Abstract
This article describes a theoretical and computational study of the dynamical assembly of a protein shell around a complex consisting of many cargo molecules and long, flexible scaffold molecules. Our study is motivated by bacterial microcompartments, which are proteinaceous organelles that assemble around a condensed droplet of enzymes and reactants. As in many examples of cytoplasmic liquid-liquid phase separation, condensation of the microcompartment interior cargo is driven by flexible scaffold proteins that have weak multivalent interactions with the cargo. Our results predict that the shell size, amount of encapsulated cargo, and assembly pathways depend sensitively on properties of the scaffold, including its length and valency of scaffold-cargo interactions. Moreover, the ability of self-assembling protein shells to change their size to accommodate scaffold molecules of different lengths depends crucially on whether the spontaneous curvature radius of the protein shell is smaller or larger than a characteristic elastic length scale of the shell. Beyond natural microcompartments, these results have important implications for synthetic biology efforts to target alternative molecules for encapsulation by microcompartments or viral shells. More broadly, the results elucidate how cells exploit coupling between self-assembly and liquid-liquid phase separation to organize their interiors.
Keywords: bacterial microcompartments, self-assembly, carboxysomes, protein shells, cargo encapsulation, liquid-liquid phase separation, simulation
Graphical Abstract
While the eukaryotic cytoplasm is organized by lipid-encased organelles, it is now clear that cells from all kingdoms of life employ other modes of compartmentalization, such as liquid-liquid phase separation (LLPS)1-4 and proteinaceous organelles.5-7 For example, bacterial microcompartments are organelles that form by assembling a protein shell around a dense complex of enzymes and reactants in certain metabolic pathways.8-15 The best-studied type of microcompartment is the carboxysome, which assembles around a dense complex of the enzyme ribulose-1,5-bisphosphate carboxylase/oxygenase (rubisco) and other proteins to facilitate the Calvin-Bensen-Bassham cycle in autotrophic bacteria.8,9,16,17
Other protein-shelled compartments are found in bacteria and archea (e.g. encapsulins18,19 and gas vesicles18,20), and eukaryotes (e.g. vault particles21). Microcompartment function depends crucially on the amount and composition of encapsulated cargo, and the integrity of the surrounding shell. Thus, understanding the mechanisms that control cargo encapsulation and shell assembly are important to elucidate the normal biological functions of microcompartments, and to reengineer microcompartments as customizable nanoreactors for synthetic biology applications (e.g.12,22-35).
More broadly, there are strong parallels between the condensed cargo within a microcompartment and liquid-liquid phase-separated fluid domains. For example, the rubisco complex within carboxysomes has a similar structure and function as the pyrenoid, which is a liquid-phase separated domain consisting of rubisco and other components that is found within plant cells.36-39 Moreover, experiments and models suggest that microcompartment assembly proceeds by phase separation of the cargo, either prior to or during assembly of the outer shell.40-48 However, the protein shell of a microcompartment confers distinct advantages over uncoated liquid domains. In addition to functioning as a selectively permeable barrier,49-51 experiments suggest that the shell plays a structural role, influencing the size and morphology during microcompartment assembly.23,26,40,52-54 Despite intense recent investigations into LLPS, we have yet to understand the role of LLPS in promoting or guiding self-assembly and cargo encapsulation, or conversely the role of assembly in promoting and regulating LLPS. Thus, models that describe coupled LLPS and microcompartment assembly are needed to identify the factors that control microcompartent formation, cargo encapsulation, and function. From a practical perspective, condensation of cargo into fluid domains is a powerful approach to develop self-assembling and self-packaging gene/drug delivery vehicles.55-65 Coupling such complexes to shell assembly could enable control of their size, amount of packaged cargo, and targeting capabilities.
Microcompartment shells are polydisperse (40-400 nm diameter), roughly icosahedral, and formed from pentameric, hexameric, and pseudo-hexameric (trimer-of-dimer) protein oligomers.8,9,17,53,66-70 Recently, Sutter et al. obtained atomic-resolution structures of small (40 nm diameter) empty microcompartment shells composed of pentamer, hexamer, and pseudo-hexamer proteins53 or smaller shells (~ 20 nm) composed of only pentamer and hexamer proteins.70 While these structures provide essential insight into microcompartment architectures, the effect of cargo on shell assembly, and the mechanisms that control cargo packaging, remain unclear. In many types of microcompartments, cargo coalescence and cargo-shell interactions are mediated by auxiliary microcompartment proteins called scaffold proteins. Scaffold proteins are typically flexible (e.g. the α-carboxysome scaffold (CsoS2) is an intrinsically disordered protein) and contain multiple interaction sites with cargo molecules.37,43,45 Thus, scaffolds drive cargo coalescence via weak multivalent interactions, paralleling mechanisms that drive liquid-liquid phase separation in cells.
Previous modeling studies have elucidated the assembly of empty icosahedral shells,71-97 the effect of an interior template such as a nanoparticle or RNA molecule on shell assembly,78,84-86,98-122 and how the interplay between template curvature and shell elasticity can control its size.78,106,107 However, the many-molecule scaffold-cargo complex within a microcompartment does not have a specific size or morphology, and thus requires alternative models. Recent computational works investigated assembly of microcompartment shell subunits123,124 or assembly of shells around a single cargo species with direct pairwise attractions driving cargo coalescence and packaging.46-48 These studies showed that the cargo can influence the size of the assembled shell through a kinetic mechanism48 or a combination of kinetic and thermodynamic effects.46,47 However, there are no models for microcompartment assembly that account for the crucial role of scaffold molecules.
Therefore, in this work we develop a computational model for microcompartment assembly that explicitly accounts for flexible scaffold molecules and scaffold-mediated cargo coalescence and packaging. We are motivated by recent experiments that investigated how changing the length of the scaffold molecule affects the size of α–carboxysome shells,45,125 but the model is sufficiently general to also provide insights into self-assembling delivery vehicles (e.g.55-64). In addition, we develop an equilibrium theory, which extends models for spherical micelles assembled from star or diblock copolymers,126-130 to describe variable packaging of the interior block, and an exterior shell with a preferred curvature radius (which may differ from the preferred size of the micelle).
Our models predict that shell sizes increase with scaffold length over a broad range, but there are minimal and maximal sizes beyond which the shell size becomes independent of scaffold length. Cargo packaging diminishes with increasing scaffold length for fixed scaffold-cargo valence (i.e. number of cargo interaction domains per scaffold molecule), eventually leading to sparsely filled shells. However, increasing the scaffold-cargo valence can restore full shells.
A scaling analysis suggests that microcompartment properties are determined by the relative values of characteristic length scales set by: (i) the scaffold length, (ii) the spontaneous curvature of the protein shell, (iii) shell elasticity, and (iv) excluded volume. Our results show how these characteristic scales can be inferred from experimental measurements of the variation of shell size with scaffold length. Importantly, such measurements could reveal the role of shell spontaneous curvature in driving microcompartment closure, which is currently a key unresolved question.
Results and discussion
Computational results
To simulate scaffold-mediated microcompartment assembly, we extend a model with direct cargo-cargo and cargo-shell pair interactions47 to include scaffold proteins (section Computational model). Although we keep the model minimal to understand general principles, we are motivated by recent experiments on α–carboxysome assembly.45,125 The α–carboxysome scaffold, CsoS2, contains three linearly connected flexible domains which include binding sites for the cargo (rubisco) and the shell proteins. Although the N-terminal domain contains multiple binding sites for rubisco, it is not known which sites interact with shell proteins. In many other microcompartment types, the scaffold molecules contain ‘encapsulation peptides’ at their C-terminal domains that interact with the shell, but these have not been identified for CsoS2. Given the current level of experimental uncertainty, we have started with a simple model for the scaffold: a flexible bead-spring polymer with three domains (section Computational model and Fig. 1). The domain at one end has multiple cargo interaction sites, the domain at the other end binds to shell subunits, and the middle domain has only repulsive interactions with cargo and shell proteins. In future work we will explore other arrangements of interaction sites on the scaffold. To minimize the number of parameters, we restrict the computational model to a single size of cargo particles and scaffold segments. Thus, the simulations do not account for the small excluded volume size of a CsoS2 segment relative to a rubisco holoenzyme. However, we analyze effects of varying excluded volume using the theoretical model described below. To further focus on scaffold-mediation, we restrict consideration to purely repulsive direct cargo-cargo and cargo-shell interactions, although attractive cargo-cargo and cargo-shell interactions have not been ruled out in the experimental systems.45,131
Figure 1:
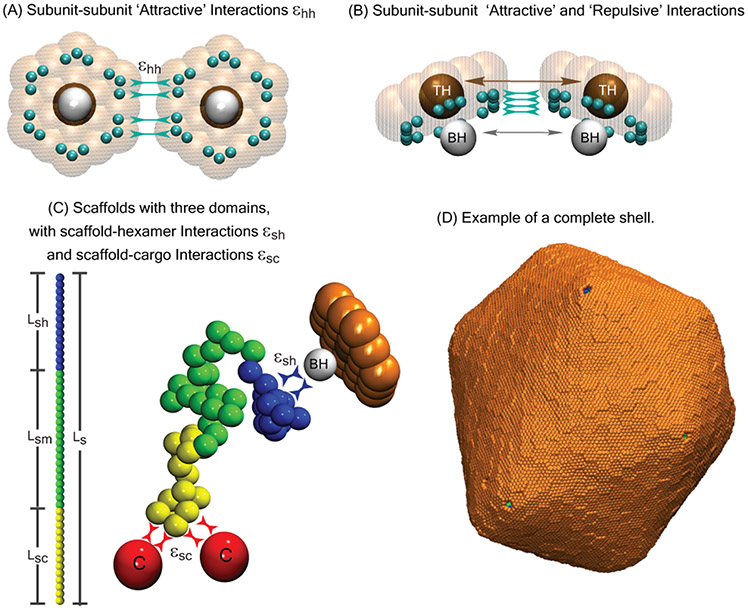
Description of the computational model. (A) Bottom and (B) side views of shell subunits. Each subunit contains ‘Attractors’ (cyan spheres) on its perimeter, and a ‘Top’ (ochre sphere, ‘TH’ ) and a ‘Bottom’ (white sphere, ‘BH’ ) in the center above and below the subunit plane. Interactions between Attractors drive subunit assembly, while Top-Top and Bottom-Bottom repulsions control the subunit-subunit angle and spontaneous curvature radius of the shell R0. (C) Scaffolds are bead-spring polymers with three domains: scaffold-cargo binding domain (yellow) beads have attractive interactions with cargo particles, middle domain (green) beads have no attractive interactions with cargo or shell subunits, and scaffold-subunit binding domain (dark blue) beads have attractive interactions with subunit Bottom pseudoatoms ‘BH’. The contour length of the scaffold with Ns beads is denoted as Ls, while the lengths of the domains are Lsc, Lsm, and Lsh, respectively. Excluder atoms (orange pseudoatoms in the plane of the ‘Top’) experience excluded volume interactions with the cargo and scaffold beads. (D) Example of a complete shell with spontaneous curvature radius R0 = 22, with encapsulated cargo and scaffold molecules with Ls = 64 (Lsc = 7, Lsm = 50, Lsh = 7). All lengths in this article are given in units of r*, the cargo diameter (the rubisco diameter in carboxysome is ≈13 nm), and energies are in units of the thermal energy kBT.
Natural microcompartment shells assemble from three classes of shell subunits (protein oligomers), each comprised of proteins with different sequences: pentamers, hexamers, and ‘pseudo-hexamers’ (trimers of heterodimers). Based on atomic-resolution structures of small empty microcompartment shells,70 each subunit species has different preferred subunit-subunit angles, but hexamers are the major species by mass in large shells. Our goal in this work is to focus on the influence of scaffold molecules on microcompartment size. To this end, we employ a minimal model for shell assembly which only includes only a single shell subunit species, which has hexamer symmetry but plays the role of both hexamers and pseudo-hexamers. Since AFM experiments have shown that microcompartment shell facets assemble from pre-formed oligomers,132 we set the model hexamer as the basic assembly subunit (irreducible species) in our simulations.
Model subunits have attractive edge-edge interactions with a preferred angle that sets the intrinsic spontaneous curvature radius R0 of the shell. The spontaneous curvature of microcompartment shell proteins is not known. Hexamers may have zero spontaneous curvature, since systems of only hexamer proteins can form tubular structures or rolled sheets (rosettes) under some conditions,124,133-140 and assemble flat sheets on surfaces or interfaces.132,141 However, in the latter systems interfacial tension exerts a strong driving force favoring flat sheets. Moreover, recombinant expression of hexamers, pseudo-hexamers, and pentamers can result in small, icosahedral, empty shells53,70,142 implying that there is a net spontaneous curvature for at least some stoichiometries of microcompartment proteins. Given this uncertainty about spontaneous curvature, and since the subunits in our model account for both hexamers and pseudo-hexamers, we treat the spontaneous curvature radius R0 as a phenomenological parameter. We have also investigated the effect of R0 on microcompartment size in the case of assembly without scaffold proteins,47 allowing us to focus on the effects of scaffold properties here. Additional model details are in the Methods section.
To elucidate assembly pathways and outcomes, we performed dynamical simulations over a range of scaffold lengths Ls, cargo-binding domain lengths Lsc, shell spontaneous curvature radii R0, and binding affinities between scaffold-cargo, scaffold-subunit, and subunit-subunit pairs (εsc, εsh, εhh). Since empty microcompartment shells are rare in most natural systems, we consider subunit-subunit interaction strengths weak enough (εhh < 3.3 at R0 = 4.5, εhh < 2.9 at R0 = 8.0, and εhh < 2.8 at R0 = 22) so that the presence of scaffold and cargo is required for nucleation. Moreover, previous computational and experimental studies have shown that assembly of well-formed shells requires moderate interaction strengths, since interactions which are too strong in comparison to the thermal energy lead to kinetic traps consisting of partial or incorrectly formed shells (e.g. 46,47,83,92,93,122,143-155). For most results in this work we maintain affinities (εsh = 2.5kBT, εsc = 1.0kBT) and a scaffold-cargo valence (number of cargo-binding sites, Lsc = 7) that are sufficiently moderate that our simulations avoid such kinetic traps. We present results for three values of the spontaneous curvature radius, R0 = 4.5, 8, and 22.0, which are respectively below, equal to, and above the size that is commensurate with the ‘wild-type’ scaffold length in our model, Ls = 24r* (see Methods).
Assembly pathways depend on scaffold-cargo interactions.
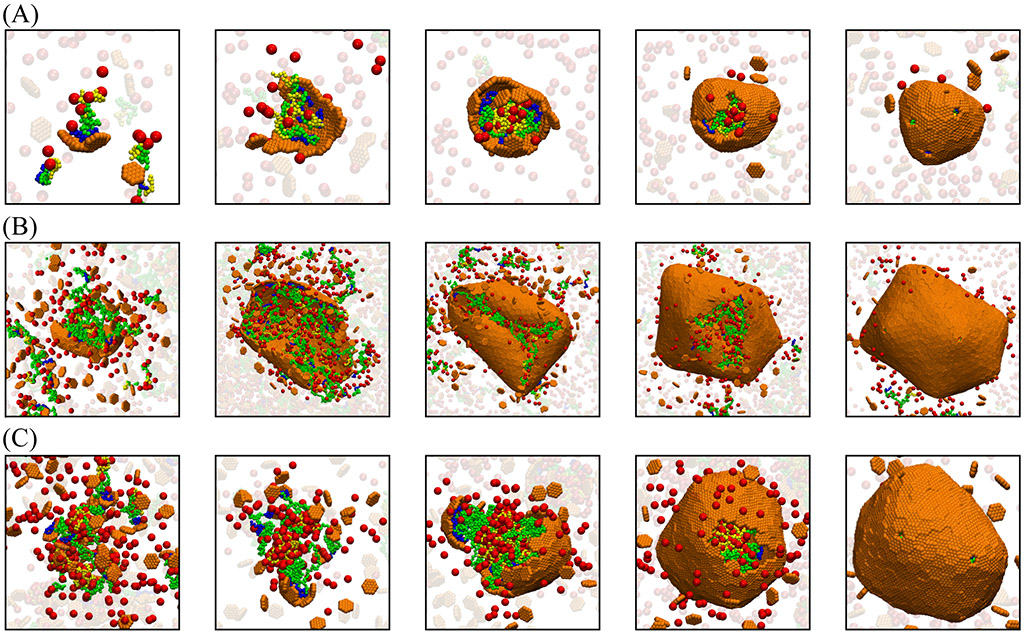
We find that the strength of scaffold-mediated cargo-cargo interactions strongly influences assembly pathways. Strong interactions (εsc ≳ 1.2 for the concentrations and wild-type cargo binding domain length used in our simulations) drive phase separation into a dilute phase and a high density liquid complex of scaffold and cargo molecules. This condition favors two-step assembly pathways (such as observed for assembly of β–carboxysomes40,41), in which the shell proteins adsorb onto the scaffold-cargo domain, and then cooperatively into ordered shell structures. For weaker scaffold-cargo interactions, we observe one-step assembly pathways with simultaneous scaffold-cargo coalescence and shell assembly (Fig. 2 A,B). To quantitatively assess the extent to which a pathway is one-step or two-step, we have developed an order parameter that measures the number of adsorbed but unassembled subunits during a trajectory46 (SI Fig. S3D).
Figure 2:
Snapshots from simulation trajectories illustrating typical assembly pathways and products (Animations corresponding to these trajectories are provided in the SI, videos S8). (A) One-step assembly pathway leading to full shells: Coalescence of the cargo and scaffold occurs concomitantly with shell assembly. The mean size of assembled shells (defined as the radius of gyration of shell subunits) is R = 6.3 ± 0.5. Parameter values are: shell spontaneous curvature radius R0 = 8.0, scaffold contour length Ls = 24 (Lsm = 10, Lsc = 7), and subunit-subunit interaction strength εhh = 2.85 (all lengths and energies are given in units of r* and kBT respectively). (B) One-step assembly with sparse cargo loading, with mean shell size R = 18 ± 3.6, for R0 = 22, Ls = 64 (Lsm = 50, Lsc = 7 ), and εhh = 2.65. (C) Two-step assembly pathway: The scaffold and cargo phase separate prior to shell assembly, due to increased valence of the scaffold-cargo binding domain fsc = 0.42. The shell size is R = 10.66 ± 0.60. Parameter values are: R0 = 22, Ls = 64 (Lsm = 30, Lsc = 27), and εhh = 2.65. For (A)-(C), the scaffold-shell and scaffold-cargo interaction strengths are εsh = 2.5 and εsc = 1.0. Snapshots are shown at different scales for clarity.
Here we are motivated by α–carboxysomes, for which experiments observe one-step pathways and that the rubisco does not undergo phase separation in the absence of shell proteins at physiological conditions.43,69,156 Therefore, for all further results we set εsc = 1.0, which drives one-step assembly pathways for the wild-type scaffold and cargo-binding domain lengths.
In addition to classifying assembly pathways as one-step or two-step, we can further subdivide the one-step pathways into those that lead to full or empty shells. A set of snapshots from a typical assembly trajectory for each of these three categories is shown in Fig. 2A,B,C respectively, for (A) all scaffold domains at wild-type lengths and a commensurate shell spontaneous curvature radius R0 = 8, (B) a long middle domain and large preferred curvature R0 = 22, and (C) a long cargo binding domain and R0 = 22. Fig. 2 (A) and (B) correspond to clear one-step assembly pathways (as is the case for most parameters considered in this work). Assembly begins with a small aggregate involving all the microcompartment constituents: shell subunits, scaffold, and cargo. Because we focus on weak binding affinities, all these interactions are required to stabilize small aggregates. Consequently, the shell grows concomitantly with further coalescence of scaffold and cargo, until shell closure terminates assembly. While the scaffold and cargo are essential for nucleating assembly in both cases, the scaffolds with longer middle domains (which do not attract cargo particles in the model) lead to a lower density of packaged scaffold and cargo (Fig. 2B) compared to the shorter middle domains (Fig. 2A).
In contrast, the higher valence cargo-binding domain (Fig. 2C) mediates cargo-cargo attractions that are nearly strong enough to drive phase separation, resulting in pathways closer to two-step assembly and full shells (SI Fig. S3D). This result is consistent with experimental observations that α-carboxysome scaffold and rubisco can phase separate without shell proteins under non-physiological conditions.37,45
Shell size depends on scaffold length.
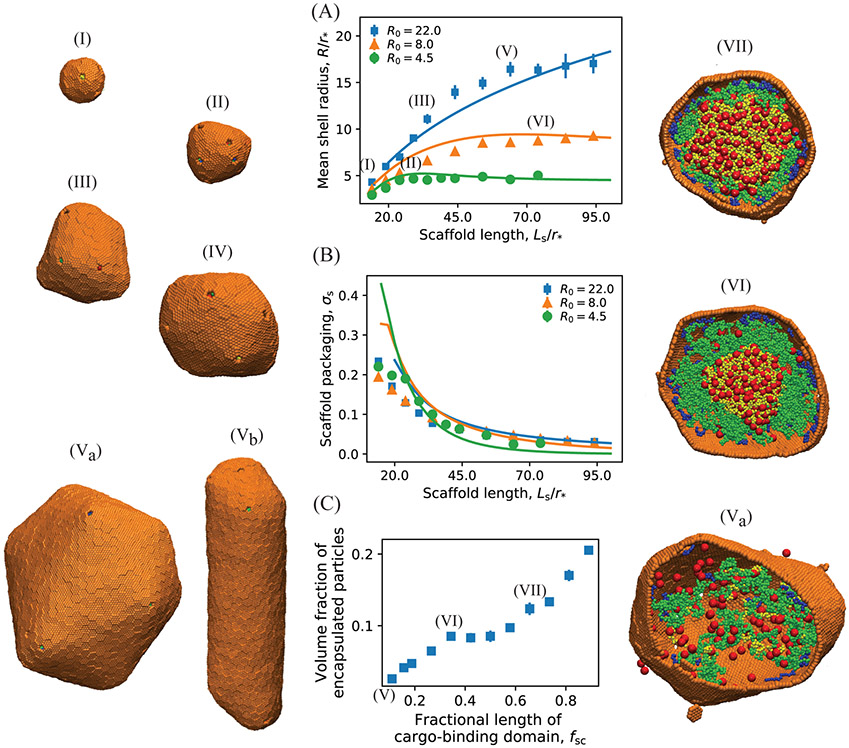
We find that the shell size depends sensitively on scaffold length and shell spontaneous curvature. Motivated by the experiments, we vary the scaffold length above and below its wild-type length, with Ls = 24 and Lsc = 7 model segments roughly corresponding to the wild-type values for the total scaffold length and cargo binding domain length (see SI section S2. Computational Model Details). Fig. 3A shows the mean size of assembled shells as a function of the middle domain length Lsm (with the other two domains at constant lengths Lsc = 7, Lsh = 7) for several values of R0. We identify two regimes, depending on whether the preferred size of the scaffold molecules (their end-to-end distance Rscaf in the absence of shell proteins, SI Fig. S2) is smaller or larger than the intrinsically preferred shell size R0. For small scaffold lengths, Rscaf < R0, shell size increases with scaffold length, consistent with experimental observations,125 until saturating at a value on the order of R0. In this limit, the number of encapsulated scaffold molecules (nscaf) relative to shell subunits (nshell), given by σs = nscaf/nshell, decreases with increasing scaffold length (Fig. 3B). Finally, for Rscaf ≫ R0 shells are unable to close around scaffold molecules, leading to incomplete assembly (SI Fig. S7).
Figure 3:
(A) The mean shell radius as a function of the scaffold length calculated from Brownian dynamics simulations (symbols) and the equilibrium theory (Eq. 1, lines). Results are shown for different shell spontaneous curvature radii: R0 = 4.5(●), 8.0(▲), 22.0(■). Example snapshots of assembled shells are shown to the left, taken from simulations with (I): R0 = 22, Ls = 14, (II): R0 = 8, Ls = 24, (III): R0 = 22, Ls = 34, and (IV): R0 = 8, Ls = 74, (Va,b): R0 = 22, Ls = 64. (B) Dependence of scaffold packaging on scaffold length and shell spontaneous curvature. The scaffold surface density (or ratio of packaged scaffold molecules to shell subunits, σs ≡ nscaf/nshell) is shown for the same parameter values as in (A). In (A) and (B) the length of the middle domain of the scaffolds Lsm is varied, with fixed shell-interacting and cargo-interacting domain lengths Lsh = 7 and Lsc = 7. The lines correspond to numerical minimization of Eq. 1, with respect to and σ, with the scaffold chemical potential as an adjustable parameter set to Δμ = −2.5kBT. Other theory parameters are taken from the simulations: the scaffold bead excluded volume and (with a the subunit area and κ the bending modulus, which was approximately determined in Ref. 47). (C) Dependence of the volume fraction of encapsulated particles (cargo and scaffolds) on the fractional length of cargo-binding domain of scaffolds fsc = Lsc/Ls, for R0 = 22, Ls = 64, and Lsh = 7. Snapshots of the interior of shells assembled at different parameter values are shown on the right: (Va): fsc = 0.11, (VI): fsc = 0.27, (VII): fsc = 0.58. Other parameter values for (A), (B) and (C) are as follows. Shell subunit-subunit affinities: εhh = 3.15 at R0 = 4.5, εhh = 2.85 at R0 = 8.0 and εhh = 2.65 at R0 = 22; scaffold-shell interaction εsh = 2.5, and scaffold-cargo interaction εsc = 1.0.
Although the total amount of packaged cargo increases with scaffold length for small lengths, due to the increasing shell size, the volume fraction of packaged cargo and scaffolds decreases monotonically with scaffold length (SI Fig. S3A and B). That is, long scaffold middle domains lead to poor cargo loading, because the additional scaffold segments do not attract cargo but increase excluded volume in our computational model.
Longer cargo binding domains increase cargo loading.
Fig. 3C shows how cargo packaging depends on increasing the fractional length of the cargo binding domain, fsc = Lsc/Ls; i.e., increasing Lsc at fixed Ls. We see that packaging increases monotonically with fsc, but there is an inflection point at fsc = 0.3 beyond which shells are nearly full. This point corresponds to the cargo binding domain length beyond which phase separation and two-step assembly pathways occur (SI Fig. S3D). We find that two-step pathways always lead to full shells, but the shell-size exhibits a very different dependence on parameters in comparison to the one-step cases we are focusing on. We plan to explore scaffold-mediated two-step assembly in detail in a future manuscript. This dependence on assembly pathways suggests that both thermodynamic and kinetic factors influence cargo packaging, as discussed further in the Discussion and Conclusions section.
Effect of binding affinity values.
Finally, the shell size is relatively insensitive to the subunit-subunit εhh and scaffold-subunit εsh affinities, provided they are strong enough to drive assembly and scaffold packaging, and weak enough to avoid kinetic traps and remain in the one-step regime (see SI Fig. S3D). For example, decreasing εhh leads to a small increase in shell size ( 20%) for spontaneous curvature radius R0 = 8.0 (SI Fig. S6), whereas increasing the scaffold length effects a three-fold increase in shell size for the same system (orange triangles in Fig. 3A). However, higher values of the scaffold-cargo affinity εsc ≳ 1.2 lead to two-step assembly pathways.
Shell morphology.
In addition to size, scaffold properties influence shell morphologies. Simulations result in complete shells (other than the 12 five-fold vacancies required by topology) for most of the parameters we focus on here (SI Fig. S7). However, the shells are not perfectly icosahedral, as shown by measurements of shell asphericity and the magnitude of icosahedral order in SI Figs. S4 and S5 respectively. These results are consistent with the fact that natural microcompartments are predominately asymmetric;69,133 in fact, Kennedy et al.133 showed that protocols and techniques used to purify and image microcompartments with electron microscopy have overrepresented the degree of icosahedral symmetry.
As discussed below, these deviations from icosahedral symmetry likely reflect a combination of kinetic effects and energetic strain due to incompatibility between the preferred scaffold and shell sizes. In support of the latter effect, varying the scaffold far from the size that is commensurate with the preferred shell size leads to distinctive morphologies; in particular, elongated but complete shells (e.g. snapshot (Vb) in Fig. 3). Short scaffolds can also result in shells with octahedral symmetry or paired five-fold vacancies (SI Fig. S3), although these defects may be model-dependent because shells are strained far from their preferred size. Finally, as noted above, varying the scaffold even further from the preferred size leads to no assembly or incomplete shells.
Equilibrium theory
Model
To further understand the interplay between scaffold and shell properties, we developed a simple equilibrium model (see SI section S1. Equilibrium Theory). Although kinetic factors may be important as noted above, the thermodynamic model captures key trends observed in the dynamical simulations.
We make the following simplifying assumptions; extensions to eliminate these approximations are straightforward. First, we restrict the theory to spherical shells as observed for most parameter values in the simulations. Second, cargo molecules are implicitly represented by a net driving force for scaffold packaging Δμ that accounts for scaffold-shell and scaffold-cargo attractive interactions, as well as the mixing entropy penalty for scaffold coalescence. We further assume that the coalesced cargo and scaffold-cargo binding domains are concentrated in the shell interior, while the other end of the scaffold, the scaffold-shell binding domain, binds to the inner shell surface. Our model system can thus be thought of as a diblock copolymer spherical micelle (e.g.126-128,157-159), except that the stoichiometry of the interior/exterior block is annealed, and there is an exterior shell with a preferred curvature that may be incommensurate with the optimal size of the micelle within. We discuss below the implications of model predictions for alternative scaffold packaging geometries.
The free energy (per shell subunit) of a shell with radius R and ratio of scaffold/shell subunits σs is given by
| (1) |
| (2) |
| (3) |
| (4) |
Here fshell gives the shell free energy, with the first term (ghh) the free energy per subunit due to subunit-subunit contacts (see SI section S1. Equilibrium Theory, Eq. S8), and the second term describing the bending energy due to deviations from the shell spontaneous curvature, with a the subunit area and κ the bending modulus. For simplicity, we neglect contributions from the 12 five-fold defects that are required by topology in real and computational microcompartments. Including these will not qualitatively change the results (see SI section S1. Equilibrium Theory and Ref. 47). Then the first two terms in fscaf give the entropic penalty for stretching or compressing scaffold molecules from Rscaf. The following two terms account for attractive scaffold-cargo and scaffold-shell interactions (Δμ), and excluded volume interactions, with ν as the scaffold segment excluded volume. Finally, fent represents the mixing entropy of encapsulated scaffolds. The equilibrium shell size and scaffold loading are obtained by minimizing the total free energy of the system. In the thermodynamic limit, the distribution of shell sizes will be strongly peaked around the size that minimizes the free energy per subunit of the shell complex (see SI section S1. Equilibrium Theory and Refs.47,160).
Comparison of theory with computational results
The solid lines in Fig. 3A,B show the theory results, with the parameters and ν = 0.065 calculated from simulations and Δμ as a fitting parameter chosen by eye. We set with lk the statistical segment length, since the theory separately accounts for chain stretching and excluded volume (as in the Flory approximation161).
We find that the theory qualitatively captures the main features observed in the simulation results. In particular, the shell size increases with scaffold length, until saturating near R0 for long scaffolds, where excluded volume limits scaffold packaging. However, for simulations with R0=22, longer scaffolds undergo limited coalescence in the center of the shell, causing the shell size to saturate at smaller scaffold lengths than predicted by the theory.
Scaling analysis, and the small excluded volume limit
Eq. (1) predicts that the system behavior depends on several characteristic length scales. In addition to the shell spontaneous curvature radius R0 and scaffold size Rscaf, we obtain length scales from the scaffold excluded volume, Rexc ~ (Nsν)1/3, and the shell elastic energy, . Specifically, RE is the radius for which a closed shell with no spontaneous curvature R0 = ∞ to would have a bending energy of kBT per subunit. Different scaling forms can be deduced from Eq. (1) depending on the relative magnitudes of these lengths.
Since our model is most applicable to biological microcompartments in the limit of small excluded volume (see discussion), we focus here on the limit of small excluded volume, ν → 0. In SI section S1. Equilibrium Theory we present a detailed derivation of these expressions and further analysis for finite excluded volume.
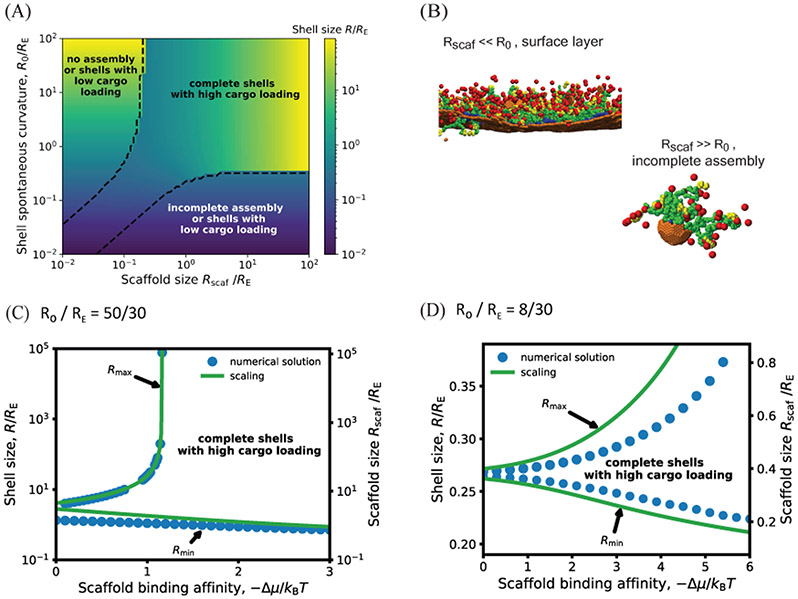
Fig. 4 shows the shell size calculated as a function of scaffold length and shell spontaneous curvature with ν = 0, by minimizing Eq. (1). The dashed black lines encompass the region with significant scaffold packaging for Δμ = −10kBT; the full dependence of scaffold packaging on parameters is shown in SI Fig. S1. We see that the range of accessible shell sizes depends crucially on the relative sizes of the preferred shell curvature and the elastic length scale. For R0 > RE the shell size is highly tunable with scaffold length, varying over orders of magnitude, while only small deviations from the preferred shell curvature are possible in the opposite limit R0 < RE. This predicted trend may be a way to experimentally probe R0 in microcompartment systems.
Figure 4:
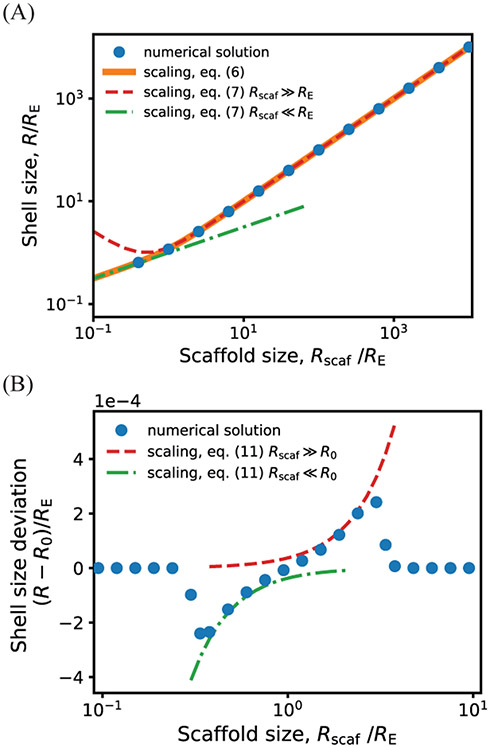
(A) Shell radius as a function of the shell spontaneous curvature radius R0 and scaffold unperturbed size Rscaf (normalized by the shell elastic energy length scale RE), calculated by numerically minimizing Eq. 1, with scaffold chemical potential Δμ = −10kBT, RE = 30, subunit area , and excluded volume parameter ν = 0. The dashed line encompasses parameter values that lead to efficient scaffold packaging (see SI Fig. S1 for the amount of packaged scaffold as a function of these parameters). Outside of this region σs ≈ 0, leading to assembly of nearly empty shells (with a surface layer of scaffold and cargo) with sizes approximately equal to R0, incomplete shells, or no assembly. The heat map in this region corresponds to the size of the complete but nearly empty shells. (B) Examples of incomplete assemblies that form in the dynamics simulations with overly short (top) or long (bottom) scaffold molecules. Parameters are (top) R0 > 300 and Ls = 34, (bottom) R0 = 4.5 and Ls = 84. Other parameters are as in Fig. 3. (C) The minimum and maximum shell radius (normalized by the shell elastic energy length scale RE) that lead to assembly and cargo packaging, predicted by the theory for varying the scaffold length as a function of the scaffold packaging driving force Δμ, for fixed shell spontaneous curvature R0 = 50. The left y-axis shows the shell size, while the right y-axis shows the corresponding scaffold length, showing that the shell size closely tracks the scaffold preferred size in this regime. The symbols correspond to maximum and minimum shell sizes obtained by numerically minimizing Eq. 1, and the lines show the asymptotic results (Eq. 7). For scaffold lengths above the maximum length, shells would be either incomplete or empty, whereas below the minimum length, shells will either be incomplete or have low packaging of scaffold and cargo. (D) The minimum and maximum shell radius (normalized by RE) in the high intrinsic shell curvature regime (R0 < RE), calculated by numerically minimizing Eq. 1 (symbols) and from the asymptotic analysis Eq. (11) (lines) for R0 = 8, RE = 30, and ν = 0. Other parameters in (C) and (D) are the same as in (A).
Scaling analysis.
Further insight can be obtained from a simple scaling analysis. First, minimizing the free energy with respect to σs gives
| (5) |
Eq. (5) shows that scaffold/cargo packaging diminishes as the shell size deviates from the preferred scaffold size Rscaf, but that scaffold can be packaged over a greater range of shell sizes by increasing ∣Δμ∣. Second, we obtain simplified expressions for the shell size and packaging depending on the relative characteristic scales as follows.
Small intrinsic shell curvature, R0 ≫ RE.
In this limit the optimal shell size becomes asymptotically independent of shell spontaneous curvature, and minimizing the free energy results in an optimal shell size
| (6) |
which can be further simplified in two limits:
| (7) |
Thus, the shell size depends on a competition between the preferred scaffold size and the tendency of the shell proteins to disfavor curvature: the shell size tracks the scaffold size Req ≈ Rscaf for long scaffolds, but adopts the geometric mean of the scaffold size and shell elastic length for short scaffolds. These scaling estimates are compared against the full free energy in Fig. 5A.
Figure 5:
Dependence of shell size on the scaffold preferred size Rscaf calculated from the asymptotic analysis, (lines, Eqs. (7) and (11), compared against numerical minimization of Eq. 1 (symbols). Results are shown in (A) and (B) respectively for shell spontaneous curvature radius values that are large or small compared to the shell elastic length scale: (A) R0 = 300 and (B) and R0 = 1, with RE = 30. Other parameter values are , Δμ = −10kBT, and ν = 0.
However, Eq. (5) shows that scaffold packaging will exponentially diminish for large deviations from Rscaf. Therefore, we estimate upper and lower bounds on the scaffold-driven changes in shell size by noting that shell bending energy must be compensated by the free energy of scaffold packaging:
| (8) |
| (9) |
with Δμeff = −(Δμ + 2kBT)σeq – fent the effective confinement free energy per shell subunit, since fscaf ≈ Δμ + 2kBT for R ≈ Rscaf, and
| (10) |
The packageable range of scaffold lengths can then be determined by combining Eqs. (8), (9) and (7) (Fig. 4C). Outside of these bounds, scaffold packaging decreases exponentially, resulting in either no assembly or assembly of empty shells with sizes near R0. Alternatively, for small scaffolds, if the scaffold-shell energy is sufficient to drive scaffold packaging without cargo, the scaffold can form a layer in the vicinity of the shell surface (Fig. 4B). That scenario is not accounted for in the theoretical model.
Importantly, in any of these scenarios, the microcompartments will saturate at a minimum shell size with decreasing scaffold length (Eq. (9)), which is an experimentally testable prediction.
High intrinsic shell curvature, R0 < RE.
In this regime the preferred curvature of the shell proteins influences the assembled shell size, so we must consider the full free energy Eq. 1. Then, the limits in which the preferred scaffold size is larger or smaller than R0 result in
| (11) |
showing that the shell size depends on the competition between the shell spontaneous curvature and scaffold size, with their relative importance determined by the shell bending modulus (via RE). As above, there are bounds on the range of scaffold lengths that can be efficiently packaged, which increase with ∣Δμ∣. Since the shell bending energy dominates in this limit, the shell size exhibits only small deviations from R0 (Fig. 5B), and the extent of scaffold incorporation is determined by the competition between the packaging driving force Δμ and the scaffold confinement free energy fscaf, resulting in:
| (12) |
The range of shell sizes (, ) can then be determined by combining Eqs. (10)-(12). Consistent with the numerical solution (Fig. 4D), the range of accessible shell sizes is considerably smaller than in the large R0 limit (Fig. 4C).
Conclusions
We have theoretically and computationally investigated the equilibrium behavior and dynamical assembly pathways of a system in which polymeric scaffold molecules drive coalescence of many cargo particles, and their packaging within an assembling protein shell. While motivated by bacterial microcompartments, we have employed minimal models allowing for generic conclusions about such multicomponent assemblies. Thus, in addition to elucidating the behaviors of natural and reengineered bacterial microcompartments, our results suggest design principles for tailoring the size, morphology, and loading of synthetic or biomimetic systems such as delivery vehicles.
We find that the shell size and the amount of packaged cargo are determined by several characteristic length scales: the preferred sizes of the protein shell and the scaffold, the scaffold excluded volume size, and a characteristic elastic length scale of the shell (which depends on its rigidity). In our computational model, we have considered a relatively low bending rigidity of the shell (motivated by experimental observations on bacterial microcompartments), and scaffold excluded volume plays a significant role. In this case, results depend on whether the preferred scaffold size is either smaller than or larger than the spontaneous curvature radius. In the limit of small scaffold molecules, assembly driving forces are dominated by stretching of the scaffold between the cargo-filled interior and the surface of the protein shell, leading to shells which are smaller than the spontaneous curvature radius (provided that the scaffold-shell interactions and scaffold-mediated cargo-cargo interactions are stronger than shell bending elasticity). In the opposite limit of long scaffold molecules, scaffold packing becomes a dominant contribution, leading to decreased scaffold-cargo packaging and a shell size that roughly saturates at the spontaneous curvature radius and/or elongated shells.
Our simulations also demonstrate that the amount and morphology of packaged cargo depends on the strength and geometry of scaffold-cargo interactions. Multivalent scaffold-cargo interactions are essential for achieving full shells, while the scaffold length and distribution of cargo binding sites on the scaffold influence the morphology of the packaged cargo. When cargo-binding sites are limited to one end of long scaffold molecules, with scaffold-shell interactions at the other end, we observe a tri-layer micelle-like complex, with an interior core of cargo, surrounded by a layer of scaffold, and finally the shell on the exterior. In contrast, longer scaffold-cargo binding domains or shorter scaffolds lead to a nearly uniform distribution of cargo and scaffold in the shell interior.
Because our primary objective was to qualitatively understand scaffold-mediated shell assembly, we did not tune the computational model parameters to match a specific biological system, and the computational model likely overestimates the scaffold excluded volume compared to bacterial microcompartments. For example, the α-carboxysome scaffold (CsoS2) accounts for only 12% by mass of a wild-type α-carboxysome,162 compared to 70% in our model. Moreover, while we have included very weak scaffold inter-segment attractions in our model, stronger inter-segment attractions among CsoS2 residues could further reduce the effective excluded volume.
Therefore, we also developed a more tractable, though simplified, equilibrium theoretical model that facilitates more direct comparisons against experiments. Using this model, we have explored a wide parameter range, including the effect of reducing the excluded volume. The theoretical analysis suggests that the ability of a scaffold to modulate shell size depends crucially on whether the protein shell spontaneous curvature radius is large or small compared to its elastic length scale. In the regime of a large spontaneous curvature radius, shell size is extremely malleable and can be tuned over a wide range by varying scaffold length. In contrast, shell proteins with a small preferred curvature radius exhibit only small size fluctuations, and relatively poor packaging of scaffold molecules with incommensurate sizes. In both regimes, the range of scaffold lengths that can be packaged effectively, and correspondingly the range of accessible shell radii, increase with the free energy driving force for scaffold incorporation. This important control parameter depends on the scaffold concentration and the valence and affinity of the scaffold-cargo and scaffold-shell domains.
Testing against experiments.
Since our models are general, these predictions could be tested in a variety of biological or synthetic systems. For example, testing in bacterial microcompartments will be enabled by the modular nature of microcompartment scaffold molecules: the CsoS2 scaffold of the α-carboxysome can be represented as a tri-block co-polymer, with the cargo-binding domain in the N-terminal block, and shell-binding sites in the C-terminal block. Our results could thus be compared against experiments in which mutagenesis45 is used to change the length of the middle domain (Fig. 3A,B) or the cargo-binding domain (Fig. 3C), although we note that the presence of shell binding sites in the middle block has not been ruled out.
Importantly, our results suggest a path to assess the magnitude and importance of the spontaneous curvature, a key unresolved question in microcompartment assembly. In particular, recent experiments on recombinant systems exhibit assembly of small (~ 20 – 30 nm) empty microcompartment shells, suggesting a small shell spontaneous curvature radius. Yet, other experiments observe extensive flat sheets of hexamers,124,132-141 suggesting the possibility of a low or zero spontaneous curvature. In this regard, both the simulations and theoretical model predict that shells with a small spontaneous curvature radius exhibit only narrow fluctuations in size when presented with scaffold in molecules of different lengths, whereas shells with a large spontaneous curvature radius can assemble over a wide range of sizes to accommodate scaffolds with different lengths. In the small spontaneous curvature radius regime, our results suggest that preferred shell curvature plays a key role in driving shell closure, whereas in the large curvature radius regime scaffold properties (this work) and cargo properties (Refs.47,48) are important for shell closure.
One readily testable prediction from our model is that there is a minimum accessible shell size. Reducing scaffold lengths below this limit will either lead to a saturating shell size with diminished scaffolding packaging, or abrogation of shell assembly.
Kinetic and thermodynamic effects drive deviations from icosahedral symmetry.
Previous equilibrium elasticity studies of shells have identified local minima as a function of size at a series of ‘magic number’ sizes, for which the structures have icosahedral symmetry or other high symmetries (e.g.71-73,89,106,107,121,122,163-165). Yet, the assembly products in our simulations are predominately asymmetric, consistent with the structures of natural microcompartments.133 This lack of symmetry can be explained by three factors, the first kinetic and the other two thermodynamic. First, trajectories in our simulations and experimental systems begin from a highly out-of-equilibrium condition of dispersed subunits, and thus are not guaranteed to approach equilibrium on the finite timescales of experiments and our simulations.154 It is well-known that overly strong interactions lead assembly into kinetic traps consisting of incomplete shells, due to free subunit starvation, or shells that cannot close due to defects (e.g.46,47,83,92,93,122,143-155,166). In this work we focus on moderate binding affinities, and thus (except for very short or long scaffolds) most simulations lead to complete shells with the 12 five-fold defects required by topology. However, once a shell is complete, reorganization of its components is slow in comparison to assembly timescales, and thus diffusion of defects or changing the number of subunits to a size that is compatible with icosahedral symmetry does not occur on experimentally relevant timescales. Further, we find that switching from one-step two-step assembly pathways is correlated to an increase in cargo loading (Fig. 3C) suggesting that kinetic effects influence cargo encapsulation. However, the relatively strong agreement between our equilibrium theory and the dynamical simulation results (Fig. 3A,B) suggests that the assembly products are near equilibrium for the moderate binding affinity parameter sets we have focused on.
In addition to kinetic effects, there are (at least) two sources of elastic strain that may suppress icosahedral symmetry. First, scaffolds with preferred sizes that are much smaller or larger than the shell spontaneous curvature radius lead to incomplete assembly. More moderate incompatibilities between preferred scaffold and shell size lead to complete but asymmetric shells, such as elongated shells (Figs. 3 and S4). Second, formation of icosahedral structures from more than 60 asymmetric subunits requires multiple subunit species and/or elastic strains. Because our minimal model includes only a single subunit species, there are necessarily strains even in symmetric ground states. However, natural microcompartments also have far fewer shell protein species than the number of distinct local symmetry environments (the triangulation number T167). Even a small shell with diameter d ~ 100 nm has T = 75, and the triangulation number grows as T ∝ d2. Thus natural microcompartments shells must have some degree of elastic strain.
Coupling of assembly to liquid-liquid phase separation (LLPS).
While the discussion above focuses on the effect of a phase separating domain on the size and morphology of the assembling shell, our results demonstrate that the coupling between assembly and LLPS is bidirectional. Shell assembly can control both the onset of LLPS and the nature of its aggregation behavior. In particular, for low scaffold-cargo valences, shell assembly is required for nucleation and subsequent coalescence of the cargo domain. For larger scaffold-cargo valences, the cargo-scaffold complex domain nucleates spontaneously, but will undergo unbounded growth (until depleting cargo or scaffold) unless restrained by shell assembly. Thus, coupling to protein assembly can qualitatively change liquid domain formation from macrophase separation to self-limited assembly (aggregation). However, we reiterate that the preferred size of the domain is controlled by properties of both the shell and the encapsulated cargo.
Outlook.
Finally, our results suggest additional physical ingredients that will be important to study for understanding biological microcompartments or guiding the design of synthetic delivery vehicles. First, increasing the rigidity of the scaffold molecules would diminish the range of variation of shell sizes. This trend can be seen from the equilibrium scaling of the shell size in Eqs. (7) and (11), since the unperturbed scaffold size increases with its rigidity. Second, combining direct cargo-cargo interactions with scaffold mediation could enhance cargo packaging within assembling shells. This proposition is based on our observation in this work that increasing effective scaffold-mediated cargo interactions promotes cargo loading, and is consistent with observations from previous models with cargo coalescence driven only by direct cargo-cargo pair interactions.46 Third, although we observe qualitative agreement between our dynamical simulation results and the equilibrium theory, kinetic effects likely play important roles in some parameter regimes. For example, we have primarily focused on parameters that lead to one-step assembly pathways as observed for α-carboxysomes, but we anticipate that kinetic effects will become more important in the case of two-step assembly pathways. Thus, models such as developed here, combined with experiments on different microcompartment systems and solution conditions, are needed to fully understand the interplay between thermodynamics and kinetics in scaffold-mediated shell assembly and cargo packaging.
Methods
Computational model
Our computational model extends a previous model for assembly of a shell around fluid cargo46,47 to include scaffold molecules and scaffold-mediated cargo-cargo and cargo-shell interactions. To focus on the effect of scaffold-mediated cargo interactions, we do not include direct cargo-cargo and cargo-shell attractive interactions, and we consider only one shell subunit species, which represents both hexamer and pseudo-hexamer proteins.
Scaffolds.
In carboxysome systems, attractions between rubisco particles are mediated by auxiliary proteins (e.g. the intrinsicallly disordered protein CsoS2 in α–carboxysomes43,45 and the protein CcmM in β–carboxysomes40). The α–carboxysome scaffold molecule, CsoS2, contains three linearly connected flexible domains, with the C-terminal domain containing multiple binding sites for the cargo molecule rubisco. While there is not yet clear experimental evidence for the location of the shell binding sequences, in β-carboxysomes and other microcompartments, shell-cargo attractions are mediated by an ‘encapsulation peptide’ sequence in the N-terminal domain of the scaffold.23,31,40,168,169 Motivated by these characteristics, we model the scaffold as a flexible bead-spring polymer with three linearly connected domains: a scaffold-cargo binding domain at one end with multiple cargo interaction sites, a scaffold-shell binding domain at the other end with multiple shell subunit binding sites, and a middle domain that has only repulsive interactions with cargo and shell proteins. Based on experimental evidence, we include weak attractive interactions between pairs of scaffold beads.
The interactions between various molecule types are modeled as follows, with further details given in SI section S2. Computational Model Details.
Scaffold-cargo interactions.
Attractive interactions between cargo particles and the ‘cargo-interacting’ beads (type ‘SC’) in scaffolds are modeled by a Lennard-Jones potential with well-depth parameter εsc.
Scaffold-shell interactions.
Attractive interactions between subunits and scaffolds are modeled by a Morse potential with well-depth parameter εsh, between beads in ‘shell interacting’ beads in polymers (blue beads in Fig. 1C) and Bottom pseudoatoms on subunits (type ‘BH’). We also add a layer of ‘Excluders’ in the plane of the ‘Top’ pseudoatoms, which account for shell-scaffold and shell-cargo excluded volume interactions.
Subunit-subunit interactions.
Interactions between edges of BMC shell proteins are primarily driven by shape complementarity and hydrophobic interactions.53 To mimic these short-ranged directionally specific interactions, each model subunit contains ‘Attractors’ on its perimeter that mediate subunint-subunit attractions. Complementary Attractors on nearby subunits have short-range interactions (modeled by a Morse potential, Eq. S28 in SI section S2. Computational Model Details). Attractors that are not complementary do not interact. The arrangement of Attractors on subunit edges is shown in Fig. 1, with pairs of complementary Attractors indicated by cyan double-headed arrows. The subunit-subunit binding affinity is proportional to the well-depth of the Morse potential between complementary Attractors, given by εhh.
To control the shell spontaneous curvature and bending modulus, each subunit contains a ‘Top’ (type ‘TH’) pseudoatom above the plane of Attractors, and a ‘Bottom’ pseudoatom (type ‘BH’) below the Attractor plane. There are repulsive interactions (WCA interactions, Eq. S27) between Top-Top, Bottom-Bottom, and Top-Bottom pairs of pseudoatoms on nearby subunits. The relative sizes of the Top and Bottom pseudoatoms set the preferred subunit-subunit binding angle (and thus the spontaneous curvature R0), while the interaction strength (controlled by the well-depth parameter εangle) controls the shell bending modulus κ. The Top-Bottom interaction ensures that subunits do not bind in inverted orientations.79 Since the subunit-subunit interaction geometries are already controlled by the Attractor, Top, and Bottom pseudoatoms, we do not consider Excluder-Excluder interactions.
Effects of simplifying the shell stoichiometry.
To focus on the effects of scaffold properties on microcompartment assembly, we have employ a minimal shell protein model with only a single hexameric subunit species with spontaneous curvature, meant to represent both hexamers and pseudo-hexamers. We neglect pentamers based on our previous computational study47 and experiments on assembly of α–carboxysome systems in the absence of pentamer proteins.170,171 In previous simulations, we found that the stoichiometric ratio of pentamers to hexamers affects the size of assembled shells, and one can expect that the stoichiometric ratio of pseudo-hexamers plays a role as well. However, based on their mass percentage in purified BMCs, pentamers are likely present in cells at very low stoichiometric ratios compared to other subunit species. We found that a system of only hexamer subunits can assemble shells with morphologies similar to those obtained at low stoichiometric ratios of pentamers, except that the shells in the hexamer-only system each contain 12 vacancies. Despite these vacancies, the entire scaffold remains inside complete shells due to scaffold-cargo and scaffold-subunit interactions on the two end-domains of the scaffold molecules. Moreover, if pentamers are introduced after assembly, they can fill in these vacancies leading to complete shells.47
These computational results are consistent with experimental observations on assembly of α–carboxysomes in the absence of pentamer proteins. Cai et al.170 showed that deleting the pentamer proteins (CsoS4) in H. neapolitanus resulted in structures that were predominantly similar to those assembled with pentamers, although there were some elongated shells. Function was impaired, but could be restored by adding pentamers to the system after assembly. More recently, Long et al.171 performed recombinant experiments in tobacco plants, showing that expressing only the scaffold (CsoS2) and hexamer protein (CsoS1A) from Cyanobium marinum PCC7001 α–carboxysomes is sufficient to obtain shells with normal appearance and at least partial function. However, while these results suggest that eliminating pentamers has only a minor effect on α–carboxysome assembly, deleting pentamers (and in some cases pseudo-hexamers) in other types of microcompartments (β–carboxysomes and Pdu) led to more significant structural aberrations, including elongated shells.124,133-140,171-176 Overexpressing hexamers also resulted in elongated structures,40 although that may be caused by in part by the increased hexamer/pseudo-hexamer stoichiometry. Intriguingly, experiments suggest that α–carboxysomes assemble by one-step assembly pathways whereas β–carboxysomes and Pdu microcompartments follow two-step pathways, suggesting that pentamers may have different effects depending on the assembly pathway.
Note that curvature in our model arises only due to angles between the rigid body subunits, whereas the experimental structure of Tanaka et al.177 suggests the possibility of intra-subunit bending for pseudo-hexamers. While we plan to explore this possibility in a future work, this additional degree of freedom should not qualitatively change the dependence of shell size on scaffold properties, which is the focus of this work.
Simulations
We simulated assembly dynamics using the Langevin dynamics algorithm in HOOMD (which uses GPUs to efficiently simulate dynamics178), and periodic boundary conditions to represent a bulk system. The subunits were modeled as rigid bodies.179 Each simulation was performed in the NVT ensemble, using a set of fundamental units180 with the unit length scale r* defined as the cargo particle diameter, and energies in units of the thermal energy, kBT. The simulation time step was 0.005 in dimensionless time units, and we performed 2 × 108 timesteps in each simulation, except the maximum simulation time was increased to 4 × 108 for Ls >= 40 and R0 = 22 (because longer timescales were required for the large shells that assemble at those parameters).
Systems.
Each system included 2300 shell subunits, 2000 cargo particles, and 213 scaffold molecules in a cubic box with side length 120r*. To avoid overlaps in the initial condition, simulations were initialized by placing subunits and cargo particles on a grid, with scaffolds in extended configurations in between. Initial subunit orientations were random. For systems near the threshold for cargo-scaffold phase separation (Lsc > 7), we eliminated correlations imposed by the grid by performing an initial dynamics with excluded volume interactions only (all attractive interactions turned off) for 5 × 106 timesteps. The attractive interactions were turned on after completion of this initialization dynamics. For other parameter sets, this initial dynamics protocol was not needed since memory of the initial condition was lost before any assembly began.
Sample sizes.
We performed a minimum of 10 independent trials at each parameter set, and performed additional trials if needed so that at least 10 complete shells formed amongst all trials at a given parameter set. In particular, simulations with a large spontaneous curvature radius and long scaffolds, R0 = 22 and Ls > 40, result in large shells, and thus fewer shells per simulation in comparison to other parameter sets, even though the fraction of subunits in shells is similar.
Connecting simulation nondimensional units to physical values.
Although the model is designed to be generic, we are particularly motivated by α-carboxysomes. We can approximately map our computational model to carboxysomes by setting the cargo diameter (the unit length scale in the model) to that of the rubisco holoenzyme, implying r* ≈ 13 nm. However, to enable tractable simulation of long assembly timescales, we have set the size ratios of subunit/cargo and scaffold bead/cargo to be larger than the ratios of these proteins relative to rubisco. In particular, our model subunits have a side length of r* and are thus about three times larger than carboxysome hexamers (side-length ≈ 4 nm). To represent the carboxysome system as closely as possible despite this approximation, we have set the bending modulus of the computational model to obtain a characteristic elastic length scale similar to that of carboxysomes. Nanoindentation measurements on β-carboxysome shells obtained κ ≈ 25kBT181 (smaller than that for a typical viral capsid), resulting in an elastic length scale of RE ≈ 47 nm. Correspondingly, we set the computational bending modulus to about 5 – 10kBT (see SI section S2. Computational Model Details), and thus RE ≈ 38 – 54 nm (using a subunit area ).
We perform a similar approximate mapping for the model scaffold molecule, by attempting to match its end-to-end vector (when unconfined) to that of a CsoS2 molecule. The model scaffold behaves as a self-avoiding polymer with a statistical segment length of about one segment, or lk ≈ 0.5r*, and thus has a end-to-end vector , with Ns = Ls/lk (see SI Fig. S2), with a proportional radius of gyration. Since most of the CsoS2 sequence is thought to be intrinsically disordered, we assume that it also behaves as a self-avoiding polymer. The Halothiobacillus neapolitanus CsoS2 molecule studied in mutagenesis experiments has 869 amino acids. While its radius of gyration has not been reported, the Prochlorococcus CsoS2 with a similar sequence length (792 amino acids) has a radius of gyration of ~ 70 nm.43 To match this value, we assign the wild-type length of the model scaffold to be Ls = 24r* (48 beads).
Supplementary Material
Table 1:
Computational model parameters and variables
| parameter / variable | symbol |
|---|---|
| shell radius | R |
| surface density of encapsulated scaffolds | σs |
| shell spontaneous curvature radius | R0 |
| total length of scaffold | Ls |
| length of scaffold shell binding domain | Lsc |
| length of scaffold cargo binding domain | Lsh |
| length of scaffold middle domain | Lsm |
| number of segments in scaffold | Ns |
| scaffold statistical segment length | lk |
| excluded volume of a scaffold segment | ν |
| subunit area | a |
| shell bending modulus | κ |
| number of subunits in a shell | nshell |
| number of encapsulated scaffolds in a shell | nscaf |
| subunit-subunit interaction | εhh |
| scaffold-subunit interaction | εsh |
| scaffold-cargo interaction | εsc |
Acknowledgement
We are grateful to Luke Oltrogge and David Savage for insightful discussions. This work was supported by Award Number R01GM108021 from the National Institute Of General Medical Sciences and the Brandeis Center for Bioinspired Soft Materials, an NSF MRSEC, DMR-1420382 and DMR-2011846. Computational resources were provided by NSF XSEDE computing resources (XStream, Bridges, and Comet) and the Brandeis HPCC which is partially supported by DMR-2011486.
Footnotes
References
- 1.Brangwynne CP Phase Transitions and Size Scaling of Membrane-Less Organelles. J. Cell Biol 2013, 203, 875–881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Weber SC; Brangwynne CP Getting RNA and Protein in Phase. Cell 2012, 149, 1188–1191. [DOI] [PubMed] [Google Scholar]
- 3.Hyman AA; Brangwynne CP Beyond Stereospecificity: Liquids and Mesoscale Organization of Cytoplasm. Dev. Cell 2011, 21, 14–16. [DOI] [PubMed] [Google Scholar]
- 4.Hyman AA; Simons K Beyond Oil and Waterphase Transitions in Cells. Science 2012, 337, 1047–1049. [DOI] [PubMed] [Google Scholar]
- 5.Yeates TO; Kerfeld CA; Heinhorst S; Cannon GC; Shively JM Protein-Based Organelles in Bacteria: Carboxysomes and Related Microcompartments. Nat. Rev. Microbiol 2008, 6, 681–691. [DOI] [PubMed] [Google Scholar]
- 6.Nott TJ; Petsalaki E; Farber P; Jervis D; Fussner E; Plochowietz A; Craggs TD; Bazett-Jones DP; Pawson T; Forman-Kay JD Phase Transition of a Disordered Nuage Protein Generates Environmentally Responsive Membraneless Organelles. Molecular Cell 2015, 57, 936–947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zaslavsky BY; Ferreira LA; Darling AL; Uversky VN The Solvent Side of Proteinaceous Membrane-Less Organelles in Light of Aqueous Two-Phase Systems. Int. J. Biol. Macromol 2018, 117, 1224–1251. [DOI] [PubMed] [Google Scholar]
- 8.Kerfeld CA; Heinhorst S; Cannon GC Bacterial Microcompartments. Microbiology 2010, 64, 391. [DOI] [PubMed] [Google Scholar]
- 9.Tanaka S; Kerfeld CA; Sawaya MR; Cai F; Heinhorst S; Cannon GC; Yeates TO Atomic-Level Models of the Bacterial Carboxysome Shell. Science 2008, 319, 1083–1086. [DOI] [PubMed] [Google Scholar]
- 10.Rae BD; Long BM; Badger MR; Price GD Functions, Compositions, and Evolution of the Two Types of Carboxysomes: Polyhedral Microcompartments That Facilitate CO2 Fixation in Cyanobacteria and Some Proteobacteria. Microbiol. Mol. Biol. Rev 2013, 77, 357–379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bobik TA; Lehman BP; Yeates TO Bacterial Microcompartments: Widespread Prokaryotic Organelles for Isolation and Optimization of Metabolic Pathways. Mol. Microbiol 2015, 98, 193–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chowdhury C; Sinha S; Chun S; Yeates TO; Bobik TA Diverse Bacterial Microcompartment Organelles. Microbiol. Mol. Biol. Rev 2014, 78, 438–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kerfeld CA; Melnicki MR Assembly, Function and Evolution of Cyanobacterial Carboxysomes. Curr. Opin. Plant Biol 2016, 31, 66–75. [DOI] [PubMed] [Google Scholar]
- 14.Polka JK; Hays SG; Silver PA Building Spatial Synthetic Biology with Compartments, Scaffolds, and Communities. Cold Spring Harb Perspect Biol 2016, 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kerfeld CA; Aussignargues C; Zarzycki J; Cai F; Sutter M Bacterial Microcompartments. Nat. Rev. Microbiol 2018, 16, 277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Schmid MF; Paredes AM; Khant HA; Soyer F; Aldrich HC; Chiu W; Shively JM Structure of Halothiobacillus neapolitanus Carboxysomes by Cryo-Electron Tomography. J. Mol. Biol 2006, 364, 526–535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Iancu CV; Ding HJ; Morris DM; Dias DP; Gonzales AD; Martino A; Jensen GJ The Structure of Isolated Synechococcus Strain WH8102 Carboxysomes as Revealed by Electron Cryotomography. J. Mol. Biol 2007, 372, 764–773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sutter M; Boehringer D; Gutmann S; Gunther S; Prangishvili D; Loessner MJ; Stetter KO; Weber-Ban E; Ban N Structural Basis of Enzyme Encapsulation into a Bacterial Nanocompartment. Nat. Struct. Mol. Biol 2008, 15, 939–947. [DOI] [PubMed] [Google Scholar]
- 19.Nichols RJ; LaFrance B; Phillips NR; Oltrogge LM; Valentin-Alvarado LE; Bischoff AJ; Nogales E; Savage D Discovery and Characterization of a Novel Family of Prokaryotic Nanocompartments Involved in Sulfur Metabolism. bioRxiv, 2020; doi: 10.1101/2020.05.24.113720, accessed June 1, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pfeifer F Distribution, Formation and Regulation of Gas Vesicles. Nat Rev Micro 2012, 10, 705–715. [DOI] [PubMed] [Google Scholar]
- 21.Kickhoefer VA; Rajavel KS; Scheffer GL; Dalton WS; Scheper RJ; Rome LH Vaults Are Up-Regulated in Multidrug-Resistant Cancer Cell Lines. J. Biol. Chem 1998, 273, 8971–8974. [DOI] [PubMed] [Google Scholar]
- 22.Chessher A; Breitling R; Takano E Bacterial Microcompartments: Biomaterials for Synthetic Biology-Based Compartmentalization Strategies. ACS Biomaterials Science & Engineering 2015, 1, 345–351. [DOI] [PubMed] [Google Scholar]
- 23.Lehman BP; Chowdhury C; Bobik TA The N Terminus of the PduB Protein Binds the Protein Shell of the Pdu Microcompartment to Its Enzymatic Core. J. Bacteriol 2017, 199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Long BM; Badger MR; Whitney SM; Price GD Analysis of Carboxysomes from Synechococcus PCC7942 Reveals Multiple Rubisco Complexes with Carboxysomal Proteins CcmM and CcaA. J. Biol. Chem 2007, 282, 29323–35. [DOI] [PubMed] [Google Scholar]
- 25.Long BM; Tucker L; Badger MR; Price GD Functional Cyanobacterial Beta-Carboxysomes Have an Absolute Requirement for Both Long and Short Forms of the CcmM Protein. Plant Physiol. 2010, 153, 285–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mayer MJ; Juodeikis R; Brown IR; Frank S; Palmer DJ; Deery E; Beal DM; Xue WF; Warren MJ Effect of Bio-Engineering on Size, Shape, Composition and Rigidity of Bacterial Microcompartments. Sci. Rep 2016, 6, 36899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Quin MB; Perdue SA; Hsu SY; Schmidt-Dannert C Encapsulation of Multiple Cargo Proteins within Recombinant Eut Nanocompartments. Appl. Microbiol. Biotechnol 2016, 100, 9187–9200. [DOI] [PubMed] [Google Scholar]
- 28.Slininger Lee M; Tullman-Ercek D Practical Considerations for the Encapsulation of Multi-Enzyme Cargos within the Bacterial Microcompartment for Metabolic Engineering. Current Opinion in Systems Biology 2017, 5, 16–22. [Google Scholar]
- 29.Slininger Lee MF; Jakobson CM; Tullman-Ercek D Evidence for Improved Encapsulated Pathway Behavior in a Bacterial Microcompartment through Shell Protein Engineering. ACS Synth. Biol 2017, 6, 1880–1891. [DOI] [PubMed] [Google Scholar]
- 30.Hagen A; Sutter M; Sloan N; Kerfeld CA Programmed Loading and Rapid Purification of Engineered Bacterial Microcompartment Shells. Nat. Comm 2018, 9, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kinney JN; Salmeen A; Cai F; Kerfeld C. a. Elucidating Essential Role of Conserved Carboxysomal Protein CcmN Reveals Common Feature of Bacterial Microcompartment Assembly. J. Biol. Chem 2012, 287, 17729–17736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ferlez B; Sutter M; Kerfeld CA A Designed Bacterial Microcompartment Shell with Tunable Composition and Precision Cargo Loading. Metab. Eng 2019, 54, 286–291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kalnins G; Cesle E-E; Jansons J; Liepins J; Filimonenko A; Tars K Encapsulation Mechanisms and Structural Studies of GRM2 Bacterial Microcompartment Particles. Nat. Comm 2020, 11, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Juodeikis R; Lee MJ; Mayer M; Mantell J; Brown IR; Verkade P; Woolfson DN; Prentice MB; Frank S; Warren MJ Effect of Metabolosome Encapsulation Peptides on Enzyme Activity, Coaggregation, Incorporation, and Bacterial Microcompartment Formation. MicrobiologyOpen 2020, 9, e1010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Künzle M; Mangler J; Lach M; Beck T Peptide-Directed Encapsulation of Inorganic Nanoparticles into Protein Containers. Nanoscale 2018, 10, 22917–22926. [DOI] [PubMed] [Google Scholar]
- 36.Rochaix J-D The Pyrenoid: An Overlooked Organelle Comes out of Age. Cell 2017, 171, 28–29. [DOI] [PubMed] [Google Scholar]
- 37.Wang H; Yan X; Aigner H; Bracher A; Nguyen ND; Hee WY; Long B; Price GD; Hartl F; Hayer-Hartl M Rubisco Condensate Formation by CcmM in β-Carboxysome Biogenesis. Nature 2019, 566, 131–135. [DOI] [PubMed] [Google Scholar]
- 38.He S; Chou H-T; Matthies D; Wunder T; Meyer MT; Atkinson N; Martinez-Sanchez A; Jeffrey PD; Port SA; Patena W; He G; Chen VK; Hughson FM; McCormick AJ; Mueller-Cajar O; Engel BD; Zhiheng Y; Jonikas MC The Structural Basis of Rubisco Phase Separation in the Pyrenoid. Nature Plants 2020, 6, 1480–1490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Meyer MT; Itakura AK; Patena W; Wang L; He S; Emrich-Mills T; Lau CS; Yates G; Mackinder LC; Jonikas MC Assembly of the Algal CO2-Fixing Organelle, the Pyrenoid, Is Guided by a Rubisco-Binding Motif. Science Advances 2020, 6, eabd2408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Cameron JC; Wilson SC; Bernstein SL; Kerfeld CA Biogenesis of a Bacterial Organelle: The Carboxysome Assembly Pathway. Cell 2013, 155, 1131–40. [DOI] [PubMed] [Google Scholar]
- 41.Chen AH; Robinson-Mosher A; Savage DF; Silver PA; Polka JK The Bacterial Carbon-Fixing Organelle Is Formed by Shell Envelopment of Preassembled Cargo. PLoS One 2013, 8, e76127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wunder T; Cheng SLH; Lai S-K; Li H-Y; Mueller-Cajar O The Phase Separation Underlying the Pyrenoid-Based Microalgal Rubisco Supercharger. Nat. Comm 2018, 9, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Cai F; Dou Z; Bernstein SL; Leverenz R; Williams EB; Heinhorst S; Shively J; Cannon GC; Kerfeld CA Advances in Understanding Carboxysome Assembly in Prochlorococcus and Synechococcus Implicate CsoS2 as a Critical Component. Life 2015, 5, 1141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chaijarasphong T; Nichols RJ; Kortright KE; Nixon CF; Teng PK; Oltrogge LM; Savage DF Programmed Ribosomal Frameshifting Mediates Expression of the α-Carboxysome. J. Mol. Biol 2016, 428, 153–164. [DOI] [PubMed] [Google Scholar]
- 45.Oltrogge LM; Chaijarasphong T; Chen AW; Bolin ER; Marqusee S; Savage DF Multivalent Interactions between CsoS2 and Rubisco Mediate α-Carboxysome Formation. Nature Structural & Molecular Biology 2020, 27, 281–287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Perlmutter JD; Mohajerani F; Hagan MF Many-Molecule Encapsulation by an Icosahedral Shell. eLife 2016, 5, e14078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Mohajerani F; Hagan MF The Role of the Encapsulated Cargo in Microcompartment Assembly. PLoS Comput. Biol. 2018, 14, e1006351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Rotskoff GM; Geissler PL Robust Nonequilibrium Pathways to Microcompartment Assembly. Proceedings of the National Academy of Sciences 2018, 115, 6341–6346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Menon BB; Heinhorst S; Shively JM; Cannon GC The Carboxysome Shell Is Permeable to Protons. Journal of Bacteriology 2010, 192, 5881–5886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Mahinthichaichan P; Morris DM; Wang Y; Jensen GJ; Tajkhorshid E Selective Permeability of Carboxysome Shell Pores to Anionic Molecules. J. Phys. Chem. B 2018, 122, 9110–9118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Faulkner M; Szabó I; Weetman SL; Sicard F; Huber RG; Bond PJ; Rosta E; Liu L-N Molecular Simulations Unravel the Molecular Principles That Mediate Selective Permeability of Carboxysome Shell Protein. Scientific reports 2020, 10, 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lassila JK; Bernstein SL; Kinney JN; Axen SD; Kerfeld CA Assembly of Robust Bacterial Microcompartment Shells Using Building Blocks from an Organelle of Unknown Function. J. Mol. Biol 2014, 426, 2217–28. [DOI] [PubMed] [Google Scholar]
- 53.Sutter M; Greber B; Aussignargues C; Kerfeld CA Assembly Principles and Structure of a 6.5-MDa Bacterial Microcompartment Shell. Science 2017, 356, 1293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Cai F; Bernstein SL; Wilson SC; Kerfeld CA Production and Characterization of Synthetic Carboxysome Shells with Incorporated Luminal Proteins. Plant Physiol. 2016, 170, 1868–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Fung SY; Yang H; Bhola PT; Sadatmousavi P; Muzar E; Liu M; Chen P Self-Assembling Peptide as a Potential Carrier for Hydrophobic Anticancer Drug Ellipticine: Complexation, Release and in Vitro Delivery. Adv. Funct. Mater 2009, 19, 74–83. [Google Scholar]
- 56.Vilaça H; Castro T; Costa FM; Melle-Franco M; Hilliou L; Hamley IW; Castanheira EM; Martins JA; Ferreira PM Self-Assembled RGD Dehydropeptide Hydrogels for Drug Delivery Applications. J. Mater. Chem. B 2017, 5, 8607–8617. [DOI] [PubMed] [Google Scholar]
- 57.Hanafy NAN; El-Kemary M; Leporatti S Micelles Structure Development as a Strategy to Improve Smart Cancer Therapy. Cancers 2018, 10, 238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Gao C; Li H; Li Y; Kewalramani S; Palmer LC; Dravid VP; Stupp SI; Olvera de la Cruz M; Bedzyk MJ Electrostatic Control of Polymorphism in Charged Amphiphile Assemblies. J. Phys. Chem. B 2017, 121, 1623–1628. [DOI] [PubMed] [Google Scholar]
- 59.Hpone Myint K; Brown JR; Shim AR; Wyslouzil BE; Hall LM Encapsulation of Nanoparticles during Polymer Micelle Formation: A Dissipative Particle Dynamics Study. J. Phys. Chem. B 2016, 120, 11582–11594. [DOI] [PubMed] [Google Scholar]
- 60.Kang M; Cui H; Loverde SM Coarse-Grained Molecular Dynamics Studies of the Structure and Stability of Peptide-Based Drug Amphiphile Filaments. Soft Matter 2017, 13, 7721–7730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Lee MT; Vishnyakov A; Neimark AV Calculations of Critical Micelle Concentration by Dissipative Particle Dynamics Simulations: The Role of Chain Rigidity. J. Phys. Chem. B 2013, 117, 10304–10. [DOI] [PubMed] [Google Scholar]
- 62.Loverde SM; Klein ML; Discher DE Nanoparticle Shape Improves Delivery: Rational Coarse Grain Molecular Dynamics (rCG-MD) of Taxol in Worm-Like PEG-PCL Micelles. Adv. Mater 2012, 24, 3823–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Loverde SM; Pantano DA; Christian DA; Mahmud A; Klein ML; Discher DE Curvature, Rigidity, and Pattern Formation in Functional Polymer Micelles and Vesicles from Dynamic Visualization to Molecular Simulation. Curr. Opin. Solid State Mater. Sci 2011, 15, 277–284. [Google Scholar]
- 64.Spaeth JR; Kevrekidis IG; Panagiotopoulos AZ Dissipative Particle Dynamics Simulations of Polymer-Protected Nanoparticle Self-Assembly. J. Chem. Phys 2011, 135, 184903. [DOI] [PubMed] [Google Scholar]
- 65.Condezo GN; San Martin C Localization of Adenovirus Morphogenesis Players, Together with Visualization of Assembly Intermediates and Failed Products, Favor a Model Where Assembly and Packaging Occur Concurrently at the Periphery of the Replication Center. PLoS pathogens 2017, 13, e1006320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Price GD; Badger MR Evidence for the Role of Carboxysomes in the Cyanobacterial CO2-Concentrating Mechanism. Canadian Journal of Botany 1991, 69, 963–973. [Google Scholar]
- 67.Shively JM; Ball F; Brown DH; Saunders RE Functional Organelles in Prokaryotes: Polyhedral Inclusions (Carboxysomes) of Thiobacillus neapolitanus. Science 1973, 182, 584–586. [DOI] [PubMed] [Google Scholar]
- 68.Shively JM; Ball FL; Kline BW Electron Microscopy of the Carboxysomes (Polyhedral Bodies) of Thiobacillus neapolitanus. J. Bacteriol 1973, 116, 1405–1411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Iancu CV; Morris DM; Dou Z; Heinhorst S; Cannon GC; Jensen GJ Organization, Structure, and Assembly of α-Carboxysomes Determined by Electron Cryotomography of Intact Cells. J. Mol. Biol 2010, 396, 105–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Sutter M; Laughlin TG; Sloan NB; Serwas D; Davies KM; Kerfeld CA Structure of a Synthetic β-Carboxysome Shell. Plant Physiol. 2019, 181, 1050–1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Chen T; Glotzer SC Simulation Studies of a Phenomenological Model for Elongated Virus Capsid Formation. Physical Review E. 2007, 75, 051504. [DOI] [PubMed] [Google Scholar]
- 72.Bruinsma RF; Gelbart WM; Reguera D; Rudnick J; Zandi R Viral Self-Assembly as a Thermodynamic Process. Phys. Rev. Lett 2003, 90, 248101. [DOI] [PubMed] [Google Scholar]
- 73.Zandi R; Reguera D; Bruinsma RF; Gelbart WM; Rudnick J Origin of Icosahedral Symmetry in Viruses. Proc. Natl. Acad. Sci. U. S. A 2004, 101, 15556–15560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Berger B; Shor PW; Tuckerkellogg L; King J Local Rule-Based Theory of Virus Shell Assembly. Proc. Natl. Acad. Sci. U. S. A 1994, 91, 7732–7736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Schwartz R; Garcea RL; Berger B “Local Rules” Theory Applied to Polyomavirus Polymorphic Capsid Assemblies. Virology 2000, 268, 461–470. [DOI] [PubMed] [Google Scholar]
- 76.Rapaport D Self-Assembly of Polyhedral Shells: A Molecular Dynamics Study. Phys. Rev. E 2004, 70, 051905. [DOI] [PubMed] [Google Scholar]
- 77.Nguyen HD; Reddy VS; Brooks CL Invariant Polymorphism in Virus Capsid Assembly. J. Am. Chem. Soc 2009, 131, 2606–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Elrad OM; Hagan MF Mechanisms of Size Control and Polymorphism in Viral Capsid Assembly. Nano Lett. 2008, 8, 3850–3857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Johnston IG; Louis AA; Doye JPK Modelling the Self-Assembly of Virus Capsids. J. Phys.: Condens. Matter 2010, 22, 104101. [DOI] [PubMed] [Google Scholar]
- 80.Rapaport DC Studies of Reversible Capsid Shell Growth. J. Phys.: Condens. Matter 2010, 22, 104115. [DOI] [PubMed] [Google Scholar]
- 81.Nguyen H; Brooks C Generalized Structural Polymorphism in Self-Assembled Viral Particles. Nano Lett. 2008, 8, 4574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Mateu MG Assembly, Stability and Dynamics of Virus Capsids. Arch. Biochem. Biophys 2013, 531, 65–79. [DOI] [PubMed] [Google Scholar]
- 83.Hagan MF Modeling Viral Capsid Assembly. Adv. Chem. Phys 2014, 155, 1–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Perlmutter JD; Hagan MF Mechanisms of Virus Assembly. Annu. Rev. Phys. Chem 2015, 66, 217–239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Bruinsma RF; Klug WS Physics of Viral Shells. Annu. Rev. Condens. Matter Phys 2015, 6, 245–268. [Google Scholar]
- 86.Hagan MF; Zandi R Recent Advances in Coarse-Grained Modeling of Virus Assembly. Current Opinion in Virology 2016, 18, 36–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Rapaport DC Molecular Dynamics Simulation of Reversibly Self-Assembling Shells in Solution Using Trapezoidal Particles. Phys. Rev. E 2012, 86, 051917. [DOI] [PubMed] [Google Scholar]
- 88.Rapaport DC; Johnson JE; Skolnick J Supramolecular Self-Assembly: Molecular Dynamics Modeling of Polyhedral Shell Formation. Comput. Phys. Commun 1999, 122, 231–235. [Google Scholar]
- 89.Mendoza CI; Reguera D Shape Selection and Mis-Assembly in Viral Capsid Formation by Elastic Frustration. eLife 2020, 9, e52525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Wagner J; Zandi R The Robust Assembly of Small Symmetric Nanoshells. Biophys. J 2015, 109, 956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Schwartz R; Shor PW; Prevelige PE; Berger B Local Rules Simulation of the Kinetics of Virus Capsid Self-Assembly. Biophys. J 1998, 75, 2626–2636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Hagan MF; Chandler D Dynamic Pathways for Viral Capsid Assembly. Biophys. J 2006, 91, 42–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Wilber AW; Doye JPK; Louis AA; Noya EG; Miller MA; Wong P Reversible Self-Assembly of Patchy Particles into Monodisperse Icosahedral Clusters. J. Chem. Phys 2007, 127, 085106. [DOI] [PubMed] [Google Scholar]
- 94.Baschek JE; Klein HCR; Schwarz US Stochastic Dynamics of Virus Capsid Formation: Direct versus Hierarchical Self-Assembly. BMC biophysics 2012, 5, 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Castelnovo M; Verdier T; Foret L Comparing Open and Closed Molecular Self-Assembly. EPL (Europhysics Letters) 2014, 105, 28006. [Google Scholar]
- 96.Castelnovo M; Muriaux D; Faivre-Moskalenko C Entropic Control of Particle Sizes during Viral Self-Assembly. New Journal of Physics 2013, 15, 035028. [Google Scholar]
- 97.Boettcher MA; Klein HCR; Schwarz US Role of Dynamic Capsomere Supply for Viral Capsid Self-Assembly. Physical biology 2015, 12, 016014. [DOI] [PubMed] [Google Scholar]
- 98.Fejer SN; Chakrabarti D; Wales DJ Emergent Complexity from Simple Anisotropic Building Blocks: Shells, Tubes, and Spirals. ACS Nano 2010, 4, 219–228. [DOI] [PubMed] [Google Scholar]
- 99.Kusters R; Lin H-K; Zandi R; Tsvetkova I; Dragnea B; van der Schoot P Role of Charge Regulation and Size Polydispersity in Nanoparticle Encapsulation by Viral Coat Proteins. J. Phys. Chem. B 2015, 119, 1869–1880. [DOI] [PubMed] [Google Scholar]
- 100.Zandi R; van der Schoot P Size Regulation of ss-RNA Viruses. Biophys. J 2009, 96, 9–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Hagan MF Controlling Viral Capsid Assembly with Templating. Phys. Rev. E 2008, 77, 051904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Hagan MF A Theory for Viral Capsid Assembly around Electrostatic Cores. J. Chem. Phys 2009, 130, 114902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Belyi VA; Muthukumar M Electrostatic Origin of the Genome Packing in Viruses. Proc. Natl. Acad. Sci. U. S. A 2006, 103, 17174–17178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Twarock R; Bingham RJ; Dykeman EC; Stockley PG A Modelling Paradigm for RNA Virus Assembly. Curr. Opin. Vir 2018, 31, 74–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Zandi R; Dragnea B; Travesset A; Podgornik R On Virus Growth and Form. Phys. Rep 2020, 847, 1–102. [Google Scholar]
- 106.Li S; Roy P; Travesset A; Zandi R Why Large Icosahedral Viruses Need Scaffolding Proteins. Proc. Natl. Acad. Sci. U. S. A 2018, 115, 10971–10976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Li S; Zandi R; Travesset A; Grason GM Ground States of Crystalline Caps: Generalized Jellium on Curved Space. Phys. Rev. Lett 2019, 123, 145501. [DOI] [PubMed] [Google Scholar]
- 108.van der Schoot P; Zandi R Impact of the Topology of Viral RNAs on Their Encapsulation by Virus Coat Proteins. J. Biol. Phys 2013, 39, 289–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Erdemci-Tandogan G; Wagner J; van der Schoot P; Podgornik R; Zandi R RNA Topology Remolds Electrostatic Stabilization of Viruses. Phys. Rev. E 2014, 89, 032707. [DOI] [PubMed] [Google Scholar]
- 110.Siber A; Zandi R; Podgornik R Thermodynamics of Nanospheres Encapsulated in Virus Capsids. Phys. Rev. E 2010, 81, 051919. [DOI] [PubMed] [Google Scholar]
- 111.Dykeman EC; Stockley PG; Twarock R Packaging Signals in Two Single-Stranded RNA Viruses Imply a Conserved Assembly Mechanism and Geometry of the Packaged Genome. J. Mol. Biol 2013, 425, 3235–49. [DOI] [PubMed] [Google Scholar]
- 112.Patel N; Dykeman EC; Coutts RHA; Lomonossoff GP; Rowlands DJ; Phillips SEV; Ranson N; Twarock R; Tuma R; Stockley PG Revealing the Density of Encoded Functions in a Viral RNA. Proc. Natl. Acad. Sci. U.S.A 2015, 112, 2227–2232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Dykeman EC; Stockley PG; Twarock R Solving a Levinthal’s Paradox for Virus Assembly Identifies a Unique Antiviral Strategy. Proc. Natl. Acad. Sci. U. S. A 2014, 111, 5361–5366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Dykeman EC; Stockley PG; Twarock R Building a Viral Capsid in the Presence of Genomic RNA. Phys Rev E 2013, 87, 022717. [DOI] [PubMed] [Google Scholar]
- 115.Morton VL; Dykeman EC; Stonehouse NJ; Ashcroft AE; Twarock R; Stockley PG The Impact of Viral RNA on Assembly Pathway Selection. J. Mol. Biol 2010, 401, 298–308. [DOI] [PubMed] [Google Scholar]
- 116.Zhang R; Wernersson E; Linse P Icosahedral Capsid Formation by Capsomer Subunits and a Semiflexible Polyion. RSC Adv. 2013, 3, 25258–25267. [Google Scholar]
- 117.Zhang R; Linse P Topological Effects on Capsomer-Polyion Co-Assembly. The Journal of chemical physics 2014, 140, 244903. [DOI] [PubMed] [Google Scholar]
- 118.Zhang R; Linse P Icosahedral Capsid Formation by Capsomers and Short Polyions. The Journal of chemical physics 2013, 138, 154901. [DOI] [PubMed] [Google Scholar]
- 119.Angelescu DG; Stenhammar J; Linse P Packaging of a Flexible Polyelectrolyte inside a Viral Capsid: Effect of Salt Concentration and Salt Valence. J. Phys. Chem. B 2007, 111, 8477–8485. [DOI] [PubMed] [Google Scholar]
- 120.Angelescu DG; Linse P Monte Carlo Simulations of Flexible Polyelectrolytes inside Viral Capsids with Dodecahedral Charge Distribution. Phys. Rev. E 2007, 75, 051905. [DOI] [PubMed] [Google Scholar]
- 121.Panahandeh S; Li S; Zandi R The Equilibrium Structure of Self-Assembled Protein NanoCages. Nanoscale 2018, 10, 22802–22809. [DOI] [PubMed] [Google Scholar]
- 122.Panahandeh S; Li S; Marichal L; Leite Rubim R; Tresset G; Zandi R How a Virus Circumvents Energy Barriers to Form Symmetric Shells. ACS Nano 2020, 14, 3170–3180. [DOI] [PubMed] [Google Scholar]
- 123.Mahalik JP; Brown KA; Cheng X; Fuentes-Cabrera M Theoretical Study of the Initial Stages of Self-Assembly of a Carboxysome’s Facet. ACS Nano 2016, 10, 5751–8. [DOI] [PubMed] [Google Scholar]
- 124.Young EJ; Burton R; Mahalik JP; Sumpter BG; Fuentes-Cabrera M; Kerfeld CA; Ducat DC Engineering the Bacterial Microcompartment Domain for Molecular Scaffolding Applications. Front. Microbiol 2017, 8, 1441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Oltrogge LM; Savage DF Unpublished work. [Google Scholar]
- 126.Halperin A Polymeric Micelles: A Star Model. Macromolecules 1987, 20, 2943–2946. [Google Scholar]
- 127.Daoud M; Cotton JP Star Shaped Polymers : A Model for the Conformation and Its Concentration Dependence. J. Phys 1982, 43, 531–538. [Google Scholar]
- 128.Hariharan R; Biver C; Mays J; Russel WB Ionic Strength and Curvature Effects in Flat and Highly Curved Polyelectrolyte Brushes. Macromolecules 1998, 31, 7506–7513. [Google Scholar]
- 129.Manandhar A; Kang M; Chakraborty K; Tang PK; Loverde SM Molecular Simulations of Peptide Amphiphiles. Organic & Biomolecular Chemistry 2017, 15, 7993–8005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Lee SM; Bond N; Callaway C; Clark B; Farmer E; Mallard M; Jang SS Dissipative Particle Dynamics Simulation of Multicompartment Micelle Nanoreactor with Channel for Reactants. RSC Adv. 2018, 8, 37866–37871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Ryan P; Forrester TJ; Wroblewski C; Kenney TM; Kitova EN; Klassen JS; Kimber MS The Small RbcS-Like Domains of the β-Carboxysome Structural Protein CcmM Bind RubisCO at a Site Distinct from that Binding the RbcS Subunit. J. Biol. Chem 2019, 294, 2593–2603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Sutter M; Faulkner M; Aussignargues C; Paasch BC; Barrett S; Kerfeld CA; Liu L-N Visualization of Bacterial Microcompartment Facet Assembly Using High-Speed Atomic Force Microscopy. Nano Lett. 2016, 16, 1590–1595, PMID: 26617073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Kennedy NW; Hershewe JM; Nichols TM; Roth EW; Wilke CD; Mills CE; Jewett MC; Tullman-Ercek D Apparent Size and Morphology of Bacterial Microcompartments Varies with Technique. Plos One 2020, 15, e0226395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Huber I; Palmer DJ; Ludwig KN; Brown IR; Warren MJ; Frunzke J Construction of Recombinant Pdu Metabolosome Shells for Small Molecule Production in Corynebacterium glutamicum. ACS Synth Biol 2017, 6, 2145–2156. [DOI] [PubMed] [Google Scholar]
- 135.Lee MJ; Mantell J; Hodgson L; Alibhai D; Fletcher JM; Brown IR; Frank S; Xue WF; Verkade P; Woolfson DN; Warren MJ Engineered Synthetic Scaffolds for Organizing Proteins within the Bacterial Cytoplasm. Nat Chem Biol 2018, 14, 142–147. [DOI] [PubMed] [Google Scholar]
- 136.Pang A; Frank S; Brown I; Warren MJ; Pickersgill RW Structural Insights into Higher Order Assembly and Function of the Bacterial Microcompartment Protein PduA. J Biol Chem 2014, 289, 22377–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Uddin I; Frank S; Warren MJ; Pickersgill RW A Generic Self-Assembly Process in Microcompartments and Synthetic Protein Nanotubes. Small 2018, 14, e1704020. [DOI] [PubMed] [Google Scholar]
- 138.Hagen AR; Plegaria JS; Sloan N; Ferlez B; Aussignargues C; Burton R; Kerfeld CA In Vitro Assembly of Diverse Bacterial Microcompartment Shell Architectures. Nano Lett 2018, 18, 7030–7037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Huang J; Ferlez BH; Young EJ; Kerfeld CA; Kramer DM; Ducat DC Functionalization of Bacterial Microcompartment Shell Proteins with Covalently Attached Heme. Front Bioeng Biotechnol 2019, 7, 432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Young EJ; Sakkos JK; Huang J; Wright JK; Kachel B; Fuentes-Cabrera M; Kerfeld CA; Ducat DC Visualizing in Vivo Dynamics of Designer Nanoscaffolds. Nano Lett 2020, 20, 208–217. [DOI] [PubMed] [Google Scholar]
- 141.Dryden KA; Crowley CS; Tanaka S; Yeates TO; Yeager M Two-Dimensional Crystals of Carboxysome Shell Proteins Recapitulate the Hexagonal Packing of ThreeDimensional Crystals. Protein Science 2009, 18, 2629–2635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Kerfeld CA; Sutter M Engineered Bacterial Microcompartments: Apps for Programming Metabolism. Current Opinion in Biotechnology 2020, 65, 225–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143.Zlotnick A; Johnson JM; Wingfield PW; Stahl SJ; Endres D A Theoretical Model Successfully Identifies Features of Hepatitis B Virus Capsid Assembly. Biochemistry 1999, 38, 14644–14652. [DOI] [PubMed] [Google Scholar]
- 144.Endres D; Zlotnick A Model-Based Analysis of Assembly Kinetics for Virus Capsids or Other Spherical Polymers. Biophysical Journal 2002, 83, 1217–1230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Zlotnick A Are Weak Protein–Protein Interactions the General Rule in Capsid Assembly? Virology 2003, 315, 269–274. [DOI] [PubMed] [Google Scholar]
- 146.Ceres P; Zlotnick A Weak Protein-Protein Interactions Are Sufficient to Drive Assembly of Hepatitis B Virus Capsids. Biochemistry 2002, 41, 11525–11531. [DOI] [PubMed] [Google Scholar]
- 147.Jack RL; Hagan MF; Chandler D Fluctuation-Dissipation Ratios in the Dynamics of Self-Assembly. Physical Review E 2007, 76, 021119. [DOI] [PubMed] [Google Scholar]
- 148.Rapaport D Role of Reversibility in Viral Capsid Growth: A Paradigm for Self-Assembly. Physical Review Letters 2008, 101, 186101. [DOI] [PubMed] [Google Scholar]
- 149.Whitelam S; Feng EH; Hagan MF; Geissler PL The Role of Collective Motion in Examples of Coarsening and Self-Assembly. Soft Matter 2009, 5, 1251–1262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150.Nguyen HD; Reddy VS; Brooks CL Deciphering the Kinetic Mechanism of Spontaneous Self-Assembly of Icosahedral Capsids. Nano Lett. 2007, 7, 338–344. [DOI] [PubMed] [Google Scholar]
- 151.Wilber AW; Doye JP; Louis AA; Lewis AC Monodisperse Self-Assembly in a Model with Protein-Like Interactions. The Journal of Chemical Physics 2009, 131, 11B602. [DOI] [PubMed] [Google Scholar]
- 152.Hagan MF; Elrad OM; Jack RL Mechanisms of Kinetic Trapping in Self-Assembly and Phase Transformation. The Journal of Chemical Physics 2011, 135, 104115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Cheng S; Fan C; Sinha S; Bobik TA The PduQ Enzyme Is an Alcohol Dehydrogenase Used to Recycle NAD+ Internally within the Pdu Microcompartment of Salmonella Enterica. PloS One 2012, 7, e47144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Whitelam S Hierarchical Assembly May Be a Way to Make Large Information-Rich Structures. Soft Matter 2015, 11, 8225–8235. [DOI] [PubMed] [Google Scholar]
- 155.Làzaro GR; Mukhopadhyay S; Hagan MF Why Enveloped Viruses Need Cores:The Contribution of a Nucleocapsid Core to Viral Budding. Biophys. J 2018, 114, 619–630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 156.Dai W; Chen M; Myers C; Ludtke SJ; Pettitt BM; King JA; Schmid MF; Chiu W Visualizing Individual RuBisCO and Its Assembly into Carboxysomes in Marine Cyanobacteria by Cryo-Electron Tomography. J. Mol. Biol 2018, 430, 4156–4167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.Alexander S Adsorption of Chain Molecules with a Polar Head a Scaling Description. J. Phys 1977, 38, 983–987. [Google Scholar]
- 158.Witten TA; Pincus PA Colloid Stabilization by Long Grafted Polymers. Macromolecules 1986, 19, 2509–2513. [Google Scholar]
- 159.Zhulina EB; Borisov OV Absorption of a Polyelectrolyte Brush into an Oppositely Charged Layer. Macromolecules 1998, 31, 7413–7422. [Google Scholar]
- 160.Hagan MF; Grason GM Equilibrium Mechanisms of Self-Limiting Assembly. arXiv.2007.01927 2020, https://arxiv.org/abs/2007.01927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161.de Gennes P Scaling Concepts in Polymer Physics; Cornell Univ. Pr.: Ithaca, 1979. [Google Scholar]
- 162.Heinhorst S; Cannon GC; Shively JM Complex Intracellular Structures in Prokaryotes; Springer: Berlin, 2006. [Google Scholar]
- 163.Paquay S; Kusumaatmaja H; Wales DJ; Zandi R; van der Schoot P Energetically Favoured Defects in Dense Packings of Particles on Spherical Surfaces. Soft Matter 2016, 12, 5708–5717. [DOI] [PubMed] [Google Scholar]
- 164.Luque A; Reguera D; Morozov A; Rudnick J; Bruinsma R Physics of Shell Assembly: Line Tension, Hole Implosion, and Closure Catastrophe. J. Chem. Phys 2012, 136, 184507. [DOI] [PubMed] [Google Scholar]
- 165.Fejer SN Minimalistic Coarse-Grained Modeling of Viral Capsid Assembly. Progress in molecular biology and translational science 2020, 170, 405–434. [DOI] [PubMed] [Google Scholar]
- 166.Asor R; Schlicksup CJ; Zhao Z; Zlotnick A; Raviv U Rapidly Forming Early Intermediate Structures Dictate the Pathway of Capsid Assembly. Journal of the American Chemical Society 2020, 142, 7868–7882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 167.Caspar DL; Klug A Physical Principles in the Construction of Regular Viruses. Cold Spring Harbor Symposia on Quantitative Biology 1962, 27, 1–24. [DOI] [PubMed] [Google Scholar]
- 168.Fan C; Cheng S; Liu Y; Escobar CM; Crowley CS; Jefferson RE; Yeates TO; Bobik T. a. Short N-Terminal Sequences Package Proteins into Bacterial Microcompartments. Proc. Natl. Acad. Sci. U. S. A 2010, 107, 7509–7514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169.Aussignargues C; Paasch BC; Gonzalez-Esquer R; Erbilgin O; Kerfeld CA Bacterial Microcompartment Assembly: The Key Role of Encapsulation Peptides. Communicative & Integrative Biology 2015, 8, e1039755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 170.Cai F; Menon BB; Cannon GC; Curry KJ; Shively JM; Heinhorst S The Pentameric Vertex Proteins Are Necessary for the Icosahedral Carboxysome Shell to Function as a CO2 Leakage Barrier. PLoS ONE 2009, 4, e7521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.Long BM; Hee WY; Sharwood RE; Rae BD; Kaines S; Lim YL; Nguyen ND; Massey B; Bala S; von Caemmerer S; Badger MR; Price GD Carboxysome Encapsulation of the CO2-Fixing Enzyme Rubisco in Tobacco Chloroplasts. Nat Commun 2018, 9, 3570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Cheng S; Sinha S; Fan C; Liu Y; Bobik TA Genetic Analysis of the Protein Shell of the Microcompartments Involved in Coenzyme B12-Dependent 1,2-Propanediol Degradation by Salmonella. J Bacteriol 2011, 193, 1385–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173.Parsons JB; Dinesh SD; Deery E; Leech HK; Brindley AA; Heldt D; Frank S; Smales CM; Lunsdorf H; Rambach A; Gass MH; Bleloch A; McClean KJ; Munro AW; Rigby SE; Warren MJ; Prentice MB Biochemical and Structural Insights into Bacterial Organelle Form and Biogenesis. J Biol Chem 2008, 283, 14366–75. [DOI] [PubMed] [Google Scholar]
- 174.Price GD; Howitt SM; Harrison K; Badger MR Analysis of a Genomic DNA Region from the Cyanobacterium Synechococcus Sp. Strain PCC7942 Involved in Carboxysome Assembly and Function. Journal of Bacteriology 1993, 175, 2871–2879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 175.Wheatley NM; Gidaniyan SD; Liu Y; Cascio D; Yeates TO Bacterial Microcompartment Shells of Diverse Functional Types Possess Pentameric Vertex Proteins. Protein Sci 2013, 22, 660–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 176.Yeates TO; Crowley CS; Tanaka S Bacterial Microcompartment Organelles: Protein Shell Structure and Evolution. Annu Rev Biophys 2010, 39, 185–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 177.Tanaka S; Sawaya MR; Yeates TO Structure and Mechanisms of a Protein-Based Organelle in Escherichia coli. Science 2010, 327, 81–84. [DOI] [PubMed] [Google Scholar]
- 178.Anderson JA; Lorenz CD; Travesset A General Purpose Molecular Dynamics Simulations Fully Implemented on Graphics Processing Units. J. Comput. Phys 2008, 227, 5342–5359. [Google Scholar]
- 179.Nguyen TD; Phillips CL; Anderson JA; Glotzer SC Rigid Body Constraints Realized in Massively-Parallel Molecular Dynamics on Graphics Processing Units. Comput. Phys. Commun 2011, 182, 2307–2313. [Google Scholar]
- 180.https://hoomd-blue.readthedocs.io/en/stable/units.html, date of access 06.30.2020.
- 181.Faulkner M; Rodriguez-Ramos J; Dykes GF; Owen SV; Casella S; Simpson DM; Beynon RJ; Liu L-N Direct Characterization of the Native Structure and Mechanics of Cyanobacterial Carboxysomes. Nanoscale 2017, 9, 10662–10673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 182.Humphrey W; Dalke A; Schulten K VMD – Visual Molecular Dynamics. Journal of Molecular Graphics 1996, 14, 33–38. [DOI] [PubMed] [Google Scholar]
- 183.Mohajerani F; Sayer E; Neil C; Inlow K; Hagan MF Mechanisms of Scaffold-Mediated Microcompartment Assembly and Size-Control. bioRxiv, 2020; doi: 10.1101/2020.10.14.338509, accessed Nov 1, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.