Soft anharmonic phonons and ultralow thermal conductivity in Mg₃(Sb, Bi)₂ thermoelectrics

The atomistic origin of ultralow thermal conductivity in promising new thermoelectrics is revealed by experiments and simulations.

Abstract

The candidate thermoelectric compounds Mg₃Sb₂ and Mg₃Bi₂ show excellent performance near ambient temperature, enabled by an anomalously low lattice thermal conductivity (κ_l) comparable to those of much heavier PbTe or Bi₂Te₃. Contrary to common mass-trend expectations, replacing Mg with heavier Ca or Yb yields a threefold increase in κ_l in CaMg₂Sb₂ and YbMg₂Bi₂. Here, we report a comprehensive analysis of phonons in the series AMg₂X₂ (A = Mg, Ca, and Yb; X = Bi and Sb) based on inelastic neutron/x-ray scattering and first-principles simulations and show that the anomalously low κ_l of Mg₃X₂ has inherent phononic origins. We uncover a large phonon softening and flattening of low-energy transverse acoustic phonons in Mg₃X₂ compared to the ternary analogs and traced to a specific Mg-X bond, which markedly enlarges the scattering phase-space, enabling the threefold tuning in κ_l. These results provide key insights for manipulating phonon scattering without the traditional reliance on heavy elements.

INTRODUCTION

Thermoelectric (TE) materials directly interconvert electrical and thermal gradients, providing opportunities in waste heat recovery and cooling applications (1–4). Improving TE conversion efficiency requires minimizing the thermal conductivity κ_tot = κ_e + κ_l (sum of electronic and lattice components) and simultaneously maximizing the electronic power factor (3, 4). While first-principles band structure calculations have enabled a predictive understanding of electronic transport properties and in silico material design, achieving a quantitative microscopic understanding of thermal transport in strongly anharmonic materials has remained challenging (3, 4). Impressive advances in TE performance have been achieved over the past decade at intermediate to high temperature (T > 450 K) (5–12), enabled in part because κ_l is strongly suppressed by anharmonic scattering for high phonon occupations (scaling with T). Around room temperature, a relative paucity of material candidates has hampered TE developments, with (Bi, Sb)₂(Te, Se)₃ alloys remaining the best for decades (13, 14). Recently, however, n-type Mg₃(Bi, Sb)₂ Zintl compounds were reported to achieve comparable performance near ambient conditions, potentially with much lower cost (15–18).

Despite their much lighter weight than conventional TE compounds PbTe or Bi₂(Te, Se)₃, these promising Zintl compounds exhibit strikingly low values of κ_l. For instance, κ_l = 1.4 W m⁻¹ K⁻¹ was achieved in polycrystalline Mg₃Sb₂ at 323 K (19), despite its low mass and relatively simple crystal structure. This low κ_l is comparable to those of 2.5× heavier compounds PbTe and Bi₂(Te, Se)₃ or barium clathrates with complex structures, contradicting the expected trend of κ_l ∝ M⁻¹ [from the inverse relationship between the square of phonon frequency, ω, and mass, M, and the proportionality of group velocity v_g and ω. κ_l of polycrystalline PbTe, Bi₂Te₃, and Ba₈Ga₁₆Ge₃₀ are 2.0, 1.2, and 1.5 W m⁻¹K⁻¹ at room temperature (20–22). The mass densities of Mg₃Sb₂, PbTe, and Bi₂Te₃ are 4.02, 8.16, and 7.74 g/cm³, respectively.] Further, this surprisingly low κ_l in Mg₃X₂ is strongly tunable upon targeted substitutions: Replacing A-site Mg with heavier Ca or Yb results in a striking anomalous increase in κ_l by a factor of 2 to 3 (23, 24), again directly contradicting the expected suppression from more complex composition and heavier mass, and suggests heretofore unknown mechanisms capable of strongly suppressing phonon propagation in simple, lightweight crystalline compounds.

Experimental and theoretical TE investigations of Mg₃X₂ have so far mainly focused on the electronic properties, for example, the origin of n-type behavior (25, 26), the multivalley character of the conduction band (27–30), and routes to increased carrier mobility (17, 18, 31–33). In contrast, the origin of the intrinsically low κ_l of Mg₃X₂ and the counterintuitive increase of κ_l in homologous ternary AMg₂X₂ have remained puzzling, although the low κ_l plays an equally important role in achieving high zT. Previous computational studies suggested that the anharmonic interlayer shearing transverse acoustic (TA) modes (23, 24) and anharmonic mid-energy optical phonons (24) suppress κ_l. Simulations of alloys also predicted that doping 25% Ca or Yb on the A-site reduces κ_l by reducing the averaged phonon velocity, while the averaged phonon lifetime remains unchanged (29). Measurements of elastic moduli revealed soft shear moduli in Mg₃Sb₂ and a higher rate of softening upon warming than in ternary AMg₂X₂, which was interpreted in terms of ionic radii, unit cell volumes, and large negative Gr$\ddot{\mathrm{u}}$neisen parameters in TA modes (23). Yet, a clear microscopic picture of phonon scattering remains elusive because of the lack of detailed phonon measurements, precluding a clear understanding of the origin of the abnormally low κ_l in Mg₃X₂.

Here, we reveal the phononic origins of the unusual thermal conductivity of Mg₃X₂ using both inelastic neutron scattering (INS) and inelastic x-ray scattering (IXS), supported by computational modeling based on density functional theory (DFT) and ab initio molecular dynamics (AIMD). We uncover a striking phonon softening (shift to lower energy) in Mg₃X₂ compared with ternary compounds (A= Ca or Yb) and an unusual flat low-frequency TA phonon branch in Mg₃X₂ that considerably stiffens upon substitution with Ca or Yb. Combining our extensive phonon measurements and simulations, we quantitatively determined the origin of the low κ_l in Mg₃X₂. In particular, we identify the importance of a weak A-X nearest-neighbor bond in Mg₃X₂. This weak bond effectively destabilizes TA phonons, leading to a soft branch along Γ − M, overcoming expected mass trends between Mg and heavier A-site ions (A = Ca and Yb). Concomitant with a suppression in group velocities, we show how the phonon softening markedly increases (fivefold) the weighted scattering phase-space, overcoming an actual suppression (50%) in third-order force constants (FC). These results quantitatively account for the anomalous two- to threefold suppression in κ_l in binary Mg₃X₂ compared to ternary AMg₂X₂ despite the lighter mass and simpler chemistry of the former. Our momentum and energy-resolved phonon measurements thus rationalize the basis of the high thermal performance of Mg₃X₂ for TE applications.

RESULTS AND DISCUSSION

Soft phonons in Mg₃X₂

The Zintl compounds AMg₂X₂ (A = Mg, Ca, and Yb; X = Sb and Bi) belong to the CaAl₂Si₂-type family that crystallize in a trigonal conventional cell with space group $P\overline{3}m1$ (no. 164). Their structures consist of alternating [Mg₂X₂] and A atom layers, as shown in Fig. 1A. Despite the structural anisotropy, the bonding and electronic structure are fairly isotropic (24). In the following, we refer to Mg on the octahedrally coordinated A-site by X atoms as Mg(1) and Mg on the tetrahedrally coordinated sites as Mg(2).

Fig. 1. Soft phonons from inelastic neutron scattering.

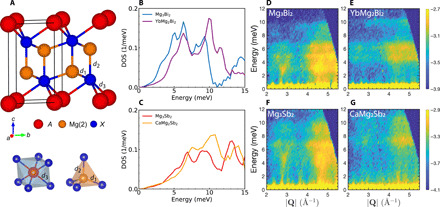
(A) Crystal structure of AMg₂X₂ and illustration of octahedral A-site and tetrahedral Mg(2) atoms. Red, orange, and blue represent A, Mg(2), and X, respectively. d₁ and d₂ are the nearest- and second-nearest-neighbor Mg(2)-X bonds. The nearest-neighbor A-X bond is d₃. Comparison of experimental neutron DOS E_i = 20 meV at 300 K of (B) Mg₃Bi₂ (blue) and YbMg₂Bi₂ (purple) and (C) Mg₃Sb₂ (red) and CaMg₂Sb₂ (orange). Significant stiffening is observed in ternary compounds despite a heavier mass of Ca or Yb than Mg. Extra shoulders at low energy are observed only in binary compounds. Neutron dynamical structure factor S(∣Q∣, ω) of (D) Mg₃Bi₂, (E) YbMg₂Bi₂, (F) Mg₃Sb₂, and (G) CaMg₂Sb₂, the same datasets as in (B) and (C). Total intensities are normalized to the value of Mg₃Bi₂. Much stronger intensities at the low-energy region can be observed in binary compared to ternary compounds.

The phonon density of states (DOS) of six AMg₂X₂ (A = Mg, Ca, and Yb; X = Sb and Bi) powder samples were measured with INS as a function of temperature, using the wide angular-range chopper spectrometer (ARCS) at the Spallation Neutron Source (34). The contributions from different atoms are spectrally well separated, as seen from the calculated partial DOS (Fig. 2A and fig. S9). For instance, in Mg₃Bi₂, Mg(2) contributes mainly at energies greater than 20 meV, Bi contributes mostly below 10 meV, and Mg(1) dominates the intermediate region. The lower vibrational frequency of Mg(1) than Mg(2) thus suggests a weaker bonding environment of Mg(1). When replacing A-site Mg(1) with Ca or Yb, the Mg(2) modes at E > 20 meV remain almost unaffected in both experiments and simulations (figs. S5 and S9). This indicates relatively unchanged local environments and bondings for Mg(2) across compositions. Considering that the atomic mass directly shifts phonon frequencies (ω² ∝ K/M, where K is the spring constant and M is the mass), all else being fixed, heavier atoms should exhibit lower phonon energies. Naturally, the heavier Yb atoms vibrate at a lower frequency than Mg or Ca (173, 24, and 40 atomic mass units, respectively). However, when comparing Mg(1) and Ca, the partial DOS of Mg(1) contributes more to the lower energy side and is substantially broader than for Ca (fig. S9). Substitution on the A-site also strongly affects the X partial DOS at low energy, reflecting a strong change in the A-X interaction, which we will explain later.

Fig. 2. Anharmonic Mg(1) phonon modes and momentum-resolved measurements from inelastic x-ray scattering.

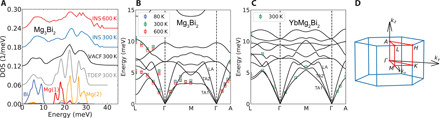
(A) Phonon DOS of Mg₃Bi₂ from INS at 300 K (blue) and 600 K (red), compared with VACF calculation at 300 K (black) and renormalized DOS from TDEP (gray). The computed total DOS is NW and convolved with the experimental resolution. (B and C) Momentum-resolved IXS measurements on single crystals (markers), compared with DFT phonon dispersions (solid lines) for Mg₃Bi₂ and YbMg₂Bi₂. Blue, green, and red markers correspond to the fitted phonon energy at 80, 300, and 600 K. (D) Brillouin zone (irreducible wedge in red) and high-symmetry points.

A strong phonon stiffening (energy increase) is observed at E < 12 meV when substituting Mg(1) with Ca or Yb. This is clearly seen in the E_i= 20 meV INS data at 300 K, as shown in Fig. 1 (B and C) and fig. S4. Compared with Mg₃X₂, all the peaks in CaMg₂X₂ below 12 meV are stiffened, with relative shifts (ΔE/E) as large as +6.4, +15.1, and +4.6% in Bi compounds, and +12.3, +12.7, and +6.2% in Sb compounds (see table S1). On the basis of mass alone, one would predict a softening of −3% in CaMg₂X₂ from DFT. Even for the heavy YbMg₂Bi₂, where Yb contributes significantly below 12 meV, stiffer phonon energies are observed compared to Mg₃Bi₂ for 8 < E < 12 meV (see fig. S4B). The frequency stiffening of the X partial DOS in ternary compounds relative to the binaries again suggests that the interactions between Ca-X and Yb-X are stronger than Mg(1)-X. While a 10% stiffening on average is observed in the DOS, specific modes stiffen significantly more. Our DFT calculations show that the lowest TA mode at the zone boundary M-point stiffens by more than 60% (E = 3.33, 5.40, and 5.53 meV for Mg₃Bi₂, CaMg₂Bi₂, and YbMg₂Bi₂; see fig. S8). Notably, an extra shoulder is seen at low energy around 3.5 meV in Mg₃Bi₂ (5 meV in Mg₃Sb₂) that does not exist in the ternaries.

The powder-averaged dynamical structure factor from INS, S(∣Q∣, ω), shown in Fig. 1 (D to G), reveals more details. In all four compounds, vertical intensity streaks disperse out from the elastic line (at 0 meV), corresponding to acoustic phonons. The top of the acoustic phonon and the low-energy optical phonons contribute to the strong intensity between 6 and 10 meV. At 2 to 4 meV, only the binary Mg₃X₂ show strong intensity, especially visible at higher Q, which originate from the softened acoustic phonons, and give rise to the extra shoulder in the DOS.

The soft phonon and low-energy shoulder seen in Mg₃X₂ with INS are well captured by our DFT simulations, as shown in fig. S6. We resolve the low-E shoulder as a softened TA branch in binaries, as shown by the red curves in fig. S7 (a peak/shoulder in the DOS arises from a less dispersive branch over an extended volume of the Brillouin zone). The lowest-energy TA branch along Γ − M is drastically less dispersive in Mg₃X₂ than in CaMg₂X₂ or YbMg₂X₂ (highlighted in red in fig. S8). We note that previous studies (24) reported an unphysical unstable phonon branch for Mg₃Bi₂, in particular around the L-point. Our simulations resolved this issue by using the Perdew-Burke-Ernzerhof revised for solids (PBEsol) functional and including spin-orbit coupling (SOC). The softer dispersion and flat TA branch in Mg₃X₂ result in suppressed phonon group velocities (v_g =∣∇_kω∣, where E = ℏω). Simultaneously, the three-phonon scattering phase-space is strongly expanded, as detailed below and in section S4.

We further compare the INS DOS with first-principles simulation including anharmonic effects. We performed temperature-dependent effective potential (TDEP) simulations, which include anharmonic frequency renormalization but no anharmonic broadening, and calculations of the velocity autocorrelation function (VACF) from AIMD, capturing anharmonic mode broadening as well as shifts. As seen in Fig. 2A, peak positions from TDEP (gray) agree well with the INS DOS for Mg(2) and Bi-dominated modes at 300 K (blue). However, a stronger broadening is seen in INS for 10 < E < 20 meV, corresponding to Mg(1) modes, reflecting an anharmonic bonding environment for Mg(1). This broadening is well captured by the VACF at 300 K (black). Additional INS results for all compounds as a function of temperature are shown in figs. S2 and S3. The entire spectrum broadens upon warming as a result of anharmonic lifetime suppression when vibrational amplitudes increase, but the Mg(1) modes broaden the most in panels (A) and (D).

Origin of soft TA modes in Mg₃X₂

To fully elucidate the origins of the anomalous low-E acoustic modes, we performed Q-resolved dispersion measurements with IXS on small single crystals of Mg₃Bi₂ (T = 80, 300, and 600 K) and YbMg₂Bi₂ (T = 300 K), using the high-energy-resolution inelastic x-ray spectrometer (HERIX) beamline (sector 30) at the Advanced Photon Source (35, 36). The IXS spectra show well-defined peaks (see fig. S16), enabling accurate estimates of the phonon energies. The phonon energies from IXS are compared with our DFT simulations in Fig. 2 (B and C). Very good agreement is observed for YbMg₂Bi₂, which exhibits strongly dispersive TA along Γ − M, Γ − A, and the long-wavelength portion of Γ − L (we track the lowest-energy TA by phonon polarization; see fig. S13). Good agreement is also found in Mg₃Bi₂. Upon warming Mg₃Bi₂ from 80 to 600 K, most phonons soften and broaden, but the TA branch at the L-point anomalously stiffens, consistent with the negative Grüneisen parameter from our quasi-harmonic simulations (fig. S10) and those in (23).

The lowest TA branch along Γ − M is significantly softer in Mg₃Bi₂ than in YbMg₂Bi₂, which explains the extra shoulder observed in the DOS. To rationalize this soft TA branch, we analyze the modulus of the second-order FC (∣Φ⁽²⁾∣) from DFT for Mg₃Sb₂ (red), CaMg₂Sb₂ (orange), Mg₃Bi₂ (blue), and YbMg₃Bi₂ (purple), respectively, as shown in Fig. 3A and as a function of bond length in fig. S14A. The two strongest bonds are the nearest-neighbor (d₁) and second-nearest-neighbor (d₂) Mg(2)-X bonds. For these bonds, ∣Φ⁽²⁾∣ varies less than 20% between binaries and ternaries. However, for the A-X nearest-neighbor bond (d₃), ∣Φ⁽²⁾∣ very strongly depends on the A cation: 1.06 and 0.52 eV/Ų in CaMg₂Sb₂ and Mg₃Sb₂ and 1.17 and 0.75 eV/Ų in YbMg₂Bi₂ and Mg₃Bi₂, respectively. This large increase in ∣Φ⁽²⁾(d₃)∣ by 105% (Sb) and 56% (Bi) in the ternary compounds reveals a strong change in A-X bonding. The much smaller ∣Φ⁽²⁾∣ for d₃ than d₁ or d₂ also leads to the lower phonon frequency of Mg(1) than Mg(2) in the DOS. The weak d₃ bond directly controls the TA branch along the Γ − M direction. As we show in fig. S14F, artificially replacing Φ⁽²⁾(d₃) in Mg₃Bi₂ with that from YbMg₂Bi₂ leads to a more dispersive TA branch along Γ − M, while changing Φ⁽²⁾ for d₁ or d₂ has relatively little effect.

Fig. 3. Weakened A-X bonds in binary Mg₃X₂ compared with ternary CaMg₂X₂.

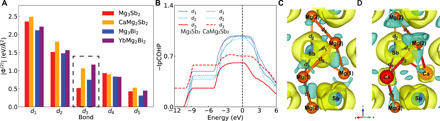
(A) Modulus of second-order FC (∣Φ⁽²⁾∣) in Mg₃Sb₂ (red), CaMg₂Sb₂ (orange), Mg₃Bi₂ (blue), and YbMg₂Bi₂ (purple). Bonds d₁ through d₅ are defined in (C) and (D). The largest change is found for the d₃ bond, which is much weaker in binaries than in ternaries. (B) The negative integrated pCOHP (−IpCOHP) for d₁, d₂, and d₃. The larger absolute value of IpCOHP at the Fermi energy of d₃ in CaMg₂Sb₂ than in Mg₃Sb₂ is in accordance with the ∣Φ⁽²⁾∣. Deformation electron density in (C) Mg₃Sb₂ and (D) CaMg₂Sb₂ at an isosurface value of 0.004 e/ų. Yellow and blue are positive and negative values, respectively.

The change in Φ⁽²⁾ can be related to the electronic bonding via the crystal orbital Hamiltonian population (COHP), here calculated with the LOBSTER software (37–40). Figure S15 shows the projected partial COHP for bonds d₁, d₂, and d₃, comparing Mg₃Sb₂ (solid lines) and CaMg₂Sb₂ (dashed lines). Bonding states are negative and antibonding states are positive. All states are bonding below −2 eV. In the valence band near the Fermi energy (E_F = 0 eV), Mg₃Sb₂ and CaMg₂Sb₂ have similar pCOHP for d₁ and d₂. However, for d₃, Mg(1)-Sb remains nonbonded down to −1 eV, while Ca-Sb has antibonding interaction in the valence band down to −2 eV. The pCOHP for Mg(1)-Mg(2) (d₅) in Mg₃Sb₂ was shown to involve nonbonding states at the valence band maximum but bonding states at the conduction band minimum in (33). The integrated pCOHP (IpCOHP) probes covalency and relative bond strength, where a more negative value corresponds to a stronger covalent bonding (41). We note that all AMg₂X₂ compounds are isostructural with only A-site substitution, so comparing their pCOHP is justified. As seen in Fig. 3B, the −IpCOHP values at E_F for d₁ are slightly larger than d₂ in both Mg₃Sb₂ and CaMg₃Sb₂, and much larger than d₃, which matches the trend of the corresponding ∣Φ⁽²⁾∣. While a slightly smaller −IpCOHP for d₁ and d₂ is found in CaMg₂Sb₂ than in Mg₃Sb₂, the −IpCOHP for d₃ is larger, which supports the observation of weaker Mg(1)-Sb than Ca-Sb bonds. Meanwhile, the deformation charge density (Fig. 3, C and D) shows that despite the larger charge transfer in the case of CaMg₂Sb₂, the charge density around Mg(2) is similar in both cases. A more ionic character was found in Ca-Mg(2) compared to Mg(1)-Mg(2) (d₅) in agreement with a prior study (29).

Differences in Mg(1)-X versus Ca-X bonding character cannot fully explain the surprising disparity in d₃ FC. The softer Mg(1)-X bonds likely arise in part from negative chemical pressure experienced by Mg(1). Although Mg is much smaller than Ca (atomic radii: 1.45 versus 1.94; ionic radii: 0.72 versus 1.00 in Å), the difference between the Ca-Sb versus Mg(1)-Sb bond lengths (d₃) is only 0.14 Å. In the binary compounds, the Mg(1) coordination environment can thus be described as an oversized pnictide cage. The MgX₆ octahedra in the binaries are highly distorted compared with the near-ideal octahedral geometry of the ternary compounds. Both binaries exhibit a high-temperature β-phase in which Mg is tetrahedrally coordinated by X (42). The formation of the Mg₃X₂ compounds in the CaAl₂Si₂ structure type at lower temperatures is a testament to the extreme chemical adaptability of Mg (43). The binaries can be seen as a textbook example of driving a system to the edge of structural stability to achieve soft TA modes by negative chemical pressure.

Thermal conductivity analysis

We now rationalize the anomalously low κ_l in Mg₃Sb₂ and Mg₃Bi₂. Replacing Mg(1) with Ca or Yb leads to two- to threefold higher κ_l in polycrystalline samples, as shown in Fig. 4 (A and B) (filled markers) (24, 44, 45). The κ_l of Mg₃X₂ is twice higher in single crystals (46) versus polycrystals owing to the absence of boundary scattering. Our calculated κ_l using TDEP (details in the Supplementary Materials) matches very well with the single-crystal measurements in Mg₃X₂ at 300 K (red and blue hollow markers versus solid lines). Further, we find an almost isotropic κ_l at all temperatures (e.g., 2.38 in-plane, 2.29 out-of-plane for Mg₃Sb₂ and 6.30 in-plane, 6.05 out-of-plane for CaMg₂Sb₂ at 300 K), in agreement with previous Mg₃Sb₂ simulations (29). The calculated κ_l of CaMg₂Sb₂ is about 3× higher than for Mg₃Sb₂ (2× in Bi compounds), matching the experimental trend (only polycrystalline data available).

Fig. 4. Lattice thermal conductivity analysis and origin of suppression in binary Mg₃X₂.

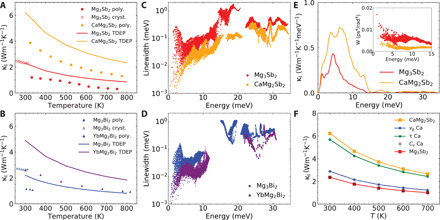
Reported κ_l of (A) AMg₂Sb₂ and (B) AMg₂Bi₂ from (24, 44–46) compared with our TDEP simulations. κ_l of Mg₃X₂ is two to three times lower than in the Ca or Yb compounds in both experiments and simulations. Comparison of phonon linewidths from TDEP for (C) AMg₂Sb₂ and (D) AMg₂Bi₂. Binary compounds exhibit a factor of 2 to 3 larger linewidths, similar to the ratio in κ_l. (E) Spectrally decomposed κ_l in Mg₃Sb₂ and CaMg₂Sb₂. Inset shows the corresponding weighted phase-space (W). A three times larger W is observed in Mg₃Sb₂ below 10 meV. (F) κ_l comparison of Mg₃Sb₂ and CaMg₂Sb₂. Red and orange markers are the same κ_l in (A). Blue, green, and black hollow markers represent the κ_l when replacing v_g, τ, and C_v with the values from CaMg₂Sb₂ (details in the main text).

Figure 4E and fig. S18 show the spectrally decomposed thermal conductivity, κ_l(E), revealing that phonons below 15 meV dominate the overall κ_l in both Mg₃Sb₂ and CaMg₂Sb₂ (12 meV in AMg₂Bi₂). The peak contribution to κ_l(E) corresponds to the top of the acoustic branches, around 5 meV in Mg₃Sb₂ and 7 meV in the CaMg₂Sb₂. A marked suppression of κ_l is observed in Mg₃Sb₂ over the range 1 < E < 15 meV. The κ_l ratios (2 to 3) between binaries and ternaries are directly reflected in their phonon linewidths ($\propto {\mathrm{\kappa }}_{\mathrm{l}}^{-1}$) in both Sb and Bi compounds (Fig. 4, C and D, and fig. S18). The much larger phonon linewidths below 4 meV in Mg₃X₂ correspond to the flat TA mode (e.g., along Γ − M). These are strongly scattered, as they satisfy the energy conservation rules for phonon-phonon scattering easily. They also have low phonon group velocities and thus contribute little to the total κ_l. In ternary compounds, these phonon branches are more dispersive, are less scattered, and carry more heat. Zhang et al. (24) emphasized these TA phonons and mid-energy optical phonon (13 to 20 meV) as the main suppression mechanism. However, this is insufficient, as the suppression happens over the entire energy range. The anharmonic scattering rates (∝ linewidth) calculated in (24), using harmonic Φ⁽²⁾, are almost 10 times larger in Mg₃Sb₂ than in CaMg₂Sb₂, leading to an underestimated κ_l even lower than polycrystalline data. We note that using harmonic phonon dispersions significantly overestimates the scattering phase-space.

We further examine the thermal transport mechanism by isolating the relative contribution of C_v, v_g, and τ in κ_l, and revealing the critical importance of the d₃ bond in modulating the scattering phase-space. We use the TDEP κ_l of Mg₃Sb₂ and CaMg₂Sb₂ as references and replace each component in Mg₃Sb₂ with its counterpart from CaMg₂Sb₂, as shown in Fig. 4F. For instance, the blue curve labeled as “v_g Ca” represents ${\mathrm{\kappa }}_{\mathrm{l}}=\frac{1}{3}\sum C_{V_{\mathrm{M}{\mathrm{g}}_3\mathrm{S}{\mathrm{b}}_2}}{v}_{g_{\text{CaM}{\mathrm{g}}_2\mathrm{S}{\mathrm{b}}_2}}^2{\mathrm{\tau }}_{\mathrm{M}{\mathrm{g}}_3\mathrm{S}{\mathrm{b}}_2}$. As one would expect, the heat capacity effect is minimal, which almost overlaps with the κ_l of Mg₃Sb₂ (black hollow circles). The energy shift observed in INS indicates a strong change in v_g. As shown in table S5, at some Q vectors, v_g is enhanced by more than 50% in CaMg₂Sb₂, showing a corresponding increase in mode κ_l compared to Mg₃Sb₂. However, the overall increase in κ_l is only 22% (blue), which is a small part of the actual difference (∼3×) in total κ_l. On the other hand, replacing τ leads to a 2.4× higher κ_l (green). The scattering rate (∝τ⁻¹) results from a product of the scattering phase-space, weighted by the phonon occupation factor, and the scattering probability $\mid V_{\mathrm{\lambda }{\mathrm{\lambda }}^{\prime }{\mathrm{\lambda }}^{\prime \prime }}^{\pm }\mid$ involving phonon modes λ, λ′, and λ″. The latter can be viewed as the mass-, frequency-, and eigenvector-weighted Fourier transform of the third-order FC (Φ⁽³⁾). Φ⁽²⁾ controls the phonon group velocity, frequency, and eigenvector and determines the scattering phase-space. Φ⁽³⁾ only determines the scattering probability. By separately replacing Φ⁽²⁾ and Φ⁽³⁾ of Mg₃Sb₂ with those of CaMg₂Sb₂, we further break down the contributions to κ_l. As can be seen in fig. S14B, ∣Φ⁽³⁾∣ only differs by 10% on average between the two Sb compounds, while weak Mg(1)-X bonds are again found. These weaker d₃ bonds result in a 50% smaller scattering probability, and substituting the Ca Φ⁽³⁾ (blue) leads to 50% decrease in κ_l (fig. S19). However, substituting the Ca Φ⁽²⁾ (green) results in a 5× increase in κ_l, arising from frequency and scattering phase-space renormalization by the d₃ bond. The weighted scattering phase-space (W), defined by equation S7, is shown in the inset of Fig. 4E. A large increase in W is observed for Mg₃Sb₂ compared with CaMg₂Sb₂, in the same energy range where κ_l is suppressed. This renormalization is controlled by Φ⁽²⁾ as shown in fig. S18E.

Through a systematic investigation of phonons and thermal transport in AMg₂X₂ compounds with INS, IXS, and first-principles modeling including AIMD, we revealed how the superior thermal properties of Mg₃X₂ for TE applications originate from specific bonding characteristics, especially a weak d₃ bond associated with Mg(1)-X. This weak bond plays a critical role in destabilizing TA phonons, leading to a soft flat branch along Γ − M, overcoming expected mass trends between Mg and heavier A-site ions (Ca and Yb). Our thermal conductivity analysis fully accounts for the unexpected threefold suppression in the κ_l of Mg₃X₂ compared to heavier ternaries, revealing the impact of this soft d₃ bond. While group velocity suppression reduces κ_l by a modest 20%, the soft anharmonic dispersion enables a threefold increase in phonon scattering primarily by enhancing the scattering phase-space. These findings rationalize the microscopic origins of the outstanding thermal properties of AMg₂X₂ compounds and provide fundamental insights into means to control thermal transport properties, which will enable the further design of highly efficient TE materials.

MATERIALS AND METHODS

For a detailed description of methods, see the Supplementary Materials. Neutron experiments were performed on AMg₂X₂ powders using the ARCS time-of-flight neutron spectrometer at the Spallation Neutron Source, Oak Ridge National Laboratory. The samples were sealed in a 1.27-centimeter-diameter thin-walled aluminum can and placed in a high-T closed-cycle refrigerator in an inert atmosphere. IXS measurements were performed on small single crystals mounted on standard copper posts with a beryllium dome and heated with high-T closed-cycle refrigerators in vacuum, using the HERIX beamline at Sector 30 at the Advanced Photon Source, Argonne National Laboratory. Powder samples were grown by solid-state reaction and single crystals were synthesized by the self-flux growth method.

Theoretical calculations were performed with the Vienna ab initio simulation package (VASP 5.4) (47–49), using PBEsol (50–52). SOC was included for Bi compounds. Phonon and thermal conductivity calculations were performed with Phonopy (53), ShengBTE (54), and TDEP (55, 56).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/21/eabg1449/DC1