Significance
Comparative analysis of samples from two biological states, such as two stages of embryonic development, is a pressing problem in single-cell RNA sequencing (scRNA-seq). A key challenge is to detect cell subpopulations whose abundance differs between the two states. To that end, we develop DA-seq, a multiscale strategy to compare two cellular distributions. In contrast to existing unsupervised clustering-based analysis, DA-seq can delineate cell subpopulations with the most significant discrepancy between two states and potentially reveal important changes in cellular processes that are undetectable using conventional methods.
Keywords: single cell, RNA-seq, local differential abundance
Abstract
Comprehensive and accurate comparisons of transcriptomic distributions of cells from samples taken from two different biological states, such as healthy versus diseased individuals, are an emerging challenge in single-cell RNA sequencing (scRNA-seq) analysis. Current methods for detecting differentially abundant (DA) subpopulations between samples rely heavily on initial clustering of all cells in both samples. Often, this clustering step is inadequate since the DA subpopulations may not align with a clear cluster structure, and important differences between the two biological states can be missed. Here, we introduce DA-seq, a targeted approach for identifying DA subpopulations not restricted to clusters. DA-seq is a multiscale method that quantifies a local DA measure for each cell, which is computed from its k nearest neighboring cells across a range of k values. Based on this measure, DA-seq delineates contiguous significant DA subpopulations in the transcriptomic space. We apply DA-seq to several scRNA-seq datasets and highlight its improved ability to detect differences between distinct phenotypes in severe versus mildly ill COVID-19 patients, melanomas subjected to immune checkpoint therapy comparing responders to nonresponders, embryonic development at two time points, and young versus aging brain tissue. DA-seq enabled us to detect differences between these phenotypes. Importantly, we find that DA-seq not only recovers the DA cell types as discovered in the original studies but also reveals additional DA subpopulations that were not described before. Analysis of these subpopulations yields biological insights that would otherwise be undetected using conventional computational approaches.
Profiling biological systems with single-cell RNA sequencing (scRNA-seq) is an invaluable tool, as it enables experimentalists to measure the expression levels of all genes over thousands to millions of individual cells (1, 2). A prevalent challenge in scRNA-seq analysis is comparing the transcriptomic profiles of cells from two biological states (3, 4). The two biological states may correspond to wild-type (WT) and knockout (KO) mice, healthy and diseased samples, two time points in a developmental process, and biological systems before and after treatment/stimulus, etc. Often, such comparison reveals cell subpopulations that are differentially abundant (DA). In DA subpopulations, the ratio between the number of cells from the two biological states differs significantly from the respective ratio in the overall data. In mathematical terms the problem is to find local differences in density between two high-dimensional distributions of points (multiple single cells in the transcriptomic space). Developing methods to accurately capture these differences is important to gain insights from scRNA-seq datasets such as COVID-19 and cancer immunotherapy.
A standard approach to detect DA subpopulations is by clustering the union of cells from both states. This step is typically done in a completely unsupervised manner. For each cluster, the proportion of cells from the two biological states is measured. A cluster in which these proportions significantly differ from the overall proportion in the data is considered differentially abundant. This approach was applied in the analysis of various biological systems, for example, to investigate immune response and mechanisms in patients with various disease severities after viral infection (5, 6), to compare responders and nonresponders to cancer treatment (7), and to study cell remodeling in inflammatory bowel disease (8). A similar cluster-based method is ClusterMap (9), where the clustering step is applied separately to cells from the two states. Subsequently, the datasets are merged by matching similar clusters. Skinnider et al. (10) developed Augur, which employs machine learning to quantify separability of cells from two states within clusters. Comparing biological states through clustering is also related to differential compositional analysis, where biological states are compared via the proportion of predetermined cell types (11). Once DA clusters are identified, marker genes characteristic of each cluster can be determined by differential expression (DE) analysis.
Clustering-based methods might be suboptimal, however, in cases where the subpopulations most responsive to the biological state do not fall into well-defined separate clusters. For example, DA subpopulations may be distributed among several adjacent clusters or, alternatively, encompass only a part of a cluster. Additionally, the clustering approach may fail for continuous processes where no clear cluster structure exists, such as cell cycles or certain developmental programs. For the above scenarios, differential abundance at a cluster level may miss the important molecular mechanisms that differentiate between the states. One approach to partially mitigate these problems is based on topic modeling, where the representation of each biological state is assessed within each topic (12). However, this approach is not designed to directly detect DA subpopulations.
Therefore, a targeted approach for identifying cell subpopulations with significant differential abundance is needed to advance comparative analysis between the cell distributions from both biological states.
An earlier work for identifying DA subpopulations that does not rely on initial clustering was derived by Lun et al. (13) for mass cytometry data. Their algorithm performs multiple local two-sample tests for hyperspheres centered at randomly selected cells. The caveat of this approach is that the selected hyperspheres may only partially overlap with the DA subpopulations or fail to form localized regions. Accurate delineation of a DA subpopulation is essential for identifying the markers that differentiate it from its immediate neighboring cells as well as markers that separate it from the rest of the cells in the dataset.
Here, we develop DA-seq, a multiscale approach for detecting DA subpopulations (https://github.com/KlugerLab/DAseq). In contrast to clustering-based methods, DA-seq detects salient DA subpopulations in a targeted manner. For each cell, we compute a multiscale differential abundance score measure. These scores are based on the nearest neighbors in the transcriptome space across a range of values. The motivation of multiscale analysis is that by employing a single scale, one may miss some of the DA subpopulations if the scale is too large or detect spurious DA subpopulations if the scale is too small. We applied DA-seq to various scRNA-seq datasets from published works as well as simulated datasets. We show that DA-seq successfully recovers findings presented in the original works. More importantly, DA-seq reveals DA cell subpopulations that were not reported before. Characterization of these subpopulations provides insights crucial to understanding the biological processes and mechanisms.
Results
The DA-seq Algorithm.
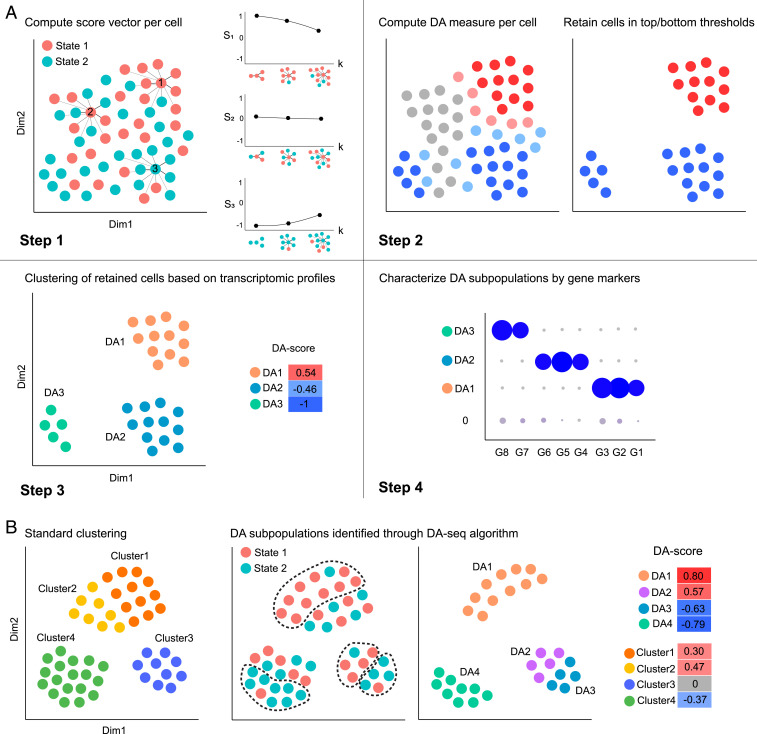
Here, we briefly outline the main four steps of the DA-seq algorithm (Fig. 1A). As a first step, DA-seq computes for each cell a score vector based on the relative prevalence of cells from both biological states in the cell’s neighborhood. Importantly, this measure is computed for neighborhoods of different size, thus providing a multiscale measure of differential abundance for each cell. The multiscale measure is referred to as the score vector of each cell. In the second step, the multiscale measure is merged into a single DA measure as quantity of differential abundance. This step is done by training a multivariate logistic regression classifier to predict for each cell its biological state (state 1 or state 2) given its score vector entries. The associated prediction probability is then transformed to a DA measure of how much a cell’s neighborhood is dominated by cells from one of the biological states. In the third step, DA-seq clusters the cells whose DA measure is above or below a certain threshold into localized regions based on gene expression profiles. The cells in each region represent cell subpopulations with a significant difference in abundance between biological states. Each DA subpopulation is associated with a DA score (SI Appendix, Note 1). It is also accompanied by a P value to assess reproducibility if there are adequate biological replicates in both biological states. In the final step, DA-seq selects genes that distinguish a DA subpopulation from the rest of the cells in the data or cells from its immediate neighborhood. For example, if the DA subpopulation is a subset of CD8 T cells, DA-seq outputs differentially expressed genes between this subset of CD8 T cells and the rest of the cells in the dataset. Additionally, DA-seq has another option to output differentially expressed genes between this subset of CD8 T cells and other CD8 T cells not included in the DA subpopulation. As detailed in Materials and Methods, for this task we employ our recently developed feature selection method based on stochastic gates (STG) (14) which identifies approximately the minimum number of genes that distinguish a DA subpopulation, as well as standard differential expression methods (15). The four steps of DA-seq are illustrated in Fig. 1A. All steps are described in detail in Materials and Methods.
Fig. 1.
Schematic demonstration of DA-seq. (A) Illustration of the DA-seq algorithm. DA-seq detects DA subpopulations by analyzing cells from two biological states. The input of the algorithm is the union of data from two states after initial dimension reduction. Step 1: Computing a multiscale score vector, based on the -nearest neighbors (NN) of each cell, for several values of (e.g., ). Step 2: Training a logistic classifier to predict the biological state of each cell based on the multiscale score to obtain a single DA measure. The algorithm retains only cells for which the DA measure is above a threshold or below and hence may reside in DA subpopulations. Step 3: Clustering the cells retained in step 2 to obtain contiguous DA subpopulations above a predefined size. These subpopulations are denoted , , and . The degree of their differential abundance is quantified by a DA score (SI Appendix, Note 1). Step 4: Detect subsets of genes that characterize each of the DA subpopulations. For example, the genes G7 and G8 characterize . (B) Standard clustering analysis vs. DA-seq. (Left) Cluster information obtained through standard clustering analysis. (Center) DA subpopulations identified through DA-seq. (Right) Normalized differential abundance of DA subpopulations and clusters, represented by DA score.
Conventional DA analysis employs a clustering procedure on cells from both biological states. This step is based on their transcriptomic profiles, but ignores the biological state of each cell. In contrast, DA-seq is a supervised approach that utilizes the biological state of each cell to identify and delineate the cell subpopulations most representative of the differences between the two biological states. Fig. 1B illustrates several cases where DA-seq has an advantage over standard clustering analysis. DA clusters found by clustering analysis often contain DA subpopulations detected by DA-seq where the latter have stronger differential abundance, such as, within and within . Moreover, unsupervised clustering may miss scenarios where its output clusters contain two or more subsets that we refer to as DA subpopulations. Some subpopulations may be enriched with cells from state 1, while others may be enriched with cells from state 2. For example, and have an opposite DA score and are entirely unseen when analyzed as a single cluster, , resulting in valuable biological data being completely lost in traditional clustering analysis pipelines.
We applied DA-seq to publicly available scRNA-seq datasets from diverse biological systems (5, 7, 16, 17). In the following sections, we present the output of steps 2, 3, and 4 of DA-seq for datasets from refs. 5, 7, and 16. We then compare the results to the findings in the original works and validate our findings. Importantly, we show that DA-seq provides invaluable biological insights through the characterization of DA subpopulations that are not revealed by standard clustering-based approaches. Additional results on a dataset from Ximerakis et al. (17) and simulated datasets can be found in SI Appendix.
Abundance of Immune Cell Subsets in Responsive vs. Nonresponsive Melanoma Patients.
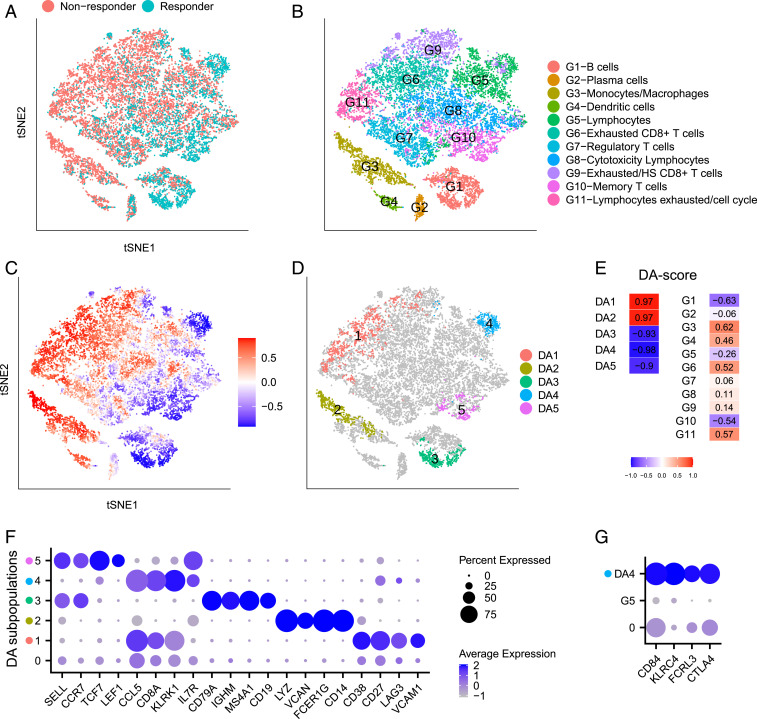
One of the goals of the Sade-Feldman et al. (7) study was to identify factors related to the success or failure of immune checkpoint therapy. To that end, 16,291 immune cells from 48 samples of melanoma patients treated with checkpoint inhibitors were profiled and analyzed. The tumor samples were classified as responders or nonresponders based on radiologic assessments. The cells originating from responding tumors and nonresponding tumors are labeled in the t-distributed stochastic neighbor embedding (t-SNE) plot of Fig. 2A. Comparisons between responders and nonresponders yielded important biological insights.
Fig. 2.
Immune cells from responding and nonresponding melanoma patients treated with checkpoint therapy. (A–D) t-SNE embedding of 16,291 cells from ref. 7. (A) Cells colored by status of response to immune therapy. (B) Cells colored by cluster labels from ref. 7. (C) Cells colored by DA measure. Large (small) values indicate a high abundance of cells from the pool of nonresponder (responder) samples. (D) Five distinct DA subpopulations obtained by clustering cells with DA measure> 0.8. (E) DA score of DA subpopulations and predefined clusters. (F) Dot plot for markers characterizing the five selected DA subpopulations. The color intensity of each dot corresponds to the average gene expression across all cells in the DA subpopulation excluding the cells with zero expression values. The lowest row in the plot corresponds to the non-DA cells (cells not included in any DA subpopulations). (G) Dot plot for markers that distinguish and the complementary cells within .
Sade-Feldman et al. (7) clustered the 16,291 immune cells into 11 distinct clusters (Fig. 2B). Subsequently, they computed the percentage of cells in each of the predefined clusters from responder and nonresponder samples and compared the relative abundance between these two groups. Two clusters () were enriched in cells from the responder samples, and four clusters () were enriched in cells from nonresponder samples. Finally, they composed a list of genes with high expression within the six differentially abundant clusters.
Fig. 2C shows the intensity of the DA measure of each cell as computed in step 2 of the algorithm, where higher values indicate an abundance of cells from nonresponder samples relative to responder samples. Five DA cell subpopulations denoted to (Fig. 2 D and E and SI Appendix, Fig. S1A) were identified. In contrast to the method applied in ref. 7, the DA subpopulations obtained by our approach are not constrained to any predefined clusters. Thus, there are some important differences between our findings and those of ref. 7 in addition to the following partial similarities. Five of the six DA clusters described in ref. 7 have partial overlaps with our DA subpopulations:
In ref. 7, the clusters and are reported as two distinct DA clusters. In contrast, our DA cell subpopulation overlaps with both and , as well as another cluster . We argue that identification of and as two separate DA clusters and the exclusion of as potentially relevant for DA are artificial. Unifying the clusters of exhausted lymphocytes allows us to detect and transcriptionally characterize cell subpopulations within this union that are more specific to differences between responders and nonresponders. We observe that DA subpopulations , and partially overlap with , and , respectively, but they are not identical; furthermore, subpopulation partially overlaps with cluster which was not identified as a DA cluster.
The cluster (dendritic cells), which was reported in ref. 7 as a DA cluster, was not detected by DA-seq as a DA subpopulation. We note, however, that this subpopulation is detected with a slight relaxation of the upper threshold in step 2 (SI Appendix, Fig. S2A).
Finally, we identified markers that characterize the DA subpopulations by both the standard differential expression approach implemented in Seurat (15, 18) and our feature selection approach via STG (Materials and Methods). A subset of the identified markers is shown in Fig. 2F. For the subpopulations to , DA-seq detected similar lists of characteristic markers to their corresponding clusters in Fig. 2B.
Interestingly, the characteristic markers LAG3 and CD27 for subpopulation define an exhausted lymphocyte population (19, 20) covering three clusters associated with lymphocyte exhaustion. Notably, VCAM1 was the most significant gene in (SI Appendix, Fig. S2B), which covers parts of clusters , and . Although VCAM1 was reported in ref. 7, it was not among the salient markers of their analysis. Analyzing these clusters separately diminished the significance of VCAM1 relative to other genes. VCAM1 expression on a class of cells discovered by the DA approach is intriguing, as it is a critically important cell adhesion and costimulatory ligand in the immune system (21). In addition, VCAM1 has been implicated as having an important role in immune escape as has been studied in refs. 22–26.
To distinguish subpopulation and its immediate neighborhood, we performed differential expression analysis comparing and cells in cluster that are not within . This uncovered the distinct transcriptional profile of (Fig. 2G). Intriguingly, the gene is highly expressed in , which is enriched in posttreatment responders (SI Appendix, Fig. S2C). Incidentally, this gene was reported as a marker for nonresponders in other cell types from ref. 7. Clustering-based DA analysis failed to detect this DA subpopulation and thus missed this important insight.
Compared with standard differential expression approaches that simply output individual genes in a univariate manner, STG provides a prediction score (Materials and Methods) as a linear combination of its selected genes that best separate each DA subpopulation from the rest of the cells. The improved discrimination by STG compared to a univariate approach is demonstrated in SI Appendix, Fig. S2 D and E for DA subpopulations and .
To assess the stability of DA-seq results, the following cross-validation procedure was performed. We split the data randomly into two sets and , each with half nonresponder and half responder samples, such that all cells of each individual sample are either in or in . To compare the two sets, the same t-SNE embedding as in Fig. 2 is used to show the response status (SI Appendix, Fig. S3 A and E) and cluster label (SI Appendix, Fig. S3 B and F) for each cell. Next, we applied DA-seq separately to each set. The DA measure for both sets is shown in SI Appendix, Fig. S3 C and G. Seven DA subpopulations denoted as to and to were detected from and , respectively (SI Appendix, Fig. S3 D and H). The characteristic genes of DA subpopulations in and are shown in SI Appendix, Fig. S3 I and J. We observe that most of the DA subpopulations detected in share common characteristic genes with their counterparts in , as well as in the full dataset. The exact match between DA subpopulations in , and the full dataset is shown in SI Appendix, Fig. S3K. We note that subpopulations , , and do not overlap with subpopulations from the other split or the full dataset when we apply the same threshold parameters. However, with relaxed on the full dataset, (SI Appendix, Fig. S3D) overlaps with in SI Appendix, Fig. S2A. The subpopulations and (SI Appendix, Fig. S3H) are enriched by cells from single patients. Further, subpopulation in the full dataset overlaps with in , but does not overlap with any subpopulations in . This may indicate that this DA subpopulation exists only in a subset of patients, as reflected by the values computed for each subpopulation (SI Appendix, Fig. S1A).
Differentiation Patterns of Early Mouse Dermal Cells.
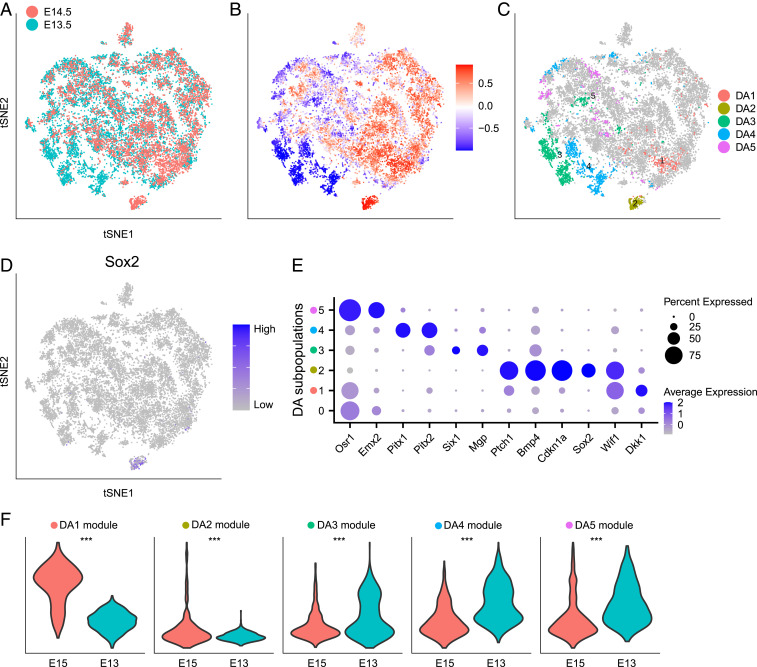
We applied DA-seq to scRNA-seq data from a study on developing embryonic mouse skin (16). Cells from dorsolateral skin were sequenced for two time points of embryonic development (days E13.5 and E14.5), each with two biological replicates (Fig. 3A). Dermal cells were selected for analysis by using the marker Col1a1 to study hair follicle dermal condensate (DC) differentiation.
Fig. 3.
Comparing embryonic mouse dermal cells in embryonic days E13.5 and E14.5. (A–E) Data from Gupta et al. (16). (A–D) t-SNE embedding of 15,325 cells. (A) Embryonic day of each cell. (B) Cells colored by DA measure. Large (small) values indicate a high abundance of cells from E14.5 (E13.5). (C) Distinct DA subpopulations obtained by clustering cells with DA measure> 0.8. (D) Normalized Sox2 gene expression. (E) Dot plot of several markers that characterize DA subpopulations. Details are as in Fig. 2F. (F) Validation on data from Fan et al. (27). Violin plots compare gene module scores between E15 and E13 samples in dermal cells of data from ref. 27. Gene modules are defined from DA subpopulations in C. Wilcoxon test is used to calculate P values. ***P < 0.001.
Gupta et al. (16) studied the transcriptional states of the cells by embedding them via diffusion map coordinates to capture the manifold structure of the scRNA-seq data. They then used the early DC marker Sox2 to identify differentiated DC cells as well as the diffusion map dimension that corresponds to DC cell differentiation, which they called the DC-specific trajectory. By observing this trajectory, they found that although it contained cells from both E13.5 and E14.5, there were notably more E14.5 cells at the terminus representing differentiated DC cells.
In ref. 16, the authors had prior knowledge that differentiated DC cells express Sox2. In contrast, DA-seq does not require prior knowledge. We obtained an unbiased comparison of dermal cells (Fig. 3A) between E13.5 and E14.5, which resulted in five DA subpopulations (Fig. 3 B and C), revealing the differentiated DC cell population discussed in ref. 16. Due to lack of replicated samples in this dataset (two replicates for both E13.5 and E14.5), we did not compute a value. Instead, we computed the DA score for these DA subpopulations for every possible pairwise comparison of these samples and observed reproducible results for all DA subpopulations (SI Appendix, Fig. S1B).
Among the identified DA subpopulations, and are more abundant in E14.5. Subpopulation corresponds to the Sox2+ differentiated DC cells (Fig. 3D). Markers of (Fig. 3E) include other genes (Cdkn1a, Bmp4, Ptch1) known to be expressed in differentiated DC cells. Subpopulation , characterized by the gene Dkk1, corresponds to a subpopulation that spatially surrounds the DC population. Although this subpopulation was acknowledged briefly in ref. 16, the localization of in our analysis provides a method to interrogate the molecular mechanisms that regulate DC maturation and hair follicle development. Other characteristic markers of provide insights on more detailed biological functions of this peri-DC subpopulation. DA subpopulations , and are more abundant in E13.5. Marker genes of these subpopulations (Fig. 3E) are associated with various developmental processes, potentially representing cell development or relocalization during early embryonic days.
To validate findings obtained by analyzing the data with DA-seq, we examined scRNA-seq data from another closely related study (27). In ref. 27, single cells isolated from the dorsal skin at embryonic days E13 and E15 were profiled. We defined gene signatures (Materials and Methods) that are enriched in each of the five DA subpopulations detected in the data from Gupta et al. (16) shown in Fig. 3C. Gene module scores (Materials and Methods) for these signatures are computed and compared between E13 and E15 in dermal cells from Fan et al. (27). The differences between the module score distributions of E15 versus E13 (Fig. 3F) are consistent with the enrichment of these signatures within the DA subpopulations in Fig. 3C.
Patients with Severe and Moderate COVID-19 Have Distinct Immunological Profiles.
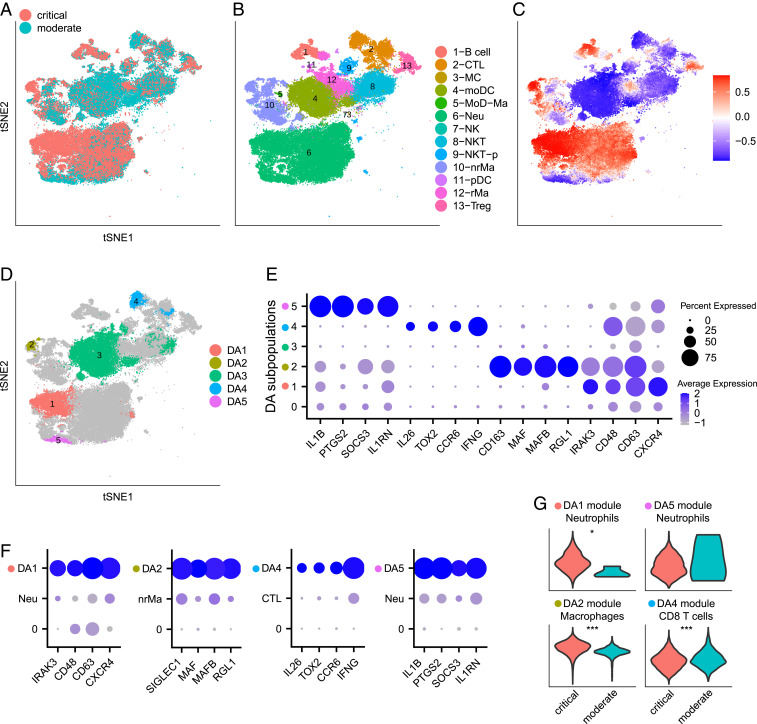
COVID-19 is a current global pandemic of a novel virus. It is crucial to understand the immunological mechanisms related to disease severity. In ref. 5, Chua et al. applied scRNA-seq on nasopharyngeal (nasopharyngeal or pooled nasopharyngeal/pharyngeal swabs [NSs]) samples from 19 patients that were clinically well characterized, with moderate or critical disease, as well as 5 healthy controls. They identified 9 epithelial and 13 immune cell types and performed comprehensive comparisons between patients with critical and moderate COVID-19 and healthy controls. In differential abundance analysis of the cellular landscape, they observed depletion in basal cells and enrichment in neutrophils in critical cases compared with both healthy controls and moderate cases. Additionally, they applied differential expression analysis comparing cells from patients with different disease severity for each cell type and identified transcriptional profiles characterizing patients with critical or moderate disease in these cell types. Specifically, they observed higher expression of some inflammatory mediators in nonresident macrophages (nrMa) and lower levels of some typical antiviral markers in cytotoxic T cells (CTL) in severe cases compared to moderate cases.
As the results derived in ref. 5 are based on initial clustering into cell types, variable behavior within cell types could be overlooked. To better interpret the differences in immunological responses between patients with critical and moderate disease, we focused on immune cells from samples from these patients (Fig. 4 A and B) and applied DA-seq. Five DA cell subpopulations were identified: and are more abundant in critical cases; , , and are more abundant in moderate cases (Fig. 4 C and D and SI Appendix, Fig. S1C). Subpopulation largely overlaps the monocyte-derived dendritic cell (moDC) cluster. The depletion of moDC in critical cases was also reported in ref. 5. Other DA subpopulations are subclusters within the 13 well-separated immune cell types, which have been overlooked in the original clustering-based analysis. To identify the distinct transcriptional profile of these subpopulations, we compared each DA subpopulation to its immediate neighborhood, i.e., complementary cells to the DA subpopulation within the corresponding cluster of known immune cell type. Characterization of these DA subpopulations by gene markers (Fig. 4E) provides important insights on mechanisms associated with COVID-19 disease severity. These DA subpopulations show distinct profiles that separate them from the complementary cells within their corresponding clusters (Fig. 4F), which clustering-based analysis performed in ref. 5 failed to report.
Fig. 4.
Comparing immune cells from patients with severe and moderate COVID-19. (A–F) Data from Chua et al. (5). (A–D) t-SNE embedding of 80,109 cells. (A) Cells colored by disease severity of COVID-19, critical or moderate. (B) Cells colored by cluster labels from ref. 5. CTL, cytotoxic T cell; MC, mast cell; moDC, monocyte-derived dendritic cell; MoD-Ma, monocyte-derived macrophage; Neu, neutrophil; NK, natural killer cell; NKT, natural killer T cell; NKT-p, proliferating NKT cell; nrMa, nonresident macrophage; pDC, plasmacytoid dendritic cell; rMa, resident macrophage; Treg, regulatory T cell. (C) Cells colored by DA measure. Large (small) values indicate a high abundance of cells from the pool of critical (moderate) cases. (D) Five distinct DA subpopulations obtained by clustering cells with DA measure> 0.8. (E) Dot plot for markers characterizing the selected DA subpopulations. Details are as in Fig. 2F. (F) Dot plots for markers of DA subpopulations, comparing each DA subpopulation to the complementary part in the corresponding cluster. (G) Validation on data from Liao et al. (6). Violin plots compare gene module scores between critical and moderate cases in matching cell types of data from ref. 6. Specifically, module scores of DA1, DA2, DA4, and DA5 are compared in neutrophils, macrophages, CD8 T cells, and neutrophils from Liao et al. (6), respectively. Of note, of the 7,101 immune cells analyzed for the moderate cases, only 4 were neutrophils. Gene modules are defined from DA subpopulations in D. Wilcoxon test is used to calculate P values. *P < 0.05, ***P < 0.001.
Both cell subpopulations and are within the neutrophil cluster. However, they represent two distinct subsets of neutrophils (Fig. 4 E and F and SI Appendix, Fig. S4 A and B). Subpopulation is more abundant in critical cases and shows elevated expression of activation markers CD48, CD63 (28, 29). Further, expression of another marker CXCR4 has been reported to be associated with acute respiratory distress syndrome (ARDS) (30) and allergic airway inflammation (31). On the contrary, subpopulation is more abundant in moderate cases and is characterized by the expression of the inhibitory and anti-inflammatory gene IL1RN (32), as well as SOCS3, an important regulator in restraining inflammation with previously characterized functions in regulating cytokine signaling and the subsequent response (33–35). Another marker enriched in is PTGS2 (COX2) which has a controversial role and can both promote and constrain inflammation. Enrichment of PTGS2 expressing neutrophils in moderate patients may suggest its inhibitory role in COVID-19. This provides invaluable insights on the use of nonsteroidal anti-inflammatory drugs (NSAIDs), which is under debate (36). We note that, while abundances of neutrophils might be affected due to sensitivity to isolation techniques, our differential abundance analysis of neutrophils could still reflect real biological processes.
Subpopulation is a subset of nrMa and is more abundant in critical cases. Markers of include RGL1, MAFB, and SIGLEC1 (Fig. 4 E and F and SI Appendix, Fig. S4C). RGL1 and MAFB are associated with M2 state or alternatively activated macrophages (37, 38). Interestingly, MAFB and SIGLEC1 have also been reported as maturation markers of alveolar macrophages (39) and may have implications in mediation of pathology by tissue resident macrophages in COVID-19 lung pathology (6).
Subpopulation is a subset of CTLs and is more abundant in moderate cases. This subpopulation is characterized by high expression of IFNG (Fig. 4 E and F and SI Appendix, Fig. S4D). This observation is consistent with the descriptions in ref. 5, where CTLs expressing antiviral markers were found in patients with moderate COVID-19.
Immunological profiles identified through DA-seq as discussed above should be predictive if they reflect real biological mechanisms in COVID-19 patients. To inspect whether these differential abundance trends are shared in another cohort of COVID-19 patients, we examined a second COVID-19 dataset from ref. 6. In ref. 6, bronchoalveolar lavage fluid immune cells from COVID-19 patients with different disease severity were sequenced and characterized. To facilitate the analysis, we defined gene signatures (Materials and Methods) that are enriched in our detected DA subpopulations , and shown in Fig. 4D. Gene module scores (Materials and Methods) for these gene signatures were computed and compared between COVID-19 patients with moderate and critical disease in matching cell types from the second COVID-19 dataset (6). The differences between the module score distributions of the critical versus moderate cases (Fig. 4G) are consistent with the enrichment of these signatures within the DA subpopulations in Fig. 4D.
Additional Datasets.
In Ximerakis et al. (17), transcriptomes of brain cells from young and old mice are profiled (SI Appendix, Fig. S5 A and B and Note 2). We applied DA-seq and detected cell subpopulations more abundant in brains from young mice with respect to old mice and vice versa (SI Appendix, Fig. S5 C and D). To demonstrate the specificity of DA-seq, we compared cell distributions between samples extracted from different young mice (SI Appendix, Fig. S5E). We verify that DA-seq did not detect any sizable DA subpopulations, as expected (SI Appendix, Fig. S5 F and G).
In addition, we applied DA-seq to two simulated datasets, in which we formed several artificial DA subpopulations (SI Appendix, Note 3). The first simulated dataset is based on the scRNA-seq data from ref. 7, in which we assessed the ability of DA-seq and Cydar (13) to determine for each cell whether it belongs to any of the artificial DA subpopulations or not (SI Appendix, Fig. S6). We observe that DA-seq captures the simulated DA subpopulations with area under the curve (AUC) of 0.97, while Cydar has a maximum AUC of 0.81 using different hyperparameters. The second simulated dataset is a perturbed Gaussian mixture model in which DA-seq successfully retrieved the artificial DA subpopulations and the characteristic features as can be verified by visual inspection (SI Appendix, Fig. S7).
Discussion
In this work we present DA-seq, a multiscale approach for detecting subpopulations of cells that have differential abundance (DA) between scRNA-seq datasets from two biological states. This approach enables us to robustly delineate regions with substantial differential abundance between these two samples. In contrast to existing methods, the subpopulations of cells we discover are not confined to any predefined clusters or cell subtypes. We applied DA-seq to several scRNA-seq datasets and compared its output to results obtained through conventional methods. DA-seq not only recovered results obtained by standard approaches but also revealed striking unreported DA subpopulations, which informs on cellular function, identifies known and additional genes in DA subpopulations, and greatly increases the resolution of cell type identity in different clinical states of disease.
Due to high dimensionality of the genetic data, it is important to avoid overfitting in statistical learning. In various steps of our algorithm, we prevent overfitting via dimensionality reduction, model regularization, and cross-validation. However, the current approach relies on large sample size and model validation to justify the results, but overfitting could remain a concern at regions where data density is low. Further developments of model regularization will benefit the method, and analysis of generalization error will be theoretically interesting.
Another potential improvement to DA-seq can be achieved by applying a neural network classifier directly on the input features (gene expression profiles or principal component analysis [PCA] coordinates) without computing the score vector in step 1. A network architecture for classification of two classes often contains a logistic regression as its last layer. The layers preceding the last layer can then be viewed as feature extractors trained in a supervised way. These features may substitute our hand-crafted, multiscale score-vector features. We conducted preliminary experiments using the full-neural-network approach. The results were comparable to those of DA-seq for the simulated datasets but inferior for the real-world datasets. We conjecture that, for our DA problem, the hand-crafted features allow for a better identification of DA cells because these cells are concentrated in two regions in the score-vector space. On the other hand, the landscape of DA cells in the original gene or PCA space is much more complex. However, it is possible that more sophisticated neural network approaches may outperform DA-seq—especially when a larger number of cell measurements is available.
In step 4 of DA-seq, we characterize each DA subpopulation by markers that differentiate it from the remaining cells by either our neural network embedded-feature selection (-based regularization) method or standard differential expression approaches. However, the genes we identified for each DA subpopulation are not inferred by a causal inference technique. Thus, augmenting step 4 by a causal inference module (40) may reveal potential causal relationships within pathways and other mechanisms. Other aspects of this characterization can be examined by biclustering (41) or biorganization (42) techniques that allow for exploration of biological mechanisms associated with the DA subpopulations.
Proper cell preparations as well as preprocessing of scRNA-seq data are required to obtain reasonable DA results. It is important to recognize that batch effect removal is a typical preprocessing step for DA-seq in cases where there are noticeable batch effects between samples. Without proper calibration, the DA subpopulations detected by DA-seq may reflect both biological and technical differences between samples. To address this open problem in the context of scRNA-seq, multiple-batch effect removal methods have been developed (15, 18, 43, 44). Furthermore, imputation or denoising for scRNA-seq datasets may also improve downstream analysis and lead to a more accurate differential abundance assessment, as cells are positioned more accurately after imputation (45–48).
In addition to the comparison between two states discussed above, potential applications of DA-seq could be extended to studies comparing multiple biological states, such as time series studies or subjecting a biological system to multiple perturbations. DA-seq can be applied to such multistate comparisons by considering all pairwise differences in abundance. Alternatively, one can propose a multistate score vector and replace the binary logistic regression classifier with a multiclass classifier, such as the softmax classifier.
Practitioners often try to detect intracluster differentially expressed genes between two states separately for each cluster (7, 17, 18). If such intracluster differentially expressed genes exist, it means that the distributions of cells from these two states are shifted with respect to each other and, hence, represent two adjacent DA subpopulations: one enriched by cells from the first state and the other enriched by cells from the latter one. One example is in the comparison between old and young mice shown in SI Appendix, Fig. S5. Cluster 21-MG (SI Appendix, Fig. S5B) consists of two DA subpopulations, one enriched with cells from old mouse brains and the other one enriched with cells from young mouse brains. In this case, differentially expressed genes from intracluster analysis will be similar to genes that characterize the DA subpopulations with respect to its immediate neighborhood. However, the intracluster analysis neither informs us about differential abundance between the states nor is applicable to data with no cluster-like structure.
In many biological systems, cell populations could be heterogeneous in terms of the expression status of certain markers. For instance, breast cancer cells from an estrogen receptor (ER)-positive patient do not express ER in all her cancer cells. This status can be measured at the transcriptional or translational level. An application of DA-seq to data generated in a single scRNA-seq experiment to compare her ER(+) or ER(−) cancer cells will enable identification of subpopulations of cancer cells enriched by ER(+) or ER(−) cells and, thus, allow exploration of the biological differences between these two populations (beyond their difference in ER status). Essentially, this approach allows us to use cells generated in a single scRNA-seq experiment and compare cells conditioned on the expression status of a single marker.
Taken together, DA-seq represents a major advance in the comparative analysis of two distinct biological states. DA-seq has the ability to uncover important, significant, and hypothesis-driving data which would normally be completely lost within a cloud of transcriptomic data restrained by strict and arbitrary clustering definitions. We envisage that DA-seq will be easily integrated into conventional scRNA-seq analysis pipelines and will facilitate major findings in all areas of biological investigation.
Materials and Methods
Overview.
Let , where is the number of cells, and is the -dimensional profile of cell . In scRNA-seq, the number of genes is , while the number of cells ranges between . The high dimensionality of the gene space is reduced to (in our experiments, ranges between 10 and 90) via standard techniques such as PCA. Every cell is assigned a binary label that represents the biological state of the sample from which the cell was extracted. In other words, the label of each cell indicates its membership in one of the two experimental samples (e.g., healthy and diseased samples) and it does not represent specific cell types. We assume that the data are generated according to the following probabilistic model: First, each label is sampled according to a Bernoulli distribution with parameter , . Next, conditioned on , the gene expression profile is sampled according to two regular probability density functions defined over , such that
The objective of DA-seq is to identify regions in where is significantly larger than and vice versa, by analyzing the set of samples .
One approach to find DA regions is based on local two-sample tests (49–52). A global two-sample test determines whether two sets of samples were generated by the same distribution. In contrast, local sample tests also detect the locations of any discrepancies between them. Such methods often compute a test statistic in local neighborhoods around selected cells. The statistics therein are associated with the difference and provide a local value for each . In refs. 13 and 50, the Benjamini–Hochberg procedure (53) was applied to correct for multiple testing.
Different approaches for obtaining DA regions were derived by Landa et al. (52) and Cazáis and Lhéritier (51), where a measure of local discrepancy is computed for all of the points in the dataset instead of a random subset. In ref. 52, the local measure of discrepancy is computed around each cell using a random walk. In ref. 51, the points with the highest measure of discrepancy are then aggregated into localized clusters in the feature space. Thus, the output of this approach is a small number of DA regions, rather than a list of cells.
In our work, we derive DA-seq, a multiscale approach for detecting DA regions in scRNA-seq datasets comprising distinct biological states. DA-seq is based on a multiscale measure of differential abundance computed for each cell. This measure enables us to robustly and efficiently detect localized differentially abundant cell populations of different sizes and scales in the gene space.
To derive a measure of discrepancy between two states, we introduce the normalized and bounded pointwise statistic
| [1] |
The statistic ranges between −1 and 1. For regions where , approaches , while for regions where , approaches 1. Applying Bayes’ rule to and , we rewrite Eq. 1 as
| [2] |
where are the posterior probabilities around a point . This representation allows us to estimate the statistic in the neighborhood of each cell in terms of estimates of these posterior probabilities and the Bernoulli parameter . For each cell, the posterior probabilities are estimated based on its nearest-neighbor cells at multiple scales (spanning a range of values). DA-seq detects localized subpopulations of cells for which the estimated local normalized differential abundances between two states are statistically significant. It further screens in an exploratory fashion of DA discrepancies whose magnitudes (effect size) are greater than user-specified thresholds.
In the following subsections, we describe the steps of our approach in detail.
Step 1: Computing a Multiscale Score Vector.
In the first step of DA-seq, we compute a multiscale score vector at each point based on its nearest neighbors (NN), which reflects differential abundance between and and is motivated by Eq. 1. We use the standard Euclidean distance in to compute cell measurement dissimilarities and identify NN for each cell. Let and be the number of cells from states 1 and 0 among the NN of , respectively. The expression is a crude estimate of the posterior , assuming that is properly scaled with respect to and that . We then estimate the two terms in the numerator (or denominator) of Eq. 2 by
| [3] |
where denotes the total number of cells from state 1, and is an estimate of . Inserting these estimates into Eq. 2 yields our NN-based score, for each cell at length scale ,
| [4] |
The score in Eq. 4 depends on the number of neighbors . An estimator based on a single global value for , however, may be appropriate only for certain regions in the data while being completely suboptimal in other regions. We therefore compute and with a vector at different nearest-neighborhood scales and define the score vector
| [5] |
Fig. 1 A, Step 1 illustrates the qualitative behavior of the score vector for three cells located in different regions of the data. The vector at the top contains positive entries and corresponds to a cell in a DA region where . Thus, the score is high for small values of . As increases, the score typically decreases since at this scale the neighbors may contain a more balanced proportion of cells from the two biological states and even include neighbors positioned outside of the DA region.
While the NN score provides an estimate of the DA measure at each , the estimation is not efficient due to the following reasons: 1) The finite-sample effect may substantially degrade the accuracy of such an estimator, and regularization of the estimator is needed to reduce variance error; 2) using multiple values of as proposed in Eq. 5 potentially resolves the difficulty of choosing optimal which is usually unknown; however, then it is unclear how to merge the ensemble of measurements within the NN framework. We overcome these challenges by a classification approach presented in step 2.
Step 2: Computing a DA Measure for Each Cell.
The output of step 1 consists of multiscale score vectors. Cells in DA subpopulations whose neighborhoods are enriched with cells from one biological state tend to be closer to each other in the -dimensional score space than cells whose neighborhoods are enriched with the other biological state or not enriched by any of the states.
Our task in step 2 is to map the -dimensional score vector , defined in Eq. 4, into a single DA measure for each cell. To that end, we use a logistic regression classifier. The classifier is trained to predict the class label of each cell given its -dimensional score vector . Specifically, we compute a vector that minimizes the following loss,
| [6] |
where is the sigmoid function and is the regularization term. The classifier is trained to increase if and decrease its value if and thus assigns a numerical value between 0 and 1, which estimates the posterior , as
We employ a regularized logistic classifier with ridge penalty by default. The importance of the regularization term is to induce smoothness of the logistic output, such that the cells chosen as DA are localized. In comparison, applying the logistic classifier without regularization produces results with more outliers.
The data are split into folds. For each fold, the model is trained on the remainder folds. The model is then applied to the (fold) test set and provides predicted probabilities. The penalty parameter for each model is selected by cross-validation. These steps are repeated in several runs and the average predicted probability is used for each cell. Notably, the properties of the logistic classifier imply that a high value of is a strong indication that the cell is located in a (score-vector space) region enriched with positive labels, and vice versa.
The logistic regression output estimates the posterior . Substitution of the posteriors in Eq. 2 with these estimated values gives an estimator of :
| [7] |
which we refer to as the DA measure.
Fig. 1 A, Step 2 illustrates the output of this step. It shows a heatmap, where each cell is colored by the prediction probability of the logistic classifier after transformation, i.e., its DA measure. The cells that reside in DA regions are determined by thresholding the DA measure from above or below and , respectively. A cell belongs to a positive DA region if and to a negative DA region if (see Choice of thresholds below).
Step 3: Clustering the DA Cells into Localized Regions.
This step involves clustering the subset of cells (DA cells) whose DA measure values are above or below into localized regions. These DA regions represent cell subpopulations with difference in abundances between biological states. Importantly, the clustering is performed in the original dimensionality reduced gene space.
We first calculate a shared nearest neighbor (SSN) graph based on the Euclidean distance between all cells. This computation is done with Seurat (15, 18), using default parameters. Next, a subgraph comprising DA cells only is extracted from the full SNN graph. A modularity optimization-based clustering algorithm implemented in Seurat is applied on this subgraph. For robustness, singletons and small clusters (containing number of cells fewer than a user-defined parameter) are removed as outliers.
A graph-based clustering approach is used here because of its widespread use in scRNA-seq analysis. We note, however, that other clustering methods can be used for this step. The output of this step is a list of DA subpopulations where each subpopulation is assigned a subset of cells. In our next section, we describe a feature selection approach to identify characteristic genes for each DA subpopulation.
Step 4: Differential Expression Analysis as a Feature Selection Problem.
Differential expression analysis (DEA) and feature selection are related tasks. In DEA, one applies univariate statistical tests to discover biological markers that are typical of a certain state or disease. This approach is typically used for its simplicity and interpretability. Univariate approaches treat each gene individually; however, they ignore multivariate correlations. Feature selection, on the other hand, seeks an interpretable, simplified, and often superior classification model that uses a small number of genes. Here, we use our recently proposed embedded-feature selection (14) method to discover for each DA subpopulation a subset of genes that collectively have a profile characteristic for that subpopulation which thus separates it from the rest of the data.
Given observations , the problem of feature selection could be formulated as an empirical risk minimization
| [8] |
where is the number of selected features, is the loss function, and are the parameters of a linear model or more complex neural net model. Due to the constraint, the problem above is intractable. In practice, the norm is typically replaced with the norm, which yields a convex optimization problem as implemented in the popular least absolute shrinkage and selection operator (LASSO) optimization approach (54). Nonetheless, we recently surmounted this obstacle by introducing a STG approach to neural networks, which provides a nonconvex relaxation of the optimization in Eq. 8. Each STG is a relaxed Bernoulli variable , where , and is the number of genes after an initial screening to remove genes with low expression. The risk minimization in Eq. 8 could be reformulated by gating the variables in and minimizing the number of expected active gates. This yields the following objective:
| [9] |
Objective Eq. 9 could be solved via gradient descent over the parameters of the model and the gates . To identify characteristic genes of a DA subpopulation, we train a model that minimizes Eq. 9 by sampling multiple balanced batches from the DA subpopulation vs. the backgrounds. Then we explore the distribution of genes that were selected by the model: all s such that . Note that is a regularization parameter that controls the number of selected genes; it could be tuned manually for extracting a certain number of genes or, alternatively, using a validation set by finding which maximizes the generalization accuracy.
An important consideration for tuning is the potential colinearity between features. Embedded feature selection methods, such as LASSO or STG, can capture all correlated features if the regularization parameter is appropriately tuned (14, 55). In ref. 55, the authors study how correlated variables influence the prediction of LASSO. The authors recommend to decrease the regularization parameter if the correlation between variables is high. A similar behavior was observed for the -based STG (14).
In this study, STG is used for binary classification (DA subpopulation vs. background cells). We use a standard cross-entropy loss in Eq. 9 defined by
where the predictions and represent the predicted probabilities that the th cell belongs to the DA subpopulation and background, respectively. To obtain a probabilistic interpretation for , we use the common sigmoid function
which is in the range of . Using the sigmoid, the predicted DA probability is computed as . Furthermore, the predicted background probability is computed by , where and are coefficients for predicting DA and background cells, respectively. We then define the STG score for the experimental section by applying a sigmoid to the difference between the linear predictions of DA and background; that is, . Training of STG is performed using gradient decent with a learning rate of 0.1 using 3,000 epochs. These values were observed to perform well across all our experiments.
Practical Considerations.
In this section we elaborate on choice of parameters and computational properties of DA-seq. Additional information is provided in SI Appendix, Table S1, in which we list the parameters used in all datasets presented in the article.
Multiscale range.
The choice of range in the vectors should be guided by the data at hand; typically, the lower limit is the smallest number of cells that a user will consider a meaningful region. The upper limit can be adjusted to the minimal value for which the score, for most cells, converges to the same value. In our experiments, is typically about 10. We explored the use of different vectors in the simulated data described in SI Appendix, Note 3 and SI Appendix, Figs. S6 and S9A show the DA measure for each cell computed in step 2, with different vectors. These results indicate that DA-seq is more sensitive to the value of (lower limit of the vector) than the upper limit , where increasing leads to a smoother DA measure.
Choice of thresholds.
We apply a permutation test to determine which of the DA measures computed for each cell in step 2 is statistically significant. To obtain the null distribution, we apply the first two steps of DA-seq on randomly permuted cell labels (biological state of each cell). The maximum and minimum values of the DA measure of the data with the scrambled labels, denoted and , are set as the upper and lower thresholds. Thus, only cells whose DA measures are greater than or smaller than are retained. For example, in the simulated data described in SI Appendix, Note 3 and Fig. S6, we show that using successfully recovers cells from our artificial DA sites (true positive DA cells) and introduces only very few false positive cells (SI Appendix, Fig. S9B). Another illustration of the permutation test is shown in SI Appendix, Fig. S5 for the aging brain dataset. For some datasets, applying the permutation test results in a substantial fraction of cells with significant DA measures. This may arise due to large biological deviations between states, inability to remove all batch effects, or a combination of both. For instance, in the melanoma dataset (7), we detect roughly 70% of cells with a significant DA measure (SI Appendix, Fig. S9C). DA-seq not only is designed to detect cells in neighborhoods with significant differential abundance but also is an exploratory tool. It allows users to adjust threshold parameters for retaining cells whose DA measures both are significant and exceed a desired magnitude of the normalized differential abundance . This exploratory option allows the users to focus on the most salient cell subpopulations for which the -statistic effect size is strong ( or ). This option is analogous to the choice of a desired differential expression fold ratio in differential expression analysis tools.
Imbalanced samples.
In many experiments that compare the cell distributions of two states there exists an imbalance between the total number of cells in the corresponding samples; i.e., is nonnegligible. DA-seq is based on the normalized statistics defined in Eq. 1, which is independent of and thus invariant to the possible imbalance between the two samples. Further, ranges between and 1, which helps users to interpret the results and naturally set symmetrical thresholds (with a symmetry axis at 0) for detecting cell neighborhoods whose differential abundance magnitudes (effect size) are larger than the absolute values of these thresholds. Refs. 49 and 52 considered the normalized statistics , whose denominator is equal to the marginal density at . We note that this latter form of normalized statistics is noninvariant to imbalances.
Initial dimension reduction and choice of metric.
Due to the high dropout rate in scRNA-seq, reduction to lower dimensionality is needed before step 1. For PCA, the number of retained principal components is typically determined by methods such as JackStraw and parallel analysis (1, 56, 57). Other dimension reduction methods or metrics other than the standard Euclidean distance may be adopted here. For the choice of metric, we also explored the use of diffusion distance (58) in the PCA feature space when calculating the NN estimator in the first simulation data (described in SI Appendix, Note 3 and Fig. S6). Significant DA cells identified with diffusion distance (SI Appendix, Fig. S8) have less overlap with true DA subpopulations.
Computational complexity.
The computation of for all cells may be a computational bottleneck for very large datasets. A standard method to compute NN is via the application of trees (59). The complexity of constructing a tree is , and the average complexity for finding nearest neighbors is bounded by . For datasets on the order of millions of cells, fast approximate approaches, such as in refs. 60 and 61, can be applied to increase the scalability of this step.
Preprocessing of scRNA-seq Datasets.
The R package Seurat was used for most preprocessing steps for the scRNA-seq datasets discussed in this paper. Details are described below. In datasets from refs. 5, 7, and 17, the preprocessing steps were exactly the same as in the original papers. In the dataset from ref. 16, data integration with Seurat (15) was used to remove batch effect, instead of regressing out batch during data scaling. t-SNE for data visualization was calculated with fast interpolation-based t-SNE (FIt-SNE) (62).
Melanoma dataset.
Transcripts per million (TPM) scRNA-seq data were obtained from ref. 7. We then performed data scaling and PCA with Seurat. Following the steps implemented in ref. 7, we calculated the variance for each gene and kept only genes with variance larger than 6 as an input for PCA; the top 10 PCs were retained for the calculation of t-SNE and DA analysis.
Mouse embryonic dataset.
Raw count matrices of scRNA-seq data from two time points E13.5 and E14.5 (two replicates each) were obtained from ref. 16. For each sample, we used Seurat to perform data normalization, scaling, variable gene selection, PCA, clustering, and t-SNE calculation. As in ref. 16, markers Col1a1, Krt10, and Krt14 were used to select dermal clusters: Only cells in clusters with expression of Col1a1 and no expression of Krt10, Krt14 were retained for further analysis. After selecting dermal cells, we used Seurat data integration to merge data and remove batch effects. PCA was performed on the integrated data, and the top 40 PCs (the same as in ref. 16) were used to calculate the t-SNE and for DA-seq analysis.
For the five detected DA subpopulations, marker genes were identified using the FindMarkers() Seurat function with the “negbinom” method, comparing each DA subpopulation to the rest of the cells. The top 100 genes enriched in the DA subpopulation (or all genes if the number of marker genes is fewer than 100) were selected as a gene signature/module for each DA subpopulation.
For validation, raw count matrices of scRNA-seq data from time points E13 and E15 were downloaded from ref. 27. For each sample, Seurat was used to process the data and generate clusters. Marker gene Col1a1 was used to select dermal cells. Only dermal cells from both samples were retained and merged for further analysis. The Seurat function AddModuleScore() was used to calculate module scores for gene modules of DA subpopulations described above.
COVID-19 datasets.
The Seurat object of integrated data from ref. 5 was downloaded. PCA was performed on the integrated data with 2,000 variable features. The top 90 PCs were retained for DA-seq analysis and as input for t-SNE. Immune cells were selected based on cell type labels obtained from the “meta.data” slot of the downloaded object. For detected DA subpopulations , and , marker genes were identified using the FindMarkers() Seurat function with the negbinom method, comparing the DA subpopulation to remaining cells in clusters 6-Neu, 10-nrMa, 2-CTL, and 6-Neu, respectively. The top 100 genes enriched in the DA subpopulation (or all genes if the number of marker genes is fewer than 100) were selected as a gene signature/module for each DA subpopulation.
For validation, the Seurat object of data from ref. 6 was downloaded. Cell type information was obtained from the meta.data slot of the downloaded object. The Seurat function AddModuleScore() was used to calculate module scores for gene modules of DA subpopulations described above.
Aging brain dataset.
The normalized expression matrix of scRNA-seq data from young and old mice was downloaded from Ximerakis et al. (17). Cell metadata—including cell type and cell sample labels (from young and old mice)—were also obtained from the original paper. As described in ref. 17, PCA was carried out after the identification of variable genes by the “mean variance plot” method from Seurat. The top 20 PCs were retained to calculate two-dimensional embedding with t-SNE and as the input for DA-seq.
Supplementary Material
Acknowledgments
We thank Rihao Qu, Manolis Roulis, Jonathan Levinsohn, Peggy Myung, and Shelli Farhadian for useful discussions and suggestions. This work was supported by NIH Grants R01GM131642, UM1 DA051410, 2P50CA121974, R01DK121948, R01GM135928, and R01HG008383.
Footnotes
The authors declare no competing interest.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2100293118/-/DCSupplemental.
Data Availability
An R package implementation of DA-seq is freely available at GitHub, https://github.com/KlugerLab/DAseq. Scripts to reproduce the analysis and figures presented in this paper are available at GitHub, https://github.com/KlugerLab/DAseq-paper.
Previously published data were used for this work. [All scRNA-seq datasets used in this manuscript are publicly available. Details are as follows. Sade-Feldman et al. (7), GSE120575; Gupta et al.(16), GSE122043; Fan et al. (27), GSE102086; Chua et al. (5), https://ndownloader.figshare.com/files/22927382; Liao et al. (6), cells.ucsc.edu/covid19-balf/nCoV.rds; and Ximerakis et al. (17), https://singlecell.broadinstitute.org/single_cell/study/SCP263/aging-mouse-brain#/.]
References
- 1.Macosko E. Z., et al. , Highly parallel genome-wide expression profiling of individual cells using nanoliter droplets. Cell 161, 1202–1214 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Zheng G. X. Y., et al. , Massively parallel digital transcriptional profiling of single cells. Nat. Commun. 8, 14049 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Burkhardt D. B., et al. , Quantifying the effect of experimental perturbations at single-cell resolution. Nat. Biotechnol., 10.1038/s41587-020-00803-5 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Laehnemann D., et al. , Eleven grand challenges in single-cell data science. Genome Biol. 21, 31 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chua R. L., et al. , Covid-19 severity correlates with airway epithelium–immune cell interactions identified by single-cell analysis. Nat. Biotechnol. 38, 970–979 (2020). [DOI] [PubMed] [Google Scholar]
- 6.Liao M., et al. , Single-cell landscape of bronchoalveolar immune cells in patients with covid-19. Nat. Med. 26, 842–844 (2020). [DOI] [PubMed] [Google Scholar]
- 7.Sade-Feldman M., et al. , Defining t cell states associated with response to checkpoint immunotherapy in melanoma. Cell 175, 998–1013 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kinchen J., et al. , Structural remodeling of the human colonic mesenchyme in inflammatory bowel disease. Cell 175, 372–386 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gao X., Hu D., Gogol M., Li H., Clustermap: Compare multiple single cell RNA-seq datasets across different experimental conditions. Bioinformatics 35, 3038–3045 (2019). [DOI] [PubMed] [Google Scholar]
- 10.Skinnider M. A., et al. , Cell type prioritization in single-cell data. Nat. Biotechnol. 39, 30–34 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cao Y., et al. , SCDC: single cell differential composition analysis. BMC Bioinf. 20, 721 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bielecki P., et al. , Skin-resident innate lymphoid cells converge on a pathogenic effector state. Nature 592, 128–132 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lun A. T. L., Richard A. C., Marioni J. C., Testing for differential abundance in mass cytometry data. Nat. Methods 14, 707 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yamada Y., Lindenbaum O., Negahban S., Kluger Y., “Feature selection using stochastic gates” in Proceedings of the 37th International Conference on Machine Learning, Daumé H. III, Singh A., Eds. (Proceedings of Machine Learning Research, PMLR, 2020), vol. 119, pp. 10648–10659. [Google Scholar]
- 15.Stuart T., et al. , Comprehensive integration of single-cell data. Cell 177, 1888–1902 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gupta K., et al. , Single-cell analysis reveals a hair follicle dermal niche molecular differentiation trajectory that begins prior to morphogenesis. Dev. Cell 48, 17–31 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ximerakis M., et al. , Single-cell transcriptomic profiling of the aging mouse brain. Nat. Neurosci. 22, 1696–1708 (2019). [DOI] [PubMed] [Google Scholar]
- 18.Butler A., Hoffman P., Smibert P., Papalexi E., Satija R., Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat. Biotechnol. 36, 411 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gandhi M. K., et al. , Expression of lag-3 by tumor-infiltrating lymphocytes is coincident with the suppression of latent membrane antigen–specific CD8+ T-cell function in Hodgkin lymphoma patients. Blood 108, 2280–2289 (2006). [DOI] [PubMed] [Google Scholar]
- 20.Buchan S. L., et al. , Ox40- and cd27-mediated costimulation synergizes with anti–pd-l1 blockade by forcing exhausted CD8+ T cells to exit quiescence. J. Immunol. 194, 125–133 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Koni P. A., et al. , Conditional vascular cell adhesion molecule 1 deletion in mice: Impaired lymphocyte migration to bone marrow. J. Exp. Med. 193, 741–754 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lin K.-Y., et al. , Ectopic expression of vascular cell adhesion molecule-1 as a new mechanism for tumor immune evasion. Canc. Res. 67, 1832–1841 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Harjunpää H., Asens M. L., Guenther C., Fagerholm S. C., Cell adhesion molecules and their roles and regulation in the immune and tumor microenvironment. Front. Immunol. 10, 1078 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wu T. C., The role of vascular cell adhesion molecule-1 in tumor immune evasion. Canc. Res. 67, 6003–6006 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Schlesinger M., Bendas G., Vascular cell adhesion molecule-1 (VCAM-1)—An increasing insight into its role in tumorigenicity and metastasis. Int. J. Canc. 136, 2504–2514 (2015). [DOI] [PubMed] [Google Scholar]
- 26.Kong D.-H., Young K., Kim M., Jang J., Lee S., Emerging roles of vascular cell adhesion molecule-1 (VCAM-1) in immunological disorders and cancer. Int. J. Mol. Sci. 19, 1057 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Fan X., et al. , Single cell and open chromatin analysis reveals molecular origin of epidermal cells of the skin. Dev. Cell 47, 21–37 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.McArdel S. L., Terhorst C., Sharpe A. H., Roles of cd48 in regulating immunity and tolerance. Clin. Immunol. 164, 10–20 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Skubitz K. M., Campbell K. D., Skubitz A. P. N., Cd63 associates with cd11/cd18 in large detergent-resistant complexes after translocation to the cell surface in human neutrophils. FEBS Lett. 469, 52–56 (2000). [DOI] [PubMed] [Google Scholar]
- 30.Grunwell J. R., et al. , Neutrophil dysfunction in the airways of children with acute respiratory failure due to lower respiratory tract viral and bacterial coinfections. Sci. Rep. 9, 2874 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Radermecker C., et al. , Locally instructed CXCR4 hi neutrophils trigger environment-driven allergic asthma through the release of neutrophil extracellular traps. Nat. Immunol. 20, 1444–1455 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ortiz L. A., et al. , Interleukin 1 receptor antagonist mediates the antiinflammatory and antifibrotic effect of mesenchymal stem cells during lung injury. Proc. Natl. Acad. Sci. U.S.A. 104, 11002–11007 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Croker B. A., et al. , Socs3 negatively regulates IL-6 signaling in vivo. Nat. Immunol. 4, 540–545 (2003). [DOI] [PubMed] [Google Scholar]
- 34.Yasukawa H., et al. , Il-6 induces an anti-inflammatory response in the absence of socs3 in macrophages. Nat. Immunol. 4, 551–556 (2003). [DOI] [PubMed] [Google Scholar]
- 35.Rottenberg M. E., Carow B., Socs3, a major regulator of infection and inflammation. Front. Immunol. 5, 58 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.FitzGerald G. A., Misguided drug advice for covid-19. Science 367, 1434 (2020). [DOI] [PubMed] [Google Scholar]
- 37.Kim H.., The transcription factor MafB promotes anti-inflammatory m2 polarization and cholesterol efflux in macrophages. Sci. Rep. 7, 7591 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Martinez F. O., et al. , Genetic programs expressed in resting and IL-4 alternatively activated mouse and human macrophages: Similarities and differences. Blood 121, e57–e69 (2013). [DOI] [PubMed] [Google Scholar]
- 39.Reyfman P. A., et al. , Single-cell transcriptomic analysis of human lung provides insights into the pathobiology of pulmonary fibrosis. Am. J. Respir. Crit. Care Med. 199, 1517–1536 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Buschur K. L., Chikina M., Benos P. V., Causal network perturbations for instance-specific analysis of single cell and disease samples. Bioinformatics 36, 2515–2521 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kluger Y., Basri R., Chang J. T., Gerstein M., Spectral biclustering of microarray data: Coclustering genes and conditions. Genome Res. 13, 703–716 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mishne G., Talmon R., Cohen I., Coifman R. R., Kluger Y., Data-driven tree transforms and metrics. IEEE Trans. Signal Inform. Process. Netw. 4, 451–466 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Shaham U., et al. , Removal of batch effects using distribution-matching residual networks. Bioinformatics 33, 2539–2546 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Haghverdi L., Lun A. T. L., Morgan M. D., Marioni J. C., Batch effects in single-cell RNA-sequencing data are corrected by matching mutual nearest neighbors. Nat. Biotechnol. 36, 421 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Eraslan G., Simon L. M., Mircea M., Mueller N. S., Theis F. J., Single-cell RNA-seq denoising using a deep count autoencoder. Nat. Commun. 10, 390 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Huang M., et al. , Saver: Gene expression recovery for single-cell RNA sequencing. Nat. Methods 15, 539 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Linderman G. C., Zhao J., Kluger Y., Zero-preserving imputation of scRNA-seq data using low-rank approximation. bioRxiv [Preprint] (2018). https://www.biorxiv.org/content/10.1101/397588v1 (Accessed 7 May 2021).
- 48.Wagner F., Barkley D., Yanai I., Accurate denoising of single-cell RNA-seq data using unbiased principal component analysis. BioRxiv [Preprint] (2019). https://www.biorxiv.org/content/10.1101/655365v2 (Accessed 7 May 2021).
- 49.Freeman P. E., Kim I., Lee A. B., Local two-sample testing: A new tool for analysing high-dimensional astronomical data. Mon. Not. R. Astron. Soc. 471, 3273–3282 (2017). [Google Scholar]
- 50.Kim I., et al. , Global and local two-sample tests via regression. Electronic J. Stat. 13, 5253–5305 (2019). [Google Scholar]
- 51.Cazáis F., Lhéritier A., “Beyond two-sample-tests: Localizing data discrepancies in high-dimensional spaces” in 2015 IEEE International Conference on Data Science and Advanced Analytics (DSAA) (IEEE, 2015), pp. 1–10. [Google Scholar]
- 52.Landa B., Qu R., Chang J., Kluger Y., Local two-sample testing over graphs and point-clouds by random-walk distributions. arXiv [Preprint] (2020). https://arxiv.org/abs/2011.03418 (Accessed 7 May 2021).
- 53.Benjamini Y., Hochberg Y., Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. B 57, 289–300 (1995). [Google Scholar]
- 54.Tibshirani R., Regression shrinkage and selection via the LASSO. J. R. Stat. Soc. B 58, 267–288 (1996). [Google Scholar]
- 55.Hebiri M., Lederer J., How correlations influence LASSO prediction. IEEE Trans. Inf. Theor. 59, 1846–1854 (2012). [Google Scholar]
- 56.Shekhar K., et al. , Comprehensive classification of retinal bipolar neurons by single-cell transcriptomics. Cell 166, 1308–1323 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Dobriban E., Permutation methods for factor analysis and PCA. Ann. Stat. 48, 2824–2847 (2020). [Google Scholar]
- 58.Richards J. W., Freeman P. E., Lee A. B., Schafer C. M., Exploiting low-dimensional structure in astronomical spectra. Astrophys. J. 691, 32 (2009). [Google Scholar]
- 59.Bentley J. L., Multidimensional binary search trees used for associative searching. Commun. ACM 18, 509–517 (1975). [Google Scholar]
- 60.Hajebi K., Abbasi-Yadkori Y., Shahbazi H., Zhang H.. “Fast approximate nearest-neighbor search with k-nearest neighbor graph” in Twenty-Second International Joint Conference on Artificial Intelligence, Walsh T., Ed. (AAAI Press, 2011), vol. 2, pp. 1312–1317. [Google Scholar]
- 61.Linderman G. C., Mishne G., Jaffe A., Kluger Y., Steinerberger S., Randomized near-neighbor graphs, giant components and applications in data science. J. Appl. Probab. 57, 458 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Linderman G. C., Rachh M., Hoskins J. G., Steinerberger S., Kluger Y., Fast interpolation-based t-SNE for improved visualization of single-cell RNA-seq data. Nat. Methods 16, 243–245 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
An R package implementation of DA-seq is freely available at GitHub, https://github.com/KlugerLab/DAseq. Scripts to reproduce the analysis and figures presented in this paper are available at GitHub, https://github.com/KlugerLab/DAseq-paper.
Previously published data were used for this work. [All scRNA-seq datasets used in this manuscript are publicly available. Details are as follows. Sade-Feldman et al. (7), GSE120575; Gupta et al.(16), GSE122043; Fan et al. (27), GSE102086; Chua et al. (5), https://ndownloader.figshare.com/files/22927382; Liao et al. (6), cells.ucsc.edu/covid19-balf/nCoV.rds; and Ximerakis et al. (17), https://singlecell.broadinstitute.org/single_cell/study/SCP263/aging-mouse-brain#/.]