Optimizing Spatial Allocation of COVID‐19 Vaccine by Agent‐Based Spatiotemporal Simulations

Abstract

Optimizing allocation of vaccine, a highly scarce resource, is an urgent and critical issue during fighting against on‐going COVID‐19 epidemic. Prior studies suggested that vaccine should be prioritized by age and risk groups, but few of them have considered the spatial prioritization strategy. This study aims to examine the spatial heterogeneity of COVID‐19 transmission in the city naturally, and optimize vaccine distribution strategies considering spatial prioritization. We proposed an integrated spatial model of agent‐based model and SEIR (susceptible‐exposed‐infected‐recovered). It simulated spatiotemporal process of COVID‐19 transmission in a realistic urban context. Individual movements were represented by trajectories of 8,146 randomly sampled mobile phone users on December 28, 2016 in Guangzhou, China, 90% of whom aged 18–60. Simulations were conducted under seven scenarios. Scenarios 1 and 2 examined natural spreading process of COVID‐19 and its final state of herd immunity. Scenarios 3–6 applied four vaccination strategies (random strategy, age strategy, space strategy, and space & age strategy), and identified the optimal vaccine strategy. Scenario 7 assessed the most appropriate vaccine coverage. The results demonstrates herd immunity is heterogeneously distributed in space, thus, vaccine intervention strategies should be spatialized. Among four strategies, space & age strategy is substantially most efficient, with 7.7% fewer in attack rate and 44 days longer than random strategy under 20% vaccine uptake. Space & age strategy requires 30%–40% vaccine coverage to control the epidemic, while the coverage for a random strategy is 60%–70% as a comparison. The application of our research would greatly improves the effectiveness of the vaccine usability.

Key Points

• Spatial heterogeneity in herd immunity rate has been identified

• Space & age strategy is substantially considered as the most efficient strategy among four vaccination strategies

• 30%–40% vaccine coverage are needed to control the epidemic under space & age strategy, while 60%–70% for a random strategy as a comparison

1. Introduction

Coronavirus disease 2019 (COVID‐19), caused by severe acute respiratory syndrome coronavirus 2 (SARS‐CoV‐2), quickly spread across the globe since it was detected in December 2019 (Bi et al., 2020), and three months later, WHO declared it a pandemic (Budd et al., 2020). At the time of this writing, there were over 140,000,000 confirmed cases and 3,000,000 total deaths, globally. The outbreak and spread of COVID‐19 are being widely concerned and bringing in big challenges all over the world. Most countries have implemented varied protection measures during the ongoing COVID‐19 pandemic. The strictest measures of lockdown have remarkably controlled the spread of COVID‐19, such as in Chinese cities (Cheng et al., 2020; Leung et al., 2020; Yin et al., 2021). However, these measures have led to massive economic losses and other underlying impacts on daily life and society. The implementation of lockdown is also not sustainable and tolerated by population in the long‐term. Many contries are gradually lifting their lock‐down and social distancing measures in the course of reopening their economies and societies. There is still a huge risk of disease resurgence particularly in densely populated urbanized areas, before the herd immunity achieved by a long‐way mass vaccination globally (Huang et al., 2021; Kissler et al., 2020; López & Rodó, 2020). Fortunately, recent vaccine research has made some promising progress, and several vaccines have received approval for emergency use (WHO, 2020). However, the supply of vaccines will not be sufficient to achieve herd immunity in the immediate future. Therefore, how to distribute vaccine effectively is an urgent and critical issue when vaccine is a highly scarce resource at this stage.

Mathematical models have been broadly used in vaccine distribution studies, such as susceptible‐exposed‐infected‐recovered (SEIR) and its variants (Gojovic et al., 2009; Medlock & Galvani, 2009; Mukandavire et al., 2020; Sah et al., 2018; Tuite et al., 2010). Object, timing and places are three important dimensions to evaluate vaccine resource allocation strategies. Based on these models, to whom vaccine should be provided (Medlock & Galvani, 2009; Sah et al., 2018; Tuite et al., 2010) and when the vaccination is initiated (Gojovic et al., 2009; Sypsa et al., 2009) were widely discussed. Most studies suggested that vaccine should be prioritized to people by age and risk (Lee et al., 2010; Medlock & Galvani, 2009; Sah et al., 2018; Tuite et al., 2010; Wallinga et al., 2010). However, spatial optimization of vaccine allocation was few explored. In the limited studies, meta‐population models were applied to explore the effectiveness of spatially targeted vaccination (Araz et al., 2012; Azman & Lessler, 2015; Dowdy et al., 2012; Engebretsen et al., 2019). Details of the complex behavior patterns of individuals were neither captured in mathematical models nor in meta‐population models. Discussions of vaccination effectiveness at the population scale could not reflect individuals’ behavior and their spatial interactions. Ignoring the spatiotemporal dimension, the vaccine's distribution strategy might be ineffective.

Integrating an agent‐based model and SEIR model may shed light on the problem. An agent‐based model is a bottom‐up modeling method which was developed from a complex adaptive system (Parker et al., 2003). It is an important tool to analyze and simulate complex urban systems (Benenson, 1998; Li & Liu, 2007; Liu et al., 2006). An agent is an autonomous computer entity capable of interacting with other agents and adapting its behavior to a changing environment. Each agent can be given specific rules and followed its own behaviors. Agents can represent heterogeneous entities, for example, people, animals or institutions etc. Agent‐based model has been widely used in uncovering the dynamic spatiotemporal process and its complex mechanism of infectious disease over the past decades (Chao et al., 2010; Crooks & Hailegiorgis, 2014; Eubank et al., 2004). As we know, the spread of the epidemic is a process in which human mobility, contact behavior and the epidemiological feature interplay with each other. Human mobility and contact have fundamental roles in shaping the transmission pattern of infectious disease (Wesolowski et al., 2012), especially for person‐to‐person contact‐transmissible infectious diseases, such as COVID‐19. Their impact on COVID‐19 spread had been extensively investigated using mobile phone data. Additionally, age was considered as a principal factor in explaining the pattern of COVID‐19 transmission dynamic. Several studies showed age‐specific differences in the biological susceptibility to infection (Ayoub et al., 2020; Zhang, Litvinova, Liang, et al., 2020). A descriptive report results of over 70,000 patient records from China CDC also showed that the age distribution of cases in China are mainly concentrated in 30–79 ages, accounting for 86.6% (Surveillances V, 2020). Hence, agent‐based model provides a perfect solution to simulate COVID‐19 transmission that individual age‐specific differences in the biological susceptibility to infection, mobility, and contact behavior between individuals are fully considered. Prior to our study, two articles used agent‐based models to evaluate the importance of the spatiotemporal dimension in vaccine's distribution (Grauer et al., 2020; Tao et al., 2018). However, the simulations of these studies were implemented on a virtual space, which is far from the fact that realistic space is highly complex, dynamic and mobile. The according vaccine distribution strategy might be ineffective based on a biased assumption. Uncovering the spatiotemporal transmission process clearly in a realistic urban space is a key to solve the problem.

Integrating the SEIR model and the agent‐based model makes a promising way to simulate how urban mobile individual interact with each other in the process of an epidemic. The former reveals the mechanism of epidemical progression, and the latter simulates the spatial interaction of individuals. The spatiotemporal simulation of COVID‐19 intra‐city transmission will help understanding how epidemic spreads naturally until achieving the state of herd immunity. Also, we can simulate epidemic spreading process in several realistic scenarios in which different strategies of vaccine intervention are employed.

With these considerations, this study proposes an individual‐based spatial model by integrating agent‐based model and SEIR. It characterizes the spatiotemporal dynamic process of COVID‐19 intra‐city transmission. It tests theoretical hypothesis that (1) the herd immunity rate is spatially heterogeneous in a city when COVID‐19 is spreading naturally; (2) the vaccine distribution can be optimized by a spatial heterogeneous strategy. By simulating the dynamics of virus infection and transmission, we obtain some valuable insights into the optimal vaccine strategies on epidemic control.

2. Data and Methods

2.1. Study Area and Mobile Phone Data

This study applied mobile phone trajectory data in Guangzhou to identify individuals’ actual movements. Guangzhou is the capital of Guangdong province, located in the south of China, near Hong Kong, Macaw and Shenzhen (Figure 1). Selecting Guangzhou as a case in scenario simulation, because Guangzhou is one of the megacities in China and an international city, with nearly 20 million population, representing a typical city with densely populated and high mobility. Furthermore, during the epidemic outbreak period in China, Guangzhou is also one of the prior targets for epidemic prevention and control besides Wuhan. Until the time of this writing, a total of 377 cases of COVID‐19, including 1 death, have been reported in Guangzhou. The city is still under severe pressure of preventing imported virus carriers from abroad. Therefore, taking Guangzhou as a case to study epidemic spread and vaccine delivery strategies is both representative and timely. The study area is a highly urbanized area located in the southwest of the city (Figure 1).

Figure 1.

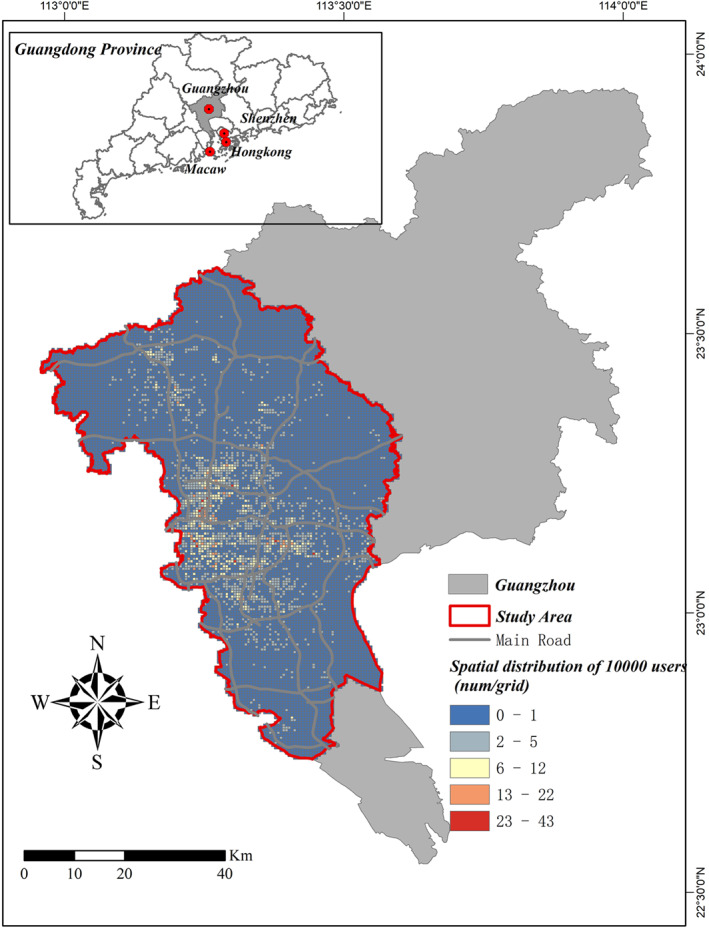
Study Area. Guangzhou is selected as a case study. It is the capital of Guangdong province, and near to Hong Kong, Macau and Shenzhen. The study area is located in the southwest of Guangzhou, a highly urbanized area.

The mobile phone trajectory data of Guangzhou was provided by a major mobile communication service company in China, which shared about 20% of the market. The data contained 1‐day trajectory of more than 5 million users on December 28, 2016, an ordinary Wednesday without major events or extreme weather. One‐day tracked data in the working day (December 28, 2016) is representative for daily mobility pattern, because previous research has found that human trajectories show a high degree of temporal and spatial regularity (Song et al., 2010), and the pattern of human daily mobility are not random and to be very predictable (Gonzalez et al., 2008). Several studies also utilized 1‐day mobile phone data to estimate human daily mobility pattern (Song et al., 2019; Xu et al., 2016). The trajectories are positioned by base stations (not users’ actual locations) that interact with the users' mobile phones. Users’ locations were recorded by 1‐h interval. When a user traveled across many base stations, the longest stayed one was identified. To protect users’ privacy, locations were geocoded by spatial units (500 × 500 m grids). In this research, 10,000 mobile phone users were randomly selected from the data set. The spatial distribution of these 10,000 users were shown in Figure 1. Filtering out samples with missing information (age), 8,146 users were taken as the final samples. These 8,146 users were distributed in 3,430 grids, accounting for 26% of the study area, with 13,390 grids in total. Samples are representative since their spatial distribution is highly consistent with the total mobile phone users in Guangzhou (correlation coefficient = 0.95, p‐value ≤ 0.05).

2.2. Agent‐Based Model

The definition of agent’ decision behavior is essential to agent‐based models. Our agent‐based model in a realistic environment is proposed as follows, based upon the mechanism of SEIR (Kermack and McKendrick, 1927; 1932) (A full description of SEIR is available in the supporting information Text S1).

The agents represent mobile phone users in our model. The life cycle of an individual agent is divided into four states: susceptible, exposed (but not yet infectious), infectious, and removed (isolated, recovered, or otherwise no longer infectious, etc.). Each agent can be in one out of the above four states with its own unique attributes (sex, age, latent duration, infectious duration, etc.). Agents are born in a “susceptible” state, except for a few initial infections. Agents are moving or stopping according to their own trajectories. Once susceptible agents meet infectious agents and get infected, the state of susceptible agents is transformed to “exposed.” At this stage, they cannot infect other agents yet. After a given “latent period,” those individuals become “infectious” which can infect other agents. Finally, after an “infectious period,” individuals become “recovered” which are immune against the disease and would never be infected again. A simplified agent‐based simulation diagram is displayed in Figure 2a. The model was performed in an open source software named “NetLogo” (version 6.1.1), which is a programmable modeling environment for simulating natural and social phenomena (Wilensky, 1999; Yang & Wilensky, 2011).

Figure 2.

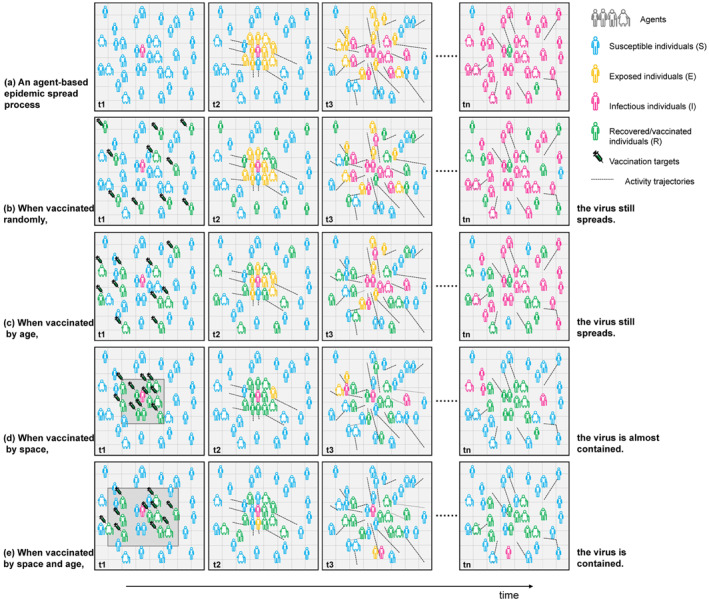
Schematic diagram of agent‐based simulation. A simplified agent‐based simulation diagram is displayed. The horizontal axis represents time, and the vertical axis represents different scenarios. A completely natural epidemic transmission process without any intervention measures (a), different vaccine intervention strategies on epidemic spreading process (b–e).

2.3. Model Parameterization

The model involves three parameters, the average latent period ${\mathit{D}}_{\mathit{e}}$, the mean infectious period $D_i$ and the probability of being infected per contact $\theta$ and its differences across age groups.

We set the latent period and infectious period based on recently published estimates, which have estimated the mean incubation period of COVID‐19 (from infection to symptom onset) is ∼5 days (Lauer et al., 2020; Li et al., 2020; Linton et al., 2020; Zhang, Litvinova, Wang, et al., 2020) and the mean infectious period (from symptom onset to hospital admission) is about 6 days, from day 4 to day 9 (Li et al., 2020; Linton et al., 2020; Tindale et al., 2020; Zhang, Litvinova, Wang, et al., 2020). However, early evidence shows that virus transmission occurs during a presymptomatic stage (Bai et al., 2020; Tindale et al., 2020; Yu et al., 2020), and infers that infection is transmitted on average about 2 days before symptom onset (Tindale et al., 2020). In other words, a latent period should be 2 days shorter and an infectious period should be 2 days longer. Given the above comprehensive considerations, eventually, we assumed the mean latent period and infectious period as 3  and 8 days respectively. Different from SEIR model, in which the mean latent period $D_e$ and infectious period $D_i$ are always constants, an agent‐based model considers the inter‐personal diversity and allows each agent to have a unique latent period and infectious period. We assume that each agent's latent period and infectious period follow normal distributions with a mean of 3 days and a standard deviation of 1 day (latent period), and a mean of 8 days and a standard deviation of 2 days (infectious period), respectively (see Table 1).

Table 1.

Model Parameter Setting

Variables	Value
Input
Population	8,146
Number of susceptible individuals	8,142
Number of exposed individuals	0
Number of infected individuals	4
Number of removed individuals	0
Latent period, $D_e$	$D_e\sim N\left(\mathrm{3,1}\right)$
Infectious period, $D_i$	$D_i\sim N(\mathrm{8,2}$)
The contact infected rate,$\theta$ (without age differences)	8‰ (R 0 = 2), 12‰ (R 0 = 3), 16‰ (R 0 = 4)
The contact infected rate,$\theta$ by age groups	See Table 2
Output
Attack rate (%)	/
Herd immunity (%)	/
The effective reproduction number, Rt	/
Durations (day)	/

Note. Attack rate means the proportion of those experiencing infection at the end of an epidemic; Herd immunity equals to attack rate when spreading naturally; Durations is the time that the epidemic lasts.

Parameter $\theta$ (the probability of being infected per contact) determines how likely an agent would be infected when contacting another agent in a 500 × 500 m grid. Although some recent studies estimated the probability of be infected from close contacts (Bi et al., 2020), it is not applicable to us because the spatial scale of our model (500 × 500 m grid) is far from close contact. We estimate parameter $\theta$ according to the basic reproduction number $R_0$, which is defined as the average number of secondary cases produced by a typical primary case during its infectious period in a completely susceptible population (Diekmann et al., 1990). Parameter $\theta$ can be inferred based on an mathematical expression (Lipsitch et al., 2003) as $R_0=k\theta D_i$, where $k$ is the average number of contacts, and $D_i$ is the average infectious period. Therefore, parameter $\theta$ is inferred as:

$$\theta =R_0/k{D}_i$$ (1)

Obviously, parameter $\theta$ depends on the above three parameter$R_0,kand{D}_i$. $D_i$ has just been determined as 8 days. $R_0$ for COVID‐19 epidemic of China has been estimated in several studies (Li et al., 2020; Liu, Hu, Kang, et al., 2020; Read et al., 2020; Sanche et al., 2020; Shen et al., 2020; Tang et al., 2020; Wu et al., 2020). It ranges from 2 to 6, with an average of about 3. Therefore, we set $R_0$ = 3 here, but we will also do a sensitivity analysis under different $R_0$ assumptions: the relatively mild ($R_0$ = 2) and severe outbreak ($R_0$ = 4). Parameter $k$ need to be known. We use another agent‐based model to simulate parameter k (how many people an agent would encounter in one day). The simulation is implemented using the mobile phone trajectory data from the 8,146 users. The simulation reproduces these users’ actual mobility and encountering process in a day (December 28, 2016). Based on the simulation, the number of encounters that an agent meets can be observed. The average number of encounters per agent estimates parameter $k$. The detailed simulation process is available in the supporting information Text S2.

The simulation values are shown in Figure S1. The mean value of $k$ is 29.45 ($\pm 0.2$), which means the average number of encounters per day for an agent is about 30 agents. According to Equation 1, parameter $\theta$ is easily calculated as 12‰ (when $R_0$ = 3), 8‰ (when $R_0$ = 2) and 16‰ (when $R_0$ = 4).

Additionally, there is evidence that the susceptibility to the infection of COVID‐19 increases with age (Ayoub et al., 2020; Zhang, Litvinova, Liang, et al., 2020). As referenced, this model divides the entire population into five age groups: under 18, 19–30, 31–45, 46–60, and above 60. The heterogeneous susceptibility to infection is modeled by a weight function $\mathrm{w}\left(\mathit{\theta }\right)$ which is a relative weight of the contact infected rate $\mathit{\theta }$ and differentiated by age groups. Age group 31–45 is taken as the reference group. The relative weight of different age groups is exhibited in Table 2.

Table 2.

Weight of the Contact Infected Rate $\mathbf{\theta }$ Among Different Age Groups

Age	Under 18	19–30	31–45	46–60	60+
w($\mathbf{\theta }$)	0.3$\mathbf{\theta }$	0.8$\mathbf{\theta }$	$\mathbf{\theta }$	1.2$\mathbf{\theta }$	1.8$\mathbf{\theta }$

Note. $\mathbf{\theta }$ is the probability of being infected per contact (i.e., the probability of an agent being infected when encountering another agent in a 500 × 500 m grid). It increases with age, Age group 31–45 is taken as the reference group. The relative weight of different age groups are shown.

Details of model parameter values are provided in Table 1. We assume that the epidemic starts with several infectious agents and the rest populations are initially susceptible. Each simulated epidemic is seeded by infecting four randomly chosen agents, and each simulation stops when there are no more transmissible agents, with only susceptible and removed agents remaining in the simulation. The attack rate (the proportion of those having experienced infection at the end of an epidemic), herd immunity and the epidemic durations would be outputted. Herd immunity equals the attack rate in a natural spreading scenario without any interventions. At the same time, the effective reproduction number $R_t$—the average number of secondary cases per primary case at time t (Nishiura, 2007)—can be also evaluated during the process of epidemic.

2.4. Model Scenarios Setting

Simulations were conducted in seven different scenarios that scenarios 1 and 2 simulated the spatiotemporal process of the epidemic, and scenarios 3–7 focused on vaccine allocation optimization.

Both scenarios 1 and 2 simulated a completely natural epidemic transmission process without any intervention measures. Considering the classical herd immunity threshold theorem (Smith, 1970)—that if population is randomly mixed without heterogeneity, the incidence of the infection would decline if the proportion of immune exceeds $1-1/R_0$, which implies that $1-1/R_0$ threshold is often used as the goal of immunization coverage. Achieving that can lead to eradication of target infectious disease. Consequently, scenario 1 assumed that all agents were equally susceptible, and equally infectious if they became infected. The simulation result of scenario 1, simulated herd immunity, was then compared with the classical herd immunity threshold ($1-1/R_0$) to validate the model. While, scenario 2 considered individual infection vulnerability (age‐specific contact infected rate). The spatiotemporal dynamic transmission process of COVID‐19 and spatial heterogeneity of herd immunity would be examined in scenario 2.

Scenarios 3–7 aimed to evaluate the impacts of vaccine intervention strategies on epidemic spreading dynamic and identify the optimal vaccine strategy, as well as the most appropriate vaccine coverage. On the basis of scenario 2 (base scenario), vaccine intervention measures were implemented using this model, in which some individuals were selected for vaccination. We evaluated four strategies of vaccine distribution. Scenario 3 distributed vaccines randomly (random strategy). Scenario 4 distributed vaccines by age vulnerability where a vaccination priority was assigned to age groups with high contact infected rates (age strategy). The order of vaccine allocation by age group was: ≥60, 46–60, 31–45, 19–30, ≤18, with each time fulfilling target group before proceeding to the next age group. Scenario 5 was a spatial vaccination strategy where a vaccination priority was assigned to areas with the highest herd immunity rate (space strategy). Specifically, vaccinated areas were ranked in a descending order of herd immunity rate, and distribution to a given area begins only after target population have been met in the higher ranker area. Scenario 6 considered both spatial risk and age vulnerability (space & age strategy). We assumed the vaccine coverage as 20% in scenario 3–6 (a simplified simulation diagram is shown in Figures 2b–2e). We considered two outcome measures to evaluate the vaccination strategies: the attack rate and durations. These two indicators were selected for the purpose of minimizing the infections, as well as slowing transmission to avoid overburdening healthcare systems (known as flattening the curve). Subsequently, we estimated different coverages (30%–80%), and identified the most appropriate vaccine coverage to control the epidemic, which aims to achieve herd immunity with minimal vaccine.

3. Results

3.1. Model Validation

The model was validated by comparing simulated herd immunity in scenario 1 with classical herd immunity threshold (1−1/$R_0,R_0$ = 3). The time evolution of simulated herd immunity and the effective reproduction number $R_t$ are shown in Figure 3. Different from $R_0$, $R_t$ shows the actual time‐dependent variation due to the decline in susceptible individuals. Figure 3 shows that $R_t$ goes up sharply above three first, then slowly down to 1, and finally down to 0. Simulated herd immunity goes up all the way, and finally approaches a balance. The whole simulation represents 150 days.

Figure 3.

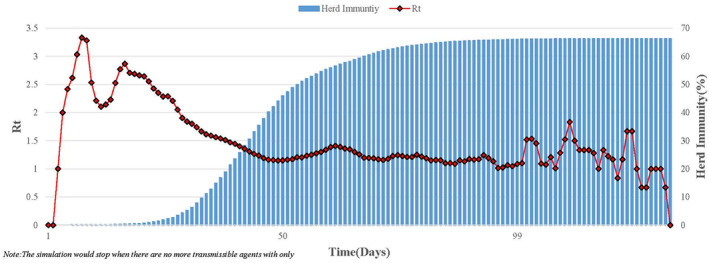
The variation of $R_t$ and herd immunity over time (${\mathcal{R}}_{\mathcal{0}}$ = 3) in Scenario 1. This simulates a completely natural transmission without any intervention measures under ${\mathcal{R}}_{\mathcal{0}}$ = 3, assuming that all agents are equally susceptible, and equally infectious. Red line represents actual time‐dependent variation of $R_t$. Blue columns represents herd immunity. The whole simulation represents 150 days.

The simulation was repeated 100 times to balance the stochastic effect. The median value (of 100 simulations) of simulated herd immunity is 66.11%. It indicates that our model is validated since the simulated herd immunity is almost equivalent to the classical herd immunity threshold 66.67% (1−1/$R_0,R_0$ = 3). We also did a sensitivity analysis under different $R_0$ assumptions: the relatively mild ($R_0$ = 2) and severe ($R_0$ = 4) outbreak. Each of these tests also had 100 simulations. The simulated herd immunity (Table 3) again is consistent with the classical herd immunity threshold, which further confirms that our model is convincing.

Table 3.

The Simulation Result When R ₀ = 2, 3 and 4 in Scenario 1

Scenarios	${\mathit{R}}_0$	Simulated herd immunity	Classical herd immunity	Durations
		%, median [1st, 3rd quartile] *	%, 1‐1/${\mathit{R}}_0$	Days, median [1st, 3rd quartile] *
Scenario 1	2	50.23 [49.67, 50.70]	50.00	150 [132, 170]
Scenario 1	3	66.11 [65.70, 66.58]	66.67	128 [120, 143]
Scenario 1	4	74.69 [74.30, 75.25]	75.00	127 [115, 139]

Note. Scenario 1 simulates a completely natural transmission without any intervention measures, assuming that all agents are equally susceptible, and equally infectious. Sensitivity analysis are implemented under different $R_0$ assumptions. Each $R_0$ hypothesis ran 100 simulations to balance the stochastic effect. The median and quartiles values of 100 simulations were included.

3.2. Spatiotemporal Process

The completely natural spatiotemporal dynamic process without any intervention measures from scenario 2 is shown in Figure 4. Compared to scenario 1, individuals’ infection vulnerability (age‐specific differences) is considered into scenario 2. Figure 4 shows that the infected cases are concentrated in space. Most of the cases appear in the city center at the beginning and then spread to the suburbs. With the simulation going on, more grids have infected cases, but grids with high attack rate were are still concentrated at locations with dense population or heavy traffic. Obviously, the transmission dynamics is geographically heterogeneous and the majority of transmissions occur in urban areas particularly the city center.

Figure 4.

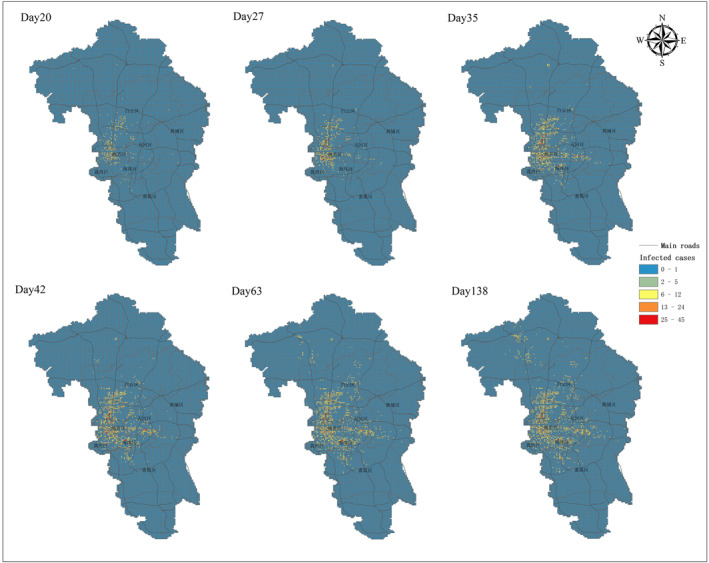
Spatiotemporal dynamic spread process of Covid‐19 in scenario 2. Scenario 2 considers individual infection vulnerability (age‐specific contact infected rate) and simulates a completely natural transmission without any intervention measures. The spatial spread process at different time points are displayed.

3.3. Spatial Heterogeneity

Eventually, herd immunity would be achieved at the end of scenario 2 simulation. The spatial distribution of herd immunity is shown in Figure 5. Notice that Figure 5 is presented at a spatial scale of Jiedao rather than a grid, because Jiedao is the smallest administrative unit in China and thus aggregating results into Jiedao scale is convenient for administrative management. Figure 5 exhibits strong spatial heterogeneity. A size‐ranking diagram of herd immunity of each Jiedao is shown in the bottom left of Figure 5, displayed in descending order of herd immunity rate from left to right. Nearly half of Jiedaos’ herd immunity is above 80%, while 16% of them have herd immunity below 20%. An indicator of Moran's I statistics was further applied to examine the level of spatial heterogeneity. Moran's I statistics is commonly used to test whether an observed spatial clustering is formed due to chance. The values of Moran's I would be approximately between +1 and −1. The higher the value is, the stronger the spatial clustering is. Global Moran's” I of Figure 4 is 0.46 (p‐value ≤ 0.05), indicating that there is a strong spatial heterogeneity of herd immunity. These evidences verify the Hypothesis 1 that ‘the herd immunity rate is spatially heterogeneous in a city when COVID‐19 is spreading naturally.

Figure 5.

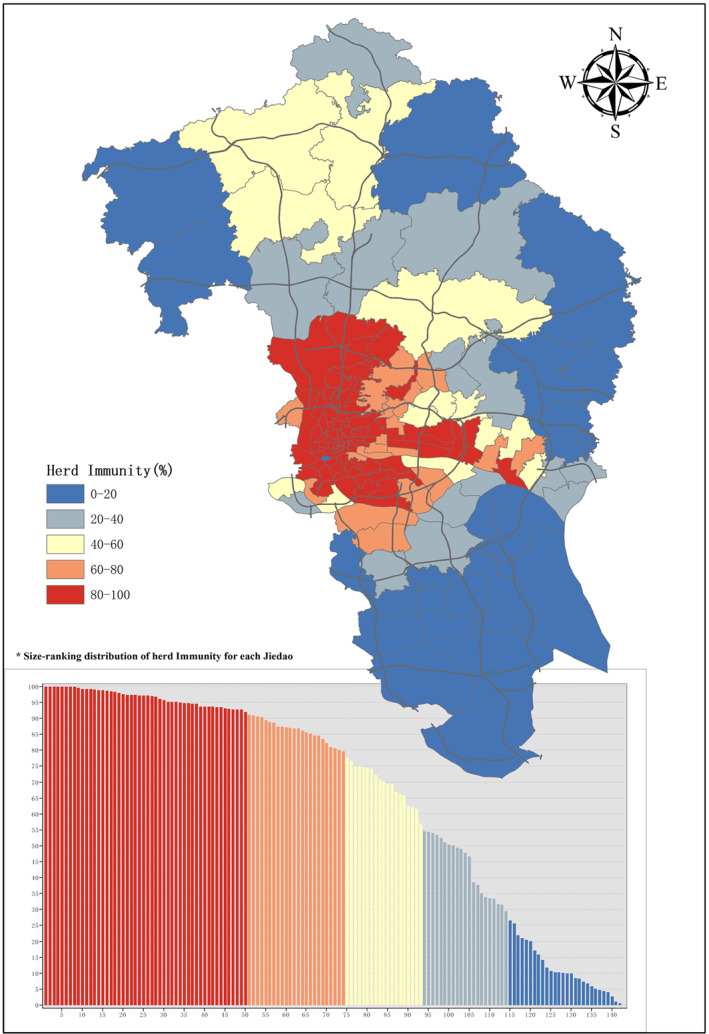
Spatial distribution of Herd Immunity at Jiedao Level from Scenario 2. The scenario simulation would stop when there are no more transmissible agents with only susceptible and removed agents remaining in the procedure. At the point, herd immunity would be achieved. The herd immunity rate of each Jiedao are displayed in colors. In the bottom left, it is displayed in descending order of herd immunity rate from left to right.

3.4. Optimizing Vaccine Distribution Strategies

The above results demonstrate that the herd immunity is not uniform in space and is spatially heterogeneous, implying that the vaccine distribution can be optimized by a spatial heterogeneous strategy (Hypothesis 2). This hypothesis was tested in scenarios 3–6. We assumed the vaccine coverage was 20%. We evaluated the attack rate and the durations among four strategies.

The results (Table 4) demonstrate that a spatial strategy has smaller attack rate and longer epidemic durations than a random or age strategy. Space optimization plays a greater role in reducing attack rate and slowing the transmission to flatten the infection curve. In “random strategy” scenario, 45.36% (45.04%–45.78%) population would eventually be infected. Compared to “random strategy,” the median value of attack rate in “age strategy” is 44.07%, a decrease of 1.29%. However, when the vaccination is distributed according to “space strategy,” the attack rate drops even more, to 39.44% (38.57%–39.94%). Eventually, a “space & age strategy” has the lowest attack rate (with a median value of 37.66%). Simultaneously, the duration under “space & age strategy” is the longest (with a median value of 175 days) among four delivery strategies, which would alleviate pressure on the emergency services and give more time to deal with the epidemic. The results verify Hypothesis 2 that the vaccine distribution can be optimized by a spatial heterogeneous strategy.

Table 4.

Four Vaccine Delivery Strategies Under 20% Vaccination Coverage

Scenarios	Attack rate	Durations
	%, median [1st, 3rd quartile]	Days, median [1st, 3rd quartile]
Scenario 3: random strategy	45.36 [45.04, 45.78]	131 [121, 163]
Scenario 4: age strategy	44.07 [43.26, 44.55]	146 [132, 159]
Scenario 5: space strategy	39.44 [38.57, 39.94]	154 [145, 171]
Scenario 6: space & age strategy	37.66 [37.12, 38.42]	175 [152, 197]

Note. On the basis of Scenario 2 (base scenario), vaccine intervention measures are implemented, in which some individuals are selected for vaccination. Four strategies of vaccine distribution are evaluated (scenarios 3–6). Each strategy was simulated for 100 times. The median and quartiles values of 100 simulations were shown.

3.5. Identifying the Optimal Vaccine Coverage

The space & age strategy has been proven to be the best vaccine allocation strategy. In subsequent analysis, we varied the level of vaccine coverage (30%, 40%, 50%, 60%, 70%, and 80%) to identify the optimal vaccine uptake (scenario 7). Our aim is to achieve herd immunity with minimal vaccine. To quantify the effect, we compared the optimal strategy (space & age strategy) with “random strategy,” under the same vaccination coverage setting. The effective reproduction number $R_t$, as mentioned earlier, is used to determine whether the epidemic is under control. If $R_t<1$ (Nishiura, 2007), it suggests that the epidemic is in decline and regarded as being under control at time t (Nishiura & Chowell, 2009). Due to the large fluctuations of $R_t$, it is necessary to smooth the calculation (Liu, Hu, Xiao, et al., 2020). $R_t$ values are smoothed over a 8‐days moving window considering the mean infectious period is 8 days in this study. The maximum value of $R_t$ is used to evaluate vaccination coverage: $R_{t\_max}=\max \left\{R_t,t\in T\right\}$, where T is the epidemic duration. If ${R_t}_{max}<1$, $R_t$in the whole epidemic spreading process would be less than 1. Similarly, each coverage setting per strategy has 100 simulations.

The results (Table 5) show that 40% vaccines are needed to control the epidemic (The median value of $R_{t\_max}$ = 0.81) under “space & age strategy,” while 70% vaccines (The median value of $R_{t\_max}$ = 0.95) for “random strategy.” Although the epidemic is under control at the corresponding vaccine coverage level, there are still 1.06% (0.1%–1.72%) and 3.89% (0.1%–6.21%) people being infected eventually in “space & age strategy” and “random strategy,” respectively. The attack rate of “space & age strategy” is much lower than that of “random strategy” under any vaccination coverage. For example, there are still 36.74% (36.08%–37.49%) people at risk of infection under “random strategy,” while only 17.96% (14.39%–19.24%) under “space & age strategy,” when the vaccination coverage is 30%. There is no doubt that “space & age strategy” plays a significant role in minimizing the number of infections compared to “random strategy,” in which 18.78% people are protected from infection under 30% vaccine coverage, and 27.58% people under 40% vaccine coverage.

Table 5.

Vaccination Coverage Evaluation Under a Space & Age Strategy and a Random Strategy in Scenario 7

Vaccine coverage	(A) Space & age strategy	(B) Random strategy
	${\mathit{R}}_{\mathit{t}}\_\mathit{max}$,	${\mathit{R}}_{\mathit{t}}\_\mathit{max}$,
	Median [1st, 3rd quartile]	Median [1st, 3rd quartile]
30% Coverage	1.23 [(1.05, 1.46]	1.70 [1.58, 1.89]
40% Coverage	0.81 [0.52, 1.13]	1.53 [1.43, 1.76]
50% Coverage	0.56 [0.30, 1.08]	1.45 [1.30, 1.62]
60% Coverage	0.52 [0.25, 0.78]	1.31 [1.18, 1.47]
70% Coverage	0.25 [0.04, 0.50]	0.95 [0.53, 1.32]
80% Coverage	0.15 [0.06, 0.44]	0.72 [0.27, 1.08]
Vaccine coverage	Attack rate,	Attack rate,
	%, median [1st, 3rd quartile]	%, median [1st, 3rd quartile]
30% Coverage	17.96 [14.39,19.24]	36.74 [36.08, 37.49]
40% Coverage	1.06 [0.10, 1.72]	28.64 [28.03, 29.09]
50% Coverage	0.12 [0.09, 0.28]	20.39 [19.83, 20.90]
60% Coverage	0.10 [0.06, 0.20]	13.10 [12.51, 13.49]
70% Coverage	0.07 [0.06, 0.09]	3.89 [0.10, 6.21]
80% Coverage	0.07 [0.06, 0.11]	0.14 [0.07, 0.47]
Vaccine coverage	Durations,	Durations,
	days, median [1st, 3rd quartile]	days, median [1st, 3rd quartile]
30% Coverage	264 [228, 299)]	134 [114, 142]
40% Coverage	43 [21, 114]	131 [117, 144]
50% Coverage	24 [15, 45]	128 [117, 143]
60% Coverage	21 [13, 33]	142 [128, 159]
70% Coverage	14 [9, 20]	108 [20, 142]
80% Coverage	14 [10, 23]	25 [15, 65]

Note. All of the above scenarios are assumed that no other intervention measures are taken but only vaccination. Similarly, each coverage hypothesis per strategy would be simulated for 100 times. The median and quartiles values of 100 simulations were taken into account.

From the perspective of durations, “space & age strategy” greatly slow the transmission to avoid overburdening healthcare systems, such as 264 [228–299] days for “space & age strategy” and 134 [114–142] days for “random strategy” when the vaccine coverage is 30%. While, the durations under “space & age strategy” are getting shorter than “random strategy,” as the coverage increased. This is because that attack rate under “space & age strategy” is much smaller than “random strategy” with the coverage increasing, which implies that epidemic only locally spreads across a small area and ends quickly under “space & age strategy.” In summary, “space & age strategy” improves the effectiveness of the vaccine usability and epidemic are under control with minimal vaccines under this strategy.

4. Discussion

Through simulating spatiotemporal transmission process of COVID‐19 in Guangzhou integrating agent‐based model and SEIR model with mobile phone trajectory data, we tested the hypothesis that herd immunity rate is spatially heterogeneous and that the vaccine distribution can be optimized by the spatial heterogeneous strategy. Our simulation results suggested that herd immunity is not uniform in space and give priority to those vulnerable individuals in high‐risk areas in vaccine allocation would greatly improve vaccine effectiveness.

4.1. Spatial Heterogeneity in Herd Immunity

We observed a high degree of spatial heterogeneity in herd immunity rate under spreading naturally in this study. Geographical heterogeneity in herd immunity suggested that not all locations need to reach the threshold of herd immunity to end the epidemic. In low‐density suburbs, the attack rate is lower when the whole city reaches herd immunity. In contrast, an extremely high attack rate is observed in dense urban areas. The underlying reason may be the different contact patterns between rural and urban areas (Read et al., 2014) or different social groups in those places (Mossong et al., 2008). The spread of the epidemic is a process in which population, individual mobility, and the epidemiological feature interplay with each other. That means heterogeneity of all these dimensions affect the distribution of infected cases and herd immunity rates. Being aware of geographical heterogeneity in herd immunity is critical. Conventionally, preventing epidemic spread though vaccination is described in terms of the herd immunity threshold (1−1/$R_0$) under the assumption of the classic mean‐field theory. Our results emphasized the existence of spatial heterogeneity in herd immunity. Previous studies also indicated that spatial heterogeneity may influence the implementation of interventions, and control strategies should aim at such heterogeneity (Dowdy et al., 2012; Nath et al., 2021; Shrestha et al., 2016; Yechezkel et al., 2020). Therefore, it is necessary to quantify the degree of spatial heterogeneity, identify the “hotspots” and apply intervention against the disease outbreak.

4.2. The Importance of Space‐Targeted Vaccination

Hypothetical scenarios on vaccine interventions strategies demonstrated that space‐targeted vaccination has better perform than vaccination targeted to specific age groups or general population when distributing the same vaccine quantity. How to deploy limited control measures to minimize transmission, and to choose target population for optimal allocation of vaccine have been an critical question that public health policy makers face with, which have been discussed in many papers (Liu & Xia, 2011; Medlock & Galvani, 2009). The selection of target populations for allocation of vaccine were usually based on socio‐demographic characteristics, such as age, sex, occupation, or other demographic characteristics (Lee et al., 2010; Medlock & Galvani, 2009; Sah et al., 2018; Shim, 2013). Actually vaccinating population by socio‐demographic attributes did not capture the essence of disease transmission. The nature of epidemic diffusion is a process in which human mobility, contact behavior, and the epidemiological feature interplay with each other. The difference of demographic characteristics (e.g., age) affect the susceptibility to the infection in the biology (Ayoub et al., 2020) on the one hand. On the other hand, it leads to different patterns of mobility or contact. Because, the patterns of mobility are highly associated with socio‐demographic factors (Mossong et al., 2008; Read et al., 2014). Peoples with different socio‐demographic attributes have different patterns of behavior or activity. Indeed, human mobility and contact behavior are known as crucial determinants for the spread of COVID‐19. In short, vaccinating population by socio‐demographic attributes actually did not capture the essence. Namely, socio‐demographic attributes are not the nature of the vaccine problem, but just the outer skin of vulnerability and contacts. Although age differences in the biology of infection has been captured in the previous studies (Medlock & Galvani, 2009; Sah et al., 2018), the actual behavior and movement of individuals were not. Integrating an agent‐based model in the study provides a perfect solution on this problem that both the susceptibility of infection and the interaction between individual behaviors are fully considered. Further, since the agent‐based simulation is ultimately embodied in the space aspects, it reveals that spatial optimization plays a greater role in vaccine allocation.

4.3. Implications for Future Policy Decisions

Results suggested that targeted high‐incidence areas (“hotspots”) vaccination is key to epidemic control, which is consistent with previous studies, where targeted vaccination in specific locations are implemented and considered as an efficient strategy (Azman & Lessler, 2015; Dowdy et al., 2012; Engebretsen et al., 2019). Targeting those high‐incidence geographic areas on the one hand would serve to directly protect the population at high risk, and on the other hand may indirectly serve to protect the general population. Consequently, quantifying spatial heterogeneity and identifying high‐incidence areas are essential to fully harness the potential advantage of spatial targeting of COVID‐19 vaccines. Public health government officials needs to know the specific hotspots of the city to fight against on‐going COVID‐19 epidemic. Furthermore, the intervention combining both spatial heterogeneity and age heterogeneity is the most effective strategy. This combined strategy requires 30%–40% vaccine coverage to control the epidemic, which is much lower than traditional herd immunity threshold (66.67%, 1−1/$R_0$). We therefore recommend immediate deployment of this strategy when determining vaccination prioritization.

4.4. Limitations of This Research

However, this study has several limitations. First, only 1‐day trajectory is available and we assume that human daily mobility patterns do not change much. Second, the current model differentiates the population only by ages but not by other demographic attributes such as sex, occupation, wealth, etc. Considering these additional attributes may lower the disease‐induced immunity level even further. Quantifying this effect and to what extend more precisely remains to be done. Third, vaccine efficacy is not considered, and we assumed vaccines with 100% efficacy. For simplicity, we also assume that all the vaccine is delivered at once by a given coverage. Indeed, the vaccine allocation is temporally constrained by the production and availability schedule. It is necessary to estimate the timing of vaccine delivery in future. Lastly, the type of location (i.e., schools, workplaces, hospitals, markets, shops, and restaurants etc.) and the travel mode (i.e., bus, subway, bike, car, etc.) were not considered in our model. Indeed, individuals in these different settings had different mixing patterns and contact intensity. These factors should be further considered in the future research.

5. Conclusions

In conclusion, we proposed an integrated spatial model of an agent‐based model and SEIR to evaluate the spatiotemporal process of COVID‐19 intra‐city transmission. Individual movements were projected by hourly mobile phone trajectory data. We found that herd immunity is not uniform in space, thus, vaccine intervention strategies should be spatialized. Among four strategies, space & age strategy is substantially more efficient than the other three strategies. Additionally, space & age strategy requires 30%–40% vaccine coverage to control the epidemic, comparatively that for a random strategy is 60%–70%. Results demonstrate the importance of spatial optimization vaccines. It also highlights that this strategy will greatly improve the effectiveness of the vaccine usability. Our methodology can help global policymakers develop optimal strategies based on their own specific spatial situations against on‐going COVID‐19 epidemic.

Conflict of Interest

The authors declare no conflict of interest relevant to this study.

Supporting information

Supporting Information S01

Zhou, S. , Zhou, S. , Zheng, Z. , & Lu, J. (2021). Optimizing spatial allocation of COVID‐19 vaccine by agent‐based spatiotemporal simulations. GeoHealth, 5, e2021GH000427. 10.1029/2021GH000427

Data Availability Statement

The raw data of this study obtained from the mobile operator are not publicly available due to limited use agreement. Access to aggregated versions of the data that support the findings of this study can be obtained from the corresponding author.