Modeling and synthesis of breast cancer optical property signatures with generative models

Abstract

Is it possible to find deterministic relationships between optical measurements and pathophysiology in an unsupervised manner and based on data alone? Optical property quantification is a rapidly growing biomedical imaging technique for characterizing biological tissues that shows promise in a range of clinical applications, such as intraoperative breast-conserving surgery margin assessment. However, translating tissue optical properties to clinical pathology information is still a cumbersome problem due to, amongst other things, inter- and intrapatient variability, calibration, and ultimately the nonlinear behavior of light in turbid media. These challenges limit the ability of standard statistical methods to generate a simple model of pathology, requiring more advanced algorithms. We present a data-driven, nonlinear model of breast cancer pathology for real-time margin assessment of resected samples using optical properties derived from spatial frequency domain imaging data. A series of deep neural network models are employed to obtain sets of latent embeddings that relate optical data signatures to the underlying tissue pathology in a tractable manner. These self-explanatory models can translate absorption and scattering properties measured from pathology, while also being able to synthesize new data. The method was tested on a total of 70 resected breast tissue samples containing 137 regions of interest, achieving rapid optical property modeling with errors only limited by current semi-empirical models, allowing for mass sample synthesis and providing a systematic understanding of dataset properties, paving the way for deep automated margin assessment algorithms using structured light imaging or, in principle, any other optical imaging technique seeking modeling. Code is available.

I. Introduction

In the past two decades, breast-conserving surgery (BCS) has become the most common procedure in the treatment of early invasive breast cancer, with clinical results similar to [1] or better [2] than those achieved via full mastectomy. In BCS, the tumor is extracted with a surrounding layer of healthy tissue (i.e. the surgical margin of the tumor). Tumor margins are visually evaluated by the surgeon and a pathologist during the resection process, and whether margins are cancer-free is determinant to the success of a given operation. Such visual assessment is referred to as the intraoperative gross examination of the resected sample. The lumpectomy sample is then processed by a histopathologist, who provides a final veredict on the prognosis of each case, hours or days afterwards. Unfortunately, about 20% to 40% of patients that undergo BCS treatment require two or more re-excision procedures [3], [4]; this percentage appears to be, among other things, inversely proportional to surgeon case volume [5]. This accuracy mismatch between gross examination and histological analysis calls for finding automated and/or standardized intraoperative margin assessment methods that can reduce current re-excision rates, by enhancing any surgeon’s ability to detect whether BCS resection margins are cancer-free.

Currently, two-dimensional projection X-ray imaging is commonplace for intraoperative margin assessment during breast-conserving surgeries, but the margins normal to the imaging axis are occluded from view, and peripheral margins may be poorly resolved. Recent studies have explored the value of three-dimensional X-ray micro-computed tomography [6] and tomosynthesis [7] for intraoperative volumetric specimen scanning. X-ray imaging provides excellent contrast between tumor and adipose tissue but lacks contrast between tumor and fibroglandular tissue that may be important for clinical decision making [8]. Thus, the BCS clinical environment is already acclimated to intraoperative imaging in an X-ray cabinet located in the surgical suite, and a rapid, wide field-of-view optical imaging solution could feasibly integrate with X-ray imaging already in place to improve sensitivity to key tissue subtypes.

Spatial frequency domain imaging (SFDI) shows potential for improving intraoperative margin assessment in this setting. Also known as wide-field structured light imaging, SFDI is a wide-field-of-view, optical imaging technique that involves projecting a series of one-dimensional sinusoidal fringe patterns at various spatial frequencies and wavelengths of light. By modifying the spatial frequency, wavelength, and phase of the fringe patterns, and after adequate demodulation, the medium’s response function is captured in the form of backscattered radiation [9], [10]. Using a diffuse or sub-diffuse light transport model, demodulated SFDI data can be used to quantify bulk optical properties (OPs) in a turbid medium [10], [11]. Absorption coefficient quantification at multiple optical wavelengths can be used to derive biological chromophore concentrations [10]. Another use of SFDI involves using different spatial frequencies of illumination to depth-resolve section samples, allowing for tomographic imaging [12]. SFDI has seen, in the past decade, its full development from an experimental procedure into a mature modality, with numerous calibration and error-correction methods [13], [14]. Recently, an SFDI system for the measurement of tissue oxygenation in patients with potential circulatory compromise gained U.S. Food and Drug Administration (FDA) clearance [15]. Several other SFDI techniques have emerged, most of which rely on numerical approximations for the behavior of light as it traverses through layered turbid media, i.e., enforcing assumptions and simplifying the Radiative Transfer Equation (RTE). Examples of these techniques include sub-diffuse SFDI for imaging surface tissue structure [16], single-snapshot imaging (SSOP) [17], qF-SSOP for fluorescence imaging [18], Diffuse Optical Tomography (DOT) [19] and Multispectral Optoacoustic Tomography (MSOT) [20]. All these techniques are currently undergoing various clinical studies, where OP quantification shows to be promising in estimating microstructural and molecular properties with some implications on modeling pathology. Notable use cases for SFDI in particular include the evaluation of burn depth and severity [21], [22], skin flap oxygen saturation monitoring during surgery [22], arterial occlusion detection [23], vascular assessment of diabetic foot revascularization [24], skin disease response to laser therapy [25], quantitative mapping of surgically resected breast tissues [26], [27] and skin cancer [28], [29], proving that there can be measurable optical, structural, and molecular differences between different tissues and pathologies. However, little work focuses on unsupervised, nonlinear modeling of optical pathophysiology, resulting in great, directed efforts to parameterize and predict disease given a dataset of labeled measurements, while potentially failing to harness the true diagnostic power of a given imaging modality.

The vast amount of information provided by SFDI methods, and the fact the relationship between OPs and image data is highly nonlinear, have prompted the generation of new analytical models [30], as well as the use of deep learning for estimating tissue properties. In the latter case, algorithms can approximate complex nonlinear functions by concatenating distributed, atomic operations called ‘units’ and applying automatic differentiation (i.e., backpropagation) on data input-output pairs to gradually generate a function that can relate them [31]. Methods such as lookup-table (LUT) OP extraction have proven less precise at extracting reduced scattering $\left({\mu }_s^{\prime }\right)$ and absorption (μ_a) coefficients than well-trained deep neural network models [32], [33]. Recently, Conditional Generative Adversarial Networks (cGAN) have been used to improve optical properties estimates from single-snapshot images [34]. These methods effectively solve simplified inverse light diffusion problems when compared to state-of-the-art solutions [35], while attempting to correct artifacts. All of these various clinical studies, deep learning classifiers and optical property estimators suggest their combination into a single framework, i.e. a deep learning system that can bidirectionally cross-reference and translate OPs to (and from) pathology. Here, we will consider four problem domains in total, namely (1) the space of possible optical signatures, (2) a representation of this space in a few dimensions, (3) the domain of possible pathologies, and (4) the domain of physical, optical properties in tissues. This work constitutes the first use of data-driven generative models for the analysis and synthesis of breast cancer SFDI data, showing that it is possible to find a tractable non-linear relationship between the wide-field data and tissue pathophysiology, recently observed via multiphoton microscopy [36]. The generative toolkit, which could be applied to other nonlinear imaging modalities, may enable future objectives such as margin delineation and real-time pathology assessment of resected samples within milliseconds, potentially reducing the number of follow-up re-excisions in current lumpectomy interventions.

II. Materials and methods

A. Breast tissue dataset

The SFDI dataset consists of 70 freshly resected BCS tissue samples, imaged in order of arrival with a multimodal scanning device at the Dartmouth Hitchcock Medical Center (DHMC) in Lebanon, New Hampshire. Each BCS sample was cut into ~5-mm thick “bread-loafed” slices of tissue, following protocol approved by the Internal Review Board at DHMC. After resection, one of the cuts was positioned between two optically-clear acrylic plates, each 1/8th of an inch in thickness. The assembly was held together by elastic bands and placed inside a custom-built micro-CT/SFDI device for imaging [37]. After image acquisition, all thick slices were processed as per standard protocol in hematoxylin and eosin (H&E) stain imaging. Analysis of histopathological slides was performed by an expert pathologist, who delineated regions of interest (ROIs) on the H&E images associated with distinct tissue subtypes. These ROIs were then conservatively co-registered with wide-field-of-view SFDI data. Each BCS sample is thus represented by SFDI data that is validated by gold standard histopathological information. Importantly, the ROIs in the sliced BCS samples imaged in this study do not represent real margins of excised tumors; instead, they simply highlight breast tissue heterogeneity and identify areas where tissue categories are certain. The SFDI data associated with each BCS sample includes 16 1024 × 1024-pixel reflectance images, corresponding to 4 spatial frequencies sampled at 4 different wavelengths, namely f_x = {0., 0.15, 0.61, 1.37} mm⁻¹ and λ = {490, 550, 600, 700} nm. Spatial resolution is 0.128 mm per pixel. A total of 136 tissue ROIs are available, with 15 distinct tissue pathologies in total, presenting in different ratios. Table I shows a detailed description of each of the tissue subtypes, samples, and ROIs imaged.

Table I.

Number of dataset samples, ROIs, and pixels

Tissue subtype	Samples with ROI	n	Total pixels
Background	2–5, 7, 9–12, 15, 16, 19–21, 23–25, 27, 29, 30, 31–33, 36, 39, 41, 42, 46, 49, 51–53, 55, 56, 57, 59, 60, 63, 64, 67	40	10,693,158
Adipose Tissue	2–5, 8, 9, 11, 12, 14, 16, 17, 22, 26, 28, 30, 34, 37, 39–42, 44, 45, 47–54, 58–60, 63, 64, 67, 69, 70	39	158,070
Connective Tissue	6, 8, 12, 13, 22, 23, 33, 35, 40, 43, 47–50, 52, 53, 55, 58, 60, 63, 64, 65	22	89,470
Myofibroblastic	38	1	11,522
Benign Phyllodes	57	1	19,201
Normal Treated	20	1	20,740
Fibroadenoma	1, 19, 27, 32	4	45,350
Fibrocystic Disease	4, 5, 7, 9, 11, 32, 36	7	61,907
IDC (Low Grade)	12, 17, 28, 40, 47, 50, 51, 54, 61, 65, 68	11	21,137
IDC (Interm. Grade)	6, 8, 13, 29, 30, 33, 35, 36, 37, 41, 42, 53, 58, 63, 66, 67, 70	17	44,219
IDC (High Grade)	5, 16, 23, 24, 25, 39, 46, 56, 59, 64	10	70,520
ILC	2, 4, 21, 22, 26, 45, 48, 49, 52, 55	10	53,612
DCIS	3, 18, 31, 34, 37, 44, 62	7	26,119
Mucinous	10, 14, 43, 60	4	26,348
Tubular	11, 69	2	3,347
Metaplastic	15	1	18,955
Total non-background	70	137	670,517

SFDI images, as presented in Fig. 1, provide information that could not be obtained via conventional multispectral acquisition. By demodulating high spatial frequency patterns, it is possible to eliminate image blurring due to light diffusion within the sample, resulting in decreased sensitivity to absorption and increased sensitivity to backscattering from the surface layer of tissue [16]. Sub-diffuse SFDI imaging enhances contrast to Rayleigh-type scatterers in surface tissues, which are mainly collagen fibrils and striations that may or may not be associated with disease [38]. This suggests that specific tissue types could respond distinctively to spatial frequency modulation, while other diseases could be detected through this contrast improvement. For example, some specific pathologies reveal an inherent texture at high frequencies that cannot be observed in the low-frequency domain, further facilitating differentiability [39], [40]. This is notably visible in Figs. 1.(e) and (k), which show demodulated images at high spatial resolution (f_x = 1.37 mm⁻¹). As the spatial frequency increases, contrast is enhanced to tumor-associated collagen structures. From now on, we will refer to scatter signatures as any behavior characteristic of a specific pathology, in terms of both textural and spectral/spatial-frequency information. We seek to find the scatter signatures of most, if not all, pathologies typically present in BCS interventions, and the similarities between them, which may hinder diagnosis for margin delineation algorithms.

Fig. 1.

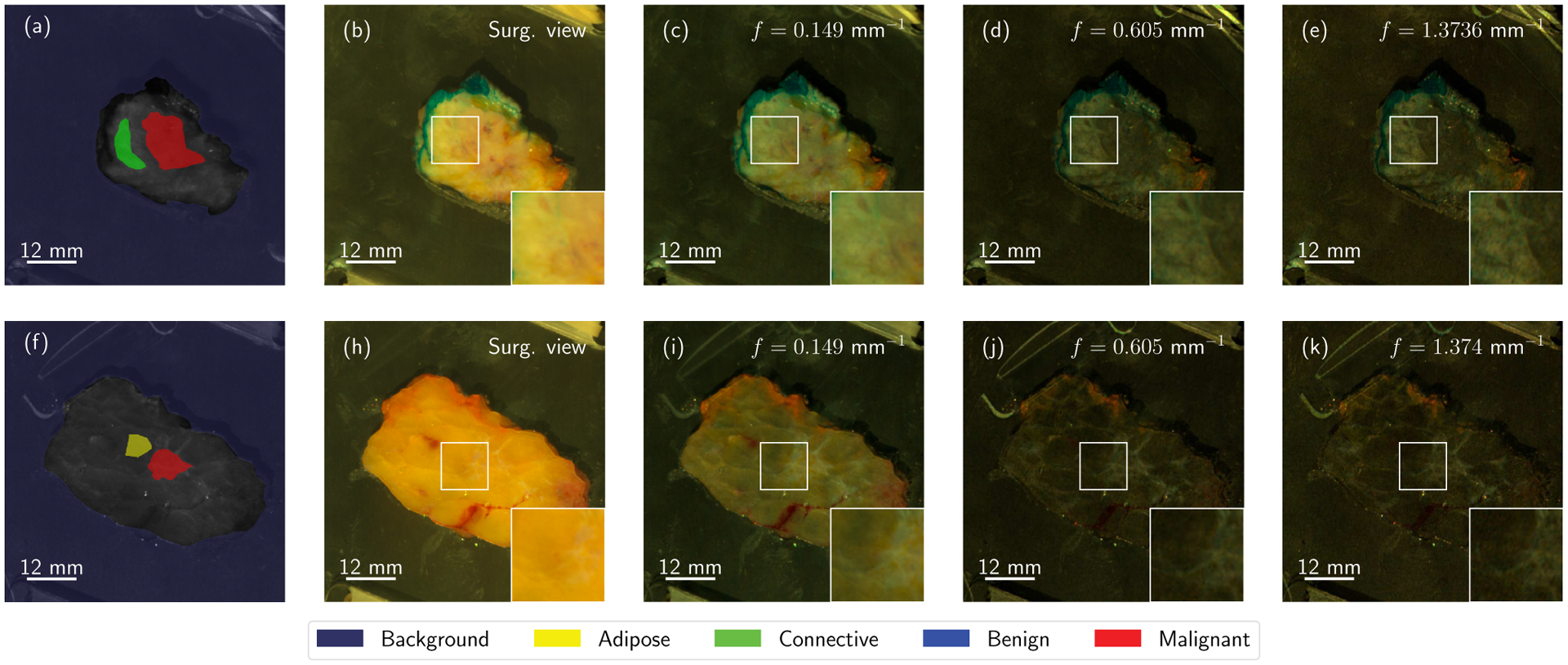
Two lumpectomy samples from the breast tissue dataset, namely samples 23 (top row) and 16 (bottom row). Structured light imaging reveals hidden textural contrast as a function of spatial frequency. Each of the specimens is accompanied by a set of Regions of Interest with known properties (a, f). Here, color reconstructions of demodulated reflectance data for f = 0.0 (b, h), f = 0.15 (c, i), f = 0.61 (d, j), and f = 1.37 mm⁻¹ (e, k) are shown to present how textural properties evolve as a function of the spatial frequency of the projected patterns. Best viewed in color.

B. Patch dataset production

Due to the limited number of available samples, and ROI pixels per sample, this preemptive study merely seeks to analyze the local texture and optical properties of SFDI images of breast cancer. Thus, a patch extraction algorithm was designed for balanced dataset production. A general outline of the process is depicted in Fig. 2. Specific tissue category quotas are initially specified for each of the known available tissue classes (12,000 patches per supercategory, resulting in a dataset of 60,000 patches). Then, a random population sub-sampling method is run iteratively until the quota is satisfied. The method proceeds as follows. First, a sample among those presenting with a specific tissue type is selected at random. Then, a random location within the ROI is selected. At this location, a square patch 31 × 31 pixels is extracted. The patch is also randomly rotated, uniformly in the range [0°, 360°] as is typical in dataset augmentation. Additional metadata is also included, namely (1) the specimen reference number, (2) the corresponding tissue category, and (3) its location within the ROI. The specific class is one-hot encoded to feed the classifier network later on. This process is repeated until the required amount of patches is obtained, guaranteeing a balanced dataset irrespective of the relative frequency of specific pathologies. The total number of patches per sample and ROI was kept under 500 (on average) to avoid redundancy in the training set. Additional measures were taken to ensure that miscalibrated or undesired data were not provided to the networks. Miscalibrated patches, i.e. data with reflectance outside of the range R_valid ∈ [0, 0.99], were automatically discarded from the generated dataset during training and validation. Finally, the fifteen categories were summarized into five main supercategories (shown in Table II), as discovered through previous successful classification experiments [41]. The initial objective of this work is to separate adipose tissue, collagen and elastin in connective tissue, benign growths, and malignant tumors. Additionally, Fibrocystic Disease (FD) should exhibit a certain connection with connective tissue and benign growths, since these particular tissue types are present in the disease.

Fig. 2.

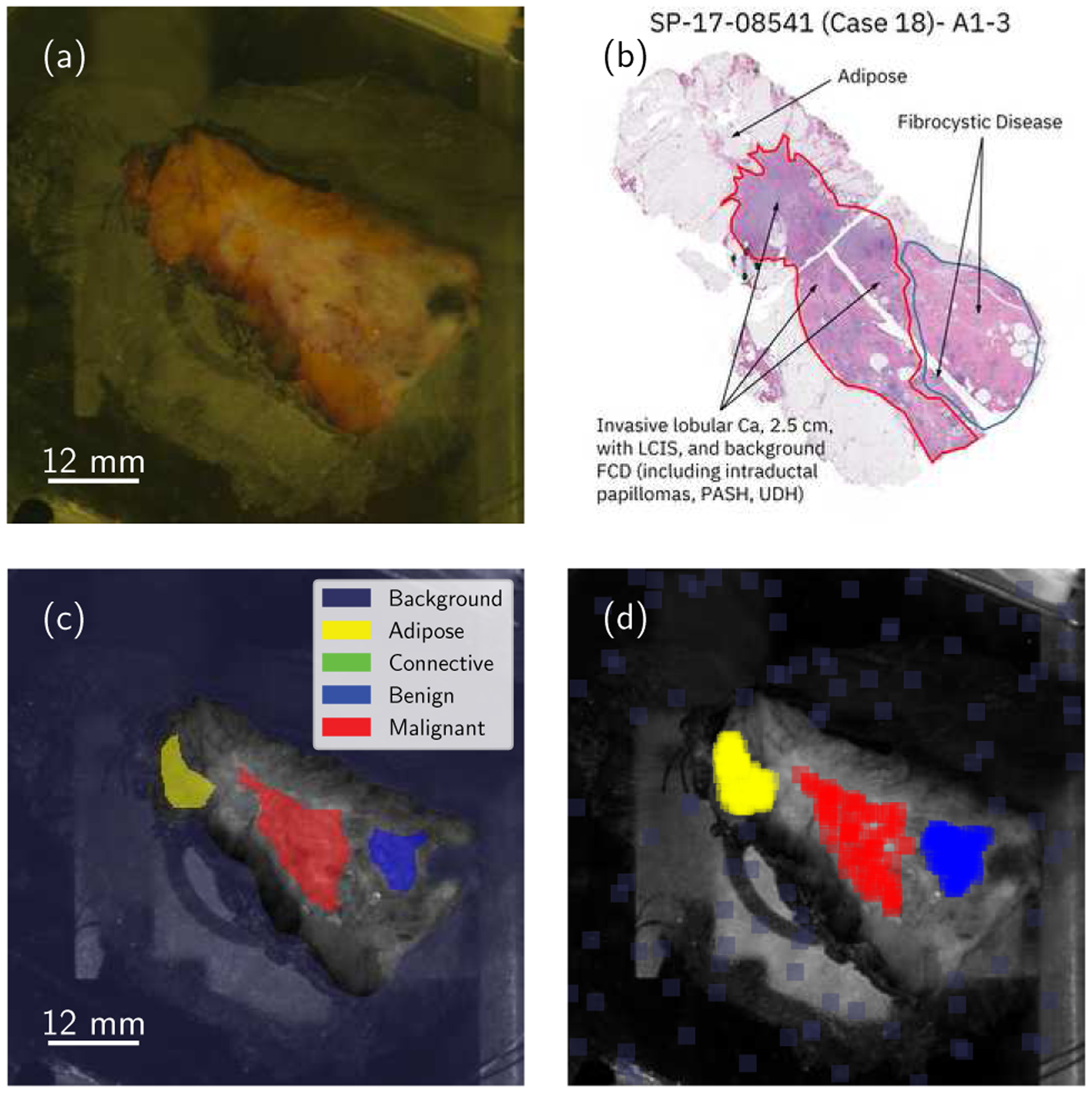
General summary of the complete data extraction protocol. Each specimen is visually inspected (a) and co-registered with H&E stain histology data (b). This analysis results in conservative, manually-generated Regions of Interest (c) which are then uniformly sampled and filtered depending on additional requirements (d). Best viewed in color.

Table II.

Tissue supercategories and total number of ROIs.

Tissue group	Tissue subtypes	n
Adipose	Adipose	39
Connective	Connective Tissue	22
Benign	Fibroadenoma, Myofibroblastic, Benign Phyllodes	6
Fibrocystic Disease	Fibrocystic Disease	7
Malignant	IDC (Low Grade), IDC (Interm. Grade), IDC (High Grade), ILC, DCIS, Mucinous, Tubular, Metaplastic	62
Total	70 samples	136 ROIs

C. The neural network pipeline

To connect the four domains described in Section I (Introduction), a series of neural networks must be prepared and trained. Fig. 3 presents a schematic that connects each of the domains of interest. First, a primary autoencoder with sufficient capacity –Fig. 3.(a)– is used to first compress textural and spectral/spatial-frequency data r into low-dimensional keywords $z\in {ℝ}^m$. This first model must be capable of reproducing textural information with sufficient fidelity, which will be measured in terms of a reconstruction loss that compares the input patches $r\in {ℝ}^{n_x\times n_y\times n_{\text{ch}}}$, with the reconstructed output $\widehat{r}\in {ℝ}^{n_x\times n_y\times n_{\text{ch}}}$ at the other side of the bottleneck, $\mathcal{L}(r,\widehat{r})$, where n_x and n_y are the width and height in pixels, respectively, and n_ch is the number of input channels ($n_{\text{ch}}=n_{\lambda }{n}_{f_x}$, with n_λ number of wavelengths and $n_{f_x}$ number of spatial frequencies per wavelength). This network is a skip-connection convolutional variational autoencoder with an auxiliary discriminator; it is composed of encoder q_θ(z|r) and decoder p_ϕ(r|z). Similar schematics have been previously shown to improve reconstruction quality when compared to ${\mathcal{L}}_2$ distances for natural images [42], [43]. Once high-dimensional textural and spectral information is compressed into low-dimensional keywords, an optional next step is to produce a human-interpretable representation. This can be achieved with a secondary autoencoder, depicted in Fig. 3.(b). The network is a multi-layer perceptron MMD-VAE [44] with skip connections [45]. The rich encoding at the primary autoencoder’s bottleneck can be used for classification, as per Fig. 3.(c). Diagnostic accuracy was used here as a measure of separability at the keyword level, z. This is done via an additional neural network, namely a multi-layer perceptron with skip connections, which allows the translation of keywords z into known pathology classes $\widehat{y}$.

Fig. 3.

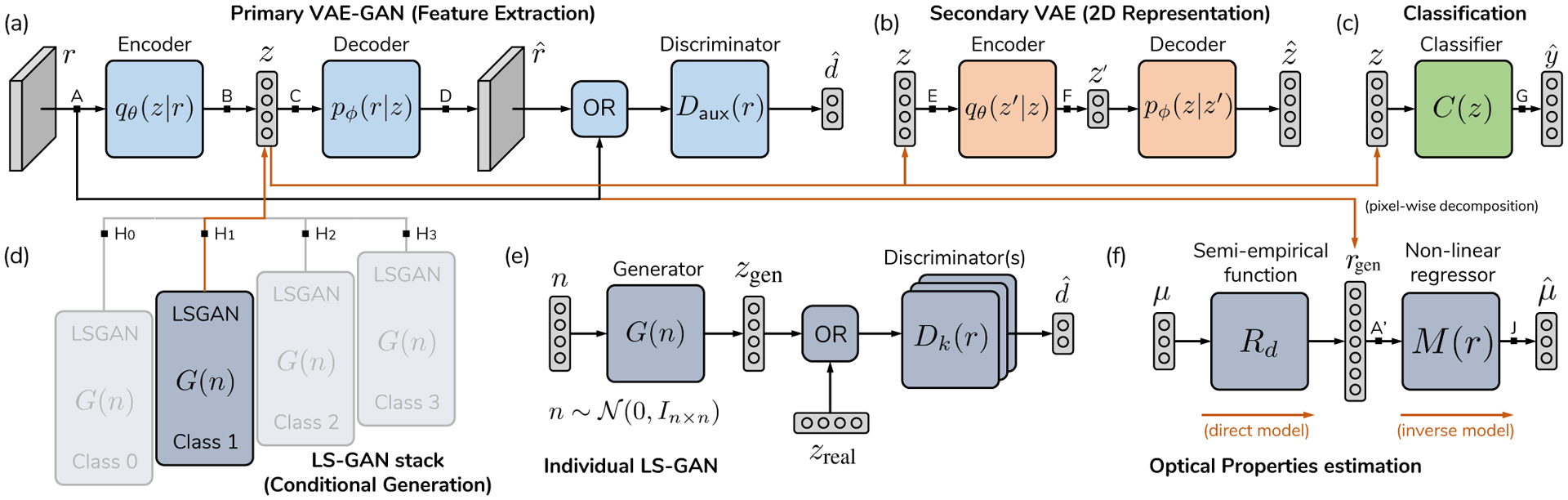
Network setup for the four domain problem. (a) Reflectance data r is introduced into a primary autoencoder (i.e. $r\to z\to \widehat{r}$), generating a low-dimensional translation of spectral and spatial data. (b) A secondary autoencoder $z\to z^{\prime }\to \widehat{z}$ transforms this first domain into a two-dimensional domain z′, where the dataset can be represented. The same codeword z can be used for classification (c). Conditional sample generation is achieved with a set of small multilayer perceptron Least-Squares GANs (d), with multiple decoders to avoid mode collapse (e). Optical properties estimation is achieved via an MLP non-linear regressor, which is trained with domain randomization, using spectra generated by giving random OP values to a deterministic semi-empirical function (f). The following paths represent each of the objectives in Fig. 1, as follows: $\overline{AB}$ (Feature Extraction), $\overline{\mathit{\text{ABEF}}}$ (Visualization), $\overline{\mathit{\text{ABG}}}$ (Classification), $\overline{H_0/\dots /H_{n}CD}$ (Generation), $\overline{A{A}^{\prime }J}$ (pixel-wise OP estimation). Black arrows are real connections in the graph, while orange connections represent copying operations.

Sample generation is achieved with a stack of skip-connected MLP Least-Squares Generative Adversarial Networks (LS-GAN) [46] which are trained on class-specific bottleneck keywords. Let $H_0,\dots ,H_{n_{\text{cls}}-1}$ be each of the possible hypotheses (tissue categories), with n_cls the total number of categories. Each LS-GAN is trained only with the fraction of the learned keywords that belong to a specific tissue category, which can be seen as a conditional variable z|H_k, with H_k the tissue type to be generated by that GAN. One single LS-GAN has an ensemble of N_disc = 10 discriminators and one generator, which is known to reduce mode collapse [47]. Gaussian noise $n\sim \mathcal{N}(0,\sigma )$ is injected into the input of the discriminators and σ is annealed towards zero during training to further regularize the generator [48]. This modular approach allows us to employ the same feature extraction network for conditional generation of pathology-specific keywords without requiring re-training of larger models. Learned textural features can consequently be reused with each independent generator. Lastly, OP estimation is achieved via uniform random sampling of the forward, semi-empirical model of reflectance in the spatial frequency domain, further explained in the Supplementary Material, Section S.I.A. The specifics of the method are explained in Section II-D.

D. Optical properties estimation via input randomization

We apply previous existing work from Zhao et al. [32] and Stier et al. [33], but with a hybrid forward model that combines diffuse and sub-diffuse regimes. The forward model is governed by the following equation:

$$R\left(f_x,\lambda \right)=\{\begin{array}{c}{R}_d\left(f_x,\lambda ;{\mu }_s^{\prime },{\mu }_a\right),f_x\le 0.2{\text{mm}}^{-1},\\ R_{d,sd}\left(f_x,\lambda ;{\mu }_s^{\prime },\gamma \right)f_x\ge 0.5{\text{mm}}^{-1},\end{array}$$ (1)

where R_d corresponds to the diffuse approximation of the RTE [10], and R_{d, sd} is the semi-empirical approximation of sub-diffuse behavior used by McClatchy et al., [38] for wide-field imaging. The former is a function of the reduced scattering coefficient ${\mu }_s^{\prime }$ and the absorption coefficient μ_a, while the latter is dependent on ${\mu }_s^{\prime }$ and a phase function parameter γ (technical specifications are provided in the Supplementary Material). Inverse function learning is illustrated in Fig. 3.(f). For this particular setup, Equation 1 was prepared to return a spectrum $R_d\left(f_x;{\mu }_s^{\prime },{\mu }_a,\gamma \right)$ from a given triplet of input parameters $\left({\mu }_s^{\prime },{\mu }_a,\gamma \right)$. This constitutes the direct model $f:\left({\mu }_s^{\prime },{\mu }_a,\gamma \right)\to R_d\left(f_x\right)$. The inverse model $f^{-1}:R_d\to \left({\mu }_s^{\prime },{\mu }_a,\gamma \right)$ is produced with a neural network, which is trained with a synthetic dataset of optical properties and reflectance pairs. The output of the forward model is given to the input of the optical properties estimator network, and the network is expected to return the exact parameters that produced such reflectance curve. This inverse operation requires minimizing the mean square error (MSE) between the actual value y and the network’s estimate $\widehat{y}$. Optical property estimation inputs were established within well-known value ranges: ${\mu }_s^{\prime }\in [0.01,4.0]\supset [0.4,1.8]{\text{mm}}^{-1}$, γ ∈ [1.0, 4.0] ⊃ [1.4, 2.2] mm⁻¹ as per Kanick et al. [11] and McClatchy et al. [38]; and μ_a ∈ [0.01, 4.0] mm⁻¹ and n = 1.4 as per Jacques [49] and Cuccia et al. [10]. Relevantly, reflectance data must be monotonically decreasing with respect to spatial frequency [9], [10], [38], [50]. This is not guaranteed for every possible triplet of $\left({\mu }_s^{\prime },{\mu }_a,\gamma \right)$ in the aforementioned ranges when combining the diffuse and sub-diffuse models, as the subdiffuse model does not consider absorption, potentially resulting in a curve that is not monotonically decreasing. For those values, such a curve is not physically possible, and hence it makes no sense to use those combinations of OP values in training. Thus, in order to train a proper model that does not misinterpret the presence of noise or miscalibrated data as physically implausible optical properties, values for $\left({\mu }_s^{\prime },{\mu }_a,\gamma \right)$ that did not result in a monotonically decreasing R_d(f_x) were discarded from the training and test sets. As a result, the network must find a combination of optical properties that fits the data and, simultaneously, results in a feasible curve. The network was trained on a synthetic dataset of 27 × 10⁶ uniformly spaced points (300 × 300 × 300 grid) and tested on a sparser grid of 216,000 points (60 × 60 × 60 grid) until reaching a test MSE of 10⁻⁴, at least two orders of magnitude below the estimation errors inherent to the direct OP model [38], and equivalent to 1–5% MSE at the lowest reflectance values.

E. Bottleneck clamping

Generally, neural networks have fixed architectures that remain constant across training and inference. This implies that an autoencoder with a fixed bottleneck size will use all of its units to represent data. This contrasts with typical dimensionality reduction methods such as the Singular Value Decomposition (SVD) and/or Principal Components Analysis (PCA), where the size of the latent space can be chosen from a set of basis vectors. In these settings, the higher the number of vectors, the better reconstructions will be. To achieve a similar effect, the primary autoencoder employed a variant of bottleneck clamping, a technique used differently in other works [51] to restrict the content available at the bottleneck during training. In the proposed variant, clamping is performed by the gradients backpropagating towards the encoder for one or multiple units in z. In our particular case, we clamped the bottleneck stochastically, as shown in Fig. 4, so that for a given minibatch, the k-th unit is selected at random and trained to improve upon the reconstruction provided by the (k−1) previous bottleneck units, by establishing the following optimization problem:

$$\begin{gathered} \underset{\theta ,\varphi }{\text{minimize}}\mathcal{L}(\widehat{r},r) \\ \text{subject to }\frac{\partial \mathcal{L}}{\partial z_i}=0,\forall i\ne k. \\ {z}_i=0,\forall i>k. \end{gathered}$$ (2)

Fig. 4.

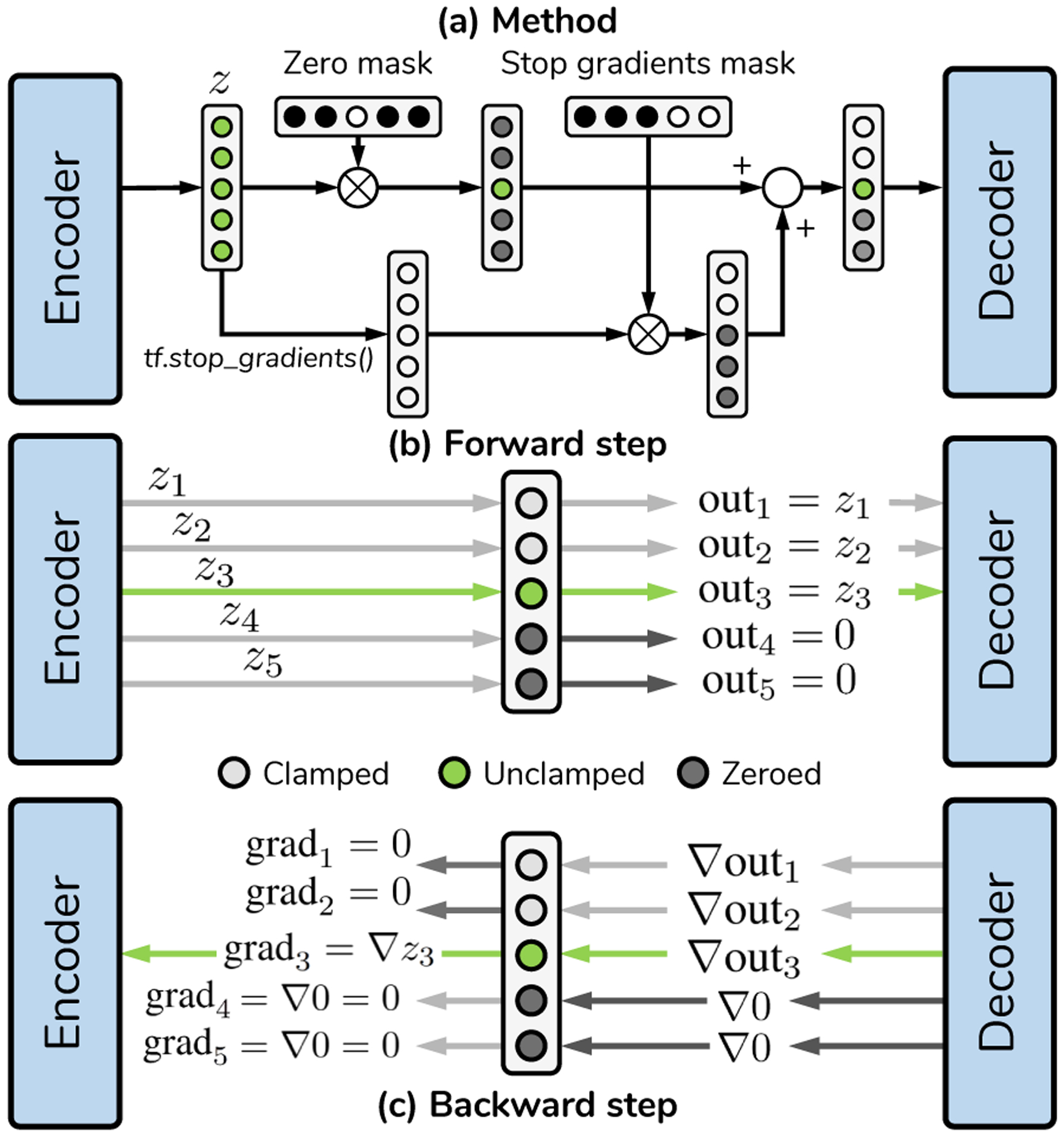
Bottleneck clamping for dimensionality reduction. Schematic analogous to [51] but for all coordinates in a bottleneck. (a) Process for generating words of length 3 (i.e. training the third unit in z) in a primary bottleneck with n_z = 5. (b) Forward step, showcasing which values are transmitted to the decoder. Units past the third one are zeroed out. (b) Gradient backpropagation of the given keyword. The gradient is cut for all coordinates except the one under training, thus in this step the encoder must modify the third coordinate to improve the reconstruction error given previous unit values. Each unit is trained stochastically within a given minibatch. After training, all units in the bottleneck are left unclamped.

A summarized schematic of the TensorFlow implementation is provided in Fig. 4. By changing k stochastically, the model attempts to minimize all the optimization problems in Equation 2 simultaneously. In general terms, the algorithm attempts to replicate the SVD but with a nonlinear network, where each individual unit is forced to improve the current reconstruction error by adding more information. This results in the network indirectly reserving parts of its capacity to solving each individual optimization problem, which we have observed results in slower convergence time at the expense of controlling reconstruction errors as a function of bottleneck size. Nonetheless, obtaining an adjustable bottleneck was fundamental in understanding the role of texture, as explained in Section III-C.

III. Results and discussion

A total of five experiments were carried out. The training regimes of each individual network are given in Table III, and do not change unless stated otherwise. The exact dimensions of the networks and layers are provided in Section S.I.C of the Supplementary Material.

Table III.

Simulations and training schedules

Parameter	(1) Competition	(2) Primary AE	(3) Secondary AE	(4) Classifier	(5) OP learning	(6) LS-GAN
Training mode	Fixed lr with linear decay	Fixed lr with linear decay	Fixed lr with linear decay	One-cycle policy	One-cycle policy	Fixed lr with linear decay
Learning rate lr	1 × 10−5 to 0.0	1 × 10−5 to 0.0	1 × 10−4 to 0.0	-	-	2 × 10−5 to 0.0
Warmup (iters)	0	0	0	50 × 103	500 × 103	0
Cooldown (iters)	150 × 103	150 × 103	100 × 103	50 × 103	500 × 103	250 × 103
Minibatch size	16	16	128	16	32	128
No. of iterations	300 × 103	300 × 103	900 × 103	100 × 103	2 × 106	500 × 103
Cycle size T	-	-	-	(100 × 103)	(1 × 106)	-
No. of cycles	-	-	-	1	1	-
lr range (min, max)	-	-	-	[0.0,1.0 × 10−4]	[0.0, 1.0 × 10−4]	-
Optimizer	Adam	Adam	Adam	Adam	Adam	Adam
Instance noise (GAN)						σ = 0.3
Evaluation	Every 1k iters	Every 1k iters	Every 1k iters	Every 1k iters	Every 1k iters	Every 1k iters
β (AEs only)	1.0	1.0	1.0	-	-	-
Dropout rate	5%	5%	5%	10%	10%	-
Patience (early stop)	-	-	-	50 epoch, accuracy	50 epoch, MSE	-
Train time per model	~ 3 to ~ 21h, model-dependent	~ 21h	~ 2 h 40 min	~ 5 min	1 h, ~ 50 min	~ 6 h, 30 min

A. Designing the primary autoencoder

The final primary autoencoder is the result of a series of design choices that are specified in Sections II.C and II.E, as well as Sections B and C in the Supplementary Material. Such decisions result in improved reconstruction errors and textural fidelity, which are crucial for the task at hand. For comparison, Fig. 5 shows a series of networks that gradually introduce each of the fundamental modifications that enable successful dataset replication. Six networks in total were tested under 3-fold sample-wise cross-validation (CV). The first four, namely (A) a Standard convolutional VAE, (B) the former VAE but including skip connections, (C) an MMD-VAE, and (D) the previous VAE with skip connections, utilize global averaging to connect the convolutional feature maps to the MLP sections. The last two are our contributions, i.e. (E) an MMD-VAE with skip connections and fully-connected layers connecting convolutional layers with MLP layers, and (F) the same network, with an auxiliary discriminator (G). All the networks are provided in the repository. Given a constant number of iterations, the final model is the best of all possible options in terms of test MSE (Fig. 5.(a)), test Structural Self-Similarity (SSIM) (violin plots of Fig. 5.(b)) and average variance of the Laplacian across channels, as shown in Fig. 5.(c). Architectures (F) and (G), which include the intermediate fully-connected layers achieve faster convergence and lower MSE/SSIM, while (G) best fits the Laplacian variance histogram. The latter metric demonstrates that (G) preserves high-frequency information, observed after applying the Laplacian operator across the x and y dimensions of the patch, has the same distribution as the real data.

Fig. 5.

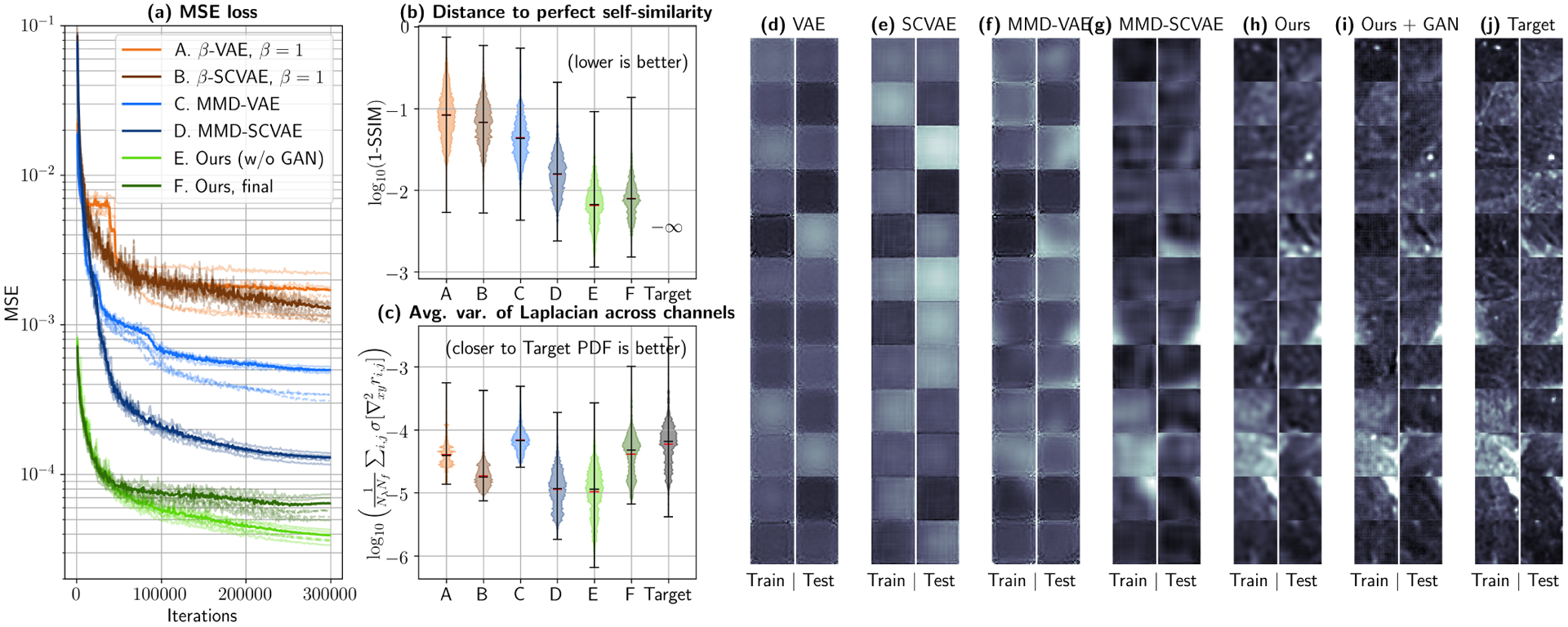
Autoencoder comparison via 3-fold cross-validation. (a) Mean Squared Error (MSE) for all the tested architectures. Transparent dashed curves depict training errors, while continuous curves correspond to test errors for each fold. The average test error is shown as a thicker, non-transparent line for each network. Architecture E (MMD-SCVAE with fully connected connections at encoder and decoder, Gradually Upscaling Network and auxiliary fully connected feature maps) achieves the lowest average test MSE in the least amount of iterations. (b) This can also observed by evaluating the distance to a perfect test SSIM (1.0), where architectures E and F show up to an order-of-magnitude improvement in self-similarity when compared to controls. (c) However, most architectures still return blurred reconstructed patches, which can be quantified by the average variance of the Laplacian across channels. By using an auxiliary GAN Discriminator (Architecture F), high frequency components can be better recovered, which translates in a variance histogram that better follows the true distribution. Reconstructions returned by each of the proposed architectures can be qualitatively observed in (d)–(i) and compared with the true data (j). Reflectance values are shown in the range [0.0, 0.04] at spatial frequency f_x = 0.61 mm⁻¹ and wavelength λ = 500 nm.

These quantitative results can be qualitatively observed in the reconstructions provided by each individual network in Fig. 5(d)–(i), by comparing them to the target images (Fig. 5(j)). While these networks work well in benchmarked datasets such as MNIST and CIFAR-10 (see provided code), modeling texture in SFDI data proves to be a much more delicate and ill-posed problem, which is challenging to most architectures. Two relevant concepts must be noted here. First, that wall clock time differs between architectures, e.g. ~3 hours for VAE (A) vs. ~24 hours for (G). However, all architectures saturate at MSE/SSIM scores orders of magnitude above (F) and (G), and all except (G) fail to replicate the variance-of-the-Laplacian histogram of the patch dataset. Secondly, it is important to note that bottleneck clamping is not implemented in networks (A) through (E), which means that convergence for the last two networks would be faster if they were allowed to train with 256-long words for all minibatch steps.

B. 2D representations

Low-dimensional, unsupervised representations of the 256-dimensional keywords, when combined with adequate validation tests, can provide significant insight with regards to how well each pathology is uniquely identifiable. Fig. 6 presents the same experiment, performed separately for 31 × 31-pixel patches (shown in the top row) and individual spectra (bottom row). In Figs. 6.(a) and (f), the 2D projection of the 256-dimensional feature-space keywords is shown, color-coded by tissue category. The point cloud corresponds to 80% of the dataset, while 20% was left aside for validation control. Identical scatter plots are given in (b) and (g), but are instead color-coded by the specimen number of origin. Generally, there appears to be a gradual change in imaging conditions. Such differences may be consequence of improvements in the acquisition protocol, given the experimental nature of the imaging device and dataset, and considering the fact that this separation becomes negligible for later samples.

Fig. 6.

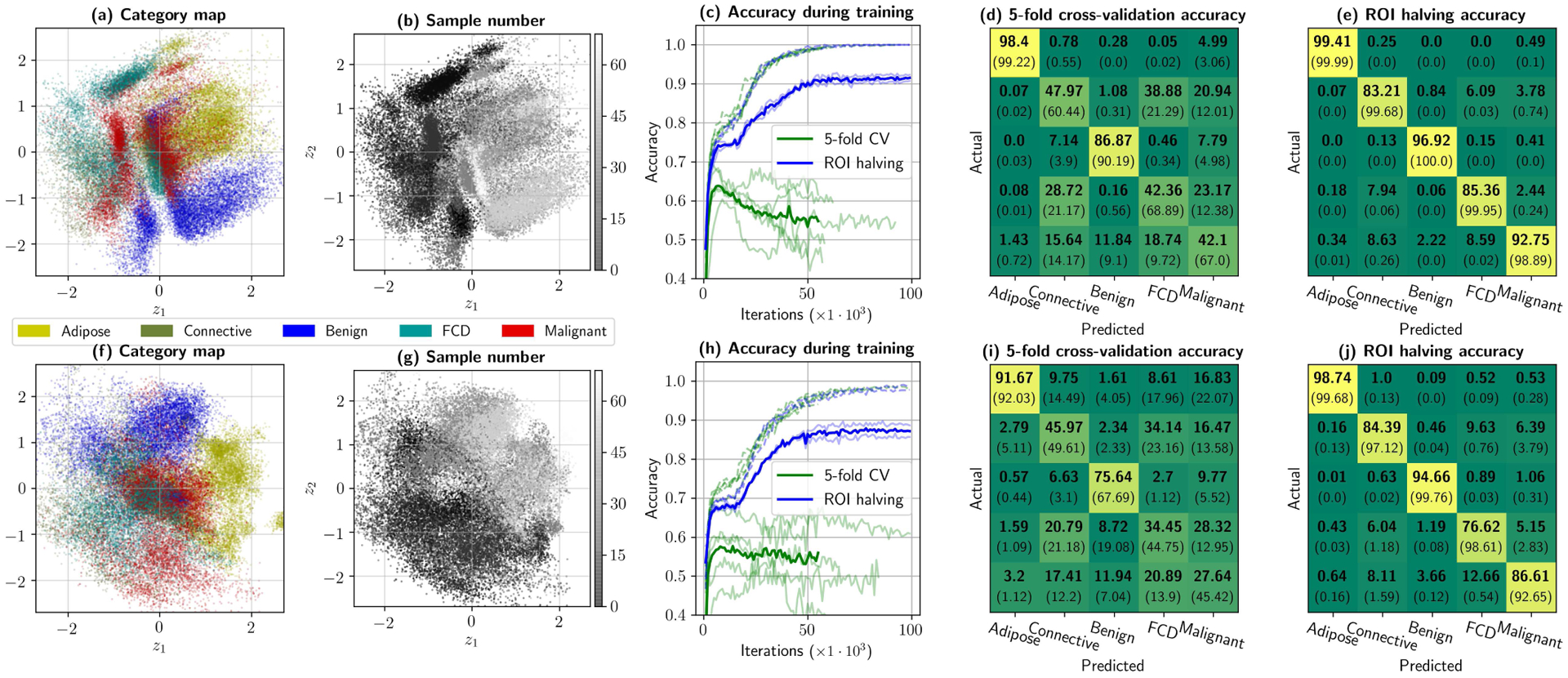
Initial dataset considerations provided by the neural framework. Top row shows (a) the 31 × 31-pixel patch dataset projected into 2D, color-coded by tissue supercategory, (b) the same plot but color-coded by sample number of origin, (c) classifier accuracies observed during training for 1000 random samples of the training and test sets in 5-fold cross-validation and ROI halving experiments. Finally, the confusion matrices in (d) and (e) provide the best test (in bold) and training (between parentheses) accuracies per category, for 5-fold cross-validation and ROI halving, respectively. Bottom row –plots (f) through (j)– provides analogous results for pixel-wise analysis. In this dataset, inter-sample variability dominates intra-sample variability by a significant margin, to the point that spectra can be nearly perfectly identified if the training set includes information from its specimen of origin.

Some conclusions can be drawn from these maps. First, that there is significant overlap between connective tissue, malignant tumors and fibrocystic disease, even with texture analysis, suggesting that there are spectral and/or textural properties shared among these categories. This is consistent with recent work in multiphoton histology, where collagen fibers have been observed providing structure to malignant tumors [36]. Macroscopically, this would present as a spectral superposition of structural (scattering) and chemical (absorption) properties, which inevitably hinder classification. Secondly, adipose tissue and benign lesions show significant unsupervised separability in both simulations, with reduced inter-sample variability in the 2D maps, implying that these particular categories consistently respond with a specific spatial frequency and spectral signature that can be identified by unsupervised means.

These unsupervised, qualitative results can be contrasted with what is returned by the classification branch of the framework. During training, a large generalization gap was reported in 5-fold CV for both pixel-wise and patch-wise analysis, as can be observed in Fig. 6.(c) and (h). In fact, both models overfit past the first ten thousand iterations for 5-fold CV. The best possible results for 5-fold CV (at 7 × 10³ and 10×10³ training iterations for patches and pixels, respectively) are left in Fig. 6.(d) and (i), showing severe accuracy deficiencies. While patch-wise analysis improves malignancy detection accuracy by about 15% (which could be observed succinctly by how point clouds for malignant subtypes are slightly more separated from connective and fibrocystic tissue in Fig. 6.(a)), these cross-validation results agree with the best global classification accuracy reported with this dataset, i.e. 75–80%, on previous work that evaluated leave-one-out cross-validation on an ensemble of patch analysis networks [41]. In contrast, using half of each ROI for training and the other half for testing shows that overfitting never truly occurs –albeit the model shows an evident, reduced generalization gap– implying that if inter-sample variability is eliminated from the problem, classification becomes trivial. Such results allow us to conclude that the presence of connective tissue in breast cancer, and the fact that Fibrocystic Disease presents in most cases as a combination of benign growths and connective tissue [52] both constitute the main sources of errors in a vanilla classification environment, indicating that a successful algorithm will require the inclusion of local, case-specific information to reliably assess tumor margin status.

C. The role of texture in classification accuracy

The previous study is demonstrably insufficient to prove that texture truly contributes in pathology identification as, perhaps, mere redundancy could be the cause of accuracy improvements observed in Fig. 6.(e). Proper empirical proof can be obtained with an ablation test on a primary AE trained with bottleneck clamping, which allows for plotting graphs analogous to those used in PCA/SVD-based dimensionality reduction, where reconstruction accuracy (or explained variance) can be plotted with respect to latent space size. The experiment required inter-sample variability to be omitted and, thus, ROI halving validation was performed: the top half of each ROI was used for training, and the bottom half was used for testing, and viceversa, resulting in two validation folds that only reflect intra-sample variability.

Results are provided in Fig. 7. In this simulation, the size of the bottleneck was iteratively increased from n_z = 1 to n_z = 256, and a classifier was trained for keywords of length n_z. This was feasible in practice thanks to clamping the bottleneck during training, and therefore a single VAE needed to be trained, following Table III.(2). The n_z-th classifier is trained with the first n_z coordinates from this autoencoder. Reconstructions with only these coordinates can be obtained as in Fig. 4.(b), by setting the remaining coordinates to zero. The proposed framework, in its current configuration, allows us to observe the effect of bottleneck size in two different domains simultaneously, namely the classification domain (Fig. 7.(a)) and the measurements domain (Fig. 7.(b) and (c)). First, classifier accuracy for each of the tissue supercategories is left in Fig. 7.(a). Fig. 7.(b) presents the MSE for the complete dataset as a function of bottleneck size, as well as the MSE between the average spectrum of each patch and the average spectrum of its reconstruction at the primary AE output. Fig. 7.(a) shows a set of patches reconstructed with n_z-long keywords (n_z = 1, … , 50) at f_x = 0.15 mm⁻¹ and λ = 550 nm.

Fig. 7.

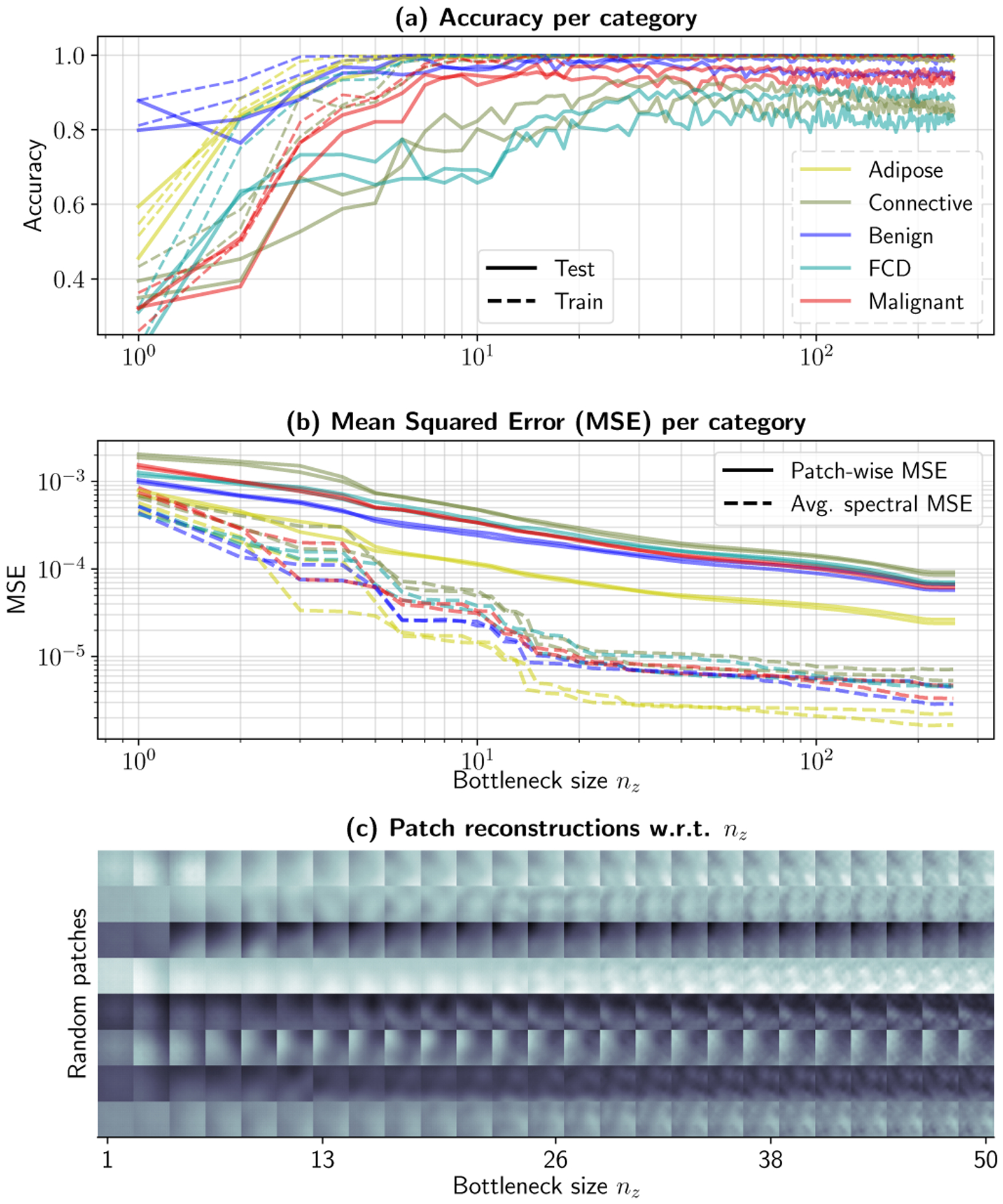
An ablation test can evaluate the effect of bottleneck size on classification accuracy and reconstruction quality. Experiment results obtained via ROI halving. Subplot (a) shows per-category classification accuracy for training and test sets for both halves, while (b) evaluates the patch-wise MSE and average spectral MSE between original and reconstructed patches. Finally, (c) shows reconstructions for different bottleneck sizes. Bottleneck clamping allows the use of a single autoencoder for this experiment. The rest of the coordinates are set to zero and the reconstruction is extracted at its output. A high-resolution version of (c) is provided in the Supplementary Material.

Interestingly, the first crucial observation is that the average spectral properties of individual patches (in both spatial frequency and wavelength) stabilize at about n_z = 20, while patch reconstruction errors consistently improve with n_z. In the patch domain –Fig. 7.(c)–, reconstructions from n_z = 1 to n_z = 20 qualitatively corroborate that low-frequency spatial information (i.e. the presence of darker or lighter corners, or the presence of millimeter-sized objects) is gradually included as n_z is increased. These phenomena would correspond to changes in illumination, tumor boundaries, or folds resulting from positioning the sample, which typically would be observed in the first Principal Components or Singular Vectors. Further information, which does not improve the average spectral properties as significantly, are introduced circa n_z = 20. These components correspond to higher frequency spatial information, i.e. finer details and texture, and as seen in Fig. 7.(c). It is during this transition, at n_z = 10, …, 40, where the introduction of finer details coincides with an improvement in classification performance for Fibrocystic Disease and Connective tissue, from ~ 70% to ~ 85% accuracy. In other words, performance improves as local structural variations surrounding a pixel is introduced and/or learned, to the point of allowing for individual identification, supporting parallel work that showed similar results on single-frequency, single-wavelength patch analysis [40]. It is important to note, however, that malignant tissue subtypes reach peak accuracy before higher-frequency texture is encoded in the keywords, suggesting the possibility of patient-specific spectral information that could be used in a case-by-case basis for margin delineation.

D. Sample generation

Prior to quantification, it is interesting to consider the qualitative properties of the generated patches in the multiple available observation domains. Fig. 8 shows real and synthesized patches for the five individual super-categories of interest. Data was obtained from an LS-GAN stack trained with 80% of the patch dataset (with 20% left for validation). The outputs of the LS-GAN stack are then provided to the primary bottleneck, where the primary decoder transforms the feature keywords into 31 × 31-pixel patches. The plots show RGB reconstructions of individual patches, where each column represents a single patch at the four available spatial frequencies. CIE 1931 Color Matching Functions with a D-65 illuminant were used for the reconstructions [53]. The same points can also be observed in 2D space, in Figs. 8.(a’) through (.e’). These scatter plots show the original training data in bright colors, and the synthesized data in a darker shade of the same color, for each of the individual pathologies. The complete 2D map is provided as a faint gray scatterplot, so that each figure can be consistently compared with Fig. 6.(a).

Fig. 8.

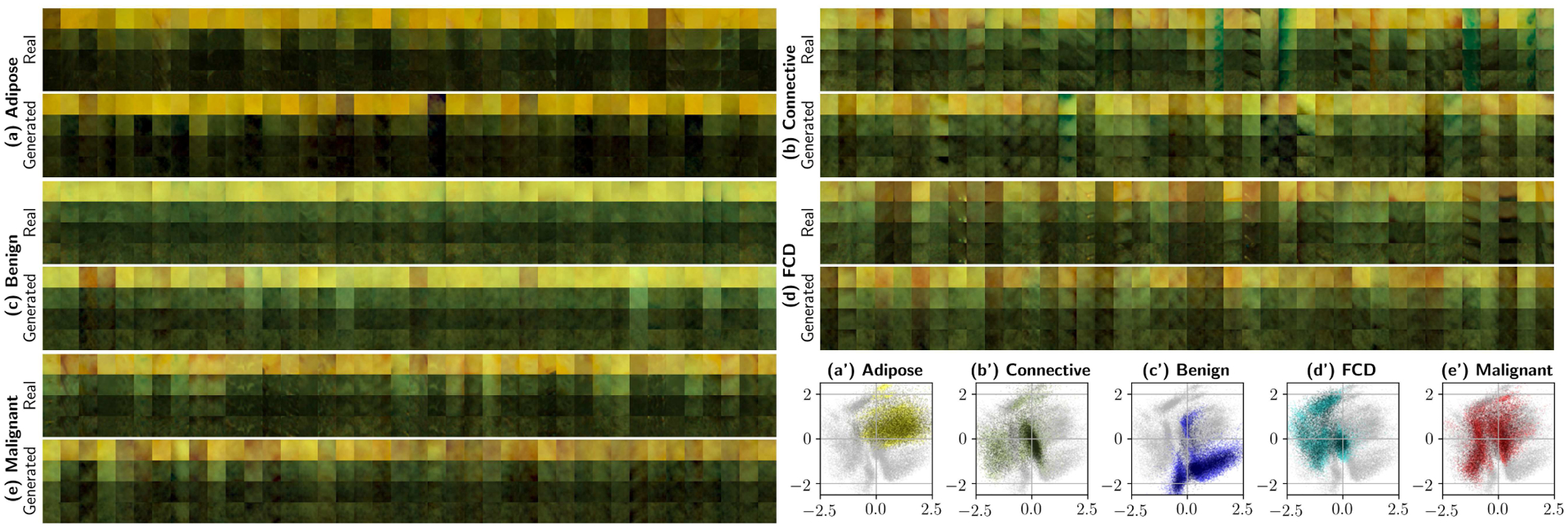
Generating patches at various frequencies with the LS-GAN stack. The following are outputs of the primary autoencoder to synthesized 256-dimensional feature keywords. This experiment uses the complete dataset (80% for training, 20% for validation). Plots (a) through (d) show spectra-to-RGB reconstructions of real and generated patches, where each column displays a patch at the four different spatial frequencies (0.0, 0.15, 0.61, and 1.37 mm⁻¹). Subplots (a’) through (e’) show 5000 artificially generated samples for each supercategory projected onto the 2D space of the secondary bottleneck (shown in Fig. 6.(a)). In these scatter plots, light colored points represent reference training data, and darker points correspond to the synthesized data. These 2D projections qualitatively ensure correct sample generation without significant mode collapse. Best viewed in color.

Many of the conclusions extracted via supervised methods can be repeated here. The 2D maps allow us to verify that each of the individual LS-GANs with multiple discriminators do not exhibit significant mode collapse, as all the different training set point clouds superimpose adequately with the original training data. Adipose and benign cysts present a very specific spectral signature, which is separable from each other and the rest of the categories. Once again, the presence of elastin and collagen in malignant subtypes and fibrocystic disease can be observed from a different perspective, as the three categories share a region in 2D space near the coordinate origin where connective tissue –Fig. 8.(b’)–is the most dominant subtype. Moreover, the presence (or lack thereof) of multiple modes or point clouds separated by specimen number in some pathologies suggests that certain signatures (e.g. adipose tissue and benign cysts showing few or no modes) are easily generalizable to all specimens, whereas others (FCD and malignant tumors) are not, again suggesting that the use of prior information would be beneficial in margin delineation with deep classifiers.

It is also important to note that some of the categories exhibit the presence of surgical ink, i.e. Fig. 8.(b), revealing that connective tissue is often marked with blue ink which, considering that all slides are intermediate cuts, implies some degree of perfusion of surgical ink, which may be obstructing proper classification. All in all, unsupervised qualitative analysis allows the observer to extract conclusions that can then be contrasted with canonical classification experiments, as in Fig. 6.(d), (e), (i), and (j).

E. Optical properties and inter-sample variability

In the following quantitative analysis, pixel optical properties are compared between real and generated data. The 80 : 20 dataset split for training/validation was used, since using ROI halving and/or 5-fold cross-validation will only show the variations in OPs between folds and/or halves, and we wish to compare how well the GAN stack can replicate and synthesize the variability observed in the complete dataset. Importantly, the OP estimator never observes actual data, and thus we only wish to analyze how well the trained GANs generate data with accurate optical properties, and how well the OP estimator fits the semi-empirical function to the data.

Two figures were devised. Fig. 9 studies how well OP estimation can reconstruct the original data, by evaluating the coefficient of determination between the input data and the estimated reflectance, which is a result of fitting R_d(f_x) (Equation 1) with the optical properties estimated by the neural network, $\left({\widehat{\mu }}_s^{\prime },{\widehat{\mu }}_a,\widehat{\gamma }\right)$. Fig. 10 indirectly compares real and synthesized data by analyzing similarities in its optical properties, given the justified assumption that the OP estimator is sufficiently accurate. Results in Fig. 9 show that this assumption is valid, for both real –Fig. 9.(a)– and generated data –Fig. 9.(b)– but that model precision changes with respect to wavelength. Particularly, the first wavelengths show average standard errors within 15%, typical of LUT and least-squares fitting of R_d [32], [33], while the 700–800 nm region stays under 6–7%. This is due to two main reasons. Firstly, at 490 and 550 nm absorption due to hemoglobin is significant, thus violating the fundamental condition for the diffuse approximation of the RTE to hold $\left({\mu }_s^{\prime }\gg {\mu }_a\right)$. Secondly, light source instabilities and changes in illumination conditions due to the various shapes and sizes of the tumors reveal inconsistencies at higher frequencies. This is expected; note that the plot is in logarithmic scale, and we refer to variations for low reflectances (1% – 5%), where low SNR and changes in illumination with respect to a flat reference phantom will cause random fluctuations that may compromise monotonicity and consistent decay in the measurements, resulting in incorrect fitting of the theoretical model.

Fig. 9.

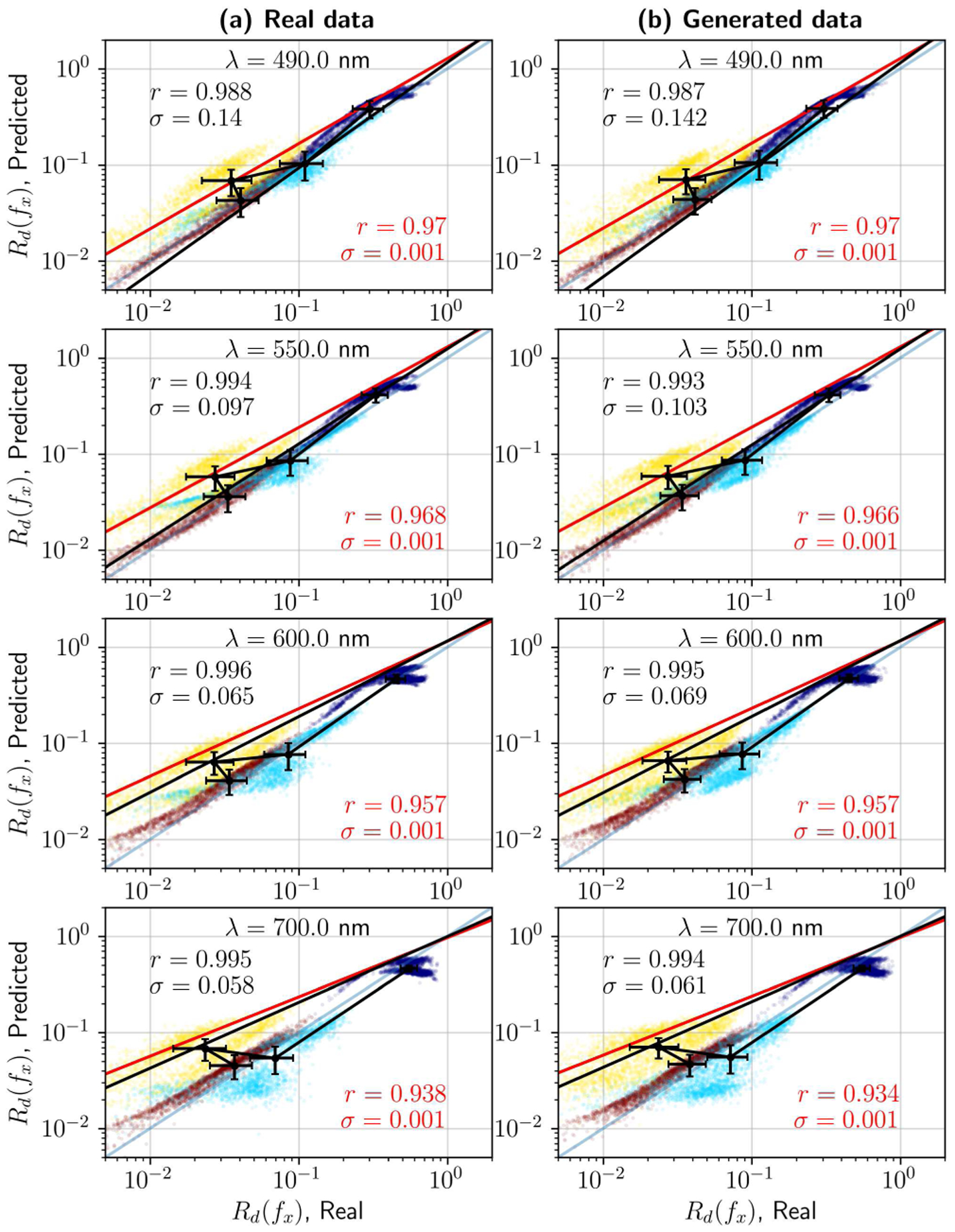
Optical properties estimation with a neural network LUT. Actual vs. predicted reflectance R_d(f_x) on the real dataset (left column) and synthetic data (right column). Average standard errors for the dataset are within 5% – 15%, as is typical in SFDI-based OP extraction. Rows show the actual and predicted reflectances for individual wavelengths. Each plot includes coefficients of determination and standard errors for the complete dataset (in red) and the dataset averages (in black).

Fig. 10.

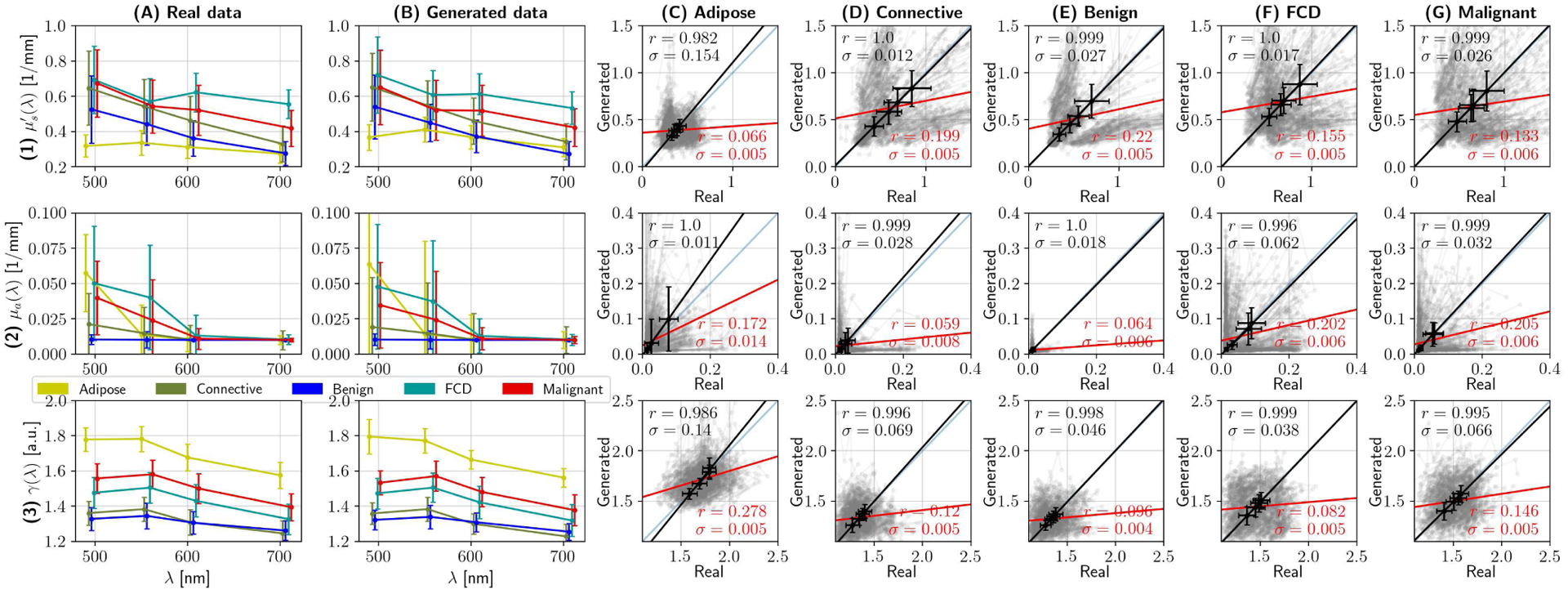
Quality assessment of synthesized spectra can be done indirectly, by analyzing optical properties. Rows (1), (2) and (3) show results pertaining to reduced scattering coefficient ${\mu }_s^{\prime }$, absorption coefficient μ_a, and phase function parameter γ, respectively. Columns (A) and (B) show the median optical properties per tissue category as error-bar plots, where whiskers represent one standard deviation, of real and synthesized spectra, respectively. Columns (C) through (G) randomly compare optical properties of real data with synthesized equivalents for each of the main tissue supercategories. In this grid, each subplot contains 500 pairs of optical properties from real and synthesized spectra in grey, the identity line y = x –plotted in blue–, and two linear regression tests. The red line and stats (namely, coefficient of determination and standard error) are the result of applying linear regression on the raw data, while the black line, errorbars and corresponding statistics correspond to analyzing average optical properties. The former provides little information due to the multimodal characteristics of the dataset; however, the latter demonstrates that, on average, the optical properties of the real and synthesized datasets match.

As a final demonstration, Fig. 10 presents the average optical properties per tissue category, as a proxy for analyzing the differences between real and synthesized data. Each row represents a different parameter, namely (1) reduced scattering coefficient ${\mu }_s^{\prime }$, (2) absorption coefficient μ_a, and phase function parameter γ, with respect to wavelength. The network extracts OPs at each wavelength individually, by processing the pixels at the center of each patch in both the real dataset (column A) and the synthesized dataset (column B). These two first columns are crucial in understanding the relevance of local information, as opposed to finding a global spectral/spatial signature for cancer. As observed by the unsupervised AEs, some tissue types present a differentiating feature (i.e. adipose tissue presents with a higher γ than other categories, and benign tumors present little absorption) but, in general, tissue optical properties are superimposed in the VisNIR regime. Further insight is revealed after analyzing the statistics between real and generated optical properties, which are shown in columns (C) through (G). In each plot, the complete category r-score is calculated, and shown in red. Its corresponding slope and intercept is plotted in red as well. Additionally, the category-average optical properties are analyzed and presented. The disparity between the average category r-score and the complete r-score is significant, but is explained by the fact that each category is multi-modal, i.e. not only one type of spectra is observed.

The presence of latent space clusters for a given tissue category has been discussed in Section III-D; its causes may include inter-sample variability, the presence of perfusing surgical ink, and minor acquisition inconsistencies, among others. For illustrative purposes, 500 randomly selected real-synthesized pairs of OPs (in transparent grey) are shown in Fig. 10, columns (C) through (G). These plots show symmetries along the y = x axis, revealing separate clusters in scattering and absorption for all categories. Such a result allows us to prove that no modes have collapsed during GAN training; otherwise, the gray plots would not be symmetrical.

IV. Summary

This work makes use of a neural network-based framework to study the effects of pathology on tissue optical properties in breast cancer. Developing a complete framework with supervised and unsupervised elements has been shown to be useful in previous work –particularly, melanoma detection– with conventional statistical tools and linear dimensionality reduction [54]. However, in many problems –as is the case in this contribution– data is rarely well conditioned and exhibits non-linear behavior, and thus a successful implementation of a similar framework requires the development of ad hoc neural architectures and methods that leverage the power of deep learning models to compensate for these problems, which cannot be resolved with conventional approaches to HSI/SFDI imaging. In the case of SFDI images of breast cancer lumpectomies, three fundamental developments were necessary prior to this work: (1) designing and training an autoencoder that could encode the ill-conditioned, subtle textural properties of tissues under modulated light, (2) finding a generator stage that could synthesize data with evident inter-sample variability without significant mode collapse, and (3) defining a neural LUT for real-time optical properties estimation that would include both diffuse and sub-diffuse reflectance data.

Interconnecting these models, once functionality is guaranteed, results in a variety of conclusions, which are indicative of the specific properties required to design a functional margin delineation system in practice. By employing bottleneck clamping, it is possible to observe that average spectral properties can be explained with few dimensions, and that texture presents as low-variance, high-dimensional fluctuations that are embedded within spectral information. Furthermore, it can be concluded that pixel-wise optical properties are sufficient for identifying malignant tissue, but that the inclusion of local textural information helps to uniquely identify categories with prominent textural features, such as Fibrocystic Disease and connective tissue, as long as inter-patient variability is compensated, supporting work that analyzes textural information exclusively [40]. Moreover, the dataset shows a detectable superposition between connective tissue and malignant tissue subtypes in feature space, suggesting that the presence of collagen and elastin in malignant growths, recently observed in multiphoton microscopy [36], could perhaps be measured macroscopically; further research is needed to ascertain if such presence of connective tissue could be quantified.

Classifying over the primary AE’s extracted features and following classical validation methods demonstrates the fundamental effects of inter-sample variability, as opposed to local variability. While textural methods are able to improve malignancy detection accuracy by up to 15% upon pixel-wise analysis, the similarities in the confusion matrices of Fig. 6 certainly suggests that a proper margin delineation tool must work locally. Solutions to this problem such as the use of one-shot deep learning, the inclusion of patient biopsy information, and/or problem constraining methods that define comparing metrics instead of absolute ones, will be researched and studied, as they seem to be the most viable option to achieving real-time assessment of tumor margins.

A functional primary AE also allows for high-fidelity sample generation with Generative Adversarial Networks, as most of the compression effort is achieved a priori, and can therefore be leveraged and reused with smaller generative networks. The alternative would be to train multiple, larger conditional GANs, or conditional VAE-GANs with more parameters and modules that ensure true conditional generation with no mode collapse, with their corresponding additional compute and time requirements. The proposed solution allows its user to produce complete datasets for multiple categories with millions of samples closely resembling the spectral and textural properties of actual patient data. By reusing the primary autoencoder features, classes and partitions of such classes could be prepared in hours’ time with relatively constrained computational resources. Furthermore, synthesized data –or the models themselves— do not need to adhere to the same ethical constraints as private patient information, and could be potentially open-sourced, as long as adequate ethical provisions are guaranteed.

The ability to observe incoming data under different scopes simultaneously could, in fact, be already useful in a clinical setting. As an example, consider the plots in Figs. 11 and 12. These individual specimen summaries show five potential ways to observe a lumpectomy specimen with this architecture, namely with reflectance data –(a) and (b)–, unsupervised features –plots (c) and (d)–, supervised and feature-based segmentation –(e) and (f)– and direct optical properties –(g), (h), and (i). Unsupervised feature maps were generated by transforming the secondary autoencoder’s output into polar coordinates, and then converting them to HSV and RGB. Features and classification maps can be combined and produced in many ways to enhance contrast in margin assessment.

Fig. 11.

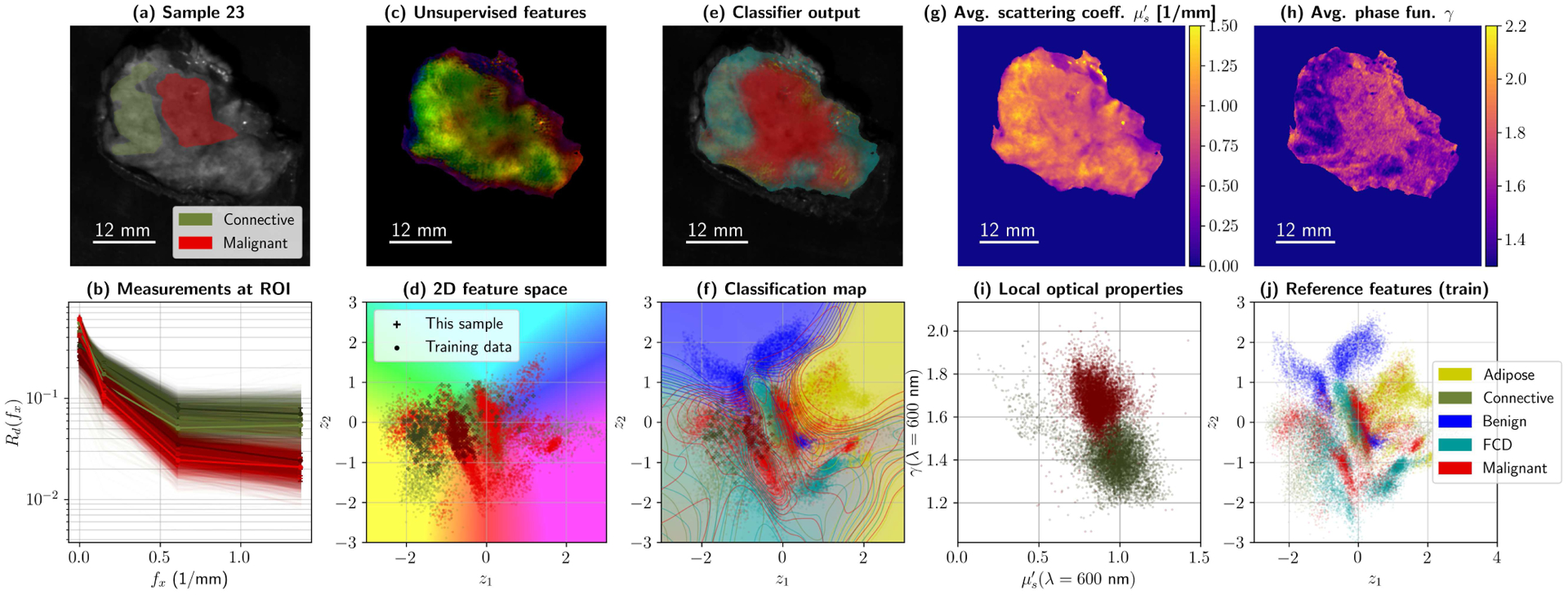
Summary for Sample 23 during 5-fold cross-validation (High Grade IDC embedded in connective tissue). Subplot (a) shows ROIs and average reflectance; (b) presents 10% of the reflectance data within those ROIs, at all four wavelengths. Processing the data with the primary and secondary autoencoder produces a map with two values per pixel, which was translated to HSV values to create a false color image (c). The corresponding colors for the false color map are shown with the test spectra from (b) –as well as training data for the categories of interest– in subplot (d). The classifier uses the 256-D pixels from the primary AE to produce a diagnostic map (e). Classification boundaries can also be projected onto 2D (f), by color-coding z-space with the classifier $\left(z^{\prime }\to \widehat{z}\to \widehat{y}\right)$. Finally, optical property maps can be plotted, namely reduced scattering ${\mu }_s^{\prime }$ (g) and phase function parameter γ (h). Local differences in OPs can be observed and plotted as usual (i). The complete training set in z-space for this fold is left, for reference, in (j).

Fig. 12.

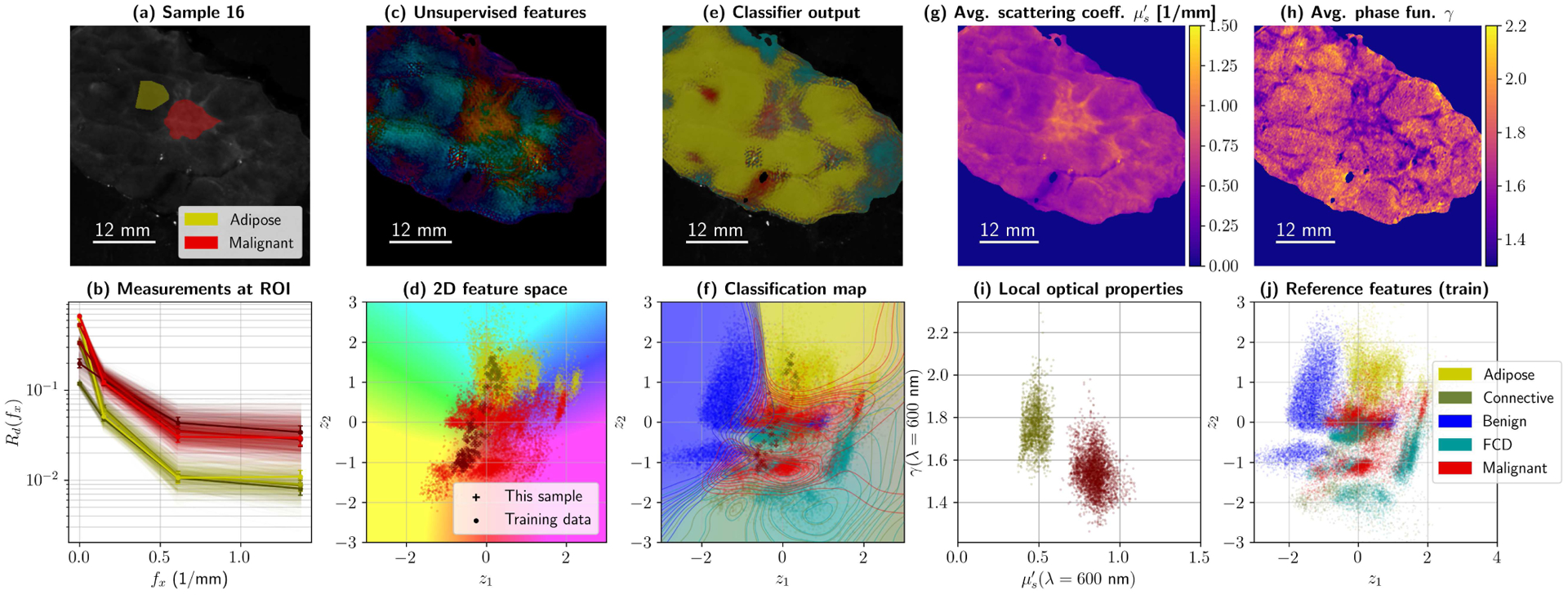
Summary for Sample 16 during 5-fold cross-validation (High Grade IDC in adipose tissue). Subplot (a) shows ROIs and average reflectance; (b) presents 10% of the reflectance data within those ROIs, at all four wavelengths. Processing the data with the primary and secondary autoencoder produces a map with two values per pixel, which was translated to HSV values to create a false color image (c). The corresponding colors for the false color map are shown with the test spectra from (b) –as well as training data for the categories of interest– in subplot (d). The classifier uses the 256-D pixels from the primary AE to produce a diagnostic map (e). Classification boundaries can also be projected onto 2D (f), by color-coding z-space with the classifier $\left(z^{\prime }\to \widehat{z}\to \widehat{y}\right)$. Finally, optical property maps can be plotted, namely reduced scattering ${\mu }_s^{\prime }$ (g) and phase function parameter γ (h). Local differences in OPs can be observed and plotted as usual (i). The complete training set in z-space for this fold is left, for reference, in (j).

Future margin delineation methods designed to consider the lessons learned in this article should certainly focus on optimizing clinical applicability. Protocols for SFDI-based margin assessment could easily be integrated into already existing 2D/3D X-ray imaging in BCS, resulting in a multimodal approach to margin delineation. We consider that this can be achievable if four issues are addressed, namely that (a) the imaging device is capable of acquiring the necessary data in a clinically negligible time frame (e.g. 10–15 minutes or less); (b) that the margin assessment algorithm can respond in a fraction of the time spent acquiring–which can be achieved with sufficient compute power, in situ or within hospital premises–; (c) that the algorithm provides some metric of certainty or accountability on the generated diagnosis, and (d) that the surgeon can interact with the diagnostic maps and provide references to compensate for inter-sample variability. The first two conditions are fundamental to their implementation in a practical surgical workflow, while the latter are essential to ensure that the algorithm can be trusted, while keeping the human in the loop in charge.