Multi-Armed Angle-Based Direct Learning for Estimating Optimal Individualized Treatment Rules With Various Outcomes

Abstract

Estimating an optimal individualized treatment rule (ITR) based on patients’ information is an important problem in precision medicine. An optimal ITR is a decision function that optimizes patients’ expected clinical outcomes. Many existing methods in the literature are designed for binary treatment settings with the interest of a continuous outcome. Much less work has been done on estimating optimal ITRs in multiple treatment settings with good interpretations. In this article, we propose angle-based direct learning (AD-learning) to efficiently estimate optimal ITRs with multiple treatments. Our proposed method can be applied to various types of outcomes, such as continuous, survival, or binary outcomes. Moreover, it has an interesting geometric interpretation on the effect of different treatments for each individual patient, which can help doctors and patients make better decisions. Finite sample error bounds have been established to provide a theoretical guarantee for AD-learning. Finally, we demonstrate the superior performance of our method via an extensive simulation study and real data applications. Supplementary materials for this article are available online.

1. Introduction

Precision medicine, which recommends different treatments for individual patients, has been a popular research area in the scientific community. Compared with traditional “one-size-fits-all” medical procedures, precision medicine provides an individualized decision for each patient based on their information, such as clinical covariates, genetics, in order to maximize the outcome of each patient. There are different types of outcomes such as time to event, health index or the disease indicator.

There are a number of existing statistical methods for estimating optimal ITRs in the literature. These methods can be roughly characterized into two types. The first type includes value-based methods such as Q-learning (Watkins 1989; Watkins and Dayan 1992; Murphy 2005; Qian and Murphy 2011) and A-learning (Murphy 2003; Robins 2004). Q-learning estimates optimal ITRs via modeling the conditional outcome function based on covariates while A-learning models the contrast between rewards of two treatments. The second type of methods directly targets the decision rules. One major approach of this type is to recast the estimating ITRs problem as weighted classification problems and use machine learning techniques to estimate optimal ITRs (Zhang et al. 2012a; Zhao et al. 2012b, 2015a; Tao and Wang 2017; Zhou et al. 2017). In order to enhance interpretability of decision rules, tree-based methods were also proposed (Foster et al. 2011; Laber and Zhao 2015; Zhang et al. 2015). Other direct-search methods include Tian et al. (2014) and Direct Learning (D-learning) (Qi and Liu 2018), which directly estimate the decision function that leads to optimal ITRs by regression techniques. Recently, a general statistical framework to estimate optimal ITRs was proposed by Chen et al. (2017).

Censored data are commonly seen in practice. Thus, it is also important to develop methods to estimate optimal ITRs for the survival outcome. Various methods have been proposed in the literature to estimate optimal ITRs for survival outcomes, such as Goldberg and Kosorok (2012), Zhao et al. (2015b), and Cui et al. (2017). Recently, Bai et al. (2016) and Jiang et al. (2017) proposed several methods to estimate the optimal ITR that can maximize the survival probability of patients. However, for general ITR problems, most of these existing methods are designed for binary treatment settings only. There are many multi-armed ITR problems in pratice (Baron et al. 2013). To the best of our knowledge, not much has been done for estimating the optimal ITR for the multiarmed treatment settings with various outcomes, such binary and survival outcomes. Thus, it is essential to develop methods to take multiple treatments into consideration simultaneously and estimate optimal ITRs for various outcomes, which can help to improve the estimating efficiency and the classification accuracy.

Besides the accurate estimation of ITRs, good interpretations are also important for multi-armed treatment settings. For binary treatment settings, value-based methods can report a single-value difference function between two treatments to illustrate the relative effectiveness. For classification based methods such as O-learning (Zhao et al. 2012b), interpretation of the decision rule for binary treatment settings may not be as clear. Meanwhile for K-armed treatment settings, at least $\frac{K(K-1)}{2}$ pairwise value difference functions need to be estimated to illustrate the relative performance of treatments for each patient. Although such an extension can be simple to implement, it does not use the data simultaneously and consequently may yield suboptimal rules.

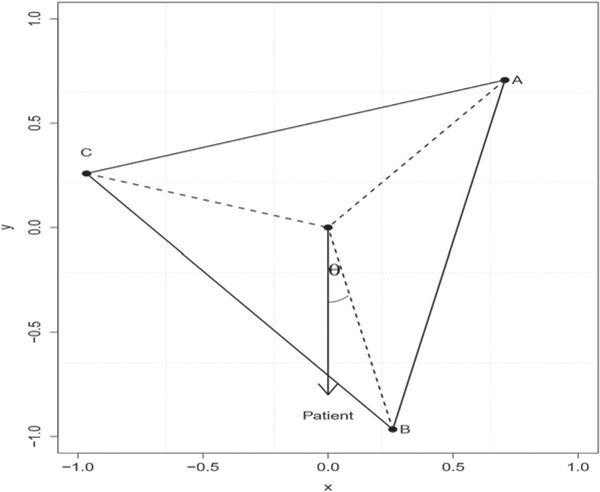
To get accurate estimation of optimal ITRs and obtain a good interpretation jointly under the multiarmed setting, we consider a K-vertex simplex structure in an Euclidean space, where each vertex represents one treatment. The simplex lies in a K − 1 dimensional space with the origin as the center and has equal inner products among vertices. Using the expression of the optimal ITR, we transform the problem of finding the optimal ITR maximizing the value function into maximizing the inner product between the decision function vector and the corresponding vertex in the simplex space. Such a transformation allows us to estimate the optimal ITR using multiple response regression methods. In particular, for each patient, our estimated decision function vector maps the covariates into this K − 1 dimensional space. The angle between each treatment vertex and the estimation function vector can be interpreted as a measure of preference to this treatment. We recommend a patient to take the corresponding treatment having the least angle with our estimated decision function vector. Figure 1 shows an example with our estimated ITR for a given patient. In this case, we recommend treatment B as the best option for this patient. In addition, we can see treatment C is more preferable than treatment A for this patient based on their angles.

Figure 1.

Graphical illustration of the estimated ITR for a given patient in a three-treatment setting. Vertices A, B, and C represent 3 treatments. The estimated ITR of the patient has the least angle with treatment B which is thus more preferable than the other two treatments.

We call our method angle-based direct learning (AD-learning) which can directly estimate optimal ITRs under multiarmed treatment settings using multiple response regression techniques. Furthermore, our proposed AD-learning can be extended to various types of outcome such as binary and survival responses. Compared with existing methods, our proposed AD-learning enjoys several advantages. In particular, our method is robust in the sense that it is not necessary to model the main effect function of the conditional outcome. Due to direct learning scheme, our method does not suffer from the mismatch problem between minimizing prediction errors and maximizing value functions in model based methods such as l₁-PLS (Qian and Murphy 2011) and can perform better in high dimensional settings. Moreover, by representing each treatment as a vertex of a standard simplex in the Euclidean space, our proposed method provides an attractive geometric interpretation of the relative effectiveness of all treatments for a given patient. The resulting relative effectiveness of different treatments can be interpreted as the angles between the decision function vector for the patient and each vertex corresponding to the treatment. These angles can be scaled between [0, π]. In addition, flexible structures such as group and low rank sparsity can be also incorporated to further improve the model interpretation and simplicity, which can be applied in high-dimensional settings. Finally, our proposed method is easy to implement with efficient algorithms.

The remainder of this article is organized as follows. In Section 2, we introduce our AD-learning to estimate optimal ITRs in multiple treatment settings. In Section 3, we discuss how to extend our proposed method to binary and survival outcomes. In Section 4, we provide a theoretical guarantee for our AD-learning under some mild assumptions. In Section 5, we conduct an extensive simulation study to evaluate the finite sample performance of our method with implementation details including algorithms. Furthermore, we illustrate our method using the AIDS data in Section 6. We conclude our article with some discussions and possible future extensions in Section 7.

2. Angle-Based Direct Learning

For notation of the article, we use boldface capital and lowercase symbols to denote matrices and vectors respectively. For a matrix B, we define a mixed l₁ and l₂ norm as ‖B‖_2,1 = Σ‖B_j‖₂, where B_j is the jth row vector of B. We use Tr(B) to denote the sum of the diagonal value of the matrix B.

We consider a randomized treatment framework for estimating optimal ITRs. For each patient, we observe a triplet random vector (x, A, R). In particular, $\mathbf{x}=\left(1,X_1,\dots ,X_p\right)\in \mathcal{X}$ denotes patients’ p-dimensional covariates with an intercept. The random variable A represents the randomized treatment that a patient receives. Here, we consider the K-treatment-armed setting where A ∈ {1, 2, …, K} with a known prior probability distribution π(A, x), which is the conditional probability depending on x. In a general setting other than the randomized trial study, π(A, x) denotes the propensity score and can be estimated by the generalized linear models such as multinomial logistic regression. The variable R is a patient’s outcome after receiving the treatment A. Without loss of generality, we assume that the outcome R is bounded and the larger R is, the better the treatment works for this patient.

One of the most important goals of our problem is to estimate the optimal ITR that can maximize the expected clinical outcome of each patient under this ITR. Mathematically speaking, an ITR is a decision function $d(\mathbf{x}):\mathcal{X}\to \mathcal{A}$, mapping from the covariate space into the treatment space. According to Qian and Murphy (2011) and Zhao et al. (2012b), the value function under the ITR d can be expressed as

$$V(d)=:\mathbf{E}[R|d(\mathbf{x})=A]=\mathbf{E}\left[\frac{R\mathbb{I}(A=d(\mathbf{x})}{\pi (A,\mathbf{x})}\right],$$ (1)

where $\mathbb{I}(•)$ is the indicator function. Then the optimal ITR is defined as

$$d_0(\mathbf{x})={\mathrm{argmax}}_{d\in D}V(d)$$ (2)

within a prespecified class of treatment rules D. Before introducing our proposed AD-learning, we first discuss the direct learning framework.

2.1. The Direct Learning Framework

Consider a binary problem with K = 2. We encode treatment A to be 1 or −1. Then from the value function and optimal ITRs defined in (1) and (2) respectively, we can further represent the optimal ITR as

$$\begin{gathered} d_0(\mathbf{x})=\mathrm{sign}(\mathbf{E}[R|\mathbf{x},A=1]-E[R|\mathbf{x},A=-1]) \\ =\mathrm{sign}(\mathbf{E}\left[\frac{RA}{\pi (A|\mathbf{x})}|\mathbf{x}\right]):=\mathrm{sign}\left(f_0(\mathbf{x})\right). \end{gathered}$$ (3)

Using Equation (3), similarly in Tian et al. (2014), the ITR problem becomes to estimate the optimal decision function $f_0(\mathbf{x})=\mathbf{E}[\frac{RA}{\pi (A|\mathbf{x})}|\mathbf{x}]$ via various regression methods such as l₁ penalized regression (LASSO). The final decision rule is determined by the sign of the estimator.

Binary D-learning directly estimates the decision rule. It is very different from the outcome weighted learning (OWL) proposed by Zhao et al. (2012b) because binary D-learning uses regression methods to estimate the optimal ITR directly. Note that binary D-learning can be simply extended to the K-treatment-arm setting by rewriting the optimal ITR as

$$\begin{gathered} d_0(\mathbf{x})=\underset{k\in \{1,\dots ,K\}}{\mathrm{argmax}}\mathbf{E}[R|\mathbf{x},A=k] \\ =\underset{k\in \{1,\dots ,K\}}{\mathrm{argmax}}K\mathbf{E}[R|\mathbf{x},A=k]-\sum _{i=1}^K\mathbf{E}[R|\mathbf{x},A=i] \\ =\underset{k\in \{1,\dots ,K\}}{\mathrm{argmax}}\sum _{i\ne k}^K\{\mathbf{E}[R|\mathbf{x},A=k]-\mathbf{E}[R|\mathbf{x}A=i]\} \\ =\underset{k\in \{1,\dots ,K\}}{\mathrm{argmax}}\sum _{i\ne k}^K\mathbf{E}[\frac{R{A}_{ki}}{{\pi }_{ki}\left(A_{ki},\mathbf{x}\right)}|\mathbf{x},A=k\text{or}i] \\ :=\underset{k\in \{1,\dots ,K\}}{\mathrm{argmax}}\sum _{i\ne k}^K{f}_{ki}(\mathbf{x}):=\underset{k\in \{1,\dots ,K\}}{\mathrm{argmax}}{f}_k(\mathbf{x}), \end{gathered}$$ (4)

where A_ki ∈ {−1, 1} represents treatments k and i, and f_ki(x) is defined as the optimal decision function between treatment k and i. Each pairwise decision function can be estimated by a binary D-learning method. The final treatment decision rule is to compare the cumulative sum of pairwise decision functions f_k(x) for k = 1, …, K, and select the largest one. We refer this pairwise method as pairwise D-learning.

Binary D-learning gives us a directed way to estimate optimal ITRs. However, pairwise D-learning, which is based on binary D-learning, focuses only on pairwise comparisons between treatments without considering all treatments simultaneously. Although the proposed effect measure f_k(x) can capture the relative strength of a treatment for a given patient, it may be suboptimal.

To handle multiarmed ITR problems with various outcomes, we propose AD-learning that considers all treatments together to estimate the optimal ITR. Moreover, the AD-learning can provide a more effective measure of treatments for patients with a good interpretation.

2.2. Angle-Based D-learning for Continuous Outcomes

For a K-armed ITR problem, one natural approach is to estimate K functions for all treatments. Since only one function is needed for the binary ITR problem, one indeed only needs K − 1 functions for a K-armed problem. Instead of using K functions with a constraint on these functions, we aim to directly estimate K − 1 functions. To that end, we project the treatment A into K simplex vertices defined ${\mathcal{R}}^{K-1}$. Specifically, we encode the jth treatment as a vector ${\mathbf{w}}_j\in {\mathcal{R}}^{K-1}$ with

$${\mathbf{w}}_j=\{\begin{array}{l}{\left(K-1\right)}^{-1/2}{\mathbf{1}}_{K-1}\\ \text{if}A=1,\\ -(1+\sqrt{K})/{(K-1)}^{3/2}{\mathbf{1}}_{K-1}+(\frac{K}{K-1}{)}^{1/2}{e}_{A-1}\\ \text{if}2\le A\le K,\end{array}$$ (5)

where e_i is a K −1 dimensional vector with every element being 0, except the i-th location being 1. Define w as a random vector with P[w = wj|x] = P[A = j|x]. This simplex encoding scheme has several properties. In particular, the center of these vertices is the origin of the space, that is ${\sum }_{j=1}^K{\mathbf{w}}_j=0$ with ‖w_j‖₂ = 1 for j = 1, …, K. The angle between each pair of vertices is equal, that is ${\mathbf{w}}_i^{\text{T}}{\mathbf{w}}_j=C(K)<1$ for i ≠ j, where the constant C only depends on K. Interestingly, we can then express the optimal ITR as

$$\begin{gathered} d_0(\mathbf{x})=\underset{k\in \{1,\dots ,K\}}{\mathrm{argmax}}\mathbf{E}[R|\mathbf{x},A=k] \\ =\underset{k\in \{1,\dots ,K\}}{\mathrm{argmax}}(1-c(K))\mathbf{E}[R|\mathbf{x},A=k] \\ =\underset{k\in \{1,\dots ,K\}}{\mathrm{argmax}}\{(1-c(K))\mathbf{E}[R|\mathbf{x},A=k] \\ +c(K)\sum _{j=1}^K\mathbf{E}[R|\mathbf{x},A=j]\} \\ =\underset{k\in \{1,\dots ,K\}}{\mathrm{argmax}}\{\mathbf{E}[R|\mathbf{x},A=k]+c(K)\sum _{j\ne k}^K\mathbf{E}[R|\mathbf{x},A=j]\} \\ =\underset{k\in \{1,\dots ,K\}}{\mathrm{argmax}}\{{\mathbf{w}}_k^{\text{T}}\mathbf{E}[R\mathbf{w}|\mathbf{x},A=k]+{\mathbf{w}}_k^{\text{T}}\sum _{j\ne k}^K\mathbf{E}[R\mathbf{w}|\mathbf{x},A=j]\} \\ =\underset{k\in \{1,\dots ,K\}}{\mathrm{argmax}}{\mathbf{w}}_k^{\text{T}}\mathbf{E}\left[\frac{R\mathbf{w}}{\pi (A,\mathbf{x})}|\mathbf{x}\right]:=\underset{k\in \{1,\dots ,K\}}{\mathrm{argmax}}{\mathbf{w}}_k^{\text{T}}{\mathbf{f}}_0(\mathbf{x}), \end{gathered}$$ (6)

where f₀(x) is a function vector from ${\mathcal{R}}^{p+1}$ to ${\mathcal{R}}^{K-1}$ with some abuse of notation. Then, the optimal ITR is given by comparing the inner product between w_k and f₀(x) for each treatment k. We define the angle between each pair of vertices in [0, π]. Then, ${\mathbf{w}}_k^{\text{T}}{\mathbf{f}}_0(\mathbf{x})$ is the largest if and only if the angle between w_k and f₀(x) is the least, for k = 1, …, K. Thus, we call our proposed method as angle-based D-learning (AD-learning). Note that the simplex coding is unique up to the orthogonal rotation.

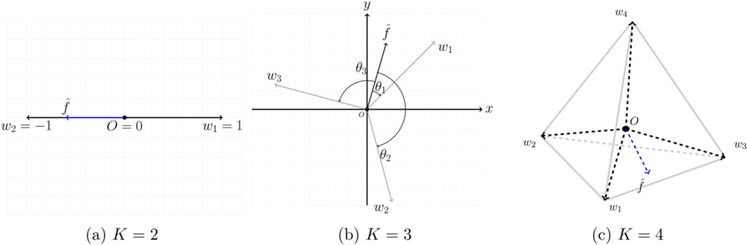
Our proposed AD-learning has an attractive geometric interpretation. In particular, this least angle decision rule can be understood through newly defined treatment regions for each patient. For example, when K = 3, as shown in Figure 2 (b), vectors w_k; k = 1, …, K form an equilateral triangle in the ${\mathcal{R}}^2$ space, where each divided region represents a treatment region. The decision function vector f₀(x) maps from the covariate space into the treatment region. One can observe that the angles between vertices are the same, and consequently each treatment is treated equally. Such a simplex coding scheme does not require a balanced group size for each treatment since treatment proportions are taken into account by the term π(A, x) in Equation (6). We name the angle between each w_k and f₀(x) as the treatment score which lies in a bounded interval [0, π]. If a patient has the angle of 0 with the ith treatment, then the i-th treatment is a perfect fit for this patient compared with other treatments. Figure 2 gives a geometric explanation of our AD-learning.

Figure 2.

Geometric interpretation of our least angle decision rule. When K = 3 or K = 4, the estimate $\widehat{f}$ has the smallest angle with treatment 1 so we recommend treatment 1 as the optimal treatment. When K = 2, we can see $\widehat{f}$ has the smallest angle with vector w₂ and the optimal rule for this patient is treatment 2.

To further illustrate our AD-learning, we propose the following alternative interpretation. Suppose the clinical outcome R can be modeled as follows:

$$R=\mu (\mathbf{x})+\sum _{i=1}^K{\delta }_i(\mathbf{x})\mathbb{I}(A=i)+ϵ,$$ (7)

where μ(x) is main effect function, δ_i(x) is the interaction effect between covariates and the ith treatment, and ϵ is mean zero random error. Then we can get

$$\begin{gathered} E\left[\frac{R\mathbf{w}}{\pi (A,\mathbf{x})}|\mathbf{x}\right]=\mu (\mathbf{x})E\left[\frac{\mathbf{w}}{\pi (A,\mathbf{x})}|\mathbf{x}\right] \\ +\sum _{i=1}^K{\delta }_i{\left(\mathbf{x}\right)}_i\mathbf{E}\left[\frac{\mathbf{w}\mathbb{I}(A=i)}{\pi (A,\mathbf{x})}|\mathbf{x}\right] \\ +E\left[\frac{\mathbf{w}}{\pi (A,\mathbf{x})}|\mathbf{x}]\mathbf{E}[ϵ|\mathbf{x}\right] \\ =\sum _{i=1}^K{\delta }_i(\mathbf{x}){\mathbf{w}}_i. \end{gathered}$$ (8)

Furthermore, the optimal ITR is

$$\begin{gathered} d_0(\mathbf{x})={\mathrm{argmax}}_{k\in \{1,\dots ,K]}{\mathbf{w}}_k^{\text{T}}\mathbf{E}\left[\frac{R\mathbf{w}}{\pi (A|\mathbf{x})}|\mathbf{x}\right] \\ ={\mathrm{argmax}}_{k\in \{1,\dots ,K\}}{\mathbf{w}}_k^{\text{T}}\sum _{i=1}^K{\delta }_i(\mathbf{x}){\text{w}}_i \\ ={\mathrm{argmax}}_{k\in \{1,\dots ,K\}}C(K)\sum _{i=1}^K{\delta }_i(\mathbf{x})+(1-C(K)){\delta }_k(\mathbf{x}) \\ ={\mathrm{argmax}}_{k\in \{1,\dots ,K\}}{\delta }_k(\mathbf{x}), \end{gathered}$$ (9)

which is exactly to compare each treatment interaction effect with the covariates.

As a remark, we note that extensions of methods for binary treatment settings to multiple treatment settings using all treatments jointly can be nontrivial since we need to account for multiple treatment effect comparisons without sacrificing too much efficiency. Our proposed AD-learning achieves this by first projecting treatments into a K − 1 dimensional space. A simplex with K vertices is used to represent the K treatments. Then, Equation (6) provides an innovative but direct way to efficiently estimate the decision function vector and considers all the data simultaneously. Inherited from the simplex structure, our proposed method has an attractive geometric interpretation to show the relative effectiveness of different treatments for a patient. Thus, it provides an informative comparison of all treatments for patients and doctors to make decisions.

Note that the simplex coding scheme was previously used by Wu and Lange (2010) and Zhang and Liu (2014) for classification problems. However, our proposed AD-learning is very different because it is not a classification method. Consequently, our method is not an extension of O-learning proposed by Zhao et al. (2012b). Instead, by transforming the problem (2) into (6), our goal is to estimate the decision function f₀(x) directly, using multiple response regression introduced in Section 2.3.

2.3. Estimation Proceduresof AD-learning

In order to estimate the optimal ITR, it is equivalent to estimating f₀(x) from Section 2.2. The next lemma provides us a way for estimation of f₀(x).

Lemma 1

Under the exchange of differential and expectation condition, f₀(x) is an optimal solution to

$$\underset{\mathbf{f}\in {\mathcal{R}}^{K-1}}{\mathrm{argmin}}\mathbf{E}\left[\frac{1}{\pi (A,\mathbf{x})}{(KR\mathbf{w}-\mathbf{f}(\mathbf{x}))}^{\text{T}}\mathrm{\Sigma }(KR\mathbf{w}-\mathbf{f}(\mathbf{x}))\right],$$ (10)

where Σ can be any positive definite matrix that characterizes the dependency among responses. Without knowing any prior knowledge, one could simply let Σ = I_K−1.

Assume we observe independent identically distributed data {(x_i, A_i, R_i), i = 1, …, n}. Then, we can estimate f₀(x) via empirical average approximation

$$\begin{gathered} \underset{\mathbf{f}\in \mathcal{F}}{\mathrm{argmin}}\frac{1}{n(K-1)}\sum _{i=1}^n\frac{1}{\pi \left(A_i,{\mathbf{x}}_i\right)} \\ \times {\left(K{R}_i{\mathbf{w}}_i-\mathbf{f}\left({\mathbf{x}}_i\right)\right)}^{\text{T}}\left(K{R}_i{\mathbf{w}}_i-\mathbf{f}\left({\mathbf{x}}_i\right)\right), \end{gathered}$$ (11)

where $\mathcal{F}$ is a prespecified class of decision functions. For simplicity, we first consider the class of linear decision rules, that is, $\mathcal{F}:=\left\{\mathbf{f}(\mathbf{x})={\mathbf{B}}^{\text{T}}\mathbf{x},\mathbf{B}\in {ℝ}^{p\times (K-1)}\right\}$. By observing KR_iw_i as multivariate responses, one can apply ordinary least square estimates for each of the responses separately. However, since the responses share the same clinical outcome R_i for the ith sample, it is clear that pooling multivariate responses together can efficiently improve the estimation of f₀(x) (Breiman and Friedman 1997). This motivates us to incorporate shrinkage and selection strategies that explore the correlations among different responses by

$$\begin{gathered} \underset{\mathbf{B}\in {ℝ}^{p\times (K-1)}}{\mathrm{argmin}}\frac{1}{n(K-1)}\sum _{i=1}^n\frac{1}{\pi \left(A_i,{\mathbf{x}}_i\right)}{\left(K{R}_i{\mathbf{w}}_i-{\mathbf{B}}^{\text{T}}{\mathbf{x}}_i\right)}^{\text{T}} \\ \times \left(K{R}_i{\mathbf{w}}_i-{\mathbf{B}}^{\text{T}}{\mathbf{x}}_i\right)+\lambda J(\mathbf{B}), \end{gathered}$$ (12)

where λ is a positive tuning parameter. Then our final least angle decision rule becomes $d_0(\mathbf{x})={\mathrm{argmax}}_{k\in \{1,\dots ,K\}}{\mathbf{w}}_k^{\text{T}}{\mathbf{B}}^{\text{T}}\mathbf{x}$. In this decision rule, the corresponding coefficient for the jth variable of x is ${\mathbf{w}}_k^{\text{T}}{\mathbf{B}}_j$, for j = 1, …, p, where B_j is the jth row vector of B. Note that for any orthogonal matrix,

$$\begin{gathered} \Vert \mathbf{B}\mathrm{\Gamma }{\Vert }_{2,1}=\sum _{j=1}^p{\Vert {\mathbf{B}}_j^{\text{T}}\mathrm{\Gamma }\Vert }_2=\sum _{j=1}^p\sqrt{{\mathbf{B}}_j^{\text{T}}\mathrm{\Gamma }{\mathrm{\Gamma }}^{\text{T}}{\mathbf{B}}_j} \\ =\sum _{j=1}^p{\Vert {\mathbf{B}}_j\Vert }_2=\Vert \mathbf{B}{\Vert }_{2,1}, \end{gathered}$$ (13)

which implies that ‖B‖_2,1 remains to be the same under any orthogonal transformation of w. This is essential since our simplex coding is unique up to the orthogonal rotation. In addition, B_j = 0_K−1 implies the jth variable has no effect on our least angle decision rule. These motivate us to use the group sparsity penalty, that is, the mixed l₁/l₂ norm as follows

$$\begin{gathered} \underset{\mathbf{B}\in {ℝ}^{p\times (K-1)}}{\mathrm{argmin}}\frac{1}{n(K-1)}\sum _{i=1}^n\frac{1}{\pi \left(A_i,{\mathbf{x}}_i\right)}{\left(K{R}_i{\mathbf{w}}_i-{\mathbf{B}}^{\text{T}}{\mathbf{x}}_i\right)}^{\text{T}} \\ \times \left(K{R}_i{\mathbf{w}}_i-{\mathbf{B}}^{\text{T}}{\mathbf{x}}_i\right)+\lambda \Vert \mathbf{B}{\Vert }_{2,1}. \end{gathered}$$ (14)

Model (14) is best suited for the case that all treatments share the common interaction covariates. The group sparsity structure of B will not change under any orthogonal transformation of w.

In the literature, it is known that group sparsity of a matrix is a special case of a low rank matrix. If B = UV^T such that $\mathbf{U}\in {ℝ}^{p\times r}$ and $\mathbf{V}\in {ℝ}^{r\times (K-1)}$ with r < min(p, K − 1). Then B^Tx = V(U^Tx) implies potential r orthogonal latent factors in the covariates. Hence, we can also use the nuclear norm penalty to control the complexity of coefficient matrix B if there is a low-rank structure or exists latent factors in the covariates by

$$\begin{gathered} \underset{\mathbf{B}\in {ℝ}^{p\times (K-1)}}{\mathrm{argmin}}\frac{1}{n(K-1)}\sum _{i=1}^n\frac{1}{\pi \left(A_i,{\mathbf{x}}_i\right)}{\left(K{R}_i{\mathbf{w}}_i-{\mathbf{B}}^{\text{T}}{\mathbf{x}}_i\right)}^{\text{T}} \\ \times \left(K{R}_i{\mathbf{w}}_i-{\mathbf{B}}^{\text{T}}{\mathbf{x}}_i\right)+\lambda \Vert \mathbf{B}{\Vert }_{*}, \end{gathered}$$ (15)

where the ‖B‖_* is the sum of all singular values of coefficient matrix B. The nuclear norm penalty, unlike the rank constraint, provides soft and stable shrinkage on the singular values. Similar to the penalty ‖B‖_2,1, other penalties including ‖B‖* that are invariant to any orthogonal rotation of w can be applied for our methods.

So far, we have only focused on linear decision rules. If f₀(x) belongs to some classes of nonlinear functions, we can adapt our method to nonlinear learning via kernel learning or basis function expansions. For kernel learning, we can apply kernel ridge regression for each response separately, using Equation (11). However, it may lose some efficiency, since it does not consider the dependence among the responses. How to perform kernel learning with multiple responses in our setting is an interesting future research direction. For basis function expansions, depending on the problem, we can use spline basis functions, interaction functions, wavelet functions, etc. to approximate the nonlinear decision function.

To summarize, Models (14) and (15) are proposed to control the complexity of coefficient matrix B and consequently enhance the estimation and prediction. As our proposed AD-learning directly targets on the decision function f₀(x), it does not suffer the mismatch problem between minimizing prediction errors and maximizing value functions happened for model-based methods such as l₁-PLS. Thus, our proposed method tends to perform better in high-dimensional settings. If there are group signals in the covariates for optimal ITRs, we recommend to use Model (14). If there are latent factors in the covariates for optimal ITRs, we recommend to use Model (15). One can also use the cross-validation procedure to choose Model (14) or (15) that maximizes the empirical value function on the validation dataset. The computation of these models involves convex optimization and thus can be solved efficiently.

3. Extensions to Other Types of Outcomes

In Sections 2, we proposed AD-learning for continuous outcomes. In practice, especially in clinical studies, other types of outcomes such as binary, count responses, or survival time can also be used. In this section, we extend our AD-learning to more general types of outcomes motivated by the following lemma.

Lemma 2

Under the exchange of differential and expectation condition, f₀(x) is an optimal solution to

$$\underset{\mathbf{f}\in \mathcal{F}}{\mathrm{argmin}}\mathbf{E}\left[\frac{1}{\pi (A,\mathbf{x})}{(\frac{K}{K-1}R-{\mathbf{w}}^{\text{T}}\mathbf{f}(\mathbf{x}))}^2\right].$$ (16)

Based on the optimization problem (16), one can write a corresponding working model as

$$\frac{K}{K-1}R={\mathbf{w}}^{\text{T}}f(\mathbf{x})+ϵ,$$ (17)

where ϵ is the random error. Note that when $\mathbf{f}\in \mathcal{F}$, w^Tf(x) = w^TB^Tx = Tr(B^T(xw^T)). Then, xw^T can be regarded as modified covariates. Then, the multiple response regression model in (11) can be extended to a more general model, namely trace regression model (Rohde et al. 2011).

Motivated by the optimization problem (16) and the corresponding working model, we can extend our proposed AD-learning to more general settings. In particular, instead of the least-squared loss for continuous outcome in (16), we can use other loss functions for corresponding outcomes.

3.1. Binary Outcomes

When R is binary, motivated by Lemma 2 and the connection between (16) and working model (17), we consider to replace the least squared loss in (16) by the deviance loss of logistic regression models. Then, we have the following lemma.

Lemma 3

Under the exchange of differential and expectation condition, an optimal solution to

$$\underset{\mathbf{f}\in \mathcal{F}}{\mathrm{argmin}}\mathbf{E}\left[-\frac{R{\mathbf{w}}^{\text{T}}\mathbf{f}}{\pi (A,\mathbf{x})}+\frac{\log \left(1+\exp \left({\mathbf{w}}^{\text{T}}\mathbf{f}\right)\right)}{\pi (A,\mathbf{x})}\right]$$ (18)

is the function f₀(x) satisfying

$$\mathbf{P}[R=1|\mathbf{x},A=i]=\frac{\exp \left({\mathbf{w}}_i^{\text{T}}{\mathbf{f}}_0(\mathbf{x})\right)}{1+\exp \left({\mathbf{w}}_i^{\text{T}}{\mathbf{f}}_0(\mathbf{x})\right)}.$$ (19)

Analogous to (17), solving (18) is equivalent to fitting a logistic regression working model (19). Based on Lemma 3, we can derive the optimal decision rule for the binary outcome as

$$\begin{gathered} d_0(\mathbf{x})={\mathrm{argmax}}_{k\in \{1,\dots ,K\}}\mathbf{P}[R=1|\mathbf{x},A=i] \\ ={\mathrm{argmax}}_{k\in \{1,\dots ,K\}}{\mathbf{w}}_i^{\text{T}}{\mathbf{f}}_0(\mathbf{x}), \end{gathered}$$ (20)

which can be also interpreted as the least angle decision rule. Then, we can fit a weighted logistic regression with modified covariates x* = xw^T by modeling

$$\mathbf{P}[R=1|\mathbf{x},A]=\frac{\exp \left(\mathrm{Tr}\left({\mathbf{B}}^{\text{T}}\mathbf{x}*\right)\right)}{1+\exp \left(\mathrm{Tr}\left({\mathbf{B}}^{\text{T}}\mathbf{x}*\right)\right)},$$ (21)

and estimate the coefficient matrix B by maximum likelihood estimation

$$\begin{gathered} \underset{\mathbf{B}\in {ℝ}^{p\times (K-1)}}{\mathrm{argmin}}l(\mathbf{B})=-\frac{1}{n}\sum _{i=1}^n\frac{R_i\mathrm{Tr}\left({\mathbf{B}}^{\text{T}}{\mathbf{x}}_i^{*}\right)}{\pi \left(A_i,{\mathbf{x}}_i\right)} \\ +\frac{1}{n}\sum _{i=1}^n\frac{\log \left(1+\exp \left(\mathrm{Tr}\left({\mathbf{B}}^{\text{T}}{\mathbf{x}}_i^{*}\right)\right)\right)}{\pi \left(A_i,{\mathbf{x}}_i\right)}+\lambda J(\mathbf{B}), \end{gathered}$$ (22)

where J(B) is either the mixed l₁/l₂ penalty or the nuclear norm penalty under different model assumptions. We can use the accelerated proximal gradient method to solve this problem (Beck and Teboulle 2009). However, the gradient of the exponential loss function for this model may need relatively large computational time. Efficient group coordinate descent proposed by Breheny and Huang (2015) can be an alternative to solve Model (22) with the mixed l₁/l₂ penalty by vectorizing the modified covariates.

3.2. Survival Outcomes

When R is the survival outcome, due to the potential censoring of observations, we do not always observe the exact outcomes of patients in clinical studies. Thus, R becomes a pair of random variables defined as $R=(Y,\delta )=(\tilde{Y}\wedge C,\delta )$, where $\tilde{Y}$ is the patient’s survival time, C is the censoring time, and δ is an indicator about whether this patient is censored or not. Motivated by Lemma 2 and a similar derivation as in Section 3.1, we can replace squared error loss in (16) for continuous outcomes by the negative log-likelihood of the Cox model for survival outcomes. Then, we have the following lemma for survival outcomes.

Lemma 4

Under the exchange of differential and expectation condition, an optimal solution to

$$\underset{\mathbf{f}\in \mathcal{F}}{\mathrm{argmin}}\mathbf{E}[{\int }_0^{\tau }\frac{\log \mathbf{E}[e^{{\mathbf{f}}^{\text{T}}\mathbf{w}}\mathbb{I}(Y\ge u)]}{\pi (A,\mathbf{x})}-\frac{{\mathbf{f}}^{\text{T}}\mathbf{w}}{\pi (A,\mathbf{x})}dN(u)]$$ (23)

is the function f* satisfying

$$\exp \left({\mathbf{w}}_i^{\text{T}}\mathbf{f}*\right)\mathbf{E}\left[\mathrm{\Lambda }*\left(Y^{(i)}\right)|\mathbf{x},A=i\right]=\mathbf{P}[\delta =1|\mathbf{x},A=i]$$ (24)

for a monotone nondecreasing function Λ*(u), where $N(u)=\mathbb{I}(\tilde{Y}\le u)\delta$, and τ is a fixed time point with $\mathbf{P}[\tilde{Y}\ge \tau ]>0$. If the censoring time is noninformative and the censoring rate for each treatment group is the same, then

$${\mathrm{argmax}}_{i\in \{1,\dots ,K\}}-{\mathbf{w}}_i^{\text{T}}f*={\mathrm{argmax}}_{i\in \{1,\dots ,K\}}\mathbf{E}[\mathrm{\Lambda }(Y)|\mathbf{x},A=i].$$ (25)

Using Lemma 4, the optimal decision rule for the survival outcome can be written as

$$d_0(\mathbf{x})={\mathrm{argmax}}_{k\in \{1,\dots ,K\}}{\mathbf{w}}_i^{\text{T}}\left(-\mathbf{f}*\right).$$ (26)

This is equivalent to fitting a weighted Cox proportional hazard (CPH) model with modified covariates x* = xw^T, by defining the hazard function as

$$\lambda (t|\mathbf{x},A)={\lambda }_0(t)e^{\mathrm{Tr}\left({\mathbf{B}}^{\text{T}}\mathbf{x}*\right)},$$ (27)

where λ₀(t) is a baseline hazard function. Then we can estimate the coefficient matrix B by maximum likelihood estimation such as

$$\begin{gathered} \underset{\mathbf{B}\in {ℝ}^{p\times (K-1)}}{\mathrm{argmin}}l(\mathbf{B})=\frac{1}{n}\sum _{i:{\delta }_i=1}\{-\frac{Y_i\mathrm{Tr}\left({\mathbf{B}}^T{\mathbf{x}}_i^{*}\right)}{\pi \left(A_i,{\mathbf{x}}_i\right)} \\ +\frac{1}{\pi \left(A_i,{\mathbf{x}}_i\right)}\log \sum _{j:Y_j\ge Y_i}\exp \left(\mathrm{Tr}\left({\mathbf{B}}^{\text{T}}{\mathbf{x}}_i^{*}\right)\right)\} \\ +\lambda J(\mathbf{B}), \end{gathered}$$ (28)

where J(B) is either the mixed l₁/l₂ penalty or the nuclear norm penalty under different model assumptions. As the gradient of the Cox loss function for this model requires heavy computation, similar to Section 3.1, efficient group coordinate descent (Breheny and Huang 2015) can be used to optimize (28) with the mixed l₁/l₂ penalty through vectorizing the modified covariates.

Note that the modified covariates x* in Equation (27) contain the treatment information that can be incorporated into the baseline hazard function. Thus, baseline hazard functions can be different for different treatments. For Lemma 4, we assume the censoring rate to be equal for all treatment groups so that our proposed method can be directly extended to the survival outcome. This assumption can possibly be removed by estimating the censoring rate for each group and then adjusting Equation (24).

4. Theoretical Properties of AD-learning

In this section, we show our proposed AD-learning is consistent under some mild conditions and establish finite value reduction bounds for our method. We first state the generalized margin condition used in our theory.

Assumption 1

For any ϵ > 0, there exists some constants C > 0 and α > 0 such that

$$\mathbf{P}[|{\left({\mathbf{w}}_i-{\mathbf{w}}_j\right)}^{\text{T}}{\mathbf{f}}_0(\mathbf{x})|\le ϵ]\le C{ϵ}^{\alpha }$$ (29)

for every i, j = 1, …, K.

Assumption 1 is an extension of margin condition used in binary classification problems to obtain sharper bounds on the excess 0–1 risk (Audibert et al. 2007). For our ITR problems, this generalized margin condition characterizes the behavior of the decision function vector f₀(x) around the boundary among different treatment regions, thus the level of difficulty in finding the optimal ITR. In the literature, Zhao et al. (2012b) used a similar assumption in the binary ITR problem. Using Assumption 1, we have the following theorem for the value reduction bound.

Theorem 1

For the estimator ${\widehat{\mathbf{f}}}_n$ by our proposed AD-learning and the corresponding ITR ${\widehat{d}}_n$, we have

$$V(d_0)-V({\widehat{d}}_n)\le \frac{2K(K-1)}{1-C(K)}{(E\Vert {\mathbf{f}}_0-{\widehat{\mathbf{f}}}_n{\Vert }_2^2)}^{\frac{1}{2}}.$$ (30)

Furthermore, if Assumption 1 holds, we can improve the bound by

$$V\left(d_0\right)-V({\widehat{d}}_n)\le C_1(K,\alpha ){(E{\Vert {\mathbf{f}}_0-{\widehat{\mathbf{f}}}_n\Vert }_2^2)}^{\frac{1+\alpha }{2+\alpha }},$$ (31)

where C₁(K, α) is the constant that only depends on K and α.

Remark 1

Based on (31), we can see that when α = 0 and C = 1, Assumption (1) always holds for any ϵ > 0. In this case, (31) reduces to (30). Based on (29), if α increases, the outcomes corresponding to various treatments become more different. As a result, the corresponding exponent $\frac{1+\alpha }{2+\alpha }$ becomes larger, and consequently a sharper bound in (31) can be obtained.

Theorem 1 gives an upper bound for the value function reduction in terms of the prediction error. For simplicity, we first consider Model (14) with equal π(A_i, x_i) for each treatment. Then, we can use the main idea from Lounici et al. (2009). We first vectorise the multiple responses and the coefficient B so that the model becomes

$$\underset{\mathit{\beta }\in {ℝ}^{p(K-1)}}{\mathrm{argmin}}\frac{1}{n(K-1)}\sum _{k=1}^{K-1}{\left({\mathbf{y}}_k-\mathbf{X}{\mathbf{\beta }}_k\right)}^{\text{T}}\left({\mathbf{y}}_k-\mathbf{X}{\mathbf{\beta }}_k\right)+\lambda \Vert \mathit{\beta }{\Vert }_{2,1},$$ (32)

where vector ${\mathbf{y}}_k=KR{\mathbf{w}}_k\in {ℝ}^n$ for k = 1, …, K − 1 and X is a design matrix with the ith row being the ith patient covariates x_i. Denote each column of the coefficients B as β_k, for k = 1, …, K − 1. Then, $\mathit{\beta }\in {ℝ}^{p(K-1)}$ is formed by stacking the coefficient β_k, for k = 1, …, K − 1. We further define the (K −1)n×p(K −1) block diagonal matrix Z with its k-th block formed by the design matrix X.

We assume the underlying true f₀ is linear with coefficient β₀. Define S(β) = {j : β_kj ≠ 0, k 1, …, K − 1 and the cardinality of S(β) as ‖S(β)‖0. We make the following two assumptions as in Lounici et al. (2009). The first one is the restricted eigenvalue (RE) assumption considered by Bickel et al. (2009) with an extension to the mixed l₁/l₂ norm.

Assumption 2

[RE(s)] For any nonzero β with ‖S‖₀ ≤ s and ${\Vert {\mathit{\beta }}_{S^c}\Vert }_{2,1}\le 3{\Vert {\mathit{\beta }}_S\Vert }_{2,1}$, there exists a positive real number ρ(s) such that

$$\sqrt{\mathit{\beta }\widehat{\mathbf{\Sigma }}\mathit{\beta }}\ge \rho (s)\Vert {\mathit{\beta }}_S\Vert ,$$ (33)

where S denotes the short notation of S(β) and $\widehat{\mathbf{\Sigma }}=\frac{1}{n}{\mathbf{Z}}^{\text{T}}\mathbf{Z}$.

The next assumption is to control the stochastic error term in Model (14) with the bounded variance assumption.

Assumption 3

1. Assume that the random error $e_{ki}=(y_{ki}-{\mathbf{x}}_i^{\text{T}}{\mathit{\beta }}_k)$; i = 1, …, n, k = 1, …, K − 1, are independent among different i with mean zero and finite variance $E\left[e_{ki}^2\right]\le {\sigma }^2$.

2. There exists a constant c such that max_1≤i≤n max_1≤j≤p |x_ij| ≤ c.

With the assumptions in place, we have the following theorem.

Theorem 2

Consider Model (14), for p ≥ 3 and K, n ≥ 1. Assume S(β₀) ≤ s, Assumptions 2 and 3 and the RE(2s) assumption hold. Let

$$\lambda =\sigma \sqrt{\frac{{(\log p)}^{1+\delta }}{n(K-1)}},$$

for any δ > 0. Then with probability at least $1-\frac{(2e\log p-e)c^2}{{(\log p)}^{1+\delta }}$, for the solution $\widehat{\mathbf{B}}$ to the Model (14), we have

$$V\left(d_0\right)-V({\widehat{d}}_n)\le \frac{\sqrt{K-1}K(K-1)}{1-C(K)}\frac{4\sqrt{10}c}{{\rho }^2(2s)}\sigma \sqrt{\frac{s{(\log p)}^{1+\delta }}{n}}.$$ (34)

Furthermore, if Assumption 1 is satisfied, we can improve the bound by

$$V\left(d_0\right)-V({\widehat{d}}_n)\le C(K,\alpha )\frac{32}{{\rho }^2(s)}{\sigma }^{2}s{\left(\frac{{(\log p)}^{1+\delta }}{n}\right)}^{\frac{1+\alpha }{2+\alpha }},$$ (35)

where C(K, α) only depends on K and the margin condition constant α.

Theorem 2 gives us the value reduction bound of order nearly $\frac{1}{n}$ as long as α is large enough. This value bound is consistent with l₁-PLS proposed by Qian and Murphy (2011) if we assume the underlying true function is linear. For a general function approximation, an additional approximation error to f₀(x) needs to be considered.

For Model (15), Rohde et al. (2011) has obtained the same rate $\mathbf{O}(\frac{1}{n})$ for the prediction error and thus the order of value reduction bound for Model (15) is the same as Theorem 2. For Model (22), it can be regarded as usual logistic regression with modified covariates. If we consider the mixed l₁/l₂ penalty, error bounds of the same order were developed in Meier et al. (2008). These results are applicable to our proposed AD-learning. However, to the best of our knowledge, the finite sample properties of other settings such as CPH models with the mixed l₁/l₂ penalty or low-rank penalty require further developments and we leave it as the future work.

5. Simulation Study

In this section, we perform an extensive simulation study to investigate the finite sample performance of AD-learning for various types of outcomes. For all simulation settings, we consider four-armed (K = 4) randomized trials with equal probabilities of patients being assigned to each treatment group. For the low-dimensional simulation setting, we set the sample size n to be 200, 400, and 800. The number of covariates p is set to be 20 and 40. For high-dimensional simulation settings, we let the sample size be 400 and p be 1000. Each simulation is repeated for 120 times. Additional simulation results are in the supplementary material, such as settings with n = 200, low-rank decision function simulation studies, etc.

For the implementation details of AD-learning, two types of algorithms can be applied. The first one is the accelerated proximal gradient method. In particular, Models (14) and (15) can be represented as follows:

$$\min F(\mathbf{B}):=L(\mathbf{B})+\lambda J(\mathbf{B}),$$ (36)

where L(B) is a smooth convex function with its gradient being Lipschitz continuous and J(B) is a nonsmooth convex function, of which the proximal operator can be computed efficiently. Then, we can use the accelerated proximal gradient method to solve it with low computational complexity. It achieves the optimal converge rate $\mathbf{O}(\frac{1}{m^2})$ for gradient methods, where m is the number of iterations for the algorithm. More details can be found in Nesterov (2013) and Toh and Yun (2010).

In binary and survival outcome settings, the gradient of function L(B) may need large computational cost to calculate. To address the problem, the stochastic block coordinate decent algorithm can be applied instead when J(B) is the mixed l₁/l₂ penalty. By using this algorithm, each gradient decent iteration can be efficiently computed. Thus, the stochastic block coordinate decent algorithm may cost less time than the accelerated proximal gradient method.

The tuning parameter λ is selected based on the cross-validation procedure. The criterion is to select λ that maximizes the average of estimated value functions on the validation data set defined as follows:

$$\widehat{V}(d)=\frac{{\mathbf{E}}_n[R\mathbb{I}(A=d(\mathbf{x}))/\pi (A,\mathbf{x})]}{{\mathbf{E}}_n[\mathbb{I}(A=d(\mathbf{x}))/\pi (A,\mathbf{x})]},$$ (37)

where E_n denotes the empirical average.

5.1. Study of Continuous Outcomes

When the clinical outcome R is continuous, we generate our data from Model (7). Specifically, for i = 1, …, n, let

$$R_i=\mu \left({\mathbf{x}}_i\right)+\delta \left({\mathbf{x}}_i\right)+{ϵ}_i,$$

where $\delta \left({\mathbf{x}}_i\right)={\sum }_{k=1}^K\left({\mathbf{x}}_i^{\text{T}}{\mathit{\beta }}_k\right)\mathbb{I}(A=k)$, each covariate is generated by the uniform distribution from −1 to 1, and ϵ_i follows from the standard normal distribution. For each simulation scenario, we consider μ(x) = 1 + X₁ + X₂ and consider other types of main effect functions in the supplementary material. We design the following three interaction functions similar to those in Zhou et al. (2017) and Zhang et al. (2015):

1. $$\begin{gathered} \delta (\mathbf{x})=\left(1+X_1+X_2+X_3+X_4\right)\mathbb{I}(A=1)+(1+X_1- \\ {X}_2-X_3+X_4)\mathbb{I}(A=2)+\left(1+X_1-X_2+X_3-X_4\right)\mathbb{I}(A= \\ 3)+\left(1-X_1-X_2+X_3+X_4\right)\mathbb{I}(A=4); \end{gathered}$$

2. $$\begin{gathered} \delta (\mathbf{x})=\left(3\mathbb{I}\left(X_1\le 0.5\right)\left(\mathbb{I}\left(X_2>-0.6\right)-1\right)\right)\mathbb{I}(A=1)+ \\ (\left(\mathbb{I}\left(X_3\le 1\right)\right)\left(2\mathbb{I}\left(X_4\le -0.3\right)-1\right)\mathbb{I}(A=2)+(4\mathbb{I}(X_5\le \\ 0)-2)\mathbb{I}(A=3)+\left(4\mathbb{I}\left(X_6\le 0\right)-2\right)\mathbb{I}(A=4); \end{gathered}$$

3. $$\begin{gathered} \delta (\mathbf{x})=\left(0.2+X_1^2+X_2^2-X_3^2-X_4^2\right)\mathbb{I}(A=1)+(0.2+X_2^2+ \\ {X}_3^2-X_2^2-X_4^2)\mathbb{I}(A=2)+\left(0.2+X_1^2+X_4^2-X_2^2-X_3^2\right)\mathbb{I}(A= \\ 3)+\left(0.2+X_2^2+X_3^2-X_1^2-X_4^2\right)\mathbb{I}(A=4). \end{gathered}$$

The first scenario corresponds to linear interaction effects. For the second scenario, we consider tree-type interaction effects. The last scenario includes polynomial interaction effects and we use degree 2 polynomials as basis functions for all methods. For each simulation scenario, we compare our proposed AD-learning using the group sparsity penalty with the following methods:

1. l₁-PLS proposed by Qian and Murphy (2011) with basis (1, x, xA);

2. pairwise D-learning;

3. the decision list (DL) method proposed by Zhang et al. (2015);

4. adaptive contrast weighted learning (ACWL-1 and ACWL-2) methods proposed by Tao and Wang (2017);

5. the method of virtual twins (VT) proposed by Foster et al. (2011),

where we use degree 2 polynomials as basis functions for all methods in the last scenario. Additional simulation study results on AD-learning using the low rank sparsity penalty are included in the supplementary material. In addition, we also perform the comparison between group l₁-PLS and l₁-PLS in the supplementary material, which shows little differences between l₁-PLS and group l₁-PLS in our simulation studies. This confirms our appropriate use of l₁-PLS instead of group l₁-PLS unless there are some prior information about strong group sparsity structures.

All the tuning parameters are selected via 10-fold cross-validation. We report the value functions and misclassification errors for p = 40 on 10,000 independently generated test data in Table 1. From Table 1, we can see that our AD-learning has competitive performance among all methods. When we consider linear interaction effect, it is expected that our proposed AD-learning and l₁-PLS perform the best compared with other methods. In particular, our method will potentially be better than l₁-PLS because l₁-PLS suffers the mismatch problem discussed previously. For the second simulation scenario that corresponds to simple tree-type interaction effect, while those tree-based methods such as VT, DL and ACWL perform well, our method is still competitive. Similar results for p = 20 are included in the supplementary material. An interesting observation for this scenario is that although VT has the largest empirical value function among all methods, its misclassification rate is similar to that of our proposed method when n = 400. One potential reason is that VT is focused on model fitting while our method directly targets on decision rules. For the last scenario, since the basis functions we used correctly identify the interaction effect, our proposed AD-learning and l₁-PLS enjoy some advantages over other methods.

Table 1.

Results of average means (standard deviations) of empirical value functions and misclassification rates for four continuous-outcome simulation scenarios with 40 covariates. The best value functions and misclassification rates are in bold.

	n = 400		n = 800
	Value	Misclassification	Value	Misclassification
Scenario 1
Pair-D	2.67(0.06)	0.49(0.02)	3.01(0.02)	0.32(0.02)
l1-PLS	3.05(0.04)	0.24(0.01)	3.15(0.01)	0.16(0.01)
DL	2.6(0.04)	0.54(0.01)	2.78(0.02)	0.47(0.01)
ACWL-1	2.69(0.05)	0.46(0.01)	2.9(0.02)	0.37(0.01)
ACWL-2	2.77(0.05)	0.43(0.01)	3.02(0.01)	0.31(0.01)
VT	2.66(0.03)	0.5(0.01)	2.81(0.02)	0.45(0.01)
Group-AD	3.06(0.05)	0.22(0.02)	3.14(0.03)	0.15(0.02)
Scenario 2
Pair-D	2.84(0.12)	0.32(0.04)	2.93(0.1)	0.3(0.03)
l1-PLS	2.93(0.11)	0.36(0.04)	3.01(0.1)	0.32(0.04)
DL	2.89(0.12)	0.34(0.04)	3.04(0.11)	0.28(0.04)
ACWL-1	2.76(0.11)	0.38(0.02)	2.96(0.11)	0.32(0.02)
ACWL-2	2.81(0.11)	0.38(0.02)	3.03(0.1)	0.29(0.03)
VT	3.07(0.09)	0.31(0.02)	3.12(0.1)	0.27(0.02)
Group-AD	2.97(0.1)	0.31(0.03)	2.97(0.1)	0.3(0.03)
Scenario 3
Pair-D	1.2(0.03)	0.75(0.03)	1.2(0.03)	0.75(0.03)
l1-PLS	1.42(0.18)	0.61(0.13)	1.58(0.22)	0.47(0.18)
DL	1.38(0.08)	0.64(0.06)	1.5(0.08)	0.57(0.06)
ACWL-1	1.29(0.08)	0.7(0.04)	1.49(0.07)	0.56(0.05)
ACWL-2	1.3(0.07)	0.69(0.04)	1.57(0.06)	0.51(0.05)
VT	1.39(0.05)	0.64(0.03)	1.44(0.04)	0.6(0.03)
Group-AD	1.57(0.14)	0.5(0.11)	1.76(0.04)	0.3(0.05)

5.2. Study of Binary and Survival Outcomes

For the binary outcome R, the dataset is independently generated by the logistic regression model

$$\mathrm{logit}\left(\mathbf{P}\left[R_i=1\right]\right)=\mu \left({\mathbf{x}}_i\right)+\sum _{k=1}^K\left({\mathbf{x}}_i^{\text{T}}{\mathit{\beta }}_k\right)\mathbb{I}(A=k),$$

where the link function $\mathrm{logit}(x)=\log \frac{x}{1-x}$. We consider same interaction effects as the first two scenarios of the continuous outcome simulation study.

Since pairwise D-learning and ACWL are not intended for the binary outcome, after modifying the l₁-PLS by using l₁ penalized logistic regression (l₁-PLR), we compare l₁-PLR, DL and VT with our AD-learning. Table 2 shows the value functions and misclassification rates for p = 40 and n = 400, 800. We can see that our proposed AD-learning has largest value functions and lowest misclassification rates in both scenarios. Moreover, there are some mismatches in model-based methods such as l₁-PLS, where the misclassification rates and the value functions are both high. One potential reason is the mismatch between the optimization criterion and the tuning procedure in l₁-PLS. The other potential reason is the mismatch between minimizing prediction error and maximizing value function in model-based methods.

Table 2.

Results of average means (standard deviations) of empirical value functions and misclassification rates for two binary-outcome simulation scenarios with 40 covariates. The best value functions and misclassification rates are in bold.

	n = 400		n = 800
	Value	Misclassification	Value	Misclassification
Scenario 1
l1-PLR	0.88(0.01)	0.58(0.02)	0.91(0)	0.45(0.02)
DL	0.85(0.01)	0.67(0.01)	0.87(0.01)	0.61(0)
VT	0.84(0.01)	0.68(0.01)	0.84(0)	0.69(0)
Binary-AD	0.9(0.01)	0.44(0.02)	0.92(0)	0.32(0.02)
Scenario 2
l1-PLR	0.83(0.01)	0.66(0.05)	0.86(0)	0.61(0.05)
DL	0.81(0.01)	0.53(0.01)	0.85(0.01)	0.44(0.01)
VT	0.83(0.01)	0.43(0.01)	0.83(0.01)	0.51(0)
Binary-AD	0.86(0.01)	0.43(0.04)	0.87(0.01)	0.4(0.04)

Next, we consider R to be the outcome of time to event. The simulated data are generated by the following model with the exponential distribution:

$$R_i=\exp \left({\lambda }_i\right),$$

where exp denotes the exponential distribution and ${\lambda }_i=\mu \left({\mathbf{x}}_i\right)+{\sum }_{k=1}^K\left({\mathbf{x}}_i^{\text{T}}{\mathit{\beta }}_k\right)\mathbb{I}(A=k)$ for i = 1, …, n. The censoring time C_i; i = 1, …, n, are generated from an exponential distribution with mean θ to induce around 25% censoring rate. We consider the same settings as those in the binary case. For comparisons, we apply the l₁ penalized CPH models and compare it with AD-learning, since other methods we use previously are not designed for the survival outcome. From Table 3 with p = 40, we can see that our proposed AD-learning has clear advantages over l₁-CPH. In addition, we also observe the mismatch phenomena of l₁-CPH in Scenario 2 of Table 3.

Table 3.

Results of average means (standard deviations) of empirical value functions and misclassification rates for two survival-outcome simulation scenarios with 40 covariates.

	n = 400		n = 800
	Value	Misclassification	Value	Misclassification
Scenario 1
l1-CPH	41.35(2.2)	0.33(0.04)	45.05(1.1)	0.21(0.02)
Surv-AD	43.91(1.3)	0.25(0.02)	45.56(1.06)	0.18(0.01)
Scenario 2
l1-CPH	21.95(0.63)	0.57(0.04)	23.21(0.59)	0.5(0.04)
Surv-AD	22.1(0.62)	0.46(0.02)	22.78(0.53)	0.44(0.02)

NOTE: The best value functions and misclassification rates are in bold.

5.3. Study of High-Dimensional Problems

We evaluate our AD-learning performance for high-dimensional settings. We consider the sample size n = 400 so that each treatment group has roughly 100 patients and number of covariates p = 800. Scenarios 1–2, 3–4, 5–6 correspond to continuous, binary, and survival outcomes, respectively. The interaction effects considered here are the same as the first two scenarios in the continuous setting in Section 5.1.

From Table 4, we can find that our proposed AD-learning performs better than l₁-PLS. One of the possible reasons is that our proposed method tends to select right covariates for the interaction effect function due to the direct learning of the decision rule. An interesting observation is that although pairwise D-learning has the lowest misclassification rate in Scenario 2, its corresponding value function is the lowest. This mismatch comes from the potential sub-optimality of pairwise comparisons.

Table 4.

Results of average means (standard deviations) of empirical value functions and misclassification rates for six high-dimensional simulation scenarios.

	Method	Value	Misclassification
Scenario 1	l1-PLS	5.3(0.02)	0.17(0.01)
	Pair-D	4.51(0.14)	0.47(0.03)
	Group-AD	5.31(0.04)	0.15(0.02)
Scenario 2	l1-PLS	5.64(0.03)	0.22(0.01)
	Pair-D	5.51(0.02)	0.2(0.01)
	Group-AD	5.65(0.04)	0.21(0.01)
Scenario 3	l1-PLR	0.88(0.02)	0.64(0.04)
	Binary-AD	0.92(0.02)	0.46(0.06)
Scenario 4	l1-PLR	0.84(0.01)	0.7(0.02)
	Binary-AD	0.87(0.01)	0.45(0.03)
Scenario 5	l1-CPH	771.35(126.2)	0.41(0.09)
	Surv-AD	1004.57(40.19)	0.2(0.02)
Scenario 6	l1-CPH	150.87(7.71)	0.63(0.02)
	Surv-AD	158.92(4.73)	0.45(0.02)

NOTE: The best value functions and misclassification rates are in bold.

6. Real Data Applications

In this section, we perform a real data analysis to further evaluate our proposed AD-learning. We consider a clinical trial dataset from “AIDS Clinical Trials Group (ACTG) 175” in Hammer et al. (1996) to study whether there is a subgroup of patients suitable for different combination treatments of AIDS. In this study, with equal probabilities, a total number of 2139 patients with HIV infection were randomly assigned into four treatment groups: zidovudine (ZDV) monotherapy, ZDV combined with didanosine (ddI), ZDV combined with zalcitabine (ZAL), and ddI monotherapy.

We choose 12 baseline covariates in our model: age (year), weight(kg), CD4+T cells amount at baseline, CD8 amount at baseline, Karnofsky score (scale at 0–100), gender (1 = male, 0 = female), race (1 = nonwhite, 0 = white), homosexual activity (1 = yes, 0 = no), history of intravenous drug use (1 = yes, 0 = no), symptomatic status (1 = symptomatic, 0 = symptomatic), antiretroviral history (1 = experienced, 0 = naive) and hemophilia (1 = yes, 0 = no). The first five covariates are continuous and have been scaled before estimation. The remaining seven covariates are binary categorical variables.

We consider two outcomes for our analysis. The first outcome is the difference between the early stage (around 25 weeks) CD4+ T (cells/mm³) cell amount and the baseline CD4+ T cells prior to the trial. This was also studied in Lu et al. (2013) and Fan et al. (2017). Using this short-term outcome, our goal is to use AD-learning to find the short-term optimal ITR for each patient with AIDS among four treatment groups. We report the estimator of the coefficient ${\mathbf{w}}_i^{\text{T}}{\mathbf{B}}^{\text{T}}$ for each treatment in Table 5.

Table 5.

Results of coefficients estimation for comparison functions.

Variable Name (1–7)	ZDV	ZDV+ddI	ZDV+Zal	ddI
Intercept	−49.86	44.66	−3.53	8.73
Age	−0.47	4.33	−3.34	−0.52
Weight	0	0	0	0
Karnofsky Score	0	0	0	0
CD4 baseline	3.58	−14.79	−14.78	9.46
Days preantiretroviral therapy	0	0	0	0
Hemophilia	0	0	0	0
Homosexual activity	−0.28	−3.96	0.65	3.60
History of drug use	−2.50	8.20	4.03	−9.74
Race	0	0	0	0
Gender	0	0	0	0
Antiretroviral history	0	0	0	0
Symptomatic indicator	0	0	0	0

In Table 5, we can see that four covariates including Age, CD4 baseline, homosexual activity and history of drug use, are identified to play an important role in our estimated optimal ITRs. These variables were also identified in the previous literature such as Lu et al. (2013) and Fan et al. (2017). According to the analysis in Hammer et al. (1996), ZDV alone is inferior to the other treatments, which is also confirmed in our estimated ITR. Based on the CD4 change in the early stage, Zal treatment is generally not recommended in our finding with one possible reason that Zal has the most serious adverse event compared with ZDV and ddI (Kakuda 2000). According to our estimated ITRs, those old patients with small amount of CD4 T cell baseline and having history of drug use but not homosexual activity, are recommended to take ZDV + ddI. The patients with large amount of CD4 T cell baseline and history of homosexual activity but not drug use history, are more advisable to take ddI alone.

To evaluate the performance of our proposed AD-learning, we randomly split the data into five folds and use four folds to train the model. We evaluate our method on the remaining one fold of data based on the empirical value function. We repeat this procedure for 1000 times. From Table 6, we can see our AD-learning has the largest value.

Table 6.

Results of empirical value functions on one fold of testing data. The best empirical value function is in bold.

l1-PLS	Pair-D	DL	ACWL-1	ACWL-2	VT	AD low rank	AD group
53.73 (0.33)	57.17 (0.40)	53.25 (0.47)	52.74 (0.45)	54.04 (0.45)	54.84 (0.45)	50.48 (0.38)	59.69(0.39)

The second outcome is patients’ time to event. Using this long-term outcome, our second goal is to find the long-term optimal ITR for patients among four treatment groups. The AIDS data consist of 2139 patient time to event responses with around 75% censor rate during the four-year long trial study. We use our proposed Model (23) to estimate the optimal ITR. We report the estimates of the coefficient ${\mathbf{w}}_i^{\text{T}}{\mathbf{B}}^{\text{T}}$ for each treatment of 12 covariates in Table 7. We can see that all covariates, except the indicator of homosexual activity and symptomatic, play an important role in the estimated optimal ITR. It may not be surprising because it is a long-term study and thus more complicated. Since we model via the hazard function, the smaller the coefficient is, the longer the survival time is.

Table 7.

Results of coefficient estimation for survival time of failure.

Variable Name (1–7)	ZDV	ZDV+ddI	ZDV+Zal	ddI
Age	0.04	−0.11	0.04	0.03
Weight	0.11	0.02	0.02	−0.14
Karnofsky Score	0.06	0.03	−0.09	0.01
CD4 baseline	−0.04	0.04	−0.00	0.00
Days preantiretroviral therapy	0.09	−0.07	−0.04	0.02
Hemophilia	0.05	−0.06	0.16	−0.15
Homosexual activity	0.00	0.00	0.00	0.00
History of drug use	0.04	−0.11	−0.12	0.18
Race	0.03	−0.04	0.01	0.01
Gender	0.31	−0.08	−0.16	−0.07
Antiretroviral history	0.17	−0.15	0.04	−0.06
Symptomatic Indicator	0.00	0.00	0.00	0.00

Compared with the previous finding based on the short-term CD4 T cells amount, covariates including age, CD4 baseline and history of drug use have the similar effect on the ZDV + ddI and ddI alone treatments. In addition, we also find that ZDV + Zal treatment may not be good to take for the female patients with hemophilia, but may be suitable for the male patients with high Karnosky score and history of drug use. The estimated optimal ITR for other treatments can be interpreted in the similar way. In general, ZDV alone is always the least preferable among other treatments for patients and ZDV+ddI is always preferable for patients. Based on time-to-event outcome, ZDV+ Zal is relatively more preferable than ddI alone. In addition, we evaluate our AD-learning with l₁-CPH using the same scheme based on value functions. Our AD-learning has an average value of911.20,compared with the average value of 905.02 for l₁-CPH.

7. Conclusion

In this article, we propose an AD-learning method to estimate the optimal ITRs in multiple treatment settings for various types of outcomes. Our proposed method provides a clear geometric interpretation about the relative effectiveness of treatments for patients, which is quantified by angles in the Euclidean space. Our proposed AD-learning is robust to model misspecification. By incorporating group or low rank sparsity, our AD-learning can further improve the estimation of decision rules and interpretation, especially for high dimensional settings. The competitive performance of our method has been demonstrated via the simulation studies and data applications.

Several possible extensions can be explored for future study. Our proposed method for the survival outcome is based on the noninformative censoring and Cox proportional hazard assumption. It will be interesting to develop methods for more complex settings. In order to use nonlinear functions to approximate f₀(x), we can use different types of basis functions such polynomials or wavelet functions. It will be also interesting to develop kernel methods for our AD-learning, such as multiple kernel learning (Bach et al. (2004)). Finally, the current AD-learning focuses on a single decision point. It will be worthwhile to develop the corresponding methods for multiple decision points (Zhao et al. 2015a; Liu et al. 2016).

Appendix

Proof of Lemma 1

Let $g(f)=\mathbf{E}[\frac{1}{\pi (A,\mathbf{x})}{(KR\mathbf{w}-\mathbf{f}(\mathbf{x}))}^{\text{T}}\mathrm{\Sigma }(KR\mathbf{w}-\mathbf{f}(\mathbf{x}))]$. Taking the derivative over f and setting it to zero, we get

$$\begin{gathered} \frac{\partial g(f)}{\partial f}=2\mathrm{\Sigma }{\mathbf{E}}_{\mathbf{x}}\left\{\mathbf{E}[(\frac{KRW}{\pi (A,\mathbf{x})}-\frac{f(\mathbf{x})}{\pi (A,\mathbf{x})})|\mathbf{x}]\right\} \\ =2\mathrm{\Sigma }{\mathbf{E}}_{\mathbf{x}}\{K\mathbf{E}[\frac{RW}{\pi (A,\mathbf{x})}|\mathbf{x}]-f(\mathbf{x})|\mathbf{x}]\}=0. \end{gathered}$$

Proof of Lemma 2

Let $g(f)=\mathbf{E}[\frac{1}{\pi (A,\mathbf{x})}{(\frac{K}{K-1}R-{\mathbf{w}}^{\text{T}}\mathbf{f}(\mathbf{x}))}^{\text{T}}(\frac{K}{K-1}R-{\mathbf{w}}^{\text{T}}\mathbf{f}(\mathbf{x}))]$. Taking the derivative over f and setting it to zero, we get

$$\begin{gathered} \frac{\partial g(f)}{\partial f}={\mathbf{E}}_{\mathbf{x}}\left\{\mathbf{E}\left[W(\frac{KR}{(K-1)\pi (A,\mathbf{x})}-\frac{W^{\text{T}}f(\mathbf{x})}{\pi (A,\mathbf{x})})|\mathbf{x}\right]\right\} \\ ={\mathbf{E}}_{\mathbf{x}}\{\frac{K}{K-1}\mathbf{E}[\frac{RW}{\pi (A,\mathbf{x})}|\mathbf{x}]-\frac{K}{K-1}f(\mathbf{x})|\mathbf{x}]\}=0, \end{gathered}$$

where the second equality holds because $\mathbf{E}[\frac{W{W}^{\text{T}}}{\pi (A,\mathbf{x})}|\mathbf{x}]=\frac{K}{K-1}{I}_{K-1}$ by definition. Thus, f₀(x) is an optimal solution.

Proof of Lemma 3

Let $g(f)=\mathbf{E}[-\frac{R{\mathbf{w}}^{\text{T}}f}{\pi (A,\mathbf{x})}+\frac{\log \left(1+\exp \left({\mathbf{w}}^{\text{T}}f\right)\right)}{\pi (A,\mathbf{x})}]$. Taking the derivative over f and setting it to zero, we get

$$\begin{gathered} \frac{\partial g(f)}{\partial f}=2{\mathbf{E}}_{\mathbf{x}}\left\{\mathbf{E}[\left(\frac{RW}{\pi (A,\mathbf{x})}-\frac{W\exp \left({\mathbf{w}}^{\text{T}}f\right)}{1+\exp \left({\mathbf{w}}^{\text{T}}f\right))\pi (A,\mathbf{x})}\right)|\mathbf{x}]\right\} \\ =2{\mathbf{E}}_{\mathbf{X}}\left\{\sum _{i=1}^K{\mathbf{w}}_i\mathbf{P}[R=1|\mathbf{x},A=i]-\sum _{i=1}^K{\mathbf{w}}_i\frac{\exp \left({\mathbf{w}}_i^{\text{T}}f\right)}{1+\exp \left({\mathbf{w}}_i^{\text{T}}f\right)}\right\} \\ =0. \end{gathered}$$

If $\mathbf{P}[R=1|\mathbf{x},A=i]=\frac{\exp \left({\mathbf{w}}_i^{\text{T}}f*\right)}{1+\exp \left({\mathbf{w}}_i^{\text{T}}f*\right)}$, then f* is an optimal solution to (18).

Proof of Lemma 4

Let $g(f)=\mathbf{E}\left[{\int }_0^{\tau }\frac{\log \mathbf{E}[e^{f^{\text{T}}\mathbf{w}}\mathbb{I}(Y\ge u)]}{\pi (A,\mathbf{x})}-\frac{f^{\text{T}}\mathbf{w}}{\pi (A,\mathbf{x})}dN(u)\right]$. Taking the derivative over f and setting it to zero, we get

$$\begin{gathered} \frac{\partial g(f)}{\partial f}={\mathbf{E}}_{\mathbf{x}}\{{\int }_0^{\tau }\sum _{i=1}^K{\mathbf{w}}_i\mathbf{E}\left[\mathbb{I}(Y\ge u){\lambda }_i(u,\mathbf{x})|\mathbf{x},A=i\right] \\ -\frac{{\mathbf{w}}_i\exp \left({\mathbf{w}}_i^{\text{T}}f\right)\mathbb{I}\left(Y^{(i)}\ge u\right)\mathbf{E}[\mathbb{I}(Y\ge u)\lambda (u,\mathbf{x})|\mathbf{x}]}{\mathbf{E}\left[\exp \left(W^{\text{T}}f\right)\mathbb{I}(Y\ge u)\right]}du\} \\ ={\mathbf{E}}_{\mathbf{x}}\{{\int }_0^{\tau }\sum _{i=1}^K{\mathbf{w}}_i(\mathbf{E}\left[\mathbb{I}(Y\ge u){\lambda }_i(u,\mathbf{x})|\mathbf{x},A=i\right] \\ -\exp \left({\mathbf{w}}_i^{\text{T}}f\right)\mathrm{\Lambda }*\left(Y^{(i)}\right))du\} \\ =0, \end{gathered}$$

where λi(u, x) is the hazard function for the i-th treatment and Λ*(Y) is the cumulative hazard function. Then, we get a sufficient condition that if $\exp \left({\mathbf{w}}_i^{\text{T}}f\right)\mathrm{\Lambda }*\left(Y^{(i)}\right)=\mathbf{P}[\delta =1|\mathbf{x},A=i]$, then f* is an optimal solution. If the censoring time in each treatment group is the same, then we get (25).

Proof of Theorem 1

For any ITR d, we have

$$\begin{gathered} V(d)=\mathbf{E}\left[\sum _{k=1}^K\mathbf{E}[R|\mathbf{x},A=k]\mathbb{I}(d(\mathbf{x})=k)\right] \\ =\mathbf{E}[\frac{1}{1-C(K)}\{\sum _{k=1}^K(1-C(K))\mathbf{E}[R|\mathbf{x},A=k]\mathbb{I}(d(\mathbf{x})=k) \\ +\sum _{j=1}^{K}C(K)\mathbf{E}[R|\mathbf{x},A=j]\}-\frac{C(K)}{1-C(K)}\sum _{j=1}^K\mathbf{E}[R|\mathbf{x},A=j]] \\ =\mathbf{E}[\frac{1}{1-C(K)}\{\sum _{k=1}^K\mathbf{E}[R|\mathbf{x},A=k]\mathbb{I}(d(\mathbf{x})=k) \\ +\sum _{j=1}^{K}C(K)\mathbf{E}[R|\mathbf{x},A=j]\sum _{i\ne j}^K\mathbb{I}(d(\mathbf{x})=i)\}]-\mathrm{\Delta } \\ =\mathbf{E}[\frac{1}{1-C(K)}\{\sum _{k=1}^K\mathbf{E}[R|\mathbf{x},A=k]\mathbb{I}(d(\mathbf{x})=k) \\ +\sum _{i=1}^K\sum _{j\ne i}^{K}C(K)\mathbf{E}[R|\mathbf{x},A=j]\mathbb{I}(d(\mathbf{x})=i)\}]-\mathrm{\Delta } \\ =\mathbf{E}[\frac{1}{1-C(K)}\sum _{k=1}^K(\mathbf{E}[R|\mathbf{x},A=k] \\ +\sum _{j\ne k}^{K}C(K)\mathbf{E}[R|\mathbf{x},A=k])\mathbb{I}(d(\mathbf{x})=k)]-\mathrm{\Delta } \\ =\mathbf{E}\left[\frac{1}{1-C(K)}\{\sum _{k=1}^K{\mathbf{w}}_k^{\text{T}}\mathbf{E}\left[\frac{RW}{\pi (A,\mathbf{x})}|\mathbf{x}\right]\mathbb{I}(d(\mathbf{x})=k)\}\right]-\mathrm{\Delta } \\ =\mathbf{E}\left[\frac{1}{1-C(K)}\{\sum _{k=1}^K{\mathbf{w}}_k^{\text{T}}{\mathbf{f}}_0(\mathbf{x})\mathbb{I}(d(\mathbf{x})=k)\}\right]-\mathrm{\Delta }, \end{gathered}$$ (A1)

where $\mathrm{\Delta }=\mathbf{E}\mathbf{[}C(K){\sum }_{j=1}^K\mathbf{E}[R|x,A=j]]$ that does not depend on the ITR d. Then we can obtain the value reduction bound between the optimal ITR d₀ and our estimated ITR $\widehat{d}$ by using (A1):

$$\begin{gathered} V\left(d_0\right)-V(\widehat{d}) \\ \le \frac{1}{1-C(K)}\mathbf{E}[\{\sum _{k=1}^K{\mathbf{w}}_k^T{\mathbf{f}}_0(\mathbf{x})(\mathbb{I}(d(\mathbf{x})=k)-\mathbb{I}(\widehat{d}(\mathbf{x})=k)\}] \\ \le \frac{1}{1-C(K)}\mathbf{E}[\{\sum _{i\ne j}|{\mathbf{w}}_i^T{\mathbf{f}}_0(\mathbf{x})-w_j^T{\mathbf{f}}_0(\mathbf{x})|\mathbb{I}(d(\mathbf{x})=i,\widehat{d}(\mathbf{x})=j)\}] \\ \le \frac{1}{1-C(K)}\mathbf{E}[\{\sum _{i\ne j}|{\mathbf{w}}_i^T{\mathbf{f}}_0(\mathbf{x})-w_j^T{\mathbf{f}}_0(\mathbf{x})|\mathbb{I}({\mathbf{w}}_i^T{\mathbf{f}}_0(\mathbf{x}) \\ -w_j^T{\mathbf{f}}_0(\mathbf{x}))({\mathbf{w}}_i^T\widehat{f}(\mathbf{x})-w_j^T\widehat{f}(\mathbf{x})<0)\}] \\ \le \frac{1}{1-C(K)}\mathbf{E}[\{\sum _{i\ne j}|{\mathbf{w}}_i^T({\mathbf{f}}_0(\mathbf{x})-\widehat{f}(\mathbf{x}))-w_j^T({\mathbf{f}}_0(\mathbf{x})-\widehat{f}(\mathbf{x}))| \\ \mathbb{I}({\mathbf{w}}_i^T({\mathbf{f}}_0(\mathbf{x})-\widehat{f}(\mathbf{x}))w_j^T({\mathbf{f}}_0(\mathbf{x})-\widehat{f}(\mathbf{x}))<0)\}] \\ \le \frac{1}{1-C(K)}\sum _{i\ne j}(\mathbf{E}\Vert {\mathbf{f}}_0(\mathbf{x})-\widehat{f}(\mathbf{x}){\Vert }_2+\mathbf{E}\text{||}{\mathbf{f}}_0(\mathbf{x})-\widehat{f}(\mathbf{x}){\Vert }_2) \\ \le \frac{2K(K-1)}{1-C(K)}{(\mathbf{E}{\Vert {\mathbf{f}}_0(\mathbf{x})-\widehat{f}(\mathbf{x})\Vert }_2^2)}^{\frac{1}{2}}, \end{gathered}$$ (A2)

where the second to last inequality holds by using the Hölder and Minkowski inequality together with ‖w_i‖ = 1 for i = 1, …, K. Furthermore, if we assume Assumption 1 holds, then we can further bound the value reduction by

$$\begin{gathered} V\left(d_0\right)-V(\widehat{d}) \\ \le \frac{1}{1-C(K)}\mathbf{E}[\{\sum _{i\ne j}|{\mathbf{w}}_i^{\text{T}}{\mathbf{f}}_0(\mathbf{x})-w_j^{\text{T}}{\mathbf{f}}_0(\mathbf{x})|\mathbb{I}({\mathbf{w}}_i^{\text{T}}{\mathbf{f}}_0(\mathbf{x}) \\ -w_j^{\text{T}}{\mathbf{f}}_0(\mathbf{x})({\mathbf{w}}_i^{\text{T}}\widehat{f}(\mathbf{x})-w_j^{\text{T}}\widehat{f}(\mathbf{x})<0)\}] \\ \le \frac{1}{1-C(K)}\mathbf{E}[\{\sum _{i\ne j}ϵ\mathbb{I}(|{\left({\mathbf{w}}_i-w_j\right)}^{\text{T}}{\mathbf{f}}_0(\mathbf{x})|<ϵ)\mathbb{I}({\left({\mathbf{w}}_i-w_j\right)}^{\text{T}} \\ {\mathbf{f}}_0(\mathbf{x}))({\left({\mathbf{w}}_i-w_j\right)}^{\text{T}}\widehat{f}(\mathbf{x}))<0)\}] \\ +\frac{1}{1-C(K)ϵ}\mathbf{E}[\{\sum _{i\ne j}{({\mathbf{w}}_i^{\text{T}}{\mathbf{f}}_0(\mathbf{x})-w_j^{\text{T}}{\mathbf{f}}_0(\mathbf{x}))}^2\mathbb{I}({\left({\mathbf{w}}_i-w_j\right)}^{\text{T}} \\ {\mathbf{f}}_0(\mathbf{x}))({\left({\mathbf{w}}_i-w_j\right)}^{\text{T}}\widehat{f}(\mathbf{x}))<0)\}] \\ \le \frac{1}{1-C(K)}\sum _{i\ne j}ϵ\mathbf{P}\left[|{\left({\mathbf{w}}_i-w_j\right)}^{\text{T}}{\mathbf{f}}_0(\mathbf{x})|<ϵ\right]+\frac{2}{ϵ}(\mathbf{E}\Vert {\mathbf{f}}_0(\mathbf{x})-\widehat{f}(\mathbf{x}){\Vert }_2^2 \\ +\mathbf{E}\Vert {\mathbf{f}}_0(\mathbf{x})-\widehat{f}(\mathbf{x}){\Vert }_2^2) \\ \le \frac{1}{1-C(K)}\sum _{i\ne j}C{ϵ}^{\alpha +1}+\frac{4}{ϵ}\mathbf{E}{\Vert {\mathbf{f}}_0(\mathbf{x})-\widehat{f}(\mathbf{x})\Vert }_2^2), \end{gathered}$$ (A3)

for any ϵ > 0. We can then minimize right-hand-side above over and get the desired bound

$$V\left(d_0\right)-V({\widehat{d}}_n)\le C_1(K,\alpha ){(E{\Vert {\mathbf{f}}_0-{\widehat{\mathbf{f}}}_n\Vert }_2^2)}^{\frac{1+\alpha }{2+\alpha }}.$$

Proof of Theorem 2

Define β^j = (β_kj, k = 1, …, (K − 1))^T, and let $\lambda =\sigma \sqrt{\frac{{(\log p)}^{1+\delta }}{n(K-1)}}$. With probability at least $1-\frac{(2e\log p-e)c}{{(\log p)}^{1+\delta }}$, we have the following inequality

$$\begin{gathered} \frac{1}{n(K-1)}{\Vert \mathbf{Z}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)\Vert }^2+\lambda \Vert \widehat{\mathit{\beta }}-\mathit{\beta }{\Vert }_{2,1}\le \\ \le \frac{1}{n(K-1)}{\Vert \mathbf{Z}\left(\mathit{\beta }-{\mathit{\beta }}_0\right)\Vert }^2+4\lambda \sum _{j\in S(\mathit{\beta })}\Vert {\widehat{\mathit{\beta }}}^j-{\mathit{\beta }}^j\Vert , \end{gathered}$$ (A4)

for any β. This was previously shown in Theorem 5.2 by Lounici et al. (2009). Let β = β₀. Then with probability at least $1-\frac{(2e\log p-e)c}{{(\log p)}^{1+\delta }}$, we have

$$\begin{gathered} \frac{1}{n(K-1)}{\Vert \mathbf{Z}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)\Vert }^2\le 4\lambda \sum _{j\in S(\mathit{\beta })}\Vert {\widehat{\mathit{\beta }}}^j-{\mathit{\beta }}^j\Vert \\ \le 4\lambda \sqrt{s}\Vert {(\widehat{\mathit{\beta }}-\mathit{\beta })}_S\Vert \end{gathered}$$

and

$$\Vert \widehat{\mathit{\beta }}-\mathit{\beta }{\Vert }_{2,1}\le 4\Vert {(\widehat{\mathit{\beta }}-\mathit{\beta })}_S\Vert ,$$

which implies $\Vert \widehat{\mathit{\beta }}-\mathit{\beta }{\Vert }_{S^c}\le 3\Vert {(\widehat{\mathit{\beta }}-\mathit{\beta })}_S\Vert$. Then by the RE(s) assumption, with probability at least $1-\frac{(2e\log p-e)c}{{(\log p)}^{1+\delta }}$, we have

$$\begin{gathered} \frac{1}{n(K-1)}{\Vert \mathbf{Z}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)\Vert }^2\le 4\lambda \sqrt{s}\Vert {(\widehat{\mathit{\beta }}-\mathit{\beta })}_S\Vert \\ \le 4\lambda \sqrt{s}\frac{\Vert \mathbf{Z}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)\Vert }{\rho (s)\sqrt{n}}, \end{gathered}$$

such that we can bound the empirical error by

$$\frac{1}{n}{\Vert \mathbf{Z}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)\Vert }^2\le \frac{16(K-1)}{\rho (s)}{\sigma }^{2}s\frac{{(\log p)}^{1+\delta }}{n}.$$

With the RE(2s) assumption, we can further show that with the same probability

$$\frac{1}{\sqrt{K-1}}\Vert \widehat{\mathit{\beta }}-{\mathit{\beta }}_0\Vert \le \frac{4\sqrt{10}}{{\rho }^2(2s)}\sigma \sqrt{\frac{s{(\log p)}^{1+\delta }}{n}}.$$

Combining with Theorem 1, we get the value reduction bound

$$V\left(d_0\right)-V({\widehat{d}}_n)\le \frac{\sqrt{K-1}K(K-1)}{1-C(K)}\frac{4\sqrt{10}c}{{\rho }^2(2s)}\sigma \sqrt{\frac{s{(\log p)}^{1+\delta }}{n}}.$$

Together with our margin condition, we can directly get the corresponding improved bound (31).