Group Testing in Mediation Analysis

Abstract

We consider the scenario where there is an exposure, multiple biologically-defined sets of biomarkers, and an outcome. We propose a new two-step procedure that tests if any of the sets of biomarkers mediate the exposure/outcome relationship, while maintaining a prespecified Family-Wise Error Rate (FWER). The first step of the proposed procedure is a screening step that removes all groups that are unlikely to be strongly associated with both the exposure and the outcome. The second step adapts recent advances in post-selection inference to test if there are true mediators in each of the remaining, candidate sets. We use simulation to show that this simple two-step procedure has higher statistical power to detect true mediating sets when compared with existing procedures. We then use our two-step procedure to identify a set of Lysine-related metabolites that potentially mediate the known relationship between increased BMI and the increased risk of ER+ breast cancer in post-menopausal women.

1. Introduction

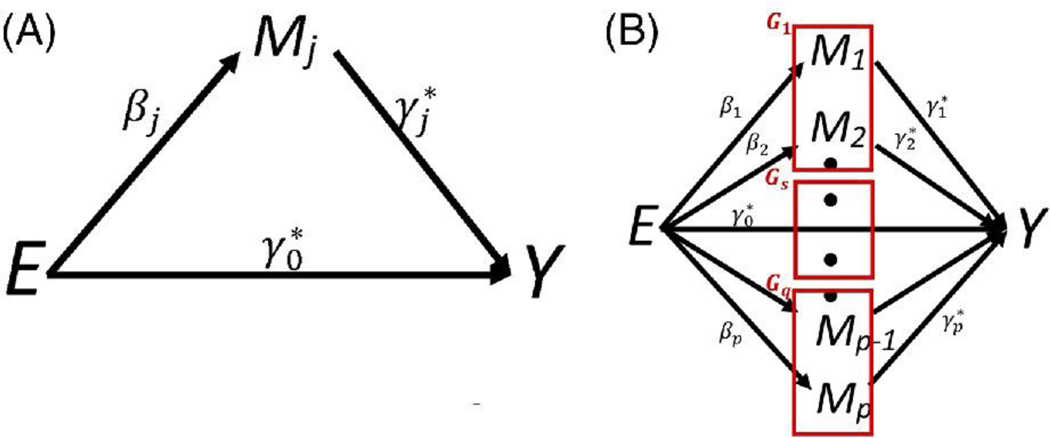
Mediation analysis explores how an exposure (E) is associated with an outcome (Y) ^1,2. Traditionally, mediation analysis assumes the exposure influences a single mediating variable (M) which, in turn influences the outcome (Figure 1A), and then aims to decompose the total effect of the exposure into a direct and indirect (i.e. via M) effect ^2–4. Initial methods explored this decomposition using parametric models ^5,6, while more modern methods use a counterfactual framework ^2,7. Recently, epidemiological studies have considered high-dimensional biomarkers as potential mediators linking an exposure and disease ^8–10. Here, we focus on the scenario when the biomarkers can be split into disjoint, biologically defined sets (i.e. groups) and the specific goal is to test whether any of these predefined sets potentially mediate the exposure/outcome relationship (Figure 1B). By pooling signals from multiple biomarkers within a set, these group level tests may increase the power to detect true mediators. Group level tests have already been demonstrated to increase the power^18–20 for testing associations when looking at groups of rare-variants in genes^12,13, groups of genetic variants in pathways^14,15, and groups of biomarkers with shared function or structure^16,17. We note, however, that we can only increase power when the mediating biomarkers belong to the same group, a condition that will strongly depend on the type and quality of set definitions.

Figure 1: Causal graphs of the mediation models.

A) Traditional mediation analysis focus on the exposure influencing individual biomarkers, B) Mediation analysis tests whether any of these predefined q sets mediate the exposure/outcome relationship.

There is a growing body of literature exploring how high-dimensional biomarkers can be used in mediation analysis, specifically discussing how to identify sets of biomarkers that collectively mediate the exposure/outcome association^9,21,22, test if individual biomarkers mediate the association ^8,21,23,24, and test if predefined groups of biomarkers mediate the association ^10,25. Here, we add to the literature by proposing a new procedure for testing groups of biomarkers. Our motivating study ²⁶ is a 843-individual case-control study of ER+ positive breast cancer where the goal is to identify if one of the 38 biologically defined sets of metabolites mediates the relationship between higher body mass index (BMI) and the increased risk of breast cancer.

The first step of our two-step (TS) procedure is a screening step that removes all sets unlikely to be strongly associated with both the exposure and the outcome. The second step of the procedure adapts a method for post-selection inference ^27–29 to attach a corrected or conditional p-value to each biomarker in the remaining sets. We then claim a set to be a mediating set if one of the included biomarkers is a statistically significant mediator based on this conditional p-value. Specifically, we define our p-value for a set of biomarkers to be the minimum of these conditional p-values. This approach builds upon two recent advances in the genetics literature, improved group tests of rare variants^30,31 and post-selection inference to identify specific associated variants within the group^27–29. This approach, screening by group and testing individual biomarkers, has higher power to detect mediating sets than the standard methods used to test groups. Moreover, our approach has the additional benefit of identifying the specific biomarkers in a set that are the actual mediators. We note that we defined our set-level p-value to be the minimum p-value, as opposed to using Fisher’s method, because the statistical distribution for the sum of the logged-conditional p-values could not be easily described.

The remainder of the paper is organized as follows. In the Materials and Methods, we describe the proposed TS procedure, the simulations used to evaluate the procedure, and the motivating study of breast cancer. In the Results, we compare the performance of the TS procedure with comparators in the simulations and report our findings from the breast cancer study. Finally, in the Discussion, we offer insights about the differences between the TS and other procedures.

2. Materials and methods

2.1. Notation

Let us consider $n$ individuals. For individual $i$, let $E_i$ be the exposure, $Y_i$ be the outcome, and ${\stackrel{⃑}{M}}_i={\left(M_{i1},\dots ,M_{im}\right)}^{\text{'}}$ be a vector of $m$ biomarkers or potential mediators. For a given biomarker j, we denote the m-1 set of biomarkers without j by ${\stackrel{⃑}{M}}_{i\backslash j}={\left(M_{i1},\dots ,M_{ij-1},M_{ij+1},\dots M_{im}\right)}^{\text{'}}$. For this paper, our potential mediators will always be biomarkers and we will use the terms interchangeably. We classify all $m$ biomarkers into $q$ predefined disjoint sets, where the $m_s$ biomarkers of set $s\in \{1,\dots ,q$} are indexed by $G_s=\{s_1,\dots ,s_{m_s}\}\subset \{1,\dots ,m\}$, and we then define ${\stackrel{⃑}{M}}_{is}=\left\{M_{i{j}^{\text{'}}}:j^{\text{'}}\in G_s\right\}$ and ${\stackrel{⃑}{M}}_{i\backslash s}=\left\{M_{i{j}^{\text{'}}}:j^{\text{'}}\notin G_s\right\}$. Finally, we let $s\left(j\right)$ be the set containing biomarker $j,G_{s\left(j\right)\backslash j}$ be the indices for all biomarkers, other than $j$, in the set $s\left(j\right)$ and ${\stackrel{⃑}{M}}_{is\left(j\right)\backslash j}=\{M_{i{j}^{\text{'}}}:j\text{'}\in G_{s\left(j\right)\backslash j}\}$.

2.2. Causal Inference

We introduce counterfactual notation. We define ${\stackrel{⃑}{M}}_i\left(e\right)={\left(M_{i1}\left(e\right),\dots ,M_{im}\left(e\right)\right)}^{\text{'}}$ to be the value of the biomarkers in subject $i$ if $E_i$ is set to $e$ and we define ${Y_i(e,\stackrel{⃑}{M}}_i\left(e\text{'}\right))$ to be the value of the outcome if $E_i$ is set to $e$ and ${\stackrel{⃑}{M}}_i$ is set to ${\stackrel{⃑}{M}}_i\left(e\text{'}\right)$. Given the number of biomarkers and their unknown and potentially bidirectional relationships, we cannot allow the biomarkers to be functions of each other (i.e. $M_{ij}(\bullet )$ is only a function of e) when using counterfactual notation.

We can then define the total effect from changing $e$ to $e^{\text{'}}$ to be $TE=E\left[Y_i\left(e^{\text{'}},{\stackrel{⃑}{M}}_i\left(e\text{'}\right)\right)-Y_i\left(e,{\stackrel{⃑}{M}}_i\left(e\right)\right)\right]$, the Natural Indirect Effect (NIE(s)) through a given set $s$ to be $NIE\left(s\right)=E\left[Y_i\left(e,{\stackrel{⃑}{M}}_{is}\left(e^{\text{'}}\right),{\stackrel{⃑}{M}}_{i\backslash s}\left(e\right)\right)–Y\left(e,{\stackrel{⃑}{M}}_i\left(e\right)\right)\right]$, and the Natural Indirect Effect (NIE(j)) through a given biomarker $j$ to be $NIE\left(j\right)=E\left[Y_i\right(e,M_{ij}\left(e^{\text{'}}\right),{\stackrel{⃑}{M}}_{i\backslash j}\left(e\right))–Y_i(e,{\stackrel{⃑}{M}}_i\left(e\right)\left)\right].$.

We would like to claim $s$ to be a mediating set if NIE(j) ≠ 0 for at least one $j\in G_s$. We emphasize that, as shown below, this statement would differ from claiming that $s$ is a mediating set if NIE(s) ≠ 0. Our formal definition of mediating set is offered in Section 2.3.

2.3. Continuous Outcome

We will first assume that the biomarkers and outcome are continuous random variables defined by

$$M_{ij}={\beta }_{0j}+{\beta }_j{E}_i+{ϵ}_{M_{ji}}\text{for}j=1,\dots ,m,$$ (3)

$$Y_i={\gamma }_0^{*}+{\gamma }_E^{*}{E}_i+{\sum }_{j=1}^m{\gamma }_j^{*}{M}_{ij}+{ϵ}_{Yi}^{*}$$ (4)

where ${\stackrel{⃑}{ϵ}}_{Mi}=({ϵ}_{1i},\dots ,{ϵ}_{mi})\text{'}\sim N\left(\stackrel{⃑}{0},{\Sigma }_M\right),{ϵ}_{Yi}^{*}~\text{N}(0,{\sigma }_Y^{*2})$, and ${\stackrel{⃑}{ϵ}}_{Mi}\perp {ϵ}_{Yi}^{*}$. Equation (4) further implies that for any set $s$

$$Y_i={\gamma }_0^s+{\gamma }_E^s{E}_i+{\sum }_{j\in G_s}{\gamma }_j{M}_{ij}+{ϵ}_{Yi}^s$$ (5)

We can define the causal effects from Section 2.2 in terms of the parameters from equations 3–5: $TE=\left(e^{\text{'}}-e\right)({\gamma }_E^{*}{\beta }_j+{\sum }_{j=1}^m{\gamma }_j^{*}{\beta }_j)$, $NIE\left(s\right)=\left(e^{\text{'}}-e\right){\sum }_{j\in G_s}{\gamma }_j^{*}{\beta }_j$, and $NIE\left(j\right)=\left(e^{\text{'}}-e\right){\gamma }_j^{*}{\beta }_j$. When equations 3–5 hold, we also note that the following assumptions, provided by Imai et al ³², will also hold and allow all causal effects to be estimable.

Assumption 1 (Sequential ignorability)

$$\left\{Y_i\left(e^{\text{'}},\stackrel{⃑}{m}\right),{\stackrel{⃑}{M}}_i\left(e\right)\perp E_i\right\}|X_i=x,$$

$$Y_i\left(e^{\text{'}},\stackrel{⃑}{m}\right)\perp {\stackrel{⃑}{M}}_i\left(e\right)|E_i=e,X_i=x,$$

$$M_{ij}\left(e^{\text{'}}\right)\perp {\stackrel{⃑}{M}}_{i\backslash j}\left(e\right)|E_i=e,X_i=x\text{for any}j=1,\dots ,m,$$

where $X$ denotes the vector of observed pre-treatment covariates.

However, when m > n, we may not be able to estimate the parameters in equation (4). Therefore, we may not be able to estimate $NIE\left(j\right)$ and test for its presence. Instead, as a pragmatic compromise, we will use the parametric models from equations (3) and (5), and formally define s to be a mediating-set if ${\gamma }_j{\beta }_j\ne 0$ for at least one $j\in G_s$, or equivalently, if ${\sum }_{j\in G_s}{\left({\beta }_j{\gamma }_j\right)}^2\ne 0$. We offer three comments regarding this definition. First, although not easily stated using the language of causal inference, our definition for a mediating-set is still well defined. Second, when the biomarkers from different sets are independent given $E_i,NIE\left(j\right)=\left(e^{\text{'}}-e\right){\gamma }_j^{*}{\beta }_j=\left(e^{\text{'}}-e\right){\gamma }_j{\beta }_j$ and our definition has the desired meaning. Third, we note that there are other powerful methods for detecting $NIE\left(s\right)=0$. One approach¹⁰ would be transforming the biomarkers using spectral decomposition and then individually testing each of the resulting linear combinations

We will fit models (3) and (5) using linear regressions to obtain the Maximum Likelihood Estimates (MLE) for set $s$. We denote the MLE by ${\widehat{\stackrel{⃑}{\beta }}}_s={\left({\widehat{\beta }}_{s_1},\dots ,{\widehat{\beta }}_{s_{m_s}}\right)}^{\text{'}}$ and ${\widehat{\stackrel{⃑}{\gamma }}}_s={\left({\widehat{\gamma }}_{s_1},\dots ,{\widehat{\gamma }}_{s_{m_s}}\right)}^{\text{'}}$; we denote the combined vector by ${\widehat{\stackrel{⃑}{\theta }}}_s={\left({\widehat{\beta }}_{s_1},\dots ,{\widehat{\beta }}_{s_{m_s}},{\widehat{\gamma }}_{s_1},\dots ,{\widehat{\gamma }}_{s_{m_s}}\right)}^{\text{'}}$. Furthermore, we denote the estimates of the covariances for ${\widehat{\stackrel{⃑}{\beta }}}_s,{\widehat{\stackrel{⃑}{\gamma }}}_s$, and ${\widehat{\stackrel{⃑}{\theta }}}_s$ by ${\widehat{\Sigma }}_{{\beta }_s},{\widehat{\Sigma }}_{{\gamma }_s}$, and ${\widehat{\Sigma }}_{{\Theta }_s}$, the standard errors of the j^th element of ${\widehat{\stackrel{⃑}{\beta }}}_s$ by ${\widehat{\sigma }}_{\beta s_j}$and the standard error of the j^th element of ${\widehat{\stackrel{⃑}{\gamma }}}_s$ by ${\widehat{\sigma }}_{\gamma s_j}$. Note, the $cor({\widehat{\beta }}_j$, ${\widehat{\gamma }}_{j^{\text{'}}})=0$ for all $j,j^{\text{'}}\in G_s.$ The latter is true because the likelihood, $f\left(Y,M|E;\beta ,\gamma \right)$, can be factored into two components, $f\left(Y,M|E;\beta ,\gamma \right)=f\left(Y|M,E;\gamma \right)f\left(M|E;\beta \right)$, each containing only one set of parameters, as described in previous literature ^8,10,24.

We can define biomarker-level p-values to test the null hypotheses $H_{0E}^j:{\beta }_j=0$ and $H_{0Y}^j:{\gamma }_j=0$ by $p_{E,j}=F_Z(-\left|Z_{Ej}\right|)$ and $p_{Y,j}=F_Z\left(-\left|Z_{Yj}\right|\right)$, where $Z_{E,j}={\widehat{\beta }}_j/{\widehat{\sigma }}_{\beta j},Z_{Y,j}={\widehat{\gamma }}_j/{\widehat{\sigma }}_{\gamma j}$, and $F_Z$ is the Cumulative Distribution Function (CDF) for the standard normal distribution. We choose the normal distribution as opposed to the t-distribution because relevant studies of high dimensional biomarkers typically have significantly more subjects than markers in per set, n >> $m_s$.

We can further define a weighted set-level p-value to test the set’s association with the exposure and outcome using one of two variance component tests ^30,31. For the first method, we test for an association between the group of biomarkers and E or Y using the following pooled test statistic

$$T_{Y,\beta }^s=T_{E,\gamma }^s={\sum }_{j\in G_s}{\left({\widehat{\beta }}_j{\widehat{\gamma }}_j\right)}^2,$$ (10)

where the complementary effect estimates are used as weights. Thus, when testing for the association between the set of biomarkers and the exposure, we treat ${\widehat{\stackrel{⃑}{\gamma }}}_s$ as fixed weights and, similarly, when testing for the association with the outcome we treat ${\widehat{\stackrel{⃑}{\beta }}}_s$ as fixed weights. Both test statistics $T_{Y,\beta }^{s}and{T}_{E,\gamma }^s$ explicitly upweights biomarkers that have large effects with exposure or outcome. The corresponding p-values for the set s, $p_{E,\gamma }^s=1-F_{{\chi }_{E,s}^2}\left(T_{E,\gamma }^s\right)$ and $p_{Y,\beta }^s=1-F_{{\chi }_{Y,s}^2}\left(T_{Y,\beta }^s\right)$, are calculated from two functions, $F_{{\chi }_{E,s}^2}$ and $F_{{\chi }_{Y,s}^2}$, that are the CDFs for a linear combinations of ${\chi }^2$ distributions with weights determined by ${\widehat{\stackrel{⃑}{\gamma }}}_s$ and ${\widehat{\stackrel{⃑}{\beta }}}_s$. For the second method, we test for an association between the group of biomarkers and the exposure or outcome without any weighting, using the statistics

$$T_{E,1}^s={\sum }_{j\in G_s}{\left({\widehat{\beta }}_j\right)}^2$$ (11)

$$T_{Y,1}^s={\sum }_{j\in G_s}{\left({\widehat{\gamma }}_j\right)}^2.$$ (12)

The corresponding p-values for the set s, $p_{E,1}^s=1-F_{{\chi }_{E1,s}^2}\left(T_{E,1}^s\right)$ and $p_{Y,1}^s=1-F_{{\chi }_{Y1,s}^2}\left(T_{Y,1}^s\right)$, are now calculated from two functions, $F_{{\chi }_{E1,s}^2}$ and $F_{{\chi }_{Y1,s}^2}$, that are the CDFs for a linear combination of ${\chi }^2$ distributions with weights set to 1. Note that sets of biomarkers only associated with the outcome or exposure will have relatively small values of $T_{Y,\beta }^{s}and{T}_{E,\gamma }^s$, compared to $T_{Y,1}^{s}and{T}_{E,1}^s$, making the former potentially more powerful at detecting true signals. However, we incorporate the unweighted tests $T_{Y,1}^{s}and{T}_{E,1}^s$ in parts of proposed methodology because of their statistical independence with each other.

2.4. Binary Outcome

Although we have thus-far considered continuous outcomes, we will also consider the scenario where the outcome is a binary random variable. We define the binary outcome, $Y_i^{*}$, by the probit model $Y_i^{*}=1(Y_i>0)$ and $Y_i$ following equations (4) and (5). Here, our definitions of the null hypotheses (i.e. equations 7–9), test statistics, and p-values remain essentially the same. The exception is that we estimate $\widehat{\gamma }$ by probit regression and for retrospective sampling (i.e. case/control models), we estimate $\widehat{\beta }$ by weighted linear regression, where the weights are proportional to the probability of being sampled. Note, the choice of the probit model ensures both that equations (4) and (5) are consistent and that the hypotheses stated in equations (2) and (7) are identical, although the only true requirement is for $E\left[{\widehat{\gamma }}_j\right]=0$ for biomarkers satisfying $H_{0Y}^j$. We note that, in practice, the procedure performs equally satisfactorily when the coefficients and p-values for the outcome associations are calculated using logistic regression, a model more familiar in epidemiology ²⁴.

2.5. Testing procedures for groups of biomarkers

We first describe existing procedures and then introduce our new, more powerful, two-step procedures for testing sets of biomarkers.

2.5.1. Minimum-P Procedure (MIN)

This procedure is a direct modification of the approach introduced by Sampson and others ²⁴. We start by calculating the FWER-corrected p-value for each biomarker using the MCP_S approach. Briefly, define ${\omega }_E=\{j:p_{E,j}\le 0.025\}$ and ${\omega }_Y=\{j:p_{Y,j}\le 0.025\}$. Let ${|\omega }_E|$ and ${|\omega }_Y|$ be the cardinality of each set (i.e. the number of elements in that set). We define a FWER-corrected p-value for each biomarker by $p_j^{FWER}=2\max ({|\omega }_E|p_{E,j},{{|\omega }_Y|p}_{Y,j})$ if ${j\in \omega }_E\cap {\omega }_Y$ and 1 otherwise. The MIN procedure then claims a set $s$ to be a mediating set if ${mi{n}_{j\in G_s}(p}_j^{FWER})<\alpha$. In other words, the MIN procedure claims a set to be a mediating set if one of the biomarkers included in that set qualifies as a mediator after adjusting for multiple testing.

2.5.2. Linear Procedures (LIN)

These procedures were introduced by Huang ²⁵.They suggest two test statistics, each with a normal distribution under the null hypotheses and some additional assumptions. For set $s$, the two statistics are $Z_{L1}^s={\widehat{\stackrel{⃑}{\beta }}}_s^{\text{'}}{\widehat{\stackrel{⃑}{\gamma }}}_s/({\widehat{\stackrel{⃑}{\beta }}}_s^{\text{'}}{\widehat{\Sigma }}_{{\beta }_s}^{-1}{\widehat{\stackrel{⃑}{\beta }}}_s+{\widehat{\stackrel{⃑}{\gamma }}}_s\text{'}{\widehat{\Sigma }}_{{\gamma }_s}^{-1}{\widehat{\stackrel{⃑}{\gamma }}}_s{)}^{\frac{1}{2}}$ and $Z_{L2}^s={\widehat{\stackrel{⃑}{\beta }}}_s^{\text{'}}{\widehat{\stackrel{⃑}{\gamma }}}_s/V_{max}^{1/2}$, where $V_{max}=ma{x}_{w\in {\Omega }_w}\left({\widehat{\stackrel{⃑}{\nu }}}_s^{\text{'}}{\widehat{\Sigma }}_{{\Theta }_s}{\widehat{\stackrel{⃑}{\nu }}}_s\right),{\widehat{\stackrel{⃑}{\nu }}}_s={\left(w_{Y1}{\widehat{\gamma }}_{s_1},\dots ,{w_{Y{m}_s}\widehat{\gamma }}_{s_{m_s}},w_{E1}{\widehat{\beta }}_{s_1},\dots ,{w_{E{m}_s}\widehat{\beta }}_{{s_m}_s}\right)}^{\text{'}}$, and the max is over all binary 2m_s-length vectors ${\Omega }_w=\left\{{\left({w_{Y1},\dots ,w_{Y{m}_s},w}_{E1},\dots ,w_{E{m}_s}\right)}^{\text{'}}:w_{Ej}\in \left\{\mathrm{0,1}\right\},w_{Yj}\in \left\{\mathrm{0,1}\right\},w_{Ej}+w_{Yj}=1\right\}$. The LIN-1 and LIN-2 procedures will, respectively, claim a set $s$ to be a mediating set if $p_{L1}^s=F_Z(-|Z_{L1}^s\left|\right)<\alpha /q$ and $p_{L2}^s=F_Z(-|Z_{L2}^s\left|\right)<\alpha /q$. For the comparison below, we consider only the more powerful, LIN-2, which we abbreviate by LIN. We note that the LIN procedure is designed to answer a slightly different problem and test the null hypothesis that $NIE\left(s\right)=0$.

2.5.3. Quadratic Procedure (QUAD)

This procedure was introduced by Huang and Pan ¹⁰. To account for the possibility of effects in different directions, they suggest the statistic $T_Q^s=\sum _{j\in G_s}{(\widehat{\beta }}_j{\widehat{\gamma }}_j{)}^2$ and a novel parametric bootstrap to obtain the corresponding p-value. Specifically, they randomly generate B bootstrap replicates of ${\widehat{\stackrel{⃑}{\theta }}}^b=\{{\widehat{\stackrel{⃑}{\beta }}}^b,{\widehat{\stackrel{⃑}{\gamma }}}^b\}$ from a normal distribution with mean ${\widehat{\stackrel{⃑}{\theta }}}_s$ and variance ${\widehat{\Sigma }}_{{\Theta }_s}$. They then calculate $T_{Q,b}^s=\sum _{j\in G_s}({\widehat{\beta }}_j^b{\widehat{\gamma }}_j^b-\frac{1}{B}\sum _b{\widehat{\beta }}_j^b{\widehat{\gamma }}_j^b{)}^2$ for each boostrapped set and define the p-value to be $p_Q^s=\frac{1}{B}{\sum }_{b}1(T_{Q,b}^s<T_Q^s)$. The QUAD procedure will claim a set $s$ to be a mediating set if $p_Q^s<\alpha /q$. We note that the original QUAD procedure offered modified methods that could handle large sets, with $m_s>n$, a scenario not considered here.

2.5.4. Marginal Procedure (MARG)

This procedure, the first to be introduced here, is a set-level modification of the MCP_s statistic ²⁴. Importantly, for reasons discussed at the end of this section, we do not suggest that this overly-simplified approach controls the FWER and include it because it provides a reference for the maximum possible power that can be reasonably expected from a test. MARG is based on p-values $p_{E,1}^s$ and $p_{Y,1}^s$ calculated from the unweighted pooled association test statistics $T_{Y,1}^{s}and{T}_{E,1}^s$. Define ${\omega }_E^G=\left\{s:p_{E,1}^s\le 0.025\right\}$ and ${\omega }_Y^G=\left\{s:p_{Y,1}^s\le 0.025\right\}$ so that they are the sets potentially associated with the exposure and outcome. Let $\left|{\omega }_E^G\right|$ and $\left|{\omega }_Y^G\right|$ be the cardinality of each set (i.e. the number of elements in that set) and the marginal p-value be $p_M^s=2\max (\left|{\omega }_E^G\right|p_{E,1}^s,\left|{\omega }_Y^G\right|p_{Y,1}^s)$ if $s\in {\omega }_E^G\cap {\omega }_Y^G$ and 1 otherwise. The MARG procedure will claim a set $s$ to be a mediating set if $p_M^s<\alpha$. However, the problem is that this procedure only marginally tests if the set is associated with both the exposure and the outcome; the procedure does not ensure that there is a common set of mediating biomarkers associated with both the exposure and the outcome (i.e. that $s$ is a true mediating set). We do note that MARG uses p-values from group tests without weights (i.e. $p_{E,1}^s$ and $p_{Y,1}^s$) because the p-values $p_{E,\gamma }^s$ and $p_{Y,\beta }^s$ are not independent under the null hypothesis (see Proposition 1 in Supplemental Material) and therefore can occasionally have lower power than the TS method proposed below. We note that Huang proposed another marginal procedure, JTV-comp³³, which again tests for sets associated with both the exposure and the outcome without ensuring that there are true mediators in that set. We offer comparisons with JTV-comp in Supplementary Material Section 4.6 and note that the method did tend to have higher statistical power, albeit with a slightly inflated type-I error rate.

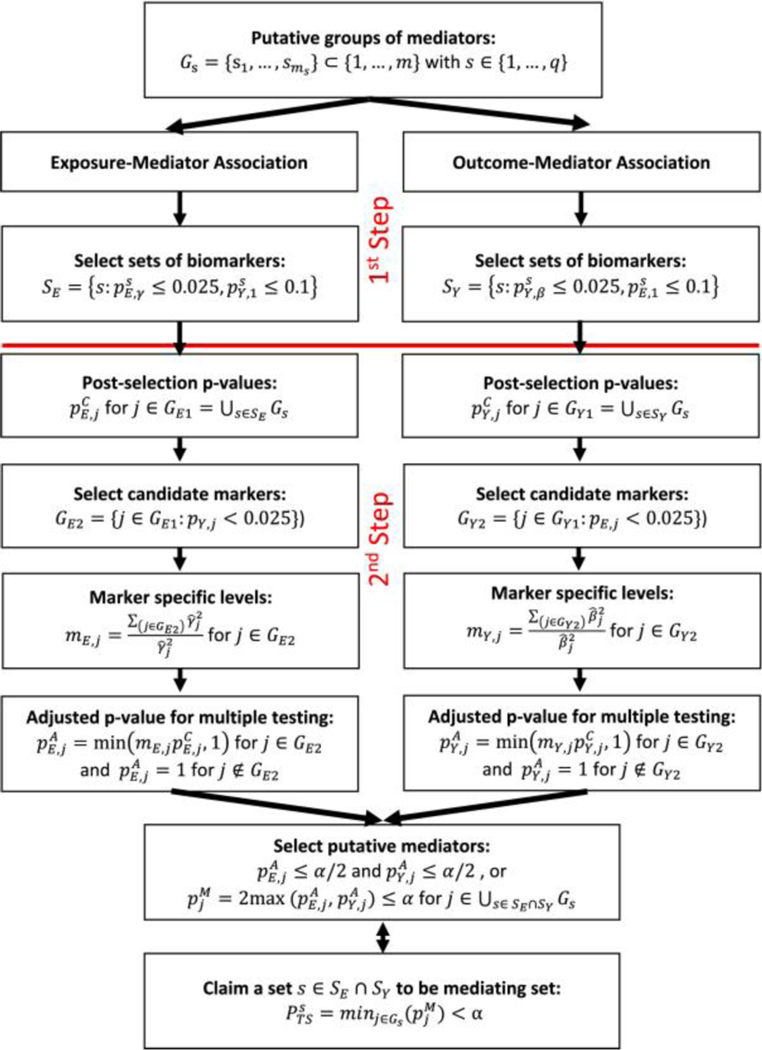
2.5.5. Two-Step Procedure (TS)

This novel procedure is described in Figure 2. In parallel analyses, we identify biomarkers associated with the exposure and we identify biomarkers conditionally associated with the outcome. Note, in each of these analyses, we perform two steps: (i) a screening step to remove sets of biomarkers that are unlikely to be strongly associated with both the exposure and outcome (ii) a testing step that assigns individual p-values to each biomarker in the remaining sets. After these parallel analyses, we define the mediating sets to be those sets with biomarkers associated with both the exposure and outcome. Below we describe the links in Figure 2 for identifying the biomarkers associated with the exposure, while omitting the near identical descriptions for identifying biomarkers associated with the outcome.

Figure 2: Diagram of Two-Step procedure (TS).

In the first step, we select sets of biomarkers that are potentially associated with the both the exposure and outcome. In the second step, we test individual biomarkers to identify mediators.

Step 1: Define $S_E=\left\{s:p_{E,\gamma }^s\le 0.025,p_{Y,1}^s\le 0.1\right\}$ based on p-values from weighted and unweighted group test statistics. Here, we screen out those sets that are unlikely to be strongly associated with both the exposure and outcome. Note, this set differs from $S_Y$. Further note that choices of 0.025 and 0.1 can be modified, but we have found these thresholds to work well in practice for the FWER-corrected p-value of 0.05.

Step 2a: For each biomarker in one of the remaining sets, ${G_{E1}\equiv \cup }_{s\in S_E}{G}_s$, we calculate a conditional p-value for association (i.e. conditioned on its set passing the screening step). Here, we define $p_{E,j}^C=1-F_{Z_{E,j}^T}\left({\widehat{\beta }}_j\right)$ for ${jG}_{E1}$ where $F_{Z_{E,j}^T}$ is the truncated normal distribution described in the Supplementary Material Section 1.3, and, for completeness, define $p_{E,j}^C=1$ for $j\notin G_{E1}$.

Step 2b: We then divide $G_{E1}$ into two complementary sets of biomarkers, $G_{E1}=G_{E2}\cup G_{E2}^C$, where $G_{E2}=\{j:p_{Y,j}<0.025\}$ is the set of candidate biomarkers. Let $m_E$ be the number of biomarkers in $G_{E2}$.

Step 2c: For each biomarker in $G_{E2}$, we now calculate an adjusted conditional p-value, where the adjustment is needed to account for multiple testing. In its simplest form, the adjusted p-value would be $p_{E,j}^A=\min \left(m_E{p}_{E,j}^C,1\right).$ However, we find it beneficial to decrease the multiple-testing penalty for those biomarkers strongly associated with the outcome (i.e. potentially true mediating biomarkers). Therefore, we define the adjusted p-value to be $p_{E,j}^A=min(m_{E,j}{p}_{E,j}^C,1)$, $m_{E,j}=\left({\sum }_{\left(j\in G_{E2}\right)}{\widehat{\gamma }}_j^2\right)/{\widehat{\gamma }}_j^2$, if ${j\in G}_{E2}$ and, for completeness, define $p_{E,j}^A=1$ for $j\notin G_{E2}.$

Step 2d: After completing steps 2a-2c for both the exposure and the outcome, we can now define an adjusted p-value for mediation by $p_j^M=2\max (p_{E,j}^A,p_{Y,j}^A)$ for markers ${j\in G}_{E2}\cap G_{Y2}$ and, for completeness, define $p_j^M$ =1 for ${j\notin G}_{E2}\cap G_{Y2}$. We then say a set, $s$, is a mediating set if $P_{TS}^s\equiv mi{n}_{j\in G_s}{p}_j^M<\alpha$. Let us formally define the FWER for the TS procedure by FWER^TS $\equiv P(mi{n}_s\left(P_{TS}^s\right)<\alpha )$. Then, in Supplementary Material Section 1.5, we prove the following theorem.

Theorem 1.

If ${\stackrel{⃑}{M}}_{is}\perp {\stackrel{⃑}{M}}_{i{s}^{\text{'}}}given{E}_{i}for\forall s,s^{\text{'}}\in \{1,..,q\}$, then $\underset{n\to \infty }{\lim }FWE{R}^{TS}\le \alpha .$

We note that the assumption, ${\stackrel{⃑}{M}}_{is}\perp {\stackrel{⃑}{M}}_{i{s}^{\text{'}}}|E_i$, is unlikely to hold in practice and violations of this assumption can lead to the TS procedure having an inflated type I error. Consider the example where E affects $M_j(j\in G_s$) and a second biomarker $M_{j\text{'}}(j\text{'}\in G_{s\text{'}}$) also affects $M_j$. Furthermore, of the two biomarkers, only $M_{j\text{'}}$ affects the outcome. Then, $s$ may be mistakenly classified as a mediating set. In Supplementary Material Section 3.1, we offer simulations to show that the effect of $M_{j\text{'}}$ on $M_j$ must be large for there to be an inflated type I error rate. We note that when $n\gg m$, we can modify our approach so that its performance does not require this assumption (Supplementary Material Section 2).

We offer a couple of remarks. First, the initial screening uses a quadratic (i.e. $T_{E,\gamma }^s={\sum }_{j\in G_s}{\left({\beta }_j{\gamma }_j\right)}^2$), as opposed to a linear (i.e. $T_L^s={\widehat{\stackrel{⃑}{\beta }}}_s^{\text{'}}{\widehat{\stackrel{⃑}{\gamma }}}_s$), test statistic. This choice offers increased power when the proportion of associated biomarkers is low or biomarkers within a set have opposing effects. Second, the initial screening steps select sets using one weighted and one unweighted test statistic. Ideally, we would have used two weighed statistics but that would greatly complicate post selection inference because of the dependence between $T_{Y,\beta }^s,T_{E,\gamma }^s$ (see Supplemental Material Section 1.2). Post-selection inference in the second step of TS allows to quantify mediating effects (i.e. $NIE\left(j\right)$) for detected potential mediators (see Supplemental Material Section 1.4).

2.6. Simulations

We compared the performance of the five previously defined procedures (MIN, LIN, QUAD, MARG, TS) for testing sets of biomarkers. Specifically, we used simulations to estimate the power to detect a mediating set of biomarkers in various scenarios defined by equations (3–5) and the parameters in Table 1.

Table 1:

Simulation Parameters

Parameter	Interpretation	Possible Values
$q$	Number of sets of biomarkers	15, 20, 50
$q_{OD},q_{TD}$	Number of one- or two-dimensional sets	0, 4, 6
$m_s$	Number of biomarkers per set	15, 20, 50
$m_M$	Number of mediating biomarkers in the mediating set	1, 3, 5
$m_E$	Number of noise biomarkers in the mediating set associated only with exposure	0, 2, 4
$m_Y$	Number of noise biomarkers in the mediating set associated only with outcome	0, 2, 4
$m_{EY}$	Number of noise biomarkers in the mediating set with half associated only with the exposure and half associated only with the outcome	0, 2, 4
$m_D$	Number of associated biomarkers in one- or two-dimensional sets	6
${\rho }_M$	Correlation between biomarkers within a set	0, 0.25, 0.5
${\beta }_j$	Non-null effect of exposure on metabolite	0.065A, 0.045B
${\gamma }_j^{*}$	Non-null effect of metabolite on outcome	0.065 A, 0.085B

^AModels with a continuous outcome

^BModels with a binary outcome

Bold values indicate default settings.

We assumed there were a total of $q\in \{15,20,50\}$ sets of biomarkers, each containing $m_s\in \{15,20,50\}$ biomarkers.

We assumed that there was $q_m=1$ mediating set, $q_{OD}\in \{0,4,6\}$ one-dimensional sets, and $q_{TD}\in \{0,4,6\}$ two-dimensional sets, where we say a set is one-dimensional if it contains $m_D=6$ biomarkers associated with only the exposure or only the outcome and two-dimensional if it contains $m_D/2=3$ biomarkers associated with only the exposure and $m_D/2=3$ biomarkers associated with only the outcome. For the one mediating set, we assumed there were $m_M\in \{1,3,5\}$ true mediators, $m_E\in \{0,2,4\}$ “noise” biomarkers associated with only the exposure, $m_Y\in \{0,2,4\}$ “noise” biomarkers associated with only the outcome, and $m_{EY}=m_E+m_Y$. In Supplemental Figure S1, we provide additional details on the simulation model.

Unless otherwise designated, we used the default parameters highlighted in black for the simulations.

In all scenarios, the exposure followed a normal distribution defined by $E_i~N\left(\mathrm{0,1}\right)$ and the $m$ biomarkers followed a multivariate normal distribution defined by equation 3. The correlation (i.e. off-diagonal element in ${\Sigma }_M$) for metabolites within a set was chosen to have AR(1) structure (i.e. ${\rho }_{ij}={\rho }_M^{\left|i-j\right|}$) with ${\rho }_M\in \left\{\mathrm{0,0.25,0.5}\right\}$. For continuous outcomes, the sample contained a total of $n=2500$ individuals and the outcome followed the normal distribution defined by equation 4. For non-null associations, we let the magnitudes of all effects be the same with ${\beta }_j={\gamma }_j^{*}=0.065$. For a binary outcome, the sample contained $n=2500$ cases and $n=2500$ controls retrospectively sampled from a large cohort with outcomes generated from a logistic model ${logit\left(P\right(Y}_i|E_i,{\stackrel{⃑}{M}}_i))={\gamma }_0^{*}+{\gamma }_E^{*}{E}_i+{\sum }_{j=1}^m{\gamma }_j^{*}{M}_{ij}$ and the incidence defined by ${\gamma }_0^{*}=\log \left(\frac{0.01}{099}\right)=-4.6$, the non-null exposure effects defined by ${\beta }_j=0.045$ and the non-null outcome effects defined by ${\gamma }_j^{*}=0.085$. The choice of effect sizes ensured similar power when testing continuous and binary outcomes. We generated 1000 simulations per scenario to estimate power of five methods at a $FWER=\alpha =0.05.$

We also conducted additional sensitivity analyses. We explore the effect of confounding in Supplementary Material Section 3.1. Specifically, we consider the scenario where there are no mediators, but there are confounders that link the exposure, biomarkers, and outcome. We also explore the methods under a wider set of parameter values in Supplementary Material Section 3.2. Specifically, we further explore the power when varying the proportion of biomarkers in a set that are mediators and the strength of the biomarkers’ combined association with both the exposure and outcome.

2.7. Metabolomic Study of Breast Cancer

Our motivating study aims to identify metabolites that mediate the known relationship between high BMI and the increased risk of estrogen-receptor positive (ER+) breast cancer. This study nested inside the Prostate, Lung, Colorectal, and Ovarian Cancer Screening Study (PLCO), includes 410 (ER+) breast cancers and 433 controls matched on study age (+/− 2 years), date of blood collection (+/− 3 months), and hormone therapy use at baseline. The study collected serum samples at the first follow up visit, one-year post-baseline, and using these specimens, measured the serum metabolites (< 1 Kilodalton molecular weight) with liquid chromatography-tandem mass-spectrometry. Metabolite peaks were normalized by dividing by batch median and then log transformed. Of the 1057 measured serum metabolites, we consider the 481 metabolites that have known identities and are present in at least 90% of the case-control population. These 481 metabolites can be divided into 38 disjoint sets defined by their biologic properties ³⁴. Details on the study have been previously published ²⁶.

3. Results

3.1. Simulations

In general, TS successfully controlled the FWER at the targeted level (0.05). The MIN, LIN, and QUAD procedures similarly controlled the FWER. However, we note that all four procedures tend to have conservative FWERs when most biomarkers are associated with neither the exposure nor the outcome. The conservative nature of the tests observed here is consistent with previous observations when testing individual biomarkers²¹. As expected, the MARG procedure had inflated FWER when the number of two-dimensional sets was greater than 0 (Supplemental Figures S3F and S8F). Again, this inflated type I error results from falsely declaring a set as a mediating set if it is marginally associated with both the exposure and outcome, regardless of whether true mediating biomarkers are present. Additionally, TS, MIN, LIN and QUAD were relatively robust to the presence of unmeasured confounders affecting the biomarkers, exposure and outcome (see Supplemental Figures S3-S12).

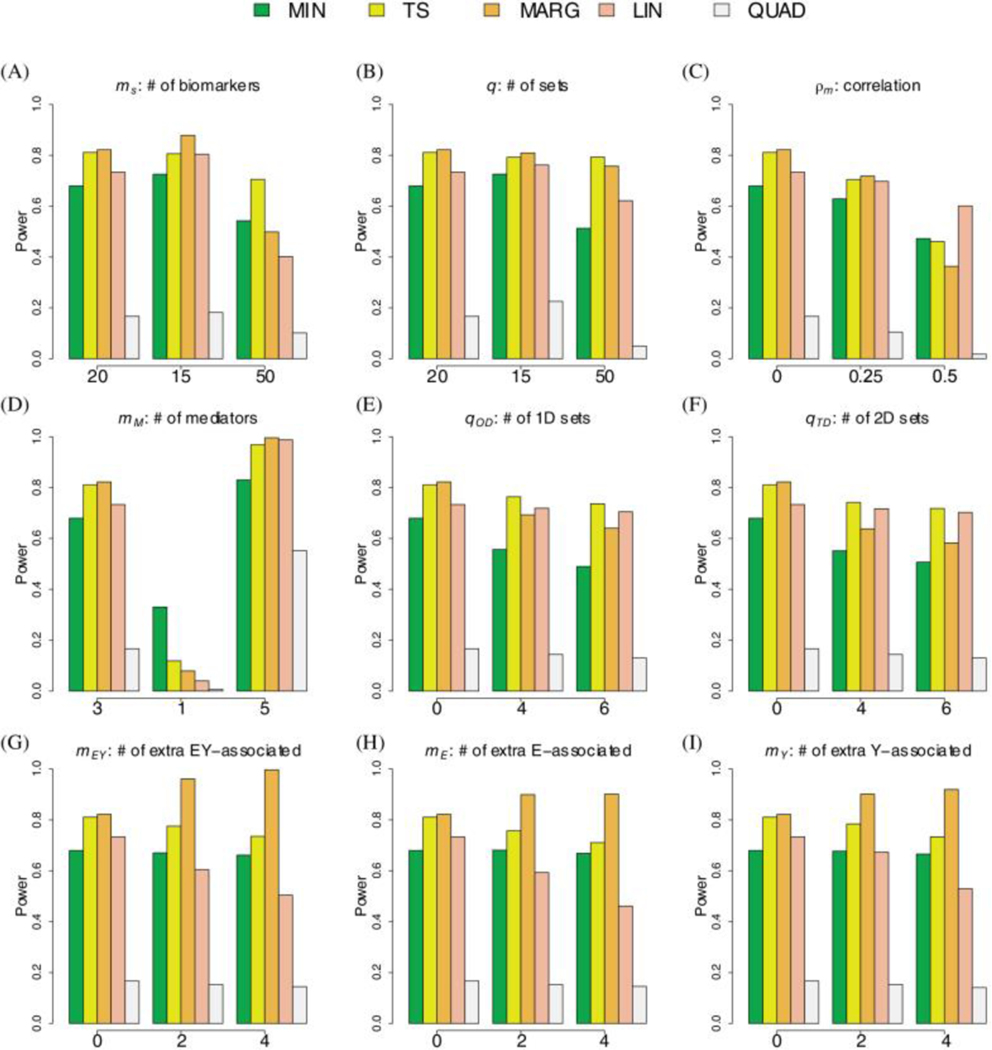
The simulations demonstrate that the newly proposed TS procedure has comparable or better performance characteristics then the competing methods in all tested scenarios. Note, we show the results for only a selection of illustrating scenarios in the main text and show additional results in the supplementary material. We focus on a baseline scenario with $q=20$ disjoint sets of size $m_s=20,q_m=1$ mediating set, $q_{OD}=0$ one-dimensional sets, $q_{TD}=0$ two-dimensional sets, $m_M=3$ mediating biomarkers, $m_E=0$ and $m_Y=0$ noise-biomarkers, and a correlation of ${\rho }_M=0$. We then vary individual parameters to assess their specific impact on the relative performance of the five procedures (Figures 3, 4 and Supplemental Figures S13-S22).

Figure 3: Simulations for Continuous Outcome.

The bar-plots show the power to detect the mediating set when using the TS (yellow), MIN (green), MARG (orange), LIN (red), and QUAD (brown) procedures. The baseline scenario includes $m_s=$ 20 biomarkers per set, $q=$ 20 disjoint sets, $q_m=$ 1 mediating set, $q_{OD}=$ 0 one-dimensional sets, $q_{TD}=$ 0 two-dimensional sets, $m_M=$ 3 mediating biomarkers, $m_E=$ 0 noise-biomarkers, and a correlation of ${\rho }_M=$ 0. We evaluate the effect of varying a single parameter, keeping all other parameters set to their baseline value.

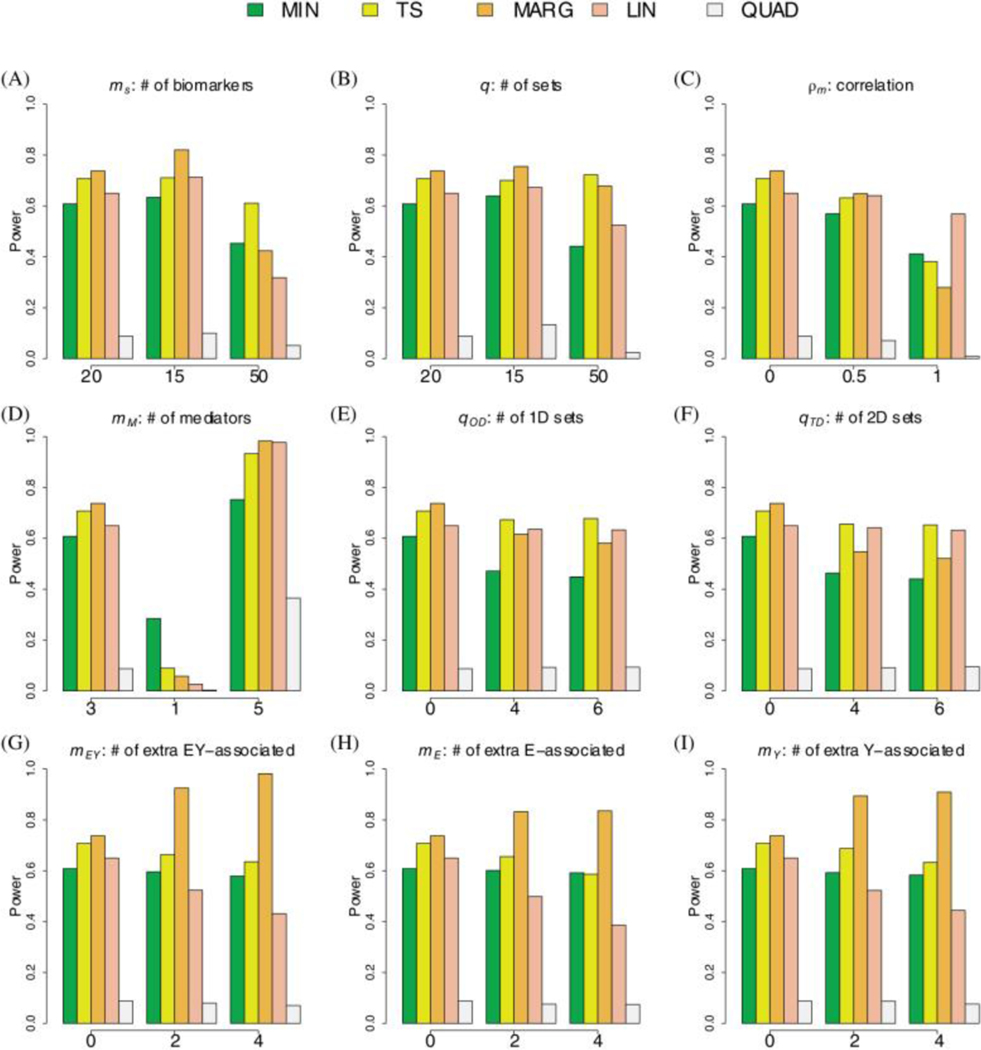
Figure 4: Simulations for Binary Outcome.

The bar-plots show the power to detect the mediating set when using the TS (yellow), MIN (green), MARG (orange), LIN (red), and QUAD (brown) procedures. The baseline scenario includes $m_s=$ 20 biomarkers per set, $q=$ 20 disjoint sets, $q_m=$ 1 mediating set, $q_{OD}=$ 0 one-dimensional sets, $q_{TD}=$ 0 two-dimensional sets, $m_M=$ 3 mediating biomarkers, $m_E=$ 0 noise-biomarkers, and a correlation of ${\rho }_M=$ 0. We evaluate the effect of varying a single parameter, keeping all other parameters set to their baseline value.

The MARG procedure unexpectedly did not have the highest power under all settings. The main disadvantage of MARG is that it uses suboptimal statistics $T_{E,1}^s$ and $T_{Y,1}^s$ to detect associations between the group of biomarkers and either the exposure or outcome. Nevertheless, MARG did have the highest power in most settings, and performed significantly better when the number of associated markers, $m_M,m_E,m_Y,and{m}_{EY}$, in the mediating set was large (Figure 3D and 3G-1I and Figure 4D and 4G-2I). JTV-comp³³, a similar procedure to MARG, also had high, if not the highest power, when included in simulations (see Supplemental Figure S21). However, this study not only had an inflated type I error when the number of two-dimensional sets was greater than 0 but also in some scenarios when the number of one-dimensional sets was greater than 0 (see Supplemental Figure S22).

QUAD generally had the lowest power to detect the mediating set in all our simulations. The power tends to be low because the parametric bootstrap procedure ¹⁰ is known to be overly-conservative. LIN generally has power only slightly lower than TS. However, LIN has higher power when either the number of mediators in a set is large (see Figure 3D and 4D for setting with $m_M=5$ and Supplemental Figures S15 and S16) or the number of test sets is small (see Figure 3A and 4A for setting with $q=15$). The power for LIN was significantly affected by the number of noise biomarkers in a mediating set (Figures 3G-1I and 4G-2I) because large values of ${\widehat{\beta }}_s$ and ${\widehat{\gamma }}_s$ increase the variance in the denominator of the statistic. We note that we did not evaluate LIN in examples where the biomarkers in the mediating set have opposing effects (i.e. ${\widehat{\stackrel{⃑}{\beta }}}_s^{\text{'}}{\widehat{\stackrel{⃑}{\gamma }}}_s\approx 0)$ as clearly LIN would have little to no power in this potentially unrealistic scenario.

The MIN procedure had reasonable power, achieving more than 80% of the power of the TS procedure for the baseline scenario. Moreover, the MIN procedure had the highest power when there was only $m_M=1$ mediating biomarker and $q=$ 20 disjoint sets (Figures 3D and 4D). However, even when there was only a single mediating biomarker, increasing the number of sets and, therefore, biomarkers, decreased the difference in power achieved by the MIN and TS procedures (see Supplemental Figures S13 and S14).

The final observation is that the TS procedure had consistently higher power than the other methods for the realistic scenarios evaluated here. We note that changing the number of one- and two- dimensional sets did not have a meaningful impact on the overall or relative performance of the TS procedure (Figures 3E-3F, 4E-4F). We note that increasing the number of noise biomarkers resulted in a slight loss of power for the TS procedure but had no effect on the MIN procedure (Figures 3D-3I, 4D-4I). In contrast to other tests, increasing the total number of sets had minimal effect on the TS procedure, but greatly reduced the power of the MIN, LIN and QUAD procedures. In the supplementary material, we compared the four procedures in a wider set of scenarios that have been more rarely observed in practice. We note that when the proportion of mediating biomarkers ($m_M/m_s$) was large or close to 1, LIN and QUAD did have higher power (see Supplemental Figures S17 and S18). However, we also note that when the proportion was low or the number of sets was large, the TS procedure had notably higher power. Specifically, when $q=$ 100 disjoint sets and $m_s=100$, the TS procedure had power above 80% while the other procedures had power below 40% (see Supplemental Figures S13 and S14). As expected, the power for all procedures, including TS, is significantly improved by increasing the number of mediating biomarkers in the set and/or reducing the correlation between biomarkers (Figures 3C, 4C). We also saw similar results when the overall effect of mediators increased (i.e. 0.1% to 2% of phenotypic variation) while the number of mediators remained constant (see Supplemental Figures S19 and S20). We note that for our TS procedure, which is based on the minimum conditional p-value, this increase in power can be mainly attributed to the increased probability that the set is selected in the first step.

Increased correlation reduces the power for all tests because ${\widehat{\sigma }}_{\gamma }$ increases significantly when the regression for the outcome includes highly correlated biomarkers. Moreover, for the TS approach, the p-values from post-selection inference tend be larger because, in theory, an association with an outcome may be caused by the association to another mediating biomarker. Finally, compared to MIN, the TS identified a larger number of true mediators (see Supplemental Figures S23 and S24), consistent with the overall improvement in power (see Figure 3 and 4).

3.2. Breast Cancer Study

We tested the 38 sets of metabolites to determine if any mediated the relationship between BMI and risk of breast cancer. We observed that TS selected three pathways associated with the exposure and seven pathways associated with the outcome at step one, but only one pathway, Lysine metabolism, was identified as a mediating set with adjusted p-value $P_{TS}^s=0.043$. TS identified that the specific mediating biomarker, 3-Methylglutarylcarnitine-1, drove the association with $p_j^M=0.043.$ LIN and MIN also detected the same pathway with adjusted p-value of 0.0001 and 0.041. Associations detected by LIN, TS and MIN were large driven by the single biomarker 3-Methylglutarylcarnitine-1 (see Table 2). On the other hand, MARG discovered a different Sterol/steroid pathway ($p_M^s=0.038$) that contains several sex hormones, suggesting that non-overlapping sets of hormones may be associated with the exposure and outcome. Lastly, QUAD did not identify any pathways that are potential mediators. However, the lowest adjusted p-value of 0.18 was for the Lysine metabolism group. In Table 2, we present the metabolites in the pathway discovered by LIN, TS and MIN and we present similar results for the Sterol/steroid pathway in the Supplementary material (Table S2).

Table 2:

Individual biomarker results for Lysine metabolism group pathway

Metabolite	P-value for association with risk of breast cancer	P-value for association with BMI
2-Aminoadipate	0.43	5.3∙10−4
3-Methylglutarylcarnitine-1*	9.5∙10−5	2.0∙10−8
3-Methylglutarylcarnitine-2	0.02	0.31
Glutarate pentanedioate	0.82	0.96
Lysine	0.35	0.25
N6-Trimethyl-L-lysine	0.13	0.02
N2-Acetyl-L-lysine	0.28	0.09
N6-Acetyl-L-lysine	0.17	0.55
Pipecolate	0.64	0.26
3-Methylglutaconate	0.62	0.82

^*Metabolite discovered by TS and MIN to mediate effect of BMI

4. Discussion

We introduced a new procedure, TS, to test if sets of biomarkers mediate the relationship between an exposure and an outcome. The TS procedure is computationally efficient, controls the family-wise error rate (FWER), and has high statistical power for detecting potentially mediating sets of biomarkers. Additionally, the TS also identifies individual biomarkers that are potential mediators. The strength of the method comes from the first, screening, step that removes all sets that are unlikely to be strongly associated with both the exposure and the outcome. As compared with standard association tests this screening step removes a significantly larger number of sets (e.g. 100 x (1–0.025 × 0.1) = 99.75% of sets removed compared to 100 x (1–0.025)=97.5% of sets removed). The statistical complication, which was solved and discussed in the supplementary material, is to calculate the adjusted, conditional p-values based on this screening approach. In addition to higher power, the added benefit of our approach is that it identifies the individual mediating biomarkers and allows practitioners to make more precise claims about the underlying biology by measuring effects mediated through biomarkers. In the remainder of this section, we focus on providing insight into the trends observed in our simulations, potential extensions to the TS procedure, and a discussion on the benefits of group testing.

One observation is that the QUAD and LIN procedures had lower power in many tested scenarios. Here, we offer some comments about those tests. First, importantly, we note that these procedures were not designed for scenarios where only a small subset of the biomarkers in the mediating set qualify as actual mediators. Second, despite having lower power, these procedures still have the advantage of offering a set-level p-value. In contrast, the TS procedure offers biomarker-level p-values for elements of the set, and then uses the minimum biomarker-level p-value as the set-level p-value. Third, the test statistic used in the QUAD procedure is similar to those statistics use in the first step of the TS procedure, $T_Q^s=T_{Y,\beta }^s=T_{E,\gamma }^s={\sum }_{j\in G_s}{\left({\widehat{\beta }}_j{\widehat{\gamma }}_j\right)}^2$ and therefore the similarity in procedures’ statistics needs to be reconciled with the dissimilarity in their performance. For the null distribution, the QUAD procedure assumes that both of the estimated vectors, ${\widehat{\beta }}_s$ and ${\widehat{\gamma }}_s$, follow multivariate normal distributions with non-zero means, while the TS procedure assumes one vector is a group of fixed weights and the other vector follows a multivariate normal variable with zero means. As further illustrated by an example in Supplementary material of the original paper ¹⁰, the variance of $T_{Q,b}^s$ under its associated null is an order of magnitude larger than the variance of $T_{Ys}$ or $T_{Es}$ under their associated nulls. Fourth, when testing a set of biomarkers, the quadratic version of the test statistics (see corresponding references ^30,31) generally have higher statistical power than their linear counterparts when only a subset of biomarkers are true positives regardless of the sign of effect. A second observation, which applies to all procedures, is that testing groups will only have higher power, as compared to testing individual biomarkers, when the groupings combine mediators together. Albeit not explicitly stated, our examples showed the cost if the groups were formed randomly. In this extreme scenario, a set would likely have at most one mediating biomarker (i.e. $m_M=1$). As Figures 3D, 4D, S17, and S18 illustrate, the power of all group tests are noticeably lower than the power of MIN, where we recall that MIN is equivalent to testing each biomarker individually. A third observation is that TS and MIN had low power when the majority of biomarkers in a set each had a small mediating effect. The last point, which we did not show by simulation, is that in the presence of alternating effects, where ${\beta }_j{\gamma }_j$ can be both positive and negative, LIN will clearly have lower power to detect mediating sets.

There are potential modifications to the TS procedure. First, as remarked previously, in the initial step of TS method, we used a combination of weighted statistics, $T_{Y,\beta }^s=T_{E,\gamma }^s={\sum }_{j\in G_s}{\left({\widehat{\beta }}_j{\widehat{\gamma }}_j\right)}^2$ and unweighted statistics, $T_{E,1}^s={\sum }_{j\in G_s}{\widehat{\beta }}_j^2$ and $T_{Y,1}^s={\sum }_{j\in G_s}{\widehat{\gamma }}_j^2$, to test the marginal null. The more powerful approach would be to select candidate sets by weighted tests only (i.e. $S=\left\{s:p_{E,\gamma }^s\le 0.025,p_{Y,\beta }^s\le 0.025\right\}$). However, in the second step of our new procedure, the adjustment of p-values would need to take into consideration selection by both of these test statistics, a complication that requires further thought. The second modification of TS would be to calculate the adjusted p-values by computing them under the global null ²⁸. Such a test can provide better power when the proportion of mediators in a set is very low. A third modification is to allow one biomarker to appear in multiple sets. However, such a modification is not straight-forward, as the assumptions in Theorem 1, would clearly fail to hold. Another potential modification is to allow there to be exposure/biomarker interactions in the outcome model. As a final note, we refer to each selected set as a potentially mediating set, as opposed to simply referring to it as a mediating set. We note that the test for an association between a set of biomarkers and the outcome ignores biomarkers from all other sets. Therefore, for these association tests, the other biomarkers are “unmeasured” confounders that could potentially bias our findings. Note, for large m, such bias is difficult to avoid because models cannot easily include all biomarkers.

We expect there to be growing interest in testing whether groups of biomarkers are mediators. In some scenarios, we might expect the exposure to affect an underlying, latent process that affects both the individual biomarkers and the outcome²². In other scenarios, we might expect the exposure to directly affect the biomarkers and the biomarkers to directly influence the outcome^8,10,22,33. Recently, for example, Chen and colleagues⁹ investigated whether a thermal stimula excited a region of the brain (e.g. sets of fMRI voxels in common areas), which in turn affected the reaction. Huang³³ recently investigated whether smoking affected methylation levels in a gene (e.g. sets of probes linked to a common gene), which in turn affected cancer risk. As another example, a study⁸ investigated whether high intake of fish, as measured by a questionnaire, influenced serum levels of sets of metabolites (e.g. sets that were associated with consumption of specific fish), which in turn were associated with a reduced risk of colorectal cancer.