Quantitative standardization of resident mouse behavior for studies of aggression and social defeat

Abstract

Territorial reactive aggression in mice is used to study the biology of aggression-related behavior and is also a critical component of procedures used to study mood disorders, such as chronic social defeat stress. However, quantifying mouse aggression in a systematic, representative, and easily adoptable way that allows direct comparison between cohorts within or between studies remains a challenge. Here, we propose a structural equation modeling approach to quantify aggression observed during the resident-intruder procedure. Using data for 658 sexually experienced CD-1 male mice generated by three research groups across three institutions over a 10-year period, we developed a higher-order confirmatory factor model wherein the combined contributions of latency to the first attack, number of attack bouts, and average attack duration on each trial day (easily observable metrics that require no specialized equipment) are used to quantify individual differences in aggression. We call our final model the Mouse Aggression Detector (MAD) model. Correlation analyses between MAD model factors estimated from multiple large datasets demonstrate generalizability of this measurement approach, and we further establish the stability of aggression scores across time within cohorts and demonstrate the utility of MAD for selecting aggressors which will generate a susceptible phenotype in social defeat experiments. Thus, this novel aggression scoring technique offers a systematic, high-throughput approach for aggressor selection in chronic social defeat stress studies and a more consistent and accurate study of mouse aggression itself.

Introduction

Aggression is a common, adaptive animal behavior that broadly defines social conflict related to competition for resources or self-defense. However, aggression is an unobservable construct, or latent factor, that cannot be directly measured. Instead, aggression is defined by a unifying constellation of observable indicators that characterize an aggressive behavioral phenotype. One such behavioral phenotype in rodents is territorial, or reactive, aggression where a dominant male confronts and expels pubescent males from its marked territory [1]. Territorial aggression is typically studied with variations of the resident-intruder procedure, a multi-day (typically 3- day) behavioral assay during which an intruder mouse is placed in the home cage of a resident, and the subsequent social interaction (SI) behaviors are observed. The severity of the resident’s aggressive behavior during resident-intruder testing is characterized by attack features, including latency to the first attack, the number of attack bouts, bout duration, attack consistency, attack site, level of tissue damage, bite number, and responsiveness to intruder submission behaviors [2–4]. However, individual variation of these measurements between and even within experimental cohorts of mice makes a consistent overall determination of aggression behavior difficult. Currently, no one indicator exists that accurately encapsulates mouse aggressive behavior for use in behavioral studies, leading to difficulty in comparing aggressive behavior between labs and decreased replicability in experimental set-ups that utilize aggressive behavior as a component.

Mouse aggression is a key component of the chronic social defeat stress (CSDS) procedure [5–7], a gold-standard model for the study of mood-related disorders in mice. Due to its etiological, predictive, discriminative, and face validity, the CSDS procedure has grown enormously in popularity over the last decade (Fig. 1a). In CSDS, inbred C57BL/6J male intruder mice are repeatedly subjected to bouts of social defeat by larger and more aggressive male outbred CD-1 resident mice, inducing enduring deficits in SI and other behavioral antecedents related to mood disorders like anhedonia and anxiety. However, the measurement of aggression exhibited by the resident CD-1 mouse is not standardized, introducing unnecessary variability into CSDS studies.

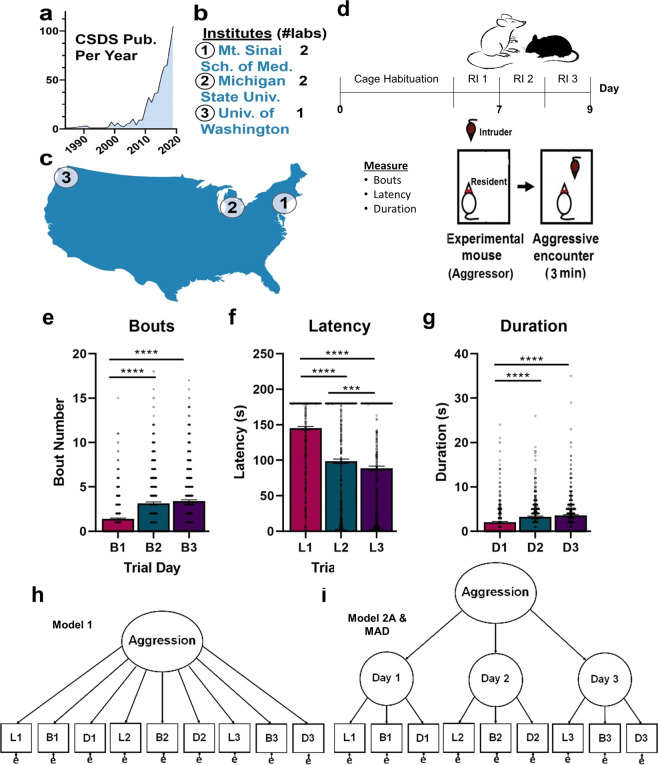
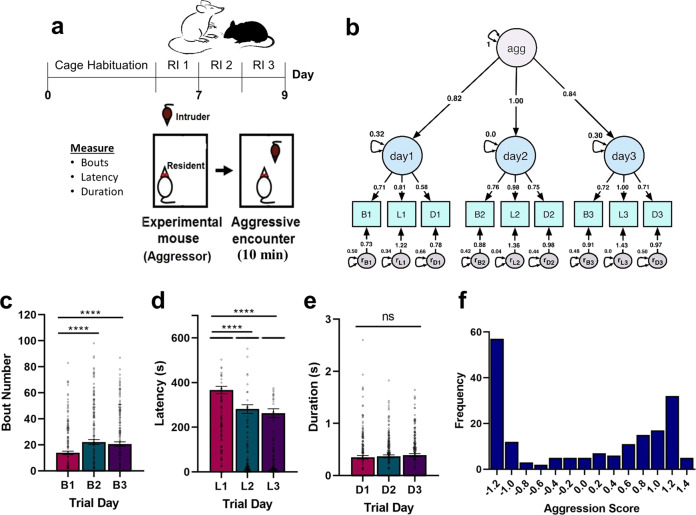
Fig. 1. Aggression is a composite measure for studies of aggression behavior and chronic social defeat.

a The number of studies using CSDS listed on NIH Pub Med each year since 1985. b Data presented in this manuscript are drawn from aggressor screenings at three different institutes located across the United States (c), performed over the course of 10 years by four separate laboratories. d The resident-intruder procedure is a 3-day behavioral assay that evaluates aggression during a timed social interaction. After habituation of retired breeder male CD-1 aggressors to the home cage, a different male C57BL/6J intruder is introduced for 3 min per day on each of 3 days. Attack features including bouts, latency, and duration are recorded for each resident mouse. e–g Among experimentally naïve aggressors (Set 3; n = 579), there was main effect of trial day for bouts (p < 0.0001), latency (p < 0.0001), and duration (p < 0.0001). e The number of bouts increased on day 2 versus day 1 (p < 0.0001) and day 3 versus day 1 (p < 0.0001). f Latency decreased across all trial days (p < 0.001). g Duration increased only on days 2 and 3 when compared to day 1 (p < 0.0001). Together, bout, latency, and duration measurements generate nine observed variables that can be structured in an (h) first-order or (i) second-order measurement model to calculate an aggression score. ****p < 0.0001, ***p < 0.001, **p < 0.01, *p < 0.05; error bars indicate SEM.

To evaluate aggression, the observed attack features may be used as dependent variables themselves, or to calculate a composite aggression score. A drawback to operationalizing aggression as any one of its observed indicators is that a single indicator may provide a limited view of behavior. This is especially true if the selected variable depends upon the escape behavior of the intruder mouse (e.g., attack duration), which can vary between intruders. Furthermore, unwanted variation due to measurement error contaminates any true score of aggression when only one indicator is used [8]. Alternatively, a composite aggression score can be generated by applying a rank or sum function to the observed indicators. This too is not optimal since, due to natural cohort-to-cohort variation, scores that depend on the group mean (e.g., z-score) will change when mice are added to analyses over time, or the same numerical score will reflect different behavior between mice in separate experimental cohorts. Furthermore, the validity of summed or aggregated indicators representing repeated measurements should also account for any expected change in behavior over the course of the behavioral assay [e.g., the “winner effect”, wherein aggressive mice become more aggressive over time as they learn to rapidly and efficiently dominate intruders; 9, 10], permitting appropriate weighting of the contribution of variables to the overall aggression score. To this end, we outline a data-driven method to model aggression and systematically generate aggression scores that are comparable across experimental cohorts, at different repeated screenings, and between labs. This is a critical tool for social defeat experiments and direct studies of territorial reactive aggression, as these methods become more prominent and reproducibility more challenging.

Structural equation modeling (SEM; see Supplemental information) provides an ideal confirmatory framework for testing theoretical relations in data measured across multiple dimensions (e.g., latency to attack, bout number, and bout duration) of a latent factor (e.g., aggression). The assumption of these models is that shared variance among observed indicators is caused by a common relationship to the latent factor. Confirmatory factory analysis (CFA) is a particularly useful measurement tool for preclinical research because it utilizes foundational research, such as extensive behavioral data, as a ground-truth to inform modeling by allowing researchers to specify the number and pattern of variable relationships [11]. Indeed, utilizing previous research to make a priori modeling decisions within this SEM framework is how CFA earns its “confirmatory” moniker.

The goal of the current study is to develop an empirically driven measurement model that explains variation in species-normative territorial reactive aggression among male CD-1 retired breeder mice. To measure aggression, we selected latency to the first attack, attack bouts, and average attack duration because these observed indicators are the most common behavioral metrics used to quantify aggression without performing in-depth ethological analysis, making them suitable for high-throughput screening. We show that CFA generates an effective and consistent measurement model, the Mouse Aggression Detector (MAD), across four different laboratories in different institutes across the United States with CD-1 mice acquired from multiple vendors over a decade of experiments (Fig. 1b, c). We then apply the model to additional, smaller cohorts of mice to further demonstrate the stability of aggression scores over repeated screening experiments and how aggressor selection predicts CSDS outcomes. Together, this approach facilitates statistically rigorous multivariate analyses of aggression to evaluate aggressor performance as well as consistent selection of aggressors for CSDS research. Use of MAD allows direct comparison of mouse aggression between labs and studies for the first time and will facilitate high-throughput screening for consistent and stable aggressors, improving the consistency and replicability of CSDS and related social stress studies. Finally, we now make the model (i.e., code) available for free use with GitHub (https://github.com/RobisonLab/MAD).

Methods

Animals

All experiments involving male CD-1 and C57BL/6J mice were approved by the Institutional Animal Care and Use Committee at the University of Washington, Icahn School of Medicine at Mount Sinai, and Michigan State University and conducted in accordance with guidelines from the Association for the Assessment and Accreditation of Laboratory Animal Care and National Institute of Health. Mice were housed in a 12:12 h light–dark cycle and provided ad libitum access to water and a standard laboratory diet.

Resident-intruder procedure

Aggression was evaluated using the resident-intruder procedure as previously described [4, 5, 12, 13]. The procedure was repeated over 3 consecutive trial days and measures of latency to the first attack, the number of attack bouts, and attack duration were collected each day.

Chronic social defeat stress

CSDS was conducted as previously described [5]. Experimental C57BL/6J mice were subsequently evaluated for susceptibility to defeat in SI, also as described [14]. See Supplementary Methods for details.

Aggregate data

The Robison and Mazei-Robison Labs at Michigan State University contributed aggression screening data from multiple cohorts for a combined total of 210 sexually experienced CD-1 male mice, 131 of which were experimentally naïve aggressors (Set 1). The Russo Lab contributed data for 448 experimentally naïve, sexually experienced aggressors (Set 2) from screenings conducted at the Icahn School of Medicine at Mount Sinai and subsequently used for other experiments [4]. We combined Sets 1 (n = 131) and 2 (n = 448) to form a large, aggregate dataset of screening information for 579 experimentally naïve mice (Set 3). Aggression scores were generated for a completely inclusive dataset of 658 experimentally naïve and experienced mice (Set 4) from the Robison, Mazei-Robison, and Russo Labs. The Golden Lab at the University of Washington contributed an independent dataset of 182 sexually experienced, experimentally naïve CD-1 male mice that underwent aggression screenings (Set 5) that were measured using the SimBA computer classification toolkit with an “attack” predictive classifier generated as previously described [15].

Data analysis

We utilized the SEM framework to model attack behaviors (i.e., latency, bouts, duration) as manifest indicators representing theoretically related facets of an underlying aggression factor. Confirmatory factor analysis was conducted using the lavaan package [16] in RStudio version 3.6.2 [17]. Models were estimated using maximum likelihood estimation with robust standard errors. To evaluate the CFA models, we examined several different indices reflecting goodness-of-fit between the hypothesized covariance structure and the observed data covariance matrix (Table S1). We explored fit indices, including the comparative fit index (CFI), Tucker–Lewis index (TLI), root mean square error of approximation (RMSEA), and standardized root mean square residual (SRMR) [18]. We evaluated our proposed measurement models using thresholds for good fit: RMSEA ≤ 0.06, CFI ≥ 0.95, TLI ≥ 0.95, and SRMR ≤ 0.08 [19]. To compare models, we performed Satorra–Bentler scaled chi-square difference tests [20]. Once the final model was established, we calculated aggression scores for smaller cohorts of mice using RStudio which inputs model parameters in a multivariate equation with novel data. To use MAD in this way, materials and instructions are publicly available on GitHub (https://github.com/RobisonLab/MAD). PRISM software 8.0 was utilized to compare aggression scores via Pearson correlation tests and analyze our observed indicators using repeated measures analysis of variance (ANOVA) tests with Tukey’s multiple comparison tests for post hoc analysis.

Results

Attack behavior varies across trial days during the resident-intruder procedure

To determine potential changes in behavior during resident-intruder screenings (Fig. 1d), we independently examined changes in latency, bouts, and duration across trial days using experimentally naïve aggressor data generated at Michigan State University in 2018–2020 (Set 1; n = 131) and the Mount Sinai School of Medicine in 2010–2014 (Set 2; n = 448), as well as in a combined, experimentally naïve aggressor dataset (Set 3; n = 579). In accordance with previous research [4, 10, 12], we show with repeated measures ANOVA that experimentally naïve, sexually experienced CD-1 male mice (Set 3) exhibit significant increases in aggression-related behavior across trial days (Fig. 1e–g): reduced latency to the first attack and increased bout number and bout duration. We established a significant main effect of trial day for bouts (F(1.999, 1156) = 120.9, p < 0.0001), latency (F(1.940, 1121) = 248.5, p < 0.0001), and duration (F(1.958, 1132) = 36.12, p < 0.0001). The number of bouts significantly increased only on day 2 versus day 1 (∆M = 1.772, SE = 0.1398, p < 0.0001) and day 3 versus day 1 (∆M = 2.005, SE = 0.1418, p < 0.0001). Latency significantly decreased across all trial days (day 2 versus day 1 ∆M = 46.77, SE = 2.772, p < 0.0001; day 3 versus day 1 ∆M = 56.64, SE = 2.881, p < 0.0001; day 2 versus day 3 ∆M = 9.874, SE = 2.474, p = 0.0002). Duration significantly increased only on days 2 and 3 compared to day 1 (day 2 versus day 1 ∆M = 1.210, SE = 0.1783, p < 0.0001; day 3 versus day 1 ∆M = 1.525, SE = 0.2020, p < 0.0001). Taken together, these data suggest that behavior changes over trial days, underscoring the importance of developing an empirical model of aggression.

Next, we developed two single-factor CFA models to determine how to best calculate a composite measure of aggression. We compared a first-order model with freely estimated factor loadings (i.e., regression weights) for all nine indicators (Fig. 1h) and a second-order model where indicators were grouped by trial day (Fig. 1i). In the latter model, the estimated residual variance for latency on day 3 was negative, suggesting that all variability in this indicator was explained by the model. Therefore, residual variance for latency on day 3 was fixed to zero to improve estimation. For both models, the loadings for all indicators on their hypothesized factors were significant, suggesting that a unifying latent construct (i.e., aggression) is driving variation in all the observed variables.

As shown in Table S1, model fit was poor for Model 1 for Set 1 (RMSEA = 0.168; CFI = 0.721; TLI = 0.628; SRMR = 0.092), Set 2 (RMSEA = 0.161; CFI = 0.713; TLI = 0.617; SRMR = 0.078), and the combined Set 3 (RMSEA = 0.167; CFI = 0.712; TLI = 0.616; SRMR = 0.079). All reported fit indices improved dramatically in Model 2A versus Model 1. Specifically, model fit for Model 2A was good for Set 1 (RMSEA = 0.058; CFI = 0.970; TLI = 0.957; SRMR = 0.050), acceptable for Set 2 (RMSEA = 0.072; CFI = 0.947; TLI = 0.924; SRMR = 0.046), and acceptable for the combined dataset, Set 3 (RMSEA = 0.076; CFI = 0.945; TLI = 0.921; SRMR = 0.040). These data show Model 2A, in which the observable variables are grouped by trial day, has the most appropriate structure for aggression measurement. Taken together, this suggests that there is a credible latent structure in measuring aggression with the resident-intruder procedure and aggression is best represented as a composite of measures from all three trial days.

To yield our final MAD model, we further refined Model 2A based on model modification indices. This reveals additional sources of shared variance between the variables in the model that may improve model fit if consistent with theoretical considerations. For example, mice that have a shorter attack latency on the first trial day tend to also have a shorter attack latency on the second and third day. Acknowledging that behavior is correlated between trial days, we inspected the modification indices for relationships between trial days and mathematically accounted for those relationships in the model without changing its overall structure (Fig. 1i). With this model, residual variance estimates for latency on days 2 and 3 were negative, suggesting not only that the model explains differences in these variables but that there was no residual covariance between them. Residual variance for latency on days 2 and 3 as well as their residual covariance were therefore fixed to zero. Model fit for MAD was excellent for Set 1 (RMSEA = 0; CFI = 1.000; TLI = 1.006; SRMR = 0.034), Set 2 (RMSEA = 0.045; CFI = 0.985; TLI = 0.971; SRMR = 0.035), and Set 3 (RMSEA = 0.042; CFI = 0.988; TLI = 0.976; SRMR = 0.028). We subsequently conducted Satorra–Bentler scaled chi-square difference tests to compare MAD to Model 1 across all three datasets [20]. Results indicate that fit is significantly better for MAD for each comparison. In sum, we generated a model demonstrating excellent fit and significant factor loadings for three datasets. This demonstrates that our decision to include preselected variables for measurement (confirmatory factor analysis does allow for the a priori specification of variable relationship) are validated by the goodness-of-fit indices, highlighting the suitability of the MAD Model for measuring aggression behavior in the resident-intruder paradigm.

Consistencies in model structure produce similar aggression scores when applied to novel data

Although the factor structure is the same, factor loadings differ between datasets (Fig. 2a–c), thereby changing the regression coefficients used in the multivariate regression formula used to estimate aggression scores. In particular, the model estimates the same patterns of factor loadings in their contribution to generating an aggression score, where latency > bouts > duration. The model diverges, however, in the estimated factor loadings for trial days. For Set 1, factor loadings for day 3 > day 2 > day 1 in their contribution to the overall aggression score, while the factor loadings for Sets 2 and 3 followed the pattern of day 2 > day 3 > day 1 in their contribution to the aggression score. However, the 95% confidence intervals for these estimates were overlapping. To ensure that the model would be generalizable to novel datasets, we investigated the extent to which these differences change aggression scoring and if the scores remain comparable. Using the different model parameters calculated from Sets 1–3, we applied three iterations of MAD to Set 4, our combined dataset of 658 animals with and without (i.e., Set 3) experimental histories, yielding three different aggression scores for each animal to be used in subsequent analyses.

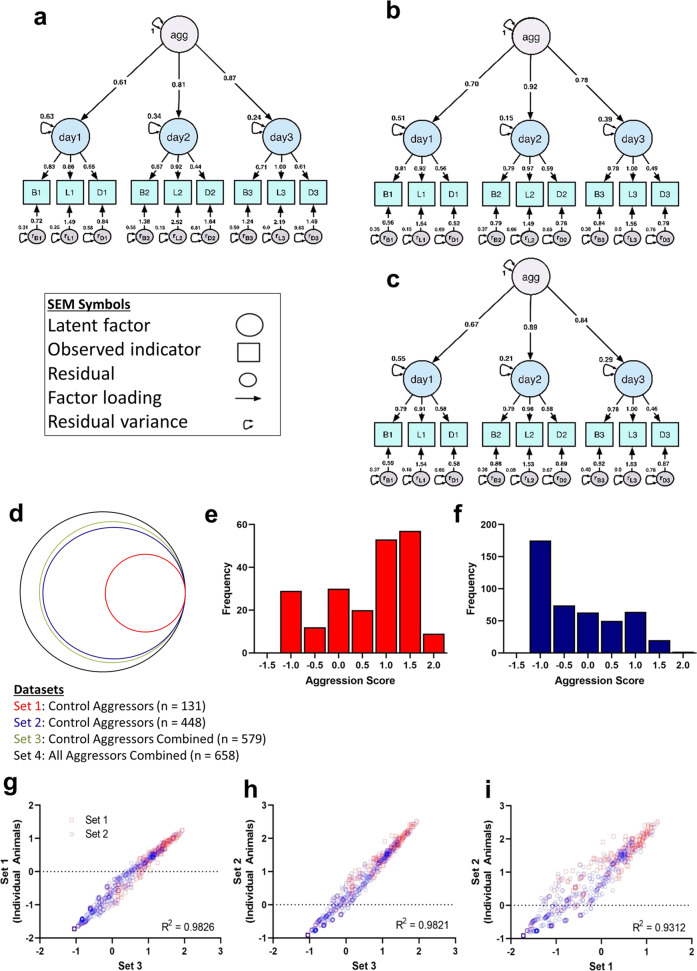
Fig. 2. Aggression scores are significantly correlated across datasets.

The final model (MAD) is a second-order measurement model wherein the observed variables are grouped by trial day before loading onto the higher-order factor, aggression. a–c In each path diagram, circles represent latent (unobservable) factors, including an overall aggression score as well as a behavior score on days 1–3, while squares represent the observed indicators, bouts, latency, and duration, on days 1–3, and small circles with double-headed arrows represent indicator residuals and residual variance. Arrows containing factors loadings, or regression weights, are interpreted as regression coefficients, denoting the change in the indicated variable, latent or observed, for every one unit change in the higher-order factor the arrow descends from. These values along with other model estimates are used in a multivariate formula to calculate aggression scores. MAD was developed three times using experimentally naïve aggressor data, thereby generating model estimates unique to (a) Set 1 (n = 131), b Set 2 (n = 448), and (c) Set 3 (n = 579). d–i Application of MAD to Sets 1–3 generated three sets of model parameters from which three sets of aggression scores were calculated for Set 4 (n = 658). d Schematic representing the four primary datasets used in this analysis. The distributions of aggression scores calculated with Set 3 model estimates are depicted in separate histograms for (e) Set 1 and (f) Set 2 datasets. Correlation analyses showed positive relationships between scores calculated using (g) Sets 1 and 3 parameters (p < 0.0001); h Sets 2 and 3 parameters (p < 0.0001); and (i) Sets 1 and 2 parameters (p < 0.0001).

To this end, we used lavaan’s predict function to separately apply each of the three patterns of estimated factors loadings (i.e., for Sets 1, 2, and 3) to the entire, aggregated sample (Set 4, n = 658) in order to generate three aggression scores for each animal (Fig. 2d). Aggression scores range from negative to positive with negative values denoting low aggression while positive values reflect high aggression (Fig. 2e, f), and the level of aggression must be interpreted with respect to the range. Unsurprisingly, summary statistics for Set 4 represent moderately aggressive animals, or the average CD-1 behavior, but the numerical values differ between calculations made using parameters generated from MAD’s application to Set 1 (M = −0.59, SD = 0.95, Mdn = −0.71, MIN = −1.73, MAX = 1.25), Set 2 (M = 0.31, SD = 1.07, Mdn = 0.16, MIN = −0.91, MAX = 2.52), and Set 3 (M = 0.06, SD = 0.94, Mdn = −0.05, MIN = −1.05, MAX = 1.94).

To assess the viability of applying MAD to different datasets, we fitted MAD to Set 4 (n = 658 aggressors from all conditions), and conducted a series of Pearson correlation tests between the three aggression scores generated for each animal. We found a significant, positive relationship between aggression scores calculated using Sets 1 and 3 (Fig. 2g; r = 0.9913, R² = 0.9826, p < 0.0001); using Sets 2 and 3 (Fig. 2h; r = 0.9910, R² = 0.9821, p < 0.0001); and using Sets 1 and 2, representing resident-intruder aggression screenings at two different institutions (Fig. 2i; r = 0.9650, R² = 0.9312, p < 0.0001). Therefore, despite these differences in absolute values, MAD aggression scores consistently represent the spectrum of aggressive behavior. Taken together, these findings strongly suggest consistent factor-variable relationships and measurement model structure that accurately and consistently quantifies aggressive behavior.

Aggression scores are stable over time

To determine if aggression scoring is consistent over time, we repeated resident-intruder screening at two different time points in a novel cohort of n = 20 CD-1 mice, beginning 7 (T1) and 21 days (T2) after animal arrival (Fig. 3a). There was a significant main effect of trial day (F(1.862, 35.39) = 10.79, p = 0.0003) as well as an interaction effect between trial day and screening time point (F(1.957, 37.19) = 5.065, p = 0.0118). At T1, there was an increase in bouts (Fig. 3b) on days 2 and 3 compared to day 1 (day 2 versus day 1 ∆M = 3.050, SE = 0.8223, p = 0.0045; day 3 versus day 1 ∆M = 3.350, SE = 0.7755, p = 0.0011). At T2, there were no differences in bout number between trial days. Between T1 and T2, we found an increase in the number of bouts on day 1 (∆M = 2.200, SE = 0.5161, p = 0.0013), but not on days 2 or 3. For latency (Fig. 3c), there were main effects of trial day (F(1.693, 32.16) = 8.901, p = 0.0014) and screening time (F(1.00, 19.00) = 9.169, p = 0.0069), as well as an interaction effect between trial day and screening time (F(1.975, 37.52) = 7.497, p = 0.0019). At T1, latency decreased on days 2 and 3 compared to day 1 (day 2 versus day 1 ∆M = 55.20, SE = 17.76, p = 0.0173; day 3 versus day 1 ∆M = 71.85, SE = 16.70, p = 0.0012), whereas only latency between days 1 and 2 at T2 decreased (∆M = 26.00, SE = 9.586, p = 0.0409). Latency on days 1 (∆M = 68.80, SE = 15.22, p = 0.0007) and 2 (∆M = 39.60, SE = 14.25, p = 0.0355) decreased between T1 and T2. At T1, we found an increase in duration (Fig. 3d) between days 1 and 3 (∆M = 2.586, SE = 0.7380, p = 0.0071), but there were no other differences at T1 or T2. Between T1 and T2, there was an increase in duration on days 1 (∆M = 2.941, SE = 0.9765, p = 0.0213) and 2 (∆M = 2.808, SE = 1.040, p = 0.0418).

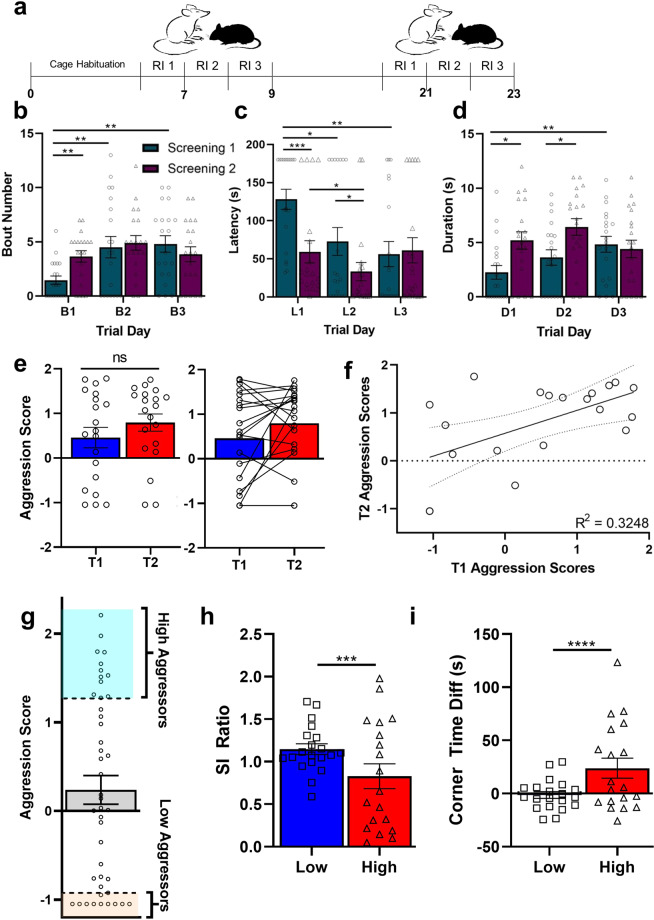
Fig. 3. Aggression scores are stable over time and predict CSDS utility.

a Schematic showing experimental timeline. Aggression was measured via the resident-intruder procedure at two different time points beginning on days 7 and 21 in a novel cohort of 20 mice. b–d The raw screening data for bouts, latency, and duration on trial days 1–3 are compared between Screening 1 (T1) and Screening 2 (T2). b Across screenings, there was a main effect of trial day (p < 0.001) as well as an interaction effect between trial day and screening (p < 0.05). At T1, there was a increase in bouts on day 2 versus day 1 (p < 0.01) and day 3 versus day 1 (p < 0.01). At T2, there were no differences in bout number between trial days. Between T1 and T2, we found a increase in the number of bouts on day 1 (p < 0.01), but not on days 2 or 3. c For latency, there were main effects of both trial day (p < 0.01) and screening (p < 0.01) as well as an interaction effect between trial day and screening (p < 0.01). At T1, latency decreased compared to day 1 on days 2 (p < 0.05) and 3 (p < 0.01) whereas only latency between days 1 and 2 at T2 (p < 0.05) decreased. Latency on days 1 (p < 0.001) and 2 (p < 0.05) decreased between T1 and T2. d At T1, we found an increase in duration between days 1 and 3 (p < 0.01), but there were no other differences at T1 or T2. Between T1 and T2, there was an increase in duration on days 1 (p < 0.05) and 2 (p < 0.05). e A paired t-test of aggression scores at Time 1 and Time 2 demonstrates no differences in aggression (p > 0.05). Among the top most aggressive animals, however, the majority maintained aggression during the two screenings. f Aggression scores are correlated for individual animals between T1 and T2 (p < 0.01). A simple linear regression analysis demonstrates a relationship between aggression scores at T1 and T2 (p < 0.01). g A cohort of 42 aggressors was screened and those with the top 10 MAD scores (high aggressors) and bottom 10 scores (low aggressors) were chosen for subsequent CSDS. Adult male C57 mice exposed to CSDS with high aggressors showed reduced social interaction (h) and increased time in the corners (i) compared to those exposed to low aggressors. ****p < 0.0001, ***p < 0.001, **p < 0.01, *p < 0.05; error bars indicate SEM.

Aggression scores were subsequently calculated by applying MAD to this novel dataset of n = 20 aggressors using parameters calculated with Set 3, our most inclusive dataset of experimentally naïve aggressors. We found that, though there were differences in the observed variables (Fig. 3b–d), there was no difference in overall aggression over time (Fig. 3e; t(19) = 1.693, p = 0.1069). However, we found that aggression scores at days 7 and 21 correlated (Fig. 3f; r = 0.5699, p = 0.0044) with aggression scores at T1 accounting for ~32% of variation in aggression scores at T2 (R² = 0.3248, m = 0.4787, p = 0.0087). Importantly, we showed that the majority of the most aggressive animals maintain their aggressive behavior between screenings (Fig. 3e), suggesting that aggressive animals behave consistently during repeated resident-intruder interactions, a typical circumstance for mice used as aggressors in multiple social defeat experiments. Taken together, these results indicate that our model provides a stable aggression score over time, making it well suited for initially selecting aggressors that will remain aggressive over multiple CSDS experiments.

MAD score predicts CSDS outcome

We next sought to determine whether a stratified aggressor exposure predicts susceptibility to CSDS-induced SI deficits. We screened 42 naïve CD-1 aggressors and conducted CSDS using aggressors with high (n = 10) and low (n = 10) aggression scores determined from the MAD model (Fig. 3g). Experimental juvenile C57BL/6J male mice were exposed to these two separate groups (n = 19 high-expose, n = 20 low-exposed). Experimental mice were subsequently evaluated for susceptibility to social avoidance in the SI task. C57 mice exposed to high aggressors showed reduced interaction ratio (Fig. 3h; t(37) = 2.038, p = 0.048) and increased corner time (Fig. 3i; t(37) = 2.539, p = 0.014) compared to mice exposed to low aggressors. Moreover, F test for inequality of variance showed that mice exposed to high aggressors had increased variance in SI (Fig. 3h; F(18,19) = 5.216, p = 0.0008) compared to mice exposed to low aggressors, indicating a separation of susceptible from resilient animals.

MAD generated aggression scores generalize to automated aggression classification

To determine the extent to which the MAD model can be applied to resident-intruder data acquired from supervised machine-learning classification of encounter videos, we used MAD to generate aggression scores for 182 experimentally naïve, sexually experienced CD-1 male mice (Set 5; Fig. 4a) that were evaluated during 10-min aggression trials using an attack classifier generated by SimBA, a supervised machine-learning tool for social behavior classification [15]. We observed the same consistent pattern of factor loadings for model estimates as seen in the primary analysis (Fig. 4b): latency > bouts > duration in their contribution to aggression score. Unlike the findings from the 3-min screening data, there were significant differences between model estimates for all three variables on all 3 days. Moreover, model estimates for trial day factor loadings showed a pattern of day 2 > day 3 > day 1 in their contribution to the aggression score. Model estimates for day 2 were different from days 1 and 3, but there was no difference between days 1 and 3. Together, these preliminary findings suggest that the behavioral characteristics defining aggression become more clearly distinguished from each other during a 10-min trial compared to a 3-min trial. However, 3- and 10-min screenings both allow efficient definition of overall aggression in each mouse.

Fig. 4. MAD for modeling SimBA data.

a Schematic showing the experimental timeline. Aggression behavior among experimentally naïve, sexually experienced CD-1 male mice (Set 5; n = 182) was measured using the resident-intruder procedure for three consecutive days under video observation, and behavior was evaluated using the SimBA classification toolkit. b Schematic showing the path diagram for MAD model estimates generated using Set 5. Circles represent latent (unobservable) factors, including an overall aggression score as well as a behavior score on days 1–3, while squares represent the observed indicators, bouts, latency, and duration, on days 1–3, and ovals represent error. c–e We found a main effect of trial day for bouts (p < 0.0001) and latency (p < 0.0001) but not duration (p > 0.05). c Bouts increased day 2 versus day 1 (p < 0.0001) and day 3 versus 1 (p < 0.0001). d Latency decreased on day 2 versus day 1 (p < 0.0001) and day 3 versus 1 (p < 0.0001). e There were no differences in average bout duration across trial days. f Histogram showing the distribution of aggression scores for Set 5. ****p < 0.0001; error bars indicate SEM.

As shown in Table S2, however, metrics indicating MAD’s goodness-of-fit for Set 5 decreased compared to the primary analyses, falling into the acceptable rather than good to excellent range. Though fit may be acceptable (RMSEA = 0.088; CFI = 0.963; TLI = 0.926; SRMR = 0.045), this finding suggests that there is additional variation in this dataset that is unaccounted for in the MAD model. Indeed, examination of the observed indicators revealed a slightly different pattern of aggression behavior across trial days. Using repeated measures ANOVA, we show that Set 5 mice demonstrate increases in only some aggression-related behaviors over time (Fig. 4c–e). Specifically, we established a main effect of trial day for bouts (F(1.930, 349.4) = 17.37, p < 0.0001) and latency (F(1.831, 331.4) = 28.97, p < 0.0001) but not duration (F(1.840, 333.1) = 0.8337, p = 0.4268). Again, the number of bouts increased only on day 2 versus day 1 (∆M = 8.313, SE = 1.607, p < 0.0001) and day 3 versus day 1 (∆M = 6.758, SE = 1.521, p < 0.0001). Likewise, latency decreased only on days 2 and 3 compared to day 1 (day 2 versus day 1 ∆M = 85.29, SE = 14.61, p < 0.0001; day 3 versus day 1 ∆M = 103.7, SE = 16.31, p < 0.0001). Overall average attack duration among mice measured with SimBA is 0.37 s (versus 2.96 s among animals scored by human experimenters in Set 3) and the number of attack bouts is higher in Set 5, certainly because screening was over three times longer, but also likely a result of SimBA parsing attacks into many shorter, independent attack bouts. Taken together, this suggests that the attack classifier used for this analysis measures aggressive behavior more granularly than human annotation, likely a function of unbiased annotation of every frame across all experimental videos. Importantly, these data show that MAD provides a useful mechanism for calculating aggression scores for high-throughput screening using automated supervised classification, as well as manual classification (Fig. 4f).

Three trial days allow for sufficient data collection for aggression scoring

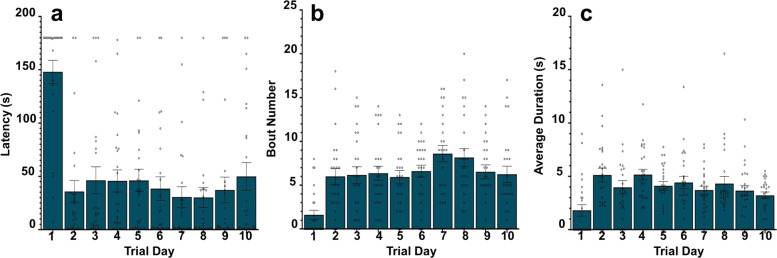
To evaluate the number of trial days necessary for appropriately assessing aggression, we conducted ten screening trials over 10 consecutive days. Results showed a significant main effect of trial day for latency (Fig. 5a; F(9) = 16.46, p < 0.0001), bouts (Fig. 5b; F(9) = 7.711, p < 0.0001), and duration (Fig. 5c; F(9) = 4.216, p < 0.001). We found some differences in measured behaviors across individual days (Tables S7–S9), but overall, we show that extended screenings do not provide substantively more information than 3-day resident-intruder procedure. Moreover, we examined measurement invariance (a test of construct measurement fidelity) across trial days during model development. Overall, we could not establish metric invariance across all 3 trial days, precluding use of a three-factor model that grouped the observed indicators by time. We further probed levels of measurement invariance between trial days. We could not establish measurement invariance between days 1 and 2, suggesting that the same construct is not being measured between these days. However, we established metric invariance between days 2 and 3, indicating that aggression behavior begins to stabilize on days 2 and 3. As such, the resident-intruder procedure is necessarily a multi-day experiment.

Fig. 5. Three trial days are sufficient to characterize aggression.

a–c The raw screening data for experimentally naïve, sexually experienced CD-1 male mice (n = 25) during a 10-day resident-intruder screening. a Bout number for days 1–10. Day 1 is different than all other trial days (p < 0.0001). Bout number on day 5 is also different from that of day 7 (p < 0.05). b Latency for days 1–10. Day 1 is different from all other trial days (p < 0.0001). There are no other differences between trial days. c Duration for days 1–10. Day 1 is different (p < 0.001) from days 2–6, but not 7–10. Duration on day 4 is also different from duration on day 10 (p < 0.05).

Discussion

We present a data-driven method to generate a composite measure of aggression behavior for sexually experienced CD-1 male mice using confirmatory factor analysis. We showed the generalizability of MAD across labs and experimenters, and the stability of MAD in quantifying aggressor performance over time, thereby demonstrating the utility of our model as a critical tool for both CSDS and aggression research.

We also showed how MAD provides a useful measurement model for data collected using automated machine-learning-based supervised classification. In short, any laboratory using the social defeat procedure can input aggressor screening data into MAD and use the resulting scores to select CD-1 residents that are most aggressive and that will remain aggressive over multiple defeat experiments. These data can be collected manually or using automated approaches. Further, these scores can be reported and incorporated into the description of CSDS experiments, standardizing (or at least accounting for) CD-1 aggression levels across experiments and laboratories.

This approach allowed us to generate an internally consistent and generalizable model that can be used to study latent mouse aggression without the need for high-speed video monitoring, specialized hardware, or behavioral analysis software, and that is readily accessible to experimenters. However, our approach can be easily extended to computational neuroethological methods [21] for the study of aggression-related behavior [22], which generate datasets that contain many more observable measures and therefore require greater dimensionality reduction. As computational neuroethology becomes more common, our approach can further be used to standardize aggression scores between labs using manual and labs using automated approaches.

Currently, there is little standardization in the measurement of aggression within the resident-intruder procedure. Many studies rely on single variable measures to quantify offensive aggressive behavior. For example, average attack latency is widely used to evaluate aggressive behavior in both aggression [e.g., 23] and CSDS research [5]. Koolhaas et al. [12] recommend summing offense behavior over three to four resident-intruder trials as a data reduction technique to score aggression across trial days. In CSDS research, Golden et al. [5] recommend selecting aggressors that attack on two consecutive days and have an attack latency of <60 s. In both cases, evaluating aggression requires the analysis of more than one aspect of aggressor behavior. The current study therefore builds on these approaches by offering a data-driven model to efficiently and systematically generate an aggression score that can be directly compared to those generated in other cohorts at different times, by different experimenters, and/or in different environments.

Confirmatory factor analysis utilizes variance and covariance to determine the structure of a measurement model, and mice are both sensitive to experimental conditions and do not often rigidly adhere to a pattern of behavior. Though there were no significant differences between the factor loadings for days 1–3, the model estimated a stronger factor loading for day 2. Looking at the raw data, we observed a small subset of animals that attacked only on day 2 and for an extended duration, likely driving this finding. As such, including cohorts of animals in aggregate data that may have been evaluated by different researchers or different screening methods (i.e., real-time versus video) certainly affects model structure, but building the model with data from multiple experimenters and institutes ensures its generalizability and thus its potential utility in all labs. We demonstrated here that aggression scores were highly correlated despite differential (but non-significant) numerical weighting of days 2 and 3 parameter estimates (Fig. 2i). Thus, though variation in screening procedures likely produced differential parameter estimates that affect scoring, this only makes the model more amenable to different datasets and applications.

Another limitation of the current study is that the experimental animals were all male. In light of an ongoing effort to broaden our understanding of affective disorders, recent adaptations of the CSDS model have been successfully applied to female mice [24, 25]. Critically, this work has revealed differences in attack behavior between intermale and rival female aggression [24]. MAD does not account for any sex differences in aggression behavior and therefore cannot necessarily be applied to female aggressors. Though there may be some overlap in model structure, additional work is required to accurately characterize rival female aggression. It is likely that female aggression may be qualitatively different, both in measurement of behavior and the underlying circumstances that produce the aggression. While given similar conditions and behavioral measurements it can be presumed that the model may accurately predict aggression scores in both males and females, additional work would be necessary to test this hypothesis. Future work should apply SEM approaches to female aggressor data to develop an appropriate measurement model to aid the study of sex as a biological variable in aggression.

Conclusion

In the current study, we sought to develop a systematic, data-driven method of measuring aggression behavior in a preclinical model of territorial aggression. SEM provides an ideal confirmatory approach that leverages foundational research to quantify aggression behavior. With this approach, we show that a multidimensional, multi-day aggression screening provides a better characterization of aggression behavior. As such, utilizing this standard measurement approach, especially in tandem with other quantitative measurement tools (e.g., SimBA), facilitates reproducibility of research and collaboration across labs. Importantly, our model, MAD, can be used for high-throughput screening to streamline aggressor selection and reduce an element of variability in CSDS research.

Funding and disclosure

This study is a part of the Avielle Foundation’s Basic Neuroscience Research Grant Program (AJR and CCK). Other funding includes NIMH R01 MH111604 (AJR), NIDA 4R00DA045662-02 (SAG), NIDA P30 DA048736 (SAG), NARSAD Young Investigator Award 27082 (SAG), and NIDA T32 5T32NS099578-04 (NG). The authors report no other relevant funding and no conflicts of interest.

Author contributions

CCK, ALE, NG, SAG, and AJR conceived and interpreted experiments; CCK, ALE, IN, and NG performed experiments; KM provided critical support for experiments; CCK, HA, and ARB performed the analysis; CCK and AJR wrote the paper; all authors revised the manuscript.

Supplementary information

The online version contains supplementary material available at 10.1038/s41386-021-01018-1.