Rapid whole-brain electric field mapping in transcranial magnetic stimulation using deep learning

Guoping Xu; Yogesh Rathi; Joan A Camprodon; Hanqiang Cao; Lipeng Ning

doi:10.1371/journal.pone.0254588

. 2021 Jul 30;16(7):e0254588. doi: 10.1371/journal.pone.0254588

Rapid whole-brain electric field mapping in transcranial magnetic stimulation using deep learning

Guoping Xu ^1,², Yogesh Rathi ^2,^3,⁴, Joan A Camprodon ^3,⁴, Hanqiang Cao ⁵, Lipeng Ning ^2,^3,^4,^*

Editor: Dzung Pham⁶

PMCID: PMC8323956 PMID: 34329328

Abstract

Transcranial magnetic stimulation (TMS) is a non-invasive neurostimulation technique that is increasingly used in the treatment of neuropsychiatric disorders and neuroscience research. Due to the complex structure of the brain and the electrical conductivity variation across subjects, identification of subject-specific brain regions for TMS is important to improve the treatment efficacy and understand the mechanism of treatment response. Numerical computations have been used to estimate the stimulated electric field (E-field) by TMS in brain tissue. But the relative long computation time limits the application of this approach. In this paper, we propose a deep-neural-network based approach to expedite the estimation of whole-brain E-field by using a neural network architecture, named 3D-MSResUnet and multimodal imaging data. The 3D-MSResUnet network integrates the 3D U-net architecture, residual modules and a mechanism to combine multi-scale feature maps. It is trained using a large dataset with finite element method (FEM) based E-field and diffusion magnetic resonance imaging (MRI) based anisotropic volume conductivity or anatomical images. The performance of 3D-MSResUnet is evaluated using several evaluation metrics and different combinations of imaging modalities and coils. The experimental results show that the output E-field of 3D-MSResUnet provides reliable estimation of the E-field estimated by the state-of-the-art FEM method with significant reduction in prediction time to about 0.24 second. Thus, this study demonstrates that neural networks are potentially useful tools to accelerate the prediction of E-field for TMS targeting.

Introduction

Transcranial magnetic stimulation (TMS) is a non-invasive neuromodulation technique increasingly used to study human physiology, cognition, brain-behavior relations and the pathophysiology of neurologic and psychiatric disorders [1]. In TMS, a magnetic coil with pulsed current is placed over the scalp to generate an electric field (E-field) in the underlying brain tissue in order to modulate neural activity in a target brain region [2]. However, due to the complex structure of the brain and the electrical conductivity variation across different tissues, the maximal stimulation strength of E-field does not always happen at the expected location [3] and the current pathways induced by electrical stimulation are not straightforward to identify [4]. Thus, it is necessary to accurately estimate the distribution of electric field (E-field) induced in the brain to improve brain targeting in TMS [5].

Several numerical approaches have been developed to estimate the E-field in TMS, including the local sphere model [6, 7], the boundary element method (BEM) [8, 9] and the FEM method [10–12]. In particular, the FEM method is based on a volume conductor model (VCM) of head tissue which not only is able to characterize complex tissue structure, brain geometry but also anisotropic tissue conductivity to potentially improve the model precision especially in white matter regions [13, 14]. Moreover, the FEM approach is able to integrate individual anatomical head models (volume conductor models) using several standard toolboxes such as SimNIBS [15], FreeSurfer [16], FSL [17], and SPM [18], to estimate the spatial distribution of stimulated tissue taking into account the impact of individual head and brain anatomy [19]. But this approach takes long time in two aspects: First, it needs a few hours to build the individual head model. Second, it takes typically several minutes to estimate the E-field, which used to construct and solve a linear system on one location and angle. Hence, it limits its application in situations when rapid adjustments for multiple coil positions and orientations are needed. To overcome the limitations, several computation algorithms [20–22] have been developed to reduce the simulation time.

The deep-learning technique has been recently applied to predict the E-field induced by TMS [21]. This approach is able to significantly reduce the simulation time to much shorter than one second, a significant reduction in prediction time. However, the original framework in [21] has several limitations which compromise the accuracy of the estimated E-field. First, it estimates the magnitude of the E-field without any information about the underlying directions which are useful to investigate the effect of TMS on axonal fiber bundles [23]. Second, the approach in [21] only predicts E-field with the coil placed near a small brain region around the motor cortex with no training and testing data examined for other brain regions. Third, the neural network takes a T_1w MRI and the position the TMS coil as input to predict the E-field and neglect the difference between coils. Thus, the trained network is only applicable to predict E-field maps for a specific coil.

In this work, we propose a new deep-learning framework that overcomes the limitations of previous method in [21]. First, our approach predicts the three-dimensional vector E-field instead of its magnitude. Second, our method can be used to predict E-field with the TMS coil placed at different positions over the whole brain. Third, our method uses the change of vector potential, i.e., the dA/dt map, of the TMS coil as input to predict E-field. Thus, the trained DNN can be applied to predict E-field for different types of coils. We have developed four deep neural networks (DNNs) that use different types of imaging data to predict vector E-field. Similar to the method in [21], the first two DNNs were trained based on T_1w MRI images to predict E-field simulated using isotropic or anisotropic tissue conductivity tensors, respectively. The other two DNNs take the anisotropic tissue conductivity maps derived from diffusion MRI as the input to predict the E-field maps. By comparing the prediction results of the four DNNs, we can examine if the additional information provided by diffusion MRI can enhance the prediction accuracy. Moreover, the proposed DNNs have a novel network architecture, named 3D-MSResUnet, which integrates the residual module and deep supervision mechanism in a multi-scale way [24, 25] to the standard 3D-Unet architecture [26] to achieve better performances. The performance of the trained DNNs has been examined using different testing datasets and different types of coils with multiple evaluation metrics.

Materials and methods

MRI data and VCM

T_1w and diffusion MRI data of 65 randomly selected subjects from the 100 unrelated subjects Human Connectome Project (HCP) database were used in this study [27]. The T_1w MPRAGE image was acquired with 0.7 mm isotropic voxels. The diffusion MRI data has 1.25 mm isotropic voxels and three non-zero b-values at b = 1000, 2000, 3000 s/mm² with 90 gradient directions at each b-shell. The HCP diffusion MRI datasets were preprocessed with corrections for head motion and distortions and were co-registered with T_1w MRI [28]. We applied the mri2mesh command from the SimNIBS software (version 3.0.8) [15] which integrates the FreeSurfer toolbox [29] to construct the volume conductor models (VCMs) for each subject using the T_1w MRI data. Then, we extracted the b = 0 and 1000 s/mm² volumes of the diffusion MRI data and applied to the dwi2cond command to estimate anisotropic tissue conductivity tensors. Higher b-values were not included in the analysis to ensure that the proposed network is also applicable to diffusion MRI acquired from clinical MRI scanners with standard protocols.

E-field simulation

We used Matlab (R2015b, Mathworks, Natic, MA) and SimNIBS (version 3.0.8) to simulate E-field maps using the HCP dataset for training and testing the neural networks. Two sets of E-field maps were simulated for each subject by using scalar-valued tissue conductivity and anisotropic conductivity tensors, respectively. The scalar-valued tissue conductivity for white matter, gray matter, CSF, bone and scalp were set as 0.126, 0.275, 0.1654, 0.01 and 0.465 S/m, respectively, which were the default values in SimNIBS. Moreover, the distance from the coil to the scalp was 4 mm which was also the default value. For anisotropic conductivity tensor based simulations, we followed the recommendation of [30] to use volume normalized conductivity tensors to model the anisotropic conductivity in brain tissue with the eigenvectors consistent with those of the diffusion tensor models and with the geometric mean of the eigenvalues identical to the standard isotropic conductivity [31]. In order to generate E-field maps with different coil centers and orientations, we sampled the position of the coil from the positions of the EEG 10–10 system and with the coil handle directed to 78 different directions with approximately 4.6^o angular resolutions. Thus, 52 coil center positions and 78 directions at each position were selected to simulate E-field maps, which provided a total number of 4056 (52x78) samples for each subject for either scalar-valued conductivity or anisotropic conductivity based E-field simulations.

Training and prediction strategies

The results in [21] have shown that a neural network trained by data from 20 subjects can accurately predict E-field simulated using T_1w MRI. Accordingly, we selected 20 subjects from the HCP dataset in an initial experiment to train the neural networks. We used two sets of input images to train the neural networks. The first set of training data included the T_1w MRI and the temporal change of vector potential map, i.e., the dA/dt map, of the magnetic coil, which provides a 4-dimensional input to the DNNs. This set of input data was applied to train two DNNs to predict E-field distributions simulated based on isotropic and anisotropic conductivity maps, respectively, with trained DNNs being denoted by T1-iso20 and T1-aniso20. The second set of training data included the principal eigenvector from the conductivity tensor and the dA/dt map of the coil, which provided a 6-dimensional input to the DNN, with the trained DNN being denoted by C-20. This set of data was used to predict anisotropic conductivity tensor-based E-field maps to investigate the additional advantage of using high-dimension data provided by diffusion MRI.

Different from the method in [21], the proposed DNNs not only predict vector E-field maps but also predict it in the whole brain as opposed to scalar E-field maps in a small region. In particular, the dimension of the output data of the proposed DNNs is 180x220x120x3, whereas dimension of the output of the method in [21] is 72x144x24x1. To examine if additional training data was needed to improve the prediction accuracy of the large dimensional output data, we added 40 more subjects to continue the training of the C-20 models, with the result being denoted by C-60. Thus, the total number of training datasets for C-60 was equal to 243,360 (4056x60), whereas the number of datasets used for T1-iso20, T1-aniso20 and C-20 was equal to 81,120 (4056x20).

In summary, four DNNs were trained to predict E-field maps based on isotropic or anisotropic tensor based tissue conductivity. The T1-iso20 model were trained using 20 subjects to predict isotropic conductivity based E-field maps by using T_1w MRI and the dA/dt vector field of the TMS coil. The T1-aniso20 model were trained using the same set of input data to predict anisotropic conductivity based E-field maps. The C-20 model was also trained using 20 subjects to predict anisotropic conductivity based E-field maps by using anisotropic conductivity tensors and the dA/dt map. The C-60 model was further trained based on the C-20 model by using additional 40 training subjects.

Network architecture

The standard network architecture that has been widely used for image-based learning, including [21], is a structure called U-net which consists of a sequence of encoder and decoder modules. In [32], a variant of U-net with the residual module was introduced to solve the exploding or vanishing gradients problem and improve the training efficiency [33]. It was shown that the residual module combined with standard U-net has better performance than the standard U-net in [32, 34]. In addition, [35, 36] proposed a different variant of U-net to pass the features extracted from early stages to later stages of decoders to improve the network prediction performance using multi-scale features.

In this work, we introduce a new network architecture, which is named 3D-MSResUnet, by combining the residual modules introduced in [33] and the approach from [35] to integrate multi-scale features based on U-net architecture. 3D-MSResUnet is a fully convolutional network whose architecture is illustrated in Fig 1. The dark arrows represent the short skip connection of residual modules, and the light arrows mean the short skip connection that pass the feature maps of decoders to the encoders. All cuboids with various colors represent the feature maps extracted from the 3D-MSResUnet. Note that the gray cuboids indicate multi-scale feature maps from the decoders.

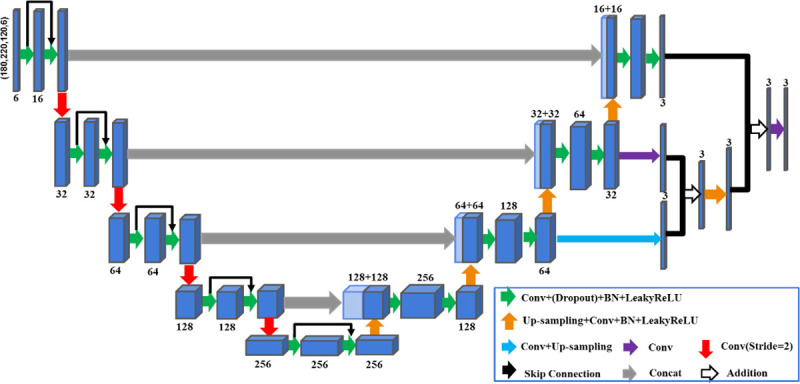
Fig 1 — The last few cuboids shown in dark gray colors represent the mechanism for integrating multi-scale features maps from decoders.

Learning strategy

Our networks were trained by minimizing the mean squared error loss between the predicted E-field and the reference data provided by SimNIBS (version 3.0.8) [15]. The network can be considered as a nonlinear regression model, which was trained to fit the E-field distribution calculated by FEM approach.

We first initialized the network weights using the method proposed in [37]. We then used the RAdam (Rectified Adam) [38] optimizer for network training with modulate parameters β₁ = 0.9, β₂ = 0.999 and the initial learning rate lr = 0.002. Step learning rate strategy was employed with the initial lr decayed by gamma = 0.5 after every 5 epochs. The total parameters were iteratively updated using backpropagation for a mini-batch size 4. The parameters were iteratively updated for 25 epochs, where each epoch had 2x10⁵ iterations. The network had 31 convolutional layers totally as illustrated in Fig 1. Four 3D-MSResUnet models, i.e., T₁-iso20, T₁-aniso20, C-20 and C-60, were trained with the same architecture. The T₁-iso20 and T₁-aniso20 models were trained by using the T_1w MRI and the dA/dt maps as input, with training data sampled from 20 subjects, to predict E-field maps simulated using isotropic scalar-valued tissue conductivity and anisotropic conductivity tensors, respectively. The size of the combined input data was 180x220x120x4. The C-20 and C-60 models were trained using the principal eigenvector scaled by the corresponding eigenvalues of the conductivity tensor and the dA/dt maps as input, with the training datasets sampled from 20 and 60 subjects, respectively, based on anisotropic conductivity tensors. The size of input data for both C-20 and C-60 was 180x220x120x6. The training of C-60 was initialized by the parameters of the C-20 model but with additional 40 independent subjects added to the training with 4x10⁵ additional iterations for each of the 25 epochs.

Testing methods

We conducted the following experiments to examine the performance of the DNN models and their dependence on the type of TMS coils, imaging protocols and the coil positions.

HCP testing subjects

We applied the four trained DNNs to predict E-field maps for 5 independent subjects from the HCP database that were not used in training. Each subject had 4,056 simulated E-field volumes with isotropic and anisotropic tissue conductivity, respectively, using three different coils. The difference between the predicted and simulated E-field maps were compared to examine the performance of the DNNs.

On the dependence of coils

We note that a major difference between the proposed approach and the method in [21] is the inclusion of the dA/dt map as a input to the DNN. Thus, the DNN model can produce different E-field maps for different coils at the same positions. In our experiment, the DNNs were trained based on simulated E-field using a Magstim-70mm-Figure8 [39] TMS coil. To examine the performance for other coils, we applied the C-60 model to predict E-field maps for the MagVenture-MC-B70 coil, which has a similar Figure-of-Eight shape as the trained coil and the Magstim-70mm-Circular coil [40].

On the dependence of imaging protocols

To examine the dependence of the prediction results on imaging protocols, we applied the trained DNNs to predict E-field maps simulated using the Ernie dataset provided by SimNIBS. This dataset was acquired using a standard clinical scanner with 2 mm resolution dMRI data which had much lower resolution compared to the 1.25 mm isotropic voxels in HCP datasets. We simulated E-field maps using both isotropic and anisotropic conductivity maps with three types of coils and compared the results with the predicted data.

On the dependence of coil positions

To examine if the trained DNNs were able to predict E-field maps with the coil placed at different positions that were not included in the training dataset, we simulated the E-field maps with coil positions sampled at different vertices of the brain surface model at the rostral middle frontal lobe from FreeSurfer [29]. This region contained about 31795 vertices (total) in the 5 testing subjects. E-field maps with anisotropic conductivity were simulated using 3 uniformly sampled orientations at each position, providing a total of 95385 volumes to evaluate the performance of trained neural networks at positions that are different from EEG nodes. The simulation results were compared with the predicted values by the C-60 model.

Evaluation metrics

We have evaluated the performance of the neural networks using the following metrics.

Target overlapping coefficient (TOC)

One main application of E-field simulation is to define the best coil position on the scalp to optimally stimulate a given cortical target with TMS. To evaluate the performance of the predicted E-field for brain targeting, we used two approaches to define the brain target in the volume space and the surface space, respectively. In the volume space, we defined the target region as the set of voxels within brain tissue whose magnitude were higher than 95% of all other brain voxels, i.e., the top 5% voxels. To define the target region in brain surface, we first mapped the magnitude of E-field to the brain surface using the mri_vol2surf command from FreeSurfer. Then we defined the target region at the set of vertices whose magnitude were higher than 95% of all vertices. To compare the target regions of the predicted E-field and the reference, we computed their Dice similarity coefficient (DSC) [41], which was named as target overlapping coefficient (TOC). We note that TOC takes value between 0 and 1. Higher TOC implies better similarity between the E-field distributions.

T O C = \frac{2 T P}{2 T P + F P + F N}

(1)

where the TP, FP and FN mean true positive, false positive and false negative between the prediction E-Field and the reference E-Field.

E-field peak distance (EPD)

To further evaluate the performance of the predicted E-field maps, we computed the distance between peaks of the predicted and reference E-field magnitude. Similar to TOC, we computed the E-field peak distance (EPD) in both the volume and the surface space, respectively, using the following definition

E P D = ‖ P e a k (E_{P}) - P e a k (E_{R}) ‖,

(2)

where E_P and E_R denote the predicted and reference E-field and Peak() obtains the coordinate of the voxel at the gray matter region or the vertex at brain surface with the maximum magnitude. To reduce the influence of outliers on EPD in the volume space, we took the average value of the E-field magnitude in 3x3x3 neighboring voxels within the gray matter region as magnitude of a voxel to determine the location of the peak value of E-field maps for Magstim-70mm-Fig8 and MagVenture-MC-B70 coils. For the less focal E-field distributions corresponding to the Magstim-70mm-circular coil, the location of the target was determined as the average position of the top 200 voxels with the highest E-field magnitude in the gray-matter region.

E-field similarity

We also computed the correlation coefficient between the magnitude of the predicted and reference E-field maps to evaluate their similarities. The E-field similarity score was computed for whole-brain E-field magnitude using the following definition

C o r r e l a t i o n = \frac{C o v (‖ E_{P} ‖, ‖ E_{R} ‖)}{\sqrt{V a r (‖ E_{P} ‖) V a r (‖ E_{R} ‖)}},

(3)

where ‖E_P‖ and ‖E_R‖ denote the magnitude of the predicted and the reference E-field, respectively.

Mean absolute error (MAE) and mean relative error (MRE)

The mean absolute error (MAE) was defined as the absolute value of the difference between the predicted E-field magnitude and the reference. The mean relative error (MRE) was defined as the ratio between MAE and the reference E-field magnitude within the corresponding target region. Here, MRE was only computed within the target region to avoid singularity when computing the ratio.

M A E = \frac{1}{K} \sum_{1}^{K} | ‖ E_{P} ‖ - ‖ E_{R} ‖ |,

(4)

M R E = \frac{1}{K} \sum_{1}^{K} (\frac{| ‖ E_{P} ‖ - ‖ E_{R} ‖ |}{‖ E_{R} ‖}),

(5)

where K denotes the number of vertices on brain surfaces.

Normalized root-mean-square error (NRMSE): To compare the vector E-field in volume space, we computed the NRMSE measure [42] using the method below

N R M S E = \frac{1}{N} \sum_{1}^{N} (\frac{‖ E_{P} - E_{R} ‖}{‖ E_{R} ‖}),

(6)

where N denotes the number of voxels. We computed the NRMSE measure using the whole-brain E-field as well as the target region that contained the 5% voxels around the peak of the reference E-field.

Mean directional error (MDE)

The direction of E-field vectors was shown to be important to understand the stimulation of white matter in TMS [43]. To this end, we evaluated the angular accuracy of the predicted E-field maps by computing the mean directional error (MDE) between predicted and reference E-field vectors within the reference target region based on the following definition

M D E = \frac{1}{N} \sum_{1}^{N} a c o s (\frac{E_{P} . E_{R}}{‖ E_{P} ‖ ‖ E_{R} ‖}) .

(7)

Similar to the NRMSE measure, we computed MDE for whole-brain E-field as well as the E-field around the target region.

Results

On network training

The neural networks were trained with PyTorch [44] on a Linux workstation equipped with two NVIDIA TITAN RTX GPUs with 48 GB graphics RAM in total. The training time for the T1-iso20, T1-aniso20 and C-20 models were about 14 days each. The training of the C-60 model took 28 days. Once the neural networks were trained, they were able to predict an E-field volume in 0.24 s.

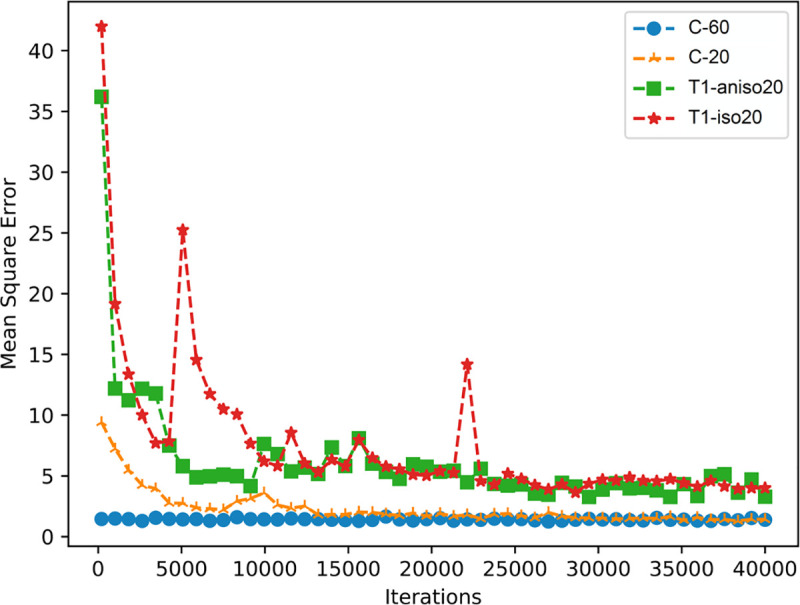
Fig 2 shows the mean square error after each epoch in the training stage of the four models. The C-20 model with anisotropic conductivity tensors in the input had a significantly lower mean square error than the T1-aniso20 model to predict the same set of E-field maps. The C-60 model was initialized by the final result of the C-20 model, which provided a relatively lower mean square error at the beginning of the training. But final mean square errors of the C-20 and C-60 models were similar and were lower than the final mean square errors of the T1-iso20 and the T1-aniso20 models.

Surface-space evaluations

Table 1 shows the evaluation metrics that compare the predicted and the reference E-field maps on brain surfaces. Overall, the T1-iso20 and T1-aniso20 models had similar performances in predicting E-field maps with isotropic and anisotropic conductivity, respectively. The C-20 model overperformed the T1-iso20 model with higher TOC and correlation measures and lower EPD, MAE and MRE measures, indicating that conductivity maps provide better performance than T_1w MRI to predict E-field maps. The C-60 model had similar performance as the C-20 indicating that using datasets from 20 subjects can provide reliable training results which is consistent to conclusions in [21]. The performance of the C-60 model at non-EEG positions that were no included in the training dataset was similar to the performance at EEG positions. In particular, the EPD was about 1.3 mm indicating that C-60 provided high accuracy for localizing TMS targets on brain surfaces.

Table 1. Target overlapping coefficient (TOC), E-field peak distance (EPD) error [mm], correlation, mean absolute error (MAE) [V/m] and mean relative error (MRE) and mean directional error (MDE) between the VCM and DNNs on gray matter region of the whole brain for T1-iso20, T1-aniso20, C-20 and C-60 and the rostral middle frontal area for C-60 on brain surfaces.

Mean (SD)	EEG positions				Non-EEG positions
Mean (SD)	T1-iso20	T1-aniso20	C-20	C-60	C-60
TOC	0.894(0.045)	0.906(0.024)	0.946(0.012)	0.956(0.009)	0.962(0.007)
EPD (mm)	3.9591(6.68)	3.736(6.055)	1.638(3.951)	1.394(3.663)	1.300(3.167)
Correlation	0.983(0.038)	0.986(0.008)	0.995(0.004)	0.997(0.004)	0.997(0.0015)
MAE	0.018(0.006)	0.017(0.005)	0.010(0.002)	0.008(0.001)	0.008(0.001)
MRE	0.154(0.059)	0.152(0.062)	0.089(0.014)	0.077(0.013)	0.077(0.009)

Open in a new tab

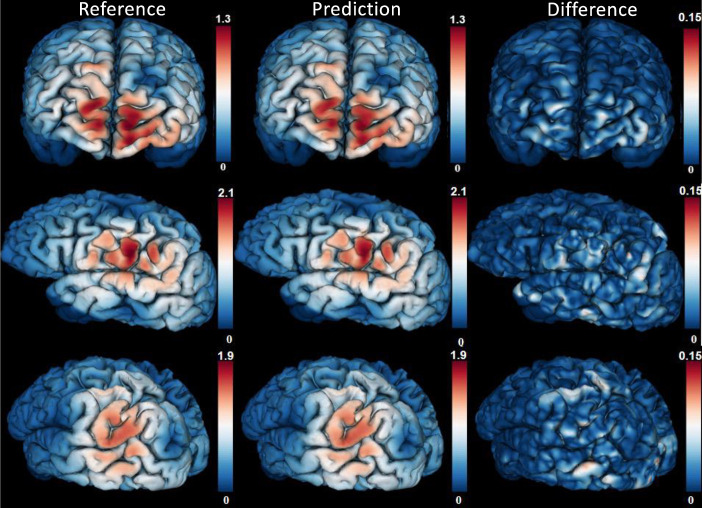
Fig 3 illustrates three samples of the predicted E-field magnitude by the C-60 model (left column), the corresponding ground truth (middle column) and their differences (right column). The coil center of the three E-field maps were at the Fpz, C5 and P5 EEG positions. Though the MRE was about 7.7% over the entire brain surface, the relative error in some regions was 10% or higher. More detailed comparisons for the E-field maps at non-EEG positions is shown in S4 Fig in S1 File. Moreover, the topographic maps for the evaluation metrics at EEG positions in surface space can be found in S5 Fig in S1 File. A detailed illustration of the evaluation metrics at non-EEG positions at the rostral middle frontal lobe is shown in S5 Fig. Moreover, a video that shows the E-field maps at different non-EEG positions is also provide in the S1 File.

Volume-space evaluations

Table 2 shows the average target overlapping coefficient (TOC), E-field peak distance (EPD), the correlation measure, the normalized root-mean-square error (NRMSE) and the mean directional error (MDE) of the E-field vectors. The NRMSE and the MDE measures were evaluated for both whole-brain E-field maps and target regions. The second to the fifth columns show the average values of these metrics from all 20280 testing volumes from 5 HCP subjects with coil placed at the same set of positions at in the training data. The last column shows the performance of the C-60 model with the coil placed at a different set of positions.

Table 2. Performance of the models using independent HCP datasets.

	EEG positions				Non-EEG positions
	T1-iso20	T1-aniso20	C-20	C-60	C-60
TOC	0.874(0.033)	0.878(0.027)	0.905(0.014)	0.914(0.012)	0.931(0.008)
EPD (mm)	8.225(8.539)	8.709(8.789)	5.588(7.112)	4.977(6.546)	3.842(5.671)
Correlation	0.978(0.026)	0.977(0.008)	0.984(0.003)	0.986(0.003)	0.989(0.001)
NRMSE	0.264(0.0744)	0.277(0.083)	0.205(0.019)	0.187(0.017)	0.217(0.019)
NRMSE (target)	0.154(0.033)	0.153(0.031)	0.107(0.010)	0.097(0.009)	0.104(0.007)
MDE	13.455(3.338)	13.770(4.039)	9.969(1.133)	9.117(0.977)	10.814(0.930)
MDE (target)	6.688(2.545)	6.605(1.299)	4.841(0.426)	4.474(0.368)	4.957(0.412)

Open in a new tab

The evaluation metrics include the target overlapping coefficient (TOC), the E-field peak distance (EPD) error, the Correlation, the Normalized root-mean-square error (NRMSE) and the Mean directional error (MDE) between the VCM and DNNs on gray matter region of the whole brain for T1-iso20, T1-aniso20, C-20 and C-60 and the rostral middle frontal area for C-60 in the volume space.

The T1-iso20 and T1-aniso20 models had similar performances for most evaluation metrics. The C-20 model had better performance than the T1-aniso20 model with increased TOC and correlation and reduced NRMSE and MDE. The NRMSE and MDE for C-20 were both lower than T1-aniso20 at target regions than the average results. The C-60 model had slightly improved performance than C-20 model. The EPD measures for all coils were higher than the surface-based results shown in Table 1. Thus, mapping the predicted E-field from the three-dimensional space to brain surfaces can improve the precision of target localization. The NRMSE and MDE both had relative lower values at target regions compared to the average results over the whole brain. The MDE for C-20 at target regions was about 4.841 degree which was lower than the 6.605-degree error for the T1-aniso20 model, indicating that the anisotropic conductivity tensor provided by diffusion MRI was helpful to improve the angular precision.

The last column of the Table 2 shows that the C-60 model had similar performance at coil positions that were not included in the training dataset. Thus, the trained networks can potentially be applied to predict E-field with arbitrary coil positions and orientations.

Table 3 shows the evaluation metrics of the C-60 model for predicting the E-field with three types of coils for the HCP data and Ernie dataset. All evaluation metrics for the Magstim-70mm-Fig8 and MagVenture-MC-B70 coils had similar values for both the HCP and Ernie datasets, but the NRMSE and MDE for the Magstim-70mm-Fig8 coil were relative lower. Moreover, the HCP datasets had lower EPD, NRMSE and MDE than the Ernie dataset, indicating the dependence of the DNN on imaging protocols and resolutions. The last column shows the results for the Magstim-70mm-Circular coil. The corresponding EPD was much higher than the result for the other two coils which may be related to the less focal distribution of the E-field.

Table 3. Performance of the C-60 model using different coils for the HCP and Ernie dataset.

		Magstim-70mm-Fig8	MagVentur-MC-B70	Magstim-70mm-Circ
TOC	HCP	0.914(0.012)	0.909(0.012)	0.890(0.012)
TOC	Ernie	0.905(0.011)	0.895(0.015)	0.8858(0.014)
EPD (mm)	HCP	4.977 (6.546)	4.789(6.636)	6.257(6.174)
EPD (mm)	Ernie	7.591(8.588)	7.236(8.951)	18.451(12.620)
Correlation	HCP	0.986(0.003)	0.986(0.003)	0.985(0.003)
Correlation	Ernie	0.982(0.004)	0.981(0.004)	0.9806(0.005)
NRMSE	HCP	0.187(0.017)	0.312(0.045)	0.244(0.056)
NRMSE	Ernie	0.3375(0.117)	0.511(0.194)	0.1123(0.3503)
NRMSE (target)	HCP	0.097(0.009)	0.116(0.012)	0.105(0.016)
NRMSE (target)	Ernie	0.121(0.016)	0.156(0.018)	0.1418(0.019)
MDE	HCP	9.117(0.977)	11.534 (1.966)	12.432(3.357)
MDE	Ernie	15.985(4.415)	18.382 (9.776)	18.3903(5.973)
MDE (target)	HCP	4.474(0.368)	4.965(0.494)	4.407(0.592)
MDE (target)	Ernie	5.474(0.889)	5.935(1.096)	5.2675(1.0954)

Open in a new tab

The evaluation metrics include the Target overlapping coefficient (TOC), the E-field peak distance (EPD) error, the Correlation, the Normalized root-mean-square error (NRMSE) and the Mean directional error (MDE) in the volume space.

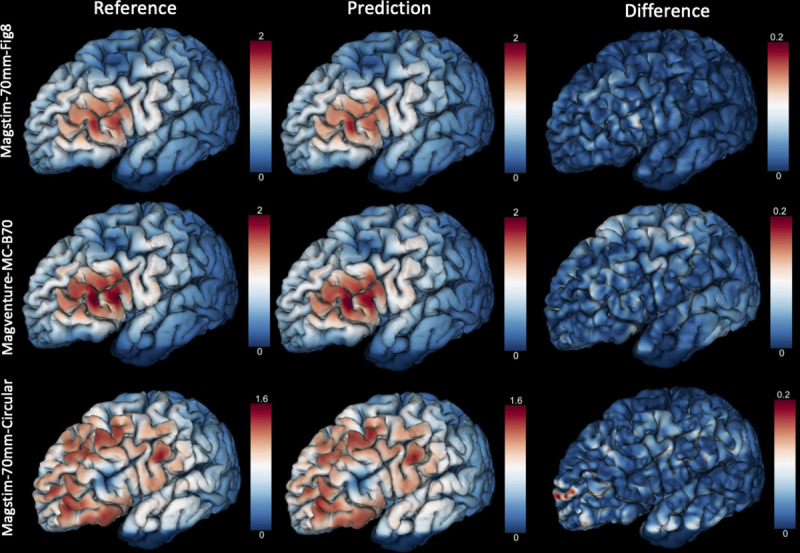
Fig 4 illustrates the simulated and the predicted E-field maps by the C-60 model for the three types of TMS coils placed at the same position of a testing subject of the HCP dataset. The E-field maps corresponding to the Magstim-70mm-Fig8 and MagVenture-MC-B70 coils have similar distributions around the target regions because the two coils have similar structure and size. But the MagVenture-MC-B70 coil had higher prediction error especially in brain areas outside of the peak regions. Though the Magstim-70mm-Circular coil has a different structure as the Magstim-70mm-Fig8 coil used in DNN training, the C-60 model can still predict similar E-field distributions as the simulated data. But the prediction error is higher than the other two coils.

Topographical illustrations

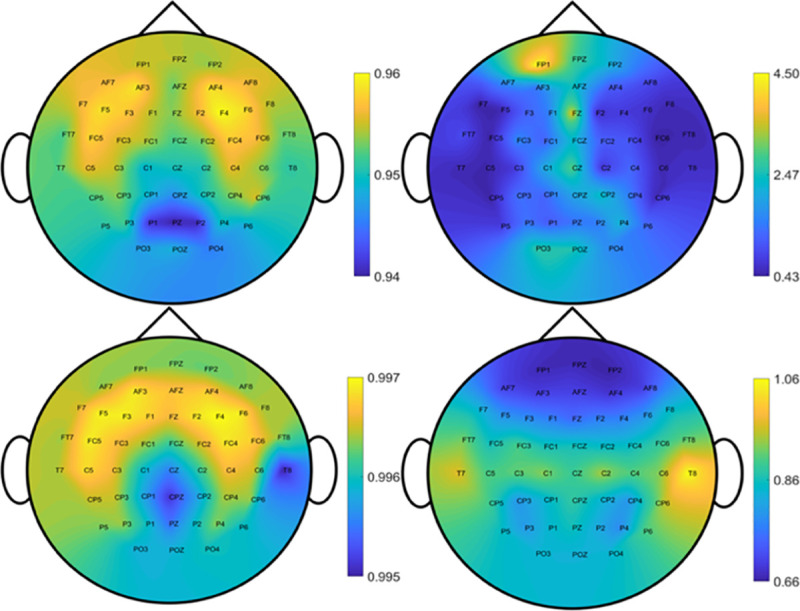
Fig 5 shows the topographic maps of the evaluation metrics associated with different coil positions. At each EEG position, the metric was the average value from 390 samples (5 subject and 78 directions). These topographic maps illustrate the dependence of the performance of network models on coil positions. In particular, the target overlapping coefficient (TOC) was symmetrical between left and right head. The larger E-field peak distance (EPD) and MAE appeared in the front of head. The correlation was more or less uniform in all brain regions except for the midline. It can be seen that the performance calculated by different metric on EEG positions. We noted that it has nearly symmetry between left head and right head, especially for TOC and MAE. Moreover, the performance is different on different EEG positions.

Discussion and conclusions

In this work, we have introduced a deep-learning based framework for E-field prediction for TMS applications. We examined its performance using different types of training data, coils and imaging protocols. Our method has several major differences compared to the DNN method in [21]. First, our method uses the dA/dt map of the magnetic coil to predict vector E-field. Thus, the trained DNN model can be applied to predict E-field maps for different TMS coils. Second, we proposed a novel architecture of neural networks, i.e., 3D-MSResUnet, to improve the prediction accuracy by combination of residual module and multi-scale feature maps into 3D-U-net architecture. Third, our method used anisotropic conductivity maps to improve the prediction accuracy of E-field maps. Several key results and limitations are summarized below:

Conductivity map vs T_1w MRI

The experimental results showed that the T1-aniso20 model can use T_1w MRI to predict E-field maps based on anisotropic conductivity with similar performance as the T1-iso20 model for predicting E-field based on isotropic models. While using T_1w MRI to predict E-field based on anisotropic models is an advantage compared to physics-based FEM method, the prediction accuracy is worse than the results of C-20 that uses anisotropic conductivity tensors for E-field prediction. On the other hand, the dependence the C-20 and C-60 models on diffusion tensors limits their applications in situations when diffusion MRI is not available.

On the dependence on positions, coils and imaging protocols

The experimental results showed that the trained DNN can predict E-field maps for coil positions that were not included in the training dataset. The whole-brain feasibility of the trained networks was attributes to the extensive training of using 243,360 data volumes which contained information about heterogeneity in brain anatomy and differences in coil positions and orientations. Moreover, the results have also shown that the performance of DNN models depend on both the shape of coils and imaging protocols. Low-resolution MRI images can reduce the targeting accuracy for the DNN models. The results for the MagVenture-MC-B70 and Magstim-70mm-Fig8 coils were similar since both coils have similar shapes. But the performance significantly degraded for the Magstim-70mm-circular coil. Thus, further training and different training strategies are needed to improve the performance for different coils and imaging protocols.

On localization accuracy

Several evaluation metrics were applied to examine the prediction accuracy of the DNN models. The experimental results showed that the target overlap ratio of the C-60 model on brain surfaces was 95.6% and the E-field peak distance was 1.3 mm and the correlation coefficient was about 0.997. The distance error increased in the volume space to about 11.3 mm. The T1-iso20 and T1-aniso20 models had reduced targeting accuracy with the E-field peak distance on brain surfaces being 3.959 mm 3.736 mm, respectively, and 8.225 mm, 12.601 mm in volume spaces. The angular error of the C-20 and C-60 models in target regions were about 4.841 and 4.474 degrees which were lower compared to the 6.688 degree for T1-iso20 and 6.605 degrees for T1-aniso20. But the angular errors were much higher than the fast quadrature method [22]. Thus, a different training strategy may be needed to improve the angular precision of the DNN models, which will be explored in our future work.

On prediction speed

The prediction of a whole-brain E-field volume using the trained neural networks took about 0.24 s. In practice, additional time is needed to apply rigid transformation to the dA/dt map according to the coil position which is expected to take much shorter computation time. Moreover, the prediction speed is still slower than the fast quadrature method [22] and the DNN based method [21] though the predicted E-field by these methods is only in a smaller region of the brain. More recently, a fast computational algorithm was introduced in [45] to estimate E-field in a selected ROI so that the E-fields generated by coils placed at 5900 different scalp positions and 360 orientation per position can be computed under 15 minutes. In [46], a rapid algorithm was introduced to compute E-field in ~100 ms on a cortical surface mesh with 120k facets and with about 5 hours of preparation time. Compared to these methods, the merits of our DNN-based method lie in the simplification in data preprocessing since it does not need mesh models and the acceleration in whole-brain E-field volume prediction. But significant improvements are needed to accelerate the prediction of E-field in target ROI to optimize coil positions and to achieve real-time prediction on brain surfaces. For this purpose, we will improve the architecture and training approach of the DNN in our future work to directly predict E-field in a selected ROI or on brain surfaces. We expect that reduced data dimension and simplified network architecture can significantly reduce the prediction time.

Finally, we note that the DNN methods have several limitations. First, the neural networks were trained to predict E-field simulated with fixed values for tissue conductivity, i.e., specific values of conductivity for different tissue types, a specific coil and specific imaging protocols, which are limitations compared to physics-based FEM algorithms. Second, the trained DNN models not only depend on the type of coils, imaging protocols but also the data processing methods. In particular, tissue segmentations in this study were obtained based on T_1w MRI, but more accurate results can be obtained by using both T_1w and T_2w MRI. Thus, further development and training of the DNN models are needed to integrate different tissue segmentation approaches for more accurate prediction results. Third, the DNN models were only trained based on data from health subjects whereas physics-based FEM algorithms have more broad applications for patients with tumors or lesions. Thus, the goal of the DNN-based method is not to replace FEM approaches. But the DNN-based methods can potentially be useful to accelerate the prediction of E-field in situations when their performances are validated. It is also a potentially useful tool to use only anatomical images, e.g., T_1w MRI, to predict E-field based on anisotropic conductivity tensors when diffusion MRI is not available in clinical settings, though further improvements in prediction accuracy are needed.

Supporting information

S1 File

(PDF)

Click here for additional data file.^{(7.3MB, pdf)}

S1 Video

(AVI)

Click here for additional data file.^{(2.2MB, avi)}

Acknowledgments

This study was partially completed while XG visited the Psychiatry Neuroimaging Laboratory at Brigham and Women’s Hospital in 2019. The authors would like to thank Fan Zhang and Joshua Goldenberg for their helpful assistance.

Data Availability

All data used in this study are freely available from public website. Results and code from this paper are available at https://github.com/LipengNing/Efield.

Funding Statement

This work was supported in part by NIH grants R21MH126396 (LN), R21MH115280 (LN and JC), K01MH117346 (LN), R21MH116352 (LN), R01MH112737(JC). XG was supported by Graduate School of Huazhong University of Science and Technology. This study was partially completed while XG visited the Psychiatry Neuroimaging Laboratory at Brigham and Women’s Hospital in 2019. No additional external funding was received for this study.

References

1.Camprodon J. A. and Pascual-Leone A., “Multimodal applications of transcranial magnetic stimulation for circuit-based psychiatry,” JAMA psychiatry, vol. 73, no. 4, pp. 407–408, 2016. doi: 10.1001/jamapsychiatry.2015.3127 [DOI] [PubMed] [Google Scholar]
2.Saturnino G. B., Madsen K. H., and Thielscher A., “Electric field simulations for transcranial brain stimulation using FEM: an efficient implementation and error analysis.,” J. Neural Eng., vol. 16, no. 6, p. 66032, 2019. doi: 10.1088/1741-2552/ab41ba [DOI] [PubMed] [Google Scholar]
3.Lee E. G., Rastogi P., Hadimani R. L., Jiles D. C., and Camprodon J. A., “Impact of non-brain anatomy and coil orientation on inter-and intra-subject variability in TMS at midline,” Clin. Neurophysiol., vol. 129, no. 9, pp. 1873–1883, 2018. doi: 10.1016/j.clinph.2018.04.749 [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Bakir A. A., Bai S., Lovell N. H., Martin D., Loo C., and Dokos S., “Finite Element Modelling Framework for Electroconvulsive Therapy and Other Transcranial Stimulations,” in Brain and Human Body Modeling, Springer, 2019, pp. 27–47. [PubMed] [Google Scholar]
5.Saturnino G. B., Thielscher A., Madsen K. H., Knösche T. R., and Weise K., “A principled approach to conductivity uncertainty analysis in electric field calculations,” Neuroimage, vol. 188, pp. 821–834, 2019. doi: 10.1016/j.neuroimage.2018.12.053 [DOI] [PubMed] [Google Scholar]
6.Ilmoniemi F. J., Ruohonen J., and Karhu J., “Transcranial magnetic stimulation–A new tool for functional imaging,” Crit. Rev. Biomed. Eng, vol. 27, pp. 241–284, 1999. [PubMed] [Google Scholar]
7.Hannula H. and Ilmoniemi R. J., “Basic principles of navigated TMS,” in Navigated transcranial magnetic stimulation in neurosurgery, Springer, 2017, pp. 3–29. [Google Scholar]
8.Salinas F. S., Lancaster J. L., and Fox P. T., “3D modeling of the total electric field induced by transcranial magnetic stimulation using the boundary element method,” Phys. Med. Biol., vol. 54, no. 12, p. 3631, 2009. doi: 10.1088/0031-9155/54/12/002 [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Nummenmaa A., Stenroos M., Ilmoniemi R. J., Okada Y. C., Hämäläinen M. S., and Raij T., “Comparison of spherical and realistically shaped boundary element head models for transcranial magnetic stimulation navigation,” Clin. Neurophysiol., vol. 124, no. 10, pp. 1995–2007, 2013. doi: 10.1016/j.clinph.2013.04.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Miranda P. C., Hallett M., and Basser P. J., “The electric field induced in the brain by magnetic stimulation: a 3-D finite-element analysis of the effect of tissue heterogeneity and anisotropy,” IEEE Trans. Biomed. Eng., vol. 50, no. 9, pp. 1074–1085, 2003. doi: 10.1109/TBME.2003.816079 [DOI] [PubMed] [Google Scholar]
11.Nielsen J. D., Madsen K. H., Puonti O., Siebner H. R., Bauer C., Madsen C. G., et al. , “Automatic skull segmentation from MR images for realistic volume conductor models of the head: Assessment of the state-of-the-art,” Neuroimage, vol. 174, pp. 587–598, 2018. doi: 10.1016/j.neuroimage.2018.03.001 [DOI] [PubMed] [Google Scholar]
12.Windhoff M., Opitz A., and Thielscher A., “Electric field calculations in brain stimulation based on finite elements: an optimized processing pipeline for the generation and usage of accurate individual head models,” Hum. Brain Mapp., vol. 34, no. 4, pp. 923–935, 2013. doi: 10.1002/hbm.21479 [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Åström M., Lemaire J.-J., and Wårdell K., “Influence of heterogeneous and anisotropic tissue conductivity on electric field distribution in deep brain stimulation,” Med. Biol. Eng. Comput., vol. 50, no. 1, pp. 23–32, 2012. doi: 10.1007/s11517-011-0842-z [DOI] [PubMed] [Google Scholar]
14.Shahid S. S., Bikson M., Salman H., Wen P., and Ahfock T., “The value and cost of complexity in predictive modelling: role of tissue anisotropic conductivity and fibre tracts in neuromodulation,” J. Neural Eng., vol. 11, no. 3, p. 36002, 2014. doi: 10.1088/1741-2560/11/3/036002 [DOI] [PubMed] [Google Scholar]
15.Saturnino G. B., Puonti O., Nielsen J. D., Antonenko D., Madsen K. H., and Thielscher A., “SimNIBS 2.1: a comprehensive pipeline for individualized electric field modelling for transcranial brain stimulation,” in Brain and Human Body Modeling, Springer, 2019, pp. 3–25. doi: 10.1007/978-3-030-21293-3_1 [DOI] [PubMed] [Google Scholar]
16.Fischl B., “FreeSurfer,” Neuroimage, vol. 62, no. 2, pp. 774–781, 2012. doi: 10.1016/j.neuroimage.2012.01.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Smith S. M., Jenkinson M., Woolrich M. W., Beckmann C. F., Behrens T. E. J., Johansen-Berg H., Bannister P. R., De Luca M., Drobnjak I., and Flitney D. E., “Advances in functional and structural MR image analysis and implementation as FSL,” Neuroimage, vol. 23, pp. S208–S219, 2004. doi: 10.1016/j.neuroimage.2004.07.051 [DOI] [PubMed] [Google Scholar]
18.Penny W. D., Friston K. J., Ashburner J. T., Kiebel S. J., and Nichols T. E., Statistical parametric mapping: the analysis of functional brain images. Elsevier, 2011. [Google Scholar]
19.Thielscher A., Antunes A., and Saturnino G. B., “Field modeling for transcranial magnetic stimulation: a useful tool to understand the physiological effects of TMS?,” in 2015 37th annual international conference of the IEEE engineering in medicine and biology society (EMBC), 2015, pp. 222–225. doi: 10.1109/EMBC.2015.7318340 [DOI] [PubMed] [Google Scholar]
20.Laakso I. and Hirata A., “Fast multigrid-based computation of the induced electric field for transcranial magnetic stimulation,” Phys. Med. Biol., vol. 57, no. 23, p. 7753, 2012. doi: 10.1088/0031-9155/57/23/7753 [DOI] [PubMed] [Google Scholar]
21.Yokota T., Maki T., Nagata T., Murakami T., Ugawa Y., Laakso I., et al. , “Real-Time Estimation of Electric Fields Induced by Transcranial Magnetic Stimulation with Deep Neural Networks,” Brain Stimul., vol. 12, no. 6, pp. 1500–1507, 2019. doi: 10.1016/j.brs.2019.06.015 [DOI] [PubMed] [Google Scholar]
22.Stenroos M. and Koponen L. M., “Real-time computation of the TMS-induced electric field in a realistic head model,” Neuroimage, p. 116159, 2019. doi: 10.1016/j.neuroimage.2019.116159 [DOI] [PubMed] [Google Scholar]
23.De Geeter N., Crevecoeur G., Leemans A., and Dupré L., “Effective electric fields along realistic DTI-based neural trajectories for modelling the stimulation mechanisms of TMS,” Phys. Med. Biol., vol. 60, no. 2, p. 453, 2014. doi: 10.1088/0031-9155/60/2/453 [DOI] [PubMed] [Google Scholar]
24.Lee C.-Y., Xie S., Gallagher P., Zhang Z., and Tu Z., “Deeply-supervised nets,” in Artificial intelligence and statistics, 2015, pp. 562–570. [Google Scholar]
25.Dou Q., Yu L., Chen H., Jin Y., Yang X., Qin J., and Heng P.-A., “3D deeply supervised network for automated segmentation of volumetric medical images,” Med. Image Anal., vol. 41, pp. 40–54, 2017. doi: 10.1016/j.media.2017.05.001 [DOI] [PubMed] [Google Scholar]
26.Çiçek Ö., Abdulkadir A., Lienkamp S. S., Brox T., and Ronneberger O., “3D U-net: Learning dense volumetric segmentation from sparse annotation,” in Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 2016, vol. 9901 LNCS. [Google Scholar]
27.Van Essen D. C., Ugurbil K., Auerbach E., Barch D., Behrens T. E. J., Bucholz R., et al. , “The Human Connectome Project: a data acquisition perspective,” Neuroimage, vol. 62, no. 4, pp. 2222–2231, 2012. doi: 10.1016/j.neuroimage.2012.02.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Sotiropoulos S. N., Jbabdi S., Xu J., Andersson J. L., Moeller S., Auerbach E. J., et al. , “Advances in diffusion MRI acquisition and processing in the Human Connectome Project,” Neuroimage, vol. 80, pp. 125–143, 2013. doi: 10.1016/j.neuroimage.2013.05.057 [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Dale A. M., Fischl B., and Sereno M. I., “Cortical surface-based analysis: I. Segmentation and surface reconstruction,” Neuroimage, vol. 9, no. 2, pp. 179–194, 1999. doi: 10.1006/nimg.1998.0395 [DOI] [PubMed] [Google Scholar]
30.Opitz A., Windhoff M., Heidemann R. M., Turner R., and Thielscher A., “How the brain tissue shapes the electric field induced by transcranial magnetic stimulation,” Neuroimage, vol. 58, no. 3, pp. 849–859, 2011. doi: 10.1016/j.neuroimage.2011.06.069 [DOI] [PubMed] [Google Scholar]
31.Güllmar D., Haueisen J., and Reichenbach J. R., “Influence of anisotropic electrical conductivity in white matter tissue on the EEG/MEG forward and inverse solution. A high-resolution whole head simulation study,” Neuroimage, vol. 51, no. 1, pp. 145–163, 2010. doi: 10.1016/j.neuroimage.2010.02.014 [DOI] [PubMed] [Google Scholar]
32.Yu L., Yang X., Chen H., Qin J., and Heng P. A., “Volumetric convnets with mixed residual connections for automated prostate segmentation from 3d MR images,” 31st AAAI Conf. Artif. Intell. AAAI 2017, pp. 66–72, 2017. [Google Scholar]
33.He K., Zhang X., Ren S., and Sun J., “Deep Residual Learning for Image Recognition,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778. [Google Scholar]
34.Lee K., Zung J., Li P., Jain V., and Seung H. S., “Superhuman accuracy on the SNEMI3D connectomics challenge,” arXiv Prepr. arXiv1706.00120, 2017. [Google Scholar]
35.Zeng G., Yang X., Li J., Yu L., Heng P.-A., and Zheng G., “3D U-net with multi-level deep supervision: fully automatic segmentation of proximal femur in 3D MR images,” in International workshop on machine learning in medical imaging, 2017, pp. 274–282. [Google Scholar]
36.Zhu Q., Du B., Turkbey B., Choyke P. L., and Yan P., “Deeply-supervised CNN for prostate segmentation,” in 2017 International Joint Conference on Neural Networks (Ijcnn), 2017, pp. 178–184. [Google Scholar]
37.He K., Zhang X., Ren S., and Sun J., “Delving deep into rectifiers: Surpassing human-level performance on imagenet classification,” in Proceedings of the IEEE international conference on computer vision, 2015, pp. 1026–1034. [Google Scholar]
38.Liu L., Jiang H., He P., Chen W., Liu X., Gao J., and Han J., “On the variance of the adaptive learning rate and beyond,” arXiv Prepr. arXiv1908.03265, 2019. [Google Scholar]
39.Thielscher A. and Kammer T., “Electric field properties of two commercial figure-8 coils in TMS: calculation of focality and efficiency,” Clin. Neurophysiol., vol. 115, no. 7, pp. 1697–1708, 2004. doi: 10.1016/j.clinph.2004.02.019 [DOI] [PubMed] [Google Scholar]
40.Deng Z.-D., Lisanby S. H., and V Peterchev A., “Electric field depth–focality tradeoff in transcranial magnetic stimulation: simulation comparison of 50 coil designs,” Brain Stimul., vol. 6, no. 1, pp. 1–13, 2013. doi: 10.1016/j.brs.2012.02.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
41.Tustison N. J. and Gee J. C., “Introducing Dice, Jaccard, and other label overlap measures to ITK,” Insight J, vol. 2, 2009. [Google Scholar]
42.Gomez L. J., Dannhauer M., Koponen L. M., and Peterchev A. V., “Conditions for numerically accurate TMS electric field simulation,” Brain Stimul., vol. 13, no. 1, pp. 157–166, 2020. doi: 10.1016/j.brs.2019.09.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
43.Nummenmaa A., McNab J. A., Savadjiev P., Okada Y., Hämäläinen M. S., Wang R., et al. , “Targeting of white matter tracts with transcranial magnetic stimulation,” Brain Stimul., vol. 7, no. 1, pp. 80–84, 2014. doi: 10.1016/j.brs.2013.10.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
44.Paszke A., Gross S., Massa F., Lerer A., Bradbury J., Chanan G., et al. , “PyTorch: An imperative style, high-performance deep learning library,” in Advances in Neural Information Processing Systems, 2019, pp. 8024–8035. [Google Scholar]
45.Gomez L.J., Dannhauer M., Peterchev A.V. Fast computational optimization of TMS coil placement for individualized electric field targeting. NeuroImage. 2021. Mar;228:117696. doi: 10.1016/j.neuroimage.2020.117696 [DOI] [PMC free article] [PubMed] [Google Scholar]
46.Daneshzand M., Makarov SN., de Lara LIN, Guerin B., McNab J., Rosen BR., et al. Rapid computation of TMS-induced E-fields using a dipole-based magnetic stimulation profile approach. Neuroimage. 2021. Apr 30:118097. doi: 10.1016/j.neuroimage.2021.118097 [DOI] [PMC free article] [PubMed] [Google Scholar]

PLoS One. doi: 10.1371/journal.pone.0254588.r001

Decision Letter 0

Dzung Pham

23 Dec 2020

PONE-D-20-30151

Toward real-time electric field mapping in transcranial magnetic stimulation using deep learning

PLOS ONE

Dear Dr. Ning,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process. In particular, both reviewers expressed significant concerns about the evaluation of the proposed approach, and a lack of comparison to competing methods. Both reviewers also raised questions about the methodology. Reviewer 1 further suggests a potential reframing of the primary results of the paper.

Please submit your revised manuscript by Feb 06 2021 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter. Guidelines for resubmitting your figure files are available below the reviewer comments at the end of this letter.

We look forward to receiving your revised manuscript.

Kind regards,

Dzung Pham

Academic Editor

PLOS ONE

Journal Requirements:

When submitting your revision, we need you to address these additional requirements.

1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at

https://journals.plos.org/plosone/s/file?id=wjVg/PLOSOne_formatting_sample_main_body.pdf and

https://journals.plos.org/plosone/s/file?id=ba62/PLOSOne_formatting_sample_title_authors_affiliations.pdf

2. Thank you for providing links to your data and code in your cover letter. We ask that you provide this information (" The data used in this paper are publicly available from the Human Connectome Project. The Python script used in this paper is available at Github via " ext-link-type="uri" xlink:type="simple">https://github.com/LipengNing/Efield.git."), along with a link to the Human Connectome Project in both your Data Availability Statement and your Methods section.

3. Please include captions for your Supporting Information files at the end of your manuscript, and update any in-text citations to match accordingly. Please see our Supporting Information guidelines for more information: http://journals.plos.org/plosone/s/supporting-information.

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: No

Reviewer #2: Partly

**********

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: N/A

Reviewer #2: Yes

**********

3. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: No

Reviewer #2: Yes

**********

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: Yes

Reviewer #2: Yes

**********

5. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: The manuscript left me with mixed feeling. It contains a good idea, but in its current state, it is unsuitable for publication.

First, the bad news: The authors use a DNN for approximate computation of a problem with known physics-based solution. They do not, however, compare their results to existing fast computation methods, but rather provide their ‘accuracy’ without any reference or comparison with either existing methods or requirements of the application the authors suggest the method to be used. The approach of using DNN to replace physics-based models is also questionable, see point 30 which paraphrases authors own critique of the earlier DNN work by (Yokota et al., 2019).

Then, the good news: their result with ‘T1-20’ model is interesting. This is an application where the DNN-based approach may shine. They did reach almost full accuracy of their approximate solver (with full input data) with limited input data. This should be the main result: with DNN, we can estimate the induced electric field of an anisotropic VCM without having to measure the anisotropy (which is expensive for subject-specific models). However, even with this change, the authors must perform additional comparisons. The accuracy of approximate DNN model must be compared to that of isotropic physics-based model. See my point 31. This alone is a reason I will currently have to suggest rejection, but most certainly with an option to resubmit.

Further, to ensure that the model is really robust to change of coil, the tested coil model should be fundamentally different from the teaching coil model. Now they are two figure-of-eight coils with fairly similar sizes (one step down in size). The testing coil could be, e.g., a circular coil or an H-coil.

Finally, it seems that the authors have used the SimNIBS with incorrect parameters (omit the T2 images, which is needed to correctly predict the thickness of the skull in the modelling pipeline). Thus, much of the results need to be re-computed.

I will begin with minor technical observations:

The authors, for no apparent reason, limit availability of their data. Their data availability statement has arbitrary requirement of “The data that support the findings of this study are available from the corresponding author upon *reasonable* request.” The authors provide no legal or ethical reason to limit access in this manner.

I further wonder why this work is submitted to PLOS ONE and not into some of the more specialized journals on neurostimulation methods.

Then, my other observations are in the order of their occurrence.

The abstract:

1. First sentence: TMS, in addition to being a ‘neuromodulation’ method is a ‘neurostimulation’ method. The latter is more descriptive, as neuromodulation is possible also with the subthreshold stimulation methods.

2. The second sentence is misleading: “Due to the complex structure of the brain and the electrical conductivity variation across different tissues, it is difficult to exactly identify the brain region stimulated by TMS, which is important to improve the treatment efficacy and understand the underlying mechanism.”

Even based on this work, this computation is very straightforward with readily available toolkits to compute this. Further, this work, at best tries to reproduce the accuracy of these existing methods. Hence, calling this problem difficult is misleading.

3. The “relative long computation time” is an incorrect claim. Realistic VCM models have been solved in under 25 ms, a further factor of 10 faster than the approximate solver shown in this work. And, compared to fast FEM implementations (such as the 3-second computation in Yokota et al., 2019) the authors speedup does not make a fundamental difference.

This is because the authors fail to define what they mean with “real-time computation”. Their computation speed is much lower than in any of the previous three methods for ‘real-time computations’ (the local spherical models, the previous magnitude-only isotropic-VCM DNN, or a hardware-accelerated, fast-quadrature, isotropic-5C-VCM BEM).

The authors current computation speed of 240 ms = 4.2 computations per second = 4.2 frames per second is still too slow for neuronavigation (where the operator needs a smooth feedback, at minimum at least 15 frames per second, i.e. below 67 ms, and ideally 30 or 60 frames per second, i.e., 33 ms and 17 ms, respectively).

The spherical model rans readily at these speeds, as did the earlier DNN which computed the fields in 10–30 ms (Yokota et al., 2019), or the real-time BEM which computed the fields in 15–23 ms based on it computing 46–65 coil positions per second (Stenroos Koponen, 2019).

In the current performance bracket, the model does not provide a quantitative improvement over the fast FEM solvers (about 3 s, not the number suggested in the work at 30-60 s), but is quantitatively too slow for the suggested ‘real-time’ application by a factor of at least 4.

4. Abbreviation FEM (finite element method) should be defined before its first use in the abstract.

Introduction:

5. Line 42: the TMS coil current is pulsed, not oscillating (which suggests a continuous stimulation instead of discrete pulses). Even at highest repetition rates, the duty cycle of TMS is less than 1%, and typically it is much less than 0.1%.

6. Line 52: the “multi-sphere method” is commonly known as “local sphere model”. This is also the case for the provided reference by the authors. Further, instead of the text-book chapter, the local spherical model should probably be attributed to its source, based on the book (Ilmoniemi et al., 1996), or as that work, similarly to the cited text-book chapter, is not readily available, their journal publication (Ilmoniemi et al., 1999).

7. Line 53: TMS-specific BEM should be attributed to more correct, older references such as (Salinas et al., 2009) or (Nummenmaa et al., 2013).

8. Line 54: TMS-specific FEM, similarly to above, should be attributed correctly (Miranda et al., 2003).

9. Line 54: remove word “sophisticated”, as it does not apply only to FEM VCM. The BEM VCM are equally, or sometimes even more sophisticated given the recent advanced in fast-multipole methods.

10. Further, related to the claim “but also anisotropic tissue conductivity, which cannot be done by other methods” (line 56), the authors glossed over FDM methods which can model the anisotropy (e.g., De Geeter et al., 2011). The authors further failed to justify why the anisotropy in particular is of such a high importance (given the uncertainty conductivity values, for both isotropic and anisotropic case).

11. Line 66: BEM is not an accelerating algorithm!

12. Further, the sentence in line 66 should contain both (Stenroos Koponen, 2019) and (Yokota et al., 2019), the existing real-time solvers.

13. Finally, I do not see any fundamental reason why (Laakso Hirata, 2012) could not include also the anisotropy. It is an FEM after all. They likely followed the common convention in TMS-stimulation literature of omitting the anisotropy as we do not really know the anisotropic conductivity tensor. (As the authors also admit when they slightly latter use one of the three rules of thumb, none of which is even based on the physics, of deriving the anisotropic conductivity values from the DTI data and the not-that-accurately-known isotropic conductivity value.)

14. Line 74: The authors again claim their method capable of real-time simulation in clinical and research setting despite it being too slow for the suggested real-time neuronavigation use.

15. Line 85: Overselling, every existing physics-based computation method (spherical models, FEMs, FDMs, BEMs) predicts the three-dimensional vector E-field: “In particular, our approach predicts the three-dimensional vector E-field instead of its magnitude.” The sole method that does not, is the previous DNN method by (Yokata et al., 2019).

16. Line 88: Advertising a weakness of the method as its strength. The ‘C-20’ and ‘C-60’ require much more time-consuming and costly DTI dataset of each individual TMS subject, compared to just T1 (and in most cases T2 for best quality) MRI. It is not a strength to require the extraordinarily high-resolution input files of the HCP, but a limitation: “Furthermore, both diffusion-MRI based conductivity tensors and T1w MRI, which integrate anisotropic conductivity of brain tissues, are used to predict the E-field.”

17. Line 90: Overselling similarly to point 15. All but the previous DNN method allow straightforward change of the coil model.

18. Lines 106–116: there are results at the end of introduction?

The methods or metrics such as “target overlapping coefficient” are not defined here!

This paragraph is entirely impossible to read for a person who has not read the rest of the work before returning here. It should be removed!

Oh, one final thing on this part: the 9-degree error is NOT much lower than a 13-degree error. They are about equal, and both are HORRIBLY BAD VALUES for such a simple quantity that can be modelled with physics-based models instead of DNN.

13-degree error is comparable to a one-shell model, and 9-degree error to omitting the whole of white matter altogether (Stenroos Koponen, 2019). This means that the “approximate DNN model with anisotropy” performs worse than much simpler and faster conventional physics-based models. This is despite requiring much more input data!

Considering this performance, or lack of thereof, the authors use FAR TOO BOLD words such as “the rich information” (line 114) and “ultra-short computational time” (line 114).

Further, if the computation time is from the extraordinarily expensive high-end GPU, it should not be used to describe the suitability to “clinical setting” (line 115).

PS. It is computation time, not computational time. This error repeats throughout the work.

Material and methods (at this point, I will shorten my observations, as I have written a tad overly long response already).

19. Line 124: define “the minimal processing pipeline” (reference or description)

20. Line 125: define “the native space” (the native space of what, a description)

21. Line 126: questionable use of SimNIBS. The VCM construction should be given both T1 and T2 images for better performance.

22. Line 126: Which SimNIBS version it was, and why there is no reference?

23. Line 128: Unnecessary sentence “We note that another command headreco can also be used to generate head models which may lead to different simulation results [Nielsen et al. 2018].”

24. Instead of unnecessary sentences like in point 23, the previous sentences should contain all relevant modelling parameters. (The work further glosses over the entire problem with selection of conductivity parameters, despite being about anisotropic conductivity, which is finicky to the choice of the isotropic baseline values.)

25. Line 137: You seem to provide exact details on version of MATLAB, but for some reason omit them from SimNIBS at all points.

26. Line 146: what does this sentence about the “average degree between the nearest handle directions being about 4.6 degrees” even mean?

27. Line 165: grossly incorrect statement. Just having the T1 image (or even the correct set for good VCM, i.e., T1 and T2) has nothing to do with not computing the direction of the E-field! Is this the reason for the ridiculous claim of point 15? The anisotropy has a (small compared to just the much larger isotropic conductivity differences) effect on the field directions. It is not a fundamental reason for the field directions. I refer now to sentence: “We note that the T1w MRI was used in [Yokota et al., 2019] to predict only the magnitude of the E-field since T1w MRI does not contain diffusion information about the axon orientation.”

28. Line 169: “field” not “filed”.

29. Line 169: I assume you refer to the spatial distribution of the change of the vector potential (dA/dt) at the beginning of the TMS pulse, and not peak temporal changes!

30. Line 177-179: The authors critique of (Yokota et al., 2019) could also be said about their own work! Let me paraphrase: “Thus, the DNN in (THE AUTHORS) is not a solver for the forward model but also needs to learn the well-known underlying physics of electromagnetic induction, which may reduce the prediction accuracy.”

This is basically my main critique of both this work and the work of (Yokota et al., 2019).

In their current state, both methods are FAR LESS accurate than any PHYSICS-BASED solvers. And, in the case of the present manuscript, they are also slower than properly implemented fast physics-based solvers. The approximation by (Yokota et al., 2019) was at least momentarily the fastest approach with more complex than spherical geometry, before being caught up and surpassed by the fast BEM solvers.

31. But, then the positive. Line 194: you actually, should the result survive through the proper cross-validation against the error for a SimNIBS model without the DTI data, try to make things that are not possible with a physics-based model.

The ‘T1-20’ model approximates the DTI dataset without needing one.

This result, however, will need to be compared to the computation against a physics-based model without the DTI data. As, if the physics-based model has prediction errors smaller than 13 degrees, then it is both faster more accurate than the proposed DNN-based model. Such comparison is missing, and without it, I will suggest rejection.

The approximation of the DTI data is only true if the ‘T1-20’ can perform better than just using a physics-based solver without the data. (For which the error is likely much less than 10 degrees.)

32. Line 231-233, rewrite this sentence to make sense of it.

33. Line 282: on scalp, not on skull.

34. Line 293: between E-field distributions, not between the brain regions.

35. Line 303: why is the word reference in quotation marks? Remove them.

36. Line 306-310: This error metric is incorrect, and underestimates the relevant prediction error. The correct method is to compute the magnitude of the vector difference (similarly to previous works with physics-based models).

Your method gives an error of 0 even if you would have predicted the field direction incorrectly by 180 degrees. (See the point about testing the coil with a different type of TMS coil, such as circular coil.)

37. Line 324: Comparing apples to oranges. The computation speed for the DNN is told with two flagship GPUs, and the computation speed for the (not exactly optimized for speed) FEM is told with an undisclosed hardware (probably no GPU acceleration).

38. Line 327: Repeating the incorrect claim that 240 ms computation is ‘real time”. The authors never mention what they actually mean with that. They give example of neuronavigation, for which such computation speed is too slow.

39. Line 339: Significantly as in statistical significance? Or, some other significance? If using the latter used criteria of visual indistinguishability, both are equally good, or rather bad.

Further, line 342: I saw not even a statistically significant difference between the results of C-20 and C-60?

40. Table is on line 345: Why is the angle error omitted from this table?

41. Line 354: what exactly do you mean with “almost visually indistinguishable”?

42. Line 362, figure 3: Is this the difference of fields or difference of magnitude of fields? If former, there is 10% errors in the fields? If latter, well…

43. Line 382: The angle errors are humongous. They are comparable to far simpler head models, not to some simple approximation. Compared to the approximation errors due to the fast quadrature of (Stenroos and Koponen, 2020), where the angle error was 0.1 degrees, the 9 degree and the 13 degree errors are unusable.

44. Line 393, table 2: the location error is also 10 mm even for the ‘C-60’. Such larger error is unusable for neuronavigation!

Also, based on this table, is the angle error rather not 14 degrees and not 13 degrees?

45. Line 407, table 3: the EPD, the correlation error, and the MDE are all unusably large! Such errors seem about the same as the error of a local sphere model? Compare to results of (Stenroos Koponen, 2019).

Discussion and conclusions:

46. Line 430: “novel advantages” what does this even mean?

47. Line 431: this is not a new feature: “First, it can be applied to predict E-field vector volumes with arbitrary coil positions and orientations”

48. Line 433: with angle error close to 10 degrees, I would not exactly call this accurate: “to accurately predict the magnitude and the direction of E-field.”

49. And, then line 439, compare to point 31. Basically, you show that your DNN is worse than a physics-based model, and not fundamentally faster. “Our work shows that deep learning can be further used as a solver for the forward model for estimating whole-brain E-field in TMS.”

I would like to point out that you have far more than 10 times more computational power than the fast-multigrid method by (Laakso and Hirata, 2012), which took just 3 s in (Yokota et al., 2019).

And, you do not even compare to such fast solver (~3 s), but rather compare your GPU-accelerated computation time to a not-optimized for real-time FEM without any GPU acceleration (30-60 s).

50. Line 444-448: No you did not show this. What was your reference model compared to which you showed that the FEM was accurate in its prediction? Did you test for the sensitivity of your solution to your input parameters (which you failed to disclose), or even just the model resolution?

51. Line 467: 9 degree error in volume is not similar in direction. It is horribly badly off.

52. Line 470: 13.7 degrees is not “as low as” but rather horribly bad prediction.

53. Line 473: how is this work applicable to clinical setting? Where do we get all the DTI data, and the computational resources?

54. Line 478: the computation time (not computational time) is not ultra-short.

55. Line 480: visualization in real-time might indeed be useful (not quite essential), but your work fails to deliver such speeds, unlike previous ‘real-time methods’

56. Line 483: Probably soon tenth repetition of this same line does not make it true. Please, do not oversell your work.

57. Line 487: Fundamental problem with understanding physics-based models. A FEM and a BEM will produce practically identical E-field predictions, e.g., (Gomez et al., 2020), and thus the DNN should not change based on which physics-based model it is trained on. This is the whole reason for physics-based models. We get the SAME result with a BEM as with a FEM, or an FDM (given adequate resolution for each).

This is why DNN is also inherently problematic for this type of problem. You essentially try to make it learn very well-known physics, instead of actually just using said physics to compute the result.

58. Line 490: There were other far more important fixed parameters than distance to scalp (which your dA/dt –based approach should in any case be fairly robust on). But then again, this revisits points 31, 57, etc.

DNN is fundamentally wrong tool for solving the forward problem. (The ‘T1-20’ to predict the DTI-FEM result is interesting, however. That is, if you compare it to no-DTI FEM to see if it can actually perform better.)

59. Line 490: for example, you now fix the conductivity parameters. And, of course you model only works for ‘normal’ brains. This makes the method unsuitable for, e.g., neuronavigation of persons with lesions etc. (which is where the physics-based models excel).

60. Line 490: based on what data is the DNN expected to be robust against the change of the long list of parameters you fail to mention at any point in the manuscript?

Reviewer #2: This paper introduces a novel U-net architecture for realtime Efield analysis of TMS. The manuscript is well written and their methods technically sound. However, some important issues need to be addressed:

1) Since they are claiming this is accurate they should mathematically define all of their error metrics.

2) The authors do not compare to standard error metrics like L2, pointwise error like in https://doi.org/10.1016/j.brs.2019.09.015 . Also, others like RDM. What is the relative performance to existing methods.

3) How long does it take to compute dA/dt?;this should be included in computation time.

4) This method has not been trained with different coils, how do we know the trained network will generalize to other coils?

5) In a sense when you move the coil the dA/dt is moved; this is equivalent to moving the brain. So their claim that passing these maps changes something needs a deeper rationale.

6) is the DNN computing both primary plus secondary E-field or just secondary?

**********

6. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email PLOS at figures@plos.org. Please note that Supporting Information files do not need this step.

PLoS One. 2021 Jul 30;16(7):e0254588. doi: 10.1371/journal.pone.0254588.r002

Author response to Decision Letter 0

20 Apr 2021

Please find our response letter to the reviewers in the attached files.

Attachment

Submitted filename: PlosOne_Response_v3.pdf

Click here for additional data file.^{(1.6MB, pdf)}

PLoS One. doi: 10.1371/journal.pone.0254588.r003

Decision Letter 1

Dzung Pham

9 Jun 2021

PONE-D-20-30151R1

Rapid whole-brain electric field mapping in transcranial magnetic stimulation using deep learning

PLOS ONE

Dear Dr. Ning,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process. Overall, there remains some difference of opinion among the reviewers on the value of this contribution and the use of deep neural networks (DNNs) for E-field modeling. In particular, as FEM/BEM models continue to improve in speed, it is not clear what niche is filled by DNN approaches. In addition to responding to reviewer comments, I suggest that the following revisions be made to the manuscript:

Please cite the references provided by Reviewer 4 and briefly discuss contributions of the proposed method compared to these references.
Please add a brief discussion on the future of DNN approaches against accelerated FEM/BEM models for E-field modeling.

Please submit your revised manuscript by Jul 24 2021 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

If applicable, we recommend that you deposit your laboratory protocols in protocols.io to enhance the reproducibility of your results. Protocols.io assigns your protocol its own identifier (DOI) so that it can be cited independently in the future. For instructions see: http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols. Additionally, PLOS ONE offers an option for publishing peer-reviewed Lab Protocol articles, which describe protocols hosted on protocols.io. Read more information on sharing protocols at https://plos.org/protocols?utm_medium=editorial-emailutm_source=authorlettersutm_campaign=protocols.

We look forward to receiving your revised manuscript.

Kind regards,

Dzung Pham

Academic Editor

PLOS ONE

Journal Requirements:

Please review your reference list to ensure that it is complete and correct. If you have cited papers that have been retracted, please include the rationale for doing so in the manuscript text, or remove these references and replace them with relevant current references. Any changes to the reference list should be mentioned in the rebuttal letter that accompanies your revised manuscript. If you need to cite a retracted article, indicate the article’s retracted status in the References list and also include a citation and full reference for the retraction notice.

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. If the authors have adequately addressed your comments raised in a previous round of review and you feel that this manuscript is now acceptable for publication, you may indicate that here to bypass the “Comments to the Author” section, enter your conflict of interest statement in the “Confidential to Editor” section, and submit your "Accept" recommendation.

Reviewer #2: All comments have been addressed

Reviewer #3: All comments have been addressed

Reviewer #4: (No Response)

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #2: Yes

Reviewer #3: Yes

Reviewer #4: No

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #2: Yes

Reviewer #3: Yes

Reviewer #4: Yes

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #2: Yes

Reviewer #3: Yes

Reviewer #4: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #2: Yes

Reviewer #3: Yes

Reviewer #4: Yes

**********

6. Review Comments to the Author

Reviewer #2: (No Response)

Reviewer #3: In this study, authors propose a method to estimate the induced E-field from the magnetic field generated by TMS coil and the MRI image, using the framework of deep learning. Since the E-field can be estimated by the forward calculation of DNN without solving the problem, the estimation can be significantly accelerated than the FEM. In the experiment, the proposed DNN is evaluated by several metrics, and the effectiveness of the proposed method is confirmed.

To my understanding, the most relevant paper to this study is [21] by Yokota et al at 2019. In terms of TMS-induced E-field estimation using DNN, this study can be considered as a kind of next step of original one [21]. The main new contributions are three folds: (1) estimation of a whole brain region, (2) vector field estimation, and (3) magnetic filed representation of TMS coil parameters.

Contributions (1) and (2) are relatively weak because both vector and whole brain extensions are straightforward by introducing some powerful computational resources. On the contrary, since weak E-fields is often majority in whole brain, the necessity of whole region estimation is unclear for TMS targeting. Moreover, the requirement of the large DNN model with powerful computation (i.e., large memory of GPU) reduces practical usefulness. That is always trade-off.

The contribution (3) is important and it make the paper acceptable in my opinion. By introducing magnetic field representation of TMS coil parameter, the DNN can be trained and applied for various types of coils. It is nice that some computational experiments have conducted by using three different coils. However, it is necessary to care that the overfitting is more easily cased in the proposed framework becasue input space is quite larger than original one [21].

Reviewer #4: Comments on the paper “Rapid whole-brain electric field mapping in transcranial magnetic stimulation using deep learning”

This is a modeling study which aims to use a neural network (DNN) to predict the TMS fields in subjects in a real time. It essentially develops the idea of Ref. [21] with an extra inclusion of the primary TMS field as an input. 65 Connectome subjects and the SimNIBS FEM solver have been used to perform numerical experiments.

While the original idea is interesting, the reviewer still tends to agree with the previous review #1 saying that “The DNN is inherently problematic for this type of problem”.

The first reason is that it is obviously hardly possible to replicate a unique gyral pattern of a subject which, in its turn, uniquely defines the resulting TMS field, based on limited numbers of computations for other subjects (20 or 60 in the paper). Even for those numbers, training the DNN takes weeks, according to the paper, and requires a specially equipped workstation.

The second reason is that, according to the manuscript, after the several weeks (!) of training, the approximate TMS field could be predicted in 0.24 sec. However, the paper does not compare this finding to the performance of the modern physical solvers, which estimate the TMS fields precisely.

As a first example, a new precise physical approach of Gomez et al

[Gomez LJ, Dannhauer M, Peterchev AV. Fast computational optimization of TMS coil placement for individualized electric field targeting. NeuroImage. 2021 Mar;228:117696. doi: 10.1016/j.neuroimage.2020.117696.] allows us to predict the E-fields generated in an MRI-derived head model when the coil is placed at 5900 different scalp positions and 360 coil orientations per position (over 2.1 million unique configurations) under 15 min on a standard laptop computer. This performance of the exact FEM physical solver simply cannot be matched to the approximate results reported by the authors.

As a second example, another new physical approach of Daneshzand et al

[Daneshzand M, Makarov SN, de Lara LIN, Guerin B, McNab J, Rosen BR, Hämäläinen MS, Raij T, Nummenmaa A. Rapid computation of TMS-induced E-fields using a dipole-based magnetic stimulation profile approach. Neuroimage. 2021 Apr 30:118097. doi: 10.1016/j.neuroimage.2021.118097.] allows computation of the E-field in ∼100 ms given ~5 hours of preprocessing time. This performance of the exact BEM physical solver cannot again be matched to the approximate results reported by the authors.

Compared to these studies, the suggested approach seems to be a step back as being less accurate and significantly more lengthy.

Minor comment:

1. Why is Ernie (one model) compared to the entire HCP dataset?

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #2: No

Reviewer #3: No

Reviewer #4: No

PLoS One. 2021 Jul 30;16(7):e0254588. doi: 10.1371/journal.pone.0254588.r004

Author response to Decision Letter 1

23 Jun 2021

See the attached response-to-reviewers letter.

Attachment

Submitted filename: Response to Reviewers.pdf

Click here for additional data file.^{(59.1KB, pdf)}

PLoS One. doi: 10.1371/journal.pone.0254588.r005

Decision Letter 2

Dzung Pham

30 Jun 2021

Rapid whole-brain electric field mapping in transcranial magnetic stimulation using deep learning

PONE-D-20-30151R2

Dear Dr. Ning,

We’re pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it meets all outstanding technical requirements.

Within one week, you’ll receive an e-mail detailing the required amendments. When these have been addressed, you’ll receive a formal acceptance letter and your manuscript will be scheduled for publication.

An invoice for payment will follow shortly after the formal acceptance. To ensure an efficient process, please log into Editorial Manager at http://www.editorialmanager.com/pone/, click the 'Update My Information' link at the top of the page, and double check that your user information is up-to-date. If you have any billing related questions, please contact our Author Billing department directly at authorbilling@plos.org.

If your institution or institutions have a press office, please notify them about your upcoming paper to help maximize its impact. If they’ll be preparing press materials, please inform our press team as soon as possible -- no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact onepress@plos.org.

Kind regards,

Dzung Pham

Academic Editor

PLOS ONE

Additional Editor Comments (optional):

Reviewers' comments:

PLoS One. doi: 10.1371/journal.pone.0254588.r006

Acceptance letter

Dzung Pham

21 Jul 2021

PONE-D-20-30151R2

Rapid whole-brain electric field mapping in transcranial magnetic stimulation using deep learning

Dear Dr. Ning:

I'm pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.

If your institution or institutions have a press office, please let them know about your upcoming paper now to help maximize its impact. If they'll be preparing press materials, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact onepress@plos.org.

If we can help with anything else, please email us at plosone@plos.org.

Thank you for submitting your work to PLOS ONE and supporting open access.

Kind regards,

PLOS ONE Editorial Office Staff

on behalf of

Dr Dzung Pham

Academic Editor

PLOS ONE

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

S1 File

(PDF)

Click here for additional data file.^{(7.3MB, pdf)}

S1 Video

(AVI)

Click here for additional data file.^{(2.2MB, avi)}

Attachment

Submitted filename: PlosOne_Response_v3.pdf

Click here for additional data file.^{(1.6MB, pdf)}

Attachment

Submitted filename: Response to Reviewers.pdf

Click here for additional data file.^{(59.1KB, pdf)}

Data Availability Statement

All data used in this study are freely available from public website. Results and code from this paper are available at https://github.com/LipengNing/Efield.

[pone.0254588.ref001] 1.Camprodon J. A. and Pascual-Leone A., “Multimodal applications of transcranial magnetic stimulation for circuit-based psychiatry,” JAMA psychiatry, vol. 73, no. 4, pp. 407–408, 2016. doi: 10.1001/jamapsychiatry.2015.3127 [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref002] 2.Saturnino G. B., Madsen K. H., and Thielscher A., “Electric field simulations for transcranial brain stimulation using FEM: an efficient implementation and error analysis.,” J. Neural Eng., vol. 16, no. 6, p. 66032, 2019. doi: 10.1088/1741-2552/ab41ba [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref003] 3.Lee E. G., Rastogi P., Hadimani R. L., Jiles D. C., and Camprodon J. A., “Impact of non-brain anatomy and coil orientation on inter-and intra-subject variability in TMS at midline,” Clin. Neurophysiol., vol. 129, no. 9, pp. 1873–1883, 2018. doi: 10.1016/j.clinph.2018.04.749 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0254588.ref004] 4.Bakir A. A., Bai S., Lovell N. H., Martin D., Loo C., and Dokos S., “Finite Element Modelling Framework for Electroconvulsive Therapy and Other Transcranial Stimulations,” in Brain and Human Body Modeling, Springer, 2019, pp. 27–47. [PubMed] [Google Scholar]

[pone.0254588.ref005] 5.Saturnino G. B., Thielscher A., Madsen K. H., Knösche T. R., and Weise K., “A principled approach to conductivity uncertainty analysis in electric field calculations,” Neuroimage, vol. 188, pp. 821–834, 2019. doi: 10.1016/j.neuroimage.2018.12.053 [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref006] 6.Ilmoniemi F. J., Ruohonen J., and Karhu J., “Transcranial magnetic stimulation–A new tool for functional imaging,” Crit. Rev. Biomed. Eng, vol. 27, pp. 241–284, 1999. [PubMed] [Google Scholar]

[pone.0254588.ref007] 7.Hannula H. and Ilmoniemi R. J., “Basic principles of navigated TMS,” in Navigated transcranial magnetic stimulation in neurosurgery, Springer, 2017, pp. 3–29. [Google Scholar]

[pone.0254588.ref008] 8.Salinas F. S., Lancaster J. L., and Fox P. T., “3D modeling of the total electric field induced by transcranial magnetic stimulation using the boundary element method,” Phys. Med. Biol., vol. 54, no. 12, p. 3631, 2009. doi: 10.1088/0031-9155/54/12/002 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0254588.ref009] 9.Nummenmaa A., Stenroos M., Ilmoniemi R. J., Okada Y. C., Hämäläinen M. S., and Raij T., “Comparison of spherical and realistically shaped boundary element head models for transcranial magnetic stimulation navigation,” Clin. Neurophysiol., vol. 124, no. 10, pp. 1995–2007, 2013. doi: 10.1016/j.clinph.2013.04.019 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0254588.ref010] 10.Miranda P. C., Hallett M., and Basser P. J., “The electric field induced in the brain by magnetic stimulation: a 3-D finite-element analysis of the effect of tissue heterogeneity and anisotropy,” IEEE Trans. Biomed. Eng., vol. 50, no. 9, pp. 1074–1085, 2003. doi: 10.1109/TBME.2003.816079 [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref011] 11.Nielsen J. D., Madsen K. H., Puonti O., Siebner H. R., Bauer C., Madsen C. G., et al. , “Automatic skull segmentation from MR images for realistic volume conductor models of the head: Assessment of the state-of-the-art,” Neuroimage, vol. 174, pp. 587–598, 2018. doi: 10.1016/j.neuroimage.2018.03.001 [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref012] 12.Windhoff M., Opitz A., and Thielscher A., “Electric field calculations in brain stimulation based on finite elements: an optimized processing pipeline for the generation and usage of accurate individual head models,” Hum. Brain Mapp., vol. 34, no. 4, pp. 923–935, 2013. doi: 10.1002/hbm.21479 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0254588.ref013] 13.Åström M., Lemaire J.-J., and Wårdell K., “Influence of heterogeneous and anisotropic tissue conductivity on electric field distribution in deep brain stimulation,” Med. Biol. Eng. Comput., vol. 50, no. 1, pp. 23–32, 2012. doi: 10.1007/s11517-011-0842-z [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref014] 14.Shahid S. S., Bikson M., Salman H., Wen P., and Ahfock T., “The value and cost of complexity in predictive modelling: role of tissue anisotropic conductivity and fibre tracts in neuromodulation,” J. Neural Eng., vol. 11, no. 3, p. 36002, 2014. doi: 10.1088/1741-2560/11/3/036002 [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref015] 15.Saturnino G. B., Puonti O., Nielsen J. D., Antonenko D., Madsen K. H., and Thielscher A., “SimNIBS 2.1: a comprehensive pipeline for individualized electric field modelling for transcranial brain stimulation,” in Brain and Human Body Modeling, Springer, 2019, pp. 3–25. doi: 10.1007/978-3-030-21293-3_1 [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref016] 16.Fischl B., “FreeSurfer,” Neuroimage, vol. 62, no. 2, pp. 774–781, 2012. doi: 10.1016/j.neuroimage.2012.01.021 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0254588.ref017] 17.Smith S. M., Jenkinson M., Woolrich M. W., Beckmann C. F., Behrens T. E. J., Johansen-Berg H., Bannister P. R., De Luca M., Drobnjak I., and Flitney D. E., “Advances in functional and structural MR image analysis and implementation as FSL,” Neuroimage, vol. 23, pp. S208–S219, 2004. doi: 10.1016/j.neuroimage.2004.07.051 [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref018] 18.Penny W. D., Friston K. J., Ashburner J. T., Kiebel S. J., and Nichols T. E., Statistical parametric mapping: the analysis of functional brain images. Elsevier, 2011. [Google Scholar]

[pone.0254588.ref019] 19.Thielscher A., Antunes A., and Saturnino G. B., “Field modeling for transcranial magnetic stimulation: a useful tool to understand the physiological effects of TMS?,” in 2015 37th annual international conference of the IEEE engineering in medicine and biology society (EMBC), 2015, pp. 222–225. doi: 10.1109/EMBC.2015.7318340 [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref020] 20.Laakso I. and Hirata A., “Fast multigrid-based computation of the induced electric field for transcranial magnetic stimulation,” Phys. Med. Biol., vol. 57, no. 23, p. 7753, 2012. doi: 10.1088/0031-9155/57/23/7753 [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref021] 21.Yokota T., Maki T., Nagata T., Murakami T., Ugawa Y., Laakso I., et al. , “Real-Time Estimation of Electric Fields Induced by Transcranial Magnetic Stimulation with Deep Neural Networks,” Brain Stimul., vol. 12, no. 6, pp. 1500–1507, 2019. doi: 10.1016/j.brs.2019.06.015 [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref022] 22.Stenroos M. and Koponen L. M., “Real-time computation of the TMS-induced electric field in a realistic head model,” Neuroimage, p. 116159, 2019. doi: 10.1016/j.neuroimage.2019.116159 [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref023] 23.De Geeter N., Crevecoeur G., Leemans A., and Dupré L., “Effective electric fields along realistic DTI-based neural trajectories for modelling the stimulation mechanisms of TMS,” Phys. Med. Biol., vol. 60, no. 2, p. 453, 2014. doi: 10.1088/0031-9155/60/2/453 [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref024] 24.Lee C.-Y., Xie S., Gallagher P., Zhang Z., and Tu Z., “Deeply-supervised nets,” in Artificial intelligence and statistics, 2015, pp. 562–570. [Google Scholar]

[pone.0254588.ref025] 25.Dou Q., Yu L., Chen H., Jin Y., Yang X., Qin J., and Heng P.-A., “3D deeply supervised network for automated segmentation of volumetric medical images,” Med. Image Anal., vol. 41, pp. 40–54, 2017. doi: 10.1016/j.media.2017.05.001 [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref026] 26.Çiçek Ö., Abdulkadir A., Lienkamp S. S., Brox T., and Ronneberger O., “3D U-net: Learning dense volumetric segmentation from sparse annotation,” in Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 2016, vol. 9901 LNCS. [Google Scholar]

[pone.0254588.ref027] 27.Van Essen D. C., Ugurbil K., Auerbach E., Barch D., Behrens T. E. J., Bucholz R., et al. , “The Human Connectome Project: a data acquisition perspective,” Neuroimage, vol. 62, no. 4, pp. 2222–2231, 2012. doi: 10.1016/j.neuroimage.2012.02.018 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0254588.ref028] 28.Sotiropoulos S. N., Jbabdi S., Xu J., Andersson J. L., Moeller S., Auerbach E. J., et al. , “Advances in diffusion MRI acquisition and processing in the Human Connectome Project,” Neuroimage, vol. 80, pp. 125–143, 2013. doi: 10.1016/j.neuroimage.2013.05.057 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0254588.ref029] 29.Dale A. M., Fischl B., and Sereno M. I., “Cortical surface-based analysis: I. Segmentation and surface reconstruction,” Neuroimage, vol. 9, no. 2, pp. 179–194, 1999. doi: 10.1006/nimg.1998.0395 [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref030] 30.Opitz A., Windhoff M., Heidemann R. M., Turner R., and Thielscher A., “How the brain tissue shapes the electric field induced by transcranial magnetic stimulation,” Neuroimage, vol. 58, no. 3, pp. 849–859, 2011. doi: 10.1016/j.neuroimage.2011.06.069 [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref031] 31.Güllmar D., Haueisen J., and Reichenbach J. R., “Influence of anisotropic electrical conductivity in white matter tissue on the EEG/MEG forward and inverse solution. A high-resolution whole head simulation study,” Neuroimage, vol. 51, no. 1, pp. 145–163, 2010. doi: 10.1016/j.neuroimage.2010.02.014 [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref032] 32.Yu L., Yang X., Chen H., Qin J., and Heng P. A., “Volumetric convnets with mixed residual connections for automated prostate segmentation from 3d MR images,” 31st AAAI Conf. Artif. Intell. AAAI 2017, pp. 66–72, 2017. [Google Scholar]

[pone.0254588.ref033] 33.He K., Zhang X., Ren S., and Sun J., “Deep Residual Learning for Image Recognition,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778. [Google Scholar]

[pone.0254588.ref034] 34.Lee K., Zung J., Li P., Jain V., and Seung H. S., “Superhuman accuracy on the SNEMI3D connectomics challenge,” arXiv Prepr. arXiv1706.00120, 2017. [Google Scholar]

[pone.0254588.ref035] 35.Zeng G., Yang X., Li J., Yu L., Heng P.-A., and Zheng G., “3D U-net with multi-level deep supervision: fully automatic segmentation of proximal femur in 3D MR images,” in International workshop on machine learning in medical imaging, 2017, pp. 274–282. [Google Scholar]

[pone.0254588.ref036] 36.Zhu Q., Du B., Turkbey B., Choyke P. L., and Yan P., “Deeply-supervised CNN for prostate segmentation,” in 2017 International Joint Conference on Neural Networks (Ijcnn), 2017, pp. 178–184. [Google Scholar]

[pone.0254588.ref037] 37.He K., Zhang X., Ren S., and Sun J., “Delving deep into rectifiers: Surpassing human-level performance on imagenet classification,” in Proceedings of the IEEE international conference on computer vision, 2015, pp. 1026–1034. [Google Scholar]

[pone.0254588.ref038] 38.Liu L., Jiang H., He P., Chen W., Liu X., Gao J., and Han J., “On the variance of the adaptive learning rate and beyond,” arXiv Prepr. arXiv1908.03265, 2019. [Google Scholar]

[pone.0254588.ref039] 39.Thielscher A. and Kammer T., “Electric field properties of two commercial figure-8 coils in TMS: calculation of focality and efficiency,” Clin. Neurophysiol., vol. 115, no. 7, pp. 1697–1708, 2004. doi: 10.1016/j.clinph.2004.02.019 [DOI] [PubMed] [Google Scholar]

[pone.0254588.ref040] 40.Deng Z.-D., Lisanby S. H., and V Peterchev A., “Electric field depth–focality tradeoff in transcranial magnetic stimulation: simulation comparison of 50 coil designs,” Brain Stimul., vol. 6, no. 1, pp. 1–13, 2013. doi: 10.1016/j.brs.2012.02.005 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0254588.ref041] 41.Tustison N. J. and Gee J. C., “Introducing Dice, Jaccard, and other label overlap measures to ITK,” Insight J, vol. 2, 2009. [Google Scholar]

[pone.0254588.ref042] 42.Gomez L. J., Dannhauer M., Koponen L. M., and Peterchev A. V., “Conditions for numerically accurate TMS electric field simulation,” Brain Stimul., vol. 13, no. 1, pp. 157–166, 2020. doi: 10.1016/j.brs.2019.09.015 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0254588.ref043] 43.Nummenmaa A., McNab J. A., Savadjiev P., Okada Y., Hämäläinen M. S., Wang R., et al. , “Targeting of white matter tracts with transcranial magnetic stimulation,” Brain Stimul., vol. 7, no. 1, pp. 80–84, 2014. doi: 10.1016/j.brs.2013.10.001 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0254588.ref044] 44.Paszke A., Gross S., Massa F., Lerer A., Bradbury J., Chanan G., et al. , “PyTorch: An imperative style, high-performance deep learning library,” in Advances in Neural Information Processing Systems, 2019, pp. 8024–8035. [Google Scholar]

[pone.0254588.ref045] 45.Gomez L.J., Dannhauer M., Peterchev A.V. Fast computational optimization of TMS coil placement for individualized electric field targeting. NeuroImage. 2021. Mar;228:117696. doi: 10.1016/j.neuroimage.2020.117696 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0254588.ref046] 46.Daneshzand M., Makarov SN., de Lara LIN, Guerin B., McNab J., Rosen BR., et al. Rapid computation of TMS-induced E-fields using a dipole-based magnetic stimulation profile approach. Neuroimage. 2021. Apr 30:118097. doi: 10.1016/j.neuroimage.2021.118097 [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Rapid whole-brain electric field mapping in transcranial magnetic stimulation using deep learning

Guoping Xu

Yogesh Rathi

Joan A Camprodon

Hanqiang Cao

Lipeng Ning

Roles

Abstract

Introduction

Materials and methods

MRI data and VCM

E-field simulation

Training and prediction strategies

Network architecture

Fig 1. Illustration of the architect of 3D-MSResUnet.

Learning strategy

Testing methods

HCP testing subjects

On the dependence of coils

On the dependence of imaging protocols

On the dependence of coil positions

Evaluation metrics

Target overlapping coefficient (TOC)

E-field peak distance (EPD)

E-field similarity

Mean absolute error (MAE) and mean relative error (MRE)

Mean directional error (MDE)

Results

On network training

Fig 2. The training loss for the four DNNs in each iteration.

Surface-space evaluations

Fig 3. The magnitude [V/m] of E-field from VCM (the first column) and C-60 (the middle column), and the absolute difference between VCM and C-60 (the last column) with the Magstim-70mm-Fig8 placed at three positions of one testing subject.

Volume-space evaluations

Table 2. Performance of the models using independent HCP datasets.

Table 3. Performance of the C-60 model using different coils for the HCP and Ernie dataset.

Fig 4. The magnitude [V/m] of E-field from VCM (the first column) and C-60 (the middle column), and the absolute difference between VCM and C-60 (the last column) for three types of TMS coils placed at the same position of a testing subject of the HCP dataset.

Topographical illustrations

Fig 5. The distribution of TOC, EPD, Correlation and MAE [mV/m] on EEG position with C-60 model on the surface space.

Discussion and conclusions

Conductivity map vs T1w MRI

On the dependence on positions, coils and imaging protocols

On localization accuracy

On prediction speed

Supporting information

Acknowledgments

Data Availability

Funding Statement

References

Decision Letter 0

Dzung Pham

Roles

Author response to Decision Letter 0

Decision Letter 1

Dzung Pham

Roles

Author response to Decision Letter 1

Decision Letter 2

Dzung Pham

Roles

Acceptance letter

Dzung Pham

Roles

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Conductivity map vs T_1w MRI