Abstract
Bayesian causal inference offers a principled approach to policy evaluation of proposed interventions on mediators or time-varying exposures. Building on the Bayesian g-formula method introduced by Keil et al., we outline a general approach for the estimation of population-level causal quantities involving dynamic and stochastic treatment regimes, including regimes related to mediation estimands such as natural direct and indirect effects. We further extend this approach to propose a Bayesian data fusion (BDF), an algorithm for performing probabilistic sensitivity analysis when a confounder unmeasured in a primary data set is available in an external data source. When the relevant relationships are causally transportable between the two source populations, BDF corrects confounding bias and supports causal inference and decision-making within the main study population without sharing of the individual-level external data set. We present results from a simulation study comparing BDF to two common frequentist correction methods for unmeasured mediator-outcome confounding bias in the mediation setting. We use these methods to analyze data on the role of stage at cancer diagnosis in contributing to Black-White colorectal cancer survival disparities.
Keywords: causal inference, data fusion, g-formula, mediation, racial disparities, unmeasured confounding
1 |. INTRODUCTION
The value of causal evidence from a statistical analysis depends on the quality and suitability of the data source. In the era of Big Data, many large data sources valuable for health research are used in ways that were not foreseen by the original collectors and are often missing one or more key covariates. For example, electronic health records and tumor registries may lack important socioeconomic and behavioral factors. If these unmeasured factors act as confounders of the relationship(s) of interest, causal quantities may not be estimated using the observed data, regardless of the sample size.
Analyses leveraging the rich, longitudinal nature of data sources like electronic health records are still vulnerable to time-varying confounding by unmeasured variables. Proper control of confounding is particularly difficult when exposure status changes over time, with later exposure determined in part by covariates influenced by previous exposure. For example, doctors often tailor treatment based on patient history and current health state. Analogous problems arise in the context of mediation analysis, within which the temporal ordering of treatments, mediators, and outcomes can yield structures analogous to time-varying exposures.
When missing important confounders, researchers typically conduct sensitivity analyses to assess whether bias due to the unmeasured confounding is likely to alter the substantive conclusions of the research. Recent methodological advances have identified sharp nonparametric bounds for common causal estimands such as average treatment effects (Ding and VanderWeele, 2016) and various mediation quantities (Ding and Vanderweele, 2016). Bias correction formulae adjust point estimates and confidence intervals based on bias values found in the literature (VanderWeele and Chiba, 2014; VanderWeele, 2015). Without information about the sources of confounding, they can be used to determine the strength of confounding needed to obtain the observed result when the truth is below some practical or statistical threshold. Individual approaches may require rare outcomes, specific link functions, or assumptions about effect modification (VanderWeele, 2015). With notable exceptions (Robins et al., 2000; Greenland, 2005; McCandless and Somers, 2017), correction methods rarely incorporate uncertainty surrounding the bias parameters. We contribute to the literature offering practical guidance in longitudinal settings or those with arbitrary confounding structures (Scharfstein et al., 1999; Tchetgen Tchetgen and Shpitser, 2012).
Fortunately, the era of Big Data is also the era of abundant data. Relationships among the outcome, confounders, and exposure of interest can be found in alternative data sets, though these sources may not be as representative of the target population as the main source. A literature on data fusion methods has arisen to meet the need to combine information from multiple sources (Bareinboim and Pearl, 2016). Recent authors have proposed Bayesian variable selection methods with validation data sets (Antonelli et al., 2017) and integration of information measured on different levels (Jackson et al., 2006).
The motivating study for our work concerns the investigation of the causal impact of stage at diagnosis in explaining Black-White racial disparities in overall survival among colorectal cancer patients. This involves estimating a variant of the randomized interventional analog to the natural direct effect, the “residual disparity” that would remain after an intervention that fixes the stage at diagnosis distribution in the Black population to match the one observed in the White population (VanderWeele and Robinson, 2014). Valeri et al. (2016) estimated this quantity using a U.S. cancer registry. Causal interpretability of that estimated requires complete adjustment for confounding of the stage-survival relationship. The analysis controlled for numerous confounders but not household-level poverty status—which was unavailable—potentially leading to bias due to unmeasured confounding. Fortunately, information on household-level poverty was collected in a separate, high-quality cohort study of cancer patients. Our goal was to incorporate information from this cohort study into the registry study analysis to reduce or eliminate the bias in the estimated residual disparity without the need to share individual-level data.
To address this question, we propose a general frame-work for incorporating information from external data sources to perform sensitivity analyses for unmeasured confounding. We first extend an existing Bayesian g-formula approach that adjusts for confounding using parametric models for covariate standardization (Keil et al., 2015) to the estimation of dynamic and stochastic treatment regimes, mediation contrasts, and direct and indirect effects in disparities research. We then outline a probabilistic sensitivity analysis that we refer to as Bayesian data fusion (BDF). If causal transportability holds (Pearl and Bareinboim, 2011), the method corrects for unmeasured confounding by generating informative priors using external data sources. We compare this data fusion approach with traditional sensitivity analysis techniques, paying particular attention to potential violations of causal transportability. Unlike existing approaches, these Bayesian g-formula methods generalize to accommodate unmeasured confounding of many different types, including time-varying confounding found in mediation and the analysis of longitudinal treatments.
Our paper is organized as follows. Section 2 develops a Bayesian g-method for the estimation of population average effects involving dynamic and stochastic treatment assignment mechanisms. Section 3 introduces Bayesian data fusion, an approach to conduct probabilistic sensitivity analysis for Bayesian g-estimators using informative priors derived from external data. This approach applies to contrasts involving dynamic and stochastic regimes—including mediation estimands—as well as static and deterministic regimes. A simulation study comparing Bayesian data fusion to traditional sensitivity analysis approaches is given in Section 4. In Section 5, we use the data fusion method from Section 3 to augment cancer registry data with information from a cohort study in order to evaluate the role of stage at diagnosis in explaining Black-White disparities in colorectal cancer survival. We conclude with a discussion in Section 6.
2 |. EXTENDING THE BAYESIAN G-FORMULA TO STATIC AND DYNAMIC REGIMES
2.1 |. Causal notation and assumptions
Let Y denote the observed outcome of interest in a causal graph G, with the central scientific question concerning two intervention regimes g and g′. One of these regimes may correspond to the “natural” assignment mechanism that generated the observed data. Let V be the intervention set (i.e., the nodes intervened on by either g or g′), and let Z be the set of baseline confounders and post-treatment variables not influenced by treatment. Let W be the set containing all other nodes in G, in which case W includes any variable influenced by treatment but not of primary interest (i.e., not the outcome Y) or directly intervened upon (i.e., W ∉ V). The complete set of observed data is O = (Z, V, W, Y). Let Yg denote the potential outcome for Y under regime g, with the causal contrast of interest . Depending on the specifics of the regime, mediators of the treatment-outcome relationship may either be in the set W or V. Potential outcomes for W and V under regime g are denoted by Wg and Vg. When one mediator is of primary interest, we will denote it by M. Throughout this paper, we must assume Bayesian analogs to positivity and consistency (Keil et al., 2015), plus exchangeability conditional on observed variables and correct specification of all parametric models. Formal statements of these four assumptions can be found in the Web Appendix A. Additional assumptions needed for the data fusion method proposed in Section 3 are stated in Section 3.1.
2.2 |. Static and deterministic treatment regimes
After adopting parametric models indexed by the parameter vector θ, the Bayesian g-formula algorithm outlined by Keil et al. (2015) gives the posterior predictive distribution for a newly observed outcome Y under intervention regime g0 ∈ {g, g′} as , where π(θ|o) is the posterior of the parameters θ given the observed data O. The posterior distribution of the causal effect τ is therefore . Keil and colleagues outline a simulation-based algorithm for estimating causal contrasts for static regimes. To facilitate our extension to the mediation setting, we introduce different notation to emphasize the distinction between covariates Z that are unaffected by treatment and covariates W that are caused by one or more variables in the intervention set. For parametric models p(z|θz), p(w|v, z, θw), and p(y|w, v, z, θY). Then the likelihood for the complete parameter vector θ = (θZ, θW, θY) is given by . We assume that θY, θw, θZ are independent a priori such that π(θ) = π(θY) × π(θw) × π(θX). The resulting parameter posterior is , and the posterior predictive distribution for the outcome under regime g0 ∈ {g, g′} is
| (1) |
We now develop a procedure for dynamic and stochastic treatment regimes g0, extending the approach of Section 3.3 to estimands like the motivating residual racial disparity.
2.3 |. Dynamic and stochastic treatment regimes
Scientific questions of interest sometimes involve contrasts of regimes that assign exposure stochastically according to different distributions depending on prior covariates. In particular, we may be interested in the “natural” assignment mechanism generating the observed data. This is exactly the case for mediation analysis, which decomposes the effect of an exposure on an outcome into component causal pathways in order to understand possible mechanisms enacting the overall effect. Figure 1 shows a classic causal structure in mediation, where the mediator M channels part of the effect of the exposure A on the outcome Y, with Z as a baseline confounder. The set W contains other mediators that also act as exposure-induced mediator-outcome confounders for the M →Y relationship.
FIGURE 1.

Mediation causal structure with outcome Y, exposure A, mediator M, baseline confounder(s) Z, and exposure-induced mediator-outcome confounder(s) W. The controlled direct effect captures the A → Y effect when M is fixed to some m. Natural direct and indirect effects are not identified under this structure due to the A → W arrow, but randomized interventional analogs are identified
All common mediation estimands can be formulated as contrasts in regimes, including controlled direct effects (CDE), natural direct and indirect effects (NDE and NIE), and randomized interventional analogs to these quantities (Didelez et al., 2012). For concreteness, we restrict attention in the main text to the randomized interventional analog to the natural direct effect (rNDE), which is identified under weaker conditions than the NDE; estimation algorithms for the CDE, NDE, NIE, and rNIE are available in Web Appendix B. The rNDE can be conceived as a contrast in dynamic regimes where part of the regime recreates the naturally occurring assignment mechanism (Didelez et al., 2012), which is unknown and must therefore be estimated. We add a parametric model for M reflecting its parents in the natural stochastic regime, and let θ = (θZ, θW, θM,θY). The likelihood is
We now outline a strategy for estimating the rNDE that compares a = 1 to a = 0 when the mediator is stochastically assigned as it would be if A were set to 0. The rNDE contrasts regime g = (A = 1,M = Hz(a = 0)) with g′ = (A = 0,M = Hz(a = 0)), where Hz(a = 0) is a draw from the distribution of M among the Z = z group if A is set to 0 through intervention (VanderWeele, 2015). For any exposure-induced mediator-outcome confounders W, p(hz(a = 0)|z) = ʃ p(m|a = 0, z, w)p(w|a = 0, z)dw.
The equation for for g′ = (A = 0,M = Hz(a = 0)) is analogous to Equation (1) with an added model for M. For the regime g = (A = 1,M = Hz(a = 0)), the W value used to assign M is different from the value for Y (i.e., a recanting witness) (Avin et al., 2005). The simulation-based Bayesian g-formula invokes an independence assumption that results in separate posterior predictive draws of for both a = 0 and a = 1. The posterior mean of the rNDE is thus given by
| (2) |
2.4 |. Targeting population causal estimands with the Bayesian bootstrap
Marginalization over the baseline confounder distribution may occur through posterior predictive sampling from , with Z modeled parametrically. In practice, Z can be high dimensional, introducing substantial risk of model misspecification. Because Z is, by definition, the same for all regimes, Keil et al. (2015) fix p(z|θz) to the empirical distribution pN(z). However, treating the baseline covariates as fixed will estimate a “conditional average” causal effect rather than a population or “superpopulation” average effect (Imbens and Rubin, 2015; Kern et al., 2016). Web Appendix C elaborates on this distinction.
To facilitate estimation of superpopulation effects, we employ the Bayesian bootstrap as a flexible model for Z in the target population (Rubin, 1981). When all Zi values are unique for i = 1, …, n, the Bayesian bootstrap assigns observation weights (d1, …, dn) sampled from a Dirichlet(1, …, 1), with weights changing every MCMC iteration; because all observations are equally weighted, the resulting closely reflects the observed empirical distribution. An expected causal contrast τi that conditions on Z is calculated for each i, and the weighted population average causal effect is given by . Many popular causal estimands have tractable closed-form solutions τ(Zi) for discrete data, which introduces an opportunity for computational efficiency when multiple observations have the same value of Z. Web Appendix D describes this, along with another source of computational gains that does not change the underlying probability model: QR decomposition for design matrices (Stan Development Team, 2018). Computational efficiencies become particularly important when adapting these models to perform sensitivity analyses for unmeasured confounding.
3 |. BAYESIAN DATA FUSION: A DATA-DRIVEN PROBABILISTIC SENSITIVITY ANALYSIS APPROACH
We now consider the problem of making causal inferences when an important confounder is unmeasured in the primary (“main”) data set but is available in a secondary (“external”) source. Although the data fusion algorithm we outline accommodates arbitrary confounding structures and many different estimands, we restrict attention to estimating the rNDE with an exposure-induced unmeasured mediator-outcome confounder U as in Figure 2; algorithms for other estimands are available in Web Appendix B. The rNDE is interesting for two reasons: (1) the additional complexity involved with estimating the natural, stochastic assignment mechanism and (2) the need to accommodate exposure-induced confounding. Under weaker assumptions, this estimator can also yield estimates important for health disparities research (VanderWeele and Robinson, 2014).
FIGURE 2.
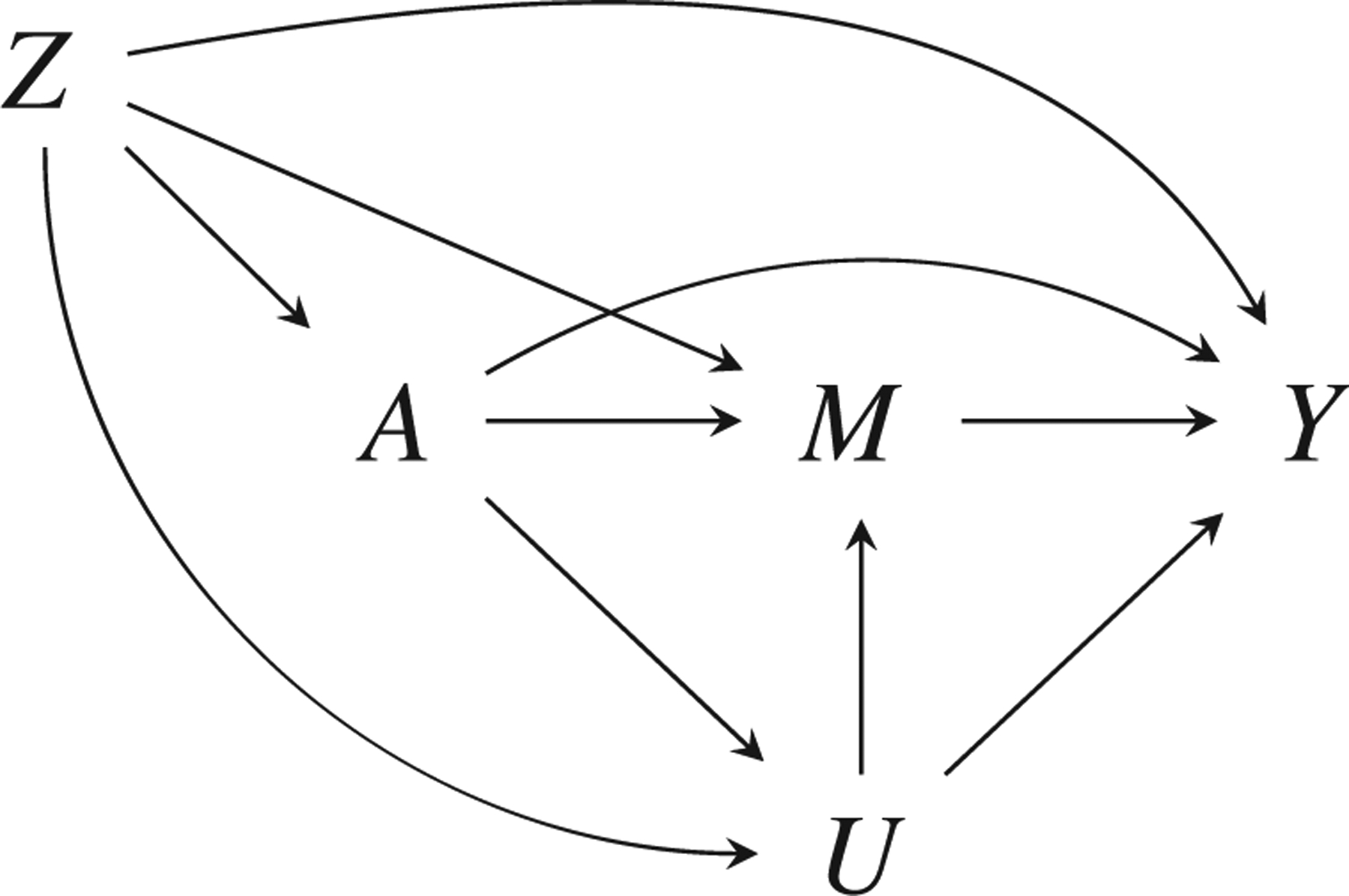
Mediation causal structure with outcome Y, exposure A, mediator M, baseline confounders Z, and exposure-induced mediator-outcome confounder U that is unmeasured in the main data
3.1 |. Notation and assumptions
Suppose an investigator wants to learn about an effect in some target population for which a large data source (N = n1) exists. The desired causal quantity is the rNDE in the population from which the n1 observations were randomly sampled. Figure 2 shows the causal structure, with outcome Y, exposure A, mediator M, and baseline confounders Z. There is also an exposure-induced mediator-outcome confounder U, which is unmeasured in the data set of size n1. Information on {Z, M, A, Y, U} exists in a smaller secondary data source (N = n2, with n2 < n1), which may or may not be from the same population. For g-computation, models for {A, M, Y} can be any univariate or multivariate generalized linear model, and there are no distributional restrictions on Z. However, imposing additional restrictions on U can dramatically improve MCMC performance. Marginalization over the distribution of U is only guaranteed to result in a closed form when U has finite support, although certain continuous distributions can also be integrated out of the likelihood.
In addition to the assumptions of the Bayesian g-formula (Keil et al., 2015)—which are formally stated as Assumptions 1–4 in Web Appendix A—Bayesian data fusion requires causal transportability to hold. That is, although the smaller data set may not be representative of the target population with respect to the distribution of baseline covariates, the underlying causal processes operate in the same way.
Assumption 5 (Parametric causal transportability). Let and denote the superpopulations for the main and external data sources. If , the causal graph structures of and must agree such that all Q ∈ {U, M, Y} have the same parent nodes pa(Q). Furthermore, the true underlying data-generative parameters and must be the same such that
| (3) |
The conditional exchangeability of Assumption 3 is still required for U (i.e., Uz ⫫ A|Z, a conditional independence that is encoded in Figure 2), but the requirements for M and Y are relaxed to allow the confounder U to be unmeasured.
Assumption 6 (Conditional exchangeability). Briefly, (Z, U) must be sufficient to control confounding. For the randomized rNDE in Figure 2, this implies
| (4) |
| (5) |
3.2 |. Specification of parametric models
To illustrate the closed-form estimator and facilitate contrasts with existing methods, we assume A, U, M, and Y are all binary with logistic link functions. The baseline confounders Z are also assumed to be discrete.
Letting πQ = P(Q = 1|pa(Q)) for Q ∈ {U, M, Y}, we adopt the following models:
| (6) |
| (7) |
| (8) |
Then θU = (γ0, γA, γZ), θM = (β0, …, βU), and θy = (α0, …, αU). For Q ∈ {U, M, Y}, . Equation (9) shows the observed data likelihood for the full parameter vector θ = (θu, θM, θy) in the main data set, marginalizing over the missing U.
| (9) |
For a generic prior π(θ), the posterior for θ marginalizing over the missing U is proportional to How to set an informative prior π(θ) using the secondary data set is the focus of the next section.
3.3 |. Specification of prior information with external data
Given that U is unmeasured in the main data source, any parameters involving U (e.g., θU, βU, and αU) cannot be identified from that data. Because the main data set is presumably more representative of the target population of interest, the sole reason for integrating the external data set is for providing information about the confounder unmeasured in the main data set. That information can be summarized through the use of informative priors.
Priors for θU, θM, and θY are derived by fitting in the external data frequentist maximum likelihood models corresponding to Equations (6) through (8). Under causal transportability, maximum likelihood estimators fit in the external data will be consistent and asymptotically normal about , the true θQ parameters for the Q ∈ {U, M, Y} outcome model in population . Let denote the maximum likelihood estimate (MLE) of θQ in the external data, and let be the estimated variance-covariance matrix. Then (, ) is a sensible choice for prior π(θQ). With moderately large n2, this prior approximates the posterior distribution for θ in a Bayesian analysis conducted using the n2 observations, assuming a noninformative prior. In fact, the BDF prior can be seen as an approximation of the power prior (Ibrahim and Chen, 2000; Chen and Ibrahim, 2006) that can be implemented using a different set of summary statistics; see the Web Appendix E for additional details on this useful connection. With a priori independence, the complete prior for θ is π(θ) = π(θU) × π(θM) × π(θY).
If , some relationships may not be transportable, suggesting the use of less informative priors wherever possible. Consider the parameter αz, about which the main data source contains substantial information. In the model formulation given by Equation (8), variance and covariance hyperparameters for αz would be found along the second row and column of . If we multiply the off-diagonal elements in that row and column by a large inflation factor σ (e.g., 100) and the diagonal element by σ2, we assert a marginal prior distribution on αz that is virtually noninformative. However—critically—the prior correlation between αz and the unidentifiable parameter αU is preserved.
3.4 |. A simulation-based Bayesian data fusion algorithm
We now outline a simulation-based Bayesian data fusion approach for g-formula causal contrasts in the context of rNDE estimation.
Fit maximum likelihood models in the external data to obtain the prior π(θ) as detailed in Section 3.3.
Use a No-U-Turn sampler (NUTS) with target probability distribution proportional to in order to obtain posterior samples of the regression parameter vector θ. The probabilistic programming language Stan has a NUTS implementation (Carpenter et al., 2016), and it is available to R users through the rstan R package (Stan Development Team, 2016). For some large B (e.g., 4,000), let θ(1), …, θ(B) denote the B posterior samples remaining after discarding warmup iterations.
- For MCMC iteration b = 1, …, B, sample a length-n1 weight vector sampled from a Dirichlet(1, …, 1). For i = 1, …, n1:
- For g0 ∈ {g, g′} and a0 ∈ {0,1}, sample as Bernoulli with success probability
- For g0 ∈ {g, g′}, sample randomized mediator as Bernoulli with success probability
- Define individual-level causal contrast as
Calculate population estimate .
Construct a point estimate for rNDE as the posterior mean , and create quantile-based 95% credible intervals.
4 |. SIMULATION STUDY
We designed a simulation study to evaluate estimator performance with rNDE in the main study superpopulation as the estimand of interest. Due to the fact that sensitivity analyses based on sharp nonparametric bounding and those based on externally derived bias parameters are not directly comparable, we focus our comparison between BDF and two standard bias correction techniques. The first, which we refer to as the δ-γ (DG) method, imposes strict assumptions about functional form and does not allow for exposure-mediator interaction (VanderWeele, 2015). A second method, which we refer to as the interaction correction (IX), allows for exposure-mediator interaction in the outcome model (VanderWeele, 2010). Neither method accommodates exposure-induced mediator-outcome confounding. For comparability with BDF, we elected to use the secondary data source, replacing component quantities in the bias formulae with maximum likelihood estimates derived from regression models in the external data. Additional details are available in Web Appendix F; Web Appendix H explores the use of inflation factors to increase robustness to certain types of violations of parametric transportability.
4.1 |. Data generation procedure
We considered a number of scenarios with varying data generation schemes. We varied: sample sizes (n1 and n2 = n1/10), causal structure (ΔU,A = 1 if the mediator-outcome confounder U is caused by A; 0 otherwise), and presence of an interaction (ΔY,AM = 1 if there is an A-M interaction in the Y model; 0 otherwise). The strength of mediator-outcome confounding by U was governed by two quantities, the log-odds ratios of U in the M and Y models, respectively. When the same βU and αU were used to generate the main and external data, causal transportability holds; this was done for strong confounding by U (βU = αU = 1.5, corresponding to odds ratios of ≈ 4.5). To investigate various estimators’ performances under violations of the transportability assumption, βU = αU = 0 was used to generate the external data, while βU = αU = 1.5 in the main data. Complete details of the data generation process are available in the Web Appendix G. For each simulation condition, estimator bias and interval coverage were assessed using 200 replicates.
4.2 |. Implementation of the Bayesian data fusion bias correction
The simulation-based Bayesian data fusion estimator was implemented for each pair of simulated main and external data sets. Priors were constructed using the external data as described in Section 3.3 with variance inflation (σ = 100) for the covariance matrix. The models in the external data were correctly specified, with ΔY,AM and ΔU,A matching the underlying generation process for the main data. Posterior samples of the bias-corrected rNDE were obtained from three MCMC chains of 2000 iterations each, with the first 1000 samples discarded as warmup. The posterior mean was taken as a point estimate, with uncertainty captured using 95% quantile-based credible intervals.
4.3 |. Simulation results
Figure 3 shows estimates from the case with exposure-induced U. When the transportability assumption holds, the BDF estimator eliminates the confounding bias at all sample sizes. In contrast, the frequentist correction methods do worse than no correction at all. Although these corrections do not purport to address exposure-induced mediator-outcome confounding, this finding underscores the danger of using these corrections when U may be caused by Z.
FIGURE 3.
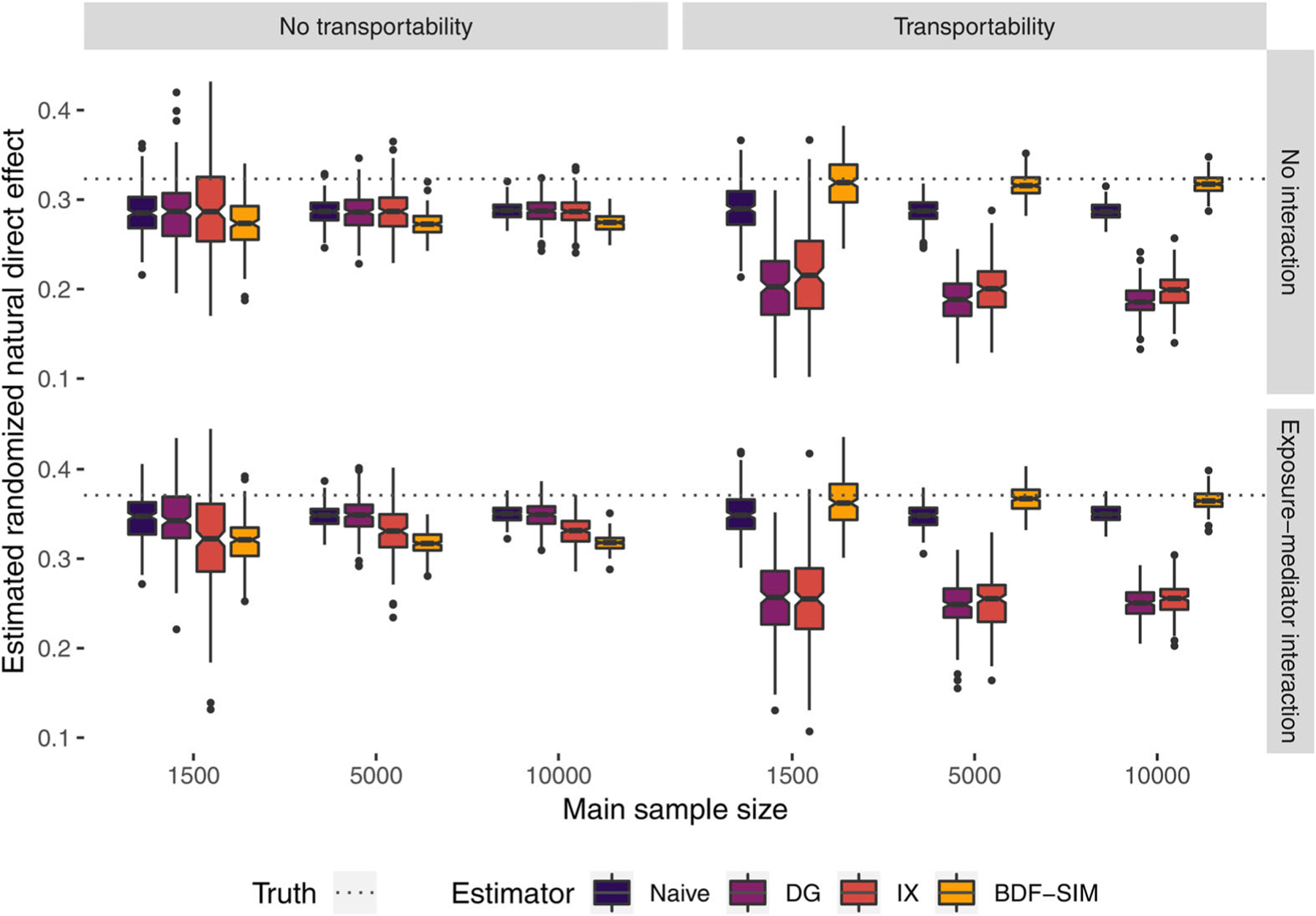
Randomized natural direct effects estimated with naive, delta-gamma (DG) correction, interaction (IX) correction, and simulation-based Bayesian data fusion (BDF-SIM), with and without exposure-mediator interaction and causal transportability between main and external data sets. This figure appears in color in the electronic version of this article, and any mention of color refers to that version
In the presence of such a severe violation of transportability, the information extracted from the external data set by the BDF procedure is misleading, and the BDF estimator performs poorly. Confounding bias is not eliminated, and the prior information leads to less posterior uncertainty. The frequentist estimators also do not correct the bias, but the uncertainty is the same as the uncorrected naive intervals.
Table 1 reports coverage for the 95% confidence and credible intervals. Since all variables were discrete, a closed-form expression of the BDF rNDE estimator was available. Simulation results for this variant demonstrated nearly identical properties as the simulation-based version; Web Appendix H reports these results. In general, credible intervals from BDF approaches had widths comparable to the naive and frequentist corrected confidence intervals. However, the classical correction methods are not unbiased, and the interval coverage is low (< 10%). Conversely, as noted previously, BDF did not perform well under serious transportability violations, achieving less than 1% coverage. Web Appendix H.4 explores using the prior variance inflation factor parameter σ to mitigate certain types of transportability issues when the external and main data sets are equal in size. Based on those findings, we recommend using moderate to large σ (e.g., 10–100) if transportability is in question for parameters with a relatively large impact on the estimand of interest (e.g., parameters relating to A for estimating the rNDE), with the caveat that credible intervals may still have less than nominal coverage. We urge caution with interpreting results if transportability violations are believed to affect parameters directly involving U.
TABLE 1.
Coverage percentages for 95% confidence and credible intervals for naive, delta-gamma (DG) and interaction (IX) frequentist corrections, and simulation-based Bayesian data fusion estimator (BDF-SIM), calculated in 200 replicates with exposure-induced mediator-outcome confounding
| Transportability | Interaction | Sample sizes | Naive | DG | IX | BDF-SIM |
|---|---|---|---|---|---|---|
| Yes | No | (150, 1500) | 73.5 | 5.0 | 15.5 | 93.5 |
| Yes | No | (500, 5000) | 25.0 | 0.0 | 0.0 | 94.0 |
| Yes | No | (1000, 10,000) | 2.5 | 0.0 | 0.0 | 91.5 |
| Yes | Yes | (150, 1500) | 69.0 | 7.0 | 12.5 | 92.5 |
| Yes | Yes | (500, 5000) | 19.5 | 0.0 | 0.0 | 95.5 |
| Yes | Yes | (1000, 10,000) | 2.5 | 0.0 | 0.0 | 93.5 |
| No | No | (150, 1500) | 66.5 | 64.0 | 54.0 | 50.0 |
| No | No | (500, 5000) | 26.0 | 31.5 | 34.0 | 3.0 |
| No | No | (1000, 10,000) | 2.5 | 10.5 | 13.0 | 0.0 |
| No | Yes | (150, 1500) | 59.5 | 72.5 | 45.0 | 53.0 |
| No | Yes | (500, 5000) | 18.0 | 55.0 | 33.0 | 3.5 |
| No | Yes | (1000, 10,000) | 3.5 | 44.0 | 13.0 | 0.0 |
5 |. EXAMINING THE ROLE OF STAGE AT DIAGNOSIS IN BLACK-WHITE SURVIVAL DISPARITIES IN COLORECTAL CANCER
5.1 |. Overview
We now use BDF to explore the extent to which differentials in stage at diagnosis contribute to apparent racial disparities in colorectal cancer survival. Our analysis estimates how much we could reasonably expect to reduce the observed survival disparity if we broke the link between race and cancer stage at the time of diagnosis, for example, by implementing targeted screening programs leading to earlier colorectal cancer detection among Blacks. This “direct effect disparity measure” or “residual disparity” can be estimated using rNDE formulae under slightly weaker identifiability conditions (VanderWeele and Robinson, 2014; VanderWeele, 2015).
Valeri et al. (2016) sought to address this question in a recent article with data from a registry of U.S. cancer patients from 1992 to 2005. The National Cancer Institute’s Surveillance, Epidemiology, and End Results (SEER) registry collects information on tumor site and stage for a sizable proportion of cancer patients from diverse geographic regions within the United States. They concluded that eliminating Black-White disparities in colorectal cancer stage at diagnosis would lead to a 35% reduction in survival disparities as measured by 5-year restricted mean survival time. Their analysis controlled for a number of covariates, including age at diagnosis, gender, time period of cancer diagnosis, geographic locale, and median county income as derived from the American Community Survey; however, it did not control for household-level poverty status, as that information was not available.
5.2 |. Analysis description
We extend the analysis of Valeri and colleagues to add information about confounding of the stage-survival relationship by individual-level income using data from the Cancer Care Outcomes Research and Surveillance (CanCORS) Consortium data. This observational study followed patients shortly after cancer diagnosis and aimed “to determine how the characteristics and beliefs of lung and colorectal cancer patients, physicians and health-care organizations influence treatments and outcomes spanning the continuum of cancer care from diagnosis to recovery or death” (Catalano et al., 2013). To support these ambitious aims, the CanCORS database contains detailed socioeconomic information, including household income for the year preceding cancer diagnosis. We chose U = 1 to correspond the lowest income group of <$40,000 per year. The goal was to assess the bias of the residual disparity measure as calculated in SEER, assuming the underlying race-poverty and poverty-survival relationships in SEER matched those in CanCORS. The survival outcome was a binary indicator Y for whether the patient was alive 5 years after diagnosis. Self-reported race was coded such that A = 1 for non-Hispanic blacks and A = 0 for non-Hispanic whites; individuals reporting Hispanic origin were excluded. The intervening variable of interest, stage at cancer diagnosis M, took on values 1–4 for stages I-IV. Adjustment covariates included in all models were: gender, age at cancer diagnosis (<60, 60–65, or >65), and geographic region (West, South, or other). Patients whose cancer was unstaged were excluded, leaving a total of 146,031 colorectal cancer cases in the SEER analysis data set.
First, we fit two naive models using maximum likelihood in the SEER data: (1) stage at cancer diagnosis as a function of race and adjustment covariates, using a baseline category logit model; and (2) 5-year survival as a function of race, stage at diagnosis, and the adjustment covariates, using a logistic link. Coefficients were used to calculate a naive estimated residual disparity measure RDnaive and bootstrapped 95% confidence intervals.
Next, we implemented the BDF estimator to obtain poverty-adjusted estimates of the Black-White survival disparity. Formally, our estimand is the population average residual disparity , where g = (M = Hz,u(0)). To construct priors, we fit three frequentist models using the 1613 CanCORS colorectal cancer patients for whom complete stage and covariate data were available. The two regression models described above were modified by adjusting for an indicator of income <40,000/year (“poverty”). Prior distributions were constructed as in Section 3.3 with no variance inflation applied due to the large sample sizes; a sensitivity analysis with σ = 10 was also performed. A third and final frequentist model was a logistic regression for poverty as a function of race, gender, region, and age category.
Using BDF, we estimated the poverty-adjusted residual disparity in the SEER data. Four chains of 2000 MCMC iterations each were run in Stan (Stan Development Team, 2016), with the first 1000 iterations discarded as warmup. Gelman-Rubin convergence diagnostics (Gelman and Rubin, 1992) were calculated for all parameters. The number of MCMC iterations was chosen based on trace plots, an absence of divergent NUTS transitions, and < 1.01 for the residual disparity parameter.
5.3 |. Residual disparity results
Posterior samples of the poverty-adjusted population residual disparity measure calculated using simulation-based and closed-form BDF are shown in Figure 4. The null value of zero, which represents Black-White equality with respect to baseline covariate-adjusted survival, lies beyond the far right of the graph. Visible as a dotted line on the left is the disparity we currently observe without an intervention on stage. With a value of 0.099 (95% CI: 0.092, 0.107), we estimate that Black patients are 9.9 percentage points less likely to survive 5 years postdiagnosis than White patients of the same gender and geographic region. The naive estimate of the residual disparity after an intervention aligning Blacks’ cancer stage distribution to the current stage suggests that the remaining disparity in 5-year survival would be 6.6% (95% CI: 5.8, 7.4). The data fusion suggests that unmeasured confounding by poverty does not substantially change the estimated residual disparity, with an estimate of 6.5% (95% CI: 5.3, 7.4). An additional analysis with inflation factor set to σ = 10 did not substantially change any results, as might be expected given the relative data set sizes.
FIGURE 4.
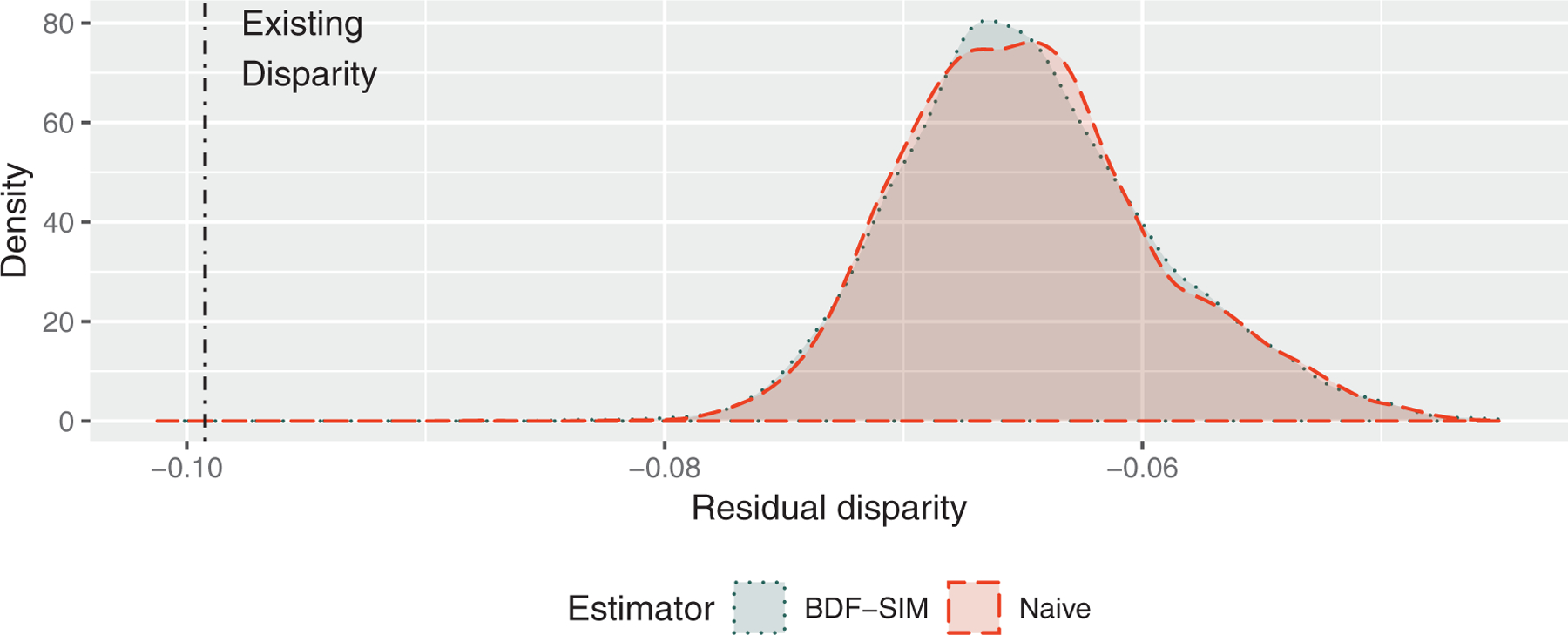
Posterior samples of average residual disparity (ARD) estimates of differences in Black-White 5-year colorectal cancer survival probabilities in the SEER population, accounting for unmeasured poverty using simulated-based Bayesian data fusion (BDF-SIM) from the CanCORS cohort study. This figure appears in color in the electronic version of this article, and any mention of color refers to that version
Given the abundant literature documenting the role of socioeconomic status in cancer outcomes (Le et al., 2008), it may be surprising to see negligible impact of poverty adjustment. One possibility is that causal transportability may not hold between the SEER and CanCORS populations in ways related to poverty. Although CanCORS may appear to be representative of the larger U.S. population appearing in SEER (Catalano et al., 2013), the causal relationships determining cancer outcomes in CanCORS may differ those in SEER because many CanCORS study sites were academic medical centers in large cities (Ayanian et al., 2004). Thus, we may not see dramatic shifts because CanCORS does not indicate strong stage-survival confounding by poverty. Alternatively, there may residual confounding due to the coarsening of socioeconomic deprivation—a complex, multifaceted problem—into a single binary indicator. Nevertheless, the analysis gives policymakers two potentially valuable pieces of information: (1) a quantitative estimate of the poverty-adjusted residual disparity and (2) a better understanding of the true uncertainty surrounding that estimate.
6 |. DISCUSSION
In this paper, we have proposed a general method for Bayesian data fusion that can be used to perform sensitivity analyses for unmeasured confounding in a variety of settings. Although there can be no substitute for a well-designed study in the target population of interest, decision makers cannot wait for the ideal analysis in the ideal data set and must often work from incomplete or imperfect information. BDF communicates the sensitivity of a research conclusion while incorporating some of what is already known about the problem.
The general nature of BDF makes it easily extendable. For example, any number of parametric models could be used for the unmeasured confounder. Although we demonstrated properties using randomized natural direct effects in mediation, these principles can be applied to any mediation estimand or to settings with time-varying confounding. Any generalized linear model can be adopted for the unmeasured confounder, allowing for both continuous and discrete distributions. The method can also adjust for multiple unmeasured confounders; information on multiple confounders could be constructed from different external data sources, although doing so requires assumptions about the joint distribution of their bias coefficients.
With respect to the motivating question of Black-White racial disparities in U.S. colorectal cancer patients, we conclude that unmeasured confounding of the stage-survival relationship by poverty leads to residual disparity reduction estimates that are slightly too optimistic. Implementing an intervention—for example, a targeted screening program—to alleviate or eliminate delayed cancer diagnosis for Black colorectal cancer patients would substantially improve 5-year survival outcomes. However, without also intervening on the complex societal factors that lead to greater poverty among black patients, we cannot realize the full benefit of such an intervention.
Bayesian data fusion relies on three major assumptions. First, BDF assumes that parametric models are otherwise correctly specified, which means it does not account for uncertainty in model misspecification, as some sensitivity analyses do (Tchetgen Tchetgen and Shpitser, 2012). A more comprehensive uncertainty quantification would incorporate additional uncertainty due to model selection. Second, as with most parametric causal inference, the models extrapolate causal effects (Vansteelandt et al., 2012), forcing analysts to detect nonoverlap. Recent advances in Bayesian nonparametrics (Roy et al., 2017) may be adapted to add flexibility to portions of the models. Third, like other data fusion methods, BDF requires causal transportability between the external and main data sets (Pearl and Bareinboim, 2014). When transportability holds completely, the proposed approach is both a data fusion technique and a sensitivity analysis with favorable bias correction properties, particularly with large external sample sizes. In the absence of transportability, we can no longer appeal to asymptotic consistency for the elimination of bias. In that context, BDF is best understood as a Monte Carlo sensitivity analysis with parameters that are informed, however, imperfectly, by the external data. The degree to which confounding bias is appropriately corrected will depend on the severity of the transportability violation. Assessing transportability is an exercise in scientific judgement and causal reasoning. Notwithstanding some useful identifiability results (Correa et al., 2018), the statistical literature needs additional research on the impact of various transportability violations. Here we proposed the use of a prior variance inflation factor as a strategy to reduce problems arising from certain types of violations, but future work should explore other solutions.
Nevertheless, our extension of the Bayesian g-formula for dynamic and stochastic regimes offers a Bayesian approach to the estimation of population average effects in the presence of time-varying confounding. BDF, a principled algorithm for data-driven sensitivity analysis, offers a significant step forward for statistical analyses to inform decision-making. As a sensitivity analysis method, BDF is flexible enough to allow for a much greater variety of causal structures and regression model specifications, and it works for any causal estimand that can be represented as a counterfactual contrast. As a data fusion approach, the underlying Bayesian principles allow for extensibility to multiple unmeasured confounders of various types. Information from the external data source enters exclusively through prior distributions, reducing computational burden, sidestepping data privacy concerns, and dramatically increasing the number of data sources that may be used as external data. Researchers cannot guarantee that the right data are always available, but developing statistical methods to rigorously synthesize information from multiple sources gives decision makers the tools to make more informed choices.
Supplementary Material
ACKNOWLEDGMENTS
LC acknowledges support from NIH grants T32CA009337 and T32ES007142 as well as a David H. Peipers Fellowship. CZ was supported by EPA grant RD-835872 and NIH grants R01ES026217 and NIH R01GM111339. LV received funding from NIH grant K01MH118477, and BC was funded by NIH grants P01CA134294 and P30ES000002, and EPA grant RD-835872. The authors thank the editor and two anonymous reviewers for helpful suggestions that substantially improved this manuscript.
Funding information
National Institute of Environmental Health Sciences, Grant/Award Numbers: P30ES000002, R01ES026217, T32ES007142; Environmental Protection Agency, Grant/Award Number: RD-835872; David H. Peipers Fellowship; National Institute of Mental Health, Grant/Award Number: K01MH118477; National Cancer Institute, Grant/Award Numbers: P01CA134294, T32CA009337; National Institute of General Medical Sciences, Grant/Award Number: R01GM111339
Footnotes
DATA AVAILABILITY STATEMENT
The data that support the findings of this paper are available from the Surveillance, Epidemiology, and End Results (SEER) Program and the Cancer Care Outcomes Research and Surveillance Consortium (CanCORS). Restrictions apply to the availability of these data, which were used under license for this study. Data can be requested at https://seer.cancer.gov/seertrack/data/request and https://www.sgim.org/communities/research/dataset-compendium/proprietary-datasets/cancors.
SUPPORTING INFORMATION
Web Appendices, Tables, Figures, and R code referenced in Sections 2– 5 are available with this paper at the Biometrics website on Wiley Online Library.
REFERENCES
- Antonelli J, Zigler C& Dominici F (2017) Guided Bayesian imputation to adjust for confounding when combining heterogeneous data sources in comparative effectiveness research. Biostatistics, 18, 553–568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avin C, Shpitser I & Pearl J (2005) Identifiability of path-specific effects. Proceedings of International Joint Conference on Artificial Intelligence, Edinburgh, Scotland, 357–363. [Google Scholar]
- Ayanian J, Chrischilles E, Wallace R, Fletcher R, Fouad M, Kiefe C et al. (2004) Understanding cancer treatment and outcomes: the cancer care outcomes research and surveillance consortium. Journal of Clinical Oncology, 22, 2992–2996. [DOI] [PubMed] [Google Scholar]
- Bareinboim E& Pearl J (2016) Causal inference and the data-fusion problem. Proceedings of the National Academy of Sciences, 113, 7345–7352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpenter B, Gelman A, Hoffman M, Lee D, Goodrich B, Betancourt M et al. (2016) Stan: a probabilistic programming language. Journal of Statistical Software, 20,1–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catalano P, Ayanian J, Weeks J, Kahn K, Landrum MB, Zaslavsky A et al. (2013) Representativeness of participants in the cancer care outcomes research and surveillance (CanCORS) consortium relative to the surveillance, epidemiology and end results (SEER) program. Medical Care, 51, e9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen M-H& Ibrahim JG (2006) The relationship between the power prior and hierarchical models. Bayesian Analysis, 1,551–574. [Google Scholar]
- Correa JD, Tian J & Bareinboim E (2018) Generalized adjustment under confounding and selection biases. Thirty-Second AAAI Conference on Artificial Intelligence, 6335–6342. [Google Scholar]
- Didelez V, Dawid P & Geneletti S (2012) Direct and indirect effects of sequential treatments. [Preprint] Available from: http://arxiv.org/abs/1206.6840.
- Ding P& VanderWeele T (2016) Sensitivity analysis without assumptions. Epidemiology, 27, 368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding P& Vanderweele T (2016) Sharp sensitivity bounds for mediation under unmeasured mediator-outcome confounding. Biometrika, 103, 483–490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman A& Rubin D (1992) Inference from iterative simulation using multiple sequences. Statistical Science, 7, 457–472. [Google Scholar]
- Greenland S (2005) Multiple-bias modelling for analysis of observational data. JRSS:A, 168, 267–306. [Google Scholar]
- Ibrahim J& Chen M-H (2000) Power prior distributions forregression models. Statistical Science, 15, 46–60. [Google Scholar]
- Imbens GW & Rubin DB (2015) Causal inference in statistics, social, and biomedical sciences. Cambridge: Cambridge University Press. [Google Scholar]
- Jackson C, Best N& Richardson S (2006) Improving ecological inference using individual-level data. Statistics in Medicine, 25, 2136–2159. [DOI] [PubMed] [Google Scholar]
- Keil A, Daza E, Engel S, Buckley J& Edwards J (2015) A Bayesian approach to the g-formula. Statistical Methods in Medical Research, 27, 3183–3204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kern HL, Stuart EA, Hill J& Green DP (2016) Assessing methods for generalizing experimental impact estimates to target populations. Journal of Research on Educational Effectiveness, 9,103–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le H, Ziogas A, Lipkin S& Zell J (2008) Effects of socioeconomic status and treatment disparities in colorectal cancer survival. Cancer Epidemiology, Prevention & Biomarkers, 17,1950–1962. [DOI] [PubMed] [Google Scholar]
- McCandless L& Somers J (2017) Bayesian sensitivity analysis for unmeasured confounding in causal mediation analysis. Statistical Methods in Medical Research, 28, 515–531. [DOI] [PubMed] [Google Scholar]
- Pearl J & Bareinboim E (2011) Transportability of causal and statistical relations: a formal approach. 2011 IEEE 11th International Conference on Data Mining Workshops. Piscataway, NJ: IEEE. pp. 540–547. [Google Scholar]
- Pearl J& Bareinboim E (2014) External validity: from do-calculus to transportability across populations. Statistical Science, 29, 579–595. [Google Scholar]
- Robins J, Rotnitzky A & Scharfstein D (2000) Sensitivity analysis for selection bias and unmeasured confounding in missing data and causal inference models. In: Halloran ME and Berry D (Eds.) Statistical models in epidemiology, the environment, and clinical trials. Berlin: Springer. pp. 1–94. [Google Scholar]
- Roy J, Lum K, Zeldow B, Dworkin J, Re VL III& Daniels M (2017) Bayesian nonparametric generative models for causal inference with missing at random covariates. Biometrics Methodology, 74,1193–1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin DB (1981) The Bayesian bootstrap. The Annals of Statistics, 9, 130–134. [Google Scholar]
- Scharfstein D, Rotnitzky A& Robins J (1999) Adjusting for nonignorable drop-out using semiparametric nonresponse models. Journal of the American Statistical Association, 94, 1096–1120. [Google Scholar]
- Stan Development Team (2016) RStan: the R interface to Stan. R package version 2.14.1
- Stan Development Team (2018) Stan modeling language users guide and reference manual, version 2.18.0
- Tchetgen Tchetgen E& Shpitser I (2012) Semiparametric theory for causal mediation analysis: efficiency bounds, multiple robustness, and sensitivity analysis. Annals of Statistics, 40,1816–1845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valeri L, Chen J, Garcia-Albeniz X, Krieger N, VanderWeele T& Coull B (2016) The role of stage at diagnosis in colorectal cancer black-white survival disparities: a counterfactual causal inference approach. Cancer Epidemiology, Prevention & Biomarkers, 25, 83–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele T (2010) Bias formulas for sensitivity analysis for direct and indirect effects. Epidemiology, 21, 540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele T (2015) Explanation in causal inference: methods for mediation and interaction. Oxford: Oxford University Press. [Google Scholar]
- VanderWeele T& Chiba Y (2014) Sensitivity analysis for direct and indirect effects in the presence of exposure-induced mediator-outcome confounders. Epidemiology, Biostatistics, and Public Health, 11, e9027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele T& Robinson W (2014) On causal interpretation of race in regressions adjusting for confounding and mediating variables. Epidemiology, 25, 473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vansteelandt S, Bekaert M& Claeskens G (2012) On model selection and model misspecification in causal inference. Statistical Methods in Medical Research, 21, 7–30. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


