Folding non-homologous proteins by coupling deep-learning contact maps with I-TASSER assembly simulations

Summary

Structure prediction for proteins lacking homologous templates in the Protein Data Bank (PDB) remains a significant unsolved problem. We developed a protocol, C-I-TASSER, to integrate interresidue contact maps from deep neural-network learning with the cutting-edge I-TASSER fragment assembly simulations. Large-scale benchmark tests showed that C-I-TASSER can fold more than twice the number of non-homologous proteins than the I-TASSER, which does not use contacts. When applied to a folding experiment on 8,266 unsolved Pfam families, C-I-TASSER successfully folded 4,162 domain families, including 504 folds that are not found in the PDB. Furthermore, it created correct folds for 85% of proteins in the SARS-CoV-2 genome, despite the quick mutation rate of the virus and sparse sequence profiles. The results demonstrated the critical importance of coupling whole-genome and metagenome-based evolutionary information with optimal structure assembly simulations for solving the problem of non-homologous protein structure prediction.

Graphical abstract

Highlights

• •C-I-TASSER adds deep-learning contact prediction to fragment assembly simulations
• •C-I-TASSER enables ab initio folding of proteins lacking homology in the PDB
• •The inherent force field is critical for proteins with poor templates and sparse MSAs
• •Half of unsolved Pfam families are foldable by C-I-TASSER

Motivation

Taking advantage of the rapid progress in deep-learning technologies, residue-residue contact-map prediction recently achieved impressive breakthroughs. However, how to efficiently convert the binary contact maps into atomic-level structure models remains an important unsolved problem in ab initio protein structure prediction. In this work, we integrated the deep-learning contact-map predictions with cutting-edge threading assembly simulations and found that the inherent force field of the structural folding simulations is essential to maximize the potential of contact-assisted protein structure prediction, especially for the targets and regions that lack spatial restraints and sufficient evolutionary data.

Zheng et al. develop C-I-TASSER, which integrates interresidue contact maps from deep neural-network learning with the cutting-edge I-TASSER fragment assembly simulations, for high-accuracy protein structure prediction. C-I-TASSER folds more than twice the number of proteins without homology than I-TASSER and has successfully folded 50% of Pfam families without solved experimental structures.

Introduction

Template-based modeling (TBM), which is designed to construct protein structure models by using known homologous structures as templates, has dominated the field of protein structure prediction for more than half a century (Browne et al., 1969; Sali and Blundell, 1993). Despite its simplicity and efficiency, TBM does not work for proteins that lack close homology to structures in the Protein Data Bank (PDB) (Sali and Blundell, 1993; Zhang, 2008).

Because of their power in dictating protein folds, residue-residue contacts were employed to address the problem of template-free structure modeling several decades ago (Gobel et al., 1994; Vendruscolo et al., 1997). Early efforts in using contact maps to fold proteins, however, enjoyed modest to little success (Kinch et al., 2011; Wu et al., 2011), mainly due to the low accuracy of contact-map predictions, which had typically less than 30% of the top L/5 long-range contacts, where L is the protein length and long range represents a sequence separation with at least 24 residues, correctly predicted (Monastyrskyy et al., 2014). Most recently, with the development of advanced algorithms in co-evolutionary decoupling (Jones et al., 2012; Marks et al., 2011; Weigt et al., 2009) and deep machine learning (Li et al., 2019a; Wang et al., 2017), contact prediction accuracy has dramatically increased. For example, in the community-wide 13th CASP experiment (CASP13), the state-of-the-art methods based on deep learning from whole-genome sequence databases achieved average precisions of up to 70% for the top L/5 long-range predicted contacts (Shrestha et al., 2019). Nevertheless, how to efficiently convert the contact maps into high-resolution atomic structure models remains a challenging problem. State-of-the-art approaches (Greener et al., 2019; Lamb et al., 2019; Marks et al., 2011; Xu, 2019) often utilize traditional distance geometry-based structure reconstruction tools such as the Crystallography & NMR System (CNS) (Brunger et al., 1998). Because CNS was originally designed for constructing structures from a high number of experimental contacts, it might not be as effective when a limited number of noisy contacts from computational predictions are provided.

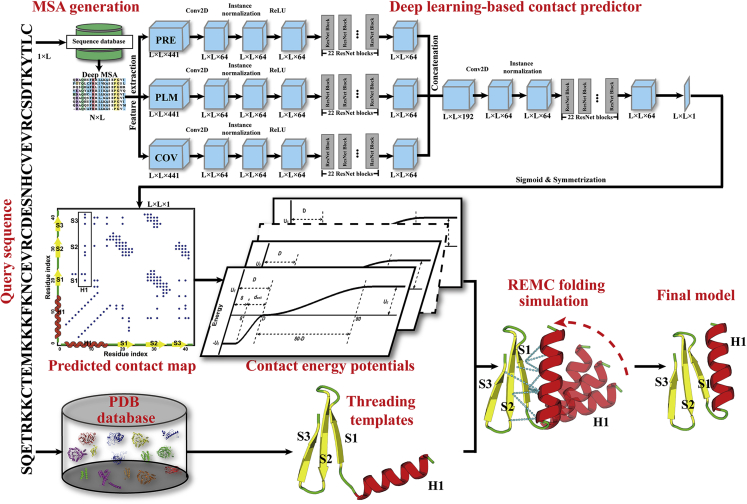
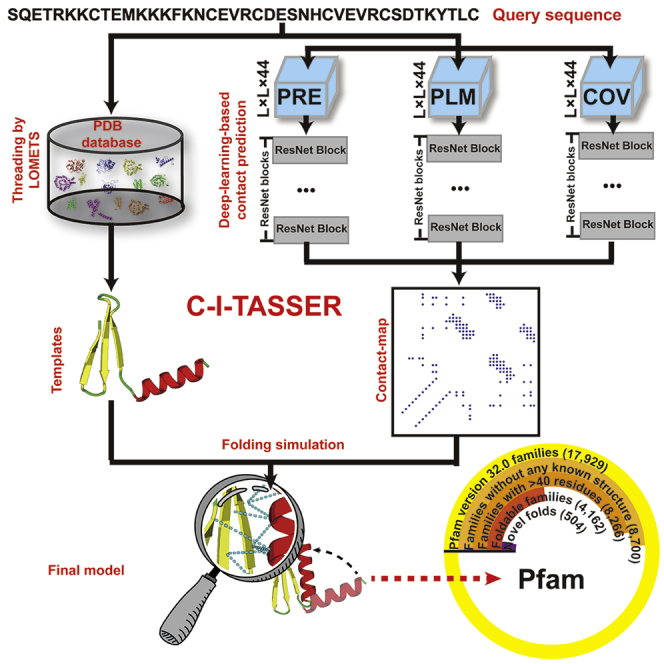
In this work, we present a different protocol, named C-I-TASSER (Figure 1), which integrates contact-map prediction with the cutting-edge threading and fragment assembly method I-TASSER (Wu et al., 2007; Yang et al., 2015) to carefully examine the capacity of using contact maps to fold distantly homologous (or non-homologous) protein targets. Here, we use “non- or distantly homologous targets” to refer to the proteins for which no good templates could be detected by the start-of-the-art threading programs (also called “hard” targets in this study). Although good templates might still exist in the PDB for some of the targets, this does not reduce the difficulty of structure modeling for them, given that modeling starts only from the templates detected by threading. As an independent structure assembly pipeline, I-TASSER was tested in former CASPs and consistently ranked as one of the most accurate methods in the past decade (Battey et al., 2007; Kryshtafovych et al., 2018). Accordingly, the online I-TASSER server (https://zhanglab.ccmb.med.umich.edu/I-TASSER/) has been widely used in the community and has served more than 130,000 users from 149 countries (see Figure S1). Thus, an essential advantage of the C-I-TASSER pipeline over traditional protocols, such as CNS, is that the inherent and highly optimized I-TASSER force field is capable of handling structural regions that lack accurate spatial restraints and therefore has the potential to maximize the benefit of contact-map predictions with false-positive noise.

Figure 1.

The C-I-TASSER pipeline for protein structure prediction

It starts with contact-map prediction from whole-genome and metagenome sequences based on deep residual convolutional neural networks (top) and LOMETS-based threading template identification (bottom). Full-length structure models are then constructed by iterative REMC fragment assembly simulations under the guidance of the deep-learning contact maps and template-based restraints. Abbreviations are as follows: MSA, multiple sequence alignment; REMC, replica-exchange Monte Carlo.

It is noted that because the work was completed, the field has witnessed considerable progress in deep-learning-based interresidue distance and torsion angle predictions (Xu, 2019; Yang et al., 2020), as well as the most recent end-to-end model training (Jumper et al., 2020), which demonstrated significant usefulness for improving 3D structure modeling accuracy. Nevertheless, given the dominantly important role of contact predictions (Shrestha et al., 2019) and the fact that the most reliable distance predictions are for short distances (Li et al., 2021), we believe it is still of significant importance to examine separately the impact of contact maps on ab initio structure prediction, especially in conjunction with the most advanced structure folding simulations that can help explore the maximum potential of contact-map predictions. Our study showed that optimized coupling of deep-learning-based spatial information with efficient structure assembly simulations is the key to improving the capability of distantly homologous protein folding.

Results

Benchmark and blind test results

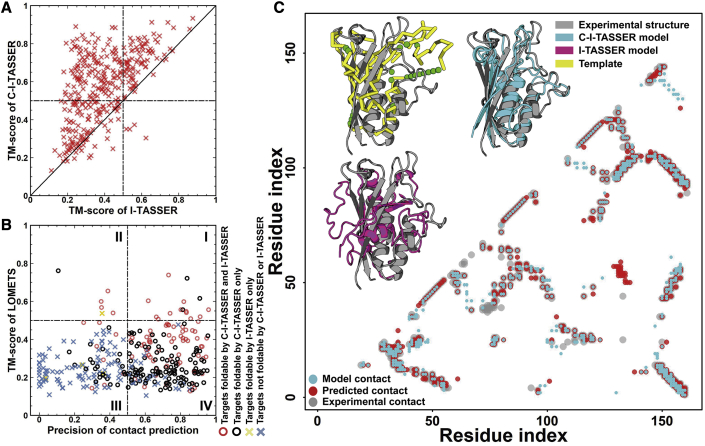
To examine the ability of C-I-TASSER to fold non-homologous proteins, we first tested the pipeline on 342 non-redundant protein domains collected from the SCOPe 2.06 database; these proteins were regarded as hard targets by LOMETS (Zheng et al., 2019c), given that there were no significant templates detected after excluding structures with a sequence identity >30% to the query (see “benchmark dataset collection” under STAR Methods). Overall, C-I-TASSER's top-ranked models attained an average TM score of 0.573, which was 46.2% higher than that of the state-of-the-art TBM approach I-TASSER (0.392); this corresponded to a p = 5.1 × 10⁻⁵⁰ by Student's t test, showing that the difference was highly statistically significant (Table S1). Here, TM score is a metric for measuring the structural similarity between predicted models and the native and has values ranging from 0 to 1, with a TM score of 1 indicating a perfect model (Zhang and Skolnick, 2004a) (see Equation S22 in the STAR Methods). Figure 2A presents a head-to-head TM-score comparison between C-I-TASSER and I-TASSER, where C-I-TASSER outperformed I-TASSER in 313 of the 342 cases (92%), whereas the reverse occurred in only 29 cases. If we define a successful fold as a model with a TM ≥ 0.5 (Xu and Zhang, 2010), C-I-TASSER correctly folded 65% (= 224 out of 342) of the hard targets, which was 2.55 times more than I-TASSER (26%, or 88 out of 342). In Figure S2A, we present the running time of C-I-TASSER simulations, which increases with the length of the protein but is largely comparable to I-TASSER, and the average running time was 5.0 h for the test proteins.

Figure 2.

C-I-TASSER modeling results on the 342 hard targets in the benchmark dataset

(A) Comparison between TM scores of the first models built by C-I-TASSER and I-TASSER.

(B) TM score of LOMETS templates versus accuracy of the contact map utilized by C-I-TASSER. The red circles denote the targets that can be folded by both C-I-TASSER and I-TASSER with a TM score ≥ 0.5; the black points are the targets that can be folded only by C-I-TASSER and not I-TASSER; the yellow crosses are the targets that can be folded only by I-TASSER and not C-I-TASSER; the blue crosses indicate the targets that cannot be folded by either C-I-TASSER or I-TASSER.

(C) An illustrative example from 2-C-methyl-D-erythritol 2,4-cyclodiphosphate synthase IspF (SCOPe: d3fpia_). The upper left shows the structure superpositions of the best LOMETS template (yellow), I-TASSER first model (pink), and C-I-TASSER first model (cyan) with the target structure (gray), and the lower right displays an overlay of predicted contacts (red) with the contacts of the target structure (gray), as well as the contacts from the C-I-TASSER model (cyan).

Contact map dominates the success rate of C-I-TASSER folding

The significant improvement demonstrated by C-I-TASSER can be mainly attributed to accurately predicted contact maps and the effective integration of the threading-based restraints and contact-map potential with the structural assembly simulations. In Figure 2B, we split the datum samples into four quadrants, depending on whether the LOMETS (see details of LOMETS in “LOMETS2 pipeline for meta-server threading” under STAR Methods) threading templates were good (TM ≥ 0.5) or the predicted contacts were accurate (precision of top L long-range contacts ≥0.5). We found that when LOMETS could detect good templates (i.e., the points in quadrants I and II, which accounted for only 21 of the 342 cases because of the nature of hard targets), both I-TASSER and C-I-TASSER could build the correct global fold, with a TM ≥ 0.5. However, if LOMETS failed to detect good templates (points in quadrants III and IV), there were still 204 cases for which C-I-TASSER was able to construct the correct fold; the majority of these cases (84%) were located in quadrant IV, indicating the dominant contribution from the contact-map predictions for folding hard targets.

In Figure 2C, we present a representative example from 2-C-methyl-D-erythritol 2,4-cyclodiphosphate synthase IspF (SCOPe: d3fpia_), for which LOMETS failed to detect any reasonable templates where the best template had a TM score of 0.172. Although I-TASSER considerably refined the template quality by multiple fragment assembly simulations, the global fold was still incorrect; TM = 0.461 and root-mean-square deviation (RMSD) = 11.9Å. The six contact programs from C-I-TASSER (TripletRes, Li et al., 2021; ResTriplet, Li et al., 2019b; ResPre, Li et al., 2019a; ResPLM, Li et al., 2019b; Zheng et al., 2019a; and NeBconA and NeBconB, He et al., 2017) generated reasonable contact-map predictions, with a top L precision of 92.5%, 93.2%, 93.2%, 91.9%, 79.5%, and 85.1%, respectively, which resulted in an overall contact precision of 96.9% for the top L-ranked contacts after combining the maps. With the aid of this combined contact map, C-I-TASSER constructed a significantly improved model with TM = 0.746 and RMSD = 3.23Å. In this example, although the precision increase of the combined contact map was quite modest compared with the best individual predictors (96.9 versus 93.2 for the top L contacts), the C-I-TASSER force field accounts for the frequency of the occurrence of top-ranked predictions from different predictors (see Equation S11 in “residue-residue contact prediction” under STAR Methods), which executed an additional contribution to the contact-map guided folding simulations (see Equation S20 in “replica-exchange Monte Carlo in C-I-TASSER” under STAR Methods and Figure S2B). In fact, if we used only the best contact-map predictor, ResTriplet, to guide the C-I-TASSER simulations in this case, the TM score of the final model was 0.721, which was 3.4% worse than that attained by combining all six contact maps.

Impact of the deepness of MSAs on contact and final model prediction

Given that our contact predictors are trained with multiple sequence alignments (MSAs), a sufficient number of homologous sequences in the MSAs is essential for both contact-map prediction and the subsequent contact-guided structural assembly simulations. In C-I-TASSER, DeepMSA (Zhang et al., 2019) is employed to generate MSAs from multiple whole-genome and metagenome databases to collect more diverse sequence homologs in the MSAs. In Figure S2C, we present the contact accuracy results of the six contact predictors versus the number of effective sequences in the MSAs (or Neff, defined in Equation S12 in “DeepMSA for MSA generation” under STAR Methods). The precision of contact prediction increases almost linearly as the Neff value of the MSA grows, indicating that providing more homologous sequences in the MSAs indeed helps improve the accuracy of contact prediction.

In Figure S2D, we further examine the dependence of the final model quality on the Neff of the MSA used. We found that as the Neff values increased, the TM scores of the final models also increased for most targets. Particularly, when the Neff reached 2³ (= 8), most targets were foldable with TM ≥ 0.5; this requirement is around 2-fold lower than the Neff value of 16 (= 2⁴) reported previously (Ovchinnikov et al., 2017).

Folding proteins with poor templates and contact prediction

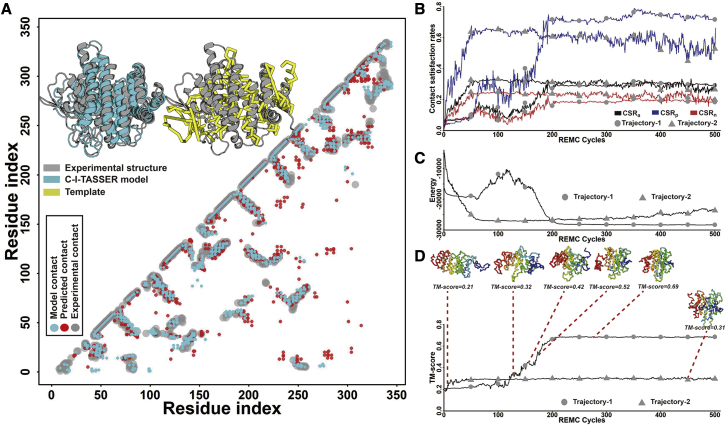
Although both correct threading alignments and accurate contact prediction are key to C-I-TASSER modeling, as demonstrated by Figure 2B, C-I-TASSER generated correct folds (TM ≥ 0.5) for 26.4% of the proteins that had neither good templates nor accurately predicted contacts (quadrant III). The successful folding of these targets can be mainly attributed to the effective coupling of the inherent C-I-TASSER force field with sparse external threading and contact restraints. To illustrate this point, in Figure 3A we analyze in detail an example from the platypus lactating protein (PDB: 4v00), which had a poor template quality (TM score of the first template 0.26) and contact prediction accuracy (top L long-range precision 0.30), yet C-I-TASSER successfully built the first model with a TM = 0.708, which was 194% higher than that of the I-TASSER model (0.241). In this case, of the 628 long-range contacts used to guide the replica-exchange Monte Carlo (REMC) simulations (see details of the REMC simulations in “replica-exchange Monte Carlo in C-I-TASSER” under STAR Methods and Figures S2E–S2G), 501 (80%) were false positives (Figure 3A). Despite the high amount of noise from the predicted contacts, the C-I-TASSER folding engine was able to select the correctly predicted contacts.

Figure 3.

Case study of C-I-TASSER folding on the platypus lactating protein (PDB: 4v00)

(A) The upper left shows the structure superpositions of the template (yellow) and the C-I-TASSER model (cyan) with the target structure (gray), and the lower right shows the overlay of the contact maps from contact predictors (red), the native structure (gray), and C-I-TASSER model (cyan).

(B) Comparison of contact satisfaction rates of the REMC trajectories of C-I-TASSER on two decoys.

(C) Comparison of the energy during the REMC cycles for two decoys.

(D) Comparison of the model TM scores during the REMC cycles. The structures are the decoy models for different simulation states.

In Figure 3B, we display two decoy trajectories of the contact satisfaction rate (CSR) collected from 500 REMC simulation steps. Three CSRs were calculated from each trajectory, including $CS{R}_a=n_a/N_a$, $CS{R}_p=n_p/N_p$, and $CS{R}_n=n_n/N_n$, where $n_a$ (or $n_p$ or $n_n$) is the number of overlaps between the contacts of the decoy structure and all (or positively or negatively) predicted contacts, and $N_a$ (or $N_p$ or $N_n$) is the total number of all (or positively or negatively) predicted contacts. From the figure, it can be seen that $CS{R}_{a,p,n}$ all increased as the Monte Carlo simulation progressed, but the $CS{R}_p$ increased much faster than the $CS{R}_n$. After around 100–200 steps, all CSRs became stable at the states where $CS{R}_p$ (>0.55) was much higher than $CS{R}_n$ (<0.25), suggesting that C-I-TASSER folding simulations tend to select more positively predicted contacts over incorrectly predicted contacts.

Interestingly, one trajectory (labeled as “1”) had a clearly higher $CS{R}_p$ (75% versus 58%) and lower $CS{R}_n$ (19% versus 22%) than the other trajectory (labeled as “2”), despite their $CS{R}_a$ (29.9% versus 30.0%) being nearly identical at the stable state. As shown in Figure 3C, the energy of the decoys in trajectory 1 was consistently lower than that in trajectory 2 at the stable state, suggesting that the C-I-TASSER force field was able to pick up correct contacts by integrating them with the inherent knowledge-based force field. As indicated by its lower energy, the final decoy pool from multiple REMC simulations was dominated by conformations similar to those in trajectory 1, which had much higher TM scores (∼0.69) than those in trajectory 2 (∼0.31) (Figure 3D). This eventually helped SPICKER in selecting a correctly folded model by clustering the structure decoys (Zhang and Skolnick, 2004b). In addition, we noticed that there were 25 long-range contacts that were correctly extracted from the initial LOMETS templates despite the fact that these templates had low TM scores; these contacts were all retained in the final models of the largest cluster from SPICKER, indicating the effect of these threading-based restraints in guiding the C-I-TASSER folding. As a result, as shown in Figure 3A, the contact map of the final C-I-TASSER model satisfied 45% (149/334) of the long-range contacts from the native structure, which was considerably higher than that from deep-learning-based contact predictors (34%) and LOMETS threading (7.5%) given the same number of total contacts. Hence, the effective coupling of the inherent I-TASSER force field with sparse threading and contact restraints is critical for folding such hard targets lacking quality contact prediction (see details of C-I-TASSER force fields in “replica-exchange Monte Carlo in C-I-TASSER” under STAR Methods).

As a comparison, we plot the CSR trajectories for the I-TASSER simulations in Figure S3A on the same target of 4v00. As expected, because of the lack of contact restraints, the $CS{R}_{a,p,n}$ values do not change much along with the REMC simulation. In Figure S3B–D, we also present a comparison of the CSRs in the final models by C-I-TASSER and I-TASSER for all 342 hard targets, where C-I-TASSER has higher CSRs than I-TASSER for nearly all targets, which demonstrates again the dominant role of deep-learning contacts on folding the hard protein targets in C-I-TASSER.

Structure folding of hard membrane proteins

Although the C-I-TASSER force field was mainly optimized on globular proteins, we list in Table S2 a summary of the structure folding results of C-I-TASSER on 80 non-redundant membrane domain proteins collected from the GPCR-EXP (Chan and Zhang, 2020) and PDBTM (Kozma et al., 2013) databases (see “collection of membrane protein dataset” under STAR Methods). Here, all homologous templates with a sequence identity >30% of the query or being membrane proteins were excluded from the LOMETS library. Therefore, all targets were categorized as hard targets by LOMETS.

It is seen from Table S2 that C-I-TASSER achieves an average TM score of 0.688, which is 55.7% higher than that of the I-TASSER models (0.429). This TM-score improvement is considerably larger than that obtained for the general benchmark dataset (46.2%). Despite the more stringent template filter, the average TM score (0.688) on the membrane proteins is also higher than that on the general hard proteins (0.573). These differences are probably due to the better conservation of membrane proteins in the sequence databases, which resulted in a higher accuracy of contact predictions. In fact, the average Neff of MSAs collected by DeepMSA is 659.1 for the membrane proteins, which is 6.2 times that for the general benchmark dataset (105.7). As a result, the precision of the top L/5 long-range contacts of the membrane proteins is ∼9% higher than that of general hard proteins (0.85 versus 0.78). Consequently, the higher-accuracy contact maps resulted in a larger impact on the C-I-TASSER structure modeling for folding membrane proteins.

Deep-learning contact maps improve TBM accuracy

To further examine the impact of contact maps on TBM, we tested C-I-TASSER on 455 non-redundant protein domains collected from SCOPe that were regarded by LOMETS as “easy” targets, given that significant templates with normalized Z scores >1 were detected after excluding templates with a sequence identity >30% of the query for all these domains (see definition of Z score in “replica-exchange Monte Carlo in C-I-TASSER” under STAR Methods).

In Figure S3E, we present a head-to-head comparison of the TM scores obtained by C-I-TASSER and I-TASSER for these easy targets. First, compared with the hard targets, the TM scores of the final models for the easy targets were dramatically higher for both C-I-TASSER and I-TASSER (Table S1), highlighting the importance of template quality in the final models. Second, despite the use of the same set of templates, C-I-TASSER outperformed I-TASSER in 343 of the 455 cases, whereas the converse was true for 112 cases. The average TM score by C-I-TASSER (0.765) was 3.2% higher than that by I-TASSER (0.741), which corresponded to p = 2.5 × 10⁻²⁸ in Student's t test, indicating that the difference was highly statistically significant.

It is important to note that sequence-based contact-map predictions have been of little to no use for TBM until the most recent CASP experiments (Kryshtafovych et al., 2018; Zhang et al., 2018). The data in Table S1 and Figure S3E suggest that the deep-learning-based approaches increased the accuracy of contact-map prediction and brought it to a level compatible with threading templates for TBM. In Figure S3F, we also plot the data with the LOMETS TM score against contact precision for the 455 easy targets. It was found that C-I-TASSER successfully folded a much higher number of cases (by 29%) than I-TASSER for targets with LOMETS TM < 0.5, demonstrating again the power of contact maps in refining incorrectly predicted templates.

Comparison with the state of the art

To further investigate the effectiveness of C-I-TASSER, we list in Table S1 the modeling results of C-I-TASSER in comparison with those by CNS (Brunger et al., 1998) and trRosetta (Yang et al., 2020). For CNS, we input the same sets of predicted contacts and secondary structure used in C-I-TASSER. Given that trRosetta generates spatial restraints (distances and orientations) on its own, we provided the same MSAs but used only the contact restraints (i.e., distances with the peak of predicted distance distribution lower than 8 Å or when the sum of probabilities below 8 Å is greater than 0.5), to have a fair comparison with C-I-TASSER. The significant improvement of C-I-TASSER over CNS/trRosetta on easy targets (TM = 0.765 versus 0.408/0.534) is largely due to the use of LOMETS templates, which by themselves had a higher TM-score (0.657) than the CNS/trRosetta models. For the hard targets, the TM score of C-I-TASSER (0.573) was also significantly higher than those of CNS (0.498) and trRosetta (0.500) with p = 7.4 × 10⁻²⁸ and 5.5 × 10⁻⁷. Given that both CNS and trRosetta create models by optimally satisfying spatial constraints, these data highlight the effectiveness of C-I-TASSER in integrating the optimized knowledge-based force field with deep-learning-based contact maps.

To examine C-I-TASSER in comparison with the state of the art, an early version of C-I-TASSER was tested in the CASP13 experiment, for which Table S3 lists a summary of the 3D structure modeling results of the best 20 groups in the Server Section, in which models were automatically created in a blind fashion, i.e., without knowledge of the experimental structures (Kryshtafovych et al., 2019). It was shown that the C-I-TASSER method (named “Zhang-Server”) outperformed all other groups based on both TM and global distance test score (GDT score); here GDT score is calculated by GDT = (GDT_P1 + GDT_P2 + GDT_P4 + GDT_P8)/4, where GDT_Pn indicates the percent of residues under the distance cut-off ≤ n Å . In Figure S4, we list the structural models created by C-I-TASSER for 32 of the 50 FM and FM/TBM targets, which lacked homologous templates, for which C-I-TASSER was able to generate correct folds with TM ≥ 0.5. These data demonstrate the superiority of C-I-TASSER over state-of-the-art structure prediction approaches.

Structure modeling for unsolved Pfam families

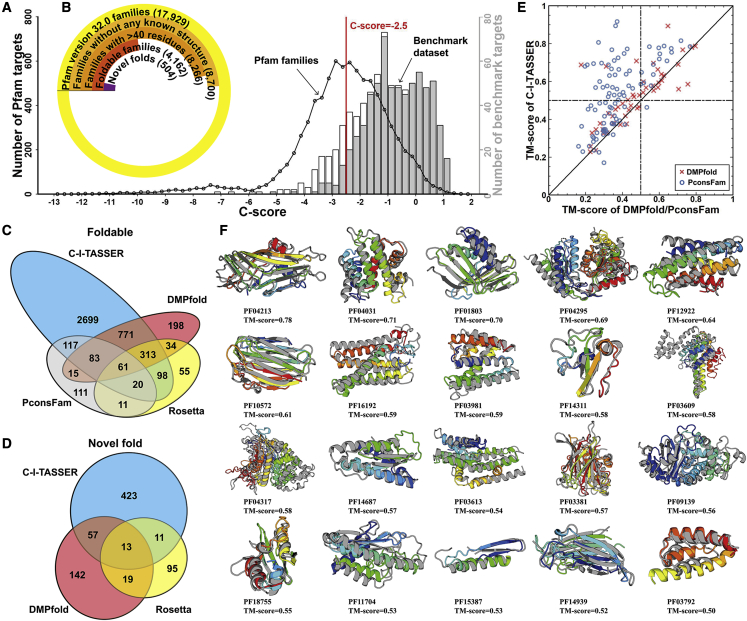
Pfam is a database of protein families (El-Gebali et al., 2018), each represented as a sequence profile of structurally and/or functionally related protein domains. There are 17,929 protein single-domain-level families in the Pfam database (version 32.0), of which 9,229 have at least one member with an experimentally determined structure in the PDB. For the proteins in the Pfam families with known structures, reliable models could be built through comparative modeling with the members with known structure. For the remaining 8,700 families, however, no structural information is available for any members; these families are named “unsolved Pfam families” for simplicity in this paper. Here, we used C-I-TASSER to predict structure models for the 8,266 unsolved Pfam families that were at least 40 amino acids long, and the details of the data collection are described in “Pfam dataset” under STAR Methods.

Overall results

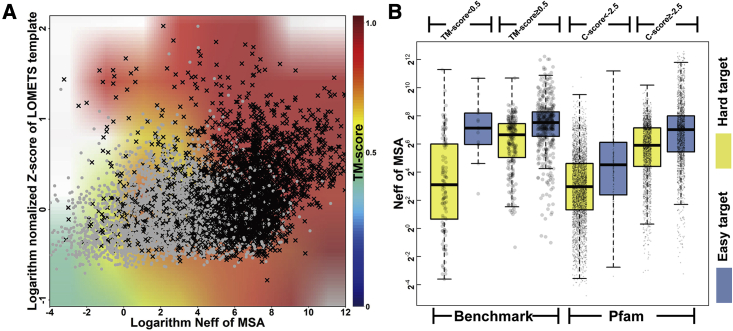
Given that the experimental structures are unknown for these unsolved Pfam families’ domains, we designed a confidence score (C score) to quantitatively estimate the quality of the C-I-TASSER models. As shown in Equation S23 in “model quality estimation of C-I-TASSER” under STAR Methods, the C score is a linear combination of three components: significance of the LOMETS threading alignments, satisfaction rate of the predicted contact maps, and the decoy convergence degree of the C-I-TASSER simulations. Based on the 797 test targets (342 hard and 455 easy) in the benchmark dataset, the C score had a Pearson correlation coefficient of 0.80 with TM score (see Figures S5A and S5B and “model quality estimation of C-I-TASSER” under STAR Methods). If we select a C-score cutoff of −2.5, which corresponds to an estimated TM = 0.5, the Matthews correlation coefficient on the benchmark dataset reached a maximum of 0.623 and the false discovery rate (FDR) only 6.88%.

In Figure 4A, we present the C-score histogram distribution of the C-I-TASSER models on the 8,266 unsolved Pfam families, where the C score from the benchmark targets is listed as a control. If we assume that the C-I-TASSER models have a similar FDR between the benchmark and the Pfam families, there should be around 3,876 (=4,162 ∗ (100% – 6.88%)) of the 4,162 high-confidence Pfam families that are foldable with an estimated TM ≥ 0.5. We further searched the 4,162 Pfam models against the PDB by TM-align (Zhang and Skolnick, 2005) and found that 504 Pfam models predicted by C-I-TASSER did not have any structure in the PDB that had a TM ≥ 0.5 in relation to the predicted model. Therefore, these Pfam families might assume novel folds; the construction of these new fold models is mainly due to the employment of the deep-learning contact maps. A summary of the Pfam modeling results is listed in Figure 4B.

Figure 4.

Structural modeling results for unsolved Pfam families

(A) The distribution of Pfam families and benchmark targets in different C-score bins. The black circles represent the number of Pfam targets in a specific C-score bin, and histograms are from benchmark proteins; the gray bars indicate the number of foldable targets with TM ≥ 0.5 and the white bars being the number of non-foldable targets.

(B) Number of Pfam families at each stage of the analysis, where each set is a subset of the previous set.

(C) Venn diagram for the number of foldable models for the Pfam families constructed by C-I-TASSER, Rosetta, DMPfold, and PconsFam.

(D) Venn diagram for the number of novel folds for the Pfam families produced by C-I-TASSER, Rosetta, and DMPfold.

(E) Comparison of the TM scores for the first models produced by C-I-TASSER versus those by DMPfold (red crosses) and PconsFam (blue circles) for 96 Pfam families that have at least one member newly solved after modeling.

(F) Case study of 20 Pfam families regarded as hard by LOMETS. In each case, the model is shown in rainbow color and the solved experimental structure of a member from the same Pfam family, if available, is shown in gray.

Comparison with other methods of Pfam family modeling

Three recent studies (Greener et al., 2019; Lamb et al., 2019; Ovchinnikov et al., 2017) performed structure prediction for the unsolved Pfam families. Among them, Rosetta (Ovchinnikov et al., 2017) generated models for 592 unsolved Pfam families, of which 138 were novel folds. DMPfold (Greener et al., 2019) attempted to fold 5,214 families for which HHsearch (Söding, 2005) was unable to detect homologous templates and reported 1,475 foldable models and 231 novel folds. Finally, PconsFam (Lamb et al., 2019) folded all 13,617 Pfam families from Pfam v.29.0 and reported only 418 foldable models (with no novel fold information reported). Although DMPfold produced a relatively high number of foldable models (1,475), the FDR reported in the DMPfold benchmark analysis was 17.5%, which was considerably higher than the C-I-TASSER FDR of 6.88% at a C-score cutoff of −2.5. Based on the FDR value, the number of trustable cases by DMPfold should be 1,217 (=1,475 ∗ (100%–17.5%)), which is also significantly lower than the reliably folded models (1,892 = 2,032 ∗ (100%–6.88%)) produced by C-I-TASSER, where 2,032 is the number of the foldable cases by C-I-TASSER on the same set of 5,214 Pfam families that DMPfold used.

In Figure 4C, we present a Venn diagram of modeling results by C-I-TASSER, Rosetta, DMPfold, and PconsFam on the unsolved Pfam families. There were overall 2,699 families that were foldable by C-I-TASSER but not by any other method; this number was 55 for Rosetta, 198 for DMPfold, and 111 for PconsFam. Furthermore, the number of novel folds discovered by C-I-TASSER (504) was considerably higher than that of either Rosetta or DMPfold (Figure 4D). Considering that different methods have modeled different sets of Pfam families, in Figures S5C–S5E we present the Venn diagrams on the same set of Pfam families folded by C-I-TASSER and the control methods. More specifically, we restricted the C-I-TASSER results to the Pfam families modeled by the Rosetta, DMPfold, and PconsFam studies to make a fairer comparison. We found that C-I-TASSER still created considerably more foldable families and novel folds than the control methods in this common dataset.

Blind test of the Pfam family models

The C-I-TASSER modeling was performed on the Pfam database version 32.0 (released in September 2018), and the modeling data are summarized in Table S4 for all 8,266 unsolved Pfam families. Pfam v.33.0 (released in March 2020) reported 305 new families with solved structures for at least one member, which provides an opportunity to assess the performance of the prediction effort. Because 192 of the structures in the 305 families were released before the C-I-TASSER threading was completed in June 2019 and the target structures were included in the template library, these families should be excluded from our assessment.

The comparison between the C-I-TASSER models and the solved experimental structures is listed in Table S4, where an average TM score of 0.532 was achieved for the 113 domains whose structures were released after June 2019, for which 63 had correctly folded models with TM > 0.5. Here, given that only one member from each Pfam family was modeled by C-I-TASSER, the modeled sequence might be different from that of the solved structure. For these cases, we superposed the structure of the solved protein to the C-I-TASSER model by using TM-align and calculated the TM score between the C-I-TASSER model and the mapped experimental structure.

Figure 4E shows a comparison of TM scores for the first models generated by C-I-TASSER, DMPfold, and PconsFam on the 96 Pfam families for which DMPfold or PconsFam also published their predicted models. DMPfold generated models for only 50 of the 96 Pfam families, whereas PconsFam produced models for 91 of the 96 Pfam families. We did not include the comparison with Rosetta here because Rosetta produced models for only 2 of the 96 Pfam families, which was insufficient for meaningful statistical analysis. Compared with the experimental structures, the TM scores of the C-I-TASSER models were higher than those of PconsFam for 93.4% (85 of 91) of the common Pfam families. Moreover, C-I-TASSER generated models with TM ≥ 0.5 for 50 of the 91 Pfam families, which was 194% higher than the number (17) by PconsFam, demonstrating the advantage of coupling contact maps with template-based restraints in C-I-TASSER compared with the CNS-based pipeline used by PconsFam, which relies only on contact prediction. Although DMPfold utilized deep-learning distance prediction in addition to contact restraints, C-I-TASSER also outperformed DMPfold on 74% (37/50) of the Pfam families. For the 50 Pfam families for which DMPfold generated models, C-I-TASSER generated models with TM ≥ 0.5 for 26 Pfam families, which was 37% higher than that by DMPfold (19).

Figure 4F lists C-I-TASSER models for 20 successfully folded Pfam families that lack homologous templates in the PDB and were regarded as hard targets by LOMETS; the structures for another 43 successfully folded families, including 38 regarded as easy and 5 regarded as hard, but with a naive fold composed of a single helix, are shown in Figure S6. Taken together, these data show that C-I-TASSER modeling guided by contact-based constraints generates useful models for unsolved Pfam families. The structural models for all 8,266 unsolved Pfam families are available at https://zhanglab.ccmb.med.umich.edu/C-I-TASSER/pfam/.

Lessons on improving C-I-TASSER for other Pfam families

Despite the fact that ∼50% of the unsolved Pfam families could be folded by C-I-TASSER with high confidence, it is important to examine why C-I-TASSER could not generate foldable models for the remaining Pfam families. In Figure 5A, we compare the benchmark targets and Pfam families in terms of template quality (measured by normalized Z score of LOMETS templates) and contact-map accuracy (indicated by the MSA Neff values), where two interesting points can be observed. First, the TM-score heatmap for the benchmark targets is highly consistent with the regions of Pfam families with low (gray) or high (black) C scores, showing that C score can indeed be used as a reliable measure for estimating the quality of unsolved Pfam family models. Second, we found that for the 4,162 Pfam models with C > −2.5, 95.5% (= 3,974/4,162) had either a high Neff value (≥ 2³) or a high template Z score (≥ 1), suggesting that successful C-I-TASSER modeling requires either good templates or relatively accurate contact prediction for most targets.

Figure 5.

Comparison of the C-I-TASSER results for the Pfam families and benchmark dataset for different C scores, Z scores, and Neff values

(A) Normalized Z score of the first LOMETS template versus the Neff of DeepMSA for the Pfam families (points) and benchmark dataset (background). The black crosses represent the Pfam targets with C ≥ −2.5, and the gray dots are Pfam targets with C < −2.5. The heatmap in the background depicts the TM scores for benchmark targets, where white regions indicate no data.

(B) The box-and-whisker chart for the logarithm Neff values of MSAs for easy and hard targets in the Pfam families and benchmark dataset. The left corresponds to the results of the benchmark dataset, and the right contains the results for the Pfam families. The yellow boxes indicate the hard targets, and the blue boxes are the easy targets.

To further examine the impact of the contact maps, we list the Neff distribution for different Pfam families in Figure 5B. We observed that the average Neff (=208.3) for the 4,162 foldable Pfam families was 7.4 times higher than that for the non-foldable Pfam families (=28.1). Among the foldable families, the easy targets (Z $\ge$ 1) generally had a slightly higher Neff than the hard targets (Z < 1); this is understandable because easy families are often more well studied by the community and therefore tend to have more homologous sequences in both structure and sequence databases. As a control, we also listed the Neff distribution of the 797 benchmark proteins, where a similar trend was seen (i.e., easy targets tend to have higher Neffs). Here it is worth noting that although both Pfam and benchmark proteins contain easy and hard targets, Pfam families seem more difficult to fold because by design we selected to model only the unsolved Pfam families containing no solved structures in the homologous members, whereas easy benchmark proteins do not have such constraints. On average, the Neff of Pfam families (118.8) is also considerably lower than that of the benchmark proteins (236.1); these data partly explain the results of Figure 4A in which the overall C-score distribution of Pfam families was shifted to the lower values compared with the benchmark proteins.

Thus, given that the majority of the Pfam families with C < −2.5 (93.8% = 3,848/4,104) were hard targets that lacked homologous templates in the PDB, it will be critically important to develop effective MSA collection and contact-map prediction methods to model the structures of these hard Pfam families. In addition, given that many newly developed LOMETS programs (Zheng et al., 2019c) utilize MSAs and deep-learning contact maps, better MSAs and contact maps will help LOMETS to reliably detect distant-homologous templates, which can convert the Pfam families from the hard to the easy category and help improve the quality of final models from the TBM aspect as well.

Application to COVID-19 structure modeling

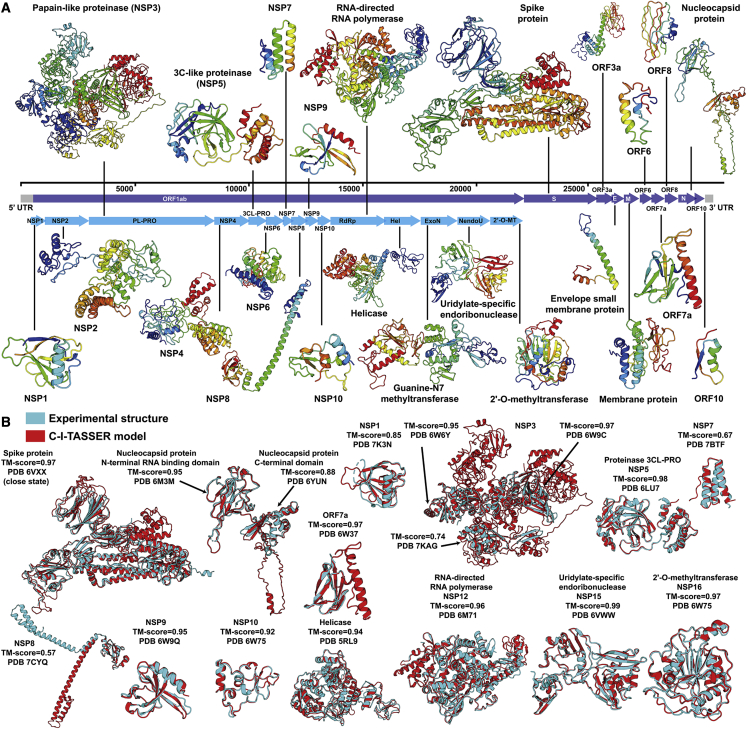
SARS-CoV-2 is a new coronavirus responsible for the ongoing COVID-19 pandemic, which has resulted in more than 80 million infections with 1.8 million deaths. To help understand the mechanism of the new virus, we applied C-I-TASSER to generate a genome-wide structure modeling study on SARS-CoV-2 (see “SARS-CoV-2 dataset” under STAR Methods). The C-I-TASSER models for all SARS-CoV-2 proteins, including 4 structural proteins (spike protein, envelope small membrane protein, membrane protein, and nucleocapsid protein) and 20 non-structural proteins, are displayed in Figure 6A; all structures are downloadable at https://zhanglab.ccmb.med.umich.edu/COVID-19/. A summary of the modeling details is also listed in Table S5. It is noted that the SARS-CoV-2 proteins have generally few homologous sequences in the sequence database, where the average Neff (=21.0) is much lower than those of the benchmark dataset (236.1) and the unsolved Pfam families (118.8), probably due to the relatively new species and the quick mutation rate of the virus.

Figure 6.

Application of C-I-TASSER to COVID-19 structure modeling

(A) C-I-TASSER models for all 24 proteins in the SARS-CoV-2 genome, including 4 structural proteins and 20 non-structural proteins.

(B) The structure superpositions of the C-I-TASSER models (red) with the experimental structures (cyan) for 17 solved SARS-CoV-2 proteins/domains, for which C-I-TASSER created models with correct fold (TM >0.5).

After the C-I-TASSER models were released in January 2020, 20 protein structures from the SARS-CoV-2 genome were experimentally solved. Compared with these experimental structures, the C-I-TASSER models have a correct fold for 17 proteins, whose structure superposition with the experimental structure and TM scores are shown in Figure 6B. For another 3 targets, including ORF3a protein (ORF3a), envelope small membrane protein (E), and ORF8 protein (ORF8), however, C-I-TASSER failed to generate correct folds because of the poor quality of template recognition and contact-map predictions. The poor quality of contact-map prediction is mainly due to the low multiplicity of the MSAs, where the Neff values are 0.4, 4.5, and 0.4, respectively, even though the metagenome database was utilized.

Overall, despite the relatively lower Neff values for the SARS-CoV-2 proteins, the average TM score of the C-I-TASSER is 0.820, which is even higher than that of the easy benchmark proteins (0.765), probably because of the better template quality identified by LOMETS for the SARS-CoV-2 proteins (TM = 0.748). These data confirm the ability of C-I-TASSER to create high-resolution models for the unknown SAR-CoV-2 genome. In Table S5, we also list the estimated TM score for each model of the SARS-CoV-2 genome proteins, which were calculated on the basis of the C score of C-I-TASSER simulations (see Equation S24 in “model quality estimation of C-I-TASSER” under STAR Methods). The estimated TM score values can be used as references for the model quality for the proteins currently without experimentally solved structures.

Discussion

We developed a pipeline, C-I-TASSER, for contact-guided protein-structure prediction. Compared with its predecessor, the I-TASSER protocol, C-I-TASSER shows a significantly improved ability to model structures of non-homologous sequences. Based on a benchmark test of 342 hard proteins lacking homologous templates in the PDB, the average TM score of C-I-TASSER was 46% higher than those of I-TASSER, and the number of foldable domains with TM > 0.5 increased by 2.55 times in relation to I-TASSER. Compared with the modest TM-score increase (4.6%) witnessed previously by contact-map-guided template-based structure prediction (Wu et al., 2011), the significant improvement of the model quality achieved in this study can be mainly attributed to the substantial increase in contact-map accuracy brought by advanced deep neural network learning techniques in combination with deep MSA collection from whole-genome and metagenome databases. Although C-I-TASSER was primarily optimized on globular proteins, it showed a stronger ability to fold hard membrane proteins with an average TM score 20% higher than those for the globular proteins, which is probably because of the more conserved sequence profiles and therefore more accurate contact-map predictions for the member proteins. The 3D structure modeling accuracy of C-I-TASSER is also significantly higher than the pipelines based purely on contact-map satisfaction (e.g., CNS) (Brunger et al., 1998, and trRosetta, Yang et al., 2020), demonstrating the importance of the effective coupling of contact maps with threading-template restraints and knowledge-based force fields by using cutting-edge structural assembly simulations. Here, it is worth noting that although the average TM score (0.573) is quite close to the baseline of correct fold (TM score = 0.5), there are 15% (= 50 out of 342) of the hard cases whose TM score is above the average TM score of easy targets (0.765), or 41% (= 140 out of 342) of hard cases whose TM score is above 0.652, which is one standard deviation away from the average TM score of easy targets; this indicates that C-I-TASSER builds models for a considerable fraction of hard targets whose quality is comparable to that obtained by traditional homology modeling approaches and shown useful in various biological applications (Zhang, 2009).

The C-I-TASSER pipeline was applied to predict models for 8,266 unsolved Pfam families. Reliable models were generated for nearly half of the domains with a low FDR of 6.88%. Among them, we found 504 novel folds that do not exist in the PDB library, demonstrating the power of the sequence-based contact map for assisting ab initio structural folding. Both numbers of reliably predicted models and novel folds were considerably higher than the recent modeling studies built on contact and distance maps. Compared with the 96 families with experimental structures recently released, it was found that the number of foldable cases by C-I-TASSER was 53, which is 66% higher than that of a combination of the best models by DMPfold and PconsFam. As a real-world application, we also applied C-I-TASSER to generate genome-wide structure models for the SARS-CoV-2 coronavirus, where a comparison with 20 newly solved experimental structures showed that 85% of the models have correct folds with an average TM = 0.820, confirming the usefulness of C-I-TASSER for modeling new genomes.

Overall, because of the advancement of new deep machine learning techniques, structure folding of distantly homologous proteins has shifted largely from fold recognition in the PDB to evolutionary pattern detection from homologous sequences, as the latter can result in high-quality contact maps to assist structural assembly. Despite the success of the C-I-TASSER pipeline, considerable challenges still exist in folding distantly homologous proteins that have little sequence homology in the sequence databases (i.e., quadrant III in Figure 2B). Therefore, development of sensitive MSA algorithms from the rapidly increasing whole-genome and metagenome sequence databases is key to addressing this problem. Meanwhile, deep-learning-based interresidue distance and torsion-angle maps along with hydrogen bond network predictions have been recently found to further assist modeling quality improvement (Li et al., 2020; Senior et al., 2020; Xu, 2019; Yang et al., 2020). In particular, the end-to-end training powered with attention networks demonstrated an unprecedented ability for folding nearly all single-domain proteins in the CASP14 experiment (Jumper et al., 2020). Studies along these lines are in progress.

Limitations of the study

To reliably fold a protein by C-I-TASSER with a high success rate, either a set of good structure templates or a highly accurate residue-residue contact-map prediction is required. Given that the contact maps are deduced from MSAs through deep learning models, an MSA with a sufficient number of effective sequences (Neff >8) is one of the essential conditions for correct folding of a non-homologous protein by C-I-TASSER.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
C-I-TASSER	This paper	https://zhanglab.ccmb.med.umich.edu/C-I-TASSER/ https://zhanglab.ccmb.med.umich.edu/C-I-TASSER/standalone/C-I-TASSER-1.0.tar.bz2 https://github.com/jlspzw/C-I-TASSER
R	The R Project for Statistical Computing	https://www.r-project.org/
LOMETS	(Wu and Zhang, 2007; Zheng et al., 2019c)	https://zhanglab.ccmb.med.umich.edu/LOMETS/
HMMER	(Eddy, 1998)	http://hmmer.org/
ResTriplet	(Li et al., 2019b)	https://zhanglab.ccmb.med.umich.edu/ResTriplet/
TripletRes	(Li et al., 2021)	https://zhanglab.ccmb.med.umich.edu/TripletRes/
ResPRE	(Li et al., 2019a)	https://zhanglab.ccmb.med.umich.edu/ResPRE/
ResPLM	(Li et al., 2019b; Zheng et al., 2019a)	N/A
NeBcon	(He et al., 2017)	https://zhanglab.ccmb.med.umich.edu/NeBcon/
Pytorch	(Paszke et al., 2017)	https://pytorch.org
DeepMSA	(Zhang et al., 2019)	https://zhanglab.ccmb.med.umich.edu/DeepMSA/
PSSpred	(Yan et al., 2013)	https://zhanglab.ccmb.med.umich.edu/PSSpred/
STRIDE	(Frishman and Argos, 1995)	http://webclu.bio.wzw.tum.de/stride/
SPICKER	(Zhang and Skolnick, 2004b)	https://zhanglab.ccmb.med.umich.edu/SPICKER/
TM-score	(Zhang and Skolnick, 2004a)	https://zhanglab.ccmb.med.umich.edu/TM-score/
TM-align	(Zhang and Skolnick, 2005)	https://zhanglab.ccmb.med.umich.edu/TM-align/
REMO	(Li and Zhang, 2009)	https://zhanglab.ccmb.med.umich.edu/REMO/
FASPR	(Huang et al., 2020)	https://zhanglab.ccmb.med.umich.edu/FASPR/
FG-MD	(Zhang et al., 2011)	https://zhanglab.ccmb.med.umich.edu/FG-MD/
ThreaDom	(Xue et al., 2013)	https://zhanglab.ccmb.med.umich.edu/ThreaDom/
DEMO	(Zhou et al., 2019)	https://zhanglab.ccmb.med.umich.edu/DEMO/
I-TASSER	(Wu et al., 2007; Yang et al., 2015)	https://zhanglab.ccmb.med.umich.edu/I-TASSER/
CNS	(Brunger et al., 1998)	https://www.mrc-lmb.cam.ac.uk/public/xtal/doc/cns/cns_1.3/tutorial/text.html
trRosetta	(Yang et al., 2020)	https://github.com/gjoni/trRosetta

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Yang Zhang (zhng@umich.edu)

Materials availability

This study did not generate new unique reagents.

Data and code availability

The C-I-TASSER server is available at Zhang Lab (https://zhanglab.ccmb.med.umich.edu/C-I-TASSER/). The standalone package of C-I-TASSER can be downloaded at https://zhanglab.ccmb.med.umich.edu/C-I-TASSER/download.html or https://github.com/jlspzw/C-I-TASSER. The datasets supporting the current study have been deposited in Zhang Lab for public use, where the benchmark and membrane datasets are available at https://zhanglab.ccmb.med.umich.edu/C-I-TASSER/dataset.tar.bz2, the structure models for Pfam domain families are available at https://zhanglab.ccmb.med.umich.edu/C-I-TASSER/pfam/, and the structural models for SARS-CoV-2 genome are available at https://zhanglab.ccmb.med.umich.edu/COVID-19/.

Experimental model and subject details

This study did not use experimental models typical in the life sciences.

Method details

Benchmark dataset collection

The benchmark dataset consists of single-domain proteins collected from the SCOPe 2.06 database (Chandonia et al., 2018) and the FM and FM/TBM targets from CASP 8–12 (Moult et al., 2009, 2011, 2014, 2016, 2018). Redundant proteins were removed using a pairwise sequence identity cutoff <30% and only sequences with lengths between 50 and 450 amino acids were kept in the benchmark dataset. Furthermore, we removed targets that had break positions where the residue indices were not consecutive or the C_α distance between two consecutive residues was greater than 5Å in the middle of the protein chain, which resulted in 797 targets with 179 α proteins, 101 β proteins, and 517 α/β or α+β proteins. Based on LOMETS (Wu and Zhang, 2007; Zheng et al., 2019c), this set contained 200 Trivial, 255 Easy, 239 Hard, and 103 Very Hard targets (see below: “LOMETS2 pipeline for meta-server threading”). In our benchmark analysis, the “Trivial” and “Easy” targets were combined into one group called “Easy targets” (455), while the “Hard” and “Very Hard” targets were integrated into one group called “Hard targets” (342). When LOMETS is performed, all homologous templates with a sequence identity >30% to the target were excluded.

Collection of membrane protein dataset

The membrane protein dataset contains 80 single domain proteins collected from GPCR-EXP (Chan and Zhang, 2020) and PDBTM (Kozma et al., 2013) databases. Similar with the benchmark dataset, redundant proteins were removed using a pairwise sequence identity cutoff <30%, and only the sequences with lengths between 50 and 450 amino acids were kept. The single-helix transmembrane proteins with a trivial topology have been removed as well. Finally, this dataset contains 73 α-helix proteins and 7 β-sheet proteins, where 30 G protein-coupled receptors (GPCRs) are included.

When LOMETS is performed on the proteins, all homologous templates either with a sequence identity >30% to the target or belonging to membrane proteins were excluded. Here, the GPCR-EXP, PDBTM, and MPstruct databases are used for determining whether a template belongs to the membrane protein. We added the additional filter in order to make the test more stringent for the membrane proteins, as we found that two proteins can share similar structures even with a low sequence identity. For example, C-C chemokine receptor type 2 (CCR2) and C5a anaphylatoxin chemotactic receptor 1 (C5AR1) share a sequence identity of 23% but have TM-score of 0.80 between their structures. Thus, to check the influence of predicted contacts to C-I-TASSER folding, we remove not only homologous templates by sequence identity cutoff, but also all membrane proteins. After excluding the templates by LOMETS, we found all 80 proteins are classified as “Hard” targets by LOMETS.

Pfam dataset

Pfam is a database of protein families (El-Gebali et al., 2018), each represented by hidden Markov models (HMMs). Typically, each Pfam entry is comprised of a seed alignment, which forms the basis to build a profile hidden Markov model using the HMMER software (http://hmmer.org/) (Eddy, 1998). The profile HMM is then queried against a sequence database, and all matches scoring above the curated threshold are aligned back to the profile HMM to generate the full alignment.

The Pfam dataset was collected from the Pfam version 32.0 database, which includes 17,929 protein families. We removed 9,229 protein families that had structural annotations concerning experimentally determined X-ray crystal, nuclear magnetic resonance (NMR), or Cryo-electron microscopy (Cryo-EM) structures. For the remaining 8,700 families, there was no structural information available for any member. We further removed Pfam families with less than 40 amino acids of sequence length, resulting in a dataset of 8,266 Pfam families.

Note that there are multiple sequences available for each Pfam family. We only picked up one representative sequence from each Pfam family, and then used C-I-TASSER to predict a structure model for the representative sequence. The representative sequence for each Pfam family was selected using the following steps. First, we ran ‘hmmsearch’ to search a specific Pfam family against uniref100 (May 2019) database (Suzek et al., 2014). Then, we ranked all of the sequences hit from uniref100 by their E-values. Finally, we selected the first sequence that satisfied the formula:

$$\frac{Cov1+Cov2}{2}>0.95$$ (Equation S1)

$$Cov1=\frac{len\left(aligned\right)}{len\left(hmm\right)}$$ (Equation S2)

$$Cov2=\frac{len\left(hmm\right)}{len\left(aligned\right)+len\left(insertion\right)}$$ (Equation S3)

where len(hmm) is the length of the HMM for a specific Pfam family, len(aligned) is the length of the alignment between the hit sequence and the Pfam HMM, and len(insertion) is the length of the hit sequence aligned to the gaps in the middle of the Pfam HMM. This criterion guaranteed that the selected representative sequences did not contain too many inserted residues compared to the Pfam HMMs, and that the selected sequences should have high coverage with respect to the HMMs.

Pfam 32.0 modeling timeline

September 2018, Pfam 32.0 database was released.

June 2019, LOMETS threading was completed for 8,266 unsolved Pfam (32.0) families, followed by C-I-TASSER folding simulation and structure refinement.

March 2020, Pfam 33.0 database was released. 305 unsolved families in Pfam 32.0 have been solved and reported in Pfam 33.0. The structures for 113 of those 305 families have been released after June 2019, and thus selected as a blind test set for C-I-TASSER (Figure 4F in main text and Figure S6) since none of the solved structure information was used during the C-I-TASSER modeling.

SARS-CoV-2 dataset

We built C-I-TASSER three-dimensional (3D) models for the proteins from the genome of the SARS-CoV-2 virus, also known as 2019-nCoV, which is the novel coronavirus that caused the COVID-19 pandemic. First, all protein sequences were translated from the complete genome of SARS-CoV-2 available at https://www.ncbi.nlm.nih.gov/nuccore/MN908947.3. For each sequence, ThreaDom (Xue et al., 2013) was used to split the target into several domains according to threading template alignment. Then, the C-I-TASSER pipeline was used to generate structure models for each domain. For multi-domain targets, the C-I-TASSER structures of individual domains were assembled by DEMO (Zhou et al., 2019) into full-length structures.

In total, we predicted 24 structures from the above SARS-CoV-2 genome, including host translation inhibitor nsp1 (NSP1), non-structural protein 2 (NSP2), papain-like proteinase (NSP3), non-structural protein 4 (NSP4), 3C-like proteinase or non-structural protein 5 (3CL-PRO), non-structural protein 6 (NSP6), non-structural protein 7 (NSP7), non-structural protein 8 (NSP8), non-structural protein 9 (NSP9), non-structural protein 10 (NSP10), RNA-directed RNA polymerase (RdRp), helicase (Hel), Guanine-N7 methyltransferase (ExoN), uridylate-specific endoribonuclease (NendoU), 2'-O-methyltransferase (2'-O-MT), spike glycoprotein (S), ORF3a protein (ORF3a), envelope small membrane protein (E), membrane protein (M), ORF6 protein (ORF6), ORF7a protein (ORF7a), ORF8 protein (ORF8), nucleocapsid protein (N), ORF10 protein (ORF10).

Methods summary

C-I-TASSER integrates contact-map prediction with the cutting-edge threading and fragment assembly method I-TASSER to make protein structure prediction. As an independent structure assembly pipeline, I-TASSER was tested in former CASPs and consistently ranked as one of the most accurate methods in the last decade. Accordingly, the online I-TASSER server (https://zhanglab.ccmb.med.umich.edu/I-TASSER/) has been widely used in the community and serving for more than 130,000 users from 149 countries (Figure S1). With the newly added features, C-I-TASSER pipeline was tested in the Server Section of the CASP13 experiment, where C-I-TASSER method (named “Zhang-Server”) outperformed all other groups based on both TM and GDT scores.

The C-I-TASSER pipeline includes five steps: deep multiple sequence alignment generation, structural template identification and residue-residue contact prediction, iterative structure assembly, atomic-level structure refinement, and model quality estimation. We describe the steps as following.

LOMETS2 pipeline for meta-server threading

LOMETS2 (Wu and Zhang, 2007; Zheng et al., 2019c) is a meta-threading server for quick template-based fold recognition and protein structure prediction. It integrates 11 state-of-the-art threading programs: one contact-based threading program CEthreader (Zheng et al., 2019b), three profile HMM-based threading programs HHpred (Meier and Söding, 2015), HHsearch (Söding, 2005), and PRC (Madera, 2008), and seven profile-based threading programs FFAS3D (Xu et al., 2013), MUSTER (Wu and Zhang, 2008), Neff-MUSTER(Zheng et al., 2019c), PPAS (Yang et al., 2015), PROSPECT2 (Xu and Xu, 2000), SP3 (Zhou and Zhou, 2005), and SparksX (Yang et al., 2011), to help improve the quality of the meta-threading results. Particularly, CEthreader (https://zhanglab.ccmb.med.umich.edu/CEthreader/) (Zheng et al., 2019b) is a fold-recognition algorithm to identify similar-fold structures from the PDB guided by predicted contact-maps. The core part of the algorithm consists of contact-map prediction, eigen-decomposition of the contact matrix, and contact-guided template search and selection.

All individual threading methods are locally installed and run on our computer cluster to ensure the quick generation of initial threading alignments. Also, template libraries are updated every week. Due to its speed and accuracy, LOMETS2 is used as the initial step of C-I-TASSER to identify structural templates and generate query-template alignments. The LOMETS2 pipeline consists of three consecutive steps: generation of sequence profiles, fold recognition through its component threading programs, and template ranking and selection.

Generation of sequence profiles

Starting from a target protein sequence, the DeepMSA (Zhang et al., 2019) method (see below: “DeepMSA for MSA generation”) is used to generate deep MSAs and further calculate deep profiles in the form of sequence profiles or profile Hidden Markov Models (HMMs), which are prerequisite to different individual threading programs.

Fold recognition through the component threading programs

The profiles generated in the first step are used by the 11 LOMETS2 threading programs to identify template structures from the template library, where profiles are pre-built for each template.

Template ranking and selection

For a given target, the top 20 templates, ranked by the Z-scores (Wu and Zhang, 2007; Zheng et al., 2019c) of their query-template alignments, are first selected for each program, resulting in a preliminary set of 220 candidate templates. The Z-scores can be calculated as follows:

$$Z-score\left(i,j\right)=\frac{S\left(i,j\right)-S\left(j\right)}{\sigma \left(j\right)}$$ (Equation S4)

where $S\left(i,j\right)$ is the alignment score of the i-th template for the j-th program, and $S\left(j\right)$ and $\sigma \left(j\right)$are the average and standard deviation of the alignment scores across all templates for the j-th program, respectively.

Then, the top N templates are selected from the 220 templates based on a scoring function that integrates Z-score, the confidence score of each method, and sequence identity between the identified templates and query sequence. These N selected templates are further used as initial constraints in the C-I-TASSER pipeline. The number of final selected templates, N, is varied with regard to different targets. The scoring function used to re-rank the templates can be calculated as follows:

$$score\left(i,j\right)=conf\left(j\right)\ast \frac{Z-score\left(i,j\right)}{Z_0\left(j\right)}+seqid\left(i,j\right)$$ (Equation S5)

where $seqid\left(i,j\right)$ is the sequence identity between the query and the i-th template for the j-th program, $conf\left(j\right)$ is the confidence score for the j-th program, which was calculated by determining the average TM-scores over the first templates to the native structures on a training set of 243 non-redundant target proteins (Wu and Zhang, 2007), and $Z_0\left(j\right)$ is the Z-score cut-off for defining good/bad templates for the j-th program, which was determined by maximizing the Matthews correlation coefficient (MCC) for distinguishing a good template (with a TM-score ≥0.5) from a bad template (TM-score <0.5) on the same training set. As a result, the parameters $Z_0\left(j\right)$ (and $conf\left(j\right)$) are 83.0 (0.589), 6.9 (0.587), 33.0 (0.574), 8.7 (0.570), 6.1 (0.569), 10.0 (0.567), 7.0 (0.566), 7.6 (0.562), 3.2 (0.558), 21.0 (0.536), and 5.6 (0.617) for HHpred, SparksX, FFAS3D, Neff-MUSTER, MUSTER, HHsearch, SP3, PPAS, PROSPECT2, PRC, and CEthreader, respectively. The normalized Z-score ($Z_N\left(i\right)$) for template i of threading program j is defined as the Z-score ($Z-score\left(i,j\right)$) of the template divided by the Z-score cutoff ($Z_0\left(j\right)$) for each threading method, which can be used as a measure to judge if a template is good (i.e., $Z_N\left(i\right)>1.0$) or not.

Since Z-score is a measure used to evaluate the quality of templates selected by LOMETS2. We found that the Z-score has a strong correlation with the real TM-score, with a Pearson Correlation Coefficient (PCC) of 0.7794 on the 797 benchmark proteins.

Based on the quality and number of threading alignments from LOMETS2, protein targets can be classified as “Trivial”, “Easy”, “Hard” or “Very Hard”. The classification of targets was utilized in the contact prediction and replica-exchange Monte Carlo (REMC) simulation sections of C-I-TASSER in order to train the parameters and weights with regard to different target types. The detailed procedure of target classification is shown as follows:

For each protein target, we first select the top template for each of the 11 threading methods in LOMETS2. Based on the selected templates, Z_a, the average normalized Z-score (divided by Z₀), is calculated for the 11 threading methods. We further calculate the pairwise TM-scores among the 11 templates selected by the 11 threading methods. There is a total of 55 ($=C_{11}^2=11\times 10/2$) distinct template-template pairs and corresponding TM-scores. We define TM1, TM2, TM3, and TM4 as the average TM-scores over the top 1/4, 2/4, 3/4 and 4/4 template-template pairs ranked by their TM-scores. Thus, we get a set of 9 measuring scores, i.e., S = {Z_a, TM1, TM2, TM3, TM4, Z_a∗TM1, Z_a∗TM2, Z_a∗TM3, Z_a∗TM4}. Based on the set S, the target can be classified by the following rule,

$$\text{Target is classified as }\{\begin{array}{l}Trivial,if\left|\left\{s\in S|s>1.8\times cut2\left(s\right)\right\}\right|\ge 8\hfill \\ Easy,elseif\left|\left\{s\in S|s>1.0\times cut2\left(s\right)\right\}\right|\ge 7\hfill \\ Veryhard,elseif\left|\left\{s\in S|s<1.0\times cut1\left(s\right)\right\}\right|\ge 6\hfill \\ Hard,otherwise\hfill \end{array}$$ (Equation S6)

where cut1(S)={0.620, 0.273, 0.250, 0.216, 0.185, 0.151, 0.137, 0.096, 0.093} and cut2(S)={1.052, 0.508, 0.396, 0.350, 0.339, 0.353, 0.279, 0.239, 0.209}. Here, $\left|\{\dots \}\right|$ means the number of items in the set $\{\dots \}$.

In order to simplify the logic of the benchmark analysis and Pfam analysis in the manuscript, we re-defined target classification as two groups of targets: easy targets and hard targets, where easy targets here include both “Trivial” and “Easy” types, while hard targets are a combination of both the “Hard” and “Very Hard” groups. On the other hand, for the parameter determination in the “Methods summary” section, we still keep the four classification groups.

Residue-residue contact prediction

C-I-TASSER utilizes contact-map models from six different contact predictors: TripletRes (Li et al., 2021), ResTriplet (Li et al., 2019b) , ResPRE (Li et al., 2019a), ResPLM (Li et al., 2019b; Zheng et al., 2019a), and NeBconA/NeBconB (He et al., 2017). Below we give an overview of the contact prediction programs.

TripletRes and ResTriplet

TripletRes (Li et al., 2021) and ResTriplet (Li et al., 2019b) starts with multiple sequence alignments created by DeepMSA (see below: “DeepMSA for MSA generation”), from which three co-evolutionary features are extracted. The first feature, COV, is the covariance matrix as proposed by DeepCov (Jones and Kandathil, 2018). Considering an MSA with N rows and L columns, we can compute a 21∙L by 21∙L sample covariance matrix as follows:

$$\begin{array}{l}{S}_{ij}^{ab}=f_{i,j}\left(a,b\right)-f_i\left(a\right)f_j\left(b\right)\end{array}$$ (Equation S7)

where $f_{i,j}\left(a,b\right)$ is the observed relative frequency of residue pair a and b at position i and j. $f_i\left(a\right)$ is the frequency of occurrence of residue type a at position i. There are 21 residue types in total (20 standard amino acid types plus a gap type).

The second feature, the precision matrix (PRE) was formulated by ResPRE, and can be obtained by minimizing the objective function:

$$\begin{array}{l}L=tr\left(S\text{Θ}\right)-log\left|\text{Θ}\right|+\rho {\left|\left|\text{Θ}\right|\right|}_2^2\end{array}$$ (Equation S8)

where the first two terms can be interpreted as the negative log-likelihood of the inverse covariance matrix, i.e., the precision matrix $\text{Θ}$, under the assumption that the data are under a multivariate Gaussian distribution. Here, $tr\left(S\text{Θ}\right)$ is the trace of matrix $S\text{Θ}$ and $log\left|\text{Θ}\right|$ is the log determinant of $\text{Θ}$. The last term is the L2 regularization of the precision matrix with $\rho$ set to $e^{-6}$.

The third feature is the coupling parameters of the inverse Potts model obtained through pseudolikelihood maximization (PLM). The starting point is approximating the probability of the sequence by the conditional probability of observing one variable conditioned on all other variables. We use CCMpred (Seemayer et al., 2014) to efficiently calculate the PLM coupling parameters.

The covariance matrix, the precision matrix, and the coupling parameters from the Potts model are all in the form of a 21∙L by 21∙L matrix, representing relationships between specific residue types at any two positions. After a reshaping procedure, three input features of size L by L by 441 are collected for each sequence.

Given the training features, two architectures were proposed based on deep residual neural networks (ResNets) (He et al., 2016), where the first version of ResNet is used as the basic residual block, defined as:

$$\begin{array}{l}y=f\left(F\left(x,W_1,W_2\right)+x\right)\end{array}$$ (Equation S9)

where x and y are the input and output vectors of the residual block considered. f denotes the activation function (ReLU is used in this work). Specifically, there are two convolutional layers in a residual block. Thus, the residual function is $F\left(x,W_1,W_2\right)=W_{2}f\left(W_{1}x\right)$ where $W_1$ and $W_2$ are the learnable weights in the first and second convolutional layers, respectively.

For the architecture of TripletRes, the three co-evolutionary features are ensembled directly by residual neural networks. Each input feature is fed into a set of residual blocks and transformed into the output feature with 64 channels. The three output features are concatenated along the channel dimension as the input of the last layers. The last set of layers try to learn patterns from the three transformed features by another 12 residual blocks. All residual blocks have a channel size of 64, and the kernel size of convolutional layers is set to 3 $\times$ 3 with a padding size equal to one. Such padding parameter set-up can keep the spatial information fixed through different layers. Here, we use a convolutional layer with a 1$\times$1 kernel size to transform each co-evolutionary input feature and the concatenated features into 64 channels. The final contact-map prediction is obtained by a sigmoid activation function.

ResTriplet is a two-stage ensemble model that uses a stacking strategy. In Stage I, three individual base models are trained separately based on the three different sets of co-evolutionary features, PRE, PLM and COV, respectively as described above. The base models have the same training data and the same neural network structure consisting of 22 residual basic blocks. In Stage II, we use a shallow neural network structure to combine the predictions of the base models from Stage I. Thus, the predicted contact-maps from the base models are considered as the input features in Stage II. To reduce the risk of over-fitting, predicted contact-maps produced by each base model are generated by 10-fold cross-validation as the input features of Stage II. The predicted secondary structures, denoted as PSS, by PSIPRED (Jones, 1999) are also adopted as an extra feature for the neural network model in Stage II. For shallow convolutional neural networks, the size of the receptive fields is usually limited. Hence, a dilated convolutional neural network structure with dilation equal to 2 is employed in order to enlarge the size of the receptive fields.

The neural networks in both TripletRes and ResTriplet are implemented in Pytorch (Paszke et al., 2017) and were trained by an Adam optimizer (Kingma and Ba, 2014) for 50 epochs.

ResPRE (Li et al., 2019a) is a novel in-house contact-map predictor, which consists of two consecutive steps of precision matrix-based feature generation and deep residual neural network-based contact inference, which are similar to those described above in “ResTriplet and TripletRes for contact prediction”. ResPRE is the average ensemble of ten base models trained by different subsets of the whole training data.

ResPLM (Li et al., 2019b; Zheng et al., 2019a) is also an in-house contact-map predictor similar to ResPRE. The only difference is that ResPLM was trained using the PLM feature.

NeBcon (He et al., 2017) is a meta-approach designed for contact-map prediction. In this study, we retrained NeBcon to improve its long-range contact prediction precision by using the naïve Bayes classifier (NBC) theorem to integrate eight state-of-the-art contact prediction methods, including four deep-learning-based methods: DeepPLM (Zheng et al., 2019a), DeepCov (Jones and Kandathil, 2018), Deepcontact (Liu et al., 2018), and DNCON2 (Adhikari et al., 2017), three co-evolution-based methods: GREMLIN (Kamisetty et al., 2013), CCMpred (Seemayer et al., 2014), and FreeContact (Kaján et al., 2014), and one meta-server-based methods MetaPSICOV2 (Buchan and Jones, 2018). A set of posterior probability scores for the NBC model are then calculated from the eight predictors. Finally, six inherent structural features are extracted from the query sequence, which are trained together with the NBC probabilities using neural networks to generate a final contact-map. Six types of intrinsic features are extracted from the query sequence, including (1) The sequence terminal information where a residue belongs to the five residues of the N- or C-terminal of the sequence; (2) The secondary structure; (3) The normalized solvent accessibile area; (4) The Shannon entropy; (5) The residue separation; (6) The residue composition generated by PSI-BLAST MSAs. NeBcon has two variants, NeBconA and NeBconB, which are designed for C_α and C_β atoms, respectively.

It has been demonstrated that the deep-learning-based predictors typically have higher prediction accuracies than the other predictors, and hence the contacts from these predictors have a higher likelihood to be the native contacts. Based on the testing on the 797 proteins in the benchmark dataset, on average, deep-learning-based methods, especially our in-house ResTriplet and TripletRes, had significantly higher precisions than other methods on both easy and hard targets. It is noteworthy that the TripletRes method was ranked as the top contact predictor in the recent CASP13 experiment (Shrestha et al., 2019).

After obtaining the contact predictions from the six methods, C-I-TASSER integrates them by selection and re-ranking.

Due to the variation of scoring schemes used by different contact predictors, we chose different confidence score cutoffs for different predictors that correspond to a contact accuracy of at least 0.5 for different ranges, including long-, medium- and short-range contacts with sequence separation $|i-j|\ge 24$, $23\ge |i-j|\ge 12$, and $\left|i-j\right|\le 11$, respectively. For each individual contact predictor p, we first rank all of the residue-residue pairs in descending order of confidence scores predicted by the predictor. A residue-residue pair (i, j) is selected as the predicted contact if $con{f}^p\left(i,j\right)>con{f}_{cut}^p\left(r\right)$ where $con{f}^p\left(i,j\right)$ is the confidence score of the residue-residue pair $(i,j)$ predicted by predictor p, and $con{f}_{cut}^p\left(r\right)$ is the confidence score cutoff for the predictor p at range type $r\in$ {short-, medium-, and long-range}, or $Lc\left(p\right)<Lcut\left(p\right)$ where $Lc\left(p\right)$ is the currently selected number of contacts by predictor p and $Lcut\left(p\right)$ is the cutoff for the minimum number of selected contacts by predictor p. It is important to note that all the confidence cutoffs and parameter sets were determined on a separate set of 243 training proteins: $Lcut\left(p\right)=L$ for all predictor p; $con{f}_{cut}^p\left(short-range\right)=$ 0.647, 0.809, 0.607, 0.604, 0.483, and 0.512; $con{f}_{cut}^p\left(medium-range\right)=$ 0.622, 0.789, 0.581, 0.598, 0.626, and 0.652; $con{f}_{cut}^p\left(long-range\right)=$ 0.678, 0.806, 0.654, 0.652, 0.849, and 0.906 for TripletRes, ResTriplet, ResPRE, ResPLM, NeBconB, and NeBconA, respectively.

After the contacts have been selected from each individual contact predictor, we normalize the contact prediction results from different predictors. For each of the predicted contacts $(i,j)$, the new normalized confidence scores over different contact predictors is calculated as follows:

$$U_{i,j}=\frac{1}{N}\cdot \sum _{p=1}^N{w}_p\left(i,j\right)$$ (Equation S10)

$$w_p\left(i,j\right)=\{\begin{array}{l}2.5\cdot \left[1+con{f}^p\left(i,j\right)-con{f}_{cut}^p\left(r\right)\right]\cdot Fw,ifpredictorpselectsout\left(i,j\right)\hfill \\ \begin{array}{llllllllllllllllllll}\hfill & 0\hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & else\hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \end{array}\hfill \end{array}$$ (Equation S11)

where N is the number of predictors. $con{f}^p\left(i,j\right)$ is the contact confidence score of the residue-residue pair $(i,j)$ predicted by predictor p, and $con{f}_{cut}^p\left(r\right)$ is the contact confidence score cutoff for predictor p at range type $r\in$ {short-, medium-, and long-range}, which is given above. Fw = 0.62, 1.25, 6.25, and 5 for Trivial, Easy, Hard, and Very hard target type, respectively, when Neff > 50; while Fw = 0.62, 1.5, 3, and 3.75 accordingly, when Neff < 50.

DeepMSA for MSA generation

Rather than generating multiple sequence alignments (MSA) by some general tools, such as PSI-BLAST (Altschul et al., 1997), HHblits (Remmert et al., 2012), or HMMsearch (Eddy, 1998), which may result in an insufficient number of homologs in an MSA, we adopted a novel MSA generation method (Zhang et al., 2019), called DeepMSA, to collect “deep” MSAs from multiple whole-genome and metagenome databases through complementary hidden Markov model (HMM) algorithms. The practical usefulness of the pipeline was examined on 614 non-redundant proteins, where DeepMSA was utilized to generate MSAs for residue-level contact prediction, which increased the accuracy of long-range contact prediction up to 24.4% compared to other MSA generation programs.

Starting from a query protein sequence, the DeepMSA approach iteratively searches for sequence homologs from multiple sequence databases in order to create deep MSAs, which in turn are utilized to build the deep sequence profiles used by the contact prediction algorithms in C-I-TASSER. In order to quantify the quality of an MSA, we define the number of effective sequences (Neff) as follows, which has been regarded as the stop criterion of the DeepMSA method:

$$Neff=\frac{1}{\sqrt{L}}{\sum }_{n=1}^N\frac{1}{1+{\sum }_{m=1,m\ne n}^{N}I\left[S_{m,n}\ge 0.8\right]}$$ (Equation S12)

where L is the length of a query protein, N is the number of sequences in the MSA, $S_{m,n}$ is the sequence identity between the m-th and n-th sequences, and I[ ] represents the Iverson bracket, which means $I\left[S_{m,n}\ge 0.8\right]=1$ if $S_{m,n}\ge 0.8$, and 0 otherwise.

A brief outline of the DeepMSA methodology is provided below, which consists of three stages.

Stage 1: Starting from the input query sequence, HHblits (Remmert et al., 2012) from the HH-suite package (Steinegger et al., 2019) is used to search against the UniClust30 database (Mirdita et al., 2016) with the same parameters used by MetaPSICOV2 (Buchan and Jones, 2018) to generate the first-level MSA. If there are not enough homologous sequences in the first-level MSA, i.e., the number of effective sequences (Neff) of the first-level MSA generated by Stage 1 is <128, Stage 2 will be performed.

Stage 2: Jump-starting from the first-level MSA, HHblits is again applied to search against a custom HHblits-formatted database to generate the second-level MSA. The custom database is constructed as follows: Jackhmmer from the HMMER package (Eddy, 1998) is used to search the query sequence against the UniRef90 database (Suzek et al., 2014) to generate a list of sequences (hits). Then esl-sfetch from the HMMER package is used to extract full-length hits from the list. These hits are finally converted into a custom HHblits-formatted database by the “hhblitdb.pl” script from HH-suite. If the Neff of the second-level MSA is still <128, Stage 3 will be performed.

Stage 3: Similar to Stage 2, the second-level MSA is used to jump-start an HHblits search against a new custom HHblits-formatted database to get the third-level MSA. The new custom database is built as follows: The second-level MSA is converted into a profile Hidden Markov Model (HMM) by HMMbuild from the HMMER package. This HMM is then searched against the Metaclust (Steinegger and Söding, 2018) metagenome sequence database by HMMsearch from HMMER to extract full-length hits. Finally, these hits from HMMsearch are built into the new custom database.

Replica-exchange Monte Carlo in C-I-TASSER

To reduce the conformational search space, only the alpha carbon (C_α) atom of each residue is treated explicitly, and the C_α trace is restricted to a three-dimensional underlying cubic lattice system with a lattice grid of 0.87 Å (Figure S2E). To preserve sufficient flexibility for the conformational movements and geometric fidelity of the structure representation, the backbone length of the structural model is allowed to fluctuate from 3.26 Å to 4.35 Å (i.e., the actual distance from C_α(i) to C_α(i+1) is required to be in the range [3.26 Å, 4.35 Å] in Figure S2E). As a result, there are 312 basic vectors representing the virtual and reasonable C_α-C_α bonds. The average vector length is about 3.8 Å, which is consistent with the value from real proteins. Additionally, to reduce the configurational entropy, the reasonable C_α-C_α bond angle is restricted to the experimental range [65°, 165°]. Note that all the allowable C_α-C_α bond combinations are pre-calculated.

The positions of three consecutive C_α atoms define the local coordinate system used for the determination of the remaining two interaction units: the beta carbon (C_β) (except glycine), and the center of side-group heavy atoms (SG) (except glycine and alanine). The approximation is shown in Figure S2F. Let V_i-1 be the vector from C_α(i-1) to C_α(i), and U_i-1 be the unit vector for V_i-1. Thus, the local Cartesian coordinate system can be given in the form of:

$$\stackrel{\rightharpoonup }{P_{\iota }}=\stackrel{\rightharpoonup }{e_{x\iota }}=\frac{\stackrel{\rightharpoonup }{U_{\iota -1}}+\stackrel{\rightharpoonup }{U_{\iota }}}{\left|\stackrel{\rightharpoonup }{U_{\iota -1}}+\stackrel{\rightharpoonup }{U_{\iota }}\right|}$$ (Equation S13)

$$\stackrel{\rightharpoonup }{H_{\iota }}=\stackrel{\rightharpoonup }{e_{y\iota }}=\frac{\stackrel{\rightharpoonup }{U_{\iota -1}}\times \stackrel{\rightharpoonup }{U_{\iota }}}{\left|\stackrel{\rightharpoonup }{U_{\iota -1}}\times \stackrel{\rightharpoonup }{U_{\iota }}\right|}$$ (Equation S14)

$$\stackrel{\rightharpoonup }{M_{\iota }}=\stackrel{\rightharpoonup }{e_{z\iota }}=\frac{\stackrel{\rightharpoonup }{U_{\iota -1}}-\stackrel{\rightharpoonup }{U_{\iota }}}{\left|\stackrel{\rightharpoonup }{U_{\iota -1}}-\stackrel{\rightharpoonup }{U_{\iota }}\right|}$$ (Equation S15)

Note that $\stackrel{\rightharpoonup }{H_{\iota }}$ is also the direction of the hydrogen bond (HB). Let C_β(i) be the position of the i-th C_β atom, and SG(i) be the position of the i-th center of the side-group heavy atoms. Therefore, the corresponding vectors relative to C_α(i) can be represented as:

$$\stackrel{\rightharpoonup }{V_{\iota }^{C\beta }\left(A{A}_{\iota }\right)}=x^{C\beta }\left(A{A}_i\right)\ast \stackrel{\rightharpoonup }{e_{x\iota }}+y^{C\beta }\left(A{A}_i\right)\ast \stackrel{\rightharpoonup }{e_{y\iota }}+z^{C\beta }\left[A{A}_i\right]\ast \stackrel{\rightharpoonup }{e_{z\iota }}$$ (Equation S16)

$$\stackrel{\rightharpoonup }{V_{\iota }^{SG}\left(A{A}_{\iota }\right)}=x^{SG}\left(A{A}_i\right)\ast \stackrel{\rightharpoonup }{e_{x\iota }}+y^{SG}\left(A{A}_i\right)\ast \stackrel{\rightharpoonup }{e_{y\iota }}+z^{SG}\left(A{A}_i\right)\ast \stackrel{\rightharpoonup }{e_{z\iota }}$$ (Equation S17)

where the parameters $x^{C\beta }\left(A{A}_i\right)$, $y^{C\beta }\left(A{A}_i\right)$, $z^{C\beta }\left(A{A}_i\right)$, $x^{SG}\left(A{A}_i\right)$, $y^{SG}\left(A{A}_i\right)$, $z^{SG}\left(A{A}_i\right)$ are amino acid type-dependent statistical values that were extracted from the PDB.

The structure reassembly in C-I-TASSER is conducted by replica-exchange Monte Carlo (REMC) simulations. There are 6 types of conformational movements used during the C-I-TASSER simulations (Figure S2G): (1) 2-bond vector walk; (2) 3-bond vector walk; (3) 4-bond vector walk; (4) 5-bond vector walk; (5) 6-bond vector walk; (6) N- or C-terminal random walk. To speed up the simulations, all of the 2-bond and 3-bond conformations for any given distance vector spanning the moving window are pre-calculated, so that movements (1) and (2) can be quickly conducted by a look-up table. Movements (3)-(5) can also be performed rapidly by recursively conducting combinations of movements (1) and (2).

Following the standard REMC protocol, there are N simulation replicas that are implemented in parallel, with the temperature of the i-th replica being:

$$T_i=T_{min}{\left(\frac{T_{max}}{T_{min}}\right)}^{\frac{i-1}{N-1}}$$ (Equation S18)

where $T_{min}$ and $T_{max}$ are the temperatures of the first and the last replicas, respectively. $N\in \left[40,80\right]$, $T_{min}\in \left[1.6k_B^{-1},1.98k_B^{-1}\right]$, and $T_{min}\in \left[66k_B^{-1},106k_B^{-1}\right]$, depend on the protein size with larger proteins having more replicas and higher temperatures. These parameter settings can result in an acceptance rate of ∼3% for the lowest-temperature replica and ∼65% for the highest- temperature replica for different size proteins.

After every 200∗L local conformational movements, where L represents the protein length, a global swap movement between each pair of neighboring replicas is attempted following the standard Metropolis criterion with a probability of $\text{min}\left(1,e^{(E_i-E_j)(\frac{1}{k{T}_i}-\frac{1}{k{T}_j})}\right)$, where k is a constant and the temperature distribution is shown in Equation S18. This parameter setting results in an approximate 40% acceptance rate for the swap movement between each neighboring replica.

The C-I-TASSER simulations are governed by different energy terms that achieve various effects on the generation of nativelike states. The overall force field used in C-I-TASSER is as follows:

$$E=w_1{E}_{Scon}^{C\alpha }+w_2{E}_{Scon}^{C\beta }+w_3{E}_{dist}^{Short}+w_4{E}_{dist}^{Long}+w_5{E}_{Tcon}^{C\alpha }+w_6{E}_{Tcon}^{SG}+w_7{E}_{burial}^{SG}+w_8{E}_{sec}^{C\alpha }+w_9{E}_{crumpling}+w_{10}{E}_{sec}^{frag}+w_{11}{E}_{pair}^{C\alpha -SG}+w_{12}{E}_{pair}^{SG}+w_{13}{E}_P^{C\alpha }+w_{14}{E}_{NP}^{C\alpha }+w_{15}{E}_{HB}+w_{16}{E}_{corr}^{C\alpha }+w_{17}{E}_{vol}^{SG}+w_{18}{E}_{mvol}^{SG}+w_{19}{E}_{Spair1-5}^{C\alpha }+w_{20}{E}_{cprof}+w_{21}{E}_{Ncon}$$ (Equation S19)

There are a total of 21 energy terms in the C-I-TASSER force field, which can be categorized into seven energy groups (or E-Groups). Those seven energy groups are (i) sequence-based contact restraints ($E_{Scon}^{C\alpha }$ and $E_{Scon}^{C\beta }$), (ii) template-based restraints ($E_{dist}^{Short}$, $E_{dist}^{Long}$, $E_{Tcon}^{C\alpha }$ and $E_{Tcon}^{SG}$), (iii) burial interaction restraints ($E_{burial}^{SG}$), (iv) secondary structure-based restraints ($E_{sec}^{C\alpha }$, $E_{crumpling}$, and $E_{sec}^{frag}$), (v) pairwise potentials ($E_{pair}^{C\alpha -SG}$, $E_{pair}^{SG}$, $E_P^{C\alpha }$, and $E_{NP}^{C\alpha }$), (vi) hydrogen bond restraints ($E_{HB}$), and (vii) statistical restraints from the PDB library ($E_{corr}^{C\alpha }$, $E_{vol}^{SG}$, $E_{mvol}^{SG}$, $E_{Spair1-5}^{C\alpha }$, $E_{cprof}$, and $E_{Ncon}$). The last six energy groups are classic I-TASSER force fields (Yang et al., 2015; Zhang et al., 2003) and the first energy group is the newly added deep learning-based contact energy potentials.

Energy terms in the first group was developed for C-I-TASSER to account for the restraints from the predicted contacts. We define it as the 3-gradient (3G) contact potential, as shown in Figure S2B, which has the following form for both C_α and C_β atoms:

$$E_{Scon}^{C\alpha /C\beta }=\sum _{i=1}^{L-1}\sum _{j>i}^L{E}_{Scon}^{C\alpha /C\beta }\left(d_{ij}\right)$$ (Equation S20)

$$E_{Scon}^{C\alpha /C\beta }\left(d_{ij}\right)=\{\begin{array}{ll}-U_{ij},& d_{ij}<d_{cut}\\ -\frac{1}{2}{U}_{ij}\left[1-sin\left(\frac{d_{ij}-\left(\frac{d_{cut}+D}{2}\right)}{D-d_{cut}}\pi \right)\right],& d_{cut}\le d_{ij}<D\\ \frac{1}{2}{U}_{ij}\left[1+sin\left(\frac{d_{ij}-\left(\frac{D+80}{2}\right)}{\left(80-D\right)}\pi \right)\right],& D\le d_{ij}<80\text{Å}\\ U_{ij},& d_{ij}\ge 80\text{Å}\end{array}$$ (Equation S21)

where $d_{ij}$ is the C_α or C_β distance between the i-th and j-th residues of the model and $U_{ij}$ is calculated by Equation S10. $d_{cut}=8\AA$ and D is a constant that depends on the protein length.

SPICKER for structural model selection

SPICKER (Zhang and Skolnick, 2004b) is a clustering algorithm to identify the near-native models from a pool of protein structure decoys. The conformations generated in the ten lowest-temperature replicas during the refinement simulation are clustered by SPICKER, with the purpose of identifying low free energy states. Cluster centroids are then obtained by averaging the 3D coordinates of all the clustered structural decoys. Since the centroid models often contain steric clashes, a second round of assembly simulations are conducted by C-I-TASSER to remove the local clashes and to further refine the global topology. Starting from the cluster centroid conformations, the REMC simulations are performed again. The distance and contact restraints in the second-round of the C-I-TASSER simulations are taken from the combination of the centroid structures and the PDB structures searched by the structure alignment program TM-align (Zhang and Skolnick, 2005) based on the cluster centroids. The conformation with the lowest energy in the second round is selected. Finally, REMO (Li and Zhang, 2009) is used to add backbone atoms (N, C, O) and FASPR (Huang et al., 2020) is used to build side-chain rotamers.

FG-MD for protein structure refinement

The FG-MD (Zhang et al., 2011) protocol is a molecular dynamics (MD) based algorithm for atomic-level protein structure refinement. Starting from a target protein structure, the sequence is split into separate secondary structure elements (SSEs). The substructures of every three consecutive SSEs, together with the full-length structure, are used as probes to search through a non-redundant PDB library by TM-align (Zhang and Skolnick, 2005) for structure fragments closest to the target. The top 20 template structures with the highest TM-scores (Zhang and Skolnick, 2004a) are used to collect spatial restraints. Simulated annealing molecular dynamics simulations are then carried out using a modified version of LAMMPS (Plimpton, 1993), which is guided by the distance map restraints, a knowledge-based hydrogen-bonding potential and AMBER99 force field (Ponder and Case, 2003). The final refined models are selected on the basis of the sum of the Z-score of the hydrogen bonds, Z-score of the number of steric clashes, and Z-score of the FG-MD energy.

Model quality estimation of C-I-TASSER

The global quality of a structural model is usually assessed by the TM-score between the model and the experimental structure:

$$TM-score=\frac{1}{L}\sum _{i=1}^{L_{ali}}\frac{1}{1+{\left(\frac{d_i}{d_0}\right)}^2}$$ (Equation S22)

where L is the number of residues, d_i is the distance between the i-th aligned residue, and $d_0=1.24\cdot \sqrt[3]{L-15}-1.8$ is a scaling factor. The TM-score ranges between 0 and 1, with TM-scores ≥0.5 indicating that the structure models have correct global topologies. Stringent statistics showed that TM-score >0.5 corresponds to a similarity with two structures having the same fold defined in SCOP/CATH (Xu and Zhang, 2010).

It should be noted that TM-score can be discrepant with the widely used root-mean-square deviation (RMSD) for some protein structure pairs. This is mainly because by definition, RMSD (=$\sqrt{\frac{1}{N}\sum _{i=1}^N{d}_i^2}$) is calculated as an average of distance error ($d_i$) with equal weight over all residue pairs. Therefore, a large local error on a few residue pairs can result in a quite large RMSD. On the other hand, by putting $d_i$ in the denominator of Equation S22, TM-score naturally weights smaller distance errors more strongly than larger distance errors. Therefore, TM-score value is more sensitive to the global structural similarity rather than to the local structural errors, compared to RMSD. Another advantage of TM-score is the introduction of the scale $d_0=1.24\sqrt[3]{\text{L}-15}-1.8$ which makes the magnitude of TM-score length-independent for random structure pairs, while RMSD is a length-dependent metric (Zhang and Skolnick, 2004a). Due to these reasons, our discussion of modeling results is mainly based on TM-score. Since RMSD is intuitively more familiar to most readers, however, we also list RMSD values when necessary in the manuscript.

In the process of real-world protein structure prediction experiment, we often do not have the experimental structure to calculate the TM-score relative to the native. Therefore, an estimation of the modeling accuracy is essential to decide how the users should utilize the models in their own research. In this study, the accuracy of the C-I-TASSER structure models is estimated through calculation of the confidence score (C-score) and the estimated TM-score (eTM-score) of the structure assembly simulations:

$$C-score=w_{1}ln\left(\frac{M}{M_{total}}\cdot \frac{1}{⟨RMSD⟩}\right)+w_2\ln \left(\prod _m\frac{Z\left(m\right)}{Z_0\left(m\right)}\right)+w_{3}ln\left(\frac{O\left(C{M}^{model},C{M}^{pred}\right)}{N\left(C{M}^{pred}\right)}\right)$$ (Equation S23)

$$eTM-score=a\cdot {\left(C-score\right)}^2+b\cdot \left(C-score\right)+c$$ (Equation S24)

where M_total is the total number of decoy conformations used for clustering, M is the number of decoys in the top cluster, and <RMSD> is the average RMSD among decoys in the same cluster. These three terms describe the extent of convergence of the structure assembly simulations. Z(m) is the score of the top template by threading method, m, and Z₀(m) is a cutoff above which templates are considered reliable/good. These Z-score related measures describe the significance of the LOMETS threading templates and alignments. $N\left(C{M}^{pred}\right)$ is the number of predicted contacts used to guide the REMC simulation, and $O(C{M}^{model},C{M}^{pred})$ is the number of overlapped contacts between the final model and the predicted contacts. These three terms account for the contact satisfaction rate. $w_1=0.77$, $w_2=1.36$ and $w_3=0.67$ are free parameters. As for the estimated TM-score, three free parameters, a=0.00098, b=0.10770, and c=0.79, were obtained by linear regression.

There were three parameters, w₁, w₂ and w₃, that were trained in the definition of C-score in Equation S23. We trained the three parameters based on the 797 proteins in the benchmark dataset. First, we equally split the 797 benchmark proteins into a training and test set. We defined the binary classification problem as follows: the positives in the true condition were the targets in the training set where the TM-score between the predicted model and the experimental structure was greater than or equal to 0.5, while the negatives in the true condition were the targets in the training set with TM-scores <0.5; the positives in the predicted condition were the targets with C-scores ≥ cutoff, while the negatives in the predicted condition were the targets with C-scores < cutoff. We varied each parameter from 0 to 3 using an interval size of 0.01. When the three parameters w₁, w₂ and w₃ were fixed, the C-score for each target in the training set could be calculated, and then the best C-score cutoff could be obtained by optimizing the Matthews correlation coefficient (MCC) on the training set. Finally, we selected the parameter values that corresponded to the highest MCC. The optimal parameters were $w_1=0.77$, $w_2=1.36$ and $w_3=0.67$, and the corresponding C-score cutoff = -2.5 produced an MCC = 0.6735. We also calculated the performance on the test set, which produced an MCC=0.6231, indicating the parameter selection was reasonable.

We also analyzed the effect of C-score and estimated TM-score on evaluating the model quality as shown in Figures S5A and S5B. We calculated the true TM-scores between the models and experimental structures, the C-scores for the predicted models, and the estimated TM-scores for the predicted models on the benchmark dataset. We found that both the C-score and estimated TM-score had a strong correlation with the real TM-score, with a Pearson Correlation Coefficient (PCC) of 0.7973 and 0.7961, respectively, on the 797 benchmark proteins.

Quantification and statistical analysis

Data were analyzed using R (4.0.3) and are presented as the average values of different datasets. Details of specific statistical analyses are included in the main text. For differences between distributions, we used the single-tailed Student’s t test of the hypothesis that both individual distributions are drawn from the same underlying distribution, as indicated in the different parts of this study. Statistical significance was defined as p < 0.05.

Published: June 21, 2021