A Big Data Pipeline: Identifying Dynamic Gene Regulatory Networks from Time Course GEO Data with Applications to Influenza Infection

Abstract

A biological host response to an external stimulus or intervention such as a disease or infection is a dynamic process, which is regulated by an intricate network of many genes and their products. Understanding the dynamics of this gene regulatory network allows us to infer the mechanisms involved in a host response to an external stimulus and hence aids the discovery of biomarkers of phenotype and biological function. In this article, we propose a modeling/analysis pipeline for dynamic gene expression data, called Pipeline4DGEData, which consists of a series of statistical modeling techniques to construct dynamic gene regulatory networks from the large volumes of high-dimensional time course gene expression data that are freely available in the Gene Expression Omnibus (GEO) repository. This pipeline has a consistent and scalable structure that allows it to simultaneously analyze a large number of time course gene expression data sets, and then integrate the results across different studies. We apply the proposed pipeline to influenza infection data from nine studies and demonstrate that interesting biological findings can be discovered with its implementation.

Introduction

Gene regulation plays a fundamental role in biological activities, such as cell growth, division, development and response to environmental stimulus. The dynamic gene regulatory network (GRN) specifies the interactions between genes, which in turn determines the expression level of each gene over time. Identifying these networks from genomic big data can shed light on the genetic mechanisms that occur when the cellular processes are impaired, for instance when they are subject to an infection or disease.

It is widely recognized that there may be hundreds or thousands of genes that harbor variations contributing to a specific illness, and there may also be a large genetic variability in host responses to an external stimulus or disease. Thus dynamic GRNs inferred from a single or a few gene expression data sets, may not be sufficient to understand the complexity and heterogeneity of the dynamic interaction process between the host and external stimulus.

Fortunately, in this Big Data era, we have an abundance of high-dimensional time course gene expression data from a variety of biological experiments and conditions. These data sets are generated from microarray, next-generation sequencing and other forms of high-throughput technologies, and are freely available in the Gene Expression Omnibus (GEO) data repository at the National Center for Biotechnology Information (NCBI) (1; 2). As of September 19, 2016, GEO has accumulated gene expression data from approximately 2 million samples from more than 73,000 studies (series) (3). As investigators must submit their genomic data to a data-sharing repository in accordance with grant or journal requirements, the number of data samples in GEO is growing rapidly (e.g., GEO obtained the data from 81,415 new samples between 2015 and 2016 (3)).

While a variety of options exist for reconstructing a gene regulatory network (GRN) based on a single experimental data set (see (4; 5) for an overview). There is limited methodology available to examine a large number of time course data sets from many different experiments to address important biological questions regarding a host genetic response to an external stimulus or disease. Examples of some fundamental questions include: (i) how do we identify genes that have a significant response over time at either population or individual level; (ii) do genes respond differently to the external stimulus or can multiple genes be grouped together based on their behavior over time? (iii) what are the similarities and differences among the genetic time-course patterns for various hosts or experimental conditions? (iv) what network of genetic interactions is formed for the host to respond to the external stimulus? (v) what are the similarities and differences among these networks for various hosts or experimental conditions?

We propose a pipeline for dynamic gene expression data, called Pipeline4DGEData, to address the above questions. This pipeline constructs dynamic gene regulatory networks from the large sets of time course gene expression data available on GEO for different biological experiments under various disease and/or stimulation conditions. We believe that this pipeline will allow us to better understand the pathogenesis of different diseases at both individual and population level. We can examine each host response to a disease or condition at a genetic level so that novel prevention and intervention targets can be discovered and personalized or precision medicine can be achieved (6; 7). We can also integrate the results from a large number of hosts that are responding to various diseases or conditions so that we can gain a better understanding of the heterogeneity that is inherent in the real world population and subsequently identify robust and reproducible signatures of disease phenotypes.

Current approaches for identification of GRNs from gene expression data have pros and cons. For example, information theory models (8; 9) are simple and easy to compute, but are essentially correlation models and do not take into account that multiple genes can co-regulate a target gene. Boolean networks (10; 11) represent the state of a gene using a binary variable, and as such do not account for the continuous nature of gene expressions. Bayesian networks (12; 13; 14) represent conditional dependencies among the genes via a directed graph, but the optimization of the network is computationally expensive, so applications are mostly limited to small-scale systems.

Linear differential equation (LDE) models (15) quantify the rate of change (derivative) of the expression level of one gene in the system as a function of the expression levels of all related genes. Let g_i represent the expression level of gene i and Dg_i denote the rate of change of this expression level, then $D{g}_i={\sum }_{j=1}^n{\beta }_{i,j}{g}_j$ for i = 1, …, n, where n denotes the number of genes and β_i,j quantifies the regulation effect of gene j on gene i. Some standard statistical methods such as the least squares or maximum likelihood estimation can be used to perform statistical inference for the parameters β_i,j from time course gene expression data for small-scale networks (15; 16). However, for LDE models that involve hundreds or even thousands of genes, the standard statistical methods often fail due to the curse-of-dimensionality.

In this article, we propose the Pipeline4DGEData which, consists of a series of cutting-edge statistical analysis and inference techniques to identify dynamic GRNs from high-dimensional time course gene expression data. The pipeline is designed to obtain time-course data from GEO automatically, analyze the data to reconstruct the dynamic GRNs, and output the results into the format of a manuscript for publication. As a consequence, a large number of data sets from GEO can be analyzed and modeled in an effective manner, and the results can be quickly disseminated. We demonstrate the utility of the Pipeline4DGEData by applying it to time course gene expression data from nine studies on viral respiratory infections that are available on GEO.

Dynamic Modelling for Genomic Big Data

The Pipeline for Dynamic Gene Expression Data is implemented in Matlab (R2016a) and is available at https://github.com/j142857z/Pipeline. It obtains GRNs from a large number of time course gene expression data sets. The pipeline has been specifically designed to have a scalable structure that allows it to simultaneously analyze the large volumes of data that are available on GEO. It consists of the following eight steps:

1. Obtain the time course gene expression data sets from GEO.

2. Pre-process the probe level data, i.e., background adjustment, normalization, and summarization.

3. Detect the genes with expression levels that change significantly with respect to time, which we call dynamic response genes (DRGs).

4. Cluster the DRGs into groups of co-expressed genes, which are referred to as temporal “gene response modules” (GRMs).

5. Obtain the functional annotation (gene ontology terms, associated pathways and a functional gene-enrichment analysis) of the GRMs.

6. Construct the high-dimensional gene regulatory networks (GRNs) that determine the interactions between the GRMs using LDE models.

7. Perform a network feature analysis on the established GRNs

8. Output the results in the form of a manuscript.

These steps are summarized in the flowchart in Figure (1). Each of these eight steps is detailed in the subsequent subsections.

Figure 1.

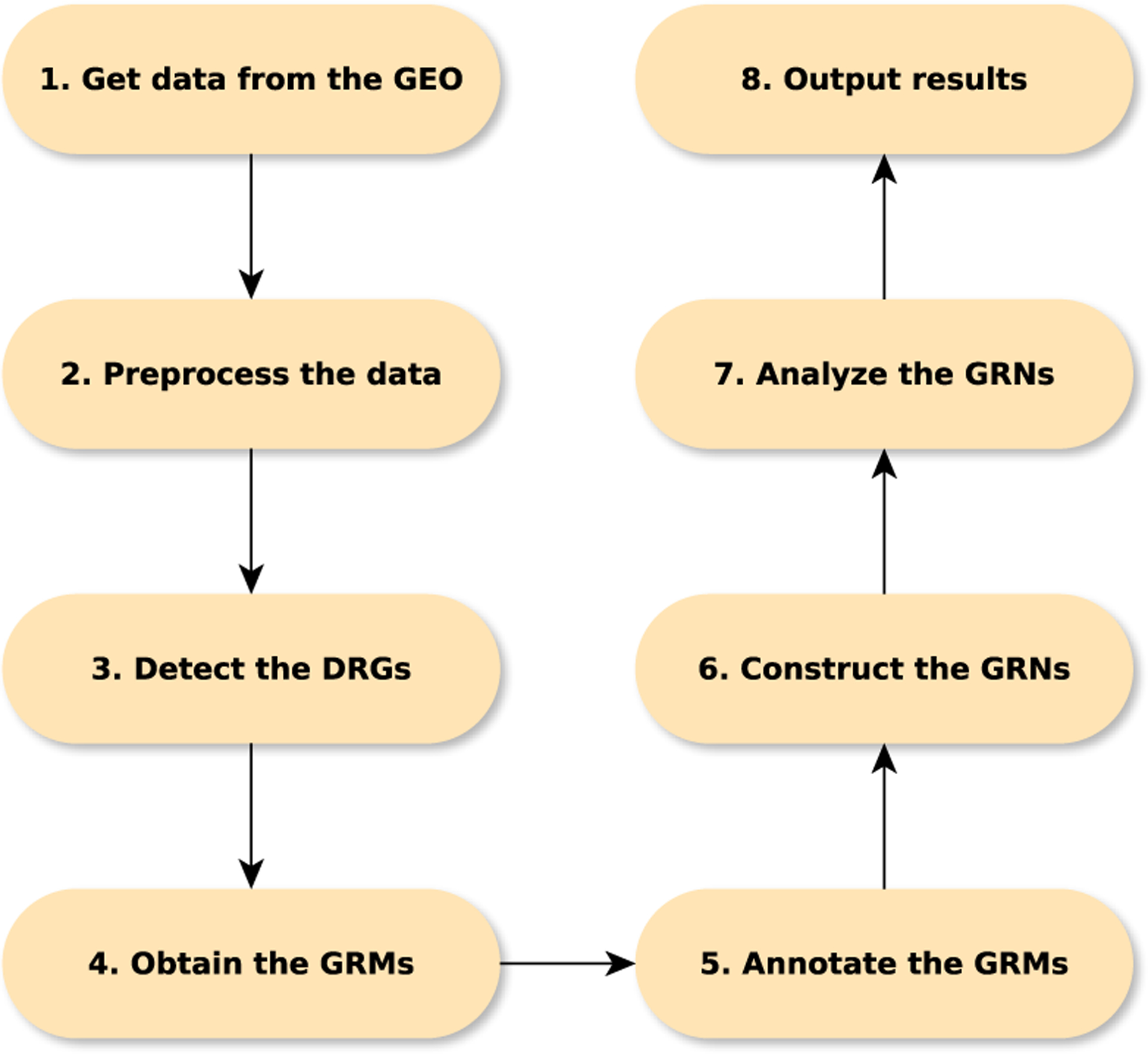
Summary of the eight steps implemented by the Pipeline4DGEData

Step 1. Get the data from GEO

Our pipeline has been developed to model time course gene expression data and is expected to produce reliable results if there are 7 or more time points available. The GEO database is not designed to easily identify the number of time points for the microarray or RNA-Seq experiments. Instead, the experimental design is documented in a text file for each study. We have used text mining, natural language processing and ontology techniques to identify, from the GEO database, potential time course data sets in addition to other characteristics or metadata including the related diseases and cell types from which the data are generated. But these text mining approaches are not the focus of this paper and will be reported elsewhere. The first step of our pipeline is to identify the time course GEO data sets related to a particular keyword, for example, influenza. The resulting GSE numbers, which identify series records in GEO are saved to a file. See (1) and (2) for further details on GEO record types. The pipeline automatically retrieves the data sets and meta information corresponding to these GSE numbers.

Step 2. Pre-process the data

Affymetrix GeneChip arrays are currently among the most widely used high-throughput technologies for the genome-wide measurement of expression profiles. To minimize mis- and cross-hybridization problems, this technology includes both perfect match (PM) and mismatch (MM) probe pairs as well as multiple probes per gene (17). As a result, significant pre-processing is required before an absolute expression level for a specific gene can be accurately assessed. In general, pre-processing probe-level expression data consists of three steps: background adjustment (remove local artefact’s and “noise”), normalization (remove array effects), and summarization at the probe set level (combine probe intensities across arrays to obtain a measure of the expression level of corresponding messenger RNA (mRNA)).

Most datasets in GEO are already pre-processed. By default, the Pipeline for Dynamic Gene Expression Data proceeds with the pre-processing technique used in the original study. However, if the .cell files are available, then the user can select from the following popular pre-processing techniques to reprocess the data if necessary: Microarray Suite 5 (MAS5) (18), Robust Multi-array Average (RMA) (19) and Guanine Cytosine Robust Multi-Array Analysis (GCRMA) (20). Table 1 provides a brief overview of the three pre-processing techniques. See (21; 22) for a detailed comparison.

Table 1.

A brief overview of the pre-processing techniques: Microarray suite 5 (MAS5), Robust Multi-array Average (RMA) and Guanine Cytosine Robust Multi-Array Analysis (GCRMA).

Technique	Background adjustment	Normalization	Summarization
MAS5	Ideal (full or partial) MM subtraction	Constant	Turkey biweight
RMA	Signal (exponential) and noise (normal) close-form transformation	Quantile	Median polish
GCRMA	Optical noise, probe affinity and MM adjustment	Quantile	Median polish

Step 3. Detect the Dynamic Response Genes (DRGs)

(a) Obtain the estimated gene expression curves

We assume that the centered expression levels of the i^th gene, belonging to subject j, denoted here by x_i,j, is a smooth function over time t and that the centered gene expression measurement ${\tilde{y}}_{i,j}$ is a discrete observation from this smooth function, which has been distorted by noise, i.e.,

$${\tilde{y}}_{i,j}=x_{i,j}\left(t_k\right)+{ϵ}_{i,j},$$

for i = 1, …, n, j = 1, …, N and k = 1, …, K_i,j, where n is the number of genes, N is the number of subjects (or experimental conditions), K_i,j is the number of time points observed for the i^th gene, belonging to subject j. The noise ϵ_i,j is assumed to be an independently identically distributed (i.i.d.) Gaussian random variable with mean 0 and variance σ².

The K_i,j × 1 vector of the estimated centered expression levels evaluated at the points t, for the i^th gene, belonging to subject j, ${\hat{x}}_{i,j}$ is obtained by spline smoothing (23; 24). This approach approximates x_i,j by a linear combination of L independent basis functions, $x_{i,j}\approx {\sum }_{l=1}^L{b}_{i,j,l}{c}_{i,j,l}=B_{i,j}{c}_{i,j}$, where the K_i,j × L matrix B_i,j denotes the basis functions evaluated at time t and the vector c_i,j provides the corresponding coefficients.

The coefficients c_i,j can be estimated by minimizing

$$\left[{\tilde{y}}_{i,j}-B_{i,j}{c}_{i,j}\right]\prime \left[{\tilde{y}}_{i,j}-B_{i,j}{c}_{i,j}\right]+{\lambda }_j{c}_{i,j}^{\prime }{R}_{i,j}{c}_{i,j}^{\prime }$$ (1)

where the first term defines the squared discrepancy between the observed centered gene expression measurements ${\tilde{y}}_{i,j}$ and the estimated measurements ${\hat{x}}_{i,j}$, and the second term contains the L × L matrix R_i,j which is the integral of the squared second derivative of B_i,j. The second term penalizes the curvature of ${\hat{x}}_{i,j}$ and hence requires it to be sufficiently smooth. The parameter λ_j controls the trade-off between the fit to the data and the smoothness requirement and hence ensures that ${\hat{x}}_{i,j}$ has an appropriate amount of regularity. All the genes for each subject are assumed to have the same λ_j.

We expect that only a small fraction of genes respond to the external stimulus and the majority of the genes have no significant response with relatively flat expression levels over time. Therefore, estimating the parameter λ_j using the conventional method of minimizing the prediction error with generalized cross validation (GCV), see (25) for details, of all the genes together is not ideal as GCV will tend to select a λ_j that is large to minimize the prediction error of the majority of unresponsive genes. As we are interested in obtaining an appropriate amount of regularity for the responsive genes, we apply an approach similar to (26) and (27) and choose a subset of the genes that exhibit time course response patterns with relatively smooth trajectories that do not fluctuate widely. Then we rank these genes by their interquartile range and select 200 of the top ranking genes as our estimation subset. The regularity parameter λ_j is estimated by minimizing the GCV of the responsive genes in our estimation subset, this parameter is then used to smooth the time course data for all the genes.

(b) Perform a hypothesis test to identify the genes with expressions that change significantly over time

Dynamic response genes (DRGs) can be defined as genes with expressions that change significantly over time. In order to determine which genes can be considered DRGs, we use an F-statistic which compares the goodness-of-fit of the null hypothesis $H_0:{\hat{x}}_{i,j}=0$ versus the alternative hypothesis $H_a:{\hat{x}}_{i,j}\ne 0$. The F-statistic is given by,

$$F_{i,j}=\frac{\frac{{\text{RSS}}_{i,j}^0-{\text{RSS}}_{i,j}^1}{{\text{df}}_{i,j}-1}}{\frac{{\text{RSS}}_{i,j}^1}{K_{i,j}-{\text{df}}_{i,j}}},$$

where df_i,j is the degrees of freedom of the estimated curve ${\hat{x}}_{i,j}$, ${\text{RSS}}_{i,j}^0={\tilde{y}}_{i,j}^{\prime }{\tilde{y}}_{i,j}$ and ${\text{RSS}}_{i,j}^1=\left[{\tilde{y}}_{i,j}-{\hat{x}}_{i,j}\right]\prime \left[{\tilde{y}}_{i,j}-{\hat{x}}_{i,j}\right]$. are the residual sum of squares under the null and the alternative models for the i-th gene, belonging to subject j. The genes with large F-ratios can be considered as exhibiting notable changes with respect to time. If we wish to have an equal amount of DRGs for each subject, we can rank the F-ratios and select nDRG the number of top ranking dynamic response genes. By default the Pipeline4DGEData sets nDRG to 3000.

As an alternative, the functional principal component analysis (FPCA) approach (27) can also be used to identify the DRGs. The FPCA method needs to borrow information across genes to estimate the covariance and the results will be subject to the estimation accuracy of the covariance matrix.

Step 4. Cluster the DRGs into temporal gene response modules (GRMs)

As many of the DRGs exhibit similar expression patterns over time, we wish to cluster them into co-expressed modules (groups of genes which have similar gene expression patterns over time). This step not only reduces the modeling dimension but also eases the identifiability problem. It is widely recognized that many co-expressed genes may follow similar temporal patterns, but at the same time, some genes may have very few or even no co-expressed genes, and thus may exhibit unique temporal response patterns. Consequently, the GRMs can vary greatly in size, with some being large and containing many genes and others being small or even containing a single gene. To obtain these clusters, we adopt the Iterative Hierarchical Clustering (IHC) method introduced in (28). This approach requires a single parameter that controls the trade-off of the between- and within-cluster correlations. In particular, the average within-cluster correlation will be approximately α, and the between-cluster correlation will be below α. The IHC algorithm is outlined below:

• Initialization: Cluster the data for the standardized DRGs using the hierarchical agglomerative clustering approach. Let the distance metric be the Spearman rank correlation with a threshold of α, and the linkage method be the average of the genes in each cluster.

• Merge: Treat each of the cluster centers as ‘new genes’ and use the same rule as in the initialization step to merge the centers into new clusters. The cluster centers provide the average time-course pattern of the cluster members.

• Prune: Let c_i be the center of cluster i. If the correlation between the cluster center and gene j, which will be denoted by ρ_i,j, is less than α, then remove gene_j from the cluster i. Let P be the number of genes removed from the existing S clusters. Assign all P genes into single-element clusters. Hence, there is now (S + P) clusters in total.

• Repeat Merge-Prune Steps until the index of clusters converges.

• Repeat Merge Step until the between-cluster correlations are less than α.

Step 5. Annotate the GRMs

The Pipeline for Dynamic Gene Expression Data outputs an annotation report which extracts biological meaning from the DRGs contained in each GRM. Specifically, it provides the gene ontology terms, associated pathways, and a functional gene enrichment analysis. This is achieved by using the Database for Annotation, Visualization and Integrated Discovery (DAVID) (29; 30).

Step 6. Construct the high-dimensional gene regulatory network (GRN) that determines the interactions between the GRMs

High-dimensional gene regulatory networks map how the change in the expression of any single gene is regulated by its own expression level and other gene expression levels. There is an abundance of literature regarding the use of ordinary differential equation (ODE) modeling to construct a high-dimensional gene regulatory network (GRN) (5; 31; 32). ODEs model gene regulations using rate equations. Here we model the interactions between GRMs using the following ODE

$$D{m}_{q,j}=\sum _{p=1}^Q{\beta }_{p,q,j}{m}_{p,j},\text{\hspace{1em} for \hspace{1em}}q=1,\dots ,Q,$$ (2)

where Dm_q,j represents the instantaneous rate of change in q^th gene response module, ${\left\{{\beta }_{p,q,j}\right\}}_{p=1}^Q$ quantifies the regulation effects of the p^th gene response module on the rate of change of the q^th gene response module Dm_q,j. The standard approach for estimating the parameters of differential equations from noisy measurements is nonlinear least squares (NLS) (33; 34). However, this method requires initial estimates of the regulation effects and initial conditions for the expression levels of the gene response modules at time t₀. Differential equation models differ from the classical regression models as they capture not only the direct effects that are strong interactions between two gene response modules but they also include indirect effects high correlations that may exist between two gene response modules that are not directly connected but influence each other via a third gene response module they both directly interact with. In general, such indirect interactions may be induced not only by the third gene response module, but equally by the entire collective dynamics of a network.

(a) Initial estimates of the regulation effects

The two-stage smoothing-based estimation method (35; 36) decouples the system of differential equations in (2) and approximates it by a set of pseudo-regression models as in (3). The first step obtains estimates of the average trajectory of the GRMs ${\hat{m}}_{p,j}$ and their derivative $D{\hat{m}}_{q,j}$ for p, q = 1, …, Q. The estimated trajectories ${\hat{m}}_{q,j}$ are the average of the smoothed trajectories attained by the spline smoothing approach in part (a) of Step 3, for all the genes contained in the q^th GRM. Similarly, $D{\hat{m}}_{q,j}$ is estimated by averaging the derivative of the smoothed trajectories obtained by the spline smoothing approach in part (a) of Step 3, for all the genes contained in the q^th GRM. The set of Q pseudo-regression models are then given by

$$D{\hat{m}}_{q,j}=\sum _{p=1}^Q{\theta }_{p,q,j}{\hat{m}}_{p,j}+{ϵ}_{p,j}q=1,\dots ,Q,$$ (3)

where θ_p,q,j denotes the direct effects that is the strong relationships between the p^th GRM and the rate of change in the q^th GRM.

It is widely accepted that gene regulatory networks are sparse, i.e., only a few of the ${\left\{{\theta }_{p,q,j}\right\}}_{p=1}^Q$ are non-zero. In order to determine which of the regulation effects are significant (i.e., non-zero) our pipeline applies the least absolute shrinkage and selection operator (LASSO) (37) approach or the adaptive LASSO (38) approach (36) to the pseudo-regression model in (3). The LASSO approach requires minimizing

$${\left[D{\hat{m}}_{q,j}-\sum _{p=1}^Q{\theta }_{p,q,j}{\hat{m}}_{p,j}\right]}^2+\gamma \sum _{p=1}^Q\Vert {\theta }_{p,q,j}\Vert q=1,\dots ,Q.$$

As the penalty term ${\sum }_{p=1}^Q\Vert {\theta }_{p,q,j}\Vert$ means that the LASSO increases, LASSO sets more coefficients θ_p,q,j to zero. This means that the LASSO estimator is a smaller model, with fewer predictors. The L1 regularization parameter γ enforces the amount of sparsity in θ and can be chosen by minimizing either the generalized cross validation criterion, the Akaike information criterion or the Bayesian information criterion. As such, LASSO is a model selection and dimensionality reduction technique that determines the significant coefficients θ_p,q,j or initial estimates of the weighted network edges by maximizing the prediction accuracy (GCV) or the trade-off between the goodness of fit and the complexity (AIC/BIC) of (3). Alternatively, the SCAD approach (31; 39) can also be used in this step. See more details in (31).

(b) Refined estimation of the regulation effects

The parameter estimates from the two-stage method in the above pseudo-regression model are not efficient in terms of estimation accuracy when the model selection is performed simultaneously, and there can be significant approximation error in ${\hat{m}}_{p,j}$ and its derivatives. The estimation of significant coefficients or network edges can be improved or refined using nonlinear least squares (NLS), maximum likelihood or other more efficient estimation methods once the model selection from part (a) of Step 6 is completed. Our pipeline adopted the NLS approach which minimizes the squared discrepancy between the numerical approximation to the solution of the differential equation (2) and the observations. The non-zero estimates of ${\left\{{\hat{\theta }}_{p,q,j}\right\}}_{p=0}^Q$ from part (a) of Step 6 are used as initial estimates for the regulation effects ${\left\{{\beta }_{p,q,j}\right\}}_{p=1}^Q$ in equation (2). Given the initial estimates, ${\beta }_0={\left\{{\hat{\theta }}_{p,q,j}\right\}}_{p=0}^Q$ and a set of p initial values, ${\hat{m}}_{p,j}$, which are attained by the spline smoothing approach in part (a) of Step 3, an initial numerical approximation of the solution to differential equation (2) can be computed as ${\hat{m}}_{p,j}\left(t,{\beta }_0\right)$. Using a linearization of the discrepancy between the data and the numerical solution, the estimated parameters $\hat{\beta }$ can be refined iteratively. In Lu et al. (31), the mixed-effects modeling approach is used for parameter refinement.

The variability in the GRN is assessed by calculating the confidence intervals of the parameters $\hat{\beta }$ using the delta method see (40) for details.

Step 7. Perform a network feature analysis on the GRN.

The reconstructed biological networks are significantly different from random networks and often exhibit ubiquitous properties in terms of their structure and organization. Many metrics have been developed to characterize biological networks, see (41) and (42) for an overview.

We use these network metrics to identify influential GRMs and to provide insight on the organization of the GRN describing the host response to the external stimulus or disease. These metrics are divided into two groups: node metrics and network metrics. Node metrics provide information on the modules within each GRN and are useful for identifying GRMs that are likely to be hubs or groups of modules that are strongly interconnected. On the other hand network metrics identify properties or features of each GRN and are useful for comparing different GRNs. The Pipeline for Dynamic Gene Expression Data uses the Matlab SBEToolbox (43) to compute the network metrics for each of the GRNs. This toolbox includes many metrics, some of the most relevant are listed in Table 2. The interaction network between GRMs was represented as as a directed graph with the gene response modules as nodes and interactions as directed edges which are given by the point estimates $\hat{\beta }$ obtained in step 6. The variability in the network metrics can be estimated by evaluating each metric at the lower endpoint of the 95% confidence interval and the upper endpoint of the 95% confidence interval for $\hat{\beta }$.

Table 2.

The node metrics which identify influential modules and the network metrics which provide insight on the organization of the host response to the external stimulus or disease.

Node Metrics
Degree centrality	is the number of links that a node has with other nodes in the network (44).
	Biological interpretation: GRMs with high metrics are likely to be hubs since they play central regulatory roles (45; 46).
Closeness centrality	is the average distance from a given node to all other nodes in the network (47).
	Biological interpretation: A measure of a GRM’s proximity to other GRMs. Identifies groups of GRMs (46).
Eccentricity	is the greatest geodesic distance between a node and any other node in the network (48).
	Biological interpretation: A GRM with a high metric may be more influential or more easily influenced by other GRMs and a GRM with a low metric is influenced or influencing neighbouring GRMs. (49).
Bridging centrality	measures the extent to which a node or an edge is located between well-connected regions (50).
	Biological interpretation: Identifies GRMs that are located between large groups of GRMs (51; 52).
Clustering Coefficient	measures the degree of interconnectivity in the neighborhood of a node (53).
	Biological interpretation: measures the extent to which the GRMs regulated by a given GRM also regulate each other. Identifies GRM cliques or groups (50).
Network Metrics
Density	The proportion of direct ties in a network relative to the total number possible (54).
	Biological interpretation: Measures the sparsity or denseness of a GRN (55).
Diameter	is the shortest distance between the two most distant nodes in the network (54).
	Biological interpretation: Lets us compare GRNs based on size and indicates how quickly something might spread through the GRN (56; 57).

Step 8. Output the results: reporting and manuscript drafting.

As GSE numbers can often contain data sets on more than one experimental condition, for example, GSE52428 contains time course gene expression data following intranasal influenza A H1N1 and H3N2 inoculation, for 24 and 17 subjects respectively. The pipeline determines if there is more than one experimental condition (subject/virus strain), and then runs steps 2–8 on each condition/subject. For example, one of the experimental conditions for the GSE52428 study was H1N1 Subject 1. Step 8 creates six folders to store the results from Steps 2–7. The folders are organized in the following hierarchal fashion: GSE number, experimental condition, and steps 2–7. Figure 2 provides a schematic of the folders and Table 3 details the contents of each folder. The folder structure allows for different experimental conditions to be computed in parallel. We have developed and tested a parallel computing version of the pipeline from which the results can be automatically saved on the OneDrive cloud. The experimental condition folder also contains a TEX document (if ran on a Mac, Linux, or Windows machine) and a Word document (if ran on a Windows machine), in the format of a biomedical journal article detailing the results. This article includes: a methods section describing the data and techniques implemented by the Pipeline for Dynamic Gene Expression Data and a draft of the results section which contains tables and figures which are automatically generated by the pipeline. The aim of this document is to facilitate with the drafting of a manuscript for publication, based on the results produced by the pipeline. An example of this article draft is provided in the supplementary material.

Figure 2.

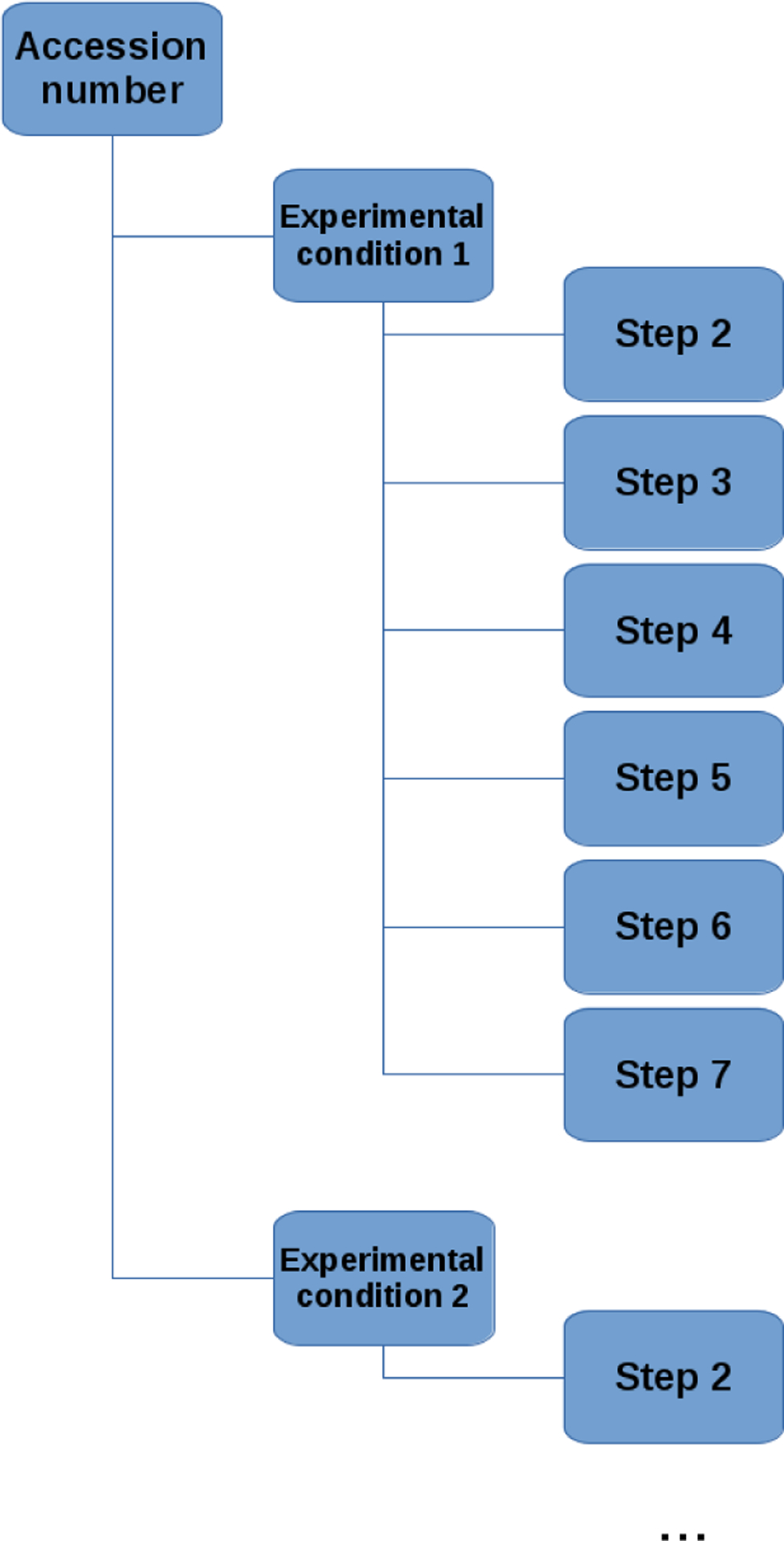
Schematic for the structure of the folders created by the Pipeline for Dynamic Gene Expression Data

Table 3.

The contents of each folder produced by Steps 2–7 of the Pipeline for Dynamic Gene Expression Data

File name	Description
Step 2
raw_data.mat	A Matlab file containing the raw unprocessed data (if .cell files are available)
processed_data.mat	A Matlab file containing the processed data (if .cell files are available)
Step 3
Matlab_Workspace3.mat	A Matlab file containing all the variables that the pipeline has required thus far.
Derivative_Fitted_Curves.csv	The first derivative of the estimated smooth trajectories of each gene expression over time.
DRG.csv	The probe set ids and the time course genes expression of each of the Dynamic Response Genes.
F_value.csv	The F-value for each gene.
Fitted_curves.csv	The estimated smooth trajectories of each gene expression over time.
Index_Ftest_DRGs.csv	The index of the DRGs ranked by their F-Statistic.
Index_Ftest.csv	The index of the probe set ids ranked by their F-Statistic.
Probe_set_ID_Ftest_DRG.csv	The probe set ids of the DRGs ranked by their F-Statistic.
Step 4
Matlab_Workspace4.mat	A Matlab file containing all the variables that the pipeline has required thus far.
Cluster_IDX.csv	The cluster index for each of the DRGs.
Cluster_MT.csv	The probe set ids for each of the DRGs and a number indicating which type of module this probe set belongs to SGM (1), SSM (2), MSM (3) and LSM (4).
GRMs.pdf	A file containing a plot of the time-course patterns for all the genes in each GRM.
Step 5
Matlab_Workspace5.mat	A Matlab file containing all the variables that the pipeline has required thus far.
M1/Chart_report_of_M1.csv	The annotation and enrichment analysis which highlights the most relevant terms associated with the genes contained in GRM 1. There is a folder and file for each GRM.
M1/Table_report_of_M1.csv	The annotation and enrichment analysis which highlights the most relevant terms associated with the genes contained in GRM 1. There is a folder and file for each GRM.
Step 6
Matlab_Workspace6.mat	A Matlab file containing all the variables that the pipeline has required thus far.
Coefficients.xls	The estimated regulation effects ${\left\{{\hat{\beta }}_{p,q,j}\right\}}_{p=0}^Q$
Dependency_matrix.xls	The GRMs inward and outward connections.
Step 7
Matlab_Workspace7.mat	A Matlab file containing all the variables that the pipeline has required thus far.
Adjacency_matrix.xls	The estimated regulation effects ${\left\{{\hat{\alpha }}_{p,q,j}\right\}}_{p=1}^Q$
Dependency_matrix.xls	The GRMs inward and outward connections.
Network_Statistics.xls	The Network metrics for the GRN.
Node_metrics.xls	The Network metrics for the GRMs.
Network_plot.pdf	A plot of the GRNs.

The Pipeline for Dynamic Gene Expression Data Applied to Influenza Studies

We demonstrate the utility of the Pipeline for Dynamic Gene Expression Data by applying it to time course gene expression data from nine studies on various influenza viruses. These viruses represent respiratory pathogens that cause either seasonal, endemic infections or unpredictable pandemics. Influenza occurs globally with an annual attack rate estimated at 5% to 10% in adults and 20% to 30% in children (58). Illnesses can result in hospitalization and death mainly among high-risk groups (the very young, elderly or chronically ill). Worldwide, these annual epidemics are estimated to result in about 3 to 5 million cases of severe illness, and about 250,000 to 500,000 deaths (58). We expect that our biological findings on these influenza virus strains, produced by the proposed Pipeline4DGEData, will have a high impact on public health.

The nine studies that we have chosen as examples for the application of the Pipeline for Dynamic Gene Expression Data consist of 58 time course data sets corresponding to different experimental conditions (hosts inoculated with various virus strands) with 1, 554 samples from either blood, epithelial cells, dendritic cells or adenocarcinoma cells (59; 60; 61; 62; 63; 64; 65; 66). Unlike a single cohort experiment study where the goal is to control as many confounding factors as possible, our analysis includes data sets with a broad biological and technical heterogeneity. These data sets include healthy controls, individuals with various types of viral or bacterial infections, and individuals that were vaccinated for influenza. These studies can be grouped into 19 virus subtypes, and Table 4 provides detailed information on these subtypes for each of the nine studies. The majority of the studies (89%) involve human subjects, and their most common (63%) bio-samples are bronchial epithelial cells. The dominating virus subtypes are seasonal influenza virus strains, H1N1 (41% of the data sets) and H3N2 (29% of the data sets). Figure 3 show the distributions of the number of time-points, the number of genes/probes from which expression-level measurements are available and the pre-processing techniques used in the original study. The number of time points range from 7 − 15, with 69% of the data sets containing more than ten time-points. The number of genes or probes range from 11, 961 – 54, 675. Here we choose to analyze the time course gene expression data using the pre-processing techniques employed in the original study. The 58 data sets were pre-processed with one of the following techniques, RMA, GCRMA, MAS5 and LIMMA. The most popular pre-processing technique is RMA (67% of the studies selected this method). The design of the pipeline allows for the systematic integration of the results at various levels. More specifically, results of the pipeline analysis can be examined on an individual by individual basis, e.g., by examining each subject’s DRGs, GRMs and GRN separately. Also, results can be examined across several subjects and experimental conditions (e.g., virus subtypes). This can be achieved by finding the DRGs that are common across groups of subjects, the similarities/differences between the patterns of the GRMs in the groups and the similarities/differences between GRNs across the groups. The following subsections examine the population level similarities/differences between the DRGs, GRMs, and GRN for all 58 time course data sets across the 19 virus subtypes.

Table 4.

The details for each of the 19 virus subtypes for the nine influenza-related studies containing genome-wide time course gene expression data obtained from the GEO database.

GSE number	Virus Subtype	No. Hosts	Bio Sample	Organism
GSE52428	H1N1/Brisbane	24	peripheral blood	Homo sapiens
GSE12254	WE (LCMV-WE)	1	liver sample	Macaca mulatta
GSE19392	delNS1 post trypsin	1	bronchial epithelial cells	Homo sapiens
GSE19392	PR8 post trypsin	1	bronchial epithelial cells	Homo sapiens
GSE19392	vRNA LTX+RNA	1	bronchial epithelial cells	Homo sapiens
GSE19392	treated with media alone	1	bronchial epithelial cells	Homo sapiens
GSE19392	treated with IFNb IFN	1	bronchial epithelial cells	Homo sapiens
GSE19392	treated with LTX transfection reagent	1	bronchial epithelial cells	Homo sapiens
GSE37571	A/CA/04/2009	1	Calu-3 lung adenocarcinoma cell line	Homo sapiens
GSE37571	Mock	1	Calu-3 lung adenocarcinoma cell line	Homo sapiens
GSE30550	H3N2/Wisconsin	17	peripheral blood	Homo sapiens
GSE40844	Mock	1	Calu-3 lung adenocarcinoma cell line	Homo sapiens
GSE41067	H1N1 influenza A/New Caledonia/20/1999	1	monocyte-derived dendritic cells	Homo sapiens
GSE47960	dORF6	1	bronchial epithelial cells	Homo sapiens
GSE47960	iSARs	1	bronchial epithelial cells	Homo sapiens
GSE47960	Mock	1	bronchial epithelial cells	Homo sapiens
GSE47961	BAT	1	bronchial epithelial cells	Homo sapiens
GSE47961	dORF6	1	bronchial epithelial cells	Homo sapiens
GSE47961	H1N1	1	bronchial epithelial cells	Homo sapiens

Figure 3.

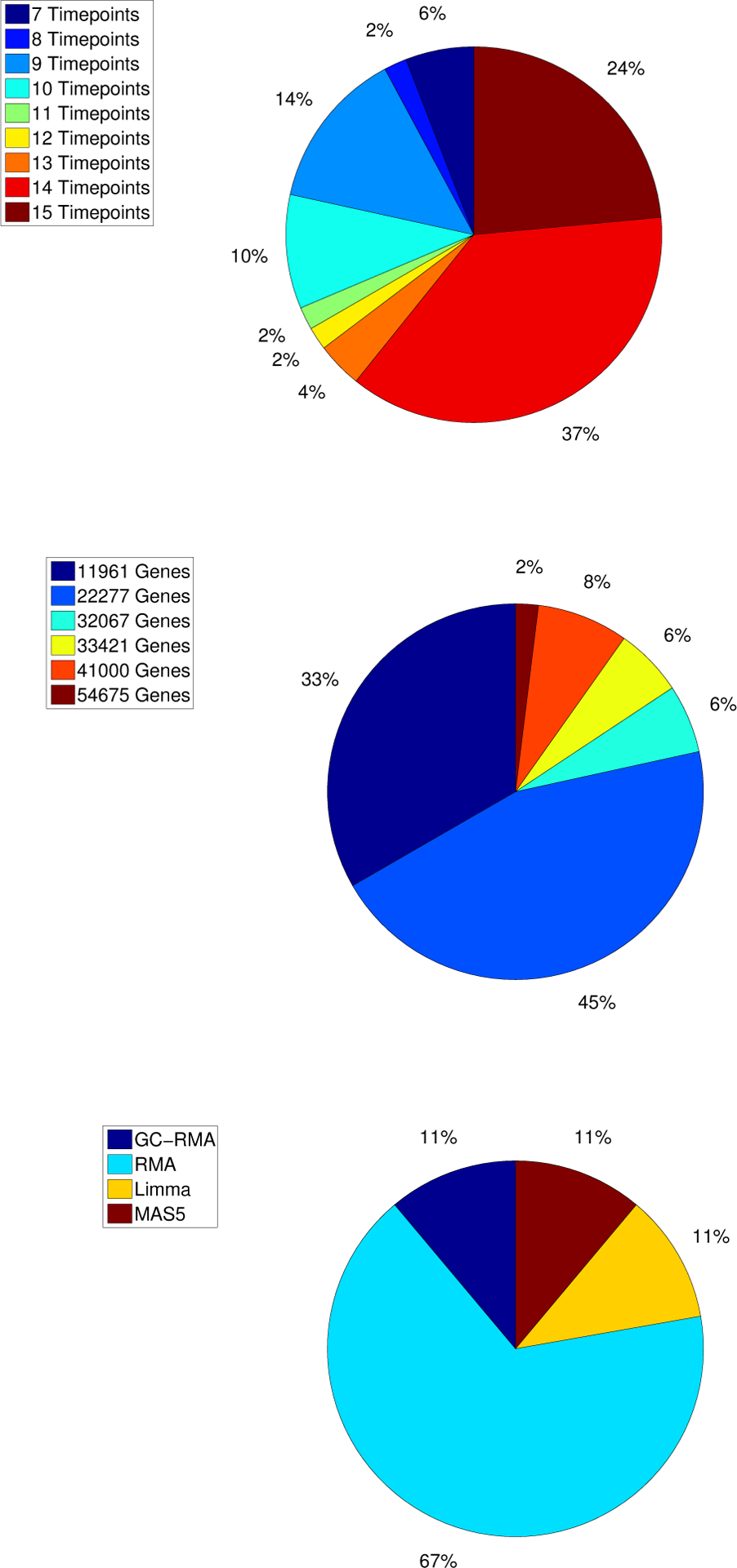
Distribution of the number of time-points and the number of genes/probes

Dynamic Response Genes for Influenza

The F-test statistic in Step 3 of the pipeline was used to identify the top 3, 000 dynamic response genes (DRGs) for each of the 58 datasets. We cut the number of DRGs nDRG = 3, 000 for all experimental conditions to avoid introducing bias due to different sample sizes for different conditions. Alternatively, one could select the number of significant DRGs for each experimental condition using a p-value (with a multiple testing adjustment), but as the number of significant DRGs can vary considerably for different conditions, it can be difficult to draw reliable comparisons between groups of experimental conditions. After careful consideration (e.g., visual inspection of the DRGs for each of the 58 datasets), we felt that 3000 was an appropriate threshold for the number of DRGs. The DRGs are genes that show a strong reaction over time after inoculation with the various virus strands. These genes might translate into clinically valuable biomarkers. The annotation of the DRGs is analysed at both virus subtype and population level in the following subsections.

Virus Subtype-Level Results:

Table 5 provides the annotation for the most significant DRG’s for each of the 19 virus subtypes based on the ranking of the F-test statistic in Step 3 of our pipeline. Many of these genes have been previously identified as been significantly related to influenza infection such as, 2’-5’-oligoadenylate synthetase-like, is part of a system activating RNase L, which is an important unspecific antiviral immune response and is also thought to play a role in the control of cell growth and differentiation (67); DnaJ (Hsp40) homolog, has been implicated in positive regulation of virus replication through co-option by influenza A virus (68); glucan (1,4-alpha-), is related to anti-infectious immunity (69) and N-acyl phosphatidylethanolamine phospholipase D, is an endogenous lipid that modulates pain and inflammation (70).

Table 5.

The most significant DRGs for each of the 19 virus subtypes.

GSE number	Virus Strand	Most Significant DRG’s
GSE52428	H1N1/Brisbane, H3N2/Wisconsin	2’-5’-oligoadenylate synthetase-like, KH domain containing, RNA binding, signal transduction associated 3
GSE12254	WE (LCMV-WE)	CHK1 checkpoint homolog, RAD58 homolog (RecA homolog, E. coli), RAD52 homolog
GSE19392	delNS1 post trypsin	DnaJ (Hsp40) homolog, subfamily A, member 1, cyclin A1, inhibitor of DNA binding 2, dominant negative helix-loop-helix protein
GSE19392	PR8 post trypsin	glucan (1,4-alpha-), branching enzyme 1, matrix metallopeptidase 1 (interstitial collagenase), ornithine decarboxylase 1
GSE19392	vRNA LTX+RNA	STAM binding protein, cysteine and glycine-rich protein 2, polymerase (RNA) III (DNA directed) polypeptide K
GSE19392	treated with media alone	bone marrow stromal cell antigen 2, interferon stimulated exonuclease gene, proteasome (prosome, macropain) subunit
GSE19392	treated with IFNb IFN	N-myc (and STAT) interactor, PHD finger protein 11, interferon-induced protein 44-like, tripartite motif-containing 22
GSE19392	treated with LTX transfection reagent	interferon induced transmembrane protein 1, interferon stimulated exonuclease gene, radical S-adenosyl methionine domain containing 2
GSE37571	A/CA/04/2009	CCAAT/enhancer binding protein (C/EBP), complement factor B, PCSK9, TUBB8, kinesin family member 4A
GSE37571	Mock	major histocompatibility complex, class I, E, complement factor B, major histocompatibility complex, class I, A, HLA-G
GSE30550	H3N2/Wisconsin	Anaphase-promoting complex subunit MND2, Bud site selection protein 22, C-8 sterol isomerase, Vacuolar-sorting protein SNF7
GSE40844	Mock	tetraspanin 8, kelch-like 24 (Drosophila), hect domain and RLD 5, DEAD (Asp-Glu-Ala-Asp) box polypeptide 60
GSE41067	H1N1 influenza A/New Caledonia/20/1999	HLA complex P5, DEXH (Asp-Glu-X-His) box polypeptide 58, interferon, alpha-inducible protein 6
GSE47960	dORF6	XIAP associated factor 1, interferon-induced protein 44-like, interferon induced transmembrane protein 1 (9–27)
GSE47960	iSARs	trafficking protein, kinesin binding 1, RAD23 homolog B (S. cerevisiae), chemokine (C-X-C motif) ligand 10
GSE47960	Mock	tribbles homolog 1 (Drosophila), tumor necrosis factor, alpha-induced protein 2, PR domain containing 1, with ZNF domain
GSE47961	BAT	eyes absent homolog 3, BAI1-associated protein 2, cardiotrophin-like cytokine factor 1, endothelin 2
GSE47961	dORF6	N-acyl phosphatidylethanolamine phospholipase D, LIM and senescent cell antigen-like domains 3, zinc finger protein 564
GSE47961	H1N1	interferon, alpha-inducible protein 27, nterferon induced transmembrane protein 4 pseudogene, MHC class I polypeptide-related seq B

Population-Level Results:

As the 58 data sets have a broad biological and technical heterogeneity, we do not expect that the annotation for the 3000 DRGs identified for each data set will contain genes that are common among all 58 data sets. Interestingly, there are 19 data sets out of the 58 that all contain the following three genes in the annotation of the DRG lists: TRADD^* which is an apothic pathway activated by TNF and linked to the H1N1 virus (71), ELMO2 which is involved in cytoskeletal rearrangements required for phagocytosis of apoptotic cells and cell motility, and STAT1^† which has been shown to be required for ISG induction and resistance to influenza infection (72). As 19 out of the 58 data sets (32% of the population) have identified these genes as having a significant response over time, we can regard them as potential bio-markers for influenza infection response at a population level. Additionally, we found that 17 out of the 58 data sets shared 15 common DRGs (fbx11, Fau, APEH, nadK, Necap1, nsfl1c, RAB6C, YCR015C, CTSS, Cdc25b, COL2A1, CRYAB, SERPING1, RTEL1, POLR2E) that are related to the regulation of cell death, proteins secreted into the cell surroundings and protein binding. Table 6 provides the official gene symbols and the functions of these DRGs. As these represent 29% of the population, they can also be regarded as potential bio-markers for influenza infection response at a population level.

Table 6.

The identified DRGs that are common across 17 or more data sets

Gene Symbol	Function
fbx11	Substrate recognition component of the a (SKP1-CUL1-F-box protein) E3 ubiquitin-protein ligase complex which mediates the ubiquitination and subsequent proteasomal degradation of target proteins
Fau	This protein is synthesized with ribosomal S30 as its C-terminal extension.
APEH	This enzyme catalyzes the hydrolysis of the N-terminal peptide bond of an N-acetylated peptide to generate an N-acetylated amino acid and a peptide with a free N-terminus.
nadK	Belongs to the NAD kinase family
Necap1	Involved in endocytosis.
nsfl1c	Reduces the ATPase activity of VCP. Necessary for the fragmentation of Golgi stacks during mitosis and for VCP-mediated reassembly of Golgi stacks after mitosis.
RAB6C	Protein transport. Regulator of membrane traffic from the Golgi apparatus towards the endoplasmic reticulum (ER).
YCR015C	Belongs to the UPF0655 family.
CTSS	Thiol protease.
Cdc25b	Tyrosine protein phosphatase which functions as a dosage-dependent inducer of mitotic progression.
COL2A1	Type II collagen is specific for cartilaginous tissues. It is essential for the normal embryonic development of the skeleton, for linear growth and for the ability of cartilage to resist compressive forces.
CRYAB	May contribute to the transparency and refractive index of the lens., mass spectrometry
SERPING1	Activation of the C1 complex is under control of the C1-inhibitor. It forms a proteolytically inactive stoichiometric complex with the C1r or C1s proteases. May play a potentially crucial role in regulating important physiological pathways including complement activation, blood coagulation, fibrinolysis and the generation of kinins.
RTEL1	ATP-dependent DNA helicase required to sup-press inappropriate homologous recombination, thereby playing a central role DNA repair and in the maintenance of genomic stability
POLR2E	DNA-dependent RNA polymerase catalyzes the transcription of DNA into RNA using the four ribonucleoside triphosphates as substrates.

Additionally, the annotation in step 5 provides the functional enrichment of the DRGs for all 58 data sets. The most enriched pathways are: Spliceosome (hsa03040), it is well known that influenza viruses have developed accurate regulation mechanisms to utilize the host spliceosome to enable the expression of specific spliced influenza virus products throughout infection (73); Proteasome (hsa03050) which has been shown to effectively block the influenza virus (74); p53 signaling pathway (hsa04115), the influenza virus infection is known to increases p53 activity (75); and other classical pathways such as cell cycle (hsa04110) and Ribosome (hsa03010) protein synthesis.

Gene Response Modules for Influenza

We use the Pipeline4DGEData Step 4, i.e., the IHC method with a correlation threshold of α = 0.7 to group the 3,000 DRGs for each of the 58 data sets, into between 15 and 476 temporal gene response modules (GRMs).

Virus Subtype-Level Results:

Table 7 shows the number of GRMs for a single data set or the range of the number of GRMs for multiple data sets, for each of the 19 virus subtypes. It also provides a brief description of the time-course patterns of the GRMs. For most virus subtypes, the time-course patterns of the GRMs have either a distinctive up/down regulated feature or multiple features denoting peaks and troughs at various time-points.

Table 7.

GRMs from different studies.

GSE number	Virus Strand	Number of GRMs	Time Course Pattern
GSE19392	delNS1 post trypsin	57	Two dominating features up/down regulation
GSE19392	PR8 post trypsin	63	Two dominating features up/down regulation
GSE19392	vRNA LTX+RNA	36	Two dominating features up/down regulation
GSE12254	WE (LCMV-WE)	57	Two dominating features up/down regulation
GSE37571	Mock	18	Two dominating features up/down regulation
GSE40844	Mock	17	Two dominating features up/down regulation
GSE41067	H1N1 influenza A/New Caledonia/20/1999	17	Two dominating features up/down regulation
GSE47960	dORF6	47	Two dominating features up/down regulation
GSE47960	Mock	83	Two dominating features up/down regulation
GSE47961	H1N1	19	Two dominating features up/down regulation
GSE19392	treated with media alone	53	A few features all denoting peaks and troughs at different timings
GSE19392	treated with LTX transfection reagent	34	A few features all denoting peaks and troughs at different timings
GSE52428	H1N1/Brisbane, H3N2/Wisconsin	200–467	Many features all denoting peaks and troughs at different timings
GSE19392	treated with IFNb IFN	56	Many features all denoting peaks and troughs at different timings
GSE37571	A/CA/04/2009	15	Many features all denoting peaks and troughs at different timings
GSE30550	H3N2/Wisconsin	291–400	Many features all denoting peaks and troughs at different timings
GSE47960	iSARs	75	Many features all denoting peaks and troughs at different timings
GSE47961	BAT	36	Many features all denoting peaks and troughs at different timings
GSE47961	dORF6	32	Many features all denoting peaks and troughs at different timings

Population-Level Results:

Figure 4 shows the time-course patterns from two different datasets. One with the distinctive up/down regulated time-course patterns (experimental condition Mock from GSE37571) and one with time course patterns that denote peaks and troughs at various time-points (experimental conditions BAT from GSE47961). In this manner, Figure 4 illustrates the different time-course patterns identified in Table 7. These preliminary results indicate that there are two categories of gene response modules for influenza infection. The first is composed of modules of approximately the same size containing genes that have different time course behaviors. The second is composed of modules of a greater size containing genes that have a similar behavior over time (dominating up/down regulated feature).

Figure 4.

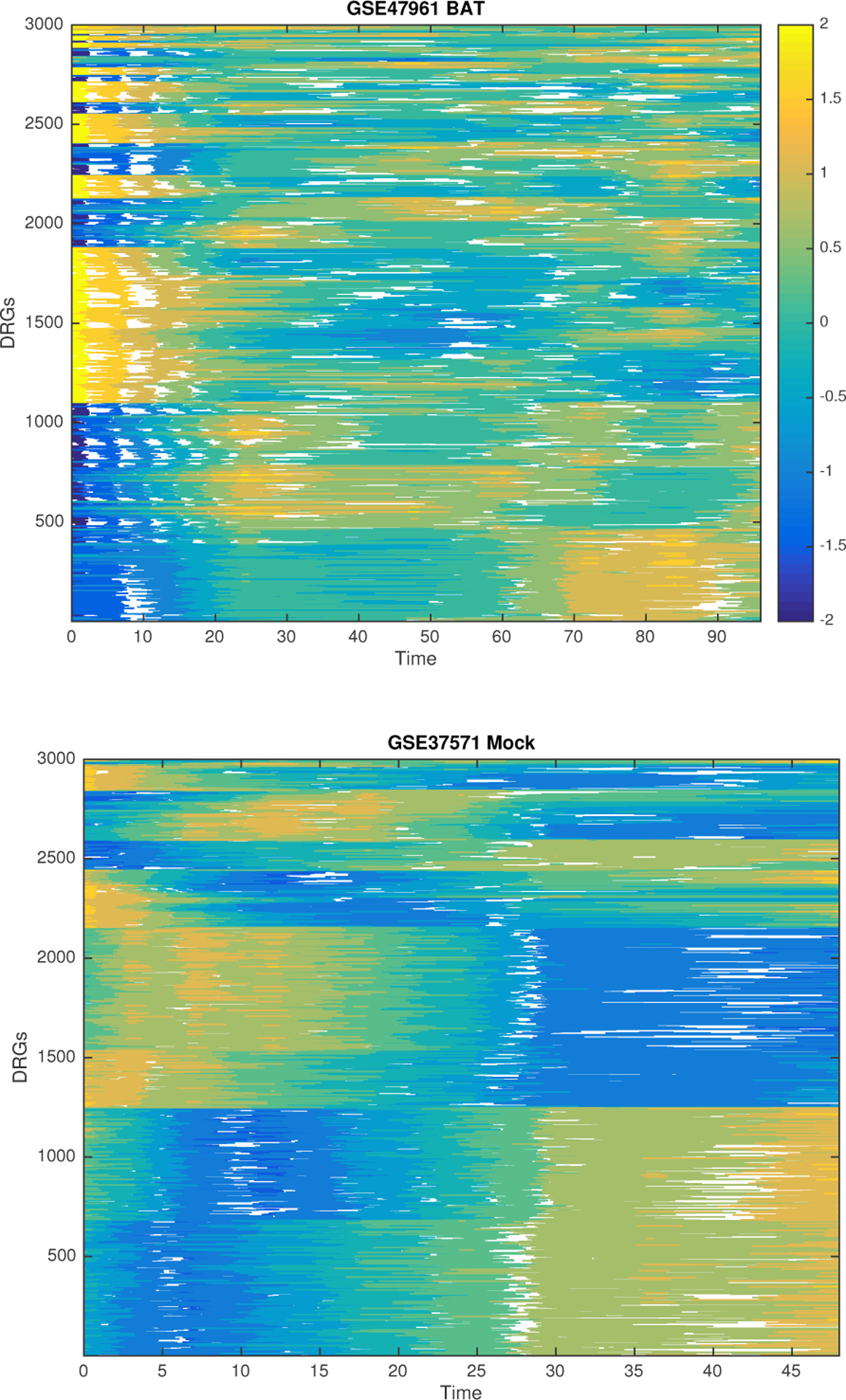
Typical Time-Course Patterns of the GRMs

Gene Regulatory Networks for Influenza

Steps 6 and 7 of our pipeline are applied to the GRMs attained from each data set contained in the 9 influenza-related studies, the gene response networks for these data sets are established and their network features are analyzed. In this section, we analyze the network features of the 58 gene regulatory networks. The nodes of these networks are the GRMs, and the edges are the regulation effects β. The results are summarized as follows.

Virus Subtype-Level Results:

Here we use the network centrality measures to compare the features of the GRNs for each of the 19 virus subtypes. Figure 5 illustrates the virus subtypes with GRNs that have relatively large centrality measures by showing the standardized clustering coefficient, density, bridging centrality and closeness centrality of the GRNs grouped by their virus subtype. For virus subtypes with multiple GRNs, we obtain the average of the metric for all experimental conditions pertaining to that particular virus subtype.

Figure 5.

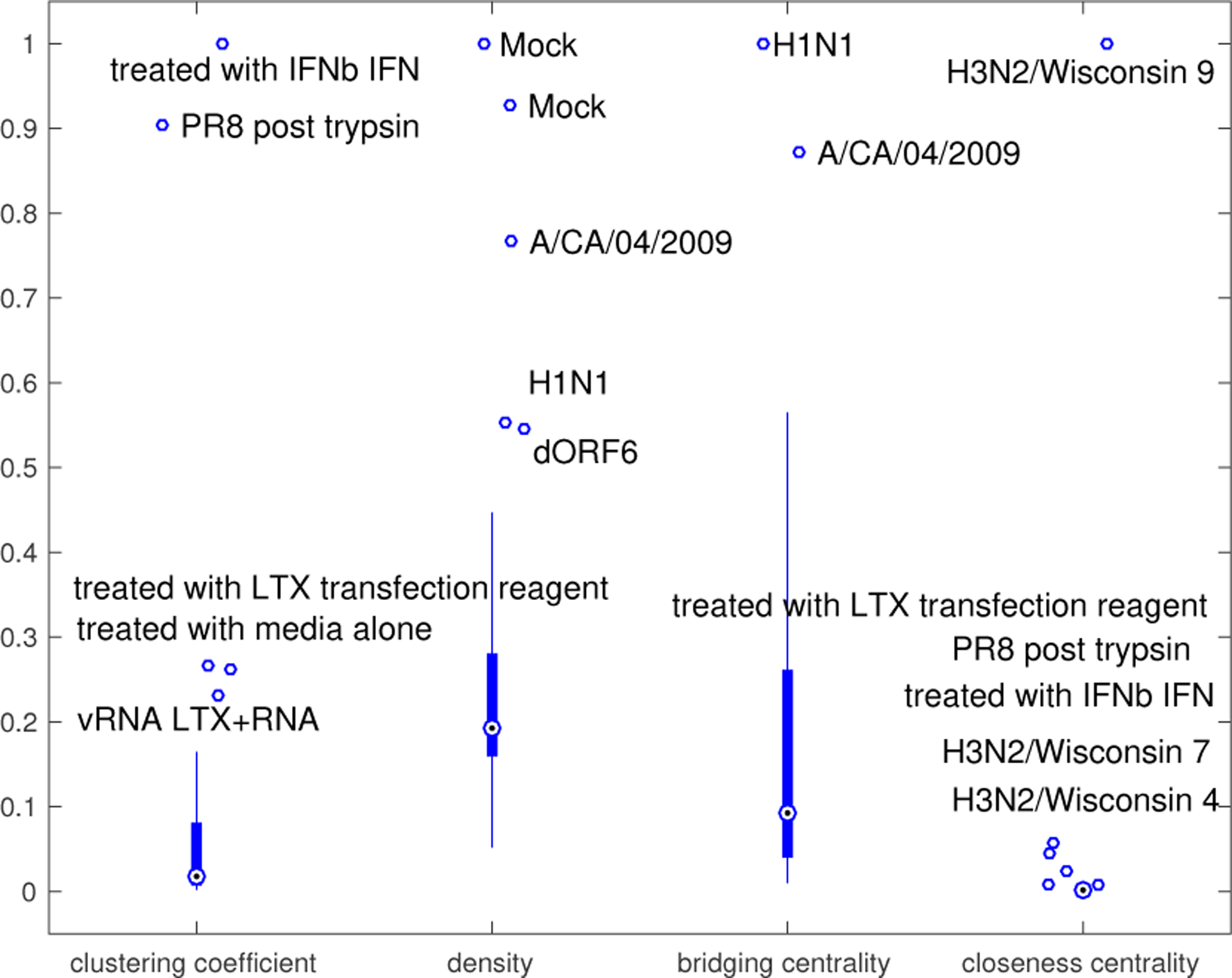
The standardized clustering coefficient, density, bridging centrality and closeness centrality of the GRNs for the 19 virus subtypes.

The virus subtypes with relatively high clustering coefficients are: In the GSE19392 study, cells treated with IFNb, treated with media alone, treated with LTX transfection reagent, vRNA LTX+RNA, and PR8 post trypsin. This suggests that there is a strong interconnectivity between the modules in the GRNs for these studies. Figure 6 illustrates the GRN for the cells treated with interferon beta (IFNb), which has a relatively high clustering coefficient (top), and the GRN for the cells infected with PR8 virus lacking the NS1 gene (DNS1), which has a relatively low clustering coefficient (bottom). The size of the nodes indicates the number of genes contained in the modules, (i.e., the larger the node, the greater the number of genes contained in that module). It is clear that both GRNs only have two very large modules containing many genes and that these modules are not closely related to each other as they have a large distance between one another. The GRN for the cells treated with interferon beta (IFNb) has a closer-knit community of modules than the cells infected with the PR8 virus lacking the NS1 gene (DNS1), which has a dispersed community of modules.

Figure 6.

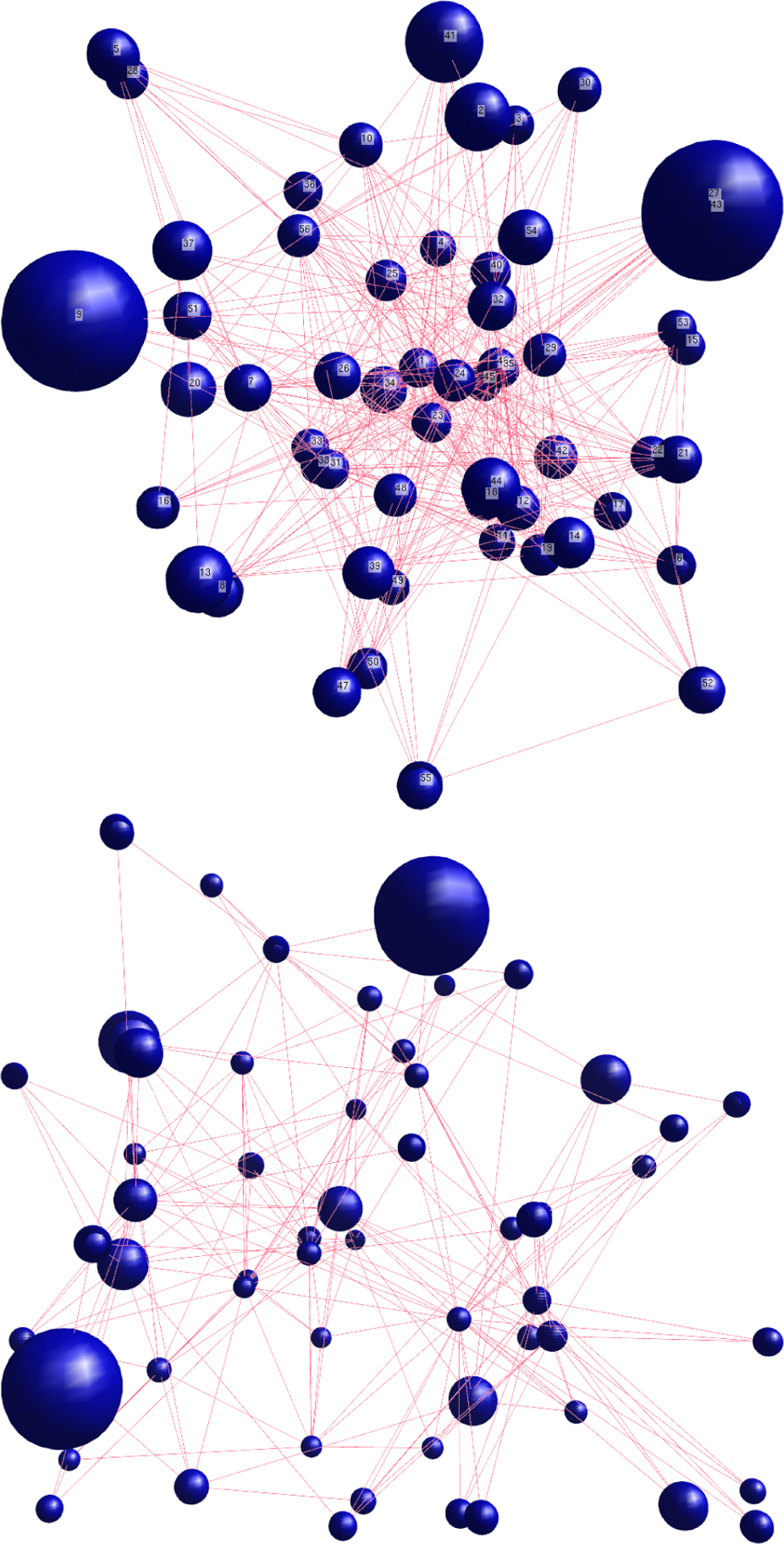
The GRNs for two experimental conditions in the study of GSE19392: cells treated with IFNb (top) and PR8 virus lacking the NS1 gene (bottom)

The studies with relatively high densities are GSE37572 Mock, GSE40844 Mock, GSE37571 A/CA/04/2009, GSE47961 H1N1 and dORF6. As Table 2 describes, this metric provides a measure of the general interdependence between all nodes in the network. GRNs with higher densities are those where the GRMs tend to be closely dependent on each other. In such networks, the expression of each module tends to be affected by many or all of the other modules. Figure 7 illustrates the GRN for GSE37571 A/CA/04/2009, which has a relatively high density (top), and the GRN for GSE52428 H3N2 Subject 9, which has a relatively low density (bottom). The GRN for GSE37571 A/CA/04/2009 contains a few GRMs, but these modules are highly connected to one another. While the GRN for GSE52428 H3N2 Subject 9 has many GRMs, but each module only regulates a relatively small proportion of the other modules.

Figure 7.

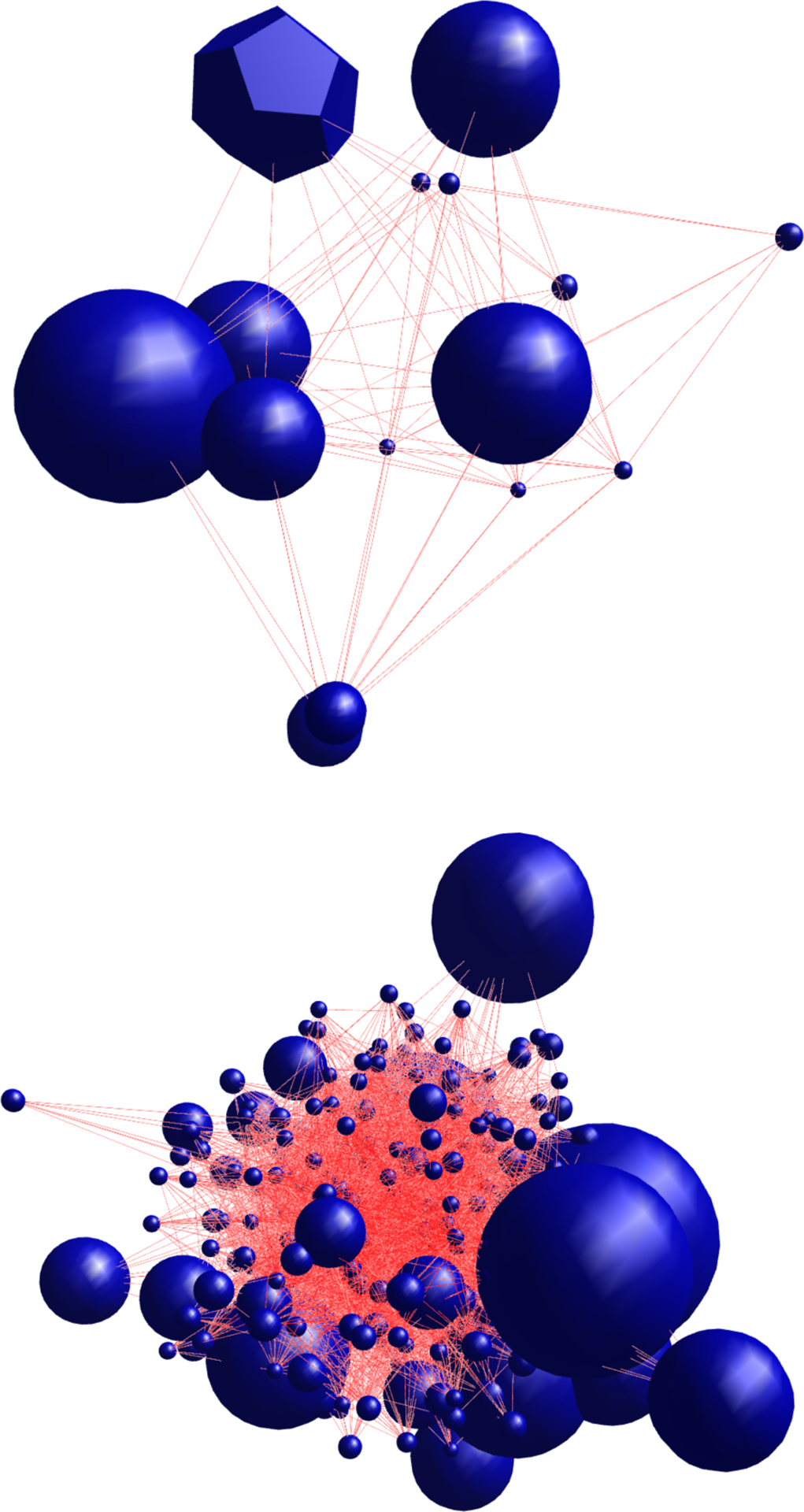
The GRNs for GSE37571 A/CA/04/2009 (top) and GSE52428 H3N2 Subject 9 (bottom)

The studies with relatively high bridging centralities are GSE19392 treated with LTX transfection reagent, GSE37572 A/CA/04/2009, and GSE47961 H1N1. This suggests that these studies have modules that regulate highly-connected groups of GRMs. Figure 6 shows the GRN for GSE37571 A/CA/04/2009. The GRM that is shaped like a dodecahedron is the module with the largest bridging centrality, from Figure 6, it is clear that this module connects different groups of highly connected GRMs. We analyzed the functional enrichment of the DRGs in this GRM. The most enriched pathways are Pathogenic Escherichia coli infection (hsa05830), Gap junction (hsa04540) and Phagosome (hsa04666), in particular, these all reference the tubulin protein superfamily as being significantly related to these DRGs. This supports recent research showing that influenza A virus induces the disruption of the microtubule network β with and α-tubulin (76; 77)

The studies with relatively high closeness centralities are GSE52428 H3N2/Wisconsin Subject 7, 4 and 9, GSE19392 study, cells treated with IFNb, treated with LTX transfection reagent, and PR8 post trypsin. Figure 7 shows the GRNs for GSE37571 A/CA/04/2009 and GSE52428 H3N2/Wisconsin Subject 9. The GRN for GSE37571 A/CA/04/2009 has a relatively low closeness centrality metric with a few modules that are relatively far apart or dispersed, while the GRN for GSE52428 H3N2/Wisconsin Subject 9 has a high closeness centrality metric with many of the modules in close proximity to one another.

Population-Level Results:

Clustering is an important property of any network as it measures the interconnectivity of the network. Our results suggest that a lower clustering coefficient may indicate an expanded response to the influenza infection. The evidence to support this claim comes from 22 data sets in the GSE19392 and GSE30550 studies which account for 43% of the population. The data sets in GSE19392 concern cells infected by the influenza virus but under five different conditions, each highlighting a distinct aspect of the response: i) cells were infected with the wild-type PR8 influenza virus that can mount a complete replicative cycle (PR8 post trypsin); ii) cells were transfected with viral RNA isolated from influenza particles. This does not result in the production of viral proteins or particles (vRNA LTX+RNA); iii) cells were treated with interferon beta, to distinguish the portion of the response which is mediated through Type I IFNs (treated with IFNb IFN); iv) cells were infected with a PR8 virus lacking the NS1 gene (delNS1 post trypsin); v) cells were treated with media alone as a control. All the conditions except for condition (iv) have an unusually high clustering coefficient (this is also true for diameter and mean distance, two alternative measures of inter-connectivity). The NS1 protein normally inhibits vRNA- or IFNb-induced pathways, and its deletion can reveal an expanded response to infection (61). We suspect that a lower clustering coefficient is an indication of an increase in a host response to influenza infection. This is further supported by the data sets in the GSE30550 study. These data sets are divided into two groups according to the clinical symptom chart based on the standardized symptom scoring (78): symptomatic (Sx) group with nine subjects (subjects 1,5,6,7,8,10,12,13,15) and asymptomatic (Asx) group with eight subjects (subjects 2,3,4,9,11,14,16,17). Interestingly, the majority of the Asx group (subjects 2,3,4,9,11,14,16), which we would expect to have a high response to influenza infection as they are not experiencing symptoms, have the lowest average clustering coefficients among all the studies.

In summary, we have briefly discussed some of the results from our analysis of several virus infection studies using Pipeline4DGEData. The primary goal of this article is to propose the methodology for the Pipeline4DGEData, a tool for the construction of gene regulatory networks from large amounts of high-dimensional time course gene expression data. Here we demonstrate the pipeline’s ability to identify potential bio-markers for influenza infection and to discern interesting characteristics of the dynamic interaction process between the host and influenza virus. More detailed biological findings from these viral infection studies will be reported elsewhere in the near future.

The Pipeline for Dynamic Gene Expression Data Applied to Simulated Data Sets

The accuracy of the results provided by Pipeline4DGEData was evaluated by examining its performance on simulated expression data. Simulation 1 is derived from previously discovered GRMs, i.e., the estimated GRMs were used to simulate the underlying time course data. The pipeline analysis was run on the simulated data in order to confirm if the new results are consistent with the original results. Simulation 2 adds various levels of random noise to the the time course gene expression data set GSE52428, subject 1. The pipeline analysis was run on the simulated data in order to confirm if the new results are consistent with the original results.

Simulation 1

The simulated data was obtained as follows. Let c_i be the average standardized expression level over time of the genes in the i^th cluster attained from Step 4 of the Pipeline. The simulated time course data for the j^th dynamic response gene in the i^th cluster can be generated as follows:

$$DR{G}_{i,j}\left(t\right)=c_i\left(t\right)+\sigma {ϵ}_{i,j}\left(t\right)$$

for j = 1, …, Q_i, where Q_i is the number of genes in the i^th cluster, also provided by the step 4, ϵ_i,j(t) is normally distributed random variable with mean 0 and variance 1 whereas σ quantifies the magnitude of the measurement error. This produces simulated time course measurements for the 3000 DRGs. The remaining non-responsive genes (NRG) were generated by

$$NR{G}_{i,j}\left(t\right)=\sigma {ϵ}_{i,j}\left(t\right).$$

The simulated data sets for the DRGs and the non-responsive genes are combined to form the test data set. The simulated data were generated for three measurement error levels: σ = 0.1, σ = 0.2 and σ = 0.3 and each simulation was performed 1000 times.

The method described above was used to simulate time course data based on the pipeline results from the data set GSE52428, subject 1. This data set contains time course measurements for 22, 277 genes. Step 3 of the pipeline identifies 3000 of these genes as DRGs and the remaining 19, 277 genes are considered non-responsive genes (NRGs). Step 4 subsequently groups these DRGs into 128 clusters. Using the method described above, simulated expression data of the 22, 277 genes were obtained from the 128 modules. The results obtained from the application of the pipeline to this simulated data is described as follows.

Dynamic Response Genes:

The F-test statistic in Step 3 of the pipeline was used to identify the top 3,000 dynamic response genes (DRGs) for each of the simulated datasets. We computed a binary vector that is one if the gene has been selected as a DRG and zero otherwise. Then we computed the difference between this binary vector and a binary vector corresponding to the true DRG assignment. If the difference is negative then the gene has been identified as DRGs but in fact is a non-responsive gene (false positive) and if its is positive then the gene has been identified as a non-responsive gene but is in fact a DRG (false positive). Table 8 shows the average percentage of false positives and percentage of false negatives. As is evidenced in Table (8) Step 3 provides an accurate identification of the top 3,000 dynamic response genes with an error which ranges from 3.74% for σ = 0.1 to 5.24% for σ = 0.3.

Table 8.

Accuracy of the DRG Identification

Error Level	False Positives	False Negatives
Simulation 1
0.10	1.87%	1.87%
0.20	2.19%	2.19%
0.30	2.62%	2.62%
Simulation 2
0.10	1.00%	1.00%
0.20	2.05%	2.05%
0.30	2.84%	2.84%

Gene Response Modules:

The IHC clustering method in Step 4 of the pipeline was used to group the top 3,000 DRGs into gene response modules for each of the simulated datasets. The adjusted rand index (ARI) (79) provides an overall similarity measure between two clustering assignments taking into account that the agreement between partitions could arise by chance alone. Thus, the ARI provides a measure of the similarity of two clustering methods. This index has an expected value of zero for independent clusterings and maximum value 1 for identical clusterings. Table 9 shows the adjusted rand index for the true cluster assignment and the cluster assignment identified by Step 4 of the pipeline. Overall, step 4 provides clusters that are very similar to the true cluster assignment with an similarity which ranges from 82% for σ = 0.1 to 75% for σ = 0.3.

Table 9.

Accuracy of the GRM identification.

Error Level	Adjusted rand index (ARI)
Simulation 1
0.10	0.82
0.20	0.79
0.30	0.75
Simulation 2
0.10	0.90
0.20	0.81
0.30	0.74

Gene Response Network:

Step 6 attains the gene response networks for each simulation data set. As these networks are likely to have differing number of nodes as different simulations can generate a different number of clusters, we cannot compare these networks directly. Instead we compare the edge weights in terms of the DRGs as opposed to the clusters by computing a 3000 × 3000 matrix which assigns the edge of each cluster to each of the DRGs in that cluster. Table 9 uses one minus the Hamming distance to compare the percentage of coordinates (i.e., nodes) that are the same. Step 6 provides networks that are very similar to the true networks with a similarity which ranges from 79% for σ = 0.1 to 73% for σ = 0.3.

Simulation 2

The simulated data was obtained as follows. Let η be a matrix size 22, 277 × 15 containing the time course gene expression data set GSE52428, subject 1. The simulated time course data can be generated as follows:

$$y_j\left(t_i\right)={\eta }_j\left(t_i\right)+{\sigma }_j{ϵ}_j\left(t_i\right)$$

for j = 1, …, 22, 277, indexing each gene and i = 1, …, 15, indexing each time point, ϵ_j(t_i) is normally distributed random variable with mean 0 and variance 1 whereas σ_j quantifies the magnitude of the measurement error. The simulated data were generated for three measurement error levels: σ_j = 0.1κ_j, σ_j = 0.2κ_j and σ_j = 0.3κ_j, where κ_j represents the sample standard deviation of the j^th gene and each simulation was performed 1000 times. The results obtained from the application of the pipeline to this simulated data is described as follows.

Dynamic Response Genes:

The F-test statistic in Step 3 of the pipeline was used to identify the top 3,000 dynamic response genes (DRGs) for each of the simulated datasets. Table 8 shows the average percentage of genes that were identified as DRGs but were in fact non-responsive genes (false positives) and average percentage of genes that were identified as non-responsive genes but were in fact DRGs (false negatives). As is evidenced in Table (8) Step 3 provides an accurate identification of the top 3,000 dynamic response genes with an error which ranges from 2% for σ = 0.1 to 5.68% for σ = 0.3.

Gene Response Modules:

The IHC clustering method in Step 4 of the pipeline was used to group the top 3,000 DRGs into gene response modules for each of the simulated datasets. The ARI provides a measure of the similarity of two clustering methods. This index has an expected value of zero for independent clusterings and maximum value 1 for identical clusterings. Table 9 shows the adjusted rand index for the true cluster assignment and the cluster assignment identified by Step 4 of the pipeline. Overall, step 4 provides clusters that are very similar to the true cluster assignment with an similarity which ranges from 90% for σ = 0.1 to 74% for σ = 0.3.

Gene Response Network:

Step 6 attains the gene response networks for each simulation data set. Table 9 uses one minus the Hamming distance to compare the percentage of coordinates (i.e., nodes) that are the same. Step 6 provides networks that are very similar to the true networks with a similarity which ranges from 81% for σ = 0.1 to 80% for σ = 0.3.

These results indicate that there is consistency in the output returned by the pipeline. In other words, given a set of genomic time course data with underlying behavioural patterns shared by groups of dynamically-responsive genes, the pipeline is able to identify these groups of genes as DRGs, cluster them into GRMs based on their expression patterns and determine the GRN that describes the interactions between these modules. This consistency is manifest in the objective correspondence between the results (DRGs, GRMs, and GRN) obtained from the original data and those obtained from the simulated data sets. Table 8 shows that rates of false positives and negatives between DRGs from real and simulated are low. In other words, if a group of genes within the dataset are dynamically responsive, then the pipeline will correctly class them, on average, as DRGs. Similarly, the high rand indices (close to 1) observed when comparing real and simulated modules, and displayed in Table 9, show that the clustering method used by the pipeline performs well. Finally, correspondence was observed between the GRNs from real and simulated data, as shown in Table 11. The coherence between the results from real and simulated data serves as strong evidence that the output returned by the pipeline is truly representative of the dynamic response patterns hidden in a large data set, such as those provided by the GEO.

Table 11.

Sensitivity of the GRN Identification

Step 3
	SS vrs SS	FPCA vrs FPCA	SS vrs FPCA
% of DRGs that differ
nDRG : 2000 vs 3000	4.48%	4.48%	11.76%
nDRG : 4000 vs 3000	4.48%	4.48%	15.76%
nDRG : 5000 vs 3000	8.97%	8.97%	18.59%
Step 3
Adjusted Rand Index (ARI)
α : 0.60 vs 0.7	0.99	0.99	0.39
α : 0.80 vs 0.7	0.99	0.99	0.39
α : 0.90 vs 0.7	0.99	0.99	0.39
Step 6
LASSO
γ : AIC vs GCV	0.87	0.64	0.90
γ : BIC vs GCV	0.88	0.77	0.91
γ : AIC vs BIC	0.87	0.64	0.90
SCAD
γ : AIC vs GCV	0.87	0.64	0.87
γ : BIC vs GCV	0.87	0.77	0.88
Y : AIC vs BIC	0.88	0.64	0.87
LASSO vs SCAD
γ = GCV	0.87	0.35

The Pipeline for Dynamic Gene Expression Data Sensitivity Analysis

Various steps of the Pipeline for Dynamic Gene Expression Data have tuning parameters that must be provided by the user or set to default for instance: step 3 either uses spline smoothing (default) or functional principal component analysis to estimate the trajectory of the genes and subsequently selects a fixed number of dynamic response genes, nDRG (default is 3000); step 4 selects the average within cluster correlations and the higher bound for the within cluster corelations (default α = 0.7); step 6 uses either LASSO (default) or SCAD to do variable selection and selects the corresponding regulation parameter γ using either GCV, AIC or BIC (default approach selects γ by minimizing GCV). In this section, we examine the sensitivity of the results to each of these parameters.

Dynamic Response Genes:

The F-test statistic in Step 3 of the pipeline was used to identify the dynamic response genes (DRGs) for the time course gene expression data set GSE52428, subject 1. We compare three different numbers of the top ranking dynamic response genes nDRG set to 2000, 4000 or 5000 to the default for that approach namely, nDRG = 3000 for both spline smoothing (SS) and functional principal components analysis (FPCA). We also compare the difference between the different approaches SS vrs FPCA for nDRG set to 2000, 4000 or 5000. Table 8 shows the sum of the percentage of genes that were identified as DRGs but were in fact non-responsive genes (false positives) and the percentage of genes that were identified as non-responsive genes but were in fact DRGs (false negatives) for each scenario. As is evidenced in Table (8) Step 3 provides an stable identification of the top dynamic response genes with a variation which ranges from 4.48% for nDRG = 2000 to 8.97% for nDRG = 5000 for SS and FPCA. As expected there are some differences between the DRGS identified by the SS and FPCA approaches with an agreement regarding DRG selection of 90.40% for nDRG = 2000 and 79.66% for nDRG = 5000.

Gene Response Modules:

The IHC clustering method in Step 4 of the pipeline was used to group the top 3,000 DRGs into gene response modules for the time course gene expression data set GSE52428, subject 1. Table 9 shows the adjusted rand index for the cluster assignment identified by Step 4 of the pipeline with α = 0.7 and the cluster assignment identified by Step 4 of the pipeline with α set to 0.6, 0.8 or 0.9 for both the SS and FPCA approaches. Overall, step 4 provides clusters that are robust to the selection of the parameter α as the ARI of the clusters is 99% for all levels of α for both the SS and FPCA approaches. As expected theres is not much similarity between clusters identified by the SS and FPCA approches with an agreement regarding cluster assignment of 39% for all levels of α.. The FPCA approach borrows information across genes to attain an estimate the trajectories of the genes, thus the estimated trajectories will be more similar to one another for this approach than SS approach where the trajectories for each gene are attained from smoothing the observations from each gene individually. In light of this the FPCA is likely to produce less clusters containing more genes.

Gene Response Network:

Step 6 attains the gene response networks for each simulation data set. Here we use one minus the Hamming distance to compare the percentage of coordinates (i.e., nodes) that are the same. Table 9 shows the percentage of common coordinates for the various approaches for selecting the regulation parameter γ, namely, GCV, AIC and BIC. For the SS approach Step 6 provides networks that are robust to the technique used to select the regulation γ parameter with an average agreement of 0.87. However, for the FPCA approach there is a considerable variability in the variable selection for various values of γ with an average agreement of 0.68. We also compare the two proposed approaches LASSO vs SCAD for the SS and FPCA. For the SS approach Step 6 provides networks that are robust to the model selection technique used with an average agreement of 0.87. However, for the FPCA approach there is a considerable variability in networks wit respect to the model selection technique used with an average agreement of 0.35.

Conclusions

In this article, we propose the Pipeline4DGEData for the statistical modeling and analysis of the time course gene expression data sets that are available on GEO. Pipeline4DGEData identifies dynamic gene regulatory networks that determine the host response to an external stimulus or disease. This pipeline incorporates the following eight steps: (i) obtain the data from GEO; (ii) pre-process the data; (iii) detect the dynamic response genes; (iv) cluster the dynamic response genes into gene response modules; (v) annotate these gene response modules; (vi) construct a gene regulatory network that describes the interactions between these gene response modules using differential equations; (vii) perform a network feature analysis to identify influential GRMs and to characterize various properties of the network and (viii) output the results in a manner that make the publication process more efficient, i.e., provide a manuscript file for a biological journal that contains all tables and figures automatically generated by the pipeline and a template for the descriptions of the studies analyzed and methodologies implemented. Furthermore, the pipeline has a consistent and scalable structure that facilitates comparative analysis across large groups of data sets.

We demonstrate the utility of the Pipeline for Dynamic Gene Expression Data by using it to analyze time course gene expression data from nine studies on various influenza viruses. The goal of our analysis is to simultaneously analyze multiple heterogeneous sources of time course gene expression data on various influenza viruses to (i) identify robust bio-markers for influenza infection and (ii) determine virus-specific bio-markers. These two goals facilitate the diagnosis of virus strains and the identification of vaccine responders at a population level.

We detect the most significant dynamic response genes for each of the 19 virus subtypes (see Table 5). Furthermore, we establish the following potential bio-markers for influenza infection response at population level (37% of the data sets reporting these genes as having a significant response over time): TRADD, an adapter molecule for TNFRSF1A/TNFR1 that specifically associates with the cytoplasmic domain of activated TNFRSF1A/TNFR1 mediating its interaction with FADD; ELMO2 involved in cytoskeletal rearrangements required for phagocytosis of apoptotic cells and cell motility; and STAT1 A signal transducer and activator of transcription that mediates signaling by interferons IFNs.

Additionally, we determine that there are two types of gene response modules for influenza infection: (i) there are approximately the same number of genes in each module and each module’s time course behavior is different (modules with many features); (ii) there are a lot of genes in each module and these have a similar behavior over time (dominating up/down regulated feature).

The network feature analysis can help identify key gene response modules in the gene regulatory network while also providing insight into the structure of the network allowing us to make comparisons across various virus subtypes. We find that a lower clustering coefficient may indicate an expanded response to the influenza infection with 43% of the data sets supporting this claim.

While the Pipeline for Dynamic Gene Expression Data is shown to produce interesting biological results, this approach does have some limitations which may warrant more research in the future. In the network construction step (Step 6), the linear ODE model is used, but for some applications, nonlinear ODE models or other network models may be more appropriate. The two-stage approach for linear ODE model selection is highly dependent on the accuracy of the estimated time course gene expression trajectories and their derivatives and can produce inaccurate results if these estimates are poor. As a result, a more robust approach to model selection would be favorable. Finally, we also need to develop more comparative tools to allow us to produce more in-depth across-study analyses.

In summary, the Pipeline for Dynamic Gene Expression Data allows us to take advantage of the vast amounts of publicly available data sets and investigate gene regulatory networks for different biological conditions efficiently. We can examine the dynamic interaction processes between many hosts and external stimulus across multiple conditions. We believe that these types of analyses will lead to a better understanding of the heterogeneity of the real world population. This approach also provides an examination of each host response to a disease or experimental condition at a genetic level, so that novel prevention and intervention targets can be discovered at an individual level and personalized or precision medicine can be achieved.

Table 10.

Accuracy of the GRN Identification

Error Level	1-Hamming Distance
Simulation 1
0.10	0.79
0.20	0.78
0.30	0.73
Simulation 2
0.10	0.81
0.20	0.81
0.30	0.80