Abstract
The steric repulsion between proteins on biological membranes is one of the most generic mechanisms that cause membrane shape changes. We present a minimal model in which a spontaneous curvature is induced by asymmetric protein crowding. Our results show that the interplay between the induced spontaneous curvature and the membrane tension determines the energy-minimizing shapes, which describes the wide range of experimentally observed membrane shapes, i.e., flat membranes, spherical vesicles, elongated tubular protrusions, and pearling structures. Moreover, the model gives precise predictions on how membrane shape changes by protein crowding can be tuned by controlling the protein size, the density of proteins, and the size of the crowded domain.
Significance
Membranes are complex environments in which proteins are often densely packed. In a crowded membrane domain, where proteins are asymmetrically bounded to the membrane, volume exclusion leads to steric repulsion, which in turn drives membrane deformation. Experiments have revealed various different shapes: spherical vesicles, pearls, and tubes. We present a theoretical model in which protein crowding induces a spontaneous curvature that depends on the protein density. The interplay between induced spontaneous curvature and membrane tension captures the wide variety of membrane shapes found in experiments. We predict the membrane shape transformation from a flat patch to spherical buds and elongated pearl-like and tubular shapes as a function of the size of the crowded domain, the membrane tension, and the protein density.
Introduction
Membrane nanotubes formed by lipid bilayers are ubiquitous in cell biology (1,2), in which they play a key role in various transport processes by facilitating the inter- and intracellular transport of fluids and macromolecules (2,3). The high surface/volume ratio inherent to tubular shapes enables rapid exchange of biomaterial across the lipid bilayer by transmembrane proteins or protein channels (4,5). As membrane tubes can bridge distances of several micrometers, they can facilitate the transport of nutrients or even entire organelles such as mitochondria and lysosomes between cells (6,7). A wide range of biophysical mechanisms cause tube formation, such as the adsorption of intrinsically curved proteins (8, 9, 10, 11), internal and external protein scaffolds (12,13,14,15), local pulling forces (16), membrane compression (17), osmotic deflation (18,19), protein phase separation (20), and protein crowding (21,22). In addition, it was shown that pearling of cylindrical tubes can be induced by an interplay of membrane bending and membrane tension (23,24) and by curvature-inducing proteins (25,26). Protein crowding, i.e., the accumulation of proteins in a confined membrane domain is a phenomenon that is ubiquitous in biological membranes, which typically contain a multitude of domains with densely packed proteins of different size and where an overexpression of specific proteins or biopolymers can be a disease marker. Tumor cells, for example, exhibit both a higher concentration of glycosylated polymers and a higher tendency to form tubular protrusions (27). Although tubulation in biological cells is complex and different mechanisms, such as scaffolded tubulation by actin polymerization and crowding, can act simultaneously, experiments of Shurer et al. (27) indicate that crowding plays an important role in cellular tubulation in cancer cells and may set apart healthy and malignant cells.
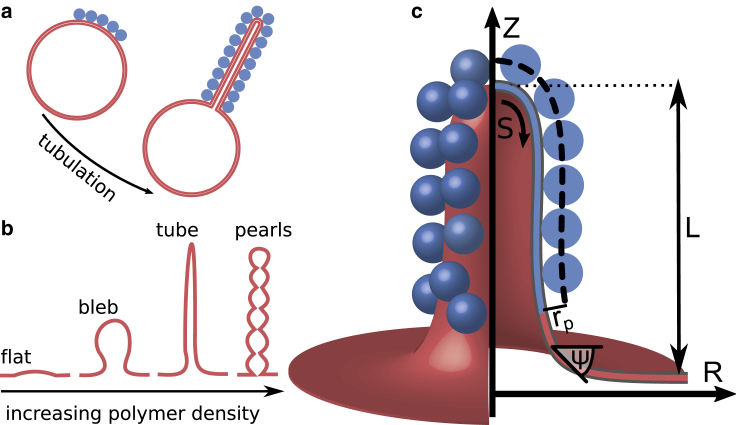
Despite the fact that protein crowding plays an essential role in many membrane remodeling phenomena, a theoretical model encompassing the protein size and density that accurately predicts the wide range of membrane shapes observed experimentally is still lacking. Theoretical studies have shown that the steric pressure between dense, unstructured proteins together with an asymmetry in the protein distribution across the lipid bilayer produces a spontaneous membrane curvature (28, 29, 30) and thus induces changes in the membrane shape. Stachowiak et al. (31) observed membrane tubes protruding from synthetic giant unilaminar vesicles (GUVs) functionalized with green fluorescent proteins (GFPs) (31). A schematic description of this experimentally observed tubulation process is shown in Fig. 1 a (31). The membrane tubes completely consume the GFP-coated membrane region and extend over a length of several micrometers, which is of the same order of magnitude as the GUV diameter (31). Other polymers containing a large unstructured region also generate a repulsive effect that leads to tube formation (27,32). Moreover, Shurer et al. (27) recently demonstrated that densely packed brush-like glycocalyx polymers induce a variety of cell membrane shapes: flat membranes, Ω-shaped membranes (referred to as blebs), tubes, and pearls, induced by densely packed brush-like glycocalyx polymers, as shown in Fig. 1 b. The wide range of polymers causing membrane tubes, including folded, intrinsically disordered, and brush-like polymers (27,31,32), suggests that the shape remodeling process does not depend on the chemical structure of the individual protein but is based on a generic mechanism that is potentially relevant for a variety of proteins in densely packed membrane domains. However, a biophysical model that reveals the minimal requirements for the formation of the different and seemingly incommensurable membrane shapes through a single mechanism has yet to be established. Inspired by these experimental observations (27,31), we study theoretically the biophysical origin leading to the zoology of different membrane shapes. We derive a minimal mathematical model describing the progressive shape transformation induced by protein crowding, i.e., from a flat membrane to a fully formed tube.
Figure 1.
(a) Schematic illustration of the membrane tube formation as observed experimentally on GUVs (31). The protein-coated domain, for which the proteins are shown as blue spheres, is completely consumed by the protruding tube. The size of the vesicle and the tube are drawn to scale to illustrate a ratio between the protrusion height L and the crowded domain Ac that is representative of the order of magnitude found in experiments (31). (b) Qualitative representation of membrane shapes observed experimentally by Shurer et al. (27) on cells with glycocalyx biopolymers with increasing polymer density. (c) The membrane shape is parameterized by the arc length S and the azimuthal angle ψ, where we treat the membrane as axially symmetrical around the z axis. The proteins that bind to the membrane within an area Ac are modeled as spheres with a radius rp.
Materials and methods
We start by formulating the membrane energy E, which takes into account the Helfrich bending energy (33,34), the membrane tension σ, and the lateral pressure p between crowded proteins:
| (1) |
with A the total membrane area, the bending rigidity κ, and the mean curvature H. The Gaussian curvature is neglected in Eq. 1 because the membrane does not change its topology (34). We refer to the area Ac, in which proteins are bound to the membrane, as the crowded domain. The crowded domain is modeled as a predefined patch on the membrane with a fixed size, representing, e.g., a domain with a specific lipid composition. Such a scenario was found in the tubulation experiments of Stachowiak et al. (31), in which GFPs bind only to a patch of distearylglycero triethyleneglycyl iminodiacetic acid lipids. Distearylglycero triethyleneglycyl iminodiacetic acid lipids form an insoluble gel phase domain within the GUV. Because lipid membranes endure only a small areal expansion of typically less than 2% (17) before rupture, we consider the area Ac to be fixed. In contrast, we allow the outer domain to expand in response to shape transformation. To justify this assumption, we note that the outer domain is considered to be much larger than the crowded domain, which is also true in experiments (27,31). Expansion of the outer domain thus leads to negligible relative area dilation. Furthermore, experimental studies have shown that thermal shape fluctuations allow effective area dilation of a few percent on GUVs (35) and cells benefit from an even larger effective membrane reservoir through membrane folding (17). The proteins are modeled as spheres with radius rp and density ρ, which experience the dominant contribution of steric repulsion along a virtual surface shifted by rp perpendicular to the membrane (dashed line in Fig. 1 c). The variables related to the shifted surface are indicated by an asterisk (∗) in Eq. 1. The lateral pressure p causes an increase of the membrane energy E with increasing protein density for a planar membrane, reflecting the steric repulsion between the proteins. Outward bending causes an effective expansion of the shifted surface and thus a reduction of the lateral pressure. In the model presented here, the proteins adsorb to one side of the lipid bilayer, i.e., the proteins are bound asymmetrically across the membrane. The same energy expression results for asymmetric transmembrane proteins, for which the protein portion protrudes from one side of the membrane with the size rp much more than the protein portion on the other side of the membrane. We consider a crowded domain much smaller than the total area, which means that also the volume of the protruding shape is small compared to the total volume of the vesicle. Therefore, the associated transmembrane pressure will not influence the membrane shape (see the Supporting materials and methods). Experimental studies have shown the simultaneous formation of multiple protrusions (27,36), which might result from a heterogeneous protein distribution. If the individual crowded domains are spatially separated, we assume that the tubulation process occurs independently in each domain but driven by the same mechanism. Therefore, we restrict the model to the formation of a single protrusion.
The membrane shape is parameterized by the arc length S and the azimuthal angle ψ (Fig. 1 c), where we model the membrane as a thin axially symmetric surface, which is valid as long as the radius of curvature is large compared to the membrane thickness (34). The height Z and the radial coordinate R are then obtained via dR/dS = cosψ and dZ/dS = −sinψ, and the principle curvatures are written as C1 = dψ/dS and C2 = sinψ/R, with the mean curvature H = (C1 + C2)/2. If the protein radius rp is small compared to the inverse of the two principle curvatures, the area element and the density along the shifted protein surface can be expressed as dA∗ = dA(1 + rpC1)(1 + rpC2) and ρ∗ = ρ/[(1 +rpC1)(1 + rpC2)] (see Supporting materials and methods). The pressure term in Eq. 1 can then be approximated by dA∗p(ρ∗) ≈ dA∗ ≈ dAp(ρ) + dArp(C1 + C2) up to first order in C1 and C2. Integration over the first term gives a constant, as we consider a homogeneous protein distribution and a fixed area of the crowded domain. The second term quantifies the release of steric pressure due to bending, where the term p − ρ is negative if the pressure increases more than linearly with ρ. Hence, the effective reduction of the lateral pressure due to bending can be written as an energy term that scales with the mean curvature analogous with a spontaneous curvature. In other words, we can write the membrane energy up to a constant as the sum of two terms, i.e., the bending energy Eκ and the tension energy Eσ (see Supporting materials and methods for a detailed derivation):
| (2) |
where the influence of the lateral pressure between the proteins is expressed by an induced spontaneous curvature Cind. We consider a homogeneous protein distribution (ρ = constant) within the crowded domain Ac and ρ = 0 in the protein-free domain. In general, proteins can diffuse within the membrane, which then can cause a spatial variation in the spontaneous curvature. However, heterogeneity of the protein or lipid distribution is counteracted by an energetic penalty ∼(ρ)2 that maintains a more uniform density (22,37). To keep the model minimal, we consider only the limit of small density gradients, assuming ρ = constant and Cind = constant. We find the following expression for the induced spontaneous curvature:
| (3) |
A detailed derivation of Eqs. 2 and 3 is presented in the Supporting materials and methods. We find that expanding the lateral pressure to quadratic terms in C1 and C2 causes two additional energy terms that only act in the crowded domain: an increase in bending stiffness Δκ and a difference in the Gaussian bending rigidity between the crowded and the outer domain κg (see Eq. S23). The additional contributions to the bending rigidities Δκ and κg scale with ∼( /Ac)2 and are therefore negligible, as the crowded domain is large compared to the size of the proteins.
To derive the relation between the induced spontaneous curvature and the lateral pressure (Eq. 3), we take into account a spatially varying membrane curvature. Equation 3 thus provides a more general version of the results previously obtained by Derganc et al. (28) under the constraint of a uniform membrane curvature and by Stachowiak et al. (36) for a perfectly cylindrical shape. Both studies find a linear relationship between the induced curvature and the lateral pressure p, which coincides with Eq. 3 if p ∼(ρ/ρmax)2. In general, however, the dependence between lateral pressure and protein coverage is more complex. In analogy to Derganc et al. (28) and Stachowiak et al. (36), we use the two-dimensional analog of the Carnahan-Starling equation (38,39) to model the lateral pressure, which is a suitable approximation if the steric repulsion of proteins is caused by volume exclusion alone:
| (4) |
where the maximal areal density is set by the protein radius with ρmax = 1/. Eq. 4 is a suitable approximation if the protein interaction is purely repulsive and if the proteins behave like two-dimensional hard disks. It is expected that attractive interactions between neighboring proteins, conformational changes, or intersection of unstructured proteins will lead to deviations from Eq. 4 and might even cause a negative spontaneous curvature, i.e., inward budding of the membrane protrusion, in line with recent observations by Yuan et al. (20). The induced spontaneous curvature following Eq. 4 reads
| (5) |
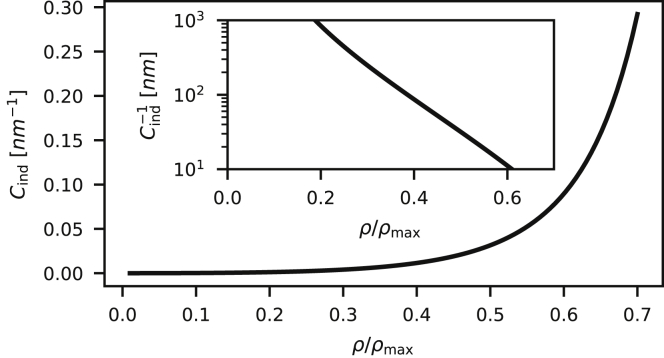
For a fixed protein coverage ρ/ρmax, the prefactor in Eq. 5 shows an inverse scaling of the induced spontaneous curvature with respect to the size of the proteins rp in accordance with previous theoretical studies (28,29). In addition, Eq. 5 provides an explicit relation between Cind and the protein coverage ρ/ρmax. In Fig. 2, Cind is shown as a function of the protein coverage ρ/ρmax (Eq. 5), with rp = 2.1 nm and κ = 10 kBT in accordance with the experimental study by Stachowiak et al. (36) on the tubulation propensity of GUVs covered with densely packed proteins with ENTH domains. The inset shows the inverse of Cind as an approximation for the diameter of a protruding cylinder that follows the induced curvature.
Figure 2.
The induced spontaneous curvature Cind is shown as a function of the protein coverage ρ/ρmax (Eq. 5), with rp = 2.1 nm and κ = 10 kBT (36). The inset shows the inverse of Cind.
We set the scaled membrane tension to σAc/κ = 25. To relate this value to experimentally relevant parameters, we note that the typical membrane tension varies in the range σ = 10−6–10−3 N/m (40). For a membrane in a liquid phase, which is a suitable approximation for most cellular membranes, the bending rigidity is on the order of κ ≈ 10kBT (41). Thus, σAc/κ = 25 corresponds to a crowded domain size of (10−3–1) μm2, which includes the submicrometer structures observed by Shurer et al. (27). Synthetic membranes in the gel phase can exhibit much higher bending rigidity on the order of κ ≈ 200 kBT (41). The corresponding crowded domain size of (0.02–20) μm2 is closer to the micrometer-sized domains observed in GUVs used by Stachowiak et al. (31). We note that the GUVs used in reference (31) have two domains. The crowded domain is in the gel phase, whereas the outer domain is in the liquid phase. To keep the mathematical description minimal, we consider here a constant bending stiffness for the entire membrane.
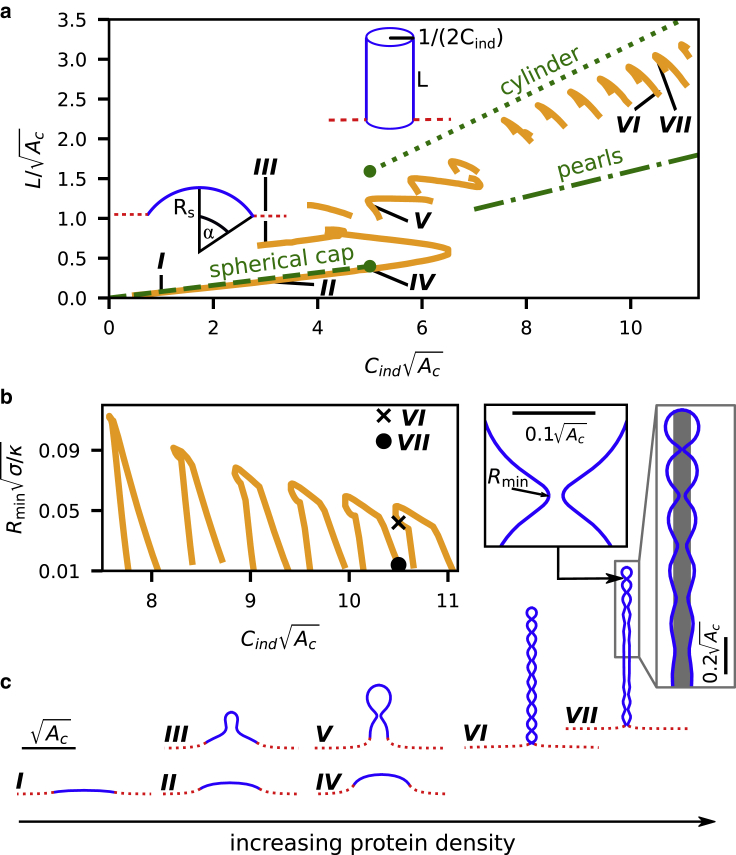
When minimizing the energy (Eq. 2) the membrane can take two characteristic shapes: a rather flat shape that minimizes Eσ or a cylindrical shape that follows the induced spontaneous curvature and minimizes Eκ. Before we derive the shape equations, we discuss two analytical approximations in the limit of small and large Cind to gain an intuitive understanding of the scaling of the protrusion height L and the energy. For small Cind, we describe the crowded domain as a spherical cap with a radius Rs and an opening angle α, and the protein-free membrane region is considered to be flat; see Fig. 3 a. The energy difference ΔE between a flat and a deformed membrane according to Eq. 2 is ΔE = 2κAc[(1/Rs − Cind)2 − ] + σ(Ac − πsin2α). The radius Rs and the angle α are related via the area as Ac = 2π(1 − cosα). Minimizing ΔE with respect to Rs for fixed Ac and Cind results in L = AcCind/[2π + σAc/(4κ)] (dashed line in Fig. 3 a). In the limit of large Cind, the membrane energy is dominated by the bending energy, and we can approximate the membrane shape by a cylinder with radius 1/(2Cind) and length L = AcCind/π (dotted line in Fig. 3 a). The energy difference between the flat and the cylindrical shape is given by ΔE/(2πκ) = −Ac/π + σAc/(2πκ) − σ/. The cylindrical shape becomes energetically advantageous compared to the spherical cap if the induced spontaneous curvature exceeds a value of Cind ≈ (see Supporting materials and methods). This simple approximation shows that, as the protein density or equivalent of the induced spontaneous curvature increases, the height of the protrusion increases linearly with Cind. We notice that the membrane shape will transition from a spherical cap shape to a cylindrical shape at the threshold of Cind ≈ 5/ (green marker in Fig. 3 a).
Figure 3.
(a) The scaled protrusion height L is shown as a function of the induced spontaneous curvature Cind. The results from the shape equations (Eqs. 7) are shown by orange solid lines. The analytic approximations for a spherical cap (dashed), a cylinder (dotted) and a string of beads (dash-dotted) are shown as green lines. At the transition point (Cind = 5, green marker), the energy of a spherical cap and a cylinder are equal. (b) The minimal neck radius Rmin as a function of the induced spontaneous curvature for tubular shapes with Cind > 7.5. (c) Seven membrane shapes are shown, with the crowded region illustrated by the solid blue line and the protein-free region shown as a red dashed line. The scale bar indicates the length that is set by the area of the crowded domain. The inset to the right of shape VII shows an undulating tubular shape together with a cylinder with radius 1/(2Cind) in gray. The inset to the left shows the smallest membrane neck along the tubular shape, with Rmin = 0.04, which corresponds to Rmin = 40 nm for Ac = 25 μm2. Hence, Rmin is still much larger than the membrane thickness.
We now turn to the energy-minimizing shapes and scale all lengths by , i.e., s = S/, r = R/, z = Z/, cind = Cind(Ac − A), with the Heaviside function Θ, ψ(S) → ψ(s), a = A/Ac, and h = H − cind. Applying the Euler-Lagrange formalism, we determine the stationary shapes of the functional :
| (6) |
where the derivative with respect to s is indicated by a prime, d()/ds = ()′. In Eq. 6, the Lagrange multiplier function λ1 constrains the geometric relation between the azimuthal angle ψ and the radius r. The Lagrange multiplier λ2 enforces a constant area at the crowded domain. The energy-minimizing membrane shapes are then described by the following set of differential equations (see Supporting materials and methods):
| (7) |
where u := λ1(2r) is an auxiliary function that becomes equal to the scaled membrane tension at the outer boundary. The boundary conditions
| (8) |
describe a membrane that is flat in the far field, whereas the mean curvature at the centerline (s = 0) is given by c0, where c0 is part of the solution of Eq. 7. To solve Eq. 7, we define the parameter u0 := u(s = 0) and treat the differential equation as an initial value problem in which the parameters c0 and u0 are systematically varied such that the boundary conditions (Eq. 8) at the outer boundary are satisfied. The parameter u0 is related to the Langrange multiplier λ2 as u0 = λ2π + σ + 2 − 2c0cind. Further details about the numerical implementation of Eq. 7 can be found in the Supporting materials and methods.
Results and discussion
In Fig. 3 a, the protrusion height L is shown as a function of Cind. L is defined as the height of the membrane in the Z-direction above the center point Z = 0, R = 0 (Fig. 1 c). Similar to the analytic approximation presented above, we see a transition from flat shapes (shape I) for small Cind to elongated shapes (shapes VI and VII) for large Cind. In the transition region around Cind ≈ 5, multiple stable shapes coexist, including shapes II and III as well as IV and V. Above Cind > 5, the elongated protrusions become more energetically favorable and are hence expected to be predominant in experiments. As we see in Fig. 3 c, the shape of the tubulating membrane does not follow a cylindrical shape; instead, the radius undulates around a value of 1/(2Cind) (gray area in shape VII), which is determined by the spontaneous curvature. The neck size of shape VII is still much larger than the typical thickness of a lipid bilayer, highlighted by the inset. We note that even though the membrane has a shape similar to a string of beads, the protrusion height is significantly longer than if it were composed of spherical beads with radius 1/Cind, with L = AcCind/(2π) (dash-dotted line in Fig. 3 a). As the induced spontaneous curvature increases, Fig. 3 a shows a series of branches. The tube length increases in a discontinuous manner (Fig. 3 a) between two consecutive branches. Each step originates from an additional bead along the tube (see shapes VI and VII). Toward the ends of each branch, the minimal neck radius Rmin decreases as shown in Fig. 3 b. As Rmin decreases, the neck is constricted and eventually reaches a size that is smaller than the thickness of the membrane. In this case, the description of the membrane as a thin elastic sheet is no longer valid. We therefore limit the results shown in Fig. 3 to shapes with a neck size that is at least Rmin = 0.01, or equivalently Rmin = 10 nm for σAc/κ = 25 and Ac = 25 μm2. Hence, in all shapes considered here, the membrane neck is sufficiently wide to prevent membrane fission.
The membrane tubes we find here differ significantly from tubes caused by a point force, in which the tube radius is determined by the ratio of the membrane tension and the bending rigidity showed only slight deviations from a cylindrical shape (16). Pearl-like structures that have a qualitatively similar shape to the elongated protrusions we find here are also observed for tubular membranes under tension (18,23,24), for which the pearling instability is driven by an interplay between the bending energy and the membrane tension. In contrast, the pearl-like structures we see in Fig. 3 (shapes VI and VII) are caused by the spontaneous curvature. To minimize the bending energy, the membrane shape must match the spontaneous curvature Cind. A cylindrical shape with a radius 1/(2Cind) has a vanishing bending energy on the cylinder side, whereas the cylinder cap causes a substantial contribution to the bending energy. If the cylinder is capped by a half-sphere with radius 1/(2Cind), this results in a bending energy of πκ. An alternative shape that minimizes the bending energy is a chain of spherical pearls of radius 1/(Cind) connected by narrow necks. Although the bending energy vanishes at the bulge of the pearl, the curvature at the neck does not follow Cind and thus raises the bending energy. To minimize the energy contributions originating from the cap of the tube and the membrane necks, the shapes VI and VII constitute an intermediate shape between a cylindrical and a pearl-like shape. We note that with an increasing number of pearls along the tube, i.e., with an increasing tube length or a larger induced spontaneous curvature, the energetic cost of the pearl necks will increase. We thus hypothesize that longer tubes approach a more cylindrical shape. Tubes induced by crowding or by a change in the area/volume ratio by osmotic deflation (18) have qualitatively similar shapes, for which the tube radius is determined by either the induced spontaneous curvature or the intrinsic membrane curvature. Despite the similar membrane shapes, there are large differences between these tubes. In the case of osmotic deflation, the area of a tube is not fixed and could, in principle, consume the entire surface of the original vesicle. In contrast, the total area of a tube induced by protein crowding is limited by the size of the crowded domain, and the spontaneous curvature is not fixed but is determined by the protein density.
As we follow the minimal energy shapes for increasing spontaneous curvature or equivalently for increasing protein density in Fig. 3, a and c, we find shapes that are qualitatively similar to those recently found experimentally by Shurer et al. (27) on cells with glycocalyx polymers (Fig. 1 b), including Ω-shapes/blebs (shape V), tubes (shape VII), and pearls or beads (shape VI). Although several of these shapes have been theoretically described before in specific analytical limits (27), we here obtain the entire variety of shapes by a single underlying physical principle, i.e., the interplay of the induced spontaneous curvature and the membrane tension, where all shapes are described by the same set of shape equations (Eqs. 7).
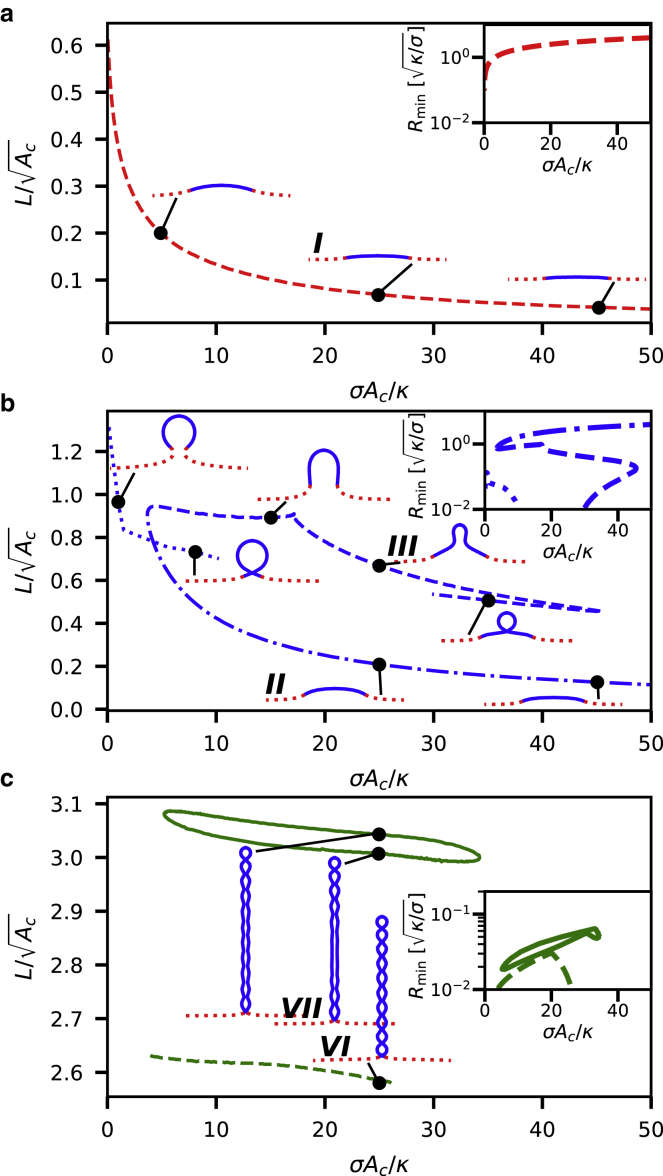
So far, we have considered a fixed value for the scaled membrane tension. We now discuss the continuous transition between different shape classes through the change in membrane tension σ for a fixed Cind. In Fig. 3, we show L as a function of the scaled membrane tension σAc/κ for three different values of Cind ∈ [1, 3, 10.5]. The inset in each panel shows the membrane neck radius Rmin. If the membrane shape does not exhibit an indentation (e.g., shape I), Rmin is defined as the radius at the outer edge of the crowded domain. As in Fig. 3, we only show membrane shapes with a neck radius of Rmin > 0.01, i.e., the neck is larger than the membrane thickness and the thin sheet description of the membrane is valid. The five shapes that are indicated by roman numbers are also shown in Fig. 3. For the lowest value, Cind = 1 (Fig. 4 a), a monotonic decrease of L with increasing membrane tension is observed, i.e., the membrane flattens (shape I).
Figure 4.
The scaled protrusion height L is shown as a function of the scaled membrane tension σAc/κ for different induced spontaneous curvatures Cind. The inset in each subfigure shows the membrane neck radius Rmin. The five shapes that are indicated by roman numbers are the same shapes shown in Fig. 3. (a) Cind = 1, (b) Cind = 3, (c) and Cind = 10.5.
Increasing the spontaneous curvature to Cind = 3, we find a more complex behavior with three different classes of membrane equilibrium shapes (shown in Fig. 4 b as dashed, dashed-dotted, and dotted lines, respectively) that can coexist. The lower line (dashed-dotted line) corresponds to flattened shapes that minimizes the tension energy. The shapes in the upper dashed line show a narrower protrusion. For σAc/κ < 12, there is a third class of equilibrium shapes that is associated with spherical membrane shapes. These shapes do not lead to tubulation, and the neck becomes narrower as σAc/κ increases. We speculate that a further increase of the membrane tension (σAc/κ > 12) would lead to an overlap of opposing sides of the neck and subsequent membrane fission. Membrane scission by protein crowding was observed experimentally by Snead et al. (42), in which the presence of unstructured proteins (an epsin1 N-terminal homology domain) on the membrane was sufficient to induce vesicle formation even in the absence of specialized proteins that facilitate membrane scission. For an even larger spontaneous curvature, Cind = 10.5, elongated tubes are formed. Although we can observe a closed line for shapes with 11 connected beads along the tube (shape VII), shapes with only 10 beads (shape VI) are limited by a constriction of the membrane neck for both low and high membrane tensions.
The minimal theoretical model presented here shows that steric repulsion between membrane-associated proteins and membrane tension can explain a variety of membrane shapes observed in experiments, providing a quantitative framework for understanding membrane remodeling induced by protein crowding. In Figs. 3 and 4, we have shown that multiple equilibrium membrane shapes can coexist: flat, spherical, and tubular shapes. Our results highlight protein crowding as a versatile mechanism for membrane shape regulation, which is a process vital to cell functionality by compartmentalizing or connecting cellular organelles.
Acknowledgments
We thank Padmini Rangamani for stimulating discussions and input to this manuscript.
The work has been enabled by funding from the Research Council of Norway (Project Grant number 263056).
Editor: Ilya Levental.
Footnotes
Susanne Liese’s present address is Max Planck Institute for the Physics of Complex Systems, Dresden, Germany.
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2021.04.029.
Contributor Information
Susanne Liese, Email: sliese@pks.mpg.de.
Andreas Carlson, Email: acarlson@math.uio.no.
Supporting citations
References (43, 44, 45, 46, 47, 48) can be found in the Supporting material.
Supporting material
References
- 1.Drab M., Stopar D., Iglič A. Inception mechanisms of tunneling nanotubes. Cells. 2019;8:6. doi: 10.3390/cells8060626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hurtig J., Chiu D.T., Onfelt B. Intercellular nanotubes: insights from imaging studies and beyond. Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol. 2010;2:260–276. doi: 10.1002/wnan.80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nixon-Abell J., Obara C.J., Lippincott-Schwartz J. Increased spatiotemporal resolution reveals highly dynamic dense tubular matrices in the peripheral ER. Science. 2016;354:aaf3928. doi: 10.1126/science.aaf3928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ellgaard L., Molinari M., Helenius A. Setting the standards: quality control in the secretory pathway. Science. 1999;286:1882–1888. doi: 10.1126/science.286.5446.1882. [DOI] [PubMed] [Google Scholar]
- 5.Manford A.G., Stefan C.J., Emr S.D. ER-to-plasma membrane tethering proteins regulate cell signaling and ER morphology. Dev. Cell. 2012;23:1129–1140. doi: 10.1016/j.devcel.2012.11.004. [DOI] [PubMed] [Google Scholar]
- 6.Watkins S.C., Salter R.D. Functional connectivity between immune cells mediated by tunneling nanotubules. Immunity. 2005;23:309–318. doi: 10.1016/j.immuni.2005.08.009. [DOI] [PubMed] [Google Scholar]
- 7.Nawaz M., Fatima F. Extracellular vesicles, tunneling nanotubes, and cellular interplay: synergies and missing links. Front. Mol. Biosci. 2017;4:50. doi: 10.3389/fmolb.2017.00050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Simunovic M., Voth G.A., Bassereau P. When physics takes over: BAR proteins and membrane curvature. Trends Cell Biol. 2015;25:780–792. doi: 10.1016/j.tcb.2015.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Simunovic M., Evergren E., Bassereau P. How curvature-generating proteins build scaffolds on membrane nanotubes. Proc. Natl. Acad. Sci. USA. 2016;113:11226–11231. doi: 10.1073/pnas.1606943113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Idema T., Kraft D.J. Interactions between model inclusions on closed lipid bilayer membranes. Curr. Opin. Colloid Interface Sci. 2019;40:58–69. [Google Scholar]
- 11.Lenz M., Crow D.J.G., Joanny J.-F. Membrane buckling induced by curved filaments. Phys. Rev. Lett. 2009;103:038101. doi: 10.1103/PhysRevLett.103.038101. [DOI] [PubMed] [Google Scholar]
- 12.Roux A., Koster G., Bassereau P. Membrane curvature controls dynamin polymerization. Proc. Natl. Acad. Sci. USA. 2010;107:4141–4146. doi: 10.1073/pnas.0913734107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jarsch I.K., Daste F., Gallop J.L. Membrane curvature in cell biology: an integration of molecular mechanisms. J. Cell Biol. 2016;214:375–387. doi: 10.1083/jcb.201604003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Iglic A., Hägerstrand H., Veranic P., Plemenitas A., Kralj-Iglic V. Curvature-induced accumulation of anisotropic membrane components and raft formation in cylindrical membrane protrusions. J. Theor Biol. 2006;240:368–373. doi: 10.1016/j.jtbi.2005.09.020. [DOI] [PubMed] [Google Scholar]
- 15.Iglic A., Slivnik T., Kralj-Iglic V. Elastic properties of biological membranes influenced by attached proteins. J Biomech. 2007;40:2492–2500. doi: 10.1016/j.jbiomech.2006.11.005. [DOI] [PubMed] [Google Scholar]
- 16.Derényi I., Jülicher F., Prost J. Formation and interaction of membrane tubes. Phys. Rev. Lett. 2002;88:238101. doi: 10.1103/PhysRevLett.88.238101. [DOI] [PubMed] [Google Scholar]
- 17.Staykova M., Holmes D.P., Stone H.A. Mechanics of surface area regulation in cells examined with confined lipid membranes. Proc. Natl. Acad. Sci. USA. 2011;108:9084–9088. doi: 10.1073/pnas.1102358108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Liu Y., Agudo-Canalejo J., Lipowsky R. Patterns of flexible nanotubes formed by liquid-ordered and liquid-disordered membranes. ACS Nano. 2016;10:463–474. doi: 10.1021/acsnano.5b05377. [DOI] [PubMed] [Google Scholar]
- 19.Bahrami A.H., Hummer G. Formation and stability of lipid membrane nanotubes. ACS Nano. 2017;11:9558–9565. doi: 10.1021/acsnano.7b05542. [DOI] [PubMed] [Google Scholar]
- 20.Yuan F., Alimohamadi H., Stachowiak J.C. Membrane bending by protein phase separation. Proc. Natl. Acad. Sci. USA. 2021;118:11. doi: 10.1073/pnas.2017435118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bassereau P., Jin R., Weikl T.R. The 2018 biomembrane curvature and remodeling roadmap. J. Phys. D Appl. Phys. 2018;51:343001. doi: 10.1088/1361-6463/aacb98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Alimohamadi H., Rangamani P. Modeling membrane curvature generation due to membrane-protein interactions. Biomolecules. 2018;8:4. doi: 10.3390/biom8040120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bar-Ziv R., Moses E. Instability and “pearling” states produced in tubular membranes by competition of curvature and tension. Phys. Rev. Lett. 1994;73:1392–1395. doi: 10.1103/PhysRevLett.73.1392. [DOI] [PubMed] [Google Scholar]
- 24.Nelson P., Powers T., Seifert U. Dynamical theory of the pearling instability in cylindrical vesicles. Phys. Rev. Lett. 1995;74:3384–3387. doi: 10.1103/PhysRevLett.74.3384. [DOI] [PubMed] [Google Scholar]
- 25.Campelo F., Hernández-Machado A. Model for curvature-driven pearling instability in membranes. Phys. Rev. Lett. 2007;99:088101. doi: 10.1103/PhysRevLett.99.088101. [DOI] [PubMed] [Google Scholar]
- 26.Jelerčič U., Gov N.S. Pearling instability of membrane tubes driven by curved proteins and actin polymerization. Phys. Biol. 2015;12:066022. doi: 10.1088/1478-3975/12/6/066022. [DOI] [PubMed] [Google Scholar]
- 27.Shurer C.R., Kuo J.C.-H., Paszek M.J. Physical principles of membrane shape regulation by the glycocalyx. Cell. 2019;177:1757–1770.e21. doi: 10.1016/j.cell.2019.04.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Derganc J., Čopič A. Membrane bending by protein crowding is affected by protein lateral confinement. Biochim. Biophys. Acta. 2016;1858:1152–1159. doi: 10.1016/j.bbamem.2016.03.009. [DOI] [PubMed] [Google Scholar]
- 29.Lipowsky R. Bending of membranes by anchored polymers. Europhys. Lett. 1995;4:197–202. [Google Scholar]
- 30.Lipowsky R. Spontaneous tubulation of membranes and vesicles reveals membrane tension generated by spontaneous curvature. Faraday Discuss. 2013;161:305–331. doi: 10.1039/c2fd20105d. discussion 419–459. [DOI] [PubMed] [Google Scholar]
- 31.Stachowiak J.C., Hayden C.C., Sasaki D.Y. Steric confinement of proteins on lipid membranes can drive curvature and tubulation. Proc. Natl. Acad. Sci. USA. 2010;107:7781–7786. doi: 10.1073/pnas.0913306107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Busch D.J., Houser J.R., Stachowiak J.C. Intrinsically disordered proteins drive membrane curvature. Nat. Commun. 2015;6:7875. doi: 10.1038/ncomms8875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 34.Deserno M. Fluid lipid membranes: from differential geometry to curvature stresses. Chem. Phys. Lipids. 2015;185:11–45. doi: 10.1016/j.chemphyslip.2014.05.001. [DOI] [PubMed] [Google Scholar]
- 35.Evans E., Rawicz W. Entropy-driven tension and bending elasticity in condensed-fluid membranes. Phys. Rev. Lett. 1990;64:2094–2097. doi: 10.1103/PhysRevLett.64.2094. [DOI] [PubMed] [Google Scholar]
- 36.Stachowiak J.C., Schmid E.M., Hayden C.C. Membrane bending by protein-protein crowding. Nat. Cell Biol. 2012;14:944–949. doi: 10.1038/ncb2561. [DOI] [PubMed] [Google Scholar]
- 37.Veksler A., Gov N.S. Phase transitions of the coupled membrane-cytoskeleton modify cellular shape. Biophys. J. 2007;93:3798–3810. doi: 10.1529/biophysj.107.113282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Carnahan N., Starling K. Equation of state for nonattracting rigid spheres. J. Chem. Phys. 1969;51:635–636. [Google Scholar]
- 39.Henderson D. A simple equation of state for hard discs. Mol. Phys. 1975;30:971–972. [Google Scholar]
- 40.Morris C.E., Homann U. Cell surface area regulation and membrane tension. J. Membr. Biol. 2001;179:79–102. doi: 10.1007/s002320010040. [DOI] [PubMed] [Google Scholar]
- 41.Et-Thakafy O., Delorme N., Guyomarc’h F. Mechanical properties of membranes composed of gel-phase or fluid-phase phospholipids probed on liposomes by atomic force spectroscopy. Langmuir. 2017;33:5117–5126. doi: 10.1021/acs.langmuir.7b00363. [DOI] [PubMed] [Google Scholar]
- 42.Snead W.T., Hayden C.C., Stachowiak J.C. Membrane fission by protein crowding. Proc. Natl. Acad. Sci. USA. 2017;114:E3258–E3267. doi: 10.1073/pnas.1616199114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Linden M.,P., Sens, Phillips R. Entropic tension in crowded membranes. PLoS Comput. Biol. 2012;8:e1002431. doi: 10.1371/journal.pcbi.1002431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Seifert U., Berndl K., Lipowsky R. Shape transformations of vesicles: phase diagram for spontaneous-curvature and bilayer-coupling models. Phys. Rev. A. 1991;44:1182–1202. doi: 10.1103/physreva.44.1182. [DOI] [PubMed] [Google Scholar]
- 45.Jülicher F., Seifert U. Shape equations for axisymmetric vesicles. a clarification. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1994;49:4728–4731. doi: 10.1103/physreve.49.4728. [DOI] [PubMed] [Google Scholar]
- 46.Jülicher F., Lipowsky R. Shape transformations of vesicles with intramembrane domains. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1996;53:2670–2683. doi: 10.1103/physreve.53.2670. [DOI] [PubMed] [Google Scholar]
- 47.Bozic B., Svetina S., Zeks B. Theoretical analysis of the formation of membrane microtubes on axially strained vesicles. Phys. Rev. E. 1997;55:5834–5842. [Google Scholar]
- 48.Goldstein H., Poole C., Safko J. Third Edition. Addison Wesley; Boston, MA: 2001. Classical Mechanics. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.