The structural heterogeneity of α-synuclein is governed by several distinct subpopulations with interconversion times slower than milliseconds

Summary:

α-Synuclein plays an important role in synaptic functions by interacting with synaptic vesicle membrane, while its oligomers and fibrils are associated with several neurodegenerative diseases. The specific monomer structures that promote its membrane-binding and self-association remain elusive due to its transient nature as an intrinsically disordered protein. Here, we use inter-dye distance distributions from bulk time-resolved Förster resonance energy transfer as restraints in discrete molecular dynamics simulations to map the conformational space of the α-synuclein monomer. We further confirm the generated conformational ensemble in orthogonal experiments utilizing far-UV circular dichroism and cross-linking mass spectrometry. Single-molecule protein-induced fluorescence enhancement measurements show that within this conformational ensemble, some of the conformations of α-synuclein are surprisingly stable, exhibiting conformational transitions slower than milliseconds. Our comprehensive analysis of the conformational ensemble reveals essential structural properties and potential conformations that promote its various functions in membrane interaction or oligomer and fibril formation.

Graphical Abstract

In brief

Structures of intrinsically disordered proteins (IDPs) are difficult to be studied by traditional biophysical methods. Chen & Zaer et al. developed a new methodology to characterize the ensemble structure of an IDP, α-synuclein. Distinct structural subpopulations of α-synuclein monomer with stable local structures might promote its physiological and pathogenic functions.

Introduction

α-Synuclein (α-syn) is a 140-residue protein containing an N-terminal segment (residues 1~60), a hydrophobic non-amyloid-β component (NAC) segment (residues 61~95), and an acidic C-terminal segment (residues 96~140) (Mane and Stepanova, 2016). It is encoded by the SNCA gene in humans and is mainly expressed in the presynaptic terminals of neurons (Iwai et al., 1995). Endogenous α-syn regulates neurotransmitter release and synaptic vesicle homeostasis through the interaction with synaptic vesicle membranes (Burré et al., 2010; Gómez-Benito et al., 2020; Mori et al., 2020; Nemani et al., 2010). An imbalance of this α-syn-membrane interaction may induce the formation of α-syn fibrils (Mori et al., 2020). These ordered aggregates of α-syn serve as a precursor in Lewy body formation, which is a hallmark of several neurodegenerative diseases (e.g. Parkinson’s disease (PD), PD dementia, dementia with Lewy bodies, and multiple system atrophy) (Galvin et al., 2001; Guerrero-Ferreira et al., 2020; Holec and Woerman, 2020; Stok and Ashkenazi; Xu and Pu, 2016). The different roles of α-syn in normal synaptic activity and as a factor in the advancement of PD may stem from different manifestations of its structure. As an intrinsically disordered protein (IDP), α-syn is characterized by a heterogeneous ensemble of dynamic conformations (Theillet et al., 2016). Although monomeric α-syn is structurally flexible, it can form ordered structures under different conditions. In the membrane-bound state, α-syn adopts two dynamically interconverting (Ferreon et al., 2009) conformations: a broken antiparallel α-helix structure (residues 3~37 and residues 45~92) (Ulmer et al., 2005), and an extended helix (residues 1~97) (Georgieva et al., 2008). Physiologically, α-syn appears as a helically folded tetramer (α-helices shown in the initial 100 residues), which is stable and resistant to protein aggregation (Bartels et al., 2011; Wang et al., 2011; Xu et al., 2018, 2019). These two conformational states of α-syn mainly composed of α-helices are essential for physiological functions (Burré et al., 2014) and disease prevention (Bartels et al., 2011). On the other hand, α-syn oligomers and fibrils, which are toxic to neuronal cells, are characterized by β-sheets rather than α-helices (Alam et al., 2019; Celej et al., 2012; Mehra et al., 2019; Zhou and Kurouski, 2020). These observations link the different roles of α-syn to its various conformational states. Can the structures of the α-syn subunit in these complexes be identified also as conformational states in the structural ensemble of the α-syn monomer? If yes, a detailed structural characterization of the α-syn monomer conformations would shed light on the specific mechanisms that lead α-syn to different functional routes.

Characterizing the structurally heterogeneous ensemble of α-syn conformations is particularly challenging because it is an IDP. Experimental methods such as nuclear magnetic resonance (NMR), small-angle X-ray scattering (SAXS), and circular dichroism (CD) frequently report the conformational ensemble average (Munari et al., 2020), which is a superposition of multiple distinct states. Due to the high concentration of proteins required in some experiments, the structural information provided might be of oligomers rather than solely of the monomer (Brodie et al., 2019). Finally, these methods (except for NMR) cannot provide atomic-resolution structural models of the conformations. Molecular dynamics (MD) simulations have been used to investigate the details of α-syn conformations. Traditional force fields used in MD, however, are designed for folded proteins (Yang et al., 2019). Simulations of IDPs using these force fields usually generate structures that are too compact and contradict experimental data (Bhattacharya and Lin, 2019; Huang et al., 2016; Song et al., 2017; Yu et al., 2020). Moreover, computational exploration of the structural ensembles of IDPs is often prohibitive due to the vast allowable conformational space. To overcome the force-field limitations and enhance sampling, experimental data from NMR (Dedmon et al., 2005), SAXS (Ullman et al., 2011), and cross-linking mass spectrometry (XL-MS) (Brodie et al., 2019) have been integrated with MD simulations (Bonomi et al., 2017; Dokholyan, 2020). These experimental methods, however, either report ensemble averages over structurally heterogeneous states or are limited by the length of crosslinkers (Bonomi et al., 2017). Time-resolved fluorescence resonance energy transfer (trFRET) reports a distribution of inter-residue distances rather than the single average of the ensemble (Bonomi et al., 2017). Therefore, we use data previously generated from trFRET experiment (Grupi and Haas, 2011a) to guide discrete molecular dynamics (DMD) simulations (Dokholyan, 2006; Ding et al., 2008; Proctor et al., 2011; Proctor et al., 2016; Shirvanyants et al., 2012) of the α-syn monomer.

Previous studies using experimentally-restrained simulations to characterize the α-syn structural ensemble provided insights into the long-range interactions and secondary structures that stabilize α-syn or stimulate early stages of aggregation (Brodie et al., 2019; Dedmon et al., 2005; Ullman et al., 2011). The long-range interaction between the N- and C-terminal segments was proposed to expose the hydrophobic NAC segment and therefore, promote protein aggregation (Ullman et al., 2011). However, recent studies showed that such interaction protects α-syn from aggregation (Bertoncini et al., 2005; Stephens et al., 2020). Whether this interaction protects or exposes the aggregation-prone NAC segment needs to be further investigated. A study based on paramagnetic relaxation enhancement (PRE) measurement showed that the multiple conformations of the α-syn monomer interconvert in the time range of nanoseconds to microseconds (Bertoncini et al., 2005). However, such rapid conformational dynamics and the outcoming short-lived conformations may decrease the probability of ligand binding to a specific conformation. Knowing the correct timescale of conformational transitions is important for understanding the functional fate of the α-syn monomer. Furthermore, although the conformational ensemble of α-syn has been studied (Brodie et al., 2019; Chitra Narayanan, Daniel S. Weinstock, Kuen-Phon Wu, Jean Baum, 2012; Dedmon et al., 2005; Ferrie et al., 2018; Kuen-Phon Wu, Daniel S. Weinstock, Chitra Narayanan, Ronald M. Levy, 2009; Nath et al., 2012; Ullman et al., 2011), the molecular mechanisms of forming diverse conformational states (e.g. membrane-bound, dimer, tetramer, oligomer, and fibril) from the monomer ensemble are still obscure. The representative structural subpopulations of the monomer that are associated with specific cellular events (e.g. membrane binding, nucleating fibrillization), have not been fully characterized yet. Identifying these subpopulations or representative monomeric structures is significant as the concrete structural features could be used to develop small molecules that regulate α-syn functions or interfere with disease progression.

Here, we use existing trFRET data as experimental restraints in DMD simulations to map the conformational ensemble of α-syn. We confirm the predicted conformational ensemble using far-UV CD spectra and XL-MS experimental data. The results of single-molecule protein-induced fluorescence enhancement (smPIFE) measurements suggest that some of the structural subpopulations, or groups of them, are stable enough to have interconversion transitions to occur in milliseconds. This finding suggests that the α-syn monomer has stable local structures. The simulations reveal that structural subpopulations of the α-syn monomer include structures that are similar to the structures of the α-syn subunit in several well-documented complexes. Therefore, these structures might promote α-syn complexation including membrane binding and the formation of various oligomers and fibrils. Taken together, we propose stable α-syn local structures are promoting specific complex formations, and, thus, link to a structure-function relationship.

Results

The conformational ensemble of α-synuclein predicted by trFRET-guided DMD (trFRET-DMD) simulations

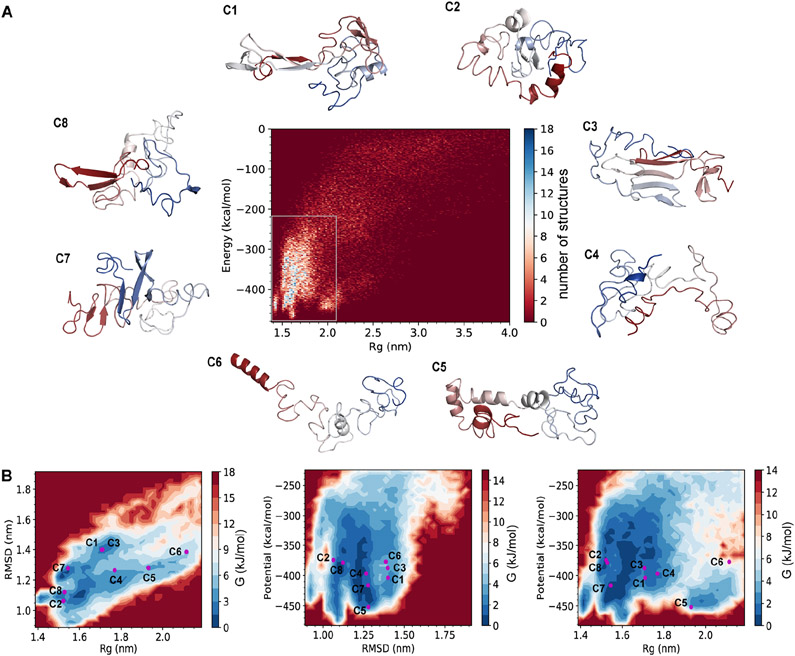
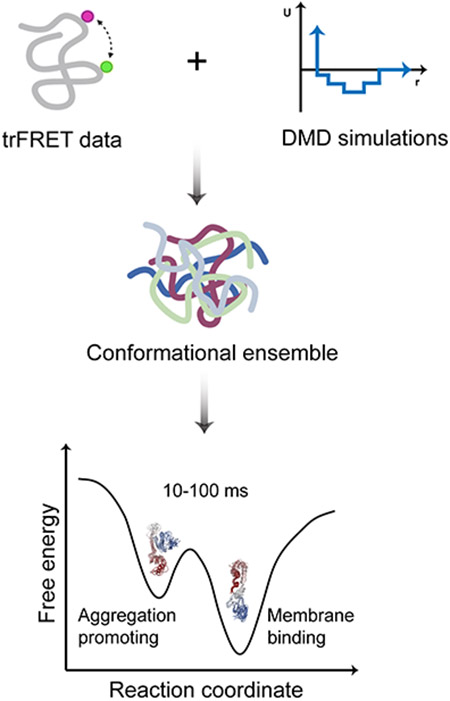
We construct the conformational ensemble of the α-syn monomer by trFRET-DMD (Figure 1, Methods). We select the most populated structures (Figure 2A) and perform hierarchical clustering, which results in the division of the conformational ensemble of α-syn into eight distinct clusters (Figure S5; further discussion in Methods). The average pairwise RMSD between the clusters is 16.7 Å (Table S2) indicating the heterogeneity of the conformational ensemble. The heterogenous conformations are also demonstrated by the centroid structures (the structure with the lowest overall RMSD to the other structures in a cluster) of the eight clusters. Some of these centroids are compact while others are more expanded and disordered, as judged by R_g (Figure 2A). Most of the clusters are structurally heterogeneous to different degrees (Table S3), and the structures within these clusters can deviate relative to their centroids. However, clusters 3 and 7 tend to be less heterogeneous and include structures that do not deviate much from their centroids (Table S3).

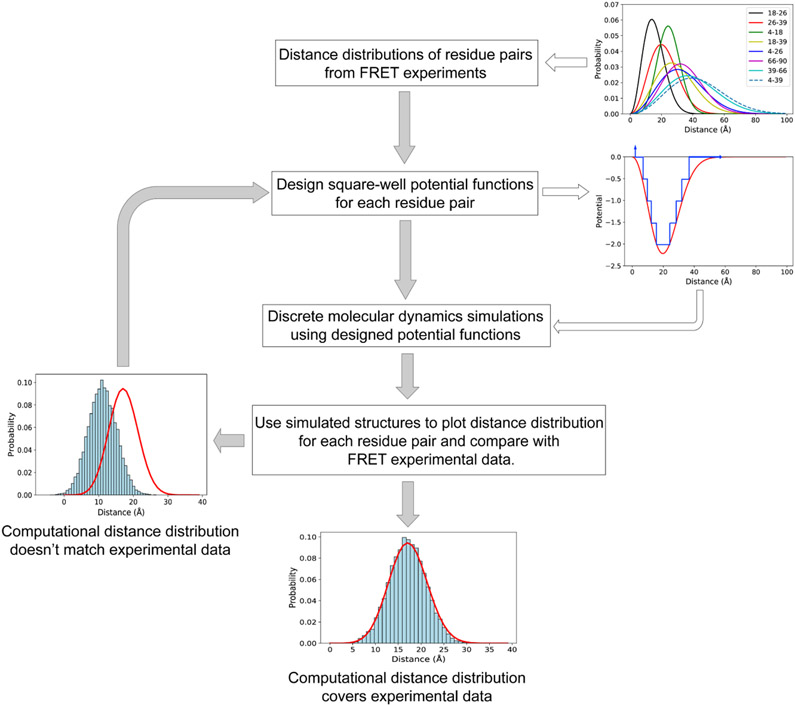
Figure 1. The schematic workflow of predicting protein conformations by the combination of trFRET and DMD simulations.

The distance distributions of the eight residue pairs are retrieved from the trFRET experiment (Grupi and Haas, 2011a). In the subplot of potential and distance, the red line indicates the continuous potential and the blue line represents the designed discrete step function potential. In the two bottom subplots, the red line indicates the experimental data and the blue histogram represents the computational distance distribution.

Figure 2. The eight distinct clusters resolved by trFRET-DMD.

(A) Energy versus radius of gyration (R_g) for the structural ensemble and the centroid structures of the eight clusters (C1-8). The structures are colored from red (N-terminus) to blue (C-terminus).

(B) The energy landscapes of α-syn based on RMSD, R_g, and/or potential. RMSD indicates the distance between each structure and the average structure of the conformational ensemble.

To visualize the relation of the eight clusters to the physical states they represent, we calculate Gibbs free energy maps (Methods) using pairs of the following parameters: (i) the level of compactness, as represented by R_g, (ii) the RMSD relative to the average structure of the ensemble, and (iii) the potential energy from DMD (Figure 2B). The centroids of clusters 1 and 3 have similar levels of compactness relative to the RMSD and hence are not separate in the free energy map (R_g vs. RMSD; Figure 2B, left panel). However, when the free energy is calculated using the potential energy and the level of compactness (potential energy vs. R_g) or using the potential energy and the RMSD (potential energy vs. RMSD), the centroids of clusters 1 and 3 are close yet separate in the free energy maps (Figure 2B, middle and right panels, respectively). This feature has occurred also between the centroids of clusters 2 and 8, when comparing the different two-dimensional representations of the free energy maps. This observation is due to reduced dimensionality in our representation of the reaction coordinates, represented here by three measures (R_g, RMSD, and the potential energy) out of many other possible representations. Indeed, visual inspection of the structures of centroids 1 and 3 as well as centroids 2 and 8 show they have markedly different secondary structures and three-dimensional organizations (Figure 2A). The centroids of other clusters, however, are distributed at different R_g, RMSD and potential energy positions on the free energy maps (Figure 2B). Therefore, these well-separated clusters represent structurally distinct conformations as judged by their levels of compactness and by the RMSD. The centroid structure of cluster 6 locates at regions with higher Gibbs free energy and the structure has a low level of compactness (R_g ≈ 21,1 Å). This expanded structure might contribute to its high free energy and therefore, might appear less frequently than the other centroids in the ensemble. The centroid of cluster 7 is found to be located near the area with the lowest Gibbs free energy. It contains a β-sheet structure, which might stabilize the conformation. Indeed, this centroid is compact (R_g ≈ 15.4 Å). After performing this computational procedure guided by trFRET-derived distance distributions, we add a validation layer against additional experimental information, which is summarized in the next section.

Experimental validation of the predicted conformational ensemble

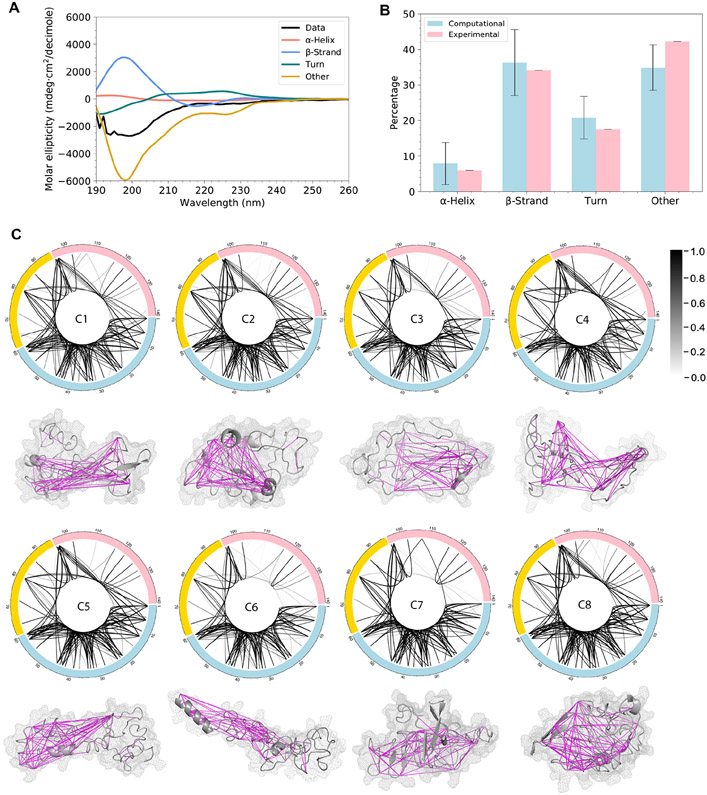
To validate the simulated ensemble structure of α-syn, we conduct orthogonal experiments using CD and XL-MS and compare the computational results with experimental data in terms of secondary structure composition and intramolecular proximities. Analysis of the far-UV CD spectrum shows that monomeric α-syn in solution consists of 6.1% α-helix, 34.1% β-strand (β-sheet and β-bridge), 17.5% turns, and 42.3% other structures (random coil, bends, 5-helix, and 3-helix; Figure 3A and B). To compare the secondary structure content of predicted conformational ensemble with CD data, we quantify secondary structures for every structure in the 8 clusters. The ensemble average of the secondary structures includes 7.9±5.9% α-helix, 36.3±9.3% β-strand, 20.8±6.0% turns, and 34.9±6.4% other structures (Figure 3B). Overall, the secondary structure content of our predicted conformational ensemble agrees with the secondary structure content measured by far-UV CD experiments.

Figure 3. Predicted conformational ensemble validated by far-UV CD and XL-MS experiments.

(A) The far-UV CD data showing the secondary structure content.

(B) The comparison of secondary structure content calculated from the simulated structures and from the analysis of the far-UV CD spectrum. Error bars indicate standard deviation.

(C) XL-MS connection maps of the eight clusters. Each line indicates a crosslink and the grayscale level indicates the probability of structures that satisfy cross-linking constraints within each cluster. The centroid structure of each cluster is shown under the connection map. Magenta lines indicate that these cross-linking constraints are satisfied by over 50% of the structures within each cluster. The calculated C_α-C_α distance of each pair of amino acids satisfies the cross-linking constraint if it is smaller than a certain threshold: ABAS < 17 Å (Brodie et al., 2015), EDC < 10 Å (Brodie et al., 2019), SDA < 15 Å (Brodie et al., 2019), TATA < 15 Å (Brodie et al., 2016), CBDPS < 28 Å (Piersimoni and Sinz, 2020), BS³ < 30 Å (Merkley et al., 2014).

XL-MS is often used to study local proximity of protein structures in three-dimensional space (Kaledhonkar et al., 2018). Previously, Nicholas et al. combined cross-linking data with DMD simulations to improve computational prediction of protein structures (Brodie et al., 2017, 2019). Here, we take advantage of these data together with additional XL-MS data that we collect in order to validate the characterized conformational ensemble of α-syn. A total of 125 pairs of amino acids that are crosslinked with various crosslinkers are summarized in Table S4 (Methods). To compare these cross-linking results with the modeled structures from DMD simulations, we calculate the distances between the 125 residue pairs and plot distance distribution for all the structures in each cluster. The maximal cross-linking length of each crosslinker is also displayed and compared with the computational distance distribution (data deposited in Zenodo) (Chen et al., 2021). The cross-linking constraints are determined to be satisfied if the maximal length falls within the computational distance distribution, since we expect the ensemble structure of α-syn includes multiple conformations and only part of the conformations are in accordance with the constraints. All the 125 constraints are satisfied by at least one of the eight clusters indicating that our predicted monomeric structures of α-syn agree with the XL-MS data. Most of the cross-linking constraints are satisfied by a high proportion of structures within each cluster (Figure 3C). The N-terminal segment is highly connected intra-segmentally and constraints within this segment are satisfied by most structures in all the 8 clusters (Figure 3C). The difference between the clusters comes in the probability of structures that satisfy the crosslinks between amino acids of different segments as well as those within the C-terminal segment (Figure 3C), indicating that long-range interactions between the three segments vary for each cluster and the C-terminal segment is more flexible than the N-terminal. The crosslinking arrests multiple conformational states of a protein, and therefore, not all crosslinks agree with one particular structure. Using our trFRET-DMD analysis, we deconvolute the contributions of predominant conformations to overall conformational ensemble of α-syn.

Structural properties of α-synuclein conformational ensemble

The conformational characteristics of our predicted α-syn ensemble may provide structural insight into the molecular mechanisms that stabilize the monomer, as well as trigger protein aggregation (Churchill et al., 2019). Therefore, we analyze the structural features including secondary structures, surface exposure, and long-range interactions and compare our results to previously published data.

The N-terminal and NAC segments have a higher propensity to form α-helices than the C-terminal segment (Figure S6), which is also captured by other studies (Dułak et al., 2020; Zhang et al., 2018). Folded α-helices in these two segments are proposed to decrease the fibrillation rate of α-syn (Bhattacharya et al., 2019; Rossetti et al., 2016). Overall, the formation of α-helix occupies a much lower probability than the other secondary structures (Figure S6). On the other hand, β-strands tend to form more frequently across the whole protein compared to the other structures (Figure S6). In clusters 1, 2, and 6, the central segment of α-syn has a higher propensity to form β-strand than the N- and C-terminal segments. Previous studies suggest that β-strand formation within the hydrophobic central segment may lead to oligomerization and fibril formation (Balupuri et al., 2019; Brodie et al., 2019; Graen et al., 2018; Healey et al., 2016; Jónsson et al., 2012; Yu et al., 2015). The average secondary structure content for each cluster (Table S5) shows that the eight clusters can be separated into two groups, one group (clusters 2, 5, 6, 8) with a higher α-helix propensity and another group (clusters 1, 3, 4, 7) with a higher β-strand propensity. Clusters with a high propensity of forming β-strands are also confirmed by their contact frequency maps (Figure S7), exhibiting lines vertical to the diagonal. The membrane-bound state and the tetramer of α-syn form stable α-helices in the N-terminal and NAC segments, while the oligomers and fibrils have an increasing amount of β-strand. The two distinct groups with different α-helix and β-strand propensity may indicate their diverse roles in physiological functions and pathogenesis of PD.

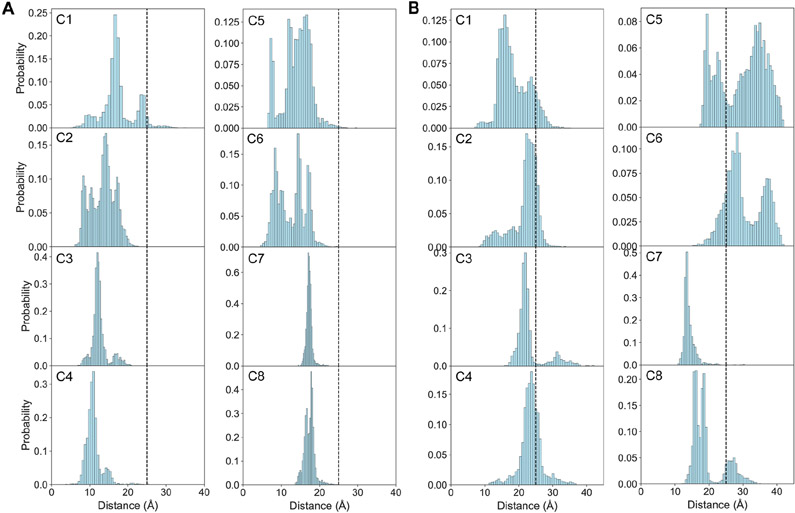
Long-range interaction between the C-terminal and NAC segments, as well as the interaction between C- and N-terminal segments of native α-syn have been detected and confirmed by several PRE experiments (Bertoncini et al., 2005; Bisaglia et al., 2009; Dedmon et al., 2005; Sung and Eliezer, 2007). These experiments measure the interactions between an attached paramagnetic nitroxide radical group and protons of a distance within 25 Å (Marius Clore and Iwahara, 2009). To determine if our conformations agree with these observations, we calculate the distances between the centers of mass of the N- and C-terminal segments, as well as the NAC and the C-terminal segments, respectively. A long-range contact is defined to occur if the distance is less than 25 Å. The majority of our predicted structures have this long-range interaction (Figure 4A), which is consistent with the PRE experimental data (Dedmon et al., 2005). This NAC and C-terminal contact is hypothesized to sequester the hydrophobic NAC segment from exposing in the solvent and therefore, is critical to retard protein aggregation (Dedmon et al., 2005; Kuen-Phon Wu, Daniel S. Weinstock, Chitra Narayanan, Ronald M. Levy, 2009). The long-range interaction between the N- and C-terminal segments was also proposed to protect monomeric α-syn from aggregating by hiding the hydrophobic core (Bertoncini et al., 2005). A recent study showed that calcium interaction with the negatively charged C-terminal segment disrupts the N- and C-terminal interaction causing the exposure of the N-terminal, which consequently increases aggregation propensity (Stephens et al., 2020). Some studies, however, found that this long-range interaction exposes the hydrophobic NAC segment, which could induce protein aggregation rather than inhibit it (Ullman et al., 2011). To solve these two contradictory statements, first, we plot the distance distribution between the N- and C-terminal segments to confirm if this long-range interaction exists in our data. Our analysis shows that over 70% of the structures in clusters 1 (90.46%), 2 (83.69%), 3 (84.04%), 4 (73.33%), 7 (99.54%), 8 (79.35%) possess the N- and C-terminal long-range interaction, while less then 35% of the structures in clusters 5 (30.94%) and 6 (15.25%) contain this interaction (Figure 4B). Then, we extract the protein structures that have this long-range interaction from each cluster and compute the average solvent accessible surface area (SASA) for each residue. Since different amino acids have different sizes, we calculate the relative solvent accessibility by dividing its average SASA by the maximum surface area of that type of residue. A cutoff of 40% is used to define the two states, buried or exposed, as this cutoff has been proved to be useful by other studies (Stultz et al., 1993; Ullman et al., 2011). Our data (Figure S8) show that most residues in the NAC segment tend to be buried except residues in cluster 7, where 57% of the residues in the hydrophobic segment are exposed. These results indicate that for most of the monomeric conformations of α-syn, N- and C-terminal contact covers the hydrophobic NAC segment, which stabilizes the protein and protects it from aggregation. However, this long-range contact also causes the NAC segment to be exposed in a small fraction of the structures that are aggregation-prone.

Figure 4. The long-rang contacts in the simulated structures of clusters 1~8 (C1~8).

(A) The simulated distance distributions between the centers of mass of NAC and C-terminal segments.

(B) The simulated distance distributions between the centers of mass of N- and C- terminal segments. Structures with distances lower than 25 Å (black dashed vertical lines) are defined to have this long-range interaction.

Millisecond transitions between some of the structural subpopulations observed by single-molecule protein-induced fluorescence enhancement

We have shown that the ensemble structure of α-syn can be divided into eight distinct clusters, describing the underlying structural subpopulations of α-syn. DMD simulations in the present study, however, do not capture the transition between structural subpopulations. The ensemble structure of an IDP may include several distinct conformational states with low activation barriers between them, in which transitions may occur as slow as a few microseconds. If this is the case, fluorescence measurements of freely-diffusing single molecules that yield photon bursts with durations of a few milliseconds would result in a single burst population that is averaged out (up to thousands of transitions between conformational states occurring within the time a single α-syn traverses the confocal spot). However, if the transitions between some of α-syn’s structural subpopulations occur slower than the millisecond timescale of bursts, such measurements would result in burst histograms including more than a single population. In order to test the conformational dynamics of α-syn monomer, we perform smPIFE experiments (Hwang and Myong, 2014; Hwang et al., 2011; Jeong et al., 2016; Lerner et al., 2016; Morten et al., 2015; Ploetz et al., 2016).

We conjugate the dye sulfo-Cy3 (referred to in this work as sCy3) to a cysteine in three different single cysteine α-syn mutants (at either residues 26, 39 or 56; Methods). Cy3-based dyes exhibit excited-state isomerization between a bright trans isomer and a dark cis isomer, leading to an overall low fluorescence quantum yield. However, if the excited-state isomerization of sCy3 is slowed down relative to its excited-state lifetime, the dwells of sCy3 in the trans isomer longer, leading to an increase in its fluorescence quantum yield. The PIFE effect tracks that change in excited-state isomerization caused by nearby segments of the protein, which impose steric obstruction on sCy3 and limit its capability to isomerize. In PIFE measurements, the increase in fluorescence quantum yield can be observed via the increase in the average fluorescence lifetime. We measure the Cy3-labeled α-syn constructs at a low concentration, in which it is found predominantly as a monomer (25 pM), where the average fluorescence lifetime is measured one α-syn molecule at a time (when it crosses a tightly focused laser beam in a few milliseconds). Importantly, the durations of the recorded single-molecule bursts are in the range of 1-8 ms.

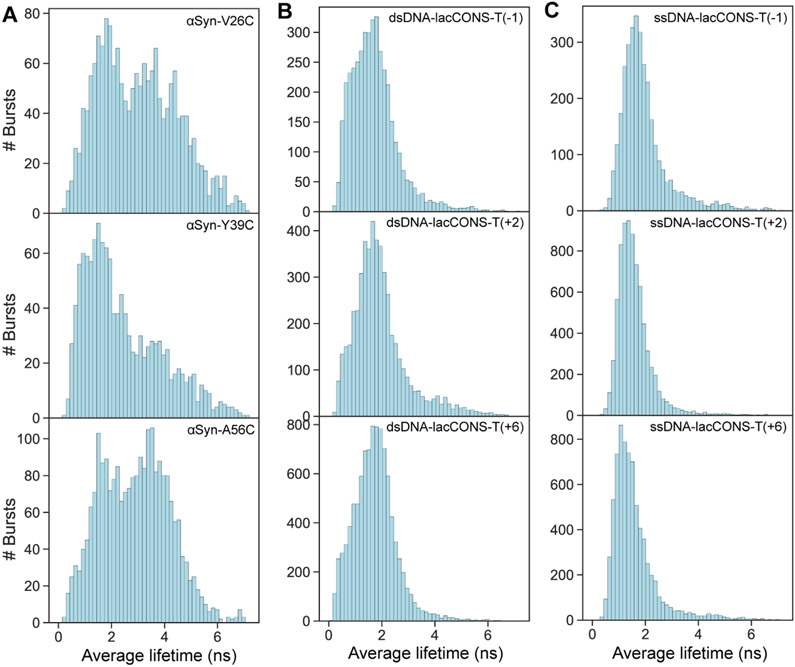
The resulting average fluorescence lifetimes of single-molecule bursts are collected in histograms (Figure 5). The results clearly show the average lifetime values of α-syn monomers (Figure 5A) can be grouped into more than a single central population. The sub-population with low average lifetime values represents α-syn species with minimal intramolecular interactions in the vicinity of sCy3-labeled residue, while the sub-populations with larger average lifetime values represent species with intramolecular interactions in the vicinity of sCy3-labeled residue, sterically interfering with the free isomerization of the exited sCy3. As a control of the smPIFE measurements, we perform the same measurements on sCy3Cy3-labeled DNA constructs at either one of three different bases along the sequence, either in double- or single-stranded form (Figure 5B and C). These measurements result in a single population of average lifetime values, showing that smPIFE yields a single population of values either in the case of a single rigid structure, such as in dsDNA, or in the case of a very flexible structure with rapid structural transitions, such as in ssDNA, that average-out in millisecond. Therefore, we show that at least some of the proposed eight clusters or structural subpopulations, interconvert in 1-8 ms or slower which is surprisingly far from what is expected for an IDP (Banerjee and Deniz, 2014; Bertoncini et al., 2005; Ferreon et al., 2009, 2010; Ferrie et al., 2018; Grupi and Haas, 2011b; Nath et al., 2010; Sahay et al., 2016; Trexler and Rhoades, 2010).

Figure 5. Slow conformational transitions of α-syn observed by smPIFE experiments.

(A) The histograms of average fluorescence lifetimes from smPIFE measurements of sCy3 labelled α-syn. sCy3 dye is conjugated at Cys in the V26C, Y39C or A56C mutants, respectively. The ensemble of α-syn includes different subpopulations with various degrees of dye available volume that interconvert slower than a few milliseconds (slower than burst durations).

(B) and (C) The histograms of average fluorescence lifetimes when sCy3 is labeling bases of double or single stranded DNA, respectively. The labeling positions were the promoter registers in the template strand of the lacCONS promoter (Kim et al., 2011; Mukhopadhyay et al., 2001; Ploetz et al., 2016). Note the low mean lifetime values in flexible single stranded DNA and the slightly higher mean values in more rigid and more sterically restricted double stranded DNA.

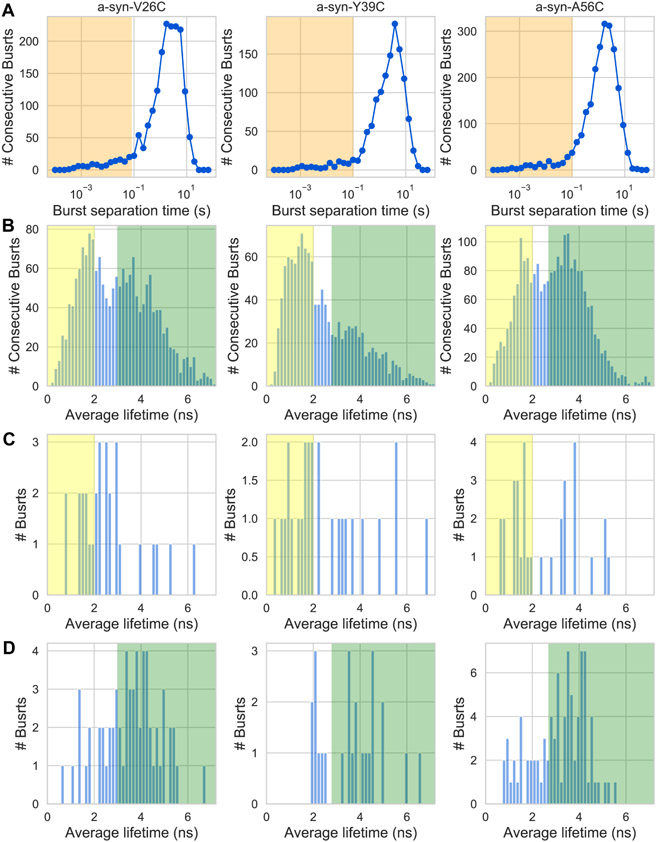
While the appearance of distinct burst-wise subpopulations is a marker of dynamics occurring slower than the burst durations, this evidence is insufficient to find the timescale of these slow transitions. To answer this question, at least qualitatively, we perform burst recurrence analysis (Hoffmann et al., 2011) based on the values of burst average lifetimes (Figure 6). Briefly, there are two types of pairs of consecutive bursts: (i) different molecules, where the pair of bursts separated by longer separation times, t_sep, the lower is the concentration. The separation times of such pairs of consecutive bursts in single-molecule experiments are at least seconds; (ii) a recurring molecule that produces a burst when crossing through the observation volume, proceeds to move outside the observation time, and then recurs back into the observation volume to produce another burst. Such pair of consecutive bursts occurs rarely, with burst separation times similar to the burst durations (few ms) that are independent of the concentration. If the two types of burst separation times are well-separated (Figure 6A), one can select pairs of consecutive bursts of recurring molecules and compare their burst properties. Out of such pairs of consecutive bursts, separated by less than a given t_sep (Figure 6A, orange shade), if the first burst has an average lifetime belonging to one subpopulation of lifetimes (Figure 6C and D) and the second burst has an average lifetime belonging to the other subpopulation of lifetimes (Figure 6C and D), then a transition occurred between these two subpopulations, within t_sep.

Figure 6. PIFE burst recurrence analysis showing individual molecules undergo transitions between different average lifetime values within 100 ms.

(A) The histogram of separation times between consecutive single-molecule bursts. The orange shade represents separation times between consecutive bursts of recurring molecules, where the first and second bursts arise from the same molecule.

(B) The average lifetime histogram of all single-molecule bursts. The yellow and green shades represent the range of average lifetime values chosen to represent values within low and high average lifetime subpopulations, respectively.

(C) or (D) The average lifetime histograms of bursts that were separated from a previous burst by a time within the orange-shaded timescale (in panel A), and where the previous burst had an average lifetime within the range represented by the yellow or green shades, respectively. Each column summarizes the PIFE burst recurrence analysis of sCy3-labelled residues at different positions (V26C, Y39C, and A56C) in α-syn.

For the smPIFE measurements of each sCy3-labeled α-syn, we define ranges of burst average lifetimes that are either within low or high values (Figure 6, yellow and green shades, respectively). Then, we seek pairs of consecutive bursts separated by < t_sep (Figure 6A, orange shade), defined as 80 ms when sCy3 is conjugated to Cys26 in the V26C mutant, or 100 ms when sCy3 is conjugated to Cys39 or Cys 56, in the Y39C or A56C mutants, respectively. Out of these burst pairs, we also seek ones where the average lifetime of the first burst is within the low or high average lifetime subpopulations, and subsequently report on the lifetime of the second burst, for all these burst pairs (Figure 6C and D, respectively). In all three sCy3-labeled positions, a fraction of burst pairs undergoes transitions between low and high average lifetime subpopulations (Figure 6C, bursts outside the yellow shade) and vice versa (Figure 6D, bursts outside the green shade). Nevertheless, the amount of these selected recurring molecule bursts is low and we cannot further use this data to estimate the exact transition rates.

Overall, our results show that α-syn undergoes structural transitions influencing the degree by which some amino acid residues in the N-terminal segment (residues 26, 39 & 56) experience steric restriction from other parts of the protein. These transitions occur within tens of milliseconds between some of the structural subpopulations of α-syn.

Discussion

The size of the α-syn monomer in aqueous solution was studied extensively by various experimental techniques including PRE, SAXS, and smFRET (Dibenedetto et al., 2013; Nath et al., 2012; Piana et al., 2015; Ramis et al., 2019; Schwalbe et al., 2014). These experiments indicate that the average structural ensemble of α-syn is more compact than a random coil. However, the R_g values differ significantly between methods ranging from 22.6 to 50 Å (Dibenedetto et al., 2013; Nath et al., 2012; Piana et al., 2015; Ramis et al., 2019; Schwalbe et al., 2014). This disagreement and the large R_g may be caused by a mixture of monomeric as well as multimeric states of α-syn under specific experimental conditions (Gurry et al., 2013; Schwalbe et al., 2014). In addition, techniques such as SAXS produce larger errors when the R_g is large (Ramis et al., 2019), because the highly extended conformations contribute more to the scattering intensity (Schwalbe et al., 2014). Our simulation data shows that most of the monomeric structures (99.6%) have R_g values ranging from 14 to 50 Å, most of which (66.6%) are populated within the range of 14 and 21 Å. The ensemble structure retrieved from our simulation captures more compact structures, which is intriguing. These compact structural subpopulations may exist and be overlooked by experimental studies due to the above-mentioned issues. Therefore, we study these compact subpopulations in the attempt to understand their potential roles as the precursors to form diverse α-syn complexes and oligomers.

The ensemble structure is split into eight clusters with distinct conformations by the agglomerative hierarchical clustering method (Methods). Our smPIFE data suggests that some of these structural subpopulations or groups of some of these subpopulations transition within tens of milliseconds, which is much slower than the reported nanosecond and microsecond timescales (Bertoncini et al., 2005). The slow dynamics support the notion that to carry out one of its multiple functions via ligand binding and complexation, the α-syn monomer has to stay in a specific conformation long enough to facilitate ligand binding. We suggest that the heterogenous conformations of α-syn follow a hierarchy of transition dynamics, in which 10-100 ms dynamics represents transitions between some of the structural subpopulations, while other transitions occur in microseconds or faster.

PRE (Marius Clore and Iwahara, 2009; Xue et al., 2009), bulk time-resolved fluorescence (Ferrie et al., 2018; Grupi and Haas, 2011b; Sahay et al., 2016), fluorescence correlation spectroscopy (Nath et al., 2010), smFRET (Banerjee and Deniz, 2014; Ferreon et al., 2009, 2010; Trexler and Rhoades, 2010), and MD simulations (Ovchinnikov et al., 2020) all point to structural dynamics as slow as microseconds, but lack identification of millisecond dynamics. Here, using smPIFE measurements, we identify the millisecond or slower dynamics of structural changes between some of α-syn’s structural subpopulations. This finding is unique, especially when compared to previous smFRET works, since PIFE identifies subpopulations on the basis of steric obstructions to sCy3 that range shorter (<3 nm) than the distance range covered by smFRET (3-10 nm) (Hwang and Myong, 2014). By that, one can assume that the slow dynamics were not identified by smFRET, because they were local, and hence did not introduce FRET subpopulations with significantly different mean values. Indeed, smFRET studies of the α-syn monomer report on a single wide FRET population when in solution (Banerjee et al., 2016; Ferreon et al., 2009; Moosa et al., 2015; Veldhuis et al., 2009). Interestingly, in the presence of the kosmotropic osmolyte trimethylamine N-oxide (TMAO), the mean FRET efficiency changes, however within a single FRET population (Moosa et al., 2015). Since TMAO stabilizes compact conformations out of an ensemble of structures, these findings come to show that multiple conformations exist, but are reported within a single millisecond-averaged population. smPIFE, however, exhibited these conformational subpopulations on the basis of a reporter that captures features that are more local than what smFRET could capture, the microenvironment of sCy3 conjugated to a given amino acid residue. Bulk trFRET can track FRET between UV-excitable dyes in shorter inter-dye distances (1-5 nm) (Ferrie et al., 2018; Grupi and Haas, 2011a). However, in bulk trFRET measurements, conformational subpopulations cannot be distinguished as in smFRET (only in exceptional cases) (Rahamim et al., 2015). Therefore, the local nature of the reported information in smPIFE, and the fact that it can be employed on single molecules rendered it useful in uncovering the multiple structural subpopulations of α-syn and the slow dynamics between them. Taken together, these results point to a possible conformational energy landscape with a hierarchy of activation barrier heights. What is still unknown to us is which pairs of conformations/clusters undergo rapid interconversions and which do not. A theory that allows mapping of smPIFE experimental findings to structural models is currently under development. Therefore, we did not attempt to compare the ensemble structure model of α-syn to the smPIFE results, but rather show that the ensemble includes distinct millisecond-stable local structures. A follow-up study that presents the transformation of smPIFE data to structural models, will identify which of the modeled structural subpopulations can be grouped into the observed smPIFE-based subpopulations.

The monomeric structures of α-syn may serve as the building block of its specific interactions with other ligands and proteins, and hence dictate which of its various functions it will follow. By that, the conformation of α-syn may determine its role in maintaining normal cellular functions as well as initiating protein aggregation that is detrimental to neuronal cells and promotes PD progression (Meade et al., 2019; Riederer et al., 2019; Sulzer and Edwards, 2019; Twohig and Nielsen, 2019). A deep investigation of α-syn structural ensemble characterized by trFRET-DMD reveals transient structures that may trigger membrane binding and protein fibrillization.

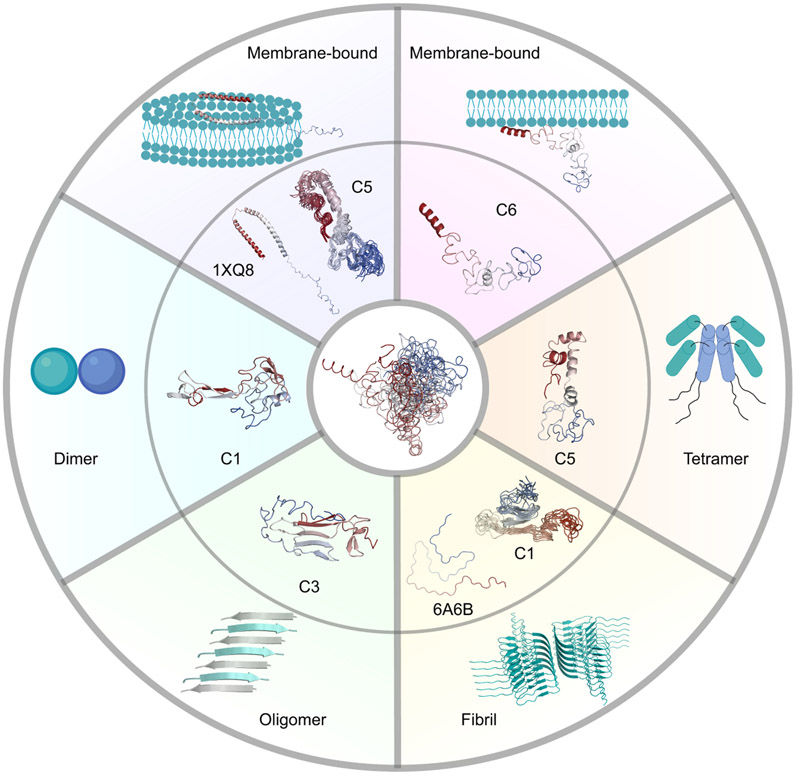
α-Syn forms two well-ordered α-helices in an anti-parallel arrangement in the N-terminal and NAC segments, followed by a disordered C-terminal segment when it interacts with micellar membranes (PDB 1XQ8 (Ulmer et al., 2005)). To find out if our predicted conformational ensemble of the α-syn monomer contains structures similar to the membrane-bound state of α-syn, we calculated the RMSD between the pairs of C_α of our simulated structures in the eight clusters and the structure of the micelle-bound α-syn. We find that several structures in cluster 5 are the most similar to this micelle-bound state, based on the RMSD distribution (Figure S9A and S10). The cluster 5 structure with the lowest RMSD (30.2 Å, p < 2.2e-16) relative to 1XQ8 displays partially folded helices in the N-terminal as well as the NAC segments (Figure 7 and Figure S11A). These two helices are arranged in an anti-parallel direction connected by the linker at the same region as that in 1XQ8. The C-terminal segment is also characterized by the highly disordered loops (Figure 7 and Figure S11A). Structural alignment of the 10 structures with the lowest RMSD in cluster 5 shows that a number of structures are closely related to the membrane-bound state of α-syn. The structures with the similar secondary structural composition and topology in cluster 5 might represent the monomeric precursor that interacts with the surface of a membrane and therefore, might be important for the synaptic functions. The organization of the N-terminal and NAC segments in these structures is more globular than the elongated structure of the end-product bound to the membrane. Gambin et al. (Gambin et al., 2011) performed smFRET measurements to track the kinetics of the conformational change upon mixing α-syn with a membrane, as viewed from the distance between the edges of the N-terminal and NAC segments, from the α-syn monomer ensemble to the membrane bound helical hairpin structure. In that study, they identified the kinetics includes an intermediate state. We propose that the first kinetic transition is the stabilization of the α-syn conformation represented by the structures in cluster 5, and the depopulation of the structures in the other clusters. Therefore, the second kinetic transition is caused by the stabilization of the elongated helical hairpin conformation by the membrane. In summary, this proposed mechanism highlights the possibility that certain structures in the structural subpopulations we identified in the α-syn monomer ensemble, serve as the preexisting intermediates for membrane binding.

Figure 7. Conformational ensemble of α-syn including dynamic structures that potentially serve as structural precursors of its various physiological and pathogenic functions.

Membrane interaction and dimer, tetramer, and oligomer formation might be stimulated by clusters 6, 1, 5, and 3 (C6, C1, C5, and C3), respectively. The membrane-bound state of α-syn with broken anti-parallel α-helices might be derived from structures in cluster 5 (C5). α-Syn fibrils might be formed by structures in cluster 1 (C1). The outer panels present the structures of the α-syn subunit in several complexes or existing models in other complexes. The inner panels present the centroid structures of specific clusters or the structural alignment of the top 10 structures with the lowest RMSD to 1XQ8 or 6A6B. The central panel describes the structural ensemble of α-syn. Structures in the figure are colored from red (N-terminus) to blue (C-terminus).

Besides the helical hairpin structure (broken-helix structure) characterized by the NMR study (Ulmer et al., 2005), an extended helix conformation associated with the membrane of a curvature larger than that of a micelle was also reported (Georgieva et al., 2008). Based on a solid-state and solution NMR spectroscopy study (Fusco et al., 2014), the N-terminal residues (first 25 residues) are found to adopt a well-defined α-helical secondary structure that targets and anchors α-syn to the membrane of synaptic vesicles. The central segment of the protein (residues 26~97), however, is more flexible in solution and forms stable α-helix when it binds to the membrane surface (Fusco et al., 2014). The C-terminus (residues 99~140) is characterized to be extremely dynamic and unstructured (Fusco et al., 2014). By comparing these experimental data with our predicted structural subpopulations, we find that the centroid structure of cluster 6 explains these essential features (Figure 7). Our results show that the first 15 residues form an α-helix followed by dynamic and partially folded α-helices in the NAC segment and a completely unstructured C-terminal segment at the end. The extended structure favors targeting of the N-terminal segment to the membrane and then brings the NAC segment close to the membrane, which further induces α-helical elongation. This proposed binding mechanism with membrane might result in the extended helix conformation rather than the broken-helix structure. Therefore, structures in cluster 6 might interact with membrane in an extended helix conformation. An overall analysis of the secondary structure composition in cluster 6 shows a high probability (>40%) of forming α-helices in the N-terminal and central segments (Figure S6). This observation further suggests that cluster 6 might represent the structural subpopulation that is important for membrane binding. The low propensity of α-helical formation in some other clusters (clusters 3, 4, 7) implicates the heterogeneity of the conformational ensemble and provides evidence that the α-syn monomer includes structural subpopulations that are prone to membrane bound and unbound states.

The α-syn tetramer was reported to be the native state in eukaryotic cells, preventing it from aggregation and reducing its pathogenicity (Bartels et al., 2011). According to the results from electron microscopy and PRE experiments, a model of the α-syn tetramer formed by hydrophobic interactions of the α-helix in the central segment (residues 50~103) was proposed (Wang et al., 2011). An α-helix in the N-terminal segment (residues 1~43) locates at the opposite direction of the hydrophobic core and forms an antiparallel arrangement with the α-helix in the NAC segment. By scrutinizing our conformational ensemble, we find that the centroid structure of cluster 5 might serve as the structural precursor of the tetramer (Figure 7). We observe discontinuous α-helices at both N-terminal and the NAC segments. An antiparallel arrangement between these two segments is also displayed. Moreover, the C-terminal segment described as disordered in the literature is also unstructured in our prediction (Wang et al., 2011). The overall hairpin-like structure exposes the hydrophobic residues in the NAC segment, which might facilitate oligomerization and benefit the formation of the tetramer hydrophobic core. Although the α-helices at the N-terminal and NAC segments are discontinuous, which is different from those in the tetramer, this can be easily explained by the monomeric state of α-syn. The structures of α-syn monomer are highly flexible in solution, while the α-helices in oligomers are elongated and stabilized by the hydrophobic interactions (Wang et al., 2011). The whole analysis of α-helix composition for all the structures in cluster 5 also reveals high probabilities of forming discontinuous α-helices at the N-terminal and NAC segments (Figure S6). We propose that these discontinuous and transient α-helices as well as the exposure of the hydrophobic NAC segment promote tetramer formation. While some structures in cluster 5 interact with membranes as discussed before, other cluster 5 structures might be involved in tetramer formation in vivo and protection from neurodegenerative disorders.

α-Syn oligomers and fibrils have been implicated in PD and other synucleinopathies. Understanding how the α-syn monomer forms oligomers and fibrils is critical to demystify the pathogenesis of PD, as well as, to assist in developing effective therapies. Dimer formation is considered to be the first step of oligomerization (Sahu et al., 2015). A high-speed atomic force microscopy (HS-AFM) study displayed two types of dimer conformations (Zhang et al., 2018). Type I is composed of two compact monomers, while type II consists of a compact monomer and a monomer with an extended protrusion. From the centroid structures of the 8 clusters, we find structures that are more globular and structures with extended tails. Because of the low-resolution of HS-AFM experiments, we have no information about the secondary structure composition of the dimers. Therefore, we propose that the conformational ensemble includes both compact and extended structures that are necessary for the formation of the α-syn dimer. Further studies are required to further clarify which cluster might promote dimer formation. Previous simulations suggested that the β-strand-rich hydrophobic NAC segment is important for dimerization (Mane and Stepanova, 2016). Since the centroid structure of cluster 1 has an exposed hydrophobic β-sheet that is extended, cluster 1 might be the potential structural subpopulation that promotes dimerization (Figure 7).

α-Syn oligomers and fibrils with varying morphologies have been reported in a large number of studies (Paslawski et al., 2014). Oligomer species are mainly divided into two groups: (i) on-pathway oligomers that can grow into fibrils, and (ii) off-pathway oligomers that are resistant to fibrillation (Chen et al., 2015). Infrared spectroscopy studies showed that the prefibrillar α-syn oligomers adopt antiparallel β-sheet structures, which is different from the parallel β-sheet structure in fibrils characterized by x-ray crystallography (Celej et al., 2012). It was proposed that on-pathway oligomers must undergo structural rearrangements to produce fibrils. Experimental evidence has already established the connection between oligomers and fibrils. If so, how does the α-syn monomer accumulate and form various oligomers? Can the α-syn monomer directly aggregate and generate fibrils? To answer these questions, we examine the centroid structures of our eight clusters and compare various fibril structures characterized by NMR and cryo-EM with the simulated structures. We identify antiparallel β-sheet structures formed in the aggregation-prone segment (NAC) of the centroid structure in cluster 3 (Figure 7). In addition, long-range interactions between the N- and C-terminal segments expose the NAC segment, which was also discovered in other studies and speculated to enhance protein aggregation³³. A comprehensive analysis of the secondary structure composition reveals that cluster 3 has a higher proportion of β-strands (Figure S6). Therefore, we deduce that cluster 3 might represent the subpopulation of forming oligomers (Figure 7), some of which are toxic to neuronal cells and promote neurodegenerative diseases.

To understand if α-syn ensemble includes structures prone to fibrillation, we compare our simulated structures with the structures of the α-syn subunit in various fibrils based on RMSD of C_αs. The comparison with the cryo-EM structure of α-syn fibril (PDB 6A6B (Li et al., 2018)) shows that clusters 1, 4, 6, and 8 contain structures with lower RMSD than the other clusters (Figure S9B). We extract the structures with the lowest RMSD in these four clusters and compare them with the subunit of 6A6B. We find that the structure in cluster 1 has the lowest RMSD (11.1 Å, p < 2.2e-16) and the most similar topology compared to 6A6B (Figure 7 and S11). The comparison of simulated structures with the other fibril structures (PDB 2N0A (Tuttle et al., 2016) and 6XYP (Schweighauser et al., 2020)) also indicates that structures in cluster 1 are the most similar to the subunits in these fibrils (Figure S9 and S11). Structural alignment of the top 10 structures with the lowest RMSD also implicates that a number of structures are similar to the subunit of the fibrils (Figure S11). Therefore, structures of cluster 1 might play a crucial role in fibril formation more than the other clusters and therefore, might represent the subpopulation that stimulates fibrillation.

The above findings suggest the α-syn monomer might use its millisecond-stable local structures to promote binding to specific biomolecular targets. This finding can be applicable to other IDPs or proteins with intrinsically disordered regions. The selected-fit (and also equilibrium shift) model is a binding model by which biomolecular association stabilizes one of the conformations of the proteins that exist also in the absence of association, as one out of several distinct conformations that dynamically interconvert. The selected-fit model of binding explains the mechanisms of many biomolecular binding events, for proteins with relatively slow conformational dynamics, where different conformations survive long enough to increase the probability of binding to it. This view may not necessarily represent the mechanism of how other IDPs associate with biomolecules, due to the previously inferred too rapid conformational dynamics, leading to conformations that do not last long before interconverting. Several principal ideas have been developed for how IDPs associate with other biomolecules, and the main question at hand is always how can a structure-less (or less structured) protein have a specific recognition mechanism for a specific binding partner, or better said, how long should the fruitful biomolecular association take, and can it occur within the time a conformation survives. Since IDPs are thought of as changing conformation too rapidly, these conformations are thought of as being too unstable, and hence the simple view of a selected fit model is not necessarily the model of choice. Variants of the induced-fit model, such as the co-folding model, have shown that some IDPs fold to specific structures upon specific binding recognition. If, however, some IDPs behave as globally disordered polymers, containing local regions with specific conformations that survive long enough, they can act as the recognizers of specific binding and their stability will increase the probability that such binding recognition will lead to a stable binding event. Therefore, we suggest that the α-syn monomer and potentially other IDPs follow a selected-fit or equilibrium shift model using stable local structures acting as recognizers of specific binding partners.

Overall, based on our predicted conformational ensemble of the α-syn monomer, we suggest potential structures that have a high propensity to bind membranes, form different oligomers, or aggregate into fibrils, which are supported by various experimental data. Experimental conditions or mutations that stabilize a specific conformational state could be explored in the future in order to verify our hypothesis. The concrete structures provided by our study may also be used in designing small molecule regulators aiming to prevent protein aggregation and interfere with the development of neurodegenerative diseases.

STAR Methods

RESOURCE AVAILABILITY

Lead contact

Further information and requests should be directed to and will be fulfilled by the Lead Contact, Nikolay V. Dokholyan (dokh@psu.edu).

Materials availability

This study did not generate new unique reagents. Plasmids will be available upon request.

Data and code availability

The mass spectrometry proteomics data have been deposited to the ProteomeXchange (Deutsch et al., 2020) Consortium via the PRIDE (Perez-Riverol et al., 2019) partner repository with the dataset identifier PXD024671. All smPIFE analyses and raw data have been deposited in Zenodo with the DOI 10.5281/zenodo.4081424 (Chen et al., 2020). Additional simulation data of α-synuclein monomer has been deposited in Zenodo with the DOI 10.5281/zenodo.4444069 (Chen et al., 2021). The models of the α-syn ensemble structure have been deposited in the PDB-Dev Database with the accession number PDBDEV_00000082 (Vallat et al., 2018).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Microbe strains

Two E. coli strains were used in this study. DH5α strain (ThermoFisher) was used for plasmid cloning and propagation. BL21(DE3) competent E.coli cells (Novagen) were used for protein expression and purification. BL21(DE3) was grown in LB media including 0.1 mg/mL ampicillin at 37 °C. Protein expression was induced by 1 mM IPTG.

METHOD DETAILS

Determination and optimization of discretized potential energy functions used as restraints

The workflow of designing discretized potential energy functions used as restraints in DMD simulations of α-syn is illustrated in Figure 1.

Conversion of distance distribution data to multi-step square-well functions

First, we retrieve the distance distributions of 8 residue pairs from analysis results of bulk trFRET data previously recorded by Grupi and Haas (Grupi and Haas, 2011a). We then convert these distributions to potential energy curves in the reaction coordinate between the residues, using the approach introduced by Haas and Steinberg (Haas and Steinberg, 1984). We discretize the resulting potential curves to produce multi-step square-well functions (Ding et al., 2008; Proctor et al., 2011; Shirvanyants et al., 2012). Usually, most populated distances have lower potential energies, while distances with low probabilities have less attractions. Initially, we design a nine-step square-well function for each residue pair. We add the designed multistep square-well functions into the Medusa force field for DMD simulations (Yin et al., 2008). The addition of these eight potentials restrains the positions of the corresponding residue pairs during simulations and reduces the degrees of freedom of the molecule.

Optimization of the square-well potential functions based on the comparison of computational and experimental distance distributions

After simulation, we calculate the eight inter-residue distances for all the structures of system equilibration and plot distance distributions for each residue pair (defined here as computational/simulated distance distributions). Next, we compare the computational and experimental distance distributions. DMD simulations using this designed multi-step square-well potential generate structures with much shorter distances as compared to the distance distribution curve characterized by trFRET. To match the long-distance distribution, we modify the previous square-well functions using the following rules. (i) If the simulated distance distribution has a higher probability than the experimental one at a given range of inter-residue distances, we increase the potential energy at these distances, which then reduces the attractions in simulations. The increasing value of the potential energy differs based on the comparison. A big difference between computational and experimental probabilities needs a large increase of the potential energy, while a small difference requires a little increase of potential energy. (ii) If the simulated distance distribution has a lower probability than the experimental one, we decrease the potential energy at these distances, which in turn allows more attractions. The decreasing level of the potential energy also depends on the comparison. Square wells can be merged or split into smaller wells in order to match local distance distribution. Then, we use the newly designed multi-step square-well functions for DMD simulations.

After several iterations of optimization, our designed potential converges to a set of square-well functions (Figure S1) that corresponds to an ensemble with the desired distance distributions (Figure S2). The distance distributions of the eight residue pairs of the simulated structures do not perfectly match the experimental data (Figure S2). This mismatch could be attributed to the skewed Gaussian distribution of the distances assumed by the trFRET experiments (Dellarole and Royer, 2014; Grupi and Haas, 2011a, 2011b). The simulations recapitulate most of the experimental distance distributions and therefore, provide structural insights of α-syn conformational ensemble.

Discrete molecular dynamics simulations of α-synuclein

Discrete step function potentials are used in DMD to define inter-atomic interactions, rather than continuous potentials widely adopted in traditional MD simulations (Ding et al., 2008; Proctor et al., 2011; Shirvanyants et al., 2012). This application greatly reduces calculations and therefore, enhances sampling and allows explorations of the dominant conformational space in a practical timescale (Brodie et al., 2019). During DMD simulations, we use the designed multi-step square-well functions as constraints for each residue pair (Brodie et al., 2017, 2019; Wang and Dokholyan, 2019) by integrating them with the Medusa force field (Ding and Dokholyan, 2006; Ding et al., 2008; Proctor et al., 2011; Shirvanyants et al., 2012; Yin et al., 2008). We use a fully extended structure of α-syn to initiate simulations. We perform the all-atom replica exchange DMD simulations with 26 replicas, which include temperatures evenly distributed from 0.35 to 0.60 kcal/(mol·k_B) (Shirvanyants et al., 2012). The simulation temperature of each replicate exchanges based on the Metropolis algorithm, which allows structures trapped at local stable states to bypass enthalpic barriers, and hence, enhances conformational sampling (Ding et al., 2008; Nymeyer et al., 2004; Ostermeir and Zacharias, 2013). The time for performing replica exchange is every 1000 time steps. We perform four million DMD time steps (~50 ps each) (Ding et al., 2008) for each simulation. After simulation, we calculate the exchange rates between adjacent replicas to ensure appropriate replica spacing and sampling (Ding et al., 2008). The rates in the range of 0.25 and 0.7 (Table S1) mean that the temperature exchange is sufficient for adequate sampling. We plot the time evolution of each replica in the temperature space to show the temperature exchange within each replica (Figure S3). We plot the system’s energy distribution specific heat curve using the weighted histogram analysis method to indicate the convergence of the system (Figure S4) (Kumar et al., 1992).

Simulation data analysis

We discard the first 0.5 x 10⁶ time steps of simulations during equilibration. Then, we calculate the radius of gyration (R_g) for all the remaining structures in the 26 trajectories. We extract the highly populated structures and cluster them using the agglomerative hierarchical clustering method based on the ward linkage algorithm from TTClust (Tubiana et al., 2018). Ward’s method determines a linkage between two clusters when the integration of these clusters causes the least increase in overall within-cluster variance (Joe H. Ward, 1963). We choose the clustering cutoff following the suggestions by Offutt et al. (Offutt et al., 2016): (i) the total number of clusters is less than 40; (ii) 90% of the structures are included in less than 7 clusters; and (iii) minimal number of clusters have only one structure. Specifically, first we rule out the cutoffs that generate too many clusters (more than 40), and then we increase the cutoff until we find one in which 90% of the structures are included in fewer clusters (~7). After structural clustering, TTClust also generates a clustering dendrogram, a bar plot showing number of structures within each cluster, and a table including pairwise root-mean-square deviation (RMSD) between clusters (Tubiana et al., 2018). We utilize GROMACS’ sham program to plot the Gibbs free energy landscape by using two of the three components including RMSD to the average structure of the ensemble, the R_g, and the potential energy. Specifically, GROMACS projects all the conformations onto a two-dimensional plane in which the axes correspond to the two selected features. Then, the program counts the number of structures occupied by each cell. It assigns the bin (in the two-dimensional plane) populated by the largest number of conformations as the reference bin and sets the free energy to zero. GROMACS calculates the free energies for the other bins using the equation: ΔG = −k_BTln[P(x,y)/P_max], where P(x,y) represents the probability of structures in a bin with respect to all the structures, P_max is the probability of the reference bin, k_B is the Boltzmann constant, and T is the temperature. We compute the secondary structure composition of the predicted conformational ensemble of α-syn using GROMACS’ DSSP program (Joosten et al., 2011; Kabsch and Sander, 1983). We calculate the solvent accessible surface area (SASA) for each residue using the SASA algorithm in GROMACS (Eisenhaber et al., 1995). We characterize the contact frequency maps for each cluster by Contact Map Explorer (https://contact-map.readthedocs.io/en/latest/examples/nb/contact_map.html).

Expression and purification of α-synuclein

We follow the protocol introduced by Grupi & Haas (Grupi and Haas, 2011a) for the expression and production of recombinant α-syn variants (WT and different single cysteine mutants V26C, Y39C or A56C). Briefly, we clone α-syn variants into pT7-7 vectors. Then, we transform the resulting plasmids verified by sequencing into BL21(DE3) cells (Novagen) for protein expression. We grow BL21(DE3) cells in Luria-Bertani media in the presence of 0.1 mg/mL ampicillin. We induce protein expression by adding 1 mM isopropyl β-d-1-thiogalactopyranoside (Sigma) when the cell density reaches an OD_λ=600nm of 0.6 ~ 0.7. After induction, we culture the cells at 37 °C for 5 h and harvest the cells by centrifugation at 6000 rpm. We resuspend the cell pellet in lysis buffer (30 mM Tris–HCl, 2 mM ethylenediaminetetraacetic acid (EDTA), 2 mM dithiothreitol (DTT), pH 8.0 - also called buffer A - and 40% sucrose) and stir it for 20 minutes at room temperature. Then, we transfer the solution to 50 mL tubes and centrifuge for 0.5 hour at 11,000 rpm. Finally, we resuspend the cell pellet in dissolution buffer (37 μL saturated MgCl₂ solution and 90 mL of buffer A) to perform osmotic shock.

We precipitate DNA by adding streptomycin sulfate (Sigma) to a final concentration of 10 mg/mL. We stir the mixture for 20 minutes at room temperature and centrifuge at 12,000 rpm for 0.5 hour. We collect the supernatant and precipitate proteins by adding 300 mg/mL ammonium sulfate (Sigma). We stir the solution for 30 minutes at room temperature and centrifuge again at 12,000 rpm for 0.5 hour. We collect the protein precipitate and resuspend in buffer A. To remove α-syn aggregates and large oligomers, we filter the solution through a 100 kDa molecular weight cutoff (MWCO) Amicon tube. We dialyze the filtered solution using 3.5 kDa MWCO dialysis bags at 4 °C overnight against buffer A. Then, we load the solution on a 1 mL MonoQ column (GE Healthcare) using an FPLC system (Äkta Explorer). We elute α-syn with a salt gradient from 0 to 500 mM NaCl. We verify the presence of α-syn in the fractions by measuring absorption spectrum in the wavelength range of 260-350 nm and running the samples in a 12% SDS-PAGE Gel. We stain the gels by fast seeBand (Gene Bio-application). We unify relevant fractions and dialyze it with 3.5 kDa MWCO dialysis bags at 4 °C overnight against buffer A. We verify the molecular mass of the recombinant α-syn by intact protein mass determination (next section). We evaluate the purity of α-syn by running a 12% SDS-PAGE gel. We use a 12% native PAGE gel to probe the presence of α-syn dimers. We store protein samples at −20 °C.

Intact protein mass determination

We dissolve proteins in 40% acetonitrile, 0.3% formic acid (all solvents are MS-grade) at a concentration of 2-5 mg/mL. Then, we inject the dissolved proteins directly via a HESI-II ion source into a Q Exactive Plus (Thermo Fisher Scientific) mass spectrometer and obtain a minimum of three scans lasting 30 seconds. The scan parameters are: scan range 1,800 to 3,000 m/z without fragmentation; resolution 140,000; positive polarity; AGC target 3x106; maximum injection time 50 ms; spray voltage 4.0 kV; capillary temperature 275 °C; S-lens RF level (Hwang and Myong, 2014). We perform scan deconvolution using Mag Tran version 1.0.3.0 (Amgen).

Cross-linking of α-synuclein

We dissolve BS³ powder (Sigma Aldrich) in HEPES buffer (pH 7.18) to a concentration of 10 mM. We add the prepared BS³ solution to α-syn to a final concentration of 1 mM and incubate at 4 °C for 1.5 h with shaking at 600 rpm. We quench the cross-linking reaction by the addition of 20 mM ammonium bicarbonate for 20 min (Kalisman et al., 2012; Tayri-Wilk et al., 2019).

Preparation of samples for mass spectrometry

The proteins were precipitated in 1 mL of acetone (−80 °C) for one hour, followed by centrifugation at 14,000 g. The pellet was resuspended in 20 μL of 8 M urea. The urea was diluted by adding 200 μL of Digestion Buffer (25 mM Tris, pH=8.0; 10% Acetonitrile). We added 0.5 μg of trypsin (Promega) to the diluted urea and digested the protein overnight at 37 °C under agitation. Following digestion, the peptides were desalted on C18 stage-tips and eluted by 55% acetonitrile. The eluted peptides were dried in a SpeedVac, reconstituted in 0.1% formic acid, and measured in the mass spectrometer (Kaledhonkar et al., 2018).

Mass spectrometry

The samples were analyzed by a 120 minute 0-40% acetonitrile gradient on a liquid chromatography system coupled to a Q-Exactive HF mass spectrometer. The analytical column was an EasySpray 25 cm heated to 40 °C. The method parameters of the run were: Data-Dependent Acquisition; Full MS resolution 70,000 ; MS1 AGC target le6 ; MS1 Maximum IT 200 ms ; Scan range 450 to 1800 ; dd-MS/MS resolution 35,000 ; MS/MS AGC target 2e5 ; MS2 Maximum IT 600 ms ; Loop count Top 12; Isolation window 1.1 ; Fixed first mass 130 ; MS2 Minimum AGC target 800 ; Peptide match - off; Exclude isotope - on ; Dynamic exclusion 45 seconds. Each cross-linked sample was measured twice in two different HCD energies (NCE): 26, and stepped 25, 30, and 35. All cross-linked samples were measured with the following charge exclusion: unassigned,1,2,3,8,>8. Proteomics samples were measured with the following charge exclusion: unassigned,1,8,>8.

Identification of cross-links

The RAW data files from the mass spectrometer were converted to MGF format by Proteome Discoverer (Thermo). The identification of BS³ cross-links used a search application (FindXL) (Kalisman et al., 2012) that exhaustively enumerates all the possible peptide pairs. The search parameters were as follows: Sequence database- α-synuclein; Protease – trypsin, allowing up to three miscleavage sites; Variable modifications: methionine oxidation, lysine with hydrolyzed mono-link; Cross-linking must occur between two lysine residues; Cross-linker is never cleaved; MS/MS fragments to consider: b-ions, y-ions; MS1 tolerance – 6 ppm; MS2 tolerance – 8 ppm; Cross-linker mass – one of three possible masses: 138.0681, 138.0681 + 1.00335, and 138.0681 + 2.0067. The three masses address the occasional incorrect assignment of the mono-isotopic mass by the mass spectrometer.

We combine the XL-MS results obtained here using BS³ crosslinker (performed as a triplicate of experiments) with those based on other crosslinkers (ABAS, SDA, TATA, CBDPS, and EDC) from the work of Brodie et al (Brodie et al., 2019). To use XL-MS data to validate our predicted conformational ensemble, we calculate the distances between the crosslinked residues for all the simulated structures in each cluster and compare these distance distributions with the maximum length of the corresponding crosslinker. Structures with distances smaller than the maximum crosslinker length are validated by the corresponding crosslinker and we calculate the proportions of these validated structures in each cluster.

Far-UV circular dichroism of α-synuclein

We measure the far-UV CD spectrum of 10 μM wild type α-syn in HEPES buffer (pH 7) at 25 °C in a CD spectrometer (J-1100ST, Jasco, Japan). We perform secondary structure estimation using Spectra Manager 2 (Jasco, Japan) in triplicate.

Single-molecule protein-induced fluorescence enhancement

Experimental setup

We perform single-molecule protein-induced fluorescence enhancement (smPIFE) (Hwang and Myong, 2014; Hwang et al., 2011; Jeong et al., 2016; Lerner et al., 2016; Morten et al., 2015; Ploetz et al., 2016) experiments using a confocal-based setup (ISS™, USA) assembled on top of an Olympus IX73 inverted microscope stand. We use a pulsed picosecond fiber laser (λ=532 nm, pulse width of 100 ps FWHM, operating at 20 MHz repetition rate and 150 μW measured at the back aperture of the objective lens) for exciting the sulfo-Cy3 (sCy3) dye (FL-532-PICO, CNI, China). The laser beam pass through a polarization-maintaining optical fiber and is then further shaped by a linear polarizer and a half-wave plate. A dichroic beam splitter with high reflectivity at 532 nm (ZT532/640rpc, Chroma, USA) reflect the light through the optical path to a high numerical aperture (NA) super Apo-chromatic objective (60X, NA=1.2, water immersion, Olympus, Japan), which focuses the light onto a small confocal volume. The microscope collects the fluorescence from the excited molecules through the same objective, and focuses it with an achromatic lens (f = 100 mm) onto a 100 μm diameter pinhole (variable pinhole, motorized, tunable from 20 μm to 1 mm), and then re-collimates it with an achromatic lens (f = 100 mm). We further filter the fluorescence from other light sources (transmitted scattering) with a 585/40 nm band-pass filter (FF01-585/40-25, Semrock Rochester NY, USA) and detect it using a hybrid photomultiplier (Model R10467U-40, Hamamatsu, Japan), routed through a 4-to-1 router to a time-correlated single photon counting (TCSPC) module (SPC-150, Becker & Hickl, GmbH) as its START signal (the STOP signal is routed from the laser controller). We perform data acquisition using the VistaVision software (version 4.2.095, 64-bit, ISS™, USA) in the time-tagged time-resolved (TTTR) file format. After acquiring the data, we transform it into the photon HDF5 file format (Ingargiola et al., 2016a) for easy dissemination of raw data to the public.

Preparation of sCy3-labeled α-synuclein

Sulfo-Cy3 (sCy3; Invitrogen) linked to the maleimide thiol-reactive group, is coupled specifically to single cysteine residues in α-syn mutants via thiol coupling reaction. We reduce the thiols of cysteine residues in α-syn mutants by 2 mM DTT (Sigma) for 1 hour at room temperature. Then, we remove DTT with two rounds of dialysis, first round against buffer A and the second one against 50 mM HEPES pH7.2, 2 mM EDTA, using dialysis bags with 3 kDa MWCO. We further activate the cysteine thiols by 50 μM Tris(2-carboxyethyl)phosphine hydrochloride (TCEP, Sigma) for an hour at room temperature. Then, we add the sCy3 dye to the protein at a molar ratio of 5:1 (dye:protein). We stir the reaction mixtures for five hours at room temperature in the dark. Then, we terminate the reaction by adding 2 mM DTT. We remove excess dyes from the solution via three rounds of dialysis against buffer A using dialysis bags with 3 kDa MWCO. Afterwards, we further purify the dye-labeled α-syn using a size exclusion column HiTrap Desalting 5 mL x 5. We assess the concentration of pure labeling products by measuring the absorption of the dye (sCy3 with an absorption coefficient of 162,000 M⁻¹cm⁻¹). Then, we further characterize the labeling products by 12 % SDS-PAGE gels based on molecular mass.

Measurement

We add 100 μL samples containing 25 pM sCy3-labeled α-syn in measurement buffer (10 mM Tris, 1 mM EDTA, pH 8, 50 mM NaCl, 10 mM cysteamine, and 1 mM (±)-6-Hydroxy-2,5,7,8-tetramethylchromane-2-carboxylic acid, TROLOX) to a microscopy well (μ-Slide 18 Well, Ibidi, GmbH), first rinsed with 1 mg/mL BSA, and then sealed with the microscopy well cover. Data acquisition lasts 1-2 hours per sample. The measured samples include α-syn V26C, Y39C, or A56C mutants labeled with sCy3, as well as sCy3-labeled ssDNA and dsDNA (the lacCONS promoter with its template labeled with sCy3 linked to either register −1, +2 or +6)(Lerner et al., 2016; Ploetz et al., 2016).

Single-molecule burst analysis

We analyze all photon HDF5 files carrying photon timestamps using the FRETbursts software (Ingargiola et al., 2016b), by first estimating the background rate per each 30 second of the measurement. Then, by using the sliding window algorithm (Eggeling et al., 1998; Fries et al., 1998; Ingargiola et al., 2017), we identify single-molecule photon bursts as having instantaneous photon rates larger than F (=6) times the background rate. We further select the identified bursts for having more than 20 photons. We store the burst data (e.g. burst sizes, widths/durations, separation times between consecutive bursts, background counts). We use the photon detection times relative to the moment of excitation (the photon nanotimes) of each single-molecule burst, to calculate the mean nanotimes of single-molecule bursts, which is equivalent to the average intrinsic fluorescence lifetime, and is referred to in the text as the burst average lifetime. We calculate it as the algebraic average of all photon nanotimes in the burst, that are higher than a minimal time threshold (the time beyond which the impulse response function, IRF, ends, and the fluorescence decay becomes exponential), and subtracted from that minimal time threshold. We use histograms of burst average lifetime to exhibit the subpopulations based on the fluorescence lifetime of sCy3.

We use the separation times between consecutive bursts, termed the burst separation times, to distinguish between consecutive bursts of two different molecules (times inversely dependent on the concentration; seconds in these measurements), and consecutive bursts of the same molecule recurring back in the confocal spot (times independent of concentration and depend only on the diffusion coefficient; milliseconds in these measurements). Inspired by the concepts behind burst recurrence analysis used in assessing conformational dynamics in single-molecule Förster resonance energy transfer (smFRET) experiments (Hoffmann et al., 2011), we report on dynamics of the sCy3 fluorescence lifetime in the following manner: the burst average lifetimes of pairs of consecutive bursts separated by less than 100 ms are compared, to qualitatively report on transitions that occur between lifetime subpopulations within 100 ms.

QUANTIFICATION AND STATISTICAL ANALYSIS

We perform CD experiments in triplicate. The average values with standard errors for each secondary structure are plotted. To determine if the structures with the lowest RMSD to the corresponding subunit in 1XQ8 and 6A6B are significant or not, we calculate the p values between the lowest RMSD and the RMSD values for all the simulated structures using one-sided Student’s t tests.

Supplementary Material

Table S4

Cross-linking data used to verify predicted conformational ensemble of α-syn, Related to Figure 3.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial strains
BL21(DE3) Singles™ Competent Cells - Novagen	Sigma-Aldrich	Cat#70235-M
MAX Efficiency™ DH5α Competent Cells	ThermoFisher	Cat#18258012
Chemicals, peptides, and recombinant proteins
Tris-HCl	Sigma-Aldrich	Cat#93363
Isopropyl β-d-1-thiogalactopyranoside (IPTG)	Sigma-Aldrich	Cat#I5502
Ethylenediaminetetraacetic acid (EDTA)	Sigma-Aldrich	Cat#E5134
Dithiothreitol (DTT)	Sigma-Aldrich	Cat#43815
Magnesium chloride	Sigma-Aldrich	Cat#63068
Streptomycin sulfate	Sigma-Aldrich	Cat#S9137
Ammonium sulfate	Sigma-Aldrich	Cat#A4418
Fast SeeBand staining solution	Gene Bio-Application	Cat#SB050
HEPES	Sigma-Aldrich	Cat#54457
TCEP	Sigma-Aldrich	Cat#75259
Sulfo-Cy3 maleimide	Abcam	Cat#ab146493
Cysteamine	Sigma-Aldrich	Cat#30070
6-Hydroxy-2,5,7,8-tetramethylchroman-2-carboxylic acid (TROLOX)	Sigma-Aldrich	Cat#238813
Deposited data
Mass spectrometry proteomics data	This paper	PRIDE: PXD024671
α-Synuclein ensemble structure	This paper	PDB-Dev: PDBDEV_00000082
smPIFE analyses and raw data	This paper	Zenodo: DOI 10.5281/zenodo.4081424
Additional simulation data of α-synuclein monomer	This paper	Zenodo: DOI 10.5281/zenodo.4444069
Micelle-bound α-synuclein	Ulmer et al. (2005)	PDB: 1XQ8
Cryo-EM structure of α-synuclein fiber	Li et al. (2018)	PDB: 6A6B
Structure of α-synuclein fibrils	Tuttle et al. (2016)	PDB: 2N0A
α-Synuclein filament structure from multiple system atrophy	Schweighauser et al., (2020)	PDB: 6XYP
Oligonucleotides
Forward Primer 5’-AAAGAGGGTGTTCTCTATGTAGGCTCCAAA ACC-3’	Integrated DNA Technologies (IDT)	N/A
Reverse Primer 5’-GGTTTTGGAGCCTACATAGAGAACACCCTCTTT-3’	Integrated DNA Technologies (IDT)	N/A
Recombinant DNA
αSyn V26C - pT7-7 plasmid	Gift from Dr. Elisha Haas Lab (See Acknowledgments)	N/A
αSyn Y39C- pT7-7 plasmid	Gift from Dr. Elisha Haas Lab (See Acknowledgments)	N/A
αSyn A56C - pT7-7 plasmid	Gift from Dr. Elisha Haas Lab (See Acknowledgments)	N/A
Wt αSyn - pT7-7 plasmid	Gift from Dr. Elisha Haas Lab (See Acknowledgments)	N/A
Software and algorithms
DMD software	Molecules in Action, LLC	http://moleculesinaction.com
GROMACS package	Abraham et al. (2015)	http://www.gromacs.org/
PyMOL (version 2.3.0)	Schrodinger LLC. The PyMOL Molecular Graphics System, Version 2.3.0	https://pymol.org/2/#download
TTClust software	Tubiana et al. (2018)	https://github.com/tubiana/TTClust
Ward linkage algorithm from TTClust	Tubiana et al. (2018)	https://github.com/tubiana/TTClust
Metropolis algorithm	Ding et al. (2008)	http://moleculesinaction.com
Medusa force field	Yin et al. (2008)	http://moleculesinaction.com
Contact Map Explorer	GNU LGPL, version 2.1	https://contact-map.readthedocs.io/en/latest/examples/nb/contact_map.html
FRETbursts software	Ingargiola et al. (2016b)	http://tritemio.github.io/FRETBursts/
Other
Dialysis bags - MEGA GeBaFlex-tube	Gene Bio-Application	Cat#MEGA320
MonoQ column	Sigma-Aldrich	Cat#54807
Amicon® Ultra-15 Centrifugal Filter Units	Merc	Cat#C7715cutoff: 100 kDa
HiTrap Desalting 5 mL	Sigma-Aldrich	Cat#GE17-1408
Rinse a μ-slide 18 (Ibidi)	Ibidi	Cat#81816
0.5 mL Protein LoBind tube	Sigma-Aldrich	Cat#EP0030108094
Presto™ Mini Plasmid Kit	Geneaid	Cat#PDH300

Highlights.

• trFRET-guided DMD simulations is used to study α-synuclein monomer conformations

• Multifunctions of α-synuclein are explained by its monomeric structures

• Millisecond conformational dynamics of α-synuclein monomer is discovered by smPIFE