Bipartite graph-based approach for clustering of cell lines by gene expression–drug response associations

Abstract

Motivation

In pharmacogenomic studies, the biological context of cell lines influences the predictive ability of drug-response models and the discovery of biomarkers. Thus, similar cell lines are often studied together based on prior knowledge of biological annotations. However, this selection approach is not scalable with the number of annotations, and the relationship between gene–drug association patterns and biological context may not be obvious.

Results

We present a procedure to compare cell lines based on their gene–drug association patterns. Starting with a grouping of cell lines from biological annotation, we model gene–drug association patterns for each group as a bipartite graph between genes and drugs. This is accomplished by applying sparse canonical correlation analysis (SCCA) to extract the gene–drug associations, and using the canonical vectors to construct the edge weights. Then, we introduce a nuclear norm-based dissimilarity measure to compare the bipartite graphs. Accompanying our procedure is a permutation test to evaluate the significance of similarity of cell line groups in terms of gene–drug associations. In the pharmacogenomic datasets CTRP2, GDSC2 and CCLE, hierarchical clustering of carcinoma groups based on this dissimilarity measure uniquely reveals clustering patterns driven by carcinoma subtype rather than primary site. Next, we show that the top associated drugs or genes from SCCA can be used to characterize the clustering patterns of haematopoietic and lymphoid malignancies. Finally, we confirm by simulation that when drug responses are linearly dependent on expression, our approach is the only one that can effectively infer the true hierarchy compared to existing approaches.

Availability and implementation

Bipartite graph-based hierarchical clustering is implemented in R and can be obtained from CRAN: https://CRAN.R-project.org/package=hierBipartite. The source code is available at https://github.com/CalvinTChi/hierBipartite. The datasets were derived from sources in the public domain, which are the Cancer Cell Line Encyclopedia (https://portals.broadinstitute.org/ccle), the Cancer Therapeutics Response Portal (https://portals.broadinstitute.org/ctrp.v2.1/?page=#ctd2BodyHome), and the Genomics of Drug Sensitivity in Cancer (https://www.cancerrxgene.org/). These datasets can be downloaded using the PharmacoGx R package (https://bioconductor.org/packages/release/bioc/html/PharmacoGx.html).

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Building predictive models of drug response from genomic profiles has been one of the long-standing goals in precision medicine (Adam et al., 2020). High throughput technologies has enabled researchers to perform genomic profiling and measure candidate drug sensitivities in vitro, resulting in pharmacogenomic datasets such as the NCI-60 drug sensitivity database (Shoemaker, 2006), the Cancer Cell Line Encyclopedia (CCLE) (Ghandi et al., 2019) dataset, the Cancer Therapeutics Response Portal (CTRP2) dataset (Seashore-Ludlow et al., 2015) and the Genomics of Drug Sensitivity in Cancer (GDSC2) dataset (Iorio et al., 2016). A standard pharmacogenomic dataset contains drug sensitivity measurements accompanied by genomic data modalities such as gene expression, copy number variation and DNA methylation, all measured in human tumor cell lines. These cell lines usually represent a diversity of malignancies, and are annotated with their biological contexts such as primary site (site of origin), histology, histology subtype.

A major challenge to predicting drug response from genomic data is conditioning on the right biological context, such as the choice of histology subtypes. Gene expression patterns and their associations with drug response are highly context-dependent (Barretina et al., 2012; Ghandi et al., 2019; Ross et al., 2000), and tissue and histology contexts have been shown to be predictive of drug sensitivity (Mannheimer et al., 2019; Yao et al., 2018). Barretina et al. demonstrated that drug response models built with only melanoma cell lines outperformed that built with all cell lines (Barretina et al., 2012). Biological context also influences gene–drug associations, from which discoveries of biomarkers and drug mechanisms of action are made (Rees et al., 2016). However, restricting models to a specific context may be overly conservative because closely related cell lines could potentially be pooled together, such as those from breast and ovarian cancers (Network et al., 2011). On the other hand, grouping diseases based on prior knowledge alone is not scalable with the number of annotations, and the relationship between gene–drug association patterns and biological context may not always obvious. Thus, a new dissimilarity measure based on gene–drug association patterns can allow investigation of the relationship between cell line groups based on biological context.

A few works have developed cell line context-aware models that pool information from similar cell lines to predict drug response. Zhang et al. (2015) modeled response for a drug, cell line pair as the sum of responses from other cell lines to the drug and the sum of responses to other drugs from the cell line. Contributions to the response are weighted by similarity to the cell line of interest and similarity to the drug of interest. Since the focus of this approach is on modeling drug response, it does not explicitly provide insight on similarity between cell lines in terms of gene–drug association patterns. Chen et al. developed a contextual heterogeneity enabled regression (CHER) method that learns a set of weights from all cell lines and a set of weights from context-specific cell lines (Chen et al., 2015). However, this approach still requires some degree of prior knowledge on which biological contexts are similar enough to include in the CHER.

On the other hand, a few methods have been developed for clustering cell lines based on multiple data modalities (e.g. expression and drug sensitivity) from pharmacogenomic datasets. Among these methods are cluster of cluster assignments (COCA), integrative clustering (iCluster) and two-way latent structure model (TWL) (Hoadley et al., 2014; Mo et al., 2013; Shen et al., 2009; Swanson et al., 2019). COCA clusters cell lines in two stages—first clustering each data modality separately, then clustering the combined cluster assignments. Both iCluster and TWL are Bayesian latent variable models. In iCluster, a joint latent variable is learned from all data modalities, assuming a common clustering across data sources. Unlike iCluster, TWL finds a clustering for each data modality while allowing cluster information to be shared. However, none of these approaches explicitly model gene–drug associations as a basis for clustering cell lines.

In this article, we present a dissimilarity measure to provide insight on which biological contexts are similar in terms of gene–drug association patterns. In the rest of the article, we assume diseases are the biological context of interest, as is typically the case. Using this dissimilarity measure, unsupervised learning can be applied for purposes such as visualization of disease similarities or deciding which diseases to include in a drug response model. For cell lines of a given disease, we start by modeling the gene–drug association patterns as a weighted undirected bipartite graph. In this bipartite graph, one disjoint set of vertices represents genes and the other represents drugs, with weighted edges in-between describing their association patterns. Edge weights are derived from sparse canonical correlation analysis (SCCA), which solves for a linear combination of genes and drugs such that the Pearson correlation between the combination of genes and drugs is maximized (Lee et al., 2011). Finally, we introduce a nuclear norm-based dissimilarity measure to compare edge weights (or equivalently bipartite graphs) from different cell line groups. Given a set of diseases, the outcome is a dissimilarity matrix. In addition, we provide a subsampling procedure to improve robustness in modeling the gene–drug associations, and a permutation test for determining the statistical significance of similarity in gene–drug associations from different groups of cell lines.

We evaluate this dissimilarity measure on the CTRP2, GDSC2 and CCLE pharmacogenomic datasets, choosing to study the association patterns between expression and drug sensitivity, because expression is strongly predictive of drug sensitivity (Aben et al., 2016; Parca et al., 2019). With hierarchical clustering as our unsupervised learning algorithm of choice, we show that our dissimilarity measure leads to clusters revealing biological insight distinct from those based on existing clustering approaches that also integrate expression and drug sensitivity data. Next, we show how SCCA coefficients can be used to characterize clustering patterns in terms of gene–drug association patterns. Finally, we demonstrate that when drug sensitivity is linearly dependent on expression by simulation, that clustering based on our dissimilarity measure is the only approach that effectively infers the true hierarchy, compared to existing approaches.

2 Overview of proposed approach

We describe the data structures involved and set up mathematical notation for the rest of the article. Assume we are interested in identifying the associations between p genes and d drugs, based on gene expression matrix $X\in {\mathbb{R}}^{n\times p}$ and drug sensitivity matrix $Y\in {\mathbb{R}}^{n\times d}$ of n cell lines. The annotated biological context (e.g. histology subtype) induces a partitioning of the cell lines into G groups. Let the expression and drug sensitivity submatrices of the n_g cell lines in group g be denoted by $X^{[g]}\in {\mathbb{R}}^{n_g\times p}$ and $Y^{[g]}\in {\mathbb{R}}^{n_g\times d}$ respectively, and assume each of these columns have been standardized with respect to the n_g cell lines. Thus, $X=\{X^{[1]},\dots ,X^{[G]}\}$ and $Y=\{Y^{[1]},\dots ,Y^{[G]}\}$ is another way to denote the entire dataset based on G groups of cell lines.

For any pair of submatrices $(X^{[g]},Y^{[g]})$ from group g, SCCA solves for canonical vectors $a\in {\mathbb{R}}^p$ and $b\in {\mathbb{R}}^d$ to specify sparse linear combinations of columns from $X^{[g]}$ and columns from $Y^{[g]}$ to maximize Pearson correlation $\mathit{Corr}(X^{[g]}a,Y^{[g]}b)$. The linear combinations $X^{[g]}a,Y^{[g]}b$ are sometimes referred to as canonical variates. For the bipartite graph describing the associations between columns of $X^{[g]}$ and columns of $Y^{[g]}$, its edge weight matrix is constructed as the cross product $B=a\otimes b$. Entry $B_{ij}\in \mathbb{R}$ describes both the direction and magnitude of association between gene i and drug j. This modeling of association patterns between two sets of features as a bipartite graph is illustrated in Figure 1A.

Fig. 1.

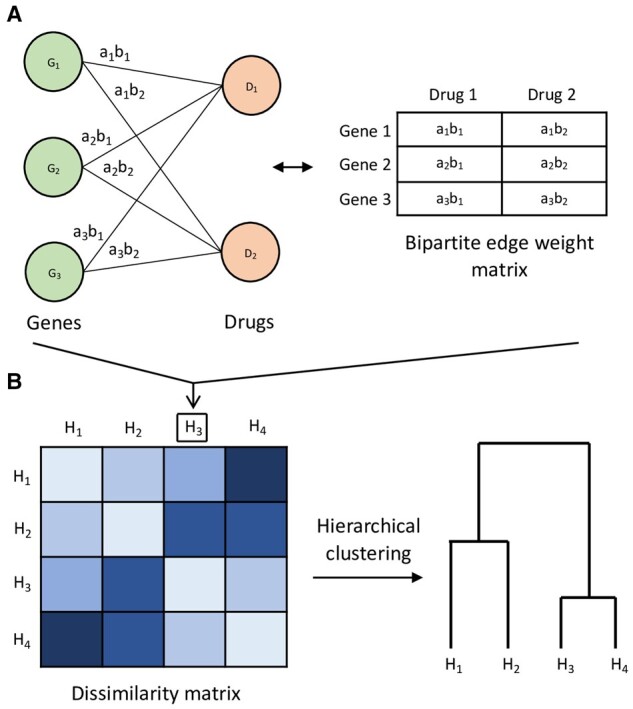
Overview of proposed approach illustrated with toy example of cell line groups $H_1,H_2,H_3,H_4$, each with genes $G_1,G_2,G_3$ and drugs D₁, D₂. (A) For example cell line group H₃, its gene–drug association patterns are modeled as a bipartite graph of gene vertices and drug vertices, with edges weighted by association strength. The edge weight between gene i and drug j is defined as $a_i{b}_j$, where a_i, b_j are elements of SCCA canonical vectors $a\in {\mathbb{R}}^3$ and $b\in {\mathbb{R}}^2$. The bipartite graph can equivalently be represented by its edge weight matrix. This modeling of gene–drug association patterns is repeated for $H_1,H_2,H_4$. (B) Using the nuclear norm-based dissimilarity measure between bipartite graphs, a matrix of dissimilarities is computed for all the cell line groups, and hierarchical clustering can be applied as an example unsupervised analysis

We then introduce a nuclear norm-based dissimilarity measure $\mathcal{D}(·,·)$ to compare a given pair of edge weight matrices (or equivalently the bipartite graphs they represent). From this we can construct a dissimilarity matrix for the G groups of cell lines, and apply an unsupervised learning algorithm such as hierarchical clustering. This is depicted in Figure 1B.

3 Materials and methods

3.1 Review of sparse canonical correlation analysis

Building upon the example from Rees et al. of using Pearson correlation to identify drug response-associated biomarkers (Rees et al., 2016), we use SCCA to identify associated genomic features and drug responses. SCCA is a penalized extension of canonical correlation analysis (CCA) developed by Hotelling (Harold, 1936). Since CCA is not scale invariant, assume each feature in X, Y is centered and scaled to variance one. In high throughput genomics data, p and sometimes d are typically much larger than n and the subset of relevant biomarkers is often small. Hence, we impose sparsity on a, b by adopting the following diagonal penalized CCA criterion developed by Witten et al. (2009), which treats sample covariance matrices $S_{XX}\in {\mathbb{R}}^{p\times p}$ and $S_{YY}\in {\mathbb{R}}^{d\times d}$ as diagonal and relaxes equality constraints for convexity

$$\begin{array}{c}\underset{a\in {\mathbb{R}}^p,b\in {\mathbb{R}}^d}{\max }{a}^{\top }{X}^{\top }Yb\hfill \\ \left|\right|a|{|}_2\le 1,|\left|b\right|{|}_2\le 1\hfill \\ p_1(a)\le c_1,p_2(b)\le c_2,\hfill \end{array}$$ (1)

where p₁ and p₂ are convex penalty functions, and c₁ and c₂ are hyperparameters that control the degree of regularization. In our application, the ${\ell }_1$ penalty is chosen as $p_1(·)=p_2(·)=\left|\right|·|{|}_1$ to induce sparse regularization (Tibshirani, 1996), and c₁ and c₂ are selected as values maximizing the objective function in Equation 1 based on k-fold cross validation. In our empirical applications, both c₁ and c₂ are searched over values in {1, 2, 3} respectively, and k = 5 for cross validation. Zero entries in a, b suggest that the corresponding genes and drugs are not associated with each other. Conversely, when the magnitudes of entries a_i, b_j for gene i and drug j respectively are large, then gene i and drug j are interpreted as strongly associated with each other. We adopt the modified NIPALS algorithm originally proposed by Lee et al. (2011) and re-implemented by Wang et al. (2015) to solve the above optimization, which is reported to have superior empirical performance than the algorithm proposed by Witten et al. (2009).

3.2 Dissimilarity measure

We introduce a nuclear norm-based dissimilarity measure to compare bipartite edge weights between a given pair of cell line groups. From canonical vectors $a\in {\mathbb{R}}^p,b\in {\mathbb{R}}^d$ solved by SCCA for a group, we form its bipartite edge weight matrix $B\in {\mathbb{R}}^{p\times d}$ as the outer product $B=a\otimes b$. Entry $B_{ij}=a_i{b}_j$ reflects the direction and magnitude of association between gene i and drug j, with negative values (e.g. a_i > 0 and b_j < 0) indicating negative association, and positive association otherwise. The dissimilarity measure between a given pair of bipartite edge weight matrices $B^{[u]}$ and $B^{[v]}$ from groups u and v respectively is based on the nuclear norm, and is defined aS  

$$\mathcal{D}(B^{[u]},B^{[v]})=\frac{\sum _i{\sigma }_i(B^{[u]}-B^{[v]})}{\sum _i{\sigma }_i(B^{[u]})+\sum _i{\sigma }_i(B^{[v]})}.$$ (2)

The denominator term normalizes the dissimilarity measure to range in $[0,1]$, and ${\sigma }_i(A)$ denotes the ith singular value of matrix A. This dissimilarity measure is based on the nuclear norm because it comprised singular value summation terms $\left|\right|A|{|}_{*}={\sum }_{i=1}^r{\sigma }_i(A)$, which is defined as the nuclear norm of matrix A with rank r. Mathematically, the nuclear norm is the convex envelope of the rank function Rank(A), meaning $\left|\right|A|{|}_{*}$ satisfies $\mathit{Rank}(A)\ge \frac{1}{M}\left|\right|A|{|}_{*}$ for all $A\in \{A\hspace{0.17em}\hspace{0.17em}|\hspace{0.17em}\hspace{0.17em}\left|\right|A\left|\right|\le M\}$ (Fazel et al., 2001).

To justify Equation 2, if $B^{[u]}$ and $B^{[v]}$ are similar, then any meaningful matrix structure in $B^{[u]}$ and $B^{[v]}$ becomes deficient in $B^{[u]}-B^{[v]}$, and the matrix difference resembles a noise matrix. If we assume noise matrices tend to have small norm (e.g. Frobenius norm), then $\left|\right|B^{[u]}-B^{[v]}|{|}_{*}$ will tend to be small as well because $\left|\right|A|{|}_{*}\le \sqrt{r}|\left|A\right|{|}_F$ holds for any matrix $A\in {\mathbb{R}}^{m\times n}$ of rank r (see Supplementary Methods for proof).

3.3 Hierarchical clustering

With the dissimilarity measure in Equation 2, one can construct a dissimilarity matrix $D\in {\mathbb{R}}^{G\times G}$ for G cell line groups, from which unsupervised analysis can be directly applied with an unsupervised algorithm of choice. In this article, we choose hierarchical clustering with Ward’s minimum variance criterion as the link function to determine the hierarchical structure among the groups. The permutation test can be used to evaluate whether two clusters at a non-leaf node of the dendrogram should be pooled together due to having similar gene–drug association patterns (details in Section 3.4).

The process starts with computing bipartite edge weight matrices $B^{[1]},\dots ,B^{[G]}$ for each group using SCCA. To improve robustness, we provide an optional subsampling procedure to produce a bipartite edge weight matrix that is instead the element-wise average of edge weight matrices, each computed using a random subsample of cell lines. This procedure produces more robust matrices $B^{[1]},\dots ,B^{[G]}$, although at greater computational cost. The subsampling procedure is summarized by Algorithm 1.

After matrices $B^{[1]},\dots ,B^{[G]}$ have been computed, the dissimilarity measure in Equation 2 is applied to all $\Theta (G^2)$ pairs of matrices to generate dissimilarity matrix $D\in {\mathbb{R}}^{G\times G}$, upon which hierarchical clustering can be applied. This entire process is summarized by Algorithm 2.

Algorithm 1 Robust bipartite edge weight matrix

1. procedure  Robust_matrix($(X^{[g]},Y^{[g]})$, m, f)

2.  Initialize $B=0\in {\mathbb{R}}^{p\times d}$

3. for i = 1 to m do

4.  Subsample f fraction of cell lines to produce ${\widehat{X}}^{[g]},{\widehat{Y}}^{[g]}$

5.  $a,b=\mathtt{SCCA}({\widehat{X}}^{[g]},{\widehat{Y}}^{[g]})$

6.  $B:=B+(a\otimes b)$

7.  Output $\frac{1}{m}B$

Algorithm 2 Unsupervised analysis

1. procedure  Hierarchical_clustering($(X^{[1]},Y^{[1]}),\dots ,(X^{[G]},Y^{[G]})$)

2. for i = 1 to G do

3.  Compute $B^{[i]}$ from $(X^{[i]},Y^{[i]})$ using $\mathtt{SCCA}(·,·)$

4.  Construct dissimilarity matrix $D\in {\mathbb{R}}^{G\times G}$

5.  Output hierarchical clustering result

3.4 Permutation test

At a given non-leaf node of the dendrogram, should cell lines from the two branches be pooled together for a drug response model? While prior biological knowledge can be informative, we provide a permutation test to help guide this decision. Between any two groups of cell lines u and v, the null and alternate hypotheses are

$$H_0:\text{No}\hspace{0.17em}\text{shared}\hspace{0.17em}\text{gene}-\text{drug}\hspace{0.17em}\text{relationship}\hspace{0.17em}\text{between}\hspace{0.17em}u\hspace{0.17em}\text{and}\hspace{0.17em}v.$$ (3)

 

$$H_1:\text{There}\hspace{0.17em}\text{are}\hspace{0.17em}\text{shared}\hspace{0.17em}\text{gene}-\text{drug}\hspace{0.17em}\text{relationships}\hspace{0.17em}\text{between}\hspace{0.17em}u\hspace{0.17em}\text{and}\hspace{0.17em}v.$$ (4)

To generate a null distribution of dissimilarities, we permute the ordering of cell lines (rows) in $X^{[u]}$ while keeping the cell line order in $Y^{[u]}$ fixed, thus breaking the gene–drug association patterns in group u. The same procedure is applied to group v. Since all biological gene–drug association patterns in both groups are broken, the association patterns common to groups u and v are broken as well. Repetition of the described procedure generates a null distribution of dissimilarities. This whole process is summarized in Algorithm 3.

Algorithm 3 Permutation test.

1. procedure  P-value($(X^{[u]},Y^{[u]}),\hspace{0.17em}(X^{[v]},\hspace{0.17em}{Y}^{[v]})$, m)

2. Initialize empty array $\mathtt{D}[·]$ of length m

3. for i = 1 to m do

4. Permute rows of $X^{[u]}$ to produce ${\tilde{X}}^{[u]}$

5. Permute rows of $X^{[v]}$ to produce ${\tilde{X}}^{[v]}$

6. $a^{[u]},b^{[u]}=\mathtt{SCCA}({\tilde{X}}^{[u]},Y^{[u]})$

7. $a^{[v]},b^{[v]}=\mathtt{SCCA}({\tilde{X}}^{[v]},Y^{[v]})$

8. $B^{[u]}=a^{[u]}\otimes b^{[u]}$

9. $B^{[v]}=a^{[v]}\otimes b^{[v]}$

10. $\mathtt{D}[i]=\mathcal{D}(B^{[u]},B^{[v]})$

11. Output $\mathtt{D}[·]$

The P-value is defined as the proportion of null dissimilarities less than or equal to the observed dissimilarity

$$\mathit{P}\text{value}=\frac{\sum _{i=1}^{m}1(d_i\le d_{\mathit{obs}})}{m},$$ (5)

where d_obs is the observed dissimilarity and d_i is the null dissimilarity from permutation i, out of m permutations. We should expect a low P-value when there are shared gene–drug association patterns between groups u and v because most null dissimilarities should be greater than the observed dissimilarity. In our implementation, we perform this test at each successive node in the dendrogram in a bottom-up fashion, until a P-value greater than a pre-defined threshold (e.g. P-value > 0.10) is encountered. We perform early stopping of P-value generation because once we have a pooling of cell lines from groups sharing little gene–drug associations, any further merging with other groups will no longer be meaningful as well. Note the permutation tests are performed after the dendrogram is generated.

3.5 Pharmacogenomic datasets

We test our approach in expression and drug sensitivity data from the CCLE, GDSC2 and CTRP2 pharmacogenomic datasets (Ghandi et al., 2019; Iorio et al., 2016; Seashore-Ludlow et al., 2015). CCLE and GDSC2 provide expression data for 55 000 transcripts and 24 000 genes respectively. We use CTRP2 only for its drug sensitivity dataset, whose cell lines are matched with those from CCLE. The datasets GDSC2 and CTRP2 are responsible for the majority of drug sensitivity data in this study. Drug sensitivity is expressed as the area over dose–response curve and expression is measured in ${\hspace{0.17em}\text{log}\hspace{0.17em}}_2\text{TPM}$, where TPM stands for transcripts per million, a normalized unit of transcript expression. Drugs with severe missingness were removed, followed by cell lines with severe missingness (details in Supplementary Methods). After processing the drug sensitivity datasets, each dataset has less than 1% values missing, and no drugs have more than 10% missing values across cell lines. The remaining missing values were median-imputed per drug.

For computational efficiency, we follow the example by Barretina et al. of pre-selecting transcripts whose expression is correlated with drug response (Barretina et al., 2012). Specifically, our processing steps for expression features are

1. Retain genomic features whose expression variance is within the 5th to 95th percentiles. This removes features that are either too uninformative, or features that potentially reflect tissue differences due to high variance.

2. Select the top 5000 transcripts by maximum absolute Pearson correlation with drug sensitivity. Specifically, if we let $x_i\in {\mathbb{R}}^n$ denote the ith genomic feature and $y_j\in {\mathbb{R}}^n$ denote the jth drug response vector, then we retain the top 5000 transcripts by ${\max }_j|\mathit{Corr}(x_i,y_j)|$.

The final number of drugs and cell lines are listed in Table 1.

Table 1.

Pharmacogenomic dataset sizes, in terms of number of candidate drugs and number of cell lines, after data processing

Dataset	Number of drugs	Number of cell lines
GDSC2	179	450
CTRP2	113	527
CCLE	20	493

3.6 Simulation

We simulate data to study the clustering behavior under the statistical model of a true linear relationship between gene expression and drug sensitivity. We compare our clustering approach against existing approaches, as well as study how the clustering results change with different simulation settings.

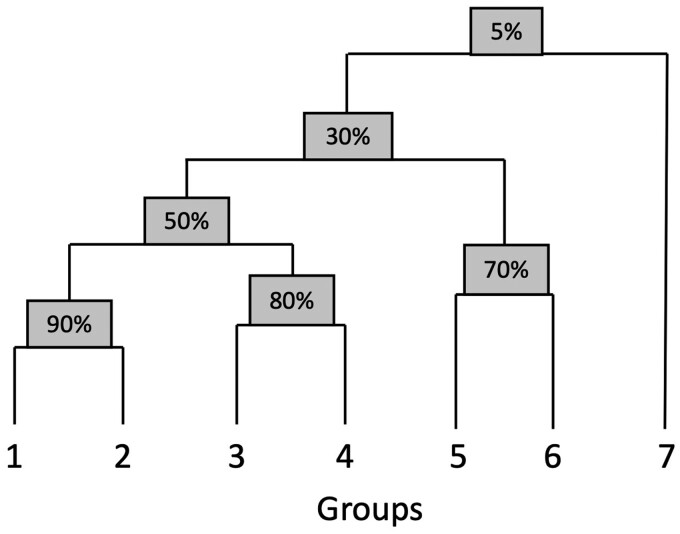
The overall setup is to simulate seven pairs of expression and drug sensitivity datasets with an imposed hierarchical structure, shown in Figure 2. The hierarchy is defined by the percentage of ‘biomarkers’ in common between the groups, where we define ‘biomarkers’ as the subset of all genes whose values contribute to drug sensitivity values. Similarly, only a subset of drugs are dependent on expression values in this simulation. For the sake of simplicity, the set of expression-dependent drugs is the same across all groups. Thus, each group is distinguished by its set of biomarkers, with its own expression covariance matrix. We simulate a given group according to the following statistical model:

Fig. 2.

Simulated hierarchy with percentage at each non-leaf node indicating percentage biomarkers shared between any group from left subtree and any group from right subtree (height not necessarily proportional to dissimilarity)

1. Generate genomic covariance matrix $\Sigma \in {\mathbb{R}}^{p\times p}$ for p genes, with only high correlation between the biomarkers. See Supplementary Methods for details on generating _Σ.

2. Generate each cell line expression as $X^{(i)}\sim \mathcal{N}(1_p,\Sigma )$ for $i=1,\dots ,n$, where $1_p\in {\mathbb{R}}^p$ is a vector of ones. We choose a mean of one so that the expected sensitivity value of an expression-dependent drug is non-zero (see step 4).

3. Initialize each drug response as noise $Y_{ij}\sim \mathcal{N}(0,s)$ for cell line i and drug j, with a pre-specified standard deviation s.

4. For each expression-dependent drug j, generate response from cell line i as $Y_{ij}:=Y_{ij}+{(X^{(i)})}^{\top }\beta$ where each ${\beta }_k\in \mathbb{R}$ is drawn independently and uniformly from the set $\{-3,-2,2,3\}$ if the kth transcript is a biomarker and ${\beta }_k=0$ otherwise.

In Figure 2, each non-leaf node in the tree shows the exact percentage of biomarkers in common between groups in the left subtree and groups in the right subtree. For example, according to Figure 2, groups 3 and 5 share 30% of their biomarkers, and groups 1 and 7 share 5% of their biomarkers. The coefficients of these shared biomarkers are the same, barring the slight perturbation described in the next paragraph.

To increase the simulation scale, we simulate multiple subgroups from each group’s Gaussian distribution and coefficient vector $\beta \in {\mathbb{R}}^p$, injecting noise between the subgroups by resampling coefficients for a random 5% of the biomarkers. Specifically, for a given group, we first generate and fix the Gaussian covariance matrix _Σ and coefficient vector $\beta \in {\mathbb{R}}^p$ according to steps above. Then for each subgroup, we generate $X\in {\mathbb{R}}^{n\times p}$ from $\mathcal{N}(1_p,\Sigma )$ and $Y\in {\mathbb{R}}^{n\times d}$ based on _β, where _β is slightly altered with a random 5% of the biomarker coefficients resampled from the set $\{-3,-2,2,3\}$. Thus, while every subgroup has the same ‘genes’ as biomarkers, their coefficients relating expression to drug sensitivity are slightly different. In this simulation, every group comprised five subgroups, each with n cell lines, p transcripts and d drugs.

We simulate all the groups according to the hierarchical structure in Figure 2 under multiple simulation settings. The first setting is a reference setting where the number of genes, drugs and cell lines in each subgroup are comparable to those in the pharmacogenomic datasets CTRP2 and GDSC2. In the second setting, we study the effect of decreasing the number of drugs, but keeping the percentage of expression-dependent drugs the same. This resembles the difference in availability of drugs between datasets CTRP2 and GDSC2 versus CCLE, which has the least number of drugs. The third setting studies the effect of increasing the sample size per subgroup. Finally, the fourth setting studies the effect of increasing drug sensitivity noise. These settings are summarized in Table 2.

Table 2.

Simulation settings

Setting	n	p	Biomarkers	d	expr-dependent drugs	s
1	20	2000	200	200	60	0.1
2	20	2000	200	20	6	0.1
3	100	2000	200	200	60	0.1
4	20	2000	200	200	60	1

Note: n, number of cell lines per subgroup; p, number of genes; d, number of drugs; expr-dependent, expression-dependent; s, baseline drug sensitivity standard deviation. The columns titled ‘biomarkers’ and ‘expr-dependent drugs’ contain number of biomarkers and number of expression-dependent drugs, respectively.

4 Results

We begin with a motivating application to the pharmacogenomic datasets CTRP2, GDSC2 and CCLE. Specifically, we test whether positive control groups created by randomly splitting primary site groups into two tend to merge together using the nuclear-norm based dissimilarity measure. The splitting was repeated 100 times to assess the proportion of times the positive controls merge. Moderate proportions may suggest primary site alone does not completely explain variation in gene–drug association patterns. All primary site groups in this experiment have sample sizes greater than 15 and Supplementary Table S1 lists the sample sizes per primary site for each dataset. The largest groups are used to generate the positive control groups, and they are skin and lung for CTRP2, and lung and haematopoietic and lymphoid tissue for both GDSC2 and CCLE.

Supplementary Figures S1–S3 show that the positive control groups merge with varying degrees of stability due to random splitting. While some positive controls merge close to 100% of the time, the CCLE lung groups merge only 60% of the time (Supplementary Fig. S3). While small sample sizes could be a contributing factor to instability, other contributing factors include heterogeneity due to the presence of multiple histology subtypes at a primary site. For example, the CCLE lung group comprises nine carcinoma subtypes, such as adenocarcinoma and squamous cell carcinoma. In Section 4.1, we investigate this further by testing if gene–drug association patterns appear to be driven more by histology subtype than site of origin in the context of carcinoma, one of the largest histology groups. In Section 4.2, we show how SCCA coefficients can be used to characterize the clustering patterns of haematopoietic and lymphoid malignancies using our dissimilarity measure. Finally, in Section 4.3 we study how factors such as sample size and drug sensitivity noise affect the performance of our method through simulation.

4.1 Bipartite graph-based clustering reveals unique biological insight

We test whether gene–drug association patterns are driven more by histology subtype than primary site in the context of carcinoma. In the former case, this means adenocarcinoma cell lines share similar gene–drug association patterns despite coming from different primary sites. We study the most prominent subtypes of squamous cell carcinoma, adenocarcinoma and ductal carcinoma in CTRP2, GDSC2 and CCLE. In the experimental setup, we group cell lines by both carcinoma subtype and primary site (e.g. adenocarcinoma, lung). Groups with less than five cell lines were removed, and the final sample size per group in each dataset is listed in Supplementary Table S2. We applied hierarchical clustering with the Ward link function based on our dissimilarity measure in Equation 2, including the subsampling procedure in Algorithm 1 ($m=100,f=0.90$). Then, permutation testing with 1000 permutations was applied, with a P = 0.10 early-stopping threshold.

Overall, the clustering results in Figure 3 suggest adenocarcinoma groups tend to have similar gene–drug association patterns. In all datasets, we observe two main clusters—one that is adenocarcinoma-dominant and one comprising the remaining groups. In the adenocarcinoma-dominant clusters from different datasets, many groups share significantly similar gene–drug association patterns (P-value $\le$ 0.05). P-values less than or equal to the early-stopping threshold of P = 0.10 are listed in Supplementary Tables S3–S5. The placement of ductal carcinoma in the adenocarcinoma-dominant cluster occurs in both CTRP2 and GDSC2. None of the groups in the non-adenocarcinoma cluster appear to share very similar gene–drug association patterns (P-value > 0.10). These results show that histology subtype could determine a cell line’s gene–drug association patterns more so than primary site, and could explain why some control primary site groups do not always merge directly.

Fig. 3.

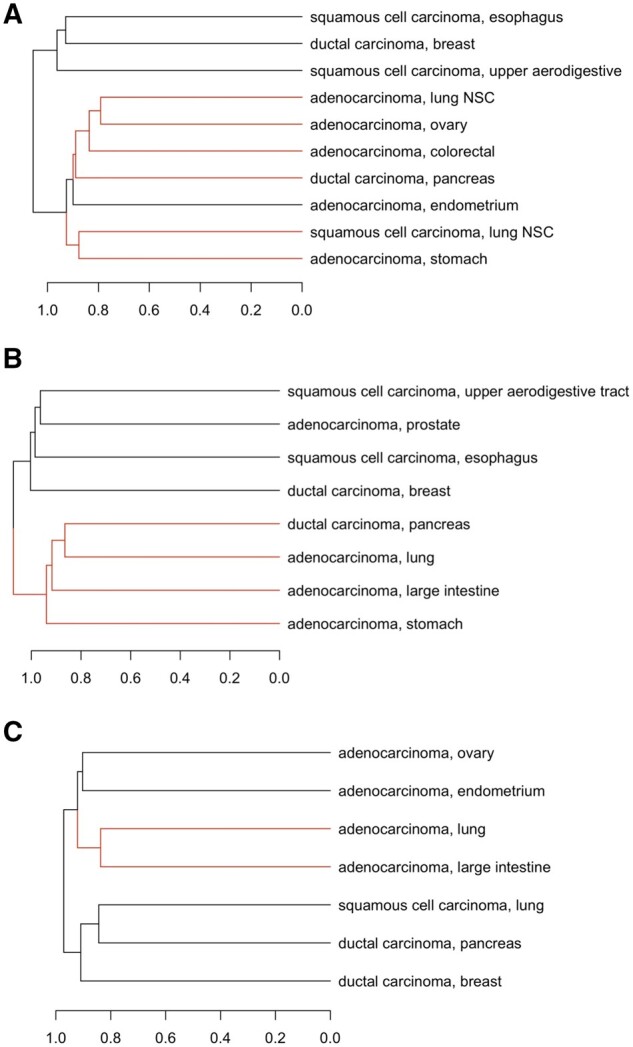
Bipartite graph-based clustering of cell line groups annotated with carcinoma subtype and primary site, for (A) CTRP2, (B) GDSC2 and (C) CCLE. Red branches highlight clusters with similar gene–drug associations according to the permutation test with P-value $\le$ 0.10. (NSC, non-small cell)

To assess the stability of this clustering result due to bootstrap resampling, we adapted an analysis similar to pvclust (Suzuki and Shimodaira, 2006). Clustering stability is measured with the proportion of times a cluster at each non-leaf node appears across b bootstrapped dendrograms, where b = 1, 000 in our experiment. A bootstrapped dendrogram is constructed by applying hierarchical clustering to the bootstrapped groups, which are generated by bootstrap resampling cell lines within each group. In contrast to the clustering in Figure 3, no subsampling was applied to generate the bipartite edge weight matrices for computational efficiency. Supplementary Figures S4–S6 show that the adenocaricnoma and non-adenocarcinoma clusters are only moderately stable, with bootstrap percentages ranging from 40% to 60% for CTRP2 and GDSC2. The CCLE clusters are not stable, with bootstrap percentages less than or equal to 23%. There are a few potential sources of instability. Given the small group sizes, the perturbation effect due to bootstrap resampling is likely enhanced since the probability of exclusion of a cell line from a bootstrap sample is approximately ${(1-1/n)}^n\approx 1/e\approx 0.368$. Small sample sizes are likely also a source of instability for our positive control application. Since CCLE has substantially less drugs compared to other datasets (Table 1), this could be a contributing factor to decreased instability compared to that of GDSC2 or CTRP2. Finally, noise in drug sensitivity measurements is likely another source of instability for all datasets (Haibe-Kains et al., 2013). In real data applications, applying the subsampling procedure in Algorithm 1 could help mitigate sources of instability.

In contrast to the bipartite graph-based clustering result, other methods that also integrate expression and drug sensitivity to cluster cell lines tend to yield results driven by primary site. These other methods include a baseline approach which we will describe shortly, iCluster and TWL (Hoadley et al., 2014; Mo et al., 2013; Shen et al., 2009). For fair comparison, hierarchical clustering with the Ward link function was again chosen as the unsupervised learning algorithm of choice for all approaches. In the baseline integrative approach, we simply applied clustering based on Euclidean distance in the combined expression and drug sensitivity feature space. Specifically, we concatenated the expression and drug sensitivity profiles $[X,Y]\in {\mathbb{R}}^{n\times (p+d)}$, computed the centroid for each group, then standardized each feature before clustering. These centroids serve as starting singletons for hierarchical clustering. Results suggest the clustering process is driven by site of origin (Supplementary Figs S7C, S8C, S9C). Many groups from similar sites of origin directly merge. For instance, the lung groups of squamous cell carcinoma and adenocarcinoma directly merge in CTRP2 and CCLE. Other suspected similar primary sites that directly merge include ovary and endometrium, stomach and colorectal and upper aerodigestive and esophagus. To determine the relative contribution of expression and drug sensitivity to this baseline clustering result, we clustered the cell line groups using each data modality separately (Supplementary Figs S7A, B, S8A, B, S9A, B). As expected, since expression accounts for most of the features, the expression dendrograms correspond to baseline dendrograms exactly. From this analysis, we confirm that expression patterns are strongly determined by primary site.

In the second approach, we cluster latent variables that are learned from expression and drug sensitivity profiles using iCluster. Specifically, iCluster learns a latent variable matrix $Z\in {\mathbb{R}}^{n\times k}$, with a latent variable vector of length k for each of the n cell lines. We follow the rule of thumb from iCluster and set k as one less than the number of starting groups. Then, hierarchical clustering was applied to Euclidean distances between the latent variable group centroids. For the CTRP2 and CCLE clusters, we still observe the influence of site of origin (e.g. upper aerodigestive and esophagus; lung groups; endometrium and ovary) (Supplementary Figs S7D and S9D). Except for the merge between ovary and endometrium for CCLE observed in our approach (Fig. 3), these direct merges between similar primary sites are absent using the nuclear norm-based dissimilarity measure. The clustering results using iCluster latent variables are shown in Supplementary Figures S7D, S8D, S9D.

In the third approach, we apply TWL to learn a clustering assignment for expression and drug sensitivity respectively (Swanson et al., 2019). Specifically, TWL learns a dissimilarity matrix for each data modality, from which we apply hierarchical clustering. In our application, we provide as input the standardized group centroids for transcript expression and drug sensitivity to the model. Overall, the clusters appear to neither be driven by histology subtype nor by site of origin, lacking a clear biological interpretation (Supplementary Figs S7E, F, S8E, F, S9E, F), except for a few cases. The first exception is the direct merge between the lung groups for drug sensitivity in CTRP2 and CCLE (Supplementary Figs S7F and S9F). The second exception is the direct merge between breast and ovary for drug sensitivity in CTRP2 and for expression in CCLE (Supplementary Figs S7F and S9E). Genomic similarities have been observed between basal-like breast cancers and high-grade serious ovarian cancers (Network et al., 2011). Again, these direct merges are absent in the bipartite graph-based clustering results in Figure 3. We observe little correspondence between the clusters for expression and the clusters for drug sensitivity under the TWL. Lastly, dendrograms based on TWL tend to be characterized by flat heights across multiple groups, suggesting an inability to resolve finer differences these groups.

From these experiments, our dissimilarity measure in Equation 2 provides biological insight that is unique compared to the other three approaches. Empirical results suggest existing approaches tend to be influenced by tissue-specific expression patterns, given that many direct merges occur between similar sites of origin. However, by clustering based on gene–drug association patterns explicitly, our approach suggests that gene–drug association patterns could be determined more by histology subtype than by primary site.

4.2 Cluster characterization with SCCA canonical vectors

In this section, we show how SCCA canonical vectors can characterize clustering results in terms of the top associated genes or drugs. For the canonical vectors $a\in {\mathbb{R}}^p,b\in {\mathbb{R}}^d$ solved by SCCA for p genes and d drugs, the magnitude of each entry is used to rank genes or drugs. Each entry in a or b is a gene or drug coefficient respectively, and the magnitude is interpreted as the strength of participation in the gene–drug associations. The strength of association between gene i and drug j is measured with $\left|a_i{b}_j\right|$, the magnitude of a bipartite graph edge weight. A network visualization of the bipartite graph for randomly selected genes and drugs for the acute myeloid leukemia (AML) group from CCLE is shown in Supplementary Figure S10. From this figure, we can see the sparsity of edge weights induced by the $\ell 1$ penalty from SCCA. We begin our experiment by clustering the haematopoietic and lymphoid tissue malignancies from CCLE. Groups with less than 5 cell lines were removed, and the number of cell lines per group in each dataset is listed in Supplementary Table S6. We again apply subsampling with $m=100,f=0.90$ for robustness, and perform permutation tests with 1000 permutations and P = 0.10 as the early-stopping threshold.

The resulting dendrogram is shown in Figure 4. Since chronic myeloid leukemia (CML) and AML are both myeloid leukemias, originating from myeloid cells instead of lymphocytes (De Kouchkovsky and Abdul-Hay, 2016), the direct merge between CML and AML aligns with intuition. However, the clusters are not always driven by disease type. Lymphoma Burkitt is separated from the other lymphomas and instead forms a cluster with multiple myeloma. This separation could be explained by clinical observations that diffuse large B-cell lymphoma (DLBCL) and lymphoma Burkitt require different treatment and management (Bellan et al., 2010; McGowan et al., 2012). The group ‘lymphoma other’ consists of a collection of other lymphomas (Fig. 4 and Supplementary Table S6), so is less interpretable. From permutation testing, cell lines from ‘lymphoma other’, T-cell acute lymphoblastic leukemia (ALL) and lymphoma DLBCL share significantly similar gene–drug associations with P-value $\le$ 0.05 (P-values less than or equal to 0.10 Supplementary Table S7). The lymphomas in ‘lymphoma other’, ALL and lymphoma DLBCL all involve lymphocytes, with differences in the type of lymphocyte and the tissue or organ affected (Abeloff et al., 2008; DeVita Junior et al., 2001; Hoffman et al., 2013). The AML and CML groups have a similarity P-value of 0.33, which suggests a weaker sharing of gene–drug association patterns. However, more cell lines are likely needed to confidently determine how similar AML and CML are (Supplementary Table S6).

Fig. 4.

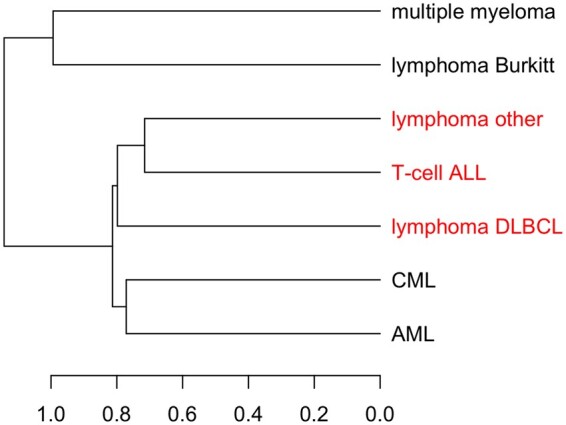
Bipartite graph-based clustering of haematopoietic and lymphoid tissue malignancies from CCLE. Red branches highlight groups with similar gene–drug associations according to the permutation test with P-value $\le$ 0.10. ALL, acute lymphoblastic leukemia; DLBCL, diffuse large B-cell lymphoma; AML, acute myeloid leukemia; CML, chronic myeloid leukemia; ‘lymphoma other’ consists of two cell lines of anaplastic large cell lymphoma, two cell lines of chronic lymphocytic leukaemia/small lymphocytic lymphoma, two cell lines of mycosis fungoides-Sezary syndrome, four cell lines of B cell lymphoma unspecified and two cell lines mantle cell lymphoma

From SCCA drug coefficients, we can identify differences in drug ranking that characterize the clustering patterns in Figure 4. For each malignancy, we applied SCCA and ranked drugs by their coefficient magnitudes. The resulting rankings are listed in Supplementary Table S8 and plotted as a heat map in Figure 5. We see a close correspondence between malignancy dendrogram based on drug rankings (Fig. 5) and the malignancy dendrogram based on the nuclear norm-based dissimilarity measure (Fig. 4), with the only difference being the T-cell ALL branch. From the heatmap itself, AML and CML appear to have similar drug rankings, with high rankings for AZD0530, L-685458, TAE684, PF2341066, 17-AAG and Sorafenib. Most of these compounds are kinase inhibitors (Barretina et al., 2012). In contrast to the myeloid leukemias, the groups ‘lymphoma other’ and lymphoma DLBCL tend to have higher rankings for drugs listed in the middle of the heatmap. The drug ranking pattern for lymphoma Burkitt differs from that of ‘lymphoma other’ or lymphoma DLBCL, and this characterizes the separation of lymphoma Burkitt from other lymphomas in Figure 4. For example, the compounds PD-0325901 and Paclitaxel are highly ranked for lymphoma Burkitt but lowly ranked for the rest of the lymphomas. PD-0325901 is a MEK1 and MEK2 kinase inhibitor, and Paclitaxel is a cytotoxic microtubule-stabilizing agent (Barretina et al., 2012). Lastly, the top two compounds for multiple myeloma, TKI258 and 17-AAG, have both been studied in clinical trials as candidate treatments for multiple myeloma (Kaufmann et al., 2011; Scheid et al., 2015).

Fig. 5.

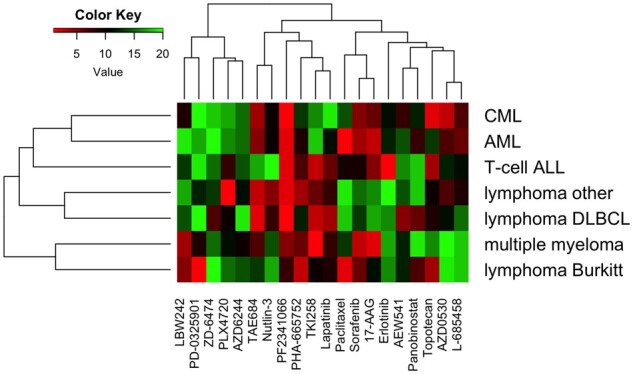
Heatmap of drug rankings for malignancies of the haematopoietic and lymphoid tissue. For each malignancy, drug ranking is determined by SCCA coefficient magnitude. In this heatmap, lower values (red) indicate higher rankings, and higher values (green) reflect lower rankings

We next interpret the top associated transcripts with respect to the biological context of the cell lines. Specifically, we investigated whether more myeloid leukemia-related genes are found among the top 10 out of 5000 transcripts when cell lines from AML and CML are pooled together, compared to when all the cell lines from haematopoietic and lymphoid tissue are pooled together. Out of the top 10 transcripts for the myeloid leukemia group, we found four genes with some relationship with either AML or CML, according to literature. These genes, which are ZNF770, RNF11, C9orf47 and PRDM2, are either associated between subtypes of AML or CML, or differentially expressed in myeloid leukemia compared to healthy conditions (Table 3) (Jiang et al., 2013; Lakshmikuttyamma et al., 2009; Noort et al., 2020; Pastural et al., 2007; Sasaki et al., 2002; Wiggers et al., 2019). In contrast, only one myeloid leukemia-related gene (C20orf197) was found among the top 10 transcripts in the general haematopoietic and lymphoid tissue group (Noort et al., 2020). No literature sources could be found connecting the remaining transcripts of the haematopoietic and lymphoid tissue group with myeloid leukemia. Instead, we found three genes with more general immune-related functions, based on descriptions provided by the National Center for Biotechnology Information (NCBI). These genes are CEBPD, SART3 and GPR35 (Table 3). SCCA transcript coefficients for both groups are listed in Supplementary Table S9. Although the comparison between the myeloid leukemia group and the haematopoietic and lymphoid tissue group is somewhat subjective, this assessment at least shows the top transcripts can be interpreted as being related to immune function.

Table 3.

Top genes with myeloid leukemia or other immune-related functions

Gene	Type	Description
ZNF770	Myeloid leukemia	This transcription factor’s binding motif is enriched in gene regulatory elements which are associated with AML relapse (Wiggers et al., 2019).
RNF11	Myeloid leukemia	This gene is differentially expressed between chronic phase CML and blast crisis CML (Jiang et al., 2013).
C9orf47	Myeloid leukemia	This gene is differentially expressed between NUP98-KDM5A+ pediatric AML and NUP98-KDM5A- pediatric AML (Noort et al., 2020).
PRDM2	Myeloid leukemia	PRDM2 expression is reduced in AML compared to normal bone marrow and is downregulated during CML progression (Lakshmikuttyamma et al., 2009; Sasaki et al., 2002). The repression of PRDM2 is involved in insulin-like growth factor-1 signaling activation in CML blast crisis cell lines (Pastural et al., 2007).
C20orf197	Other immune	This gene is differentially expressed between NUP98-KDM5A+ pediatric AML and NUP98-KDM5A- pediatric AML (Noort et al., 2020).
CEBPD	Other immune	The encoded protein is important in the regulation of genes involved in immune and inflammatory responses, and may be involved in the regulation of genes associated with activation and/or differentiation of macrophages.
SART3	Other immune	The protein encoded by this gene is an RNA-binding nuclear protein that is a tumor-rejection antigen. This antigen possesses tumor epitopes capable of inducing HLA-A24-restricted and tumor-specific cytotoxic T lymphocytes in cancer patients and may be useful for specific immunotherapy. This gene product is found to be an important cellular factor for HIV-1 gene expression and viral replication.
GPR35	Other immune	This gene is expressed by monocytes and mast cells (Amir et al., 2018).

Note: Genes are ranked by SCCA coefficient magnitude. Unless cited, descriptions are provided by NCBI.

4.3 Hierarchy inference in simulated data

From visual inspection of the dendrograms, bipartite graph-based clustering clearly outperforms the baseline approach, iCluster and TWL, for reference simulation setting 1 (Fig. 6 and Supplementary Fig. S11). None of the existing approaches could cluster subgroups within a group effectively (Supplementary Fig. S11), let alone generate a hierarchical structure resembling the true structure in Figure 2. In contrast, our approach clusters subgroups within groups almost perfectly, with the only exception of placing group 4B in the group 3 cluster (Fig. 6). Other than the placement of group 7, the hierarchical structure resembles the ground truth. Group 7 is an outlier group by design, only sharing 5% of biomarkers with other groups, so should be the last one to merge according to the ground truth. However, the merging of group 7 with groups 5 and 6 likely results from the choice of the Ward link function, which tends to favor balanced trees (Ward Jr, 1963).

Fig. 6.

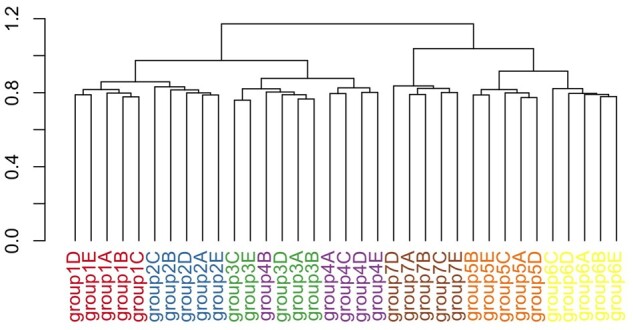
Bipartite graph-based clustering of simulated data under setting 1. Hierarchical clustering with Ward link function was used as the clustering algorithm, applied to nuclear norm-based dissimilarity measure for gene–drug association patterns

We study clustering behavior under different simulation settings. In simulation setting 2, we decrease the number of drugs from 200 to 20, while keeping the proportion of expression-dependent drugs the same at 30%. This corresponds to the drop in number of drugs in CCLE compared to either CTRP2 or GDSC2. This change resulted in a poorer recovery of the ground truth compared to setting 1 (Fig. 6 and Supplementary Fig. S12A). The clusters are more heterogenous, and the hierarchical structure deviated more from the ground truth. Specifically, groups 1–2 now merge with groups 5–6 before merging with groups 3–4, which have more biomarkers in common with groups 1–2. This supports the intuition that more drugs enables better resolution of gene–drug association differences. In simulation setting 3, we see that increasing the number of cell lines leads to perfect clustering of subgroups within each group (Supplementary Fig. S12B). The hierarchical structure is similar to that in setting 1, with the only minor difference being the merge of group 4 with groups 1–2 first before merging with group 3. Finally, in setting 4, we observe the effect of increasing the noise in drug sensitivity values, corresponding to the real data scenario where drug sensitivity values have been observed to be noisy or inconsistent (Haibe-Kains et al., 2013) (Supplementary Fig. S12C). We observe a similar detrimental effect on performance as in setting 2. The clusters for some groups are heterogenous, and the dissimilarity measure was unable to resolve differences between groups 5 and 6 since their subgroups are fairly mixed. Together, these simulations support the intuition that more drugs and cell lines allow better resolution of gene–drug association differences.

5 Conclusion and discussion

Given the diversity of cell lines in pharmacogenomic datasets, the choice of cell lines for a drug response model influences prediction performance and biomarker discovery (Barretina et al., 2012; Ghandi et al., 2019; Mannheimer et al., 2019; Ross et al., 2000; Yao et al., 2018). Our main contribution in this article is a dissimilarity measure that enables unsupervised analysis of cell lines based on gene–drug associations. In the pharmacogenomic datasets CTRP2, GDSC2 and CCLE, our approach shows that gene–drug association patterns could be driven more by histology subtype than by primary site, which is not observed under existing clustering approaches. Modeling gene–drug associations with SCCA allows us to characterize clustering patterns in terms of top associated genes and drugs. In this article, we also present a permutation test to evaluate the significance of gene–drug association similarity, which can be used to guide the decision on pooling cell lines together for further study. Finally, our simulation study shows that when drug sensitivity values have a true linear dependence on expression values, our approach is the only effective one at inferring the hierarchy in the data.

Limitations of working with pharmacogenomic datasets include potential inconsistency in drug sensitivity measurements and small sample sizes per group (Haibe-Kains et al., 2013). In our carcinoma analysis, we observe an adenocarcinoma-dominant cluster in CTRP2, GDSC2 and CCLE respectively, with permutation tests revealing significant similarity between many groups in these clusters at P-value $\le 0.05$ (Fig. 3). However, since we have more adenocarcinoma groups than either squamous cell carcinoma or ductal carcinoma groups, we cannot confidently conclude whether the other carcinoma subtypes cluster primarily by histology subtype or by site of origin. Limitations in the data, along with missingness in drug sensitivity values, both contribute to small sample sizes. Although a SCCA implementation that can accept missing values can mitigate this (Van de Velden and Takane, 2012), this still cannot address the systematic missingness across drugs or cell lines we observe in pharmacogenomic datasets. Small sample sizes likely contribute to increased clustering instability due to sampling of cell lines. Our simulation study indicates that larger sample sizes tend to improve clustering performance.

Although significant P-values can provide confidence in the similarity of gene–drug associations, P-values that fail to reach cutoff do not necessarily imply absence of shared gene–drug relationships. For example, non-linear gene–drug relationships would not be captured by the SCCA presented in Equation 1. In addition, due to the high dimensional nature of pharmacogenomic data, the signal-to-noise ratio could be low when only a few genes are truly related to drug sensitivity. Finally, small sample sizes could inflate observed P-values even when the alternate hypothesis is true. For these reasons, prior biological knowledge could still be important for the decision on which cell lines to pool together for further study.

Although the development of the bipartite graph-based approach for clustering cell lines is motivated by interest in gene–drug associations, our method can be applied to study the relationship between any two sets of variables. For example, one may be interested in relating expression with clinical phenotypes instead of drug sensitivity values. Another application can be found in genomics, such as the study of the relationship between genotype and DNA methylation, where genetic variants are known to modulate DNA methylation levels (Banovich et al., 2014; Bell et al., 2011; Liu et al., 2014). In some applications, it may be reasonable to impose connectivity constraints to the bipartite graph, such as when modeling the relationship between cis-DNA methylation quantitative trait loci and DNA methylation.

Empirically, SCCA is responsible for most of the runtime, which is further increased by running the subsampling procedure in Algorithm 1 and generating P-values according to Algorithm 3. Since the subsampling and permutation steps are independent, our implementation provides the option of parallelizing these steps using the parallel R package for improved runtime. As a reference, CTRP2 carcinoma analysis took 4.13 h to complete on a MacBook Pro with 2.4 GHz Quad-Core Intel Core i5 processor with 8 GB of RAM. The analysis involved 100 trials of subsampling and 1000 trials for P-value generation.

Finally, there are multiple other approaches to the CCA problem besides the one formulated in Equation 1. Solari et al. (2019) recently proposed a two-step algorithm which first infers sparsity before solving for canonical vectors, an approach which reduces the search space to offer greater computational efficiency. Other CCA approaches serving various purposes include Bayesian CCA (Klami et al., 2012), deep neural network-based CCA (Andrew et al., 2013) and kernel CCA (Larson et al., 2014), which could substitute the $\mathtt{SCCA}(·,·)$ procedure in Algorithm 1.

Funding

This work was supported by the National Science Foundation Graduate Research Fellowship Program [DGE 1106400 to C.C.]. The work of H.H., B.C. and Y.Y. was partially supported by National Institutes of Health [R01 GM134307-01].

Conflict of Interest: none declared.