A strong nonequilibrium bound for sorting of cross-linkers on growing biopolymers

Significance

Understanding the connection between microscopic driving forces in biological systems and their emergent structures remains an outstanding challenge. We tackle this problem by deriving a fluctuation–response bound in the context of actin polymerization and bundling and verify its robustness far from equilibrium through simulation. Our results show how actin polymerization, molecular fluxes of cross-linker binding, and the morphology of the growing bundle are associated quantitatively; when the bound is saturated, it becomes a nonequilibrium linear-response relation. Molecular driving forces are difficult to measure directly in biological systems, and this work represents a first step toward estimating them from experimentally accessible quantities such as molecular fluxes and compositions.

Abstract

Understanding the role of nonequilibrium driving in self-organization is crucial for developing a predictive description of biological systems, yet it is impeded by their complexity. The actin cytoskeleton serves as a paradigm for how equilibrium and nonequilibrium forces combine to give rise to self-organization. Motivated by recent experiments that show that actin filament growth rates can tune the morphology of a growing actin bundle cross-linked by two competing types of actin-binding proteins [S. L. Freedman et al., Proc. Natl. Acad. Sci. U.S.A. 116, 16192–16197 (2019)], we construct a minimal model for such a system and show that the dynamics of a growing actin bundle are subject to a set of thermodynamic constraints that relate its nonequilibrium driving, morphology, and molecular fluxes. The thermodynamic constraints reveal the importance of correlations between these molecular fluxes and offer a route to estimating microscopic driving forces from microscopy experiments.

Nonequilibrium driving is a crucial prerequisite for the function of many biological systems. Examples include kinetic proofreading (1–5), adaptation in molecular motors (6–8), and the suppression of phase decoherence in biochemical oscillators (9–14), among others. Given the ubiquitous role played by nonequilibrium driving in biology, much recent work has focused on establishing the general tradeoffs between energy consumption and organization (15–20). Here, motivated by recent experimental work (21–23), we consider growth and bundling of actin filaments and demonstrate that energy–speed–morphology relations can be obtained for such systems.

The actin cytoskeleton harnesses chemical energy to perform mechanical work that enables cells to migrate, divide, and exert forces on their surroundings, among other functions (7, 24–28). To perform these varied functions, a cell must be able to control the organization of its many components in both space and time. A growing body of evidence suggests, surprisingly, that much of this organization can be kinetically determined (29, 30) and can arise due to passive competition between actin-binding proteins (ABPs) (31). At the same time, other processes such as the formation of a cytokinetic ring require irreversible polymerization and motor activity (32, 33). This suggests that cells can regulate their internal structures and, in turn, their functions by tuning the relative contributions of passive and active processes. Support for this idea comes from recent in vitro experiments and simulations that demonstrate that the morphology of a growing actin bundle can be tuned not only by the binding affinities of the cross-linkers but also by the actin polymerization rates (22).

These observations, together with recent advances in nonequilibrium statistical mechanics (5, 9, 17, 34–36), raise the question of whether the nonequilibrium driving—here due to polymerization—can be related to the emergent structure quantitatively. Here, we address this question and present a theoretical framework that bounds the dynamics of a growing actin bundle. In particular, we derive constraints on a set of three matrices characterizing the actin growth and bundling process—a matrix containing the various nonequilibrium driving forces ($\mathit{\delta }\mathit{\mu }$, Eq. 11), a matrix encoding the equilibrium and nonequilibrium morphologies ($\mathbf{D}$, Eq. 12), and a matrix characterizing the covariance of the molecular fluxes (${\mathbf{L}}^{-1}$). For these three matrices, we show that

$$\text{Tr}\left[\mathit{\delta }\mathit{\mu }-\mathbf{D}-{\mathbf{L}}^{-1}\right]\ge 0\hspace{0.17em},\mathrm{D}\mathrm{e}\mathrm{t}\left[\mathit{\delta }\mathit{\mu }-\mathbf{D}-{\mathbf{L}}^{-1}\right]\ge 0.$$ [1]

Eq. 1 has the flavor of a fluctuation–response relation for the actin growth and bundling dynamics and can offer a route to generalize the classical linear irreversible thermodynamics framework to far-from-equilibrium conditions. Indeed, when the equality is satisfied, Eq. 1 can be used to obtain a linear-response–like formula (Eq. 13). This formula and, more generally, Eq. 1 provide strong thermodynamic constraints on the nonequilibrium forcing, the bundle morphology, and the response to fluctuations in molecular fluxes (i.e., the speed of growth). Notably, $\mathbf{D}$ and ${\mathbf{L}}^{-1}$ are in principle experimentally accessible, such that Eq. 1 can be used to bound $\mathit{\delta }\mathit{\mu }$, which is not straightforward to measure directly. In what follows, we first outline a minimal model that captures the salient features of actin polymerization and bundling and show that it captures the observations described above. We then proceed to derive our central results and show how these thermodynamic uncertainty relations constrain the dynamics.

Actin Polymerization Drives Sorting of Cross-Linkers

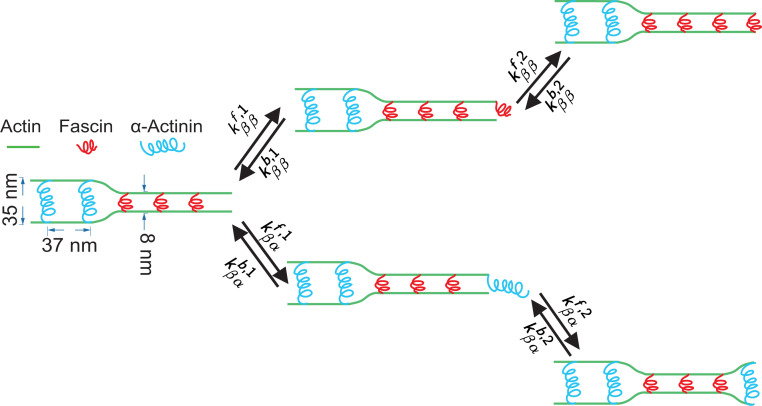
Inspired by the experiments in refs. 21 and 22, we consider a bundle consisting of two parallel actin filaments and two types of ABPs, $\alpha$ and $\beta$. The growth of a parallel actin bundle involves continuous actin monomer addition at one end, as well as continual ABP binding and “zipping” of the bundle at that same end. Refs. 29 and 30 indicate that the unbinding of ABPs in actin bundles is slow and occurs on the timescale of hours, and, under the conditions in ref. 21, bundle morphology is entirely determined by addition of cross-linkers at the growing end, on which we thus focus. In the specific case shown in Fig. 1, $\alpha$ and $\beta$ represent cross-linking proteins $\alpha$-actinin and fascin, respectively, such that the bundles formed by the $\alpha$ ABPs are substantially more widely spaced than those formed by the $\beta$ ABPs. Consequently, the bending penalty of actin favors addition of the current cross-linker at the growing end, as it costs energy to switch from one type to the other. The cost of bending actin favors the formation of distinct domains of only $\alpha$ or $\beta$ ABPs. In the case of in vitro experiments using an equimolar mixture of fluorescently labeled $\alpha$-actinin and fascin binding to growing actin bundles, these domains are on the order of several micrometers ($\sim$100 cross-linkers) long (21). The statistics of the domain lengths may vary as different labeling strategies are used. Nevertheless, it has been demonstrated in ref. 22 that regardless of different labeling strategies, the domain length statistics are modulated by the rate of actin polymerization.

Fig. 1.

Schematic of adding one ABP at the tip of a growing actin bundle. Here, $\alpha$ and $\beta$ represent $\alpha$-actinin and fascin, which are 35 and 8 nm in size, respectively. The energetic cost of bending actin disfavors binding a fascin after an $\alpha$-actinin, or vice versa, resulting in domains of consecutive $\alpha$ or $\beta$ types of ABPs. $k_{ij}^{f,1}$ and $k_{ij}^{b,1}$ ($k_{ij}^{f,2}$ and $k_{ij}^{b,2}$) are the forward and backward rates for the first (second) site of an ABP binding, where $i$ and $j$ are the types of the last two ABPs at the tip; $k_{\alpha \alpha }^{f,1}=k_{\beta \alpha }^{f,1}$ because both rates represent the binding of the first site of an $\alpha$ ABP (similarly, $k_{\beta \beta }^{f,1}=k_{\alpha \beta }^{f,1}$). An analogous schematic can be drawn for the case that the second-to-last ABP is $\alpha$, and this case introduces four additional pairs of forward and backward rates with corresponding constraints.

We construct a minimal model of this system with the following simplifications: First, we assume that the ABPs can bind and unbind only from the sites at the leading edge and not from the bulk of the bundle, and second, we assume that the two binding sites of each ABP bind sequentially and do not allow an ABP to bind to a single filament with both of its sites. As a result, we need two pairs of forward rates $k_{ij}^{f,1}$ and backward rates $k_{ij}^{b,1}$ to describe the binding of the first site of each ABP and two other pairs, $k_{ij}^{f,2}$ and $k_{ij}^{b,2}$, for their second site (Fig. 1). The consideration of both ABP binding sites independently is more sophisticated than the kinetic Monte Carlo (KMC) models considered in refs. 21 and 22 but is consistent with the experimental and simulation data therein.

Here, we further decompose the forward rate of $k_{ij}^{f,m}$ into an equilibrium component, $k_{ij,eq}^{f,m}$, that satisfies a local detailed balance rule and accounts for all the energetics associated with ABP binding and filament deformations, and a component $d{k}_{ij}^{f,m}$ that can model any nonequilibrium contributions to the rate:

$$k_{ij}^{f,m}=k_{ij,eq}^{f,m}d{k}_{ij}^{f,m}.$$ [2]

We assert that only the forward rates are modified by any nonequilibrium effects including actin polymerization and we set all the $k_{ij}^{b,m}$ to unity. The equilibrium factor $k_{ij,eq}^{f,m}$ accounts for the binding affinity of an ABP. In cases where an attached ABP binds to the second actin filament, this equilibrium part also accounts for the energy penalty associated with bending the actin filament if the newly bound ABP is different from the previous ABP at the tip (e.g., rate $k_{\beta \alpha ,eq}^{f,2}$ in Fig. 1) and the free energy associated with zipping the actin bundle (e.g., rates $k_{\beta \beta ,eq}^{f,2}$ and $k_{\beta \alpha ,eq}^{f,2}$ in Fig. 1).

The nonequilibrium component in our model, $d{k}_{ij}^{f,m}$, heuristically accounts for any effects due to the finite rate of actin growth and polymerization, excess concentration or chemical potential of various ABPs in solution, and their molecular structure. Given this, we generically decompose the nonequilibrium components as

$$d{k}_{ij}^{f,m}=d{k}_j=1+f_{\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{r},j}{f}_{\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{y},j}{f}_{\mathrm{p}\mathrm{o}\mathrm{l},j},$$ [3]

where $i$ and $j$ are the types of ABPs at the bundle tip, and type $j$ can be either the same as or different from $i$. The factor $f_{\mathrm{p}\mathrm{o}\mathrm{l}}$ models the modulation of the rates due to the finite rate of growth of the actin filaments ($k_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}$). Specifically, over a time scale $\tau$, the average increase in the number of binding sites on the filaments is $k_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}\tau$ and $k_{ij,eq}^{f,1}\tau$ is the number of binding events per binding site. Assuming Poisson statistics, the net rate of ABP binding is hence modulated by the factor,

$$f_{\mathrm{p}\mathrm{o}\mathrm{l},j}=1-e^{-k_{ij,eq}^{f,1}{k}_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}{\tau }^2}.$$ [4]

The factor $f_{\mathrm{p}\mathrm{o}\mathrm{l}}$ is essentially the probability of binding at least one ABP within time $\tau$. $f_{\mathrm{p}\mathrm{o}\mathrm{l}}$ increases from a value of zero when $k_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}$ is negligible to a value of one for rapid actin polymerization. It acts as a scaling factor that tunes the rates from their equilibrium values $k_{ij,eq}^{f,m}$ to their maximum rates.

The rates of ABP binding are also influenced by the ABP concentrations in solution around the actin filaments. The phenomenological factor $f_{\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{y}}$ accounts for these effects. Finally, we introduce the phenomenological factor $f_{\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{r}}$ to account for any remaining kinetic differences between the ABPs. Such factors could modulate the maximum rates of adding ABPs in fast-growing bundles, but they do not affect the equilibrium rates $k_{ij,eq}^{f,m}$ and the corresponding equilibrium structure of the bundle (22).

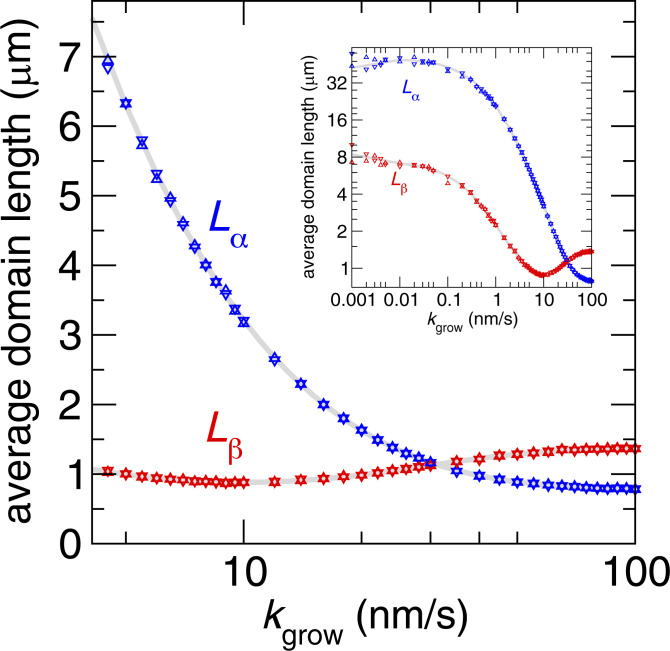
KMC simulations of this minimal model (described in Methods) reproduce a cross-over of domain lengths previously observed in growing actin bundles with $\alpha$-actinin and fascin as the actin polymerization rate was varied (22) (Fig. 2). It thus captures the essential physics of the system and serves as a meaningful starting point for the development of a theoretical framework that shows that the behavior is bounded by an energy–speed–morphology relation.

Fig. 2.

Average domain length of $\alpha$ and $\beta$ ABPs as a function of polymerization rate $k_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}$. The distance between neighboring ABPs is assumed to be 0.037 $\mathrm{\mu }$m in computing domain lengths (21). Blue and red triangles are average domain lengths $L_{\alpha }$ and $L_{\beta }$ measured from KMC simulations. Up and down triangles represent the average domain lengths measured in simulations with initial configurations composed of either all $\alpha$ or all $\beta$ types of ABPs, respectively. Each data point is computed from a single KMC simulation of $10^6$ steps. Gray lines (SI Appendix, Eq. S16) are the domain lengths computed by self-consistently solving the master equation (Eq. 5). The parameters for both KMC simulations and the master equation are $k_{\alpha \alpha ,eq}^{f,1}=6$, $k_{\beta \beta ,eq}^{f,1}=2$, $f_{density,\alpha }=f_{density,\beta }=100$, $f_{molecular,\alpha }=0.4$, $f_{molecular,\beta }=1$, $L_{\alpha ,\mathrm{e}\mathrm{q}}=900$ ($33.3\hspace{0.17em}\mathrm{\mu }$m), $L_{\beta ,\mathrm{e}\mathrm{q}}=300$ ($11.1\hspace{0.17em}\mathrm{\mu }$m), and $\tau =\mathrm{1}\hspace{0.17em}\text{s}$. Inset shows the domain lengths over a wider range of polymerization rates with the same symbols. The plateaus toward the left of Inset represent the domain lengths approaching their equilibrium values.

Connections between the Growth and Morphology of Actin Bundles: A Markov State Model

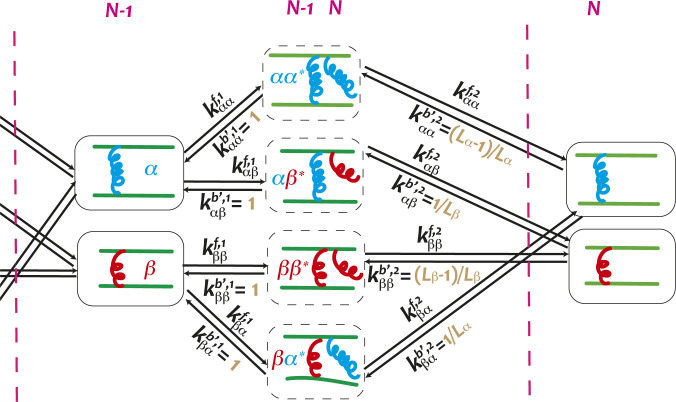
The number of accessible states of the Markov chain for actin polymerization and bundling, as defined in the previous section, grows exponentially as a function of time. Writing down thermodynamic relations for such growing systems becomes cumbersome. Here, we show that it is in fact possible to account for the behavior of the growing system using only a tractable, finite-state, Markov model. Using this model, we derive thermodynamic bounds for the nonequilibrium sorting process in Fig. 2.

We begin by introducing a mean-field treatment for the various configurations that arise at the tip as ABPs associate and dissociate sequentially (Fig. 3). The forward rates $k_{ij}^{f,m}$ are consistent with those used in the KMC simulations, accounting for the energies of binding ABPs and the effect of actin polymerization. The backward rates in the finite-state model self-consistently account for the probability of finding the appropriate ABP in the bulk of the actin bundle. For instance, using $L_{\alpha }$ to denote the domain lengths of $\alpha$-type ABPs and $L_{\beta }$ for its $\beta$ counterpart, the probability of finding one $\alpha$ at the bundle tip is $L_{\alpha }/\left(L_{\alpha }+L_{\beta }\right)$ and the probability of finding a consecutive pair $\alpha \alpha$ is $\left(L_{\alpha }-1\right)/\left(L_{\alpha }+L_{\beta }\right)$. The chance of reaching an $\alpha \alpha *$ configuration (where $*$ stands for a half-bound state as in Fig. 3) after unbinding an $\alpha$ at the bundle tip is essentially the conditional probability of finding $\alpha \alpha$ in the bundle given that the bundle tip is an $\alpha$, which can be computed by dividing the $\alpha \alpha$ probability by the $\alpha$ probability to obtain $\left(L_{\alpha }-1\right)/L_{\alpha }$.

Fig. 3.

Schematic of the model. The states between the two pink dashed lines contribute to the $N$th ABP binding. Arrows link states between which transitions are allowed. $k_{ij}^{f,m}$ and $k_{ij}^{b,m}$ are the forward and backward rates, where $i$ and $j$ are the types of the last two ABPs at the tip and $*$ represents a half-bound state. The rates used in the KMC simulations and in the master equation are compared in SI Appendix, Table S1.

In computing the unbinding rate $k_{ij}^{b^{\prime },m}$ used in the finite-state model, we multiply the backward rates $k_{ij}^{b,m}$ in KMC simulations by these corresponding conditional probabilities. Note that the effective backward rate for unbinding the first head of an ABP, $k_{ij}^{b^{\prime },1}$, is simply equal to the corresponding rate $k_{ij}^{b,1}$ used in KMC simulations. We confirm the expressions of these conditional probabilities by extracting the effective backward rates and domain length ratios from the full KMC simulations (SI Appendix, Fig. S1).

Given these expressions for the rates, we can write a master equation describing the evolution of probabilities of the various tip configurations, $P_{ij}$ at steady state:

$$\begin{array}{c}\hfill \frac{\partial P}{\partial t}=\sum _{i,j\in \alpha ,\beta }\left(k_{ij}^{f,1}{P}_i-k_{ij}^{b^{\prime },1}{P}_{ij*}\right.\\ \hfill +\hspace{0.17em}& \left.k_{ij}^{f,2}{P}_{ij*}-k_{ij}^{b^{\prime },2}{P}_j\right)=0.\hfill \end{array}$$ [5]

However, this master equation depends on the average domain lengths $L_{\alpha }$ and $L_{\beta }$. To solve the master equation of this system and get closed-form expressions for $P_{ij}$ at the steady state, we require a relation that connects the tip configuration probabilities to the domain lengths. Such a connection can be obtained by noting that the tip configuration merges into the bulk of the bundle as growth continues. The probabilities of tip configurations at steady state together with their corresponding rates of growth determine the relative amounts of the two types of ABPs being incorporated into the bulk. In other words, the fluxes $J_{N-1,i,N,j}$, defined as $k_{ij}^{f,1}{P}_i-k_{ij}^{b^{\prime },1}{P}_{ij*}$ (or equivalently $k_{ij}^{f,2}{P}_{ij*}-k_{ij}^{b^{\prime },2}{P}_j$ due to current conservation at a node), are proportional to the probabilities of sampling the corresponding ABPs in the bulk (SI Appendix, Eq. S14).

Indeed, this reasoning can be put on a firm mathematical footing by adapting the calculations in ref. 37. Specifically, as described in SI Appendix, section S1, we derive self-consistency conditions that relate the currents at which various tip configurations grow to the domain lengths in the bulk:

$$\begin{array}{cc}\hfill J_{N-1,\alpha ,N,\alpha }& =\frac{L_{\alpha }-1}{L_{\mathrm{t}\mathrm{o}\mathrm{t}}}{J}_{\mathrm{t}\mathrm{o}\mathrm{t}}\hfill \\ \hfill J_{N-1,\beta ,N,\beta }& =\frac{L_{\beta }-1}{L_{\mathrm{t}\mathrm{o}\mathrm{t}}}{J}_{\mathrm{t}\mathrm{o}\mathrm{t}}\hfill \\ \hfill J_{N-1,\alpha ,N,\beta }=J_{N-1,\beta ,N,\alpha }& =\frac{1}{L_{\mathrm{t}\mathrm{o}\mathrm{t}}}{J}_{\mathrm{t}\mathrm{o}\mathrm{t}},\hfill \end{array}$$ [6]

where $N-1,i,N,j$ denotes the tip configurations at positions $N-1$ and $N$, $J_{\mathrm{t}\mathrm{o}\mathrm{t}}$ is the sum of the four currents, and $L_{\mathrm{t}\mathrm{o}\mathrm{t}}\equiv L_{\alpha }+L_{\beta }$. We measure the currents and domain lengths from KMC simulations, and SI Appendix, Fig. S2 demonstrates the validity of the relations between the fluxes and domain lengths in Eq. 6.

The master equation (Eq. 5) can now be solved with these additional self-consistency conditions. Expressions for the nonequilibrium domain lengths $L_{\alpha }$ and $L_{\beta }$ can also be readily obtained (SI Appendix, Eq. S16). The gray lines in Fig. 2 illustrate that these predictions are in excellent agreement with the domain lengths in KMC simulations for the full range of actin polymerization rates. This model also recovers the trend shown previously by simulations (22) that as the binding affinity of the short cross-linker (the $\beta$ ABP in our model) is weakened, the crossover of domain lengths is deferred to a faster growth speed (SI Appendix, Fig. S3). Thus, our mean-field treatment is able to capture the behavior of the model quantitatively.

Thermodynamic Constraints between the Nonequilibrium Forcing, Fluctuations, and Morphology

The nonequilibrium thermodynamics of the growing actin bundle can now be probed. Using the master equation (Eq. 5) and the finite-state Markov model in Fig. 3, we write down the entropy production rate for our effective Markov model following ref. 38 as described in SI Appendix, section S2:

$$\dot{\sigma }=J_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(\mathrm{\Delta }\mu -{\epsilon }_{diss}\right)\ge 0.$$ [7]

The factor $\mathrm{\Delta }\mu$ represents the nonequilibrium forces that drive polymerization; in SI Appendix, section S2, we show that

$$\mathrm{\Delta }\mu =\frac{2}{L_{\mathrm{t}\mathrm{o}\mathrm{t}}}\left(\sum _{i\in \alpha ,\beta }{L}_i\log d{k}_i\right).$$ [8]

The factor ${\epsilon }_{diss}$ is a measure of the difference between the nonequilibrium and equilibrium morphologies as characterized by the respective average domain lengths $L_{\beta ,\mathrm{e}\mathrm{q}}$ and $L_{\alpha ,\mathrm{e}\mathrm{q}}$. SI Appendix, section S2 demonstrates that

$$\begin{array}{cc}\hfill {\epsilon }_{diss}=-\frac{1}{L_{\mathrm{t}\mathrm{o}\mathrm{t}}}& \left(\sum _{i\in \alpha ,\beta }{L}_i\log \frac{L_i}{L_{i,\mathrm{e}\mathrm{q}}}\right.\hfill \\ \hfill & \left.-\sum _{i\in \alpha ,\beta }\left(L_i-1\right)\log \frac{L_i-1}{L_{i,\mathrm{e}\mathrm{q}}-1}\right).\hfill \end{array}$$ [9]

Eq. 7 is a statement of the second law of thermodynamics. However, we can improve on this bound substantially by adapting recent work from refs. 39 and 40. Specifically, we show in SI Appendix, section S3 that a stronger matrix relation can be obtained that is valid far from equilibrium. This is our main result, Eq. 1, which we reproduce here for convenience:

$$\text{Tr}\left[\mathit{\delta }\mathit{\mu }-\mathbf{D}-{\mathbf{L}}^{-\mathbf{1}}\right]\ge 0\hspace{0.17em},\mathrm{D}\mathrm{e}\mathrm{t}\left[\mathit{\delta }\mathit{\mu }-\mathbf{D}-{\mathbf{L}}^{-\mathbf{1}}\right]\ge 0.$$ [10]

We now define the matrices $\mathit{\delta }\mathit{\mu }$, $\mathbf{D}$, and ${\mathbf{L}}^{-1}$ precisely. The matrix $\mathit{\delta }\mathit{\mu }$ depends on the nonequilibrium driving forces $\delta {\mu }_{\alpha /\beta }\equiv \log d{k}_{\alpha /\beta }$ in Eq. 3 and the average nonequilibrium domain lengths $L_{\alpha /\beta }$:

$$\mathit{\delta }\mathit{\mu }=\left(\begin{array}{cc}\hfill \delta {\mu }_{\alpha }{\gamma }_1^{\alpha }+\delta {\mu }_{\beta }{\gamma }_2^{\beta }\hfill & \hfill \delta {\mu }_{\alpha }{\gamma }_3^{\alpha }+\delta {\mu }_{\beta }{\gamma }_3^{\beta }\hfill \\ \hfill \delta {\mu }_{\alpha }{\gamma }_3^{\alpha }+\delta {\mu }_{\beta }{\gamma }_3^{\beta }\hfill & \hfill \delta {\mu }_{\alpha }{\gamma }_2^{\alpha }+\delta {\mu }_{\beta }{\gamma }_1^{\beta }\hfill \end{array}\right),$$ [11]

where ${\gamma }_1^{\alpha /\beta }\equiv \left[{\left(L_{\mathrm{t}\mathrm{o}\mathrm{t}}-1\right)}^2/\left(L_{\alpha /\beta }-1\right)+1\right]/L_{\mathrm{t}\mathrm{o}\mathrm{t}}$, ${\gamma }_2^{\alpha /\beta }\equiv \left[1/\left(L_{\alpha /\beta }-1\right)+1\right]/L_{\mathrm{t}\mathrm{o}\mathrm{t}}$, and ${\gamma }_3^{\alpha /\beta }\equiv -L_{\beta /\alpha }/\left[L_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(L_{\alpha /\beta }-1\right)\right]$. The matrix $\mathbf{D}$ depends on the nonequilibrium and equilibrium domain lengths of ABPs and is defined as

$$\mathbf{D}=\left(\begin{array}{cc}\hfill d{p}_{\alpha }{\gamma }_1^{\alpha }+d{p}_{\beta }{\gamma }_2^{\beta }+ϵ\hfill & \hfill d{p}_{\alpha }{\gamma }_3^{\alpha }+d{p}_{\beta }{\gamma }_3^{\beta }+ϵ\hfill \\ \hfill d{p}_{\alpha }{\gamma }_3^{\alpha }+d{p}_{\beta }{\gamma }_3^{\beta }+ϵ\hfill & \hfill d{p}_{\alpha }{\gamma }_2^{\alpha }+d{p}_{\beta }{\gamma }_1^{\beta }+ϵ\hfill \end{array}\right),$$ [12]

where $d{p}_{\alpha /\beta }\equiv \left(1/2\right)\left(\ln \left[\left(L_{\alpha /\beta }-1\right)/L_{\alpha /\beta }\right]-\ln \left[\left(L_{\alpha /\beta }^{\mathrm{e}\mathrm{q}}-1\right)/L_{\alpha /\beta }^{\mathrm{e}\mathrm{q}}\right]\right)$ and $ϵ\equiv \left(1/\left(2L_{\mathrm{t}\mathrm{o}\mathrm{t}}\right)\right)\hspace{0.17em}\left(\ln \left[\left(\hspace{0.17em}{L}_{\alpha }^{\mathrm{e}\mathrm{q}}-1\right)/\left(L_{\alpha }-1\right)\right]+\ln \left[\left(\hspace{0.17em}{L}_{\beta }^{\mathrm{e}\mathrm{q}}-1\right)/\left(L_{\beta }-1\right)\right]\right)$. 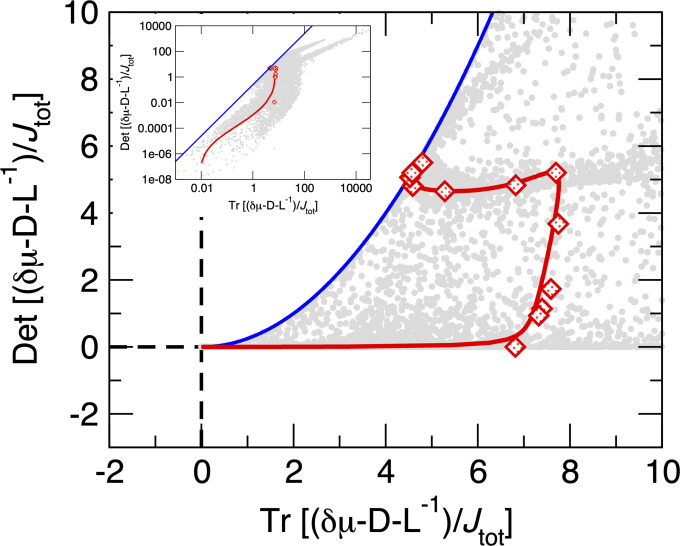The $\mathbf{D}$ matrix depends only on the equilibrium and nonequilibrium morphologies of the bundle. ${\mathbf{L}}^{-\mathbf{1}}$ is proportional to the inverse of the covariance matrix of fluxes and is computed as ${\mathbf{L}}^{-\mathbf{1}}\equiv \underset{t\to \infty }{lim}{J}_{\mathrm{t}\mathrm{o}\mathrm{t}}{\mathbf{M}}^{-1}/t$, in which $\mathbf{M}$ has the elements $M_{ij}=⟨\delta J_i\delta J_j⟩$, $\delta J_i=J_i-⟨J_i⟩$, and $t$ is the time of growth. In Fig. 4, we numerically verify Eq. 1/Eq. 10 for various parameter combinations.

Fig. 4.

Numerical verification of Eq. 10. The blue boundary marks the location of the inequality $\text{Tr}\left[A\right]\ge 2\sqrt{Det\left[A\right]}$ for a two dimensional square matrix $A$. The red diamonds are results from the nonequilibrium KMC simulations with the parameters used in Fig. 2 and the red line is the theoretical mean-field prediction for those same parameters. Gray dots are computed by constructing the matrices $\mathit{\delta }\mathit{\mu }$, $\mathbf{D}$, and ${\mathbf{L}}^{-1}$ using the the master equation results and computing the eigenvalues of $\left(\mathit{\delta }\mathit{\mu }-\mathbf{D}-{\mathbf{L}}^{-\mathbf{1}}\right)/J_{\mathrm{t}\mathrm{o}\mathrm{t}}$ using Mathematica (47) for randomly selected parameters from $L_{\beta ,\mathrm{e}\mathrm{q}}=\left[\mathrm{1,90,000}\right]$, $f_{density,\beta }=\left[\mathrm{1,100}\right]$, and $k_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}=\left[0.001,100\right]$ nm/s, with all other parameters the same as the red line. Inset shows these two quantities for a wider range, with both axes on logarithmic scales. We do not consider $k_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}<0.001$ nm/s due to limitations of numerical precision. Eq. 1/Eq. 10 provides strong constraints between the nonequilibrium forcing, morphology, and speed of growth.

The equality in Eq. 10 holds only when $\mathit{\delta }\mathit{\mu }-\mathbf{D}={\mathbf{L}}^{-\mathbf{1}}$. In that case, multiplying Eq. 10 by the column vector $\mathbf{J}$, containing the average fluxes $J_{\alpha /\beta }$ computed using Eq. 6 as $J_{\alpha /\beta }=J_{N-1,\alpha ,N,\alpha /\beta }+J_{N-1,\beta ,N,\alpha /\beta }$ (detailed in SI Appendix, section S4), we readily obtain

$$\mathbf{d}\mathbf{k}-\mathbf{D}\left[\mathbf{p}\right]={\tilde{\mathbf{L}}}^{-1}\cdot \mathbf{J},$$ [13]

where ${\tilde{\mathbf{L}}}^{-1}\equiv {\mathbf{L}}^{-1}/J_{\mathrm{t}\mathrm{o}\mathrm{t}}$, $\mathbf{d}\mathbf{k}$ is a column vector with elements $\log d{k}_{\alpha /\beta }$ (Eq. 3), and $\mathbf{D}\left[\mathbf{p}\right]$ is a column vector with elements that are the relative entropies between the equilibrium and nonequilibrium domain morphologies of the two cross-linkers in the bundle (SI Appendix, Eqs. S37 and S38). Eq. 13 relates the fluxes $\mathbf{J}$ and the thermodynamic driving $\mathbf{d}\mathbf{k}-\mathbf{D}\left[\mathbf{p}\right]$ with a correlation matrix ${\tilde{\mathbf{L}}}^{-1}$ in a form reminiscent of linear irreversible thermodynamics. Indeed, for weak driving near equilibrium conditions, we expect the correlation matrix ${\tilde{\mathbf{L}}}^{-1}$ to approach its equilibrium limit and Eq. 13 reduces to the standard linear irreversible thermodynamics identity. Furthermore, the entropy production of this bundling process can be rewritten in the following way when the equality in Eq. 10 holds:

$$\dot{\sigma }=2{\mathbf{J}}^T\left(\mathbf{d}\mathbf{k}-\mathbf{D}\left[\mathbf{p}\right]\right)=2{\left(\mathbf{d}\mathbf{k}-\mathbf{D}\left[\mathbf{p}\right]\right)}^T\cdot \tilde{\mathbf{L}}\cdot \left(\mathbf{d}\mathbf{k}-\mathbf{D}\left[\mathbf{p}\right]\right).$$ [14]

Eqs. 13 and 14 can be viewed as an extension of the classical linear irreversible thermodynamics framework (41) to our nonequilibrium bundling and polymerization process. It relates the various driving forces $\mathbf{d}\mathbf{k}$ and a relative entropic measure of the distance between the nonequilibrium and equilibrium structures, $\mathbf{D}\left[\mathbf{p}\right]$, to the various observed fluxes $\mathbf{J}$ through the flux covariance matrix ${\tilde{\mathbf{L}}}^{-1}$.

Thermodynamic uncertainty relations (TURs) (35, 36, 39, 40, 42) can also be readily derived from Eq. 10. TURs impose constraints on the fluctuations of currents in nonequilibrium processes, which present tighter bounds than the second law (Eq. 7). Specifically, our central result in Eq. 1/Eq. 10 implies that ${\mathbf{J}}^T\cdot \left[\mathit{\delta }\mathit{\mu }-\mathbf{D}-{\mathbf{L}}^{-\mathbf{1}}\right]\cdot \mathbf{J}\ge 0$. From this relation we can readily derive the following multidimensional thermodynamic uncertainty relation (MTUR) (40) (SI Appendix, section S5) for the actin bundling and growth process:

$$J_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(\mathrm{\Delta }\mu -{\epsilon }_{diss}\right)=2{\mathbf{J}}^{⊺}\cdot \left(\mathbf{d}\mathbf{k}-\mathbf{D}\left[\mathbf{p}\right]\right)⩾2{\mathbf{J}}^{⊺}\cdot {\tilde{\mathbf{L}}}^{-\mathbf{1}}\mathbf{J}.$$ [15]

This TUR-like bound takes into account the correlation between individual molecular fluxes.

Our central result provides a connection between the microscopic driving forces represented by $\mathit{\delta }\mathit{\mu }$ or $\mathbf{d}\mathbf{k}$, the nonequilibrium structure of the bundle as encoded by $\mathbf{D}$ or $\mathbf{D}\left[\mathbf{p}\right]$, and the fluctuations of the various fluxes denoted by ${\mathbf{L}}^{-\mathbf{1}}$ (obtained in the nonequilibrium steady state). Experimentally, it may be possible to measure the fluxes of various cross-linkers and the structures of their bundles. In which case, one could use Eq. 1 to bound the microscopic driving forces. These microscopic forces generally cannot be measured directly. Further, in nonequilibrium regimes where the ${\mathbf{L}}^{-\mathbf{1}}$ matrix exhibits singular or close to singular behavior, our results suggest that the system might be insensitive to perturbations that tune the various microscopic driving forces, $\mathbf{d}\mathbf{k}$. SI Appendix, Fig. S7 shows that the covariance of the molecular fluxes in our system does not have any singular behavior, suggesting that the nonequilibrium bundle morphology can be effectively tuned in the parameter regimes considered in this work.

Finally, Eq. 1/Eq. 10 can also be used to assess the relative importance of accounting for the statistics of the individual fluxes. To do so, we use the TURs (35, 36, 39, 40, 42) to derive a bound for the rate of entropy production in terms of the total flux, $J_{\mathrm{t}\mathrm{o}\mathrm{t}}$:

$$\mathrm{\Delta }\mu ⩾{\epsilon }_{diss}+\frac{2⟨J_{\mathrm{t}\mathrm{o}\mathrm{t}}⟩}{t⟨\delta J_{\mathrm{t}\mathrm{o}\mathrm{t}}^2⟩}.$$ [16]

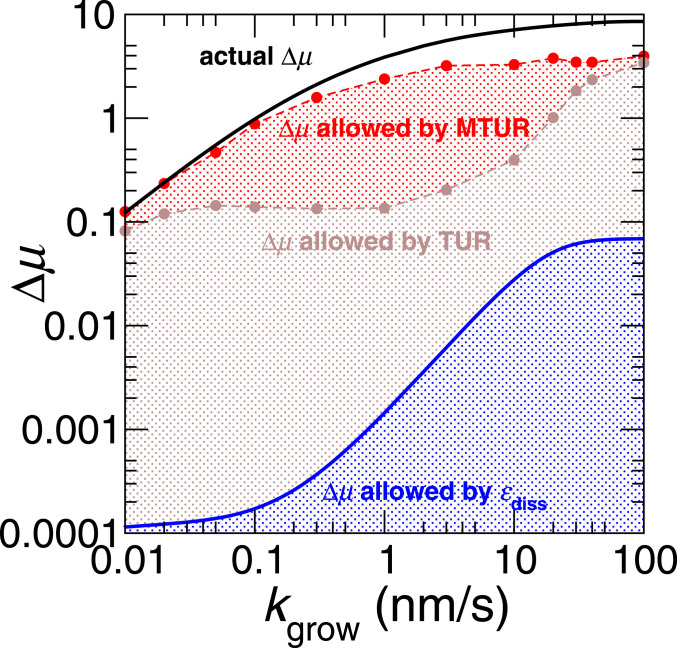
Here, $t$ is the growth time of the bundle, $⟨J_{\mathrm{t}\mathrm{o}\mathrm{t}}⟩$ is the average total flux of adding ABPs to the bundle, and $⟨\delta J_{\mathrm{t}\mathrm{o}\mathrm{t}}^2⟩$ is its variance. In Fig. 5, we compare the performance of Eq. 16 (brown) with that of Eq. 7 (blue). We see that the TUR bound is closer to the real driving $\mathrm{\Delta }\mu$ compared with the second-law bound. Nevertheless, it still fails significantly at $k_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}\approx 1$ nm/s, where it recovers only about 6% of the actual driving. This implies that controlling the overall kinetics is not enough for facilitating the sorting of ABPs.

Fig. 5.

Comparison of bounds on the nonequilibrium driving force $\mathrm{\Delta }\mu$. The black line (Eq. 8) is the actual driving force predicted by the master equation. The blue line (Eq. 7) is the driving force required for morphology change. The brown (Eq. 16) and red (Eq. 15) lines are the TUR and MTUR bounds computed from KMC simulations. Each of the brown and red data points is generated with 500 independent KMC simulations, each of $10^7$ steps. All parameters of the KMC simulations are the same as in Fig. 2.

In Fig. 5, we also plot the MTUR bound (Eq. 15) using cumulants of fluctuations in the individual fluxes from KMC simulations. Although not perfect, this bound recovers at least 46% of the actual driving $\mathrm{\Delta }\mu$ for the full range of polymerization rates. The gap between the MTUR bound and the actual driving is consistent with previous observations (36) that TUR bounds become weaker at stronger driving.

The MTUR bound in Eq. 15 can also be obtained by replacing $J_{\mathrm{t}\mathrm{o}\mathrm{t}}$ in Eq. 16 with a scalar observable $J_{\varphi }=\cos \varphi J_{\alpha }+\sin \varphi J_{\beta }$ and then maximizing $2{⟨J_{\varphi }⟩}^2/\left(t{J}_{\mathrm{t}\mathrm{o}\mathrm{t}}⟨\delta J_{\varphi }^2⟩\right)$ by varying $\varphi$ (SI Appendix, section S5). When $\tan \varphi =1$, the scalar observable $J_{\varphi }=J_{\mathrm{t}\mathrm{o}\mathrm{t}}$ and the MTUR bound in SI Appendix, Eq. S40 reduces to the TUR bound in Eq. 16. Compared with this TUR bound, we find that the MTUR bound is mostly improved where the optimized $\tan \varphi$ values deviate significantly from 1 (SI Appendix, Fig. S5), and the fluxes are strongly correlated. Hence it is crucial to take into consideration the statistics of the individual fluxes. Indeed, the analytical expression of $\tan \varphi$ (SI Appendix, Eq. S44) and the empirical results in SI Appendix, Figs. S6 and S7 show that $\tan \varphi$ is mainly governed by the ratio of the domain lengths, $L_{\alpha }/L_{\beta }$. In the regime $k_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}\approx 0.1$ to 10 nm/s, the domain lengths of the two ABPs differ significantly and so $\tan \varphi$ deviates significantly from 1 in this regime. Consequently, the MTUR bound (Eq. 15) is significantly tighter than the simple TUR bound (Eq. 16) for $k_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}\approx 0.1$ to 10 nm/s. We conclude that thermodynamic costs can be underestimated in regimes where the two ABPs display remarkably different sorting behavior if only the total flux, rather than individual ones, is considered.

Conclusions

We have derived a strong thermodynamic constraint relating the microscopic driving of a growing bundle (denoted by $\mathit{\delta }\mathit{\mu }$ in Eq. 1), the morphology of the bundle in its nonequilibrium steady state as described by the matrix $\mathbf{D}$, and the statistics of the rates of incorporation of cross-linkers as described by the matrix ${\mathbf{L}}^{-\mathbf{1}}$. Our central results, which are validated in the context of growing actin bundles, can be viewed as extensions of the linear irreversible thermodynamics framework (41). They also have practical applications. As an example, with proper extension, they potentially provide a route to estimate microscopic driving forces (contained in the $\mathit{\delta }\mathit{\mu }$ matrix) from experiments in which the various fluxes and morphologies are measured using microscopy and quantitative image analysis.

While this current work is focused exclusively on the growth dynamics of bundled actin networks, we anticipate that the approach presented here can be used in other contexts, such as the interplay between structure, speed, and nonequilibrium forcing in the growth dynamics of branched actin networks (43–45); the self-organization of other ABPs to distinct actin network architectures (e.g., networks initiated by formin or the Arp2/3 complex) (31); and the sorting of ABPs to distinct networks under confinement (23).

Methods

We simulate the growth of an actin bundle with two types of ABPs using KMC simulations. Two initial configurations are selected for each simulation: an actin bundle composed of 100 $\alpha$-type ABPs or a bundle composed of 100 $\beta$-type ABPs. We exclude the first 100 ABPs when measuring the final structure and find that domain lengths in the bundle are independent of its initial configuration in the parameter range that we explore. For each step in the KMC simulations, we identify the state of the bundle tip and all the possible forward and backward moves that can be initiated from this state. The KMC simulations are performed using the Gillespie algorithm (46). We summarize the rates used in the KMC simulations in SI Appendix, Table S1. To compute domain lengths in Fig. 2, we run one simulation of $S=10^6$ steps at each $k_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}$ and measure domain lengths $L_{\alpha }$ and $L_{\beta }$ from the full bundle by counting the number of consecutive ABPs of the same type and averaging their lengths. To generate the KMC data points in Figs. 4 and 5, we run 500 simulations of $S=10^6$ steps at each actin polymerization rate $k_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}>0.01$ nm/s; at $k_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}=0.01$ nm/s, we run 5,000 simulations of $S=2\times 10^8$ steps to ensure the convergence of the covariance of the fluxes.

Data Availability

All study data are included in this article and/or SI Appendix.