Automated design of pulse sequences for magnetic resonance fingerprinting using physics-inspired optimization

Significance

Magnetic resonance is a widely used noninvasive medical imaging technology. Most clinical MRI scans generate qualitative or “weighted” images. A recent new technology, magnetic resonance fingerprinting (MRF), simultaneously extracts quantitative voxel-by-voxel measurements of multiple intrinsic tissue properties such as $T_1$ and $T_2$ relaxation rates in a single scan, rapid enough for clinical use. These have been used for tumor characterization, epilepsy lesion detection, and for estimating variability of tissues in asymptomatic subjects. Here, we find that detailed computer models of random and systematic errors can be combined with physics-inspired optimization heuristics to discover MRF pulse sequences achieving substantially improved performance relative to MRF pulse sequences previously designed by human experts.

Abstract

Magnetic resonance fingerprinting (MRF) is a method to extract quantitative tissue properties such as $T_1$ and $T_2$ relaxation rates from arbitrary pulse sequences using conventional MRI hardware. MRF pulse sequences have thousands of tunable parameters, which can be chosen to maximize precision and minimize scan time. Here, we perform de novo automated design of MRF pulse sequences by applying physics-inspired optimization heuristics. Our experimental data suggest that systematic errors dominate over random errors in MRF scans under clinically relevant conditions of high undersampling. Thus, in contrast to prior optimization efforts, which focused on statistical error models, we use a cost function based on explicit first-principles simulation of systematic errors arising from Fourier undersampling and phase variation. The resulting pulse sequences display features qualitatively different from previously used MRF pulse sequences and achieve fourfold shorter scan time than prior human-designed sequences of equivalent precision in $T_1$ and $T_2$. Furthermore, the optimization algorithm has discovered the existence of MRF pulse sequences with intrinsic robustness against shading artifacts due to phase variation.

In contrast to traditional MRI, which relies on simple pulse sequences with analytically solvable dynamics, magnetic resonance fingerprinting (MRF) extracts tissue properties such as $T_1$ and $T_2$ from arbitrary pulse sequences by pattern matching measured signals to a dictionary of numerically computed signals for different tissue types. This can be done by interpreting the signals as complex vectors and finding the dictionary entry whose inner product with the observed signal has the largest magnitude (1). MRF has been explored for several clinical applications (2–9). By allowing arbitrary pulse sequences, MRF opens up a design space of thousands of tunable parameters over which to search for pulse sequences achieving greater precision at shorter scan time.

Optimization of MRF acquisition parameters, such as radiofrequency pulses, timing, and magnetic field gradients, is needed to achieve the best signal-to-noise ratio, image quality, precision, and reproducibility. However, the design and optimization of pulse sequences is very challenging for two main reasons. First, it is difficult to design an efficiently computable cost function that accurately predicts in vivo performance of MRF pulse sequences. Second, the resulting optimization problem is computationally difficult, as the space of possible pulse sequences is too high-dimensional and nonconvex for simple methods, such as exhaustive search or gradient descent. In this work, we use optimization algorithms to choose the flip angle and repetition time (TR) duration for each TR. Thus, the search space for a pulse sequence of $n$ pulses is $2n$-dimensional, where for two-dimensional (2D) scans, $n$ is typically on the order of 1,000 and is even larger for three-dimensional (3D) scans.

In clinical settings, it is typical to accelerate MRF scans by sampling only a small fraction of the relevant Fourier coefficients (“$k$-space”) after each pulse. For example, acceleration factors of 48 to 400 (sampling only 2 to 0.2%, as compared to the Nyquist sampling requirement) have been reported in 2D or 3D MRF in vivo scans (5, 10–12). Through extensive in vivo experimentation, we find that the dominant sources of error in MRF brain scans in this regime are Fourier undersampling artifacts and system-based phase-variation-induced shading artifacts. The interplay of these two errors results in temporally and spatially dependent artifacts in the reconstructed images and causes aliasing and shading artifacts in the resulting tissue maps (5). Random error due to background noise in the receive coils is also present, but appears to play a secondary role.

To design MRF pulse sequences through optimization, one first needs a cost function, which, given a proposed pulse sequence, produces a metric of its predicted effectiveness. In previous work, several cost functions have been proposed. Under the assumption of zero-mean independent Gaussian random error at each time step in the raw signal, lower bounds on the SD in the inferred values of $T_1$ and $T_2$ from an MRF scan can be obtained by using the Cramer–Rao bound. Taking a linear combination of these bounds as a cost function, optimized MRF pulse sequences are obtained in ref. 13 by sequential quadratic programming, in ref. 14 using the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm, in ref. 15 using an interior point method, and in ref. 16 using dynamic programming. In ref. 17, the Gaussian model of random error is supplemented by a model of Fourier undersampling artifacts in which an additional Gaussian noise term is added, whose magnitude is signal-dependent. Optimized sequences are then obtained by using a genetic algorithm. In ref. 18, the magnetization vs. pulse index time-series for a given tissue is interpreted as a vector, and inner product between the normalized vectors determined by different tissues is interpreted as a metric of distinguishability. Minimization of these inner products is then performed with simulated annealing, branch and bound, an interior point method, and brute-force search. Several works have been devoted exclusively to the design of a cost function predictive of in vivo performance of MRF sequences, without also pursuing optimization (19–21).

In the highly undersampled regime most relevant to clinical settings, we find that cost functions based on simple statistical noise models or crude heuristics, such as minimizing inner product between signal vectors, are insufficient to accurately predict in vivo performance of MRF pulse sequences. An obvious alternative is to use a comprehensive first-principles computer simulation of the MRF scan using explicit models of a tissue distribution, a choice of acquisition parameters including $k$-space trajectories, and an image-reconstruction algorithm. Such computer models have been constructed in prior work and are referred to as “digital phantoms.”* Digital phantoms that directly model undersampling artifacts by carrying out nonuniform Fourier transforms are computationally costly, often taking several minutes to evaluate, even on powerful workstations. This makes them challenging to use as a cost function within an optimization, as our computational experiments show that even carefully tuned optimization algorithms often require tens of thousands of cost-function evaluations to find good pulse sequences.

Here, we introduce an accelerated digital phantom that makes use of a simplified model of brain tissue distribution. This approximation speeds up the evaluation by approximately two orders of magnitude. Further detail on the accelerated digital phantom is given in Methods and SI Appendix. A preliminary report also appears in ref. 22.

Our computational experiments show that, even when allowed thousands of cost-function evaluations, standard “off-the-shelf” optimization methods, such as sequential quadratic programming and BFGS, yield poor pulse sequences. However, with careful parameterization of the search space, judicious generation of moves within the search space, and well-tuned hyperparameters, we find that good pulse sequences can be found with both simulated annealing and substochastic Monte Carlo optimization methods. Use of Monte Carlo methods, such as simulated annealing, for optimizing magnetic resonance (MR) protocols has a long history (23). Our experiments show that such methods can be used to design high-speed MRF pulse sequences “from scratch”—i.e., without human-designed pulse sequences as starting points—but that this requires careful design of the cost function as well as the moves by which the search space is explored, as discussed in Methods. In recent work, reinforcement learning has been used for de novo design of MRI pulse sequences (24).

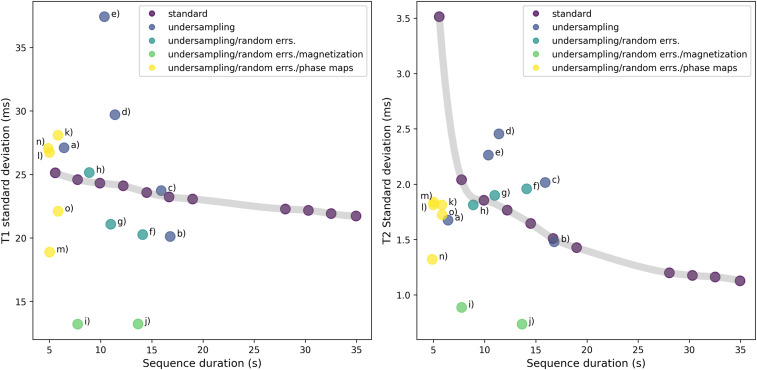
Using these methods, the optimization algorithms yield pulse sequences that display superior performance to prior state-of-the-art MRF pulse sequences designed by human experts. Improved precision can be achieved by increasing the number of pulses (and hence the scan time). Thus, a performance comparison can be made by plotting optimized pulse sequences against the precision vs. duration tradeoff curve obtained by taking truncations of the human-designed pulse sequence to different numbers of pulses. (see Fig. 5.)

Fig. 5.

Precision vs. duration tradeoff in T1 (Left panel) and T2 (Right panel) for optimized and unoptimized sequences. Here, the metrics of precision are the SDs in inferred $T_1$ and $T_2$ values, which we estimate from in vivo data using bootstrap statistics, as described in ref. 41. The standard sequence from (1) is truncated to TR counts from 480 to 3,000 in order to obtain scans of different durations, as illustrated by the gray tradeoff curve. The optimized data points are classified according to which terms were included in the cost function. Unsurprisingly, the sequences with best robustness against random error (err.) are obtained by heavily incentivizing large signal magnitude (i.e., magnetization) in the cost function. In vivo images corresponding the labeled data points (a–o) are shown in SI Appendix. Note that these bootstrap statistics are derived from in vivo experimental data, for which exact ground truth values of $T_1$ and $T_2$ are inaccessible. Thus, they can only assess scatter, and not bias.

In addition to higher precision at given scan time or shorter scan time at given precision (by up to a factor of four), the optimized sequences display a feature of intrinsic robustness to highly undersampled scans with phase variation, such as can arise from magnetic field inhomogeneities. The interplay between these two sources of error has typically resulted in shading artifacts in $T_1$ and $T_2$ maps obtained from low-pulse-count MRF scans via direct dictionary matching. Alternatives to direct dictionary matching, such as iterative reconstruction (25–28), have different characteristics regarding systematic error. In future work, the optimization framework presented here can be applied to these alternative schemes.

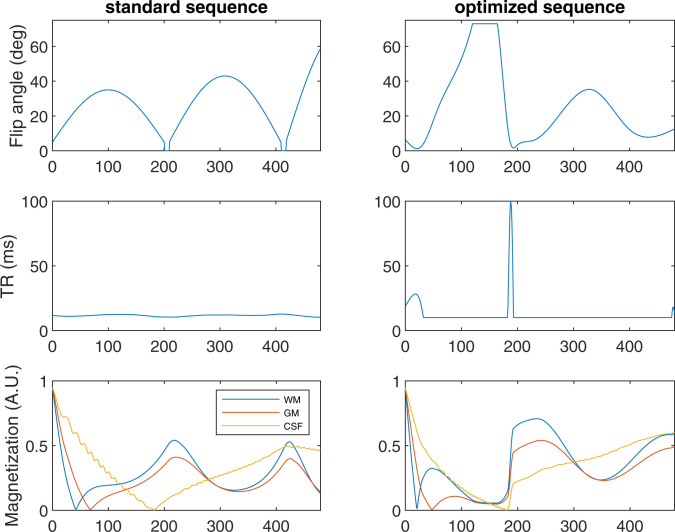
To maximize the chance of finding novel pulse sequences, we initialize the optimization algorithms from an ensemble of randomly generated pulse sequences, rather than from an existing human-designed pulse sequence. Over many repetitions from different starting points, the optimization algorithm produces a large number of distinct pulse sequences, which, nevertheless, consistently display certain qualitative features. Some of these reproduce features that were previously incorporated into MRF pulse sequences designed by human experts, while others are qualitatively distinct, as discussed in Discussion (see Fig. 3). These algorithmically discovered design patterns can inform future MRF pulse-sequence design by human experts.

Fig. 3.

The optimized sequences (Left column) display qualitatively different features than the standard human-designed sequence (Right column). In particular, the optimization algorithm consistently produces pulse sequences in which the TR duration is at its minimum allowed value for most of the TRs, but briefly spikes to much longer duration. The predicted magnitude of the magnetizations for white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) are shown for each sequence in units such that the initial inversion pulse achieves magnetization of magnitude 0.95. (The considerations behind modeling the initial magnetization as 0.95 are discussed in ref. 42.) Optimized sequence $o$ is chosen here as a representative example, about which further information is available in Fig. 5 and SI Appendix, Tables 1–4. The optimization that produced this sequence used $w_{\mathrm{C}\mathrm{S}\mathrm{F}}=0.024\hspace{0.17em}52$, $w_{\mathrm{W}\mathrm{M}}=1.000$, $w_2=12.02$, and $w_{\mathrm{m}\mathrm{a}\mathrm{g}}=0$. The pulse sequences are available for noncommercial research purposes from https://github.com/madan6711/Automatic-MRF-seq-design. A.U., arbitrary units; deg, degrees.

Methods

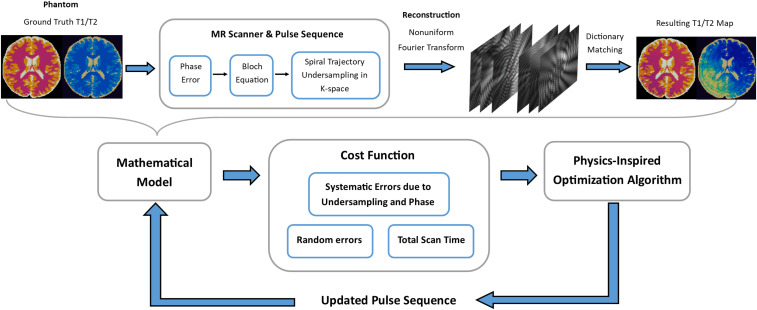
We define the sequence optimization problem with three main components: a cost function, a search space of possible pulse sequences, and an optimization algorithm. Fig. 1 summarizes the optimization workflow. The theory and implementation of each component are described in the following sections.

Fig. 1.

Here, the overall structure of the pulse-sequence optimization process is illustrated. A physics-inspired optimization algorithm proposes one or more randomly generated initial pulse sequences, which are then given to a cost function, which returns a quality metric assessing their speed and accuracy. Based on this feedback, the optimization algorithm proposes updated sequences. The cycle of updating and reevaluation is repeated for a fixed number of iterations. The best sequence found during this process, as judged by the cost function, is produced as final output. Within the cost function, a full simulation of MRF process is performed. The discrepancy between the simulated ground truth $T_1$ and $T_2$ values in a brain slice and the corresponding values inferred by the standard MRF dictionary-matching procedure are used as a metric of accuracy.

MRF Pulse Sequences.

The specific class of MRF pulse sequences that we consider are Fast Imaging with Steady-State Progression (FISP) sequences (10), applied in the context of making 2D $T_1$, $T_2$, and proton density maps of the brain.^† At the start of a FISP pulse sequence, an inversion pulse is applied to initialize the spins of hydrogen nuclei as close as possible to antialignment with the background $B_0$ field, which is taken to be in the positive $z$ direction. In such a sequence, step $\mathrm{s}$ has total duration ${\mathrm{T}\mathrm{R}}_s$, consisting of the following pieces. First, polar rotation ${\alpha }_s$ is applied followed by phase rotation ${\theta }_s$. Then, a wait time of ${\mathrm{T}\mathrm{E}}_s<{\mathrm{T}\mathrm{R}}_s$ is imposed during which the spins evolve according to exponential decay determined by $T_1$ and $T_2$. Next, the magnetization measurements are performed. Then, further exponential decay occurs during the remaining time ${\mathrm{T}\mathrm{R}}_s-{\mathrm{T}\mathrm{E}}_s$. Lastly, a strong “spoiling” gradient is applied to mitigate the effects of magnetic field inhomogeneity. (For a sequence diagram, see ref. 10.)

An MRF pulse sequence consists of hundreds or thousands of such steps, with flip angle and TR duration varying from one to the next. In practical settings, MRF scans typically sample Fourier space very sparsely in order to achieve short scan time. Commonly used Fourier undersampling patterns include radial (29), spiral (1), and 3D Cartesian (30). Here, we consider the “single-shot” setting, in which one spiral trajectory through $k$-space is sampled after each pulse. The spiral trajectory employed in this study is a variable-density spiral, which needs 48 interleaves to cover $k$-space (31). The readout duration is 5.9 ms, with a field of view of 300 × 300 ${\mathrm{m}\mathrm{m}}^2$ and matrix size of 256 × 256 (1, 10, 12, 31). The spiral sampling is varied temporally from one TR to the next, so the aliasing artifacts do not cause constant bias in the signals. A Nonuniform Fast Fourier Transform (32) is then applied to reconstruct images from an MRF scan using measured $k$-space trajectories (33). Quantification of tissue properties, such as $T_1$ and $T_2$ relaxation times, is performed in each image voxel by comparing the observed magnetization time-series against the entries of a dictionary that contains a list of potential such signals. For each voxel, one can assign ($T_1$, $T_2$) based on the dictionary entry that most closely matches the observed signal. Considering system limitations and scan time, we constrain the TR duration to the range of 10 to 100 ms, resulting in a total scan time of in the range of a few seconds for a 2D MRF scan; 3D MRF scans with duration of a few minutes have been reported in refs. 5 and 34.

Mathematical Model.

The dynamics of nuclear spins in a magnetic field are described phenomenologically by the Bloch equation (35). Given the magnetic field as a function of time at a given location, an initial condition for all the spins in a voxel,^‡tissue parameters $T_1$, $T_2$, and acquisition parameters (flip angles, TRs, unbalanced gradients), the Bloch equation predicts the state of the spins at subsequent times. Here, we consider MRF pulse sequences for 2D slices through brain tissue consisting of 256 × 256 voxels, each 1.2-mm by 1.2-mm spatial resolution. Correspondingly, our mathematical model consists of a value of $T_1$, $T_2$, and $m_0$ (proton density) assigned to each voxel. The proton density only affects the magnetization of the voxel by acting as a time-independent multiplicative factor. For a given pulse sequence, we solve the Bloch equations (in the hard-pulse approximation) to obtain magnetization vs. time for each ($T_1,T_2$) pair appearing within the voxels of the simulated tissue distribution.

MR scans are complicated processes involving many sources of random and systematic errors. An accurate model of these is a necessary ingredient for an optimization algorithm to produce sequences with good in vivo performance. Here, we model three main sources of error and their interactions: Fourier undersampling artifacts, spatially dependent phase variation, and random error. Many subtle effects can be present in the interactions. For example, aliasing artifacts are often observed in the $T_1$ and $T_2$ maps derived by applying dictionary matching to Fourier undersampled MRF scans. To minimize these, it is thought to be beneficial to design flip angles and TR times so that the Bloch dynamics spreads signal intensity as uniformly as possible between the sets of TRs associated with each of the $k$-space sampling trajectories. Similarly, shading artifacts are thought to arise through the interplay of two sources of systematic error, which individually do not cause shading artifacts, as described below. With a direct first-principles simulation in the cost function, pulse sequences can be designed to suppress such errors without needing to identify and enumerate them.

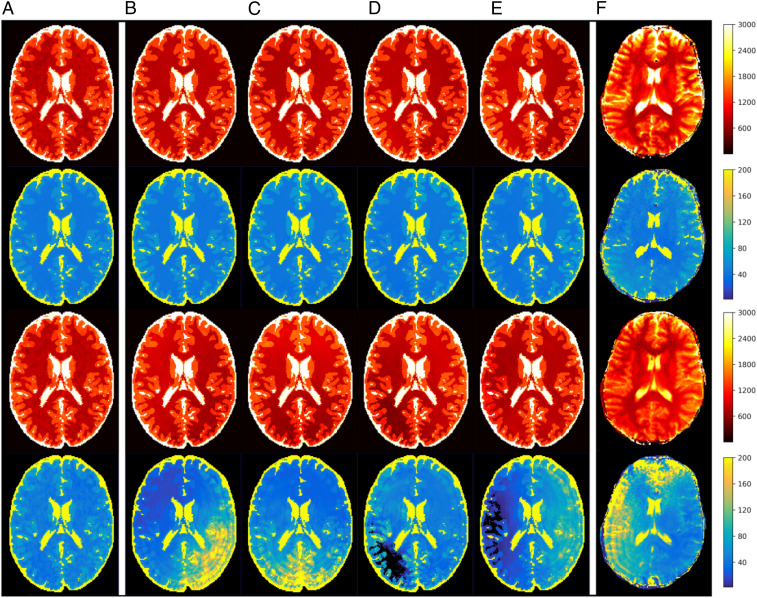
It is common to observe spatial phase variation in MR scans, which could be from spatially varying $B_0$ or $B_1$ field inhomogeneities or temporally varying motion. If not explicitly modeled, such phase variation can contribute a source of systematic error in MRF scans. Although the phase variations observed experimentally vary from scan to scan, even on the same machine, they tend to be smoothly varying across the field of view and differ between scans mainly in the direction across which they vary. In our model, we consider static spatially varying phases, which are among the most common sources of systematic error in MR scans and have been reported to cause artifacts and distortion in MR images (36, 37). Furthermore, the interplay between phase variation and aliasing due to Fourier undersampling introduces spatially and temporally varying artifacts that affect both magnitude and phase of the measured signals, which causes a commonly seen “shading artifact” shown in Fig. 2F from in vivo MRF scans. The shading is not seen when only the undersampling is modeled (Fig. 2A). Such interactions of artifacts have not been considered in previous work, which is one of the main sources of discrepancy between simulated sequence performance and in vivo scan performance.

Fig. 2.

$T_1$ (red) and $T_2$ (blue) map simulations of an optimized sequence (top two rows) and a standard human-designed sequence (1) (bottom two rows) incorporating phase variation. The error is modeled as a time-independent phase that varies quadratically along a chosen direction. Experimentally, one finds that this direction varies randomly from one scan to the next. In this figure, A includes no phase variation. B–E correspond to four example orientations for the phase variation. In vivo results for both sequences are shown in F.

In addition to systematic errors, scans exhibit random error, the dominant source of which is Johnson noise in the receive coils. Following refs. 17 and 19, we model this as independent complex Gaussian zero-mean error at each data point, i.e., white noise.

Cost Function.

For an MRF scan, we wish to minimize $T_1$ error, $T_2$ error, and scan time. We use a weighted combination of the predicted values for these quantities as a cost function to minimize. Using the formulas from refs. 17 and 19 and an assumed value of variance ${\sigma }^2$ of a Gaussian noise distribution, one can obtain predicted SD on $T_1$ and $T_2$ for a given tissue due to random errors. By simulating Fourier undersampling artifacts and phase variation, we obtain predictions of discrepancies between the theoretical and measured values of $T_1$ and $T_2$ associated with each voxel. Averaging over voxels of a given tissue type, we can obtain rms values of systematic error for each of the three tissue types in our model. Correspondingly, an estimate of total error is obtained by taking the sum in quadrature of these rms systematic errors with the predicted SDs due to random error. We thus obtain six numbers, which are the predicted rms errors in inferred $T_1$ and $T_2$ for each of the three tissue types in our model (gray matter, white matter, and cerebrospinal fluid). Ultimately, we wish to minimize these six errors and the total duration of the pulse sequence. Thus, we need to combine these seven quantities into a single aggregate measure, which our optimization algorithm will attempt to minimize. Optionally, we may add a term incentivizing large average magnetization of the tissues, as this is clearly advantageous for signal to noise ratio.

The cost function $C$ is defined as follows.

$$C=\left({\sigma }^{\left(T_1\right)}+w_2\hspace{0.17em}{\sigma }^{\left(T_2\right)}\right)\sqrt{t}+\frac{w_{\mathrm{m}\mathrm{a}\mathrm{g}}}{{\overline{m}}_{min}},$$ [1]

$${\sigma }^{\left(p\right)}={\sigma }_{\mathrm{G}\mathrm{M}}^{\left(p\right)}+w_{\mathrm{W}\mathrm{M}}\hspace{0.17em}{\sigma }_{\mathrm{W}\mathrm{M}}^{\left(p\right)}+w_{\mathrm{C}\mathrm{S}\mathrm{F}}\hspace{0.17em}{\sigma }_{\mathrm{C}\mathrm{S}\mathrm{F}}^{\left(p\right)}\hspace{1em}p\in \left\{T_1,T_2\right\}.$$ [2]

Here, $t$ is the total duration of the sequence, $w_2$ is a tunable “weight” quantifying the importance of $T_2$ errors relative to $T_1$ errors, and $w_{\mathrm{W}\mathrm{M}}$ and $w_{\mathrm{C}\mathrm{S}\mathrm{F}}$ are tunable weights quantifying the importance of errors in white matter and cerebrospinal fluid voxels relative to errors in gray matter voxels. ${\overline{m}}_{min}$ is magnetization, averaged over TRs and minimized over modeled tissues. $w_{\mathrm{m}\mathrm{a}\mathrm{g}}$ is the weight of the incentive on magnetization, which can be set nonzero if a stronger incentive is desired than that provided indirectly through the modeling of random error. The motivation for the form of the $t$-dependence of Eq. 1 is that, by standard sampling statistics, one expects that by using $n$ measurements, one can obtain SD scaling as $1/\sqrt{n}$. Consequently, multiplying the total error by $t$ raised to the power $1/2$ or higher should steer the optimizer toward shorter duration sequences. In practice, we find that the factor of $\sqrt{t}$ is usually effective. The motivation behind the functional form of the optional magnetization term is that, if magnetization vanishes completely, there is no signal and error formally diverges.

Direct evaluation of errors due to Fourier undersampling and phase variation is problematic to incorporate into a cost function due to high computational cost. To speed up evaluation, we here introduce a simplifying approximation. Specifically, rather than assigning each voxel to a unique $T_1$, $T_2$ pair, the voxels are all assumed to arise from one of three brain tissue types: gray matter, white matter, and cerebrospinal fluid, each of which has fixed values of $T_1$, $T_2$, and proton density. As a result, the magnetization of the voxels in response to a pulse sequence can be computed by solving the Bloch equations for only three $\left(T_1,T_2\right)$ pairs. More importantly, the artifacts due to Fourier undersampling and phase variation can be precomputed based on the spatial distributions of the three tissue types, for each of the 48 $k$-space trajectories. Given these 144 precomputed response functions, a simulation of the reconstructed $T_1$ and $T_2$ maps arising from a 1,000-pulse MRF sequence can be completed in 2.0 s on a 24-core computer (Azure NC-24 virtual machine). (See Fig. 2 for examples of simulated maps and comparison to in vivo data.)

Optimization Algorithms.

We formulate the design of MRF pulse sequences as a global optimization program over continuous variables. The cost function is treated as a black box. There is no formula for the gradient of the cost function; strictly speaking, the cost function is not differentiable due to the discrete dictionary matching. Due to the highly nonconvex nature of the cost function, we relied on optimization heuristics capable of escaping from local minima. The best performing of these, according to our experimentation, were simulated annealing and substochastic Monte Carlo. The latter is a quantum-inspired optimization algorithm in which quantum fluctuations are modeled in order to escape from local minima. The method used here is a continuous-variable generalization of the substochastic Monte Carlo method described in ref. 38.

Here, we perform optimization with physics-inspired optimization algorithms, which have been tuned specifically for the MRF pulse-sequence optimization problem. To obtain good pulse sequences, we first reduce the dimension of the search space by only considering pulse sequences that vary smoothly over time. In prior work, it has been observed^§ that such pulse sequences, when used with dictionary matching, yield $T_1$ and $T_2$ maps with milder Fourier undersampling artifacts than highly discontinuous sequences (13–15, 39). We achieve this by parameterizing the pulse sequences using cubic splines, as has been done in other contexts (15, 40). The two optimization algorithms found to be most successful (variants of simulated annealing and substochastic Monte Carlo) are both based on biased random walks in the search space. The random perturbations that generate these walks are not only varied in time such that larger, exploratory perturbations are followed by smaller, fine-tuning perturbations, but are also nonisotropic, such that different classes of variables are perturbed by different amounts. These nonisotropic updates appear to be crucial to the success of the algorithms, as discussed in SI Appendix. After a number of runs of the optimization algorithms with different hyperparameters and random seeds, the most promising sequences are selected for in vivo testing.

In Vivo Experiments.

The optimized pulse sequences were tested by using in vivo scans to validate our mathematical modeling and directly evaluate the precision, robustness, and image quality of the quantitative tissue maps obtained by using optimized MRF pulse sequences. In vivo scans were performed in a Siemens Magnetom Skyra 3T scanner on volunteers following informed consent and approval from the Institutional Review Board of University Hospitals Cleveland Medical Center. The scan was acquired with a field of view of 300 × 300 ${\mathrm{m}\mathrm{m}}^2$, matrix size of 256 × 256, and slice thickness of 5 mm. As a supplement to subjective judgement of image quality, data from these scans were combined with experimentally measured noise levels in the receive coils to obtain quantitative estimates of random error via bootstrapping statistics, as described in ref. 41. The SD in inferred $T_1$ and $T_2$ values from the bootstrap method is calculated within regions of interest in the white matter and is used as a metric of precision.

Results

Optimized Pulse Sequences.

Fig. 3 compares an optimized sequence against a standard MRF scan. The optimized sequences display qualitatively distinct features from prior human-designed sequences, such as “spiked” TR durations. Although the details of optimized sequences vary, this spiked TR duration feature is observed consistently for sequences optimized with and without models of phase variation in the cost function. Note that the magnetization curves shown depict the total magnitudes of the magnetization vectors, not just the magnitudes of their projections onto the $xy$-plane, which determine the signal strength of the immediate measurement. However, the latter is strongly sensitive to the flip angle of the given pulse, whereas the former gives a more meaningful metric of the reservoir of available magnetization to be exploited in subsequent pulses. Note also that the optimized sequence shown in Fig. 3 has total duration only slightly longer than the standard sequence (5.85 s vs. 5.57 s), despite having some TRs that are vastly longer than any TRs in the standard sequence. The optimization algorithm achieves this by setting almost all other TRs to the minimum allowable duration (10 ms), whereas the majority of the TRs in the standard sequence have duration between 11 and 13 ms.

Convergence of Optimization Algorithms.

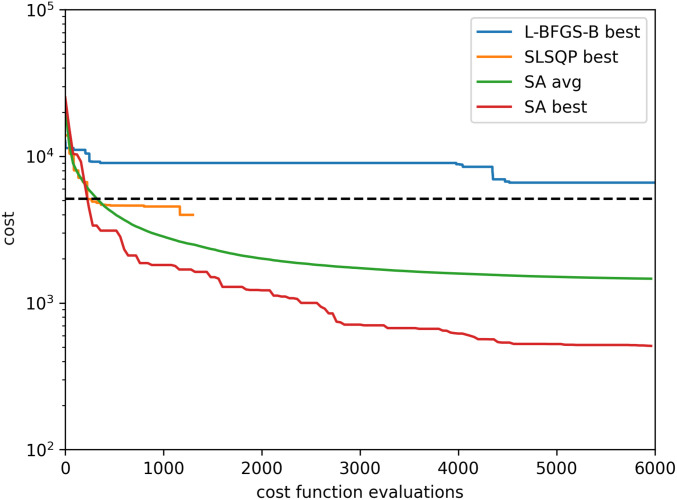
Here, we compare three optimization algorithms on the MRF cost function (Eq. 1) with a spline-parameterized search space. First, we apply Limited-memory Broyden-Fletcher-Goldfarb-Shanno algorithm with Bounds (L-BFGS-B), which is a quasi-Newton method that uses gradient information to find local minima of smoothly varying cost functions (43). (A variant of BFGS was used to optimize MRF pulse sequences in ref. 14.) Our cost function is not formally differentiable, due to dictionary matching. Nevertheless, it is smooth on length scales that are not too short, thus yielding meaningful gradient-like information via finite differences. As can be observed from Fig. 4, the cost function is sufficiently nonconvex that, even by starting L-BFGS-B from several random starting points and selecting the best local minimum found yields poor optimization performance. Similarly, we compare to sequential least-squares programming (SLSQP) (44) from multiple random starting points, which also arrives at relatively poor optima upon reaching the algorithm’s termination condition. SLSQP is a widely used optimization method closely related to the sequential quadratic programming algorithm employed to optimize MRF pulse sequences in ref. 13. The best performance is shown by the physics-inspired Monte Carlo method. Nevertheless, by initiating this with random seeds, one never finds precisely the same optima, and, thus, one can conclude that the global optimum is almost certainly not found.

Fig. 4.

Comparison of standard optimization routines from SciPy (L-BFGS-B and SLSQP) against our simulated annealing implementation with nonisotropic moves (SA). The decrease in cost is plotted as a function of the number of queries made to the cost function. As the evaluation of the cost function is by far the most computationally intensive part of the algorithm, this is therefore a metric of the efficiency of the optimization method. The physics-inspired method’s performance varies depending on random seed. Here, the average performance across 200 trials is shown alongside the performance from the best of these trials. (As a meta-algorithm, one can run such trials in parallel and select the resulting sequence with lowest cost-function value.) For comparison, the cost-function value achieved by the standard sequence is shown as a dashed line.

Robustness Against Random Error.

Fig. 5 compares the precision of $T_1$ and $T_2$ values between the standard and optimized sequences using various choices of weight parameters $w_2$, $w_{\mathrm{m}\mathrm{a}\mathrm{g}}$, $w_{\mathrm{W}\mathrm{M}}$, and $w_{\mathrm{C}\mathrm{S}\mathrm{F}}$. Unoptimized sequences of different duration are obtained by truncating the sequence from ref. 1. These then define a tradeoff curve between precision and duration. As shown in Fig. 5, the optimizer can yield sequences achieving greater precision at given duration or, equivalently, shorter duration to achieve a given precision, relative to the unoptimized sequences. Specifically, at a given duration, the best optimized sequences achieve over twofold error reduction in inferred $T_1$ and $T_2$. Alternatively, optimized sequences are found that can achieve over 4.5x speedup relative to unoptimized sequences of comparable precision, as detailed in SI Appendix. Note however, that bootstrap statistics measure only random errors, and not systematic. Therefore, the optimized sequences that appear best according to bootstrapping may not coincide with the optimized sequences that yield best subjective image quality.

Robustness Against Systematic Error.

Robustness against aliasing and systematic errors were estimated in simulations and tested with in vivo scans. Fig. 2 compares the $T_1$ and $T_2$ maps obtained from standard and optimized MRF scans, according to simulation and experiment. In both simulation and experiment, Fourier undersampling artifacts are visible as circular rings, and shading artifacts induced by phase variation are visible as nonsymmetric image intensity variations. Such errors are quite significant in state-of-the-art short-duration human-designed pulse sequences, as can be seen in the bottom two rows of F.

In addition to in vivo results (F), Fig. 2 shows simulation results under five different assumptions. A shows simulations incorporating only Fourier undersampling artifacts. B–E show simulations that additionally incorporate phase variations in four orientations. (The phase is modeled as varying quadratically across the chosen direction.) Due to the unpredictability of the orientation of phase variation from one scan to the next, maps from simulation do not match in detail the results from individual in vivo scans. However, the simulations that incorporate phase variation accurately predict the relative image quality achieved in vivo by different pulse sequences. Furthermore, the rank-ordering of pulse-sequence quality is largely independent of the orientation of the phase homogeneity. Thus, high-quality (i.e., robust) sequences can be obtained by optimization using a cost function in which a single orientation of variation has been chosen arbitrarily.

It is not a priori obvious that choice of pulse sequence can influence robustness against phase variation. To our knowledge, prior to the algorithmically discovered pulse sequences shown here, no pulse sequences were known to yield $T_1$ and $T_2$ maps via direct dictionary matching with intrinsic robustness against phase variation.

Discussion

Here, we present an automatic pulse-sequence design framework for MRF scans using physics-inspired optimization. The cost function is built upon explicit first-principles modeling of MRF scans, incorporating random error, as well as errors induced by the interplay of Fourier undersampling, phase variation, and image-reconstruction algorithms. This realistic modeling, combined with tailored optimization algorithms, yields MRF pulse sequences that strongly outperform standard MRF pulse sequences, according to in vivo experiments.

Although the optimization algorithms producing these MRF pulse sequences are essentially inscrutable, by examining the qualitative features of the optimized sequences, one may obtain insights that can be fed back to human-led MRF pulse-sequence design efforts. The first of these is that careful design of MRF pulse sequences can greatly reduce susceptibility to shading artifacts. This is an important finding in this study, because the shading artifacts represent a unique interaction of static phase variation, spatially and temporally varying undersampling errors, and signal intensity variation from temporally varying flip angles and timings. Second, the flip angle vs. pulse index in high-performing sequences is consistently observed to consist of a modest number (three to six) of “humps.” This is a feature present in prior MRF pulse sequences designed by human experts. That optimization algorithms reproduce it when proceeding from randomly generated starting points is strong confirmation of the intuitions behind this design. Third, plots of TR duration (i.e., time between pulses) vs. pulse index arising from optimized sequences consistently show spike patterns. That is, all but a small number of the TRs are of minimum allowed duration, with a small number of TRs with vastly longer duration.

We propose the following interpretation for why the optimizer finds spiked TR patterns to be beneficial. Rapidly gathering data that efficiently distinguish tissues is aided by short TR times and large flip angles. However, repeated application of pulses with these features gradually depletes magnetization levels and, hence, signal strength. One might interpret the TR duration spikes as “rest periods” during which data collection is temporarily sacrificed in favor of allowing $T_1$ relaxation to proceed unimpeded and thereby “recharge” magnetization levels. This interpretation is bolstered by the observation that, across large ensembles of optimized sequences, the TR duration spikes are generally coordinated with low flip angles, as illustrated in SI Appendix, Fig. 1. This is a feature absent in prior human-designed sequences and may be a significant contributor to the improved duration vs. accuracy tradeoff.

Our optimized sequences achieve increased scan speed at a given precision target relative to standard sequences and can simultaneously yield intrinsic robustness against phase variation. Although our in vivo scans were performed on a scanner with 3 Tesla field strength, optimization of sequences to achieve robustness against systematic variations may, in future work, serve as an enabling technology for low-cost, low-field-strength portable scanners, which are likely to have large field inhomogeneities and low signal-to-noise ratio.

In this study, we modeled three types of errors that are commonly seen in the in vivo MRF scan. In addition to Gaussian random noise, we explicitly modeled 2D spatially and temporally dependent artifacts due to undersampling and phase variation. The need to incorporate phase variation is a unique finding in this study. In a fully sampled MRF scan, this phase variation is time-independent and would have no effect on the maps derived from dictionary matching. However, in an actual in vivo MRF scan, which typically employs high acceleration rate and time-varying sampling trajectories, the phase variation combined with Fourier aliasing to generate spatially and temporally varying artifacts that cause shading artifacts in the maps. Fig. 2 compares simulation with and without incorporating phase variation. Only the simulation incorporating phase variation reproduces shading from the in vivo scan. Due to the interplay of multiple error sources, the optimal MRF sequence design should be a comprehensive consideration of flip-angle series, timing, sampling trajectories, and reconstruction.

Our cost function is based on a digital brain phantom from the Montreal Neurological Institute Brain Imaging Center (45, 46). For practical implementation, we simplified the model by mapping all voxels to three tissue types: gray matter, white matter, and cerebrospinal fluid. Although optimization using this limited model yielded sequences with good in vivo performance, one could, in future work, consider more detailed models involving additional tissue types and geometries, including pathological cases. Furthermore, with enough computational resources, optimization could be performed by using a cost function that incorporates a complete nonuniform Fourier transform, rather than precomputed response functions. This would enable $k$-space trajectories to be co-optimized with the other acquisition parameters, such as flip angles and TR durations.

The general framework developed here for automated design of pulse sequences via physics-inspired optimization algorithms could be applied in many other contexts. The framework would be straightforward to adapt to optimize pulse sequences for 3D scans or for operation with alternative image-reconstruction schemes, such as iterative reconstruction. Furthermore, the optimization algorithms, parameterization of the search space, and cost function described here could be adapted to the development of MRF pulse sequences specialized for body parts other than the brain, as well as for MRF scans measuring quantities beyond $T_1$ and $T_2$, such as diffusion rates. More ambitiously, because our cost function explicitly models the systematic errors arising from specific tissue distributions, it could be used to generate MRF pulse sequences tailored to specific disorders or even specific patients. In the opposite direction, repeatability of pulse-sequence results across different scans and different patients could be addressed by large scale in vivo studies. Such repeatability is an especially important feature for monitoring disease progression or age-related tissue changes (7–9) and helps to fulfill the promise of quantitative MR scanning for objective clinical diagnostic criteria (8, 47).

Data Availability

Some study data are available. Four tables in .csv files listing detailed results of the proposed model and optimization algorithms and a readme.md file providing detailed explanation of the experiments performed to generate numbers in each table, in addition to the 15 optimized pulse sequences reported on in the manuscript, are available in GitHub (https://github.com/madan6711/Automatic-MRF-seq-design) (48).