Tumor-immune ecosystem dynamics define an individual Radiation Immune Score to predict pan-cancer radiocurability

Abstract

Radiotherapy efficacy is the result of radiation-mediated cytotoxicity coupled with stimulation of antitumor immune responses. We develop an in silico 3-dimensional agent-based model of diverse tumor-immune ecosystems (TIES) represented as anti- or pro-tumor immune phenotypes. We validate the model in 10,469 patients across 31 tumor types by demonstrating that clinically detected tumors have pro-tumor TIES. We then quantify the likelihood radiation induces antitumor TIES shifts toward immune-mediated tumor elimination by developing the individual Radiation Immune Score (iRIS). We show iRIS distribution across 31 tumor types is consistent with the clinical effectiveness of radiotherapy, and in combination with a molecular radiosensitivity index (RSI) combines to predict pan-cancer radiocurability. We show that iRIS correlates with local control and survival in a separate cohort of 59 lung cancer patients treated with radiation. In combination, iRIS and RSI predict radiation-induced TIES shifts in individual patients and identify candidates for radiation de-escalation and treatment escalation. This is the first clinically and biologically validated computational model to simulate and predict pan-cancer response and outcomes via the perturbation of the TIES by radiotherapy.

Introduction

Radiation therapy is the single most utilized therapeutic agent in oncology [1], yet in the biology-driven medicine era, advances in radiation oncology have primarily focused on improving physical dose properties. As a result, the field of radiation oncology currently does not individualize radiation dose prescription based on the intrinsic biology of a patient's tumor.

Tumors, which contain a diverse cellular architecture comprising heterogeneous cancer cell populations, evolving vascular networks, and immune cell infiltrates, increase the complexity of the tumor radiation response [2]. An extensive body of literature has emerged describing the immune-activating ability of radiation [3]. In fact, radiotherapy efficacy may result from the combined effect of direct radiation-mediated cytotoxicity and, possibly, the subsequent indirect stimulation of an antitumor immune response. Functional tumor immunity encompasses 2 main conceptual components: immune effector populations inducing tumor regression (including natural killer (NK) cells, CD4+ helper T (Th) cells, CD8+ cytotoxic T cells (CTL), M1 macrophages and mature dendritic cells (DC)) and immune suppressor cells facilitating tumor escape (including regulatory T (Treg) cells, M2 macrophages and tolerogenic DC) [4]. The mechanisms regulating the balance of immune activation vs suppression is the foundation for several clinically approved therapeutics preventing autoimmune flares or enhancing antitumor immune responses, thus are important to consider when integrating radiotherapy. A diverse range of tactics are being investigated to modulate the immune response in combination with radiotherapy [5,6] and though synergism has been identified between radiotherapy and the immune system, it is not clear how to optimally integrate radiotherapy in the era of immune-modulating agents [7].

Despite the monumental preclinical and clinical efforts, it is impossible to rigorously analyze all possible radiation doses with and without immunotherapy while encompassing all possible dosing, sequencing, and timing variables [8]. Recent advances in integrated mathematical modeling may help provide a mechanistic understanding of the many biologic modifiers and their interactions [9], [10], [11], [12], [13]. Mathematical modeling has a long history in radiation oncology; the linear-quadratic model, biologically effective dose calculations, tumor control probability and normal tissue complication probability models are used daily in hospitals around the world [1]. Simulating the highly dynamic tumor responses to radiation based on individual patient properties holds promise for innovative translational opportunities [14], [15], [16], [17], 18, [19], [20]. Similarly, significant inroads have been made in mathematical modeling of tumor-immune interactions and immunotherapy response prediction [21], [22], [23], [24], [25], [26], [27], [28], [29], [30], as well as understanding the local and systemic mechanistic consequences of radio-immunotherapy combinations [31], [32], [33], [34].

In addition to, and in synergy with mechanistic modeling, systems biology, machine learning, and bioinformatics approaches have taken root in radiation oncology [35,36]. The clinical response to radiotherapy occurs in the evolutionary context of complex cellular ecosystems and varying intrinsic differences in tumor cell radiosensitivity. Heterogeneity in radiosensitivity between patients and different cancer types has been evaluated using the radiosensitivity index (RSI), a 10-gene molecular radiation response signature that has been independently validated across multiple human tumor types [37,38]. There are significant data to support that radiosensitivity has at least in part, a genetic basis, which we hypothesize acts in concert with the complex and highly dynamic tumor immune milieu to dictate response to therapy. However, radiosensitivity and immune signatures are almost exclusively derived from static measurements. Integrating such signatures with dynamic modeling may hold the key to better understanding, simulating, and predicting radiation responses for individual patients.

To explore this hypothesis, we developed an in silico 3-dimensional agent-based model to study the relationship between the tumor-immune ecosystem (TIES) and solid tumor response to radiotherapy, with and without consideration for patient-specific tumor radiosensitivity. The model explores the dynamic interplay between tumor cells and the influx/efflux of immune cell populations during tumor growth and following fractionated schedules of radiation. In this model, the TIES is represented as a juxtaposition of 2 balancing phenotypes, antitumor vs pro-tumor, which is based on the proportion of suppressor and effector immune cell infiltrates within the ecosystem. We validate the in silico agent-based model by demonstrating the TIES composition for all 10,469 clinical samples in our cohort is characterized by a phenotype of tumor immune evasion as predicted. Next, we model the impact of radiation on the TIES and demonstrate it predicts that radiation can drive shifts in TIES composition to promote tumor elimination. To validate this prediction, we develop a novel metric of individual Radiation Immune Score (iRIS), which quantifies the likelihood radiation will induce TIES shifts toward immune-mediated tumor eradication. Furthermore, the distribution of iRIS scores in clinical samples is consistent with the radiocurability of solid tumors. We also demonstrate that iRIS predicts both the local control and overall survival of a cohort of 59 non–small cell lung cancer patients treated with postoperative radiotherapy.

Materials and methods

Herein, we combine computational modeling with pan-cancer tissue analyses to simulate tumor-immune interactions and predict radiation-induced shifts in the tumor-immune ecosystem (Fig. 1).

Fig. 1.

Schematic of the modeling, data-collection, and radiation response prediction pipeline.

Patient tumor data set

Patients were consented to the Total Cancer Care (TCC) protocol (IRB-approved, Liberty IRB #12.11.0023) [39]. Pathology quality control evaluation of tumors was performed as part of the TCC tissue collection protocol, which includes percent malignant cellularity, necrosis and stromal cell presence. Tumor samples were assayed using the custom Rosetta/Merck HuRSTA_2a520709 Affymetrix gene expression microarray platform (GEO: GPL15048). CEL files were normalized against the median CEL file using IRON [40], which yields Log₂ intensity values per probeset. Principal component analysis (PCA) of all samples revealed that the first component was highly correlated to RIN value, suggesting an RNA quality difference among samples. A partial least squares (PLS) model was trained upon the fresh frozen samples for which RIN was available and used to re-estimate the RNA quality of all samples. Then the first component was removed to correct the signals for RNA quality. 10,469 fresh frozen macrodissected primary tumors were identified for the related analyses.

Non–small cell lung cancer cohort

This cohort was obtained from archived tumors that were resected between 2000 and 2010 from patients in the TCC and Moffitt Cancer Center database. All patients provided written informed consent tissue acquisition, molecular profiling and follow-up. We identified 59 tissue samples, which were surgically resected and pathologically confirmed, American Joint Committee on Cancer version 6, stage IIIA-IIIB tumors. Each patient underwent postoperative radiotherapy. Time to locoregional recurrence and overall survival was assessed by determination of the treating physician based on clinical source documentation. Gene expression data were obtained from the TCC.

ESTIMATE

The ESTIMATE algorithm [41] was used to calculate tumor purity from gene expression of the primary tumor (Estimate R package v1.0.13). Normalized gene expression probeset identifiers were mapped to Entrez GeneIDs. As defined in the Estimate package, the data were filtered to only the common genes. A single probeset was then selected per gene by choosing the probeset having the highest median expression across all tumors.

CIBERSORT

The HuRSTA array was reduced to the LM22 signature genes as defined by CIBERSORT [42] by choosing a representative probeset that detects the gene and has the highest median expression among matching probesets. The CIBERSORT web tool (https://cibersort.stanford.edu/index.php) was accessed on 2017-05-19 to generate signature scores (using quantile normalization).

Immune cell infiltrate normalized content abundance

Immune cell infiltrate composition proportions from CIBERSORT [42] were extracted in relative mode, where the proportions are relative to the total immune cell fraction of the tumor. To normalize the content across tumors, we scaled the ESTIMATE [41] immune scores such that the lowest immune score was 0 (rather than negative) and analyzed multiple immune cell infiltrate fractions by this adjusted immune score, to yield the Normalized Content Abundance (NCA).

Immune cell infiltrate PCA plots

Relative immune cell infiltrate composition proportions (CIBERSORT estimates) were used to compute principal components across the entire TCC cohort using prcomp (R3.6.0) with scaling. The loadings and scores were visualized using R packages ggplot2 (3.2.1), ggrepel (0.8.1), and ggpubr (v0.2.3).

Calculation of RSI

RSI was calculated for each sample using the within-sample rank coefficients as described [37]. The following 10 probesets, corresponding to the originally defined HG-U133plus2 probesets, were used: merck-NM_007313_s_at (ABL1), merck-NM_000044_a_at (AR), merck-NM_004964_at (HDAC1), merck-NM_002198_at (IRF1), merck-NM_002228_at (JUN), merck-BQ646444_a_at (PAK2, CDK1), merck2-X06318_at (PRKCB), merck2-BC069248_at (RELA), merck-NM_139266_at (STAT1), merck-NM_001005782_s_at (SUMO1).

In silico agent-based model

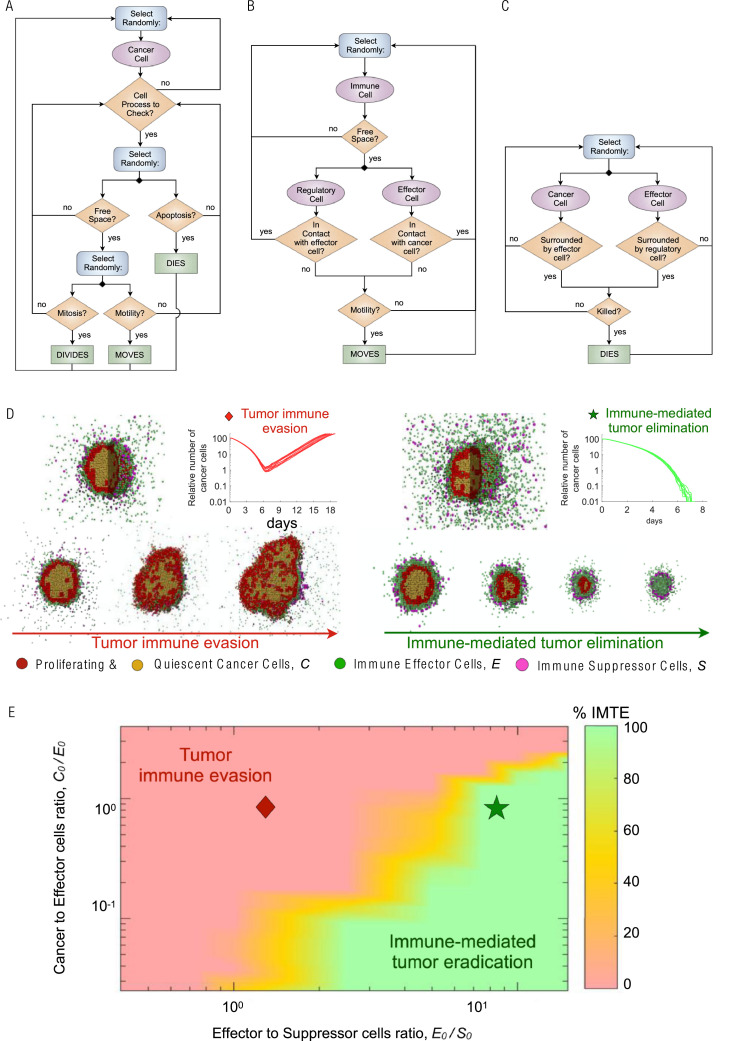
We developed a 3-dimensional (3D) multiscale agent-based model (ABM) that simulates the interactions of cancer cells with antitumor immune effector T-cells and immune-inhibitory suppressor cells. Each cell is considered as an individual agent, and their behavior at any time is determined by a stochastic decision-making process based on biological-driven mechanistic rules (see refs. [43], [44], [45], [46], [47], [48], [49] for similar modeling approaches). Immune cells are simulated on a 3D regular lattice divided into 200 × 200 × 200 nodes representing a volume of 65 mm³, with a lattice constant of 20 μm (average cell diameter, [46]). Cancer cells occupy an irregular 3D lattice that is initialized by randomly placing one lattice node inside each cube of the regular lattice for immune cells. These interconnected lattices are then used to simulate the infiltration of immune cells into the tumor bulk, thus avoiding contact inhibition between immune and tumor cells. A Moore neighborhood is considered for nodes in the same lattice, i.e., 26 orthogonally and diagonally adjacent lattice sites, where each node has 8 neighbor nodes in the opposing lattice given by the nodes surrounding it.

Model simulations are initiated with a single cancer cell at the center of the 3D simulation domain. At each time-step (Δt = 1 h), trafficking, motility, cytotoxic function and suppressing activity of immune cells, as well as tumor cell processes are executed through an iterative procedure (Fig. 2). Every time-step the state and dynamics of all cancer and immune cells are updated in random order to avoid order biases. When the tumor reaches a population of 10⁵ cancer cells, the number of cancer cells, immune effectors and suppressor cells define the preradiation tumor-immune ecosystem (TIES). The direct dose-dependent cytotoxic effect of radiotherapy (RT) on all participating cell types is simulated using the established Linear-Quadratic (LQ) model [50], [51], [52]. Model simulations continue after RT until either the immune system eradicates remaining cancer cells, or recurrent tumors reach the pretreatment number of 10⁵ tumor cells.

Fig. 2.

Integrative in silico modeling defines the tumor immune ecosystem (TIES). (A) Cancer cell decision flowchart. (B) Immune cells motility process. C. Cell-cell interactions process. (C) Biologically defined mechanistic rules guiding tumor and immune cell interactions in the 3D agent based in silico model. A fixed starting malignant cell burden and varying proportions of effector or suppressor immune cell infiltrates were inputted into the model and 10 independent simulations resulted in D. Tumor immune evasion (left panel) or immune-mediated tumor elimination (right panel). Different populations of cells in the agent-based model are depicted as follows: red (proliferating tumor cells), tan (quiescent tumor cells), green (effector immune cells) and purple (suppressor immune cells). (E) Representation of the probability of immune-mediated tumor elimination (IMTE) based on individual tumor immune ecosystems (TIES); y-axis: ratio of malignant cell burden/effector immune cell infiltrate (C₀/E₀); x-axis: ratio of effector/suppressor immune cell infiltrate (E₀/S₀). Color coded: Percent of computer simulations that resulted in immune-mediated tumor elimination (IMTE). Red region, TIES characterized by tumor immune evasion; green region, TIES representing immune-mediated tumor elimination.

Cancer cell dynamics

Cancer cells proliferate, migrate or undergo programmed cell death (apoptosis) at predefined intrinsic probabilities modulated by the local microenvironment (Fig. 2A). Proliferation and migration attempts are only successfully executed for cells residing at a lattice node with at least one vacant adjacent node. During mitosis, the new cancer cell is placed on a randomly selected free neighbor node. Similarly, cells migrate into adjacent vacant lattice nodes with equal probability to simulate random walks and cell diffusion (Brownian motion). The ability of the tumor cell to proliferate and move is temporarily lost due to contact inhibition, and this quiescent state is abandoned as soon as at least one neighbor lattice site becomes free. Cancer cells that undergo programmed cell death with specified probability are removed from the simulation domain instantaneously. For demonstration purpose, we assume commonly used generic cancer cell parameters, including a cell cycle duration of 35 hr (which results in a proliferation probability p_p = 0.02 × 10⁻² per time-step (Δt = 1 h) [53]), and apoptotic and migration probabilities as p_a = 4.17 × 10⁻³ (approximately every 10 days [54]) and p_m = 4.17 × 10⁻¹ (about 10 cell widths per day [55]).

Immune cell infiltration into the tumor microenvironment

Immune cells arrive in the tumor microenvironment after extravasation from the vasculature [56], [57], [58]. Blood vessels are assumed to be homogeneously distributed throughout the simulation domain, and immune cells enter the simulation at randomly selected free lattice nodes in the domain. At each simulation time-step t_i, the number of effector and suppressor cells that are recruited in response to tumor burden ($\nabla E_i$, $\nabla S_i$) are given as:

$$\nabla E_i=\{\begin{array}{c}{r}_E·C_i-E_{i}if\left(r_E·C_i\right)>E_i\\ 0,otherwise\end{array}$$ (1)

$$\nabla S_i=\{\begin{array}{c}{r}_S·C_i-S_{i}if\left(r_S·C_i\right)>S_i\\ 0,otherwise\end{array}$$ (2)

where (C_i, E_i, S_i) are respectively the number of cancer, immune effector, and immune suppressor cells at time t_i. By setting $r_E=E_0/C_0$ and $r_S=S_0/C_0$ we obtain the desired cancer-to-effector cell ratio ($C_0/E_0$) and effector-to-suppressor cell ratio ($E_0/S_0$) at the beginning of radiation therapy as derivable from patient tissues.

Immune cell motility

Immune cells migrate and infiltrate tumors via chemotaxis along cytokine and chemokine gradients that are secreted by cancer cells or other immune cells [59]. The mean velocity of immune cells in nonlymphoid tissues have been estimated at 4–10 μm min⁻¹, with a peak velocity as high as 25 μm min⁻¹ in the lymph nodes [60], [61], [62]. Here, we set the mean immune cell velocity to 10 μm min⁻¹, which results in a lattice move probability of h_r = 0.37 per min⁻¹. The waiting time for immune cell movement follows an exponential probability distribution. Immune cell motility is updated 60 times (every minute) per simulation time-step (Δt = 1 h). Both effector and suppressor cells move toward the tumor center of mass subject to at least one vacant lattice node in their immediate neighborhood and direction (Fig. 2B). Immune effector and suppressor cells only move while not performing cytotoxic or suppressing functions, i.e., when not in contact with cancer cells or effector cells, respectively.

Immune cells select free neighbor lattice nodes with a certain probability depending on their distance to the center mass of the tumor. The transition probability for the directed movement of an immune cell from a lattice site r to a free neighbor r' is given by

$$p\left(r\to r^{\prime }\right)=\frac{e^{\eta \Delta H}}{{\sum }_{r\in V\left(r\right)}{e}^{\eta \Delta H}},$$

where V(r) is the set of free neighbor lattice nodes of r, ΔH = H(r') - H(r), and H(j) is the distance of a lattice site j to the tumor center of mass $\frac{1}{N}\sum _{i=1}^N{\overline{r}}_i$. Here the vector ${\overline{r}}_i$ denotes the spatial coordinates of the lattice node r_i occupied by a tumor cell and N is the total amount of tumor cells. A random number is generated to select a free neighbor lattice site for movement, which is determined from the set of probabilities into which the generated number falls in. We fixed $\eta =0.25$, which results in a nondeterministic biased random walk.

Cell–cell interactions

Accumulating evidence demonstrates cancer cells secrete a wide array of different chemokines and chemotactic cytokines that recruit pro- and antitumor immune cell subsets to the tumor microenvironment [59]. While cytotoxic effector T cells have the potential to kill cancer cells by inducing different forms of cell death, suppressor T cells suppress antitumor immunity by inhibiting the cytotoxic responses of effector T-cells which is simulated as removal of effector cells in the model [63]. Accordingly, effector T cells can kill cancer cells by direct contact with probability p_E = 0.03 per time-step, and suppressor T cells can suppress effector-dependent responses by repressing effector T cells when they are in contact at a probability p_R = 0.01 per time-step (Fig. 2C). Tumor cell killing and effector T cell inactivation probabilities increase proportionally with the number of immune cells of the same types in the immediate cancer cell neighborhood. The target cell is removed from the simulation domain.

Effect of radiation on tumor and immune cells

The cytotoxic effect of radiotherapy on cancer cells was simulated by using the standard Linear-Quadratic (LQ) model [50], [51], [52]. The radiation dose D (Gy) dependent surviving fraction (SF) is given by:

$$SF\left(D\right)=e^{-\xi \left(\alpha D+\beta D^2\right)},$$

where α (Gy⁻¹) and β (Gy⁻²) are cell type-specific radiosensitivity parameters. Growth arrested cells are approximately 3 times more resistant to radiation than normoxic cycling cells [64]; we set ξ = 1 and ξ = 1/3 to respectively scale the radiosensitivity of proliferative and quiescent tumor cells as previously discussed [45,48].

As the simulated in silico tumors with 10⁵ cells are about 6 orders of magnitude smaller than clinically apparent tumors, simulating 7 weeks of radiation will overestimate tumor control. With generic cancer radiosensitivity of α = 0.3 Gy^-1 and β = 0.03 Gy^-2, the linear quadric model predicts the survival after 30 fractions to be on the order of SF(2 Gy x 30) ≅ 4e-10. Radiation with 10 fractions gives SF(2 Gy x 10) ≅ 7e-4, about 6 orders of magnitude less than 30 fractions. Thus, simulating 10 fractions on tumors with 10⁵ cells provides a comparable means to clinical radiation responses. Thus, each RT dose in silico may be assumed to equate 3 actual radiotherapy doses. For RT simulations for an individual NSCLC patient k, we set SF_k (2 Gy) = RSI_k.

Immunosuppressive cells are intrinsically more resistant to radiation than cytotoxic effector T cells [65,66], in line with estimates of radiation-induced lymphocyte death after increasing radiation doses in vitro [67]. From these dose-response curves we derive SF_S(1.8Gy) = 0.81 and SF_S(2.0Gy) = 0.79 for suppressor immune cells, and SF_E(1.8Gy) = 0.63 and SF_E(2.0Gy) = 0.61 for immune effector cells.

Radiation-induced recruitment of immune cells

Radiation induces immunogenic cell death, and this releases immune-stimulating signals and enhances T cell infiltration into the TME [3,6,68]. Radiation-induced tumor cell death occurs during the first hours after irradiation [5] and is marked by increased infiltration and recruitment of T lymphocytes [69]. Radiation-induced effector and suppressor cells recruited at time t_i is simulated by:

$$\begin{array}{c}\hfill E_i=\sum _{j=1}^{N_{\mathit{RT}}}{K}_{T_j}·\left({\delta }_E{e}^{-\gamma (t_i-t_j)}\right),\\ \hfill S_i=\sum _{j=1}^{N_{\mathit{RT}}}{K}_{T_j}·\left({\delta }_S{e}^{-\gamma (t_i-t_j)}\right)\end{array}$$

where N_RT is the number of radiation fractions, and K_Tj is the amount of cancer cells eradicated by radiation at fraction j delivered at time t_j. The parameters δ_E and δ_S describe radiation-induced recruitment rates of effector and suppressor cells, and γ is the decay of radiation-induced immune stimulation. Parameter values δ_E = 0.05 h⁻¹, δ_S = 0.01 h⁻¹ and γ = 0.05 were used for all model simulations. Model parameters are summarized in Supplementary Table 1.

Individual Radiation Immune Score (iRIS): The TIES composition prior to therapy combines cancer-to-effector cell and effector-to-suppressor cell ratios with the absolute number of suppressor cells. Effector (antitumor) immune cells were represented by CD8 T, activated CD4 memory T, activated NK, and M1-polarized macrophage cells. Suppressor (pro-tumor) immune cells were represented by regulatory T, M2-polarized macrophage and neutrophil cells. These immune cell types were chosen in line with previous literature [4] and clean signal on PCA. Including all the immune cell infiltrate populations following PCA stratification yields comparable results, but lower significance due to ambitious stratification. To correlate TIES composition with radiation responses the individual radiation immune score (iRIS) score is defined as:

$$\mathit{iRIS}=\frac{1}{2}\min \left(d_{\mathit{IMTE}}\right)+{\log }_{10}\left(S_0\right),$$

where$d_{\mathit{IMTE}}=\sqrt{{({\log }_{10}\left(\frac{E_0}{S_0}\right)-{\log }_{10}X)}^2+{({\log }_{10}\left(\frac{C_0}{E_0}\right)-{\log }_{10}Y)}^2}$ is the distance of preradiation TIES to the immune mediated tumor elimination (IMTE) region, and $E_0$, $S_0$ and -$C_0$ are the number of effector, suppressor and cancer cells, respectively. The X and Y vectors are the coordinates of all simulated points in the IMTE region in the immune contexture matrix. d_IMTE is specific to each patient sample, and independent on the number of simulated points in the IMTE region. As the TIES map is a 2D projection, to sufficiently weigh the contribution of the order of magnitude of suppressor immune cells in iRIS, the effect of d_IMTE is reduced by the factor ½.

Results

Agent-based model simulations identify 2 functional tumor-immune ecosystem phenotypes: Immune-mediated tumor elimination vs tumor immune evasion

The TIES is a dynamic and diverse network of cellular and noncellular constituents that either perpetuate or attenuate tumor growth. The absolute numbers of effector and suppressor immune cells in conjunction with the cancer cell burden were used to define the TIES (see Methods). Simulations of tumor growth in various TIES reveal that in our model, the tumor-immune ecosystem yields 2 functional phenotypes: TIES where tumors evade immune predation (Fig. 2D, left panel) and TIES where tumors are eradicated by the immune system (Fig. 2D, right panel). These distinct phenotypes are characterized by the ratio of cancer cells to effector immune cells at the beginning of the simulation (C₀/E₀, y-axis) vs the ratio of immune effector to immune suppressor cells (E₀/S₀, x-axis). Outcome statistics (immune-mediated tumor eradication; IMTE) for ten independent simulations for each initial TIES (C₀, E₀, S₀) identifies TIES compositions that will lead to IMTE or will lead to tumor escape (Fig. 2E).

Validation of TIES model in 10,469 patient tumor samples across 31 tumor types

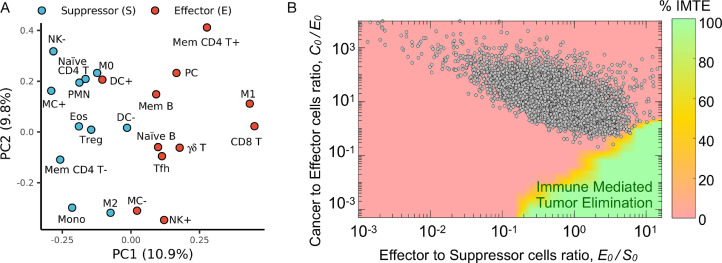
We hypothesized that clinically detectable tumors should exclusively present with TIES representative of an immune escape phenotype. To validate the TIES model, we estimated the TIES for 10,469 solid tumor patient samples across 31 tumor types, which were prospectively collected through the Total Cancer Care (TCC) protocol [39], by quantifying immune cell infiltrate counts and malignant cell burden in each sample using the CIBERSORT [42] and ESTIMATE [41] algorithms, respectively. The immune cell infiltrates across all tumor samples were grouped into effector and suppressor types based on principal component analysis (Fig. 3A). All 10,469 tumor samples demonstrated a TIES with an immune evasion phenotype, as predicted by the in silico model (Fig. 3B, Supplementary Fig. 1). Although the initial in silico model parameters (Fig. 2) were derived from the literature for a ‘generic tumor’, the derived TIES composition of all tumor samples across the 31 tumor types confirmed the model prediction of a phenotype characterized by immune evasion.

Fig. 3.

Validation of TIES model in 10,469 patient tumor samples across 31 tumor types. (A) Loading of principal component analysis (PCA) of the CIBERSORT-derived immune cell infiltrate composition across 10,469 tumors stratified as antitumor (E; effector) or pro-tumor (S; suppressor). Immune type nomenclature is listed in Supplementary Table 2. (B) The cellular composition (normalized immune cell infiltrate counts and malignant cell burden estimated by CIBERSORT and ESTIMATE, respectively) for each of the 10,469 tumors was derived and plotted onto the TIES map; all tumors localized in regions with a TIES leading to tumor immune evasion.

The agent-based TIES model predicts radiation-induced shifts in TIES composition to drive tumor elimination: individual Radiation Immune Score (iRIS)

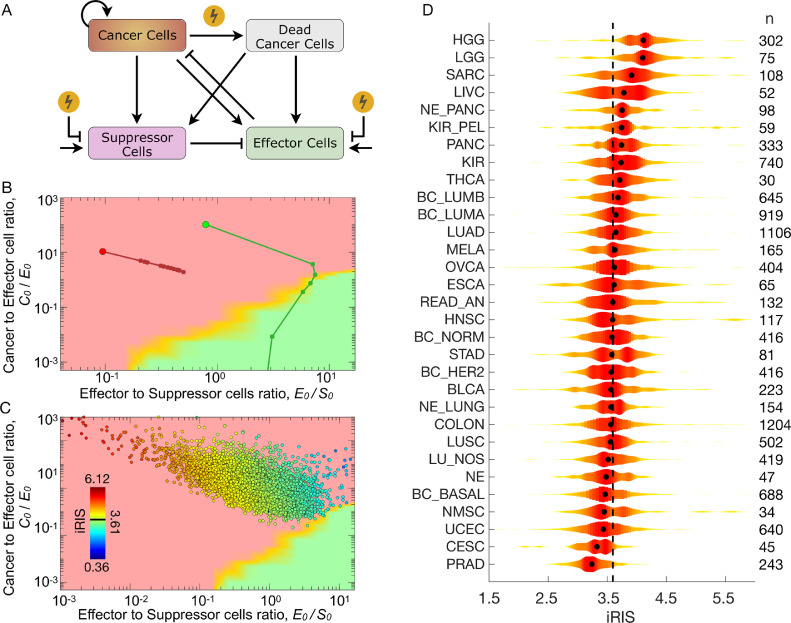
To explore the effects of radiation therapy on the tumor and its immune microenvironment, we extended the in silico agent-based TIES model to incorporate the cytotoxic impact of radiation on both tumor/immune cells and the influx/efflux of immune infiltrates (Fig. 4A, see Methods). In this simulation, we initialized the growth of 2 tumors with an identical number of cancer cells (C₀=1.0 × 10⁵), but different pretreatment immune cell infiltrates (E₀, S₀) and thus different distances of preradiation TIES to the immune mediated tumor elimination region, d_IMTE. Both tumors were then simulated to be exposed to 20 Gy of radiation in 10 daily 2 Gy fractions (equivalent of 60 Gy in 30 fractions for clinical tumor sizes) with identical radiation response parameters (see Methods for details). The in silico agent-based TIES model visualizes the predicted shifts in the TIES composition after each radiation dose (Fig. 4B). Importantly, the model incorporates tumor repopulation and regression dynamics before, between and after radiation doses. Interestingly, the in silico agent-based TIES model predicts that in some circumstances, radiation shifts the TIES into a functional phenotype driving immune-mediated tumor elimination. These tumors are the most likely to be eradicated even if viable cancer cells remain after radiation. Conversely, tumors that do not experience this shift in TIES phenotype are predicted to regrow after completion of radiation, possibly due to propagation of an immunosuppressive milieu.

Fig. 4.

Agent-based TIES model predicts radiation-induced shifts in TIES composition to drive tumor elimination: the individual Radiation Immune Score (iRIS). (A) Schema of biologically-defined mechanistic rules guiding tumor and immune cell interactions during exposure to radiation in the 3D agent based in silico model. (B) Modeled trajectories of TIES composition evolution of a given pretreatment TIES following radiation treatment. Each closed circle on the trajectory represents a radiation dose of 2 Gy/day. The simulation was continued until a total of 20 Gy was delivered over 10 fractions. This demonstrates that radiation causes shifts in the TIES, which result in different trajectories despite being equivalent closest Euclidean distances from the IMTE region (green). (C) The individual Radiation Immune SensitivityScore (iRIS) score for each tumor, which describes the specific position in the TIES map with respect to the shortest Euclidean distance from the IMTE region, penalized by the absolute number of suppressor immune cell infiltrates. A lower iRIS value represents a more radiation responsive TIES. (D) Violin plots depicting distribution of iRIS values, highlighting heterogeneity within and across tumor types. The black dot in each violin plot represents median iRIS value for each tumor type. Numbers to the right of each cancer type represents the sample numbers. Tumor type nomenclature is listed in Supplementary Table 3.

Furthermore, these simulations revealed that tumor compositions with higher initial E₀/S₀ ratios and less absolute number of suppressor cells (S₀) are predicted to have a higher probability of being shifted by radiation to the functional TIES phenotype that promotes immune eradication of tumor cells. From these findings, we derived a new individual Radiation Immune Score (iRIS), which quantifies the likelihood radiation will shift the TIES composition to the immune-eradication TIES phenotype (see Methods).

Clinical validation of iRIS

The agent-based in silico TIES model predicts tumors with a high iRIS (iRIS^hi) score are less likely to experience radiation-induced shifts to a TIES phenotype characterized by immune-mediated tumor eradication. In contrast, tumors with a low iRIS score (iRIS^lo) have a higher chance of radiation promoting immune-mediated tumor eradication. To clinically-validate iRIS, we generated iRIS scores for all patients in the TCC cohort (n=10,469) and each tumor was placed on the TIES map (Fig. 4C). The distribution of iRIS scores is presented in Fig. 4D, which shows significant heterogeneity within and across tumor types. Interestingly, prostate, cervical and nonmelanoma skin cancers constitute 3 of the 4 tumor types with the lowest median iRIS scores. Importantly, these are all radiocurable diseases where radiation and surgery have equal oncologic outcomes based on clinical experience. Gliomas (high and low grade) and sarcomas have the highest median iRIS scores, which is also consistent with the radiation-resistant phenotype of these tumors. Other observations consistent with clinical experience include lung adenocarcinomas having a higher median iRIS than lung squamous (P = 9.6 × 10⁻⁹). In breast cancer, the PAM50 molecular subtypes, such as luminal A and B had the highest median iRIS scores, whereas the HER2 and basal subtypes had the lowest median iRIS, which were significantly different (P < 0.001; Supplementary Fig. 2).

iRIS correlates with radiotherapy outcomes in non–small cell lung cancer

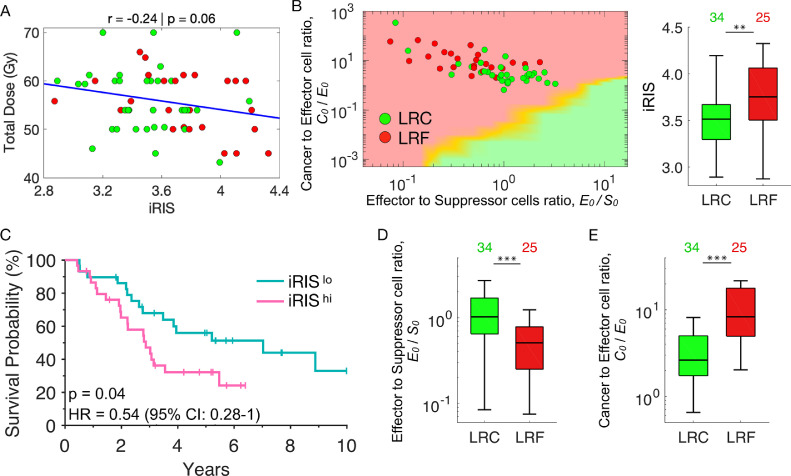
As an independent clinical validation, we tested iRIS in a cohort of 59 non–small cell lung cancer (NSCLC) patients treated with postoperative radiation. Patients received total radiation doses of 42 to 70 Gy in daily fractions of 1.8 to 2 Gy. Total dose was prescribed based on clinical guidelines and was independent of iRIS (Fig. 5A, r = -0.24, P = 0.06). As predicted, patients that achieve locoregional control (LRC) had significantly lower iRIS scores compared to patients with locoregional failure (LRF; P < 0.01; Fig. 5B). Furthermore, iRIS^lo patients had improved overall survival (OS) when compared to iRIS^hi (HR = 0.54; 95% CI: 0.28–1.0, P = 0.04, Fig. 5C). Also, we found that patients who achieved LRC had higher pretreatment E₀/S₀ ratios (median 1.02 ± 0.74 vs median 0.51 ± 0.55, P < 0.001; Fig. 5D) and lower C₀/E₀ ratios (median 2.62 ± 58.25 vs median 8.3 ± 18.16, P < 0.001; Fig. 5E).

Fig. 5.

Clinical validation of iRIS in independent non–small cell lung cancer cohort. An independent cohort of 59 non–small cell lung cancer (NSCLC) patients treated with postoperative radiation at various doses (range: 42–70 Gy) were analyzed for locoregional control (LRC), failure (LRF) or overall survival (OS). (A) iRIS is not correlated with the total radiation dose delivered to the 59 NSCLC patients (r = -0.24, P < 0.06). Color code: patient samples with locoregional control (LRC, green) and locoregional failure (LRF, red). (B) left panel, The inferred cellular composition (immune cell infiltrates and malignant cell burden) of each patient tumor was plotted onto the TIES map and actual clinical outcomes of LRC (green) and LRF (red) were evaluated with respect to their given TIES. Right panel, boxplots show patient tumors that achieved LRC had lower iRIS values compared to those with LRF (** represents P < 0.01). (C) Kaplan-Meier estimates for OS demonstrate patients with tumors classified as iRIS^lo vs iRIS^hi have improved OS (HR: 0.54, 95% CI: 0.28–1.0; P = 0.04). Boxplots show that patients who achieved LRC have (D) higher E₀/S₀ and E) lower C₀/E₀ ratios than those with LRF (*** P < 0.001).

The combination of iRIS and radiation sensitivity index, RSI, correlate with favorable outcomes in patients treated with radiation

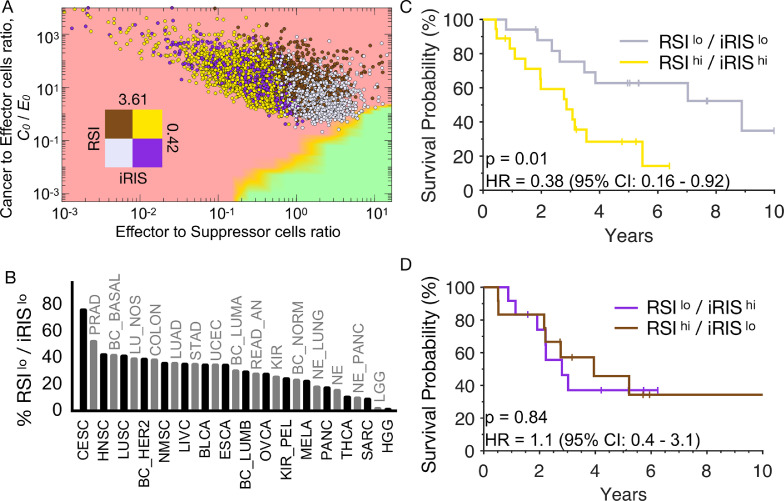
To evaluate the immune microenvironmental role in radiation response with cell-intrinsic molecular radiosensitivity, we combined iRIS with the RSI, a radiation response signature that is agnostic to cancer type and has been independently validated as a marker of radio-responsiveness across multiple human tumor types [37,38]. Combining the RSI and iRIS distributions across the 31 tumor types followed by stratification into RSI^lo and RSI^hi (median = 0.42) and iRIS^lo and iRIS^hi (median = 3.61) by global medians respectively, visualizes separation of molecularly and immunologically radiosensitive and radioresistant tumors on the in silico TIES map (Fig. 6A). Classifying tumor types based on the proportion of patients in the most favorable quadrant (e.g., iRIS^lo/RSI^lo), demonstrates cervical, prostate, and head and neck cancers have the highest proportion of tumors in this quadrant, consistent with the high radiocurability of these tumor types in clinic (Fig. 6B). In contrast, gliomas and sarcomas had the lowest proportion of tumors in the iRIS^lo/RSI^lo quadrant, which is also consistent with known clinical radioresistance.

Fig. 6.

RSI and iRIS are mutually related to improved outcomes in patients treated with radiation. (A) Tumors were separated into quadrants by RSI^lo and RSI^hi (population median RSI, 0.42), as well as iRIS^lo and iRIS^hi (population median iRIS, 3.61) and represented on the TIES map. (B) Tumor types were classified based on the proportion of patients in the most ‘favorable’ quadrant (e.g., iRIS^lo/RSI^lo). (C) Patient NSCLC tumors with dual RSI^lo/iRIS^lo phenotypes have improved OS (HR 0.38, 95% CI: 0.16–0.92; P < 0.01) compared to those with RSI^hi/iRIS^hi. (D) A RSI^lo phenotype with an unfavorable TIES (iRIS^hi) or vice versa, cannot compensate for the other (HR 1.1, 95% CI: 0.4–3.1; P = 0.84).

In the NSCLC clinical cohort, patients with favorable radiation sensitivity and immune phenotypes (RSI^lo/iRIS^lo) had significantly higher rates of LRC vs those with unfavorable (e.g., RSI^hi/iRIS^hi) pretreatment conditions (83% vs 41%; P < 0.001). Similarly, patients with dual RSI^lo/iRIS^lo vs RSI^hi/iRIS^hi tumor phenotypes have superior OS (HR = 0.38, P = 0.01; Fig. 6C). Interestingly, an RSI^lo tumor phenotype with an unfavorable TIES (iRIS^hi) or vice versa, does not connote improved OS (Fig. 6D); thus, both metrics in combination correlate with patient-specific outcomes in this cohort.

RSI/iRIS model-predicted minimum required dose for tumor control

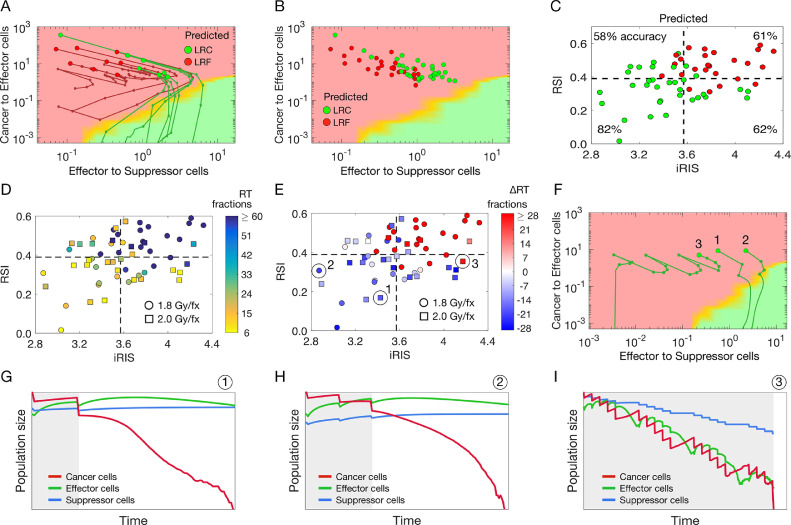
We then used the in silico model, informed with patient-specific pretreatment TIES composition, RSI and iRIS to simulate the clinically applied individual radiation dosing regimen (total dose applied in 1.8 to 2 Gy per fraction for a total of 42–70 Gy) to predicted RT-induced shifts in TIES composition. For patients with immune ‘cold’ TIES (i.e., low effector to suppressor immune cell ratios, or iRIS^hi) radiation does not perturb the TIES sufficiently to promote immune-mediated tumor elimination, resulting in LRF. For patients predicted to be controlled by radiation, RT facilitates shifts toward more favorable TIES compositions that support tumor elimination. If RT fails to eradicate all cancer cells, postradiation TIES composition facilitates immune-modulated elimination of residual cancer cells that lead to LRC (Fig. 7A,B). The highest prediction accuracy was achieved for RSI^lo/iRIS^lo patients (82% correctly predicted), followed by RSI^lo/iRIS^hi (62%), RSI^hi/iRIS^hi (61%) and RSI^hi/iRIS^lo (58%) (Fig. 7C). We then used the in silico ABM to predict the minimum required number of 1.8 Gy or 2 Gy RT fractions to eliminate the tumor. For selected RSI^lo/iRIS^lo patients, as few as 6 to 10 fractions (10.8–20 Gy total dose) may be sufficient to provide LRC via robust stimulation of antitumor immunity. For unfavorable TIES compositions with RSI^hi/iRIS^hi, we found that up to 60+ fractions (>120 Gy total dose) may be necessary to sterilize every single cancer cell with radiation (Fig. 7D). Of the analyzed 59 NSCLC patients, 6 patients (10%) received RT within +/- 5 fractions of the RSI/iRIS calculated required dose, 30 patients (51%) are predicted to be candidates for RT de-escalation, and 23 patients (39%) would require dose escalation by more than 5 fractions based on RSI/iRIS (Fig. 7E). Analysis of the shifts in the TIES during RT for 3 select patients (Fig. 7F) and the corresponding change in cancer, effector and suppressor cell population over time indicate 2 different radiation prescription purposes: RT as an immune-stimulating agent with opportunity for de-escalated doses (tumors 1 and 2; Fig. 7G,H) vs radiation as a purely cytotoxic agent that has to eradicate every cancer clonogen without the support of the immune system (tumor 3; Fig. 7I). Consequently, many more radiation fractions and a higher cumulative dose are required for tumor 3 compared to tumors 1 and 2.

Fig. 7.

Optimal patient-specific radiation doses to induce favorable TIES shifts. (A) Proof-of-principle simulation of radiation-induced shifts in the TIES composition. Big circles mark the TIES composition prior to radiation, smaller circles mark TIES composition after each radiation fraction (2 Gy x 10). After radiation, tumor-immune dynamics are simulated until the tumor either becomes extinct (green trajectories) or regrows to pretreatment size (red trajectories). (B) Model-predicted locoregional control (LRC, green) or locoregional failure (LRF, red) for the patient-specific radiation dose, RSI, and initial TIES composition for 59 NSCLC patients. (C) Model predictions of locoregional control (LRC, green) or locoregional failure (LRF, red) for 59 NSCLC patients. Percentages denote prediction accuracy for each quadrant of RSI^lo/hi and iRIS^lo/hi. (D) Model-derived minimum required number of radiation fractions to control individual patient tumors with their respective RSI, iRIS, and delivered dose per fraction (1.8 Gy/fx, circles; 2 Gy/fx, squares). (E) Model-derived difference in clinically prescribed number of fractions and model-derived minimum required number of radiation fractions to control individual patient tumors. (F) Simulated shifts in TIES composition of 3 individual patients marked in panel E. (G–I). Population dynamics for the 3 individual patients marked in panels E and F. Gray shaded background denotes times of radiation therapy.

Discussion

Mathematical modeling has become integrated into cancer biology and clinical oncology to move from molecular reductionism to quantitative holism [9]. Prospective clinical trials are currently evaluating promising modeling-derived concepts in radiation oncology, including temporally feathered radiotherapy to reduce cumulative doses to organs at risk [15], and the use of a proliferation saturation index, PSI, to personalize radiation fractionation [16,18,70]. Though laboratory techniques can perform experiments in a controlled model, there is limitation to the included variables, which results in an oversimplification of patient tumor biology. To address this complexity, we developed an in silico model of tumor-immune interactions that simulates the diverse contexts in which the tumor escapes immune surveillance and what immune environments can successfully control or eliminate tumors.

While mathematical models of tumor-immune interactions and radiation response are plentiful, here we demonstrate for the first time predictions derived from an in silico agent-based model that are validated in 10,469 clinical samples across 31 cancer types. This agent-based model stratifies TIES composition into the 3 E's of immunoediting—tumor elimination, tumor-immune equilibrium, and tumor escape [71]. Tumors that are clinically apparent must have evolved to escape immune surveillance, and in our analysis all clinical samples correctly mapped onto model-predicted TIES compositions of tumor escape.

Quantitative simulations of radiotherapy suggest that most protocols will leave cancer cells behind. However, radiation-induced shifts in TIES composition can provoke immune-mediated tumor elimination, whereas unfavorable TIES with a large proportion of immune suppressive cells will facilitate tumor regrowth and local failure. From these observations we developed the iRIS score and demonstrated that favorable iRIS values correlate with radiocurability across different clinical samples and cancer types. These results challenge the prevailing dogma of intrinsic cancer cell sensitivity to radiotherapy and suggest a significant role of the cell-extrinsic immune environment mediation to radiation response. These data complement preclinical observations of radiation-immune synergy, and suggests that in patient tumors, radioresponse and TIES composition are linked.

Combination of iRIS as a cancer cell-extrinsic immune environment metric with cancer cell molecular radiosensitivity identifies RSI^lo/iRIS^lo patients as most radiocurable, which aligns with clinical observations of locoregional control in specific tumor types enriched in RSI^lo/iRIS^lo patients. While RSI^lo/iRIS^lo NSCLC had significantly improved overall survivals compared to RSI^hi/iRIS^hi patients, survival curves of patients with mixed phenotypes (RSI^lo/iRIS^hi and RSI^hi/iRIS^lo) did not separate. Taken together, patient-specific responses to radiation may be a combination of the direct cytotoxic effect of radiation, encoded in the cell-intrinsic RSI molecular profile, and the contexture of the immune microenvironment, encoded in the iRIS model.

Of importance, protracted fractionated radiation regimens may select for more radiation-resistant (RSI^hi) tumors as the tumor evolves [72]. Combined with radiation-induced shifts in the TIES composition, radiation response may in itself visualize a complex adaptive dynamic system. The inflamed milieu of a tumor [73,74] following radiotherapy facilitates or suppresses tumor growth, thus each patient tumor is unique and may require varying approaches based on underlying TIES and molecular composition. More integrated radiobiological, mathematical, and radiation oncology studies are needed to decipher how to best use radiation dose and dose fractionation to steer TIES composition toward immune-mediated tumor elimination.

This study provides the first step toward the ability to predict which patients are prone to radiation-induced immune destruction, which patients will require priming radiation to shift to a more favorable TIES composition, and which patients have a resistant tumor immune environment where radiation alone will be ineffective. Our findings strongly support the notion that the pretreatment TIES composition and intrinsic radiosensitivity, defined by iRIS and RSI, respectively, could be actionable tumor metrics to evaluate when making these decisions. Herein we focused on qualitative understanding of the pan-cancer TIES, without calibration and validation of the model to individual cancer sites. Before any conclusions about treatment adaptations can be drawn, future work will include rigorous model training and testing for each cancer [75].

There are a plethora of active clinical trials exploring combinations of radiation and immunotherapy, but as of yet, there is no consensus on how both therapies should be integrated to optimize patient outcomes. This is a major question to address in oncology as both therapies independently and jointly may lead to adverse side effects with minimal oncologic benefit to the patient. With over 300 ongoing clinical trials to date combining radiotherapy and immunotherapy [76], invaluable biological and clinical insights into the immunogenic consequences of radiation are expected in the years to come.

In conclusion, the presented work is the first step toward a conceptual understanding of the contribution of cell intrinsic molecular radiosensitivity and cancer cell-extrinsic immune environmental modulation of the radiation response. To translate this work, rigorous calibration, validation, and evaluation of predictive power for individual responses and outcomes for specific tumor types are of utmost importance [1], which will be the topic of future work.

Author contributions

Juan C.L. Alfonso: Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Validation; Visualization; Roles/Writing – original draft; Writing – review & editing.

G. Daniel Grass: Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Validation; Visualization; Roles/Writing – original draft; Writing – review & editing.

Eric Welsh: Formal analysis; Investigation; Methodology

Kamran A. Ahmed: Formal analysis; Investigation; Methodology;

Jamie K. Teer: Formal analysis; Investigation; Methodology;

Sharon Pilon-Thomas: Conceptualization; Writing – review & editing

Louis B. Harrison: Conceptualization; Writing – review & editing

John L. Cleveland: Conceptualization; Writing – review & editing

James J. Mulé: Conceptualization; Writing – review & editing

Steven A. Eschrich: Formal analysis; Investigation; Methodology; Roles/Writing – original draft; Writing – review & editing.

Javier F. Torres-Roca: Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Validation; Visualization; Roles/Writing – original draft; Writing – review & editing.

Heiko Enderling: Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Validation; Visualization; Roles/Writing – original draft; Writing – review & editing.

Conflict of interests

G.D.G, JC.L.A., H.E., J.T-R have filed a provisional patent application for iRIS under the Innovation and Industry Alliances Office of the Moffitt Cancer Center and Research Institute. J.T-R. and S.A.E report intellectual property (RSI) and stock in Cvergenx. J.K.T. consults and has ownership stake in Interpares Biomedicine. J.J.M has ownership interest (including patents) in Fulgent Genetics, Inc., Aleta Biotherapeutics, Inc., Cold Genesys, Inc., Myst Pharma, Inc., Verseau Therapeutics, Inc., and Tailored Therapeutics, Inc., and is a consultant/advisory board member for Celgene Corporation, ONCoPEP, Inc., Cold Genesys, Inc., Morphogenesis, Inc., Mersana Therapeutics, Inc., GammaDelta Therapeutics, Ltd., Myst Pharma, Inc., Tailored Therapeutics, Inc., Verseau Therapeutics, Inc., Iovance Biotherapeutics, Inc., Vault Pharma, Inc., Noble Life Sciences Partners, Fulgent Genetics, Inc., Orpheus Therapeutics, Inc., UbiVac, LLC, Vycellix, Inc., and Aleta Biotherapeutics, Inc.