Abstract
Protein sequences and structures evolve by satisfying varied physical and biochemical constraints. This multi-level selection is enabled not just by the patterning of amino acids on the sequence, but also via coupling between residues in the native structure. Here, we employ an energetically detailed statistical mechanical model with millions of microstates to extract such long-range structural correlations, i.e. thermodynamic coupling free energies, from a diverse family of protein structures. We find that despite the intricate and anisotropic distribution of coupling patterns, the majority of residues (>70%) are only marginally coupled contributing to functional motions and catalysis. Physical origins of ‘sectors’, determinants of native ensemble heterogeneity in extant, ancient and designed proteins, and the basis for allostery emerge naturally from coupling free energies. The statistical framework highlights how evolutionary selection and optimization occur at the level of global interaction network for a given protein fold impacting folding, function, and allosteric outputs.
Keywords: Thermodynamics, Energetic coupling, Stability, Energy landscape, Function, Allostery
Graphical abstract
Highlights
-
•
Evolution of protein structures occurs at the level of global interaction network.
-
•
More than 70% of the protein residues are weakly or marginally coupled.
-
•
Functional ‘sector’ regions are a manifestation of marginal coupling.
-
•
Coupling indices vary across the entire proteins in extant-ancient and natural-designed pairs.
-
•
The proposed methodology can be used to understand allostery and epistasis.
Abbreviations
- WSME
Wako-Saitô-Muñoz-Eaton
- SSA
single sequence approximation
- DSA
double sequence approximation
- SCA
statistical coupling analysis
- NMR
nuclear magnetic resonance
- MD
molecular dynamics
1. Introduction
Protein sequence and structural evolution are driven by a multitude of factors arising from requirements for efficient folding, function, stability, regulation and inter-molecular interactions, to name a few. Every random mutation that modulates the physico-chemical property of an amino-acid could influence any of the biophysical selection factors, thus influencing organismal fitness. Of these, foldability and stability are critical as any mutation that reduces the folded population will quickly be weeded out of the population via natural selection (Tokuriki and Tawfik, 2009; Bershtein et al., 2017; Bastolla et al., 2017). Extant protein structures are therefore the product of an uncountable number of such selection and adaptation events along the evolutionary timeline. One of the unique properties of proteins that make them robust to mutations (up till a certain threshold) is the intra-molecular interaction network. Intra-protein interaction networks are highly pliable with the ability to adjust and accommodate substitutions while still maintaining the native fold (Gassner et al., 1996; Riddle et al., 1997; Kurnik et al., 2012; Ben-David et al., 2019). The pliability, a feature that is also likely selected, enables proteins to navigate through the mutational space contributing to the evolution of novel functions, drug resistance and allostery. In fact, in directed evolution, ancestral sequence construction, and deep mutagenesis based approaches, it is these interactions and forces that are modulated (through mutations) resulting in improved catalytic efficiency, promiscuity or adaptability to a particular condition (Dougherty and Arnold, 2009; Goldsmith and Tawfik, 2012; Risso et al., 2018; Gupta and Varadarajan, 2018; Bolognesi et al., 2019; Hochberg and Thornton, 2017).
While functional readouts of large-scale mutagenesis studies are becoming increasingly possible, understanding the origins of functional changes on mutations from the perspective of basic thermodynamic factors will enable the targeted design of proteins with altered or specific functionalities. To design natural-protein-like enzymes with marginal stability and specific activity, it is necessary to understand how residues in the native structure are ‘thermodynamically coupled’ to each other and the magnitude of this coupling, which in turn determines epistasis or context-dependence of mutations (Domingo et al., 2019; Horovitz et al., 2019). The extent of thermodynamic coupling of a residue arises not merely from the number of direct contacts but also via the second- or third-shell effects through intervening residues and their interactions (Yang et al., 2016; Rajasekaran et al., 2017a, 2017b). Importantly, the statistical nature of the protein with numerous conformational states lends itself to more subtle effects in coupling; specifically, if two residues i and j are always folded in a sub-ensemble or a collection of states, it contributes to a coupling free energy in the thermodynamic sense, even if they are distant in the native structure, as perturbation of i will necessarily influence j (Hilser et al., 1998).
Thermodynamic coupling free energies are, however, challenging to estimate given the diversity and the weak non-covalent nature of the numerous intra-molecular interactions in a protein, and the multitude of conformational states in the native ensemble. One avenue to generate this is via molecular simulations (coarse-grained or all-atom), where conformations are accumulated as a function of time to construct a native ensemble. However, sampling limitations and the long time-scales associated with structural transitions in large proteins (milliseconds or slower) would mean that a reasonable statistical description of a protein's conformational space is not straightforward from this method. An alternate possibility is to employ statistical mechanical treatments of protein folding, wherein a fixed ensemble of conformational states is constructed through physically reasonable assumptions thus enabling access to the total partition function and hence the relative population of states. In this regard, earlier attempts at estimating coupling free energies from statistical treatments employed the COREX algorithm and empirical energies derived from the accessible surface area of conformations (Hilser et al., 1998, 2006). On the other hand, the Wako-Saitô-Muñoz-Eaton (WSME) model (Wako and Saito, 1978; Muñoz and Eaton, 1999) provides an attractive and alternate avenue to estimate thermodynamic coupling free energies from just a single structure with detailed energetic-entropic terms (Naganathan, 2012; Rajasekaran et al., 2016). The WSME model explicitly accounts for the statistical nature of the folding problem by a diverse collection of microstates employing an Ising-like description and is arguably one of the most successful models of protein folding despite its simplicity. It has been employed to study the folding behavior of single-domain proteins (Naganathan, 2012; Rajasekaran et al., 2016), multi-domain systems (Inanami et al., 2014) and repeat proteins (Sivanandan and Naganathan, 2013; Hutton et al., 2015), characterize experimental data at different levels of resolution and to reproduce and understand phenomena such as cold denaturation (Naganathan, 2016), allostery (Itoh and Sasai, 2011) and quinary effects on folding-binding (Gopi and Naganathan, 2020; Munshi et al., 2018). The model is also rigorous enough to capture folding pathway heterogeneity at a level comparable to all-atom MD simulations (Henry et al., 2013; Gopi et al., 2017) and single-molecule force spectroscopy measurements (Gopi et al., 2017). In addition, the energy-entropy terms of the model are sufficiently detailed enough to reproduce changes in stability and folding mechanisms arising from mutations involving charged residues (Naganathan, 2013), apolar residues (Rajasekaran et al., 2017b), post-translational modifications (Gopi et al., 2015) and disordered loop insertions (Gopi et al., 2015).
In this work, we show how the WSME model can be used to simultaneously generate native ensembles, understand folding mechanisms and estimate thermodynamic coupling free energies employing a single structure as an input. Our results highlight the robustness and tunability of interaction network in proteins, and provide a complementary viewpoint to sequence- and function-based methods with implications in protein structural organization, design and allostery.
2. Methods
2.1. Wako-Saitô-Muñoz-Eaton (WSME) model
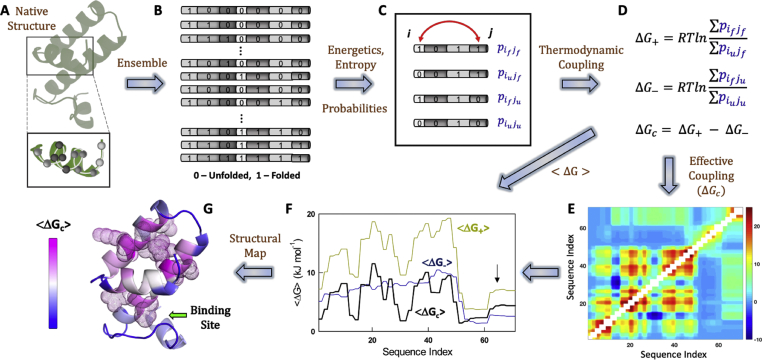
The WSME model employs a binary treatment for the folded status of residues with 1 and 0 representing folded and unfolded conformations, respectively. While many flavors of the WSME model are available (Wako and Saito, 1978; Muñoz and Eaton, 1999; Naganathan, 2012; Gopi et al., 2017; Henry and Eaton, 2004; Bruscolini and Naganathan, 2011), we employ the bWSME model (with b standing for block, a set of consecutive residues (Gopi et al., 2019)) that partitions the protein's phase space into single stretches of folded residues or blocks (single-sequence approximation, SSA), two stretches of folded residues or blocks (double-sequence approximation, DSA) and DSA with interaction across the folded islands even if the intervening residues or blocks are unfolded (DSAw/L, i.e. DSA with loop). The block-size can vary from 1 to 5, depending on the number of residues in the protein, to reduce the number of microstates that can otherwise number in several hundreds of millions (Fig. 1A and B). For example, generating the residue-level conformational landscape of Kemp Eliminase (299 residues) would require the algorithmic enumeration of more than 661 million states. However, treating a set of 5 consecutive residues as a block reduces the number of conformations to just over 2 million making the calculations less intensive a coarse-graining that does not affect the conformational landscape or the folding mechanism (Gopi et al., 2019).
Fig. 1.
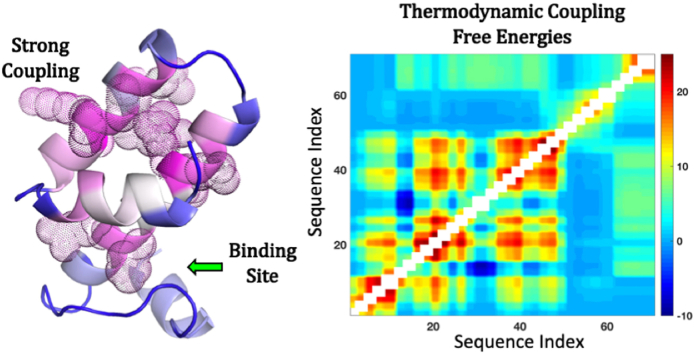
Steps involved in the calculation of thermodynamic coupling free energies from the WSME model. The native protein structure is considered as either residues or blocks (panel A) from which the ensemble is constructed (panel B) with 0 and 1 representing unfolded and folded residue (block) status, respectively. Since the WSME model is structure-centric, the energetics can be directly derived from the interactions present in the native state (vdW interactions, electrostatics, solvation free energy) while the entropic penalties are invoked based on the secondary-structure type identified in the PDB, following which the statistical weights and probabilities of every microstate are calculated. The resulting ensemble is partitioned into four sub-ensembles depending on the conditional folded status of residue j with respect to residue i (panel C). Positive, negative and effective thermodynamic coupling free energies are estimated (panel D) that can either be represented as a coupling matrix (panel E) or as vectors as a function of protein sequence index (panel F). In addition to this, the effective coupling free energies are mapped on to the structure, and those residues exhibiting strong coupling (Z-score > 1) are shown as dots (panel G). The arrow in panel G points to the direction in which the ligand binds.
The total partition function (Z) of the bWSME model is calculated as
| (1) |
where is the total number of microstates considered in the model framework (SSA, DSA and DSAw/L), R is the gas constant and T is the temperature, which is set to 310 K. Free energy of microstates with folded structure between and involving blocks p and q (p, q) is:
| (2) |
The stabilization free energy for the microstate (p, q) is written as,
| (3) |
where L is the set of residues comprising the protein, L(i) and L(j) represent the set of residues in blocks i and j, respectively, while also accounting for interactions between residues within the same block. The stabilization free energy includes contributions from van der Waals interactions (a uniform interaction energy for the vdW contacts identified from the native structure with a 5 Å cut-off; supporting Table S1), charge-charge interactions without a distance cut-off via the Debye-Hückel formalism (at a fixed ionic strength of 0.1 M, with an effective dielectric constant of 29 for soluble proteins (Naganathan, 2012; Naganathan, 2013) and 4 for membrane proteins) and contacts-scaled implicit solvation term (Naganathan, 2012) (ΔGSolv, calculated as the heat capacity change per native contact that is fixed to −0.36 J mol−1 K−1 per native contact). The entropic penalty associated with fixing all residues in the microstate (p, q) is given as,
| (4) |
here, is the entropic cost of fixing residue j in the native conformation (set to −14.5 J mol−1 K−1 per residue), L(i) includes the set of residues within block i. An excess entropic penalty (Rajasekaran et al., 2016) (ΔΔS = −6.1 J mol−1 K−1 per residue) is additionally assigned to residues identified as unstructured (coil) by STRIDE (Heinig and Frishman, 2004) and glycine residues. The entropic penalty of fixing proline in the native conformation is set to 0 J mol−1 K−1 per residue, owing to its limited backbone flexibility. Partial partition functions are calculated by lumping together microstates with a specific number of structured residues from which the one-dimensional free energy profiles are generated.
3. Results
3.1. Thermodynamic coupling free energies
The steps involved in calculating the extent of thermodynamic coupling of protein residues from the perspective of the bWSME model are outlined in Fig. 1. The model description, ensemble generation and parameterization are discussed in the Methods section. In the current work, we adjusted the van der Waals interaction energy () of every protein to generate a folding free-energy profile such that the native ensemble is 30 kJ mol−1 more stable than the unfolded ensemble. Fixing the relative stability of the native ensemble, in turn, fixes the probability () of every microstate following which four sub-ensembles are generated (Liu et al., 2006) for every residue i taking into consideration the folded status of any other residue j – both i and j are folded (), both i and j are unfolded (), i is folded and j is unfolded (), and i is unfolded and j is folded () – with the summation running over all microstates that fit the criteria (Fig. 1C). Positive () and negative () thermodynamic coupling free energies for a residue i, adapted from Chowdhury and Chanda (2010), are defined as (Fig. 1D),
| (5) |
| (6) |
Note that in the definition of and , the (un)folded status of all other residues is held fixed while that of i varies; this referencing facilitates the calculation of the true degree of coupling of i with j (also see Fig. 1C). Specifically, if residues i and j interact strongly – through direct interactions, via spatially intervening residues, or if they display little change in folding probability on perturbations amongst a collection of microstates – then the equilibrium constant will be significantly greater than 1 as the total probability of microstates in which both residues are folded (numerator in equation (5)) will be higher than those in which i is unfolded and j is folded (denominator in equation (5)), and hence . On the other hand, if i and j do not interact directly or through mediated interactions will be greater than 1 as the probability of both residues being unfolded is infinitesimally low (under folding conditions), and thus . The coupling free energies (equations (5), (6))) can be calculated for every residue i with respect to every other residue j. The resulting matrix is not symmetric since the impact of residue i on j is not the same as j on i due to differences in residue environments, and can be symmetrized by averaging the effects.
The balance between positive and negative coupling free energy of a residue will in turn determine the effective coupling free energy between different residues in the native ensemble:
| (7) |
The resulting two-dimensional (2D) matrices (Supporting Fig. S1) can be averaged as a function of residue index to calculate the mean coupling free energies , and (Fig. 1E and F). Intuitively, the effective thermodynamic coupling free energies are a measure of the extent to which local stabilities and hence the conformational status of individual residues are connected to other residues. Strong effective coupling between a pair of residues will mean that they exhibit similar behavior on perturbations and are correlated at the ensemble level, while weak effective coupling would translate to little correlation and by extension larger dynamics. The connection to dynamics can be explicitly made for weakly coupled residues as they are not held in place by multiple stabilizing interactions and thus enabling relatively uninhibited structural movements. It is important to note that changes in protein stability would redistribute the populations, which would in turn alter the magnitude of coupling free energies. However, as long as the calculations are performed under conditions in which the native state is more stable than the unfolded state with finite populations of partially structured states ( 0 and 0 at T < Tm), the rank ordering of coupling free energy magnitudes are insensitive to the choices of vdW interaction energies or stabilities (Fig. S2).
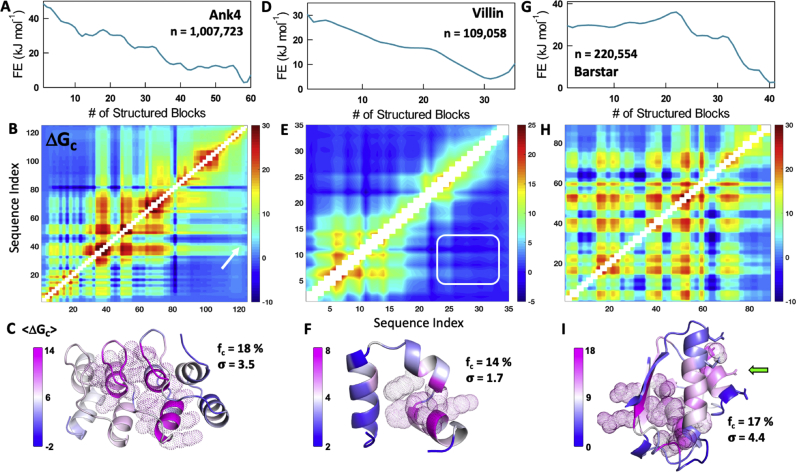
As a representative example, consider the Ankyrin repeat protein (Ank4, the first four repeats of the full-length domain, Table S1). The WSME model representation of Ank4 with more than a million microstates captures the expected multi-state folding in the one-dimensional (1D) free energy profile (Fig. 2A). The matrix exhibits strong effective coupling close to the main diagonal, as repeat domains are primarily stabilized by nearest neighbor interactions, and weak effective coupling for off-diagonal elements (Fig. 2B). The mean effective coupling, when mapped on to the structure, reveals that 18% of Ank4 residues are very strongly coupled (fc) to the rest of the structure (Z-score of greater than 1) while the rest of the structure is only weakly (Z-score of less than −1) or moderately coupled (Z-scored between 1 and -1) with an overall standard deviation (σ) in the effective coupling free energy of 3.5 kJ mol−1 (Fig. 2C). It is interesting to note that some off-diagonal regions exhibit finite coupling despite making no direct interactions in the structure. For example, the arrow in Fig. 2B points to a moderate effective coupling of ∼5 kJ mol−1 between residues A40 and L120 located in the 2nd and 4th repeats, respectively, but separated by 21 Å (Cα-Cα distance). The residues do not interact directly but are still ‘thermodynamically coupled’ via interactions mediated through the third repeat and due to the high intrinsic stability of the second repeat.
Fig. 2.
Representative examples of coupling free energy calculations on Ank4, Villin and Barstar. Shown are the one-dimensional free energy profiles (panels A, D, G), effective coupling free energy matrices (panels B, E, H) and the structural maps (panels C, F, I). The parameters n, fc and σ indicate the total number of microstates, the fraction of strongly coupled residues and the standard deviation in effective coupling free energy, respectively. The arrow in panel B signals the weak coupling between 2nd and 4th repeat residues in Ank4 while the white block in panel E shows near-zero coupling between helices 1–2 and 3 in Villin. The green arrow in panel I represents the binding surface on Barstar. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
We further tested our approach on the popular model system, villin head piece domain. The model predicts a folding free energy profile with a shallow intermediate like state at ∼18 structured residues (Fig. 2D). The constructed matrix reveals a strong coupling between the first two helices (residues 1–20) while the third helix is only weakly coupled to the first two (white rectangle in Fig. 2E). This weak coupling likely contributes to the population of a partially structured state wherein the third helix samples conformations independent of the first two helices (Fig. S3), in good agreement with triplet-triplet energy transfer experiments (Reiner et al., 2010). The fraction of strongly coupled residues is estimated to be 14% with a smaller standard deviation (just 1.4 kJ mol−1) compared to the Ank4 protein, which is likely to do with the smaller size of the protein (Fig. 2F).
3.2. Functional connect of marginally coupled residues
The simpler helical architecture of Ank4 and Villin allows for a straightforward interpretation of the effective coupling matrix. In contrast, most proteins exhibit a complex topology with an intricate distribution of energetics. We therefore constructed the native ensemble for Barstar, the inhibitor of Barnase, which not only exhibits a complex α-β topology but also displays a multi-state folding mechanism (Sarkar et al., 2013). The current version of the model captures the multi-state nature of Barstar folding with at least 3 intermediates or partially structured states in the native side of the folding barrier (Fig. 2G) in agreement with an earlier work (Naganathan et al., 2015). The effective coupling matrix derived from the native ensemble shows a non-intuitive grouping of strong positive and strong negative effective coupling with no apparent trend (Fig. 2H). However, when mapped on to the structure, the majority of strongly coupled residues cluster together and more importantly form a strong ‘base’ to enable binding of Barnase via the weakly coupled helices 2 and 4 (green arrow in Fig. 2I that points to the direction of Barnase binding). In other words, functional sites are only marginally coupled (either weakly or moderately coupled) to the rest of the structure and appear to be supported by the strongly coupled residues.
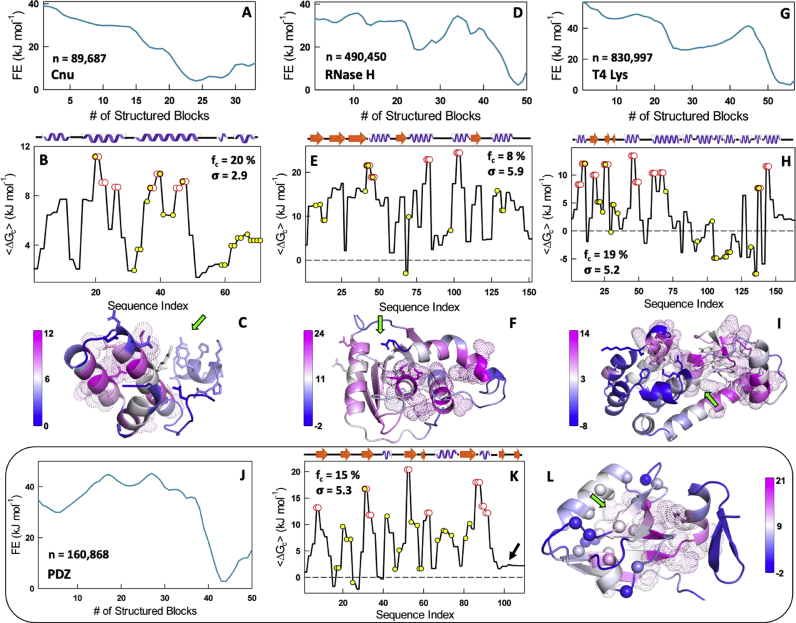
To explore this feature further, we constructed the native ensembles, coupling matrices and average coupling free energies of three domains: (a) Cnu, a protein that acts as a sensor of environmental changes in uropathogenic E. coli, (b) RNase H, an enzyme that cleaves DNA-RNA hybrids, and (c) T4 lysozyme, an enzyme that breaks down peptidoglycan in bacterial cell walls. The free energy profiles range from downhill to multi-state (Fig. 3A, D, 3G) while being consistent with experiments, as shown in earlier works (Rajasekaran et al., 2017b; Narayan et al., 2017; Cecconi et al., 2005; Narayan and Naganathan, 2014; Llinás et al., 1999). Specifically, the C-terminal helix of Cnu is observed partially structured at 310 K (note the low positive coupling for residues 60–71 in Figs. 3B and 1E) (Narayan et al., 2017), the RNase H folding pathway agrees with the order of formation observed in HX experiments (Narayan and Naganathan, 2014), while the C-terminal half of the structure is predicted to fold first for T4 lysozyme again in accordance with experiments (Rajasekaran et al., 2017b). In each of the three cases, the number of strongly coupled residues that form a part of the binding or catalytic site are 4/14, 3/12 and 7/31, respectively (red in Fig. 3B, E, 3H). Thus, more than 70% of the strongly coupled residues do not contribute to function directly. However, structural mapping points to a clustering of the strongly coupled residues while placing them right next to the ligand binding site and forming a base to support binding and catalysis (green arrow in Fig. 3C, F and 3I point to the direction of ligand binding), similar to the observation in Barstar. The fraction of strongly coupled residues ranges between 8 and 20% for the four proteins with a standard deviation of ∼3–6 kJ mol−1.
Fig. 3.
Functional connect of marginally coupled residues. Free energy profiles of Cnu, RNase H, T4 lysozyme and PDZ (panels A, D, G, J), the effective coupling free energies with the strongly coupled residues in red and functional residues in yellow (panels B, E, H, K), and the structural map of the effective coupling free energies (panels C, F, I, L). The green arrows in panels C, F and I represent the binding surface. The black arrow in panel K signals the weak coupling of the C-terminal hairpin in PDZ to the rest of the structure, while the spheres in panel L represent ‘sector’ residues. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
Functional sites induce strong co-evolution of residues around them even up till the second and third shell to maintain activity above a certain threshold (Lockless and Ranganathan, 1999). The physical origins of such ‘sectors’ around the active site have remained elusive. Since thermodynamic coupling analysis provides an alternate avenue to study long-range correlations, we generated the native conformational ensemble of PDZ, a popular model system for allostery and in which the concept of sector was first established (Lockless and Ranganathan, 1999). The free-energy profile of PDZ points to a two-state-like system (Fig. 3J) with a native ensemble in which the C-terminal hairpin only partially folded (arrow in Fig. 3K). Strongly coupled residues constitute only 15% of the total number and again cluster together in the region between the ligand binding site and the C-terminal hairpin (dots in Figure 3L). Remarkably, none of the strongly coupled residues, except for I31 (I336 in the PDB numbering scheme), fall within the sector region (Fig. 3K). In other words, sector residues are only marginally coupled to the rest of the structure, a feature that is likely driven by the requirement of dynamics to function, and in this case, to accommodate the ligand. In fact, MD simulations point to the ligand binding regions (all of which form a part of the sector) exhibiting large dynamics in the native ensemble (Bozovic et al., 2020; Kumawat and Chakrabarty, 2020) consistent with our observations of marginal coupling. A similar observation can also be made in the enzyme dihydrofolate reductase (DHFR) where the strongly coupled residues constitute one face of the protein acting as a base while the marginally coupled residues are involved in ligand-cofactor binding and catalysis (Fig. S4). Only 20% of the sector residues in DHFR (Reynolds et al., 2011) (7 out of 36) form a part of the strongly coupled residues subset (32 residues), again highlighting that sector residues identified around the ligand binding site are predominantly characterized by marginal thermodynamic coupling to the rest of the protein.
3.3. Marginal coupling and structural transitions
The marginal thermodynamic coupling of specific helices in both Villin and Cnu manifest as conformational changes in equilibrium. Do larger proteins exhibit a similar distribution of coupling energies favoring conformational transitions?
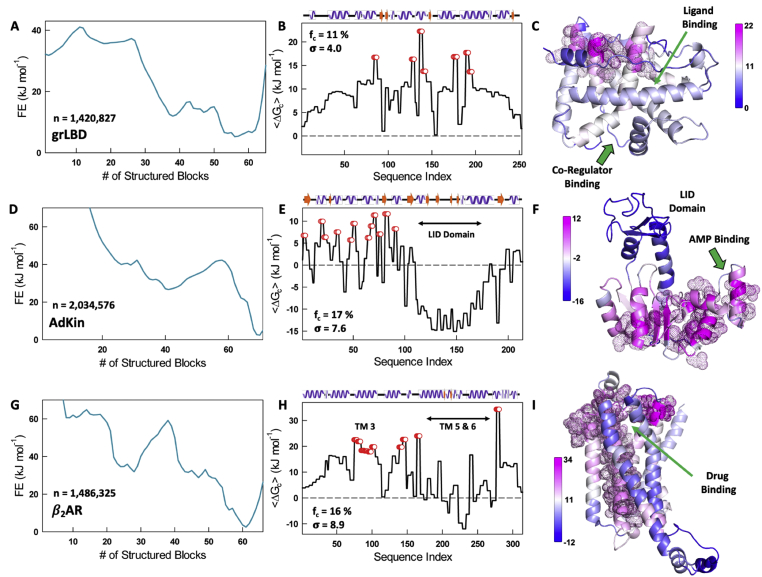
To test this, we studied the 253-residue ligand binding domain of glucocorticoid receptor (grLBD) that binds multiple ligands (both small molecules and proteins). The WSME model predicts a broad native well for this domain indicative of numerous conformations in equilibrium (Fig. 4A, left column) mirroring experimental observations (Köhler et al., 2020; Suren et al., 2018). Mapping the effective thermodynamic coupling free energies onto the structure reveal a feature similar to the smaller domains presented earlier – strongly coupled residues are physically close in space (Fig. 4B and C). The experimentally observed diversity in ligand binding is exclusively driven by marginally coupled residues that constitute a remarkable 89% of residues (225 of the 253 residues). The N-terminal lid (1–25 residues) and C-terminal helix that undergo conformational transitions to enable binding are weakly coupled ( ∼5 kJ mol−1 or less; Fig. 4B, Fig. S5A), consistent with the experimentally observed partially structured states involving these segments (Köhler et al., 2020; Suren et al., 2018).
Fig. 4.
Larger proteins display a similar anisotropic distribution of coupling free energies. The color code is maintained the same as Fig. 3 for the proteins glucocorticoid receptor (panels A, B, C), adenylate kinase (panels D, E, F) and beta-2 adrenergic receptor (panels G, H, I). (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
Adenylate Kinase is another protein that undergoes a dramatic ‘open’ to ‘close’ transition on binding AMP (Schrank et al., 2009; Aviram et al., 2018) whose conformational features are not directly evident from the one-dimensional free energy profile (Fig. 4D). However, the residue-level effective thermodynamic coupling free energy constructed from the native ensemble displays strong positive in the N-terminal half of the structure (close to the regions where AMP binds), while the ‘LID Domain’ that undergoes a large conformational transition is negative coupled (Fig. 4E). The strong negative coupling arises when the folding status of specific residues are not correlated to others due to weaker interactions and partial unfolding resulting in dominating over (Fig. S5B). Mapping of effective coupling free energies onto to the structure provides a clear view of the demarcation of the two domains from a structural-functional viewpoint and their anisotropic distribution (Fig. 4F).
The observation that only <30% of protein residues are strongly coupled to the rest of the structure also holds true for a collection of 12 domains that span all three classes of structure (Fig. S6). Surprisingly, such anisotropic distribution is also seen in the membrane protein, the β2-adrenergic receptor, a GPCR (G-Protein Coupled Receptor) involved in various physiological processes. Activation of the β2-adrenergic receptor has been shown to cause major structural changes on the intracellular side of the GPCR involving movements in transmembrane (TM) helices 5, 6, and 7. TM6, in particular, undergoes a 14 Å movement away from the center of the helical bundle (Latorraca et al., 2017). The free energy profile generated from an ensemble of ∼1.5 million microstates signals a complex folding mechanism (Fig. 4G). Interestingly, the values point to zero or negative coupling in TM5 and TM6 indicative of partially structured states in equilibrium involving residues in these helices (Fig. 4H, Fig. S5C). The strongly coupled residues are distributed across the structure but still form a spatially contiguous set accounting for 16% of the residues (Fig. 4H and I). Except for D85 in TM2, all other residues that form the binding pocket for partial inverse agonist carazolol exhibit marginal thermodynamic coupling.
3.4. Natural vs. designed and extant vs. ancient proteins
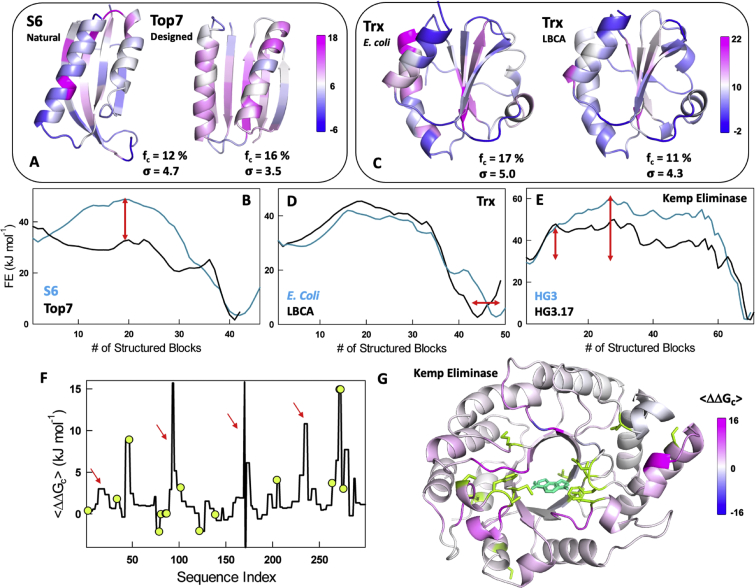
In this section, we showcase the advantages of the WSME-model derived thermodynamic coupling free energies from the perspective of protein design, evolution and function. One of the earliest designed proteins is Top7 from the group of Baker and co-workers who identified that it folds via multi-phasic kinetics while concluding that designed proteins are likely characterized by a ‘rough’ folding landscape as they do not go through the process of evolution to weed out conflicting interactions (Walters et al., 2007). Here, we compare two proteins of similar topology S6 and Top7 (Fig. 5A), with the former being a natural protein, to explore differences in coupling patterns, if any. S6 displays a two-state-like folding behavior in contrast to Top7 whose profile appears multi-state-like with a significantly lower free-energy barrier (Fig. 5B), consistent with experiments (Olofsson et al., 2007) and coarse-grained simulations (Zhang and Chan, 2010). Mapping the onto the structure, we find that Top7 has a larger fraction of strongly coupled residues with a smaller standard deviation compared to S6 (Fig. 5A). Importantly, the strongly coupled residues are more uniformly distributed in Top7 compared to S6 suggesting that the differences in folding behaviors could also be a consequence of energy functions in design algorithms that excessively stabilize pockets of structure locally to build up higher order structures, thus ensuring their high stability.
Fig. 5.
Insights into structural partitioning of coupling free energies in designed proteins and enzymes. (A, B) Mapping of coupling free energies onto the structure (panel A) for S6 and the designed protein Top7 together with their free energy profiles (panel B). The red arrow in panel B indicates the large difference in barrier heights between the two proteins. (C, D) Structural mapping of the coupling free energies of thioredoxins from E. coli and the resurrected LBCA ancestor (panel C), and their corresponding free energy profiles (panel D). The red arrow signals the more ‘disordered’ native ensemble for the LBCA ancestor. (E) Free energy profiles of the designed Kemp Eliminases HG3 and HG3.17. The red arrow signals the large difference in barrier heights between the two and the overall tilting of the HG3.17 towards the folded state (black). (F) The difference in coupling free energies between the two variants HG3 and HG3.17. The positions of additional mutations in HG3.17 are shown in green circles while the red arrows displays the non-intuitive changes in coupling free energies at positions far from the mutated sites. (G) Mapping of the coupling free energy differences onto the structure. The transition state analog is shown in cyan. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
At the other end of the spectrum are ancient or ‘resurrected’ proteins whose sequences are generated via ancestral sequence reconstruction methods (Hochberg and Thornton, 2017). Structures of thioredoxins (Trxs), conserved oxidoreductases in cells, are available for both extant and ancient proteins (Ingles-Prieto et al., 2013) allowing for a direct comparison of coupling behaviors and hence their design principles. Though the extant and ancient Trxs from the bacterial branch display no specific structural differences (Fig. 5C), the ancient proteins that are supposed to have existed 4 billion years ago (LBCA, the last bacterial common ancestor, for example) display an order of magnitude faster disulfide bond reduction rate (Perez-Jimenez et al., 2011). The native ensemble of the LBCA Trx is predicted to be less structured than the extant counterpart from E. coli (arrow in Fig. 5D) with the latter exhibiting strong coupling across the entire structure (with a larger fc) in contrast to the ancient cousin that is weakly coupled (with a smaller fc) (Fig. 5C). This observation is in line with earlier computational treatments that point to ancient proteins being more flexible (a consequence of weak coupling) that in turn contribute to their rapid catalytic turnover and even promiscuity (Zou et al., 2015; Del Galdo et al., 2019).
An alternate approach to enhance enzyme activity involves ‘directed evolution’ that has been exploited to improve the activity of many enzymes (Arnold, 2015). Particularly, the activity of Kemp Eliminase that catalyzes the deprotonation and ring opening of 5-nitrobenzisoxazole resulting in 4-nitro-2- cyanophenol has been improved by several orders of magnitude starting from the original de novo design (Khersonsky et al., 2010; Röthlisberger et al., 2008; Broom et al., 2020). Here, we compare two of the representative enzymes, HG2 S265T (HG3) and HG3.17 E47N/N300D (HG3.17) with the latter being the evolved variant, that differ in their catalytic activity by nearly 700-fold due to accumulation of additional mutations closer and far from the active site. We find that these additional mutations tilt the folding landscape towards the folded state by enabling the population of more partially structured states in the native ensemble, visible from the lower free energies of states all along the reaction coordinate and with the folding transition state ensemble being more stable by 15 kJ mol−1 in the evolved variant (Fig. 5E). The population of partially structured states translates to weaker coupling free energies in the evolved variant and this can be observed via the positive values () across nearly the entire structure (Fig. 5F and G). It is interesting to note that the differences are not concentrated around the mutated site, but can span different regions of protein (arrows in Fig. 5F) including the second- and third-shells around the ligand binding site (Fig. 5G).
3.5. Insights into allostery from thermodynamic coupling free energies
The results above signal that mutational effects can contribute to non-intuitive variations in coupling free energies across the structure, hinting at the origins of epistatic effects. Moreover, since coupling estimates explicitly account for populations of various substates in the native ensemble and their thermodynamic interconnectivity, they provide an alternate framework to understand and address allostery as originally proposed by Freire, Hilser and co-workers (Hilser et al., 1998, 2006; Liu et al., 2006). In this section, we explore the extent to which different residues are coupled in proteins from the perspective of the WSME model and without explicitly introducing mutations or modeling ligand binding effects.
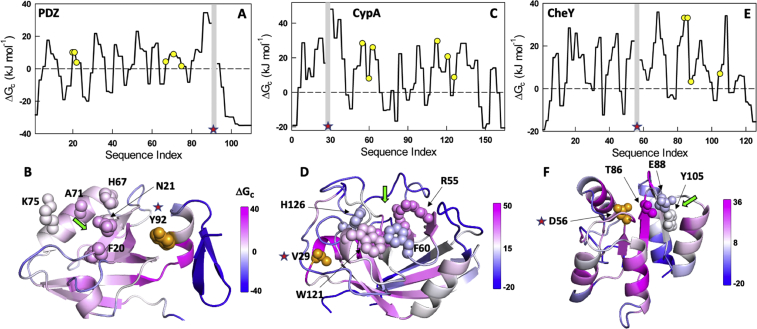
The protein PDZ is also a popular model system to study allostery given its small size (100 residues), α-β topology and its ability to bind a peptide ligand derived from its binding partner CRIPT. NMR experiments show that truncation of the C-terminal helical region, which also harbors a phosphorylation site on Y92 (Y307 in the PDB numbering) and that does not directly interact with the binding site, reduces the binding affinity of the peptide by ∼8 kJ mol−1 (Petit et al., 2009). To understand the origins of such long-range coupling, we extracted the per-residue coupling free energies of Y92 with all other residues in the protein. Fig. 6A shows that Y92 is positively coupled to the binding site residues with a mean coupling free energy of ∼6 kJ mol−1. Mapping the pair-wise coupling free energy (and not the average) on to the structure reveals that the entire protein is differentially coupled to the C-terminal helix (Fig. 6B). This observation signals the likely origins of pervasive chemical shift perturbations and order parameter variations in the entire PDZ domain on phosphorylation, truncation of C-terminal helix, ligand binding and mutations (Petit et al., 2009; Gautier et al., 2018; Chi et al., 2008; Hultqvist et al., 2013).
Fig. 6.
Coupling of experimentally known sites to active site residues in PDZ (Y92; panels A, B), CypA (V29; panels C, D) and CheY (D56; panels E, F). In panels A, C, and E, the star and the shaded block highlight the position in consideration, i.e. the residue whose coupling with other residues is considered (a residue is infinitely coupled with itself and hence no coupling free energy value is shown). The yellow circles are the active site residues in panels A and C, while they represent the known allosteric quartet in CheY. Coupling free energies mapped on to the respective structures are shown in panels B, D, and F with the spheres representing the corresponding active site residues in panel B and D, and the allosteric quartet in panel F. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
CypA, a peptidyl-prolyl isomerase, is another popular model enzyme that has been extensively employed to study allostery (Doshi et al., 2016; Holliday et al., 2017). The mapping of effective coupling matrix on to the structure reveals that the first 40 residues of CypA are more strongly coupled to the rest of the structure (Fig. 6C and D). This observation is also consistent with MD simulations that point to a strongly coupled network in this region of the protein (Doshi et al., 2016). This region also harbors one of the hotspot residues V29, the mutation of which to Leucine reduces the isomerization activity by 30% despite being far from the active site. Extracting only the contribution of V29, we find that it is differentially coupled to different protein regions (as in PDZ) and more coupled to a farther active site residue (R55, ∼25 Å) than H126 that is closer (∼13 Å) (Fig. 6C). Similarly, CheY, a regulator of chemotaxis in E. coli displays an allosteric behavior wherein the phosphorylation of D56 regulates the binding of the flagellar motor protein FliM at a site ∼10 Å away (McDonald et al., 2013). We find that Y105, a part of the binding site, is moderately coupled (∼7 kJ mol−1) to D56 emphasizing its role as an allosteric site (green arrow in Fig. 6E and F). (Itoh and Sasai, 2011; Amor et al., 2016) However, as observed in Fig. 6F, it need not be the only site that is connected to D56 as any mutation or perturbation around it (even distant) will invariably perturb the interaction energetics and hence the coupling.
4. Discussion
We find that residue environmental effects, from a combination of energetic heterogeneity and conformational diversity, could be condensed into effective thermodynamic coupling free energies providing a unique picture on the structural-thermodynamic design principles of proteins. It is important to emphasize here that such residue level effective thermodynamic coupling free energies arise from differences in positive and negative coupling free energies that are in turn related to the distribution of states in the native ensemble. Strongly coupled residues cluster to specific regions, independent of protein topology, size or secondary structure content, revealing that protein stability determinants are distributed in an anisotropic manner. Remarkably, only ∼8–24% of the residues are strongly coupled to the rest of the structure, i.e. nearly 70% of the protein residues are available to perform functional roles including ligand binding and catalysis. The strongly coupled residues are observed to form a structural ‘base’ with minimal fluctuations on average (a consequence of strong coupling) to ‘present’ the active site and binding residues that by necessity should be dynamic (moderate or weak coupling) to accommodate the ligand, at least in the systems studied in the current work. This is consistent with the marginal stability and minimal cooperativity of proteins (Malhotra and Udgaonkar, 2016; Muñoz et al., 2016) (as only a small fraction of residues exhibit strong long-range coupling) and the expected selection for large flexibility in functional sites (Petrovic et al., 2018; Wand, 2013; Henzler-Wildman et al., 2007). It should be possible to test this observation of differential dynamics by performing long time-scale MD simulations and checking for the correlated folded status of every residue versus every other residue that could, in principle, be directly related to the coupling free energies we extract. However, the challenges are that the conformational sampling should be extensive (not restricted to a local minimum) and estimates of pairwise folded status in the unfolded minimum should also be known, so as to enable precise quantification of coupling free energies.
It is of interest to note that the earliest works employing the COREX ensemble model found a similar contiguous stretch of coupled residues (Hilser et al., 1998) and structural-functional connection (Freire, 1999) (from the residue-level stability constants without accounting for the folded status of other residues), further underscoring the robustness of our observations. However, it is still possible that some proteins present a rigid surface for binding with the binding partner being selected for larger dynamics on the binding site, an aspect that can be studied only on a case-by-case basis. An understanding of such co-evolving coupling free energies across two binding partners would therefore be the next important step towards rationalizing the anisotropic distribution of protein stabilities across the structure. We also present here the elusive physical basis for the presence of ‘sectors’ in proteins. More than 80% of sector residues in both PDZ and DHFR exhibit marginal thermodynamic coupling despite forming a near-contiguous pattern around the binding site residues. Therefore, the selection for dynamics likely contributes to the co-evolution of sector-like functional regions while highlighting the power of sequence-based approaches to infer dynamical patterns without explicitly considering them.
The activity and substrate specificity of proteins can be manipulated via an array of high-throughput approaches with the endpoint being a mutation or a collection of mutations that meet the set criteria. Functional studies also show that multiple combinations of mutations (and just not one set) could rescue non-functional variants (Leander et al., 2020) and context-dependence contributes to varied allosteric outcomes (Tang and Fenton, 2017; Wang et al., 2020). But it is still not clear as to how the identified mutations affect the folding conformational landscape and hence, the interaction work or the distribution of conformational states to modulate activities. We provide a plausible answer to this by comparing the folding landscapes of diverse but related pairs of proteins and find significant differences in coupling free energies despite very little changes in the overall structure; importantly, the differences are not localized to the mutated site but are distributed throughout the structure. Moreover, experimental and computational works show that even single-point mutations and perturbations involving ligand binding can contribute to widespread changes in hydrogen-exchange protection factors, NMR order parameters, chemical shifts (Petit et al., 2009; Henzler-Wildman et al., 2007; Roche et al., 2013; Whitley et al., 2008; Naganathan, 2019; Tzeng and Kalodimos, 2012; Kumar et al., 2018; Boehr et al., 2006) and structural measures of connectivity in a variety of systems (Zheng et al., 2006; Atilgan et al., 2010; Rajasekaran and Naganathan, 2017; Guarnera and Berezovsky, 2019). Taken together with the results of the current work, it can be concluded that the majority of residues in a protein are thermodynamically coupled to different extents contributing to non-intuitive context-dependence of mutations and allosteric effects. Thus, natural selection works at the level of global interaction network with mutations in the second- or third-shell (or even distant) around the active site fine tuning the catalytic activity and specificity, the likely outcome of which is the observed long-range evolutionary coupling of active site residues (Jack et al., 2016).
To summarize, the thermodynamic framework of the WSME model provides information on not just the folding mechanism and relative barrier heights, but also the extent of native ensemble heterogeneity that manifests as a hierarchy of coupling free energies. The results presented here are consistent with the alternate thermodynamic treatments of Freire and Hilser, and provide a structural viewpoint on proteins that is complementary to sequence- and function-based approaches. In addition, given our observation that the majority of protein residues are coupled to each other in a given protein, it is necessary to think of selection at the level of the global interaction network to understand not just allostery but also in the evolution of enzymatic activity and selectivity; these features can be studied in the proposed model framework by introducing mutations and exploring the extent to which coupling free energies are modulated. The current methodology can also be extended to study the impact of disease-causing mutations even in large systems and in the absence of structural information on the mutant by merely generating coupling free energy maps.
CRediT authorship contribution statement
Athi N. Naganathan: Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. Adithi Kannan: Formal analysis, Investigation, Validation, Writing – original draft, Writing – review & editing.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was supported by grants BT/PR26099/BID/7/811/2017 from Department of Biotechnology (DBT, India) and MTR/2019/000392 from Science, Engineering and Research Board (SERB, India). A. K. acknowledges funding from the PMRF scheme (Ministry of Education, Government of India).
Handling editor: Nagasuma Chandra
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.crstbi.2021.09.003.
Data availability statement
The data presented are available in the article and in its online supplementary material.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- Amor B.R., Schaub M.T., Yaliraki S.N., Barahona M. Prediction of allosteric sites and mediating interactions through bond-to-bond propensities. Nat. Commun. 2016;7:12477. doi: 10.1038/ncomms12477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnold F.H. The nature of chemical innovation: new enzymes by evolution. Q. Rev. Biophys. 2015;48(4):404–410. doi: 10.1017/S003358351500013X. [DOI] [PubMed] [Google Scholar]
- Atilgan C., Gerek Z.N., Ozkan S.B., Atilgan A.R. Manipulation of conformational change in proteins by single-residue perturbations. Biophys. J. 2010;99(3):933–943. doi: 10.1016/j.bpj.2010.05.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aviram H.Y., Pirchi M., Mazal H., Barak Y., Riven I., Haran G. Direct observation of ultrafast large-scale dynamics of an enzyme under turnover conditions. Proc. Natl. Acad. Sci. U. S. A. 2018;115(13):3243–3248. doi: 10.1073/pnas.1720448115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastolla U., Dehouck Y., Echave J. What evolution tells us about protein physics, and protein physics tells us about evolution. Curr. Opin. Struct. Biol. 2017;42:59–66. doi: 10.1016/j.sbi.2016.10.020. [DOI] [PubMed] [Google Scholar]
- Ben-David M., Huang H., Sun M.G.F., Corbi-Verge C., Petsalaki E., Liu K., Gfeller D., Garg P., Tempel W., Sochirca I., Shifman J.M., Davidson A., Min J., Kim P.M., Sidhu S.S. Allosteric modulation of binding specificity by alternative packing of protein cores. J. Mol. Biol. 2019;431(2):336–350. doi: 10.1016/j.jmb.2018.11.018. [DOI] [PubMed] [Google Scholar]
- Bershtein S., Serohijos A.W., Shakhnovich E.I. Bridging the physical scales in evolutionary biology: from protein sequence space to fitness of organisms and populations. Curr. Opin. Struct. Biol. 2017;42:31–40. doi: 10.1016/j.sbi.2016.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boehr D.D., McElheny D., Dyson H.J., Wright P.E. The dynamic energy landscape of dihydrofolate reductase catalysis. Science (80-. ) 2006;313(5793):1638–1642. doi: 10.1126/science.1130258. [DOI] [PubMed] [Google Scholar]
- Bolognesi B., Faure A.J., Seuma M., Schmiedel J.M., Tartaglia G.G., Lehner B. The mutational landscape of a prion-like domain. Nat. Commun. 2019;10(1):4162. doi: 10.1038/s41467-019-12101-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bozovic O., Zanobini C., Gulzar A., Jankovic B., Buhrke D., Post M., Wolf S., Stock G., Hamm P. Real-time observation of ligand-induced allosteric transitions in a PDZ domain. Proc. Nat. Acad. Sci. USA. 2020;117(42):26031–26039. doi: 10.1073/pnas.2012999117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broom A., Rakotoharisoa R.V., Thompson M.C., Zarifi N., Nguyen E., Mukhametzhanov N., Liu L., Fraser J.S., Chica R.A. Ensemble-based enzyme design can recapitulate the effects of laboratory directed evolution in silico. Nat. Commun. 2020;11(1):4808. doi: 10.1038/s41467-020-18619-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruscolini P., Naganathan A.N. Quantitative prediction of protein folding behaviors from a simple statistical model. J. Am. Chem. Soc. 2011;133(14):5372–5379. doi: 10.1021/ja110884m. [DOI] [PubMed] [Google Scholar]
- Cecconi C., Shank E.A., Bustamante C., Marqusee S. Direct observation of the three-state folding of a single protein molecule. Science (80-. ) 2005;309(5743):2057–2060. doi: 10.1126/science.1116702. [DOI] [PubMed] [Google Scholar]
- Chi C.N., Elfstrom L., Shi Y., Snall T., Engstrom A., Jemth P. Reassessing a sparse energetic network within a single protein domain. Proc. Natl. Acad. Sci. U.S.A. 2008;105(12):4679–4684. doi: 10.1073/pnas.0711732105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chowdhury S., Chanda B. Deconstructing thermodynamic parameters of a coupled system from site-specific observables. Proc. Nat. Acad. Sci. USA. 2010;107(44):18856–18861. doi: 10.1073/pnas.1003609107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Del Galdo S., Alba J., Amadei A., D'Abramo M. Evolutionary modes in protein observable space: the case of thioredoxins. J. Mol. Evol. 2019;87(4–6):175–183. doi: 10.1007/s00239-019-09894-4. [DOI] [PubMed] [Google Scholar]
- Domingo J., Baeza-Centurion P., Lehner B. The causes and consequences of genetic interactions (epistasis) Annu. Rev. Genom. Hum. Genet. 2019;20:433–460. doi: 10.1146/annurev-genom-083118-014857. [DOI] [PubMed] [Google Scholar]
- Doshi U., Holliday M.J., Eisenmesser E.Z., Hamelberg D. Dynamical network of residue-residue contacts reveals coupled allosteric effects in recognition, catalysis, and mutation. Proc. Natl. Acad. Sci. U.S.A. 2016;113(17):4735–4740. doi: 10.1073/pnas.1523573113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dougherty M.J., Arnold F.H. Directed evolution: new parts and optimized function. Curr. Opin. Biotechnol. 2009;20(4):486–491. doi: 10.1016/j.copbio.2009.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freire E. The propagation of binding interactions to remote sites in proteins: analysis of the binding of the monoclonal antibody D1.3 to lysozyme. Proc. Nat. Acad. Sci. USA. 1999;96(18):10118–10122. doi: 10.1073/pnas.96.18.10118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gassner N.C., Baase W.A., Matthews B.W. A test of the “jigsaw puzzle” model for protein folding by multiple methionine substitutions within the core of T4 lysozyme. Proc. Natl. Acad. Sci. U. S. A. 1996;93(22):12155–12158. doi: 10.1073/pnas.93.22.12155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gautier C., Laursen L., Jemth P., Gianni S. Seeking allosteric networks in PDZ domains. Protein Eng. Des. Sel. 2018;31(10):367–373. doi: 10.1093/protein/gzy033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldsmith M., Tawfik D.S. Directed enzyme evolution: beyond the low-hanging fruit. Curr. Opin. Struct. Biol. 2012;22(4):406–412. doi: 10.1016/j.sbi.2012.03.010. [DOI] [PubMed] [Google Scholar]
- Gopi S., Naganathan A.N. Non-specific DNA-driven quinary interactions promote structural transitions in proteins. Phys. Chem. Chem. Phys. 2020;22(22):12671–12677. doi: 10.1039/d0cp01758b. [DOI] [PubMed] [Google Scholar]
- Gopi S., Rajasekaran N., Singh A., Ranu S., Naganathan A.N. Energetic and topological determinants of a phosphorylation-induced disorder-to-order protein conformational switch. Phys. Chem. Chem. Phys. 2015;17:27264–27269. doi: 10.1039/c5cp04765j. [DOI] [PubMed] [Google Scholar]
- Gopi S., Singh A., Suresh S., Paul S., Ranu S., Naganathan A.N. Toward a quantitative description of microscopic pathway heterogeneity in protein folding. Phys. Chem. Chem. Phys. 2017;19(31):20891–20903. doi: 10.1039/c7cp03011h. [DOI] [PubMed] [Google Scholar]
- Gopi S., Aranganathan A., Naganathan A.N. Thermodynamics and folding landscapes of large proteins from a statistical mechanical model. Curr. Res. Struct. Biol. 2019;1:6–12. doi: 10.1016/j.crstbi.2019.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guarnera E., Berezovsky I.N. On the perturbation nature of allostery: sites, mutations, and signal modulation. Curr. Opin. Struct. Biol. 2019;56:18–27. doi: 10.1016/j.sbi.2018.10.008. [DOI] [PubMed] [Google Scholar]
- Gupta K., Varadarajan R. Insights into protein structure, stability and function from saturation mutagenesis. Curr. Opin. Struct. Biol. 2018;50:117–125. doi: 10.1016/j.sbi.2018.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heinig M., Frishman D. STRIDE: a web server for secondary structure assignment from known atomic coordinates of proteins. Nucleic Acids Res. 2004;32:W500–W502. doi: 10.1093/nar/gkh429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henry E.R., Eaton W.A. Combinatorial modeling of protein folding kinetics: free energy profiles and rates. Chem. Phys. 2004;307:163–185. [Google Scholar]
- Henry E.R., Best R.B., Eaton W.A. Comparing a simple theoretical model for protein folding with all-atom molecular dynamics simulations. Proc. Natl. Acad. Sci. U.S.A. 2013;110(44):17880–17885. doi: 10.1073/pnas.1317105110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henzler-Wildman K.A., Lei M., Thai V., Kerns S.J., Karplus M., Kern D. A hierarchy of timescales in protein dynamics is linked to enzyme catalysis. Nature. 2007;450:913–916. doi: 10.1038/nature06407. [DOI] [PubMed] [Google Scholar]
- Hilser V.J., Dowdy D., Oas T.G., Freire E. The structural distribution of cooperative interactions in proteins: analysis of the native state ensemble. Proc. Natl. Acad. Sci. U.S.A. 1998;95(17):9903–9908. doi: 10.1073/pnas.95.17.9903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hilser V.J., Garcia-Moreno B., Oas T.G., Kapp G., Whitten S.T. A statistical thermodynamic model of the protein ensemble. Chem. Rev. 2006;106(5):1545–1558. doi: 10.1021/cr040423+. [DOI] [PubMed] [Google Scholar]
- Hochberg G.K.A., Thornton J.W. Reconstructing ancient proteins to understand the causes of structure and function. Annu. Rev. Biophys. 2017;46:247–269. doi: 10.1146/annurev-biophys-070816-033631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holliday M.J., Camilloni C., Armstrong G.S., Vendruscolo M., Eisenmesser E.Z. Networks of dynamic allostery regulate enzyme function. Structure. 2017;25(2):276–286. doi: 10.1016/j.str.2016.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horovitz A., Fleisher R.C., Mondal T. Double-mutant cycles: new directions and applications. Curr. Opin. Struct. Biol. 2019;58:10–17. doi: 10.1016/j.sbi.2019.03.025. [DOI] [PubMed] [Google Scholar]
- Hultqvist G., Haq S.R., Punekar A.S., Chi C.N., Engstrom A., Bach A., Stromgaard K., Selmer M., Gianni S., Jemth P. Energetic pathway sampling in a protein interaction domain. Structure. 2013;21(7):1193–1202. doi: 10.1016/j.str.2013.05.010. [DOI] [PubMed] [Google Scholar]
- Hutton R.D., Wilkinson J., Faccin M., Sivertsson E.M., Pelizzola A., Lowe A.R., Bruscolini P., Itzhaki L.S. Mapping the topography of a protein energy landscape. J. Am. Chem. Soc. 2015;137(46):14610–14625. doi: 10.1021/jacs.5b07370. [DOI] [PubMed] [Google Scholar]
- Inanami T., Terada T.P., Sasai M. Folding pathway of a multidomain protein depends on its topology of domain connectivity. Proc. Natl. Acad. Sci. U.S.A. 2014;111(45):15969–15974. doi: 10.1073/pnas.1406244111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingles-Prieto A., Ibarra-Molero B., Delgado-Delgado A., Perez-Jimenez R., Fernandez J.M., Gaucher E.A., Sanchez-Ruiz J.M., Gavira J.A. Conservation of protein structure over four billion years. Structure. 2013;21(9):1690–1697. doi: 10.1016/j.str.2013.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Itoh K., Sasai M. Statistical mechanics of protein allostery: roles of backbone and side-chain structural fluctuations. J. Chem. Phys. 2011;134(12):125102. doi: 10.1063/1.3565025. [DOI] [PubMed] [Google Scholar]
- Jack B.R., Meyer A.G., Echave J., Wilke C.O. Functional sites induce long-range evolutionary constraints in enzymes. PLoS Biol. 2016;14 doi: 10.1371/journal.pbio.1002452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khersonsky O., Röthlisberger D., Dym O., Albeck S., Jackson C.J., Baker D., Tawfik D.S. Evolutionary optimization of computationally designed enzymes: Kemp Eliminases of the KE07 series. J. Mol. Biol. 2010;396(4):1025–1042. doi: 10.1016/j.jmb.2009.12.031. [DOI] [PubMed] [Google Scholar]
- Köhler C., Carlström G., Gunnarsson A., Weininger U., Tångefjord S., Ullah V., Lepistö M., Karlsson U., Papavoine T., Edman K., Akke M. Dynamic allosteric communication pathway directing differential activation of the glucocorticoid receptor. Sci. Adv. 2020;6(29):eabb5277. doi: 10.1126/sciadv.abb5277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar G.S., Clarkson M.W., Kunze M.B.A., Granata D., Wand A.J., Lindorff-Larsen K., Page R., Peti W. Dynamic activation and regulation of the mitogen-activated protein kinase P38. Proc. Nat. Acad. Sci. USA. 2018;115(18):4655–4660. doi: 10.1073/pnas.1721441115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumawat A., Chakrabarty S. Protonation-induced dynamic allostery in PDZ domain: evidence of perturbation-independent universal response network. J. Phys. Chem. Lett. 2020;11(21):9026–9031. doi: 10.1021/acs.jpclett.0c02885. [DOI] [PubMed] [Google Scholar]
- Kurnik M., Hedberg L., Danielsson J., Oliveberg M. Folding without charges. Proc. Natl. Acad. Sci. U. S. A. 2012;109(15):5705–5710. doi: 10.1073/pnas.1118640109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latorraca N.R., Venkatakrishnan A.J., Dror R.O. GPCR dynamics: structures in motion. Chem. Rev. 2017;117(1):139–155. doi: 10.1021/acs.chemrev.6b00177. [DOI] [PubMed] [Google Scholar]
- Leander M., Yuan Y., Meger A., Cui Q., Raman S. Functional plasticity and evolutionary adaptation of allosteric regulation. Proc. Nat. Acad. Sci. USA. 2020;117(41):25445–25454. doi: 10.1073/pnas.2002613117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu T., Whitten S.T., Hilser V.J. Ensemble-based signatures of energy propagation in proteins: a new view of an old phenomenon. Proteins: Struct. Funct. Bioinf. 2006;62:728–738. doi: 10.1002/prot.20749. [DOI] [PubMed] [Google Scholar]
- Llinás M., Gillespie B., Dahlquist F.W., Marqusee S. The energetics of T4 lysozyme reveal a hierarchy of conformations. Nat. Struct. Biol. 1999;6(11):1072–1078. doi: 10.1038/14956. [DOI] [PubMed] [Google Scholar]
- Lockless S.W., Ranganathan R. Evolutionarily conserved pathways of energetic connectivity in protein families. Science (80-. ) 1999;286(5438):295–299. doi: 10.1126/science.286.5438.295. [DOI] [PubMed] [Google Scholar]
- Malhotra P., Udgaonkar J.B. How cooperative are protein folding and unfolding transitions? Protein Sci. 2016;25:1924–1941. doi: 10.1002/pro.3015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDonald L.R., Whitley M.J., Boyer J.A., Lee A.L. Colocalization of fast and slow timescale dynamics in the allosteric signaling protein CheY. J. Mol. Biol. 2013;425:2372–2381. doi: 10.1016/j.jmb.2013.04.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muñoz V., Eaton W.A. A simple model for calculating the kinetics of protein folding from three-dimensional structures. Proc. Natl. Acad. Sci. U.S.A. 1999;96(20):11311–11316. doi: 10.1073/pnas.96.20.11311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muñoz V., Campos L.A., Sadqi M. Limited cooperativity in protein folding. Curr. Opin. Struct. Biol. 2016;36:58–66. doi: 10.1016/j.sbi.2015.12.001. [DOI] [PubMed] [Google Scholar]
- Munshi S., Gopi S., Asampille G., Subramanian S., Campos L.A., Atreya H.S., Naganathan A.N. Tunable order-disorder continuum in protein-DNA interactions. Nucleic Acids Res. 2018;46(17):8700–8709. doi: 10.1093/nar/gky732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naganathan A.N. Predictions from an ising-like statistical mechanical model on the dynamic and thermodynamic effects of protein surface electrostatics. J. Chem. Theor. Comput. 2012;8(11):4646–4656. doi: 10.1021/ct300676w. [DOI] [PubMed] [Google Scholar]
- Naganathan A.N.A. Rapid, ensemble and free energy based method for engineering protein stabilities. J. Phys. Chem. B. 2013;117(17):4956–4964. doi: 10.1021/jp401588x. [DOI] [PubMed] [Google Scholar]
- Naganathan A.N. Predictive modeling of protein folding thermodynamics, mutational effects and free-energy landscapes. Proc. Indian Natl. Sci. Acad. 2016;82:1211–1228. [Google Scholar]
- Naganathan A.N. Modulation of allosteric coupling by mutations: from protein dynamics and packing to altered native ensembles and function. Curr. Opin. Struct. Biol. 2019;54:1–9. doi: 10.1016/j.sbi.2018.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naganathan A.N., Sanchez-Ruiz J.M., Munshi S., Suresh S. Are protein folding intermediates the evolutionary consequence of functional constraints? J. Phys. Chem. B. 2015;119:1323–1333. doi: 10.1021/jp510342m. [DOI] [PubMed] [Google Scholar]
- Narayan A., Naganathan A.N. Evidence for the sequential folding mechanism in RNase H from an ensemble-based model. J. Phys. Chem. B. 2014;118:5050–5058. doi: 10.1021/jp500934f. [DOI] [PubMed] [Google Scholar]
- Narayan A., Campos L.A., Bhatia S., Fushman D., Naganathan A.N. Graded structural polymorphism in a bacterial thermosensor protein. J. Am. Chem. Soc. 2017;139:792–802. doi: 10.1021/jacs.6b10608. [DOI] [PubMed] [Google Scholar]
- Olofsson M., Hansson S., Hedberg L., Logan D.T., Oliveberg M. Folding of S6 structures with divergent amino acid composition: pathway flexibility within partly overlapping foldons. J. Mol. Biol. 2007;365(1):237–248. doi: 10.1016/j.jmb.2006.09.016. [DOI] [PubMed] [Google Scholar]
- Perez-Jimenez R., Ingles-Prieto A., Zhao Z.M., Sanchez-Romero I., Alegre-Cebollada J., Kosuri P., Garcia-Manyes S., Kappock T.J., Tanokura M., Holmgren A., Sanchez-Ruiz J.M., Gaucher E.A., Fernandez J.M. Single-molecule paleoenzymology probes the chemistry of resurrected enzymes. Nat. Struct. Mol. Biol. 2011;18(5):592–596. doi: 10.1038/nsmb.2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petit C.M., Zhang J., Sapienza P.J., Fuentes E.J., Lee A.L. Hidden dynamic allostery in a PDZ domain. Proc. Natl. Acad. Sci. U.S.A. 2009;106(43):18249–18254. doi: 10.1073/pnas.0904492106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrovic D., Risso V.A., Kamerlin S.C.L., Sanchez-Ruiz J.M. Conformational dynamics and enzyme evolution. J. R. Soc. Interface. 2018;15(144) doi: 10.1098/rsif.2018.0330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajasekaran N., Naganathan A.N. A self-consistent structural perturbation approach for determining the magnitude and extent of allosteric coupling in proteins. Biochem. J. 2017;474:2379–2388. doi: 10.1042/BCJ20170304. [DOI] [PubMed] [Google Scholar]
- Rajasekaran N., Gopi S., Narayan A., Naganathan A.N. Quantifying protein disorder through measures of excess conformational entropy. J. Phys. Chem. B. 2016;120:4341–4350. doi: 10.1021/acs.jpcb.6b00658. [DOI] [PubMed] [Google Scholar]
- Rajasekaran N., Sekhar A., Naganathan A.N. A universal pattern in the percolation and dissipation of protein structural perturbations. J. Phys. Chem. Lett. 2017;8(19):4779–4784. doi: 10.1021/acs.jpclett.7b02021. [DOI] [PubMed] [Google Scholar]
- Rajasekaran N., Suresh S., Gopi S., Raman K., Naganathan A.N. A general mechanism for the propagation of mutational effects in proteins. Biochemistry. 2017;56:294–305. doi: 10.1021/acs.biochem.6b00798. [DOI] [PubMed] [Google Scholar]
- Reiner A., Henklein P., Kiefhaber T. An unlocking/relocking barrier in conformational fluctuations of villin headpiece subdomain. Proc. Natl. Acad. Sci. U.S.A. 2010;107(11):4955–4960. doi: 10.1073/pnas.0910001107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reynolds K.A., McLaughlin R.N., Ranganathan R. Hotspots for allosteric regulation on protein surfaces. Cell. 2011;147:1564–1575. doi: 10.1016/j.cell.2011.10.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riddle D.S., Santiago J.V., Bray-Hall S.T., Doshi N., Grantcharova V.P., Yi Q., Baker D. Functional rapidly folding proteins from simplified amino acid sequences. Nat. Struct. Biol. 1997;4(10):805–809. doi: 10.1038/nsb1097-805. [DOI] [PubMed] [Google Scholar]
- Risso V.A., Sanchez-Ruiz J.M., Ozkan S.B. Biotechnological and protein-engineering implications of ancestral protein resurrection. Curr. Opin. Struct. Biol. 2018;51:106–115. doi: 10.1016/j.sbi.2018.02.007. [DOI] [PubMed] [Google Scholar]
- Roche J., Caro J.A., Dellarole M., Guca E., Royer C.A., Garcia-Moreno B.E., Garcia A.E., Roumestand C. Structural, energetic, and dynamic responses of the native state ensemble of staphylococcal nuclease to cavity-creating mutations. Proteins. 2013;81(6):1069–1080. doi: 10.1002/prot.24231. [DOI] [PubMed] [Google Scholar]
- Röthlisberger D., Khersonsky O., Wollacott A.M., Jiang L., DeChancie J., Betker J., Gallaher J.L., Althoff E.A., Zanghellini A., Dym O., Albeck S., Houk K.N., Tawfik D.S., Baker D. Kemp elimination catalysts by computational enzyme design. Nature. 2008;453(7192):190–195. doi: 10.1038/nature06879. [DOI] [PubMed] [Google Scholar]
- Sarkar S.S., Udgaonkar J.B., Krishnamoorthy G. Unfolding of a small protein proceeds via dry and wet globules and a solvated transition state. Biophys. J. 2013;105:2392–2402. doi: 10.1016/j.bpj.2013.09.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrank T.P., Bolen D.W., Hilser V.J. Rational modulation of conformational fluctuations in adenylate kinase reveals a local unfolding mechanism for allostery and functional adaptation in proteins. Proc. Natl. Acad. Sci. U.S.A. 2009;106:16984–16989. doi: 10.1073/pnas.0906510106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sivanandan S., Naganathan A.N. A disorder-induced domino-like destabilization mechanism governs the folding and functional dynamics of the repeat protein IκBα. PLoS Comput. Biol. 2013;9 doi: 10.1371/journal.pcbi.1003403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suren T., Rutz D., Mößmer P., Merkel U., Buchner J., Rief M. Single-molecule force spectroscopy reveals folding steps associated with hormone binding and activation of the glucocorticoid receptor. Proc. Natl. Acad. Sci. U.S.A. 2018;115(46):11688–11693. doi: 10.1073/pnas.1807618115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang Q., Fenton A.W. Whole-protein alanine-scanning mutagenesis of allostery: a large percentage of a protein can contribute to mechanism. Hum. Mutat. 2017;38(9):1132–1143. doi: 10.1002/humu.23231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tokuriki N., Tawfik D.S. Stability effects of mutations and protein evolvability. Curr. Opin. Struct. Biol. 2009;19(5):596–604. doi: 10.1016/j.sbi.2009.08.003. [DOI] [PubMed] [Google Scholar]
- Tzeng S.R., Kalodimos C.G. Protein activity regulation by conformational entropy. Nature. 2012;488(7410):236–240. doi: 10.1038/nature11271. [DOI] [PubMed] [Google Scholar]
- Wako H., Saito N. Statistical mechanical theory of protein conformation .2. Folding pathway for protein. J. Phys. Soc. Japan. 1978;44(6):1939–1945. [Google Scholar]
- Walters A.L., Deka P., Corrent C., Callender D., Varani G., Sosnick T., Baker D. The highly cooperative folding of small naturally occurring proteins is likely the result of natural selection. Cell. 2007;128:613–624. doi: 10.1016/j.cell.2006.12.042. [DOI] [PubMed] [Google Scholar]
- Wand A.J. The dark energy of proteins comes to light: conformational entropy and its role in protein function revealed by NMR relaxation. Curr. Opin. Struct. Biol. 2013;23(1):75–81. doi: 10.1016/j.sbi.2012.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J., Samanta R., Custer G., Look C., Matysiak S., Beckett D. Tuning allostery through integration of disorder to order with a residue network. Biochemistry. 2020;59(6):790–801. doi: 10.1021/acs.biochem.9b01006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitley M.J., Zhang J., Lee A.L. Hydrophobic core mutations in CI2 globally perturb fast side-chain dynamics similarly without regard to position. Biochemistry. 2008;47(33):8566–8576. doi: 10.1021/bi8007966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang G., Hong N., Baier F., Jackson C.J., Tokuriki N. Conformational tinkering drives evolution of a promiscuous activity through indirect mutational effects. Biochemistry. 2016;55(32):4583–4593. doi: 10.1021/acs.biochem.6b00561. [DOI] [PubMed] [Google Scholar]
- Zhang Z., Chan H.S. Competition between native topology and nonnative interactions in simple and complex folding kinetics of natural and designed proteins. Proc. Nat. Acad. Sci. USA. 2010;107(7):2920–2925. doi: 10.1073/pnas.0911844107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng W., Brooks B.R., Thirumalai D. Low-frequency normal modes that describe allosteric transitions in biological nanomachines are robust to sequence variations. Proc. Natl. Acad. Sci. U.S.A. 2006;103:7664–7669. doi: 10.1073/pnas.0510426103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou T., Risso V.A., Gavira J.A., Sanchez-Ruiz J.M., Ozkan S.B. Evolution of conformational dynamics determines the conversion of a promiscuous generalist into a specialist enzyme. Mol. Biol. Evol. 2015;32(1):132–143. doi: 10.1093/molbev/msu281. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data presented are available in the article and in its online supplementary material.