MRSaiFE: An AI-based Approach Towards the Real-Time Prediction of Specific Absorption Rate

Abstract

The purpose of this study is to investigate feasibility of estimating the specific absorption rate (SAR) in MRI in real time. To this goal, SAR maps are predicted from 3T- and 7T-simulated magnetic resonance (MR) images in 10 realistic human body models via a convolutional neural network. Two-dimensional (2-D) U-Net architectures with varying contraction layers and different convolutional filters were designed to estimate the SAR distribution in realistic body models. Sim4Life (ZMT, Switzerland) was used to create simulated anatomical images and SAR maps at 3T and 7T imaging frequencies for Duke, Ella, Charlie, and Pregnant Women (at 3, 7, and 9 month gestational stages) body models. Mean squared error (MSE) was used as the cost function and the structural similarity index (SSIM) was reported. A 2-D U-Net with 4 contracting (and 4 expanding) layers and 64 convolutional filters at the initial stage showed the best compromise to estimate SAR distributions. Adam optimizer outperformed stochastic gradient descent (SGD) for all cases with an average SSIM of 90.5∓3.6 % and an average MSE of 0.7∓0.6% for head images at 7T, and an SSIM of >85.1∓6.2 % and an MSE of 0.4∓0.4% for 3T body imaging. Algorithms estimated the SAR maps for 224×224 slices under 30 ms. The proposed methodology shows promise to predict real-time SAR in clinical imaging settings without using extra mapping techniques or patient-specific calibrations.

I. INTRODUCTION

Modern neuroscience relies on understanding the brain in health and disease. Thus, the availability of technology that can significantly increase the spatial resolution and sensitivity achievable with magnetic resonance (MR) neuroimaging at the current used field strength of 3T and emerging ultra-high field (UHF) strengths of 7T and higher, consistent with safety, would offer the potential to advance our understanding of brain structure and function by enabling investigations with greater specificity and granularity [1].

A key limitation to the high potential of UHF magnetic resonance imaging (MRI) in neuroscience research and clinical or diagnostic applications [2, 3] is the safety concern related to the nonuniform deposition of radiofrequency (RF) power in the body [4], quantified by the specific absorption rate (SAR), which can lead to dangerous tissue heating and damage [5]. Not only does the average SAR possess a quadratic dependence on the static magnetic field strength (B₀) [6], increasing 4-fold from 3T to 7T, but due to the higher Larmor frequency and thus shortened in-tissue wavelength, it also exhibits a spatial variation that can lead to “local SAR” patterns or “hotspots” of focused high RF power deposition and localized tissue heating [7–13]. This results in significant SAR nonuniformity at anatomical dimensions similar to the brain at 7T (wavelength ~11 cm in tissue) as well as the body at 3T (wavelength ~26 cm in tissue) [14].

Moreover, parallel transmit (pTx) technology with multiple independent transmit RF channels [15–17] is now common in UHF applications and can lead to even stronger hotspots because of potential constructive interference of the electric fields [18, 19].

While a small portion of UHF MRI has received Food and Drug Administration (FDA) approval [20, 21], most clinical imaging has been performed at 3T to date. This is because substantial safety and technological hurdles still need to be surmounted before the potential benefits of higher sensitivity and spatial resolution can be fully realized. Specifically, there is a lack of technology that can measure local SAR due to anatomical and positional variations between patients, and between transmit coils. Current technology is not equipped to measure spatially varying local SAR; the only quantity that can be determined in vivo is the overall average, or global, SAR, delivered to the entire anatomy under investigation.

Local SAR variation is highly difficult to predict due to anatomical and positional variations between patients, as well as variations in transmit coils. Many institutions use a conservative estimate of the peak local SAR via its ratio to the measurable global SAR; typically, ~20:1 [19], thereby severely limiting the applied transmit power and thus the imaging performance achievable by UHF MRI, in particular resolution and/or scan time. This critical barrier is one of the main reasons 7T has not yet reached the patient in its full capacity and holds back its success as an extremely powerful imaging modality with unprecedented ability to decipher fine structures.

MR thermometry as an alternative approach suffers from a coarse temperature resolution [22]. The advent of artificial intelligence (AI) and machine learning in MRI [23–36] has opened up new avenues for the prediction of various imaging characteristics, among them the recent prediction of local SAR in prostate imaging [37–39], as well as the prediction of temperature rise in the brain for 33 different tissue types [40].

In this paper, we expand these pioneering techniques by use of a comprehensive training set of anatomical models and predict local SAR both at the 3T and 7T field strengths, for a large variety of landmarks and thus imaging anatomies. We propose MRSaiFE [41–43], which is eventually expected to become an AI-based, exam-integrated, MRI safety prediction software facilitating the safe generation of 3T and 7T images. In this work, we demonstrate proof of concept and feasibility for MRSaiFE using a database of 10 human body models. The algorithm is trained and evaluated for use at (1) 3T body dimensions and (2) 7T brain dimensions – significant SAR non-uniformity can occur at both field strengths and provides good basis to train the network on a variety of scenarios. Our results suggest SAR-monitoring with >90% structural similarity index (SSIM) [44] and <1% mean squared error (MSE) for high resolution imaging at UHF.

II. METHODS

A. DATA GENERATION

The input data for this study were acquired from Sim4Life simulations (ZMT, Zurich, Switzerland) using Virtual Population (IT’IS, Zurich, Switzerland) body models (Figure 1). Figure 2 shows an illustration of the proposed neural network. An anatomical image is used as the input to a neural network and predicts a SAR map in image form at the output.

FIGURE 1.

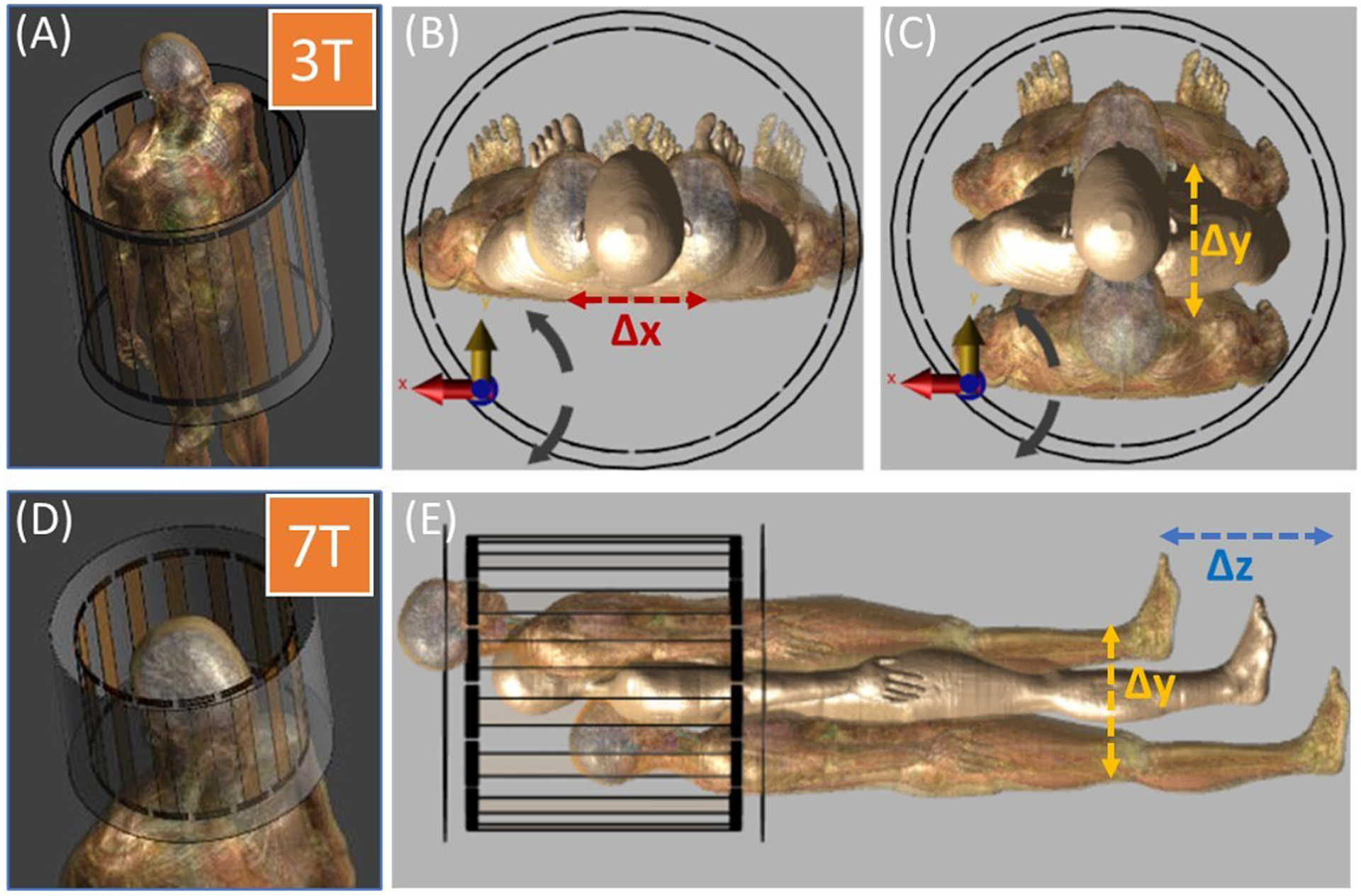
Data were generated with Sim4Life (ZMT, Zurich, Switzerland). (A) Body coil is used for 3T body imaging. Since there is no body coil available at 7T, a head coil (D) is used for 7T imaging. Positions of the realistic body models were translated in (B) x direction, (C) y direction, and (E) z direction.

FIGURE 2.

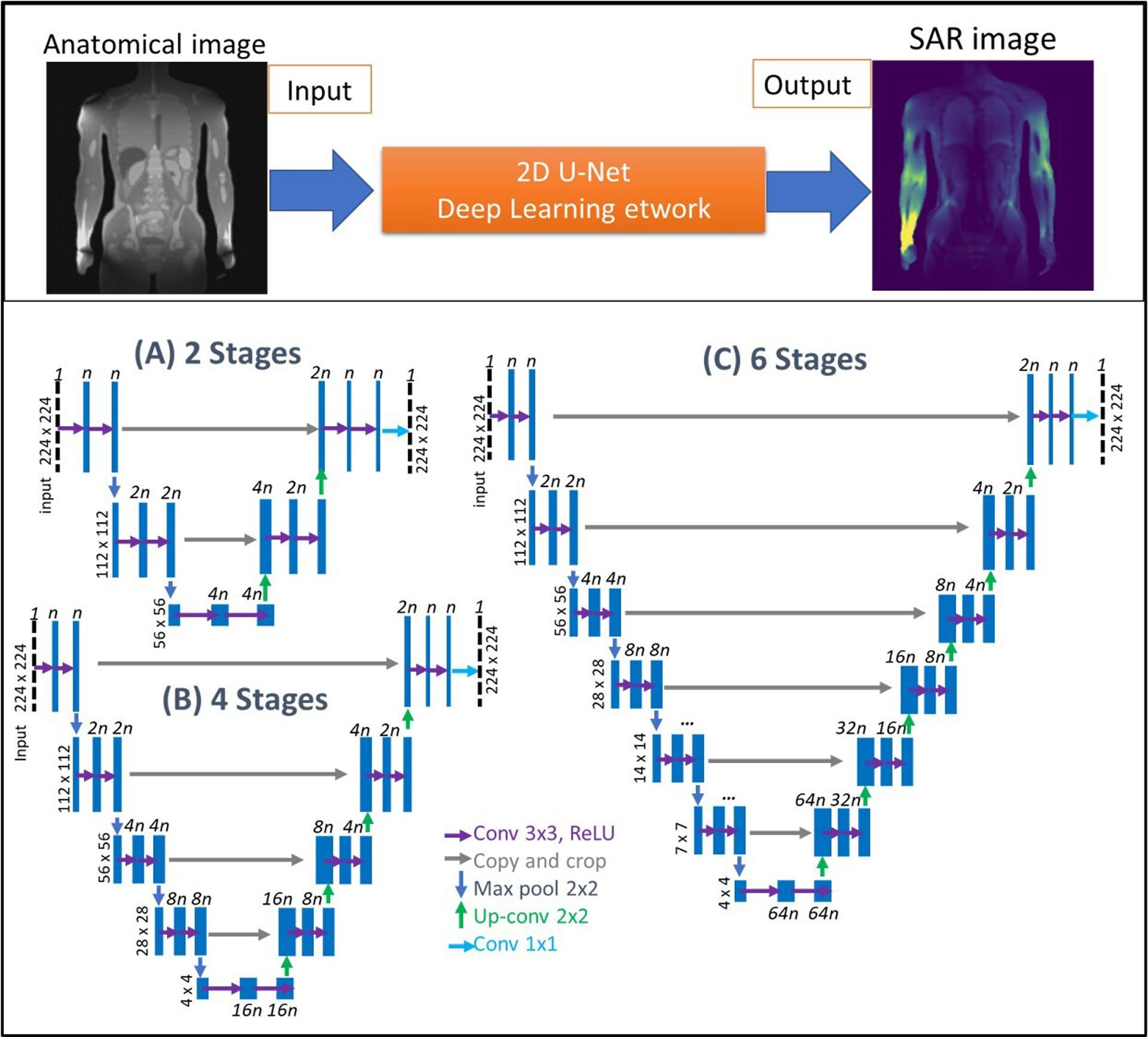
2-D U-Net architectures used in this study. (A) 2 stages, (B) 4 stages, and (C) 6 stages of encoder layers were implemented. Length of feature vectors was defined by n and varied between 32 to 256 as powers of 2. Increasing n improved the network capacity, with costs of increased memory requirements, and longer training and testing durations.

The anatomical input image that would come from an MRI scanner in a real experiment was approximated by using black/white images of the body models. Image data sets were synthesized for 1 mm anatomical resolution and down sampled to 224 × 224 × 224 pixels for a field of view (FoV) of 30 cm × 30 cm × 30 cm for head imaging (1.3 mm isotropic resolution) and for a FoV of 60 cm × 60 cm × 60 cm for body imaging (2.7 mm isotropic resolution). In order to encode landmark information as part of a neural network with a single input and output image, these anatomical images were weighted by the normalized B₁⁺ field of the unloaded RF coils [42].

For 3T body MRI SAR prediction, a 16-rung body coil model (65 cm diameter, 67 cm length) made for a standard bore size of 60 cm was used in conjunction with the body models Ella (26y, body mass index (BMI) 21.6 kg/m²), Duke (34y, BMI 22.4 kg/m²), and pregnant women at gestational stages of 3, 7, and 9 months (26y, BMI not available). Duke was positioned at 225 different imaging landmarks spanning ∓40 mm, ∓60 mm, and +60/−100 mm along the x-, y-, and z- axes (axial: xy-plane, coronal: yz-plane, sagittal: xz-plane). Similarly, Ella and the pregnant women were positioned at 125 different imaging landmarks varying between ∓40 mm in x- and y-axes, and ∓200 mm in z-axis. The 1-gram averaged peak local SAR outputs were evaluated for 1 W of simulated input power and coronal SAR slices were extracted. Here, the iterations where the body models intersected with the coil, and slices containing no information, were discarded from the dataset. This resulted in a set of 67,861 input anatomical and 67,861 output SAR images at 3T.

For 7T head MRI SAR prediction, a 16-rung birdcage head coil model (30 cm diameter, 25 cm length) was used with the body models Ella (26y female, BMI 21.6 kg/m²), Charlie (8w female, weight 4.3 kg, BMI not available), and pregnant women at different gestational stages (3, 7, and 9 months, 26y, BMI not available). All models were positioned at the same imaging landmarks within the coil ranging from ∓20 mm in x- and y-axes, and ∓60 mm in z-axis. Input anatomical image and output SAR image generation followed the same steps as for the 3T analysis, resulting in in a set of 52,806 input anatomical and 52,806 output SAR images at 7T.

The data were split into three categories for each body model separately with an approximate ratio of 80, 10, and 10% for training, validation, and testing, respectively. A summary of the dataset is provided in Table 1. Algorithms were trained and tested for each body model separately.

Table 1.

Dataset generated in this study.

Field Strength	Body Model	Total # Images	Training	Validation	Testing
3T	Ella	10,340	8272	1034	1034
	Duke	16,766	13332	1616	1818
	Preg3M	11,070	8820	1080	1170
	Preg7M	14,605	11684	1397	1524
	Preg9M	15,080	12035	1450	1595
7T	Ella	12,600	10080	1296	1224
	Charlie	12,075	9660	1242	1173
	Preg3M	12,702	10147	1241	1314
	Preg7M	7,548	6052	748	748
	Preg9M	7,881	6319	781	781
TOTAL		120,667	88,129	10,851	11,347

B. NEURAL NETWORK ARCHITECTURE

A 2D U-Net architecture [45] estimated SAR maps (y) of a given MRI image (x) by learning a transformation, y=f(x), between the two. Here, y is the simulated SAR map of a given slice, which was also used as the ground truth (GT).

We implemented a set of U-Net architectures using a cascade of 2D convolutional filters (Figure 2). Convolutional layers were paired with nonlinear rectified linear unit (reLU) activation functions [46], batch normalization [47], and He initialization [48]. The input image size was set to 224 × 224 pixels, zero padding was used for convolutions, and the output was cropped to the size of the input image. In order to analyze the effect of different hyperparameters on the network performance, we designed 3 U-Nets with varying number of contraction (encoder) and expansion (decoder) layers, using different filter feature map lengths (n) and learning rates (LR). The first, second, and third architectures used 2, 4, and 6 encoder and decoder stages, respectively (Figure 2. A, B, and C). Each stage contained 2 cascaded convolutional filters [36] with the first layer feature map lengths varied from 32 to 256 and orders of 2 (i.e., n= 32, 64, 128, and 256). These filter lengths decreased to 16 and 32 for the 6-stage network due to limited memory. The feature maps of the first layers were incremented by a factor of 2 for the subsequent encoding stages and decremented by a factor of 2 for the consequent decoding stages. All networks used 3×3 convolution filters, a 1×1 stride length, 2×2 max pooling, and up-convolutions. The final layer of each architecture included 1×1 convolutional filters with a sigmoid activation function.

C. TRAINING AND VALIDATION

We used a 3T body imaging data set generated by using Ella with the 3 different U-Net configurations to determine the best performing architecture and optimized the hyperparameters using SSIM, MSE, and training time per image as performance metrics.

Many deep learning image processing algorithms use MSE and SSIM as a basis of comparison between the ground truth and predicted images. The most traditional comparison uses the MSE and represents the cumulative mean squared error between ground truth and predicted images. The SSIM is often used in addition to measure the perceived change in structural information from ground truth to prediction. Given our need to predict anatomical outlines and SAR hotspots, this metric is a good indicator of general structural correctness of the predicted image.

Training was performed using adaptive moment estimation (Adam)[49] and stochastic gradient descent (SGD) [50] optimizers with constant exponential decay rates and momentum values (i.e., β₁=0.90, β₂=0.99, and ε=10⁻⁷ for Adam, as well as a momentum=0.9 for SGD). To optimize the hyperparameters, the MSE between the simulated and predicted SAR maps was minimized on the validation dataset by using (1).

$$MSE=1/N*\Sigma {\left(y-\widehat{y}\right)}^2$$ (1)

Here N is the total number of pixels in the images. A dynamic learning rate (LR) approach was used with initial LRs of 10⁻³, 10⁻⁴, 10⁻⁵, and 10⁻⁶, and these rates were decreased to 80% at every 5^th epoch. The maximum number of epochs was set to 200, and the best model was determined and saved using the Keras and Tensorflow backends (Google, Mountain View, CA). All training algorithms were run twice for validation purposes, and the batch size for training, validation, and test datasets was set to 1. All algorithms were run on an NVIDIA Titan RTX (NVIDIA, Santa Clara, CA) Graphics Processing Unit (GPU).

D. TESTING

Testing was performed on the testing datasets prepared for each body model. Quantitative image comparisons were performed between the GT images (simulated SAR) and the predicted SAR maps using MSE. In addition, SSIM was evaluated to provide a perceptual image quality comparison.

We also introduced a hotspot analysis by masking the images only using the pixels that fell within a percentage of highest local SAR values. We evaluated the similarity in location between ground truth and prediction by use of SSIM between ground truth and predicted hotspots. We also evaluated the maximum SAR values for all hotspots and calculated the relative error between prediction and ground truth.

III. RESULTS

A. HYPERPARAMETER ANALYSIS

SSIM results and the training time of the 3 U-Nets for different hyperparameters are given in Figure 3 (Adam) for 3T body MRI. Increasing the learning rate of the 2-stage network (Figure 3A) from 10⁻⁶ to a higher level (e.g., 10⁻³) increased the average SSIM from 68.9∓17.6% to 81.1∓4.8%. LRs chosen over a range from 10⁻³ to 10⁻⁵ resulted in similar SSIM. Additionally, increasing the feature map length from 32 to 64 improved the SSIM from 77.3∓1.2% to 81.7∓1.0%. The use of 128-layer feature maps led to the highest variation in SSIM (i.e., ∓23.2%) among all LRs and feature map sizes for all body models. Increasing the feature map length from 16 to 256 increased the time required to train each slice from 8 to 80 ms with limited improvement in SSIM.

FIGURE 3.

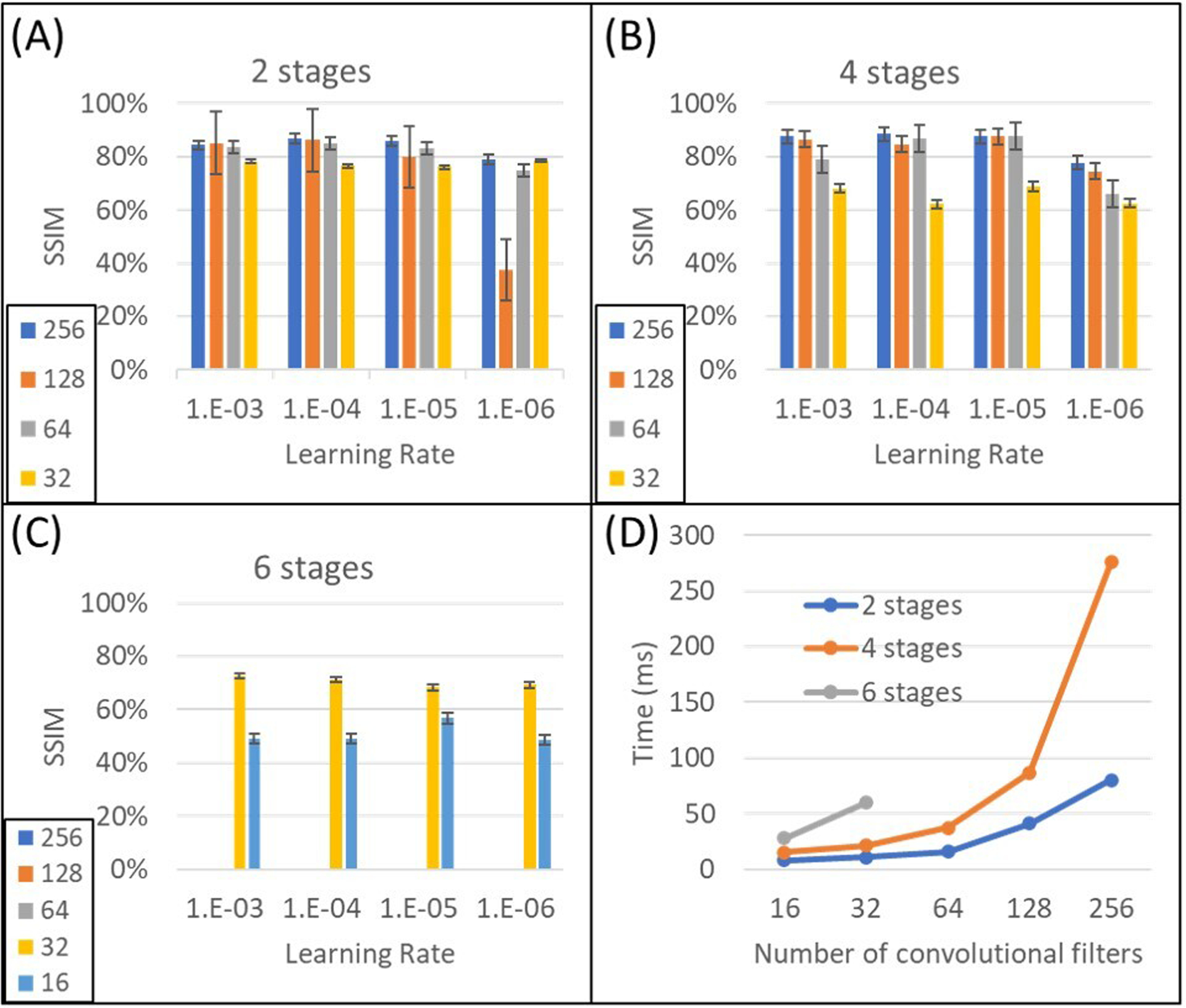
Performance comparison of three U-Nets due to different hyperparameters and time budget. All structures were trained and tested on the same realistic body model (Ella) for 3T body imaging. SSIM of (A) 2-stage, (B) 4-stage, and (C) 6-stage U-Nets are depicted. (D) Time to train each image showed exponential increase among different U-Nets. Increasing the length of feature maps (n) showed linear increase on training time for the same network up to n=128.

The architecture containing 4 stages exhibited more variation for different LRs and feature map lengths (Figure 3B). The use of 32 convolution filter layers at the initial stage generated the lowest SSIM (i.e., 65.4∓3.5%), which clearly demonstrates the importance of the length of the feature map at the initial layer. The best average SSIM, i.e., 83.0∓9.4%, was reached when the LR was 10⁻⁵. Although changing the initial layer feature map length from 64 to 256 increased the capacity of the network, it improved the average SSIM only slightly (i.e., 79.9∓10.2% to 85.4∓5.1%) but decreased the dependence on hyperparameter variations significantly (i.e., the variation of SSIM decreased from 10.2% to 5.1%). Additionally, the training time for the 256-layer feature map was increased by a factor >2 compared to 128 layers. Thus, among the investigated 4-stage U-Net architectures, the use of either 64 or 128 feature maps at the initial stage produced the best trade-off for all LRs.

The results for the 6-stage U-Net architecture are reported in Figure 3C. Using 32 feature map layers at the initial stage improved the average SSIM to 70.3∓2.0% compared to the case with 16 layers (i.e., 51.0∓4.0%), again highlighting the importance of the initial layer size. This result was also slightly improved compared to the 4-stage U-Net (i.e., 65.4∓3.5%), emphasizing the merely incremental contribution of higher number of stages for this problem. Similarly, although the number of layers and networks capacity is much higher than in the 2-stage architecture, the 6-stage network with 32 feature maps (SSIM = 70.3∓2.0%) was not able to outperform the 2-stage architecture with 64 feature maps (SSIM = 81.7∓4.6%).

In summary, the initial layer feature map length was a key factor contributing to model performance and led us to the selection of a 4-stage U-Net architecture with 64 initial layer convolutional filters, using a LR of 10⁻⁵.

B. PERFORMANCE EVALUATION OF DIFFERENT BODY MODELS AND OPTIMIZERS

We used the optimized 4-stage U-Net architecture to analyze performance metrics for different body models and different field strengths (Figure 4).

FIGURE 4.

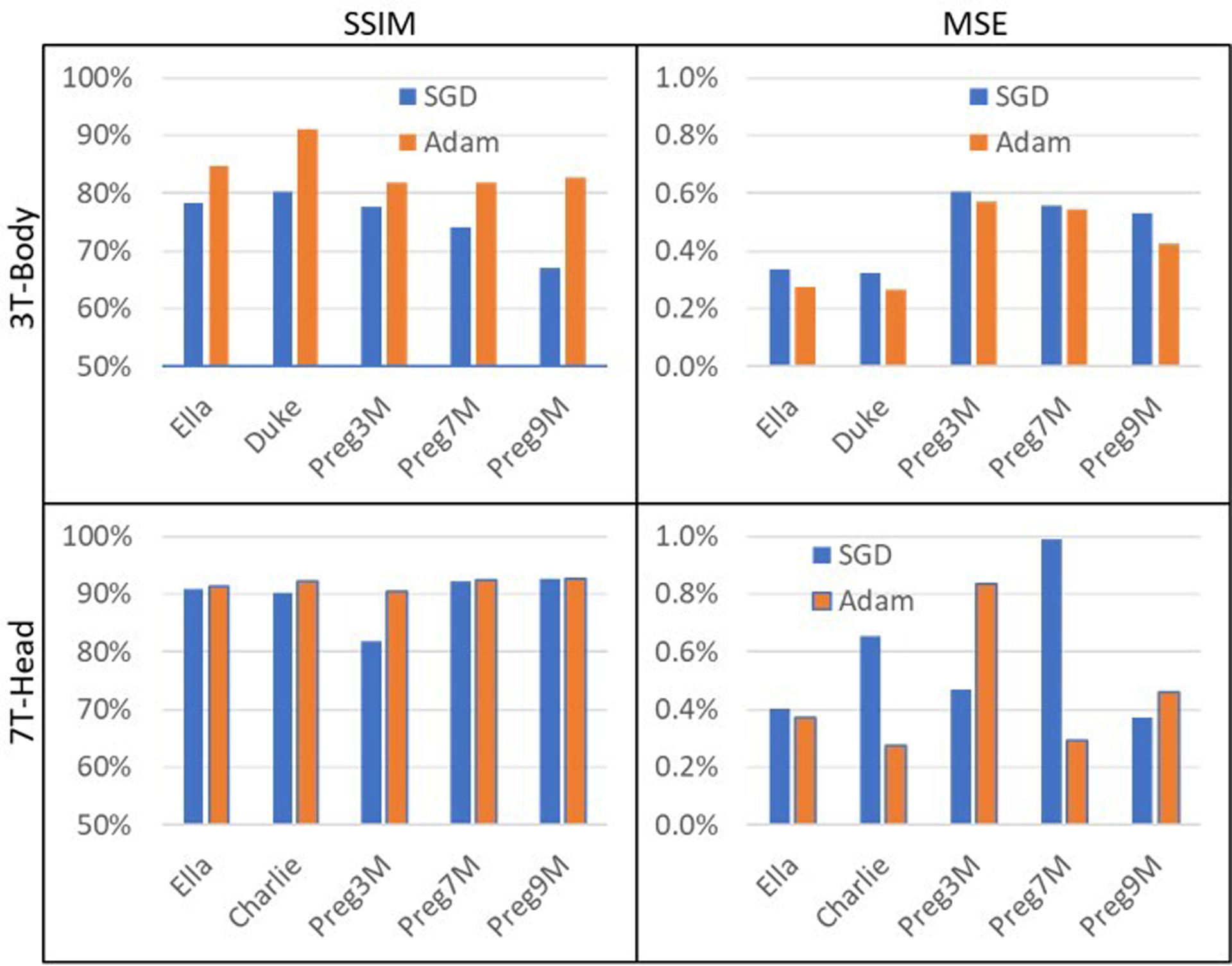
Inter-subject performance analysis of the 4-stage U-Net with 64 convolutional filters at the initial layer. Adam optimizer worked better than SGD in terms of SSIM for all scenarios. (Top Row) For 3T Body SAR prediction, an average SSIM of 85.1∓6.2% and an average MSE of 0.4∓0.4% was observed (Adam), as opposed to an SSIM of 69.3∓4.5% and an MSE of 0.5∓0.4% (SGD). (Bottom Row) In the 7T brain SAR prediction, we observed an average SSIM of 90.5∓3.6% and an average MSE of 0.7∓0.6% (Adam), compared to an SSIM of 81.4∓2.6% and an MSE of 0.5∓0.5% (SGD). The higher spatial resolution of the 7T data (i.e., isotropic pixel size of ~1.33 mm compared to 2.67 mm at 3T) resulted in improved SSIM and MSE.

Adam outperformed SGD for all body models and all field strengths according to SSIM metrics (Figure 4). For 3T body SAR prediction (top row), an average SSIM of 85.1∓6.2% and an average MSE of 0.4∓0.4% was observed (Adam), as opposed to an SSIM of 69.3∓4.5% and an MSE of 0.5∓0.4% (SGD). Specifically, for Ella, we observed an SSIM of 87.9∓8.0% and an MSE of 0.2∓0.2%. At the same field strength for Duke, we observed 91.0∓3.7% SSIM and 0.3∓0.2% MSE. Similarly, SSIM of 81.9∓4.9%, 81.9∓7.8%, and 82.7∓6.6% were obtained for the 3-, 7-, and 9-month pregnant women, respectively. An average MSE of 0.5% with a standard deviation of <0.5% was observed for the pregnant women.

In the 7T brain SAR prediction (Figure 4, bottom row), we observed similar performance for all body models, with an average SSIM of 90.5∓3.6% and an average MSE of 0.7∓0.6% (Adam), compared to an SSIM of 81.4∓2.6% and an MSE of 0.5∓0.5% (SGD). The higher spatial resolution of the 7T data (i.e., isotropic pixel size of ~1.33 mm compared to 2.67 mm at 3T) resulted in improved SSIM and MSE. For the baby body model Charlie, an SSIM of 92.2∓1.7% and an MSE of 0.8∓0.5% was achieved. Similarly, SSIM results of 91.3∓3.6%, 84.1∓5.8%, 92.5∓3.6%, and 92.6∓3.4% were obtained for Ella as well as the 3-, 7-, and 9-month pregnant women, respectively.

C. HOTSPOT ANALYSIS

Visual representation showed good agreement of ground truth and predicted hotspots in 10 subjects (Figure 5 and 6, hotspot columns). Using the top 15% of local SAR values, we obtained a mean SSIM of 97.3%±2.5% denoting good agreement on hotspot locations, as well as a relative mean error of 1.5%±1.1% of maximum SAR values when the SAR map was normalized to the mean of the ground truth. This corresponds to normalizing the predicted SAR map to the, measurable, global SAR at the time of the patient exam. Mean errors without normalization were found to be 11%, still reasonable given the small training dataset. An added underestimation constraint that will be part of the full MRSaiFE algorithm is proposed in the discussion and is expected to help with hotspot prediction accuracy.

FIGURE 5.

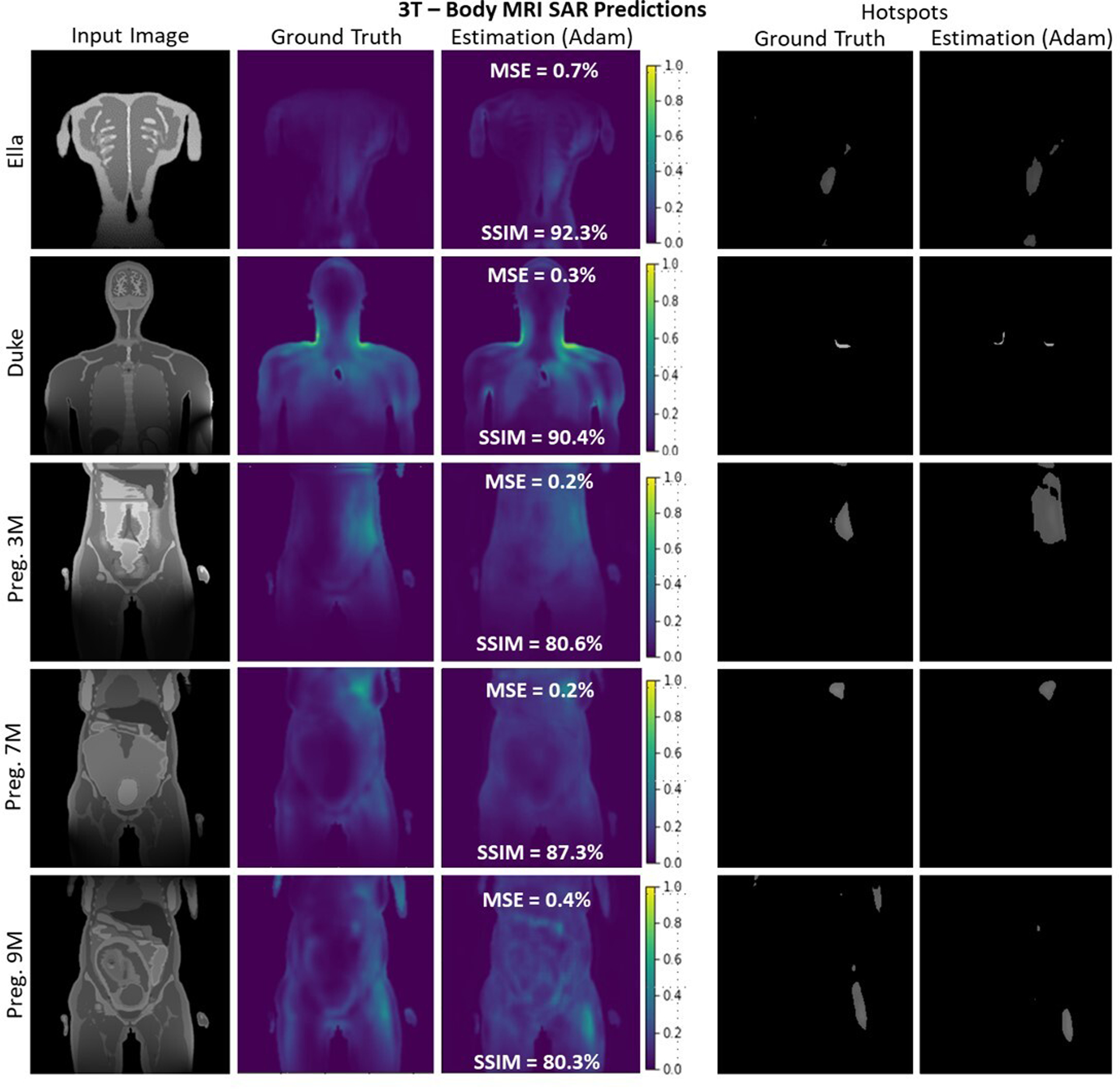
A selection of slices for Ella, Duke, and Pregnant Women of different gestational stages at 3T body imaging. Despite very high variation of SAR maps and input images, the proposed 4-stage U-Net architecture successfully recovered the distribution with better than 80% average SSIM and less than 0.5% average MSE for all body models.

FIGURE 6.

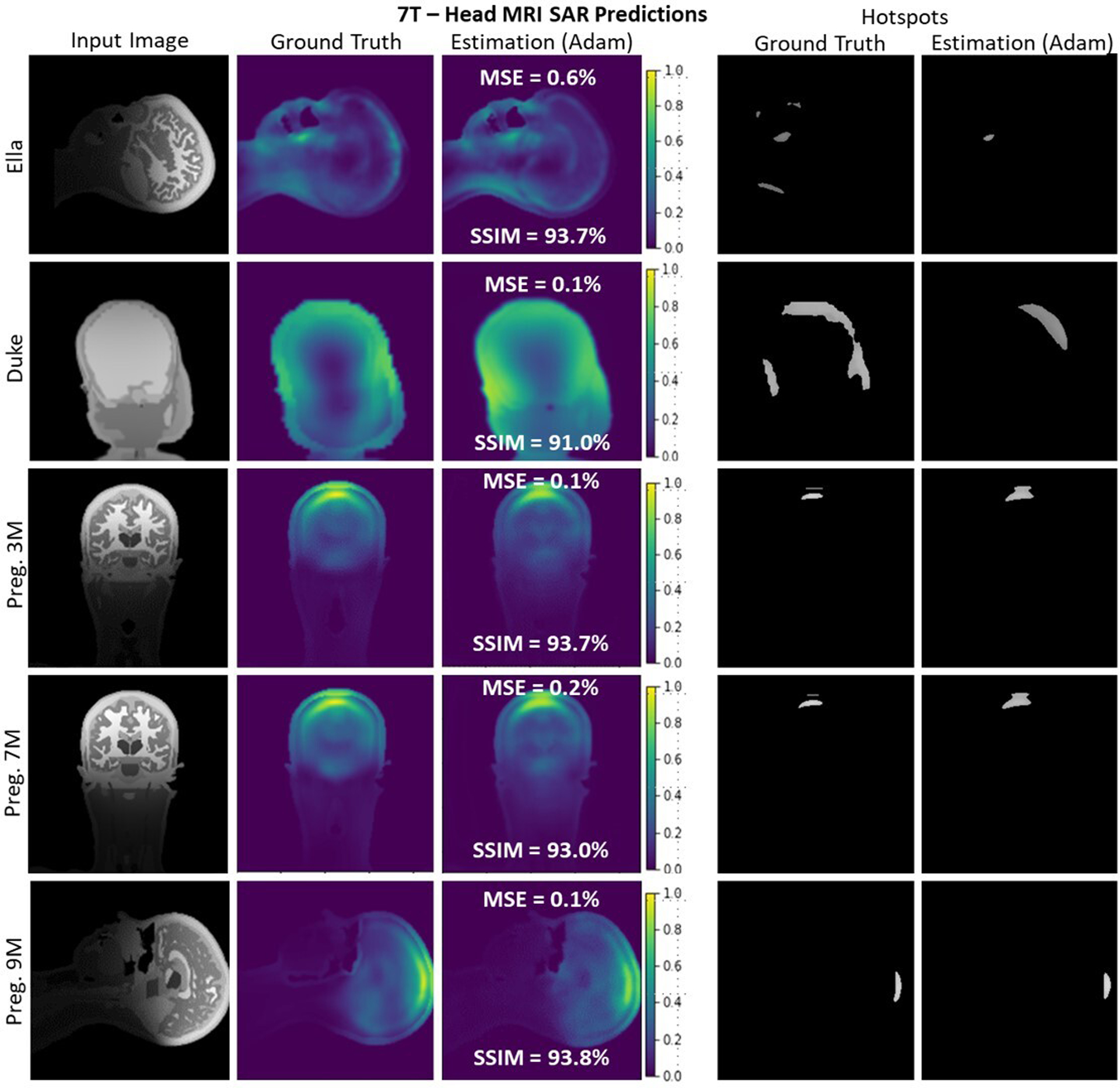
A selection of slices for different body models at 7T. 4-stage U-Net architecture successfully recovers the SAR distribution for all body models (SSIM >91%, MSE<0.5%). It is seen that the spatial information provided by the input images also carried to estimation results without any memorization.

D. PERCEPTUAL IMAGE QUALITY ANALYSIS

Representative 3T body imaging slices randomly selected from each body model are depicted in Figure 5. Qualitatively, the 4-stage U-Net designed in this work successfully estimated the SAR distributions for the given slices.

Similarly, a selection of slices and performance metrics for 7T head imaging are depicted in Figure 6. A representative anatomical input image for Ella with very fine detail is shown and yielded a predicted SAR with low spatial detail as expected from the GT SAR simulation (top row). The proposed U-Net successfully (i.e., with 93.7% SSIM and with 0.6% MSE) estimated this distribution. Similarly, a slice taken from Charlie simulations with low anatomical detail (second row) was used. The U-Net architecture successfully estimated its SAR distribution with a SSIM of 91.0% and an MSE of 0.1%. For the high-resolution head imaging simulations conducted on the 3 pregnant body models (rows 3, 4, and 5), the proposed U-Net yielded an SSIM of ≥93%. Regardless of the spatial information encoded in the anatomical input slices, the 4-stage U-Net architecture successfully recovered the SAR maps of the corresponding slices.

IV. DISCUSSION

The U-Net architecture is assumed to be one of the workhorses of biomedical image segmentation and classification. In its optimization for the purposes of our application, we found that the number of convolutional filters at the input layer is tremendously important for overall network performance. From the MRI perspective, the spatial and intensity information encoded in the MR image is limited compared to electrooptical images used in daily life. This is mainly due to lower spatial resolution (i.e., ~1 mm) and lower image sizes (e.g., 256×256 pixels) in MRI. As a result, the overall network complexity of the U-Net has to be adapted to estimate SAR maps without overfitting or underfitting. In this work, we found that using a 4-stage U-Net structure with 64 or 128 convolutional filters at the initial stage results in optimal performance and reasonable training time. Additional stages without a concurrent increase in the number of filters at the first layer did not improve performance due to the information loss incurred at the first layer.

It was also seen in Figure 4 that the prediction using whole-body anatomies yielded higher inter-subject standard deviations compared to head sized imaging. This could be attributed to the higher variation of anatomical image detail at the input level.

The relatively small database used in this proof-of-concept study in conjunction with the excellent agreement between predicted SAR and simulated SAR suggested that a large-scale SAR database along with experimental verification would lead to small SAR errors for a future real-time implementation of MRSaiFE.

One of the limitations in this work is the use of MRI-like anatomical input images. The final algorithm when used at the console will use an acquired MR image. In order to estimate whether the algorithm performs similarly we will develop our algorithm further using simulated MR images from the MRI scanner simulator platform (SYSSIM) [51] offered by Sim4Life.

Future work beyond this proof-of-concept stage will include the use of experimental in vivo and in vitro thermometry data. For patient safety reasons, we will use an underestimation bound of no greater than 5% as our metric to ensure that the actual SAR never significantly exceeds predicted SAR. To this goal, we will add a weighted L1-norm term that introduces a slight overestimation, weighting the difference between ground truth and generator output.

In this application, a 3D convolutional neural network could prove useful and will be tested as part of future work because heating from neighboring slices could prove important for training performance. We will therefore analyze the performance of both 3D networks and choose the network that provides the best training performance.

Overall, MRSaiFE could eventually provide UHF MRI with consistent tissue heating monitoring for use as a safe, practical, and non-invasive mainstream tool for clinical understanding, diagnostics, monitoring, and treatment guidance at sub-mm resolution. In practice, the existing conservative SAR margins of 20:1 could become exchangeable with optimized, patient-specific margins, and will free up valuable transmit power that can be used towards better sensitivity, resolution, or scan time.

This work could also significantly impact the safety of scanning patients with medical implants. Implants present a great cause for tissue heating concerns [29, 52, 53]. The tissue heating incurred from implants can be introduced by modifying the predicted SAR map via the implant trajectory and transfer function [54]. This ultimately would result in such patients being able to undergo MRI exams more routinely, and not only in critical situations or not at all.

The expansion of the technique to parallel transmission is straightforward: the SAR map from each channel can be predicted separately and superimposes linearly to form the total SAR. These maps can then be used in real-time SAR monitoring directly, or as an input metric in SAR-aware pTx pulse design.

The advent of even higher field strengths such as 9.4T and 10.5T, for human MRI has brought about even greater scrutiny, and valid concerns about patient safety [30, 55]. The spatial SAR variations and average global SAR are increased compared to 7T, and MRSaiFE can be of great use in bringing these technologies to clinical practice.

The effects of B₀ inhomogeneities on SAR are negligible due to their very small magnitude compared to the B₁ inhomogeneities (variations on the order of 10⁻⁶ for B₀ vs 10¹ for B₁) and are thus not included in this tool.

In hyperthermia, tissue heating is directed at specific tissue regions with the goal of ablation. UHF MRI, with its intrinsic short wavelength and state-of-the-art parallel transmit capability, can be used to tailor these heating hotspots by tailoring local SAR. MRSaiFE offers the potential to enable targeted treatment planning in MR hyperthermia for cancer and other diseases in the long term.

V. CONCLUSION

We developed a proof of concept for MRSaiFE, which is an AI-based, exam-integrated, real-time MRI safety prediction software tool that facilitates the safe generation of UHF MRI images by means of accurate local SAR-monitoring at sub-W/kg levels with less than 1% MSE error. We trained the software, with a small database of images, to perform a feasibility study and have achieved successful proof of concept for both the 3T and 7T field strengths. SAR maps were predicted with a residual MSE of <1% for both 7T head imaging and 3T body imaging. A SSIM of >90% for 7T head imaging and >80% for 3T body imaging was also achieved.

Biographies

DR. SAYIM GOKYAR obtained a B.Sc., M.Sc., and Ph.D. degrees, all from electrical and electronics engineering in 2009, 2011 and 2018 respectively.

He worked as senior associate of defense industry in Turkey from 2014 to 2019, and currently working as a postdoctoral researcher at the Department of Radiology, Weill Cornell Medicine, NY, USA. His research interests include MRI instrumentation, implantable electronics, metamaterials, RF design, safety evaluation of implantable devices, and artificial intelligence for image processing.

Dr. Gokyar is a trainee member of ISMRM and also a reviewer of various journals including MRM, JMR, and IEEE TBME. He is a valedictorian of B.Sc., in 2009. He was awarded with a graduate level scholarship of The Scientific and Technological Research Council of Turkey (TUBİTAK), between 2011 and 2017.

DR. FRASER J. L. ROBB has been in the field of MRI hardware since starting his graduate school studies at the University of Aberdeen 1990. His PhD thesis title was Field-Cycled Proton Electron Double Resonance Imaging of Dissolved Oxygen which gave him both wonderful hardware training and an appreciation for physiology and metabolism.

Subsequently he was a Research Assistant Professor of Radiology at Dartmouth College in New Hampshire from 1997–1999 working for Professor Harold Swartz on 1.1GHz ESR spectroscopic hardware. Most of his career has been heavily focused on commercial MRI coil design since starting with USA Instruments / GE Healthcare, Inc in 2000 and has more than 40 patents approved or in process on MRI coils.

In recent years he has been pioneering advanced prototyping and simulation methods for MRI coils and developed the strategy which led to the Air Technology MRI Coil revolution. He has been recognized internally as one of GE’s most prolific inventors of recent times and led the strategy that led to the development of Air Coil Technology and has an Honorary Professorship from the University of Sheffield, UK.

DR. WOLFGANG KAINZ received the Ph.D. degree in technical science from the Vienna University of Technology, Vienna, Austria, in 2000. After working for the Austrian Research Center Seibersdorf, he joined the Foundation for Research on Information Technologies in Society (IT’IS), Zurich, Switzerland, as an Associate Director. At IT’IS, he worked on the development of in vivo and in vitro exposure setups for bioexperiments. Since 2002, he has been a Research Biomedical Engineer with the Center for Devices and Radiological Health, Food and Drug Administration, Silver Spring, MD, USA.

He has authored or coauthored more than 200 peer-reviewed articles and book chapters. In 2004, he initiated the Virtual Family Project in cooperation with IT’IS and Prof. J. Chen from the University of Houston. In 2016, he initiated o2S2PARC (Open Online Simulations for Stimulating Peripheral Activity to Relieve Conditions, https://osparc.io/) in cooperation with IT’IS. His research interest is focused on the safety and effectiveness of medical devices and the safety of humans in electromagnetic fields. This includes novel computational life science methods for safety and effectiveness evaluations using the functionalized anatomical models of the human anatomy; magnetic resonance imaging (MRI) safety; performance and safety of wireless technology used in medical devices; electromagnetic compatibility of medical devices; dosimetric exposure assessments from dc to light; and novel methods to computationally assess the safety and effectiveness of new neuroprosthetics, e.g., electroceuticals, and therapeutic stimulation methods.,

Dr. Kainz was a recipient of the prestigious FDA Award of Merit in 2010 for exceptional leadership in performance in addressing the issues of compatibility of medical devices during MRI by applying transparently scientific research to device regulation. He is a Senior Member of the Administrative Committee of the IEEE International Committee on Electromagnetic Safety and a Member of many International Standards Committees.

DR. AKSHAY CHAUDHARI is an Assistant Professor of research in the Integrative Biomedical Imaging Informatics at Stanford (IBIIS) section in the Department of Radiology. His primary research interests lie at the intersection of artificial intelligence and medical imaging. Dr. Chaudhari graduated from UCSD with a B.S. in Bioengineering in 2012. He completed his Ph.D. from Stanford University’s Department of Bioengineering in 2017, focusing on novel MRI methods for musculoskeletal imaging; supported through the National Science Foundation Graduate Research Fellowship, the Whitaker Fellowship, and the Siebel Fellowship.

Dr. Chaudhari trained as a postdoctoral fellow in Radiology at Stanford University, where he combined machine learning with medical imaging acquisition and analysis.

Dr. Chaudhari has won many awards, including the W.S. Moore Young Investigator Award, the Junior Fellow Award, and an Outstanding Teacher Award from the ISMRM. He has 6 additional young investigator awards for his work on advanced medical imaging acquisition and analysis techniques. Dr. Chaudhari is the Associate Director of Research and Education at the Stanford AIMI Center and is an internal advisory board member of the Precision Health and Integrated Diagnostics Center.

DR. SIMONE ANGELA WINKLER is a Stanford-trained NIH K99/R00 funded assistant professor of Radiology at Weill Cornell Medicine and leading expert in the Ultra High-Field (UHF) MRI community.

Her research centers primarily on the development of technology for the detection of subtle brain features for the diagnostics and monitoring of neurodegenerative and neuropsychiatric diseases, which ultimately provides a pathway to therapy through MR guidance.

She was awarded with the 1st place in the MR engineering competition at the 2015 Annual Meeting of the ISMRM for a thermoacoustic MRI safety system and has earned a 2015, 2018, and 2021 Summa and Magna Cum Laude Merit Award for her oral presentations on RF coil designs, all of which are key components for Ultra High-Field MRI. Her research has appeared in over 60 journal, conference, and patent submissions. She was also honored for her position as lecturer in electromagnetic theory and has served on the editorial board of 9 international journals and a scientific book publisher. Prof. Winkler graduated majoring in mechatronics with distinction and in less than minimum time from the J. Kepler University of Linz, Austria. She pursued her graduate studies in electrical engineering at the École Polytechnique Montréal, Canada, where she specialized in RF/microwave engineering, funded by two fellowships (DOC fellowship/Austrian Academy of Science; first rank in the competition for a PhD fellowship from the FQRNT Québec). For her research work during her MSc and PhD degrees, she has received numerous scientific awards and scholarships. During her post-doctoral work at McGill University, Montréal, Canada, she developed a microwave near-field imaging system for breast cancer detection. She committed to a post-doctoral fellow position at Stanford University in Ultra High-Field MRI engineering (funded by a Canadian NSERC research fellowship from 2012–2014) in 2012, where she became Research Associate in 2015.