Abstract
Uncovering the complex network of the brain is of great interest to the field of neuroimaging. Mining from these rich datasets, scientists try to unveil the fundamental biological mechanisms in the human brain. However, neuroimaging data collected for constructing brain networks is generally costly, and thus extracting useful information from a limited sample size of brain networks is demanding. Currently, there are two common trends in neuroimaging data collection that could be exploited to gain more information: 1) multimodal data, and 2) longitudinal data. It has been shown that these two types of data provide complementary information. Nonetheless, it is challenging to learn brain network representations that can simultaneously capture network properties from multimodal as well as longitudinal datasets. Here we propose a general fusion framework for multi-source learning of brain networks – multimodal brain network fusion with longitudinal coupling (MMLC). In our framework, three layers of information are considered, including cross-sectional similarity, multimodal coupling, and longitudinal consistency. Specifically, we jointly factorize multimodal networks and construct a rotation-based constraint to couple network variance across time. We also adopt the consensus factorization as the group consistent pattern. Using two publicly available brain imaging datasets, we demonstrate that MMLC may better predict psychometric scores than some other state-of-the-art brain network representation learning algorithms. Additionally, the discovered significant brain regions are synergistic with previous literature. Our new approach may boost statistical power and sheds new light on neuroimaging network biomarkers for future psychometric prediction research by integrating longitudinal and multimodal neuroimaging data.
Keywords: Multimodality, Longitudinal, Brain Network Fusion, Representation
1. Introduction
It is widely accepted that the human brain has one of the most complex networks known to humanity and acts as the biological hardware to control our cognition and behaviors. Recently, advanced noninvasive neuroimaging techniques, e.g., magnetic resonance imaging (MRI), have revealed brain functional activities and anatomical structures in vivo. One of the modern approaches in neuroscience is to consider brain region interactions as a graph network, referred to as brain connectome or brain network [41,13]. Unlike the traditional voxel-wise statistics, a brain network describes the system in terms of a node-wise graph where graph-theoretical methods can be applied to model and simulate brain functions. By learning network properties, researchers could draw a broad picture about how the brain controls and regulates information through the orderly transfer of neural signals across brain regions [47]. Brain network analysis has been demonstrated to be effective for the diagnosis and prognosis of neurological disorders [10,67,69].
In the study of normal brain development or disease-related degeneration, useful biological information is encoded by different sources, e.g., multimodal and longitudinal data, which are not mutually exclusive but complement each other for a comprehensive description of brain activities and structures. For example, as an important period of brain neural development, early adolescence reveals a significant maturation of the brain functional architectures in terms of increasing functional connectivity between core brain regions [58]. Meanwhile, brain structures support these functional architectures exhibit plasticity in inter-regional fiber connectivity accompanying the functional maturation [39,50]. On the other hand, findings of longitudinal brain changes in multimodal data detail a trajectory map of neural development over time and these patterns may be significantly disturbed by neuropsychiatric disorders [48,22]. However, longitudinal studies of brain networks using single modality, e.g., functional MRI (fMRI) or diffusion tensor imaging (DTI), present discrepant patterns of functional and structural connectivity among some brain regions. Multimodal fusion makes it possible to systematically evaluate cross-modality relationships underlying neural processes. Previous research investigated the relationship between brain structural and functional connectivity in healthy and clinical populations [26,37,38,65] without considering progression and future changes. However, investigations combining longitudinal variations of brain connectivity with multimodal information are rarely conducted due to lack of efficient computational models.
In the present paper, we aim to integrate multiple sources, e.g., longitudinal and multimodal information, in brain network analysis. Specifically, we employ longitudinal multimodal neuroimaging data fusion with brain network representation learning. Motivated by the fact that both brain functional and structural networks reflect the brain regional interactions and they are partially shaped by each other [60,63], we design a linear coupling model to extract the similar and dissimilar factors of network structure to reveal such interactions. The proposed linear coupling model allows weighted emphasis on brain region interactions that are consistently strong or week in all modalities. Such linear cross-modality relationship is prevalent and has been observed in many brain regions [33,51,57,29,15]. Meanwhile, we incorporate the longitudinal consistency to further improve our linear coupling model by adding a homology constraint [34]. As a result, multiple sources of network data have been unified in our model to provide a better description of brain organization. Our model eventually learns a subject-level brain network representation that can be fed into any statistical models for various diagnosis or prognosis analyses. Further, the network representation contains node and edge features which may help interpret the relationship between import brain regions. This is the first work which proposes a comprehensive and mathematically rigorous model to integrate multimodal and longitudinal information of brain network data in a single framework. We hypothesize that the integrated network learning scheme may improve brain network analysis efficacy by providing statistically powerful representations. In our experiments, we will evaluate our novel framework, named multimodal brain network fusion with longitudinal couplings (MMLC), on two publicly available brain imaging datasets (both are the healthy subjects with 3 scans; n=105 and n=77, as detailed in Sec. 2.1). Tasks for the prediction of psychometric scores will be conducted on these two dataset separately, i.e. predicting anxiety [28] and depression [31] scores, respectively. We will also compare our work with several other representative and state-of-the-art network representation learning algorithms to validate our hypothesis.
2. Subjects and Methods
2.1. Subjects
The datasets used in this study are all from Southwest University Longitudinal Imaging Multimodal Brain Data Repository (SLIM) [1]. It contains a large sample of healthy participants who are university students from the local community. Each participant has multi-modal neuroimaging data, i.e. functional magnetic resonance imaging (fMRI) and diffusion tensor imaging (DTI), and multi-visit scans, i.e. three consecutive scans within three and a half years. We use two sub-datasets from this data repository. The first dataset (Dataset 1) contains 105 healthy participants and each of them was evaluated based on their level of anxiety using the State Trait Anxiety Inventory [28] before each scan. The trait anxiety score (TAIs) was used in analyses. The second dataset (Dataset 2) includes 77 participants assessed with the Automatic Thoughts Questionnaire (ATQ) [31], a self-report measure which reflects mental states associated with depression and was recorded before imaging acquisition. All participants were right-handed, with no history of neurological or psychiatric problems. All participants provided written informed consent prior to the imaging acquisitions, which was approved by the Institutional Human Participants Review Board of Southwest University Imaging Center for Brain Research. Table 1 provides their detailed demographic information.
Table 1:
Demographic Information of Anxiety and Depression Datasets. Mental states is evaluated through TAIs for Anxiety data and ATQs for Depression data. Three consecutive scans within three and a half years.
| Dataset | Age | Gender(F/M) | Scan1 | Scan2 | Scan3 |
|---|---|---|---|---|---|
| Anxiety | 20.5 ± 0.77 | 55/50 | 39.14 ± 8.47 | 41.39 ± 9.03 | 40.75 ± 9.29 |
| Depression | 20.2 ± 0.60 | 39/38 | 7.87 ± 6.62 | 7.69 ± 6.91 | 5.83 ± 5.13 |
2.2. Data Pre-Processing and Network Construction
The pre-processing of the resting state fMRI data was performed using both FSL [2] and AFNI (Automated Functional Neuroimaging) [3] toolbox. In brief, the pre-processing steps were as follows: (1) discarding the first 10 volumes in each scan series to allow for signal equilibration; (2) slice-timing correction for the remaining images; (3) performing motion correction; (4) time series despiking; (5) spatial smoothing with a Gaussian kernel of 6 mm full-width at half maximum (FWHM); (6) normalizing the mean-based intensity; (7) temporal band-pass filtering (0.01–0.08 Hz); (8) removing linear and quadratic trends; (9) structural MR image processing including brain masking, tissue classification, linear and nonlinear spatial normalization to the MNI152 brain template and other anatomical data processing steps; (10) co-registering the anatomical volume with the mean functional volume; (11) performing nuisance signal regression (nuisance signals from white matter, cerebrospinal fluid, the global signal, and 6 motion parameters); (12) resampling of the functional data into MNI space with the concatenated transformations. In the end, a 4-dimensional (4D) residual time series dataset was built for each brain regions in standard MNI space. We construct the fMRI brain networks by computing the edge weights as Pearson correlations between each pair of regional time series. The nodes in the networks are accordant with brain regions defined in the chosen brain atlas.
The pre-processing of the DTI data follows the standard process of a previous DTI study [74]. The DTI images were corrected for eddy current-related distortion and head motion via FSL software. Then, based on the structural T1 images, all DTI images were registered to a standard space, i.e. MNI152, to be consistent with that in the fMRI pre-processing. Here, the fiber probability connections across brain regions are set as the graph edge weights in the structural brain networks. More specifically, the fiber connections are measured through the probtrackx function in FSL toolbox with the default parameters. Given brain regions i and j, we further normalize the output of probtrackx Di,j, as , where Di,j stands for the number of fibers reaching region vi seeded from region vj, and Di represents the total number of fibers seeded in region i, i.e. . Such normalization results in asymmetry of fiber tracking between two regions. To overcome this, we took the average of two directions of tracking, .
2.3. Methods
The pipeline of our multi-source brain network fusion is shown in Figure 1. Briefly, an individual brain network representation is extracted concurrently through 3 stages of fusions: 1) The cross-sectional fusion among a group of participants, where the group average network representations are measured and forced to align with a group of participants; 2) The longitudinal fusion along scans to capture the consistency of longitudinal changes, where we use a homology transformation [34], i.e., rotations of network representations, to represent the time-dependent variants; and, 3) The multimodal fusion between functional and structural brain networks, where linear relations between multimodal brain networks are pursued with matrix factorizations.
Fig. 1:
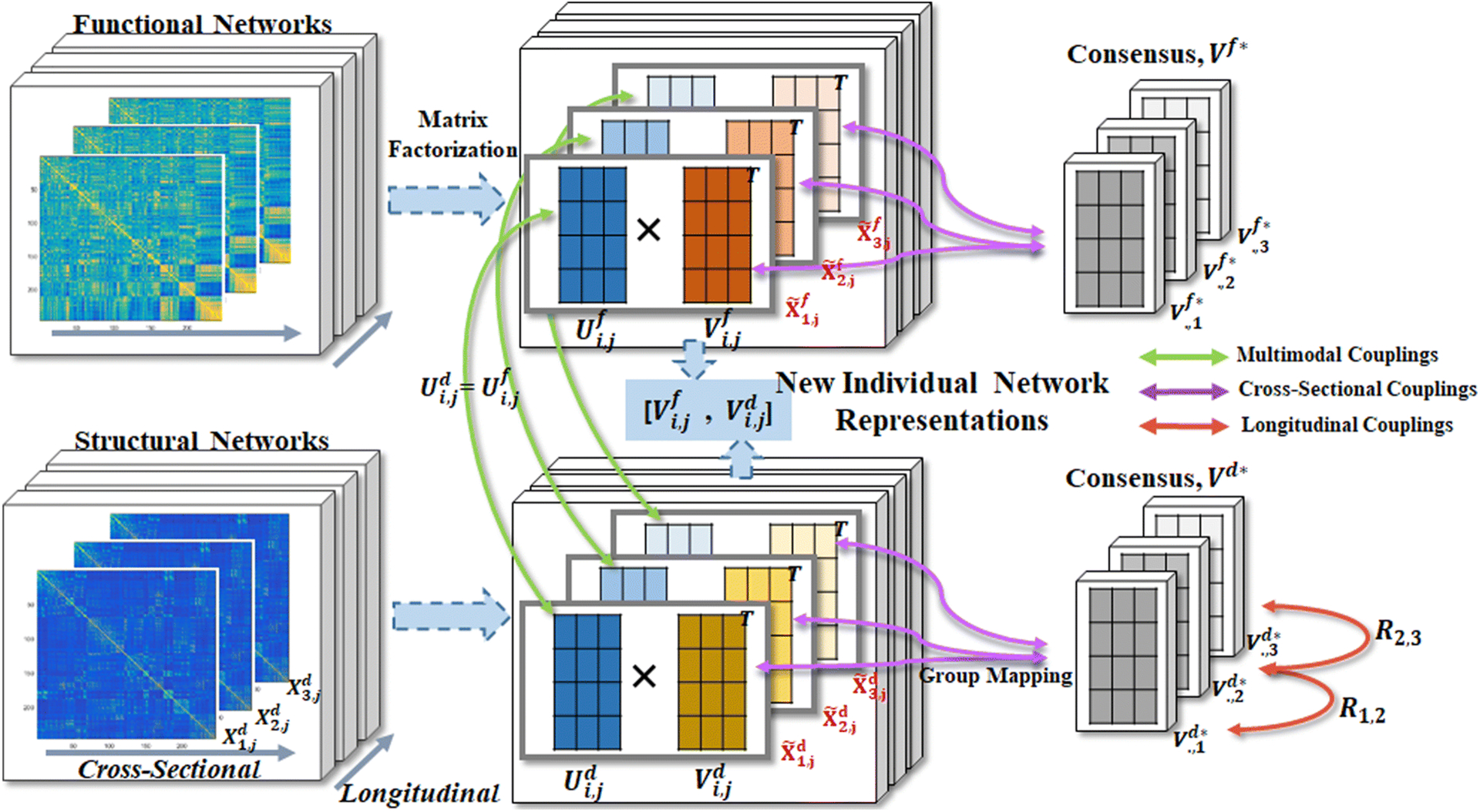
The pipeline of the proposed multimodal brain network fusion with longitudinal couplings (MMLC) framework. Three levels of information couplings are considered: cross-sectional coupling, longitudinal coupling, and multimodal coupling. First, each single modality brain network in a given scan (left column) is decomposed into two matrices (middle column), U and V. We force U to be shared across modalities (green arrows) and V of a group of subjects similar to the estimated consensus matrix V* (purple arrows). Furthermore, the consensus matrices of structural brain networks (bottom right) are aligned by rotation mappings, i.e. matrix R (red arrows), which manipulate the time consistency. Eventually, after solving these 3 coupling strategy, the new individual network representation at a given scan time is the concatenation of Vf and Vd.
2.3.1. The Cross-Sectional Fusion
It is customary to couple subjects in a population to achieve the individual and group properties. We defined a graph g = (V, X) for the individual brain network, where V = {v1, …, vn} is the set of all n brain regions and is the connectivity matrix, where epq is the edge weight (connectivity strength) between node vp and vq. In an fMRI network, , where Sp is the average time series of all the vertexes inside brain subregion vp and Cor(., .) is the correlation function evaluating similarities between signals Sp and Sq. In a DTI network, . For both fMRI and DTI networks, the number of nodes n is defined as the number of subregions in the applied brain atlas. For each subject, we have two connectivity matrices, Xf (the functional network) and Xd (the structural network). Thus, for the whole dataset, suppose we have N subjects and each subject was scanned T times, we have a set of functional and structural connectivity matrices, . We conduct network embedding with matrix factorization to map the graph data into a lower dimensional latent space. In other words, given a network Xi,j, we identify an optimal approximation matrix factorization, and will be the new representation of network. To this end, one of the standard reconstruction processes can be formulated as a Frobenius norm optimization problem:
| (1) |
Let {X1,j, X2,j, …, XN,j} denote the set of networks for a group of N subjects at a given scan j, where for each network , we have factorizations that and . The coefficient vector v(i,j),t is the new representation of the tth node of subject i’s network matrix in a low dimensional space (p dimensions) based on the new basis Ui,j. To look for the consistent patterns among a population of participants, we adopt the concept of consensus matrix. If participants are from the same group, it is natural to hypothesize that they have a similar representation matrix (Vi,j) but only differ on the basis matrix (Ui,·). Hence, Vi,· should be the target to measure disagreement of the network patterns. Here, we introduce a new variable named the consensus matrix of Vi,· and the following loss function to couple the network representations within a group of subjects,
| (2) |
Note that all Vi,· are at the same scale because entries of all the network matrix Xi,· locate within the range of [−1, 1]. Even though the general factorization problem might exist multiple solutions due to the uncertainty of basis matrix, the inter-subjects coupling problem described as below is solvable with the added consensus matrix term and assumption that Xi,· are within the same range.
| (3) |
2.3.2. The Multimodal Fusion
For a given participant, the edge weights of graph matrix in functional and structural networks fall in the same range and their number of nodes are identical. The node definition follows the organization of brain atlas used in this study. There are various brain atlases that have been widely applied in neuroimaging studies for brain intra- or inter-regional analysis. Previous research has shown the influence of different brain atlas to brain network analysis [41]. Ideally, a brain network created from fine-grained atlas contains more details of the regional interaction. Thus, in this study, we chose a newly proposed brain atlas, called human Brainnetome Atlas [21], which has 246 brain regions and contains both functional and structural connectivity patterns extracted from neuroimaging data with multiple modalities.
After reconstructing brain functional and structural networks based on the defined brain atlas, we get two new network representations for each subject i as and with the corresponding basis matrices and . As we discussed before, the structural network draws the picture of fiber connections that are regarded as the structural foundation of brain functional network. Thus we hypothesize that there are quite significant similarities between those two kinds of networks that can be interpreted by a shared presentation in the latent space. In other words, given a subject i, we let the functional and structural networks share the same basis matrix . Therefore, together with the inter-subject coupling model, we propose the multi-modality coupling model as below:
| (4) |
with α as the control parameter to modify emphasis of multi-modal network coupling, for example, α > 1 means more weights on searching topological consistency of structural connectivity and α < 1 otherwise. To be noted that, both and have the same range of weight definition. This property makes the inter-nodality coupling solvable as the general matrix factorization problem.
2.3.3. The Longitudinal Fusion
In the longitudinal coupling, we track how the brain evolves over time. We model the smooth variation of brain networks as a Procrustes problem which maps the consensus matrix to a same effect space [45]. Therefore, the longitudinal fusion is a group level fusion strategy. More specifically, first, we improve our proposed multi-modality coupling model by adding an orthogonality constraint to the consensus matrix in structural network part with two reasons: (1) Previous research has suggested the pattern that several brain regions structurally form a small subnetwork. Those subnetworks might uniquely handle some low-level functions and be eventually integrated with each other to solve high-level functions. The matrix factorization with orthogonality constraint plays a similar role as the clustering [54] which is consistent with the subgraph organization in human brain networks. (2) Human brain functional activities could be easily influenced by some sorts of the external stimulus or hormone level [23] while the fiber connection or other anatomical biomarkers are more stable to reflect current brain structure status [65].
After adding the orthogonality constraint to the objective function in every scan, we further model the relationships between each consecutive pair of consensus matrices. Suppose we have two consensus matrices and from two consecutive time points j and j + 1 for a group. Due to the relative stability of structural network within subject than cross-subjects, we expect that shares a rotation relationship with , i.e.
| (5) |
is a rotation matrix thus det(Rj,j+1) = 1 and . As is satisfied for all j, taking the rotation relationship with this orthogonality, we construct a new symmetric matrix,
| (6) |
that . Then we merge the consecutive relations from time j to j + 1 of into a single time variable as below:
| (7) |
Eventually, we model the longitudinal coupling with a homology constraint to the structural network for a given subject i and a total of T scans.
| (8) |
The above constraint is called the generalized Stiefel constrain [5] with the mass matrix Mi,j. In this paper, we applied an optimization algorithm which involves the Stiefel manifold based on the Cayley transform for preserving the constraints [70,35].
2.3.4. The Proposed Multi-Stage Fusion Model
We reformulate the problem for all N subjects and T time points. The multimodal brain network fusion with longitudinal coupling framework is to solve the problem of minimizing the following objective function, L, with the corresponding constraint:
| (9) |
where is the regularization term to prevent overfitting. To solve this optimization problem, we propose an iterative update procedure together with a Stochastic block coordinate descent algorithm. The mathematical details to optimize Eq. 9 are described in Appendix and their implementation source code is publicly available at http://gsl.lab.asu.edu/software/multimodal-longitudinal-brain-network-coupling/. It is worth noting that the objective function in Eq. 9 is non-convex and thus the solution we provided here is guaranteed to reach a local optimum. Formally, the MMLC is summarised in Algorithm 1.
2.4. Experimental Setting
We compare the performance of MMLC with several representative and state-of-the-art brain network representation learning algorithms. It is worth noting that, for a fair comparison, the hyperparameters in each model are fine-tuned with the same strategy of parameter searching applied for MMLC. Details of settings are explained as below.
-
MFCSMC - matrix factorization with the cross-sectional multimodality couplings: We apply collective matrix factorization (MF) [59] for functional and structural networks with the cross-sectional couplings. This method is the backbone of MMLC but does not consider the cross-modality coupling and the longitudinal coupling. The loss function is defined as,
where α = 1 and λ1 = 10 for both anxiety and depression score predictions. The feature dimensions of Vf and Vd are the same as in MMLC, i.e., P = 10, although they are not necessary to be the same between modalities in this model. is controlled by an empirically chosen weight λ2 = 0.1.(10)

-
EigLC - eigen longitudinal couplings: EigLC [34] is a state-of-the-art method that models the longitudinal coupling on a single modality, i.e., structural networks. EigLC transforms structural network to the corresponding Laplacian matrix and solves the eigenvalue problems with the coupling constraints.
-
sMFLC - structural-network matrix factorization with the longitudinal couplings: A variant of MMLC by removing the terms concerning functional networks in our model. It is an MF version with the longitudinal coupling of structural networks, thus it is a single modality analysis with longitudinal coupling. This model is designed to compare with EigLC. Its loss is defined as Eq. 8. The weight of MF is set as α = 1 and the cross-sectional weight λ1 = 10.
-
MFCSLC - matrix factorization with the cross-sectional longitudinal couplings: Another variant of MMLC, i.e., MF with cross-sectional and longitudinal coupling. Both functional and structural networks are processed with MF without sharing the basis matrix, U. The cross-sectional coupling is also considered by adding the consensus matrix for both modalities independently. In addition, the longitudinal coupling of the structural network is considered in this model. The objective function of this variant model is similar to Eq. 9 except the shared basis matrix U, which is formulated as:
However, different to the parameter settings in Eq. 9, α = 5 and λ1 = 10 reveal the best performance during parameter searching.(11)
We carry out a regression analysis to predict the given observations S (e.g., psychometric evaluation scores) based on the extracted network representations. Specifically, subject i will obtain his/her new feature set at time point j as the new representation of their original network graphs. We then feed the vectorized features and the corresponding predicting scores into a linear regression model to encode their relationship by using the LIBSVM toolbox [11]. In this experiment, we randomly pick 70% subjects as the training set and test on the rest. This process is repeated 20 times and, in the end, the average performance and standard deviation are reported. Two widely used evaluation metrics, i.e., mean absolute error (MAE) and root mean square error (RMSE), are adopted to evaluate the prediction performance. Specifically, MAE is defined as and RMSE is defined as . In both metrics, Si,j denotes the real observations of subject i at given time j while denotes the predicted value based on the extracted network representations. We treat the longitudinal scans of a subject as independent experiments. Thus the total size of data is equal to the number of subjects N times the number of longitudinal scans T.
It is worth noting that the objective function Eq. 9 is non-convex, thus different initialization would result in different local optima. The choice of initialization is non-trivial in MF and some strategies has been proposed [8,20]. Here, we follow the strategy in [8] to apply principal component analysis (PCA) of the network matrices to obtain initial V and U. More specifically, given feature dimension P, the singular value decomposition (SVD) of the original network matrices is carried out and the top-P principal components are chosen to construct V and the corresponding U. Such a process also naturally provides orthogonality of the initial structural representation Vd. After that, the consensus matrix V* is computed as the average of the initial V.
3. Results
3.1. Parameter Analysis
3.1.1. Weights of Cross-Sectional (λ1) and Cross-Modality (α) Couplings.
The proposed framework has two important parameters, i.e., α controls the contribution of multimodal coupling and λ1 controls cross-sectional coupling. In this section, we evaluate the influence of the settings of α and λ1 on MMLC via a metric searching. Specifically, we vary α as {0.5, 1, 5, 10, 20} and λ1 as {1, 10, 20, 30, 40}. Similarly, we use the aforementioned data splitting strategy for training and testing. By changing α and λ1 independently, we show changes of performance measured by MAE and RMSE in two experiments (Figure 2 and Figure 3). We observe that: (i) In Dataset 1, both MAE and RMSE values reach the relatively small values when α = 1, which means both functional and structural networks have equal roles in the prediction task. Besides, there is a tendency that MAE and RMSE values go up along with the increase of α. In Dataset 2, obvious downgrade of prediction performance, i.e., increasing of MAE and RMSE, is observed when α increases beyond a higher value, e.g., α > 10. (ii) Moreover, when λ1 = 20, our framework has the relatively best performance in both datasets. In this experiment, we observe the different optimal parameter settings of tasks on two different domains, i.e., anxiety and depression. It shows that our framework can be generalized to different prediction tasks via unsupervised network representation learning. The result is consistent with the previous discovery in brain networks that the distinct roles of functional and structural connectivities shift in different cognitive tasks [53].
Fig. 2:
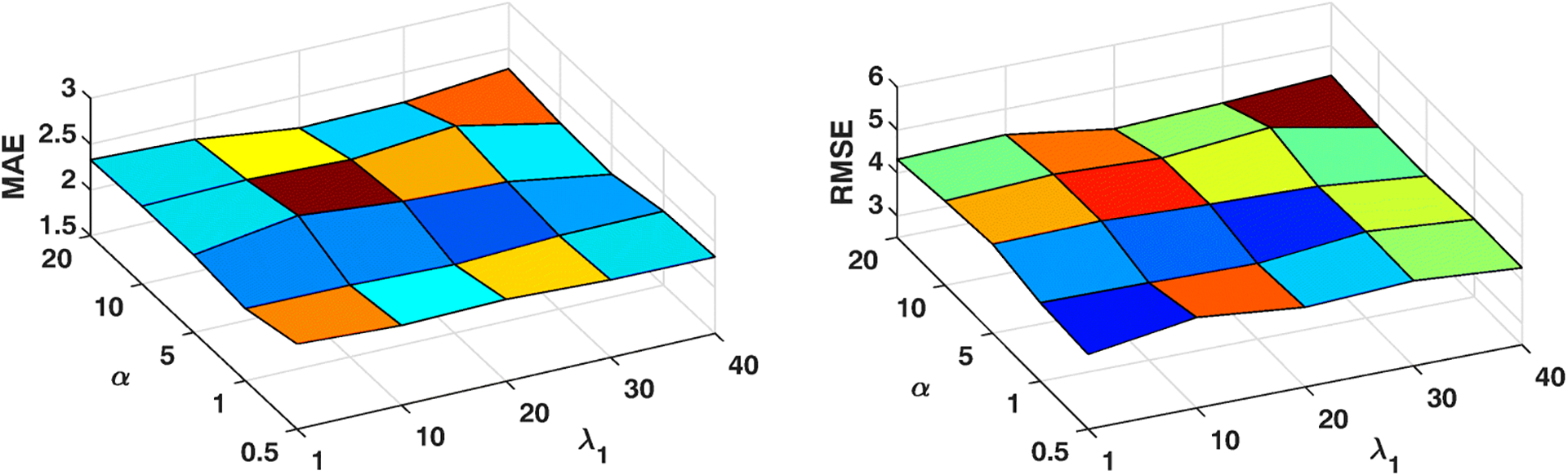
Parameter Analysis of Dataset 1 (Anxiety)
Fig. 3:
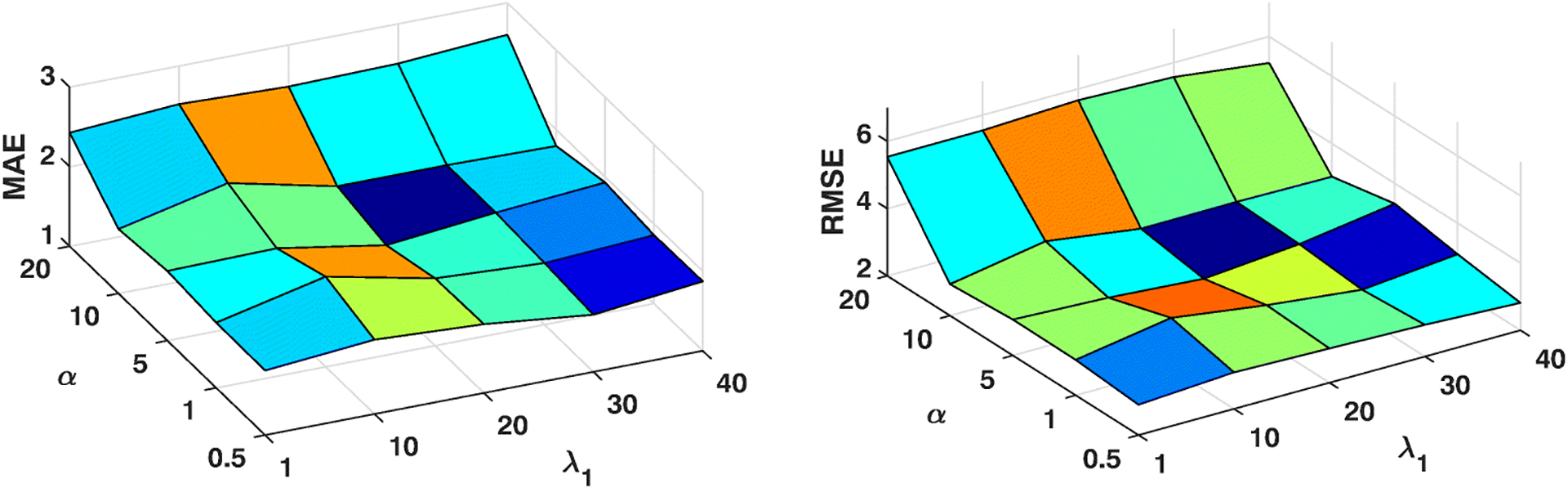
Parameter Analysis of Dataset 2 (Depression)
3.1.2. Dimension of Feature Space P
The choice of feature dimension is another key hyperparameter that affects the encoding of the brain network matrices. With a smaller P, the new network representations, Vf and Vd, focus on the core network topological changes but meanwhile might suffer from information loss. On the other hand, high dimension features with a larger P, although more informative, downgrade the following supervised learning tasks due to added signal noises. Therefore, we explore the influence of different settings of P and select the smallest P with acceptable accuracy level. The searching space of P is defined as [5,10,15,20]. The evaluation results of the metric MSE and MAE are shown in Fig. 4. We observe that P = 5 provides insufficient knowledge of network structures given the prediction performance and there is no significant change when P increases beyond 10. For both anxiety and depression tasks, the learned representations with P = 10 give satisfying accuracy in a relatively low dimension space. In other words, for each brain node, its top-10 connectivity patterns contain informative biomarkers related to these tasks. As a side note, we set P the same in MFCSLC for a fair comparison to MMLC. The larger P is also explored and P = 20 for the structural network in MFCSLC exhibit a close performance to MMLC in the anxiety prediction, e.g., MAE=2.145 ± 0.11 and RMSE=3.98 ± 0.89. However, it achieves this level of accuracy with twice the size of parameters of MMLC.
Fig. 4:
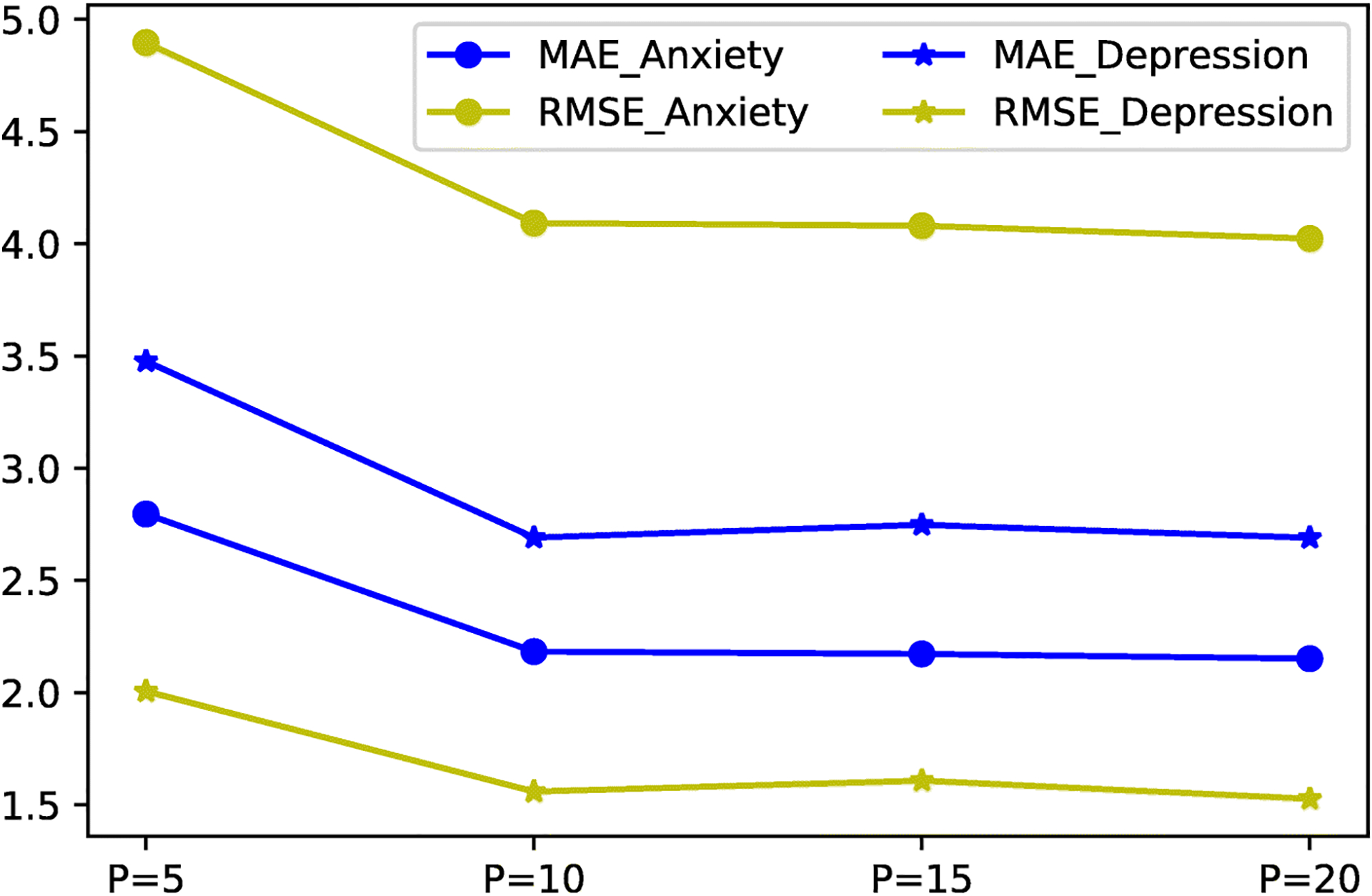
Performance of prediction tasks with various settings of P. MAE and RMSE scores do not yield significant changes when P > 10, which suggest the optimal choice of P is 10 in both Anxiety and Depression prediction tasks.
3.2. Prediction Performance
We present the regression performance of our proposed model as opposite to other comparison methods in Table 2. We set α = 1, λ1 = 20 for Dataset 1 and α = 5, λ1 = 20 for Dataset 2 according to the parameter selections. We also empirically chose λ2 to be 0.1 and dimension of the new feature space P = 10. The prediction is made for each individual in each scan since the unsupervised network representation learning (Eq. 9) derives individual-level features per scan, denoted by [Vf, Vd]. Therefore, the statistical results reported in Table 2 reflect the variance (averaged errors) of the individual predictions. From Table 2, we see that our proposed model outperforms other methods in both experiments. For example, sMFLC, the single modality version of our proposed model with longitudinal coupling, has a significantly better performance than EigLC (in Dataset 1, it decreases MAE by 1.072, p < 1e − 4 and RMSE by 0.615, p < 0.047; in Dataset 2, it decreases MAE by 1.664, p < 1e − 4 and RMSE by 2.11, p < 1e − 4). The difference of regression analysis between the full coupling and partial coupling of multimodal or longitudinal fusions is small but significant. In Dataset 2, the result of partial coupling of brain networks in the multimodal fusion (MFCSMC) has the higher value of MAE (p < 0.0006) and RMSE (p < 0.153) than MMLC. Meanwhile, MMLC outperforms MFCSLC which contains only longitudinal coupling in both datasets. Overall, MMLC has the smallest MAE and RMSE values together with the relatively low variance compared with other baseline methods in our experiments. This shows that the proposed MMLC framework could effectively extract the key properties of multimodal brain networks with longitudinal development which underlie normal variation in depression or anxiety.
Table 2:
Performance comparison regarding MAE and RMSE on Anxiety and Depression Datasets
| Methods | Dataset 1 (Anxiety) | Dataset 2 (Depression) | ||
|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | |
| EigLC | 3.401 ± 0.931 | 5.037 ± 1.464 | 3.536 ± 0.729 | 5.227 ± 0.886 |
| sMFLC | 2.329 ± 0.135 | 4.422 ± 0.770 | 1.872 ± 0.556 | 3.117 ± 1.405 |
| MFCSLC | 2.225 ± 0.185 | 4.223 ± 1.120 | 1.788 ± 0.092 | 3.050 ± 0.504 |
| MFCSMC | 2.285 ± 0.151 | 4.340 ± 0.918 | 1.741 ± 0.080 | 2.924 ± 0.392 |
| MMLC | 2.173±0.098* | 4.015±0.751* | 1.672±0.067* | 2.773±0.416* |
Significant with p < 0.05, two-sample t-test between MMLC and the compared methods.
The statistical results prove several assumptions brought forward in this study. For example, the role of cross-modality coupling via the shared basis matrix U can be evaluated through MFCSLC vs. MMLC. It leverages the prediction of anxiety scores by 0.05 in MAE and 0.2 in RMSE, and depression scores by 0.1 in MAE and 0.3 in RMSE. Besides, the orthogonality of V and its linear rotation across scans are included in the constraint term Eq. 6. Therefore, by comparing MFCSMC and MMLC, we observe the benefits of adding such constraint to the structural representation, which improves the prediction of anxiety scores by 0.1 in MAE and 0.3 in RMSE, and depression scores by 0.07 in MAE and 0.15 in RMSE. These discoveries might help us to improve the current MMLC model in our future work.
3.3. Feature Evaluation with Subnetworks
To further validate our framework, we study the subnetwork patterns in each dataset. Based on the regression model, we evaluate the node-wise sensitivities and identify the top 5 brain regions whose new representations learned from our framework have the greatest sensitivities with the psychometric evaluation scores. In the anxiety data, 5 key regions are: left and right middle frontal gyrus (MFG_L_7_7, MFG_R_7_3 in Brainnetome Atlas), left superior frontal gyrus (SFG_L_7_5), right basal ganglia (BG_R_6_1) and hippocampus (Hipp_R_2_1). In the depression data, 5 key brain regions on the right hemisphere are found: superior temporal gyrus (STG_R_6_1), parahippocampal gyrus (PhG_R_6_2), Thalamus (Tha_R_8_3), medioventral occipital cortex (MVOcC_R_5_4) and precentral gyrus (PrG_R_6_1). We present the subnetwork patterns consisting of the 5 key regions extracted from the group mean network in Fig. 5 (the plot guideline can be found at [43]). Due to the analogical topology of subnetwork patterns in longitudinal data (differs in strength weight), we only shows results from scan 1. In Fig. 5, multimodal subnetworks reflect their specific region-wise functional or structural connections. They were generated using different thresholds relatively to the level of their connection weights. Generally speaking, comparing with the fMRI subnetworks which usually possesses homogeneous connection patterns, DTI networks have much weaker connections among several key brain regions, i.e., high variance in weights. Therefore, node embeddings of the structural network through factorization potentially carry sparse features and are robust to signal noises. It is also part of the reason why we use DTI networks as the longitudinal coupling bases.
Fig. 5:
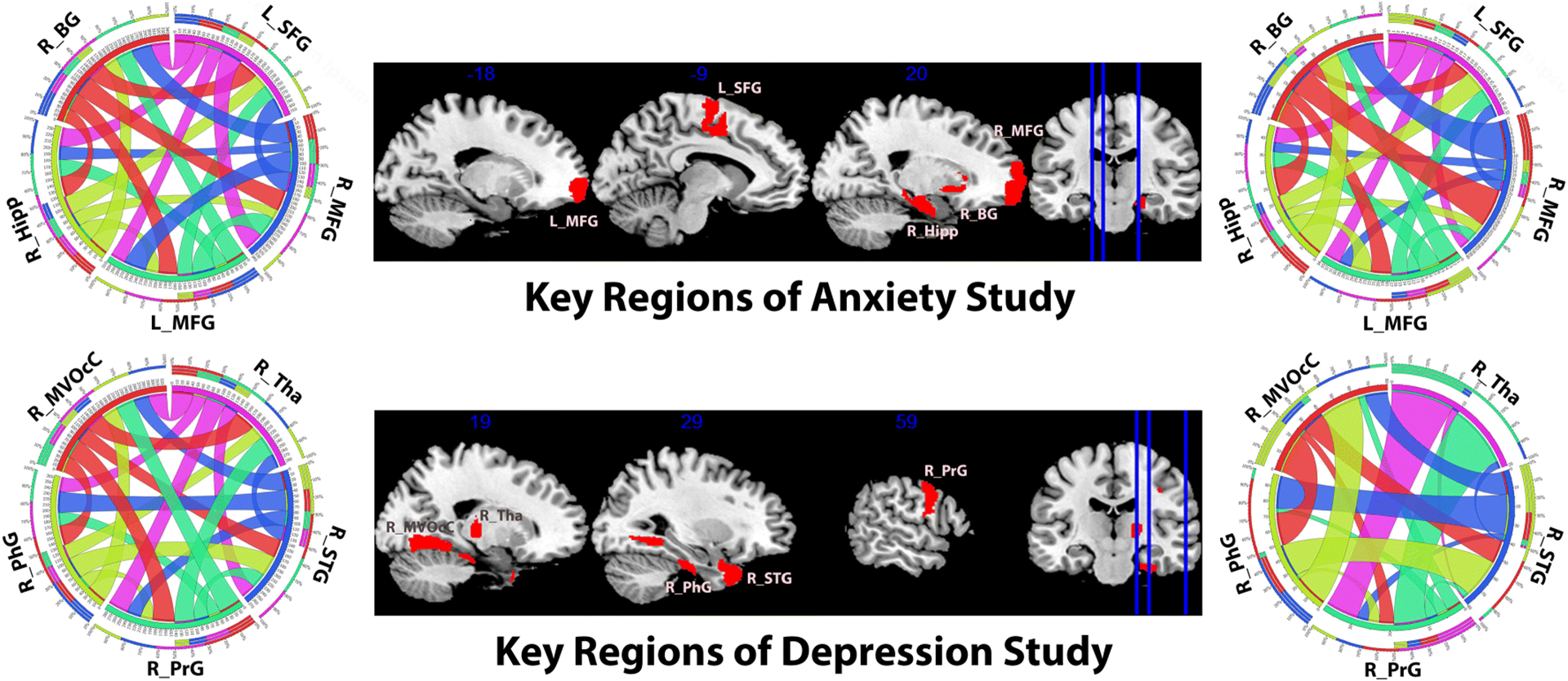
Slice view of five key brain regions (middle) and their inter-connection strength visualization. The top row shows results for the anxiety study (Dataset 1) and the second row for the depression study (Dataset 2). On each row, the left circos [43] describes the functional connection network and the right circos describes the structural connection network. In each circos, the arc widths indicate the connection strengths. Abbreviation: left and right middle frontal gyrus (L/R_MFG), left superior frontal gyrus (L_SFG), right basal ganglia (R_BG), hippocampus (R_Hipp), superior temporal gyrus (R_STG), parahippocampal gyrus (R_PhG), Thalamus (R_Tha), medioventral occipital cortex (R_MVOcC) and precentral gyrus (R_PrG).
4. Discussion
In this study, we investigate a unique problem, i.e., the longitudinal coupling with multiple modality information at the network level. A multi-source learning model for brain network analysis is then presented. Dealing with the prediction tasks, our model learns the network representations in terms of the node embeddings. We investigate the intrinsic cross-modality and longitudinal relationships inside brain networks and design a unified fusion strategy to combine those relationships. We also propose an effective numerical scheme to optimize the proposed objective function. To the best of our knowledge, this is the first work that fuses multimodal and longitudinal brain networks simultaneously. The experimental results demonstrate the effectiveness of our model in psychological state prediction. We expect the current study to bring new insights for brain connectivity analysis and help better understand the neural basis of cognitive functions along normal and abnormal brain development.
Generally, there are two types of studies in brain network analysis. One emphasizes the analysis of network topology reflected by node-wise connections. By applying knowledge from graph theory, previous studies proposed to extract some topological measures, such as centrality, similarity and motif patterns, from either binary or weighted brain networks. Recently, new trends aim to address network dynamics and higher order dependencies among nodes [7]. Comparing the local or global properties of network topology across participants, researchers could draw biologically meaningful conclusions about altered patterns on brain network efficiency in patients of Alzheimer’s disease [66] and depression [67]. The second type is to study network graph as a collection of edges; thus, the traditional statistical analysis would be conducted on the edge weights. From a data mining perspective, individual brain networks represented as a weighted graph matrix is preferred so that informative features could be learned. For example, tensor-based network embedding has been recently introduced to uncover brain networks [9]. It derives the latent features, or namely new representations, of a network to which conventional machine learning techniques could then be applied. Our current work follows the second type of approach and may enrich the edge-collection analysis-based brain network methods.
In this study, we analyzed two modalities of brain networks, functional network and structural network, where one type might interact with or underpin the other. The functional network is extracted from fMRI which records brain activity through the variation of blood oxygen level and has good temporal resolution. The structural network is computed from diffusion MRI (dMRI) which measures the water diffusion process in the white matter and depicts accurate structural neural connections. The two modalities yield complementary information to benefit the consistent graph pattern learning across modalities. Several studies proposed linear [4] or non-linear [49] multimodal integration approaches for brain network analysis, which significantly improve the statistical power to identify brain structural or cognitive changes than using single modality data. For example, Chen et al. [12] applied multi-view spectral clustering to infer the group-wise consistency in multimodal brain networks and obtained several consistent multimodal brain sub-networks within the group. Besides, Dodero et al. [17] conducted the joint diagonalization of graph Laplacians for multimodal brain networks and extracted the group-wise coherent sub-graphs. Benefits of such multi-source network integration have been discussed in [68]. Since network estimation for neuroimaging data might suffer from many false connections due to the signal noise and acquisition limitations in data collection, effectively learning features from few noisy brain networks is challenging. Therefore, we include more brain network data, e.g., longitudinal scans, as a supplement to multimodal analysis of the baseline scans. Because the multimodal and longitudinal studies are inherently related, it is promising to explore multimodal fusion with longitudinal coupling to learn effective brain network representations.
It is worth noting that the joint factorization of connectivity matrices is equivalent to the linear fusion of the node-wise connectivity patterns and the process is controlled by the consensus term to maximize the group consistency. Evidence from previous research supports our linear multimodality combination. For example, the DTI- and fMRI-derived connectivity topology is proved to be similar [62]. Brain regions in some important functional subnetworks, e.g., core resting-state networks, are found interconnected by anatomical white matter tracts [30]. Other research observed strong agreement of structure-function connectivity in the default mode network [33]. Those discoveries suggest that there may exist a linear mapping relationship between part of the functional network and its structural counterpart [46]. We also observe that, without the joint factorization across modalities, our variant model (i.e., MFCSLC) shows comparable performance to MMLC with a higher P value. Theoretically, MFCSLC has more freedom of factorization that allows each modality to independently encode its network topology. However, benefits of this quality are achieved with a solid optimization strategy that is usually non-trivial and may easily overfit the downstream prediction tasks when P is increasing. Consequently, to leverage encoding accuracy, MFCSLC requires considerably more efforts to search optimal hyperparameters, α, and, λ, at a higher P value. It may also significantly increase memory consumption for high dimensional embedding features. It may become a serious problem if we study high resolution brain networks with more nodes (i.e., brain regions). Therefore, we propose a practical approach by adding multimodal coupling as a constraint to capture a low level of cross-modality association that creates an efficient feature embedding.
In the experiment of anxiety prediction, MMLC identified five regions associated with anxiety self-report (TAI) that are synergistic with previous literature: left and right middle frontal gyrus (MFG), left superior frontal gyrus (SFG), right basal ganglia (BG), and right hippocampus (Hipp). Regions distribute on both hemispheres, suggesting bilaterally anxiety processing [44]. The hippocampus has a central role in processing emotions and long-term memories and a recent study also found the structural development of hippocampus, e.g., neurogenesis, is affected by anxiety-related behaviours [55]. Hippocampal volumes correlate with TAI in both healthy controls and depressed patients [56]. Participants with elevated TAI scores show reduced bilateral MFG activity during socioemotional processing [40]. Further, neuromodulation of MFG improves attentional control [36] and emotional memory retrieval [6] in high TAI endorsers. Using EEG, increased SFG theta has been observed in participants with high TAI scorers during risky decision making. A smaller body of literature notes relationships between anxiety and basal ganglia measures. Using proton magnetic resonance spectroscopy in healthy participants, TAI was associated with neurotransmitter levels in the nucleus accumbens [64]. Moreover, generalized anxiety patients show decreased metabolism in the basal ganglia [71]. There are notable regions associated with anxiety and depression constructs missing in our results (e.g., amygdala and cingulate cortex) that are likely due to our healthy population and the self-report measures used. As others have noted, instruments such as the STAI capture sub-dimensions of personality linked to anxiety, rather than the clinical expression of anxiety disorders [18]. Future analyses in clinical populations of depression and anxiety are warranted to determine the full utility of MMLC for detecting the neural substrates of symptoms.
In the depression score prediction study, we find regions within the right side of brain dominate associations, a pattern that has been seen in other studies as well [27]. MMLC identified five regions associated with the ATQ that are synergistic with previous literature: superior temporal gyrus (STG), parahippocampal gyrus (PhG), Thalamus (Tha), medioventral occipital cortex (MVOcC) and precentral gyrus (PrG). Two previous studies found right PhG gray matter volume predicts ATQ scores in healthy participants [19,14]. [14] also examined DTI data and found that white matter connections to the right STG was an additional significant predictor. In patients with major depression disorder (MDD), ATQ scores were related to activity of the right STG as measured by multi-channel near-infrared spectroscopy [42]. Using EEG, MDD patients who score high on the ATQ also show excessive high-beta activity specifically in right hemisphere frontal, temporal, and parahippocampal regions that reduces with effective treatment [52]. Moreover, [72] found ATQ scores were correlated with functional connectivity of the cingulo-opercular network, which includes the PrG, in MDD patients. While no previous literature has associated ATQ scores with the MVOcC, reduced connectivity of this region to the insula in MDD patients has been noted [25]. Lastly, the thalamus is an important brain region in MDD because of its connecting role between limbic subcortical structures and relevant cortical regions. This structure shows greater functional connectivity to the subgenual cingulate at rest in MDD patients, compared to healthy controls [24], as well as a greater number of neurons at autopsy, compared to other psychiatric conditions [73]. Notably, no one study has been able to identify all five of these regions associated with depressive symptoms in healthy controls. Several of these brain regions have only been related to the ATQ in MDD patients. This highlights the capabilities of MMLC to detect subtle relationships between psychological process and brain measures, compared to traditional unimodal or single time point methods. Thus, this new technique has the potential to address reproducibility and reliability concerns in brain-behavior relationship research.
Despite the promising results obtained by applying the MMLC framework to analyze longitudinal multimodal imaging data, there are three important caveats. First, the current work takes the linear coupling approach to integrate multimodal brain networks. However, recent research also shows that functional organization of the human brain has a dynamic system which may partially stem from the structural foundations of the white matter [61]. Thus, regional-wise functional activities may possess both linear and non-linear elements related to the regional patterns of structural connectivities. Moreover, formulations of brain networks, e.g., regional connections, can also be categorized into the linear [4] or non-linear [16,32] methods, which further affects multimodal brain network coupling, locally and globally. A possible solution to these problems is to obtain a hierarchical map of function-structure matching for each brain region. On each level of the hierarchy, brain functional connectivities have a linear relation with white matter connections. This can be understood as the sub-networks. The different linear patterns in the subnetworks further consist of non-linear multimodal relationship in the whole brain. Second, for a convenient modeling, we adopt a rotation matrix for the longitudinal coupling in the structural networks. We could potentially apply non-linear deformations as well for the longitudinal coupling in both structural and functional networks. As a result, the high order graph matching between the functional networks may provide additional constraints to our model and it may further improve the sensitivity of our entire network analysis framework. Third, in our current model, we empirically set the same weights, λ1, for the cross-sectional couplings of Vf and Vd (Eq. 9). By this setting, individual Vf and Vd are equally forced to align cross-sectionally. Since subjects in this study are normal young college students, we hypothesize that these two network representations contain the strong topological patterns which are shared among the group and therefore equally important. On the other hand, this setting reduces the complexity of parameter searching. However, we also believe, by assigning different cross-sectional weights for functional and structural modalities, the proposed model may enjoy more flexibility in learning tasks. We will carefully explore these approaches in our future work.
5. Conclusion
This paper describes a novel network fusion framework, named multimodal brain network fusion with longitudinal coupling (MMLC), which simultaneously considers multiple levels of information such as relationships between brain functional and structural organizations and longitudinal brain changes. We construct a linear combination of multimodal networks with matrix factorization on the target domain, and couple the longitudinal variants to enhance the network representation learning. We test our proposed framework with two relatively large datasets, and experimental results demonstrate the effectiveness of the generated network representations for predicting psychological characteristics. We demonstrate MMLC is better able to predict psychometric scores than several representative and state-of-the-art brain network learning algorithms. There are several interesting directions that are warranted for further investigation. For example, in this paper, we evaluate the learned brain network representation performance for regression tasks. In the future, we will derive subnetwork patters from the learned network representations and evaluate contributions to early disease diagnosis and prevention. The current work focuses on studying how to fuse different brain modality networks. However, it would be also interesting to investigate the generated subnetwork patterns. For example, it could be interesting to show that strong topological patterns which are shared among the groups are equally important and justify identical cross-sectional weights for functional and structural modalities. We plan to study these important questions in our future work.
7. Acknowledgments
This work was partially supported by National Institutes of Health (R21AG065942, R21AG049216, RF1AG051710, R01EB025032, and K01MH116098), and the Arizona Alzheimer’s Consortium.
8. Appendix
We present the formulation of iterative optimization to obtain the local optimal solution. Basically, for the five learning parameters, i.e. , , Ui,j, and , each update step learns one of them by fixing the rest. The algorithm details are described in Algorithm 1.
Fixing and , minimize L over Ui,j, and
Under the defined condition, objective function L only depends on Ui,j, , . For brevity in this subsection, we use U, Vf, Vd, Vf* and Vd* to represent Ui,j, , , and . Therefore, the new objective function can be simplified as:
| (12) |
First, we further fix Vf and Vd to update U. For a given subject i and time point j, we could take the derivative of L1 with respect to U.
| (13) |
Here, G′(U) is the derivative of U with respect to U. Given a step size l, we update U as . Then, we fix Vd and U to update Vf. The objective function in functional network part is related to Vf, thus the gradient of L1 with respect to Vf is:
| (14) |
Similarly, we update Vd with the same procedure as Vf,
| (15) |
Fixing Ui,j, and , minimize L over and
For brevity in this subsection, we use , , Vf* and Vd* to represent , , and . We observe that for each time j, the framework will generate a group-wise and . Therefore we can reorganize the objective function L to make it only relate to those two parameters, as below:
| (16) |
After updating all individual Ui, and , we could take the derivative of L2 with respect to Vf*.
| (17) |
For Vd*, an equality constraint (Vd*)TMVd* = I will regulate the gradient direction of L2 with respect to Vd*, which makes the solution difficult. Instead of directly finding an optimal direction with gradient descent on the surface described by original objective function, we construct the descent curves on the constraint-based Stiefel manifold [34]. Specifically, Vd* will be divided into two submatrixes , where is the free variable to be solved and is the fixed variable treated as constants. Then we rearrange the constraint as:
| (18) |
It is easy to conclude that M11 is a full rank positive definite matrix. Then a descent curve based on the previous Vd* will be constructed and it starts at the point which is the initial point for the line search on the generalized Stiefel manifold. Given the descending gradient at point P, we further project onto the tangent space of the Stiefel manifold by constructing a skew-symmetric matrix:
| (19) |
This will lead to a curve function Y(τ) by the Crank-Nicolson-like design as in the paper [70].
| (20) |
The above function gives a linear search procedure of updating point P by Pnew = Y(τ) for small τ which results sufficient decrease in L2. Finally, the next feasible will be given as:
| (21) |
Optimization of the variant models. In this study, different variants of the model are studied to test how each coupling term affects the outcome of the learning tasks. Their MP parameters, e.g., dimension P, are deliberately set to be the same as the proposed model MMLC. We find relatively similar patterns of MFCSMC and MFCSLC that both of them have a close performance to MMLC with larger P values, i.e., in high dimensional feature space. As we discussed in Sec. 4, the proposed MMLC enjoys better computational efficiency for high dimensional feature space. Meanwhile, sMFLC yields a relatively stable pattern as EigLC, which has no significant improvements by increasing P beyond 10. It is partially because the knowledge solely comes from the structural modality containing sparse connections. For the purpose of replicating our investigation, we provide the details on how to optimize these comparison algorithm as follows. Specifically, to optimize MFCSMC, in Algorithm 1, we skip steps in line 11–19 and update as in line 9. To optimize sMFLC, we skip steps in line 5,6,9 to avoid updates of , and . As for MFCSLC, we update and independently but keep the rest of Algorithm 1. For all algorithms, Their learning rates are all set as 1e − 5.
Footnotes
Data Availability
The datasets used in this study are all from Southwest University Longitudinal Imaging Multimodal Brain Data Repository (SLIM) [1]. The algorithm implementation source code is publicly available at http://gsl.lab.asu.edu/software/multimodal-longitudinal-brain-network-coupling.
Contributor Information
Wen Zhang, School of Computing, Informatics, and Decision Systems Engineering, Arizona State University, Tempe, AZ, USA.
B. Blair Braden, College of Health Solutions, Arizona State University, Tempe, AZ, USA.
Yalin Wang, School of Computing, Informatics, and Decision Systems Engineering, Arizona State University, P.O. Box 878809, Tempe, AZ 85287 USA.
References
- 1. http://fcon_1000.projects.nitrc.org/indi/retro/southwestuni_qiu_index.html .
- 2. https://fsl.fmrib.ox.ac.uk/fsl/fslwiki .
- 3. http://afni.nimh.nih.gov/afni .
- 4.Abdelnour F, Voss HU, Raj A: Network diffusion accurately models the relationship between structural and functional brain connectivity networks. Neuroimage 90, 335–347 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Absil PA, Mahony R, Sepulchre R: Optimization algorithms on matrix manifolds. Princeton University Press (2009) [Google Scholar]
- 6.Balconi M, Ferrari C: Repeated transcranial magnetic stimulation on dorsolateral prefrontal cortex improves performance in emotional memory retrieval as a function of level of anxiety and stimulus valence. Psychiatry Clin. Neurosci 67(4), 210–218 (2013) [DOI] [PubMed] [Google Scholar]
- 7.Bassett DS, Sporns O: Network neuroscience. Nature neuroscience 20(3), 353 (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Boutsidis C, Gallopoulos E: Svd based initialization: A head start for nonnegative matrix factorization. Pattern recognition 41(4), 1350–1362 (2008) [Google Scholar]
- 9.Cao B, He L, Wei X, Xing M, Yu PS, Klumpp H, Leow AD: t-BNE: Tensor-based brain network embedding. In: SIAM International Conference on Data Mining. SIAM (2017) [Google Scholar]
- 10.Cao B, Kong X, Zhang J, Yu PS, Ragin AB: Mining brain networks using multiple side views for neurological disorder identification. In: Proceedings of IEEE International Conference on Data Mining (ICDM) (2015) [Google Scholar]
- 11.Chang CC, Lin CJ: Libsvm: a library for support vector machines. ACM transactions on intelligent systems and technology (TIST) 2(3), 27 (2011) [Google Scholar]
- 12.Chen H, Li K, Zhu D, Jiang X, Yuan Y, Lv P, Zhang T, Guo L, Shen D, Liu T: Inferring group-wise consistent multimodal brain networks via multi-view spectral clustering. IEEE transactions on medical imaging 32(9), 1576–1586 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chung MK: Brain Network Analysis. Cambridge University Press (2019) [Google Scholar]
- 14.Cun L, Wang Y, Zhang S, Wei D, Qiu J: The contribution of regional gray/white matter volume in preclinical depression assessed by the Automatic Thoughts Questionnaire: a voxel-based morphometry study. Neuroreport 25(13), 1030–1037 (2014) [DOI] [PubMed] [Google Scholar]
- 15.Deco G, McIntosh AR, Shen K, Hutchison RM, Menon RS, Everling S, Hagmann P, Jirsa VK: Identification of optimal structural connectivity using functional connectivity and neural modeling. Journal of Neuroscience 34(23), 7910–7916 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Deco G, Ponce-Alvarez A, Mantini D, Romani GL, Hagmann P, Corbetta M: Resting-state functional connectivity emerges from structurally and dynamically shaped slow linear fluctuations. Journal of Neuroscience 33(27), 11239–11252 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dodero L, Gozzi A, Liska A, Murino V, Sona D: Group-wise functional community detection through joint laplacian diagonalization. In: MICCAI (2), pp. 708–715 (2014) [DOI] [PubMed] [Google Scholar]
- 18.Donzuso G, Cerasa A, Gioia MC, Caracciolo M, Quattrone A: The neuroanatomical correlates of anxiety in a healthy population: differences between the State-Trait Anxiety Inventory and the Hamilton Anxiety Rating Scale. Brain Behav 4(4), 504–514 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Du X, Luo W, Shen Y, Wei D, Xie P, Zhang J, Zhang Q, Qiu J: Brain structure associated with automatic thoughts predicted depression symptoms in healthy individuals. Psychiatry Res 232(3), 257–263 (2015) [DOI] [PubMed] [Google Scholar]
- 20.Eldén L: Matrix methods in data mining and pattern recognition. SIAM (2007) [Google Scholar]
- 21.Fan L, Li H, Zhuo J, Zhang Y, Wang J, Chen L, Yang Z, Chu C, Xie S, Laird AR, Fox PT, Eickhoff SB, Yu C, Jiang T: The Human Brainnetome Atlas: A New Brain Atlas Based on Connectional Architecture. Cereb. Cortex 26(8), 3508–3526 (2016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Giedd JN, Rapoport JL: Structural MRI of pediatric brain development: what have we learned and where are we going? Neuron 67(5), 728–734 (2010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gleason CE, Schmitz TW, Hess T, Koscik RL, Trivedi MA, Ries ML, Carlsson CM, Sager MA, Asthana S, Johnson SC: Hormone effects on fMRI and cognitive measures of encoding: importance of hormone preparation. Neurology 67(11), 2039–2041 (2006) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Greicius MD, Flores BH, Menon V, Glover GH, Solvason HB, Kenna H, Reiss AL, Schatzberg AF: Resting-state functional connectivity in major depression: abnormally increased contributions from subgenual cingulate cortex and thalamus. Biol. Psychiatry 62(5), 429–437 (2007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Guo W, Liu F, Xiao C, Zhang Z, Liu J, Yu M, Zhang J, Zhao J: Decreased insular connectivity in drug-naive major depressive disorder at rest. J Affect Disord 179, 31–37 (2015) [DOI] [PubMed] [Google Scholar]
- 26.Hao X, Xu D, Bansal R, Dong Z, Liu J, Wang Z, Kangarlu A, Liu F, Duan Y, Shova S, Gerber AJ, Peterson BS: Multimodal magnetic resonance imaging: The coordinated use of multiple, mutually informative probes to understand brain structure and function. Hum Brain Mapp 34(2), 253–271 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hecht D: Depression and the hyperactive right-hemisphere. Neurosci. Res 68(2), 77–87 (2010) [DOI] [PubMed] [Google Scholar]
- 28.Hedberg AG: Review of state-trait anxiety inventory. Professional Psychology 3(4), 389–390 (1972) [Google Scholar]
- 29.Hermundstad AM, Brown KS, Bassett DS, Amino EM, Frithsen A, Johnson A, Tipper CM, Miller MB, Grafton ST, Carlson JM: Structurally-constrained relationships between cognitive states in the human brain. PLoS computational biology 10(5), e1003591 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.van den Heuvel MP, Mandl RC, Kahn RS, Hulshoff Pol HE: Functionally linked resting-state networks reflect the underlying structural connectivity architecture of the human brain. Hum Brain Mapp 30(10), 3127–3141 (2009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hollon SD, Kendall PC: Cognitive self-statements in depression: Development of an automatic thoughts questionnaire. Cognitive Therapy and Research 4(4), 383–395 (1980). DOI 10.1007/BF01178214. URL 10.1007/BF01178214 [DOI] [Google Scholar]
- 32.Honey CJ, Kötter R, Breakspear M, Sporns O: Network structure of cerebral cortex shapes functional connectivity on multiple time scales. Proceedings of the National Academy of Sciences 104(24), 10240–10245 (2007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Horn A, Ostwald D, Reisert M, Blankenburg F: The structural–functional connectome and the default mode network of the human brain. Neuroimage 102, 142–151 (2014) [DOI] [PubMed] [Google Scholar]
- 34.Hwang SJ, Adluru N, Collins MD, Ravi SN, Bendlin BB, Johnson SC, Singh V: Coupled harmonic bases for longitudinal characterization of brain networks. In: Proc IEEE Comput Soc Conf Comput Vis Pattern Recognit, pp. 2517–2525 (2016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hwang SJ, Collins MD, Ravi SN, Ithapu VK, Adluru N, Johnson SC, Singh V: A projection free method for generalized eigenvalue problem with a nonsmooth regularizer. In: Proc IEEE Int Conf Comput Vis, pp. 1841–1849 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ironside M, Browning M, Ansari TL, Harvey CJ, Sekyi-Djan MN, Bishop SJ, Harmer CJ, O’Shea J: Effect of Prefrontal Cortex Stimulation on Regulation of Amygdala Response to Threat in Individuals With Trait Anxiety: A Randomized Clinical Trial. JAMA Psychiatry (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Isobe M, Miyata J, Hazama M, Fukuyama H, Murai T, Takahashi H: Multimodal neuroimaging as a window into the pathological physiology of schizophrenia: Current trends and issues. Neurosci. Res 102, 29–38 (2016) [DOI] [PubMed] [Google Scholar]
- 38.Jacobson S, Kelleher I, Harley M, Murtagh A, Clarke M, Blanchard M, Connolly C, O’Hanlon E, Garavan H, Cannon M: Structural and functional brain correlates of subclinical psychotic symptoms in 11–13 year old schoolchildren. Neuroimage 49(2), 1875–1885 (2010) [DOI] [PubMed] [Google Scholar]
- 39.Khundrakpam BS, Reid A, Brauer J, Carbonell F, Lewis J, Ameis S, Karama S, Lee J, Chen Z, Das S, Evans AC, Ball WS, Byars AW, Schapiro M, Bommer W, Carr A, German A, Dunn S, Rivkin MJ, Waber D, Mulkern R, Vajapeyam S, Chiverton A, Davis P, Koo J, Marmor J, Mrakotsky C, Robertson R, McAnulty G, Brandt ME, Fletcher JM, Kramer LA, Yang G, McCormack C, Hebert KM, Volero H, Botteron K, McKinstry RC, Warren W, Nishino T, Robert Almli C, Todd R, Constantino J, McCracken JT, Levitt J, Alger J, O’Neil J, Toga A, Asarnow R, Fadale D, Heinichen L, Ireland C, Wang DJ, Moss E, Zimmerman RA, Bintliff B, Bradford R, Newman J, Evans AC, Arnaoutelis R, Bruce Pike G, Louis Collins D, Leonard G, Paus T, Zijdenbos A, Das S, Fonov V, Fu L, Harlap J, Leppert I, Milovan D, Vins D, Zeffiro T, Van Meter J, Lange N, Froimowitz MP, Botteron K, Robert Almli C, Rainey C, Henderson S, Nishino T, Warren W, Edwards JL, Dubois D, Smith K, Singer T, Wilber AA, Pierpaoli C, Basser PJ, Chang LC, Koay CG, Walker L, Freund L, Rumsey J, Baskir L, Stanford L, Sirocco K, Gwinn-Hardy K, Spinella G, McCracken JT, Alger JR, Levitt J, O’Neill J: Developmental changes in organization of structural brain networks. Cereb. Cortex 23(9), 2072–2085 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Knight LK, Stoica T, Fogleman ND, Depue BE: Convergent Neural Correlates of Empathy and Anxiety During Socioemotional Processing. Front Hum Neurosci 13, 94 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kong X, Yu PS: Brain network analysis: a data mining perspective. ACM SIGKDD Explorations Newsletter 15(2), 30–38 (2014) [Google Scholar]
- 42.Koseki S, Noda T, Yokoyama S, Kunisato Y, Ito D, Suyama H, Matsuda T, Sugimura Y, Ishihara N, Shimizu Y, Nakazawa K, Yoshida S, Arima K, Suzuki S: The relationship between positive and negative automatic thought and activity in the prefrontal and temporal cortices: a multi-channel near-infrared spectroscopy (NIRS) study. J Affect Disord 151(1), 352–359 (2013) [DOI] [PubMed] [Google Scholar]
- 43.Krzywinski M, Schein J, Birol I, Connors J, Gascoyne R, Horsman D, Jones SJ, Marra MA: Circos: an information aesthetic for comparative genomics. Genome research 19(9), 1639–1645 (2009). DOI 10.1101/gr.092759.109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Martin EI, Ressler KJ, Binder E, Nemeroff CB: The neurobiology of anxiety disorders: brain imaging, genetics, and psychoneuroendocrinology. Clin. Lab. Med 30(4), 865–891 (2010) [DOI] [PubMed] [Google Scholar]
- 45.McIntosh AR, Lobaugh NJ: Partial least squares analysis of neuroimaging data: applications and advances. Neuroimage 23, S250–S263 (2004) [DOI] [PubMed] [Google Scholar]
- 46.Meier J, Tewarie P, Hillebrand A, Douw L, van Dijk BW, Stufflebeam SM, Van Mieghem P: A Mapping Between Structural and Functional Brain Networks. Brain Connect 6(4), 298–311 (2016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Mesulam M: Brain, mind, and the evolution of connectivity. Brain Cogn 42(1), 4–6 (2000) [DOI] [PubMed] [Google Scholar]
- 48.Miguel-Hidalgo JJ: Brain structural and functional changes in adolescents with psychiatric disorders. International journal of adolescent medicine and health 25(3), 245–256 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ng B, Varoquaux G, Poline JB, Thirion B: A novel sparse graphical approach for multimodal brain connectivity inference. MICCAI pp. 707–714 (2012) [DOI] [PubMed] [Google Scholar]
- 50.Nie J, Li G, Shen D: Development of cortical anatomical properties from early childhood to early adulthood. Neuroimage 76, 216–224 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Osmanlıoğlu Y, Tunç B, Parker D, Elliott MA, Baum GL, Ciric R, Satterthwaite TD, Gur RE, Gur RC, Verma R: System-level matching of structural and functional connectomes in the human brain. NeuroImage 199, 93–104 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Paquette V, Beauregard M, Beaulieu-Prevost D: Effect of a psychoneurotherapy on brain electromagnetic tomography in individuals with major depressive disorder. Psychiatry Res 174(3), 231–239 (2009) [DOI] [PubMed] [Google Scholar]
- 53.Park HJ, Friston K: Structural and functional brain networks: from connections to cognition. Science 342(6158), 1238411 (2013) [DOI] [PubMed] [Google Scholar]
- 54.Pompili F, Gillis N, Absil PA, Glineur F: Two algorithms for orthogonal nonnegative matrix factorization with application to clustering. Neurocomputing 141, 15–25 (2014) [Google Scholar]
- 55.Revest JM, Dupret D, Koehl M, Funk-Reiter C, Grosjean N, Piazza PV, Abrous DN: Adult hippocampal neurogenesis is involved in anxiety-related behaviors. Mol. Psychiatry 14(10), 959–967 (2009) [DOI] [PubMed] [Google Scholar]
- 56.Rusch BD, Abercrombie HC, Oakes TR, Schaefer SM, Davidson RJ: Hippocampal morphometry in depressed patients and control subjects: relations to anxiety symptoms. Biol. Psychiatry 50(12), 960–964 (2001) [DOI] [PubMed] [Google Scholar]
- 57.Shen K, Bezgin G, Hutchison RM, Gati JS, Menon RS, Everling S, McIntosh AR: Information processing architecture of functionally defined clusters in the macaque cortex. Journal of Neuroscience 32(48), 17465–17476 (2012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sherman LE, Rudie JD, Pfeifer JH, Masten CL, McNealy K, Dapretto M: Development of the default mode and central executive networks across early adolescence: a longitudinal study. Dev Cogn Neurosci 10, 148–159 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Singh AP, Gordon GJ: Relational learning via collective matrix factorization. In: SIGKDD, pp. 650–658. ACM; (2008) [Google Scholar]
- 60.Skudlarski P, Jagannathan K, Calhoun VD, Hampson M, Skudlarska BA, Pearlson G: Measuring brain connectivity: diffusion tensor imaging validates resting state temporal correlations. Neuroimage 43(3), 554–561 (2008) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Sporns O: Structure and function of complex brain networks. Dialogues in clinical neuroscience 15(3), 247 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Staempfli P, Reischauer C, Jaermann T, Valavanis A, Kollias S, Boesiger P: Combining fMRI and DTI: a framework for exploring the limits of fMRI-guided DTI fiber tracking and for verifying DTI-based fiber tractography results. Neuroimage 39(1), 119–126 (2008) [DOI] [PubMed] [Google Scholar]
- 63.Stam C, Van Straaten E, Van Dellen E, Tewarie P, Gong G, Hillebrand A, Meier J, Van Mieghem P: The relation between structural and functional connectivity patterns in complex brain networks. International Journal of Psychophysiology 103, 149–160 (2016) [DOI] [PubMed] [Google Scholar]
- 64.Strasser A, Xin L, Gruetter R, Sandi C: Nucleus accumbens neurochemistry in human anxiety: A 7 T 1H-MRS study. Eur Neuropsychopharmacol 29(3), 365–375 (2019) [DOI] [PubMed] [Google Scholar]
- 65.Sui J, Huster R, Yu Q, Segall JM, Calhoun VD: Function-structure associations of the brain: evidence from multimodal connectivity and covariance studies. Neuroimage 102 Pt 1, 11–23 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Supekar K, Menon V, Rubin D, Musen M, Greicius MD: Network analysis of intrinsic functional brain connectivity in alzheimer’s disease. PLoS computational biology 4(6), e1000100 (2008) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Tadayonnejad R, Ajilore O: Brain network dysfunction in late-life depression: a literature review. Journal of geriatric psychiatry and neurology 27(1), 5–12 (2014) [DOI] [PubMed] [Google Scholar]
- 68.Venkataraman A, Rathi Y, Kubicki M, Westin CF, Golland P: Joint modeling of anatomical and functional connectivity for population studies. IEEE transactions on medical imaging 31(2), 164–182 (2012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Wang C, Ng B, Abugharbieh R: Multimodal brain subnetwork extraction using provincial hub guided random walks. In: International Conference on Information Processing in Medical Imaging, pp. 287–298. Springer (2017) [Google Scholar]
- 70.Wen Z, Yin W: A feasible method for optimization with orthogonality constraints. Mathematical Programming 142(1–2), 397–434 (2013) [Google Scholar]
- 71.Wu JC, Buchsbaum MS, Hershey TG, Hazlett E, Sicotte N, Johnson JC: PET in generalized anxiety disorder. Biol. Psychiatry 29(12), 1181–1199 (1991) [DOI] [PubMed] [Google Scholar]
- 72.Wu X, Lin P, Yang J, Song H, Yang R, Yang J: Dysfunction of the cingulo-opercular network in first-episode medication-naive patients with major depressive disorder. J A ect Disord 200, 275–283 (2016) [DOI] [PubMed] [Google Scholar]
- 73.Young KA, Holcomb LA, Yazdani U, Hicks PB, German DC: Elevated neuron number in the limbic thalamus in major depression. Am J Psychiatry 161(7), 1270–1277 (2004) [DOI] [PubMed] [Google Scholar]
- 74.Zhang W, Wang J, Fan L, Zhang Y, Fox PT, Eickhoff SB, Yu C, Jiang T: Functional organization of the fusiform gyrus revealed with connectivity profiles. Hum Brain Mapp 37(8), 3003–3016 (2016) [DOI] [PMC free article] [PubMed] [Google Scholar]


