c-CSN: Single-cell RNA Sequencing Data Analysis by Conditional Cell-specific Network

Abstract

The rapid advancement of single-cell technologies has shed new light on the complex mechanisms of cellular heterogeneity. However, compared to bulk RNA sequencing (RNA-seq), single-cell RNA-seq (scRNA-seq) suffers from higher noise and lower coverage, which brings new computational difficulties. Based on statistical independence, cell-specific network (CSN) is able to quantify the overall associations between genes for each cell, yet suffering from a problem of overestimation related to indirect effects. To overcome this problem, we propose the c-CSN method, which can construct the conditional cell-specific network (CCSN) for each cell. c-CSN method can measure the direct associations between genes by eliminating the indirect associations. c-CSN can be used for cell clustering and dimension reduction on a network basis of single cells. Intuitively, each CCSN can be viewed as the transformation from less “reliable” gene expression to more “reliable” gene–gene associations in a cell. Based on CCSN, we further design network flow entropy (NFE) to estimate the differentiation potency of a single cell. A number of scRNA-seq datasets were used to demonstrate the advantages of our approach. 1) One direct association network is generated for one cell. 2) Most existing scRNA-seq methods designed for gene expression matrices are also applicable to c-CSN-transformed degree matrices. 3) CCSN-based NFE helps resolving the direction of differentiation trajectories by quantifying the potency of each cell. c-CSN is publicly available at https://github.com/LinLi-0909/c-CSN.

Introduction

With the development of high-throughput single-cell RNA sequencing (scRNA-seq), novel cell populations in complex tissues [1], [2], [3], [4], [5] can be identified and the differentiation trajectory of cell states [6], [7], [8] can be obtained, which opens a new way to understand the heterogeneity and transition of cells [9], [10], [11]. However, compared to traditional bulk RNA-seq data, the prevalence of high technical noise and dropout events is a major problem in scRNA-seq [12], [13], [14], [15], [16], [17], which raises substantial challenges for data analysis. To analyze high-dimensional scRNA-seq data, principal component analysis (PCA), nonnegative matrix factorization (NMF), and t-distributed Stochastic Neighbor Embedding (t-SNE) are widely used for dimension reduction. Subsequently, clustering methods such as hierarchical clustering, K-means, SNN-Cliq [18], Corr [19], SC3 [20], and SIMLR [21] could be applied to identify potential cell types, further corroborated with known marker genes. For developmental or differentiation studies, trajectory inference methods such as Monocle [22], TSCAN [23], and DPT [24] can be used to order cells along a pseudo temporal trajectory. Besides these approaches, several methods have been developed to offer special treatments of the dropouts in scRNA-seq data. One way is to explicitly model the dropout events during dimension reduction, e.g., the zero-inflated factor analysis model developed in ZIFA [25]. Another way is to incorporate biological information, especially functional gene–gene association networks. In this direction, SCRL [26] takes another step forward by leveraging gene–gene interactions, learning a more meaningful low-dimensional projection. A recent method, netNMF-sc [27] derives a robust factorization or clustering against dropouts, by regularizing the original NMF model with a given gene correlation network. Furthermore, gene–gene correlations could also be employed to directly estimate the ‘true’ expression values for those observed zero counts, which is known as the data imputation approach, as exemplified by several well-known methods including SAVER [28], MAGIC [29], and scImpute [30]. However, data imputation is with some limitations, such as over-imputation of genes unexpressed in certain cell types and inducing artificial effects that may confound downstream analyses [31].

Several network inference algorithms were also developed for scRNA-seq. MTGO-SC [32] can detect the network modules of genes for each cell cluster though combing the information of network structures and annotations of genes. SCODE [33] can construct regulatory networks and expression dynamics through linear ordinary differential equations (ODEs). These methods only infer the network of a group or cluster of cells, and do not construct networks for individual cells. Recently, cell-specific network (CSN) has been proposed to infer CSNs based on scRNA-seq data [34], which elegantly infers a network for each cell. Moreover, unlike imputation methods, CSN employs a data transformation strategy, and successfully transforms the noisy and “unreliable” gene expression data to the more “reliable” gene association data, thereby alleviating the dropout problem to a certain extent. The network degree matrix (NDM) derived from CSN can be further applied in downstream single-cell analyses, which performs better than traditional expression-based methods in terms of robustness and accuracy. CSN is able to identify the dependency between two genes from single-cell data based on statistical independence. However, CSN suffers from a problem of overestimation on gene–gene associations and includes both direct and indirect associations due to interactive effects from other genes in a network. In other words, a gene pair without direct association can be falsely identified to have a link just because they both have true associations with some other genes. Thus, the gene–gene network of a cell constructed by CSN may be much denser than the real molecular network in this cell, in particular when there are many complex associations among genes.

To overcome these shortcomings of CSN, we introduce a novel computational method c-CSN, which can construct a conditional cell-specific network (CCSN) from scRNA-seq data. Specifically, c-CSN identifies direct associations between genes by filtering out indirect associations in the gene–gene network based on conditional independence. Thus, c-CSN can transform the original gene expression data of each cell to the direct and robust gene–gene association data (or network data) of the same cell. In this study, we first demonstrate that the transformed gene–gene association data not only are fully compatible with traditional analyses such as dimension reduction and clustering, but also enable us to delineate the CSN topology and its dynamics along developmental trajectories. Then, by defining the network flow entropy (NFE) on the gene–gene association data of each cell based on c-CSN, we estimate the differentiation potency of individual cells. We show that NFE can illustrate the lineage dynamics of cell differentiation by quantifying the differentiation potency of cells, which is also one of the most challenging tasks in developmental biology.

Method

Assume that x and y are two random variables, and z is the third random variable. If x and y are independent, then

$$p\left(x\right)p\left(y\right)=p(x,y)$$ (1)

where $p(x,y)$ is the joint probability distribution of x and y; $p\left(x\right)$ and $p\left(y\right)$ are the marginal probability distributions of x and y, respectively.

If x and y with the condition z are conditionally independent, then

$$p\left(x|z\right)p\left(y|z\right)=p\left(x,y|z\right)$$ (2)

where $p(x,y|z)$ is the joint probability distribution of x and y with the condition z, $p\left(x\right|z)$ and $p\left(y\right|z)$ are conditionally marginal probability distributions. Note that Equations (1), (2) are both necessary and sufficient conditions on mutual independence and conditional independence, respectively. Here, we define

$${\rho }_{\mathit{xy}}=p\left(x,y\right)-p\left(x\right)p\left(y\right)$$ (3)

$${\rho }_{\mathit{xy}|z}=p\left(x,y|z\right)-p\left(x|z\right)p\left(y\right|z)$$ (4)

The original CSN method uses ${\rho }_{\mathit{xy}}$ to distinguish the independency and association between x and y (File S1 Note 1). However, if two independent variables x and y are both associated with a third random variable z, ${\rho }_{\mathit{xy}}$ cannot measure the direct independency because there is an indirect association between x and y. In other words, the associations defined by CSN or Equation (3) include both direct and indirect dependencies, thus resulting in the overestimation on gene–gene associations. To overcome this problem of CSN, we develop a novel method, c-CSN, which measures the direct gene–gene associations based on the conditional independency ${\rho }_{\mathit{xy}|z}$, i.e., Equation (4), by filtering out the indirect associations in the reconstructed network. The computational framework of c-CSN is shown in Figure 1, and the method is described in next sections.

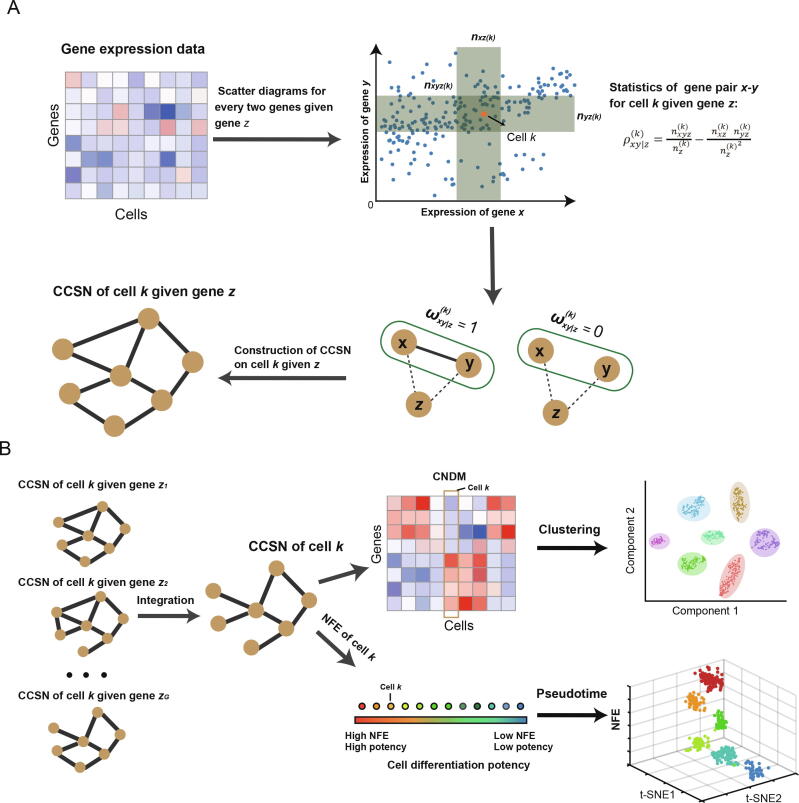
Figure 1.

Overview of c-CSN method

A. The CCSN of each cell, e.g., cell k, is constructed given a conditional gene z using gene expression data. For every two genes, e.g., gene x and gene y, we use the statistics ${\rho }_{\mathit{xy}|z}^{\left(k\right)}$ to measure whether gene x and gene y are conditionally independent given gene z. If gene x and gene y are directly dependent (${\omega }_{\mathit{xy}|z}^{\left(k\right)}=1$), there is an edge between gene x and gene y in CCSN of cell k given gene z. Otherwise, there is no edge between gene x and gene y in CCSN of cell k given gene z. B. Construction of CCSNs of cell k given conditional gene $z_i$ (i = 1, 2, 3,$\cdots$,G). These CCSNs of cell k given conditional gene $z_i$ (i = 1, 2, 3,$\cdots$,G) can be integrated into a CCSN of cell k. On the one hand, CCSN of cell k can be applied to compute NFE of cell k. The pseudotime of cells can be obtained based on NFE of cells. On the other hand, CNDM can be calculated by obtaining the CCSN of each cell. The CNDM can be further applied to clustering analysis. CCSN, conditional cell-specific network; CNDM, conditional network degree matrix; NFE, network flow entropy; t-SNE, t-distributed Stochastic Neighbor Embedding.

Probability distribution estimation

We numerically estimate the value of ${\rho }_{\mathit{xy}|z}$ by making a scatter diagram based on gene expression data. Suppose there are m genes and n cells in the data. We depict the expression values of gene x, gene y, and the conditional gene z in a three-dimensional space (Figure S1A–G), where each dot represents one cell. First, we draw two parallel planes which are orthogonal with z axis near the dot k to represent the upper and lower bounds of the neighborhoods of $z_k$. And the number of dots in the space between the two parallel planes (i.e., the neighborhood of $z_k$) is $n_z^{\left(k\right)}$ (Figure S1D). Now we get a subspace on condition of gene z. Then, we draw other four planes near the dot k, where two planes are orthogonal with x axis and the other two planes are orthogonal with y axis. We can get the neighborhoods of $\left(x_k,z_k\right)$, $\left(y_k,z_k\right)$, and $\left(x_k,{y_k,z}_k\right)$ according to the intersection space of six planes (Figure S1E–G), where the numbers of dots are $n_{\mathit{xz}}^{\left(k\right)}$, $n_{\mathit{yz}}^{\left(k\right)}$, and $n_{\mathit{xyz}}^{\left(k\right)}$, respectively. Then, we can get the estimation of probability distributions:

$$p^{\left(k\right)}\left(x,y|z\right)\approx \frac{n_{\mathit{xyz}}^{\left(k\right)}}{n_z^{\left(k\right)}},p^{\left(k\right)}\left(x|z\right)\approx \frac{n_{\mathit{xz}}^{\left(k\right)}}{n_z^{\left(k\right)}},p^{\left(k\right)}\left(y|z\right)\approx \frac{n_{\mathit{yz}}^{\left(k\right)}}{n_z^{\left(k\right)}}$$

Based on Equation (4), we construct a statistic

$${\rho }_{\mathit{xy}|z}^{\left(k\right)}=\frac{n_{\mathit{xyz}}^{\left(k\right)}}{n_z^{\left(k\right)}}-\frac{n_{\mathit{xz}}^{\left(k\right)}{n}_{\mathit{yz}}^{\left(k\right)}}{{n_z^{\left(k\right)}}^2}$$ (5)

to measure the conditional independence between gene x and gene y on the condition of gene z in cell k. And when gene x and gene y given gene z are conditionally independent, the expectation ${\mu }_{\mathit{xy}|z}^{\left(k\right)}$ and standard deviation ${\sigma }_{\mathit{xy}|z}^{\left(k\right)}$ (File S1) of the statistic ${\rho }_{\mathit{xy}|z}^{\left(k\right)}$ can be obtained:

$${\mu }_{\mathit{xy}|z}^{\left(k\right)}=0$$

$${\sigma }_{\mathit{xy}|z}^{\left(k\right)}=\sqrt{\frac{n_{\mathit{xz}}^{\left(k\right)}{n}_{\mathit{yz}}^{\left(k\right)}.\left(n_z^{\left(k\right)}-n_{\mathit{xz}}^{\left(k\right)}\right).(n_z^{\left(k\right)}-n_{\mathit{yz}}^{\left(k\right)})}{{n_z^{\left(k\right)}}^4\left(n_z^{\left(k\right)}-1\right)}}$$

Then, we normalize the statistic as

$${\widehat{\rho }}_{\mathit{xy}|z}^{\left(k\right)}=\frac{{\rho }_{\mathit{xy}|z}^{\left(k\right)}-{\mu }_{\mathit{xy}|z}^{\left(k\right)}}{{\sigma }_{\mathit{xy}|z}^{\left(k\right)}}$$ (6)

If gene x and y are conditionally independent on the condition of gene z, it can be proved that the normalized statistic follows the standard normal distribution (File S1 Note 1; Figure S2), and it is less than or equal to 0 when gene x and y are conditionally independent (File S1 Note 2).

Construction of CCSN

To estimate the conditional independency of gene x and gene y given the conditional gene z in cell k, we first use CSN or Equation (3) to distinguish the independence of gene x and gene y and we then use the following hypothesis test. $H_0\left(\mathrm{null}\mathrm{hypothesis}\right)$: gene x and gene y are conditionally independent given gene z in cell k. $H_1\left(\mathrm{alternative}\mathrm{hypothesis}\right)$: gene x and gene y are conditionally dependent given gene z in cell k. If ${\widehat{\rho }}_{\mathit{xy}|z}^{\left(k\right)}$, the normalized statistic, is larger than ${\mathcal{N}}_{\alpha }$ (significance level $\alpha$, ${\mathcal{N}}_{\alpha }$ is the alpha quantile of the standard normal distribution), the null hypothesis will be rejected and then ${\omega }_{\mathit{xy}|z}^{\left(k\right)}=1$ (${\omega }_{\mathit{xy}|z}^{\left(k\right)}$ is the edge weight of genes x and y on condition of gene z).

$${\omega }_{\mathit{xy}|z}^{\left(k\right)}=\left\{\begin{array}{c}1\\ 0\end{array}\frac{\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{es}x\mathrm{a}\mathrm{n}\mathrm{d}y\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{l}\mathrm{y}\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{g}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{e}z}{\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{es}x\mathrm{a}\mathrm{n}\mathrm{d}y\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{y}\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{g}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{e}z}\right)$$ (7)

All gene pairs can be tested if they are conditionally independent given gene z in cell k. And the CCSN $C_z^{\left(k\right)}$ given conditional gene z is obtained for cell k.

Then, to estimate the direct association between a pair of genes in a cell, theoretically we should use all the remaining m − 2 genes as conditional genes, which is computationally intensive. Suppose there are m genes in our analysis, then m$\times$(m − 1)/2 gene pairs should be tested. Fortunately, a molecular network is generally sparse, which means that a pair of genes (i.e., genes x and y) are expected to have a very small number of commonly interactive genes (as conditional genes z). In other words, numerically we can use a small number of conditional genes to identify the direct association between a pair of genes in a cell, which can significantly reduce the computational cost (File S1 Note 3; Table S1). For each gene pair in a cell, we choose G (1 ≤ G ≤ m − 2) genes as the conditional genes to test if the gene pair is conditionally independent or not. Generally, the conditional genes may be the key regulatory genes in a biological process, such as transcription factor genes and kinase genes. From a network viewpoint, these genes are usually hub genes in the gene–gene network, and the network degrees of these genes would be higher.

Practically, the conditional genes could be obtained from many available methods, such as highly expressed genes, highly variable genes, key transcription factor genes, and the hub genes in the CSN. For the c-CSN method, the conditional gene sets were defined by CSN. Two steps were used to obtain the conditional genes although other appropriate schemes can also be used.

• 1)For a given cell, we first construct a CSN without the consideration of conditional genes, where the edge between gene x and gene y in cell k is determined by the following hypothesis test:

• ${\mathit{H}}_{\text{0}}\left(\text{null hypothesis}\right)$: gene x and gene y are independent in cell k.

• ${\mathit{H}}_{\text{1}}\text{(alternative hypothesis)}$: gene x and gene y are dependent in cell k.

• The statistic ${\rho }_{\mathit{xy}}$ can be used to measure the independency of genes x and y (File S1 Note 1). If ${\rho }_{\mathit{xy}}$ is larger than a significant level, we will reject the null hypothesis and ${\mathit{edge}}_{\mathit{xy}}^{\left(k\right)}$ = 1, otherwise ${\mathit{edge}}_{\mathit{xy}}^{\left(k\right)}$ = 0.

$${\mathit{edge}}_{\mathit{xy}}^{\left(k\right)}=\left\{\begin{array}{c}1\\ 0\end{array}\frac{\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{s}x\mathrm{a}\mathrm{n}\mathrm{d}y\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}}{\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{s}x\mathrm{a}\mathrm{n}\mathrm{d}y\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}}\right)$$

Then we use ${\mathit{D}}_{\mathit{z}}^{\text{(}\mathit{k}\text{)}}$ to measure the importance of conditional gene z in cell k:

$$D_z^{\left(k\right)}=\sum _{y=1,y\ne z}^{M}edg{e}_{\mathit{zy}}^{\left(k\right)}$$ (8)

Equation (8) means that if a gene is connected to more other genes, this gene is more important.

• 2)For a given cell k, we choose the top $G\left(G\ge 1\right)$ largest ‘importance’ genes as the conditional genes. We assume that the conditional gene set is $\left\{z_g,g=1,2,3,\cdots ,G\right\}$, and CCSN $C_{z_g}^{\left(k\right)}$ is obtained for cell k given conditional gene $z_g$. The CCSNs of the cell k on the condition of gene set $\left\{z_g,g=1,2,3,\cdots ,G\right\}$ are {$C_{z_1}^{\left(k\right)}$,$C_{z_2}^{\left(k\right)},{\cdots ,C}_{z_G}^{\left(k\right)}$}. Then, we use

$${\stackrel{-}{C}}_k=\frac{1}{G}\sum _{g=1}^G{C}_{z_g}^{\left(k\right)}=\left(c_{\mathit{ij}}^{\left(k\right)}\right)$$ (9)

to represent the degrees of gene–gene interaction network of cell k, where $c_{\mathit{ij}}^{\left(k\right)}$ for $i,j=1,\cdots ,m$ is the (i, j) element of the matrix ${\stackrel{-}{C}}_k$.

For scRNA-seq data with all n cells, we can construct n CCSNs, which can be used for further dimension reduction and clustering. In other words, instead of the originally measured gene expression data with n cells, we use the n transformed CCSNs for further analysis.

Network degree matrix from CCSN

CCSN could be used for various biological studies by exploiting the gene–gene conditional association network from a network viewpoint. We transform Equation (9) to a conditional network degree vector based on the following transformation

$$v_{\mathit{ik}}=\sum _{j=1}^m{c}_{\mathit{ij}}^{\left(k\right)}$$ (10)

Then, for ${\{\stackrel{-}{C}}_1,{\stackrel{-}{C}}_2,\cdots ,{\stackrel{-}{C}}_n\}$, an m × n matrix conditional network degree matrix (CNDM) is obtained.

$$\mathit{CNDM}=\left(v_{\mathit{ik}}\right)\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}i=1,\cdots ,m;k=1,\cdots ,n$$ (11)

The matrix has the same dimension with the gene expression matrix (GEM), i.e., GEM = $\left(x_{\mathit{ik}}\right)$ (with i = 1,⋯,m; k = 1,⋯,n), but CNDM can reflect the gene–gene direct association in terms of interaction degrees. Moreover, this CNDM matrix after normalization could be further analyzed by most traditional scRNA-seq methods for dimension reduction and clustering analysis. The input/output settings as well as application fields of our c-CSN method are listed in File S1 Note 4.

Network analysis of c-CSN

The relationship between gene pairs can be obtained by c-CSN at a single-cell level. c-CSN also provides a new way to build gene–gene interaction network for each cell. And the CNDM derived from CCSNs can be further used in dimension reduction, clustering and NFE analysis by many existing methods.

Dimension reduction

We used PCA [35] and t-SNE [36] which respectively represent linear and nonlinear methods, to perform dimension reduction on public scRNA-seq datasets with known cell types.

Clustering

To validate the good performance of c-CSN in clustering analysis, several traditional clustering methods such as K-means, Hierarchical clustering analysis, and K-medoids were applied to clustering analysis. Furthermore, state-of-the-art scRNA-seq data clustering methods such as SC3, SIMLR, and Seurat [20], [21], [37] were also used for comparison.

NFE analysis

Quantifying the differentiation potency of a single cell is one of the important tasks in scRNA-seq studies [15], [38], [39]. A recent study developed SCENT [40], which uses protein–protein interaction (PPI) network and gene expression data as input to obtain the potency of cells. However, SCENT depends on the PPI network, which may ignore many important relationships between genes in specific cells. In this study, we developed NFE to estimate the differentiation potency of a cell from its CSN or CCSN, which is constructed for each cell. The normalized gene expression profile and CSN/CCSN are used when we compute the NFE. The value of NFE is expected to be lower for differentiated cells, since differentiation is accompanied by activation of a specific subnetwork, which actually diverts the signaling flux from other parts of the network.

Estimating NFE requires a background network, which could be provided by CSN or CCSN. Based on CSN or CCSN, we could know whether or not there is an edge between gene i and gene j. We assume that the weight of an edge between gene i and gene j, $p_{\mathit{ij}}$, is proportional to the normalized expression levels of gene i and gene j, that is $p_{\mathit{ij}}\propto x_i{x}_j$ with ${\sum }_{j=1}^m{p}_{\mathit{ij}}=1$. These weights are interpreted as interaction probabilities. Then, we normalize the weighted network as a stochastic matrix, P = ${(p}_{\mathit{ij}})$ with

$$p_{\mathit{ij}}=\frac{x_j}{\sum _{k\in E\left(i\right)}{x}_k}=\frac{x_j}{{\left(Ax\right)}_i}\mathrm{f}\mathrm{o}\mathrm{r}i,j=1,\cdots ,m$$

where $E\left(i\right)$ contains the neighbors of gene i, and A is the CSN or CCSN ($A_{\mathit{ij}}=1$ if i and j are connected, otherwise $A_{\mathit{ij}}=0$).

And then, we define the NFE as:

$$\mathit{NFE}=-{\sum }_{i,j}{x}_i{p}_{\mathit{ij}}\mathrm{l}\mathrm{o}\mathrm{g}\left(x_i{p}_{\mathit{ij}}\right)$$ (12)

where $x_i$ is the normalized gene expression of gene i. From the definition, NFE is clearly different from network entropy.

Datasets used

Twelve scRNA-seq datasets and one bulk RNA-seq dataset [15], [40], [41], [42], [43], [44], [45], [46], [47] were used to validate our c-CSN method. The number of cells in these datasets ranges from 100 to 20,000. Table S2 gives a brief introduction of these datasets.

Results and discussion

Visualization and clustering of scRNA-seq datasets with CNDM

Characterizing cell heterogeneity is one of the important tasks for scRNA-seq data analysis. To test whether CCSN-transformed network data can help segregate cell types, we performed dimension reduction and clustering on the CNDMs of gold-standard scRNA-seq datasets, using algorithms widely employed in scRNA-seq studies. The numbers of conditional genes used in CCSN construction are listed in Table S2.

For visualizing the structure of these datasets in a two-dimensional space, we used the representative linear and nonlinear dimension reduction methods, PCA [48] and t-SNE [36], respectively. As shown in Figure 2 and Figure S3, CNDMs can separate different cell types clearly in the low-dimensional space by both PCA and t-SNE. Notably, they generally perform even better than GEM (Figure 2, Figure S3). Hence, the network data of CNDMs contain sufficient information for separating cell types in scRNA-seq datasets.

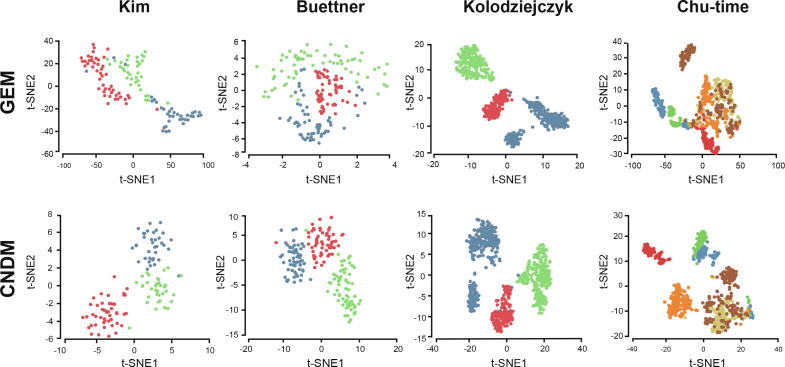
Figure 2.

Comparison of traditional GEM and CNDM on visualization

GEM (top panel) and CNDM (bottom panel) are benchmarked for visualizing four scRNA-seq datasets (Kim [43], Buettner [15], Kolodziejczyk [41], and Chu-time [42]) with t-SNE. Different colors represent different cell types. GEM, gene express matrix.

To quantitatively evaluate the power of CNDMs in cell type identification, we performed clustering on CNDMs and computed the adjusted Rand index (ARI) for each dataset based on the background truth (File S1 Note 5; Figure S4). As shown in Table 1 and Figure S5, CNDM performs obviously better than GEM on all datasets. These provide a strong support of the notion that the CCSN-transformed network data are highly informative for characterizing single-cell populations. Interestingly, when further compared to NDM, CNDM also shows a good performance (Table 2; Figure S6).

Table 1.

Performance comparison of CNDM and GEM in clustering of scRNA-seq data

Method	Input	Buettner[15]	Kolodziejczyk[41]	Gokce[46]	Chu-time[42]	Chu-type[42]	Kim[43]
K-means	GEM	0.29	0.54	0.42	0.17	0.22	0.20
	CNDM	0.87	0.85	0.75	0.45	0.57	0.81
Hierarchical	GEM	0.32	0.49	0.47	0.22	0.22	0.12
	CNDM	0.73	0.65	0.92	0.47	0.61	0.77
K-means (t-SNE)	GEM	0.41	0.87	0.43	0.33	0.55	0.53
	CNDM	0.95	0.91	0.36	0.56	0.70	0.93
Hierarchical (t-SNE)	GEM	0.55	0.99	0.50	0.39	0.67	0.73
	CNDM	0.95	0.99	0.39	0.61	0.80	0.95
K-medoids	GEM	0.23	0.29	0.40	0.33	0.33	0.79
	CNDM	0.53	0.63	0.81	0.17	0.38	0.61
SC3	GEM	0.89	1	0.56	0.66	0.78	0.89
	CNDM	0.98	0.72	0.72	0.63	0.98	0.96
SIMLR	GEM	0.89	0.49	0.43	0.30	0.48	0.38
	CNDM	0.63	0.52	0.85	0.58	0.54	0.95
Seurat	GEM	0.67	0.43	0.35	0.52	0.52	0.41
	CNDM	0.90	0.56	0.32	0.56	0.69	0.84

Note: The performance of clustering is evaluated by ARI. Hierarchical (t-SNE) and K-means (t-SNE) indicate clustering after t-SNE. CNDM, conditional network degree matrix; GEM, gene expression matrix; ARI, adjusted Rand index; t-SNE, t-distributed Stochastic Neighbor Embedding. Bold font (ARI) indicates that CNDM performs better.

Table 2.

Performance comparison of CNDM and NDM in clustering of scRNA-seq data

Method	Input	Buettner[15]	Kim[43]	Wang[45]	Gokce[46]	Tabula Muris[47](aorta)	Tabula Muris[47](limb muscle)
K-means	NDM	0.50	0.50	0.30	0.79	0.21	0.58
	CNDM	0.87	0.81	0.45	0.75	0.63	0.66
Hierarchical	NDM	0.69	0.59	0.38	0.95	0.12	0.65
	CNDM	0.73	0.77	0.45	0.92	0.75	0.76
K-means (t-SNE)	NDM	0.83	0.84	0.61	0.38	0.46	0.62
	CNDM	0.95	0.93	0.67	0.36	0.61	0.65
Hierarchical (t-SNE)	NDM	0.89	0.98	0.58	0.47	0.50	0.66
	CNDM	0.95	0.95	0.72	0.39	0.50	0.66
K-medoids	NDM	0.26	0.49	0.31	0.60	0.35	0.14
	CNDM	0.53	0.61	0.21	0.81	0.53	0.39
SC3	NDM	0.67	1	0.70	0.45	0.29	0.66
	CNDM	0.98	0.96	0.86	0.72	0.73	0.76
SIMLR	NDM	0.64	0.75	0.29	0.74	0.40	0.60
	CNDM	0.63	0.95	0.60	0.85	0.70	0.71
Seurat	NDM	0.82	0.97	0.59	0.44	0.45	0.66
	CNDM	0.90	0.84	0.59	0.32	0.76	0.75

Note: The performance of clustering is evaluated by ARI. Hierarchical (t-SNE) and K-means (t-SNE) indicate clustering after t-SNE. NDM, network degree matrix. Bold font (ARI) indicates that CNDM performs better.

We further evaluated the performance of c-CSN in larger datasets. The Tabula Muris droplet1 dataset [47] comprising more than 20,000 cells from three tissues (bladder, trachea, and spleen) were tested. The Seurat package was used to perform dimension reduction and clustering analysis on the CNDM [37]. The cells were clearly segregated into three dominant groups in the t-SNE map, which were largely defined by their cell origins (ARI = 0.73 and Figure S7). This indicates that CCSN can be effectively extended to larger datasets in addition to the relatively small gold-standard datasets benchmarked above.

CCSN reveals network structure and dynamics on a single-cell basis

In this study, we applied c-CSN to Wang dataset [45], which comes from a study of neural progenitor cells (NPCs) that differentiate into mature neurons. The dataset contains six time points over a 30-day period.

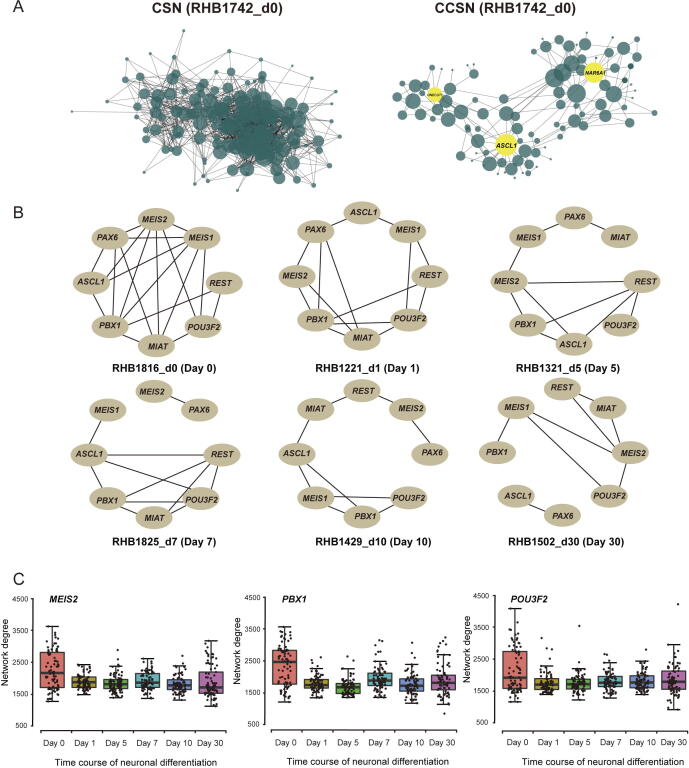
The CSN and c-CSN were performed on a single cell (Day 0, RHB1742_d0) using 195 transcription factors that are differentially expressed across all the cell subpopulations and all time points. In CCSN, two genes (HMGB1 and SOX11) of high coefficients of variation (CV) were chosen as the conditional genes. The results (Figure 3A) illustrate that the network of CCSN is much sparser than the network of CSN. There are three modules in the CCSN, while there is only one dense network in the CSN. Furthermore, three hub genes were obtained in three modules in the CCSN. One of the hub genes is ASCL1, which plays an important role in neural development [13], [49]. Thus, by removing indirect associations, c-CSN can extract a more informative network structure than CSN, which could improve the characterization of key regulatory factors in individual cells.

Figure 3.

The network analyses for single cells based on CCSN

A. CSN and CCSN of the same single cell (RHB1742_d0) from Wang dataset [45]. The same genes are used in network construction. Three hub genes ONECUT1, ASCL1, and NAR6A1 are highlighted in yellow. B. CCSNs of six cells from six time points (from Day 0 to Day 30) with eight genes that are involved in neuronal differentiation. The edge between two genes means the direct dependency of genes. C. The network degrees of MEIS2, PBX1, and POU3F2 along six time points of the neuronal differentiation. Each point indicates a single cell, colored according to the time point of sampling (from Day 0 to Day 30). The midlines indicate the median levels of network degree at six time points.

c-CSN also reveals the network dynamics over the differentiation trajectory. As illustrated in Figure 3B, a core neural differentiation network composed of eight regulatory genes was dynamically modulated through the temporal progression of NPC differentiation. At Day 0, the associations among these genes were the strongest, consistent with the high potency of progenitor cells. As NPC differentiates, the network became much sparser, suggesting more specified cell fates. In addition, when constructing CCSN from all genes, the degrees of MEIS2, PBX1 and POU3F2 were also larger at Day 0 and quickly decreases afterward (Figure 3C). These indicate that these genes are highly connected with other genes in NPCs, which is consistent with their known important roles in early differentiation of NPCs [45].

Both theoretically and computationally, c-CSN can also construct a gene–gene network for a single bulk RNA-seq sample, in addition to a single cell. To validate this biologically, we applied c-CSN to the TCGA lung adenocarcinoma (LUAD) RNA-seq dataset. The t-SNE plot based on CNDM reveals two obvious clusters, which respectively corresponding to normal adjacent lung tissues and lung tumors (Figure S8A), supporting the effective application of c-CSN to bulk RNA-seq data as well. Moreover, the EGFR pathway, a well-known oncogenic driver pathway for LUAD [50], [51], [52], was densely connected in tumor samples but not in benign tissues, as illustrated in the representative single-sample EGFR networks (Figure S8B), and the CCSN degrees of EGF and EGFR in each normal and tumor samples (Figure S8C). These data demonstrate that c-CSN well extends to single sample bulk RNA-seq data analysis and uncovers important biological connections related to disease states.

CCSN-based NFE analysis

To quantify the differentiation state of cells, we further develop a new method, NFE, to estimate the differentiation potency of cells by exploiting the gene–gene network constructed by c-CSN.

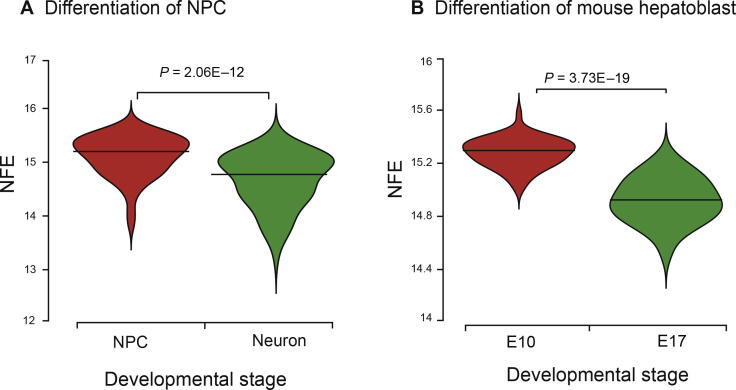
To assess the performance of NFE, we applied it to two datasets. In Wang dataset [45], there were 483 cells with 6 stages (Day 0, Day 1, Day 5, Day 7, Day 10, Day 30) and the CCSNs with one conditional gene were used to compute the NFE. We compared NPCs at Day 0 and Day 1 with mature neurons at Day 30 (Figure 4A). In Yang dataset [44], we compared the cells at embryonic day 10 (E10) with those at embryonic day 17 (E17)  in differentiation of mouse hepatoblasts (Figure 4B) and the CSN was used to compute the NFE. In both datasets, NFE assigned significantly higher scores to the progenitors than the differentiated cells (one-sided Wilcox rank sum test, P = 2.062E−12 in Wang dataset, P = 3.756E−19 in Yang dataset).

Figure 4.

NFE analyses for differentiated cells and progenitors

A. Violin plot comparing NFE of NPCs at Day 0 and Day 1 and mature neurons at Day 30 during the differentiation of NPCs. B. Violin plot of NFE values for cells at embryonic day 10 (E10) and embryonic day 17 (E17) during differentiation of mouse hepatoblasts. Cells of various differentiation states are compared for their differentiation potency by NFE. Red represents more pluripotent cells; green represents more differentiated cells. The midlines indicate the median levels of NFE in each cell type. P values are from one-sided Wilcoxon rank-sum test. NPC, neural progenitor cell.

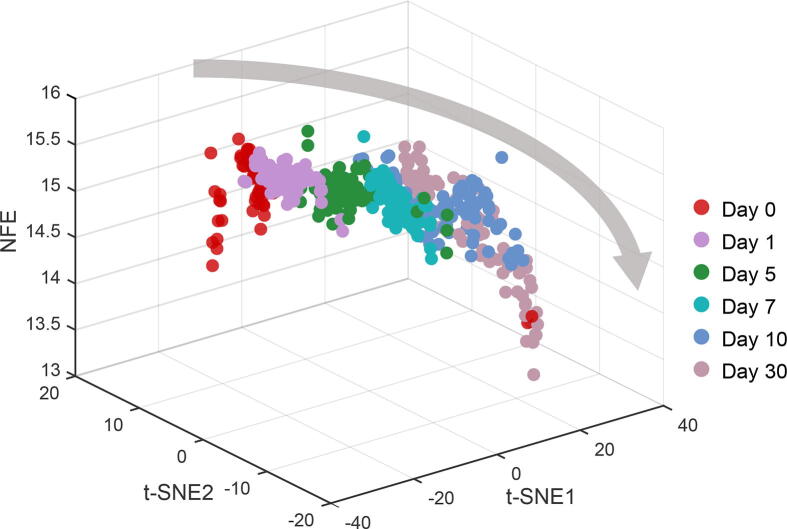
To further validate the accuracy of NFE, we generated a three-dimensional representation of the cell-lineage trajectory for the Wang dataset [45]. In the time-course differentiation experiment of NPCs into neurons [45], NFE correctly predicted a gradual decrease in differentiation potency (Figure 5). Therefore, NFE is effectively applicable to single-cell differentiation studies and highly predictive of developmental states and directions.

Figure 5.

Differentiation landscape of single-cell data according to NFE

The three-dimensional plot shows that NFE of single cells gradually decreases along the differentiation time course of NPCs (at Day 0 and Day 1) into mature neurons (at Day 30). The grey arrow depicts the overall differentiation trajectory from stem cells to differentiated cells, consistent with the trend of decrease of NFE. Cells from the same time point are assigned the same color. The z axis represents the NFE. The x axis and y axis represent respectively the two components of t-SNE (t-SNE1 and t-SNE2).

Conclusion

Estimating functional gene networks from noisy single-cell data has been a challenging task. Motivated by network-based data transformation, we have previously developed CSN to uncover CSNs and successfully applied it to extract biologically important gene interactions. However, CSN does not distinguish direct and indirect associations and thus suffers from the so-called overestimation problem. In this study, we propose a more sophisticated approach termed c-CSN, which constructs direct gene–gene associations (network) of each cell by eliminating false connections introduced by indirect effects.

c-CSN can transform GEM to CNDM for downstream dimension reduction and clustering analysis. These allow us to identify cell populations, generally better than GEM in the datasets tested above. In addition, c-CSN also shows good performance when compared to CSN. Moreover, we can construct one direct gene–gene association network by one cell based on c-CSN. From the networks of the individual cells, we can obtain the dynamically changed networks. As shown in Figure 3B, the CCSNs of these cells dynamically changed at different time points, and the network at Day 0 shows the strongest associations. Moreover, the hub genes of the networks constructed by c-CSN method may play an important role in biological processes. As shown in Figure 3A, the hub genes of three modules in the network constructed by c-CSN play a vital role in neural development. These clearly demonstrate the advantages of CCSN. In addition, individual networks of cells constructed by c-CSN can also be applied to construct network biomarkers [53], [54] for accurate disease diagnosis/prognosis, or dynamic network biomarkers [55], [56], [57], [58], [59] for reliable disease prediction.

According to the Waddington’s landscape model of cellular differentiation, cellular differentiation potency is decreased as a pluripotent cell “rolls” down from a “hill” to nearby “valleys”, and cell fate transitions could be modeled as “canalization” events [60], [61], [62]. The differentiation potency quantifies the relative number of fate choices that a cell may have and provides a useful indicator of cellular “stemness”. Recently, SCENT [40] and MCE [63] use PPI network and gene expression data as input to obtain the potency of cells. However, these methods estimate the entropy of cells based on the available PPI network across various tissues, which may ignore many important relationships between genes in specific cells. Here, we develop the NFE to integrate the scRNA-seq profile of a cell with its gene–gene association network, and the results show that NFE performs well in distinguishing various cells of differential potency.

Nonetheless, the computational cost of c-CSN generally increases by G times comparing with the original CSN due to G conditional genes. Thus, a parallel computation scheme is desired to reduce the computation time. Also, c-CSN is not designed to construct the causal gene association networks, and the directions of the gene associations cannot be obtained. These could be our future research topics.

Code availability

CCSN is available at https://github.com/LinLi-0909/c-CSN.

CRediT author statement

Lin Li: Conceptualization, Methodology, Writing - review & editing. Hao Dai: Methodology, Writing - review & editing. Zhaoyuan Fang: Conceptualization, Methodology, Writing - review & editing. Luonan Chen: Conceptualization, Writing - review & editing. All authors read and approved the final manuscript.

Competing interests

The authors have declared no competing interests.

Supplementary material

The following are the Supplementary data to this article:

Supplementary File S1

c-CSN implementation details and additional notes

Supplementary Figure S1

Scatter diagram of the expression values of gene x, gene y, and gene z for cell k A. The red plot k represents the cell k, and x axis, y axis and z axis represent the expression levels of gene x, gene y and gene z respectively. Gene z is set as the conditional gene. n is the number of cells in the dataset. B. Draw two parallel planes $P_x^1$,$P_x^2$ that are orthogonal with x-axis. The space between the two planes represent the neighborhood of $x_k$, in which the number of the dots is$n_x^{\left(k\right)}$. C. Draw two parallel planes $P_y^1$,$P_y^2$ that are orthogonal with y-axis. The space between the two planes represent the neighborhood of $y_k$, in which the number of the dots is$n_y^{\left(k\right)}$. D. Draw two parallel planes ${\mathcal{P}}_z^1$, ${\mathcal{P}}_z^2$ that are orthogonal with z-axis. The space between the two planes represent the neighborhood of $z_k$, in which the number of the dots is$n_z^{\left(k\right)}$. E. The space surrounded by $P_x^1$,$P_x^2$, ${\mathcal{P}}_z^1$, ${\mathcal{P}}_z^2$ (green box) represents the neighborhood of $(x_k,z_k)$, in which the number of dots is $n_{\mathit{xz}}^{\left(k\right)}$. F. The space surrounded by $P_y^1$,$P_y^2$, ${\mathcal{P}}_z^1$, ${\mathcal{P}}_z^2$ (green box) represents the neighborhood of $(y_k,z_k)$, in which the number of dots is $n_{\mathit{yz}}^{\left(k\right)}$. (G) The space enclosed by $P_x^1$,$P_x^2$, $P_y^1$,$P_y^2$, ${\mathcal{P}}_z^1$, ${\mathcal{P}}_z^2$ (green box) represents the neighborhood of $(x_k,y_k,z_k)$, in which the number of dots is $n_{\mathit{xyz}}^{\left(k\right)}$.

Supplementary Figure S2

The comparison of standard normal distribution and the distribution of${\widehat{\mathit{\rho }}}_{\mathit{x}\mathit{y}|\mathit{z}}^{\left(\mathit{k}\right)}$ The density function is calculated by kernel density estimation based on 20,000 plots (File S1), and $n_x$, $n_y$, $n_z$ are equal to 0.2$\ast$n, n = 200 (A), n = 500 (B). The gene x and gene y are conditional independent given gene z.

Supplementary Figure S3

Comparison of GEM and CNDM by PCA plots on four datasets Different colors represent different cell types.

Supplementary Figure S4

The clustering results of CNDM with different parameters ARI is used to evaluate the clustering performance of k-means and HCA on CNDM. Eight datasets are used. The x-axis represents the ‘boxsize’ parameter of CCSN and the y-axis represents the ARI values. Each line is colored by the number of conditional genes.

Supplementary Figure S5

Clustering performance (evaluated by ARI) of CNDM and GEM on six datasets by five clustering algorithms 100 tests were repeated for each dataset and each clustering algorithm, which were represented as small black dots. And the bars represent the average of the dots. t-SNE + K-means and t-SNE + Hierarchical represent the clustering analysis of K-means/ Hierarchical is performed after dimension-reduction by t-SNE.

Supplementary Figure S6

Clustering performance (evaluated by ARI) of CNDM and NDM on six datasets by five clustering algorithms 100 tests were repeated for each dataset and each clustering algorithm, which were represented as small black dots. And the bars represent the average of the dots. t-SNE + K-means and t-SNE + Hierarchical represent the clustering analysis of K-means/Hierarchical is performed after dimension-reduction by t-SNE.

Supplementary Figure S7

Visualization of 23,321 cells by t-SNE In the two-dimensional t-SNE plot, each dot represents a single cell of the Tabula Muris dataset. Different colors represent different tissues (blue: bladder; red: trachea; green: spleen).

Supplementary Figure S8

Analysis of TCGA-LUAD dataset based on CCSNs c-CSN is applied to the TCGA-LUAD bulk RNA-seq data A. t-SNE plots are used for visualization based on CCSN. The normal samples and tumor samples are represented by different colors. B. CCSNs of representative samples for 18 genes involved in the EGFR pathway. C. Conditional network degrees of EGF and EGGR in the normal samples and the tumor samples.

Supplementary Table S1

The running time of c-CSN with different numbers of conditional genes

Supplementary Table S2

Datasets used in this study