ASYMPTOTICALLY INDEPENDENT U-STATISTICS IN HIGH-DIMENSIONAL TESTING

Abstract

Many high-dimensional hypothesis tests aim to globally examine marginal or low-dimensional features of a high-dimensional joint distribution, such as testing of mean vectors, covariance matrices and regression coefficients. This paper constructs a family of U-statistics as unbiased estimators of the ℓ_p-norms of those features. We show that under the null hypothesis, the U-statistics of different finite orders are asymptotically independent and normally distributed. Moreover, they are also asymptotically independent with the maximum-type test statistic, whose limiting distribution is an extreme value distribution. Based on the asymptotic independence property, we propose an adaptive testing procedure which combines p-values computed from the U-statistics of different orders. We further establish power analysis results and show that the proposed adaptive procedure maintains high power against various alternatives.

1. Introduction.

Motivation.

Analysis of high-dimensional data, whose dimension p could be much larger than the sample size n, has emerged as an important and active research area (e.g., [19, 21, 23, 63]). In many large-scale inference problems, one is often interested in globally testing some overall patterns of low-dimensional features of the high-dimensional random observations. One example is genome-wide association studies (GWAS), whose primary goal is to identify single nucleotide polymorphisms (SNPs) associated with certain complex diseases of interest. A popular approach in GWAS is to perform univariate tests, which examine each SNP one by one. This, however, may lead to low statistical power due to the weak effect size of each SNP [47] and the small statistical significance threshold (~ 10⁻⁸) chosen to control the multiple-comparison type I error [40]. Researchers therefore have proposed to globally test a genetic marker set with many SNPs [40, 64] in order to achieve higher statistical power and to better understand the underlying genetic mechanisms.

In this paper, we focus on a family of global testing problems in the high-dimensional setting, including testing of mean vectors, covariance matrices and regression coefficients in generalized linear models. These problems can be formulated as $H_0:\mathcal{E}=0$, where 0 is an all zero vector, $\mathcal{E}=\{e_l:l\in \mathcal{L}\}$ is a parameter vector with $\mathcal{L}$ being the index set, and e_l’s being the corresponding parameters of interest, for example, elements in mean vectors, covariance matrices or coefficients in generalized linear models. For the global testing problem $H_0:\mathcal{E}=0$ versus $H_A:\mathcal{E}\ne 0$, two different types of methods are often used in the literature. One is sum-of-squares-type statistics. They are usually powerful against “dense” alternatives, where $\mathcal{E}$ has a high proportion of nonzero elements with a large $\Vert \mathcal{E}{\Vert }_2={\sum }_{l\in \mathcal{L}}{e}_l^2$ or its weighted variants. See examples in mean testing (e.g., [4, 11, 12, 25, 26, 60, 62]) and covariance testing (e.g., [3, 13, 42, 45]). The other is maximum-type statistics. They are usually powerful against “sparse” alternatives, where $\mathcal{E}$ has few nonzero elements with a large $\Vert \mathcal{E}{\Vert }_{\infty }$ (e.g., [6, 8, 9, 27, 36, 46, 58]). More recently, [20, 70] also proposed to combine these two kinds of test statistics. However, for denser or only moderately dense alternatives, neither of these two types of statistics may be powerful, as will be further illustrated in this paper both theoretically and numerically. Importantly, in real applications, the underlying truth is usually unknown, which could be either sparse, dense or in-between. As global testing could be highly underpowered if an inappropriate testing method is used (e.g., [15]), it is desired in practice to have a testing procedure with high statistical power against a variety of alternatives.

A family of asymptotically independent U-statistics.

To address these issues, we propose a U-statistics framework and introduce its applications to adaptive high-dimensional testing. The U-statistics framework constructs unbiased and asymptotically independent estimators of $\Vert \mathcal{E}{\Vert }_a^a≔{\sum }_{l\in \mathcal{L}}{e}_l^a$ for different (positive) integers a, where a = 2 corresponds to a sum-of-squares-type statistic, and an even integer a → ∞ yields a maximum-type statistic. The adaptive testing then combines the information from different $\Vert \mathcal{E}{\Vert }_a^a$’s, and our power analysis shows that it is powerful against a wide range of alternatives, from highly sparse, moderately sparse to dense, to highly dense.

To illustrate our idea, suppose z₁, … , z_n are n independent and identically distributed (i.i.d.) copies of a random vector z. We consider the setting where each parameter e_l has an unbiased kernel function estimator K_l(z_i1, … , z_iγl), and γ_l is the smallest integer such that for any 1 ≤ i₁ ≠ ⋯ ≠ i_γl ≤ n, E[K_l(z_i1, … , z_iγl)] = e_l. This includes many testing problems on moments of low orders, such as entries in mean vectors, covariance matrices and score vectors of generalized linear models, which shall be discussed in detail. The family of U-statistics can be constructed generally as follows. For integers a ≥ 1 and 1 ≤ i₁ ≠ ⋯ ≠ i_γl ≠ ⋯ ≠ i_{(a−1)×γl+1} ⋯ ≠ i_a×γl ≤ n, since the z’s are i.i.d., we have $\mathrm{E}[K_l({\mathbf{z}}_{i_1},\dots ,{\mathbf{z}}_{i_{{\gamma }_l}})\cdots K_l({\mathbf{z}}_{i_{(a-1)\times {\gamma }_l+1}},\dots ,{\mathbf{z}}_{i_{a\times {\gamma }_l}})]=e_l^a$. Therefore, we can construct an unbiased estimator of the parameters of augmented powers $e_l^a$ with different a. Then $\Vert \mathcal{E}{\Vert }_a^a$ has an unbiased estimator

$$\mathcal{U}(a)=\sum _{l\in \mathcal{L}}(P_{a\times {\gamma }_l}^n{)}^{-1}\sum _{1\le i_1\ne \cdots \ne i_{a\times {\gamma }_l}\le n}\prod _{k=1}^a{K}_l({\mathbf{z}}_{i_{(k-1)\times {\gamma }_l+1}},\dots ,{\mathbf{z}}_{i_{k\times {\gamma }_l}}),$$ (1.1)

where $P_k^n=n!∕(n-k)!$ denotes the number of k-permutations of n. We call a the order of the U-statistic $\mathcal{U}(a)$. If a > b, we say $\mathcal{U}(a)$ is of higher order than $\mathcal{U}(b)$ and vice versa.

This construction procedure can be applied to many testing problems. We give three common examples below for illustration and more detailed case studies will be discussed in Sections 2 and 4.

Example 1. Consider one-sample mean testing of H₀ : μ = 0, where $\mathcal{E}=\mu$ is the mean vector of a p-dimensional random vector x. Suppose x₁, … , x_n are n i.i.d. copies of x. For each i = 1, … , n, j = 1, … , p, x_i,j is a simple unbiased estimator of μ_j, then we can take the kernel function K_j(x_i) = x_i,j. Following (1.1), we know the U-statistic

$$\mathcal{U}(a)=(P_a^n{)}^{-1}\sum _{j=1}^p\sum _{1\le i_1\ne \cdots \ne i_a\le n}\prod _{k=1}^a{x}_{i_k,j}$$

is an unbiased estimator of $\Vert \mathcal{E}{\Vert }_a^a=\Vert \mu {\Vert }_a^a={\sum }_{j=1}^p{\mu }_j^a$. Please see Section 4.1 for the two-sample mean testing example and related theoretical properties.

Example 2. Suppose x₁, … , x_n are n i.i.d. copies of a random vector x with mean vector μ = 0 and covariance matrix Σ = {σ_j1,j2}_p×p. For covariance testing H₀ : σ_j1,j2} = 0 for any 1 ≤ j₁ ≠ j₂ ≤ p, we have $\mathcal{E}=\{{\sigma }_l:l\in \mathcal{L}\}$ with $\mathcal{L}=\{(j_1,j_2):1\le j_1\ne j_2\le p\}$. Since x_i,j1x_i,j2 is a simple unbiased estimator of σ_j1,j2, then for each pair $l=(j_1,j_2)\in \mathcal{L}$, we can take the kernel function K_l(x_i) = x_i,j1x_i,j2. Following (1.1), the U-statistic

$$\mathcal{U}(a)=(P_a^n{)}^{-1}\sum _{1\le j_1\ne j_2\le p}\sum _{1\le i_1\ne \cdots \ne i_a\le n}\prod _{k=1}^a(x_{i_k,j_1}{x}_{i_k,j_2})$$

is an unbiased estimator of $\Vert \mathcal{E}{\Vert }_a^a={\sum }_{1\le j_1\ne j_2\le p}{\sigma }_{j_1,j_2}^a$. Please see Section 2 for one-sample covariance testing with unknown μ, and Section 4.2 for two-sample covariance testing.

Example 3. Consider a response variable y and its covariates $\mathbf{x}\in {\mathbb{R}}^p$ following a generalized linear model: E(y∣x) = g⁻¹(x^⊤β), where g is the canonical link function and $\beta \in {\mathbb{R}}^p$ are the regression coefficients. Suppose that (x_i, y_i), i = 1, … , n, are i.i.d. copies of (x, y). For testing H₀ : β = β₀, the score vectors (S_i,j = (y_i − μ_0,i)x_i,j : j = 1, … , p)^⊤ are often used in the literature, where ${\mu }_{0,i}=g^{-1}({\mathbf{x}}_i^{⊺}{\beta }_0)$. Note that E(S_i,j) = 0 under H₀. Thus to test H₀, we can take $\mathcal{E}=\{\mathrm{E}(S_{i,j}):j=1,\dots ,p\}$ and use the U-statistic

$$\mathcal{U}(a)=(P_a^n{)}^{-1}\sum _{j=1}^p\sum _{1\le i_1\ne \cdots \ne i_a\le n}\prod _{k=1}^a{S}_{i_k,j},$$

which is an unbiased estimator of $\Vert \mathcal{E}{\Vert }_a^a={\sum }_{j=1}^p\{\mathrm{E}(S_{i,j}){\}}^a$. Please see Section 4.3.

Related literature.

For high-dimensional testing, some other adaptive testing procedures have recently been proposed in [52, 65, 67]. These works combine the p-values of a family of sum-of-powered statistics that are powerful against different $\Vert \mathcal{E}{\Vert }_a^a$’s. However, in these existing works, to evaluate the p-value of the adaptive test statistic, the joint asymptotic distribution of the statistics is difficult to obtain or calculate. Accordingly, computationally expensive resampling methods are often used in practice [40, 52, 69]. For some special cases such as testing means and the coefficients of generalized linear models, [67] and [65] derived the limiting distributions of the test statistics under the framework of a family of von Mises V-statistics. However, the constructed V-statistics are usually correlated and biased estimators of the target $\Vert \mathcal{E}{\Vert }_a^a$. It follows that in [67] and [65], numerical approximations are still needed to calculate the tail probabilities of the adaptive test statistics; see Remark 4.1 and Section 4.3. In addition, these existing adaptive testing works mainly focus on the first-order moments, and their results do not directly apply to testing second-order moments, such as covariance matrices.

To overcome these issues, this paper considers the proposed family of unbiased U-statistics. There are some other recent works providing important results on high-dimensional U-statistics (e.g., [14, 43, 72]). For instance, [72] considered testing the regression coefficients in linear models using the fourth-order U-statistic; [43] studied the limiting distributions of rank-based U-statistics; and [14] studied bootstrap approximation of the second-order U-statistics. However, these results do not directly apply to the high-order U-statistics considered in this paper.

Our contributions.

We establish the theoretical properties of the U-statistics in various high dimensional testing problems, including testing mean vectors, regression coefficients of generalized linear models, and covariance matrices. Our contributions are summarized as follows.

Under the null hypothesis, we show that the normalized U-statistics of different finite orders are jointly normally distributed. The result applies generally for any asymptotic regime with n → ∞ and p → ∞. In addition, we prove that all the finite-order U-statistics are asymptotically independent with each other under the null hypothesis. Moreover, we prove that U-statistics of finite orders are also asymptotically independent of the maximum-type test statistic with a limiting extreme value distribution.

Under the alternative hypothesis, we further analyze the asymptotic power for U-statistics of different orders. We show that when $\mathcal{E}$ has denser nonzero entries, $\mathcal{U}(a)$’s of lower orders tend to be more powerful; and when $\mathcal{E}$ has sparser nonzero entries, $\mathcal{U}(a)$’s of higher orders tend to be more powerful. More interestingly, we show that in the boundary case of “moderate” sparsity levels, $\mathcal{U}(a)$ with a finite a > 2 gives the highest power among the family of U-statistics, clearly indicating the inadequacy of both the sum-of-squares- and the maximum-type statistics.

An important application of the independence property among $\mathcal{U}(a)$’s is to construct adaptive testing procedures by combining the information of different $\mathcal{U}(a)$’s, whose univariate distributions or p-values can be easily combined to form a joint distribution to calculate the p-value of an adaptive test statistic. Compared with other existing works (e.g., [65, 67]), numerical approximations of tail probabilities are no longer needed. As shown in the power analysis, an adaptive integration of information across different tests leads to a powerful testing procedure.

The rest of the paper is organized as follows. In Sections 2 and 3, we illustrate the framework by a covariance testing problem. Particularly, in Section 2.1, we study the U-statistics under null hypothesis; in Section 2.2, we analyze the power of the U-statistics; in Section 2.3, we develop an adaptive testing procedure. In Sections 3.1 and 3.2, we report simulations and a real dataset analysis. In Section 4, we study other high-dimensional testing problems, including testing means, regression coefficients, and two-sample covariances. In Section 5, we discuss several extensions of the proposed framework. We give proofs and other stimulations in Supplementary Material [28].

2. Motivating example: One-sample covariance testing.

The constructed family of U-statistics and adaptive testing procedure can be applied to various high-dimensional testing problems. In this section, we illustrate the framework with a motivating example of one-sample covariance testing. Analogous results for other high-dimensional testing problems in Section 4 can be obtained following similar analyses. We showcase the study of one-sample covariance testing problem since this is more challenging than mean testing due to the two-way dependency structure and the one-sample problem can be used as the building block for more general cases.

Specifically, we focus on testing

$$H_0:{\sigma }_{j_1,j_2}=0\forall 1\le j_1\ne j_2\le p,$$ (2.1)

where Σ = {σ_j1,j2 : 1 ≤ j₁, j₂ ≤ p} is the covariance matrix of a p-dimensional real-valued random vector x = (x₁, … , x_p)^⊤ with E(x) = μ = (μ₁, … , μ_p)^⊤. The observed data include n i.i.d. copies of x, denoted by x₁, … , x_n with x_i = (x_i,1, … , x_i,p)^⊤. In factor analysis, testing H₀ in (2.1) can be used to examine whether Σ has any significant factor or not [1].

Global testing of covariance structure plays an important role in many statistical analysis and applications; see a review in [7]. Conventional tests include the likelihood ratio test, John’s test and Nagao’s test, etc. [1, 50]. These methods, however, often fail in the high-dimensional setting when both n, p → ∞. To address this issue, new procedures have been recently proposed (e.g., [3, 8, 13, 36-38, 41, 42, 45, 46, 53, 57-59]). However, these methods might suffer from loss of power when the sparsity level of the alternative covariance matrix varies. In the following subsections, we introduce the general U-statistics framework, study their asymptotic properties and develop a powerful adaptive testing procedure.

We introduce some notation. For two series of numbers u_n,p, v_n,p that depend on n, p: u_n,p = o(v_n,p) denotes $\text{lim}{\text{sup}}_{n,p\to \infty }\mid u_{n,p}∕v_{n,p}\mid =0;u_{n,p}=O(v_{n,p})$ denotes $\text{lim}{\text{sup}}_{n,p\to \infty }\mid u_{n,p}∕v_{n,p}\mid <\infty$; u_n,p = Θ(v_n,p) denotes $0<\text{lim}{\text{inf}}_{n,p\to \infty }\mid u_{n,p}∕v_{n,p}\mid \le \text{lim}{\text{sup}}_{n,p\to \infty }\mid u_{n,p}∕v_{n,p}\mid <\infty$; u_n,p ≃ v_n,p denotes ${\text{lim}}_{n,p\to \infty }{u}_{n,p}∕v_{n,p}=1$. Moreover, $\stackrel{P}{\to }$ and $\stackrel{D}{\to }$ represent the convergence in probability and distribution, respectively. For p-dimensional random vector x with mean μ and ∀j₁, … , j_t ∈ {1, … , p}, we write the central moment as

$${\Pi }_{j_1,\dots ,j_t}=\mathrm{E}\left[(x_{j_1}-{\mu }_{j_1})\cdots (x_{j_t}-{\mu }_{j_t})\right].$$ (2.2)

2.1. Asymptotically independent U-statistics.

For testing (2.1), the set of parameters that we are interested in is $\mathcal{E}=\{{\sigma }_{j_1,j_2}:1\le j_1\ne j_2\le p\}$. Following the previous analysis of (1.1), since σ_j1,j2 has a simple unbiased estimator x_i1,j1x_i1,j2 − x_i1,j1x_i2,j2 with 1 ≤ i₁ ≠ i₂ ≤ n, then for integers a ≥ 1, an unbiased U-statistic of $\Vert \mathcal{E}{\Vert }_a^a={\sum }_{1\le j_1\ne j_2\le p}{\sigma }_{j_1,j_2}^a$ is

$$\mathcal{U}(a)=(P_{2a}^n{)}^{-1}\sum _{1\le j_1\ne j_2\le p}\sum _{1\le i_1\ne \cdots \ne i_{2a}\le n}\prod _{k=1}^a(x_{i_{2k-1},j_1}{x}_{i_{2k-1},j_2}-x_{i_{2k-1},j_1}{x}_{i_{2k},j_2}).$$

This is equivalent to

$$\begin{gathered} \mathcal{U}(a)=\sum _{1\le j_1\ne j_2\le p}\sum _{c=0}^a(-1{)}^c\left(\begin{array}{c}\hfill a\hfill \\ \hfill c\hfill \end{array}\right)\frac{1}{P_{a+c}^n}\sum _{1\le i_1\ne \cdots \ne i_{a+c}\le n} \\ \prod _{k=1}^{a-c}(x_{i_k,j_1}{x}_{i_k,j_2})\prod _{s=a-c+1}^a{x}_{i_s,j_1}\prod _{t=a+1}^{a+c}{x}_{i_t,j_2}. \end{gathered}$$ (2.3)

Remark 2.1. The U-statistics can be constructed by another method equivalently. Given 1 ≤ j₁ ≠ j₂ ≤ p, define φ_j1,j2 = σ_j1,j2 + μ_j1μ_j2. Then

$$\sum _{1\le j_1\ne j_2\le p}{\sigma }_{j_1,j_2}^a=\sum _{1\le j_1\ne j_2\le p}\sum _{c=0}^a\left(\begin{array}{c}\hfill a\hfill \\ \hfill c\hfill \end{array}\right){\phi }_{j_1,j_2}^{a-c}\times (-{\mu }_{j_1}{\mu }_{j_2}{)}^c,$$ (2.4)

which is a polynomial function of the moments μ_j and φ_j1,j2. Since μ_j and φ_j1,j2 have unbiased estimators x_i,j and x_i,j1x_i,j2 respectively, then for 1 ≤ i₁ ≠ ⋯ ≠ i_a+c ≤ n, $\mathrm{E}({\prod }_{k=1}^{a-c}{x}_{i_k,j_1}{x}_{i_k,j_2}{\prod }_{s=a-c+1}^a{x}_{i_s,j_1}{\prod }_{t=a+1}^{a+c}{x}_{i_t,j_2})={\phi }_{j_1,j_2}^{a-c}{\mu }_{j_1}^c{\mu }_{j_2}^c$. Given this and (2.4), the U-statistics (2.3) can be obtained.

Remark 2.2. The summed term with c = 0 in (2.3) is

$$\tilde{\mathcal{U}}(a)≔(P_a^n{)}^{-1}\sum _{1\le i_1\ne \cdots \ne i_a\le n}\sum _{1\le j_1\ne j_2\le p}\prod _{k=1}^a(x_{i_k,j_1}{x}_{i_k,j_2}),$$ (2.5)

which has the same form as the simplified U-statistic for mean zero observations in Example 2, and is shown to be the leading term of (2.3) in proof.

We next introduce some nice properties of the U-statistics (2.3). The first one is the following location invariant property.

Proposition 2.1. $\mathcal{U}(a)$ constructed as in (2.3) is location invariant; that is, for any vector $\Delta \in {\mathbb{R}}^p$, the U-statistic constructed based on the transformed data {x_i + Δ : i = 1, … , n} is still $\mathcal{U}(a)$.

The following proposition verifies that the constructed U-statistics are unbiased estimators of $\Vert \mathcal{E}{\Vert }_a^a={\sum }_{1\le j_1\ne j_2\le p}{\sigma }_{j_1,j_2}^a$.

Proposition 2.2. For any integer a, $\mathrm{E}[\mathcal{U}(a)]={\sum }_{1\le j_1\ne j_2\le p}{\sigma }_{j_1,j_2}^a$. Under H₀ in (2.1), $\mathrm{E}[\mathcal{U}(a)]=0$.

We next study the limiting properties of the constructed U-statistics under H₀ given the following assumptions on the random vector x = (x₁, … , x_p)^⊤.

Condition 2.1 (Moment assumption). ${\text{lim}}_{p\to \infty }{\max }_{1\le j\le p}\mathrm{E}(x_j-{\mu }_j{)}^8<\infty$ and ${\text{lim}}_{p\to \infty }{\text{min}}_{1\le j\le p}\mathrm{E}(x_j-{\mu }_j{)}^2>0$.

Condition 2.2 (Dependence assumption). For a sequence of random variables z = {z_j : j ≥ 1} and integers a < b, let ${\mathcal{Z}}_a^b$ be the σ-algebra generated by {z_j : j ∈ {a, … , b}}. For each s ≥ 1, define the α-mixing coefficient ${\alpha }_{\mathbf{z}}(s)={\text{sup}}_{t\ge 1}\{\mid P(A\cap B)-P(A)P(B)\mid :A\in {\mathcal{Z}}_1^t,B\in {\mathcal{Z}}_{t+s}^{\infty }\}$. We assume that under H₀, x is α-mixing with α_x(s) ≤ Mδ^s, where δ ∈ (0, 1) and M > 0 are some constants.

Condition 2.2* (Alternative dependence assumption to Condition 2.2). Following the notation in (2.2), we assume that under H₀, for any j₁, j₂, j₃ ∈ {1, … , p}, Π_j1,j2,j3 = 0; for any j₁, j₂, j₃, j₄ ∈ {1, … , p}, Π_j1,j2,j3,j4 = κ₁(σ_j1,_j2σ_j3,_j4 + σ_j1,_j3σ_j2,_j4 + σ_j1,_j4σ_j2,_j3) for some constant κ₁ < ∞; and for t = 6, 8, and any j₁, … , j_t ∈ {1, …, p}, Π_j1,…,jt = 0 when at least one of these indexes appears odd times in {j₁, …, j_t}.

Condition 2.1 assumes that the eighth marginal moments of x are uniformly bounded from above and the second moments are uniformly bounded from below, which are true for most light-tailed distributions. Condition 2.2 assumes weak dependence among different x_j’s under H₀, since the uncorrelatedness of x_j’s under H₀ may not imply the independence of them, especially when x_j’s are non-Gaussian. Under H₀, Condition 2.2 automatically holds when x is Gaussian or m-dependent. The mixing-type weak dependence is similarly considered in previous works such as [5, 11, 67] and also commonly assumed in time series and spatial statistics [24, 55]. Moreover, the variables in our motivating genome-wide association studies have a local dependence structure, with their associations often decreasing to zero as the corresponding physical distances on a chromosome increase. We note that it suffices to have Condition 2.2 hold up to a permutation of the variables.

Alternatively, we can substitute Condition 2.2 with Condition 2.2*. Condition 2.2* specifies some higher-order moments of x and is satisfied when x follows an elliptical distribution with finite eighth moments and covariance Σ (see [1, 22, 50, 51]). Conditions 2.2* and 2.2 become equivalent when x follows a multivariate Gaussian distribution. The fourth moment condition is also assumed in other high-dimensional research [6]. In this work, the eighth moment condition is needed to establish the asymptotic joint distribution of different U-statistics.

The following theorem specifies the asymptotic variances of the finite order U-statistics and their joint limiting distribution. Since the U-statistics are degenerate under H₀, an analysis different from the asymptotic theory on nondegenerate U-statistics (e.g., [32]) is needed in the proof.

Theorem 2.1. Under H₀ in (2.1) and Conditions 2.1 and 2.2 (or 2.2*), for $\mathcal{U}(a)$’s defined in (2.3) and any distinct finite (and positive) integers {a₁, … , a_m}, as n, p → ∞,

$${\left[\frac{\mathcal{U}(a_1)}{\sigma (a_1)},\dots ,\frac{\mathcal{U}(a_m)}{\sigma (a_m)}\right]}^{⊺}\stackrel{D}{\to }\mathcal{N}(0,I_m),$$ (2.6)

where

$${\sigma }^2(a)≔\text{var}[\mathcal{U}(a)]\simeq \frac{a!}{P_a^n}\sum _{1\le j_1\ne j_2\le p;1\le j_3\ne j_4\le p}({\Pi }_{j_1,j_2,j_3,j_4}{)}^a,$$ (2.7)

with Π_j1,j2,j3,j4 defined in (2.2). Note that σ²(a) = Θ(p²n^−a).

Theorem 2.1 shows that after normalization, the finite-order U-statistics have a joint normal limiting distribution with an identity covariance matrix, which implies that they are asymptotically independent as n, p → ∞. The nice independence property makes it easy to combine these U-statistics and apply our proposed adaptive testing later. Moreover, the conclusion holds on general asymptotic regime for n, p → ∞, without any constraint on the relationship between n and p. We will also see in Section 4 that similar results hold generally for some other testing problems.

Remark 2.3. Theorem 2.1 discusses the U-statistics of finite orders, that is, the a values do not grow with n, p. When {x₁, … , x_p} are independent, Theorem 2.1 can be extended when a = O(1) min{log^ϵ n, log^ϵ p} for some ϵ > 0. On the other hand, we will show in Section 2.2 that it is usually enough to include $\mathcal{U}(a)$’s of finite a. Therefore, we do not pursue the general case when a grows with n, p in this work.

In the following, we further discuss the maximum-type test statistic $\mathcal{U}(\infty )$, which corresponds to the ℓ_∞-norm of the parameter vector $\mathcal{E}=\{e_l:l\in \mathcal{L}\}$, that is, $\Vert \mathcal{E}{\Vert }_{\infty }={\max }_{l\in \mathcal{L}}\mid e_l\mid$. In the existing literature, there is already some corresponding established work [8, 36] on the test statistic:

$$M_n^{\ast }≔\underset{1\le j_1\ne j_2\le p}{\max }\mid {\widehat{\sigma }}_{j_1,j_2}∕\sqrt{{\widehat{\sigma }}_{j_1,j_1}{\widehat{\sigma }}_{j_2,j_2}}\mid ,$$ (2.8)

where $({\widehat{\sigma }}_{j_1,j_2}{)}_{p\times p}={\sum }_{i=1}^n({\mathbf{x}}_i-\overline{\mathbf{x}})({\mathbf{x}}_i-\overline{\mathbf{x}}{)}^{⊺}∕n$ and $\overline{\mathbf{x}}={\sum }_{i=1}^n{\mathbf{x}}_i∕n$. We will take $\mathcal{U}(\infty )=M_n^{\ast }$ below. The limiting distribution of $\mathcal{U}(\infty )$ was first studied in [36] and extended by [8, 46, 58]. Next, we restate the result in [8], which gives the limiting distribution of (2.8) under the following condition.

Condition 2.3. Consider the random vector x = (x₁, … , x_p)^⊤ with mean vector μ = (μ₁, … , μ_p)^⊤ and covariance matrix Σ = dia(σ_1,1,… , σ_p,p). $(x_j-{\mu }_j)∕\sqrt{{\sigma }_{j,j}}$ are i.i.d. for j = 1, … , p. Furthermore, $\mathrm{E}{e}^{t_0(\mid x_1-{\mu }_1\mid ∕\sqrt{{\sigma }_{1,1}}{)}^{\varsigma }}<\infty$ for some 0 < ς ≤ 2 and t₀ > 0.

Theorem 2.2 (Cai and Jiang [8], Theorem 2). Assume Condition 2.3 and log p = o(n^β), where β = ς/(4 + ς). Then $P(n\times \mathcal{U}(\infty {)}^2+{\varpi }_p\le u)\to G(u)=e^{-(1∕\sqrt{8\pi })e^{-u∕2}}$, where ${\varpi }_p=-4\log p+\log \log p$ and G(u) is an extreme value distribution of type I.

Theorems 2.1 and 2.2 give the limiting distributions of $\mathcal{U}(a)$ of finite orders and $\mathcal{U}(\infty )$ respectively; it is of interest to examine their joint distribution. The following theorem shows that although $\mathcal{U}(\infty )$ has limiting distribution different from $\mathcal{U}(a)$, a < ∞, they are still asymptotically independent.

Theorem 2.3. Assume that Condition 2.1 is satisfied, Condition 2.3 holds for ς = 2, and log p = o(n^1/7). For finite integers {a₁, … , a_m}, under H₀, $\mathcal{U}(a_1),\dots ,\mathcal{U}(a_m)$ and $\mathcal{U}(\infty )$ are mutually asymptotically independent. Specifically, ∀z₁, … , z_m, $y\in \mathbb{R}$, as n, p → ∞,

$$\begin{gathered} \mid P\left(n\mathcal{U}(\infty {)}^2+{\varpi }_p\ge y,\frac{\mathcal{U}(a_1)}{\sigma (a_1)}\le z_1,\dots ,\frac{\mathcal{U}(a_m)}{\sigma (a_m)}\le z_m\right)\phantom{\mid } \\ \phantom{\mid }-P(n\mathcal{U}(\infty {)}^2+{\varpi }_p\ge y)\times \prod _{r=1}^{m}P\left(\frac{\mathcal{U}(a_r)}{\sigma (a_r)}\le z_r\right)\mid \to 0. \end{gathered}$$

Theorem 2.1 suggests that all the finite-order U-statistics are asymptotically independent with each other. Given this, Theorem 2.3 further shows that the maximum-type test statistic $\mathcal{U}(\infty )$ is also asymptotically mutually independent with those finite-order U-statistics. The conclusion shares similarity with some classical results on the asymptotic independence between the sum-of-squares-type and maximum-type statistics. Specifically, for random variables w₁,… , w_n, [30, 33] proved the asymptotic independence between ${\sum }_{i=1}^n{w}_i^2$ and max_i=1,…,n ∣w_i∣ for weakly dependent observations. The similar independence properties were extensively studied in literature (e.g., [31, 34, 44, 48, 54, 67]). However, there are several differences between existing literature and the results in this paper. First, we discuss a family of U-statistics $\mathcal{U}(a)$’s, which takes different a values, and $\mathcal{U}(2)$ here corresponding to the sum-of-squares-type statistic is only a special case of general $\mathcal{U}(a)$. Furthermore, we have shown not only the asymptotic independence between $\mathcal{U}(a)$ and $\mathcal{U}(\infty )$, but also the asymptotic independence among $\mathcal{U}(a)$’s of finite a values. Second, the constructed $\mathcal{U}(a)$’s are unbiased estimators, which are different from the sum-of-squares statistics usually examined in the literature. Moreover, the x’s are allowed to be dependent and the theoretical development in the covariance testing involves a two-way dependence structure, which requires different proof techniques from the existing studies.

Remark 2.4. An alternative way to construct $\mathcal{U}(\infty )$ is to standardize ${\widehat{\sigma }}_{j_1,j_2}$ by its variance $\widehat{\text{var}}({\widehat{\sigma }}_{j_1,j_2})$. Specifically, following Cai et al. [6], we take $\widehat{\text{var}}({\widehat{\sigma }}_{j_1,j_2})=n^{-1}{\sum }_{i=1}^n\{(x_{i,j_1}-{\overline{x}}_{j_1})(x_{i,j_2}-{\overline{x}}_{j_2})-{\widehat{\sigma }}_{j_1,j_2}{\}}^2$. Define $M_n^{†}={\max }_{1\le j_1\ne j_2\le p}\mid {\widehat{\sigma }}_{j_1,j_2}\mid ∕\{\widehat{\text{var}}({\widehat{\sigma }}_{j_1,j_2}){\}}^{1∕2}$ and we take $\mathcal{U}(\infty )=M_n^{†}$. Theoretically, we prove that Theorem 2.3 still holds with $\mathcal{U}(\infty )=M_n^{†}$ in Supplementary Material [28], Section B.11. Numerically, we provide the simulations in Supplementary Material [28], Section C.2, which shows that $M_n^{\ast }$ in (2.8) generally has higher power than $M_n^{†}$.

To apply hypothesis testing using the asymptotic results in Theorems 2.1 and 2.3, we need to estimate $\text{var}\{\mathcal{U}(a)\}$. In particular, we propose the following moment estimator of (2.7):

$${\mathbb{V}}_u(a)=\frac{2a!}{(P_a^n{)}^2}\sum _{1\le j_1\ne j_2\le p}\sum _{1\le i_1\ne \cdots \ne i_a\le n}\prod _{t=1}^a(x_{i_t,j_1}-{\overline{x}}_{j_1}{)}^2(x_{i_t,j_2}-{\overline{x}}_{j_2}{)}^2.$$ (2.9)

The next result establishes the statistical consistency of ${\mathbb{V}}_u(a)$.

Condition 2.4. For integer a, ${\text{lim}}_{p\to \infty }{\max }_{1\le j\le p}\mathrm{E}(x_j-{\mu }_j{)}^{8a}<\infty$.

Theorem 2.4. Under H₀ in (2.1), assume Conditions 2.1, 2.2 and 2.4 hold. Then ${\mathbb{V}}_u(a)∕\text{var}\{\mathcal{U}(a)\}\stackrel{P}{\to }1$.

Theorem 2.4 implies that the asymptotic results in Theorems 2.1 and 2.3 still hold by replacing $\text{var}\{\mathcal{U}(a)\}$ with its estimator ${\mathbb{V}}_u(a)$. Specifically, under $H_0,[\mathcal{U}(a_1)∕\sqrt{{\mathbb{V}}_u(a_1)},\dots ,\mathcal{U}(a_m)∕\sqrt{{\mathbb{V}}_u(a_m)}{]}^{⊺}\stackrel{D}{\to }\mathcal{N}(0,I_m)$ under Conditions 2.1, 2.2 and 2.4. Moreover, Theorem 2.3 implies that $\{\mathcal{U}(a)∕\sqrt{{\mathbb{V}}_u(a)}\}$’s are asymptotically independent with $\mathcal{U}(\infty )$.

2.2. Power analysis.

In this section, we analyze the asymptotic power of the U-statistics. The power of $\mathcal{U}(2)$ has been studied in the literature. In particular, [10] studied the hypothesis testing of a high-dimensional covariance matrix with H₀ : Σ = I_p. The authors characterized the boundary that distinguishes the testable region from the nontestable region in terms of the Frobenius norm ∥Σ − I_p∥_F, and showed that the test statistic proposed by [10, 13], which corresponds to $\mathcal{U}(2)$ in this paper, is rate optimal over their considered regime. However in practice, $\mathcal{U}(2)$ may be not powerful if the alternative covariance matrix is sparse with a small ∥Σ − I_p∥_F. When the alternative covariance has different sparsity levels, it is of interest to further examine which $\mathcal{U}(a)$ achieves the best power performance among the constructed family of U-statistics.

To study the test power, we establish the limiting distributions of $\mathcal{U}(a)$’s under the alternative hypothesis H_A : Σ = Σ_A, where the alternative covariance matrix Σ_A = (σ_j1,j2)_p×p is specified in the following Condition 2.5. Define J_A = {(j₁, j₂) : σ_j1,j2 ≠ 0, 1 ≤ j₁ ≠ j₂ ≤ p}, which indicates the nonzero off-diagonal entries in Σ_A. The cardinality of J_A, denoted by ∣J_A∣, then represents the sparsity level of Σ_A.

Condition 2.5. Assume ∣J_A∣ = o(p²) and for (j₁, j₂) ∈ J_A, ∣σ_j1,j2∣ = Θ(ρ), where ρ = Σ_(j1,j2)∈JA∣σ_j1,j2∣/∣J_A∣.

Here ρ represents the average signal strength of Σ_A. In our following power comparison of two U-statistics $\mathcal{U}(a)$ and $\mathcal{U}(b)$, we say $\mathcal{U}(a)$ is “better” than $\mathcal{U}(b)$, if, under the same test power, $\mathcal{U}(a)$ can detect a smaller average signal strength ρ (please see the specific definition in Criterion 1 on page 163). Condition 2.5 specifies a general family of “local” alternatives, which include banded covariance matrices, block covariance matrices and sparse covariance matrices whose nonzero entries are randomly located.

Theorem 2.5. Suppose Conditions 2.1, 2.5 and A.1 (an analogous condition to Condition 2.2* under H_A) in Supplementary Material [28] hold. For $\mathcal{U}(a)$ in (2.3) and finite integers {a₁, … , a_m}, if ρ = O(∣J_A∣^−1/a_tp^1/a_tn^−1/2) for t = 1, … , m, then as n, p → ∞,

$${\left[\frac{\mathcal{U}(a_1)-\mathrm{E}[\mathcal{U}(a_1)]}{\sigma (a_1)},\dots ,\frac{\mathcal{U}(a_m)-\mathrm{E}[\mathcal{U}(a_m)]}{\sigma (a_m)}\right]}^{⊺}\stackrel{D}{\to }\mathcal{N}(0,I_m),$$

where for a ∈ {a₁, … , a_m}, $\mathrm{E}[\mathcal{U}(a)]={\sum }_{(j_1,j_2)\in J_A}{\sigma }_{j_1,j_2}^a$ and ${\sigma }^2(a)=\text{var}[\mathcal{U}(a)]\simeq 2a!{\kappa }_1^a\times n^{-a}{\sum }_{1\le j_1\ne j_2\le p}{\sigma }_{j_1,j_1}^a{\sigma }_{j_2,j_2}^a$, which is of order Θ(p²n^−a).

Theorem 2.5 shows that for a single U-statistic $\mathcal{U}(a)$ of finite order a,

$$P\left(\frac{\mathcal{U}(a)}{\sqrt{\text{var}[\mathcal{U}(a)]}}>z_{1-\alpha }\right)\to 1-\Phi \left(z_{1-\alpha }-\frac{\mathrm{E}[\mathcal{U}(a)]}{\sqrt{\text{var}[\mathcal{U}(a)]}}\right),$$ (2.10)

where z_1−α is the upper α quantile of $\mathcal{N}(0,1)$ and Φ(·) is the cumulative distribution function of $\mathcal{N}(0,1)$. By Theorem 2.5, the asymptotic power of $\mathcal{U}(a)$ of the one-sided test depends on

$$\frac{\mathrm{E}[\mathcal{U}(a)]}{\sqrt{\text{var}[\mathcal{U}(a)]}}\simeq \frac{{\sum }_{(j_1,j_2)\in J_A}{\sigma }_{j_1,j_2}^a}{\{2a!{\kappa }_1^a{n}^{-a}{\sum }_{1\le j_1\ne j_2\le p}({\sigma }_{j_1,j_1}{\sigma }_{j_2,j_2}{)}^a{\}}^{1∕2}},$$ (2.11)

where (2.11) = Θ(∣J_A∣ρ^ap⁻¹n^a/2). It follows that when $\mathrm{E}[\mathcal{U}(a)]$ is of the same order of $\sqrt{\text{var}[\mathcal{U}(a)]}$, that is, $\mathrm{E}[\mathcal{U}(a)]=O(1)\sqrt{\text{var}[\mathcal{U}(a)]}$, the constraint of ρ in Theorem 2.5 is satisfied.

In the following power analysis, we will first compare $\mathcal{U}(a)$’s of finite a and then compare them with $\mathcal{U}(\infty )$. As we focus on studying the relationship between the sparsity level and power, we consider an ideal case where σ_j1,j2 = ρ > 0 for (j₁, j₂) ∈ J_A and σ_{j, j} = v² > 0 for j = 1, … , p. Then

$$(2.11)\simeq \mid J_A\mid {\rho }^a∕\left(\sqrt{2a!{\kappa }_1^a}{v}^{2a}p{n}^{-a∕2}\right).$$ (2.12)

We next show how the order of the “best” U-statistics changes when the sparsity level ∣J_A∣ varies. To be specific of the meaning of “best,” we compare the ρ values needed by different U-statistics to achieve the same asymptotic power. Particularly, we fix $\mathrm{E}[\mathcal{U}(a)]∕\sqrt{\text{var}[\mathcal{U}(a)]}$, that is, (2.12) to be some constant $M∕\sqrt{2}$ for different a’s and the asymptotic power of each $\mathcal{U}(a)$ is (2.10) = $1-\Phi (z_{1-\alpha }-M∕\sqrt{2})$. Then by (2.12), the ρ value such that $\mathcal{U}(a)$ attains the power above is

$${\rho }_a=\sqrt{{\kappa }_1}(a!{)}^{\frac{1}{2a}}{v}^2(Mp∕\mid J_A\mid {)}^{\frac{1}{a}}{n}^{-\frac{1}{2}}.$$ (2.13)

By the definition in (2.13), we compare the power of two U-statistics $\mathcal{U}(a)$ and $\mathcal{U}(b)$ with a ≠ b following the Criterion 1 below:

Criterion 1. We say $\mathcal{U}(a)$ is “better” than $\mathcal{U}(b)$ if ρ_a < ρ_b.

Given values of n, p, ∣J_A∣ and M, (2.13) is a function of a. Therefore, to find the “best” $\mathcal{U}(a)$, it suffices to find the order, denoted by a₀, that gives the smallest ρ_a value in (2.13). We then have the following proposition discussing the optimality among the U-statistics of finite orders in (2.3).

Proposition 2.3. Given n, p, ∣J_A∣ and any constant M ∈ (0, +∞), we consider ρ_a in (2.13) as a function of integer a, then:

(i) when ∣J_A∣ ≥ M_p, the minimum of ρ_a is achieved at a₀ = 1;

(ii) when ∣J_A∣ < M_p, the minimum of ρ_a is achieved at some a₀, which increases as M_p/∣J_A∣ increases.

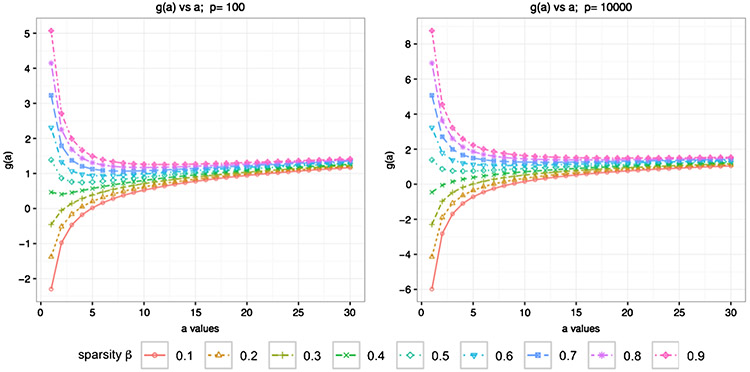
By Proposition 2.3, the order a₀ that attains the smallest value of ρ_a depends on the value of M_p/∣J_A∣ and does not have a closed-form solution. We use numerical plots to demonstrate the relationship between a₀ and the sparsity level. Particularly, let ∣J_A∣= p^2(1–β), where β ∈ (0, 1) denotes the sparsity level. To have a better visualization, we use $g(a)=\log ({\rho }_a{n}^{1∕2}{\kappa }_1^{-1∕2}{v}^{-2})=(1∕2a)\log a!+a^{-1}\log (M{p}^{2\beta -1})$ instead of ρ_a. We plot g(a) curves in Figure 1 for each β ∈ {0.1,…, 0.9} with M = 4 and p ∈ {100, 10000}. Other values of M and p are also taken, which give similar patterns to Figure 1 and are not presented.

Fig. 1.

g(a) versus a with different sparsity level β for p = 100, 10000.

Figure 1 shows that the a₀ such that g(a) attains the smallest value increases when the sparsity level β increases. In particular, when the sparsity level β ≤ 0.3, that is, when ∣J_A∣ is “very” large and then Σ_A is “very” dense, g(a) has the smallest value at a₀ = 1. This is consistent with the conclusion in Proposition 2.3 (i). When the sparsity level β is between 0.4 and 0.5, we note that a₀ = 2 achieves the minimum of g(a). This shows that when ∣J_A∣ is “moderately” large and Σ_A is “moderately” dense, $\mathcal{U}(2)$ is more powerful than $\mathcal{U}(1)$. When the sparsity level β > 0.5, we find that a₀ > 2. This implies that when ∣J_A∣ becomes smaller and Σ_A becomes sparser, U-statistics of higher orders are more powerful. Additionally, we note that a₀ increases slowly as β increases, which verifies Proposition 2.3(ii). Moreover, the curves converge as a increases and the differences of g(a) for large a values (a ≥ 6) are small. This implies that when selecting the range of considered orders of U-statistics, it suffices to select an upper bound with a = 6 or 8, which gives better or similar ρ_a values to those larger a’s.

In summary, when ∣J_A∣ is large, that is, Σ_A is dense, a small a tends to obtain a smaller lower bound in terms of ρ. But when ∣J_A∣ decreases, that is, Σ_A becomes sparse, a U-statistic of large finite order (or the maximum-type U-statistic as shown next) tends to obtain a smaller lower bound in ρ. This observation is consistent with the existing literature [7, 8, 10, 13].

Next, we proceed to examine the power of the maximum-type test statistic $\mathcal{U}(\infty )$, and compare it with the U-statistics $\mathcal{U}(a)$ of finite a defined in (2.3). By [8], the rejection region for $\mathcal{U}(\infty )$ with significance level α is

$$\mid \mathcal{U}(\infty )\mid \ge t_p≔n^{-1∕2}\sqrt{4\log p-\log \log p-\log (8\pi )-2\log \log (1-\alpha {)}^{-1}}.$$

Note $t_p\simeq 2\sqrt{\log p∕n}$ and under alternative, the power for $\mathcal{U}(\infty )$ is

$$P(\mid \mathcal{U}(\infty )\mid \ge t_p).$$ (2.14)

As discussed, we consider the alternatives satisfying Conditions 2.2* and 2.5, σ_{j1, j2} = ρ > 0 for (j₁, j₂) ∈ J_A, and σ_{j, j} = ν² for j = 1,…,p. For simplicity, we assume E(x) = μ and ν² are given, and focus on the simplified

$$\mathcal{U}(\infty )=\underset{1\le j_1<j_2\le p}{\max }\mid v^{-2}{n}^{-1}\sum _{i=1}^n(x_{i,j_1}-{\mu }_{j_1})(x_{i,j_2}-{\mu }_{j_2})\mid .$$ (2.15)

We show in the following proposition when the power of $\mathcal{U}(\infty )$ asymptotically converges to 1 or is strictly smaller than 1 under alternative.

Proposition 2.4. Under the considered alternative Σ_A above, suppose max_j=1,…,p Ee^{t₀∣x_j–μ_j∣ς} < ∞ for some 0 < ς ≤ 2 and t₀ > 0, and log p = o(n^β) with β = ς/(4 + ς). Then for (2.15), when n, p → ∞:

(i) there exists a constant c₁ > 2 such that if $\rho \ge c_1\sqrt{\log p∕n}$, (2.14) → 1;

(ii) there exists another constant 0 < c₂ < 2 such that when $\rho \le c_2\sqrt{\log p∕n}$, Condition 2.2* holds for κ₁ ≤ 1 and $\mid J_A\mid =o(1)p^{\frac{2(1-c_2∕2{)}^2}{{\kappa }_1+m}}(\log p{)}^{\frac{1}{2}-\frac{1}{2({\kappa }_1+m)}}$ for some m > 0, we have (2.14) ≤ log(1 – α)⁻¹.

Recall that Proposition 2.3 shows that there exists a finite integer a₀, such that ρ_a0 is the minimum of (2.13), and ρ_a0 is a lower bound of ρ value for the finite-order U-statistics to achieve the given asymptotic power. With Propositions 2.3 and 2.4, we next compare the finite-order U-statistics defined in (2.3) with the maximum-type test statistic $\mathcal{U}(\infty )$.

Proposition 2.5. Under the conditions of Theorem 2.5 and Proposition 2.4, for any finite integer a, there exist constants c₁ and c₂ such that when p is sufficiently large:

(i) For any M, when $\mid J_A\mid <c_1^{-a}(a!{)}^{\frac{1}{2}}{\kappa }_1^{\frac{a}{2}}(\log p{)}^{-\frac{a}{2}}Mp$, $\mathcal{U}(\infty )$ has higher asymptotic power than $\mathcal{U}(a)$.

(ii) When M is big enough and $\mid J_A\mid >c_2^{-a}(a!{)}^{\frac{1}{2}}{\kappa }_1^{\frac{a}{2}}(\log p{)}^{-\frac{a}{2}}Mp$, $\mathcal{U}(a)$ has higher asymptotic power than $\mathcal{U}(\infty )$.

From Proposition 2.3, we know when M_p/∣J_A∣ = O(1), there exists a finite a₀ such that $\mathcal{U}(a_0)$ is the “best” among all the finite-order U-statistics; in this case, Proposition 2.5(ii) further indicates that $\mathcal{U}(a_0)$ has higher asymptotic power than $\mathcal{U}(\infty )$. Specifically, if M_p/∣J_A∣ < 1, a₀ = 1, then $\mathcal{U}(1)$ is the “best” and its lowest detectable order of ρ is Θ(p∣J_A∣⁻¹n^−1/2). More interestingly, when Σ_A is moderately dense or moderately sparse with M_p/∣J_A∣ > 1 and bounded, some U-statistic of finite order a₀ > 1 would become the “best.” By Figure 1, the value of a₀ increases as Σ_A becomes denser. On the other hand, when Σ_A is “very” sparse with $\mid J_A\mid <c_1^{-a_0}(a_0!{)}^{\frac{1}{2}}{\kappa }_1^{\frac{a_0}{2}}(\log p{)}^{-\frac{a_0}{2}}Mp$, $\mathcal{U}(\infty )$ is the “best” and its lowest detectable order of ρ is $\Theta (\sqrt{\log p∕n})$.

Remark 2.5. The above power comparison results are under the constructed family of U-statistics. We note that additional formulation may further enhance the test power. For instance, [11, 73] showed that an adaptive thresholding in certain ℓ_p-type test statistics can achieve high power under the alternatives with sparse and faint signals. It is of interest to incorporate the adaptive thresholding into the constructed family of U-statistics, which is left for future study.

R_emark 2.6. The analysis above focuses on the ideal case where the nonzero off-diagonal entries of Σ_A are the same for illustration. When these entries of Σ_A are different, similar analysis still applies by Theorem 2.5 for general covariance matrices. In particular, the asymptotic power of $\mathcal{U}(a)$ depends on the mean variance ratio (2.11) and ${\rho }_a=\sqrt{{\kappa }_1}{n}^{-1∕2}(a!{)}^{1∕2a}\times (M{\sum }_{j=1}^p{\sigma }_{j,j}^a∕{\sum }_{1\le j_1,j_2\le p}{\sigma }_{j_1,j_2}^a{)}^{1∕a}$. We can then obtain conclusions similar to Propositions 2.3-2.5. One interesting case is when Σ_A contains both positive and negative entries; the same analysis applies for even-order U-statistics, since ${\sigma }_{j_1,j_2}^a$’s are all nonnegative for even a. On the other hand, the odd-order U-statistics would have low power, since ${\sum }_{1\le j_1\ne j_2\le p}{\sigma }_{j_1,j_2}^a$’s could be small due to the cancellation of positive and negative ${\sigma }_{j_1,j_2}^a$. We have conducted simulations when the nonzero σ_j1,j2’s are different in Section 3.1, and the results exhibit consistent patterns as expected.

2.3. Application to adaptive testing and computation.

Adaptive testing.

Power analysis in Section 2.2 shows that when the sparsity level of the alternative changes, the test statistic that achieves the highest power could vary. However, since the truth is often unknown in practice, it is unclear which test statistic should be chosen. Therefore, we develop an adaptive testing procedure by combining the information from U-statistics of different orders, which would yield high power against various alternatives.

In particular, we propose to combine the U-statistics through their p-values, which is widely used in literature [49, 52, 71]. One popular method is the minimum combination, whose idea is to take the minimum p-value to approximate the maximum power [52, 67, 71]. Specifically, let Γ be a candidate set of the orders of U-statistics, which contains both finite values and TO. We compute p-values p_a’s of the U-statistics $\mathcal{U}(a)$’s satisfying a ∈ Γ. The minimum combination takes the statistic T_adpUmin = min{p_a : a ∈ Γ} and has the asymptotic p-value p_adpUmin = 1 – (1 – T_adpUmin)^∣Γ∣, where ∣Γ∣ denotes the size of the candidate set Γ. We reject H₀ if p_adpUmin < α. Under H₀, p_a’s are asymptotically independent and uniformly distributed by the theoretical results in Section 2.1. The type I error is asymptotically controlled as $P(p_{\text{adpUmin}}<\alpha )=P({\text{min}}_{a\in \Gamma }{p}_a<p_{\alpha }^{\ast })\to \alpha$, where $p_{\alpha }^{\ast }=1-(1-\alpha {)}^{1∕\mid \Gamma \mid }$. Since $P({\text{min}}_{a\in \Gamma }{p}_a<p_{\alpha }^{\ast })\ge P(p_a<p_{\alpha }^{\ast })$, the power of the adaptive test goes to 1 if there exists a ∈ Γ such that the power of $\mathcal{U}(a)$ goes to 1. We note that the power of the adaptive test is not necessarily higher than that of all the U-statistics. This is because the power of $\mathcal{U}(a)$ is P(p_a < α), and is different from $P(p_a<p_{\alpha }^{\ast })$ since $p_{\alpha }^{\ast }<\alpha$ when ∣Γ∣ > 1. Based on our extensive simulations, we find that the adaptive test is usually close to or even higher than the maximum power of the U-statistics.

Remark 2.7. Fisher’s method [49] is another popular method for combining independent p-values. It has the test statistic $T_{\text{adpUf}}=-2{\sum }_{k=1}^{\mid \Gamma \mid }\log p_k$, which converges to ${\chi }_{2\mid \Gamma \mid }^2$ under H₀. By our simulations, the minimum combination and Fisher’s method are generally comparable, while Fisher’s method has higher power under several cases. Moreover, we can also use other methods to combine the p-values, such as higher criticism [16, 17]. We leave the study of how to efficiently combine the p-values for future research.

We select the candidate set Γ by the power analysis in Section 2.2. We would recommend including {1, 2,…, 6, ∞}, which can be powerful against a wide spectrum of alternatives. In particular, by Propositions 2.3 and 2.5, we include a = 1, 2 that are powerful against dense signals; a = ∞ that is powerful against sparse signals; and also a = {3,…, 6} for the moderately dense and moderately sparse signals. By Figure 1, it generally suffices to choose finite a up to 6–8, which often give similar/better performance to/than larger a values. The simulations in Section 3.1 confirm the good performance of this choice of Γ; and the proposed adaptive test appears to well approximate the “best” performance even when Γ may not always contain the unknown “optimal” U-statistics.

We would like to mention that the adaptive procedure can be generalized to other testing problems, as long as similar theoretical properties are given, such as the examples in Section 4.

Computation.

Next, we discuss the computation in the adaptive testing. A direct calculation following the form of $\mathcal{U}(a)$ in (2.3) and $\mathbb{V}(a)$ in (2.9) would be computationally expensive for large a with a cost of O(p²n^2a). To address this issue, we introduce a method that can reduce the cost.

We first consider a simplified setting when E(x_i,j) = 0 to illustrate the idea. As discussed in Remark 2.2, we examine $\tilde{\mathcal{U}}(a)$ defined in (2.5). Let $\mathcal{L}=\{(j_1,j_2):1\le j_1\ne j_2\le p\}$ denote the set of index tuples, and for each index tuple $l=(j_1,j_2)\in \mathcal{L}$, define s_i,l = x_i,j1 x_i,j2. Note that $\tilde{\mathcal{U}}(a)=(P_a^n{)}^{-1}{\sum }_{l\in \mathcal{L}}{\mathcal{U}}_l(a)$, where ${\mathcal{U}}_l(a)={\sum }_{1\le i_1\ne \cdots \ne i_a\le n}{\prod }_{k=1}^a{s}_{i_k,l}$. Calculating ${\mathcal{U}}_l(a)$ directly is of order O(n^a). We then focus on reducing the computational cost of ${\mathcal{U}}_l(a)$. For $l\in \mathcal{L}$ and finite integers t₁,…,t_k, define

$$V_l^{(t_1,\dots ,t_k)}=\prod _{r=1}^k\left(\sum _{i=1}^n{s}_{i,l}^{t_r}\right),U_l^{(t_1,\dots ,t_k)}=\sum _{1\le i_1\ne \cdots \ne i_k\le n}\prod _{r=1}^k{s}_{i_1,l}^{t_r}.$$ (2.16)

We can see that ${\mathcal{U}}_l(a)=U_l^{1_a}$ with 1_a being an a-dimensional vector of all ones, and $U_l^{(a)}=V_l^{(a)}$ for any finite integer a. To reduce the computational cost of ${\mathcal{U}}_l(a)$, the main idea is to obtain $U_l^{1_a}$ from $V_l^{(t_1,\dots ,t_k)}$, whose computational cost is O(n). In particular, ${\mathcal{U}}_l(a)$ can be attained iteratively from $V_l^{(t_1,\dots ,t_k)}$ based on the following equation:

$$U_l^{(k,1_{r-k})}=V_l^{(k)}\times U_l^{1_{r-k}}-(r-k)\times U_l^{(k+1,1_{r-k-1})},$$ (2.17)

which follows from the definitions. Algorithm 1 below summarizes the steps.

Algorithm 1:

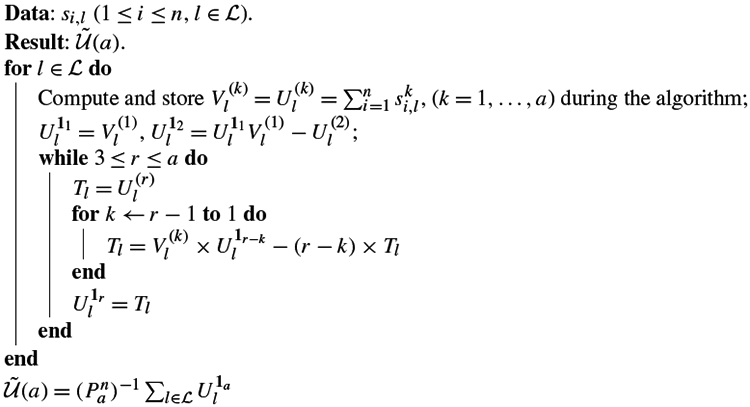
Iterative computation implementation

We illustrate the idea of the algorithm by some examples. By definition, $U_l^{(1)}=V_l^{(1)}$, which can be computed with cost O(n). Next, consider in (2.17), if r = 2 and k = 1, then $U_l^{(1,1)}=V_l^{(1)}\times U_l^{(1)}-(2-1)\times U_l^{(2)}=V_l^{(1)}\times V_l^{(1)}-V_l^{(2)}$, which yields $U_l^{1_2}$ with cost O(n). For $U_l^{1_3}$, we first take r = 3 and k = 2 in (2.17), then with cost O(n), we have $U_l^{(2,1)}=V_l^{(2)}\times U_l^{(1)}-U_l^{(3)}=V_l^{(2)}\times V_l^{(1)}-V_l^{(3)}$, as $V_l^{(k)}=U_l^{(k)}$ by the definition. Given $U_l^{1_2}$ and $U_l^{(2,1)}$, we obtain $U_l^{(1,1_2)}=V_l^{(1)}\times U_l^{1_2}-2\times U_l^{(2,1_1)}$. Thus $U_l^{1_3}$ is also computed with cost O(n). Iteratively, for any finite integer a, we can obtain $U_l^{1_a}$ from $V_l^{(t_1,\dots ,t_k)}$ whose computational cost is O(n). More closed-form formulae representing $U_l^{1_a}$ by $V_l^{(t_1,\dots ,t_k)}$ are given in Section C.1.1 of Supplementary Material [28].

Algorithm 1 reduces the computational cost of $\tilde{\mathcal{U}}(a)$ from O(p²n^a) to O(p²n). Its idea is general and can be extended to compute other different U-statistics by changing the input s_i,l. In particular, the variance estimator $\mathbb{V}(a)$ can be computed with cost O(p²n) by specifying $s_{i,l}=(x_{i,j_1}-{\overline{x}}_{j_1}{)}^2(x_{i,j_2}-{\overline{x}}_{j_2}{)}^2$, for each $l\in \mathcal{L}=\{(j_1,j_2):1\le j_1\ne j_2\le p\}$. Then $\mathbb{V}(a)=2a!(P_a^n{)}^{-2}{\sum }_{l\in \mathcal{L}}{\sum }_{l\le i_1\ne \cdots \ne i_a\le n}{\prod }_{k=1}^a{s}_{i_k,l}$ and Algorithm 1 can be applied. Moreover, when E(x_i,j) is unknown, $\mathcal{U}(a)$ can still be computed with cost O(p²n) using the iterative method similar to Algorithm 1. The details are provided in Section C.1.2 of Supplementary Material [28].

3. Simulations and real data analysis.

3.1. Simulations.

We conduct simulation studies to evaluate the performance of the proposed adaptive testing procedures, and investigate the relationship between the power and sparsity levels. For one-sample covariance testing discussed in Section 2, we generate n i.i.d. p-dimensional x_i for i = 1,…,n, and consider the following five simulation settings.

Setting 1: x_i has p i.i.d. entries of $\mathcal{N}(0,1)$ and Gamma(2, 0.5), respectively. Under each case, we take n = 100 and p ∈ {50, 100, 200,400, 600, 800, 1000} to verify the theoretical results under H₀ and the validity of the adaptive test across different n and p combinations.

For the following settings 2–5, we generate x_i from multivariate Gaussian distributions with mean zero and different covariance matrices Σ_A’s.

Setting 2: ${\Sigma }_A=(1-\rho )I_p+\rho 1_{p,k_0}{1}_{p,k_0}^{⊺}$, where 1_p,k0 is a p-dimensional vector with the first k₀ elements one and the rest zero. We take (n, p) ∈ {(100, 300), (100, 600), (100, 1000)}, and study the power with respect to different signal sizes ρ and sparsity levels k₀.

Setting 3: The diagonal elements of Σ_A are all one and ∣J_A∣ number of off-diagonal elements are ρ with random positions. We take (n, p) ∈ {(100, 600), (100, 1000)} and let the signal size ρ and sparsity level ∣J_A∣ vary to examine how the power changes accordingly.

Setting 4: The diagonal elements of Σ_A are all one and ∣J_A∣ number of off-diagonal elements are uniformly generated from (0, 2ρ) with random positions. We take (n, p) = (100, 1000) and similarly let the signal size ρ and sparsity level ∣J_A∣ vary to examine how the power changes accordingly.

Setting 5: We consider the multivariate models in [13]. Specifically, for each i = 1,…,n, x_i = Ξz_i + μ, where Ξ is a matrix of dimension p × m, and z_i’s are i.i.d. Gaussian or Gamma random vectors. Under null hypothesis, m = p, Ξ = I_p, μ = 21_p; under alternative hypothesis, m = p + 1, $\Xi =(\sqrt{1-\rho }{I}_p,\sqrt{2\rho }{1}_p)$, $\mu =2(\sqrt{1-\rho }+\sqrt{2\rho })1_p$. We also take the n and p combination in [13] with (n, p) ∈ {(40, 159), (40, 331), (80, 159), (80, 331), (80, 642)}.

We compare several methods in the literature, including both maximum-type and sum-of-squares-type tests. In particular, the maximum-type test statistic in Jiang [36] is taken as $\mathcal{U}(\infty )$ in this framework. Since the convergence in [36] is known to be slow, we use permutation to approximate the distribution in the simulations. In addition, we consider some sum-of-squares-type methods. Specifically, we examine the identity and sphericity tests in Chen et al. [13], which are denoted as “Equal” and “Spher,” respectively. We also compare the methods in Ledoit and Wolf [42] and Schott [57], which are referred to as “LW” and “Schott,” respectively.

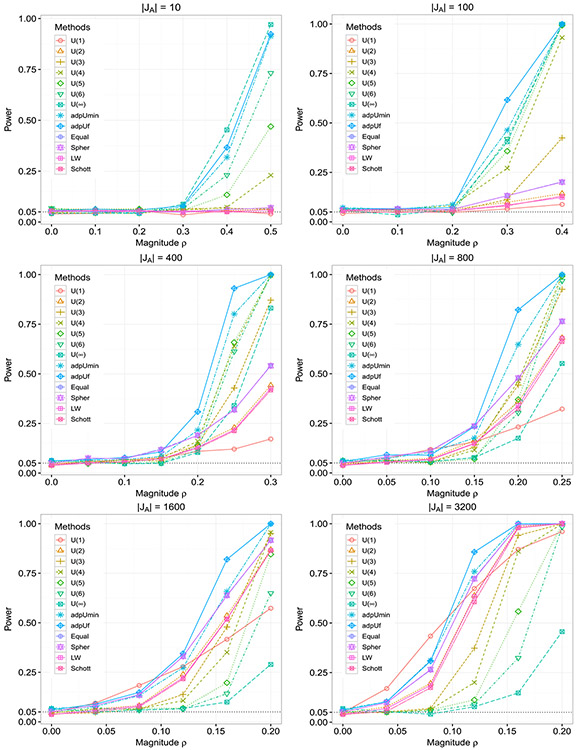
To illustrate, Figure 2 summarizes the numerical results for the setting 3 when n = 100 and p = 1000. All the results are based on 1000 simulations at the 5% nominal significance level. In Figure 2, we present the power of single U-statistics with orders in {1,…, 6, ∞}. “adpUmin” and “adpUf” represent the results of the adaptive testing procedure using the minimum combination and Fisher’s method in Section 2.2, respectively. The simulation results show that the type I error rates of the U-statistics and adaptive test are well controlled under H₀. In addition, Figure 2 exhibits several patterns that are consistent with the power analysis in Section 2.2. First, it shows that among the U-statistics, when ∣J_A∣ is very small, $\mathcal{U}(\infty )$ performs best; and when ∣J_A∣ increases, the performances of some U-statistics of finite orders catch up. For instance, when ∣J_A∣ = 100, $\mathcal{U}(6)$ and $\mathcal{U}(\infty )$ are similar and are better than the other U-statistics; when ∣J_A∣ = 400, $\mathcal{U}(4)$ and $\mathcal{U}(5)$ are similar and better than the other U-statistics. When Σ_A is relatively dense, $\mathcal{U}(2)$ and $\mathcal{U}(1)$ become more powerful. Particularly, when ∣J_A∣ = 1600, $\mathcal{U}(2)$ is powerful; when ∣J_A∣ becomes larger, such as when ∣J_A∣ = 3200, $\mathcal{U}(1)$ is overall the most powerful. Second, Figure 2 shows that “LW,” “Schott,” “Equal,” “Spher” and $\mathcal{U}(2)$ perform similarly under various cases. In particular, these methods are not powerful when the alternative is sparse but becomes more powerful when the alternative gets denser. This is because they are all sum-of-squares-type statistics that target at dense alternatives. Third and importantly, the two adaptive tests “adpUmin” and “adpUf” maintain high power across different settings. Specifically, they perform better than most single U-statistics: their powers are usually close to or even higher than the best single U-statistic. Moreover, “adpUmin” and “adpUf” generally have higher power than the compared existing methods. We also note that “adpUf” overall performs better than “adpUmin” in this simulation setting. In summary, Figure 2 demonstrates the relationship between the sparsity levels of alternatives and the power of the tests, confirming the theoretical conclusions in Section 2.2. Notably, the proposed adaptive testing procedure is powerful against a wide range of alternatives, and thus advantageous in practice when the true alternative is unknown.

Fig. 2.

Power comparison.

Due to the space limitation, we provide other extensive numerical studies in Supplementary Material [28], Section C.2. The conclusions are similar to those of Figure 2, and consistent with the theoretical results in Section 2.2. In particular, the results show that the empirical sizes of the tests are close to the nominal level, suggesting the good finite-sample performance of the asymptotic approximations. Moreover, under highly dense alternatives with only nonnegative entries in the covariance matrix, $\mathcal{U}(1)$ is the most powerful one among the $\mathcal{U}(a)$’s and the other tests in [13, 42, 57], in agreement with the results in Propositions 2.3 and 2.5. Furthermore, the proposed adaptive testing procedures often have higher power than most single U-statistics.

3.2. Real data analysis.

Alzheimer’s disease (AD) is the most prevalent neurodegenerative disease [56] and is ranked as the sixth leading cause of death in the US [68]. Every 65 seconds, someone in the US develops AD [2]. To advance our understanding of AD, the Alzheimer’s Disease Neuroimaging Initiative (ADNI) was started in 2004, collecting extensive genetic data for both healthy individuals and AD patients. To gain insight into the genetic mechanisms of AD, one can test a single SNP a time. However, due to a relatively small sample size of the ADNI data, scanning across all SNPs failed to identify any genomewide significant SNP (with p-value < 5 × 10⁻⁸) [40]. To date, the largest meta-analysis of more than 600,000 individuals identified 29 significant risk loci [35] and can only explain a small proportion of AD variance. On the other hand, a group of functionally related genes as annotated in a biological pathway are often involved in the same disease susceptibility and progression [29]. Thus, pathway-based analyses, which jointly analyze a group of SNPs in a biological pathway, have become increasingly popular. We retrieve a total of 214 pathways from the KEGG database [39] for the subsequent analysis.

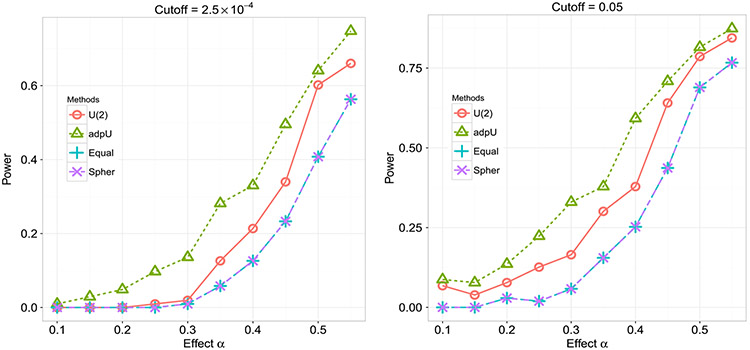
Although pathway-based analyses with KEGG pathways are common in real studies, formally testing the correlations of the genes in a KEGG pathway has been largely untouched. Here, we apply our method and other competing methods in [13] to test if all the genes in a pathway have correlated gene expression levels. Perhaps as expected, all methods reject the null hypothesis for all pathways with highly significant p-values, since the KEGG pathways are constructed to include only the genes with similar function into the same pathway [39], while similar function often implies co-expression (and vice versa). To compare the performance of the different tests, for each pathway we randomly select 50 subjects and restrict our analysis to pathways of at least 50 genes, leading to 103 pathways for the following analysis. Then we perturb the data by shuffling the gene expression levels of randomly selected 100(1 – α)% genes in a pathway before applying each test. Figure 3 shows the performance of the tests with two significance cutoffs, where “$\mathcal{U}(2)$” represents the single $\mathcal{U}(2)$ statistic, “adpU” represents our proposed adaptive testing procedure using the minimum combination with candidate U-statistics of orders in {1,…, 6, ∞}, and “Equal” and “Spher” represent the identity and sphericity tests in [13], respectively. Because all pathways are highly significant with all samples, we can treat all pathways as the true positives. Due to the adaptiveness of our proposed testing procedure, “adpU” identifies more significant pathways than the competing methods across all the levels of data perturbation (mimicking the varying sparsity levels of the alternatives).

Fig. 3.

Power comparison of different methods with ADNI data.

4. Other high-dimensional examples.

In this section, we apply the proposed U-statistics framework to other high-dimensional testing problems, including testing means, two-sample covariances, and regression coefficients in generalized linear regression models. Similar theoretical results to Section 2 are developed, with detailed proofs and related simulation studies provided in Supplementary Material [28].

4.1. Mean testing.

Testing mean vectors is widely used in many statistical analysis and applications [1, 50]. Under high-dimensional scenarios, for example, in genome-wide studies, dimension of the data is often much larger than the sample size, so traditional multivariate tests such as Hotelling’s T²-test either cannot be directly applied or have low power [18]. To address this issue, several new procedures for testing high-dimensional mean vectors have been proposed [4, 9, 11, 12, 16, 17, 25-27, 60, 62, 67]. However, many of the statistics only target at either sparse or dense alternatives, and suffer from loss of power for other types of alternatives. We next apply the U-statistics framework to one-sample and two-sample mean testing problems.

One-sample mean testing.

We first discuss the one-sample mean vector testing. Assume that x₁,…, x_n are n i.i.d. copies of a p-dimensional real-valued random vector x = (x₁,…,x_p)^⊤ with mean vector μ = (μ₁,…,μ_p)^⊤, covariance matrix Σ = {σ_j1,j2 : 1 ≤ j₁, j₂ ≤ p}. We want to conduct the global test on H₀ : μ = μ₀ where μ₀ = (μ_1,0,…,μ_p,0)^⊤ is given.

Similar to previous discussion, the parameter set that we are interested in is $\mathcal{E}=\{{\mu }_1-{\mu }_{1,0},\dots ,{\mu }_p-{\mu }_{p,0}\}$. For each j = 1,…, p, E(x_i,j) = μ_j, so K_j(x_i) = x_i,j – μ_j,0 is a kernel function, which is a simple unbiased estimator of the target. Following our construction, the U-statistic for finite a is

$$\mathcal{U}(a)=\sum _{j=1}^p\frac{1}{P_a^n}\sum _{1\le i_1\ne \cdots \ne i_a\le n}\prod _{k=1}^a(x_{i_k,j}-{\mu }_{j,0}),$$ (4.1)

which targets at $\Vert \mathcal{E}{\Vert }_a^a={\sum }_{j=1}^p({\mu }_j-{\mu }_{j,0}{)}^a$, and the U-statistic corresponding to $\Vert \mathcal{E}{\Vert }_{\infty }$ is $\mathcal{U}(\infty )={\max }_{1\le j\le p}{\sigma }_{j,j}^{-1}({\overline{x}}_j-{\mu }_{0,j}{)}^2$ with ${\overline{x}}_j={\sum }_{i=1}^n{x}_{i,j}∕n$.

Given the statistics, we have the theoretical results similar to Theorems 2.1-2.3. The following Theorems 4.1-4.2 are established under similar conditions to that of Theorems 2.1-2.3. Due to the limited space, we provide the conditions and corresponding discussions in Supplementary Material [28].

Theorem 4.1. Under H₀: μ = μ₀, assume Condition A.2 in Supplementary Material [28]. Then for any finite integers {a₁,…,a_m}, as n, p → ∞, $[\mathcal{U}(a_1)∕\sigma (a_1),\dots ,\mathcal{U}(a_m)∕\sigma (a_m){]}^{⊺}\stackrel{D}{\to }\mathcal{N}(0,I_m)$, where ${\sigma }^2(a)=\text{var}[\mathcal{U}(a)]={\sum }_{i=1}^p{\sum }_{j=1}^{p}a!{\sigma }_{i,j}^a∕P_a^n$ with the order of Θ(a!pn^−a).

Theorem 4.2. Under H₀: μ = μ₀, assume Condition A.3 in Supplementary Material [28]. Then $\forall u\in \mathbb{R}$, $P(n\mathcal{U}(\infty )-{\tau }_p\le u)\to \text{exp}\{-{\pi }^{-1∕2}\text{exp}(-u∕2)\}$, as n, p → ∞, where τ_p = 2 log p – log log p. In addition, for any finite integer a, $\{\mathcal{U}(a)∕\sigma (a)\}and\{n\mathcal{U}(\infty )-{\tau }_p\}$ are asymptotically independent.

By Theorems 4.1 and 4.2, we obtain the asymptotic independence among the U-statistics and the corresponding limiting distributions of the U-statistics under H₀. Under the alternative hypothesis, since the power analysis of the one-sample mean testing is similar to that of the two-sample case, we delay the power analysis after presenting the asymptotic independence property of the proposed U-statistics in the two-sample mean testing problem.

Two-sample mean testing.

Next, we discuss the two-sample mean testing problem. Suppose we have two groups of p-dimensional observations $\{{\mathbf{x}}_i{\}}_{i=1}^{n_x}$ and $\{{\mathbf{y}}_i{\}}_{i=1}^{n_y}$, which are i.i.d. copies of two independent random vectors x = (x₁, … , x_p)^⊤ and y = (y₁, … , y_p)^⊤, respectively. Suppose E(x) = μ = (μ₁, … , μ_p)^⊤, E(y) = ν = (ν₁, … , ν_p)^⊤, cov(x) = Σ_x and cov(y) = Σ_y. We write n = n_x + n_y and assume n_x = Θ(n_y). For easy illustration, we first consider Σ_x = Σ_y = Σ = {σ_{j1, j2} : 1 ≤ j₁, j₂ ≤ p}. We will then discuss the case when Σ_x ≠ Σ_y, where similar analysis applies.

The two-sample mean testing examines H₀: μ = ν versus H_A: μ ≠ ν, then $\mathcal{E}=({\mu }_1-v_1,\dots ,{\mu }_p-v_p{)}^{⊺}$. For 1 ≤ j ≤ p, 1 ≤ k ≤ n_x, 1 ≤ s ≤ n_y, K_j(x_k, y_s) = x_k,j − y_s,j is a simple unbiased estimator of μ_j − ν_j, and thus we construct $\mathcal{U}(a)={\sum }_{j=1}^p(P_a^{n_x}{P}_a^{n_y}{)}^{-1}\times {\sum }_{1\le k_1\ne \cdots \ne k_a\le n_x;1\le s_1\ne \cdots \ne s_a\le n_y}{\prod }_{t=1}^a(x_{k_t,j}-y_{s_t,j})$, which is also equivalent to

$$\mathcal{U}(a)=\sum _{j=1}^p\sum _{c=0}^a\left(\begin{array}{c}\hfill a\hfill \\ \hfill c\hfill \end{array}\right)\frac{(-1{)}^{a-c}}{P_c^{n_x}{P}_{a-c}^{n_y}}\sum _{\begin{array}{c}\hfill 1\le k_1\ne \cdots \ne k_c\le n_x\hfill \\ \hfill 1\le s_1\ne \cdots \ne s_{a-c}\le n_y\hfill \end{array}}\prod _{t=1}^c{x}_{k_t,j}\prod _{m=1}^{a-c}{y}_{s_m,j}.$$ (4.2)

We can check that (4.2) satisfies $\mathrm{E}\{\mathcal{U}(a)\}={\sum }_{j=1}^p({\mu }_j-v_j{)}^a$, so $\mathcal{U}(a)$ is an unbiased estimator of $\Vert \mathcal{E}{\Vert }_a^a={\sum }_{j=1}^p({\mu }_j-v_j{)}^a$. On the other hand, for $\Vert \mathcal{E}{\Vert }_{\infty }$, following the maximum-type test statistic in Cai et al. [9], we have

$$\mathcal{U}(\infty )=\underset{1\le j\le p}{\max }{\sigma }_{j,j}^{-1}({\overline{x}}_j-{\overline{y}}_j{)}^2,$$ (4.3)

where ${\overline{x}}_j={\sum }_{i=1}^{n_x}{x}_{i,j}∕n_x$, ${\overline{y}}_j={\sum }_{i=1}^{n_y}{y}_{i,j}∕n_y$. We then obtain results similar to Theorems 2.1, 2.3 and 2.5. As the conditions are similar to those in Section 2, we only keep the key conclusions, and the details of conditions and discussions are given in Supplementary Material [28], Section A.8.

Theorem 4.3. Under Condition A.4 in Supplementary Material [28], Σ_x = Σ_y and H₀: μ = ν, for any finite integers (a₁, … , a_m), as n, p → ∞, $[\mathcal{U}(a_1)∕\sigma (a_1),\dots ,\mathcal{U}(a_m)∕\sigma (a_m){]}^{⊺}\stackrel{D}{\to }\mathcal{N}(0,I_m)$, where ${\sigma }^2(a)\simeq a!{\sum }_{j_1,j_2=1}^p(n_x+n_y{)}^a{\sigma }_{j_1,j_2}^a∕(n_x{n}_y{)}^a$ is of the order Θ(a!pn^−a).

Theorem 4.4. Under Condition A.4 in Supplementary Material [28], Σ_x = Σ_y and H₀: μ = ν, $\forall u\in \mathbb{R}$, $P(\frac{n_x{n}_y}{n_x+n_y}\mathcal{U}(\infty )-{\tau }_p\le u)\to \text{exp}\{-{\pi }^{-1∕2}\text{exp}(-u∕2)\}$, as n, p → ∞, where τ_p = 2log p − log log p. Moreover, $\{\mathcal{U}(a)∕\sigma (a)\}$ of finite integer a and $\{n_x{n}_y\mathcal{U}(\infty )∕(n_x+n_y)-{\tau }_p\}$ are asymptotically independent.

Theorems 4.3 and 4.4 provide the asymptotic properties of finite-order U-statistics and $\mathcal{U}(\infty )$ under H₀. To analyze the power of $\mathcal{U}(a)$’s, we derive the asymptotic results of $\mathcal{U}(a)$’s under the alternative hypotheses. We focus on the two-sample mean testing problem, while one-sample mean testing can be obtained similarly. Specifically, we consider the alternative ${\mathcal{E}}_A=\{{\mu }_j-v_j=\rho >0$ for j = 1, … , k₀; μ_j − ν_j = 0 for j = k₀ + 1, … , p}. We then obtain similar conclusions to Theorem 2.5.

Theorem 4.5. Assume Condition A.4 in Supplementary Material [28] and k₀ = o(p). For any finite integers {a₁, … , a_m}, if ρ in ${\mathcal{E}}_A$ satisfies $\rho =O(k_0^{-1∕a_t}{p}^{1∕(2a_t)}{n}^{-1∕2})$ for t = 1, … , m, then $[\mathcal{U}(a_1)-\mathrm{E}\{\mathcal{U}(a_1)\}]∕\sigma (a_1),\dots ,[\mathcal{U}(a_m)-\mathrm{E}\{\mathcal{U}(a_m)\}]∕\sigma (a_m){]}^{⊺}\stackrel{D}{\to }\mathcal{N}(0,I_m)$, as n, p → ∞. Here, $\mathrm{E}[\mathcal{U}(a)]=\Vert {\mathcal{E}}_A{\Vert }_a^a=k_0{\rho }^a$ and ${\sigma }^2(a)=\text{var}\{\mathcal{U}(a)\}\simeq V_a$, with $V_a=a!{\sum }_{j_1,j_2=k_0+1}^p(n_x+n_y{)}^a{\sigma }_{j_1,j_2}^a∕(n_x{n}_y{)}^a$ of the order Θ(a!pn^−a).

Next, we compare the power of different U-statistics under alternatives with different sparsity levels. Theorem 4.5 shows that under the local alternatives, the asymptotic power of $\mathcal{U}(a)$ mainly depends on $\mathrm{E}\{\mathcal{U}(a)\}∕\sqrt{\text{var}\{\mathcal{U}(a)\}}$. Therefore, by Theorem 4.5, given constant M > 0, for each $\mathcal{U}(a)$, if $\rho =M^{1∕a}{k}_0^{-1∕a}{V}_a^{1∕(2a)}$, then $\mathrm{E}\{\mathcal{U}(a)\}∕\sqrt{\text{var}\{\mathcal{U}(a)\}}\simeq M$; that is, different $\mathcal{U}(a)$’s have the same power asymptotically. For easy illustration, we consider σ_{j1, j2} = 1 when j₁ = j₂ ∈ {k₀ + 1, … , p}, and σ_{j1, j2} = 0 when j₁ ≠ j₂ ∈ {k₀ + 1, … , p}, then $M^{1∕a}{k}_0^{-1∕a}{V}_a^{1∕(2a)}\simeq {\rho }_a$ with

$${\rho }_a≔a{!}^{\frac{1}{2a}}(M\sqrt{p}∕k_0{)}^{\frac{1}{a}}\{(n_x+n_y)∕(n_x{n}_y){\}}^{\frac{1}{2}}.$$ (4.4)

Therefore, similar to the analysis in Section 2.2, to find the “best” $\mathcal{U}(a)$, it suffices to find the order, denoted by a₀, that gives the minimum ρ_a in (4.4). We have the following result similar to Proposition 2.3.

Proposition 4.1. Given any constant M ∈ (0, + ∞) and n, p, k₀, we consider ρ_a in (4.4) as a function of positive integers a, then:

(i) when $k_0\ge M\sqrt{p}$, the minimum of ρ_a is achieved at a₀ = 1;

(ii) when $k_0<M\sqrt{p}$, the minimum of ρ_a is achieved at some a₀, which increases as $M\sqrt{p}∕\mid J_D\mid$ increases.

Proposition 4.1 shows that when the sparsity level k₀ is large, that is, ${\mathcal{E}}_a$ is dense, a small a tends to obtain a smaller lower bound in ρ, and vice versa. As (4.4) and (2.13) are similar, we have similar patterns to that in Figure 1 when examining the corresponding numerical plots of ρ_a. In addition, [9] shows that when $\rho ={\rho }_{\infty }≔C_1\sqrt{\log p∕n}$ for a large C₁, the power of $\mathcal{U}(\infty )$ converges to 1, and $\sqrt{\log p∕n}$ is minimax rate optimal for sparse alternatives; see also [17]. Thus, if ρ_∞ < ρ_a0, that is, $k_0<M{C}_1^{-a_0}\sqrt{p{a}_0!}∕{\log }^{a_0∕2}p$, $\mathcal{U}(\infty )$ is the “best” and its lowest detectable order of ρ is $\Theta (\sqrt{\log p∕n})$. On the other hand, Proposition 4.1 shows that when ${\mathcal{E}}_A$ is dense with $k_0>\sqrt{Mp}$, $\mathcal{U}(1)$ is the “best” and its lowest detectable order of ρ is $\Theta (\sqrt{p}{k}_0^{-1}{n}^{-1∕2})$. Moreover, for some large M and C₂, when ${\mathcal{E}}_A$ is “moderately dense” or “moderately sparse” with $C_2\sqrt{p{a}_0!}∕{\log }^{a_0∕2}p<k_0<\sqrt{Mp}$, $\mathcal{U}(a_0)$ is the “best” and its lowest detectable order of ρ is $\Theta \{(\sqrt{p}∕k_0{)}^{\frac{1}{a_0}}{n}^{-1∕2}\}$, which is of a smaller order than the optimal detection boundary of the sparse case $\Theta (\sqrt{\log p∕n})$.

More generally, when Σ_x ≠ Σ_y, similar results to Theorems 4.3 and 4.5 can be obtained. In particular, we have the following corollary.

Corollary 4.1. When Σ_x ≠ Σ_y, under Condition A.4 in Supplementary Material [28], Theorem 4.3 holds with ${\sigma }^2(a)\simeq a!{\sum }_{j_1,j_2=1}^p({\sigma }_{x,j_1,j_2}∕n_x+{\sigma }_{y,j_1,j_2}∕n_y{)}^a$ and Theorem 4.5 holds with $V_a=a!{\sum }_{j_1,j_2=k_0+1}^p({\sigma }_{x,j_1,j_2}∕n_x+{\sigma }_{y,j_1,j_2}∕n_y{)}^a$.

Corollary 4.1 shows that the asymptotic power of finite-order U-statistics depends on $\mathrm{E}\{\mathcal{U}(a)\}∕\sqrt{\text{var}\{\mathcal{U}(a)\}}$. By the construction of finite-order U-statistics and the proof, we obtain that $\mathrm{E}\{\mathcal{U}(a)\}=k_0{\rho }^a$ and $\text{var}\{\mathcal{U}(a)\}=\Theta (a!p{n}^{-a})$. We then know that for finite-order U-statistics, similar results to Proposition 4.1 still hold by examining $\mathrm{E}\{\mathcal{U}(a)\}∕\sqrt{\text{var}\{\mathcal{U}(a)\}}$.

The above power analysis shows that the optimal U-statistic varies when the alternative hypothesis changes. To achieve high power across various alternatives, we can develop an adaptive test similar to that in Section 2.3. Specifically, we calculate the p-values of the U-statistics (4.1) and (4.2) following the theoretical results above and the algorithm in Section 2.3. By combining the p-values as discussed in Section 2.3, the asymptotic power of the adaptive test goes to 1 if there exists one $\mathcal{U}(a)$ whose power goes to 1.

Remark 4.1. Xu et al. [67] has also discussed the adaptive testing of two-sample mean that is powerful against various ℓ_p-norm-like sums of μ − ν. But [67] is under the framework of a family of von Mises V-statistics where $\mathcal{V}(a)={\sum }_{j=1}^p({\overline{x}}_j-{\overline{y}}_j{)}^a$. We note that $\mathcal{V}(a)$ is equivalent to

$$\mathcal{V}(a)=\sum _{j=1}^p\sum _{c=0}^a(-1{)}^{a-c}\left(\begin{array}{c}\hfill a\hfill \\ \hfill c\hfill \end{array}\right)(n_x^c{n}_y^{a-c}{)}^{-1}\sum _{\begin{array}{c}\hfill 1\le k_1,\dots ,k_c\le n_x\hfill \\ \hfill 1\le s_1,\dots ,s_{a-c}\le n_y\hfill \end{array}}\prod _{t=1}^c{x}_{k_t,j}\prod _{m=1}^{a-c}{y}_{s_m,j},$$

which allows the indexes k’s and s’s to be the same, and thus is different from the U-statistics in (4.2). [67] shows that the constructed V-statistics are biased estimators of $\Vert \mu -\mathit{v}{\Vert }_a^a$, and $\mathcal{V}(a)$ and $\mathcal{V}(b)$ are asymptotically independent if a + b is odd, but are asymptotically correlated if a + b is even. The constructed U-statistics in this work extend the properties of those V-statistics such that $\mathcal{U}(a)$ in (4.2) is an unbiased estimator of $\Vert \mu -\mathit{v}{\Vert }_a^a$, and all $\mathcal{U}(a)$’s are asymptotically independent with each other. Given these nice statistical properties, it becomes easier to obtain the joint asymptotic distribution of the U-statistics, and then apply the adaptive test.

4.2. Two-sample covariance testing.

The U-statistics framework can be applied similar to testing the equality of two covariance matrices. Suppose $\{{\mathbf{x}}_i{\}}_{i=1}^{n_x}$ and $\{{\mathbf{y}}_i{\}}_{i=1}^{n_y}$ are i.i.d. copies of two independent random vectors x = (x₁, … , x_p)^⊤ and y = (y₁, … , y_p)^⊤, respectively. Denote E(x) = μ = (μ₁, … , μ_p)⊤, E(y) = ν = (ν₁, … , ν_p)^⊤; cov(x) = Σ_x = [σ_{x, j1, j2} : 1 ≤ j₁, j₂ ≤ p} and cov(y) = Σ_y = [σ_{y, j1, j2} : 1 ≤ j₁, j₂ ≤ p}. Consider H₀ : Σ_x = Σ_y = Σ = (σ_{j1, j2})_p×p. Given 1 ≤ j₁, j₂ ≤ p, 1 ≤ k₁ ≠ k₂ ≤ n_x, and 1 ≤ s₁ ≠ s₂ ≤ n_y, K_{j1, j2} (x_k1, x_k2, y_s1, y_s2 ) = (x_k1,j1 x_k1,j2 − x_k1,j1 x_k2,j2) − (y_s1,j1 y_s1,j2 − y_s1,j1 y_s2,j2) is a simple unbiased estimator of σ_{x, j1, j2} − σ_{y, j1, j2}. Therefore, for a finite positive integer a, we have the U-statistic

$$\mathcal{U}(a)=\sum _{1\le j_1,j_2\le p}\frac{1}{P_{2a}^{n_x}{P}_{2a}^{n_y}}\sum _{\begin{array}{c}\hfill 1\le k_{1,1}\ne k_{1,2}\ne \cdots \hfill \\ \hfill \ne k_{a,1}\ne k_{a,2}\le n_x\hfill \end{array}}\sum _{\begin{array}{c}\hfill 1\le s_{1,1}\ne s_{1,2}\ne \cdots \hfill \\ \hfill \ne s_{a,1}\ne s_{a,2}\le n_y\hfill \end{array}}\prod _{t=1}^a{K}_{j_1,j_2}({\mathbf{x}}_{k_{t,1}},{\mathbf{x}}_{k_{t,2}},{\mathbf{y}}_{s_{t,1}},{\mathbf{y}}_{s_{t,2}}).$$ (4.5)

As in Remark 2.1, another formulation of $\mathcal{U}(a)$ equivalent to (4.5) is

$$\begin{gathered} \mathcal{U}(a)=\sum _{c=0}^a\sum _{b_1=0}^c\sum _{b_2=0}^{a-c}(-1{)}^{c-b_1+b_2}\sum _{1\le j_1,j_2\le p}\sum _{\begin{array}{c}1\le i_1\ne \cdots \ne \hfill \\ i_{2c-b_1}\le n_x\hfill \end{array}}\sum _{\begin{array}{c}\hfill 1\le w_1\ne \cdots \ne \hfill \\ \hfill w_{2(a-c)-b_2}\le n_y\hfill \end{array}} \\ {C}_{n_x,n_y,a,c,b_1,b_2}\times \prod _{k=1}^{b_1}(x_{i_k,j_1}{x}_{i_k,j_2})\prod _{s=b_1+1}^c{x}_{i_s,j_1}\prod _{t=c+1}^{2c-b_1}{x}_{i_t,j_2} \\ \times \prod _{m=1}^{b_2}(y_{w_m,j_1}{y}_{w_m,j_2})\prod _{l=b_2+1}^{a-c}{y}_{w_l,j_1}\prod _{q=a-c+1}^{2(a-c)-b_2}{y}_{w_q,j_2}, \end{gathered}$$ (4.6)

where $C_{n_x,n_y,c,b_1,b_2}=(P_{2c-b_1}^{n_x}{P}_{2(a-c)-b_2}^{n_y}{)}^{-1}a!∕\{b_1!(c-b_1)!b_2!(a-c-b_2)!\}$, and (4.6) shall be used in the theoretical developments.

We next present the asymptotic results of the constructed U-statistics under the null hypothesis. Here, we assume the regularity Condition A.5 or A.6, whose details and discussions are provided in Section A.13.1 of Supplementary Material [28] due to the space limitation. We mention that Condition A.5 is a mixing-type dependence assumption similar to Condition 2.2, and Condition A.6 is a moment-type dependence assumption similar to Condition 2.2*. Particularly, Condition A.6 extends the moment assumption for second-order U-statistics in Li and Chen [45] to U-statistics of general orders; please see the detailed discussions in Section A.13.1.

Theorem 4.6. Under H₀ and Condition A.5 or A.6 in Supplementary Material [28], for finite integers {a₁, … , a_m}, $[\mathcal{U}(a_1)∕\sigma (a_1),\dots ,\mathcal{U}(a_m)∕\sigma (a_m){]}^{⊺}\stackrel{D}{\to }\mathcal{N}(0,I_m)$, where for a ∈ {a₁, … , a_m},

$$\begin{gathered} {\sigma }^2(a)=\text{var}\{\mathcal{U}(a)\} \\ \simeq \sum _{1\le j_1,j_2,j_3,j_4\le p}a!{\left\{\frac{1}{n_x}({\Pi }_{j_1,j_2,j_3,j_4}^x-{\sigma }_{j_1,j_2}{\sigma }_{j_3,j_4})+\frac{1}{n_y}({\Pi }_{j_1,j_2,j_3,j_4}^y-{\sigma }_{j_1,j_2}{\sigma }_{j_3,j_4})\right\}}^a \end{gathered}$$

with ${\Pi }_{j_1,j_2,j_3,j_4}^x=\mathrm{E}\{{\prod }_{t=1}^4(x_{1,j_t}-{\mu }_{j_t})\}$ and ${\Pi }_{j_1,j_2,j_3,j_4}^y=\mathrm{E}\{{\prod }_{t=1}^4(y_{1,j_t}-v_{j_t})\}$.

Theorem 4.6 provides the asymptotic independence and joint normality of the finite-order U-statistics, which are similar to Theorems 2.1, 4.1 and 4.3. To further study the power of these finite-order U-statistics, we next consider the alternative hypotheses where Σ_x ≠ Σ_y. Let ${\mathbb{J}}_0$ be the largest subset of {1, … , p} such that σ_{x, j1, j2} = σ_{y, j1, j2} = σ_{j1, j2} for any j₁, $j_2\in {\mathbb{J}}_0$. We then obtain the following theorem under the regularity conditions given in Section A.14 of Supplementary Material [28].

Theorem 4.7. Under Conditions A.7 and A.8 in Supplementary Material [28], for finite integers {a₁, … , a_m}, $[\mathcal{U}(a_1)-\mathrm{E}\{\mathcal{U}(a_1)\}]∕\sigma (a_1),\dots ,[\mathcal{U}(a_m)-\mathrm{E}\{\mathcal{U}(a_m)\}]∕\sigma (a_m){]}^{⊺}\stackrel{D}{\to }\mathcal{N}(0,I_m)$, where

$${\sigma }^2(a)=\text{var}\{\mathcal{U}(a)\}\simeq a!C_{\kappa ,a}\sum _{j_1,j_2,j_3,j_4\in {\mathbb{J}}_0}{\sigma }_{j_1,j_2}^a{\sigma }_{j_3,j_4}^a,$$

and C_κ,a = {(κ_x − 1)/n_x + (κ_y − 1)/n_y}^a + 2(κ_x/n_x + κ_y/n_y)^a with κ_x and κ_y given in Condition A.7.

Given the asymptotic results under the alternatives, we next analyze the power of the finite-order U-statistics. By Theorem 4.7, the asymptotic power of $\mathcal{U}(a)$ depends on $\mathrm{E}\{\mathcal{U}(a)\}∕\sqrt{\text{var}\{\mathcal{U}(a)\}}$. Let J_D = {(j₁, j₂) : σ_{x, j1, j2} ≠ σ_{y, j1, j2}, 1 ≤ j₁, j₂ ≤ p}, then $\mathrm{E}\{\mathcal{U}(a)\}={\sum }_{(j_1,j_2)\in J_D}({\sigma }_{x,j_1,j_2}-{\sigma }_{y,j_1,j_2}{)}^a$. Similar to Section 2.2, to study the relationship between the sparsity level of Σ_x − Σ_y and the power of U-statistics, we consider the case where the nonzero differences between Σ_x and Σ_y are the same. Specifically, let σ_{x, j1, j2} − σ_{y, j1, j2} = ρ for (j₁, j₂) ∈ J_D, and then $\mathrm{E}\{\mathcal{U}(a)\}=\mid J_D\mid {\rho }^a$. Following the analysis in Section 2.2, we compare the ρ values needed by different $\mathcal{U}(a)$’s to achieve $\mathrm{E}\{\mathcal{U}(a)\}∕\sqrt{\text{var}\{\mathcal{U}(a)\}}\simeq M$ for a given constant M. In particular, for given integer a, suppose $\mathrm{E}\{\mathcal{U}(a)\}∕\sqrt{\text{var}\{\mathcal{U}(a)\}}\simeq M$ is achieved when ρ = ρ_a. For any a ≠ b, we compare $\mathcal{U}(a)$ and $\mathcal{U}(b)$ following Criterion 1.

We use the following example as an illustration, where Σ_x and Σ_y satisfy the conditions of Theorem 4.7. Specifically, we assume that Σ_x = (σ_{x, j1, j2})_p×p has the diagonal elements σ_{x, j, j} = ν²; and the off-diagonal elements σ_{x, j1, j2} = h_{∣j1−j2∣} ∈ (0, ν²) with h_{∣j1−j2∣} = Θ(ν²) when ∣j₁ − j₂∣ ≤ s, while σ_{x, j1, j2} = 0 when ∣j₁ − j₂∣ > s. This covers the moving average covariance structure of order s, and Σ_x is a banded matrix with bandwidth s. In addition, we assume the bandwidth s = o(p) and $p-\mid {\mathbb{J}}_0\mid =o(p)$. By the definition of ${\mathbb{J}}_0$, the assumption $p-\mid {\mathbb{J}}_0\mid =o(p)$ implies that a large square sub-matrix of Σ_x and Σ_y are the same. For simplicity, we let n_x = n_y with n = n_x + n_y, and a similar analysis can be applied when n_x ≠ n_y. By Theorem 4.7, $\text{var}\{\mathcal{U}(a)\}\simeq (n∕2{)}^{-a}a!\{2{\kappa }_1^a+{\kappa }_2^a\}\{p{v}^{2a}+2{\sum }_{t=1}^s{h}_t^a(p-t){\}}^2$, where κ₁ = κ_x + κ_y and κ₂ = κ_x + κ_y − 2. Therefore, we know for given finite integer a, $\mathrm{E}\{\mathcal{U}(a)\}∕\sqrt{\text{var}\{\mathcal{U}(a)\}}\simeq M$ holds when ρ = ρ_a defined as

$${\rho }_a=\frac{(a!{)}^{\frac{1}{2a}}\sqrt{{\kappa }_1}v}{(n∕2{)}^{1∕2}}{\left(\frac{Mp}{\mid J_D\mid }\right)}^{1∕a}{\left\{2+{\left(\frac{{\kappa }_2}{{\kappa }_1}\right)}^a\right\}}^{\frac{1}{2a}}{\left\{1+2\sum _{t=1}^s{\left(\frac{h_t}{v^2}\right)}^a\left(1-\frac{t}{p}\right)\right\}}^{\frac{1}{a}}.$$

We next compare the ρ_a’s and obtain the following proposition.

Proposition 4.2. There exists ${\mathbb{D}}_0$ that only depends on the given κ_x, κ_y, ν², s, and h_t, t = 1, … , s, and satisfies ${\mathbb{D}}_0=\Theta (1∕s^2)$ such that:

(i) When $\mid J_D\mid \ge Mp∕\sqrt{{\mathbb{D}}_0}$, the minimum of ρ_a is achieved at a₀ = 1.

(ii) When $\mid J_D\mid <Mp∕\sqrt{{\mathbb{D}}_0}$, the minimum of ρ_a is achieved at some a₀, which increases as M_p/∣J_D∣ increases.

Proposition 4.2 is similar to Propositions 2.3 and 4.1. Following the analysis in Section 2.2, Proposition 4.2 shows that when the difference Σ_x − Σ_y is “very” dense with $\mid J_D\mid \ge Mp∕\sqrt{{\mathbb{D}}_0}$, $\mathcal{U}(1)$ is the most powerful U-statistic; when Σ_x − Σ_y becomes sparser as M_p/∣J_D∣ decreases, a higher-order U-statistic is more powerful; when the Σ_x − Σ_y is “moderately” dense or sparse, a U-statistic of finite order a₀ > 1 would be the most powerful one.

The power analysis above shows that the power of the U-statistics varies when the alternative changes. To maintain high power across different alternatives, we can develop an adaptive testing procedure similar to that in Section 2.3. Given the asymptotic independence in Theorem 4.6, an adaptive testing procedure using the constructed $\mathcal{U}(a)$’s is valid with the type I error asymptotically controlled. Also, the adaptive test achieves high power by combining the U-statistics as discussed in Section 2.3.

We provide simulation studies on two-sample covariance testing in Supplementary Material [28], Section C.3. By the simulations, we first find that the type I errors of the U statistics and the adaptive test are well controlled under H₀. This verifies the theoretical results in Theorem 4.7. Second, similar to the one-sample covariance testing, we find that generally when the difference Σ_x − Σ_y is sparser, a U-statistic of higher order is more powerful, and vice versa. Moreover, under moderately sparse/dense alternatives, $\mathcal{U}(a_0)$ with a₀ > 1 could achieve the highest power. The results are consistent with Proposition 4.2. Third, we compare the proposed adaptive test with existing methods in literature including [6, 45, 57, 61], and find that the proposed adaptive testing procedure maintains high power across various alternatives.

Remark 4.2. Similar to Section 2, we can let $\mathcal{U}(\infty )$ be the maximum-type test statistic in [6], and expect that the result similar to Theorem 2.3 holds under certain regularity conditions. However, as the dependence structure of two-sample covariance matrices is more complicated than the one-sample case, it is more challenging to establish the asymptotic joint distribution of $\mathcal{U}(\infty )$ and finite-order U-statistics. We leave this interesting problem for future study, while find in simulations that the performance of $\mathcal{U}(\infty )$ is similar to high-order U-statistics $\mathcal{U}(a)$’s.

4.3. Generalized linear model.

In this section, we consider Example 3 of generalized linear models (on page 156) to show that the proposed framework can be extended to other testing problems. Similar to the results in Section 4.1, we show that the constructed U-statistics are asymptotically independent and normally distributed, and also establish the power analysis results of the U-statistics. We provide the details in Section A.16 of Supplementary Material [28]. Recently, Wu et al. [65] also discussed the adaptive testing of generalized linear model. But [65] is under the framework of a family of von Mises V-statistics, and thus is different from the current paper as discussed in Remark 4.1. Moreover, the current work provides the theoretical power analysis while [65] did not.

5. Discussion.

This paper introduces a general U-statistics framework for applications to high-dimensional adaptive testing. Particularly, we focus on the examples including testing of means, covariances and regression coefficients in generalized linear models. Under the null hypothesis, we prove that the U-statistics of finite orders have asymptotic joint normality, and establish the asymptotic mutual independence among the finite-order U-statistics and $\mathcal{U}(\infty )$. Moreover, under alternative hypotheses, we analyze the power of different U-statistics and demonstrate how the most powerful U-statistic changes with the sparsity level of the alternative parameters. Based on the theoretical results, we propose an adaptive testing procedure, which is powerful against different alternatives. The superior performance of this adaptive testing is confirmed in the simulations and real data analysis.

There are several possible extensions of the U-statistics framework in this paper. First, by our current proof, the convergence rate in Theorem 2.3 is bounded by O(log^−1/2 p), which is an upper bound and not sharp. From our extensive simulations, we find that the type I error rate of the adaptive testing is well controlled with a relatively small p, for example, p = 50. We might obtain a shaper bound of the convergence rate, but more refined concentration property of the high-dimensional and high-order U-statistics is needed. Second, the proposed framework requires that the elements in the parameter set $\mathcal{E}$ have unbiased estimates. When we cannot obtain unbiased estimates easily, for example, for the precision matrix, the proposed construction may not follow directly. Nevertheless we may use “nearly” unbiased estimators to construct “U-statistics” for hypothesis testing, such as the “nearly” unbiased estimator of the precision matrix proposed in [66]; the main challenge is then to control the accumulative bias over the parameters under high dimensions. Third, this paper discusses the examples where the elements in $\mathcal{E}$ are comparable. When the parameters in $\mathcal{E}$ are not comparable, such as $\mathcal{E}$ containing both means and covariances parameters, the construction of U-statistics still follows but the theoretical derivation may require a careful case-by-case examination. Fourth, the construction of the U-statistics treats the parameters in $\mathcal{E}$ with equal weight. More generally, we could assign different weights to different parameter estimators. For instance, standardizing the data is one example of assigning different weights. As inappropriate weight assignments could lead to power loss, when the truth is unknown, how to effectively assign weights to maximize the test power is an interesting research question. We shall discuss these extensions in the future as a significant amount of additional work is still needed.

In addition to the examples in this paper, the proposed U-statistics framework can be applied to other high-dimensional hypothesis testing problems. For example, it can be applied to testing the block-diagonality of a covariance matrix, whose theoretical analysis would be similar to the considered one sample and two sample covariance testing problems. It can also be used to test high-dimensional regression coefficients in complex regression models other than the generalized linear models, following a similar construction based on the score functions. A key step is then to characterize the impact of nuisance parameters that are estimated under the null hypothesis, and challenges arise especially when the nuisance parameters are high dimensional. Such interesting extensions will be further explored in our follow-up studies.