Deep propensity network using a sparse autoencoder for estimation of treatment effects

Abstract

Objective

Drawing causal estimates from observational data is problematic, because datasets often contain underlying bias (eg, discrimination in treatment assignment). To examine causal effects, it is important to evaluate what-if scenarios—the so-called “counterfactuals.” We propose a novel deep learning architecture for propensity score matching and counterfactual prediction—the deep propensity network using a sparse autoencoder (DPN-SA)—to tackle the problems of high dimensionality, nonlinear/nonparallel treatment assignment, and residual confounding when estimating treatment effects.

Materials and Methods

We used 2 randomized prospective datasets, a semisynthetic one with nonlinear/nonparallel treatment selection bias and simulated counterfactual outcomes from the Infant Health and Development Program and a real-world dataset from the LaLonde’s employment training program. We compared different configurations of the DPN-SA against logistic regression and LASSO as well as deep counterfactual networks with propensity dropout (DCN-PD). Models’ performances were assessed in terms of average treatment effects, mean squared error in precision on effect’s heterogeneity, and average treatment effect on the treated, over multiple training/test runs.

Results

The DPN-SA outperformed logistic regression and LASSO by 36%–63%, and DCN-PD by 6%–10% across all datasets. All deep learning architectures yielded average treatment effects close to the true ones with low variance. Results were also robust to noise-injection and addition of correlated variables. Code is publicly available at https://github.com/Shantanu48114860/DPN-SAz.

Discussion and Conclusion

Deep sparse autoencoders are particularly suited for treatment effect estimation studies using electronic health records because they can handle high-dimensional covariate sets, large sample sizes, and complex heterogeneity in treatment assignments.

INTRODUCTION

In many research fields, especially in biomedical sciences, observational data are abundant but may contain underlying bias, arising in various steps of the data generation or collation process, for which datasets cannot be used seamlessly to draw causal claims.¹ For instance, one may be interested in studying the effectiveness of a medical treatment or an intervention in a population, but the way in which people access the healthcare system could be different (eg, due to social inequality or systemic racism); or, simply, one may not be able to account for the heterogeneity in the population in terms of age groups, prior comorbidities, surgical procedures, etc. Due to such bias, the causal effects of the treatment or intervention often cannot be estimated properly. One solution would be to force the intervention to be nondifferentiated, performing a randomized controlled trial (RCT).^2,3 In an RCT, individuals are assigned to different treatment groups (or a control group) at random, regardless of their background characteristics (ie, a pretreatment covariate or feature space). The randomization process leads to strong ignorability of individuals’ pretreatment characteristics, and thus the causal effect of the treatment versus control can be evaluated objectively.⁴ The mean difference between the observed treatment outcomes of the 2 different groups (eg, treatment vs control) is called the average treatment effect (ATE). Note that estimating the individual treatment effect (ITE) is a missing data problem^5,6 because only 1 factual outcome can be observed (ie, a person cannot be assigned to both the treatment and control groups at the same time).

Since RCTs are not always feasible due to ethical or operational constraints, for example, conducting a RCT to ask individuals to smoke and then assess the effect of smoking toward the development of lung cancer, observational data are used in attempts to draw causal conclusions. Nevertheless, when using observational data, one must account for possible types of underlying bias such as confounders, which represent true causal effects to be distinguished from other correlated, spurious variables associated with an outcome of interest.⁷

Propensity score matching (PSM) is a popular statistical approach for observational data that attempts to estimate the causal effect of a treatment variable with respect to an outcome, taking into account possible confounding bias from other pretreatment characteristics.^4,8 The propensity score is a scalar estimate $\pi \left(x\right)$ representing the conditional probability of receiving a certain treatment $T\mathrm{ }=\mathrm{ }1$, versus the control group or no treatment $T\mathrm{ }=\mathrm{ }0$, given a set of measured pretreatment covariates $X,$ denoted as

$$\pi \left(x\right)=P\left(T=1|X=x\right),$$ (1)

Hence, PSM balances the pretreatment confounders by achieving a quasi-randomization of the different treatment group assignments, allowing more unbiased estimation of the treatment effect. However, traditional PSM approach accounts only for measured (and measurable) covariates, and latent bias may remain after matching.⁹

PSM has been implemented historically through logistic regression, which calculates the probability of treatment assignment given the pretreatment covariates.¹⁰ In the presence of high-dimensional datasets, eg, those compiled from large electronic health record (EHR) databases,¹¹ different feature selection methods within PSM have been employed, such as the high-dimensional propensity score¹² or LASSO logistic regression.¹³ However, logistic regression is limited because it calculates a linear combination of input variables, and thus unable to capture the complex relationships between the pretreatment covariates and the treatment assignment. This is particularly true in high-dimensional settings, where it is difficult to explicitly define variable-to-variable interactions (eg, as higher-order terms in the logistic function) and computationally burdensome to scan all possible interaction terms.

An artificial neural network is a universal approximator and can smooth polynomial functions regardless of the order of the polynomial or the number of interaction terms.^14–16 In addition, it does not require a priori knowledge of what interactions and functional forms are likely to be relevant among covariates. Therefore, it is suited to overcome the issues in the logistic regression-based PSM approach. In fact, a number of neural deep learning approaches have been devised to provide the estimation of nonlinear treatment group assignment probability and predict treatment outcomes with improved estimation of treatment effects. Popular frameworks with available software implementations include the deep counterfactual network with propensity dropout (DCN-PD)¹⁷ and the Dragonnet.¹⁸ However, current deep learning approaches, even those that exploit weight regularization, do not explicitly address the problem of reducing the complexity of large covariate spaces, which can be common when designing studies on EHR databases.

In this work, we propose a novel deep neural architecture—the deep propensity network using a sparse autoencoder (DPN-SA)—that addresses the problems of (1) high-dimensional PSM, and (2) nonlinear/nonparallel treatment assignment bias, while maintaining or outperforming other algorithms in terms of mean squared error (MSE) and variance on estimated effects. The DPN-SA estimates the propensity score using a sparse autoencoder¹⁹ which at the same time learns a nonlinear feature representation and reduces the dimensionality of the pretreatment covariate space. Code is publicly available at https://github.com/Shantanu48114860/DPN-SA.

MATERIALS AND METHODS

Problem formulation

Let us assume a population sample (independent and identically distributed) of $\mathit{N}\mathrm{ }\left(1\dots \mathit{i}\dots \mathit{n}\right)$ individuals, given a background set of pretreatment covariates $\mathit{X}\mathrm{ }$, a treatment $\mathit{T}$ (binary, for simplicity of demonstration), and a health outcome $\mathit{Y}$. Each subject $\mathit{i}$ is represented by a tuple {X_i, T_i, Y_i}. Let Y_i⁰ and Y_i¹ be the potential outcomes for individual i under treatment T_i = 0 and T_i = 1, respectively.^20,21 Given X_i = x, the ITE $\mathbf{\tau }\left(\mathit{x}\right)$ is defined as the difference in the mean potential outcomes for the individual $\mathit{i}\mathrm{ }$under both treatments, conditional on the observed covariate vector $\mathit{x}$

$$\mathrm{\tau }\left(x\right)=E\left[Y_i^1-Y_i^0∣X_i=x\right]$$ (2)

The ITE formulation as $\mathbf{\tau }\left(\mathit{x}\right)$—called the counterfactual framework—is usually incalculable in reality, since an individual cannot be assigned to 2 different treatments at the same time. However, under the assumption of strongly ignorable treatment assignment (SITA), the potential outcomes are independent of treatment conditional on background variables, that is, ${\{\mathit{Y}}_{\mathit{i}}^1,\mathrm{ }{\mathit{Y}}_{\mathit{i}}^{0\mathrm{ }}\}\perp \mathbf{T}\mid \mathbf{X}.$^5,22–24 Thus, under the assumption of SITA, the ITE can then be calculated as

$$\mathbf{\tau }\left(\mathit{x}\right)=\mathit{E}\left[{\mathit{Y}}^1∣\mathit{T}=1,\mathit{X}\mathrm{ }=\mathrm{ }\mathit{x}\right]-\mathit{E}\left[{\mathit{Y}}^0∣\mathit{T}=0,\mathrm{ }\mathit{X}\mathrm{ }=\mathrm{ }\mathit{x}\right]=\mathit{E}\left[\mathit{Y}∣\mathit{T}=1,\mathit{X}=\mathit{x}\right]-\mathit{E}\left[\mathit{Y}∣\mathit{T}=0,\mathit{X}=\mathit{x}\right]$$

Further, under SITA and by averaging over the distribution of $\mathit{X}$, the ATE ${\mathbf{\tau }}_{01}$ can be calculated as

$${\mathrm{\tau }}_{01}=E\left[\mathrm{\tau }\left(X\right)\right]=E\left[Y∣T=1\right]-E\left[Y∣T=0\right]$$ (3)

However, by assuming SITA, ITE, and ATE can be calculated only with $\mathit{x}$ being the same in the different treatment groups, which becomes quickly unfeasible with observational data, such as EHRs, when the dimension of $\mathit{x}$ grows. PSM, through the conditional probability $\mathbf{\pi }\left(\mathit{x}\right)$ (see Equation 1), attempts at balancing the probability of receiving $\mathit{T}$ given $\mathit{X}=\mathit{x}$. Once propensity scores are obtained for a population sample, the individuals in the treatment group must be matched with those in the control group to make sure that they are balanced with respect to the background covariates $\mathit{x}$. The matching process can be solved with a number of (approximate) solutions, including k-nearest neighbor, Caliper matching,²⁵ and propensity weighing.²⁶

The DCN-PD framework

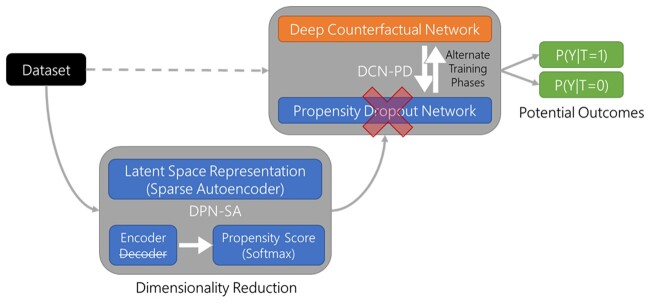
As shown in Figure 1, our approach extends the DCN-PD framework,¹⁷ by incorporating 2 interconnected neural networks: 1 for the prediction of potential outcomes (DCN) and the other for the calculation of propensity-dropout scores (PD). Both the DCN and the PD components take the same input covariates. The DCN has a classical feed-forward architecture with first a set of shared hidden layers and then a bifurcation into 2 separate sets of hidden layers (ie, the idiosyncratic layers) that predict factual and counterfactual outcomes, respectively. The PD component is designed to ameliorate the impact of treatment assignment bias, by regularizing the DCN training through propensity scores. The PD idea can be thought of as the conceptual analog of propensity weighting,²⁶ which has been previously applied to neural networks.^27,28 The propensity score of each training sample is transformed into a dropout probability, which is higher for subjects with features that belong in a region of poor treatment assignment overlap. The worse the propensity score of one example is, the larger the penalty that the PD scheme imposes, preventing the hidden units in the neural network from adapting to unreliable examples. In conjunction with the PD scheme, the DCN is trained in alternate phases. In each phase, either the data from the treatment group or from the control group are used for training only 1 idiosyncratic layer, respectively, at a time (while the shared layer is trained in all epochs).

Figure 1.

Schematic of the Deep Propensity Network using a Sparse Autoencoder (DPN-SA) framework. The DPN-SA module performs dimensionality reduction of the input through a latent variable space and then provides propensity scores to the Deep Counterfactual Network with Propensity Dropout (DCN-PD) that calculates the potential outcomes for treatment exposures vs controls.

Proposed approach

DCN-PD can be affected by the curse of dimensionality, with associated residual confounding in study settings where the covariate space has very high cardinality (eg, in study designs that use EHR data).^29,30 Our DPN-SA exploits a deep stacked sparse autoencoder to encode the covariate space $\mathit{X}$ into a lower dimensional, nonlinear feature representation, which can then be used to calculate the propensity scores replacing the PD component of the DCN-PD, as shown in Figure 1.³¹ An autoencoder is a neural network that learns to copy its input to its output (encoder-decoder), but the input is coded into a lower dimension within the hidden layers.³² In its simplest form (ie, with a single layer), the autoencoder is closely related to principal component analysis (PCA), while highly nonlinear codes can be achieved by augmenting the layer architecture (eg, with deep beliefs networks).³³ Autoencoders have been employed in a number of applications, from machine translation to drug discovery.^34,35 The sparse autoencoder is an approach that includes extra units (more than inputs) in the hidden layer, but only a small number of those units are activated depending on the input.^19,36 It has been broadly applied in biomedical studies, including imaging and -omics datasets.^37–40

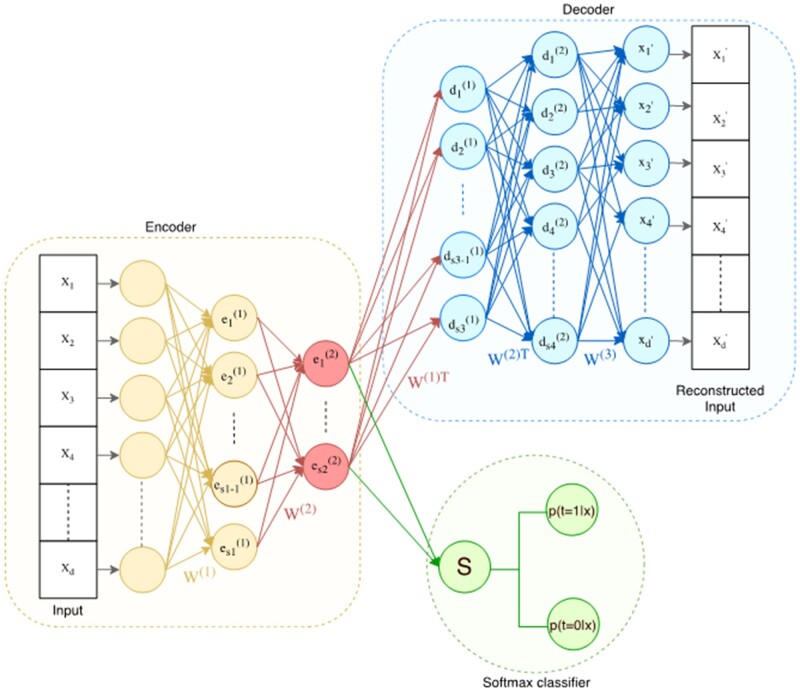
In Figure 2, we show a detailed schematic of the DPN-SA exploiting multiple layer depths and sparsity. Technical details on the architectural design and training procedure are given in the Supplementary Material. In brief, the DPN-SA is trained using dataset batches on which a forward propagation algorithm is executed. For each batch, the network parameters are optimized using a gradient-descent optimization algorithm, namely the Adam optimizer.⁴¹ The autoencoder is composed by an encoder, which is used to derive a nonlinear (lower-dimensional) latent feature space, and by a decoder, which reconstructs the original input. After training, the decoder is removed and replaced by a softmax classifier (attached to the last layer of the encoder) that calculates the probability of treatment $\mathit{T}$ assignment, thus estimating the propensity score $\mathbf{\pi }\left(\mathit{X}=\mathit{x}\right)$. The softmax function σ is a generalization of the sigmoid logistic function for multiple dimensions, that is, $\mathbf{\sigma }{\left(\mathit{z}\right)}_{\mathit{i}}=\frac{{\mathit{e}}^{{\mathit{z}}_{\mathit{i}}}}{{\sum }_{\mathit{j}=1}^{\mathit{K}}{\mathit{z}}_{\mathit{j}}}$, for i = 1…K, z = (z₁…z_K) ∈ R^K; thus, it can be used to calculate multinomial probability over multiple treatment groups. The matching procedure uses the PD component of the DCN-PD, which is also used downstream for treatment effect calculations. In this work, we evaluated different training (end-to-end vs greedy stacked/current) procedures and layer (multiple vs single) architectures, as detailed in the next sections.

Figure 2.

Architecture of a deep stacked sparse autoencoder. The encoder progressively reduces the input space dimensions from the input layer through a number of layers (in light orange) down to the innermost layer (displayed in red), which represents the latent space. Some of the units of the inner layer are/are not active given an input, depending on the sparsity constraint. The decoder reconstructs back the latent space into the original input through another set of layers (displayed in blue). In our framework, after training, the decoder is replaced by a softmax function that uses the latent space to calculate propensity scores.

Experimental setup

Datasets

We used the Infant Health and Development Program (IHDP) dataset, a multisite, longitudinal RCT designed to evaluate the efficacy of comprehensive early intervention in enhancing the outcomes of low birth weight, prematurely born infants in the United States.⁴² The original IHDP dataset was resampled by throwing away a nonrandom subset of the treatment group (based on the race/ethnicity variable), thus inducing treatment imbalance. The counterfactual outcomes (which are not available in the original RCT) were then simulated using either a linear or nonlinear/nonparallel surface, creating a semisynthetic dataset at this point. This process allows to have the knowledge of the true average treatment effect because the outcomes are drawn from a known function and the treatment assignment bias is known. In detail, the bias in the treated group is made by selecting only children with a particular ethnicity, while the control group contains all the races and ethnicities in the original RCT study (dichotomized into white vs nonwhite). Such design ensures that the overlap assumption is satisfied for the treatment group. In regards to counterfactual outcomes, they are generated using the full covariate set, thus ensuring ignorability (because the conditioning is only on observed covariates). Outcomes are drawn from a standardized distribution using 2 different surface functions. The first one is a linear combination of covariates with a different intercept for the treated group, that is, Y(0) =$\mathrm{ }\mathcal{N}$(Xβ,1) and Y(1) =$\mathrm{ }\mathcal{N}$(Xβ + 4,1), which indicates no treatment heterogeneity and an average treatment effect equal to 4. The second one is an exponential family function Y(0) =$\mathrm{ }\mathcal{N}$(exp((X + W)β),1) for the control group with an offset matrix W, and a linear function Y(1) =$\mathrm{ }\mathcal{N}$(Xβ-ω,1) for the treated, with an offset vector on the variables, where ω is made such that the average effect on the treated is also 4. Here, we used the second nonlinear surface because the first one would have been easily solved by regular PSM linear regression, as previously shown by Hill.⁴² The nonlinear surface dataset consisted of 747 subjects (139 in the treatment group and 608 controls) with 25 associated covariates, describing characteristics of the infants and their mothers (excluding the ethnicity).

In order to evaluate the performance of the proposed framework with larger covariate spaces to resemble EHR-based studies, we quadruplicated the original IHDP feature set through the creation of 25 random variables (shuffling the original ones) and then another set of 50 covariates partially correlated to the original ones (approx. $\mathbf{\rho }=0.4$), using a Gaussian noise addition $\mathit{N}\left(0,2\mathrm{*}\mathbf{\sigma }\left({\mathit{x}}_{\mathit{k}}\right)\right)$ to each original variable ${\mathit{x}}_{\mathit{k}}$. The factual and counterfactual outcomes matched those of IHDP.

Finally, we tested the framework on a real-world dataset (with only factual outcomes), using the LaLonde’s National Supported Work Demonstration experimental sample (297 treated, 425 control) and the Population Survey of Income Dynamics comparison group (2490 control), collectively known as the Jobs dataset.⁴³ The treatment variable is job training, there are 46 sociodemographic and behavioral covariates, and the outcome is posttraining employment status/income, with 15% of the subjects being unemployed by the end of the study.

DPN-SA configurations and other comparison methods

Three different configurations of the DPN-SA were tested on all datasets, given the number of input variables N, all using the sparsity constraints: (i) N-20-10-20-N; (ii) N-10-N, which is similar to PCA; (iii) N-1-N, which is similar to regularized logistic regression. For all 3, end-to-end and stacked/current greedy layer-wise training were executed for 2000 epochs. The end-to-end training means that the whole network is trained at one go. For the greedy layer-wise training, we employed two strategies. In the first one, called stacked, the network is optimized 1 layer at a time. After a layer is trained, its weights are frozen, and the next layers attached are trained. The second strategy, called stacked current, also trains layers iteratively, but when passing from one layer to the next, the weights of the prior layer are not frozen and get updated. Layer-wise training is an older method compared to end-to-end and dropout; however, it can be effective in finding a good initialization for the network in order to facilitate convergence when a high number of layers are employed. The learning rates for the sparse autoencoder and for the softmax were 0.001 and 0.01, respectively. We set weight decay ($\mathit{\lambda }$), sparsity parameter ($\mathit{\rho }$), and sparse penalty ($\mathit{\beta }$) to 0.0003, 0.8, and 0.1, respectively, with a batch size of 32. The softmax classifier was run for 50 epochs (${\mathit{K}}_{\mathit{c}}$) with a batch size of 32. The DPN-SA was implemented using the Pytorch framework (https://pytorch.org/). In addition to the DPN-SA, we ran and compared: (i) the original DCN-PD, (ii) standard logistic regression, and (iii) logistic regression with LASSO regularization, where its shrinkage parameter was optimized through cross-validation.

Performance measures and validation

On the IHDP data, models were trained on 80% of the data and validated on the remaining 20%, repeating the procedure for 100 times; while on the Jobs data, the training/test split was 90%/10% with a variable preselection (from 46 to 17), over 10 validation runs, to be consistent with prior literature setup and results (https://www.fredjo.com/). All parameter optimization for DPN-SA, DCN-PD, and LASSO (eg, the shrinkage parameter) were done within the training subsamples. On each test set, we calculated the ATE for each method (knowing the true value), and the MSE on the empirical precision in estimation of heterogeneous effect, defined as ε_PEHE = $\frac{1}{\mathit{N}}{\sum }_{\mathit{n}=0}^{\mathit{N}}{({(\mathit{y}}_{\mathit{n}}\left(1\right)-{\mathit{y}}_{\mathit{n}}\left(0\right))-({{\mathit{y}}^{\mathrm{\text{'}}}}_{\mathit{n}}\left(1\right)-{{\mathit{y}}^{\mathrm{\text{'}}}}_{\mathit{n}}\left(0\right)))}^2$, which evaluates the ability of the method to capture treatment effect heterogeneity.^17,42

For the Jobs dataset, in the absence of counterfactual truth, we calculated the average treatment effect on the treated (ATT) and the error ε_ATT as follows:

$$\mathit{ATT}=\mid \mathit{T}{\mid }^{-1}{\sum }_{\mathit{i}\in \mathit{T}}{\mathit{y}}_{\mathit{i}}-\mid \mathit{C}\cap \mathit{E}{\mid }^{-1}{\sum }_{\mathit{i}\in \mathit{C}\cap \mathit{E}}{\mathit{y}}_{\mathit{i}}$$

$${\epsilon }_{\mathit{ATT}}=\mid \mathit{ATT}-\frac{1}{\mid \mathit{T}\mid }{\sum }_{\mathit{i}\in \mathit{T}}\left(\mathit{f}\left({\mathit{x}}_{\mathit{i}}\right),1\right)-\left(\mathit{f}\left({\mathit{x}}_{\mathit{i}}\right),0\right)$$

where C is the control group and T is the treated, out of the original randomized sample E, f is the outcome prediction over the covariate vector x, and y is the factual outcome. The performance distributions were compared by means of a t-test with adjustment for sample overlap.⁴⁴

RESULTS

A summary of the population characteristics for the IHDP and Jobs datasets is given in Table 1. As explained in the methods, the original data were processed before being fed to the models (eg, treatment-bias induction by selection in IHDP and counterfactual outcome simulation) and normalized. The IHDP dataset shows high balance among the covariates before the sample selection, while the Jobs dataset is more diverse among intervention groups. Complete, descriptive statistics for all variables of the original and processed datasets are available in the Supplementary Material.

Table 1.

Summary of population characteristics for the IHDP and Jobs datasets (original samples)

IHDP dataset
Variable mean (SD) [or %]	Treated (n = 377)	Controls (n = 608)
Newborn weight g	1819 (439)	1781 (469)
Newborn head cm	29.5 (2.5)	29.0 (2.5)
Mother’s age yrs	24.6 (5.9)	24.9 (6.1)
Mother’s race/ethnicity white	37%	37%
Mother’s race/ethnicity black	53%	52%
Mother’s race/ethnicity Hispanic	8%	12%
Mother’s marital status married	42%	48%
Mother’s high school degree	28%	27%
Mother’s education	17%	22%
Mother’s smoking	35%	35%
Mother’s first pregnancy	47%	60%
Mother’s alcohol drinking	11%	13%
Mother’s substance abuse	95%	96%
Newborn sex (male)	50%	51%
Newborn twins	10%	9%
Jobs dataset
Variable mean (SD) [or %]	LaLonde (n = 297 + 425)	PSID (n = 2490)
Age yrs	24.52 (6.63)	34.85 (10.44)
No high school degree	48%	31%
Black	80%	25%
Hispanic	11%	3%
Married	16%	47%
Real earnings in 1974 $	3631 (6221)	19 429 (13 407)
Real earnings in 1975 $	3043 (5066)	19 063 (13 597)
Zero earnings in 1974	45%	9%
Zero earnings in 1975	40%	10%

Abbreviations: IHDP, Infant Health and Development Program; PSID, Population Survey of Income Dynamics; SD, standard deviation.

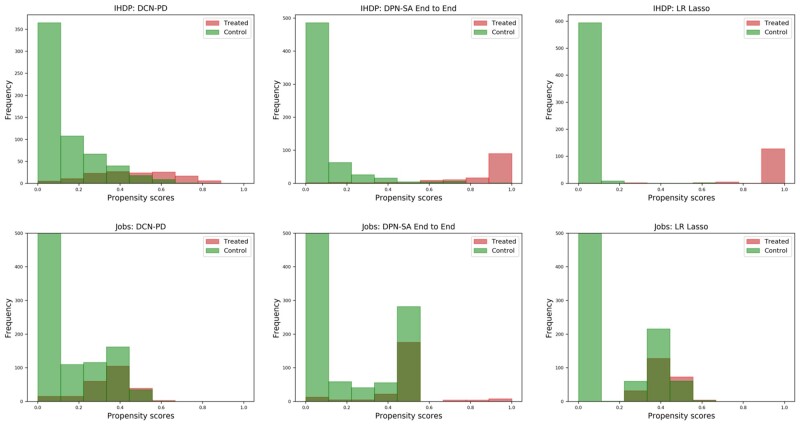
On the IHDP dataset, the propensity scores among all nonlinear (ie, N-20-10- or N-10-) DPN-SA were moderately-to-highly correlated (Pearson’s ρ between 0.67 and 0.82). However, the correlations between nonlinear vs linear (ie, N-1-) DPN-SA configurations were lower (ρ between 0.45 and 0.58). The correlation between DPN-SA N-20-10 and DCN-PD was also moderate-to-high (ρ = 0.72). Logistic regression and LASSO were very highly correlated (ρ = 0.99) and exhibited a moderate-to-high correlation with DPN-SA 20-10 (ρ = 0.72), while the correlation between LASSO and DCN-PD was lower (ρ = 0.62). In terms of score distributions, as shown in Figure 3, the DCN-PD covered low- and mid-probability ranges, with few instances showing high propensity scores. On the other hand, the DPN-SA covered all spectrum of propensity scores, while logistic regression and LASSO yielded primarily low- and high-probability values. On the Jobs dataset, similar correlations were observed among the methods. Logistic/LASSO showed scores in the low-probability ranges, DCN-PD in the low- and medium-, while DCN-PD covered all ranges.

Figure 3.

Histograms of the propensity score distributions (stratified by treatment group) for the Deep Propensity Network using a Sparse Autoencoder (DPN-SA), Deep Counterfactual Network with Propensity Dropout (DCN-PD), and LASSO logistic regression (LR) on the Infant Health and Development Program (IHDP) and Jobs datasets.

Table 2 shows the MSE results for all models on the IHDP, augmented IHDP, and Jobs datasets. On the IHDP dataset, the DPN-SA configured with the N-20-10-layer encoder stacking, trained in an end-to-end manner, yielded the best performance in terms of MSE, with an improvement of 6% over the DCN-PD, and 62% over logistic regression. The 1-neuron DPN-SA N-1- configuration was better than LASSO, perhaps due to the attachment to the DCN-PD, but worse than all the neural network-based classifiers, while the PCA-like DPN-SA N-10- had performance comparable to all other networks. On the augmented IHDP dataset, performance of all models decreased due to the artificial noise and correlated variables addition, but the regularization/sparsity constraints demonstrated to be robust against such noise and the additional correlated variables. The DPN-SA (N-10-) was the best model, 11% better than the DCN-PD and 63% better than logistic regression and LASSO. On the Jobs dataset, the DPN-SA with a single layer (N-1-) exhibited the lowest error among the sparse autoencoders, better than logistic regression/LASSO by 36%, and better than DCN-PD by 46% (which in turn exhibited a higher error than logistic/LASSO); the difference between linear and nonlinear methods was less marked. Overall, the null hypothesis of no difference could not be rejected at the 0.05 significance level for DPN-SA architectures and DCN-PD (except for the Jobs dataset), while it was highly supported against logistic regression and LASSO.

Table 2.

Performance of the models on the IHDP, the augmented IHDP (adding noise/correlated variables), and the Jobs dataset

Dataset	# Covariates/Samples	Model	MSE (SD) εPEHE/εATT	Bengio’s P value	Raw P value
IHDP	25/747	DPN-SA (N-20-10-) end-to-end	2.09 (0.22)	Ref.	Ref.
		DPN-SA (N-20-10-) greedy stack.	2.10 (0.20)	0.95	0.74
		DPN-SA (N-20-10-) greedy stack. curr.	2.11 (0.20)	0.89	0.50
		DPN-SA (N-10-)	2.14 (0.22)	0.75	0.11
		DPN-SA (N-1-)	2.52 (0.37)	0.05	2.23E-18
		DCN-PD	2.22 (0.21)	0.40	3.37E-05
		Logistic Regression	6.02 (1.19)	1.56E-09	2.88E-70
		LASSO Logistic Regression	5.51 (1.03)	1.56E-09	2.92E-70
Augmented IHDP (noise and correlated variables)	100/747	DPN-SA (N-20-10-) end-to-end	3.15 (0.50)	0.02	1.14E-23
		DPN-SA (N-20-10-) greedy stack.	2.72 (0.39)	0.30	4.59E-07
		DPN-SA (N-20-10-) greedy stack. curr.	2.72 (0.37)	0.28	1.92E-07
		DPN-SA (N-10-)	2.47 (0.27)	Ref.	Ref.
		DPN-SA (N-1-)	2.50 (0.27)	0.88	4.33E-01
		DCN-PD	2.77 (0.46)	0.27	8.69E-08
		Logistic Regression	6.85 (1.16)	1.65E-11	1.49E-77
		LASSO Logistic Regression	6.71 (1.11)	1.18E-11	4.72E-78
Jobs	46 (17)/3212	DPN-SA (N-20-10-) end-to-end	0.09 (0.10)	0.28	0.17
		DPN-SA (N-20-10-) greedy stack.	0.12 (0.10)	0.01	2.08E-03
		DPN-SA (N-20-10-) greedy stack. curr.	0.11 (0.09)	0.03	0.01
		DPN-SA (N-10-)	0.12 (0.10)	0.01	2.08E-03
		DPN-SA (N-1-)	0.07 (0.10)	Ref.	Ref.
		DCN-PD	0.13 (0.11)	4.71E-03	6.47E-04
		Logistic Regression	0.11 (0.09)	0.03	0.01
		LASSO Logistic Regression	0.15 (0.12)	6.48E-04	5.20E-05

Abbreviations: DCN-PD, deep counterfactual networks with propensity dropout; DPN-SA, deep propensity network-sparse autoencoder; IHDP, Infant Health and Development Program

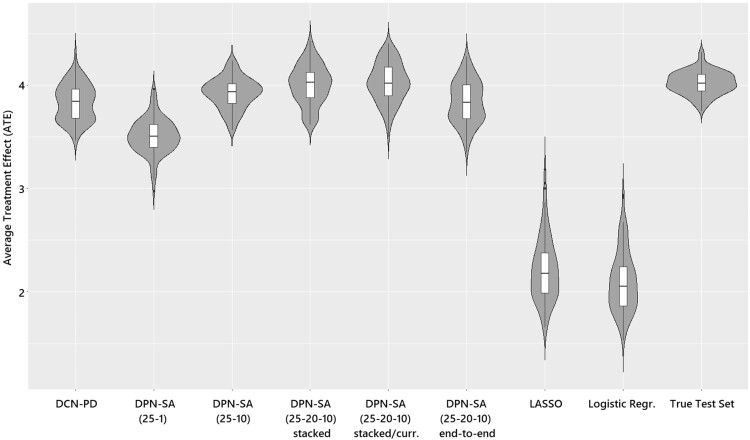
Figure 4 shows the violin plots of each model’s ATE estimation compared to the true ATE on the IHDP data. The DPN-SA (N-20-10-) with greedy stacked-current configuration showed the closest resemblance to the test set ATE followed by the end-to-end and the (N-10-) configurations that were similar to the DCN-PD. The DPN-SA (N-1-) significantly underestimated the test set ATE but was closer to the neural architectures than both logistic regression and LASSO which exhibited a much lower ATE (as expected, since the IHDP outcome surface is nonlinear by design) and a higher variance. Of note, on the Jobs dataset there is no true ATE to display; yet, differently from IHDP, the variance of ε_ATTwas similar among all methods.

Figure 4.

Violin plots of average treatment effect (ATE) estimation comparing the different methods and test/true values on the Infant Health and Development Program (IHDP) dataset.

When comparing training times, the fastest methods were logistic regression and LASSO as expected, followed by the DCN-PD and DPN-SA, with the stacked configuration being slower than the end-to-end. In detail, on an i7 Mac laptop mounting OSX with 16GB RAM, in a single IHDP training/test run, the DPN-SA stacked configuration completed in 6m15s, the DPN-SA end-to-end in 5m, the DCN-PD in 3m, while logistic regression and LASSO took less than 1m.

DISCUSSION

The DPN-SA architecture conjugates the ability to calculate nonlinear propensity scores with dimension reduction and demonstrates advantage over other methods in treatment effect estimation. In both semisynthetic and real-world datasets the DPN-SA exhibited best or near-best performance. In the IHDP counterfactual datasets, the response surface was made nonlinear across treatment groups, thus the true ATE could not be estimated by means of a single linear model, demonstrating the utility of a deep learning approach. In real-world observational data, nonparallel assignments and response surfaces are common, (eg, when investigating the effect of an investigational drug which is indicated on a population with prior comorbidities, at different ages, likely producing nonmonotonic responses). Therefore, the DPN-SA and related deep learning approaches are advantageous over linear estimators, as they do not require investigating explicitly interactional terms. Further, the DPN-SA architecture allows flexibility in configurations, from the simple 1-neuron akin to LASSO, to the single-layer PCA-like, to the fully nonlinear multilayer setup. All the multilayer DPN-SA gave ATE estimates close to the true ones, and even the simpler configurations yielded ATE better than the linear models. However, the DPN-SA—as any other deep learning approaches—neither provide an explicit, interpretable characterization of the propensity score in relation to the input, nor of the outcome surface. While variable importance can be directly ascertained using logistic regression (ie, through odds ratios), the black box nature of deep learners allows only for indirect, marginal representations. Lack of explainability can hinder the choice of a model in clinical settings—even if potentially better than others—especially when treatment decisions solely depend on ‘blind trust.’ Even after extensive validation in different populations, black-box models might be more widely accepted as aiders, not as rulers, in decision-making (eg, helping to choose among a set of already viable options. A number of recent perspective and review articles have explored the topic of black-box models, explainability, and the impact of their use in clinical practice extensively.^45,46

The advantage in MSE of DPN-SA over the DCN-PD, which also employs regularization, is small and would need to be assessed on larger and more diverse datasets. The DPN-SA might be preferable because of its latent space encoding that can be directly chosen and compared (eg, linear vs PCA vs more complex nonlinear setup).

This work has some limitations. First, the choice of a softmax classifier as a replacement to the decoder is relatively simplistic; nonetheless, it provided lower MSE and lower variance in treatment effect estimation. The softmax also allows for multiple treatment arms. Other solutions for embedding the sparse autoencoder within the DCN-PD framework or within alternative approaches could be devised, such as individual treatment effects estimation with generalized adversarial networks.⁴⁷ Another limitation is that the IHDP datasets had limited sample size (747 subjects) and relatively small covariate space (25 variables), and, therefore, the differences in average performance between models are subject to uncertainty. Nonetheless, the performance of the method proved stable with the covariate-augmented IHDP (100 variables) and the larger Jobs dataset (3000+ samples). Finally, the distribution of propensity scores among treatment/control groups is often highly dependent on the dataset and can be highly imbalanced, therefore, the results obtained with one experimental dataset are not assured to be reproducible with others.

Although the DPN-SA and other deep learning approaches allow for a flexible representation of the treatment propensity of the outcome surface and doubly robust estimation, they are not a panacea for estimating treatment effects from observational data. Alaa and Schaar⁴⁸ pointed out that “relative importance of the different aspects of observational data vary with the sample size … selection bias matters only in small-sample regimes, whereas with a large sample size, the way an algorithm models the control and treated outcomes is what bottlenecks its performance.” Therefore, in real-world situations, the number of available observations (also in relation to the number of covariates) must be taken into account when choosing between simpler approaches such as logistic regression/LASSO or a deep learning framework.

CONCLUSION

Deep learning frameworks for propensity score-based treatment effect estimation are particularly suited for large-scale EHR studies because they can take account of high-dimensional covariate sets, large sample sizes, and model complex heterogeneity in treatment assignments. In these cases, regularized linear propensity score methods (eg, high-dimensional propensity score or LASSO) would not be able to provide reliable estimates of treatment effects, likely yielding biased predictions. The DPN-SA provides a valid, possibly improved, alternative to DCN-PD and to more traditional PSM methods.

FUNDING

This work was supported in part by US NIH grants number R01AI145552, R01CA246418, U18DP006512, R21AG068717, and R21CA245858.

AUTHOR CONTRIBUTIONS

SG devised the idea, implemented the code, performed analyses, and wrote parts of the article. JB contributed to study design, methods evaluation, interpretation, and wrote parts of the article. YG provided statistical review and support for the analysis, and wrote parts of the article. MP contributed to the architectural design, methods’ evaluation, methods’ comparisons, interpretation, and wrote parts of the article. All authors reviewed, approved the final version of the paper, and agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

SUPPLEMENTARY MATERIAL

Supplementary material is available at Journal of the American Medical Informatics Association online.

DATA AVAILABILITY

The data underlying this article are available in public repositories at: https://github.com/vdorie/npci/tree/master/examples/ihdp_sim (original IHDP dataset); https://users.nber.org/∼rdehejia/data/.nswdata2.html (original Jobs dataset); https://www.fredjo.com/ (processed datasets).

CONFLICT OF INTEREST STATEMENT

None declared.