Gaussian graphical model for identifying significantly responsive regulatory networks from time course high‐throughput data

Abstract

With rapid accumulation of functional relationships between biological molecules, knowledge‐based networks have been constructed and stocked in many databases. These networks provide curated and comprehensive information for functional linkages among genes and proteins, whereas their activities are highly related with specific phenotypes and conditions. To evaluate a knowledge‐based network in a specific condition, the consistency between its structure and conditionally specific gene expression profiling data are an important criterion. In this study, the authors propose a Gaussian graphical model to evaluate the documented regulatory networks by the consistency between network architectures and time course gene expression profiles. They derive a dynamic Bayesian network model to evaluate gene regulatory networks in both simulated and true time course microarray data. The regulatory networks are evaluated by matching network structure with gene expression to achieve consistency measurement. To demonstrate the effectiveness of the authors method, they identify significant regulatory networks in response to the time course of circadian rhythm. The knowledge‐based networks are screened and ranked by their structural consistencies with dynamic gene expression profiling.

1 Introduction

The gene regulatory network provides a basic framework for the regulation relationship between transcription factors and their target genes [1, 2]. The network architecture indicates the regulatory relationships. It is a promising way to reconstruct gene regulatory network by reverse engineering [3–5]. The DREAM (Dialogue for Reverse Engineering Assessment and Methods) challenge provides evidence for the effectiveness of network reconstruction algorithms [6], but there are still many difficulties in these inferences because of the curse of dimensionality. It is also difficult to assess the inference results. Simultaneously, there is more and more available information about gene regulations. Evaluating a knowledge‐based network with gene expression data will provide a valuable alternative to study gene regulatory networks [3, 7]. The documented networks or pathways are often based on literature‐retrieved information about the relationships among genes and proteins [8]. The match between reference networks and expression profiles will indicate the enrichment information of these functional linkages.

The existing approaches of analysing gene expression data generally start from the identification of differentially expressed genes by comparing the expressions in different conditions or phenotypes. They often include statistical tests, such as t ‐test and significance analysis of microarrays (SAM) [9]. However, genes perform their functions by interacting with each other in the form of network or pathway. Then, there are some methods which have been proposed for pathway analysis [10, 11]. Gene set enrichment analysis (GSEA) [12] and gene set analysis (GSA) [13] provide the significance test for the predefined gene sets in certain gene expression profiling. The geneset will provide more information for the interrelationship of genes and imply their regulations from a system level [14]. However, network structures or topologies have not been considered in most of the existing methods [15]. Moreover, the analysis has not been conducted to consider the true gene expressions efficiently and there are lots of constraints for network structures in the assessment [16, 17]. The relationship of gene regulation defines the core network architecture underlying these genes during biological processes [2, 18]. In response to certain conditions, these gene regulatory networks will perform very different biological functions and show obvious structure dynamics [19]. Here, we aim to provide an evaluation method for the documented gene regulatory networks based on the consistency between network structure and time course gene expression data. The consistency between network structures and measured data are well known in statistical casual hypothesis [3]. The architecture of topological linkages will provide regulatory implications which will underlie gene expression. If we identify the functional linkages and their responses matching with the gene expression, network activity and importance will be identified. There are some methods which have been developed to reconcile network structure and gene expression. Herrgard et al. [7] provided a linear regression method to measure consistency, but it cannot handle the amount of large networks in parallel. Draghici et al. [16] proposed a scoring scheme for assessing the significance of pathways by their ranks corresponding to gene expressions. However, it ignores the regulatory interactions between genes as well as fails to detect the correspondence between gene expression and network structure. We have provided a method to screen the consistency between network structure and gene expression, whereas the method cannot handle the network with cycles and loops [3, 20]. To evaluate biological networks with consideration of general network structures including dynamic networks, it is necessary to develop a new method to identify the consistency between regulatory network structures and gene expression profiles.

In this work, we proposed a dynamic Bayesian network model to identify significant regulatory networks from knowledge‐based reference networks in response to conditional gene expression. Instead of reconstructing gene regulatory networks from high‐throughput data, significant regulatory networks are identified from the reference network library. We validated our method in both simulated data and circadian rhythm time course data. The documented network structures of transcription factors and targets are evaluated from random samplings. The possibility of graph architectures existing in certain conditions was measured by the consistency between network structure and gene expression profile. In particular, we ranked the referred regulatory networks by structural consistency in response to specific time course gene expression data. As shown in the results, the statistical significance as well as the potential regulation architecture provide detailed information for alternative regulatory networks responding to gene expression in specific conditions.

2 Materials and methods

2.1 Framework

Fig. 1 shows the framework of our method to identify significantly responsive regulatory networks by evaluating the consistency between network structure and gene expression. For the reference regulatory networks documented in databases shown in Fig. 1 a, we mapped the time course gene expression information to these regulatory networks shown in Fig. 1 b. By employing a dynamic Bayesian network model, we generated a likelihood value to measure the consistency between the regulatory network structure and the gene expression data (shown in Fig. 1 c). In Fig. 1 d, each of the reference regulatory networks is assigned a statistical significance of consistency with time course gene expression profiling. The significant networks are the outputs as the identified responsive gene regulatory networks.

Fig. 1.

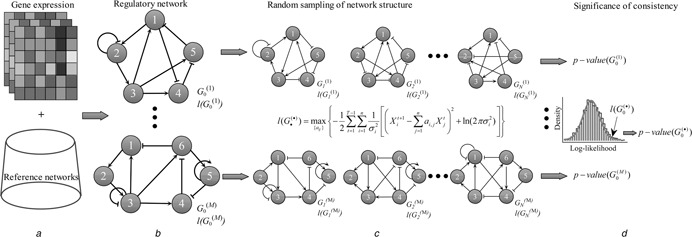
Framework to identify significant regulatory networks in response to condition‐specific gene expression data

2.2 Datasets

We implemented our method in both simulated data and real time course gene expression data of circadian rhythm.

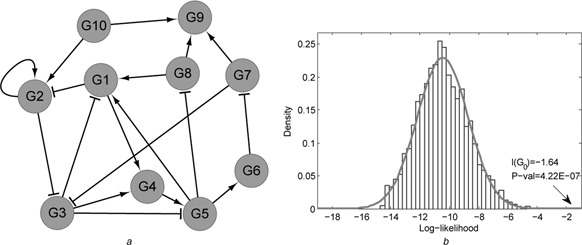
In the simulation study, we firstly generated the simulation data by the following equations representing a self‐defined regulatory architecture shown in Fig. 2 a where ε_it ∼ N (0, σ ²), i = 1, …, 10. After setting x_i,1 ∼ N (0, 1), i = 1, …, 10, σ ² = 0.1, we produced the corresponding time course gene expression data in six time points of the defined regulatory system

$$\begin{array}{cc}{x}_{1,t}=-0.5x_{3,t-1}+0.5x_{5,t-1}+0.5x_{8,t-1}& +{\epsilon }_{1t}\\ x_{2,t}=-0.5x_{1,t-1}+0.5x_{2,t-1}+0.5x_{10,t-1}& +{\epsilon }_{2t}\\ x_{3,t}=-0.5x_{2,t-1}-0.5x_{7,t-1}& +{\epsilon }_{3t}\\ x_{4,t}=0.5x_{1,t-1}+0.5x_{3,t-1}& +{\epsilon }_{4t}\\ x_{5,t}=-0.5x_{3,t-1}+0.5x_{4,t-1}& +{\epsilon }_{5t}\\ x_{6,t}=0.5x_{5,t-1}& +{\epsilon }_{6t}\\ x_{7,t}=-0.5x_{6,t-1}& +{\epsilon }_{7t}\\ x_{8,t}=-0.5x_{5,t-1}& +{\epsilon }_{8t}\\ x_{9,t}=0.5x_{7,t-1}+0.5x_{8,t-1}+0.5x_{10,t-1}& +{\epsilon }_{9t}\\ x_{10,t}=& {\epsilon }_{10t}\end{array}$$

Fig. 2.

Self‐defined regulatory architectures

a Simulated gene regulatory network refers to the ordinary differential equation systems

b Llikelihood distribution of the consistency between network structure and gene expression in the permutation study

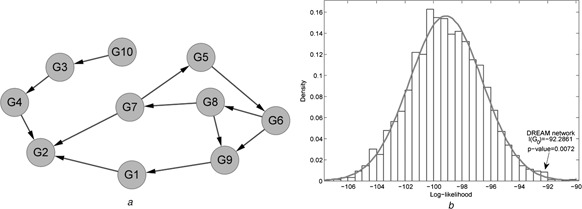
Secondly, for availability of the standard regulatory network and its corresponding time course gene expression, we employed a benchmark regulatory network and its expression from DREAM ‘In Silico’ network challenge [6, 21], which is a competition of reverse engineering to infer the simulated regulatory network from its generated gene expression data [21]. We selected one gene regulatory network and its generated gene expression data for evaluation, which contains 10 genes and 12 regulations as shown in Fig. 4 a. We evaluated the consistency between the network structure and its gene expression. The gene expression profiling of time course data contains 21 time points in two conditions, that is, perturbation and normal [21].

Fig. 4.

Simulated gene expression data were generated by designed regulatory network structures

a Network architecture of a gene regulatory network in DREAM challenge

b Distribution of the log‐likelihood values between network structures and gene expressions in the perturbation condition

In the real high‐throughput data, the true time course gene expression data are about circadian regulation in rat lung and white adipose which was downloaded from NCBI GEO database [22] (ID:GSE25612 and ID:GSE20635 for lung and adipose, respectively). The gene expression profiles were generated from the tissues of Wistar rats by Affymetrix microarray (Rat Genome 230 2.0), which was designed for examining fluctuations in gene expression in lungs and adiposes within the 24 h circadian cycle in normal animals [23, 24]. The experiments are performed in a controlled stress free environment with light:dark cycles of 12 h:12 h within 24 h. Both datasets contain 18 selected time points in the 12:12 (light:dark) cycle. Their objectives are to identify and analyse circadian oscillations in gene expression of lung and white adipose tissue, respectively.

To build the reference gene regulatory networks for evaluation, we downloaded the KEGG pathways in rat [8]. We built the regulatory networks by extracted information for every interaction between two genes. The linkages of ‘GErel’ relationship with activation and repression information are used to construct the regulatory relationships between transcription factors and target genes [8]. In total, there are 207 KEGG pathways which can identify their gene expression information in the rat time course gene expression data and resulted in 37 gene regulatory networks which contain more than 5 genes. These networks formed the reference regulatory networks which are used to identify the consistency between network structure and gene expression. Compared with inferring gene regulatory networks in reverse engineering from high‐throughput data, we identify these significantly responsive regulatory networks in the gene expression profiles of circadian rhythm in a forward manner from the high‐throughput data and the reference networks.

2.3 Significance of networks

In a graphical model, joint distribution probability of a certain directed network architecture can be represented as a product of the individual density functions with conditions on their parent variables by recursive factorisation [3, 25], that is, $f(G)=f\left(X_1,X_2,\dots ,X_n\right)={\prod }_{i=1}^{n}f\left(X_i|\text{parent}\left\{X_i\right\}\right)$ in graph G. Let ${\mathit{X}}^t={\left(X_1^t,\dots ,,X_n^t\right)}^{\mathrm{T}}$ be the gene expression vector of n genes at time t. Thus, for the time points {1, …, t, t, …, T }, under the first‐order Markovian assumption that X ^{t+ 1} is independent of X ^t′ for t ′ < t given X ^t , we have

$$f\left({\mathit{X}}^1,\dots ,{\mathit{X}}^t,\dots ,{\mathit{X}}^{\mathrm{T}}\right)=f\left({\mathit{X}}^1\right)\prod _{t=2}^{\mathrm{T}}\prod _{i=1}^{n}f\left(X_i^t|\text{parent}\left(X_i^t\right)\right)$$

in the time course data. Assume

$$\begin{array}{rl}& {\mathit{X}}^{t+1}={\mathit{\text{AX}}}^t+\mathit{E}\end{array}$$

where

$$\begin{array}{rl}& \mathit{A}=\left(\begin{array}{ccc}{a}_{1,1}& \cdots & a_{1,n}\\ ⋮& \ddots & ⋮\\ a_{n,1}& \cdots & a_{n,n}\end{array}\right)=\left(\begin{array}{c}{\alpha }_1\\ ⋮\\ {\alpha }_n\end{array}\right),a_{i,j}\end{array}$$

is the regulatory coefficient of $X_j^t\to X_i^{t+1}$; E ∼ N (0, Σ), and $\mathrm{\Sigma }=\text{diag}\left({\sigma }_1^2,\dots ,{\sigma }_n^2\right)$. According to the linear Gaussian model [26, 27] and

$$f\left(X_i^{t+1}|{\mathit{X}}^t\right)=\frac{1}{\sqrt{2\pi {\sigma }_i^2}}\text{exp}\left[-\frac{1}{2{\sigma }_i^2}\left(X_i^{t+1}-{\alpha }_i{\mathit{X}}^t\right)\right]$$

we have (see equation at the bottom of the page)

$$\begin{array}{rl}f\left({\mathit{X}}^1,{\mathit{X}}^2,\dots ,{\mathit{X}}^{\mathrm{T}}\right)& =f\left({\mathbf{X}}^1\right)\prod _{t=1}^{T-1}\prod _{i=1}^{n}f\left(X_i^{t+1}|{\mathit{X}}^t\right)\\ & =f\left({\mathbf{X}}^1\right)\prod _{t=1}^{T-1}\prod _{i=1}^n\frac{1}{\sqrt{2\pi {\sigma }_i^2}}\text{exp}\left[-\frac{1}{2{\sigma }_i^2}{\left(X_i^{t+1}-\sum _{j=1}^n{a}_{i,j}{X}_j^t\right)}^2\right]\end{array}$$

Then, the log‐likelihood function

$$\begin{array}{rl}& \ln f\left({\mathit{X}}^1,\dots ,{\mathit{X}}^t,\dots ,{\mathit{X}}^{\mathrm{T}}\right)\propto \\ & -\frac{1}{2}\sum _{t=1}^{T-1}\sum _{i=1}^n\frac{1}{{\sigma }_i^2}\left[{\left(X_i^{t+1}-\sum _{j=1}^n{a}_{i,j}{X}_j^t\right)}^2+\ln \left(2\pi {\sigma }_i^2\right)\right]\end{array}$$

Although the binary regulatory relationship between i and j is available, however, the details of upregulation (→), downregulation $(⊣)$, no regulation (↮) as well as the regulation strength are often unknown, especially for specific conditions. Hence, we employed a quadratic programming method to calculate the likelihood value by optimising the coefficients $a_{i,j}$, (i, j = 1, …, n) (Shown in Fig. 1), that is,

$$\begin{array}{c}\text{Max}-\frac{1}{2}\sum _{t=1}^{T-1}\sum _{i=1}^n\frac{1}{{\sigma }_i^2}\left[{\left(X_i^{t+1}-\sum _{j=1}^n{a}_{i,j}{X}_j^t\right)}^2+\ln \left(2\pi {\sigma }_i^2\right)\right]\\ \mathrm{s}.\mathrm{t}.a_{i,j}\ge 0\text{if}i\to j\\ a_{i,j}\le 0\text{if}i⊣j\\ a_{i,j}=0\text{if}i\nleftrightarrow j\\ 2ci,j=1,\dots ,n\end{array}$$

The constraints of a_i,j ≥ 0 if i → j, a_i,j ≤ 0, $a_{i,j}\le 0\text{if}i⊣j\text{and}{a}_{i,j}=0\text{if}i\nleftrightarrow j$ represent the regulatory strength between i and j. Thus, the likelihood value was determined by the time course gene expression data. Based on the log‐likelihood value, the significance of a network architecture was evaluated by a random sampling process [3]. As shown in Fig. 1, for each regulatory network, we randomly generated N networks by rewiring the same number of regulations between the nodes of the evaluating network. After fitting the log‐likelihood values of the random network structures by a normal distribution, we calculated the consistency probability between the evaluating regulatory architecture and gene expression profiling for each network individually. The statistical significance P ‐value of one regulatory network $G_0^{(i)}(i=1,\dots ,M)$ was calculated by a two‐tailed test. The null hypothesis is that the log‐likelihood of $G_0^{(i)}$ is equal to the mean of that of the N randomly generated networks in the same genes. We set N = 2000 in this work and the significant threshold of P ‐value was set as 0.05. All regulatory networks were implemented in the same process to obtain their effects of consistency with gene expression profiles individually. The ranking by the significant P ‐value is clearly able to provide the enrichment measure of these regulatory structures in response to the time‐series gene expression profiles.

3 Results

3.1 Simulation studies

Firstly, we generated the simulated gene expression data for the network shown in Fig. 2 a. Thus, we obtained a gene regulatory network and its time course gene expression data. The consistency between the regulatory architecture and the corresponding expression data can then be evaluated by our proposed method. After achieving the log‐likelihood value of the evaluating gene regulatory network, each randomly rewired regulatory structure was also calculated for its likelihood value of measuring the consistency with gene expression profiling in the permutation study. The log‐likelihood value between network structure and gene expression data was obtained as −1.64 with the significance P ‐value 4.22 × 10^–7. Fig. 2 b shows the distribution of the frequency of likelihood values. We can find that the regulatory network structure is significant responding to the gene expression data generated by its architecture. The simulation proves the effectiveness and efficiency of our proposed method of identifying the significant network structures in condition‐specific time course gene expression profiles.

We tested the robustness of our proposed method for detecting the strength of regulations by generating large amount of expression datasets, and calculating the significance of the consistency between network structure and expression data. Specifically, we generated 100 gene expression datasets using the former regulatory architecture fluctuated with different noise by gradually increasing the standard deviation σ from 0.1, 0.2, …, to 1 individually. We implemented our method to identify the significance P ‐values of the consistency between the network structure and these generated datasets. Fig. 3 shows the box‐plots of these P ‐values in each simulated 100 datasets for each standard deviation. We found that the P ‐values are more stable in the datasets generated with smaller deviation. The results show the robustness of our method on noise with ten‐stepwise increasing σ from 0.1 to 1 in the ten‐node network architecture. In calculation of the likelihood function, we built quadratic mathematical programming to optimise the regulatory coefficients between these genes. The robustness to noise also indicates the efficiency of our method in identifying the regulatory coefficients of the network.

Fig. 3.

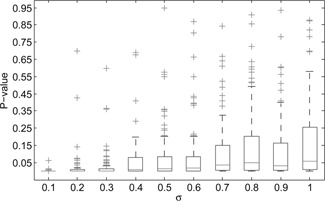
Box plots of robustness in the identification of consistency p‐values

For the benchmark gene regulatory network in the DREAM challenge [5, 21], we presented the results to demonstrate our proposed method as follows. The simulated gene expression data were generated by designed regulatory network structures shown in Fig. 4 a, which contains a cycle of ‘gene 5 → gene 6 → gene 8 → gene 7’. We implemented our method to access the consistency between the time course expression data and the gene regulatory network. For two conditions of perturbation and normal, the standard network structure achieved its significance P ‐values of 0.0072 and 0.0034, respectively. In the perturbation data, the distribution of likelihood value in these random samplings of network structures is shown in Fig. 4 b. The results provided evidence of the high consistency between network structures and its corresponding gene expression data. Compared with the original goal in the ‘in silico’ network challenge of inferring gene regulatory network from simulated expression data, we evaluated the significance of the consistency between regulatory structures and gene expressions. From the results, we identified the consistency underlying the structure of regulations with the gene expression data. The significant gene regulatory network structure responsive to specific gene expression was identified effectively. The results also indicate the rationale of inferring gene regulatory networks from expression data.

3.2 Significant regulatory networks in real gene expression data

To test the effectiveness of our method in real time course gene expression data of circadian rhythm, we implemented the proposed method to identify the significantly responsive regulatory networks enroled from KEGG [8]. Fig. 5 shows the documented regulatory network of circadian rhythm. Obviously, it contains cycles and loops. The gene expression data of circadian rhythm in rat lungs can be divided into two segments, that is, light and dark, in the rhythm of 24 h. Each knowledge‐based gene regulatory network was evaluated by calculating its consistency value with gene expression profiling data in light and black segments, respectively.

Fig. 5.

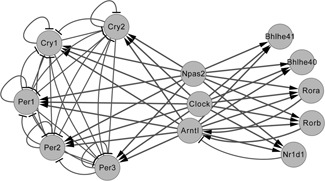
Documented gene regulatory network of circadian rhythm in KEGG

Table 1 lists the significance P ‐values of these reference gene regulatory networks in response to the circadian rhythm gene expression profiles in lungs. They are simply ranked by the significance P ‐values in light. False discovery rate (FDR) (Benjamini and Hochberg's procedure) is also listed. In the evaluation, these documented regulatory networks were screened to be significant or not by their consistency with the gene expression data. The enriched regulatory networks in response to gene expression were identified simultaneously. We found that the regulatory network of ‘circadian rhythm – mammal’ has been identified as one of the most significant networks in both the segments of light and dark. The significant regulatory network of ‘tuberculosis’ indicates the active regulations in this pathway under rhythm transition of day and night in lung cells. It is consistent with the knowledge of circadian oscillation in gene expression in lungs [23]. The significant ‘pathways of cancer’ illustrate active regulation associations between genes in cancer pathways in response to the circadian rhythm, which also indicates the importance of circadian rhythm for cancer [28]. These significant networks as well as the ‘wnt signal pathway’ also imply the interplay among these regulatory networks. The crosstalk between pathways is often crucial to generate complex responses to allow global regulations for specific mechanisms [29]. The enriched regulatory architectures might be highly related to the circadian rhythm of rat lung cells in light and dark conditions. Interestingly, we found that ‘peroxisome proliferator‐activated receptors (PPAR) signalling pathway’ is significant in the dark, whereas it is not significant in light. The pathway is known to be important in clearance of circulating or cellular lipids [8]. This indicates that specific regulations are related to lipid metabolism during night in the rhythm. In contrast, ‘Jak‐STAT signalling pathway’ was identified as significant in light, whereas not in the dark. Their different significance in two segments hints at different active modulation of regulations in response to the rhythm of different conditions [28].

Table 1.

Evaluation of gene regulatory networks in response to the GSE25612 lung gene expression data

KEGG ID	Descriptor	Node	Edge	Light		Dark
				P ‐value	FDR	P ‐value	FDR
rno05152	tuberculosis	42	163	7.59 × 10–8	3.11 × 10–6	1.04 × 10–3	9.40 × 10–3
rno04710	circadian rhythm – mammal	13	58	1.00 × 10–5	1.37 × 10–4	5.34 × 10–5	1.09 × 10–3
rno05200	pathways in cancer	82	170	6.99 × 10–5	4.29 × 10–4	9.84 × 10–3	0.0576
rno04630	Jak‐STAT signalling pathway	25	90	7.33 × 10–5	4.29 × 10–4	0.9450	0.9587
rno04310	wnt signalling pathway	13	40	2.52 × 10–3	0.0115	6.61 × 10–3	0.0451
rno05216	thyroid cancer	7	10	0.0210	0.0860	0.1150	0.2946
rno05213	endometrial cancer	7	10	0.0252	0.0938	0.1101	0.2946
rno05211	renal cell carcinoma	13	22	0.0463	0.1582	0.0981	0.2871
rno05212	pancreatic cancer	9	20	0.0527	0.1661	0.1942	0.3520
rno05143	African trypanosomiasis	6	5	0.0874	0.2561	0.1875	0.3520
rno05215	prostate cancer	9	7	0.1147	0.2985	0.2408	0.3901
rno04350	TGF‐beta signalling pathway	20	26	0.1219	0.2985	0.1865	0.3520
rno04510	focal adhesion	5	6	0.1238	0.2985	0.0319	0.1191
rno04978	mineral absorption	6	5	0.1547	0.3375	0.2185	0.3732
rno05217	basal cell carcinoma	19	38	0.1564	0.3375	0.7837	0.8902
rno04916	melanogenesis	15	14	0.2001	0.3935	0.3057	0.4643
rno04976	bile secretion	13	12	0.2102	0.3935	0.4905	0.6487
rno05134	legionellosis	14	12	0.2244	0.3935	0.4397	0.6217
rno05218	melanoma	6	5	0.2257	0.3935	0.9124	0.9587
rno04210	apoptosis	8	12	0.2436	0.3935	0.1367	0.3297
rno04150	mTOR signalling pathway	6	5	0.2560	0.3935	0.7494	0.8778
rno04961	endocrine and other factor‐regulated calcium reabsorption	6	7	0.2614	0.3935	0.8818	0.9514
rno04960	aldosterone‐regulated sodium reabsorption	16	15	0.2645	0.3935	0.1703	0.3520
rno04340	hedgehog signalling pathway	22	40	0.2773	0.3935	0.7093	0.8778
rno04962	vasopressin‐regulated water reabsorption	7	6	0.2783	0.3935	0.7470	0.8778
rno05031	amphetamine addiction	13	28	0.2883	0.3941	0.1974	0.3520
rno05222	small cell lung cancer	25	38	0.2997	0.3964	0.0270	0.1107
rno04910	insulin signalling pathway	6	5	0.3211	0.4114	0.0200	0.0913
rno04950	maturity onset diabetes of the young	20	28	0.5106	0.6214	0.9587	0.9587
rno04115	p53 signalling pathway	32	31	0.5153	0.6214	0.4777	0.6487
rno04620	toll‐like receptor signalling pathway	12	11	0.6041	0.7077	0.6175	0.7912
rno05220	chronic myeloid leukaemia	5	3	0.7017	0.7992	0.3982	0.5830
rno04110	cell cycle	20	26	0.7254	0.8038	0.0495	0.1690
rno04920	adipocytokine signalling pathway	9	10	0.8524	0.8997	0.8034	0.8902
rno05030	cocaine addiction	16	22	0.8558	0.8997	0.1461	0.3328
rno03320	PPAR signalling pathway	64	258	0.9756	0.9956	5.26 × 10–13	2.16 × 10–11
rno05221	acute myeloid leukaemia	12	10	0.9956	0.9956	0.2473	0.3901

Similarly, we identified the significance of these gene regulatory networks responding to circadian rhythm in rat white adipose tissues. The results are shown in Table 2. We found that ‘circadian rhythm’ regulations are also identified as one of the most significant pathways in both light and dark cycles. Compare with that in lungs, ‘tuberculosis’ is not significant any more. Although some signalling pathways are highlighted in white adiposes, such as ‘Hedgehog signalling pathway’. We also found that the diabetic pathways of ‘Maturity onset diabetes of the young’ and ‘Insulin signalling pathway’ are highly ranked, which are known to be closely related to metabolism. White adipose tissue is an important metabolic place of performing energy transformation [24]. The regulatory network structures are evaluated by the consistency value in our model which shows that significant regulatory networks are prioritised from the network library. The results in adipose provided more evidence for the effectiveness of the proposed method for identifying responsive regulatory networks from time course gene expression data. The enriched pathways indicates the roles of circadian regulation in coordinating the physiological functions of two dynamic tissues.

Table 2.

Evaluation of gene regulatory networks in response to the GSE20635 adipose gene expression data.

KEGG ID	Descriptor	Node	Edge	Light		Dark
				P ‐value	FDR	P ‐value	FDR
rno04340	hedgehog signalling pathway	22	40	2.89 × 10–6	0.0001	0.2773	0.8443
rno05217	basal cell carcinoma	19	38	2.87 × 10–5	0.0007	0.2734	0.8443
rno04710	circadian rhythm – mammal	13	58	0.0008	0.0072	0.0390	0.4951
rno04950	maturity onset diabetes of the young	20	28	0.0369	0.2355	0.3360	0.8443
rno04976	nile secretion	13	12	0.0446	0.2528	0.3514	0.8443
rno05031	amphetamine addiction	13	28	0.0662	0.3188	0.0362	0.4951
rno04115	p53 signalling pathway	32	31	0.0687	0.3187	0.0717	0.6097
rno04960	aldosterone‐regulated sodium reabsorption	16	15	0.0981	0.4171	0.1387	0.7860
rno04910	insulin signalling pathway	6	5	0.1233	0.4836	0.1959	0.8443
rno05134	legionellosis	14	12	0.1988	0.6521	0.1951	0.8443
rno05143	African trypanosomiasis	6	5	0.2133	0.6521	0.2385	0.8443
rno04150	mTOR signalling pathway	6	5	0.2174	0.6521	0.3564	0.8443
rno04961	endocrine and other factor‐regulated calcium reabsorption	6	7	0.2729	0.7212	0.8806	0.9166
rno04350	TGF‐beta signalling pathway	20	26	0.2744	0.7212	0.3830	0.8443
rno05030	cocaine addiction	16	22	0.2828	0.7212	0.2840	0.8443
rno05218	melanoma	6	5	0.3131	0.7380	0.4150	0.8443
rno04978	mineral absorption	6	5	0.3184	0.7380	0.9756	0.9756
rno04920	adipocytokine signalling pathway	9	10	0.3618	0.7687	0.5896	0.8943
rno05215	prostate cancer	9	7	0.3879	0.7908	0.5105	0.8443
rno04962	vasopressin‐regulated water reabsorption	7	6	0.4031	0.7908	0.2313	0.8443
rno05211	renal cell carcinoma	13	22	0.4369	0.8252	0.4897	0.8443
rno05213	endometrial cancer	7	10	0.4564	0.8312	0.8180	0.9166
rno05216	thyroid cancer	7	10	0.4754	0.8361	0.8243	0.9166
rno04110	cell cycle	20	26	0.5110	0.8386	0.4408	0.8443
rno05222	small cell lung cancer	25	38	0.5599	0.8386	0.8768	0.9166
rno05221	acute myeloid leukaemia	12	10	0.5768	0.8386	0.4365	0.8443
rno05212	pancreatic cancer	9	20	0.5774	0.8386	0.7734	0.9166
rno05220	chronic myeloid leukaemia	5	3	0.5830	0.8386	0.9307	0.9493
rno04620	toll‐like receptor signalling pathway	12	11	0.6032	0.8386	0.6339	0.9166
rno05200	pathways in cancer	82	170	0.6136	0.8386	0.8633	0.9167
rno05152	tuberculosis	42	163	0.6314	0.8386	0.7440	0.9166
rno04310	wnt signalling pathway	13	40	0.6413	0.8386	0.7301	0.9166
rno03320	PPAR signalling pathway	64	258	0.6763	0.8412	0.6592	0.9166
rno04630	Jak‐STAT signalling pathway	25	90	0.7192	0.8506	0.7465	0.9166
rno04210	apoptosis	8	12	0.7266	0.8506	0.7406	0.9166
rno04510	focal adhesion	5	6	0.8867	0.9504	0.5178	0.8443
rno04916	melanogenesis	15	14	0.9362	0.9504	0.5246	0.8443

The structure of regulations was measured by their consistency with the time course gene expression data in lung and adipose, respectively. Each knowledge‐based regulatory network achieved its significance evaluated by the P ‐values of measuring the match between network structures and expression profiles. In our scheme, we randomly rewired the regulatory linkages among these genes by keeping the number of regulations. The significance has been identified in a statistical test framework. Fig. 6 shows the log‐likelihood density plots for the regulatory network of circadian rhythm in permutation studies, where Figs. 6 a and b refer to the results of light and dark in lung, and Figs. 6 c and d are the results of light and dark in adipose, respectively. Compared with random samples, we found that the likelihood values of the known regulatory structure are located at the tail parts of these bell‐shape‐like normal distributions. The statistical significance of rejecting the null hypothesis was calculated for the known regulation structure. Note that we implemented two‐tailed tests to prioritise these networks with many distinguished likelihoods. In the two tissues, the circadian rhythm regulation relationships are significant in both segments of light and black. This clearly proved the effectiveness of our method for identifying the consistency between network architecture and gene expression. The results show the importance of these gene regulations during the temporal stages of rhythm. Simultaneously, the stability of gene regulation networks has been evaluated in the permutation processes because there are few structures which can achieve higher likelihood values in response to specific gene expression data.

Fig. 6.

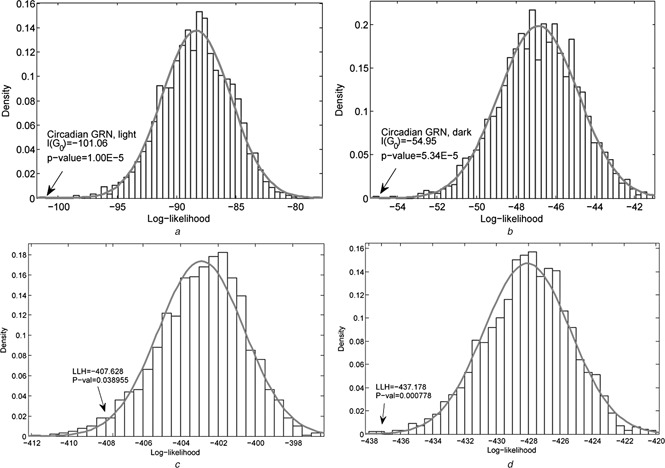
Density distribution of log‐likelihood values in the permutation study for circadian rhythm regulatory network

a In the light

b In the dark in lung

c In the light

d In the dark in white adipose

3.3 Comparison study

There are some methods which have been developed to identify the statistical significance of gene sets, such as GSEA [12] and GSA [13], but the importance of network architecture has not been embedded in the analysis. There are also some methods which have been proposed to detect the significance by the relationship between gene expression and network structure, whereas there are no specific methods available for time course gene expression data. For instance, Herrgard et al. [7] developed a method based on linear regression to assess the agreement between gene regulatory network structure and expression profiling by decomposing the network into blocks. We also proposed a Bayesian network method to identify the consistency between network structure and expression [3]. In this work, we developed a dynamic Bayesian network model to assess the consistency between network structure and time course gene expression data. Our method can handle gene regulatory networks without any constraints of acyclic, which will be applicable in many general conditions.

In our method, we calculated the network likelihoods and evaluated their statistical significance. For comparison, we also tested the effectiveness of a simple correlation based method. In the real gene expression datasets, we evaluated the significance of network structure by the consistency between the correlation and the edge for each regulatory network. Specifically, we calculated the ratios of positive and negative correlations which are consistent with the existing regulations in each pathway, that is, positive correlation coincides with active regulation, and negative correlation coincides with repression. Then, we generated N = 2000 random networks by rewiring the linkages in each gene set. For each generated network, we also calculated the consistency ratio between correlations and regulatory relationships in these rewired linkages. After fitting the ratio with a Gaussian distribution, we got the significance P ‐value by the two‐side test which we had implemented before. Table 3 lists the top 5 ranked regulatory networks in the real datasets. We found that there are no specificities of these most significant regulatory networks in the two datasets of lung and adipose. For instance, the lung related pathways are also enriched in adipose. The results provided by the proposed dynamic Bayesian network model show that the known circadian rhythm regulatory networks will be enriched, whereas the results in the correlation method cannot give this implication. The comparison study indicates the effectiveness and advantage of our proposed method.

Table 3.

Top ranked 5 significant regulatory networks of lung and adipose identified by correlation‐based method in the real gene expression datasets

Tissue	KEGG ID	Descriptor	Node	Edge	Light		Dark
					P ‐value	FDR	P ‐value	FDR
lung	rno05200	pathways in cancer	82	170	3.59 × 10–6	1.83 × 10–4	3.56 × 10–12	1.82 × 10–10
	rno04630	Jak‐STAT signalling pathway	25	90	1.22 × 10–5	3.11 × 10–4	1.56 × 10–6	1.99 × 10–5
	rno05152	tuberculosis	42	163	7.54 × 10–5	1.28 × 10–3	1.48 × 10–7	3.77 × 10–6
	rno03320	PPAR signalling pathway	64	258	0.0014	0.0173	0.0001	0.0009
	rno05222	small cell lung cancer	25	38	0.0033	0.0321	3.04 × 10–5	0.0003
adipose	rno03320	PPAR signalling pathway	64	258	<1.0 × 10–16	<1.0 × 10–15	<1.0 × 10–15	<1.0 × 10–13
	rno04630	Jak‐STAT signalling pathway	25	90	2.22 × 10–16	3.77 × 10–15	<1.0 × 10–15	<1.0 × 10–13
	rno05200	pathways in cancer	82	170	2.22 × 10–16	3.77 × 10–15	<1.0 × 10–15	<1.0 × 10–13
	rno05152	tuberculosis	42	163	2.92 × 10–12	3.73 × 10–11	8.44 × 10–15	1.08 × 10–13
	rno05222	small cell lung cancer	25	38	2.56 × 10–5	1.87 × 10–4	4.93 × 10–8	5.02 × 10–7

4 Discussions

In this paper, we proposed a dynamic Bayesian network model to identify the consistency between regulatory structure and time course gene expression data. The results show that our method can effectively identify significant regulatory networks both in simulated and real gene expression data. The simulation studies indicate the feasibility and efficiency of our method in both the defined and benchmark datasets. The results in real datasets prioritised regulatory networks which are consistent with the knowledge about circadian rhythm and were also validated by the original experiments. Our method can be used to identify large‐scale regulatory networks without any constraints of acyclic and loop‐less regulations. Note that regulatory cycles and loops usually exist in biological systems.

4.1 From reconstruction to evaluation

Owing to the complexity of gene expression, the methods for reconstructing a gene regulatory network encounter difficulties not only from the dimensional curse of high‐throughput data, but also from various assumptions of gene regulations [6]. Based on the knowledge‐based regulatory networks or documented reference networks, we measured the consistency between their architectures and expressions, which provided a powerful alternative to investigate the regulatory relationship from gene expression data. We assessed the significance of these reference networks by their structures. The identified significance provides the implication of responsive regulations in certain conditions. In our method, the likelihood of network structures meeting time course gene expression provides sequential checks on the architecture of gene regulations. However, network reconstruction is to infer the network structure from the gene expression data, which often have inherent barrier of environmental and phenotype flexibility. On the other hand, as shown in the paper, based on the knowledge‐based regulatory networks, we can identify significantly regulatory relationships in specific conditions. Clearly, the forward‐like process provides a novel approach to bridge the relationship with phenotypes and molecular data. In the future, we can efficiently identify network biomarkers [30] or dynamic network biomarkers [31] for complex diseases, for example, diabetes and cancers, by further combining the proposed technique with module‐based approaches [32].

4.2 Effect of network structure

We measured the consistency between network structure and time course gene expression in a dynamic Bayesian network formulation. In particular, we calculated the consistency possibility between network structure and gene expression data by a random sampling process. The random samples are based on the same geneset by rewiring of linkages between these genes, that is, the same number of regulations will be assigned in the same geneset. Each generated network was also evaluated for its likelihood of the connection architecture in response to gene expression profiling data. From the likelihood values, we obtained the assessment between network structures and expressions, and the documented regulatory networks achieved their consistency significance with data. However, in certain gene expression, a few random networks with rewiring linkages also achieved their significance of high consistency with gene expressions. The other alternative structures in these random samples also imply the difficulty of inferring gene regulatory networks only from gene expression data.

4.3 Improvement of directed network

The proposed method of dynamic Bayesian network model in this paper improves our former methods for network screening on acyclic and loop‐free networks of gene regulations [3, 20], and it certainly can cover more types of networks for evaluation. The proposed graphical model is designed for directed networks. However, there are many undirected biomolecular interactions, for example, protein–protein interactions, which form undirected networks. Therefore it is necessary in the future to develop a new theoretical model to consider undirected networks and hybrid networks with both directed and undirected edges, which would cover all forms of regulations, interactions and cooperations between biological molecules. As another topic, in our algorithm, the random samples can also be extended to identify more reasonable network structures and potential regulatory relationships by assessing the generated networks with higher significance given the available gene expression. The network structure coherent with the expression indicates possibly crucial meanings, which will provide valuable information for disease mechanism and drug target design.

5 Conclusion

In this work, we developed a novel dynamic Bayesian network model to measure the consistency between network structure and gene expression. We identified the significant regulatory networks from the documented reference networks in response to circadian rhythm conditions. The directed regulatory networks achieved their significance measured by the consistency possibility between network regulatory architectures and gene expression profiles. Clearly, our method provides an alternative way to detect responsive biomolecular networks responding to certain conditions and phenotypes. Our model can handle large‐scale regulations as well as general directed networks. Moreover, our method can provide potential regulations in the networking genes. The analysis of the dynamics in the regulatory networks of circadian rhythm related data provides evidence for the effectiveness of our method as well as biological insights for rhythm mechanism.