Bayesian model comparison for rare-variant association studies

Summary

Whole-genome sequencing studies applied to large populations or biobanks with extensive phenotyping raise new analytic challenges. The need to consider many variants at a locus or group of genes simultaneously and the potential to study many correlated phenotypes with shared genetic architecture provide opportunities for discovery not addressed by the traditional one variant, one phenotype association study. Here, we introduce a Bayesian model comparison approach called MRP (multiple rare variants and phenotypes) for rare-variant association studies that considers correlation, scale, and direction of genetic effects across a group of genetic variants, phenotypes, and studies, requiring only summary statistic data. We apply our method to exome sequencing data (n = 184,698) across 2,019 traits from the UK Biobank, aggregating signals in genes. MRP demonstrates an ability to recover signals such as associations between PCSK9 and LDL cholesterol levels. We additionally find MRP effective in conducting meta-analyses in exome data. Non-biomarker findings include associations between MC1R and red hair color and skin color, IL17RA and monocyte count, and IQGAP2 and mean platelet volume. Finally, we apply MRP in a multi-phenotype setting; after clustering the 35 biomarker phenotypes based on genetic correlation estimates, we find that joint analysis of these phenotypes results in substantial power gains for gene-trait associations, such as in TNFRSF13B in one of the clusters containing diabetes- and lipid-related traits. Overall, we show that the MRP model comparison approach improves upon useful features from widely used meta-analysis approaches for rare-variant association analyses and prioritizes protective modifiers of disease risk.

Introduction

Sequencing technologies are quickly transforming human genetic studies of complex traits. It is increasingly possible to obtain whole-genome sequence data on thousands of samples at manageable costs. As a result, the genome-wide study of rare variants (minor allele frequency [MAF] $<$ 1%) and their contribution to disease susceptibility and phenotype variation is now feasible.1, 2, 3, 4

In genetic studies of diseases or continuous phenotypes, rare variants are hard to assess individually because of the limited number of observations of each rare variant. Hence, to boost the power to detect a signal, evidence is usually aggregated across variants in blocks. When designing an aggregation method, there are three questions that are usually considered. First, across which biological units should variants be combined (e.g., genes); second, which variants within those units should be included;⁵ and third, which statistical model should be used?⁶ Given the widespread observations of shared genetic risk factors across distinct diseases, there is also considerable motivation to use gene discovery approaches that leverage the information from multiple phenotypes jointly. In other words, rather than only aggregating variants that may have effects on a single phenotype, we can also bring together sets of phenotypes for which a single variant or set of variants might have effects.

In this paper, we present a Bayesian multiple rare variants and phenotypes (MRP) model comparison approach for identifying rare-variant associations as an alternative to current, widely used univariate statistical tests. The MRP framework exploits correlation, scale, and/or direction of genetic effects in a broad range of rare-variant association study designs including case-control, multiple diseases and shared controls, a single continuous phenotype, multiple continuous phenotypes, or a mixture of case-control and multiple continuous phenotypes (Figure 1). MRP makes use of Bayesian model comparison whereby we compute a Bayes factor (BF) defined as the ratio of the marginal likelihoods under two models: (1) a null model where all genetic effects are zero and (2) an alternative model where factors such as correlation, scale, and direction of genetic effects are considered. For MRP, the BF represents the statistical evidence for a non-zero effect for a particular group of rare variants on the phenotype(s) of interest and can be used as an alternative to p values from traditional significance testing.

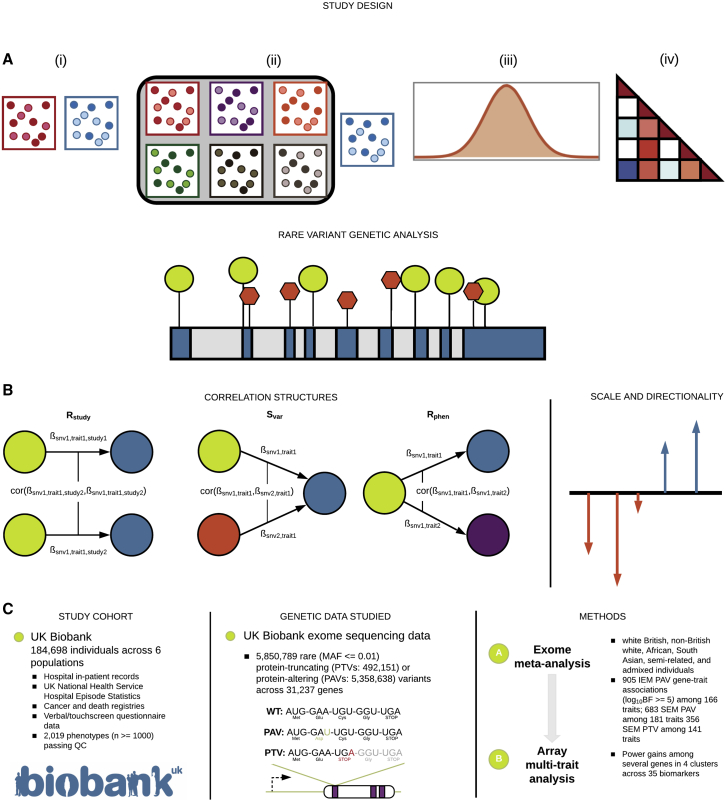
Figure 1.

MRP study overview

(A) MRP is suitable for a broad range of rare variant association study designs, including, from left to right, (i) case-control, (ii) multiple diseases with shared controls, (iii) single quantitative phenotype, and (iv) mixtures of case-control and quantitative phenotypes.

(B) Diagram of factors considered in rare variant association analysis including the correlation matrices: ${\mathbf{R}}_{\text{study}}$ (expected correlation of genetic effects among a group of studies), ${\mathbf{S}}_{\text{var}}$ (expected covariance of genetic effects among a group of variants, potentially accounting for annotation of variants), and ${\mathbf{R}}_{\text{phen}}$ (expected correlation of genetic effects among a group of phenotypes). MRP can take into account both scale and direction of effects.

(C) We focused on 184,698 individuals across six ancestry groups in the UK Biobank and analyzed 5,850,789 rare coding variants (492,151 PTVs and 5,358,638 PAVs) in the whole-exome sequencing data via single-trait and multi-trait meta-analyses with a specific focus on 35 biomarker traits.

While many large genetic consortia collect both raw genotype and phenotype data, in practice, sharing of individual genotype and phenotype data across groups is difficult to achieve. To address this, MRP can use summary statistics, such as estimates of effect size and corresponding standard errors from typical single-variant/single-phenotype linear or logistic regressions, as input. Furthermore, we use insights from Liu et al.⁷ and Cichonska et al.,⁸ which suggest the use of additional summary statistics such as covariance estimates across variants and studies, respectively, for the lossless ability to detect gene-based association signals with summary statistics alone.

Prior work has explored the use of model comparison and BFs in multi-trait settings. The model comparison in Stephens, 2013⁹ is slightly different in usage. Whereas MRP can be used for meta-analysis and the combining of signal across multiple variants within a block, the method explored in Stephens is used for identifying a distinction between direct and indirect associations. Both have strengths relative to the other.

The multi-trait model comparison approach that is referenced in Pickrell et al., 2016¹⁰ focuses on the two-phenotype case. In other words, a null (where the SNP is associated to neither trait) is compared to the alternatives of the SNP being associated to one, the other, or both traits. MRP can generalize beyond the two-phenotype case and assumes a more holistic prior across phenotypes by using correlation coefficients.

Aggregation techniques rely on variant annotations to assign variants to groups for analysis. MRP allows for the inclusion of priors on the scale of effect sizes that can be adjusted depending on what type of variants are included in the analysis. For instance, protein-truncating variants (PTVs)^11,12 are highly likely to be functional because they often disrupt the normal function of a gene. Additional deleteriousness metrics, such as MPC (a metric that combines subgenic constraints with variant-level data for deleteriousness prediction)¹³ and pLI (a metric derived from a comparison of the observed number of PTVs in a sample to the number expected in the absence of fitness effects, i.e., under neutrality, given an estimated mutation rate for the gene),¹⁴ can further attenuate or accentuate these granular signals. Furthermore, because PTVs typically abolish or severely alter gene function, there is particular interest in identifying protective PTV modifiers of human disease risk that may serve as targets for future therapeutics.15, 16, 17 We therefore demonstrate how the MRP model comparison approach can improve discovery of such protective signals by modeling the direction of genetic effects; this prioritizes variants or genes that are consistent with protecting against disease.

To evaluate the performance of MRP, we use simulations and compare it to other commonly used approaches. Some simple alternatives to MRP include univariate approaches for rare-variant association studies, including the sequence kernel association test (SKAT)¹⁸ and the burden test,⁶ which are special cases of the MRP model comparison when we assign the prior correlation of genetic effects across different variants to be zero or one, respectively.

We apply MRP to summary statistics computed on a tranche of n = 184,698 exomes for thousands of traits in the UK Biobank for which we have exome data for n $\ge$ 1,000 white British individuals, focusing on a meta-analysis context across six UK Biobank subpopulations as defined previously (material and methods).¹⁹ We additionally apply multi-phenotype MRP on clusters of biomarker traits within a single-population context (white British individuals). These analyses show that MRP recovers results from single-variant-single-phenotype association analyses while increasing the power to detect new rare-variant associations, including protective modifiers of disease risk.

Material and methods

Description of MRP

In this section, we provide an overview of the MRP model comparison approach. MRP models genome-wide association study (GWAS) summary statistics as being distributed according to one of two models: the null model, where the effect sizes across all studies for a group of variants and a group of phenotypes is zero, and the alternative model, where effect sizes are distributed according to a multivariate normal distribution with a non-zero mean and/or covariance matrix. MRP compares the evidence between the alternative model and the null model with a BF, which is the ratio of the marginal likelihoods under the two models given the observed data.

To define the alternative model, we must specify the prior correlation structure, scale, and direction of the effect sizes. Let N be the number of individuals and K the number of phenotype measurements on each individual. Let M be the number of variants in a testing unit G, where G can be, for example, a gene, a pathway, or a network. Let S be the number of studies from which data is obtained—this data may be in the form of (1) raw genotypes and phenotypes or (2) summary statistics including linkage-disequilibrium (LD) coefficients, effect sizes, and corresponding standard errors. When considering multiple studies (S $>$ 1), multiple rare variants (M $>$ 1), and multiple phenotypes (K $>$ 1), we define the prior correlation structure of the effect sizes as an SMK × SMK matrix, U. In practice, we define U as a Kronecker product of three sub-matrices:

• •an S × S matrix ${\mathbf{R}}_{study}$ containing the correlations of genetic effects among studies that can model the level of heterogeneity in effect sizes between populations;²⁰
• •an M × M matrix ${\mathbf{S}}_{var}$ containing the covariances of genetic effects among genetic variants, which may reflect, e.g., the assumption that all the PTVs in a gene may have the same biological consequence^11,12,21 or prior information on scale of the effects obtained through integration of additional functional data;^5,22 by assuming zero correlation of genetic effects, MRP becomes a dispersion test similar to C-alpha^23,24 and SKAT;¹⁸ and
• •a K × K ${\mathbf{R}}_{phen}$ matrix containing the correlations of genetic effects among phenotypes, which may be estimated from common variant data.25, 26, 27

The variance-covariance matrix of the effect size estimates may be obtained from readily available summary statistics such as in-study LD matrices, effect size estimates (or log odds ratios), and the standard errors of the effect size estimates.

MRP allows users to specify priors that reflect knowledge of the variants and phenotypes under study. For instance, we can define an independent effects model (IEM) where the effect sizes of different variants are not correlated at all. In this case, ${\mathbf{S}}_{var}$ is the identity matrix, and MRP behaves similarly to dispersion tests such as C-alpha^23,24 and SKAT.¹⁸ We can also define a similar effects model (SEM) by setting every value of ${\mathbf{R}}_{var}$ to $\sim$ 1, where ${\mathbf{R}}_{var}$ is the correlation matrix corresponding to covariance matrix ${\mathbf{S}}_{var}$. This model assumes that all variants under consideration have similar effect sizes (with, possibly, differences in scale, such as in the burden test). Such a model may be appropriate for PTVs, where each variant completely disrupts the function of the gene, leading to a gene knockout. The prior on the scale of effect sizes can be used to denote which variants may have larger effect sizes. For instance, emerging empirical genetic studies have shown that within a gene, PTVs may have stronger effects than missense variants.²⁸ This can be reflected by adjusting the prior variances of effect sizes (σ) for different categories of variants.

Finally, we can utilize a prior on the expected location/direction of effects to specify alternative models where we seek to identify variants with protective effects against disease. By default, we have assumed that the prior mean of genetic effects is zero, which makes it possible to analyze a large number of phenotypes without enumerating the prior mean across all phenotypes. To proactively identify genetic variants that are consistent with a protective profile for a disease, we can include a non-zero vector as a prior mean of genetic effects. For this, we can exploit information from Mendelian randomization studies of common variants, such as recent findings where rare protein-truncating loss-of-function variants in PCSK9 were found to decrease low-density lipoprotein (LDL) and triglyceride levels and decrease coronary artery disease risk,^15,29,30 to identify situations where such a prior is warranted.

Applying MRP to variants from a testing unit G yields a BF for that testing unit that describes the evidence that rare variants in that testing unit have a non-zero effect on the traits used in the model. We can turn this evidence into probability via Bayes’ rule. Namely, a multiplication of prior-odds of association by BF transforms the prior-odds to posterior-odds. For example, if our prior probability for one particular gene to be associated with a phenotype is ${10}^{-4}$, then an observed BF of ${10}^5$ means that our posterior probability of association between the gene and the phenotype is over 90%. Although we see advantages in adopting a Bayesian interpretation for MRP, our approach could also be used in a frequentist context by using BF as a test statistic to compute p values.

MRP details

MRP model comparison for association testing

We consider the multivariate linear regression model

$$\underset{\left(N\times K\right)}{\text{Y}}=\underset{\left(N\times K\right)}{\mathbf{\Psi }}+\underset{\left(N\times M\right)}{\text{X}}\underset{\left(M\times K\right)}{\text{B}}+\underset{\left(N\times K\right)}{\text{E}},$$

where the matrices $\text{Y}=\left[y_{ik}\right]$, $\text{X}=\left[x_{im}\right]$, $\text{B}=\left[{\beta }_{mk}\right]$, and $\text{E}=\left[e_{ik}\right]$ describe the phenotype values $\left(y_{ik}\right)$, copies of minor allele $\left(x_{im}\right)$, variant-phenotype effects $\left({\beta }_{mk}\right)$, and residual errors $\left(e_{ik}\right)$, for individual i, phenotype k, and variant m.

We assume that each phenotype has been transformed to a standard normal distribution and that the columns of X have been centered, which means that the estimate for the intercept term $\mathbf{\Psi }$ is 0 and independent of the estimate of B. We use vectorized notation where the rows of B form vector $\beta ={\left({\beta }_1,\dots ,{\beta }_M\right)}^{⊺}$ of length $MK$.

We define the MRP model comparison as a BF between the alternative model, where at least one variant affects at least one phenotype, and the null model, where all variant-phenotype effects are zero. BF is the ratio of the marginal likelihoods for these two models:

$$\text{BF}=\frac{{\int }_{\beta }p\left(\text{Data}|\beta )p(\beta |\text{ALT}\right)d\beta }{{\int }_{\beta }p\left(\text{Data}|\beta )p(\beta |\text{NULL}\right)d\beta },$$

where Data can correspond either to the effect size estimates $\hat{\beta }$ and the estimated variance-covariance matrix of $\hat{\beta }$, ${\hat{\text{V}}}_{\beta }$, or to the original phenotypes and genotypes, $\underset{\left(N\times K\right)}{\text{Y}}$ and $\underset{\left(N\times M\right)}{\text{X}}$, and any other covariates that we want to regress out from the phenotypes.

The prior distribution for the null model, $p\left(\beta |\text{NULL}\right)$, is simply the point mass at $\beta =0$.

Likelihood function

A maximum likelihood estimator of B is given by the ordinary least-squares method

$$\hat{\text{B}}={\left({\text{X}}^{⊺}\text{X}\right)}^{-1}{\text{X}}^{⊺}\text{Y},$$

which in vectorized form is denoted $\hat{\beta }={\left({\hat{\beta }}_1,\dots ,{\hat{\beta }}_M\right)}^{⊺}.$ An estimator of the variance-covariance of $\hat{\beta }$ is given by

$${\hat{\text{V}}}_{\mathbf{\beta }}={\left({\text{X}}^{⊺}\text{X}\right)}^{-1}\otimes {\hat{\text{V}}}_{\text{Y}},$$

where ${\hat{\text{V}}}_{\text{Y}}$ is the estimated residual variance-covariance matrix of Y given X.

Following Band et al.,²⁰ we approximate the likelihood function of β by a multivariate normal distribution with mean $\hat{\beta }$ and variance-covariance matrix ${\hat{\text{V}}}_{\beta }$. Note that by approximating ${\hat{\text{V}}}_{\text{Y}}$ via the trait correlation matrix, this likelihood approximation does not require access to the individual-level data X and Y but only to the summary data of effect sizes $\hat{\beta }$, LD-matrix ${\text{X}}^{⊺}\text{X}$, and a trait correlation estimate.

Prior of β in the alternative model

We construct the prior distribution $p\left(\beta |\text{ALT}\right)$ for the alternative model in three steps, allowing the user to specify correlations between effects of different variants on different traits across different studies.

In a single study, the prior density for β incorporates the expected correlation of genetic effects among a group of variants $\left({\mathbf{R}}_{\text{var}}\right)$ and among a group of phenotypes $\left({\mathbf{R}}_{\text{phen}}\right)$. In addition, we incorporate an expected spread of the effect size of each variant by scaling ${\mathbf{R}}_{\text{var}}$ as

$${\mathbf{S}}_{\text{var}}=\text{Δ}\left({\sigma }_m\right){\mathbf{R}}_{\text{var}}\text{Δ}\left({\sigma }_m\right),$$

where $\text{Δ}\left({\sigma }_m\right)$ is a diagonal matrix with entries ${\sigma }_m$ determining the spread of the effect size distribution for each variant $m\le M$. Thus, we can model settings where, e.g., PTVs have larger effect sizes $\left(\sigma =0.5\right)$ than missense variants $\left(\sigma =0.2\right)$. Note that when ${\sigma }_m=1$ for all m, then ${\mathbf{S}}_{\text{var}}={\mathbf{R}}_{\text{var}}$. All in all, our prior density for β under alternative model is

$$\beta |\text{ALT}\sim \mathcal{N}\left(0,\mathbf{U}\right),\text{ where }\mathbf{U}={\mathbf{S}}_{\text{var}}\otimes {\mathbf{R}}_{\text{phen}}.$$

When we have data from multiple studies, we allow for possible differences in genetic effects across ethnicities or populations, extending the approximate BFs of Band et al.²⁰ and the summary statistics approach of RAREMETAL⁷ from univariate to multivariate phenotypes. Let

$$\hat{\beta }=\left({\hat{\beta }}_{s,m,k}\right)=\left({\hat{\beta }}_{\mathrm{1,1,1}},{\hat{\beta }}_{\mathrm{1,1,2}},\dots ,{\hat{\beta }}_{\mathrm{1,1},K},{\hat{\beta }}_{\mathrm{1,2,1}},\dots ,{\hat{\beta }}_{\mathrm{1,2},K},\dots ,{\hat{\beta }}_{1,M,K},{\hat{\beta }}_{\mathrm{2,1,1}},\dots ,{\hat{\beta }}_{S,M,K}\right),$$

where S is the number of studies, M is the number of variants, and K is the number of phenotypes. As with a single study, we incorporate the expected correlation of genetic effects between a pair of variants and a single phenotype by using the matrix ${\mathbf{S}}_{\text{var}}$, between a variant and a pair of phenotypes by using the matrix ${\mathbf{R}}_{\text{phen}}$, and we introduce the matrix ${\mathbf{R}}_{\text{study}}$ to specify a prior on the similarity in effect sizes across the studies. Thus, the prior is

$$\beta \sim \mathcal{N}\left(0,\mathbf{U}\right),\text{ where }\mathbf{U}={\mathbf{R}}_{\text{study}}\otimes \left({\mathbf{S}}_{\text{var}}\otimes {\mathbf{R}}_{\text{phen}}\right).$$

It is also straightforward to include a non-zero vector μ as a prior mean of genetic effects, in which case the prior is $\beta \sim \mathcal{N}\left(\mu ,\mathbf{U}\right).$ We use this, for example, when screening for protective rare variants that have a pre-specified beneficial profile on a set of risk factors.

${\text{BF}}_{\text{MRP}}$

The BF is the ratio of the marginal likelihoods between the alternative and the null model. The marginal likelihood for the alternative model is

$$\underset{\beta }{\int }p\left(\text{Data}|\beta )p(\beta |\text{ALT}\right)d\beta =c\times \mathcal{N}\left(\hat{\beta };\mu ,{\hat{\text{V}}}_{\beta }+\mathbf{U}\right)$$

and the marginal likelihood for the null model is

$$\underset{\beta }{\int }p\left(\text{Data}|\beta )p(\beta |\text{NULL}\right)d\beta =c\times \mathcal{N}\left(\hat{\beta };0,{\hat{\text{V}}}_{\beta }\right).$$

The BF is given by

$${\text{BF}}_{\text{MRP}}=\frac{\text{det}{\left({\hat{\text{V}}}_{\beta }+\mathbf{U}\right)}^{-\frac{1}{2}}\text{exp}\left[-\frac{1}{2}{\left(\hat{\beta }-\mu \right)}^{⊺}{\left({\hat{\text{V}}}_{\beta }+\mathbf{U}\right)}^{-1}\left(\hat{\beta }-\mu \right)\right]}{\text{det}{\left({\hat{\text{V}}}_{\beta }\right)}^{-\frac{1}{2}}\text{exp}\left[-\frac{1}{2}{\hat{\beta }}^{⊺}{\hat{\text{V}}}_{\beta }^{-1}\hat{\beta }\right]}.$$

When $\mu =0$, ${\text{BF}}_{\text{MRP}}$ is an increasing function of the following quadratic form:

$$Q\left(\hat{\beta };{\hat{\text{V}}}_{\beta },\mathbf{U}\right)={\hat{\beta }}^{⊺}\left({\hat{\text{V}}}_{\beta }^{-1}-{\left({\hat{\text{V}}}_{\beta }+\mathbf{U}\right)}^{-1}\right)\hat{\beta }.$$

Furthermore, this quadratic form is the only part of the ${\text{BF}}_{\text{MRP}}$ that depends on $\hat{\beta }$. Thus, by deriving a distribution of $Q\left(\hat{\beta };{\hat{\text{V}}}_{\beta },\mathbf{U}\right)$ under the null model, we can compute a p value (by using the Imhof, Davies, or Farebrother methods) when ${\text{BF}}_{\text{MRP}}$ is used as a test statistic. We include support for computing these p values in the software package for MRP. According to basic properties of quadratic forms of Gaussian variables, $Q\left(\hat{\beta };{\hat{\text{V}}}_{\beta },\mathbf{U}\right)\sim {\sum }_{i=1}^n{d}_i{\chi }_i^2$, where ${\chi }_i^2$ is an independent sample from a ${\chi }_1^2$ distribution (chi-square with one degree of freedom) and $d_i$ are the eigenvalues of matrix $I-{\left({\hat{\text{V}}}_{\beta }+\mathbf{U}\right)}^{-1}{\hat{\text{V}}}_{\beta }$. The distribution function for a mixture of chi-squares can be numerically evaluated by the R package “CompQuadForm,”³¹ incorporated in the MRP software directly.

To compute the BF

$${\text{BF}}_{\text{MRP}}=\frac{\text{det}{\left({\hat{\text{V}}}_{\beta }+\mathbf{U}\right)}^{-\frac{1}{2}}\text{exp}\left[-\frac{1}{2}{\left(\hat{\beta }-\mu \right)}^{⊺}{\left({\hat{\text{V}}}_{\beta }+\mathbf{U}\right)}^{-1}\left(\hat{\beta }-\mu \right)\right]}{\text{det}{\left({\hat{\text{V}}}_{\beta }\right)}^{-\frac{1}{2}}\text{exp}\left[-\frac{1}{2}{\hat{\beta }}^{⊺}{\hat{\text{V}}}_{\beta }^{-1}\hat{\beta }\right]},$$

we first consider the term inside the exponential function:

$$\mathcal{E}\left(\hat{\beta },\mu ,{\hat{\text{V}}}_{\beta },\mathbf{U}\right)=\frac{1}{2}{\hat{\beta }}^{⊺}{\hat{\text{V}}}_{\beta }^{-1}\hat{\beta }-\frac{1}{2}{\left(\hat{\beta }-\mu \right)}^{⊺}{\left({\hat{\text{V}}}_{\beta }+\mathbf{U}\right)}^{-1}\left(\hat{\beta }-\mu \right).$$

Because ${\hat{\text{V}}}_{\beta }$ and $\mathbf{U}$ are typically defined through Kronecker products of smaller matrices, their inverses are easier to compute than the inverse of their sum. Hence, we use the Woodbury matrix identity to write

$$\mathcal{E}\left(\hat{\beta },\mu ,{\hat{\text{V}}}_{\beta },\mathbf{U}\right)=\frac{1}{2}{\hat{\beta }}^{⊺}{\hat{\text{V}}}_{\beta }^{-1}\hat{\beta }-\frac{1}{2}{\left(\hat{\beta }-\mu \right)}^{⊺}\left({\hat{\text{V}}}_{\beta }^{-1}-{\hat{\text{V}}}_{\beta }^{-1}{\left({\mathbf{U}}^{-1}+{\hat{\text{V}}}_{\beta }^{-1}\right)}^{-1}{\hat{\text{V}}}_{\beta }^{-1}\right)\left(\hat{\beta }-\mu \right).$$

To simplify the determinant calculation, we write

$$\text{det}\left({\hat{\text{V}}}_{\beta }+\mathbf{U}\right)=\text{det}\left({\hat{\text{V}}}_{\beta }\right)\text{det}\left(\mathbf{I}+{\hat{\text{V}}}_{\beta }^{-1}\mathbf{U}\right).$$

The logarithm of the BF is then

$$\text{log}\left({\text{BF}}_{\text{MRP}}\right)=-\frac{1}{2}\text{log}\left(\text{det}\left(\mathbf{I}+{\hat{\text{V}}}_{\beta }^{-1}\mathbf{U}\right)\right)+\mathcal{E}\left(\hat{\beta },\mu ,{\hat{\text{V}}}_{\beta },\mathbf{U}\right).$$

If studies do not share individuals, ${\hat{\text{V}}}_{\beta }$ is a block-diagonal matrix

$${\hat{\text{V}}}_{\beta }=\left[\begin{array}{llll}{\hat{\text{V}}}_{\beta }^1\hfill & 0\hfill & \cdots \hfill & 0\hfill \\ 0\hfill & {\hat{\text{V}}}_{\beta }^2\hfill & \cdots \hfill & 0\hfill \\ ⋮\hfill & \hfill & \ddots \hfill & ⋮\hfill \\ 0\hfill & 0\hfill & \cdots \hfill & {\hat{\text{V}}}_{\beta }^S\hfill \end{array}\right].$$

If studies share individuals, e.g., controls, we can take the approach of Cichonska et al.⁸ to use summary-level data to estimate the correlation structure of the non-diagonal blocks caused by overlapping individuals.

UK Biobank data

Population definitions

We used a combination of self-reported ancestry (UK Biobank field ID 21000) and principal-component analysis to identify six subpopulations in the study: white British, African, South Asian, non-British white, semi-related, and an admixed population (Table 1). To determine the first four populations, which contain samples not related closer than the third degree, we first used the principal components of the genotyped variants from the UK Biobank, defined thresholds on principal component 1 and principal component 2, and further refined the population definition.¹⁹ Semi-related individuals were grouped as individuals whose genetic data (after passing UK Biobank quality control [QC] filters; sufficiently low missingness rates; and genetically inferred sex matching reported sex), via a KING relationship table, were between conditional third and conditional second degrees of relatedness to samples in the first four groups. Admixed individuals were grouped as unrelated individuals who were flagged as “used_in_pca_calculation” by the UK Biobank and were not assigned to any of the other populations.

Table 1.

Number of individuals per population per genotyping platform (exome/array)

Population	${\text{n}}_{exome}$	${\text{n}}_{array}$
White British	137,920	337,138
Non-British white	10,432	24,905
African	2,716	6,497
South Asian	3,569	7,885
Semi-related	18,100	44,632
Admixed	11,961	28,551
Total	184,698	449,608

GWAS summary statistics

We performed genome-wide association analysis on 2,019 UK Biobank traits in the six population subgroups as defined above by using PLINK v2.00a (20 October 2020). We used the “--glm” Firth fallback option in PLINK to apply an additive-effect model across all sites. Quantitative trait values were rank normalized with the “--pheno-quantile-normalize” flag. We used the following covariates in our analysis: age, sex, array type, and the first ten genetic principal components, where array type is a binary variable that represents whether an individual was genotyped with UK Biobank Axiom Array or UK BiLEVE Axiom Array. For variants that were specific to one array and exome data, we did not use array as a covariate.

For the admixed population, we conducted a local ancestry-corrected GWAS. We first assembled a reference panel from 1,380 single-ancestry samples in the 1000 Genomes Project,³² the Human Genome Diversity Project,³³ and the Simons Genome Diversity Project,³⁴ choosing appropriate ancestry clusters by running ADMIXTURE³⁵ with the unsupervised setting. Using cross-validation, we identified eight well-supported ancestral population clusters: African, African hunter-gatherer, East Asian, European, Native American, Oceanian, South Asian, and West Asian. We then used RFMix v2.03³⁶ to assign each of the 20,727 windows across the phased genomes to one of these eight ancestry clusters (for all individuals in the UK Biobank). These local ancestry assignments were subsequently used with PLINK2 as local covariates in the GWAS for the admixed individuals for SNPs within those respective windows. PLINK2 allows for the direct input of the RFMix output (the MSP file, which contains the most likely subpopulation assignment per conditional random field [CRF] point) as local covariates with the “--local-cov,” “--local-psam,” and “--local-haps” flags, the “--local-cats0=n” flag (where n is the number of assignments), and the “--local-pos-cols=2,1,2,7” flag (for a typical RFMix MSP output file, see “Association Analysis” page on PLINK website [web resources]).

Variant quality control and metadata generation

For quality control (QC), we ensured that variant-level missingness was less than 10%, that the p value for the Hardy-Weinberg equilibrium test (computed within unrelated individuals of white British ancestry) was greater than ${10}^{-15}$, and that the variant was uniquely represented (the “CHROM:POS:REF:ALT” variant string was uniquely identified) in the PLINK dataset file. In total, we removed 195,920 variants that failed to meet all of these criteria, except for 134 variants on the Y chromosome.

For the remainder, we used Variant Effect Predictor (VEP)³⁷ to annotate the most severe consequence, the gene symbol, and HGVSp (the Human Genome Variation Society protein sequence name) of each variant in the UK Biobank exome and array data. We calculated MAFs by using PLINK. MPC¹³ values (variant-level) and pLI gene memberships¹⁴ were annotated from source. To determine LD independence criteria, we used PLINK’s “--indep-pairwise” function with a window size of 1,000 kb, a step size of 1, and an $r^2$ threshold of 0.1 on those variants that pass QC. As our analyses focused on PTVs and protein-altering variants (PAVs), we then performed this same LD independence analysis on only these, overriding assignments in the first analysis if necessary. We provide these essential metadata, which are necessary for MRP, in exome and array tables, available for direct download via the Global Biobank Engine (web resources).³⁸

Prior matrix selection

For exome applications, we chose variants that had MAF $\le$ 1% and that were LD independent according to the criteria mentioned above. For quantitative traits, we removed variants whose regression effect size had standard error greater than 100, and for binary traits, we removed variants whose regression effect size had standard error greater than 0.2. For array applications, we chose variants with MAF $\le$ 1% and removed variants whose regression effect size had standard error greater than 0.2. While MRP is capable of handling all variant types (e.g., proximal coding and intronic variants), we included only PAVs and PTVs in both exome and array analyses (exome data feature many more PAVs and thus potential for power gain; Table S1; Figure S1). These sets respectively contain the following consequence annotations:

• •PAVs: protein_altering_variant, inframe_deletion, inframe_insertion, splice_region_variant, start_retained_variant, stop_retained_variant, missense_variant
• •PTVs: frameshift_variant, splice_acceptor_variant, splice_donor_variant, stop_gained, start_lost, stop_lost

For the exome meta-analysis, we assumed a SEM across studies $\left({\mathbf{R}}_{\text{study}}\right)$ and an IEM across variants $\left({\mathbf{R}}_{\text{var}}\right)$. For example, if we have three studies, e.g., white British, African, and South Asian, assuming a SEM would mean that

$${\mathbf{R}}_{\text{study}}=\left[\begin{array}{lll}1\hfill & 0.99\hfill & 0.99\hfill \\ 0.99\hfill & 1\hfill & 0.99\hfill \\ 0.99\hfill & 0.99\hfill & 1\hfill \end{array}\right].$$

The off-diagonals are slightly lower than 1 so as to maintain that the matrix is positive definite and invertible. Likewise, an IEM would imply

$${\mathbf{R}}_{\text{study}}=\left[\begin{array}{lll}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill \end{array}\right].$$

The same principle would apply when constructing ${\mathbf{R}}_{\text{var}}$ for a gene with an arbitrary number of variants. We additionally incorporated information about the variant in order to formulate the matrix that is used in the calculation of $\mathbf{U}$ $\left({\mathbf{S}}_{\text{var}}\right)$. For both quantitative and binary traits, PTVs were assigned a σ (standard deviation of prior on effect size) of 0.2, whereas PAVs were assigned a σ value of 0.05. We also incorporated MPC and pLI deleteriousness metrics into our exome analyses. For those PTVs with a pLI of $>$0.8, we increased σ to 0.5, and for those PAVs with an MPC $\ge$ 1, we set σ = 0.05 × MPC. The ${\mathbf{R}}_{\text{var}}$ matrix was then dotted with a diagonalized version of the σ vector (see MRP details above). These adjustments serve to further granularize and weight MRP results in biologically meaningful ways (Table S2; Figure S2).

We also studied how the application of MRP to multiple phenotypes together would potentially boost power to detect rare-variant associations. We calculated pairwise genetic correlations between 35 biomarker phenotypes¹⁹ by using LD score regression²⁷ and then used the “hclust” algorithm in the R stats package³⁹ to generate phenotype clusters. For each of these clusters, using the array data, we performed MRP in the multi-phenotype setting. For this application, we calculated ${\mathbf{R}}_{\text{phen}}$ empirically by using correlation coefficients computed with summary statistics from significant (p $\le 1$ × ${10}^{-5}$), LD-independent, common (MAF $\ge$ 0.01) variants.

Results

Simulations

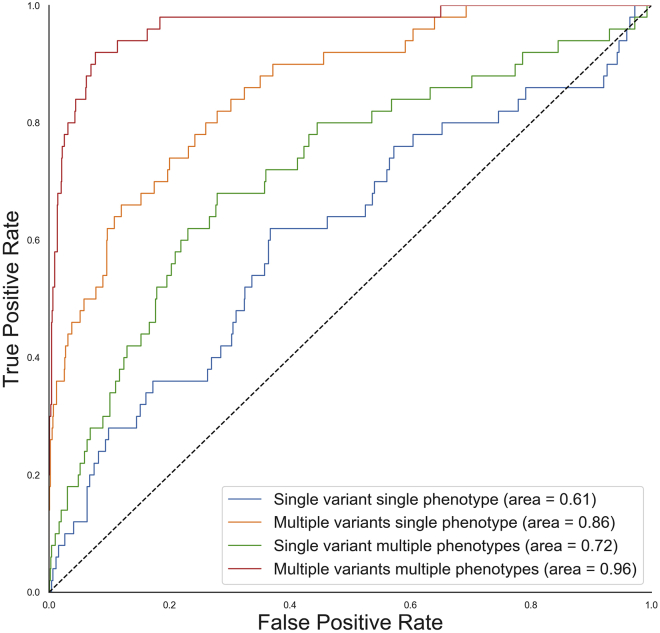
To study the behavior of MRP going from a single phenotype to multiple phenotypes, we conducted a simulation study where we assumed an allelic architecture consistent to that discovered for APOC3 in relation to triglycerides, low-density lipoprotein cholesterol (LDL-C), and high-density lipoprotein cholesterol (HDL-C).^30,40,41 We simulated three continuous phenotypes with a total correlation consistent with that observed for triglycerides, LDL-C, and HDL-C. Furthermore, we introduced effects to four variants consistent with the effects observed in four PTVs (approximately 0.35 standard deviations away from the population mean) and to another four variants consistent with the effects observed for missense variants (approximately 0.2 standard deviations away from the population mean), all with MAF of 0.05%. The PTV group of variants had the same effects, whereas out of the missense variants, half had positive and the other half had negative effect sizes. The correlation of effects between the group of phenotypes was set to be directionally consistent with the direction of genetic effects observed for lipid phenotypes and PTVs in APOC3, i.e., proportional effects for triglycerides and LDL-C, and inversely proportional for LDL-C and HDL-C and triglycerides and HDL-C. We simulated 1,000 genes where 50 of the genes contained non-zero effects on the multivariate phenotype. Given we know which of the 1,000 genes contained non-zero effects, we could compute the true positive rates and false positive rates for a given BF threshold. We find MRP with an IEM across variants to be comparable to SKAT and MRP with a SEM across variants to be comparable to the burden test (Figures S3 and S4). We analyze the data as follows: (1) single-variant and single-phenotype, (2) multiple variants and single-phenotype, (3) single-variant and multiple phenotypes, and (4) multiple variants and multiple phenotypes (Figure 2). We find that in some scenarios, analyzing multiple variants and multiple phenotypes jointly improved the ability to detect signals; however, this improvement is only specific to situations in which multiple variants have a true effect and/or the variants have effects on the multiple phenotypes in question (Figures S5 and S6).

Figure 2.

From single-variant and single-phenotype to multiple-variant and multiple-phenotype gene discovery

Receiver operating characteristic (ROC) curves for detecting simulated gene association to any of the phenotypes via single-variant and single-phenotype association (blue) to multiple-variant and multiple-phenotype association (red).

Exome single-phenotype meta-analyses

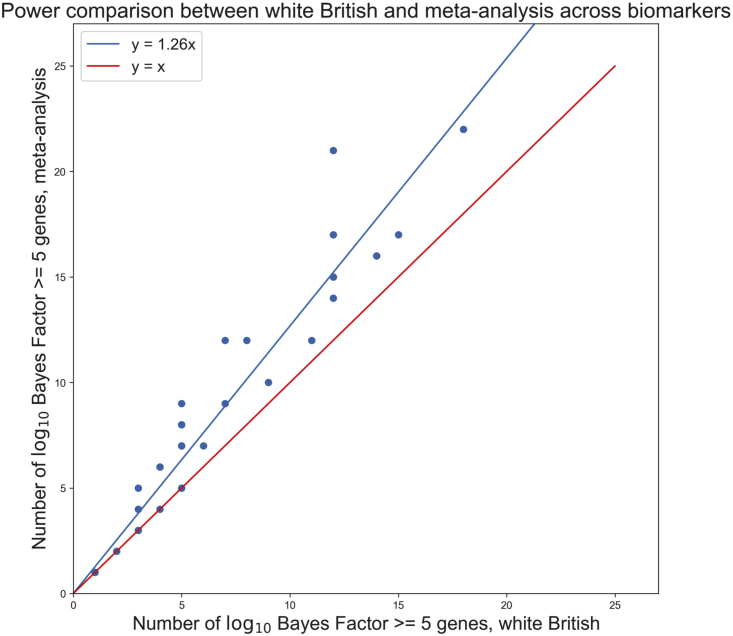
We used MRP to perform exome meta-analysis on 2,019 traits across six UK Biobank populations as described in material and methods. Among the best-powered and -represented traits were a set of 35 biomarkers, the focus of a previous publication.¹⁹ We see the number of ${\text{log}}_{10}\mathrm{BF}\ge$ 5 genes increasing from a single-population to a meta-analysis setting. Because we expect that the meta-analysis over different ancestries cannot be more confounded than the analysis of a single ancestry, we interpret the increase in the number of genes as an increase in the statistical power to detect rare-variant associations (Figure 3).

Figure 3.

From single to multiple populations

Scatterplot showing number of genes with ${\text{log}}_{10}$ BF $\ge$ 5 for white British population only (x axis) versus meta-analysis (y axis) across 35 biomarkers. Assuming that BFs are correctly calibrated in both analyses and that meta-analysis is not inflated compared to white British-only MRP, this figure suggests a 26% increase in power when incorporating summary statistics across multiple populations.

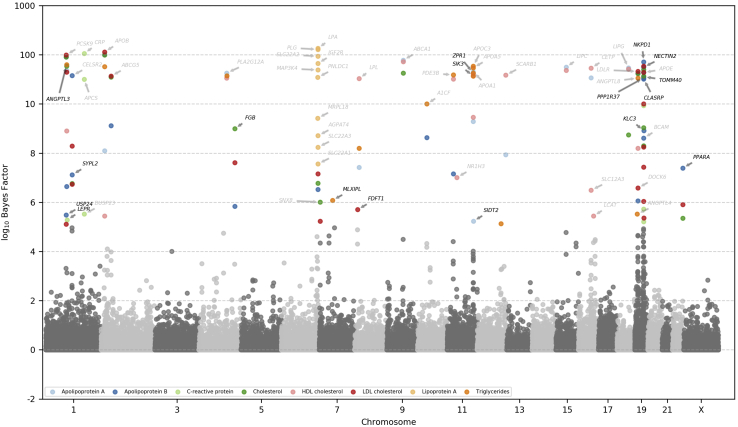
We categorize these biomarkers into six categories as in Sinnott-Armstrong et al.¹⁹ (cardiovascular, bone and joint, diabetes, hormone, liver, and renal; Figure 4 and S7–S11), and we recover several known gene-trait associations and discover several others.

Figure 4.

Manhattan plot showing ${\text{log}}_{10}$ BF under an independent effects variant model among protein-altering variants for cardiovascular phenotypes

Scale is logarithmic after ${\text{log}}_{10}$ BF $\ge$ 10. Genes found in Sinnott-Armstrong et al.¹⁹ are annotated in gray, whereas the other genes are annotated in black.

Among the “bone and joint” biomarkers (alkaline phosphatase, calcium, and vitamin D), we recover associations between CASR and calcium⁴² and HAL and vitamin D.⁴³ As compared to results from array data as found in Sinnott-Armstrong et al.,¹⁹ we also recover exome-specific associations between ALDH5A1 and alkaline phosphatase⁴⁴ and PDE3B and vitamin D.⁴³

For the “cardiovascular” phenotypes (apolipoprotein A, apolipoprotein B, C-reactive protein, total cholesterol, HDL-C, LDL-C, lipoprotein A, and triglycerides), MRP recovers array associations between the following: PLG, LPA, and lipoprotein A;⁴⁵ APOC3 and triglycerides;⁴⁶ ANGPTL3 and triglycerides;⁴⁷ APOB and apolipoprotein B⁴⁸ and LDL-C;⁴⁹ ABCA1 and apolipoprotein A⁴⁶ and HDL-C;⁴⁹ PCSK9 and total cholesterol;⁵⁰ and CRP and C-reactive protein.⁵¹ Exome-only signals recover associations such as between ZPR150 and SIK344 and triglycerides.

In the two diabetes-related phenotypes (glucose and HbA1c), we recover associations between G6PC2 and glucose⁵⁰ as well as PIEZO1 and HbA1c⁵² and an additional exome association between G6PD and HbA1c.⁵² Hormonal recoveries include those between SHBG and SHBG and testosterone levels and GH1 and IGF-1 levels.

MRP applied to liver-related phenotypes recover known associations between the following: UGT genes and bilirubins;⁵³ GOT1 and aspartate aminotransferase;⁵⁴ FCGRT and albumin;⁴⁴ and GPT and AST-ALT ratio.⁵¹ In the exome sequencing, we additionally recover associations between GGT1 and gamma glutamyltransferase,⁵⁵ TMEM236 and aspartate aminotransferase,⁴⁴ and SLCO1B3 and bilirubin.⁵⁶

The renal traits similarly feature a mix of array recoveries and exome discoveries. We recover signal between the following: SLC22A2 and creatinine;⁵⁷ CST3 and cystatin C;⁴⁸ COL4A4 and microalbumin;⁵⁸ TNFRSF13B and non-albumin protein;⁴⁴ FCGRT and total protein; WDR1, RASGRP2, DRD5, and urate;^59,60 and LRP2 and eGFR levels.⁶¹ We additionally discover novel gene-trait associations (not found in the NHGRI-EBI catalog or Open Targets Genetics) across these biomarker categories, including the following: GLPD1 and alkaline phosphatase; NKPD1 and apolipoprotein B; RENBP/MAP3K15 and Hba1c; PARPBP and IGF-1; NLGN2 and SHBG; ALB and albumin; ALPL and phosphate; RBM47 and urea; ALDH16A1 and urate; THBD and cystatin C; ITPR3 and phosphate; SLC22A7 and creatinine; and FCGR2B and non-albumin protein.

For the 2,019 traits for which MRP was performed, there were also a considerable number of associations found among non-biomarker traits. We found associations between TUBB1 and platelet distribution width and mean platelet volume;⁶² IL17RA and monocyte count and percentage;⁶² OCA2/MC1R and skin color/hair color;63, 64, 65, 66 IQGAP2 and mean platelet volume;⁶² SLC24A5, HERC2, TCF25, and TYR and skin color;⁶⁷ SH2B3 and JAK2 and platelet crit⁶⁸ and count;⁶⁹ KALRN and mean platelet volume;⁶² HBB and mean corpuscular volume,⁷⁰ mean corpuscular hemoglobin,⁷¹ and red blood cell count;⁷² and CXCR2 and neutrophil count.⁶²

The average runtime for these analyses was around 1 day for quantitative traits and 5 h for binary traits with a machine with 16 cores and 200 GB RAM (Table S3).

Array single-population multi-phenotype analyses

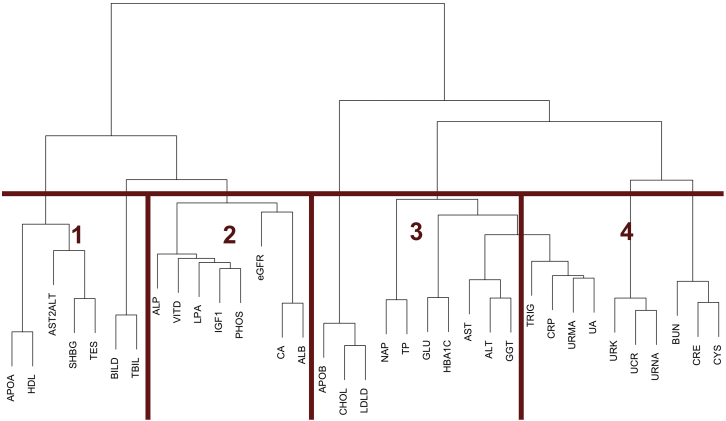
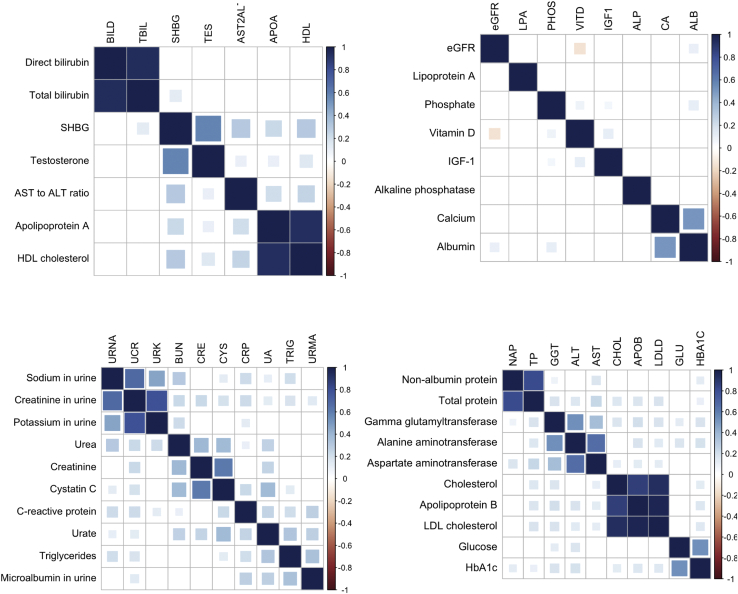
In order to demonstrate the effectiveness of MRP to boost signal in a multi-phenotype context, we used LD-score regression²⁷ to determine genetic correlations between the 35 biomarker traits (Figure S12) that were a focus of a previous paper.¹⁹ This correlation matrix was then used for hierarchical clustering followed by dynamic tree cutting, which formed four clusters of between seven and ten traits each (Figure 5). We generated the correlation plots as shown in Figure 6.

Figure 5.

Hierarchical clustering dendrogram and derived clusters from dynamic tree cutting algorithm

Based on genetic correlation derived from an LD-score-regression-based distance matrix between 35 biomarker traits.

Figure 6.

LD-score-regression-based genetic correlation plots of candidate clusters

Derived from the dendrogram in Figure 5 via a dynamic tree cutting algorithm.

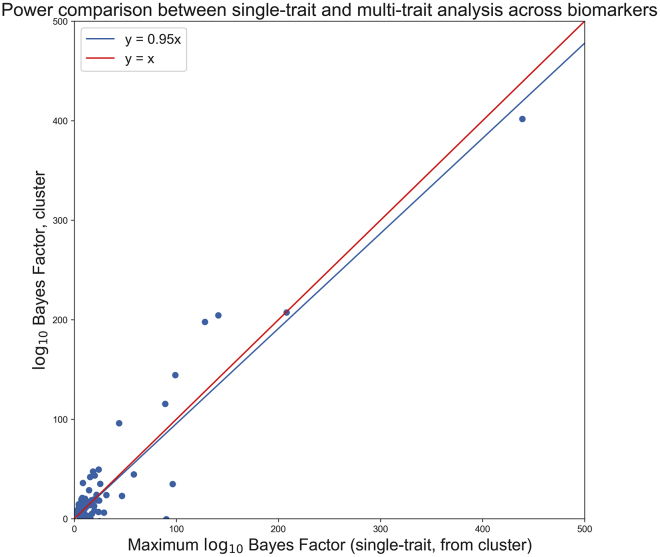
Multi-phenotype MRP results in several substantial power gains throughout the four clusters; one of these clusters is highlighted in Figure 7. As compared to the maximum ${\text{log}}_{10}\mathrm{BF}$ from the constituent phenotypes, the multi-phenotype analysis generally fares comparably while also highlighting clear targets. We found evidence for association between rare coding variants in several genes and the clusters above; TNFRSF13B (${\text{log}}_{10}{\mathrm{BF}}_{multi-trait}$ = 204.5, max$\left[{\text{log}}_{10}{\mathrm{BF}}_{single-trait}\right]$ = 141.0), APOB (${\text{log}}_{10}{\mathrm{BF}}_{multi-trait}$ = 197.9, max$\left[{\text{log}}_{10}{\mathrm{BF}}_{single-trait}\right]$ = 128.0), and SNX8 (${\text{log}}_{10}{\mathrm{BF}}_{multi-trait}$ = 96.0, max$\left[{\text{log}}_{10}{\mathrm{BF}}_{single-trait}\right]$ = 43.8) receive a boost in ${\text{log}}_{10}\mathrm{BF}$ of over 50 units for cluster 1 (alanine aminotransferase, aspartate aminotransferase, gamma glutamyltransferase, glucose, HbA1c, total protein, apolipoprotein B, cholesterol, LDL-C, and non-albumin protein). Several other genes that are clearly below 5 (in ${\text{log}}_{10}\mathrm{BF}$) in the single-trait settings become above 5 in the joint setting (e.g., G6PC; ${\text{log}}_{10}{\mathrm{BF}}_{multi-trait}$ = 5.3, max$\left[{\text{log}}_{10}{\mathrm{BF}}_{single-trait}\right]$ = 1.3). The G6PC gene provides instructions for making the glucose 6-phosphatase enzyme, found on the membrane of the endoplasmic reticulum. The enzyme is expressed in active form in the liver, kidneys, and intestines and is the main regulator of glucose production in the liver; given the traits included in cluster 1, the increase in power may be biologically relevant.⁷³ These results demonstrate that MRP can identify biologically meaningful targets that may be missed by standard GWAS approaches.

Figure 7.

Cluster versus single-trait power analysis

Power comparison of genes with ${\text{log}}_{10}$ BF $\ge$ 5 in either (i) any of the single-trait analyses of the traits within the cluster or (ii) the multi-trait analysis for a cluster of biomarkers (alanine aminotransferase, aspartate aminotransferase, gamma glutamyltransferase, glucose, HbA1c, total protein, apolipoprotein B, cholesterol, LDL-C, and non-albumin protein). x axis depicts the maximum ${\text{log}}_{10}$ BF of the gene among any of the constituent single-trait analyses, and y axis depicts the multi-trait result. Multi-trait analyses roughly equal the highest-powered single-trait analyses while also substantially boosting signal in some genes.

The average runtime for these analyses was around 5 h with a machine with 16 cores and 200 GB RAM (Table S3).

Discussion

In this study, we developed MRP, a Bayesian model comparison approach that shares information across variants, phenotypes, and studies to identify rare-variant associations. We used simulations to verify that jointly considering both variants and phenotypes can improve the ability to detect associations. We also applied the MRP model comparison framework in a meta-analysis setting to exome summary statistics across the UK Biobank, identifying strong evidence for the previously described associations between, for example, HAL and vitamin D,⁴³ and discovering several novel associations, such as between GLPD1 and alkaline phosphatase. We made the full results set available on the Global Biobank Engine (web resources).³⁸ We also leveraged MRP to boost signal in a multi-phenotype setting by using the array data (which has many more samples than the exome data), finding genes such as G6PC that do not come up in the single-trait context but show strong evidence in the joint analysis. These results demonstrate the ability of the MRP model comparison approach to leverage information across multiple phenotypes and variants to discover rare-variant associations.

MRP enjoys distinct advantages over prior techniques such as (trans-ancestry) meta-analysis and MultiSKAT in that it allows for both multiple studies as well as multiple phenotypes simultaneously, whereas (trans-ancestry) meta-analysis only allows for multiple studies and not multiple phenotypes and MultiSKAT only allows for multiple phenotypes and not multiple studies. MRP’s closest relative, MetaMultiSKAT,⁷⁴ allows for these two simultaneously as well. In comparison to MetaMultiSKAT, the novelty in MRP is the flexibility in the models/choices one can make in the priors and the inferential framework. In particular, one can directly compare any two MRP models against each other by comparing their BFs against each other. For example, one can assess the heterogeneity of effects across studies by comparing similar and IEMs for ${\mathbf{R}}_{\text{study}}$; if done on a per-variant basis, this can be a useful QC statistic. We can also assess the degree to which variants within a block (genes, annotation categories, etc.) have similar or disparate effects with a proper choice of ${\mathbf{R}}_{\text{var}}$. Such inferences are not easily available when p values are used as a basis for inference.

Analogous to the work presented in Rivas et al.,¹¹ we see MRP as a natural extension for the analysis of rare variants in gene-based settings. The same advantages we see in using BFs over p values exist here as well. To briefly summarize, studies that follow both discovery and replication phases seek to rank genes for follow-up according to departure from a null. Power in frequentist studies will change with the number of samples and the number of variants included in the analysis, whereas BFs can easily be compared naturally agnostic of the number of variants included as well as the sample size.

We acknowledge some limitations in this study. First, we are pruning variants that are LD dependent. Ancestry misspecification could have a dramatic effect on the computation of LD, especially in the setting of rare variants, whose MAFs could very well be population specific; one could obtain LD estimates that are inaccurate and inapplicable to the study at hand. We propose that if variants in LD are to be used, then LD independence should be computed within the studies that are being meta-analyzed. Many of the rare variants will not be present in external reference panels. Extensions to incorporate in-study LD matrices, as in the work by Feng et al. in RAREMETAL and RAREMETALWORKER,⁷⁵ are a logical extension to MRP. Second, in the ultra-rare variant setting and/or when case-control numbers are particularly imbalanced, the assumption that effect sizes follow a Gaussian may be invalid.⁷⁶ Third, removing related individuals as in this study results in a loss of power. Because MRP is agnostic of summary statistic type, though, one can explore models such as SAIGE,⁷⁶ REGENIE,⁷⁷ or BOLT-LMM⁷⁸ that better account for related individuals so as to improve power.

As genetic data linked to high-dimensional phenotype data are increasingly being made available through biobanks, health systems, and research programs, there is a large need for statistical approaches that can leverage information across different genetic variants, phenotypes, and studies to make strong inferences about disease-associated genes. The approach presented here relies only on summary statistics from marginal association analyses, which can be shared with less privacy concerns compared to raw genotype and phenotype data. Combining joint analysis of variants and phenotypes with meta-analysis across studies offers new opportunities to identify gene-disease associations.

Published: November 24, 2021

Web resources

• Basis of UK Biobank participation, https://www.ukbiobank.ac.uk/explore-your-participation/basis-of-your-participation

• MRP, https://github.com/rivas-lab/mrp

• PLINK, https://www.cog-genomics.org/plink/1.9/assoc

• Rare variant association analysis of 200k exomes with MRP, https://biobankengine.stanford.edu/RIVAS_HG38/mrpgene/all

• Rare variant association analysis of 500k array coding variant data with MRP, https://biobankengine.stanford.edu/RIVAS_HG19/mrpgene/all

• UK Biobank Array Metadata for MRP, https://biobankengine.stanford.edu/static/ukb_cal-consequence_wb_maf_gene_ld_indep_mpc_pli.tsv.gz

• UK Biobank Exome Metadata for MRP, https://biobankengine.stanford.edu/static/ukb_exm_oqfe-consequence_wb_maf_gene_ld_indep_mpc_pli.tsv.gz