Using the COREX/BEST Server to Model the Native-State Ensemble

Abstract

Protein structures under normal conditions exist as ensembles of interconverting, transient microstates. A computer algorithm known as COREX/BEST (Biology using Ensemble-based Structural Thermodynamics) was developed to model microstate structures and describe the native ensembles of proteins in statistical thermodynamic terms. This algorithm has been tested extensively and validated through experimental comparisons examining a range of biophysical and functional phenomena, such as structural cooperativity, pH-dependent stability, and cold denaturation. Here, we describe a Web-based implementation of the COREX/BEST algorithm, called the COREX/BEST Server, and demonstrate how to use this online resource to characterize the structural and thermodynamic properties of the native protein ensemble.

1. Introduction

Protein macromolecules often couple structural rearrangements to biological function [1–3] and show significant conformational heterogeneity under normal solution conditions [4–10]. Characterizations of these structural fluctuations are thus needed to understand the physicochemical properties of proteins and the molecular origins to their biological roles. In this chapter, we discuss a statistical thermodynamic model of the protein conformational ensemble known as COREX/BEST [11, 12]. This model uses an algorithm to compute a distribution of states a protein structure may populate under a given set of conditions (e.g., pH and temperature) to provide an ensemble description of protein dynamics. By calculating state probabilities and monitoring quantitatively the population distributions within an ensemble, COREX/BEST has shown an ability to reproduce diverse phenomena such as regional stability variations within protein structures [13–15], long-range intramolecular signaling [16, 17], electrostatic contributions to cooperative transitions [18, 19], non-cooperative cold denaturation [20,21], and functional adaptation [22]. AWeb-based implementation of the COREX/BEST algorithm [23] is freely available to the scientific community and may be accessed by visiting http://best.bio.jhu.edu. A demonstration of using the COREX/BEST Server to characterize the structural and energetic properties of a protein conformational ensemble is presented here.

Detailed descriptions of the COREX/BEST algorithm can be found elsewhere [11, 12]. Briefly, this algorithm uses a user-supplied structure (e.g., a PDB file) as a template to generate a large number of partially folded “microstates” that possess a dual structural-thermodynamic character [21]. Each microstate is generated by treating local structural fluctuations as folding-unfolding reactions that occur in an otherwise folded and native-like protein. By combinatorial unfolding of “folding units”, which are contiguous blocks of residues that fold and unfold independently, and an incremental shift in the boundaries of the folding units, an exhaustive enumeration of partially folded states is achieved. The relative Gibbs free energy for each microstate i, ΔG_i, is determined by structure-based parameterization of the intrinsic energetics: ΔC_p,i, ΔH_i, and ΔS_i (see Note 1). This parameterization gives temperature-dependent stabilities for the microstates that can be converted to probabilities (P_i) by the Boltzmann relation,

$$P_i=\frac{K_i}{\sum _i{K}_i},$$ (1)

where the statistical weight of each microstate (K_i) is determined by the relative Gibbs free energy of that microstate ($K_i={\text{e}}^{-\mathrm{\Delta }{G}_i/RT}$, where R is the gas constant and T is absolute temperature), and the summation is over all ensemble states. Figure 1 shows a representative ensemble calculated for the staphylococcal nuclease protein [24].

Fig. 1.

The nuclease conformational ensemble as calculated by the COREX/BEST Server. Calculations in this figure used 25°C as the temperature setting and the PDB file 1STN [24]. (a) Relative stability (ΔG_i) of each microstate plotted as a function of the fraction native (number of residues in folded segments/total number of residues). Each point corresponds to a particular microstate, and the ΔG values were calculated relative the fully folded state (i.e., the relative stability of the fully folded state in the ensemble was 0). (b) Relative populations (P_i) of the 20 microstates with highest computed probability. The filled black circles represent the positions of unfolded residues in a microstate. The fully folded native state, which has no unfolded residues, is shown by the red circle located at residue position = 0. The line of black circles stretching uninterrupted from residue position 6 to residue position 141 represents the fully unfolded state, which had a computed probability of P = 0.00015 at this temperature. The locations of secondary structural elements among the residue positions are as indicated. (c) Cartoon representation of the most probable microstate of the nuclease ensemble. Segments of protein colored red indicate regions that would be folded and regions colored yellow would be unfolded (positions 44–51). To illustrate the concept that the unfolded segment freely samples accessible conformational space, this region was modeled in the figure as multiple flexible loops

The statistical formula to calculate state probabilities (Eq. 1) can be expanded to account for additional system perturbations [25], such as proton-binding energies,

$$P{(\text{pH})}_i=\frac{K_i\cdot \prod _j\left(1+{10}^{\text{p}{K}_{\text{a},i,j}-\text{pH}}\right)}{\sum _i\left(K_i\cdot \prod _j\left(1+{10}^{\text{p}{K}_{\text{a},i,j}-\text{pH}}\right)\right)},$$ (2)

where pK_a,i,j is the pK_a value of residue j in microstate i (see Note 2). The addition of the proton-binding energies to the state probabilities yields a structural ensemble sensitive to pH changes and can be used to investigate electrostatic contributions to protein energetics [18, 19]. Currently, the COREX/BEST Server can perform the following tasks: (1) calculate a conformational ensemble based upon an input protein structure, (2) determine the temperature-sensitivity of the computed ensemble, and (3) determine the pH-sensitivity of the ensemble if pK_a values for the ionizable protein groups are supplied. Our discussions in this chapter are limited to the current capabilities of the COREX/BEST Server.

2. Materials

The COREX/BEST Server [23] provides online access to the COREX/BEST algorithm [12]. A computer with a Web browser and internet capabilities is required. The Web site, which can be found at http://best.bio.jhu.edu, was designed to work with standards compliant browsers (e.g., Mozilla’s Firefox). Most modern browsers, however, should be sufficient. Adequate data storage space is required to download the results of COREX/BEST calculations to a user’s computer.

2.1. Input Structure for Generating an Ensemble

The calculations performed by the COREX/BEST Server require uploading a protein structure file written in plain text and in standard PDB file format [26]. Refer to Note 3 for common errors encountered by COREX/BEST calculations due to protein structure files that are not properly prepared.

2.2. Native pK_a Values to Calculate pH Sensitivity

Calculating the pH sensitivity of an ensemble using Eq. 2 requires uploading a file written in plain text that contains a list of the pK_a values for the ionizable groups in the uploaded PDB structure file (i.e., a list of “native” pK_a values). Each ionizable group should be listed on a separate line in this file, with each line containing: (1) the three letter code for the amino acid type that has the ionizable group, (2) the residue number identifying the amino acid position in the structure file, and (3) the pK_a value of the ionizable group in the uploaded structure. For example, consider a protein containing a ε-amino group that belongs to a lysine at residue position 25 and ionizes under native conditions with a pK_a value of 11.55. The uploaded file of pK_a values should contain a line specifying “LYS 25 11.55”, as well as additional lines of text for each additional ionizable group in the structure file. Native pK_a values for the carboxyl and amino ends of a protein chain should not be listed in the uploaded file; the COREX/BEST algorithm assumes that the C-and N-termini ionize with the same pK_a values as model compounds, (i.e., 3.5 and 7.4, respectively) in all ensemble states and thus the two end groups do not contribute to the pH sensitivity of the ensemble in COREX/BEST calculations.

3. Methods

To perform ensemble calculations using the COREX/BEST Server, a user must first register with the Web site. Registration involves providing a name, a valid e-mail address, and a login password. The e-mail address is required so that users can be contacted when calculations have completed. Following successful registration, a typical user session consists of the following: (1) the user logs into the COREX/BEST Server through their Web browser, (2) the user defines workspaces for each project, (3) the user uploads protein structure file(s) to appropriate workspace(s), (4) the user submits jobs (i.e., calculations) to the COREX/BEST Server, and (5) the user may download all or a subset of the calculated data contained within that user’s workspace. Below is the example of performing calculations on the staphylococcal nuclease protein (PDB ID 1STN [24]) using the COREX/BEST Server.

3.1. Creating a Workspace

After login to the COREX/BEST Server, a workspace can be created by clicking on the “Create Workspace” link on the left side of the webpage under the heading “WORKSPACE OPTIONS”. The user is required to provide a name for this workspace and will create the workspace by clicking on the “Create!” button. Created workspaces can be accessed by clicking on links on the left side of the webpage under the heading “MY WORKSPACES”. Accessing a newly created workspace, the user is presented with the options to: (1) upload a new PDB file, or (2) delete the workspace. Click on the link “Upload New PDB” to upload a plain text PDB file. If the file was uploaded correctly, the server displays a cartoon picture of the structure file in the workspace. Also, the user can click on an “Upload Report” link in the workspace that notifies a user of potential errors detected in the PDB file. For example, uploading 1STN gives the following report due to missing the first five and last eight residues in the crystallographic structure:

PDB Upload Report for 1STN on 2012/11/20, 16:55:15:

* SEQRES Chain ‘A’ contains 149 residues

* missing coordinates for residues 1 thru 5, line number 323

* missing coordinates for residues 142 thru 149 (end of sequence)

Upload Recap:

* structure contains 2 atom/residue sequence errors or missing coordinates

Upload complete: coordinates for 136 residues with 1092 atoms

Warnings:

* 2 Discrepancies in uploaded file may cause unexpected results in calculations

END PDB Upload Report for 1STN

3.2. Generating a Conformational Ensemble

Next, a user would calculate a conformational ensemble for nuclease based upon the 1STN structure. To do this, click on the “Perform COREX/BEST Calculations” link under the “Protein Options” heading of the workspace. The user is directed to a webpage titled “Choosing COREX/BEST Jobs”. On this webpage, click the link “Run the Ensemble Generator!”. Next, the user is required to specify the size of the folding unit, referred to as the “Window Size”, which is used to calculate the ensemble. Briefly, the window size is the number of contiguous residues that constitute a folding unit. A window size of 8 means that the protein is folded and unfolded in blocks of eight residues. Smaller window sizes create larger ensembles, since a greater number of folding units can fit along a given chain length for minimally sized folding units. In general, smaller window sizes are good, but larger ensembles require longer run times on the server and COREX/BEST jobs are limited to 24 h each. Any job estimated to run longer than 1 day will not be performed. For reference, the PDB file upload report also contains a table that lists the total number of states (i.e., microstates) that would be generated and estimated run times for ensembles calculated using different window sizes. The table generated for 1STN in its upload report is reproduced in Table 1.

Table 1.

Estimates for fully enumerated ensemble generation

Window size	Total states	Estimated time (h:min:s)	MB data
6	37,748,724	1 days 17:22:40	2,208
7	5,242,866	5:44:48	306
8	1,179,632	1:17:34	69
9	393,198	0:25:51	23

In our experience, COREX/BEST ensembles seem to be able to reproduce experimental results with better accuracy when window sizes of eight to ten residues are used to generate the microstates. For proteins larger than 150 residues in length, using a recommended window size can create ensembles that exceed the run-time limits of the Server. To handle large proteins, a Monte Carlo option is available when generating ensembles [16]. Using this option, ensemble microstates are randomly generated and selected or “sampled” using standard Monte Carlo methods [27] via the computed state statistical weight (Eq. 1). Briefly, microstates with higher probabilities are more likely to be sampled in a Monte Carlo generated ensemble (see Note 4).

The user is also required to specify a “Minimum Window Size” for an ensemble. Since a protein chain isn’t necessarily an integer multiple of the user-defined window size, residues at the C-terminal end often don’t fit neatly into a standard folding unit. For example, the 1STN structure contains 136 residues. If the user chooses a window size of 9, this would mean that 15 folding units could be overlaid on the first 135 residue positions of the chain, with a C-terminal residue (i.e., the 136th residue) left by itself. For any protein, the C-terminal “left over” residues are given their own folding unit if their number is equal to or exceeds the minimum window size, otherwise those residues are added to the preceding folding unit. This parameter is also needed for the N-terminal end, as the folding unit boundaries are incrementally shifted one residue at a time toward the C-terminal end to exhaustively generate the ensemble microstates, leaving “left over” N-terminal residues [12]. The incremental shifts in folding unit boundaries are used to remove any boundary-related bias in COREX/BEST results.

3.3. Determining Entropy Weighting

The structure-based energy function utilized in COREX/BEST is coarse and provides a rough estimate of the thermodynamic parameters for each microstate (i.e., ΔH_i, ΔC_p,i, and ΔS_i). Coarse approximation of the conformational entropy of a microstate (ΔS_conf,i), which represents the number of conformational variations that a particular energetic state can occupy, is especially troubling for COREX/BEST simulations. Variations of ±5 % in the computed ΔS_conf term can cause shifts in the unfolding temperature by ~20°C [12]. The conformational entropy term of each micro-state is thus normalized using an entropy-weighting factor,

$$\mathrm{\Delta }{S}_i=\mathrm{\Delta }{S}_{\text{solv},i}+W\cdot \mathrm{\Delta }{S}_{\text{conf},i},$$ (3)

where ΔS_solv is the solvent entropy (owing to water ordering at the protein surface) and W is the applied weighting factor, typically a value between 0.95 and 1.05. In practice, a common entropy-weighting factor is applied to each microstate of an ensemble. The COREX/BEST algorithm determines an appropriate weighting factor by calculating the value of W that is needed to set the energetic separation between the native and fully unfolded states in the simulation as equal to an experimentally determined free energy difference. For example, the free energy difference between native and unfolded nuclease has been measured to be ~5 kcal/mol at 25°C via guanidine hydrochloride-induced unfolding [28]. To determine an appropriate weighting factor to use in COREX/BEST calculations with 1STN, the user would click on the link “Perform COREX/BEST Calculations” under the “Protein Options’’ heading of the 1STN workspace. The user will be directed to a webpage titled “Choosing COREX/BEST Jobs”. On this webpage, click on the link “Determining the Entropy Weighting Factor”. Next, the user is asked to specify the overall free energy difference measured and the temperature at which the measurement was made. For 1STN, a value of 5.0 would be input into the “Target Delta G” field, and 25°C entered for the temperature. Next, click on “Calc. W”. For 1STN, COREX/BEST calculates that a value of 0.968 should be used for the weighting factor, W.

3.4. Calculating the Temperature-Dependent Stability of an Ensemble

To test the ability of the COREX/BEST algorithm to accurately describe a conformational ensemble, this algorithm was initially designed to reproduce regional stability variations within protein structures as observed by site-specific hydrogen exchange data [13–15]. As demonstrated [11], the propensity of any region in a protein to undergo structural fluctuations can be determined from the microstate probabilities (Eq. 1). Defined as the residue stability constant, k_f, the local stability of each residue for the native fold is calculated as the ratio of the summed probabilities of all microstates in the ensemble in which a particular residue j is in a folded conformation, P_f,j, to the summed probability of all microstates in which residue j is in an unfolded (or nonfolded) conformation, P_nf,j,

$$k_{\text{f},j}=\frac{P_{\text{f},j}}{P_{\text{nf},j}}.$$ (4)

Residue stability constants for 1STN can be calculated using the COREX/BEST server by the following: After generating an ensemble for 1STN and determining an appropriate entropy weighting (Subheadings 3.2 and 3.3), click on the link “Perform COREX/BEST Calculations” under the “Protein Options” heading of the 1STN workspace. The user will be directed to a webpage titled “Choosing COREX/BEST Jobs”. On this webpage, click on “Calculate the Residue Specific Stability Constants”. Next, the user will need to specify the entropy weighting factor and the temperature (in °C) to use in the calculation. Also, the user will need to specify which previously generated ensemble should be used. Ensembles are classified by the parameters that were defined in the generation step, namely, window size, minimum window size, and if Monte Carlo sampling was employed. Shown in Fig. 2 are the stability constants calculated for 1STN using a temperature setting of 25°C, an entropy weighting factor of 0.968, and an ensemble generated with a window size of 8 and a minimum window size of 4. High stability constants identify residues that are folded in the majority of the most probable microstates at this temperature, whereas lower stability constants identify residues that are unfolded in many of those microstates. In nuclease, most residues with higher stability constants were located in β-strands 3–6 and in the α-helices. Lower stability constants were found in residues in β-strands 1 and 2, and, most dramatically, the loop connecting β-strand 4 to α-helix 1. In addition to providing residue stability constants, the COREX/BEST Server also outputs a file listing the 50 most probable microstates, giving data that can be used to generate Fig. 1b.

Fig. 2.

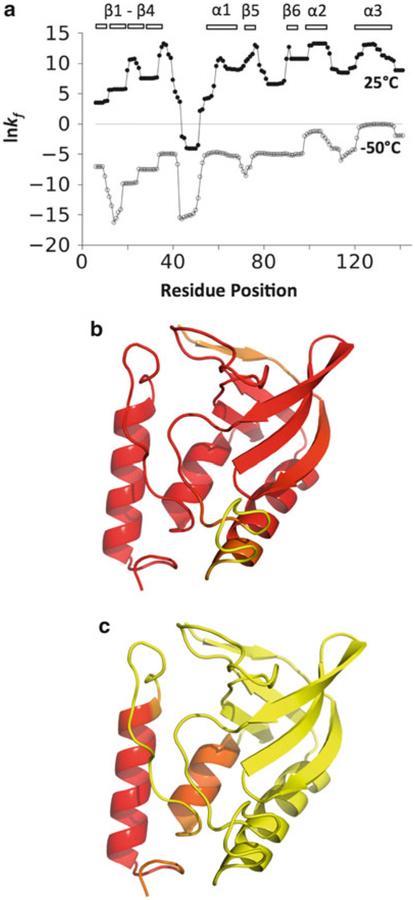
The effect of temperature on the nuclease ensemble as calculated by the COREX/BEST Server. (a) Natural logarithm of the residue stability constants, k_f, for 1STN calculated using the temperature settings of 25°C (filled circles) and −50°C (open circles). The locations of secondary structural elements are as indicated. (b) Projection of the residue stability constants onto the nuclease structure where yellow represents residue positions with the lowest k_f values and red the highest. Red colored residue positions were calculated as stable at 25°C, having large and positive k_f values, whereas yellow residues were calculated to have the least stability and lowest k_f values. (c) The nuclease structure color-coded the same as in panel b, except the stability constants were calculated using a temperature setting of −50°C

Notable to the COREX/BEST calculations is the recent suggestion that protein cold denaturation offers experimental access to the native ensemble, allowing for its structural characterization [21]. It’s thought that cold temperatures promote non-cooperative unfolding of a protein [29, 30] by minimizing the favorable energetics related to the nonspecific burial of hydrophobic groups in aqueous solution [31–33]. As such, the nonspecific hydrophobic packing that favors compact protein structures appears to be minimized at low temperatures in a manner that disrupts globular folds into sub-global structural units. The COREX/BEST Server can be used to simulate protein cold denaturation. For example, repeating the calculation of stability constants at −50°C demonstrates that at low temperatures nuclease prefers partially folded states that are mostly unfolded except for the two C-terminal helices (Fig. 2c).

3.5. Calculating the pH Sensitivity of the Conformational Ensemble

The COREX/BEST algorithm can also model the coupling between H⁺ binding reactions, local fluctuations in structure, and global conformational transitions [18, 19]. COREX/BEST performs this calculation by quantifying how the population distribution of the ensemble of microstates is affected by proton binding via Eq. 2. In this calculation, two sets of pK_a values are used to describe the affinity of each H⁺ binding site (see Note 2). One set describes H⁺ binding to sites in folded and native-like regions of the protein. The pK_a values in this set are referred to as “native” pK_a values and are supplied by the user (see Subheading 2.2). In practice, standard continuum electrostatics methods have been used to generate the set of pK_a,native values for use with COREX/BEST [18]. The second set of pK_a values describes H⁺ binding to sites in unfolded regions, using the intrinsic pK_a values of model compounds [34, 35]. pK_a,intrinsic values are supplied by the COREX/BEST algorithm.

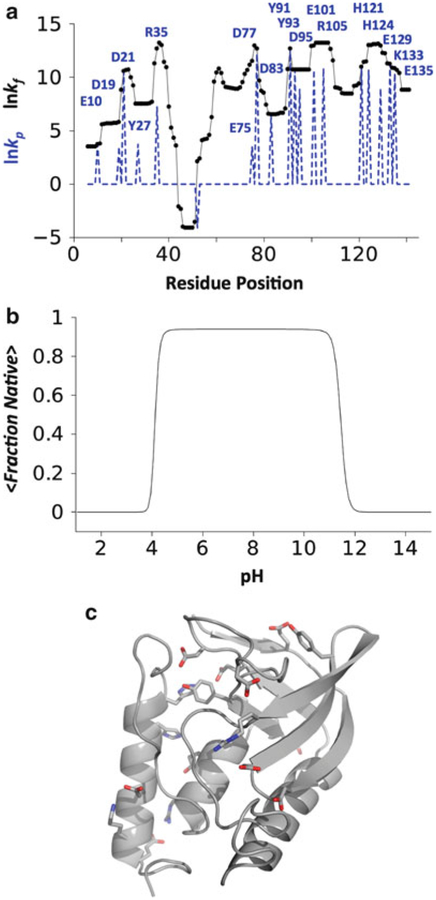
Figure 3 shows the pH sensitivity of the 1STN ensemble calculated by the COREX/BEST Server and identifies which of the ionizable residues were responsible for its pH-dependent stability in the calculation. For nuclease, mutagenic tests involving alanine substitutions of the ionizable residues provided experimental support for the COREX/BEST results [18]. To perform this simulation using the COREX/BEST Server, a user should first generate an ensemble by the steps outlined above, but also check the “pH Ensemble?” box when specifying window size and minimum window size. The COREX/BEST Server saves structural information needed to assign “native” or “intrinsic” pK_a values to each ionizable group in each microstate only when the “pH Ensemble?” box is checked. After the ensemble has been generated, the user should click on the “Calculate the pH Sensitivity an Ensemble” on the “Choosing COREX/BEST Jobs” page.

Fig. 3.

The effect of pH on the nuclease ensemble as calculated by the COREX/BEST Server. (a) Natural logarithm of the stability constants (black), k_f, and the residue-specific protection constants (blue dashed line), k_p. Protection constants identify which ionizable residues are folded and in a native-like environment in the most probable microstates [19]. In general, ionizable residues with high protection constant values (labeled in the figure) contribute to the pH-dependent population shifts of the ensemble (if pK_a,native ≠ pK_a,intrinsic), whereas those with low protection constant values do not. (b) pH dependent folding of the nuclease ensemble determined by 〈fraction native〉 = Σ fraction native_i•P(pH)_i where P(pH)_i was calculated by Eq. 2 and the fraction native value of each microstate was calculated as the number of residues in folded segments divided by the total number of residues. These data show that solution changes to acidic or basic conditions promote cooperative unfolding of the 1STN ensemble. (c) Cartoon representation of the nuclease structure. The ionizable residues with high k_p values (labeled in a) highlighted by showing the positions of their side chain atoms

4. Notes

1. The relative Gibbs free energy for each microstate, ΔG_i, is determined by structure-based parameterization of ΔC_p,i, ΔH_i, and ΔS_i [12]. The heat capacity, ΔC_p,i, is known to originate primarily from changes in hydration and has been parameterized in terms of changes in solvent accessible apolar (ΔASA_apol) and polar (ΔASA_pol) surface area,

   $$\mathrm{\Delta }{C}_{p,i}=\mathrm{\Delta }{C}_{p,\text{ apol },i}+\mathrm{\Delta }{C}_{p,\text{ pol },i},$$ (5)

   and

   $$\mathrm{\Delta }{C}_{p,i}=a_{\mathrm{\Delta }{C}_p}\cdot \mathrm{\Delta }{\text{ASA}}_{\text{apol},i}+b_{\mathrm{\Delta }{C}_p}\cdot \mathrm{\Delta }{\text{ASA}}_{\text{pol},i},$$ (6)

   Where a_ΔCp = 0.44 cal/mol KŲ and b_ΔCp = 0.26 cal mol KŲ [36–38]. The enthalpy change, ΔH_i, also scales with accessible surface areas and can be written as,

   $$\mathrm{\Delta }H{\left({60}^{°}\text{C}\right)}_i=a_{\mathrm{\Delta }H}\cdot \mathrm{\Delta }{\text{ASA}}_{\text{apol},i}+b_{\mathrm{\Delta }H}\cdot \mathrm{\Delta }{\text{ASA}}_{\text{pol},i},$$ (7)

   and

   $$\mathrm{\Delta }H{(T)}_i=\mathrm{\Delta }H{\left({60}^{°}\text{C}\right)}_i+\mathrm{\Delta }{C}_{p,i}\left(T-{60}^{°}\text{C}\right),$$ (8)

   where T is the temperature a_ΔH = −8.44 cal/mol a² and b_ΔH = 31.4 cal/mol Ų [36, 39]. The entropy change, ΔS_i, includes two contributions, one from changes in solvation and the other from changes in the conformational entropy,

   $$\mathrm{\Delta }{S}_i=\mathrm{\Delta }{S}_{\text{solv},i}+\mathrm{\Delta }{S}_{\text{conf},i},$$ (9)

   The solvation contribution can be written in terms of the polar and apolar values of ΔC_p if the temperatures at which ΔS_solv,apol = 0 and ΔS_solv,pol = 0 are known (T_s,apol and T_s,pol, respectively),

   $$\mathrm{\Delta }S{(T)}_{\text{solv},i}=\mathrm{\Delta }{C}_{p,\text{ apol, }}\text{ln}\left(T/T_{s,\text{apol}}\right)+\mathrm{\Delta }{C}_{p,\text{ pol, }}\text{ln}\left(T/T_{s,\text{pol}}\right).$$ (10)
   T_s,apol has been shown to be 385 K [31], while T_s,pol has been shown to be 335 K [40]. The conformational entropies are calculated by considering three contributions,

   $$\mathrm{\Delta }{S}_{\text{conf},i}=\mathrm{\Delta }{S}_{\text{bu}-\text{ex},i}+\mathrm{\Delta }{S}_{\text{ex}-\text{un},i}+\mathrm{\Delta }{S}_{\text{bb},i},$$ (11)

   where ΔS_bu-ex,i is the summed entropy change for all side chains that are buried in the fully folded state and become exposed in a microstate, ΔS_ex-un,i is the summed entropy change of solvent-exposed side chains upon unfolding of the peptide backbone, and ΔS_bb,i is the backbone entropy change for residues that become unfolded in a microstate. The magnitudes of the conformational entropy contributions for each amino acid type have been determined from computational analysis of the probabilities of the different dihedral and torsion angles and are reported elsewhere [40, 41]. The temperature-dependent Gibbs free energy for each ensemble state, ΔG(T)_i, is then expressed in terms of the standard thermodynamic equation,

   $$\mathrm{\Delta }G{(T)}_i=\mathrm{\Delta }H{(T)}_i-T\left(\mathrm{\Delta }S{(T)}_{\text{solv},i}+\mathrm{\Delta }{S}_{\text{conf},i}\right).$$ (12)

2. For each microstate, each ionizable group can have one of two values: the pK_a value in the native conformation (pK_a,native, which are user-supplied) or that of the unfolded state (pK_a,intrinsic, which are supplied by COREX/BEST). The set of pK_a,intrinsic values are those of model compounds in water [34, 35]. It’s recommended to calculate pK_a,native values using continuum electrostatic methods based on solution of the linearized Poisson-Boltzmann equation [42] applied to the high-resolution structure (e.g., 1STN). For each microstate, titratable residues in unfolded regions are assigned the model compound pK_a values (pK_a,intrinsic). Titratable groups in folded regions are assigned pK_a values based on the solvent accessibility of the titratable atoms. This was done to correct for the case in which a residue may reside in a folded region, however, due to the unfolding of segments of the protein that pack against the titratable site, the ionizable group is exposed to solvent. To apply this correction term in a general manner, a cutoff threshold was determined by comparison of COREX/BEST calculated and experimentally measured proton binding curves [18,19]. When the averaged solvent accessibility of the ionizable atoms of a titratable group is <31 % (for Glu, Asp, Tyr, Lys, and Arg) or <45 % (for His), these groups are assigned pK_a,native values. Otherwise, groups are assigned pK_a,intrinsic values. The COREX/BEST Server allows the user to change these two cutoff thresholds when calculating the pH sensitivity of an ensemble.

3. All lines of an uploaded PDB file that begin with the characters “ATOM” are used for COREX/BEST calculations; the algorithm is blindly unaware of the possibility that a PDB file may contain multiple models of the same structure. If a PDB file contains multiple models, either in terms of the whole chain (e.g., NMR model structures) or for the side chain conformations of individual residues, the Server will incorrectly assume that each model represents new atoms. Accordingly, additional atoms that physically aren’t present in a structure produce nonsensical COREX/BEST results. Also, PDB files that are missing side chain atoms should be avoided. The energy function used by COREX/BEST (see Note 1) was parameterized and trained using protein structures that contained side chain atoms for each residue.

4. The COREX/BEST algorithm can use a Metropolis Monte Carlo method of sampling [27] to decrease the run-time required to generate an ensemble by decreasing the number of microstates generated. By design, this method uses the microstate probabilities calculated from the COREX/BEST energy function (see Note 1 and Eq. 1) to bias sampling in favor of the more probable microstates. The COREX/BEST energy function, however, depends on temperature and pH. The Monte Carlo sampling routine uses a default temperature setting of 25°C and includes no proton binding energies when calculating microstate probabilities. Thus, Monte Carlo sampled ensembles work best (i.e., produce equivalent results compared to fully enumerated and non-sampled ensembles) for calculations designed to simulate temperatures at or near 25°C and that include no proton binding energies.