Weakly supervised individual ganglion cell segmentation from adaptive optics OCT images for glaucomatous damage assessment

Abstract

Cell-level quantitative features of retinal ganglion cells (GCs) are potentially important biomarkers for improved diagnosis and treatment monitoring of neurodegenerative diseases such as glaucoma, Parkinson’s disease, and Alzheimer’s disease. Yet, due to limited resolution, individual GCs cannot be visualized by commonly used ophthalmic imaging systems, including optical coherence tomography (OCT), and assessment is limited to gross layer thickness analysis. Adaptive optics OCT (AO-OCT) enables in vivo imaging of individual retinal GCs. We present an automated segmentation of GC layer (GCL) somas from AO-OCT volumes based on weakly supervised deep learning (named WeakGCSeg), which effectively utilizes weak annotations in the training process. Experimental results show that WeakGCSeg is on par with or superior to human experts and is superior to other state-of-the-art networks. The automated quantitative features of individual GCLs show an increase in structure–function correlation in glaucoma subjects compared to using thickness measures from OCT images. Our results suggest that by automatic quantification of GC morphology, WeakGCSeg can potentially alleviate a major bottleneck in using AO-OCT for vision research.

1. INTRODUCTION

Ganglion cells (GCs) are one of the primary retinal neurons that process and transmit visual information to the brain. These cells degenerate in optic neuropathies such as glaucoma, which can lead to irreversible blindness if not managed properly [1]. In clinical practice, measuring the intraocular pressure (IOP) and monitoring for functional and structural abnormalities are routinely used, either alone or in combination, to diagnose and manage glaucoma [1]. Visual function is measured through standard automated perimetry, and structural testing commonly consists of evaluating conventional ophthalmoscopy images. Although elevated IOP is considered a major risk factor, only one-third to half of glaucoma patients exhibit elevated IOP at the initial stages of the disease [2,3]. Thus, measuring IOP alone is not an effective method for screening populations for glaucoma. The visual field test is subjective, has poor sensitivity to early disease [1,4], and its high variability limits reliable identification of vision loss [5,6]. Optical coherence tomography (OCT) has been increasingly incorporated into clinical practice to improve disease care, with the thickness of the nerve fiber layer (NFL) a widely used metric [7,8]. While the NFL is composed of GC axons, it also contains significant glial tissue, which varies across the retina [9], and at advanced stages of glaucoma, the NFL thickness reaches a nadir despite continued progression of the disease [10,11]. Alternatively, the GC complex (GCC) thickness [comprising the NFL, GC layer (GCL), and inner plexiform layer] or its components have been suggested as alternative and complementary candidates for monitoring glaucoma progression [12]. Although the GCC thickness measured through OCT is promising, it reflects the coarse aggregate of underlying cells, and therefore does not finely capture soma loss and morphology changes at the cellular level. Since using one of the aforementioned data alone does not provide a complete picture of glaucomatous damage, more recent studies have employed different combinations of these structural and functional datasets—some with machine learning approaches—to assess disease damage [13-15]. The study of these methods remains ongoing.

In principle, quantifying features of individual GCs offers the potential of highly sensitive biomarkers for improved diagnosis and treatment monitoring of GC loss in neurodegenerative diseases. The incorporation of adaptive optics (AO) with OCT [16-18] and scanning light ophthalmoscopy (SLO) [19] allows visualization of GC somas in the living human eye. While successful, the current standard approach for quantification—manual marking of AO-OCT volumes—is subjective, time consuming, and not practical for large-scale studies and clinical use. Thus, there is a need for an automatic technique for rapid, high-throughput, and objective quantification of GCL somas and their morphological properties.

To date, many automated methods for localizing various retinal structures [20-26] and cell types [27-30] from ophthalmic images have been proposed. Previous methods range from mathematical model-based techniques to deep-learning-based algorithms. In deep learning, convolutional neural networks (CNNs) have become a staple in image analysis tasks due to their exceptional performance. Previous deep-learning-based ophthalmic image processing studies used mainly CNNs with two-dimensional (2D) filters to segment different retinal structures. However, depending on the imaging system resolution and sampling scheme, some structures such as GCs cannot be summarized into a single 2D image. Therefore, CNNs that use 3D information, e.g., by using 3D convolutional operations [31-34], can outperform 2D CNNs when processing volumetric data.

Fully supervised training of CNNs usually requires large training datasets to achieve acceptable performance. To circumvent this when detecting photoreceptors—light-sensitive cells that form a 2D mosaic—from AO-OCT images, Heisler et al. [29] took advantage of existing manually labeled AO-SLO datasets. Unfortunately, a dataset of manual volumetric segmentation for GCs from any imaging system does not currently exist. Adding to the difficulty of training CNNs, the pixel-level annotations needed for semantic segmentation is a strenuous task for densely packed GCs in AO-OCT volumes.

Currently, there is growing interest in weakly supervised segmentation schemes using different levels of weak annotation. Studies that use image-level labels often utilize class activation maps [35] to localize objects and a segmentation proposal technique to obtain the final object masks. In other studies, graphical models are combined with bounding boxes or seeds to obtain initial object masks for fully supervised training. Although segmentation masks are iteratively updated during training, errors in the initial steps could negatively affect the training process. To avoid this problem, criteria from unsupervised segmentation techniques have been incorporated into the training loss function [36]. Such intricate measures are often necessary for weakly supervised segmentation of objects with complex structures frequently present in natural images. In contrast, CGL somas are sphere-shaped structures.

Previous weakly supervised methods, if not supervised through bounding boxes, often do not account for separating touching instances of the same class. In our application of densely packed GCL somas, collecting the 3D bounding boxes of all somas for training is extremely prohibitive and requires significant human effort. Additionally, there has been little work on weakly supervised instance segmentation in the context of volumetric medical images.

In this paper, we designed a fully convolutional network for localizing GCL somas and measuring their diameters from AO-OCT scans. Our main contributions are as follows.(1) Our work is the first to automatically detect and segment individual GCL somas in AO-OCT volume image datasets. We used weak annotations in the form of human click-points in the training process to obtain the soma segmentation masks, requiring minimal annotation effort. Based on how our method works, we refer to it as WeakGCSeg. (2) We comprehensively evaluated the performance of WeakGCSeg on data acquired with two different imagers from healthy and glaucoma subjects across various retinal locations. We directly compared our method with state-of-the-art CNNs. (3) We demonstrated the utility of our automatic method in segregating glaucomatous eyes from healthy eyes using the extracted cellular-level characteristics. We also showed that these characteristics increased the structure–function correlation in glaucoma subjects.

2. MATERIALS AND METHODS

A. AO-OCT Datasets

We used two separate datasets acquired by the AO-OCT systems developed at Indiana University (IU) and the U.S. Food and Drug Administration (FDA), previously described [16,17]. Briefly, IU’s resolution in retinal tissue was 2.4 × 2.4 × 4.7 μm³ (width × length × depth; Rayleigh resolution limit). The dataset consisted of 1.5° × 1.5° AO-OCT volumes (450 × 450 × 490 voxels) from eight healthy subjects (Table S1) at 3°–4.5°, 8°–9.5°, and 12°–13.5° temporal to the fovea. Since the 3°–4.5° and 8°–9.5° retinal locations are densely packed with somas (Text Section 1 of Supplement 1), the volumes from these locations were cropped to 0.67° × 0.67° (centered at 3.75°; 200 × 200 × 250 voxels) and 0.83° × 0.83° (centered at 8.5°; 250 × 250 × 130 voxels), respectively, to facilitate manual marking. For brevity, we refer to these three retinal locations as 3.75°, 8.5°, and 12.75°.

The FDA dataset consisted of 1.5° × 1.5° volumes (297 × 259 × 450 voxels) at 12° temporal to the fovea, 2.5° superior and inferior of the raphe (for brevity, we refer to both locations as 12°) from five glaucoma patients with hemifield defect (10 volumes; Table S2) and four healthy age-matched subjects (six volumes; two subjects were imaged at one location). These volumes were acquired by the multimodal AO retinal imaging system with a retinal tissue resolution of 2.5 × 2.5 × 3.7 μm³ (Rayleigh resolution limit). Volumes from both institutions were the average of 100–250 registered AO-OCT volumes of the same retinal patch. All protocols adhered to the tenets of the Helsinki declaration and were approved by the Institutional Review Boards of IU and the FDA. Text Section 2 of Supplement 1 provides details on the ophthalmic examination of the subjects.

B. GCL Soma Instance Segmentation with Weakly Supervised Deep Learning

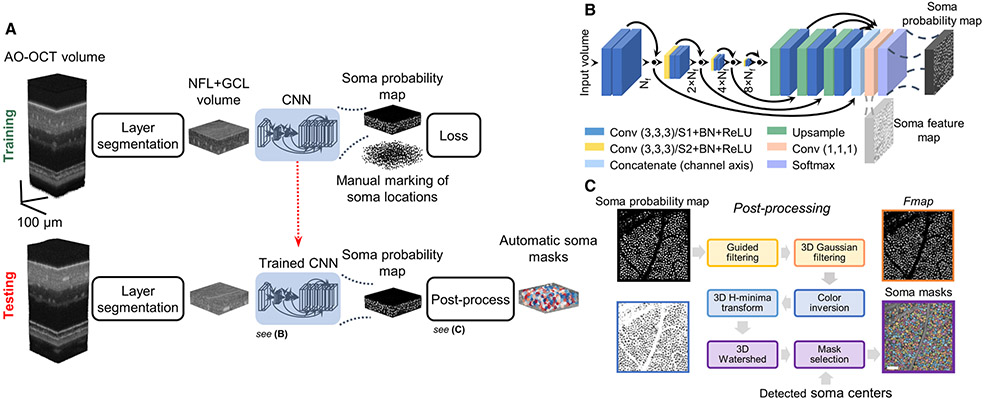
The overall framework, named WeakGCSeg, is shown in Fig. 1A. The input to the framework is the entire AO-OCT stack. First, we narrowed the search space for GCL somas by automatically extracting this retinal layer. The extracted volumes were then used for further processing. During the network training phase, instead of directly training our CNN (Fig. 1B) to learn the instance segmentation task, the CNN was trained to localize GCL somas using manually marked soma locations. Thus, the network’s output was a probability volume indicating the locations of potential somas. With additional post-processing steps applied to the CNN output, we segmented individual somas (Fig. 1C).

Fig. 1.

Details of WeakGCSeg for instance segmentation of GCL somas from AO-OCT volumes. (A) Overview of WeakGCSeg. (B) Network architecture. The numbers in parentheses denote the filter size. The number of filters for each conv. layer is written under each level. Nf = 32 is the base number of filters. Black circles denote summation. Conv, convolution; ReLU, rectified linear unit; BN, batch-normalization; S, stride. (C) Post-processing the CNN’s output to segment GCL somas without human supervision. The colored boxes correspond to steps with matching colors. Scale bar: 50 μm.

1. Data Pre-Processing

We performed retinal layer segmentation as a pre-processing step to narrow the search space for GCL somas. For each volume, we identified the vitreous-NFL and GCL-inner plexiform layer boundaries using the graph theory and dynamic programming method described previously [37]. Details of this step can be found in Supplement 1 and Fig. S1.

2. Neural Network and Training Process

Our neural network is an encoder–decoder CNN with 3D convolutional filters, with its encoder path computing feature maps at multiple scales with skip connections to a single-level decoder path (Fig. 1B). Similar to VNet [32], we used convolutional layers with a stride of two for down-sampling and to double the number of feature channels. We incorporated residual learning into the encoder path. To upscale the feature maps to the input resolution, we used the nearest neighbor up-sampling followed by a single convolutional layer. After concatenating the up-sampled feature maps, a final convolutional layer with two filters and Softmax activation estimated probabilities for the background and soma classes for each voxel. All convolutional layers used filters of size 3 × 3 × 3 and, except for the last layer, were followed by batch normalization and rectified linear unit activation.

Our network differs from the commonly used UNet3D [31] in that (1) instead of maxpooling, we used convolutional layers with stride two for downsampling, (2) we used interpolation for upsampling the feature maps instead of deconvolution, which reduces the number of network parameters, (3) our network has a single decoder level, and (4) we used residual connections. Overall, our network’s trainable parameters are about one-third of UNet3D’s parameters.

We formulated the localization problem as a segmentation task by creating training labels containing a small sphere (radius of 2 μm) at each manually annotated soma location. Small spheres were used to ensure the labels were entirely positioned within each soma body. In these training labels, most pixels belonged to the background class. We thus used the weighted binary cross-entropy loss to account for this class-imbalanced problem. The loss, L, is defined as

$$L=-\sum _i[w_{pos}{y}_i\log (p_i)+w_{neg}(1-y_i)\log (1-p_i)],$$ (1)

where y_i is the true class label (zero for background, one for soma) of voxel i, p_i is the predicted probability for voxel i to be located on a soma, and w_neg and w_pos are the weights for the background and soma classes, respectively. To reduce the bias towards the background class with its higher number of samples, we set w_neg to a lower value than w_pos. Specifically, we set w_pos = 1 and w_neg = 0.008 for the IU dataset and w_pos = 1 and w_neg = 0.002 for the FDA dataset, determined based on the ratio between the number of voxels in the soma and background classes.

During training, we sampled random batches of two 120 × 120 × 32 voxel volumes. To improve the generalization abilities of our model, we applied random combinations of rotations (90°, 180°, and 270° in the lateral plane) and flips (around all three axes) over the input and label volumes. In addition to these data augmentations, we applied additive zero-mean Gaussian noise with a standard deviation (SD) of 1.5 to the input volume. We used the Adam optimizer with learning rates of 0.005 and 0.001 for the IU and FDA datasets, respectively. We trained the network for a maximum of 100 epochs with 100 training steps per epoch, during which the loss function converged in all our experiments. We used the network weights that resulted in the highest detection score (see Section 2.D) on the validation data for further analysis.

During the CNN training on the 3.75° and 12.75° volumes, we accounted for the different size distributions of somas (i.e., midget and parasol GCs are more homogenous in size at 3° than at 12°–13°) by exposing the CNN to the 12.75° volumes more often than to the 3.75° location. Specifically, we set the probability of selecting the 12.75° volumes to be five times higher than the 3.75° volumes.

3. Soma Localization and Segmentation

We post-processed the output probability map to localize and segment individual GCL somas. We input AO-OCT volumes into the trained network using a 256 × 256 × 32 voxel sliding window with a step size equal to half the window size. In the overlapping regions, we averaged the output probabilities. Additionally, we considered using test-time augmentation (TTA) to potentially improve performance, which consisted of averaging network outputs for eight rotations and flips in the en face plane of the input volume. Next, we applied a median filter of size 3 × 3 × 3 to the probability maps to remove spurious maxima. We then located somas from the filtered maps by finding points that were local maxima in a 3 × 3 × 3 (3 × 3 × 7 for FDA) window with values greater than T. The validation data were used to find the value of T that maximized the detection performance (see Section 2.D).

To segment individual cells, we used the network’s probability map for the soma class (Fig. 1C). First, we applied self-guided filtering [38] to each en face plane of the input probability volume using MATLAB’s (MathWorks) imguidedfilter function. Next, after smoothing the filtered map in the axial direction using an elongated Gaussian filter, denoting the result as Fmap, we inverted the intensities (zero became one and vice versa). We set the Gaussian filter’s SD to (0.1, 1) pixels (en face and axial planes, respectively) and (0.1, 1.6) pixels for the IU and FDA datasets, respectively. We ultimately used the 3D watershed algorithm to obtain individual soma masks. To further prevent over-segmentation by the watershed algorithm, we applied the H-minima transform using MATLAB’s imhmin function with parameter 0.01 to the inverted Fmap. We removed voxels with intensity values greater than TH = 0.96 in the filtered Fmap from the set of watershed masks. As we are interested only in the segmentation masks of the localized somas in the previous step, we kept only the watershed masks that overlapped with the identified cell centers. To measure soma diameters, we used the en face image of each individual soma mask at its predicted center. We estimated soma diameter as the diameter of a circle with area equal to that of the soma’s en face mask image. In practice, we used information from one C-scan below to one C-scan above the soma center to obtain more accurate estimates. Eye length was used to scale the results to millimeters [39].

C. Study Design

We conducted four main experiments to evaluate the performance of our algorithm in: (1) healthy subjects at two trained retinal locations, (2) healthy subjects at an untrained retinal location (generalizability test), (3) glaucomatous subjects at trained retinal locations, and (4) healthy subjects imaged by two different AO-OCT imagers with training on one and testing on the other (generalizability test). The number of training and test samples for each experiment are summarized in Table S3.

In the first experiment, we used IU’s 3.75° and 12.75° volumes to train and validate our algorithm through leave-one-subject-out cross-validation and compared it against expert-level performance. In each fold of cross-validation, we separated the data of one subject as the test data, selected one 12.75° volume from the remaining subjects as the validation data for monitoring the training process and optimizing the post-processing parameter, and used the remaining data for training the CNN. Thus, there was no overlap among the test, validation, and training data. To attain the gold-standard ground truth GCL soma locations, two expert graders sequentially marked the data. After the first grader marked the soma locations, the second grader reviewed the labeled somas and corrected the markings as needed. To obtain expert-level performance, we performed an inter-grader variability test in which we obtained a second set of manual markings by assigning graders to previously unseen volumes. In total, nine graders were involved in the creation of the manual markings (Table S1). In the second experiment, we used the trained CNNs from the first experiment and tested their performances on the 8.5° volumes of the corresponding test subjects without any modification.

For the third experiment, we used the FDA dataset to evaluate performance on glaucomatous eyes. To create the gold-standard ground truth, two expert graders sequentially marked the soma locations, with the second grader reviewing the first grader’s labels and correcting them as needed. A third independent grader created the “2nd Grading” set, serving as the expert-level performance. We optimized our method for the two subject groups independently through leave-one-subject-out cross-validation in which we separated the data of one subject as the test data, and selected one volume from the remaining subjects as the validation data and the rest for training the CNN. To test the generalizability of the method between healthy and diseased eyes, we applied the CNN trained on all subjects of one group (healthy or glaucoma) to the other set.

In the last experiment, we tested generalizability between different devices through three studies. In the first two cases, we applied the optimized pipeline on data from one device to data from the other device. Specifically, we used the 3.75° and 12.75° volumes from IU and the 12° healthy subject volumes from FDA. In the third case, we trained and tested our network on the mixture of data from the devices. Subjects were divided into four groups, each group containing two subjects imaged with IU’s system and one subject with FDA’s device. We trained and tested performance through four-fold cross-validation. Since the devices had different voxel sizes (IU: 0.97 × 0.97 × 0.94 μm³, FDA: 1.5 × 1.5 × 0.685 μm³), we quantified performance with and without test data resized to the training data voxel size (through cubic interpolation).

In addition to these four main experiments, we conducted ablation tests, which are explained in Methods Section 2 of Supplement 1.

D. Performance Evaluation

We applied the trained network to the hold-out data for testing the performance. We evaluated the detection performance using recall, precision, and F₁ score, defined as

$$\text{Recall}=\frac{N_{TP}}{N_{GT}},$$ (2)

$$\text{Precision}=\frac{N_{TP}}{N_{\text{detected}}},$$ (3)

$$F_1=2\frac{\text{Recall}\times \text{Precision}}{\text{Recall}+\text{Precision}}.$$ (4)

In the above equations, N_GT is the number of manually marked GCL somas, N_detected denotes the number of detected somas by our automatic algorithm, and N_TP is the number of true positive somas. To determine the true positive somas, we used the Euclidean distance between the automatically found and manually marked somas. Each manually marked soma was matched to its nearest automatic soma if the distance between them was smaller than D. We set the value for D to half of the previously reported mean GCL soma diameters in healthy eyes for each retinal location [16]. For the glaucoma cases, we used 0.75 times the median spacing between manually marked somas for D. This yielded D values of 5.85 μm and 8.78 μm for the 3.75° and 12°–12.75° volumes for healthy subjects, respectively, and 10.78 μm for the 12° volumes from glaucoma patients. To remove border artifacts, we disregarded somas within 10 pixels of the volume edges. For inter-observer variability, we compared the markings of the second grading to the gold-standard markings in the same way.

To compare the performance of different CNNs, we used the average precision (AP) score, defined as the area under the precision-recall curve. AP quantifies the overall performance of any detector (CNNs in our case) in localizing GCL somas and is insensitive to the exact selection of the hyperparameter T. We also compared our estimated cell densities to gold-standard values. We measured cell density by dividing the cell count to the image area after accounting for large blood vessels and image edges. Finally, we compared our predicted soma diameters to data from previous histological [40-44] and in vivo semi-automatic studies [16,19], and to the 2D manual segmentation of a subset of the somas.

E. Implementation

We implemented our network in Python using Keras with Tensorflow backend. The soma localization and performance evaluation were implemented in Python, and the pre-processing and segmentation were coded in MATLAB (MathWorks). We used a Windows 10 computer with Intel Core i9-9820X CPU and NVIDIA GeForce GTX 1080TiGPU.

3. RESULTS

A. Achieving Expert Performance on Healthy Subjects and Generalizing to an Unseen Retinal Location (Experiments 1 and 2)

Using the characteristically different 3.75° and 12.75° volumes (in terms of GCL soma sizes and size distributions), we trained our CNN through leave-one-subject-out cross-validation. The layer segmentation step of our method cropped the original AO-OCT volumes in the axial direction to 69–85 pixels and 30–40 pixels for the 3.75° and 12.75° volumes, respectively. The results in Table 1 show that WeakGCSeg surpassed or was on par with the expert performance in detecting GCL somas (p—values = 0.008 and 0.078 for 3.75° and 12.75° volumes, respectively; two-sided Wilcoxon signed-rank test over F₁ scores of eight subjects).

Table 1.

GCL Soma Detection Scores, Reported as Mean ± Standard Deviation Calculated across Eight Subjects for 3.75° and 12.75° (Experiment 1) and a Subset of Five Subjects for the 8.5° Location (Experiment 2)^a

		GCL Soma Detection
Dataset	Method	Recall	Precision	F1
IU 3.75°	WeakGCSeg	0.88 ± 0.09	0.87 ± 0.06	0.87 ± 0.04
	2nd Grading	0.77 ± 0.16	0.80 ± 0.08	0.77 ± 0.06
IU 12.75°	WeakGCSeg	0.88 ± 0.07	0.85 ± 0.06	0.87 ± 0.04
	2nd Grading	0.83 ± 0.10	0.82 ± 0.12	0.81 ± 0.05
IU 8.5°	WeakGCSeg	0.90 ± 0.05	0.85 ± 0.04	0.87 ± 0.02
	2nd Grading	0.79 ± 0.02	0.90 ± 0.03	0.84 ± 0.02

^aThe same sets of trained WeakGCSeg networks were used in both experiments.

Next, we used the optimized WeakGCSeg (on the 3.75° and 12.75° data) and tested its performance on the unseen 8.5° data. The layer segmentation step axially cropped the 8.5° volumes down to 46–52 pixels. On the 8.5° data, WeakGCSeg achieved the same F1 score as the former locations (Table 1) and was on par with expert performance (p — value = 0.063; two-sided Wilcoxon signed-rank test over five subjects). The average precision-recall curves of WeakGCSeg compared to the average expert grading in Fig. 2A provide a more complete picture of the performance. The average curves were obtained by taking the mean of the precision and recall values of all the trained networks at the same threshold value T. At the average expert grader precision score, WeakGCSeg’s average recall was 0.16, 0.08, and 0.08 higher at the 3.75°, 8.5°, and 12.75° locations, respectively. WeakGCSeg’s generalizability and expert-level performance persisted with whitening the input data or disregarding TTA [Table S4 and Fig. S2(A)] and was superior to other variations of the network architecture (Table S5 and Fig. S3).

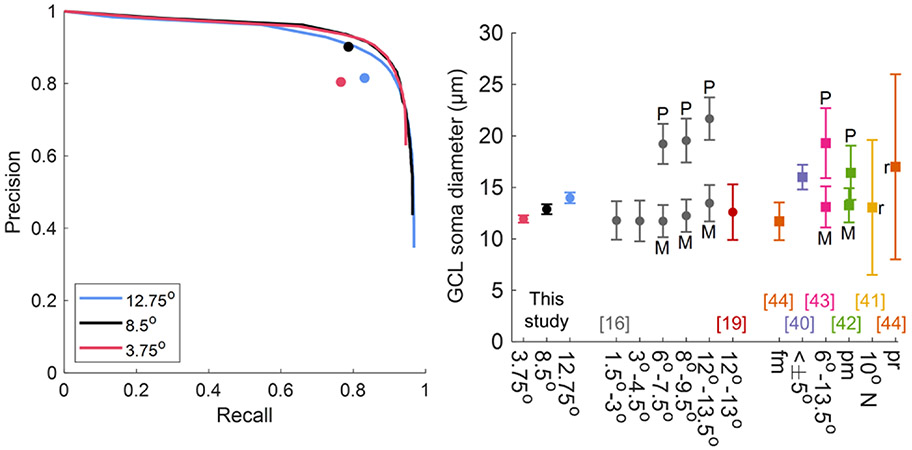
Fig. 2.

Results on IU’s dataset. (A) Average precision-recall curves of WeakGCSeg compared to average expert grader performances (circle markers). Each plotted curve is the average of eight and five curves at the same threshold values for the 3.75°/12.75° and 8.5° data, respectively. (B) GCL soma diameters across all subjects compared to previously reported values. Circle and square markers denote mean soma diameters from in vivo and histology studies, respectively. Error bars denote one standard deviation. “r” denotes the range of values. P, parasol GCs; M, midget GCs; fm, foveal margin; pm, papillomacular; pr, peripheral retina.

Using WeakGCSeg’s soma segmentation masks, we estimated the GCL soma diameters. The histograms of soma diameters in Fig. S4 reflect the trend of gradual increase in soma size from 3.75° to 12.75°, which is consistent with the GC populations at these locations. Figure 2B indicates that our predicted values (mean ± SD: 11.9 ± 0.4 μm, 12.9 ± 0.5 μm, and 14.0 ± 0.5 μm for 3.75°, 8.5°, and 12.75°, respectively) were in line with histological and in vivo semi-automatic measurements and outperformed simple thresholding of the CNN output [Section 2.B.1 of Supplement 1 and Fig. S5(A)-(B)]. To further validate the segmentation accuracy, we manually segmented 300–340 randomly selected somas in 2D from the 8.5° and 12.75° volumes of three subjects. The automatic segmentation masks agreed with the manual masks for both retinal locations [mean (95% confidence interval) Dice similarity coefficients at 8.5°/12.75° = 0.83 (0.82, 0.84)/0.84 (0.83, 0.85), 0.81 (0.80, 0.82)/0.82 (0.80, 0.83), and 0.84 (0.83, 0.85)/0.85 (0.83, 0.86) for subjects S1, S4, and S5, respectively; Fig. S6(A)]. Furthermore, the results of the ablation experiments (Methods Sections 2.B.2-3 of Supplement 1) showed that the thresholding and Gaussian smoothing steps of our post-processing framework were effective in accurately estimating the soma diameters. Specifically, the inclusion of the thresholding step (parameter TH) in our framework reduced the difference between the estimated diameters from manual and automatic segmentation masks (average difference of −0.005 μm versus −0.795 μm for TH = 0.96 and 1, respectively; TH = 1 corresponds to no thresholding, as the maximum value in the output maps is one). The smoothing step also improved the soma estimates for the less frequent larger GCL somas [Fig. S5(C)].

Example results with comparison to manual markings are illustrated in Fig. 3 and Visualization 1, Visualization 2, and Visualization 3. The cyan, red, and yellow markers indicate correctly identified (true positive; TP), missed (false negative; FN), and incorrectly identified (false positive; FP) somas, respectively. A 3D flythrough of the segmented somas for the 3.75° data in Fig. 3 is illustrated in Visualization 4 . The prediction times were 2.0 ± 0.5, 1.3 ± 0.1, and 3.2 ± 0.5 min/volume for the 3.75°, 8.5°, and 12.75° data, respectively, which were at least two orders of magnitude faster than that of manual grading (7–8 h/volume).

Fig. 3.

En face (XY) and cross-sectional (XZ and YZ) slices illustrate (top) soma detection results compared to the gold-standard manual markings and (bottom) overlay of soma segmentation masks, with each soma represented by a randomly assigned color. Cyan, red, and yellow markers denote TP, FN, and FP, respectively. Only somas with centers located within 5 μm from the depicted slices are marked in the top row. The intensities of AO-OCT images are shown in log-scale. Scale bars: 50 μm and 25 μm for en face and cross-sectional slices, respectively.

B. Achieving Expert Performance on Glaucoma Patients (Experiment 3)

We next applied WeakGCSeg to images taken from glaucomatous eyes. We whitened each extracted NFL + GCL volume (42–55 pixels and 25–53 pixels in the axial direction for the healthy and glaucoma volumes, respectively) by subtracting its mean and dividing by its SD. We then trained our method separately on the two groups of subjects. WeakGCSeg’s automatically estimated cell densities were similar to the gold standard for both groups (p – values = 0.125 and 1 across n = 4 and 5 healthy and glaucoma subjects, respectively; two-sided Wilcoxon signed-rank test). Table 2 summarizes the detection performance and the inter-observer test results. For both groups, our results were on par with expert performance based on the average F₁ scores of each subject (p – values = 0.125 and 0.063 over n = 4 and 5 healthy and glaucoma subjects, respectively; two-sided Wilcoxon signed rank test).

Table 2.

GCL Soma Detection Scores, Reported as Mean ± Standard Deviation Calculated across Six Healthy and 10 Glaucoma Volumes^a

		GCL Soma Detection
Dataset	Method	Recall	Precision	F1
FDA	WeakGCSeg	0.90 ± 0.04	0.78 ± 0.07	0.84 ± 0.05
Healthy	2nd Grading	0.93 ± 0.02	0.72 ± 0.09	0.81 ± 0.06
FDA	WeakGCSeg	0.75 ± 0.14	0.78 ± 0.15	0.75 ± 0.11
Glaucoma	2nd Grading	0.88 ± 0.07	0.53 ± 0.16	0.64 ± 0.13

^aWeakGCSeg was trained separately for the two groups.

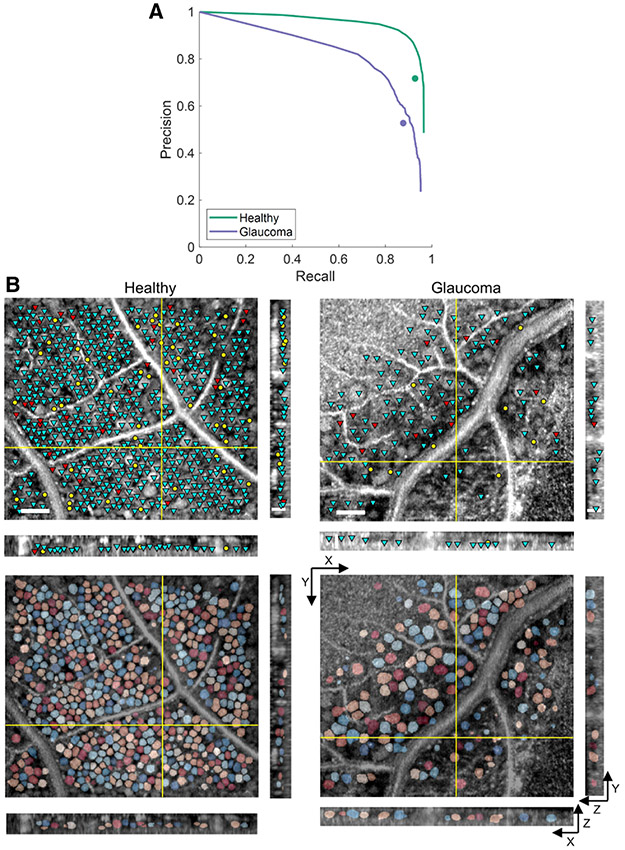
Figure 4A depicts the average precision-recall curves of our trained networks compared to the average expert grader performance; at the same level of average grader precision, our method achieved 0.04 and 0.03 higher average recall scores for the healthy and glaucoma subjects, respectively. Our method achieved high detection scores even without data whitening or TTA [Table S6 and Fig. S2(B)] and was superior to other variations of the network (Table S5 and Fig. S3). Moreover, the method retained expert-level performance when tested on a group not used during training [Table S7 and Fig. S2(C)], reflecting its generalizability between healthy and diseased eyes. Example results are illustrated in Fig. 4B.

Fig. 4.

Results on FDA’s healthy and glaucoma subjects. (A) Average precision-recall curves compared to average expert grader performances (circle markers). Each plotted curve is the average of six and 10 curves for the healthy and glaucoma volumes, respectively. (B) En face (XY) and cross-sectional (XZ and YZ) slices illustrating soma detection and segmentation results. See Fig. 3 for further details.

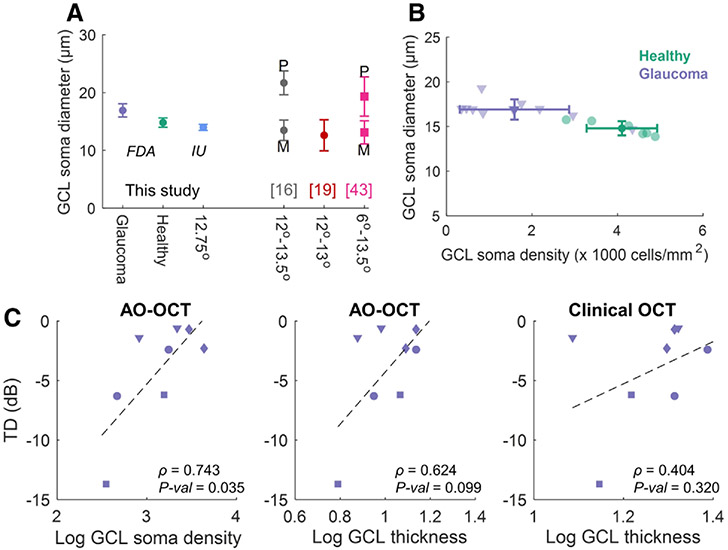
Using the soma segmentation masks, we estimated cell diameters. As Fig. 5A shows, the estimated diameters on the healthy cohort (mean ± SD: 14.8 ± 0.8 μm) agreed with the estimates from the IU dataset and previous studies at 12°–13°. The results also reflect an increase of 2.1 μm (p – value = 0.03, Wilcoxon rank-sum test, five glaucoma and four healthy subjects, respectively) in the average soma size of glaucoma subjects (mean ± SD: 16.9 ± 1.1 μm) compared to healthy individuals, which is in line with recent reports [45]. Figure 5B illustrates soma size against cell densities for all volumes, reflecting that glaucoma subjects exhibited larger somas at lower cell densities than the controls.

Fig. 5.

Structural and functional characteristics of glaucomatous eyes compared to controls. (A) GCL soma diameters compared to values reported in the literature. (B) Automatic cell densities and average diameters for all volumes from FDA’s device. (C) TD measurements versus cell densities and GCL thickness values for four glaucoma subjects. ρ, Pearson corr. coef. Subjects are shown with different marker shapes.

C. Structural and Functional Characteristics of Glaucomatous Eyes Differ from Control Eyes

AO enables cellular-level examination of GCL morphological changes and their relation to vision loss in glaucoma [45]. Our automatic method makes this possible clinically. To demonstrate this, we examined the cellular-level characteristics and clinical data of glaucomatous eyes. To remove potential bias in analysis, one subject was omitted from the structure–function study because imaging of this subject was done with an instrument (Optovue, Fremont, CA, USA) different from the predefined protocol used for all other subjects. The automatically determined cell densities exhibited stronger correlation with GCL thicknesses measured from AO-OCT [Pearson correlation coefficient, ρ = 0.851, p – value < 0.001; Fig. S7(A)] compared to measurement from clinical OCT (ρ = 0.668, p – value = 0.009). When comparing local functional measures [total deviation (TD) and pattern deviation (PD); Table S2] with the local structural characteristics [Fig. 5C and Fig. S7(B)], the soma density in log-scale strongly correlated with TD (ρ = 0.743, p — value = 0.035) and PD (ρ = 0.806, p — value = 0.016) for glaucoma subjects. The log-scale GCL thickness from AO-OCT correlated moderately with these measures (ρ = 0.624 and 0.699, p – values = 0.099 and 0.054 for TD and PD, respectively), while the measurements from clinical OCT had low correlation with the functional data (ρ = 0.404 and 0.310, p – values = 0.320 and 0.454 for TD and PD, respectively). Including the soma diameters as an additional independent variable to the AO-OCT measured GCL thickness and soma density (all in log-scale) increased the structure–function correlation (coefficient of multiple correlations = 0.892 and 0.975 for TD and PD, respectively).

D. Generalization Between Imaging Devices (Experiment 4)

Previous results were obtained by separately training models for two imagers with different scan and sampling characteristics. To evaluate the generalizability between these devices, we applied the trained and optimized method on data from one device to volumes acquired by the other system (rows 2 and 4 in Table S8). After resizing the test volumes to the same voxel size as the training data, the detection performance of the inter-device testing scheme was similar to that of the intra-device framework (rows 1 and 5; p — values = 0.547 and 0.125 over n = 8 and 4 subjects, respectively; two-sided Wilcoxon sign rank test on the average F₁ scores of each subject) without additional parameter optimization. Without test volume resizing and parameter tuning, the trained method on one device could not necessarily generalize to the other imager (p — values = 0.008 and 0.125 over n = 8 and 4 subjects, respectively).

In addition to the above experiments, we evaluated the detection performance when training and testing on the mixture of data from both devices. To this end, we resized the data from IU’s system to have the same pixel size as FDA’s data. The results in rows 3 and 6 in Table S8 show that we achieved the same level of cell detection performance as the intra-device scheme (p — values = 0.313 and 0.250 over n = 8 and 4 subjects for IU and FDA datasets, respectively).

E. Comparison with State of the Art

Finally, we compared the detection performance of our network to other state-of-the-art CNNs, which included UNet3D, VNet, and a nested version of UNet3D with the redesigned skip connections of Zhou et al. [46], which we call Unet3D++. We implemented the redesigned skip connections into the Unet3D backbone using the source code at [47] and using all 3D operations. For a fair comparison, we used the same training and soma localization procedures as WeakGCSeg for these CNNs. For VNet and Unet3D++, based on the original publications, we used learning rates of 10⁻⁶ and 3 × 10⁻⁴, respectively. We used the same learning rate for UNet3D as WeakGCSeg.

As the AP scores in Table 3 and the precision-recall curves in Fig. S8 show, WeakGCSeg’s performance was higher than these architectures. We used the Friedman ranking test with the Holm’s post-hoc procedure to conduct non-parametric multiple comparison tests [48] using the open-source JAVA program developed in [49]. We analyzed the overall performances by pooling the data in Table 3 at the subject level (17 subjects). Specifically, for each subject with multiple measurements, we averaged the AP scores. Thus, the null hypothesis here states that all methods perform equally over the entire dataset presented in this study. For completeness, we also included the two-sided Wilcoxon signed rank test between WeakGCSeg and every other CNN. We used α = 0.05 as the significance level. The Freidman test yielded p-value of 6.4 × 10⁻⁸, thus rejecting the null hypothesis. The adjusted p-values for the Holm’s 1 × N comparisons and the p-values from the Wilcoxon test additionally show that overall, WeakGCSeg’s performance is significantly better than other CNNs.

Table 3.

Comparison among the Average Precision Scores of Different CNNs for Each Dataset and Statistical Analyses across All Subjects^a

Dataset	WeakGCSeg	UNet3D++	UNet3D	VNet
IU 3.75°	0.90 ± 0.06	0.87 ± 0.06	0.89 ± 0.06	0.75 ± 0.06
IU 8.5°	0.91 ± 0.02	0.89 ± 0.03	0.90 ± 0.03	0.72 ± 0.02
IU 12.75°	0.90 ± 0.05	0.89 ± 0.05	0.86 ± 0.12	0.76 ± 0.06
FDA Healthy	0.92 ± 0.05	0.85 ± 0.05	0.85 ± 0.05	0.57 ± 0.19
FDA Glaucoma	0.77 ± 0.14	0.75 ± 0.14	0.74 ± 0.12	0.47 ± 0.18
Statistical analysis
Friedman’s avg. rank	1.29 (1st)	2.41 (3rd)	2.35 (2nd)	3.94 (4th)
Holm’s adjusted p	—	0.0232	0.0232	6.8 × 10−9
Wilcoxon p	—	0.0023	0.0086	2.9 × 10−4

^aStatistical tests are conducted at the subject level over all the data. Avg., average; p, p-value.

4. DISCUSSION

Our work provides the first step toward automatic quantification of GCL somas from AO-OCT volumes. We developed a weakly supervised deep learning-based method to automatically segment individual somas without manual segmentation masks. Compared to manual marking, which took between 7–8 h/volume, WeakGCSeg was at least two orders of magnitude faster with a speed of less than 3 min/volume.

Our method achieved high detection performance regardless of retinal eccentricity, imaging device, or the presence of pathology, which matched or exceeded that of expert graders. Our method outperformed other state-of-the-art CNNs as well. Also, WeakGCSeg’s segmentation masks agreed with manually labeled masks, and the estimated soma diameters were comparable to previously reported values.

Although our method’s performance on the glaucoma dataset was lower than that on the healthy group, the expert performance on these data was even lower. This reflects the inherent differences between the data from the two groups and the difficulty of identifying cells within glaucoma volumes. Additionally, when trained on the glaucoma dataset and applied to the data from the healthy group, WeakGCSeg retained expert-level performance even if the post-processing parameter T was set by the glaucoma data. However, when trained on healthy individuals, WeakGCSeg could achieve human-level performance on the glaucoma dataset only if labeled glaucoma data were used to optimize T (Table S7). Future work could incorporate semi-supervised or unsupervised learning techniques into our framework to further remove the need of labeling AO-OCT images from diseased eyes.

Our estimated soma diameters differed from previous studies in two aspects. First, the inter-subject SD of mean soma diameters for individuals involved in this study (error bars in Fig. 2B) were smaller than the values reported by Liu et al. [16], which were derived from a subset of our IU dataset. This dissimilarity could be due to differences between the approaches taken by us and this study. We approximated soma diameters using automatic segmentation masks, whereas Liu et al. used the circumferential intensity averaged trace around the soma center. The other in vivo diameter measurement study by Rossi et al. [19] measured soma diameters from AO-SLO images, which are different from AO-OCT images in terms of image quality. The inherent inter- and intra-variability of human graders in marking images due to the subjective nature of the task, as has been demonstrated for OCT and AO-SLO images [23,30,50], could also contribute to the higher SD values of previous studies. In contrast, our automatic method provides objective segmentations of GCL somas. The second difference was the distribution of the measured soma diameters. Previous literature [16,41] has reported a bimodal distribution for the soma size at retinal eccentricities above 6°. Although the distributions of our automatic diameter estimates for the 8.5° and 12.75° volumes did not appear bimodal for all subjects, a second smaller peak at higher diameter values was apparent for some [e.g., S1 and S4 in Fig. S4 and Fig. S6(C)]. The difference between the estimated diameters [Fig. S6(B)] reflects that the automatic masks yielded larger diameters for smaller somas (diameters <15 μm) and smaller diameters for larger cells compared to manual masks. These differences might ultimately render the two underlying peaks in the diameter distributions less distinguishable from each other.

To show the generalizability of our method to an unseen retinal location, we used the AO-OCT volumes recorded at 3.75° and 12.75° locations as the training data. When evaluated on the 8.5° volumes, the trained model achieved a performance similar to the 3.75° and 12.75° dataset. As the two extreme locations involved in training encompassed the range of spatially varying GC size, type, and density across much of the retina (see Text Section 1 of Supplement 1), we anticipate that the trained model would generalize to other untested retinal locations without additional training. In the case of training only on one retinal location, or limited locations close to each other, we anticipate that WeakGCSeg’s performance would decrease when tested on other regions with different GC characteristics. Future work could extend our method to avoid this problem, if needed. We also demonstrated our trained models’ generalizability from one imager (the source) to a different system (the target) through scaling the target data to the source data voxel size. Further studies with larger datasets across different retinal diseases and imaging systems are required to fully characterize the generalizability of WeakGCSeg. Other approaches for domain adaptation, as demonstrated previously for other imaging modalities [51,52], could also be incorporated into our framework to potentially improve the generalizability in scenarios where there is a significant difference in the resolution or quality of the captured images.

Our approach could be used by others for similar applications. For tissues with more complex structures, future work could extend our framework by adding regularization terms into the loss function or using graph-based post-processing approaches. Our work could also be extended by exploiting interactive instance segmentation techniques [53,54] to correct errors in the automatically obtained segmentation masks with active guidance from an expert. Such approaches may increase robustness to inaccuracies in the initial user-provided labels.

Despite the great potential of AO-OCT for early disease diagnosis and treatment outcome assessment, the lack of reliable automated soma quantification methods has impeded clinical translation. We presented the first automated GCL soma quantification method for AO-OCT volumes, which achieved high detection performance and precise soma diameter estimates, thus offering an attractive alternative to the costly and time-consuming manual marking process. We demonstrated the utility of our framework by investigating the relationships between GCL’s automatically measured cellular-level characteristics, its thickness values from AO-OCT and clinical OCT images, and local functional measures from the visual field test. In addition to reporting larger soma diameters in glaucoma subjects compared to healthy individuals, the structural analysis demonstrated a strong linear correlation between local GCL cell density and AO-OCT measured thickness. Thickness values obtained from clinical OCT exhibited a weak correlation to the local cell density. As the population of glaucoma patients in this work was relatively small and the subjects varied in the stage of disease, further studies are needed to investigate the structure–function relationship at different stages of glaucoma. Our work paves the way towards these clinical studies. We envision that our automated method would enable large-scale, multi-site clinical studies to further understand cellular-level pathological changes in retinal diseases.

Data Availability.

AO-OCT images and their corresponding manual annotations used in this paper are available at [55].