Surface tension and super-stoichiometric surface enrichment in two-component biomolecular condensates

Summary

Cells can achieve internal organization by exploiting liquid-liquid phase separation to form biomolecular condensates. Here we focus on the surface properties of condensates composed of two multivalent associative polymers held together by one-to-one “sticker” bonds. Using coarse-grained molecular-dynamics simulations, we study the influence of component stoichiometry on condensate surface properties. We find that unequal stoichiometry results in enrichment of the majority species at the interface and a sharp reduction of surface tension. To relate these two effects, we show that the reduction in surface tension scales linearly with the excess concentration of free binding sites at the interface. Our results imply that each excess free site contributes an approximately fixed additional energy and entropy to the interface, with the latter dominating such that enrichment of free majority sites lowers the surface tension. Our work provides insight into novel physical mechanisms by which cells can regulate condensate surface properties.

Graphical abstract

Highlights

• •Stoichiometry controls the surface tension of two-component biomolecular condensates
• •Unequal stoichiometry leads to enrichment of the majority species at the interface
• •Enrichment of the free majority binding sites increases the interfacial entropy
• •Surface tension is drastically reduced at unequal stoichiometry

Biophysical chemistry; Molecular dynamics; Mathematical biosciences

Introduction

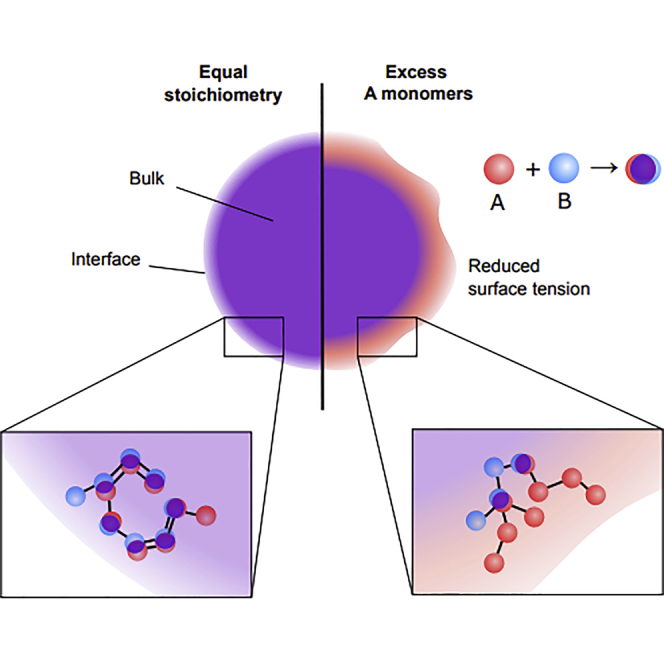
One mechanism by which eukaryotic cells achieve compartmentalization is through the formation of biomolecular condensates. These condensates have been found to be associated with a host of cellular functions, including signaling (Su et al., 2016), metabolism (An et al., 2008), and gene regulation (Sabari et al., 2018). In many cases, the formation of biomolecular condensates is driven by liquid-liquid phase separation of multivalent proteins or nucleic acids (Brangwynne et al., 2009; Li et al., 2012; Nott et al., 2015). An important class is two-component condensates that are formed by one-to-one heterotypic association among binding sites on the two components (Choi et al., 2020). One example of such a two-component condensate found in nature is the algal pyrenoid, a CO₂-fixing organelle which in the model photosynthetic alga Chlamydomonas reinhardtii is formed via condensation of the enzyme Rubisco and the linker protein Essential PYrenoid Component 1 (EPYC 1). The formation of the pyrenoid is driven by multivalent interactions between the specific binding sites of Rubisco and EPYC1 (Freeman Rosenzweig et al., 2017; Wunder et al., 2018; He et al., 2020). It has been found experimentally and theoretically that the stoichiometry of the components has a major influence on the properties of the condensates (Case et al., 2019; Choi et al., 2019; Sanders et al., 2020; Alshareedah et al., 2021; Zhang et al., 2021).

Phase separation is necessarily accompanied by the emergence of surface tension. Surface tension between the dense and dilute phases is a key material property that determines the morphology and the coarsening behavior of condensates (Caragine et al., 2018; Mitrea et al., 2018). Surface tension also plays an important role in the internal organization of biomolecular condensates, as it governs the hierarchical structure observed in multiphasic condensates such as nucleoli, stress granules, and nuclear speckles (Feric et al., 2016; Jain et al., 2016; Fei et al., 2017). Using coarse-grained molecular-dynamics simulations, we investigate how the stoichiometry of two-component condensate systems influences their internal structure and surface tension. We find that an unequal binding-site stoichiometry leads to the enrichment of the majority component in the interface region between the dense and the dilute phases. This enrichment correlates with a substantial decrease in the surface tension of the condensate, such that there is a sharp peak in surface tension at equal stoichiometry. We attribute the origin of this enrichment and the decrease in the surface tension to an increase in the entropy at the interface, which is associated with additional unbound sites of the majority species in systems with unequal component stoichiometry. As component stoichiometry can be regulated in either native or engineered biological settings, these results suggest a possible mechanism by which the physical properties and the internal organization of biomolecular condensates can be controlled.

Results

Component stoichiometry is a key determinant of the formation of biomolecular condensates, and can also have a profound influence on their internal organization. One experimental example is the observation that the majority component is enriched at the surface of the condensate, encapsulating the minority components (Kaur et al., 2021; Alshareedah et al., 2021). These observations led us to ask the question: How does the component stoichiometry influence the surface properties of the condensate? To address this question, we studied two-component multivalent associative polymers at varying stoichiometries using coarse-grained molecular-dynamics simulations. Specifically, we simulated polymers consisting of eight consecutive type A or type B stickers/interacting domains connected by stretchable bonds (Equation 1) (Figure 1A). For computational feasibility, we used a coarse-grained model of biopolymers with an implicit solvent, where the interaction potentials are considered to account for both sticker-sticker and sticker-solvent interactions. Such implicit-solvent models have been utilized in previous studies to investigate the effect of sequence (Dignon et al., 2018; Statt et al., 2020) and valence (Sanchez-Burgos and Espinosa, 2021) in the context of biomolecular condensates. One-to-one interactions are implemented by enforcing stickers of different types to interact through an associative potential (Equation 2), whereas stickers of the same type interact through a repulsive potential to prevent many-to-one binding (Equation 3) (Figure 1B). This coarse-grained model describes specific and saturable interactions between interacting residues or larger domains of proteins. Therefore, it does not reflect the behavior of systems where phase separation is driven by promiscuously interacting domains (e.g., due to hydrophobicity), or long-range and nonstoichiometric interactions (e.g., between domains of net charge). (Also note that our implementation of specific interactions results in two “bound” stickers sharing the same volume. Typically, we find that the sticker concentration in the dense phase is ∼20mM, which for our 3nm diameter stickers corresponds to a sticker volume fraction of <10%. As the sticker volume fraction in the dense phase is low, the fact that bound stickers overlap their volumes does not substantially influence dense phase properties.)

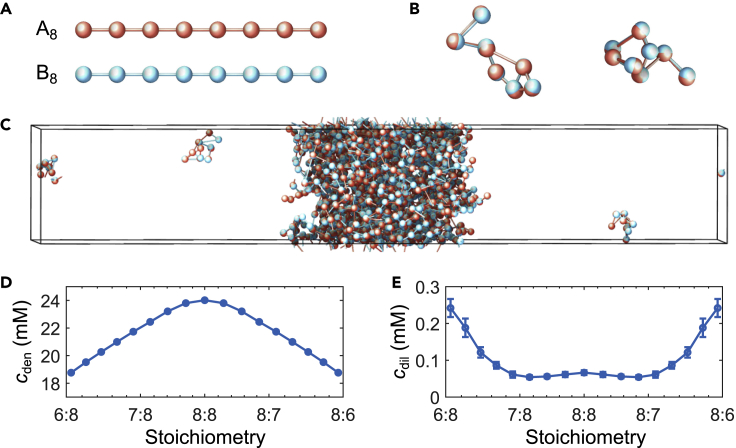
Figure 1.

Schematic of two-component multivalent associative polymers

(A) The system consists of two types of polymers with varying concentrations. Each polymer is composed of eight monomers (“stickers”) of type A or B, denoted as A₈ (red) and B₈ (blue), respectively, and modeled as a linear chain of spherical particles with a diameter of 3nm, connected by stretchable bonds with an equilibrium length of 6nm. Stickers of different types have an attractive interaction, whereas stickers of the same type interact repulsively, ensuring one-to-one binding between the A and B stickers.

(B) Examples of dimers of A and B polymers formed by one-to-one sticker bonds.

(C) Snapshot of coarse-grained molecular-dynamics simulation of 156 A polymers and 156 B polymers in a $300\text{nm}\times 50\text{nm}\times 50\text{nm}$ box with periodic boundary conditions. The system undergoes phase separation into a dense phase (middle region) and a dilute phase (two sides), driven by the one-to-one A–B bonds.

(D and E) The sticker concentrations in the dense phase (D) and the dilute phase (E) from coarse-grained molecular dynamics simulations are shown as a function of component stoichiometry $N_{\text{A}}/N_{\text{B}}$, where $N_{\text{A}/\text{B}}$ is the total number of A/B stickers in the simulation. Error bars represent standard deviations across 10 simulation replicates. All simulations were performed and snapshots were obtained using LAMMPS (Plimpton, 1995).

Since our simulated polymers have the same valence (of 8), the overall sticker stoichiometry is equal to the overall polymer stoichiometry. We simulated hundreds of polymers in a box with periodic boundary conditions. The stoichiometry was adjusted by changing the relative number of A and B polymers while keeping their total number fixed. The system evolved according to Langevin dynamics. Figure 1C shows a snapshot of coexisting dense and dilute phases after equilibration. For details of simulations see STAR Methods. We found that an imbalance in sticker stoichiometry reduces the dense phase density (Figure 1D) and increases the dilute phase density (Figure 1E). (Note that the slight change in concavity in the dilute phase density around the equal stoichiometry point in Figure 1E reflects the onset of the magic-ratio effect (Zhang et al., 2021).

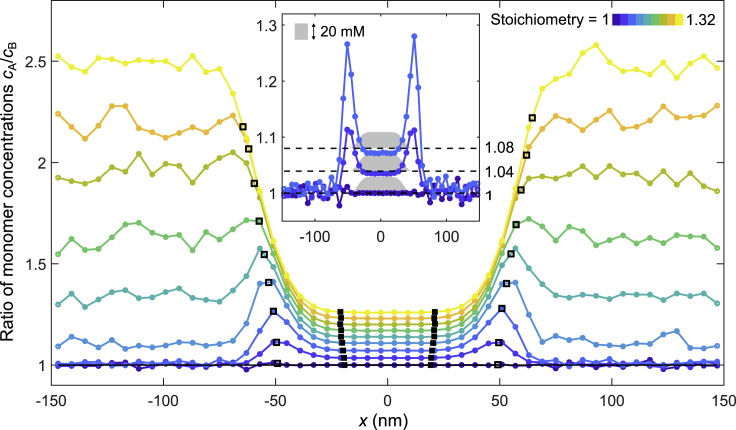
The organization of the interface between the dense and dilute phases is reflected by the ratio of sticker concentrations as a function of position along the axis (x axis) perpendicular to the surface of the condensate (Figure 2). At equal 1:1 stoichiometry, as expected, the ratio of sticker concentrations remains constant at 1.0 across positions (Figure 2, dark blue). In contrast, at unequal sticker stoichiometries, we observed substantial enrichment of the majority sticker at the surface of the dense phase, which can appear as a sharp peak in the ratio of sticker concentrations in the interface region (Figure 2, inset). For sufficiently unbalanced stoichiometry, the sticker ratio in the dilute phase becomes even larger than the ratio in the interface, masking the peak (Figure 2). Strikingly, the ratio of sticker concentration in the interface regions is very sensitive to the global stoichiometry, with a peak enrichment of 11% (28%) observed at only 4% (8%) stoichiometric mismatch in the global sticker concentrations (Figure 2, inset).

Figure 2.

Simulations of multivalent associative polymers reveal enrichment of the majority sticker species in the interface region

Spatial dependence of the ratio of sticker concentrations $c_{\text{A}}/c_{\text{B}}$ is shown for varying A₈:B₈ polymer stoichiometries, ranging from 1 (blue) to 1.32 (yellow). Open and filled black squares indicate the locations of the outer and inner boundaries of the interface, respectively (defined at 2% and 98% of the way from the dilute phase density to the dense phase density, for details see STAR Methods). (Inset, center) In depth view of the ratio of sticker concentration for component stoichiometry of 1 (dark blue), 1.04 (blue), and 1.08 (light blue) is shown with superimposed overall sticker concentration profile (gray shaded region) and the global sticker stoichiometry (dashed black line) to guide the eye. The regions where the overall sticker concentration transitions between the high-density plateau in the middle and low-density plateaus on the two sides are called the “interface regions”. The ratio of sticker concentrations $c_{\text{A}}/c_{\text{B}}$ is peaked in the interface regions

Intuitively, this enrichment effect can be understood through a kinetic argument. Consider a condensate with an unequal sticker stoichiometry, but initially arranged such that the sticker ratio in the interface region is constant and equal to the sticker ratio of the bulk dense phase. Throughout the interface there will be an excess of unbonded majority stickers. When bonds in this region break because of thermal fluctuations, consequently the transiently unbound minority sticker is more likely to collide and re-bond with a free majority sticker located closer to the dense phase (internal to the condensate), because there is a higher concentration of free majority stickers in that direction. Repetition of this process after each bond-breaking event leads to the minority stickers effectively “swimming upstream” toward the dense phase. The resulting depletion of minority stickers in the interface region implies the enrichment of the majority stickers that we observed.

We note that at unequal sticker stoichiometries (Figure 2 inset), the ratio of sticker concentrations within the dense phase is lower than the global sticker stoichiometry, whereas the ratio of sticker concentrations in the dilute phase remains close to 1.0. However, in the thermodynamic limit, where the contribution from the interface is negligible, if the dilute phase sticker ratio remains constant at ∼1.0, i.e., lower than the global sticker ratio, the dense phase sticker ratio must be correspondingly higher than the global sticker ratio. This discrepancy is likely an effect of the finite simulation domain which limits the volume of the bulk phase with respect to the volume of the interface region. We expect that for a sufficiently large dense phase, the sticker ratio in the dense phase will exceed the global ratio, as it must according to the thermodynamic argument.

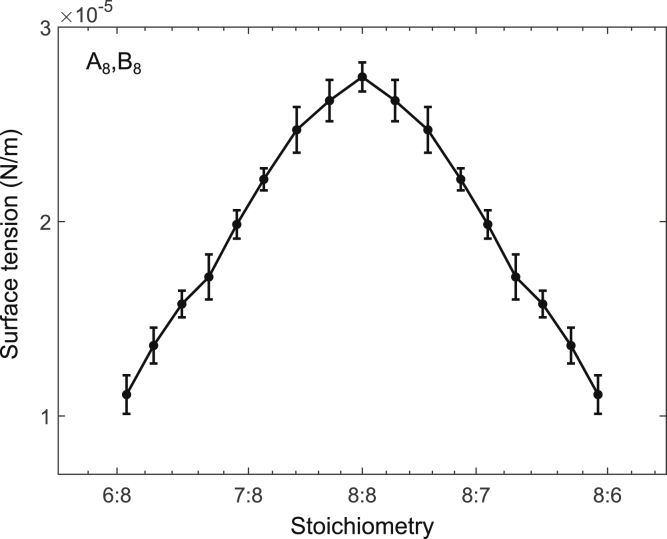
Since unbalanced sticker stoichiometry leads to substantial changes in the interface composition, we were curious whether these changes influenced the surface tension. Therefore, we applied the Kirkwood-Buff formula (Kirkwood and Buff, 1949) (Equation 4) to our simulations in order to calculate the surface tension at varying sticker stoichiometries. As seen in Figure 3, the surface tension has a maximum at equal stoichiometry and decreases monotonically away from the maximum. The monotonic trend continues until the surface tension diminishes to the point where no condensate forms. We found that, like the interface sticker ratio, the surface tension is strongly affected by the sticker stoichiometry, e.g., a 30% excess of one sticker type translates to a 60% decrease in the surface tension (Figure 3).

Figure 3.

Surface tension is peaked at equal A and B sticker stoichiometry

Surface tension between the dense and the dilute phases of polymer systems composed of A₈ and B₈ polymers is shown as a function of sticker stoichiometry. The surface tension was calculated from molecular-dynamics simulations using the Kirkwood-Buff expression (Equation 4). Error bars represent standard deviations across 10 simulation replicates.

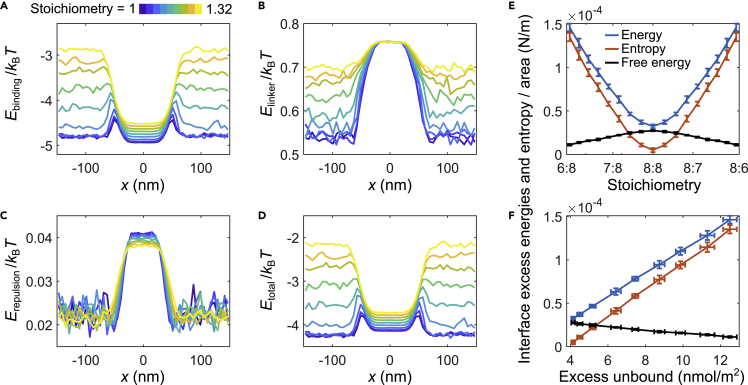
In general, we expect stoichiometric imbalance to move the system closer to the critical point by decreasing the critical temperature (Zhang et al., 2021). Because the surface tension must vanish at the critical point, unequal stoichiometry naturally leads to a decrease in surface tension, as we observed (Figure 3). At a more microscopic level, how can we understand this reduced surface tension at unequal stoichiometry? To answer this question, we calculated the average energetic contributions per sticker, arising from specific bonds (Figure 4A), linker interactions (Figure 4B), and repulsive interactions (Figure 4C) along the x axis. As expected, most of the energetic contributions come from the specific bonds, whereas the linker and repulsive interactions make only a modest contribution to the total energy (Figure 4D). Interestingly, the spatial profiles of the energy per sticker (Figure 4D) are qualitatively similar to the sticker ratio profiles shown in Figure 2, displaying peaks in the interface region for systems with a modest imbalance in sticker stoichiometry. As the surface tension arises from the excess free energy required to maintain an interface between the two bulk phases, knowing both the surface tension and the excess energy per sticker in the interface region compared to the dense phase, we are able to calculate the excess energetic and entropic components of the free energy at the interface with respect to the dense phase (Figures 4E and 4F and STAR Methods). As seen in Figure 4E, the entropic component of the free energy (red) increases faster than the energetic component (blue); this accounts for the overall decrease in the excess free energy at the interface (black) as a function of sticker stoichiometry.

Figure 4.

Energetic and entropic contributions to the free energy

(A–C)Spatial profile of the average energetic contributions per sticker arising from (A) associative specific bonds, (B) stretchable linker bonds, and (C) repulsive interactions between like stickers are shown for varying component stoichiometry, ranging from 1 (blue) to 1.32 (yellow). The energetic contributions were calculated from molecular-dynamics simulations, using (Equation 1), (Equation 2), (Equation 3).

(D) Profile of total energetic contribution per sticker, corresponding to the sum of specific, linker, and repulsive energies as a function of position.

(E) Energetic (blue) and entropic (red) contributions to the total excess free energy (black) of the interface per unit area at different component stoichiometries. Error bars represent standard deviations across 10 simulation replicates.

(F) As in (E), but as functions of the number of excess unbound stickers per area in the interface region. For details see STAR Methods

To connect the decrease in the surface tension for unequal sticker stoichiometry to the enrichment effect seen in Figure 2, notice that in Figure 4F both the energetic and entropic components of the excess free energy at the interface depend linearly on the “excess” unbound sticker concentration. (This “excess” is defined relative to the fraction of unbound stickers in the dense phase, see STAR Methods.) A natural interpretation of this observed linear relationship is that each unbound free sticker in the interface region contributes a fixed amount of both additional energy and additional entropy. The addition of each unbound sticker in the interface region results in a larger entropic gain (Figure 4F, red) than energy penalty, leading to an overall net decrease in the interface excess free energy. Therefore, the reduction in surface tension for unequal sticker stoichiometry and the enrichment effect can be viewed as two sides of the same coin: When viewed from one side, the imbalance in the sticker ratio at the interface increases the concentration of unbound stickers which in turn decreases the surface tension; however, when viewed from the other side, the system is able to reduce the free energy of the interface, i.e., the surface tension, by creating an imbalance in the interface sticker ratio.

Discussion

Component stoichiometry can strongly influence the surface properties of biological condensates. To develop a mechanistic understanding of these effects for two-component condensates held together by heterotypic stickers, we employed coarse-grained molecular-dynamics simulations. At unequal component stoichiometry, we observed enrichment of unbound stickers at the interface, most of which were of the majority type, accompanied by a decrease in the surface tension. We found that the decrease in the surface tension was due to the entropy gain associated with the excess unbound stickers in the interface region.

Our model employed some simplifying assumptions – how might these assumptions influence the simulations? In this study, we considered linkers with zero effective solvation volume. However, it has been shown that space-filling linkers can change phase properties, with positive (negative) solvation volume of the linkers suppressing (promoting) phase separation (Harmon et al., 2017). The role of space-filling linkers on surface properties will be an interesting area for future exploration. In this study, we considered strong specific interactions, such that nearly all possible sticker bonds are formed. In the future, it will be interesting to consider the regime of weak specific interactions, or systems with a combination of strong/weak and specific/nonspecific interactions, all of which are known to be biologically relevant (Li et al., 2012; Falkenberg et al., 2013; Wippich et al., 2013; He et al., 2020; Schuler et al., 2020). In this study, we varied sticker stoichiometry by varying the polymer ratio while keeping the valence of the two polymers equal. The sticker stoichiometry can also be adjusted by changing the relative valence of the two polymers while keeping the number of the polymers of each type the same. In this unequal valence case, we expect to see the same enrichment of the majority species at the interface as the “swimming upstream” kinetic argument should apply independent of the relative valence of the polymers.

Although the polymers in our simulations were assumed to be flexible, some biological systems have rigid components, such as Rubisco in the Rubisco-EPYC1 system (Mackinder et al., 2016). Rigidity implies little or no loss in conformational entropy upon binding; therefore, in two-component sticker models, component rigidity has been found to favor the dilute phase which otherwise suffers from lower conformational entropy per sticker (Xu et al., 2020). How might rigidity influence surface enrichment? In the case where only one component is rigid, as in the Rubisco-EPYC1 system, our current understanding of entropy-driven enrichment may still apply. However, we expect that the enrichment effect will be weakened if the rigid component is in excess, because of the lack of conformational entropy gain from each unbound rigid sticker. That said, how a rigid component influences interface properties requires further exploration, and will be the subject of future work.

It is informative to compare our system to related sticker models. For example, in coarse-grained scaffold-client systems where the components are modeled as monomeric spherical particles with multiple specific binding sites on their surfaces, a reduction in the surface tension was observed in the presence of excess low-valence client species (Sanchez-Burgos and Joseph, 2021). In contrast to polymeric systems, the decrease in the surface tension in this case is associated with a reduction of the specific-bond density in the interface regime (Espinosa et al., 2020; Sanchez-Burgos and Joseph, 2021). Sticker models have also been used to study the coalescence of droplets. The formation of metastable, long-living condensates has been associated with the saturation of available specific bonds at the surface (Ranganathan and Shakhnovich, 2020), which could also occur as a consequence of the surface enrichment of the excess component discussed in our work.

Although there is good experimental evidence that the surface properties of condensates depend on stoichiometry (Alshareedah et al., 2021; Kaur et al., 2021), systematic experimental investigation on these effects, isolated from the influence of sequence or mismatch in valence, is still lacking. The type of two-component polymer system we considered here is experimentally realizable using engineered polymers composed of tandem repeats of heterotypic interacting domains, such as (SUMO)_n-(SIM)_n or (SH3)_n-(PRM)_n. Furthermore, the surface tension can be characterized by monitoring the fusion/deformation events (Brangwynne et al., 2009; Zhou, 2020; Alshareedah et al., 2021) or using micropipette aspiration assays (Wang et al., 2021), and the enrichment effects can be quantified through the use of fluorescently labeled polymers.

From a biological perspective, the observed surface effects could drastically influence the coarsening behavior of condensates – with the enriched majority species playing a surfactant-like (or self-Pickering) role – suggesting a mode of droplet size regulation. The surface enrichment effect could also facilitate the formation of conventional Pickering emulsions (Folkmann et al., 2021), which can also reduce the surface tension. Furthermore, the surface enrichment of the majority species could serve as a general mechanism to regulate the surface absorption of client molecules. For example, a client that preferentially and noncompetitively binds to the majority species will be enriched at the surface of the condensate, with the extent of enrichment depending on the imbalance in polymer stoichiometry. In the case where the client competitively binds to the majority sticker with respect to the sticker-sticker binding, the ternary system could exhibit various multiphasic morphologies, as has been observed in a recent study (Kaur et al., 2021). For sticker interactions resembling polyelectrolyte mixtures (heterotypic associative and self-repulsive interactions), the addition of physical constraints such as differing polymer lengths or sequence dependence, along with the surface enrichment effect, could facilitate the formation of more complex morphologies such as micelles and vesicles (Statt et al., 2020), possibly through secondary phase transitions under extreme imbalance in stoichiometry (Alshareedah et al., 2020). Finally, in a biological setting the drastic reduction in surface tension for unequal stoichiometry could serve as a control mechanism for condensate formation and dissolution. Recently, the surface properties of condensates have been found to be relevant in autophagy (Fujioka and Noda, 2021) and in the nucleation of microtubules (Setru et al., 2021). The growing appreciation of the significance of condensate surface properties makes understanding the physical mechanisms underpinning their regulation an important goal.

Limitations of the study

In this study, we utilized a coarse-grained model to simulate strong, short-ranged, specific, and saturable interactions between the interacting domains of biopolymers. Therefore, our model is not applicable to systems driven by weak, nonstoichiometric, and/or long-ranged interactions.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
Matlab codes for generating LAMMPS input files	This paper	github.com/yaojunz/matlab-lammps-surfacetension
Inkscape	Inkscape's Contributors	inkscape.org/
Matlab 2020b	MathWorks	www.mathworks.com/
LAMMPS 2020	Sandia National Laboratories	www.lammps.org/

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Ned S. Wingreen (wingreen@princeton.edu).

Materials availability

This study did not generate new unique reagents.

Method details

Coarse-grained molecular-dynamics simulations are performed using LAMMPS (Plimpton, 1995). Two-component multivalent associative polymers are modeled as a linear chain of beads, where each bead represents one associative domain/sticker of the polymer (Figure 1A). The beads are connected by stretchable bonds, given by

$$U_{\mathrm{b}}\left(r\right)=-\frac{1}{2}K{R}_0^2\ln \left[1-{\left(\frac{r-\sigma }{R_0}\right)}^2\right],$$ (Equation 1)

where r is the center-to-center distance between beads, and $K=0.15k_{\text{B}}T/{\text{nm}}^2$, $R_0=14\text{nm}$, $\sigma =3\text{nm}$, $k_{\text{B}}$ is the Boltzmann constant, and $T=300\text{K}$ is room temperature. Stickers of different types interact through an attractive potential given by

$$U_{\mathrm{a}}\left(r\right)=-\frac{1}{2}{U}_0\left[1+\text{cos}\left(\frac{\pi r}{r_0}\right)\right],r<r_0,$$ (Equation 2)

where $U_0=12k_{\text{B}}T$ and $r_0=1.5\text{nm}$. In order to enforce one-to-one binding, stickers of the same type interact through a purely-repulsive Lennard-Jones potential given by

$$U_{\mathrm{r}}\left(r\right)=4ϵ\left[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6+\frac{1}{4}\right],r<2^{1/6}\sigma ,$$ (Equation 3)

where $ϵ=1k_{\text{B}}T$. All of the parameters are fixed at these values across the simulations.

In order to determine the surface properties at different component stoichiometries, 312 total polymers of length 8 (A₈:B₈ system) are simulated in a 300nm $\times$ 50nm $\times$ 50nm box with periodic boundary conditions. The stoichiometry (1, 1.04, …, 1.32) is adjusted by changing the relative polymer concentrations of A₈ and B₈ polymers while keeping the total number of polymers constant. To promote phase equilibrium and ensure that only a single dense condensate is formed, the polymers are initially confined to a slab in the middle of the box $-60\text{nm}\le x\le 60\text{nm}$ (Dignon et al., 2018). The attractive interaction between A and B stickers is gradually switched on from $U_0=0$ to $U_0=12k_{\text{B}}T$ over 10⁷ time steps. This annealing within the confined walls leads to the formation of a dense phase close to its equilibrated concentration. The dense condensate is equilibrated for another 10⁷ steps and then the confinement is removed. The system is equilibrated for 10⁸ more steps to allow the formation of a dilute phase and relaxation of the dense phase (Figure 1C). Through the entire simulation, the system is evolved according to Langevin dynamics, implemented using LAMMPS commands fix nve and fix langevin. The Langevin thermostat is applied at with a damping parameter $\tau =20\text{ns}$ and mass of sticker $m=565.5\text{ag}$. The simulation time step is $dt=0.2\text{ns}$. The above simulation procedure follows that of Zhang et al., 2021. The positions of all stickers are recorded every 10⁶ steps for 800 recordings. For each recording, the simulation box is recentered at the center of mass of the dense phase. These recordings are then used to calculate quantities in Figures 1, 2, and 4. The mean pressures in the simulation box along x, y, and z directions are calculated using LAMMPS command fix ave/time over the last 4 $\times$ 10⁸ steps. The mean pressures are used to calculate surface tension in Figure 3. For each choice of stoichiometry, we perform 10 simulation replicates with different random seeds. Error bars in all figures represent standard deviations across the 10 replicates.

The concentration profiles for each type of sticker, $c_{\text{A}}\left(x\right)$ and $c_{\text{B}}\left(x\right)$, are calculated by averaging the sticker concentration histogram in the region $-150\text{nm}\le x\le 150\text{nm}$ over all recordings, where $x$ represents the coordinate along the axis perpendicular to the surface of the dense phase (Figure 1C). The ratio of sticker concentrations $c_{\text{A}}/c_{\text{B}}$ is reported in Figure 2. Surface tension, $\gamma$, for each system (Figure 3) is calculated using the Kirkwood-Buff formula (Kirkwood and Buff, 1949; Ismail et al., 2006),

(Equation 4)

where $L_x$ is the length of the box along the $x$ axis, and $p_j$ is the average pressure along the $j$ th axis (output from LAMMPS).

In order to define the interface region, the profile of total concentration across the interface is fit to the Cahn-Hilliard profile (Cahn and Hilliard, 1958) given by

$$c_{\text{CH}}\left(x\right)=\frac{1}{2}\left(c_{\text{den}}+c_{\text{dil}}\right)+\frac{1}{2}(c_{\text{den}}-c_{\text{dil}})\tanh \left[\frac{2\left(x-x_0\right)}{\xi }\right],$$ (Equation 5)

where $\xi$ is the interface width. The dense and dilute phase densities, $c_{\text{den}}$ and $c_{\text{dil}}$, for each system are reported in Figures 1D and 1E. We define the interface region as ${\text{Ω}}_{\text{int}}\equiv \left[x_0-\xi ,x_0+\xi \right]$. We first calculate the profile of average energies per sticker, arising from specific bonds (Figure 4A), linker interactions (Figure 4B), repulsive interactions (Figure 4C), and their sum (Figure 4D) along the x-axis using (Equation 1), (Equation 2), (Equation 3). As each interaction involves a pair of stickers, we assign half of the interaction energy to each sticker. The excess interface energies (Figure 4E) are determined by calculating the difference in total energies for stickers in the interface region versus if they were in the dense phase. We note that by definition, the excess free energy at the interface per unit area is the surface tension. We therefore report excess energies and entropies also in the unit of per area. The entropic contribution to the surface tension is calculated as the difference between the surface tension and the excess energy per unit area. The excess unbound stickers per unit area in Figure 4F, $n_{\text{ex}}$, is calculated relative to the dense phase, using the relation

$$n_{\text{ex}}=n_{\text{int}}^{\text{ub}}-f_{\text{den}}^{\text{ub}}{n}_{\text{int}},$$ (Equation 6)

where $n_{\text{int}}^{\text{ub}}$ is the total unbound and $n_{\text{int}}$ the total stickers in the interface region per unit area, and $f_{\text{den}}^{\text{ub}}$ is the fraction of unbound stickers in the dense phase.

Quantification and statistical analysis

For each simulated system, we perform $N=10$ replicates with different random seeds. Error bars in all figures represent standard deviations across the 10 replicates. As the standard error of the mean is the standard error divided by $\sqrt{N}$, we conclude that $N=10$ is large enough to ensure the accuracy of the simulation results.

Published: February 18, 2022

Data and code availability

• •All data reported in this paper can be regenerated using deposited codes and will be shared by the lead contact upon reasonable request.
• •MatLab codes for generating LAMMPS input files have been deposited on GitHub: https://github.com/yaojunz/matlab-lammps-surfacetension and are publicly available.
• •Any additional information/codes required to reanalyze the data reported in this paper are available from the lead contact upon reasonable request.