Abstract
While large-scale genome-wide association studies (GWAS) have identified hundreds of loci associated with brain-related traits, identifying the variants, genes and molecular mechanisms underlying these traits remains challenging. Integrating GWAS with expression quantitative trait loci (eQTLs) and identifying shared genetic architecture has been widely adopted to nominate genes and candidate causal variants. However, this approach is limited by sample size, statistical power, and linkage disequilibrium. We developed the multivariate multiple QTL (mmQTL) approach and performed a large-scale multi-ancestry eQTL meta-analysis to increase power and fine-mapping resolution. Analyzing 3,983 RNA-seq samples from 2,119 donors, including 474 non-European individuals, yields an effective sample size of 3,154. Joint statistical fine-mapping of eQTL and GWAS identified 329 variant-trait pairs for 24 brain-related traits driven by 204 unique candidate causal variants for 189 unique genes. This integrative analysis identifies candidate causal variants and elucidates potential regulatory mechanisms for genes underlying schizophrenia, bipolar disorder and Alzheimer’s disease.
Introduction
Genome-wide association studies (GWAS) have associated hundreds of loci with neuropsychiatric and neurodegenerative traits1–5. Yet elucidating the molecular mechanisms underlying these traits remains challenging since most risk variants are non-coding and highly correlated due to linkage disequilibrium3,6. Integration of risk loci with expression quantitative trait loci (eQTL) has been widely adopted to identify genes and candidate causal variants7–9. Recent work by the Genotype-Tissue Expression (GTEx) consortium across 838 individuals and 49 tissues, detected eQTLs for 95% of protein-coding and >60% of long non-coding RNA genes8. While the power to detect primary (i.e. the most significant association) eQTLs is very high, advances in identifying tissue- and cell-type-specific effects, conditionally independent effects, and candidate causal variants in trait-relevant tissues and cell types promises to further inform the molecular etiology of disease8–12.
Large-scale efforts have been undertaken to catalogue human brain eQTLs8,13–16. All these efforts focus on homogenate brain tissue, which is composed of multiple cell types17–20, and, therefore, cell type-specific eQTLs are not fully captured21–23. This is an important limitation given that disease variants act through cell-type-specific biological effects21,24,25. Initial efforts have performed cell type-specific eQTL analysis in the human brain by experimentally purifying specific cell types26–28, but the sample size of such studies are necessarily limited by the increased experimental costs, and data quality can be affected by the additional experimental steps. An alternative strategy to capture cell type-specific effects is to statistically define conditional- or context-dependent eQTL10,11. While existing studies have sufficient power to detect primary eQTLs, identifying conditionally independent eQTLs that capture more subtle cell type- specific effects requires large sample sizes29,30.
Following eQTL detection, statistical fine-mapping can identify candidate causal variants likely to drive variation in expression6,9,31,32. Going one step further, joint statistical fine-mapping integrating GWAS and gene expression traits can define the candidate causal variants that increase disease risk through alterations of gene expression9. Interpreting and validating such variants can pinpoint genes such as FURIN33, BIN134 and C435 along with molecular mechanisms that can be further studied in experimental systems. Yet the resolution of statistical fine-mapping for eQTL and GWAS is incomplete due to limited sample sizes and lack of trans-ancestry analysis6. Sample size of more than 2,000 donors is needed to detect eQTLs and perform GWAS colocalization for identification of causal variants explaining 1% of heritability9. The large human brain eQTL mega-analysis by PsychENCODE included 1,387 unique donors from multiple cohorts15. Moreover, most eQTL analyses have been limited to European populations, despite the fact that much shorter linkage disequilibrium in individuals of African or African-American ancestry can substantially increase the resolution of statistical fine-mapping6,36–38.
Given the limited availability of human brain samples, it is critical to maximize power and fine-mapping resolution by combining existing datasets. Yet differences in study designs have, thus far, hindered such efforts. Multi-ancestry studies have long been challenging in genetics, but linear mixed models can control the false positive rate in the presence of complex population structure39–41. Moreover, expression measurements from multiple brain regions in GTEx are not statistically independent, so combining these data entails explicit modelling of these correlated measurements from the same set of individuals42.
In order to realize the potential of multi-ancestry eQTL fine-mapping and integration with brain-related GWAS results, we developed the multivariate multiple QTL (mmQTL) pipeline and applied it to a combined analysis of brain tissues from PsychENCODE, Religious Orders Study and Memory and Aging Project (ROSMAP) and GTEx. Our pipeline performs eQTL detection with a linear mixed model, identifies conditionally independent eQTL and combines results across datasets with a random effects meta-analysis that models the correlation between multiple brain regions from a shared set of individuals. Joint fine-mapping then identifies candidate causal variants shared between gene expression and GWAS traits. This integrative analysis identifies candidate causal variants and elucidates potential regulatory mechanisms for genes underlying schizophrenia (SZ), bipolar disorder (BD) and Alzheimer’s disease (AD).
Results
Analysis overview
We performed a multi-ancestry eQTL meta-analysis on RNA-seq gene expression data from non-overlapping samples from the dorsolateral prefrontal cortex (DLPFC) from PsychENCODE15 and ROSMAP43, and 13 brain regions from GTEx44 (Figure 1A). We accounted for diverse ancestry (Figure 1B) by applying a linear mixed model to the full data within each resource, and then combined summary statistics from these 15 eQTL analyses using a random effects meta-analysis to account for effect size heterogeneity and donor overlap in between brain regions in GTEx (Figure 1C). This statistical framework is implemented in our mmQTL software (see Methods). Statistical fine-mapping of the eQTL meta-analysis was integrated with GWAS fine-mapping from CAUSALdb45 to identify candidate causal variants shared between gene expression and neuropsychiatric traits.
Figure 1: Workflow for multi-ancestry eQTL meta-analysis.
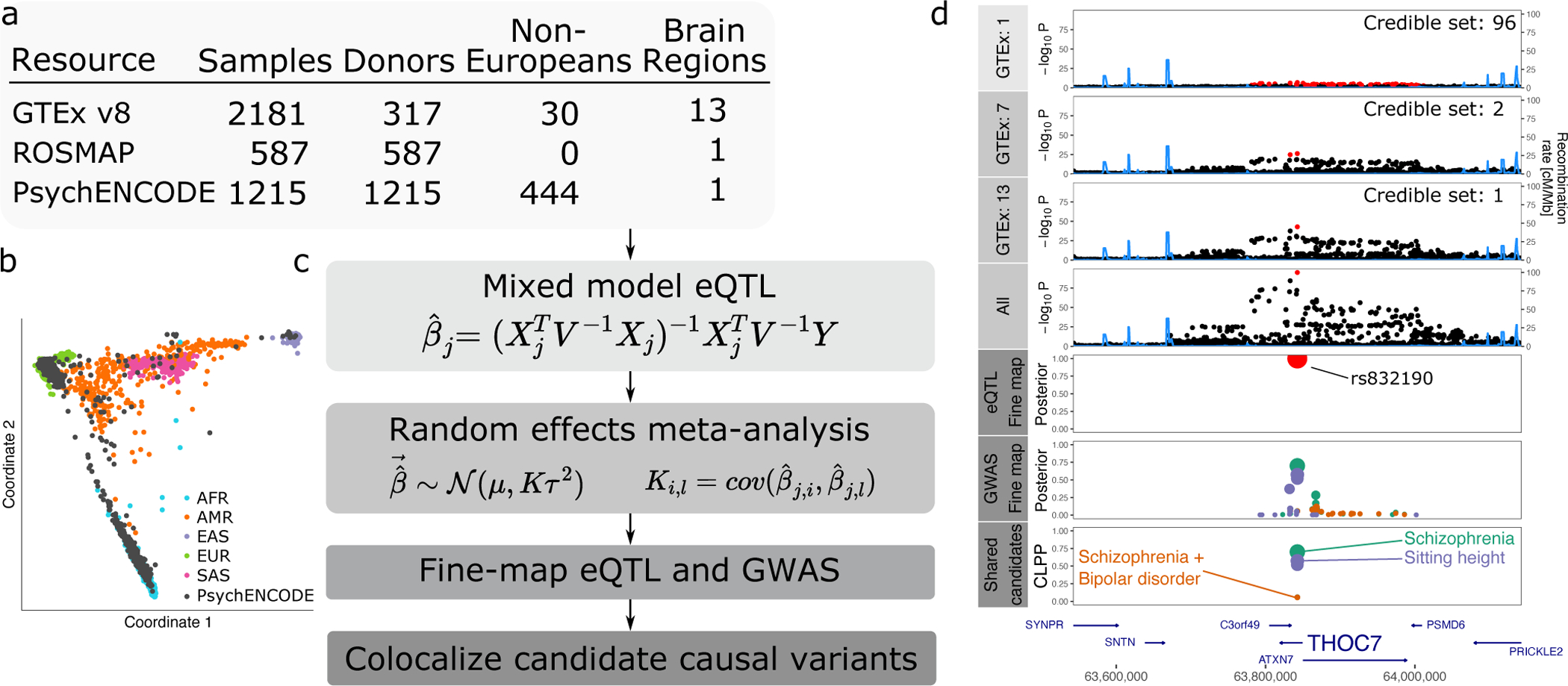
A) RNA-seq datasets with details about ancestry and repeated measures. B) Multidimensional scaling illustrating diverse ancestry of donors from PsychENCODE resource. C) mmQTL workflow is composed of eQTL analysis within each brain region for each resource using a linear mixed model to account for population stratification. Each analysis is then combined using a random effects meta-analysis that accounts for repeated measures from GTEx sample and effect size heterogeneity across brain regions and resources. Statistical fine-mapping is performed on GWAS and combined eQTL results separately. Finally, fine-mapping posterior probabilities from the eQTL analysis and each GWAS are combined to produce colocalization posterior probabilities (CLPP). D) Analysis of data for THOC7 from 1, 7 and 13 GTEx brain tissues, and addition of PsychENCODE and ROSMAP, reduces the size of the 95% credible sets indicated by red points. Statistical fine-mapping for this gene and integration with GWAS nominates a single candidate causal variant, rs832190, affecting SZ, a combined risk for SZ and BD, and sitting height in this region.
For example, results for THOC7 illustrate that increasing the number of GTEx tissue from 1 to 7 to 13 enhances power and decreases the size of the 95% credible sets, while integration with PsychENCODE and ROSMAP nominates a single candidate causal variant (Figure 1D). Integrating GWAS and eQTL results produces colocalization posterior probabilities (CLPP) > 0.05 for SZ, BD and sitting height, and identifies rs832190 and THOC7 as the candidate causal variant and gene, respectively, for this locus.
Biologically motivated simulations
Simulations motivated by the scenarios considered here (i.e. diverse ancestry and repeated measures design of the human brain datasets) were used to evaluate mmQTL performance in terms of: 1) controlling the false positive rate, 2) leveraging eQTL effects shared across multiple tissues and 3) reducing the size of the credible set from statistical fine-mapping (Figure 2). For the eQTL analysis we considered a linear regression model including 5 genotype PC’s and a linear mixed model that counts for the genetic similarity between all pairs of samples39–41. The summary statistics for each SNP-gene pair were aggregated across tissues using a fixed- or random-effects meta-analysis, or simply the minimum p-value with a Sidak correction to account for the number of tissues. The first two explicitly account for the repeated measures design by modeling the correlation between summary statistics under the null, while the Sidak-corrected minimum p-values assume independence.
Figure 2: Biologically motivated simulations demonstrate performance of mmQTL workflow: high correlation scenario.
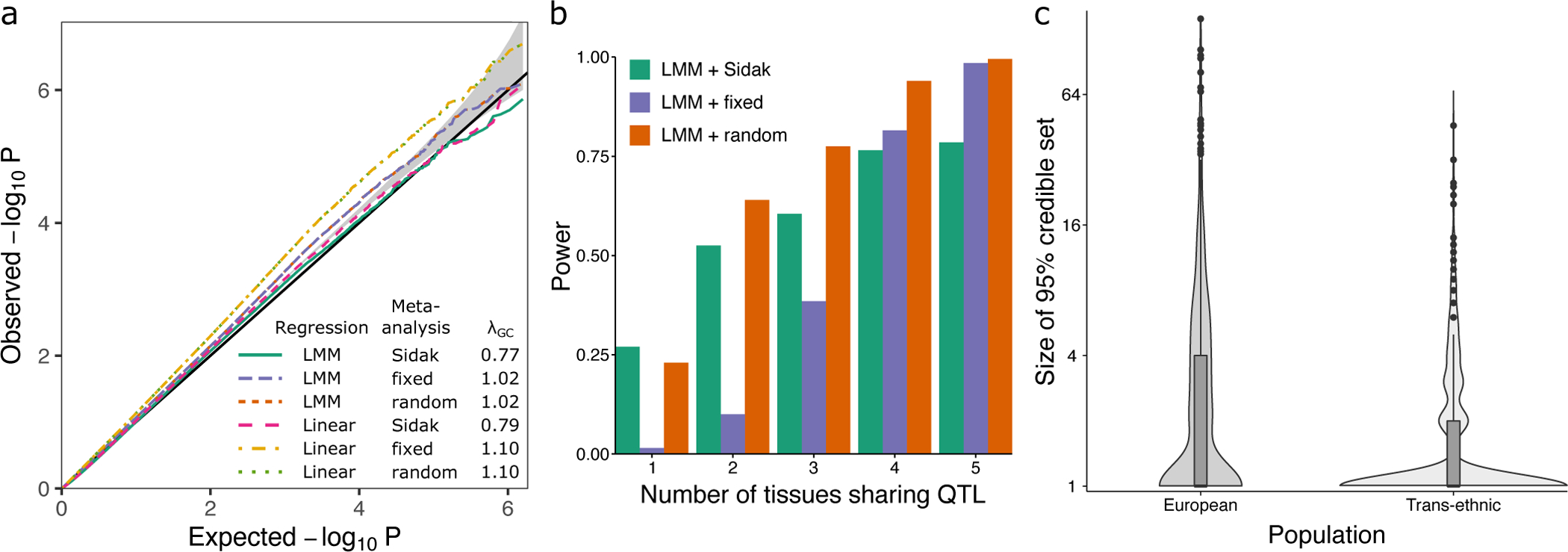
A) QQ plot of results from null simulation shows that the linear mixed model (LMM) with fixed or random effect meta-analysis accurately controls the false positive rate, while linear regression with 5 genotype principal components did not. The Sidak method was very conservative in both cases. λGC indicates the genomic control inflation factor. Gray band indicates 95% confidence interval under the null. B) Power from LMM followed by 3 types of meta-analysis versus the number of tissues sharing an eQTL. C) Size of the 95% credible sets from statistical fine-mapping for a dataset of European samples versus a multi-ancestry dataset of the same size. Box plot indicates median, interquartile range (IQR) and 1.5*IQR.
We simulated genotypes for 500 individuals in each of three distinct populations: European, African, and Asian. A single causal eQTL explaining 1–2% of expression variation in up to 5 tissues for these 1,500 individuals was simulated for 800 randomly chosen genes where the number of tissues with a shared effect varied from 1 to 5. Correlation between the same gene expression trait measured in two tissues was simulated to be low (r=0.12) or high (r=0.45) (see Methods).
In a null simulation with all genetic effects set to zero in both the low and high correlation scenarios, the linear mixed model accurately controlled the false positive rate when summary statistics from multiple tissues were aggregated using the Sidak method as well as fixed or random effects meta-analysis (Figure 2A, Extended Data Figure 1). As expected, the linear model did not adequately account for the complex population structure and showed an inflated false positive rate. Therefore, it was not included in subsequent simulations.
Power analyses were performed on the same set of samples of diverse ancestry where the number of tissues with a shared eQTL effect varied between 1 and 5 (Figure 2B). Using a p-value cutoff of 10−6, the random effects meta-analysis following a linear mixed model eQTL analysis had the highest power under most levels of eQTL sharing across tissues because it models heterogeneity in effect sizes across tissues. The fixed-effect meta-analysis was less powerful because it assumes a shared effect size across tissues. The Sidak corrected minimum p-value only performed best when the eQTL was tissue-specific (i.e. no cross-tissue sharing) since it assumes statistical independence of the results from each tissue.
The mmQTL workflow with linear mixed model followed by a random-effects meta-analysis demonstrated accurate control of the false positive rate while retaining high power under biologically motivated simulations. With the goal of identifying candidate causal variants shared with brain-related traits, we evaluated the benefit of using a dataset of diverse ancestry. A dataset of 1,500 European individuals was simulated in addition to the multi-ancestry cohort above. One causal variant with effect size 1% ± 0.09% was used to simulate gene expression traits. Statistical fine-mapping of eQTL results from the multi-ancestry cohort produced 95% credible sets containing a mean of 2.0 SNP’s compared to a mean of 4.8 for the European only cohort (Figure 2C). In the multi-ancestry cohort, 73.0% of genes have a single candidate causal variant compared to 51.6% in the European cohort. Moreover, random-effects meta-analysis reduces the credible set by 10.0% compared to fixed effects meta-analysis.
Evaluating mmQTL workflow on real data
Here we evaluate the empirical performance of our mmQTL workflow on real data by analyzing an increasing number of brain regions (k=1,4,7,13) from GTEx (Figure 3). As expected, mmQTL is able to borrow information across multiple brain regions using a random-effects meta-analysis so that increasing k substantially increases the empirical effective sample size (Neff) (Figure 3A). With k=13, there are 2,181 RNA-seq samples from 317 individuals producing empirical Neff = 1,070. Moreover, increasing k decreases the median size of the 95% credible sets from statistical fine-mapping (Figure 3B).
Figure 3: Evaluation of mmQTL workflow on real data.
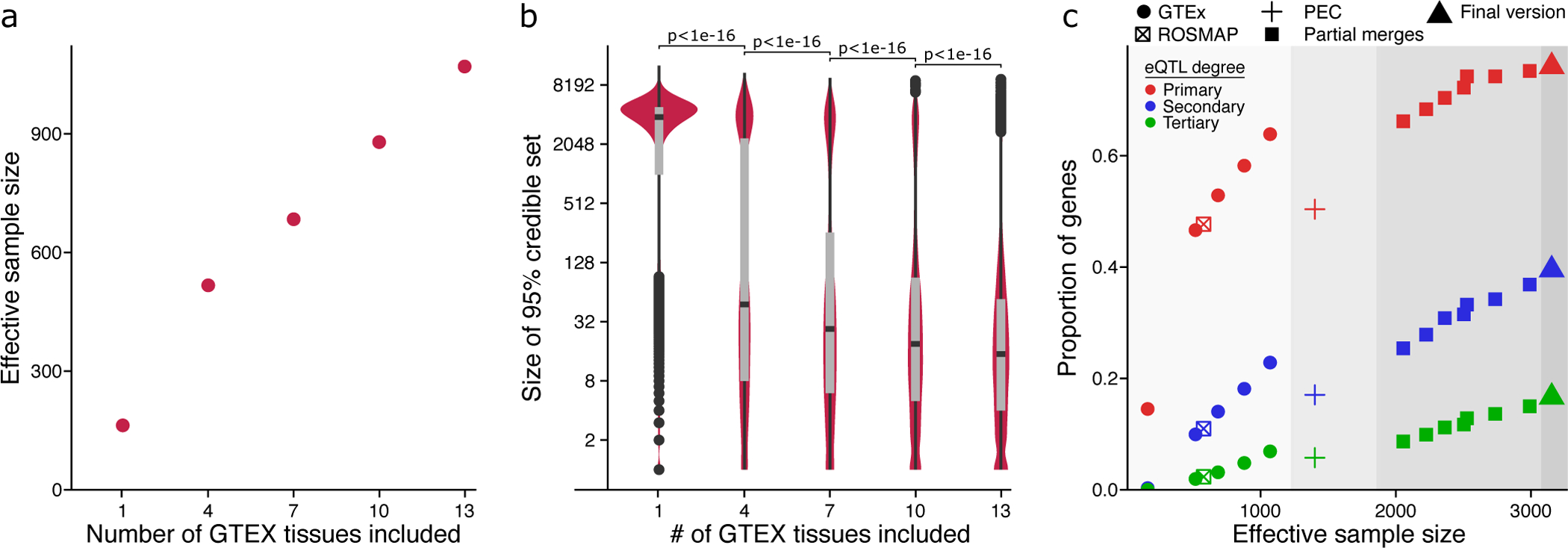
A) Increasing the number of brain regions from GTEx increases the effective sample size. B) Increasing the number of brain regions from GTEx decreases the median 95% credible set size. P-values are shown from a one-sided Kolmogorov–Smirnov test between adjacent categories. Box plot indicates median, interquartile range (IQR) and 1.5*IQR. C) Including additional datasets increases the proportion of genes with a detectable primary or conditional eQTL. Colors indicate degree of eQTL. Panel is divided into regions showing 1) GTEx and ROSMAP results; 2) PsychENCODE (PEC) data analyzed here, and published PEC summary statistics15; 3) adding an increasing number of GTEx brain tissues to the PEC+ROSMAP results; 4) final version merging PEC+ROSMAP+GTEx.
The value of adding each successive study to the meta-analysis was evaluated for primary eQTLs as well as secondary and tertiary conditional eQTLs using a conservative p-value cutoff of 10−6 (Figure 3C, see Methods). The PsychENCODE study included a large cohort and yielded 50.4% of genes having genome-wide significant primary eQTLs. Adding data from GTEx and ROSMAP produced a combined eQTL analysis comprising 3,983 RNA-seq samples from 2,119 donors to give Neff = 3,154. Powered by this substantial increase in Neff, eQTLs were detected for 76% of genes analyzed in the final meta-analysis.
Properties of brain eQTL meta-analysis
Our brain eQTL meta-analysis identifies 10,769 genes with a genome-wide significant eQTL, including 5,336 with at least one conditional eQTL using a conservative p-value threshold of 10−6 (Figure 4A). These eQTL results are highly reproducible with estimated replicated rate π1=73.6% when evaluated in an independent dataset of bulk brain tissue46 using Storey’s π1 statistic47. The increased power from our meta-analysis enables detection of cell-type-specific eQTL not detectable in smaller studies of bulk brain tissue. eQTLs detected in the granule cell layer of the dentate gyrus enriched for excitatory neurons27, are replicated in our analysis at π1=77.8% compared to π1=65.2% in the PsychENCODE analysis (one-sided Mann-Whitney U test p < 1×10−16), and eQTLs detected in purified microglia (Kosoy, et al, in preparation) are replicated in our analysis at π1=68.4% compared to π1=55.0%, from the PsychENCODE analysis (one-sided Mann-Whitney U test p < 1×10−16) (Figure 4B). Moreover, the concordance in the sign of the estimated effect sizes between our meta-analysis and the cell-type specific analyses increased with stricter p-value cutoffs (Extended Data Figure 2). Overlaying variants in 95% credible sets with ATAC-seq regions identified by fluorescence activated nuclei sorting for 4 cell populations (GABAergic neurons, glutamatergic neurons, oligodendrocytes, and a mixture of microglia and astrocytes)48 identifies significant enrichment within open chromatin regions for each cell population (Figure 4C).
Figure 4: Properties of brain eQTL meta-analysis.
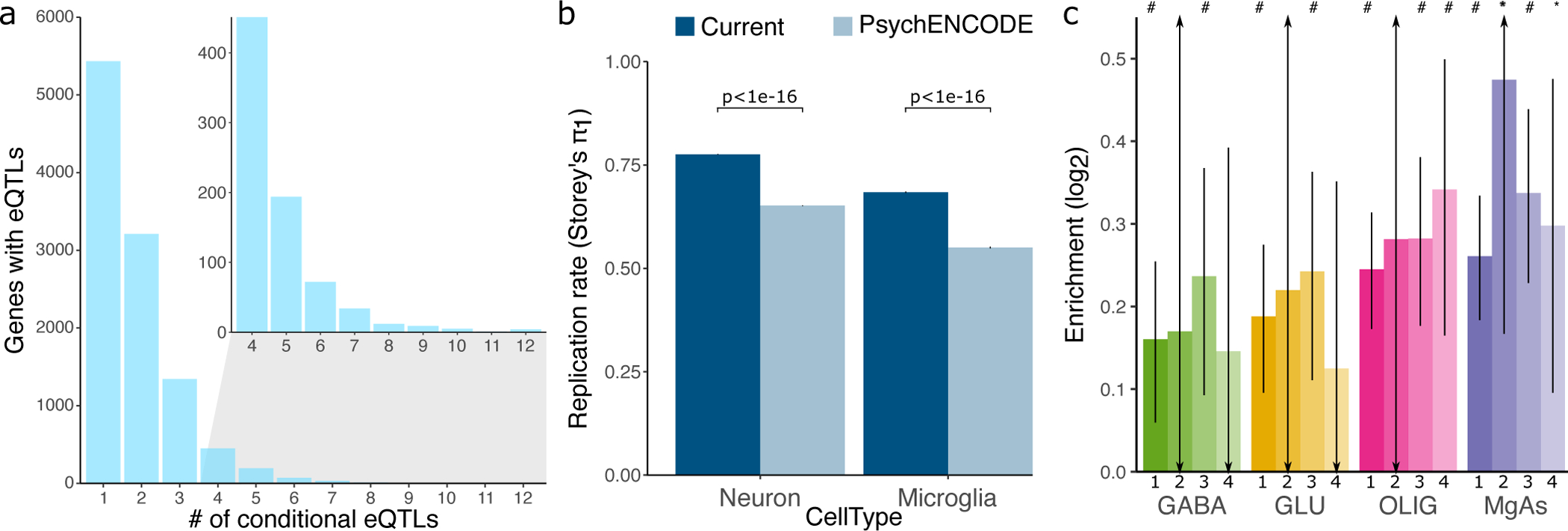
A) Number of genes having a significant primary or conditional eQTL for degree up to 12. Inset shows number of genes for eQTL degree 4 to 12. B) Replication rate measured by Storey’s π1 in the current study and PsychENCODE for eQTLs discovered in the granule cell layer of the dentate gyrus enriched for excitatory neurons27, and purified microglia (Kosoy, in preparation). Error bar indicates standard error of the mean from 100 bootstrap samplings. P-value indicates one-sided Mann-Whitney U test. C) Bar plot indicates log2 enrichment of variants in the 95% causal sets for each gene in open chromatin regions assayed in each of 4 cell populations. Results are shown for eQTL degree 1 to 4. Error bars indicate standard deviation, ‘#’ indicates Bonferroni adjusted p-value < 0.05 and ‘*’ indicates nominal p-value < 0.05 for the Fisher exact test.
The test statistic for random effect meta-analysis used here is composed of the sum of statistics testing the mean (Smean) and variance (Svariance) of the estimated effect sizes across datasets49. So statistical power to detect eQTLs depends on both the effect size as well as the effect size heterogeneity across brain regions. In our analysis an average of 72.2% of power for primary eQTL analysis is attributable to effect size, while the rest is attributable to heterogeneity (Extended Data Figure 3). Considering only cortical brain regions reduces effect size heterogeneity and reduces the number of genes with detected eQTLs from 10,769 to 9,431, but, more importantly, reduces the number of genes with conditional eQTLs from 5,336 to 3,533.
Conditional eQTLs have different properties than primary eQTLs. While primary eQTLs are a median of 22.8 kb from the transcription start site, conditional eQTL are more distal with median distances of 35.7 kb for secondary, 50.6 kb for tertiary and 52.7 kb for quaternary eQTL (p < 1.6×10−14 for all comparisons between primary, secondary and tertiary eQTLs using one sided Mann–Whitney U test) (Extended Data Figure 4A). This is consistent with primary eQTLs often affecting promoters and conditional eQTL more often affecting enhancers. In addition, genes with more independent eQTLs have higher cell type specificity in human18 (Spearman rho = 0.0621, p = 1.93×10−10) and mouse50 (Spearman rho: 0.0617, p = 2.50×10−10) brain (Extended Data Figure 4B). Finally, genes with more conditional eQTLs tend to be under lower evolutionary constraint, as measured by the probability of loss intolerance (pLI) calculated from large-scale exome sequencing51. While 29.9% of genes with no detectable eQTLs are highly constrained (pLI > 0.9), only 6.5% of genes with 4 eQTLs exceed this cutoff (Extended Data Figure 4C). While the distribution of estimated effect sizes is similar for increasing conditional eQTL degree, the minor allele frequency decreases markedly (Extended Data Figure 5). Interpretation of the estimated effect sizes from bulk and cell type specific data is challenging and is affected by multiple factors (Extended Data Figure 6, see Methods)
Credible set variants are enriched for risk to brain-related traits
Integration of variants in the 95% credible set for primary and conditional eQTLs with large-scale GWAS summary statistics using stratified linkage disequilibrium scores regression52 finds significant enrichments across 22 complex traits after accounting for baseline annotations (Figure 5). Variants in the 95% credible set for primary eQTLs were enriched for 21 traits, including 8 neuropsychiatric and behavioral traits, and 4 neurodegenerative diseases. Meanwhile, the enrichment for conditional eQTLs was limited to AD, BD and alcohol use. These enrichments indicate that our meta-analysis and statistical fine-mapping captures risk variants for brain-related phenotypes.
Figure 5. Heritability enrichment of variants in the 95% causal set for 22 complex traits.
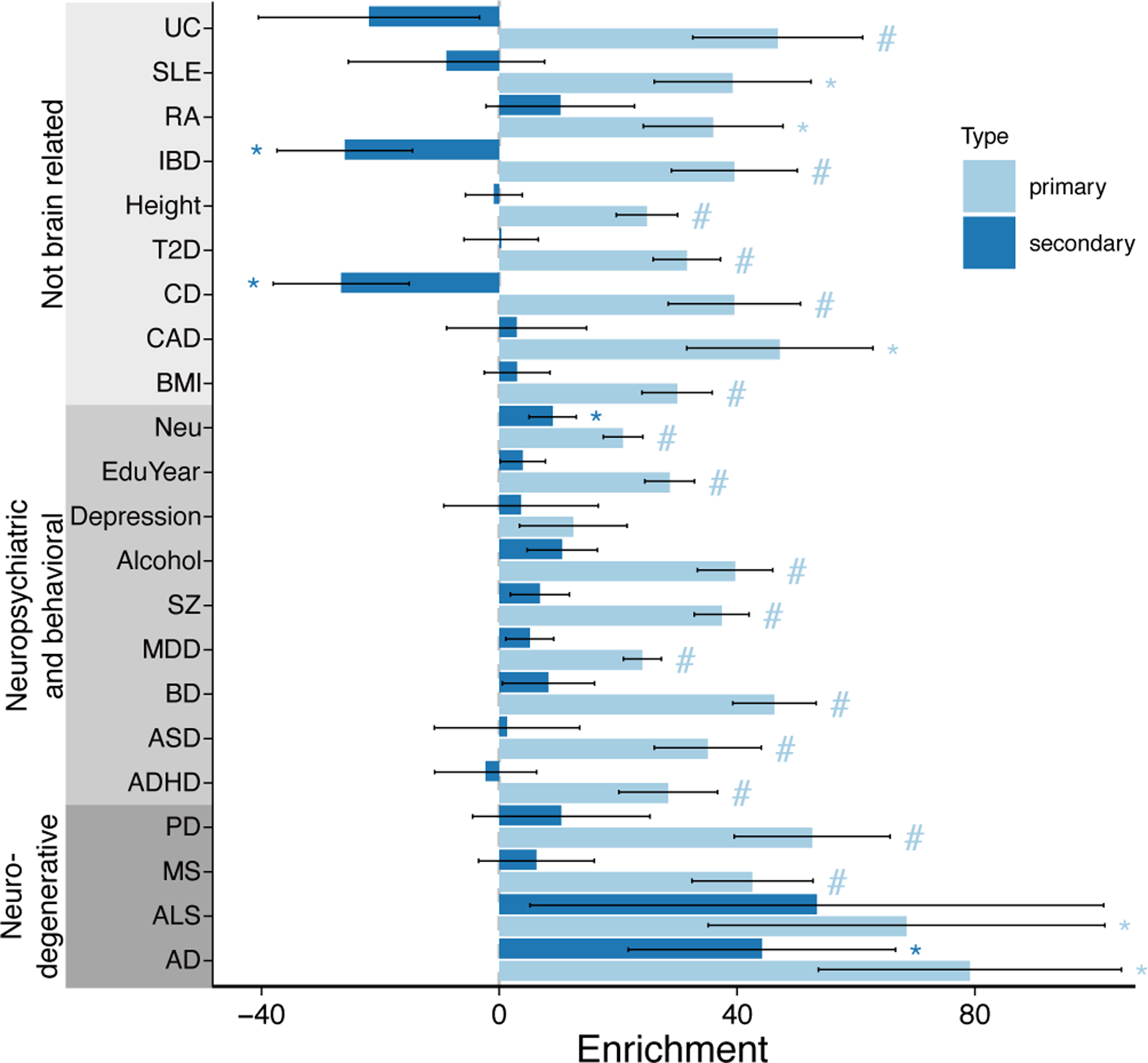
Bar plot indicates linkage disequilibrium score regression (LDSC) enrichments for variants in the 95% causal set for primary and secondary eQTLs. Error bars indicate standard errors. ‘#’ indicates p-value passes 5% Bonferroni cutoff for 44 tests and ‘*’ indicates p-value < 0.05 from 2 sided one-sample z-test. See Supplementary Table 1 for trait abbreviations and references.
Identifying candidate causal risk variants for brain-related traits
Integrating our eQTL fine-mapping results with candidate causal variants from large-scale GWAS45 using a joint fine-mapping approach9 identifies 7,564 variant-trait pairs (CLPP > 0.01) including 2,102 unique candidate causal variants and 1,666 unique genes among 668 complex traits (Extended Data Figure 7). These results include 329 variant-trait pairs for 24 brain-related traits for 204 and 189 unique candidate causal variants and genes, respectively (Figure 6A). Analysis of SZ and BD, two neuropsychiatric diseases with high genetic co-heritability53–55 identified candidate causal variants for 20 genes predicted to confer risk for one or both diseases (Figure 6B). The top genes with CLPP > 0.5 for either of these diseases include ZNF823, THOC7 and FURIN. While these genes have been implicated in SZ or BP previously, and in fact the candidate causal variant for FURIN, rs4702, has been validated experimentally33, candidate causal variants for the other two genes have not been previously identified. Moreover, integrating results from analysis of SZ, BP and SZ+BP versus controls indicates the specificity of these candidate causal variants. ZNF823 is predicted to confer risk to SZ, but not BD. THOC7 has a substantially larger CLPP score for SZ compared to the joint SZ+BP GWAS. Conversely, FURIN has a higher CLPP for the joint SZ+BP GWAS than for SZ alone. Notably, the candidate causal variants driving the colocalization with SZ and BD for CACNA1C is in fact a secondary eQTL, emphasizing the importance of including conditional eQTL analysis.
Figure 6: Summary of joint fine-mapping colocalization with brain-related traits.
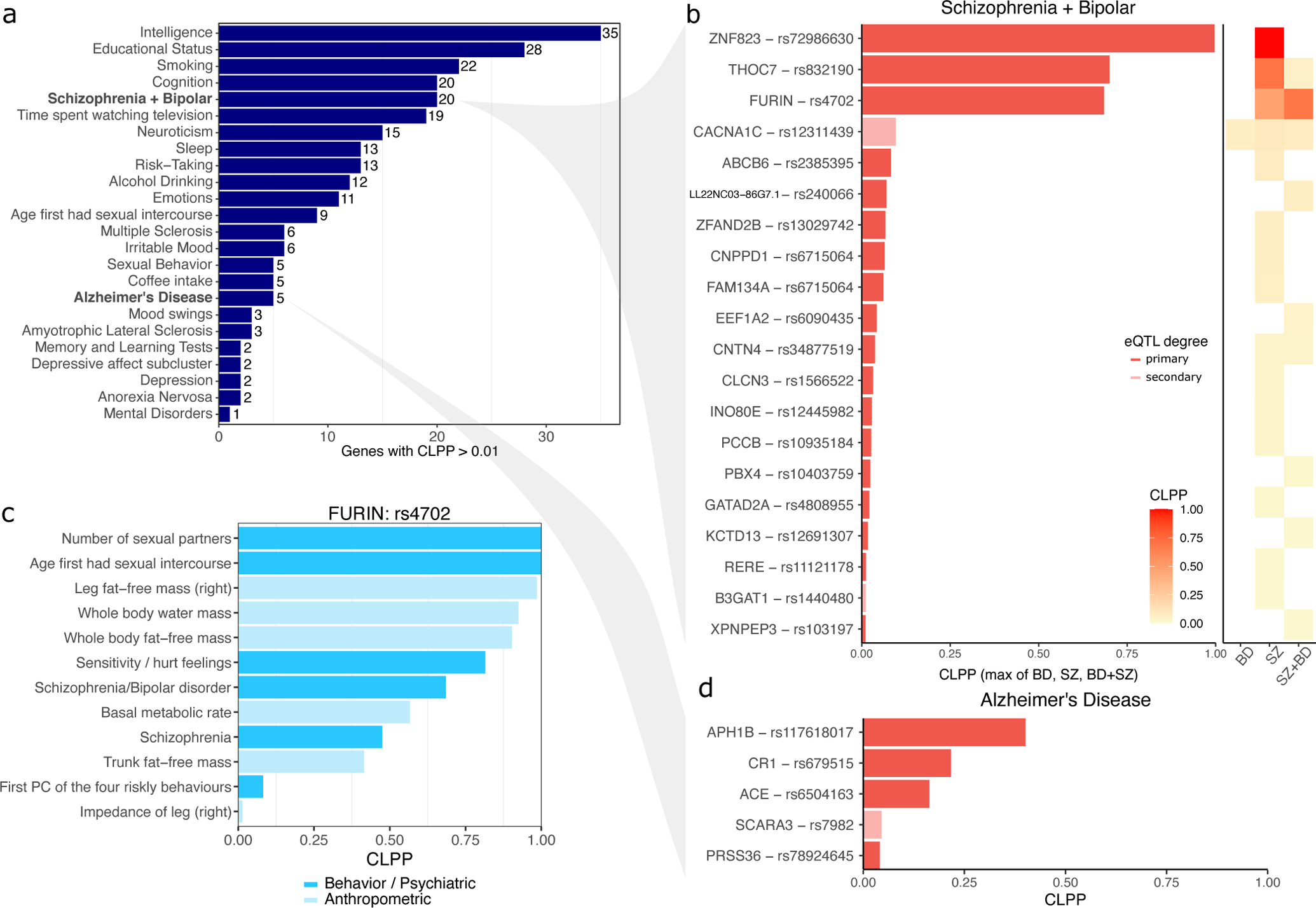
A) Number of genes with colocalization posterior probability (CLPP) > 0.01 for B) Genes with CLPP > 0.01 for Schizophrenia (SZ) and Bipolar Disorder (BP) and a joint GWAS of SZ+BP versus controls. For each gene, the max CLPP across SZ, BP and SZ+BP is shown. Right Panel shows CLPP for BP, SCZ and SZ+BP compared to controls. C) A validated casual variant, rs4702, that affects expression of FURIN is predicted to affect risk for multiple complex behavioral, psychiatric and anthropometric traits. D) Genes with CLPP > 0.01 for AD.
In addition, analysis of candidate causal variables across many phenotypes enables insight into pleiotropy. FURIN and rs4702 are also implicated in the number of sexual partners, age at first sexual intercourse, risk taking behavior, and emotional sensitivity / hurt feelings, and multiple anthropometric traits (Figure 6C, Extended Data Figure 8). Sharing of a candidate causal variant and gene between SZ+BP and these risk-taking behavior traits is particularly interesting given that impulsiveness is a clinical feature of both SZ and BD57,58, and is associated with more severe psychiatric symptoms and decreased level of functioning59.
Analysis of AD identified candidate causal variants for 5 genes. While these genes have been highlighted previously1, our analysis highlights variants and their mechanistic link to disease (Figure 6D).
Candidate causal variants elucidate potential molecular mechanisms
rs117618017 is the top causal variant for AD and drives the expression of APH1B, a subunit of the gamma-secretase complex, which includes multiple AD risk genes as components (Figure 7A). This missense coding variant was identified in a GWAS meta-analysis for AD1, but an attempt to experimentally validate a functional effect from this single amino acid change yielded only negative results60. Yet our analysis indicates an alternative molecular mechanism, whereby, instead of acting by changing protein sequence, the minor allele of rs117618017 increases AD risk by directly increasing gene expression of APH1B.
Figure 7: GWAS-eQTL colocalization by joint fine-mapping.
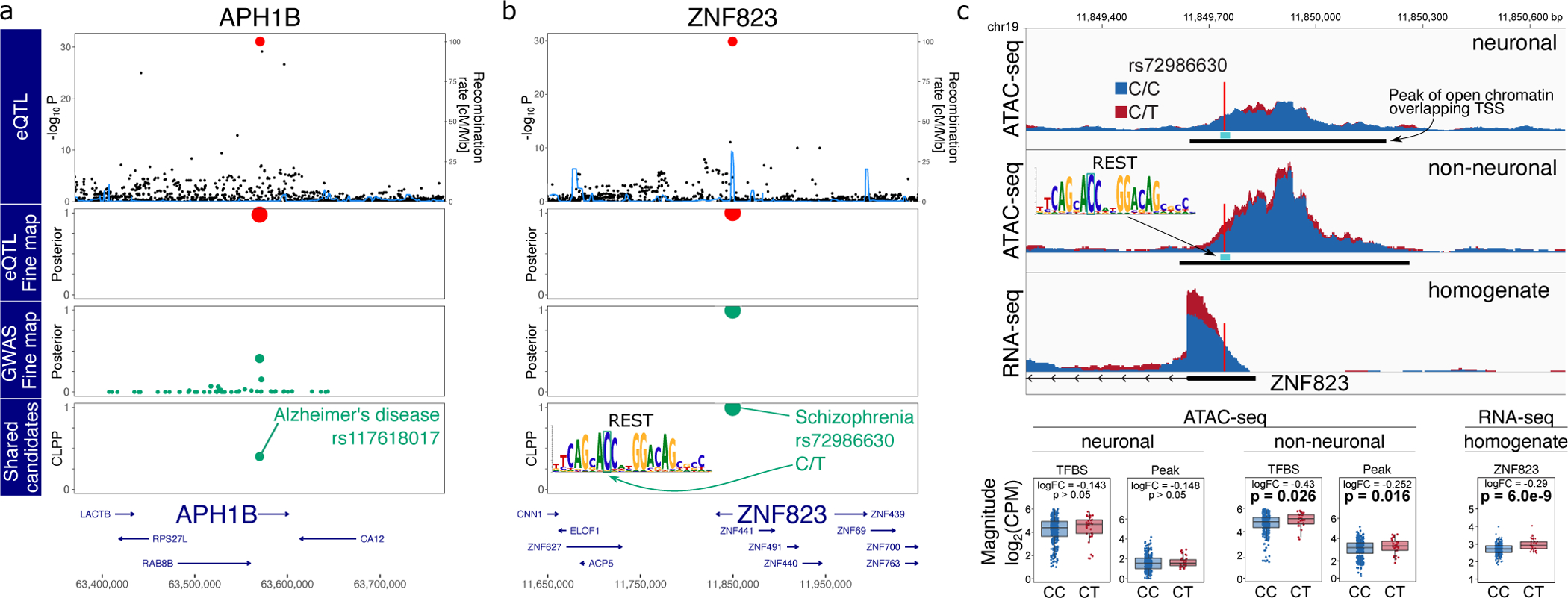
A,B) Starting from the top, the plot shows −log10 p-values from eQTL analysis, poster probabilities from statistical fine-mapping of eQTL results, poster probabilities from statistical fine-mapping of GWAS results, and colocalization posterior probabilities (CLPP) for combining eQTL and GWAS fine-mapping. A) Expression of APH1B and AD risk share rs117618017 as a candidate causal variant. B) Expression of ZNF823 and SZ risk share rs72986630 as a candidate causal variant. This variant is predicted to disrupt a REST binding site motif. C) Individuals heterozygous for rs72986630 have increased chromatin accessibility at the peak and REST binding site in non-neuronal cells. Genome-plot shows chromatin accessibility for neuronal (top) and non-neuronal (middle) nuclei, and gene expression from brain homogenate bottom. The lower panel shows boxplots comparing chromatin accessibility and gene expression between individuals with two reference alleles (i.e. CC) compared to CT heterozygotes. Box plots indicate median, interquartile range (IQR) and 1.5*IQR. Hypothesis tests were performed with limma/voom.
The top hit for SZ is rs72986630, which is predicted to drive expression of ZNF823, a zinc finger protein with little additional annotation (Figure 7B). This C/T SNP is located in the 5’ UTR of the gene and the minor allele, T (MAF ~6%), is protective against SZ. This variant is predicted to disrupt a binding site for the RE1 silencing transcription factor (REST), also known as neuron-restrictive silencing factor. REST is upregulated during neurogenesis and in adult non-neuronal cells, and acts by silencing neuron specific genes61,62. Analysis of chromatin accessibility in this region using a large-scale ATAC-seq dataset from purified neuronal and non-neuronal nuclei from the anterior cingulate cortex (ACC) of post mortem brains of 368 donors elucidated the molecular mechanism (Bendl, et al. in preparation) (Figure 7C). In non-neuronal cells, but not in neuronal cells, individuals heterozygous at this site have higher chromatin accessibility at both the 644 bp ATAC-seq peak (p = 0.016) and the 21 bp motif (p = 0.026), and this corresponds to decreased binding of REST at this site. Since REST is a transcriptional silencer, decreased binding of REST should lead to increased expression of ZNF823. Querying RNA-seq data from brain homogenate from these samples confirms that heterozygous individuals have increased expression of ZNF823 (p=6.01×10−9).
Discussion
Integration of eQTL and GWAS is a powerful method to understand the molecular mechanism influencing complex traits. While transcript-wide association studies aim to identify genes underlying a complex trait, correlated expression and co-regulation can be challenging to overcome63,64. Joint fine-mapping focuses instead on identifying variants that drive both gene expression and a downstream trait9. Despite recent successes, fine-mapping is often limited by statistical power and linkage disequilibrium6,9. Our mmQTL workflow addresses both of these issues by performing a multi-ancestry eQTL meta-analysis of 3,983 RNA-seq samples from 2,119 donors, with an effective sample size of 3,154, to produce a large resource characterizing the genetics of gene expression in the human brain. This analysis has substantially boosted the catalog of genes with detected conditional eQTLs, while increasing the resolution of statistical fine-mapping.
Despite being performed on bulk RNA-seq data, our analysis is able to replicate eQTLs discovered in purified microglia (Kosoy, in preparation) and neurons27, and the replication rate is substantially higher than for PsychENCODE15. Moreover, we identify candidate causal variants enriched in cell type specific open chromatin regions. While much recent work has pursued generating eQTLs from purified cell populations26–28, and eQTL discovery from single cell/nucleus RNA-seq is becoming tractable65,66, our eQTL meta-analysis from bulk tissue illustrates that large sample size and sophisticated statistical modelling has substantial power to replicate eQTLs from smaller studies of purified cell types.
While the number of genes with detectable eQTLs approaches saturation, there is substantial value in increasing sample size. Here, we use individuals of diverse ancestry paired with a linear mixed model in our mmQTL workflow to increase the resolution of statistical fine-mapping. Moreover, we perform conditional eQTL analysis to identify genes with up to 12 independent eQTLs. These conditional eQTLs tend to have smaller minor allele frequencies, be farther from transcription start sites, and affect genes that are more cell type specific. The number of genes with secondary and tertiary eQTL does not appear close to saturation, underscoring the regulatory variation that remains to be identified.
Integrating statistical fine-mapping for eQTLs and GWAS across hundreds of complex traits enabled insight into candidate causal variants, mechanisms of disease genetics and pleiotropy. Focusing on regulatory mechanisms for genes underlying brain-related traits, we identified 20 genes and candidate causal variants predicted to drive risk for SZ and BD, plus another 5 for AD. While other methods focus on discovering disease genes, here we focus on discovering gene-variant pairs underlying disease risk in order to elucidate the molecular mechanisms that convey risk.
Here we highlighted two examples. The SNP rs117618017 is a candidate causal variant causing a single amino acid change in APH1B. While experimental results of the impact of this amino acid change were negative60, our analysis instead supports a mechanism where this variant increases disease risk by increasing expression of APH1B. Our analysis predicts that rs72986630 drives expression of ZNF823 and is protective against SZ. By integrating chromatin accessibility data from post mortem brains, we traced the predicted chain of causality and found that the minor allele disrupts binding of REST in non-neuronal cells, which then increases expression of ZNF823. The lack of an effect in neuronal nuclei is consistent with the higher expression of REST in non-neuronal cells during adulthood, silencing neuron-specific genes61,62.
While we focused on regulatory mechanisms for genes underlying SZ, BD and AD, all results are available from the Brain eQTL meta-analysis (BREMA) resource (icahn.mssm.edu/brema).
Further integration of multi-omics data with multi-ancestry fine-mapping and large-scale GWAS promises to yield further insight into the molecular mechanisms underlying disease risk. Future studies are poised to perform multiple genomic assays, namely RNA-seq and ATAC-seq, on multiple tissues or brain regions, and target multiple cell types either by sorting or single cell/nucleus methods65,66. Moreover, these studies will increasingly include individuals of diverse ancestry67. Our mmQTL method will enable the field to take advantage of these repeated measures datasets while modeling effect size heterogeneity and controlling the false positive rate. Efforts to trace the chain of causality from variants and molecular mechanisms to pleiotropy across complex phenotypes are poised to yield insight into novel therapeutic targets.
Methods
Obtaining and processing of RNA-seq datasets
Imputed genotypes from GTEx v8 were downloaded from dbGAP (Accession phs000424.v8.p2). For ROSMAP, imputed genotypes were downloaded from the Synapse website (id: syn3157329). Imputed genotypes for each cohort in the PsychENCODE study were downloaded from Synapse website (id: syn21052530), and were then filtered to retain variants with imputation quality ≥0.3. Filtered genotypes from each cohort were merged and variants with MAF ≥ 1% and Hardy-Weinberg Equilibrium p-value ≥ 10−6 were retained.
The original PsychENCODE analysis performed eQTL detection using 1,387 individuals15. In the current work we exclude a small fraction of these individuals. First, the full PsychENCODE dataset contains GTEx samples which we excluded in order to avoid redundancy with our separate GTEx analysis. Second, the original analysis used ~5 million imputed SNPs. Since accurate statistical fine-mapping depends on including the true causal variant in the analysis, we included additional well-imputed SNPs at the cost of excluding a small set of samples. Excluding samples with < 8 million well-imputed (info score >0.3) variants yielded 1,215 individuals used in this study.
The normalized gene expression of GTEx v8 was downloaded from GTEx Portal (GTEx_Analysis_v8_eQTL_expression_matrices.tar, https://gtexportal.org/), and we regressed out covariates from the companion file GTEx_Analysis_v8_eQTL_covariates.tar with linear regression. Normalized data from PsychENCODE (DER-01_PEC_Gene_expression_matrix_normalized.txt) was downloaded from http://resource.psychencode.org/, and as the downloaded gene expression is already normalized regressing out the effect of covariates, no further normalization was taken. Data from ROSMAP (syn3388564, ROSMAP_RNAseq_FPKM_gene.tsv) was downloaded from https://adknowledgeportal.synapse.org. The provided FPKM abundance values were quantile normalized, log2 transformed, standardized to normal distribution, and 20 principal components of the gene expression matrix were regressed out.
Linear mixed model eQTL analysis
Given expression abundance of a gene measured in n tissues from same set of individuals, the gene expression in tissue t can be modeled as:
| (1) |
where, yi,t is the measured gene expression value for individual i in tissue t which has been normalized so that it has mean 0 and variance 1, xi,jis the genotype dosage for individual i at variant j normalized so that it has mean 0 and variance 1, βj,t is effect size for variant j and tissue t. The next term models the polygenic background across m variants where xi,k is the genotype dosage value for individuali at variant k and αk,t is the effect size for variant k and tissue t with distribution , where is the tissue-specific parameter for genetic background. Finally, εi,t is the normally distributed error variance for individuali and tissue t with distribution , where is the tissue-specific parameter for random noise.
This linear mixed model can be transformed for practical estimation the effect size βj,t. Equation (1) can be rewritten as
| (2) |
where and has a distribution , where K is a genetic relatedness matrix estimated based on genome-wide genotypes.
Considering that the phenotype was collected among l individuals, we can write formula (2) into a vector format:
| (3) |
where Yt, Xj and are l-dimensional vectors, and contain normalized phenotype, normalized genotype of variant j, and noise, respectively.
From Equation (3), βj,t can be estimated as
| (4) |
where and produces an unbiased estimator since
Modeling covariance across tissues
While standard meta-analysis assumes effect size estimates are statistically independent, analysis of multiple tissues from the same set of subjects produces covariance between the coefficient estimates. Here we explicitly model this covariance in order to control the false positive rate.
Denote the estimate for variant j across all tissues as the vector . Since individuals overlap across the multiple tissues, the entries of will be correlated. Estimating coefficients for tissues 1 and 2 using Equation 4 gives
| (5) |
| (6) |
where an index is added to distinguish the two tissues which may have partial sample overlapping. These estimates are not statistically independent since
where is only involved with transformed genotypes projected by a covariance matrix. Noting that and are the summed contribution from polygenic background and noise, if there are sample overlapping and the phenotypes share causal variants in two tissues, then
where Nshared is the number of shared individuals, and σg,1 and σg,2 are the genetic component for polygenic background in tissue 1 and tissue 2. Finally, we note that
explicitly indicating that there is nonzero covariance between estimators. Our mmQTL method estimates the covariance matrix among n tissues based on the non-significant z-score in tissues, and set it to be . This matrix is defined so that the covariance between tissuesi andj is estimated by the covariance between z-scores from non-significant variants (p>0.05) according to:
where Zi and Zj are vectors containing statistical Z-scores.
Fixed-and random effects meta-analysis
The results from multiple analyses are aggregated using either a fixed or random effects meta-analysis. The true effects sized are assumed to be drawn from a normal distribution centered at the true effect size β with variance . For a fixed effect model, the true effect size is fixed at a constant value which is equivalent to setting and for the random effects model . From this hierarchical framework, we obtain estimators for variant j among tissues, denoted as a vector which has a distribution . We applied the Brent-method implemented in C++ Boost library to estimate βj and . To test the difference with null hypothesis, we applied the random-effect model42,49 to obtain a p-value.
Statistically, the standard fixed effect mega-analysis combines all data into a single regression model and assumes a fixed effect size across all studies as well as constant error variance across all studies. These assumptions are not satisfied in multi-tissue eQTL analyses due to variation in effect size and variation in error variance across tissues68. Using a random effect meta-analysis addresses both of these issues to retain control of false positive rate while leveraging the effect size heterogeneity to increase power.
Detection of conditional eQTLs
We applied a stepwise selection strategy explore cis-region and identify conditionally independent eQTL associations. An iterative strategy is applied to find conditional independent eQTL: previously detected eQTL signals are regressed out and another round of eQTL detection was initiated. If one or more variants with p-value less than 10−6, the variant with the smallest p-value is added to the list of conditionally independent effects. The process is repeated until no additional variant has a p-value < 10−6. If a high-order eQTL is in high LD with low-order eQTL (r2>=0.3), the high-order eQTL will be excluded in order to avoid attenuating the estimated effect size of low-order eQTL.
Importantly, we demonstrate statistically that the order in which conditional eQTLs are detected is biologically meaningful: large-effect eQTL shared among tissues are likely to be detected first, while and small-effect eQTL or tissue-specific effect will be detected as higher-order eQTL.
Consider two true causal variantsi andj where the estimated effect has the distribution around the true value according to , where is defined above. The non-centrality parameter (NCP) reflecting the statistical power for this variant is
The ratio between the NPC of variants i and j is
| (7) |
From empirical observation that the effect size (with the genotype and response normalized) of primary eQTL is larger than that of non-primary eQTL, and both are positive definite, and can be decomposed into UΣU, in which U consists of the eigenvectors, and Σ is a diagonal matrix with elements being eigenvalues, denoted as diag(λ1, λ2, λ3, …, λN). can be decomposed into , and to be . Therefore, Equation (7) can be rewritten as
It is apparent that the difference in statistical power for variants i and j is mainly determined by effect size, and its variance. For a variant with larger effect size, and smaller variance, it has a higher statistical power, which is consistent with the empirical that primary eQTL has a much larger normalized effect size (βi > βj), and smaller variance because of the sharing among tissues , so . It follows that on average, mmQTL will pick the independent eQTL signal in a biologically meaningful manner, so that eQTL with a larger influence on expression abundance among conditions tends to be selected first.
Multiple testing
Multiple testing correction is performed at the locus-level as well as genome-wide. Empirically, we performed the locus-level control applying Bonferroni correction, which is a most conservative strategy, and Benjamini-Hochberg method69 on genome-wide correction, and we found that a p-value 10−6 is enough for two-level multiple test correction. While studies often use more liberal multiple testing cutoffs because of the limited statistical power, the statistical fine-mapping that is the focus of this analysis can perform poorly on genes that only pass a liberal cutoff9,12.
We note that Wang, et al.15 performed a mega-analysis of the PsychENCODE data and used a permutation method in order to compute the FDR and p-value cutoff. Their FDR 5% cutoff empirically corresponds to p<8.3×10−4 in their analysis. Yet the complexity of applying a permutation approach to linear mixed models70, and the use of a random effects meta-analysis afterwards in this analysis made a computationally efficient permutation approach impractical here.
Computing empirical effective sample size
In linear regression model for QTL analysis, given that both phenotype and genotype were normalized, the estimator for the allelic effect size is , and its variance is . Letting be the variance explained by the explored variant and Ni be the (effective) sample size for study i, the variance of the effect size estimate is . Consider two studies, where the (effective) sample size of the first study is easy to estimate just by using the number of samples, and the second has some confounding factors such as repeat measurements or population structure. Assuming that the effect size of a given causal variant is constant in the two studies, the ratio of the variances is determined only by N1 and N2:
Therefore, the effective sample size, N2, can be computed from known values by .
We used individual brain tissue in GTEx dataset as study 1 to define N1, and eQTL results from fixed-effect meta-analysis as study 2. The genome-wide variance ratio was set to be the median ratio of variances based on all variants with abs(z-score)>=10 in the fixed-effect meta-analysis. When evaluating the effective size of a meta-analysis, the effective sample size was computed by treating each brain tissue in GTEx as baseline and then taking the mean estimated effective sample size over 13 brain regions.
Replication of eQTLs from purified cell types
In order to assess the replication of eQTLs discovered in independent datasets, we considered the lead SNP for each gene with a genome-wide significant eQTL in the granule cell layer of the dentate gyrus enriched for excitatory neurons27 and purified microglia (Kosoy, et al., in preparation). For the set of lead SNPs from each dataset, the p-values were extracted from the current eQTL analysis as well as the PsychENCODE analysis15 and Storey’s π1 was evaluated using qvalue47. The PsychENCODE p-values were obtained from http://resource.psychencode.org/Datasets/Derived/QTLs/Full_hg19_cis-eQTL.txt.gz. Uncertainty in π1 estimates were evaluated using 100 bootstraps where SNPs were sampled with replacement and π1 was recomputed each time. A p-value comparing the replication rate for the current and PsychENCODE analysis was computed using a one-sided z-test using the estimated π1 values and their bootstrap variances.
Interpretation of estimated effect sizes
In the scenario where a SNP has a large cell type specific effect on gene expression, the true biological effect will be attenuated in bulk data that is composed of multiple cell types. Yet testing this biological intuition through eQTL analysis is challenging for a number of technical reasons. Unfortunately, eQTL analysis does not directly estimate the biological effect size because the gene expression is typically log2 transformed, scaled to have variance 1, and often quantile normalized. In addition, the inclusion of PEER factors, or other covariates can account for cell type heterogeneity across samples in the data. Therefore, the estimated eQTL effect size reflects the association between SNP and (transformed) gene expression after accounting for other variables.
Furthermore, the technical process of obtaining gene expression from bulk tissue versus cell type specific samples is susceptible to different noise profiles based on differing protocols and the biological condition of the physical samples. In fact Young, et al.26 found that cell-type specific samples from microglia are noisier than those from bulk samples, and that reported estimated effect size in purified cells are attenuated.
We performed an empirical analysis of the estimated allelic effect sizes from the lead eQTL variants for each gene in our meta-analysis of bulk data compared to estimates from cell type specific data from neurons27 and microglia from Kosoy, et al. (in preparation) and Young, et al.26. The comparison between bulk and neuron-enriched data gives a slope of 0.59, indicating that the slope is on average actually smaller in the cell type data. Comparison to the Kosoy microglia data gives a slope of 1.15 and to the Young microglia data gives a slope 0.59. These results are difficult to interpret, especially given the caveats above.
These results are not unexpected given the statistical and technical challenges outlined above. In fact, these findings are not unique to our data. Recently, Ota, et al71 generated eQTLs four immune cell types and compared the estimated effect sizes to bulk immune data from Ishigaki et al,72. Our analysis recapitulates their finding that effect size estimates are smaller in the cell type specific data.
Rigorous analysis of effect size estimates is challenging both statistically and due to different noise profiles of bulk and cell type data. Mohammadi et al.73 developed a method to estimate a biologically interpretable allelic effect size. Further research on this challenge in the field could yield further insight into cell type specific gene regulation.
Simulation pipeline to evaluate mmQTL performance
Genotype and gene expression data were simulated to compare to empirical performance of eQTL analysis using a linear model with 5 genotype principal components compared to a linear mixed model. Results from eQTL analysis of 5 simulated tissues were then aggregated using either Sidak correction, or a fixed- or random-effects meta-analysis.
Biologically realistic genotype data reflecting real human populations was simulated with a sampling-based simulation package, hapgen274, and haplotype information for European, African, and Asian populations from the 1000 Genomes Project (https://mathgen.stats.ox.ac.uk/impute/data_download_1000G_2010_interim.html). We simulated 500 individuals for each population, and merged these individuals into a single trans-ancestry dataset with sample size 1,500. We also simulated 1,500 individuals solely based on European haplotype information.
Based on these genotypes, we adapted the phenotypesimulator pipeline75 to perform 800 simulations for each scenario, simulating one gene expression trait for each simulation. For each gene a single eQTL was simulated to affect expression abundance explaining 1% phenotypic variance, and the contribution due to polygenic background was set to be 30%. We applied phenotypesimulator’s simulating strategy to account for shared environmental factors, measurement noise, and polygenic background to create correlated phenotypes. In the simulation, we simulated phenotypes in 5 tissues, and set the number of tissues that the causal genetic variant affects to be 1, 2, 3, 4, 5. To demonstrate the robustness of mmQTL to control for population structure and batch effect, we set two different levels of phenotype correlation, a low level, r=0.12, and the high level r=0.45. For power analysis, any simulated causal variants located in high LD (r2 >= 0.8) with a variant passing the multiple testing cutoff was considered to be detected.
We also performed a null simulation with no true causal variants where all effect sizes were set to zero. Results from 50 simulations were aggregated and we used genomic inflation factor76 and QQ plots to assess the false positive rate.
Comparison of fine-mapping resolution between a European and multi-ancestry population was performed using simulated pure 1,500 European individuals and multi-ancestry 1,500 individuals with 500 individuals in each of European, African and Asian population. Gene expression phenotype was simulated in a single tissue, and a causal variant was randomly chosen to explain 2% phenotypic variance. For 1,500 European individuals, we applied standard linear regression model to detect eQTL and then fine-mapping was conducted to obtain a 95% credible set candidate for causal variants, while for 1,500 multi-ancestry individuals, we used mixed linear model to detect eQTL and then fine-mapping was taken to find a 95% credible set. The size of the 95% credible set was used to compare the fine-mapping resolution, a smaller number indicating a higher fine-mapping resolution.
Integration with ATAC-seq data
Variants in the 95% credible set were overlaid with open chromatin regions from four distinct populations of cells (glutamatergic neurons, GABAergic neurons, oligodendrocytes, and a mixture of microglia/astrocytes) identified by ATAC-seq48. In order to reduce the influence of the low fine-mapping resolution of conditional eQTL, if the size of the 95% credible set for a single gene contained >10 variants, only the 10 variants with highest PIP were included. Enrichment of variants within open chromatin regions was evaluated using a Fisher’s exact test implemented in QTLTools77.
Evaluating GWAS enrichments for variants in credible sets
We applied a strategy developed in Hormozdiari et al.12: for each eQTL, we performed fine-mapping and compute the causal posterior probability (CPP) of each cis-SNP and only variants in the fine-mapped 95% credible set are retained. For each SNP in cis-regions, we assign an annotation value based on the maximum value of CPP across all molecular phenotypes; SNPs that do not belong to any 95% Credible Set are assigned an annotation value of 0, which is referred as MaxCPP in12. Stratified linkage disequilibrium score regression (S-LDSC)52 was then used to partition trait heritability using the constructed functional annotations, and the estimated enrichment was used to measure the importance of each eQTL category on human complex traits or diseases. To rule out the potential influences of the correlation among eQTL categories, we aggregate the baselineLD model, which includes a set of 75 functional annotations, and functional annotations for eQTL categories and run S-LDSR simultaneously.
GWAS summary statistics were obtained for 22 human complex traits or diseases, which contain both brain traits and non-brain traits (Supplementary Table 1).
eQTL detection in cell type specific datasets
Microglia from fresh human brain specimens (101 samples, including 27 non-Europeans) were prepared using the Adult Brain Dissociation Kit (Miltenyi Biotech). Tissue homogenates were incubated in antibody (CD45: BD Pharmingen, Clone HI30 and CD11b: BD Pharmingen, Clone ICRF44) at 1:500 for 1 hour in the dark at 4°C with end-over-end rotation. Prior to FACS, DAPI (Thermoscientific) was added at 1:1000 to facilitate identification of dead cells. Viable (DAPI negative) CD45+/CD11b+ cells were isolated by FACS using a FACSAria flow cytometer (BD Biosciences) (Kosoy et al., in preparation). RNA was extracted from FACS sorted cells (Arcturus PicoPure RNA Isolation Kit, Life Technologies) and sequencing libraries generated using the SMARTer Stranded RNA-seq kit (Clontech), according to manufacturer’s instructions. Variants with MAF > 5%, and Hardy-Weinberg equilibrium test p-value > 10−6 were retained and analyzed using a linear mixed model implemented in mmQTL. Gene expression was normalized using log2 CPM and eQTL analysis was performed on residuals after regression out 15 principal components of the gene expression. For each gene, a Benjamini-Hochberg (BH) FDR correction was applied across all variants tested in the cis regulatory region to obtain the minimum q-value. Then, the minimum q-values across all genes are adjusted again by the BH FDR method to compute the genome-wide FDR. Limited by the small sample size, we chose a less conservative FDR cutoff of 10%.
Statistical fine-mapping
For each detected eQTL, we conducted a fine-mapping analysis applying the CAVIAR method32 implemented in mmQTL to find a 95% credible set for causal variants. Briefly, meta-analysis p-value based on a random-effect model in each round of conditional eQTL detection was firstly converted to z-score, which was then used as input for fine-mapping. CAVIAR will calculate the posterior inclusion probability (PIP) of each variant to causal, and a set of variants prioritized by PIP score were outputted with summed PIP equal to 0.95.
Detecting colocalization between eQTL and GWAS signals
Joint statistical fine-mapping of eQTL’s and GWAS signals9 was performed by multiplying the estimated posterior inclusion probability (PIP) for a given variant from the eQTL analysis by the PIP for this variant from GWAS of traits compiled in CausalDB45 to obtain a colocalization posterior probability (CLPP). A gene is considered to share a candidate causal variant with a GWAS trait if at least one variant has a CLPP > 0.019.
Trait classification
CausalDB45 provided the MeSH Category for each GWAS trait. However, brain-related traits fall in multiple MeSH categories and there is no single criterion to identify such traits. We performed manual inspection of traits in CausalDB that could be considered neuropsychiatric, neurodegenerative or behavioral and termed them ‘brain related’.
Extended Data
Extended Data Fig. 1. Biologically motivated simulations demonstrate performance of mmQTL workflow: low correlation scenario.
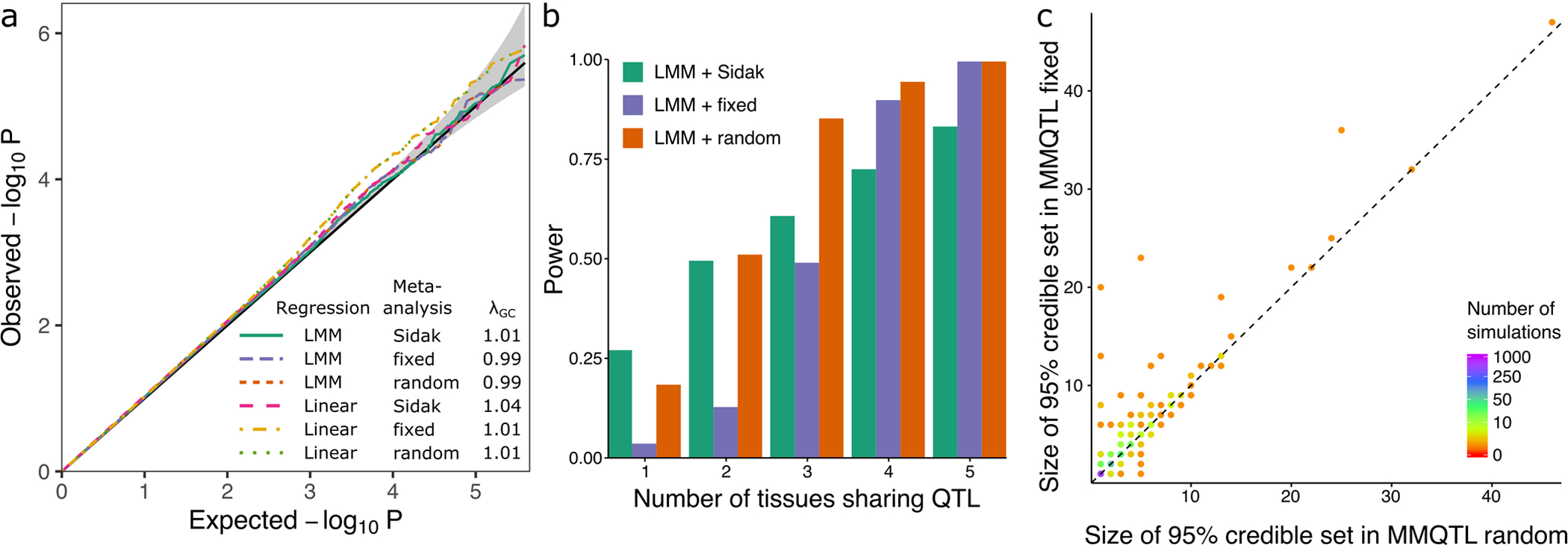
A) QQ plot of results from null simulation shows that the linear mixed model (LMM) with fixed or random effect meta-analysis accurately controls the false positive rate for, while linear regression with 5 genotype principal components did not. The Sidak method was very conservative in both cases. λGC indicates the genomic control inflation factor. Gray band indicates 95% confidence interval under the null. B) Power from LMM followed by 3 types of meta-analysis versus the number of tissues sharing an eQTL. C) Size of the 95% credible sets from fixed- (y-axis) and random- (x-axis) effects meta-analysis from simulations in Figure 2C.
Extended Data Fig. 2. Lead eQTL SNP sign concordance.
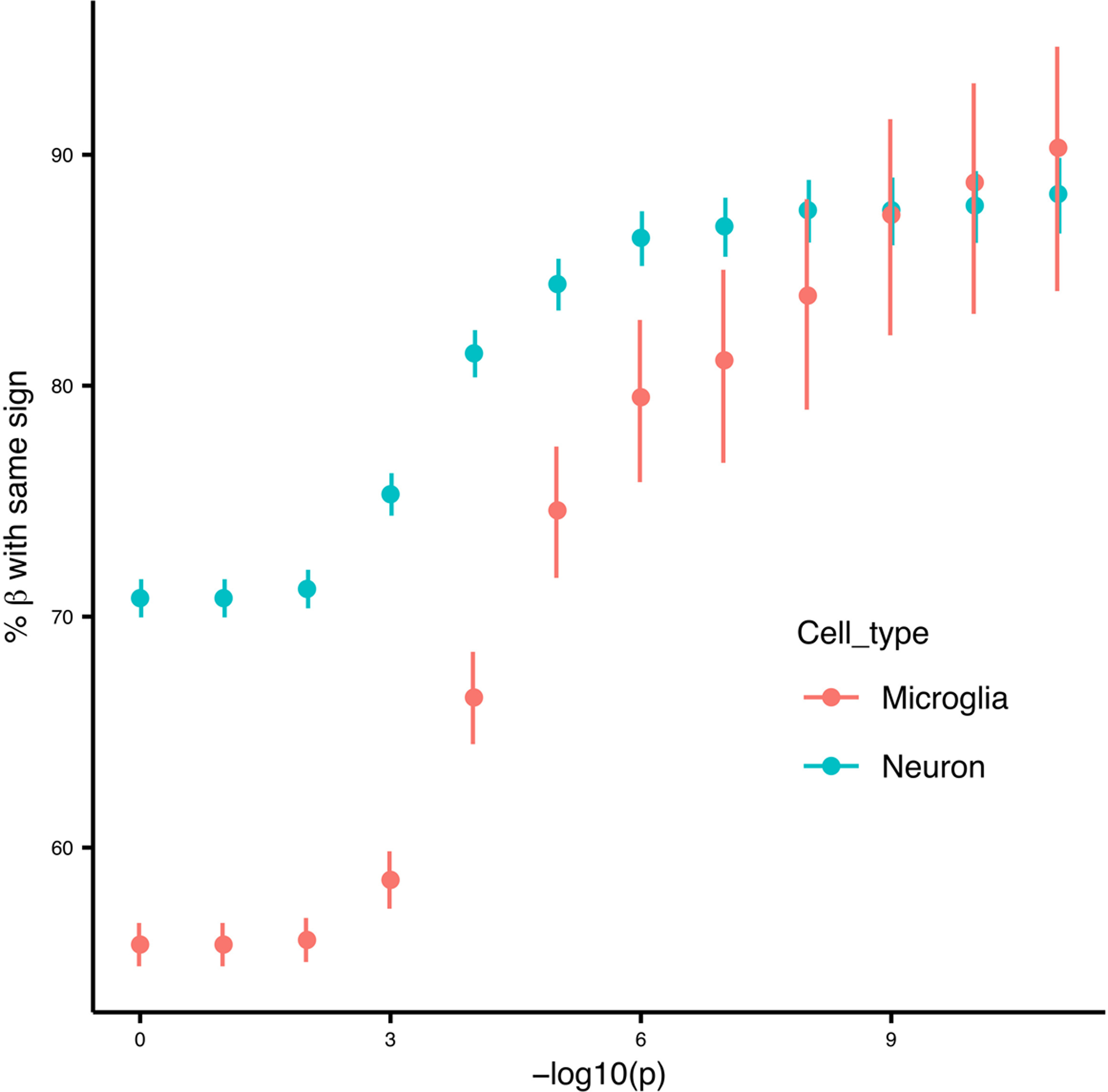
For the lead eQTL SNP of each gene in the meta-analysis, the sign of the mean estimated effect size is compared to the estimated effect sign from neuron and microglia eQTL analyses. The concordance rate increases with the strictness of the p-value cutoff, so a smaller p-value indicates a higher concordance rate. Error bars indicate 95% confidence interval for a binomial proportion. Analysis included 11,709 variants for neuron, and 10,865 variants for microglia.
Extended Data Fig. 3. Impact of effect size heterogeneity.
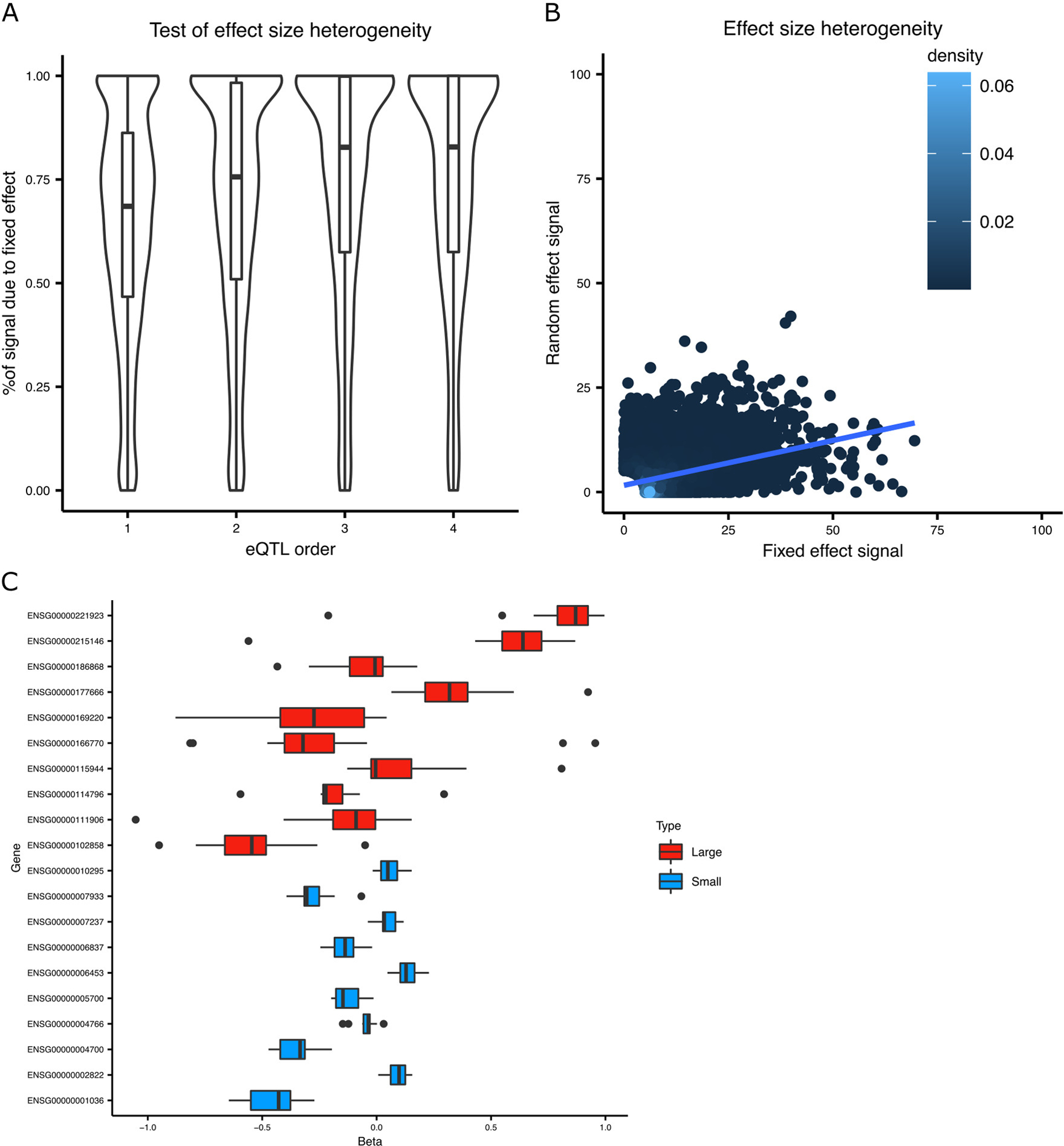
The test statistic from the random effect meta-analysis used here (Han and Eskin, 2011) is the sum of statistics testing the mean (Smean) and variance (Svariance) of the estimated effect sizes. A) The percent of total signal contributed by the fixed effect (i.e. Smean / (Smean + Svariance)) is shown for the lead eQTL SNP for multiple orders of conditional analysis. Box plot indicates median, interquartile range (IQR) and 1.5*IQR. B) The relationship between the test statistics is visualized by plotting Svariance against Smean from the lead eQTL SNP from the primary eQTL analysis. C) The estimated effect sizes from the lead eQTL SNP for genes with high and low levels of effect size heterogeneity is shown. Box plot indicates median, interquartile range (IQR) and 1.5*IQR.
Extended Data Fig. 4. Properties of conditional eQTLs.
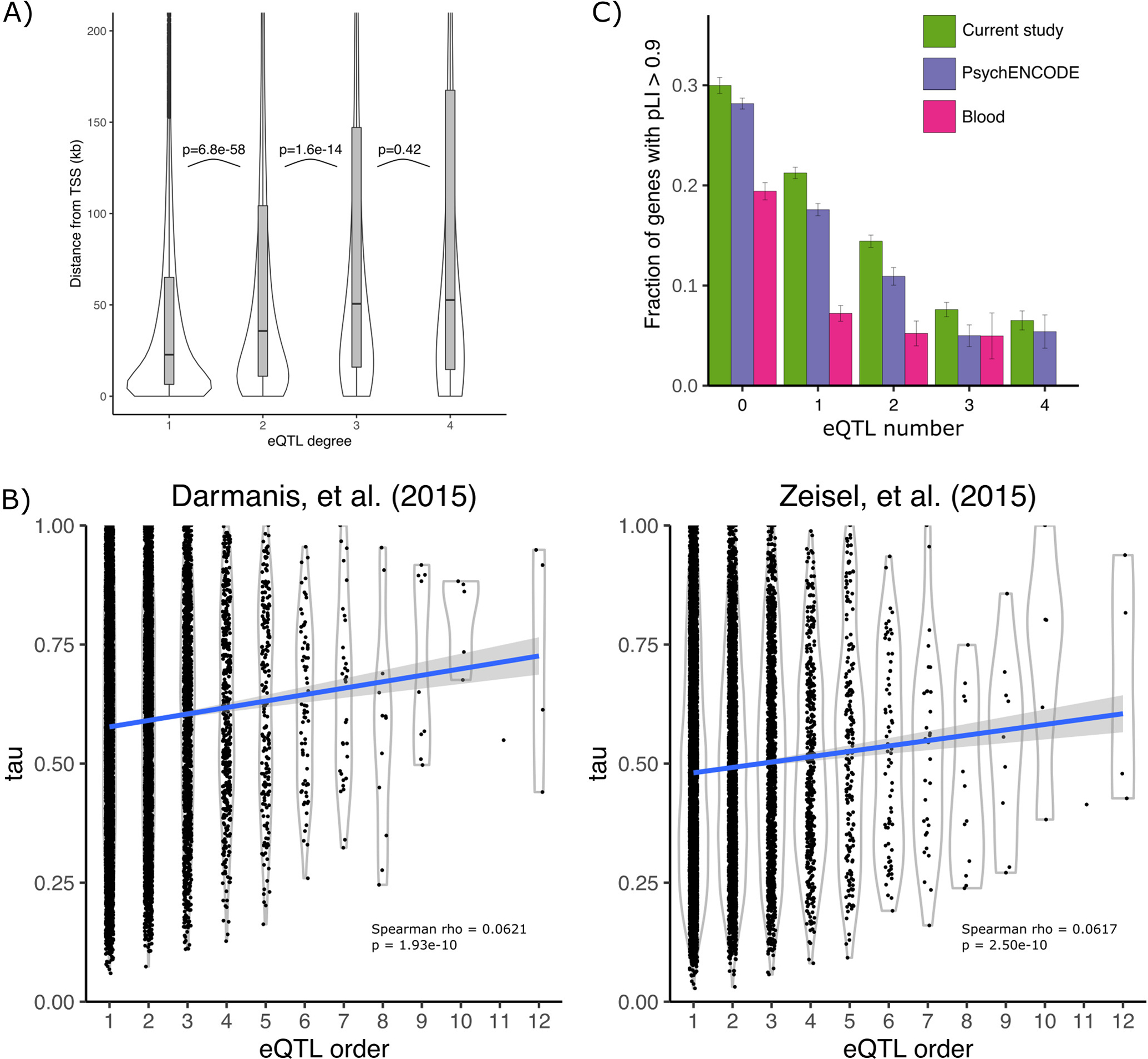
A) The distribution of the distance to the transcription start site is shown for the lead variant for eQTL analysis of increasing degree. P-values indicate significance of one-sided Mann–Whitney U test between adjacent groups. Box plot indicates median, interquartile range (IQR) and 1.5*IQR. B) Cell type specificity metric tau plotted against the number of independent eQTLs discovered for each gene. Gray band indicates 95% confidence interval. C) Bar plot shows that the fraction of genes with high evolutionary constraint (pLI > 0.9) decreases with eQTL degree for the current study, PsychENCODE15, and whole blood78. Error bars indicate standard error based on asymptotic estimate of binomial proportion. Analysis included 10769 genes with eQTLs.
Extended Data Fig. 5. Estimated effect size and minor allele frequencies from conditional eQTL analysis.
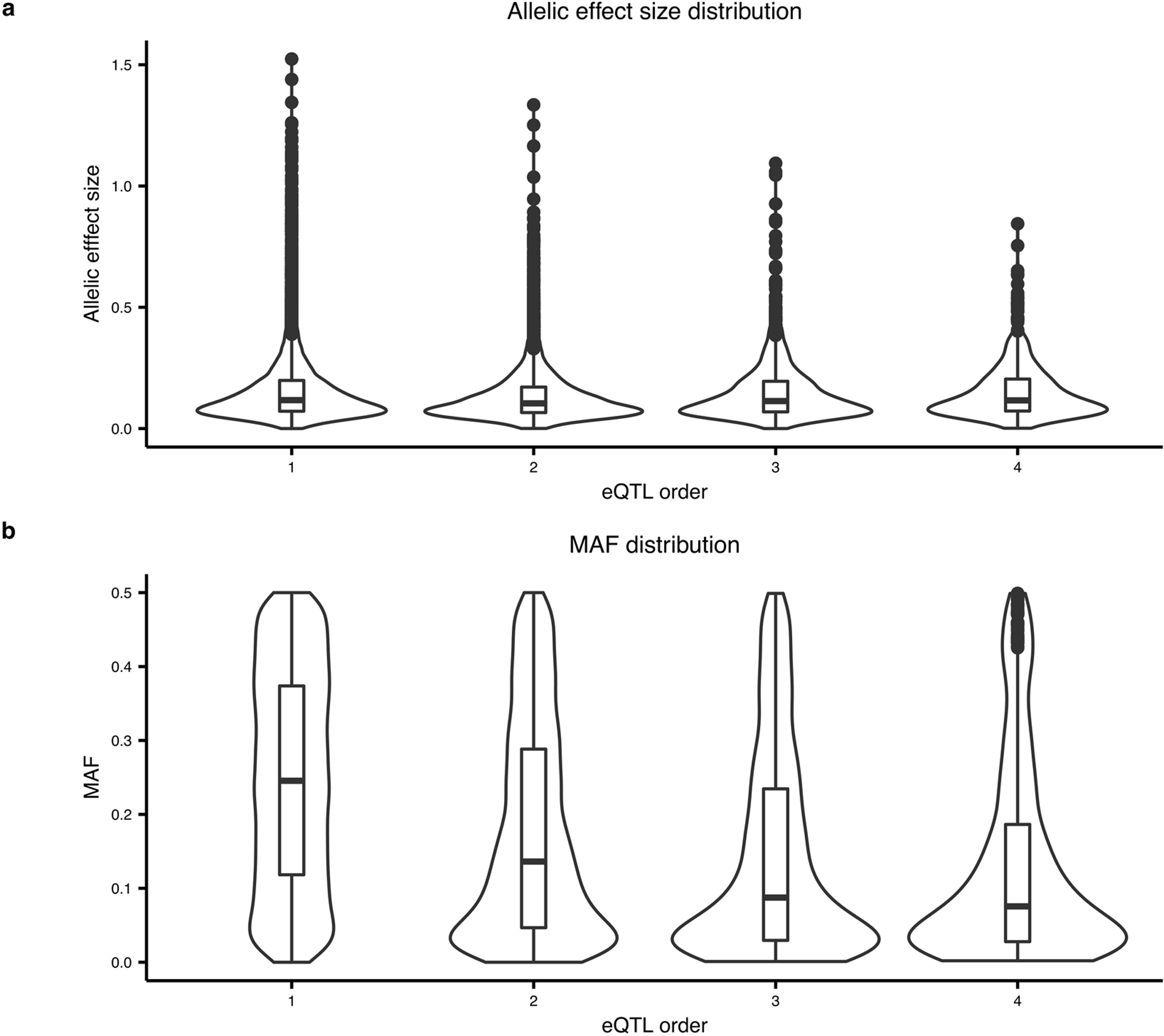
The estimated effect size (A) and MAF (B) are shown for the lead eQTL SNP of significant genes for increasing order to conditional eQTL analysis. A) The distribution of estimated effect size is similar for all conditional analyses. B) The MAF shows a marked decrease with increasing order of conditional analysis. Box plot indicates median, interquartile range (IQR) and 1.5*IQR.
Extended Data Fig. 6. Comparison of estimated effect size for bulk and cell-type specific data.
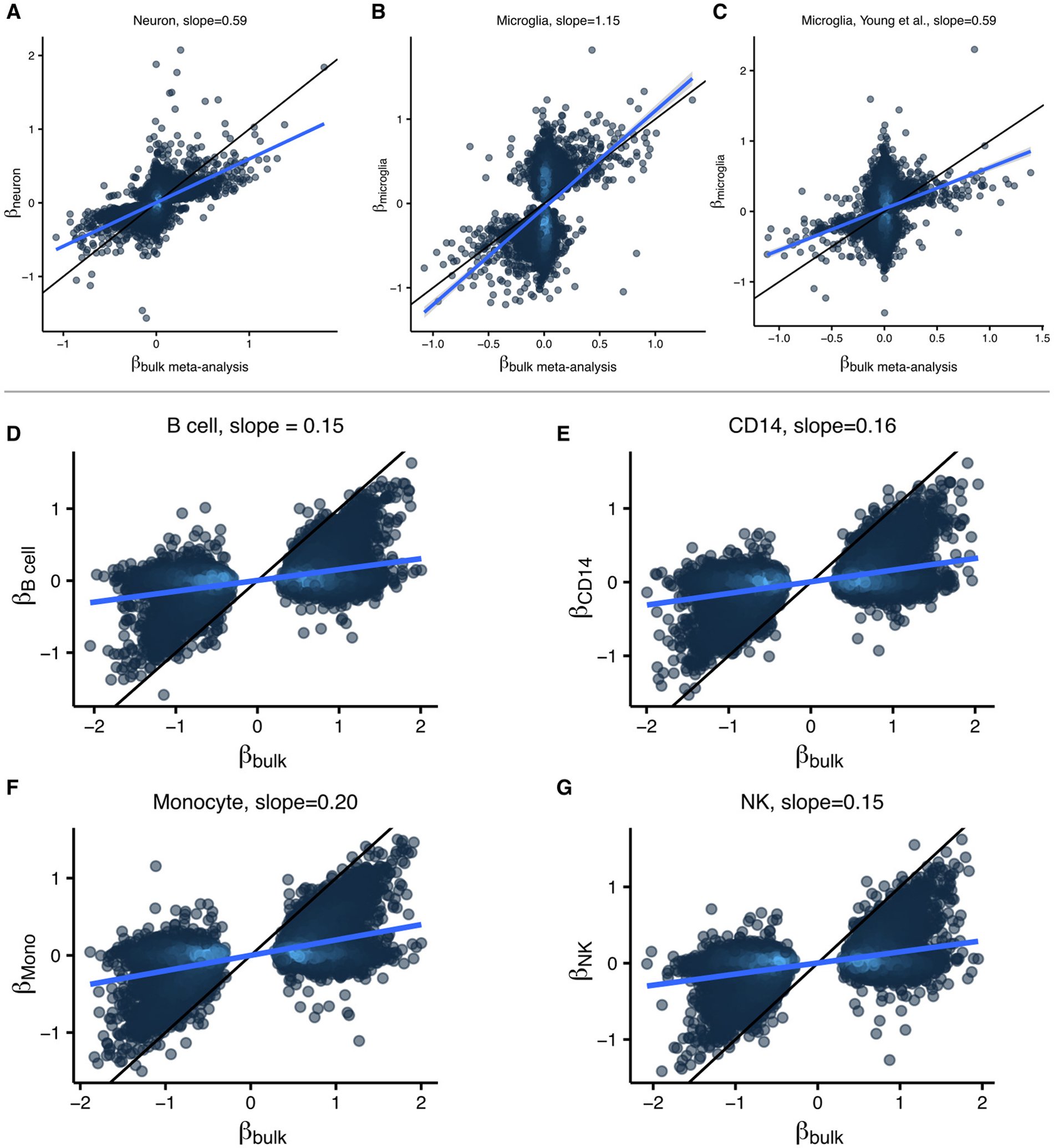
(A-C) Estimated allelic effect size for eQTL lead in (A) neurons (Jaffe, et al. 2020), (B) microglia from Kosoy, et al. (in preparation) and (C) microglia from Young, et al. (2021) compared to effect size estimates from meta-analysis of bulk data from the current study. (D-G) Estimated allelic effect size for eQTL lead SNP in four immune cell types including (D) B cells, (E) CD14, (F) monocytes, (G) NK cells from Ota, et al. (2021) compared to estimates from bulk samples (Ishigaki, et al. 2017).
Extended Data Fig. 7. Number of genes colocalizing for each MeSH category with CLPP > 0.01.
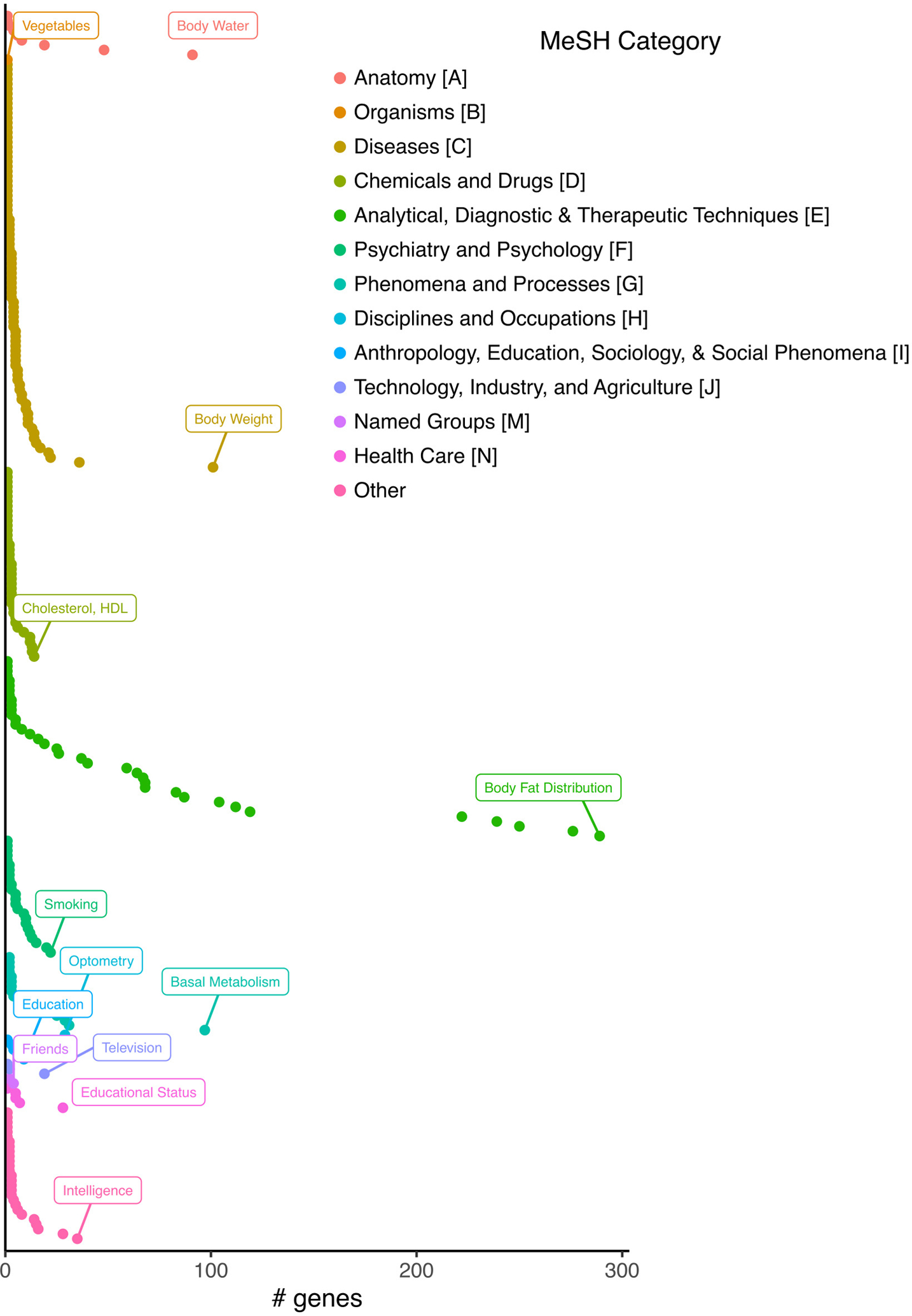
The phenotype with the highest number of colocalized genes for each MeSH category is indicated.
Extended Data Fig. 8. Expression of FURIN and risk for multiple complex traits share rs4702 as a candidate causal variant.
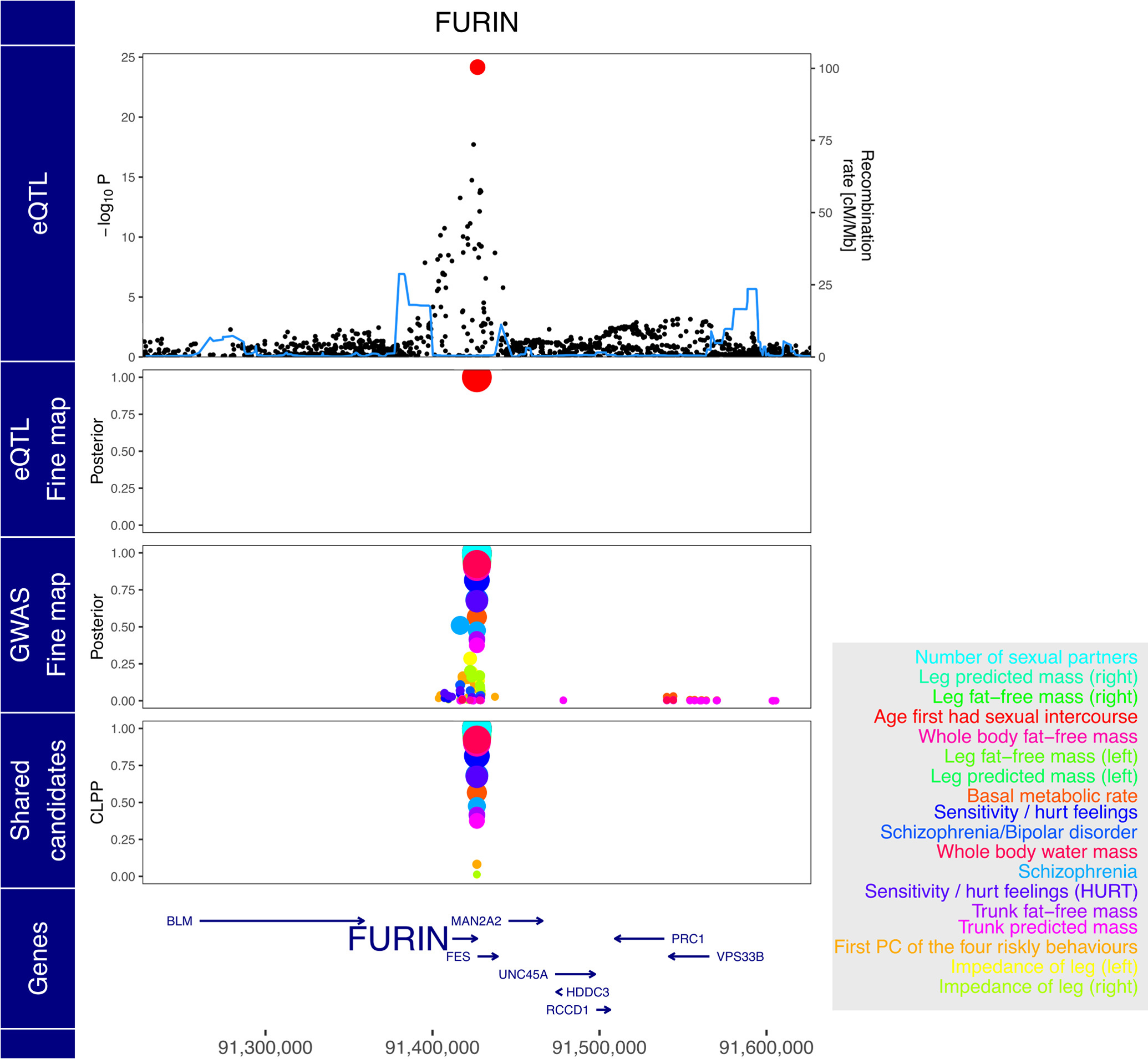
Starting from the top, the plot shows −log10 p-values from eQTL analysis, poster probabilities from statistical fine-mapping of eQTL results, poster probabilities from statistical fine-mapping of GWAS results, and colocalization posterior probabilities (CLPP) for combining eQTL and GWAS fine-mapping. Traits are shown in the box on the right in decreasing order to CLPP value.
Supplementary Material
Acknowledgements
The project was supported by the National Institute of Mental Health, NIH grants R01-MH109677, U01-MH116442, R01-MH125246 and R01-MH109897, the National Institute on Aging, NIH grants R01-AG050986, R01-AG067025 and R01-AG065582, and the Veterans Affairs Merit BX004189 to P.R. G.E.H. was supported in part by NARSAD Young Investigator Grant 26313 from the Brain & Behavior Research Foundation. J.B. was supported in part by NARSAD Young Investigator Grant 27209 from the Brain & Behavior Research Foundation. Research reported in this paper was supported by the Office of Research Infrastructure of the National Institutes of Health under award numbers S10OD018522 and S10OD026880. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
Competing Interests
The authors declare no competing interests.
Code Availability
mmQTL: https://github.com/jxzb1988/mmQTL and Zenodo79 (https://doi.org/10.5281/zenodo.5560014)
Data Availability
Brain eQTL meta-analysis resource: http://icahn.mssm.edu/brema
References
- 1.Jansen IE et al. Genome-wide meta-analysis identifies new loci and functional pathways influencing Alzheimer’s disease risk. Nat. Genet 51, 404–413 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Schizophrenia Working Group of the Psychiatric Genomics Consortium. Biological insights from 108 schizophrenia-associated genetic loci. Nature 511, 421–427 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Visscher PM et al. 10 years of GWAS discovery: biology, function, and translation. Am. J. Hum. Genet 101, 5–22 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Nalls MA et al. Identification of novel risk loci, causal insights, and heritable risk for Parkinson’s disease: a meta-analysis of genome-wide association studies. Lancet Neurol 18, 1091–1102 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wray NR et al. Genome-wide association analyses identify 44 risk variants and refine the genetic architecture of major depression. Nat. Genet 50, 668–681 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Schaid DJ, Chen W & Larson NB From genome-wide associations to candidate causal variants by statistical fine-mapping. Nat. Rev. Genet 19, 491–504 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gallagher MD & Chen-Plotkin AS The Post-GWAS Era: From Association to Function. Am. J. Hum. Genet 102, 717–730 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.GTEx Consortium. The GTEx Consortium atlas of genetic regulatory effects across human tissues. Science 369, 1318–1330 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hormozdiari F et al. Colocalization of GWAS and eQTL Signals Detects Target Genes. Am. J. Hum. Genet 99, 1245–1260 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kim-Hellmuth S et al. Cell type-specific genetic regulation of gene expression across human tissues. Science 369, (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dobbyn A et al. Landscape of Conditional eQTL in Dorsolateral Prefrontal Cortex and Colocalization with Schizophrenia GWAS. Am. J. Hum. Genet 102, 1169–1184 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hormozdiari F et al. Leveraging molecular quantitative trait loci to understand the genetic architecture of diseases and complex traits. Nat. Genet 50, 1041–1047 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fromer M et al. Gene expression elucidates functional impact of polygenic risk for schizophrenia. Nat. Neurosci 19, 1442–1453 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ng B et al. An xQTL map integrates the genetic architecture of the human brain’s transcriptome and epigenome. Nat. Neurosci 20, 1418–1426 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang D et al. Comprehensive functional genomic resource and integrative model for the human brain. Science 362, (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jaffe AE et al. Developmental and genetic regulation of the human cortex transcriptome illuminate schizophrenia pathogenesis. Nat. Neurosci 21, 1117–1125 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Habib N et al. Massively parallel single-nucleus RNA-seq with DroNc-seq. Nat. Methods 14, 955–958 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Darmanis S et al. A survey of human brain transcriptome diversity at the single cell level. Proc Natl Acad Sci USA 112, 7285–7290 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lake BB et al. Integrative single-cell analysis of transcriptional and epigenetic states in the human adult brain. Nat. Biotechnol 36, 70–80 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cao J et al. A human cell atlas of fetal gene expression. Science 370, (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Raj T et al. Polarization of the effects of autoimmune and neurodegenerative risk alleles in leukocytes. Science 344, 519–523 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.van der Wijst MGP et al. Single-cell RNA sequencing identifies celltype-specific cis-eQTLs and co-expression QTLs. Nat. Genet 50, 493–497 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fairfax BP et al. Innate immune activity conditions the effect of regulatory variants upon monocyte gene expression. Science 343, 1246949 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Finucane HK et al. Heritability enrichment of specifically expressed genes identifies disease-relevant tissues and cell types. Nat. Genet 50, 621–629 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Farh KK-H et al. Genetic and epigenetic fine mapping of causal autoimmune disease variants. Nature 518, 337–343 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Young AMH et al. A map of transcriptional heterogeneity and regulatory variation in human microglia. Nat. Genet (2021) doi: 10.1038/s41588-021-00875-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jaffe AE et al. Profiling gene expression in the human dentate gyrus granule cell layer reveals insights into schizophrenia and its genetic risk. Nat. Neurosci 23, 510–519 (2020). [DOI] [PubMed] [Google Scholar]
- 28.de Paiva Lopes K et al. Atlas of genetic effects in human microglia transcriptome across brain regions, aging and disease pathologies. BioRxiv (2020) doi: 10.1101/2020.10.27.356113. [DOI] [Google Scholar]
- 29.Jansen R et al. Conditional eQTL analysis reveals allelic heterogeneity of gene expression. Hum. Mol. Genet 26, 1444–1451 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhernakova DV et al. Identification of context-dependent expression quantitative trait loci in whole blood. Nat. Genet 49, 139–145 (2017). [DOI] [PubMed] [Google Scholar]
- 31.Benner C et al. FINEMAP: efficient variable selection using summary data from genome-wide association studies. Bioinformatics 32, 1493–1501 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hormozdiari F, Kostem E, Kang EY, Pasaniuc B & Eskin E Identifying causal variants at loci with multiple signals of association. Genetics 198, 497–508 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Schrode N et al. Synergistic effects of common schizophrenia risk variants. Nat. Genet 51, 1475–1485 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Nott A et al. Brain cell type-specific enhancer-promoter interactome maps and disease-risk association. Science 366, 1134–1139 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sekar A et al. Schizophrenia risk from complex variation of complement component 4. Nature 530, 177–183 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zaitlen N, Paşaniuc B, Gur T, Ziv E & Halperin E Leveraging genetic variability across populations for the identification of causal variants. Am. J. Hum. Genet 86, 23–33 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Asimit JL, Hatzikotoulas K, McCarthy M, Morris AP & Zeggini E Trans-ethnic study design approaches for fine-mapping. Eur. J. Hum. Genet 24, 1330–1336 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Morris AP Transethnic meta-analysis of genomewide association studies. Genet. Epidemiol 35, 809–822 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zhou X & Stephens M Genome-wide efficient mixed-model analysis for association studies. Nat. Genet 44, 821–824 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Yang J, Zaitlen NA, Goddard ME, Visscher PM & Price AL Advantages and pitfalls in the application of mixed-model association methods. Nat. Genet 46, 100–106 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sul JH, Martin LS & Eskin E Population structure in genetic studies: Confounding factors and mixed models. PLoS Genet 14, e1007309 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Han B et al. A general framework for meta-analyzing dependent studies with overlapping subjects in association mapping. Hum. Mol. Genet 25, 1857–1866 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bennett DA et al. Religious orders study and rush memory and aging project. J Alzheimers Dis 64, S161–S189 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.GTEx Consortium et al. Genetic effects on gene expression across human tissues. Nature 550, 204–213 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Wang J et al. CAUSALdb: a database for disease/trait causal variants identified using summary statistics of genome-wide association studies. Nucleic Acids Res 48, D807–D816 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wang M et al. The Mount Sinai cohort of large-scale genomic, transcriptomic and proteomic data in Alzheimer’s disease. Sci. Data 5, 180185 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Storey JD & Tibshirani R Statistical significance for genomewide studies. Proc Natl Acad Sci USA 100, 9440–9445 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hauberg ME et al. Common schizophrenia risk variants are enriched in open chromatin regions of human glutamatergic neurons. Nat. Commun 11, 5581 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Han B & Eskin E Random-effects model aimed at discovering associations in meta-analysis of genome-wide association studies. Am. J. Hum. Genet 88, 586–598 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zeisel A et al. Brain structure. Cell types in the mouse cortex and hippocampus revealed by single-cell RNA-seq. Science 347, 1138–1142 (2015). [DOI] [PubMed] [Google Scholar]
- 51.Lek M et al. Analysis of protein-coding genetic variation in 60,706 humans. Nature 536, 285–291 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Finucane HK et al. Partitioning heritability by functional annotation using genome-wide association summary statistics. Nat. Genet 47, 1228–1235 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Pardiñas AF et al. Common schizophrenia alleles are enriched in mutation-intolerant genes and in regions under strong background selection. Nat. Genet 50, 381–389 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Bipolar Disorder and Schizophrenia Working Group of the Psychiatric Genomics Consortium. Genomic Dissection of Bipolar Disorder and Schizophrenia, Including 28 Subphenotypes. Cell 173, 1705–1715 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Cross-Disorder Group of the Psychiatric Genomics Consortium. Genomic Relationships, Novel Loci, and Pleiotropic Mechanisms across Eight Psychiatric Disorders. Cell 179, 1469–1482.e11 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Roussos P et al. A role for noncoding variation in schizophrenia. Cell Rep 9, 1417–1429 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Najt P et al. Impulsivity and bipolar disorder. Eur. Neuropsychopharmacol 17, 313–320 (2007). [DOI] [PubMed] [Google Scholar]
- 58.Ouzir M Impulsivity in schizophrenia: A comprehensive update. Aggress. Violent Behav 18, 247–254 (2013). [Google Scholar]
- 59.Cerimele JM & Katon WJ Associations between health risk behaviors and symptoms of schizophrenia and bipolar disorder: a systematic review. Gen. Hosp. Psychiatry 35, 16–22 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Zhang X et al. Negative evidence for a role of APH1B T27I variant in Alzheimer’s disease. Hum. Mol. Genet 29, 955–966 (2020). [DOI] [PubMed] [Google Scholar]
- 61.Hwang J-Y & Zukin RS REST, a master transcriptional regulator in neurodegenerative disease. Curr. Opin. Neurobiol 48, 193–200 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Schoenherr CJ & Anderson DJ The neuron-restrictive silencer factor (NRSF): a coordinate repressor of multiple neuron-specific genes. Science 267, 1360–1363 (1995). [DOI] [PubMed] [Google Scholar]
- 63.Mancuso N et al. Probabilistic fine-mapping of transcriptome-wide association studies. Nat. Genet 51, 675–682 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Wainberg M et al. Opportunities and challenges for transcriptome-wide association studies. Nat. Genet 51, 592–599 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.van der Wijst M et al. The single-cell eQTLGen consortium. elife 9, (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Mandric I et al. Optimized design of single-cell RNA sequencing experiments for cell-type-specific eQTL analysis. Nat. Commun 11, 5504 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Wojcik GL et al. Genetic analyses of diverse populations improves discovery for complex traits. Nature 570, 514–518 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Sul JH, Han B, Ye C, Choi T & Eskin E Effectively identifying eQTLs from multiple tissues by combining mixed model and meta-analytic approaches. PLoS Genet 9, e1003491 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Benjamini Y & Hochberg Y Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society: Series B (Methodological) 57, 289–300 (1995). [Google Scholar]
- 70.Joo JWJ, Hormozdiari F, Han B & Eskin E Multiple testing correction in linear mixed models. Genome Biol 17, 62 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Ota M et al. Dynamic landscape of immune cell-specific gene regulation in immune-mediated diseases. Cell 184, 3006–3021.e17 (2021). [DOI] [PubMed] [Google Scholar]
- 72.Ishigaki K et al. Polygenic burdens on cell-specific pathways underlie the risk of rheumatoid arthritis. Nat. Genet 49, 1120–1125 (2017). [DOI] [PubMed] [Google Scholar]
- 73.Mohammadi P, Castel SE, Brown AA & Lappalainen T Quantifying the regulatory effect size of cis-acting genetic variation using allelic fold change. Genome Res 27, 1872–1884 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Su Z, Marchini J & Donnelly P HAPGEN2: simulation of multiple disease SNPs. Bioinformatics 27, 2304–2305 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Meyer HV & Birney E PhenotypeSimulator: A comprehensive framework for simulating multi-trait, multi-locus genotype to phenotype relationships. Bioinformatics 34, 2951–2956 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Devlin B & Roeder K Genomic control for association studies. Biometrics 55, 997–1004 (1999). [DOI] [PubMed] [Google Scholar]
- 77.Delaneau O et al. A complete tool set for molecular QTL discovery and analysis. Nat. Commun 8, 15452 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Glassberg EC, Gao Z, Harpak A, Lan X & Pritchard JK Evidence for weak selective constraint on human gene expression. Genetics 211, 757–772 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Zeng B mmQTL v1.2.0. Zenodo url: 10.5281/zenodo.5560014 [DOI]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Brain eQTL meta-analysis resource: http://icahn.mssm.edu/brema


