The evolution, evolvability, and engineering of gene regulatory DNA

Abstract

Mutations in non-coding regulatory DNA sequences can alter gene expression, organismal phenotype, and fitness^1–3. Constructing complete fitness landscapes, mapping DNA sequences to fitness, is a long-standing goal in biology, but has remained elusive because it is challenging to generalize reliably to vast sequence spaces^4–6. Here, we construct sequence-to-expression models that capture fitness landscapes and use them to decipher principles of regulatory evolution. Using millions of randomly-sampled promoter DNA sequences and their measured expression levels in the yeast Saccharomyces cerevisiae, we learn deep neural network models that generalize with excellent prediction performance, and enable sequence design for expression engineering. Using our models, we study expression divergence under genetic drift and strong-selection weak-mutation regimes to find that regulatory evolution is rapid and subject to diminishing returns epistasis, that conflicting expression objectives in different environments constrain expression adaptation, and that stabilizing selection on gene expression leads to the moderation of regulatory complexity. We present an approach for using our models to detect signatures of selection on expression from natural variation in regulatory sequences and use it to discover an instance of convergent regulatory evolution. We assess mutational robustness, finding that regulatory mutation effect sizes follow a power law, characterize regulatory evolvability, visualize promoter fitness landscapes, discover evolvability archetypes and highlight the mutational robustness of natural regulatory sequence populations. Our work provides a general framework for addressing fundamental questions in regulatory evolution.

INTRODUCTION

Changes in cis-regulatory elements (CREs) play a major role in the evolution of gene expression¹. Mutations in CREs can affect their interactions with transcription factors (TFs), change the timing, location, and level of gene expression, and impact organismal phenotype and fitness^2,3. While TFs evolve slowly because they each regulate many target genes, CREs evolve much faster and are thought to drive substantial phenotypic variation⁷. Thus, understanding how cis-regulatory sequence variation affects gene expression, phenotype and organismal fitness is fundamental to our understanding of regulatory evolution².

A fitness function maps genotypes (which vary through mutations) to their corresponding organismal fitness values (where selection operates)⁸. A complete fitness landscape⁹ is defined by a fitness function that maps each sequence in a sequence space to its associated fitness, coupled with an approach for visualizing the sequence space. Partial fitness landscapes have been characterized empirically^4,5,10, often defining fitness as the maximum growth rate of single-cell organisms^4,11. Many recent empirical fitness landscape studies of proteins¹², adeno-associated viruses¹³, catalytic RNAs¹⁴, promoters¹⁵, and TF binding sites¹⁶ have favored molecular activities as fitness proxies because they are less susceptible to experimental biases and measurement noise¹⁷. In particular, the molecular activity of a promoter sequence as reflected in the expression of the regulated gene has been used to build a ‘promoter fitness landscape’¹⁸. However, despite advances in high-throughput measurements, empirical fitness landscape studies often sample sequences in the local neighborhood of natural ones and thus remain limited to a tiny subset of the complete sequence space whose size grows exponentially with sequence length (4^L for DNA or RNA, where L is the length of sequence)^4–6.

Understanding the relationship between promoter sequence, expression phenotype, and fitness would allow us to answer fundamental questions⁶ in evolution and gene regulation, and provide an invaluable bioengineering tool^6,19. A model that accurately approximates the relationship between sequence and expression can serve as an “oracle” in evolutionary studies to conduct and interpret in-silico experiments^20–23, predict which regulatory mutations affect expression and fitness (when coupled with expression-to-fitness curves¹¹), design or evolve new sequences with desired characteristics, determine how quickly selection achieves an expression optimum, identify signatures of selective pressures on extant regulatory sequences, visualize fitness landscapes and characterize mutational robustness and evolvability^{2,4–6,24,25}.

Here, we address these long-standing problems by developing a framework for studying regulatory evolution and fitness landscapes (Fig. 1a) based on Saccharomyces cerevisiae promoter sequence-to-expression models.

Fig. 1 |. The evolution, evolvability, and engineering of gene regulatory DNA.

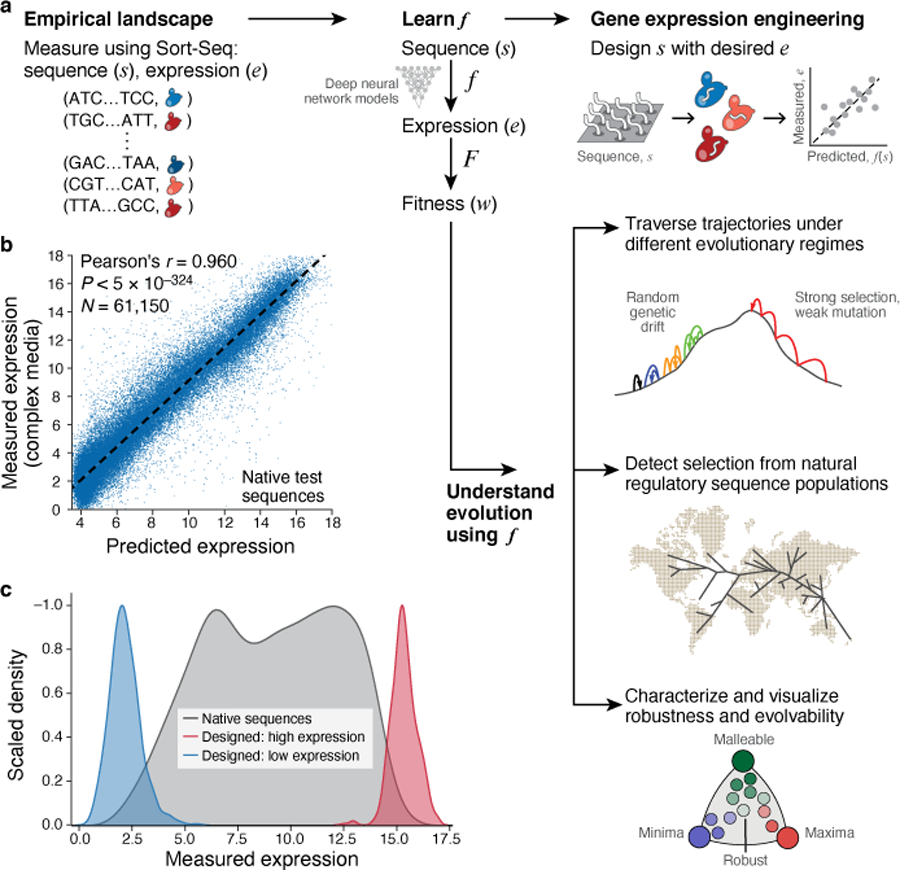
a, Project overview. b, Prediction of expression from sequence using the model. b, Predicted (x axis) and experimentally measured (y axis) expression in complex media (YPD) for native yeast promoter sequences. Pearson’s r and associated two-tailed p-values are shown; dashed line: line of best fit. c, Engineering extreme expression values beyond the range of native sequences using a genetic algorithm (GA) and the sequence-to-expression model. Normalized kernel density estimates of the distributions of measured expression levels for native yeast promoter sequences (grey), and sequences designed (by the GA) to have high (red) or low (blue) expression.

RESULTS

Models predict expression from sequence

We begin by building models that predict gene expression given an 80 bp promoter DNA sequence. To train these models, we measure the expression driven by promoter sequences using an approach we previously described²⁶, where 80 bp of DNA are embedded within a promoter construct and the associated expression is assayed in the S. cerevisiae (Methods). We clone promoter sequences into an episomal low copy number YFP expression vector, transform them into yeast, culture the yeast in the desired media, sort the yeast into 18 expression bins, and sequence the promoters present from the yeast in each bin to estimate expression (Methods and Supplementary Information). To avoid biases⁵ towards extant sequences, we measured the expression of 80 bp random DNA sequences, where each base is randomly sampled from the four bases. For training data, we measured each of >30 million sequences in complex media (YPD, Methods) and >20 million sequences in defined media (SD-Ura, synthetic defined lacking uracil). Using the resulting pairs of sequences and measured YFP expression levels, we trained convolutional neural network models (“convolutional models”) that predict expression from sequence in each medium (Methods).

To show that the learned convolutional models generalize to new sequences, we predicted the expression for several sets of test sequences not seen during model training, and compared them to their experimentally measured levels (Methods). For these test sequences, we quantified expression in independent experiments using the same experimental approach and in the same media. Our convolutional models had excellent prediction performance on native yeast promoter test sequences (Pearson’s r = 0.960, P < 5*10⁻³²⁴, n=61,150; Fig. 1b), and on multiple other test sets in both complex and defined media (Extended Data Fig. 1).

These results represent a ~45% decrease in error compared to the performance of biochemical models we previouly²⁶ trained on the same data (complex media; native yeast promoter test sequences; Supplementary Notes and Methods). Other published genomic model architectures adapted to and trained using our data also had excellent performance (Supplementary Fig. 4a), highlighting the predictive power of deep neural network models trained using our large-scale data. Finally, the expression measurements were highly correlated for the same sequences between the two media (Pearson’s r = 0.978, Extended Data Fig. 2a) and models trained on defined medium predicted expression in complex medium well (Pearson’s r = 0.966, Extended Data Fig. 2b). However, for some sequences we expect differences between growth conditions (below).

Models enable expression engineering

We leveraged the high predictive performance of our convolutional models for a synthetic biology application of gene expression engineering, by using model predictions as a ‘fitness function’ for genetic algorithms (GA) to design sequences with extreme expression values. We initialized the GA with a population of 100,000 randomly-generated samples from the sequence space, and simulated 10 generations to maximize (or minimize) the expression output from the convolutional model (Methods). We then synthesized the 500 sequences with the top predicted maximum (or minimum) expression levels and tested them experimentally. The GA-designed sequences drove, on average, more extreme expression than >99% of native sequences (99.6% for high expressing; 99.3% for low), with ~20% of designed sequences yielding more extreme expression than any native sequence tested (23.5% for high; 18.4% for low) (Fig. 1c). Thus, our sequence-to-expression model can be used for gene expression engineering.

Expression diverges under genetic drift

We next assessed the evolutionary malleability of expression under different evolutionary scenarios: random genetic drift, stabilizing selection, and directional selection for extreme expression levels (Fig. 2). In each case, we first simulated the scenario, using our convolutional model to predict the expression for each sequence, and then tested the model’s evolved sequences experimentally, where possible (Methods).

Fig. 2 |. The evolutionary malleability of gene expression.

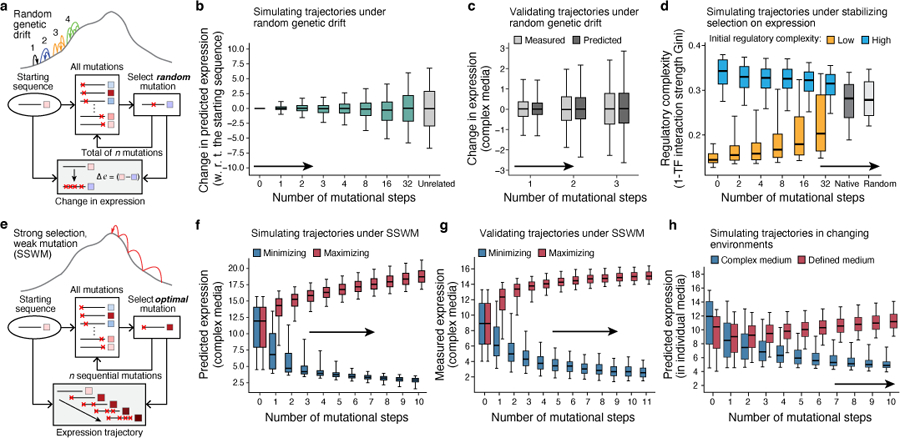
a-c, Expression divergence under genetic drift. a. Simulation procedure. b, Predicted expression divergence. Distribution of the change in predicted expression (y axis) for random starting sequences (n=5,720) at each mutational step (x axis) for simulated trajectories. Silver bar: expression differences between unrelated sequences. c, Experimental validation. Distribution of measured (light grey) and predicted (dark gray) changes in expression in complex media (y axis) for synthesized randomly-designed sequences (n=2,983) at each mutational step (x axis). d, Stabilizing selection on gene expression leads to moderation of regulatory complexity extremes. Regulatory complexity (y axis) of sequences from sequential mutational steps (x axis) under stabilizing selection to maintain the starting expression levels, where the regulatory interactions of starting sequences are complex (blue; n=192) or simple (orange, n=172). Right bars: regulatory complexity for native (dark gray) and random (light gray) sequences. e-g, Sequences under strong-selection weak-mutation (SSWM) can rapidly evolve to expression optima. e. Simulation procedure. f, Predicted expression evolution. Distribution of predicted expression levels (y axis) in complex media at each mutational step (x axis) for trajectories favoring high (red) or low (blue) expression, starting with native promoter sequences (n=5,720). g, Experimental validation. Measured expression distribution in complex media (y axis) for the synthesized sequences (n=10,322 sequences; 877 trajectories) at each mutational step (x axis), favoring high (red) or low (blue) expression. Axis scales differ due to variation in measurement procedure (Supplementary Information). h, Competing expression objectives constrain expression adaptation. Distribution of predicted expression (y axis) in complex (blue) and defined (red) media at each mutational step (x axis) for a starting set of native promoter sequences (n=5,720) optimizing for high expression in defined (red) and simultaneous low expression in complex (blue) media. (b-d,f-h) Midline: median; boxes: interquartile range; whiskers: 5^th and 95^th percentile range.

We first simulated random genetic drift of regulatory sequences, with no selection on expression levels. We randomly introduced a single mutation in each random starting sequence, repeated this process for multiple consecutive generations, and used our convolutional model to predict the difference in expression between the mutated sequences in each trajectory relative to the corresponding starting sequence (Fig. 2a-c). Expression levels diverged as the number of mutations increased, with 32 mutations in the 80 bp region resulting in nearly as different expression from the original sequence as two unrelated sequences (Fig. 2b). We validated our results experimentally by synthesizing sequences with zero to three random mutations and measuring their expression in our assay (Methods). The experimental measurements closely matched our predictions in both complex (Fig. 2c) and defined (Extended Data Fig. 1e) media, both in expression change (Pearson’s r: 0.869 and 0.847, respectively; Extended Data Fig. 1h,i) and level (Pearson’s r: 0.973 and 0.963 respectively; Extended Data Fig. 1l,m).

Stabilizing selection tempers complexity

Although gene regulatory networks often appear to be highly interconnected^26,27, the sources of this regulatory complexity and how it changes with the turnover of regulatory mechanisms²⁸ remain unclear. We used our model to study the evolution of regulatory complexity in the context of stabilizing selection, which favors the maintenance of existing expression levels. We first quantified regulatory complexity, defined as 1 minus the Gini coefficient (a measure of inequality of continuous values within a population) of TF regulatory interaction strengths. For this, we used an interpretable biochemical model we previously developed²⁶ (Methods) because it has parameters that explicitly correspond to TFs, and we can directly query their contributions to model predictions. Next, starting with native sequences whose regulatory complexity is either extremely high (many TFs with similar contributions to expression) or low (few TFs contribute disproportionately to expression) and spanning a range of expression levels, we introduced single mutations into each starting native sequence for each of 32 consecutive generations, identified the sequences that conserved the original expression level using the convolutional model, and selected one of them at random for the next generation. We then assessed the regulatory complexity of the evolved sequences.

As random mutations accumulated, the regulatory complexity of sequences starting at both complexity extremes shifted towards moderate complexities (Fig. 2d, rightmost blue and orange), closer to the averages for both random and native sequences (Fig. 2d, greys). This suggests that stabilizing selection on expression leads to a moderation of regulatory complexity, resulting from gradual drift in the roles of the different regulators, such as an increase in complexity due to a decrease in the relative contribution of one predominant TF (e.g. Abf1p for AIF1), or a decrease in complexity through smaller changes in a much larger number of sites (e.g. YDR476C; Supplementary Fig. 8). The overall distribution of regulatory complexity of native yeast promoters is similar to that of random sequences (Fig. 2d, grey boxes), suggesting that there is little selection on the regulatory complexity of native sequences in a single environment.

Strong selection rapidly finds extrema

To study the impact of directional selection on expression, we simulated the strong-selection weak-mutation (SSWM) regime²⁹ (Fig. 2e, Methods), where each mutation is either beneficial or deleterious (strong selection, with mutations surviving drift and fixing in an asexual population), and mutation rates are low enough to only consider single base substitutions during adaptive walks (weak mutation). Starting with a set of native promoter sequences, at each iteration (generation), for a given starting sequence of length L, we considered all of its 3L single-base mutational neighbors, used our convolutional model to predict their expression, and took the sequence with the largest increase (or separately, decrease) in expression at each iteration (generation) as the starting sequence for the next generation (Fig. 2e, Methods).

Sequences that started with diverse initial expression levels rapidly evolved to high (or separately, low) expression, with the vast majority evolving close to saturating extreme levels within 3–4 mutations in both the complex (Fig. 2f) and defined (Extended Data Fig. 1f) media. Sequences took diverse paths to evolve either high or low expression (Supplementary Fig. 7). We validated these trajectories experimentally for select series of sequences (Fig. 2g, Extended Data Fig. 1g), measuring the expression driven by synthesized sequences from several generations along simulated mutational trajectories for complex media (10,322 sequences from 877 trajectories) and defined media (6,304 sequences from 637 trajectories). We observed extreme expression within 3–4 mutational steps, with high agreement between measured and predicted expression change (Extended Data Fig. 1j,k; Pearson’s r: 0.977 and 0.948, respectively) and expression levels (Extended Data Fig. 1n,o; Pearson’s r: 0.980 and 0.963) along the trajectories in both complex and defined media. Thus, cis-regulatory sequence evolution is rapid and subject to diminishing returns epistasis³⁰.

Opposing objectives constrain adaptation

In contrast to the rapid evolution towards expression extremes, we found that evolution to satisfy two opposing expression requirements (one in each growth media) was more constrained. A concrete example is the expression of the URA3 gene: organismal fitness increases with increased URA3 expression in defined media lacking uracil, because Ura3p is required for uracil biosynthesis, but fitness decreases with increased URA3 expression in complex media containing 5-FOA due to Ura3p-mediated conversion of 5-FOA to toxic 5-fluorouracil (Extended Data Fig. 2c). To study this regime³¹, we started with a set of native promoter sequences (and separately, a set of random sequences) and used the convolutional model to simulate SSWM trajectories (Methods) that maximize the difference in expression between the two media (defined and complex). While the difference in expression increased with each generation (Extended Data Fig. 2d,e), the vast majority of sequences achieved neither the maximal nor the minimal expression in either condition after 10 generations (Fig. 2h, Extended Data Fig. 2f), for both native and random starting sequences. The evolved sequences became enriched for motifs for TFs involved in nutrient sensing and metabolism, compared to the starting sequences (Extended Data Fig. 2g), suggesting that the model is taking advantage of subtle differential activity of certain regulators between the two conditions to evolve condition specificity. Thus, while evolving a sequence to achieve a single expression optimum requires very few mutations, encoding multiple opposing objectives in the same sequence is more difficult, limiting expression adaptation.

Transformers enable inference at scale

We next turned to the evolution and evolvability of regulatory sequences in extant strains and species. This required us to predict expression for billions of sequences and, although our convolutional model had excellent predictive power, our implementation was limited in its scalability and incompatible with the Tensor Processing Units (TPUs), available to us for larger-scale computational tasks (Methods). To enable large-scale expression prediction, we developed “transformer” models that used transformer encoders³² with other building blocks attempting to implicitly capture known aspects of regulation³³ (Methods, Supplementary Fig. 12). The transformer models had ~20x fewer parameters than the convolutional models (Methods, Supplementary Information), predicted expression as well as the convolutional models (Extended Data Fig. 3), and better captured the propensity for expression to plateau under SSWM (Supplementary Fig. 19). The convolutional and transformer models had highly correlated predictions in both media (Supplementary Fig. 4e-h, Pearson’s r=0.967–0.985), and yielded equivalent conclusions from the analyses of genetic drift, directional selection and conflicting objectives (Extended Data Fig. 3, Supplementary Fig. 17-18).

The Expression Conservation Coefficient

We applied our sequence-to-expression transformer model to detect evidence of selective pressures on natural regulatory sequences, inspired by the way in which the ratio of non-synonymous (“non-neutral”) to synonymous (“neutral”) substitutions (d_N/d_S) in protein coding sequences is used estimate the strength and mode of natural selection³⁴. By analogy^2,35, for regulatory sequences², we used the transformer model to quantitatively assess the impact of naturally occurring regulatory genetic variation on expression, compared to that expected with random mutations, and summarized this with an Expression Conservation Coefficient (ECC) (Methods). To compute the ECC, we compared, for each gene’s promoter, the standard deviation of the expression distribution predicted by the transformer model for a set of naturally varying orthologous promoters (σ_B) to the standard deviation of the expression distribution predicted for a matched set of random variation introduced to that promoter (σ_C; related to the mutational variance³⁶; Fig. 3a). We define the ECC for a gene as log(σ_c/σ_B), such that a positive ECC indicates stabilizing selection on expression (lower variance in native sequences than expected by chance), a negative ECC indicates diversifying (disruptive) selection or local adaptation (greater variance in native sequences), and values near 0 suggest neutral drift.

Fig. 3 |. The Expression Conservation Coefficient (ECC) detects signatures of stabilizing selection on gene expression using natural genetic variation in regulatory DNA.

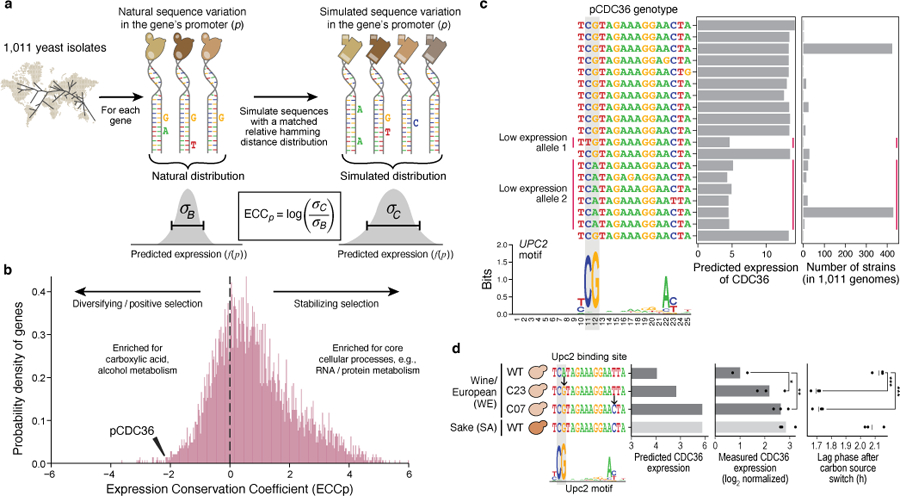
a, ECC calculation from 1,011 S. cerevisiae genomes³⁷. b, ECC distribution for S. cerevisiae genes. Frequency distribution of ECC values (x axis). Dashed line separates regions corresponding to disruptive/positive selection (left) and stabilizing selection (right). GO terms enriched by the ECC ranking are shown. Arrowhead: ECC value for the CDC36 promoter sequence. c, Convergent regulatory evolution in the CDC36 promoter. Predicted expression (x axis, left bar plot) and associated number of strains (x axis, right bar plot) of all alleles among the analyzed CDC36 promoter sequence within 1,011 yeast isolates, along with an alignment of their Upc2p binding site sequences (left; Upc2p binding motif below). Red vertical lines: two independently evolved low-expressing alleles. Grey vertical boxes: key positions in the Upc2p motif with single nucleotide polymorphisms. d, Validation of CDC36 promoter allele expression and organismal phenotype. Strains (y axis) with different Upc2p binding site alleles for both model-predicted CDC36 expression (left; predicted on −170:−90 region to capture entire Upc2p binding site), measured CDC36 expression (middle), and lag phase duration (right). Points: biological replicates (n=3); bars/vertical lines: means. Bar color: strain background. Student’s t-test p-values, unpaired, equal variance, one-sided (expression, WE WT vs. C23 p=0.044, C07 p=6.69*10⁻³) or two-sided (lag phase, WE WT vs. C23 p=1.34*10⁻⁴, C07 p=2*10⁻⁴); *p<0.05; **p<0.01; ***p<0.001.

We calculated the ECC for 5,569 S. cerevisiae genes using the natural variation observed across over 4.73 million orthologous promoter sequences from the 1,011 S. cerevisiae isolates³⁷ in the −160 to −80 regions (with respect to the Transcription Start Site (TSS)), a critical location for TF binding³⁸ and determinant of promoter activity²⁶ (Fig. 3a,b, Supplementary Table 1), using our transformer model to predict the expression for each sequence. To assess the robustness of the ECC values, we recomputed the ECC using multiple published sequence-to-expression model architectures that we adapted and trained using our data and found that models with similarly high predictive power resulted in similar ECC values (Supplementary Fig. 4b-d, 5g).

Over 70% of promoters had positive ECCs, suggesting stabilizing selection (and conserved expression) (binomial test P < 10⁻²¹⁵) (Fig. 3b), consistent with previous reports based on direct measurements of gene expression³⁹. Genes with high ECCs were enriched in highly-conserved core cellular processes (e.g., RNA and protein metabolism) (Fig. 3b, Supplementary Table 2), and those with low ECCs were most enriched in processes related to carboxylic acid and alcohol metabolism (Fig. 3b, Supplementary Table 2), potentially reflecting adaptation of fermentation genes to the diverse environments of these isolates³⁷.

The ECC discovers convergent evolution

A striking example of predicted positive selection is the promoter of CDC36 (NOT2; ECC= −2.138, Fig. 3b), which has common natural alleles with either low or high (predicted) expression across the isolates (Fig. 3c). Analysis of CDC36 promoter sequences (Methods) suggests that low-expression evolved at least twice independently, resulting in two distinct variants with reduced expression (Fig. 3c, allele 1 and 2). Interrogation with the biochemical model²⁶ to identify factors impacting these expression differences (Extended Data Fig. 4a) suggested that both low-expression alleles are explained by disruption of the same binding site for Upc2p, an ergosterol sensing TF (Fig. 3c). To validate this, we restored the putative Upc2p binding site in a strain (WE), where it is otherwise disrupted, and measured expression levels by qPCR and growth upon changing carbon source (Methods). Restoration of the Upc2p binding site increased actual expression, confirming the model’s prediction (Pearson’s r=0.96, p=0.039, n=4; Fig. 3d). We hypothesized that these variants could alter the rate of transcriptional reprogramming when changing environments via Cdc36p-regulated mRNA turnover⁴⁰. Indeed, restoration of the Upc2 binding site reduced the strains’ lag time to growth when switching carbon sources (Fig. 3d, right; Methods), and they grew to a higher culture density (Supplementary Fig. 10). Thus, convergent evolution of the CDC36 promoter, discovered using the ECC, independently produced two alleles that result in similar perturbations to TF binding, expression, and growth.

ECC vs. cross-species RNAseq and fitness

ECC values were consistent with expression conservation as measured for yeast orthologs across clades at short (Saccharomyces), medium (Ascomycota), or long (mammals) evolutionary scales (Extended Data Fig. 4b). In Saccharomyces, 1:1 orthologs with conserved expression levels across species (as measured by RNA-seq⁴¹) had significantly higher ECC (computed from the 1,011 yeast isolates) than genes whose expression was not conserved (two-sided Wilcoxon rank-sum P = 3.1*10⁻⁴, Extended Data Fig. 4b, bottom left, Methods). Next, we performed RNA-seq across 11 Ascomycota yeast species (Methods), finding that 1:1 orthologs with conserved expression across Ascomycota had significantly higher ECC values (Extended Data Fig. 4b, bottom center, P = 1.16*10⁻⁶). Finally, the 1:1 orthologs of genes with high ECC values in the 1,011 S. cerevisiae isolates also had more conserved expression within mammals⁴² (Extended Data Fig. 4b, bottom right, P = 1.07*10⁻⁴, Methods). Thus, while 1:1 yeast-mammal orthologs are likely critical to an organism’s fitness, only a subset of these may be under stabilizing selection on expression, and this subset tends to be under such selection in both yeasts and mammals. Thus, the ECC quantifies stabilizing selection on expression in yeast and may predict stabilizing selection on orthologs’ expression in other species.

Genes with higher ECCs also had a stronger effect on fitness in S. cerevisiae upon changing their expression level. We interrogated the total variation of previously measured expression-to-fitness curves¹¹ to calculate a ‘fitness responsivity’ score that captures the dependence of fitness on expression (Extended Data Fig. 5, Methods). Fitness responsivity was significantly positively correlated with the ECC (Supplementary Fig. 2e, P = 0.003, Spearman ρ = 0.326). Fitness responsivity was not associated with regulatory sequence divergence per se across the promoter sequence (as estimated by mean Hamming distance among orthologous promoters, Methods, Supplementary Fig. 2d, P = 0.46, Spearman ρ = 0.083). Thus, while stabilizing selection on gene expression (as captured by the ECC) can shape the types of mutations that accumulate in the population, it may have little effect on the overall rate at which mutations accumulate in promoter regions within populations, which has been previously used to test for evidence of selection.

Stabilizing selection shapes robustness

While a gene’s ECC (computed from the natural genetic variation in regulatory DNA) represents the imprint of its evolutionary history, its mutational robustness (assessed directly from the gene’s promoter sequence) should describe how future mutations would affect its expression⁴³. Across all native yeast promoters, the magnitude of expression changes predicted by the transformer model due to single base-pair mutations follows a power law with an exponent of 2.252 (standard error of fit σ = +/− 0.002, P = 2.4*10⁻²⁶³), such that a small number of mutations have an outsized effect on expression (~10% of mutations account for ~50% of the changes in expression, Extended Data Fig. 4d). In individual genes, the distribution can vary substantially (below).

For a given promoter sequence, we defined the mutational robustness of a sequence length L, as the percent of its 3L single nucleotide mutational neighbors predicted by the transformer model to result in a negligible change in expression (Extended Data Fig. 4c, Methods), following previous definitions of mutational robustness^25,43. The mutational robustness of a gene’s promoter sequence was positively correlated with the gene’s fitness responsivity (Supplementary Fig. 2f, Spearman ρ = 0.476, P = 8.18*10⁻⁶), suggesting that fitness-responsive genes have evolved more mutationally robust regulatory sequences. Mutational robustness, which, unlike the ECC, is computed for single sequences without a set of variants across a population, was also correlated to the ECC (Supplementary Fig. 2g, Spearman ρ = 0.515, P = 9.99*10⁻⁷). Similarly, the promoter sequences of yeast genes with conserved expression across Saccharomyces strains⁴¹, Ascomycota species, or mammals⁴² had higher mutational robustness (P = 8.4*10⁻³, 6.5*10⁻⁵, and 0.00377, respectively, two-sided Wilcoxon rank-sum test).

Thus, genes whose expression levels are under stabilizing selection have regulatory sequences that tend to be more robust to the impact of mutations, which may reflect their history and constrain their future.

Fitness landscapes in evolvability space

Mutational robustness enables the exploration of novel genotypes that could subsequently facilitate adaptation and thus promote evolvability, the ability of a system to generate heritable phenotypic variation²⁵. To characterize regulatory evolvability, we extended our description of mutational robustness by representing each sequence using a sorted vector of expression changes (predicted by the transformer model) that are accessible through single nucleotide mutations (Fig. 4a, left, Methods). This ‘evolvability vector’ captures the capacity for changes in genotype to alter expression phenotype, in line with previous definitions of evolvability²⁵.

Fig. 4 |. The evolvability vector captures fitness landscapes.

a, Characterizing regulatory evolvability by computing an evolvability vector. Left and middle: Generating evolvability vectors for a sequence. Right: training an autoencoder with evolvability vectors to generate a 2D representation to visualize sequences in archetypal evolvability space. b, Evolvability archetypes discovered by the autoencoder. Left: Evolvability vectors of the rank ordered (x axis) predicted change in expression (y axis) for native sequences closest to each of the malleable (green), maxima (red) or minima (blue) archetypes and the ‘robustness cleft’ (black). Right: all native yeast (S. cerevisiae S288C) promoter sequences (grey points) projected onto the archetypal evolvability space by their evolvability vectors. Evolvability archetypes (colored circles) and their closest native sequences (s₁-s₄ as on left) are marked. c,d, Evolvability space captures mutational robustness and expression levels. Evolvability vectors (points) of all native yeast promoter sequences projected onto the evolvability space (archetypes are large colored circles, as in b) and colored by mutational robustness (c) or predicted expression levels (d). e, ABF1 promoter fitness landscape. Evolvability vectors of promoter sequences projected onto the evolvability space and colored by computed fitness (color, Methods). f,g, Malleable promoter sequences dynamically traverse the evolvability space. Evolvability vector projections of native sequences (points) from all 1,011 S. cerevisiae isolates. Red points: natural promoter sequence variants for DBP7, the promoter closest to the malleable archetype (f) and for UTH1, the promoter closest to the robustness cleft (g). h, The robustness of native promoter sequences. Density (color) of all native yeast promoter sequences when their evolvability vectors are projected onto the evolvability space.

We next asked whether regulatory evolvability vectors fell into distinct classes by identifying evolvability ‘archetypes’. Archetypes⁴⁴ represent the extremes of canonical patterns, such that the evolvability vector of each individual sequence can be represented by its similarity to each of several archetypes representing these extremes. Applying this paradigm, we used our transformer model to compute evolvability vectors for a new random sample of a million sequences and then learned a two-dimensional representation of these evolvability vectors (referred to as the ‘evolvability space’) using an autoencoder⁴⁵ (Fig. 4a, right, Methods). This archetypal evolvability space, that is bounded by a simplex whose vertices represent evolvability archetypes (Fig. 4a, right, Methods) and where the evolvability vector of each sequence is a single point, allows us to effectively visualize arbitrarily large sequence spaces in two dimensions.

Three archetypes captured most of the variation in evolvability vectors (Extended Data Fig. 6a,b; Methods), corresponding to local expression minimum (A_minima), local expression maximum (A_maxima), and malleable expression (A_malleable) (Fig. 4b). A_minima and A_maxima correspond to sequences where most 3L mutational neighbors do not change expression, and the ones that do, increase it (for A_minima) or decrease it (for A_maxima). Conversely, for A_malleable sequences, most 3L mutational neighbors change expression and are equally likely to decrease or increase it (Fig. 4b). In addition to these three archetypes, mutationally robust sequences were present as a central cleft in the evolvability space (Fig. 4b,c; “robust”). The evolvability space also distinguishes native regulatory sequences by their associated expression level (Fig. 4d), with intermediate expression more likely to be near the malleable archetype (A_malleable) and depleted near the robustness cleft (Fig. 4d, Supplementary Information).

The location of sequences in evolvability space reflects the selective pressures operating on the sequence. Sequences under strong stabilizing selection on gene expression tend to be located far away from the malleable archetype: there is a strong negative correlation between malleable archetype proximity and mutational robustness (Extended Data Fig. 6c,e; Spearman’s ρ = −0.746, P = 1.97*10⁻¹⁵), the ECC (Extended Data Fig. 6d,f,g; ρ = −0.596, P = 5.4*10⁻⁹), fitness responsivity (Extended Data Fig. 6h; ρ = −0.413, P = 1.4*10⁻⁴), and expression conservation across species as measured by RNA-seq (Saccharomyces: P = 0.000251, Ascomycota: P = 0.00002, Mammals: P = 0.00114; two-sided Wilcoxon rank-sum test).

To visualize promoter fitness landscapes in two dimensions we combined our sequence-to-expression transformer model with previously measured expression-to-fitness curves¹¹, and integrated them with the two-dimensional archetypal evolvability space (Fig. 4e, Extended Data Fig. 7, Methods). Unlike prior visualizations of fitness landscapes, which group sequences by their sequence similarity, here, sequences are arranged by the similarity in their evolvability. This approach effectively visualizes arbitrarily large sequence spaces in two-dimensions, as well as groups sequences by their evolutionary properties. This addresses the challenges otherwise posed by sequence similarity-based landscapes since highly similar regulatory sequences can have different functional properties (e.g., due to a loss of a TF binding site), while very different sequences can be functionally similar (e.g., due to shared TF binding sites). When organismal fitness is available for a particular gene and overlaid on the landscape (Fig. 4e, Extended Data Fig. 7), the resulting patterns depend on both the condition-specific sequence-to-expression function (e.g., governing color (fitness) through predicted expression, and embedded position, through evolvability) and the gene- and condition-specific expression-to-fitness functions.

Finally, we studied how natural yeast sequences explored evolutionary space, by placing the evolvability vectors of each of set of orthologous promoters of the 1,011 sequenced S. cerevisiae isolates³⁷ in the archetypal evolvability space. When a gene’s promoter from one strain is near the malleable archetype, its orthologs in the other strains tended to broadly distribute in the evolvability space (Extended Data Fig. 6i), but avoid the robustness cleft (e.g., the DBP7 promoter from strain S288C; Fig. 4f). Conversely, when a promoter is near the robustness cleft (e.g., the UTH1 promoter from S288C), so are its orthologs (Fig. 4g, Extended Data Fig. 6i). Using in silico mutagenesis to interpret our model, we found that the DBP7 promoter is particularly malleable partly as a result of an intermediate affinity Rap1p binding site, where the most impactful mutations increased or decreased the Rap1p affinity for this site, impacting expression (Extended Data Fig. 8a). By contrast, the UTH1 promoter requires many sequential mutations, each of which has minimal impact individually, to reduce expression appreciably (Extended Data Fig. 8b). This could reflect the ways in which stabilizing selection constrains evolvability: promoters that are not under strong stabilizing selection explore expression space more freely and can quickly adapt to a new expression optimum, since the population likely already contains multiple alleles that achieve diverse expression levels (e.g. Fig. 4f). Interestingly, many of the native sequences in S. cerevisiae are near the robustness cleft (Fig. 4h).

Thus, the evolvability vector, which can be computed using our model directly for any sequence (without any population genetics data), encodes information about a sequence’s evolutionary history and potential futures.

DISCUSSION

Here, we presented a framework that addresses fundamental questions in the evolution and evolvability of regulatory sequences^2,25. Our models, developed using a combination of large scale random sequence libraries, sensitive reporter assays and deep learning (Methods), are useful as “oracles” for model-guided biological sequence design¹⁹, and answering important questions in the study of fitness landscapes^4–6, evolutionary malleability of expression and its variation across strains and species², mutational robustness⁴³, and evolvability²⁵. The framework presented here will help advance synthetic biology, cell and gene therapy, and metabolic engineering in addition to the study of evolution.

Previous studies suggested that evolution favors more complex regulatory solutions⁴⁶, but we showed that if stabilizing selection acts only on expression, regulatory complexity extremes gradually move towards the moderate complexity levels observed in native and random sequences (Fig. 2d). This supports a model where most extant regulatory sequences evolved by sampling constraint-satisfying solutions in proportion to their frequency in the sequence space, without specific consideration of the solution’s complexity.

In our study, evolving condition-specificity in a promoter sequence was much slower than simply modifying the expression level. Some yeast genes achieve condition-specificity by including multiple binding sites for condition-responsive TFs. For instance, the GAL1–10 Upstream Activating Sequence contains multiple binding sites for the galactose-responsive Gal4, which are conserved across millions of years, suggesting an ancient origin⁴⁷. Because the size of the regulatory region restricts the number of TF binding site locations, including more TFs and more regulatory sequences per gene (e.g. enhancers) may be required for more complex regulatory programs observed in higher eukaryotes⁴⁸.

The d_N/d_S ratio has been used extensively to characterize the evolutionary rates of protein coding genes³⁴, and we developed an analogous^2,35 coefficient, the ECC, for detecting evidence of selection on expression from natural variation across multiple orthologous regulatory sequences in strains of one species. The ECC complements and extends existing measures of expression conservation, since it integrates across the regulatory sequence and is not limited to specific TFs or binding motifs, does not require additional experiments to test the functions of mutations for each regulatory region, and does not rely on detecting non-uniformity in mutation distributions.

Complementing the ECC, mutational robustness as calculated with our model is predictive of selective pressures on individual sequences (Supplementary Fig. 2f-g). While we find that strong constraint on the function of regulatory sequences can shape them to be robust to future mutations, it is unlikely that robustness itself is the selected trait, since increased robustness to future mutations is likely to be of little marginal benefit⁴³. Instead, this may reflect a secondary benefit of having evolved decreased expression noise^49,50, or another as-yet-unknown mechanism. It may also reflect the fact that the sequences of some ancestral promoters may be similar to the mutational neighbors of extant sequences, and, if selective constraints on expression have remained stable, these ancestral and extant sequences likely have similar expression levels.

Based on our model-derived evolvability vectors, sequences spanned an evolvability spectrum from robust to malleable (Fig. 4c-d,f-h), and for native regulatory sequences, the magnitudes of accessible mutation effects follows a power law. Evolvability vectors also help visualize fitness landscapes⁴ (Fig. 4e, Extended Data Fig. 7) and future work can further improve our understanding of their topography^4,5.

Our sequence-to-expression models are currently limited by regulatory region and species. For example, sequence mutations that affect other regulatory mechanisms (e.g., genomic context, mRNA processing and degradation, regulation by RNA-binding proteins, translational efficiency) can compensate for those that affect transcription. While our models emulated the biological process of our experimental system, as demonstrated by their excellent predictive power, future interpretability studies will shed further light on molecular mechanisms. Finally, for multicellular organisms, selection acts simultaneously on expression levels in many different cell types and environments. As models of gene regulation are created for other species, environments, and regulatory regions, our framework will help provide further insights into regulatory evolution.

METHODS

Experimental measurement of sequence-expression pairs using a Sort-seq strategy

We experimentally measured expression using a Sort-seq^2,3,51–59 strategy called the Gigantic Parallel Reporter Assay (GPRA) we previously described²⁶ (Supplementary Fig. 1). Briefly, for each set of expression measurements mentioned, random or designed single stranded oligonucleotides were ordered from IDT (random; Supplementary Table 3) or Twist Biosciences (designed; sequences on GEO; accession GSE163045), cloned into the promoter of a Yellow Fluorescent Protein (YFP) gene within a CEN plasmid (Addgene: 127546) as previously described²⁶ and transformed into yeast (strain Y8205 for the training dataset of random sequences, and strain S288C::ura3 for all the rest of the sequences measured). The library is maintained in yeast as an episomal low copy number plasmid. It was previously reported that the expression measurements are highly correlated with expression levels as measured using integrated reporters (R²=0.97)⁵⁴. Yeast were grown in continuous log phase, diluting as necessary to maintain an OD between 0.05 and 0.6 for 8–10 generations up until the time of harvest. Cells were harvested, washed once in ice cold PBS, and kept on ice in PBS until sorting. Cells were sorted into 18 uniformly-sized expression bins covering the majority of the expression distribution. Post sort, cells were re-grown in SD-Ura until saturation, plasmids isolated, and sequencing libraries created sequenced with a 150 cycle NextSeq kit. For libraries with random 80 bp sequences, sequences were consolidated as previously described²⁶. Reads from other (defined, non-random) libraries were aligned to the pre-defined sequences using Bowtie2⁶⁰, including only reads that perfectly matched a designed sequence. For each sequence, the expression level was the average of the expression bins in which it was observed, weighted by the number of times it was observed in each bin. These expression measurements were carried out separately in defined media lacking uracil (SD-Ura (Sunrise Science, #1703–500)) and complex media (YPD: yeast extract, peptone, dextrose).

Architecture of the convolutional model

A deep neural network model^{20,21,23,61–69} with convolutional layers was constructed and used for designing sequences with high and low expression (Fig. 1c), and running evolutionary simulations under stabilizing selection, genetic drift, and SSWM (Fig. 2) for each condition. These designed sequences, whose expression was experimentally quantified (e.g. Fig. 1c and 2d,g), were designed using models with the following architecture:

Input.

The input is the DNA sequence (s) represented in one-hot encoding. Input Shape: (1, 110, 4)

Convolution Block

• For the forward and reverse strand, separately,

  • Strand-specific convolution layer 1. Kernel Shape: (1, 30, 4, 256)
  • Strand-specific convolution layer 2. Kernel Shape: (30, 1, 256, 256)

• Concatenation of features from the forward and reverse strand

• Convolution layer 3. Kernel Shape: (30, 1, 512, 256)

• Convolution layer 4. Kernel Shape: (30, 1, 256, 256)

• A bias term and a ReLU activation was added to each convolution layer in this block.

Fully Connected Layers

• Fully connected layer 1. Kernel Shape: (110*256, 256).

• Fully connected layer 2. Kernel Shape: (256, 256)

• A bias term and a ReLU activation were added to each layer in this block.

Output.

Linear combination of the 256 features extracted as a result of all the previous operations on the sequence (s) to generate the predicted expression (e).

Every fully connected layer was L2 regularized with a 0.0001 weight and had a dropout probability of 0.2.

Training of the convolutional model

For training, 20,616,659 random sequences for the defined medium and 30,722,376 random sequences for the complex medium (each to train a separate model) were used, along with their experimentally measured expression as described above. A mini-batch size of 1,024 was used for training and a mean squared error loss was optimized using the Adam optimizer⁷⁰ with an initial learning rate of 0.0005. The model was trained for 5 epochs. Model architecture was written in TensorFlow⁷¹ 1.14 using Python 3.6.7. The convolutional model used TensorFlow graphs and sessions in its implementation and was thus incompatible with the Tensor Processing Units (TPUs)⁷². These convolutional models (for both media) were used for all the predictions in Fig. 1 and 2 and Extended Data Fig. 1, 2.

The models were tested by predicting expression on sequences that the model had never seen before (Supplementary Fig. 21) that were measured in separate experiments, where the library was lower complexity (fewer sequences) than the experiments that generated the training data, such that the expression associated with each sequence was measured with high accuracy (~100 yeast cells per sequence on average). The test libraries included random, native (i.e. present in the yeast genome), and designed sequences.

Training and evaluation were carried out on 4 Tesla M60 GPUs. All code for training and using the convolutional model is available here: https://github.com/1edv/evolution/tree/master/manuscript_code/model/gpu_only_model.

Architecture of the transformer model

A transformer model^23,32,73 was developed to run inference faster than the convolutional model, as needed for the evolutionary analyses in Fig. 3 and 4. The transformer model had ~20x fewer parameters (~1.3 million, compared to the ~24 million parameters of the convolutional model) and was able to leverage Tensor Processing Units (TPUs) for computation. Transformer models are used in all the analyses in Fig. 3 and 4 and Extended Data Fig. 3-4, and 6-8. Benchmarking analyses and ablation analyses for the transformer model are available in the Supplementary Information.

The deep transformer model has the following architecture (Supplementary Fig. 12):

Input.

The input is the DNA sequence (s) represented in one-hot encoding. Input Shape: (110, 4)

Convolution Block.

The convolution block is constructed in the following order (Supplementary Fig. 12b):

• Revere Complement Aware 1D Convolution. The forward and reverse strand are operated on separately with a convolutional kernel to generate strand specific sequence-environment interaction features. Kernel Shape: (30, 4, 256).

• Batch Normalization

• Rectified Linear Unit (ReLU)

• Concatenation of Features from the forward and reverse strand

• 2D Convolution: Convolve over the combined features from both the strands to capture interactions between strands. Kernel Shape: (2, 30, 4, 256)

• Batch Normalization

• ReLU

• 1D Convolution. Kernel Shape: (30, 64, 64)

• Batch Normalization

• ReLU

Transformer Encoder Blocks.

Two transformer encoder blocks^32,74,75 are constructed in the following order (Supplementary Fig. 12c):

• Multi-Head Attention: 8 heads, capturing relations between features from different positions of (s) to compute a representation for the features extracted from the convolution block from (s).

• Residual Connection

• Layer Normalization

• Feed Forward Layer with 8 units

• Residual connection

• Layer Normalization

Bidirectional LSTM layer.

A bidirectional LSTM layer to capture the long-range interactions between different regions of the sequence with 8 units and 0.05 dropout probability.

Fully Connected Layers (Supplementary Fig. 12d).

Two Fully connected layers with 64 Hidden Units, each consisting of ReLU and Dropout (0.05 dropout probability).

Output.

Linear Combination of 64 features extracted as a result of all the previous operations on the sequence (s) to generate the predicted expression (e).

Training of the transformer model

20,616,659 random sequences (defined medium) and 30,722,376 random sequences (complex medium), along with their experimentally measured expression, were used to train separate models for each media. Model architecture was written in TensorFlow⁷¹ 1.14 using Python 3.6.7 with multiple open source libraries (citations, where relevant, are included in code for them). A mini-batch size of 1,024 was used for training and a mean squared error loss was optimized using a RMSProp optimizer⁷⁶ with a learning rate of 0.001. The stopping criterion monitored was the ‘r-squared’ value and the model was allowed to train for 10 epochs without improvement before stopping training. Training was carried out on a Google Cloud Tensor Processing Unit (TPU)⁷² v3–8. Evaluation was carried out on 4 Tesla M60 GPUs. The model architecture visualization was generated using Netron 4.5.1. All processed data and models are publicly available on Zenodo at https://zenodo.org/record/4436477 and all code is available on GitHub at https://github.com/1edv/evolution/tree/master/manuscript_code/model/tpu_model. Transformer models are used in all the analyses in Fig. 3 and 4 and Extended Data Fig. 3-4, and 6-8.

The models were tested by predicting expression on test sequences that the model had never seen before (Supplementary Fig. 21) that were measured in separate experiments, which included random, native (i.e. present in the yeast genome), and designed sequences. To obtain expression measurements for each tested sequence that are more accurate than those from the high-complexity training data experiment, library complexity was limited such that each test promoter sequence is observed in ~100 yeast cells (Methods, Supplementary Information).

Gene expression engineering using a genetic algorithm for sequence design

To design^77–80 new sequences with desired expression, a genetic algorithm (GA) was implemented with the distributed evolutionary algorithms in python (DEAP) package⁸¹. The mutation probability and the two-point crossover probability were set to 0.1 and the selection tournament size was 3. The initial population size was 100,000 and the GA was run for 10 generations. The convolutional model was used as the basis for the objective function for GA, which was maximized for high expression and minimized for low expression (maximizing negative predicted expression). The top 500 sequences were synthesized (by Twist Biosciences) and expression was measured experimentally using our reporter assay, as described above.

Characterizing random genetic drift

Simulation of random genetic drift (Fig. 2a) was initialized with a set of 5,720 random sequences, in generation 0. For each sequence in this starting set, a new single sequence was randomly picked from its 3L mutational neighborhood (the set of all sequences at a Hamming distance of 1 from a sequence of length L) and the difference in expression between the new sequence and the starting sequence was calculated using the convolutional model (Fig. 2b). This was done for each starting sequence to get generation 1. Each subsequent generation n was produced by picking a single sequence randomly from the 3L mutational neighborhood of each sequence in the preceding generation n-1. The simulation was carried out for 40 generations. Simulations were also subsequently repeated with the transformer model (Extended Data Fig. 3f), yielding concordant results.

For experimental validation, 1,000 random starting sequences were synthesized, introducing between one to three random mutations to these sequences. The expression levels of starting and mutated sequences were measured in both complex and defined media experimentally using our reporter assay. For 990 of these 1,000 starting sequences, experimental measurements were available for all three mutational distances. Additionally, 20 (median) separate single mutations were introduced to each of 196 native sequences, the sequences were synthesized, and their associated expression was measured similarly for both of these media; these were also included in the boxes for one mutational step in Fig. 2c and Extended Data Fig. 1e.

Characterizing the regulatory complexity of a sequence

To estimate the regulatory complexity^82,83 of a sequence, the Gini coefficient of the regulatory interaction strengths for each TF was calculated. A new biochemical model was first trained with our defined media data to complement the existing one trained on complex media, using our published model architecture of TF binding and position-aware activity²⁶ and the training procedure previously described²⁶ (Supplementary Notes). The regulatory interaction strength was then individually calculated for each regulator by setting the concentration parameter for that TF (individually) to 0 in the learned model, and the biochemical model was used to quantify the resulting change in expression, as previously described²⁶. The resulting vector of interaction strengths was used to calculate a Gini coefficient for each sequence, separately for the complex and defined media models. The Gini coefficient is a measure of inequality of continuous values within a population, most commonly applied to wealth or income, and ranges from 0 (all members of the population have equal wealth) to 1 (the wealth of a population is held by a single individual). Regulatory complexity for a sequence is then 1-Gini, such that 1 indicates that all TFs contribute equally to the regulation of the gene and 0 indicates that a single TF is solely responsible for its regulation. As starting points for our trajectories, 200 native promoter sequences (from −160 to −80, relative to the TSS) were chosen with relatively high regulatory complexity and another 200 were chosen with relatively low regulatory complexity, spanning the range of predicted expression levels, as starting points for our trajectories.

Trajectories for stabilizing selection on gene expression were designed using the convolutional model (Fig. 2d). Here, all sequences were required to maintain a predicted expression level within 0.5 of the original expression levels at all steps along the trajectory. There was no explicit constraint on regulatory complexity in this simulation of stabilizing selection. In order to ensure that expression was unchanged, expression levels were measured experimentally for sequences along a trajectory at growing mutational steps from the initial sequence (2, 4, 8, 16, 32 mutations). Any trajectories for which an expression measurement was missing for any experimentally tested sequence were excluded from all analyses, retaining 172 trajectories with initial low regulatory complexity and 192 trajectories with initial high regulatory complexity. Testing whether observed trends in regulatory complexity were affected by the degree to which expression was either predicted (by the convolutional model for 1–32 mutations) or observed (by the experiment at 2, 4, 8, 16, or 32 mutations) to be conserved, showed that the trends were robust to the degree of expression conservation (Supplementary Fig. 11).

Characterizing directional trajectories under SSWM

Simulations of trajectories under a Strong Selection-Weak Mutation (SSWM)^84–86 regime were initialized with a set of native yeast promoter sequences (defined here as the subset from −160 to −80 relative to the TSS for all the genes in the yeast reference genome for which we had a good TSS estimate (Supplementary Table 3 in ²⁶) as the starting generation 0. For each sequence in generation n, the sequence from its 3L mutational neighborhood that had the maximal (or separately, minimal) predicted expression using the convolutional model was picked to get generation n+1. The simulation was carried out for 10 rounds separately in the complex (Fig. 2f) and defined (Extended Data Fig. 1f) media. The simulations were subsequently repeated using the transformer model (Extended Data Fig. 3i-j).

For experimental validation, a subset of sequences from several generations were synthesized along mutational trajectories simulated by the convolutional model for complex media (10,322 sequences from 877 trajectories, 805 of which had every sequence along the trajectory successfully measured) and one for defined media (6,304 sequences from 637 trajectories, 591 of which had every sequence along the trajectory successfully measured) and their expression was measured in the corresponding media experimentally using our reporter assay (Fig. 2g, Extended Data Fig. 1g).

Measuring the URA3 expression-to-fitness relationship

Two complementary environments were studied with opposite selective pressures on the expression of URA3 (encoding an enzyme responsible for uracil synthesis): defined media, where organismal fitness increases with gene expression (up to saturation) and complex media + 5-FOA, where fitness decreases with Ura3p expression.

Convolutional models trained on defined and complex media were used to choose a set of 11 sequences that span a broad range of predicted expression levels in the two media when cloned into a YFP expression vector²⁶. The relationship between expression of URA3 and organismal fitness in yeast was estimated from experimental measurements with these 11 sequences, by cloning promoter sequence in front of YFP to measure expression level and in front of URA3 to measure fitness. Unless otherwise noted, yeast were grown at 30°C, in an orbital shaker incubator at 225 RPM. Each vector was transformed into yeast (S288C::ura3), and three independent transformants were selected per vector to serve as biological replicates. For measuring expression, yeast were grown overnight in either YPD+NAT (yeast extract, peptone, dextrose, with 75µg/ml nourseothricin) or SD-Ura (synthetic defined media, lacking uracil; Sunrise Science 1703–500), and then re-inoculated in the morning and allowed to grow for 6 hours prior to measuring expression by flow cytometry for each replicate as the log ratio of YFP to the constant background RFP, including only cells obtaining the top 50% of RFP expression. Fitness was obtained by measuring the growth rate of each yeast strain in either SD-Ura or YPD+NAT+5-FOA (0.25 mg/ml 5-FOA). Yeast were grown continuously in triplicate in log phase, with linear shaking at 30°C in a Synergy H1 plate reader (Biotek), by diluting each well to maintain OD<0.7, with OD measured at 15 minute intervals. Growth rate was defined for each replicate as the median of the instantaneous smoothed growth rates over 5 measurements in log phase, considering only time points where 0.05<OD<0.5. Each promoter’s expression and growth rate were summarized as the mean of the three replicates.

Characterizing trajectories under conflicting expression objectives in different environments

Simulations of sequence evolution in two complementary environments with opposite selective pressures (defined media and complex media) were initialized with a set of native yeast promoter sequences (present at −160 to −80 relative to the TSS) as the starting generation 0, with the objective function defined as the difference in predicted expression between defined and complex media (Fig. 2h, Extended Data Fig. 2d-g) using convolutional models trained in the respective media. The difference in expression between the two conditions was maximized at each iteration, which assumes that the cells are exposed to both environments before the mutations can reach fixation, an example of evolution in rapidly fluctuating environments³¹. For simplicity, it is assumed that fitness is directly proportional to higher expression in one condition and to lower expression in the other, such that mutations will be considered favorable even if they decrease fitness in one condition so long as they increase it in the other condition by a greater amount.

One simulation aimed to maximize the expression difference (defined minus complex), and the other to minimize it (maximizing complex minus defined). For each sequence in generation n, the sequence from its 3L mutational neighborhood that had the maximum (or separately, minimum) value for the objective function based on the convolutional model prediction is picked for generation n+1, to a total of 10 generations. The simulations were subsequently repeated using the transformer model yielding similar results (Supplementary Fig. 17b-f).

Motifs that were enriched in the sequences of generation 10 compared to the starting sequences were identified de novo using DREME⁸⁷, and each of the top 5 consensus motifs were used as queries to search the YeTFaSCo database⁸⁸, reporting the closest match, or one of multiple similar matches.

Finding orthologous promoters in the 1,011 S. cerevisiae genomes dataset

To identify orthologs of S288C promoters in the whole genome sequences of the 1,011 yeast strains³⁷, BLAT⁸⁹ was used to identify regions of ≥80% identity with each −160 to −80 region (relative to the TSS) annotated in the reference S288C genome sequence (R64)⁹⁰. Any strains with more than one such match, where the match contained insertions or deletions, or had incomplete matches, were excluded on a gene-by-gene basis. Genes with more than 1.2 matches with ≥80% identity per genome, on average, were excluded altogether.

Computing the expression conservation coefficient (ECC)

To calculate the ECC (a regulatory analog^2,35,91,92 of d_N/d_S^34,93,94), for each yeast gene promoter, the transformer model was used to predict an expression value for each orthologous promoter in the 1,011 yeast genomes (above), defining an expression distribution with a standard deviation σ_B. Next, a set of sequences with random mutations was generated from each gene’s consensus promoter sequence (defined as the most abundant base at each position across the strains), such that the number of sequences at each Hamming distance from the consensus promoter sequence was the same for the natural and simulated sets. Here, mutations introduced to create random variation sampled each base with equal probability; using observed mutation rates yielded similar results (Supplementary Information). The same transformer model to predict the expression of the simulated sequences, and calculate its standard deviation σ_C. The nominal ECC is log(σ_C/σ_B). Because the variance on simulated sequences is better estimated than in natural orthologs (whose sequences may be more constrained), a constant correction factor is subtracted, calculated by creating a second simulated set of randomly mutated sequences whose diversity is limited to the same extent as in the natural set, by creating only one random mutation for every unique sequence in the set of native orthologs. Finally, the expression for this second set of sequences is predicted by the transformer model, and its standard deviation (σ_C’) is used to calculate a null ECC for each gene (log(σ_C/σ_C’)); the median of these null ECCs over all the genes is used as the constant correction factor $\text{C}={\text{median}}_{\forall \text{genes}, i}\left({\text{log}}_2\left(\frac{{\sigma }_{C_i}}{{\sigma }_{C{\text{'}}_i}}\right)\right)$. (An extensive description of the correction factor is provided in the “ECC calculation details and considerations” section of the Supplementary Information.)

The corrected ECC for gene g is then:

$$EC{C}_g={\text{log}}_2\left(\frac{{\sigma }_{C_g}}{{\sigma }_{B_g}}\right)-\text{C}$$

The computed ECC values for all yeast genes, available in Supplementary Table 1, were used to identify cases or presumed stabilizing selection (selection favoring a fixed non-extreme value of a trait), diversifying (disruptive) selection (selection favoring more than one extreme values of a trait; as opposed to a single fixed intermediate value), and directional (positive) selection (selection favoring a single extreme value of a trait over all other possible values of the trait). Re-computing the ECC values for all yeast genes using the S288C reference sequences instead of the consensus sequence for the promoters of each gene yielded very similar results.

In addition to each ECC value, a Z-score and p-values for the confidence that the observed ECC values differ from neutrality were also calculated. For each gene’s true ECC, a set of matched random ECC values were calculated, where the denominator is a set of sequences matched for Hamming distance distribution and the total number of unique sequences. The null ECC mean and standard deviation were calculated from 1,111 such simulations, and used to calculate a Z-score for how extreme the actual ECC would be under this null distribution. This Z-score acts as a signed p-value (negative representing divergent expression and positive representing conservation), from which p-values (using the ‘scipy.stats.norm.sf’ function on the absolute value of the Z-score in Scipy⁹⁵ and multiplying the function’s output by 2 to get a two-sided p-value) (Supplementary Table 1).

Inferring expression conservation across Saccharomyces species using RNA-seq data and comparing with ECC values

Published RPKM values for orthologs of S. cerevisiae genes in closely related Saccharomyces species⁴¹ were obtained from the Gene Expression Omnibus (GEO) (accession GSE83120). Only genes for which expression was quantified in all species were used in subsequent analysis. RPKM values were log₂ scaled after adding a pseudo count of 2, and the variance in expression of each gene across the species was calculated. Genes were ranked by their gene expression variance, and the 2% of genes with the lowest variance were considered as having conserved gene expression levels (‘expression conserved’), while the 2% with the highest variance were considered ‘expression not-conserved’. The significance of the differences was robust to the choice of these thresholds (Supplementary Information). To compare to ECC values, the p-value of a two-sided Wilcoxon rank-sum test was estimated comparing the ECC values for genes in the ‘expression conserved’ and ‘expression not-conserved’ categories (implemented using the scipy.stats.ranksums SciPy⁹⁵ function). To control for the dependence between expression mean and variance, the analysis was repeated using the coefficient of variation (P = 1.05*10⁻⁴) and the coefficient of dispersion (P = 2.42*10⁻⁴) instead of variance, yielding similar results.

Experimental protocol for RNA-seq measurements from 11 Ascomycota species

RNA-seq was performed on samples from the following 11 Ascomycota yeast species: Saccharomyces cerevisiae, Saccharomyces bayanus, Naumovozyma (Saccharomyces) castellii, Candida glabrata, Kluyveromyces lactis, Kluyveromyces waltii, Candida albicans, Yarrowia lipolytica, Schizosaccharomyces japonicus, Schizosaccharomyces octosporus, and Schizosaccharomyces pombe. Each of the 11 species was grown in BMW medium, chosen to minimize cross-species growth differences, as previously described⁹⁶. N. castellii was grown at 25℃ while the other species were grown at 30℃. RNeasy Midi or Mini Kits (Qiagen, Valencia, CA) were used to isolate total RNA from log-phase cells by mechanical lysis using the manufacturer instructions as previously described⁹⁶. dUTP strand-specific RNA-seq libraries were constructed as previously described⁹⁷ with the following modifications. (1) The polyA⁺-selected RNA was fragmented in a 40µl reaction containing 1x Fragmentation Buffer (Affymetrix) by heating at 80℃ for 4 minutes followed by cleanup via ethanol precipitation for all libraries (except Y. lipolytica, S. pombe, S. japonicus, and S. octosporus; for these species, the conditions described previously were used⁹⁷), followed by cleanup via 1.8x RNAClean XP beads (Beckman Coulter Genomics). (2) For C. glabrata, K. lactis, S. bayanus, S. pombe, S. japonicus, and S. octosporus libraries, the adapter ligation was performed overnight at 16℃. For the rest, this was done at 16℃ for 2 hours as described previously⁹⁷. (3) Normalization was carried out based on the cDNA input and pooling of selected Illumina barcoded-adaptor-ligated cDNA products followed by gel size selection occurred as follows: range of 275 to 575 bp for pooled C. albicans, K. waltii, and N. castellii libraries, and 375 to 575 bp for C. glabrata, K. lactis, and S. bayanus libraries. For the other libraries, no pooling was performed before gel size-selection – range of 310 to 510 bp for Y. lipolytica and 350 to 550 bp for S. pombe, S. japonicus, and S. octosporus. (4) The final PCR product was purified by 1.8x AMPure XP beads (Beckman Coulter Genomics) followed by a second gel size-selection for the range of 300 to 575 bp for C. albicans, K. waltii, and S. castellii libraries, but no second gel size-selection was performed for the other libraries. The pooled final library was sequenced on one to four lanes of HiSeq2000 (Illumina) with 68 base (Y. lipolytica had 76 base) paired-end reads and 8 base index reads.

Transcript assembly, mapping and expression calculation for the 11 Ascomycota species RNA-seq

For each of the 11 Ascomycota yeast species above, reads were assembled using Trinity⁹⁸(version ‘trinityrnaseq_r2012–05-18’) and the assembled transcripts were mapped onto the assemblies to the respective genomes using GMAP⁹⁹. The Jaccard coefficient was used to join adjacent assemblies given enough connecting reads (using the Trinity default of 0.35 for the Jaccard cutoff). Finally, upon mapping all assembled transcripts, the Jaccard coefficient was used to clip assemblies which did not have enough support over a certain region. For each of the species, assembled transcripts were mapped to the genome sequence¹⁰⁰ using BLAT⁸⁹. Estimated expression values were calculated for each transcript using RSEM¹⁰¹ (defined in RSEM as the estimate of the number of fragments that are derived from a given isoform or gene, or the expectation of the number of alignable and unfiltered fragments that are derived from an isoform or gene given the maximum likelihood abundances). Only reads mapping to the sense mRNA strand were considered. Orthology between genes in different species was used as previously described¹⁰⁰.

Inferring expression conservation across Ascomycota species using our RNA-seq data and comparing with ECC values

Estimated expression values from the 11 Ascomycota species RNA-seq data were used after removing all genes with NA values in expression for more than three species. Estimated expression values were log₂ scaled after adding a pseudo count of 1, and the variance in expression for each gene across the species was calculated. Genes were ordered by their variance in expression across the reported fungal species. Here, the 10% of genes with the lowest expression variance were considered to have ‘conserved’ expression, and the 10% with highest expression variance were considered to have expression ‘not conserved’. To compare to ECC values, the p-value of a two-sided Wilcoxon rank-sum test was estimated comparing the ECC values for genes in the ‘conserved’ and ‘not conserved’ categories (implemented using the scipy.stats.ranksums SciPy⁹⁵ function). Similar results were obtained when repeating the analysis using the coefficient of variation (P = 4.22*10⁻⁵) and the coefficient of dispersion (P = 8.05*10⁻⁵) instead of variance.

Inferring expression conservation across mammalian species using RNA-seq data and comparing with ECC values

Ensembl Biomart¹⁰² was used to find one to one orthologs of S. cerevisiae genes in humans (of ‘Human homology type’ ‘ortholog_one2one’; all ‘ortholog_one2many’ and ‘many2many’ orthologs were excluded). For these human orthologs of yeast genes, the previously reported ‘evolutionary variance’ values across mammalian species from the original publication⁴² (based on an Ornstein Uhlenbeck (OU model)⁴²) were directly used. Here, the 25% of genes with the lowest ‘evolutionary variance’ were considered to have conserved expression and the top 25% were considered to be not conserved (the same thresholds used in the original study⁴²). This was done separately for each profiled tissue (brain, heart, kidney, liver, lung and skeletal muscle). Subsequently, a human ortholog for a yeast gene was considered to have conserved (or non-conserved) expression if it was found to have conserved (or non-conserved) expression in at least one of the profiled tissues. Genes with conflicting expression conservation classes across tissues were excluded from the analysis. To compare to ECC values, the p-value of a two-sided Wilcoxon rank-sum test was estimated comparing the ECC values for genes in the “conserved” and “not conserved” categories (implemented using the scipy.stats.ranksums SciPy⁹⁵ function).

Quantifying sequence dissimilarity using mean Hamming distance

For each group of orthologous yeast gene promoters (with ungapped alignments), the mean of Hamming distances between each pair of orthologous promoters across the 1,011 isolates was calculated.

Generation of CDC36 promoter strains by allele swapping

Strains with a restored Upc2p binding site in the CDC36 promoter region were obtained using a previously described CRISPR-Cas9 method¹⁰³. Guide RNAs (gRNAs) were designed using the Benchling online tool (https://www.benchling.com/) and cloned in a pGZ110 derived plasmid¹⁰⁴, using standard “Golden Gate Assembly”¹⁰⁵. Plasmids carrying the gRNA and Cas9 gene were then co-transformed with a synthetic DNA fragment (ssODN) composed of a 100 bp sequence with perfect complementarity to the background promoter sequence (WE) but for the centrally-located targeted alleles that overlap the Upc2p binding site. Allele swapping was confirmed by Sanger sequencing (Macrogen, South Korea). Sequences were analyzed using the SGRP (Saccharomyces Genome Resequencing Project) BLAST server (http://www.moseslab.csb.utoronto.ca/sgrp/blast_new/) and MUSCLE tool in Geneious v10.1. All primers and ssODNs used are listed in Supplementary Table 2.

RNA extraction and qPCR of CDC36

Gene expression analysis was performed by qPCR from cultures growth in SD medium supplemented with uracil (0.02% p/v). Samples were grown until exponential phase (OD 0.6–0.8), collected by centrifugation and treated with 10 units of Zymolyase 20T (50mg/ml) for 30 min at 37°C. RNA was extracted using E.Z.N.A Total RNA kit I (OMEGA) according to manufacturers’ instructions. Genomic DNA traces were then removed by treating samples with DNase I (Promega). RNA concentrations were estimated using a Qubit system and verified by 1.5% agarose gel. RNA extractions were performed in three biological replicates.

cDNA was synthesized using 200 units of M-MLV Reverse transcriptase (Promega), 0.5 µg of Oligo (dT)15 primer and 1 µg of RNA in a final volume of 25 µL according to manufacturers’ instructions. qPCR reactions were carried out using Brilliant II SYBR® Green QPCR Master Mix (Agilent Technologies) in a final volume of 10 µL, containing 0.2 µM of each primer and 1 µL of the cDNA previously synthesized. qPCR reactions were carried out in three technical replicates per biological replicate using an Eco Real-Time PCR system (Illumina, Inc.) under the following conditions: 95°C for 15 min and 40 cycles at 95°C for 10 s and 58°C for 30 s. Primers used are listed in Supplementary Table 2. The relative expression of CDC36 was quantified using the 2(-ΔΔCt) approach¹⁰⁶, and normalized with two housekeeping genes as previously described¹⁰⁷, using the median Ct of the three technical replicates for each sample. The housekeeping genes ACT1 and RPN2 were used as previously described¹⁰⁸.

Growth curves of CDC36 mutant and wild type alleles

Growth curves incorporating carbon source switching from glucose to galactose were generated as previously described¹⁰⁹. Pre-cultures were grown in YNB containing 5% glucose medium at 30ºC for 24 h. Cultures were then diluted to an initial OD600nm of 0.1 in fresh YNB 5% glucose medium for an extra overnight growth. The next day, cultures were used to inoculate a 96-well plate with a final volume of 200μL YNB with 5% galactose with an initial OD600nm of 0.1. In parallel, a control plate containing YNB with 5% glucose was similarly inoculated. All experiments were performed in triplicate. OD600nm was monitored every 30 min using a Tecan Sunrise absorbance microplate reader (Tecan Group Ltd.). The kinetic parameters of lag phase, growth efficiency (ΔOD600 nm) and maximum specific growth rate (µ_max) were determined as previously described¹¹⁰, fitting the curves with the Gompertz function using R version 3.3.2. All growth parameters are expressed as the ratio of growth within YNB+galactose to YNB+glucose to control for phenotypic variation that results from something other than the carbon source switch.

Fitness responsivity

The empirically-determined relationships between the expression levels to organismal fitness for each of 80 genes ¹¹ were re-analyzed. Published expression-to-fitness curves in glucose media for each of 80 genes were obtained from the Supplementary Data of the original publication¹¹. For each of these curves, the total variation (Extended Data Fig. 5) was calculated by partitioning the expression range into 36 regular intervals (as reported in the ‘impulse fit’ of the expression-to-fitness curves in the original publication¹¹) and summing the absolute difference in fitness at the endpoints of each partition as follows $\sum \left|F_{GENE}\left(e_{i+1}\right)- F_{GENE}\left(e_i\right)\right|$, for each gene’s expression-to-fitness function, $F_{GENE}\left(e\right)$. The same qualitative relationship between a gene’s ECC and fitness responsivity as reported in other studies^111–113 was observed, including LCB2 (ECC 2.15 and high fitness responsivity¹¹²) and MLS1 (ECC −1.32 and extremely low fitness responsivity¹¹³).

Mutational robustness

For every sequence, mutational robustness was defined as the fraction of sequences in its 3L mutational neighborhood that altered the expression by an amount less than ϵ, where ϵ is set at two times the standard deviation of expression variance across all genes with an ECC >0 (here, ϵ = 0.1616; ECC calculated using the 1,011 S. cerevisiae genomes, Extended Data Fig. 4c). Using different values for ϵ yielded very similar results.

The evolvability vector

To derive the evolvability vector for a given sequence, expression changes associated with single base changes in every possible position were sorted to obtain a monotonically increasing vector of length 3L for each sequence of length L (here, L=80; 3L=240; Fig. 4a, left, Methods). Formally, to compute an evolvability vector for a sequence s₀, for each sequence s_i in the 3L mutational neighborhood of s₀, the difference between the predicted expression of s_i and that of s₀ : $d_i=f\left(s_i\right)-f\left(s_0\right)$ was calculated, where $f\left(s\right)$ represents the predicted expression of the transformer model. The evolvability vector is defined as the vector D $\left(\{d_1,d_2, \dots ,d_{3L}\}\right)$, sorted such that $d_i\ge d_{i-1} , \forall i$ (i.e. d_i values are in ascending order).

Power law distribution analysis

The list of the absolute values of the evolvability vectors for all native sequences was used to define the distribution of the magnitude of the expression effect of mutations. The powerlaw¹¹⁴ Python package was used to determine whether the data fit a power law distribution. The ‘Fit’ function with an ‘xmin’ parameter of 0.5 was used to determine the exponent and the ‘distribution_compare’ function was used to determine the p-value for the fit (Extended Data Fig. 4d, Supplementary Fig. 2h).

Characterizing the archetypal evolvability space

The evolvability vectors for a new random sample of a million sequences were used as input to an autoencoder with an archetypal regularization constraint⁴⁵ on the embedding layer. The autoencoder was trained using the AANet implementation made available with the publication⁴⁵ with no noise added to the archetypal layer during training, a linear activation on the output layer, an equal weight of 1 on each of the loss terms (the mean squared error loss term along with the non-negativity and convexity constraints), a learning rate of 0.001, and a minibatch size of 4,096. The autoencoder accepts an evolvability vector (of length 240 for an 80bp sequence) as input to the first encoder layer, where each node in the input layer is connected to each node in the encoder layer (fully connected layer). Every layer in the autoencoder was fully connected. The encoder architecture used was [1024, 512, 256, 128, 64], where each entry corresponds to the number of nodes in the corresponding hidden layer and the decoder architecture was the encoder’s mirror image. The output layer was the same shape as input layer and each node in the last decoder layer was connected to each node in the output layer. To select the optimal number of archetypes, the autoencoder was first trained for a 1,000 minibatches separately for 1 to 9 archetypes. Following the recommended approach⁴⁵ for picking the optimal number of archetypes, we used an elbow plot of mean squared error on the evolvability vectors (here, using native sequences) vs. the number of archetypes in the autoencoder (Extended Data Fig. 6a).

The autoencoder was then trained from scratch with 3 archetypes, using the full training data and parameters for 250,000 batches. Since this autoencoder aims to reconstruct the original evolvability vector for each sequence by learning feature representations after passing them through an information bottleneck, its reconstruction accuracy was first verified on the set of native yeast promoter sequences (Extended Data Fig. 6b, Pearson’s r = 0.992). To visualize the evolvability vectors corresponding to sequences in 2 dimensions (2D), the evolvability vectors corresponding to the three archetypes were first generated by decoding their archetypal latent space coordinates ((1,0,0), (0,1,0) and (0,0,1)) through the decoder, and MDS was performed on the decoded evolvability vectors of the archetypes. Then, as previously described⁴⁵, the encoded evolvability vector of each new sequence was projected into the 2D MDS space by representing it as a mixture of the archetypes and interpolating them between the MDS coordinates of each archetype. For every sequence, the following equivalent representations can now be computed: (i) its evolvability vector, (ii) an archetypal triplet quantifying the similarity of its encoded (latent space) evolvability vector to the three archetypes and (iii) a two-dimensional multidimensional scaling (MDS) coordinate⁴⁵ for visualizing the evolvability vectors. The representation of the evolvability vector for each sequence in this archetypal space is now bounded by a simplex (whose vertices correspond to the 3 evolvability archetypes). For each native and natural yeast promoter sequence from the sequence space, the archetypal triplet and MDS coordinates were inferred using its evolvability vector with this trained autoencoder. The MDS coordinates for the archetypes and the native yeast promoter sequences were used to generate the visualizations of the sequence space shown. This archetypal characterization of evolvability vectors allows the encoding and visualization of sequences by their evolvability in the context of a fitness landscape.

Visualizing promoter fitness landscapes

1000 random sequences were sampled and projected onto the MDS coordinate system for visualizing the sequence space described above. The expression level of each sequence was calculated using our model, and expression values were scaled so that the minimum was 0 and maximum was 1. Previously quantified expression-to-fitness relationships¹¹ to compute fitness (fraction of wildtype growth rate) by using cubic spline interpolation (implemented using the scipy.interpolate.CubicSpline SciPy⁹⁵ function) on the expression level after scaling the measured expression-to-fitness curves to have an expression range of 0 to 1. These fitness values were then used to generate the contour plots (implemented using the matplotlib.pyplot.tricontourf function; Fig. 4e, Extended Data Fig. 7) that visualize the fitness landscape in that gene’s promoter sequence space.

Extended Data

Extended Data Fig. 1: The convolutional sequence-to-expression model generalizes reliably and helps characterize sequence trajectories under different evolutionary regimes.

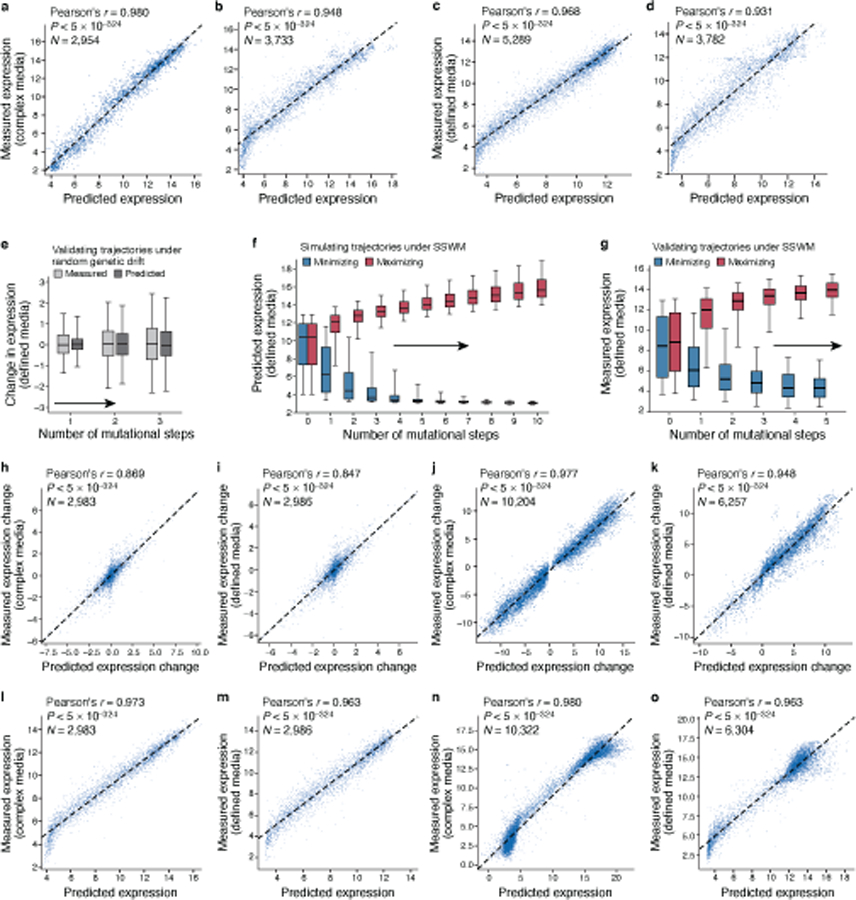
(a-d) Prediction of expression from sequence in complex (YPD) (a-b) and defined (SD-Uracil) (c-d) media. Predicted (x axis) and experimentally measured (y axis) expression for (a,c) random test sequences (sampled separately from and not overlapping with the training data) and (b,d) native yeast promoter sequences containing random single base mutations. Top left: Pearson’s r and associated two-tailed p-value. Compression of predictions in the lower left results from binning differences during cell sorting in different experiments (Supplementary Notes). e, Experimental validation of trajectories from simulations of random genetic drift. Distribution of measured (light grey) and predicted (dark gray) changes in expression in the defined media (SD-Uracil) (y axis) for the synthesized randomly-designed sequences (n=2,986) at each mutational step (x axis). Midline: median; boxes: interquartile range; whiskers: 5^th and 95^th percentile range. f, g, Simulation and validation of expression trajectories under SSWM in defined media (SD-Uracil). f, Distribution of predicted expression levels (y axis) in defined media at each evolutionary time step (x axis) for sequences under SSWM favoring high (red) or low (blue) expression, starting with native promoter sequences (n=5,720). Midline: median; boxes: interquartile range; whiskers: 5^th and 95^th percentile range. g, Experimentally-measured expression distribution in defined media (y axis) for the synthesized sequences (n=6,304 sequences; 637 trajectories) at each mutational step (x axis) from predicted mutational trajectories under SSWM, favoring high (red) or low (blue) expression. Midline: median; boxes: interquartile range; whiskers: 5^th and 95^th percentile range. h-o, Experimental validation of predicted expression for sequences from the random genetic drift and SSWM simulations. Experimentally measured (y axis) and predicted (x axis) expression level (l-o) or expression change from the starting sequence (h-k) in complex (h,j,l,n) or defined (i,k,m,o) media using sequences from the random genetic drift (Fig. 2c and (e); h,i,l,m here) and SSWM (Fig. 2g and (g); j,k,n,o here) validation experiments. Top left: Pearson’s r and associated two-tailed p-values.

Extended Data Fig. 2 |. Characterization of sequence trajectories under strong competing selection pressures using the convolutional model.

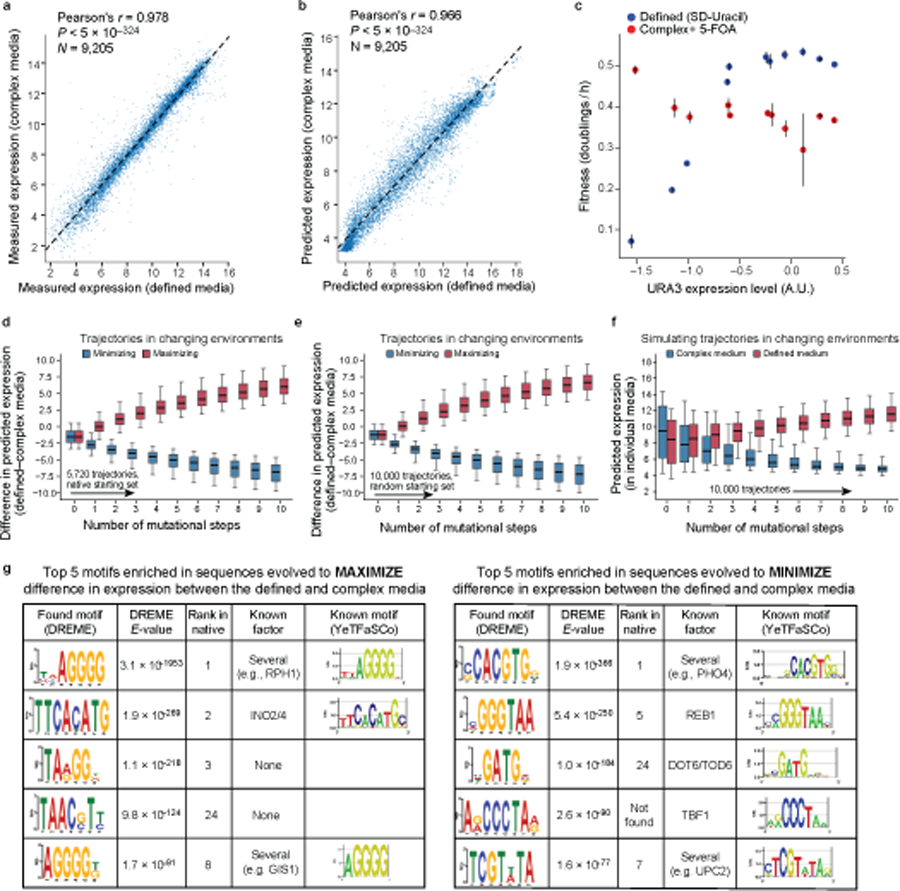
a,b, Expression is highly correlated between defined and complex media. Measured (a) and predicted (b) expression in defined (x axis) and complex (y axis) media for a set of test sequences measured in both media. Top left: Pearson’s r and associated two-tailed p-values. c, Opposing relationships between organismal fitness and URA3 expression in two environments. Measured expression (x axis, using a YFP reporter) and fitness (y axis; when used as the promoter sequence for the URA3 gene) for yeast with each of 11 promoters predicted to span a wide range of expression levels in complex media with 5-FOA (red), where higher expression of URA3 is toxic due to URA3-mediated conversion of 5-FOA to 5-fluorouracil, and in defined media lacking uracil (blue), where URA3 is required for uracil synthesis. Error bars: Standard error of the mean (n=3 replicate experiments). d-f, Competing expression objectives are slow to reach saturation. d,e, Difference in predicted expression (y axis) at each evolutionary time step (x axis) under selection to maximize (red) or minimize (blue) the difference between expression in defined and complex media, starting with either native sequences (d, as Fig. 2h, n=5,720) or random sequences (e, n=10,000). f, Distribution of predicted expression (y axis) in complex (blue) and defined (red) media at each evolutionary time step (x axis) for a starting set of random sequences (n=10,000). Midline: median; boxes: interquartile range; whiskers: 5^th and 95^th percentile range. g, Motifs enriched within sequences evolved for competing objectives in different environments. Top five most enriched motifs, found using DREME⁸⁷ (Methods) within sequences computationally evolved from a starting set of random sequences to either maximize (left) or minimize (right) the difference in expression between defined and complex media, along with DREME E-values, the corresponding rank of the same motif when using native sequences as a starting point, the likely cognate TF and that TF’s known motif.

Extended Data Fig. 3 |. The transformer sequence-to-expression model generalizes reliably and helps characterize sequence trajectories under different evolutionary regimes.

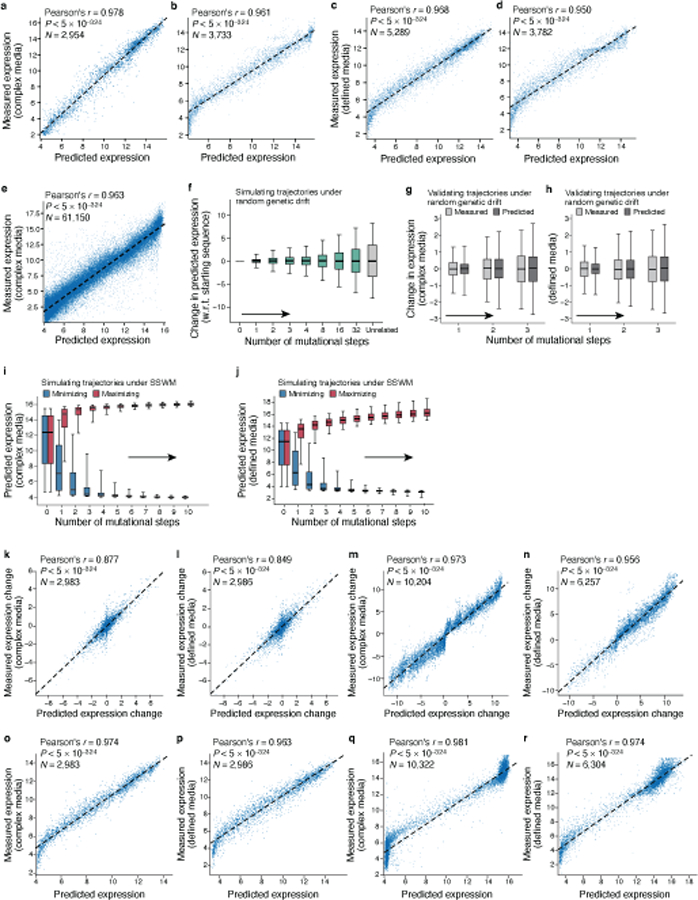
a-d, Prediction of expression from sequence in the complex (a-b) and defined (c-d) media. Predicted (x axis) and experimentally measured (y axis) expression for (a,c) random test sequences (sampled separately from and not overlapping with the training data) and (b,d) native yeast promoter sequences containing random single base mutations. Top left: Pearson’s r and associated two-tailed p-value. Compression of predictions in the lower left results from binning differences during cell sorting in different experiments (Supplementary Notes). e, Predicted (x axis) and experimentally measured (y axis) expression in complex media (YPD) for all native yeast promoter sequences. Pearson’s r and associated two-tailed p-values are shown. f, Predicted expression divergence under random genetic drift. Distribution of the change in predicted expression (y axis) for random starting sequences (n=5,720) at each mutational step (x axis) for trajectories simulated under random genetic drift. Silver bar: differences in expression between unrelated sequences. g,h, Comparison of the distribution of measured (light grey) and transformer model predicted (dark gray) changes in expression (y axis) in complex media (g, n=2,983) and defined media (h, n=2,986) for synthesized randomly-designed sequences at each mutational step (x axis). i,j Predicted expression evolution under SSWM. Distribution of predicted expression levels (y axis) in complex media (i, n=10,322) and defined media (j, n=6,304) at each mutational step (x axis) for sequence trajectories under SSWM favoring high (red) or low (blue) expression, starting with 5,720 native promoter sequences. (f-j) Midline: median; boxes: interquartile range; whiskers: 5^th and 95^th percentile range. k-r, Comparison of model predicted expression for sequences synthesized previously for the random genetic drift and SSWM analyses. Experimentally measured (y axis) and transformer model predicted (x axis) expression level (o-r) or expression change from the starting sequence (k-n) in complex (k,m,o,q) or defined (l,n,p,r) media using sequences from the random genetic drift (Fig. 2c and (Extended Data Fig. 1e); k,l,o,p here) and SSWM (Fig. 2g and (Extended Data Fig. 1g); m,n,q,r here) validation experiments. Top left: Pearson’s r and associated two-tailed p-values.

Extended Data Fig. 4 |. Signatures of stabilizing selection on gene expression detected from regulatory DNA across natural populations.

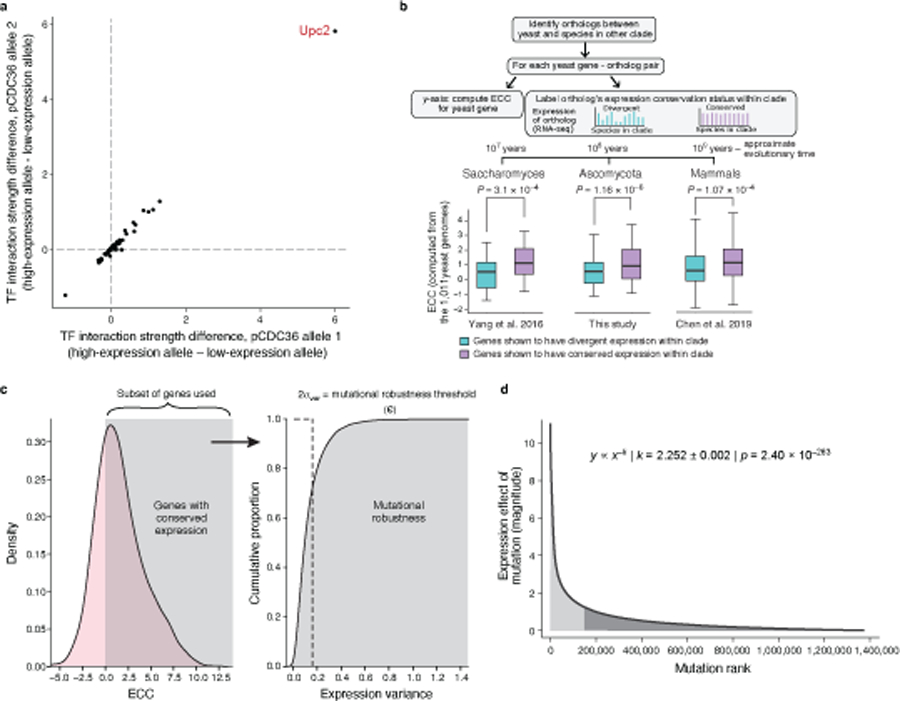
a, Expression-altering alleles in the CDC36 promoter are attributed primarily to altered UPC2 binding. TF interaction strength²⁶ (expression attributable to each TF) difference between the high and low alleles (each point is a TF) for each of two low expression alleles (allele 1: x axis; allele 2: y axis). Each low-expressing allele is compared to the high-expression allele with the most similar sequence (across all promoter sequences analyzed from the 1,011 strains; $e_{TF,A_{high}}-e_{TF,A_{low}}$). b, Distribution of ECC (y axis, calculated from 1,011 S. cerevisiae genomes, top left) for S. cerevisiae genes whose orthologs have divergent (blue) or conserved (purple) expression (within Saccharomyces (left, n=4,191), Ascomycota (middle, n=4,910), or mammals (right, n=199) (as determined by cross species RNA-seq, top right). p-values: two-sided Wilcoxon rank-sum test. Midline: median; boxes: interquartile range; whiskers: 5^th and 95^th percentile range. c, Determination of expression change threshold for defining a “tolerated mutation” to compute mutational robustness. We used all genes with an ECC consistent with stabilizing selection (ECC>0; left), calculated the variance in predicted expression across the 1011 yeast strains for each gene, and chose the tolerable mutation threshold, ϵ, as two standard deviations of the distribution of the variance (right). ~73% of genes with ECC>0 had an expression variation lower than ϵ. d, Distribution of the effects of mutations (magnitude) on expression for all native regulatory sequences follows a power law with an exponent of 2.252. Shaded regions are equal in area.

Extended Data Fig. 5 |. Fitness responsivity of a gene as the total variation of its expression-to-fitness relationship F_GENE curves.

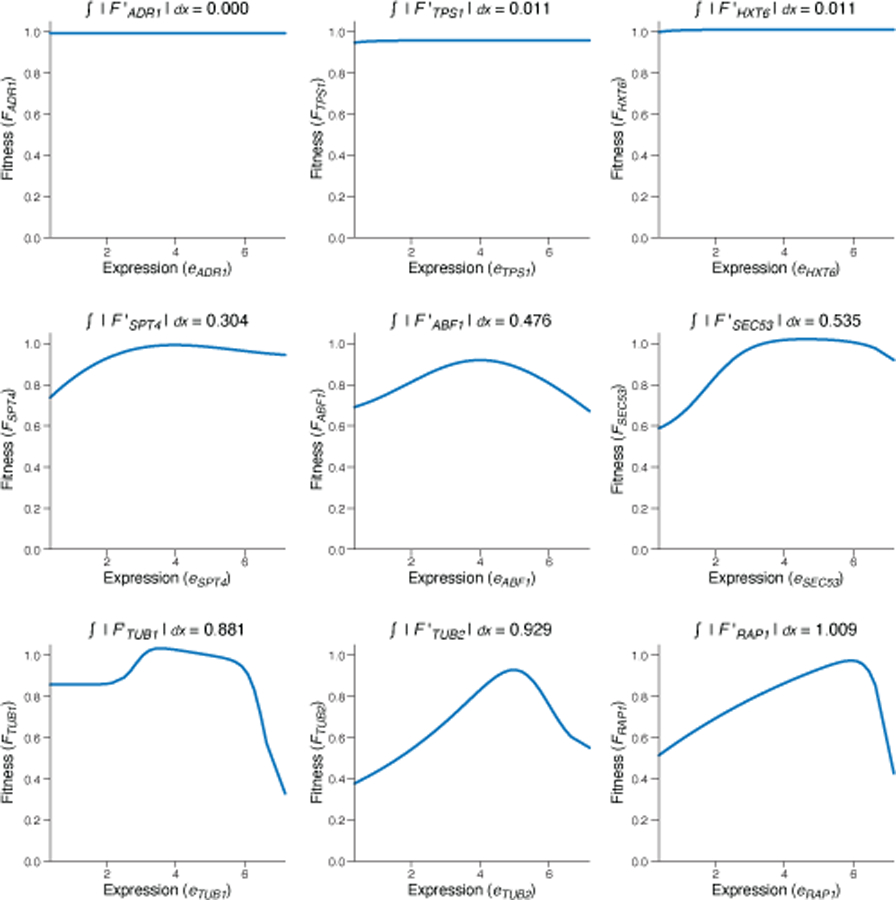
Expression (x axis) and fitness (y axis) levels for different promoter variants for each select gene fit from experimental measurements by Keren et al¹¹. Fitness responsivity calculated as the total variation in each curve is noted above each panel.

Extended Data Fig. 6 |. Analysis of regulatory evolvability reveals sequence-encoded signatures of expression conservation from solitary sequences.

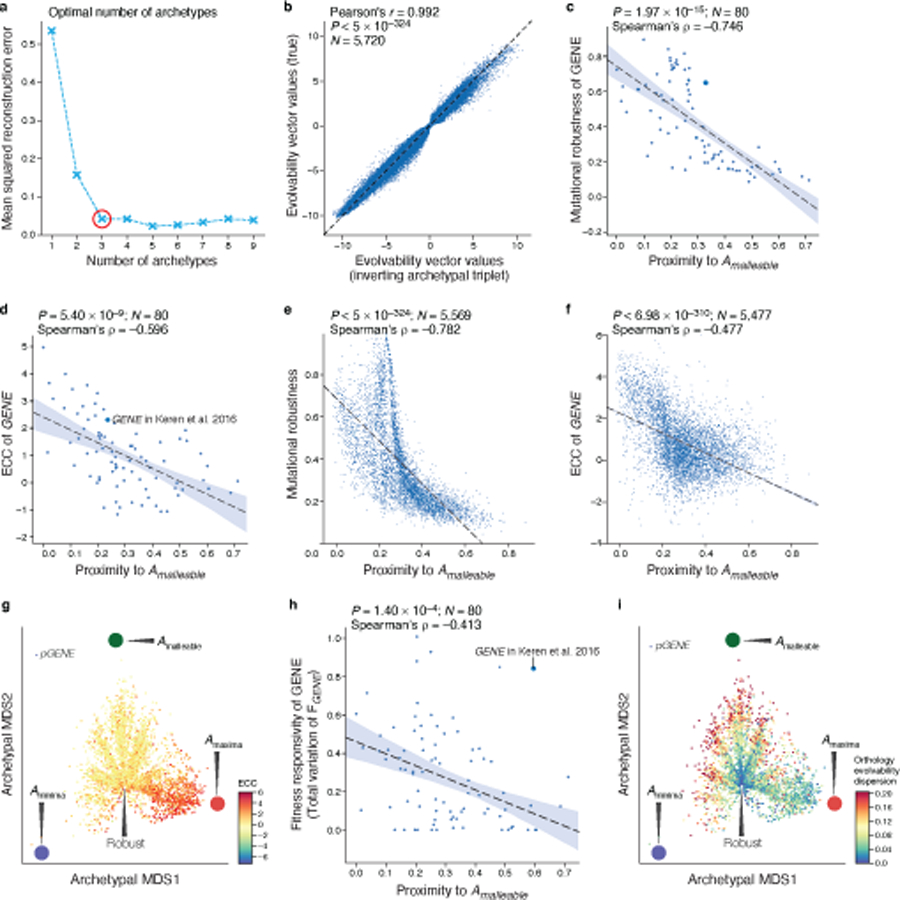
a, Selection of optimal number of archetypes. Mean-square-reconstruction error (y axis) for reconstructing the evolvability vectors from the embeddings learned by the autoencoder for an increasing number of archetypes (x axis). Red circle: optimal number of archetypes selected as prescribed⁴⁵ by the “elbow method”. b, The archetypal embeddings learned by the autoencoder accurately capture evolvability vectors. Original (y axis) and reconstructed (x axis) expression changes (the values in the evolvability vectors) for each native sequence (none seen by the autoencoder in training). Top left: Pearson’s r and associated two-tailed p-values. c-f, Evolvability space captures regulatory sequences’ evolutionary properties. Proximity to the malleable archetype (A_malleable) (x axis) and mutational robustness (c,e y axis) or ECC (d,f y axis) for all yeast genes (e,f) or the gene for which fitness responsivity was quantified (c,d). Top right: Spearman’s ρ and associated two-sided p-value. “L”-shape of relationship in e results from the robust cleft, A_maxima, and A_minima all being distal to A_malleable (left side of plot). g, All native (S288C reference) promoter sequences (points) projected onto the archetypal evolvability space learned from random sequences; colored by their ECC. Large colored circles: evolvability archetypes. h, The proximity to the malleable archetype (x axis) and fitness responsivity (y axis) for the 80 genes with measured fitness responsivity. Top right: Spearman’s ρ and associated two-tailed p-values. Light blue error band: 95% confidence interval. i, All native (S288C reference) promoter sequences (points) projected on the evolvability space learned from random sequences; colored by their mean pairwise distance in the archetypal evolvability space between all promoter alleles across the 1,011 yeast isolates for that gene (ortholog evolvability dispersion). Large colored circles: evolvability archetypes.

Extended Data Fig. 7 |. Visualizing promoter fitness landscapes in sequence space.

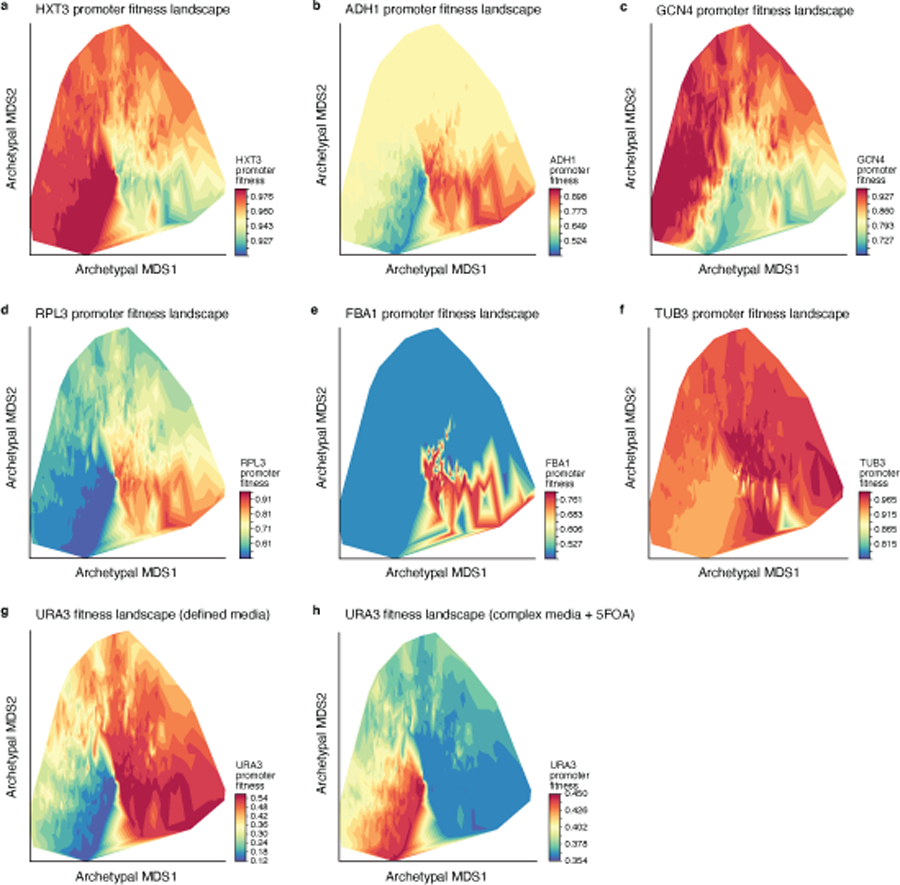
Visualizing the fitness landscapes for the promoters of HXT3 (a), ADH1 (b), GCN4 (c), RPL3 (d), FBA1 (e), TUB3 (f), URA3 (in defined media) (g), URA3 (in complex media + 5FOA) (h). 1000 promoter sequences represented by their evolvability vectors projected onto the 2D archetypal evolvability space and colored by their associated fitness as reflected by their predicted growth rate relative to wildtype (color, Methods), estimated by first mapping sequences to expression with our model and then expression to fitness as measured and estimated previously¹¹.

Extended Data Fig. 8 |. In silico mutagenesis (ISM) of malleable and robust promoters.

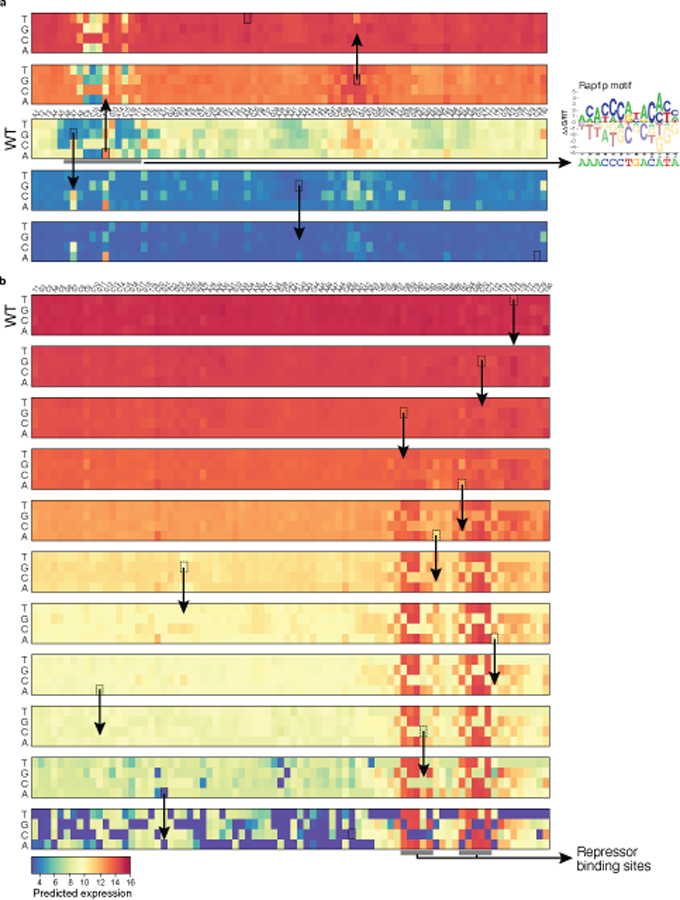
SSWM trajectories for (a) DBP7, a malleable promoter, and (b) UTH1, a robust promoter. Each subplot shows the in silico mutagenesis effects for how expression level (color) changes when mutating each position (x axis) to each of the four bases (y axis) of each sequence (subplots) in the trajectories. The DNA sequence is indicated above each wildtype subplot (indicated with “WT” at left). Arrows indicate the mutations selected at each step, which always correspond to the mutation of maximal effect; increasing expression goes up the figure from wildtype and decreasing expression goes down. Part of the malleability of the DBP7 promoter results from an intermediate-affinity Rap1p binding site (gray bar). The first mutations in increasing- and decreasing-expression trajectories either increase or decrease (respectively) the affinity of this site. The UTH1 promoter changes gradually in expression and evolves proximal repressor binding sites to dampen expression (gray bars).

Data Availability

Data generated for this study are available on NCBI’s GEO, accession numbers GSE163045 and GSE163866. All models and processed data are available on Zenodo at https://zenodo.org/record/4436477.