Modeling bursty transcription and splicing with the chemical master equation

Abstract

Splicing cascades that alter gene products posttranscriptionally also affect expression dynamics. We study a class of processes and associated distributions that emerge from models of bursty promoters coupled to directed acyclic graphs of splicing. These solutions provide full time-dependent joint distributions for an arbitrary number of species with general noise behaviors and transient phenomena, offering qualitative and quantitative insights about how splicing can regulate expression dynamics. Finally, we derive a set of quantitative constraints on the minimum complexity necessary to reproduce gene coexpression patterns using synchronized burst models. We validate these findings by analyzing long-read sequencing data, where we find evidence of expression patterns largely consistent with these constraints.

Significance

Understanding mRNA transcription requires an arsenal of tractable and versatile Markov models. Bursty transcription is ubiquitous in mammalian cells; however, only a few such systems have been mathematically characterized. We expand their scope and present full probabilistic solutions for bursty transcription at multiple, potentially synchronized, gene loci, coupled to arbitrary directed acyclic graphs of splicing. We use these general results to derive quantitative constraints on transcript count correlations, motivate physically plausible classes of burst models, and validate the constraints using single-cell sequencing data.

Introduction

Recent advances in the analysis of single-cell RNA sequencing (scRNA-seq) (1) enable the quantification of pre-mRNA molecules alongside mature mRNA. These experimental data provide an opportunity to infer the topologies and biophysical parameters governing the processes of mRNA transcription, processing, export, and degradation in living cells. In particular, they provide a novel approach to inferring and studying the dynamics of mammalian splicing cascades (2).

Faced with the enormous volume of genome-wide information accessible through this technology (3), we seek to produce models that can represent their data-generating mechanism. If the model matches the physiology, fits can be physically interpreted in terms of biological parameters, analyzed using standard Bayesian machinery, and enormously compress data sets by representing thousands of observations by a few parameters. The choice of models is informed by a variety of considerations: physiologically plausible mechanisms based on orthogonal experiments, the form and granularity of the data, phenomenological observations that we strive to explain, and computational tractability. In this section, we use these considerations to circumscribe the scope of investigation.

We leverage the past two decades of fluorescence transcriptomics to develop consistent models. Results from live-cell profiling are consistent with Markovian dynamics; in vivo reactions, such as mRNA transcription and degradation, are well described by memoryless models dependent only on the instantaneous molecule counts (4,5). This also appears to be the most general class of models that affords straightforward analytical and numerical recipes; as we discuss in section S6, the complementary class of delay master equations, which encode molecular memory, resists systematic analysis at this time. If we do adopt the assumption of memorylessness, previous experiments immediately offer plausible models for transcriptional dynamics: mRNA transcription occurs in bursts of activity (6,7), with geometrically distributed bursts prevalent in bacterial and mammalian cells. We treat the problem in more generality, considering arbitrary burst distributions, which are mandatory for describing coexpression. Since our methods are designed for scRNA-seq, we omit all mechanistic discussion of regulation: feedback is usually modeled through protein interactions (8,9). Joint quantification of mRNA and proteins is in its nascence, and requires targeted antibodies, preventing genome-wide quantification (10, 11, 12). Thus, we omit stochastic regulation, although we propose that some of our results can be used to describe deterministic regulation without feedback.

Commercially available scRNA-seq data are intrinsically discrete: they report integer counts of molecular barcodes in each cell (13). To fit these counts, we need to solve for state probabilities induced by the chemical master equation (CME), which formalizes probability flow between microstates representing copy numbers. In the most general form, the CME is an infinite series of ordinary differential equations represented by the matrix equation $\frac{dp\left(t\right)}{dt}=\mathcal{A}p\left(t\right)$, where p is a vector of probabilities and $\mathcal{A}$ encodes the state-specific fluxes; the form of the equation, dependent only on $p\left(t\right)$ rather than any history, encodes the Markov property of memorylessness. The scRNA-seq protocols also provide base-level information, which can be used to identify specific transcripts. Inspired by the RNA velocity framework, which quantifies unspliced RNA along with mature, coding transcripts to infer regulatory dynamics (1), we seek to lay the groundwork for more general problems: the microstates represent joint copy-number quantities of intermediate transcripts with various introns. We do not treat the specifics of technical noise arising from the sequencing chemistry (14) and bioinformatics (15), although our solutions are modular with respect to simple noise models (16).

We would like to use physical models to encode the full scope of available data, particularly gene-gene correlations. At this time, the modeling field either uses single-gene results (treating the marginals and omitting correlations altogether) (17,18) or explicitly treats small systems (explaining correlations using concrete, usually autoregulatory schema) (19,20), whereas the sequencing field uses fully phenomenological descriptions (omitting mechanistic details of coupling) (21, 22, 23). We seek a middle ground that retains mechanistic interpretability, but offers straightforward, physically informed, and tractable recipes for representing gene-gene correlations. Finally, scRNA-seq data are particularly appealing because they can provide genome-wide information about numerous cell types and transient processes. We describe a procedure to treat random and deterministic variation in gene parameters, extending and unifying conventional models for extrinsic cell-to-cell noise (24), cell-type heterogeneity (17), and cell-cycle dynamics (25).

To enable inference, the solutions must be computationally facile. In principle, the CME can always be solved by matrix exponentiation: the solution is simply $p\left(t\right)=p\left(0\right)e^{\mathcal{A}t}$. However, this approach does not scale very well: if the state space size is truncated to $\mathcal{N}$, the matrix exponential has ${\mathcal{N}}^3$ time complexity. Although reformulating the problem can ameliorate this—for example, by tensor decomposition (26,27) or treating the CME in terms of the reaction counts (28)—these approaches are poorly compatible with bursty systems, which can have an infinite number of possible reaction channels, corresponding to the infinite support of the burst distribution. More problematically, these numerical methods are not amenable to treating simpler subproblems. For example, finding lower moments or computing a single marginal requires solving the entire system, then summing probabilities, so the method complexity is far out of proportion with the difficulty of the problem. On the other hand, true analytical solutions are unavailable for any but the simplest problems, such as constitutive transcription. Inspired by methods in biological and financial stochastic analysis (29,30), we seek to write down generating function solutions that can be evaluated using well-established algorithms, such as numerical quadrature and the fast Fourier transform.

Therefore, we seek to solve systems characterized by the reactions in Eq. 1. We define a set of n transcripts $\left\{{\mathcal{T}}_i\right\}$, whose abundances are represented by the count variables $m_1,\dots ,m_n:=\mathbf{m}$. The “parent” transcripts are produced with bursts of size $B_i$; by intron splicing, they are converted to downstream products and eventually degraded. The splicing reactions can be naturally represented by a directed graph, a discrete structure that encodes causal relationships between states, defined as transcripts in our case. At least one of $c_{ij}$ and $c_{ji}$ must be zero, encoding the intuition that splicing is irreversible and a shorter transcript cannot turn into a longer one. This constraint implies that it is impossible to leave a transcript ${\mathcal{T}}_i$ and return to it by the process of splicing: the reactions encode an acyclic digraph or directed acyclic graph (DAG) (31,32).

$$\begin{array}{l}\varnothing \stackrel{k_i}{\to }{B}_i\times {\mathcal{T}}_i\text{ with the propensity }{k}_i\\ {\mathcal{T}}_i\stackrel{c_{i0}}{\to }\varnothing \text{ with the propensity }{c}_{i0}{m}_i\\ {\mathcal{T}}_i\stackrel{c_{ij}}{\to }{\mathcal{T}}_j\text{ with the propensity }{c}_{ij}{m}_i.\end{array}$$ (1)

Methods

In this section, we take a modular approach to the CME, and describe how to construct tractable solutions to systems defined by Eq. 1, with the DAG constraint. As outlined in the discussion of scope, we are interested in broad classes of models, and focus on strategies for developing highly general solutions.

The section is organized as follows. For each class of phenomena, we introduce and solve its most general modular formulation, but limit the other system components to their simplest form: for general splicing graphs, we discuss geometric bursts; for more complex burst models, we discuss only a single RNA species. Finally, we describe specific examples, and use the results derived from the general solution to provide qualitative results and constraints.

Definition of the CME

To solve the systems described by Eq. 1, we need to encode them in a CME, which describes probability flux between microstates. We suppose the system has n species, with counts $m_1,\dots ,m_n:=\mathbf{m}$. The random variables describing the distributions over counts are $\left\{X_i\right\}$, with joint probability mass function (PMF) $P\left(\mathbf{m},t\right)$. The reactions in Eq. 1 naively correspond to the following fluxes for each species i:

$$\begin{array}{l}{R}_{tx,i}=k_i\left[\sum _{z=0}^{m_i}{p}_{i,z}P\left(m_i-z,t\right)-P\left(m_i,t\right)\right]\\ R_{deg,i}=c_{i0}[\left(m_i+1\right)P\left(m_i+1,t\right)-m_{i}P\left(m_i,t\right)]\\ R_{splic,ij}=c_{ij}[\left(m_i+1\right)P\left(m_i+1,m_j-1,t\right)-m_{i}P\left(m_i,m_j,t\right)].\end{array}$$ (2)

For convenience of notation, Eq. 2 omits the indices of species not involved in a particular reaction. The derivation is provided in section S1.1. The full master equation takes the following generic form:

$$\frac{dP\left(\mathbf{m},t\right)}{dt}=R_{tx}+\sum _{i=1}^n\left[R_{deg,i}+\stackrel{n}{\sum _{j=1}}{R}_{splic,ij}\right],$$ (3)

i.e., the net flux into any state is the sum of contributions from all reactions for all species. If the burst processes are mutually independent, they can simply be added to yield $R_{tx}={\sum }_i{R}_{tx,i}$, but this is not true in general. Unfortunately, in all but the simplest cases, the PMF is unwieldy to manipulate. Therefore, we convert the CME to the corresponding probability generating function (PGF) $G\left(x_1,\dots ,x_n,t\right):=G\left(\mathbf{x},t\right)$:

$$G\left(\mathbf{x},t\right):=\sum _{m_1,\dots ,m_n}{x}_1^{m_1}\dots x_n^{m_n}P\left(\mathbf{m},t\right).$$ (4)

If we suppose the burst processes are independent, this partial differential equation (PDE) takes the following form:

$$\frac{\partial G\left(\mathbf{x},t\right)}{\partial t}=\sum _{i=1}^n{k}_i\left(F_i\left(x_i\right)-1\right)G+\sum _{i=1}^n{c}_{i0}\left(1-x_i\right)\frac{\partial G}{\partial x_i}+\sum _{i,j=1}^n{c}_{ij}\left(x_j-x_i\right)\frac{\partial G}{\partial x_i},$$ (5)

where $F_i$ is the PGF of the burst random variable $B_i$. The derivation of this PDE is provided in section S1.2. It is generally easier to treat the logarithm of G; applying the transformations $u_i:=x_i-1$ and $\phi :=\text{ln}G$ yields the equation:

$$\frac{\partial \phi \left(\mathbf{u},t\right)}{\partial t}=\sum _{i=1}^n{k}_i\left(M_i\left(u_i\right)-1\right)-\sum _{i=1}^n{u}_i{c}_{i0}\frac{\partial \phi }{\partial u_i}+\sum _{i,j=1}^n\left(u_j-u_i\right)c_{ij}\frac{\partial \phi }{\partial u_i},$$ (6)

where $M_i\left(u_i\right)=F_i\left(1+u_i\right)$ is the appropriate transformation of the burst PGF. To compute $P\left(\mathbf{m},t\right)$, we can evaluate $G\left(\mathbf{x},t\right)$ around the n-dimensional unit sphere and take an inverse fast Fourier transform (30,33).

Certain CMEs are isomorphic to SDEs

Before treating the discrete system defined by Eq. 2, we need to establish a crucial connection to a set of stochastic differential equations (SDEs), allowing us to use SDE tools to solve CMEs. Specifically, it is possible to treat $X_i$ as a random variable with the distribution $Poisson\left({\text{Λ}}_i\right)$, where ${\text{Λ}}_i$ is the intensity of the discrete process. In the general multivariate case, the following identity can be used to relate a set of stochastic processes ${\text{Λ}}_1,\dots ,{\text{Λ}}_n$ with joint distribution $F_{{\text{Λ}}_1,\dots ,{\text{Λ}}_n}$ to the solution of the CME (5,17,34,35):

$$P\left(\mathbf{m},t\right)=\int \prod _{i=1}^n\frac{e^{-{\text{Λ}}_i}{\text{Λ}}_i^{m_i}}{m_i!}d{F}_{{\text{Λ}}_1,\dots ,{\text{Λ}}_n}.$$ (7)

The Poisson representation was introduced by Gardiner (5,35), and successfully applied to modeling regulated gene loci (9,36,37). This representation is always viable, but does not guarantee that the law of ${\text{Λ}}_i$ is a probability: for example, if the variance of marginal random variable $X_i$ is lower than its mean, some probability densities must be negative. Nevertheless, in some cases, we can define a relationship between the CME and the “proper” probability laws of SDEs. If the distribution of burst sizes is a Poisson mixture, we can write it down as an equivalent Lévy jump process; for example, the geometric burst size distribution is an exponential-Poisson mixture, and may be interpreted as the Poisson mixture of the underlying compound Poisson process with exponential jumps. This class of models has previously been invoked to explain high trajectory variation observed in living cells (38, 39, 40). Thus, if species i undergoes jumps governed by the process $L_{i,t}$, the three prototypical reactions in Eq. 1 take the following form in the continuous worldview:

$$d{\text{Λ}}_i=d{L}_{i,t}-{\text{Λ}}_i\sum _{j=0}^n{c}_{ij}dt+\sum _{j=1}^n{c}_{ji}{\text{Λ}}_{j}dt,$$ (8)

where the left-hand term denotes the evolution of the process, the first term on the right-hand side represents bursting, the second term represents efflux by isomerization and degradation, and the third represents influx by isomerization. If $d{L}_{i,t}=k_{i}dt$, this formulation recovers the deterministic reaction rate equations and the well-known Poisson form for constitutive production (34).

This representation has three features that are occasionally useful to solving CME systems. The first is theoretical: the standard properties of Poisson mixtures mean that the moment-generating function (MGF) of the SDE is simply $G\left(\mathbf{x}-1,t\right)$, allowing easy conversion between the two (41,42). Therefore, CME solutions can be used as SDE solutions and vice versa; although we discuss the CME, the solutions generalize to classes of continuous-valued stochastic models explored in the biological (38) and financial (43) literature.

The second feature is qualitative: if the solution to an SDE is available, we can draw conclusions about the isomorphic CME without actually having to solve this CME. For example, the CME in Eq. 9 is isomorphic to the SDE in Eq. 10, as they share the generating function in Eq. 11 (17,44):

$$\frac{dP\left(m,t\right)}{dt}=k_1\sum _{z=0}^m[p_{z,1}P\left(m-z,t\right)-P\left(m,t\right)]-\gamma [\left(m+1\right)P\left(m+1,t\right)-mP\left(m,t\right)]$$ (9)

$$d\text{Λ}=d{L}_t-\gamma \text{Λ}dt$$ (10)

$$G\left(u,t\right)={\left(\frac{1-bu{e}^{-\gamma t}}{1-bu}\right)}^{\frac{k_1}{\gamma }},$$ (11)

where we suppose the burst distribution is geometric with mean b, the jump distribution is exponential with mean b, bursts arrive according to a Poisson process with rate $k_1$, the degradation rate is γ, and the process begins at $\text{Λ}=X=0$. ${\text{Λ}}_1$ is the gamma Ornstein-Uhlenbeck process (29,43, 44, 45). Inspired by a highly general result for constitutive transcription, which states that Poisson distributions always remain Poisson for a birth-death process (34), we may reasonably ask whether equivalent results are available for bursty processes. This intuition turns out to be incorrect, and straightforward to disconfirm using SDE results: $G\left(u,t\right)$ is not the gamma MGF, so the distribution of the process is not gamma for any finite $t\in \left(0,\infty \right)$—although it does approach a gamma law exponentially fast (44). Therefore, the corresponding Poisson mixture is not simply a time-varying negative binomial, and adopting such a model to describe gene expression over time (46) is theoretically problematic.

The third feature is quantitative: the Poisson representation facilitates analysis, both in the notation and the computation. The variance $\mathbb{V}\left[X_i\right]$ of the CME is simply given by $\mathbb{V}\left[{\text{Λ}}_i\right]+\mathbb{E}\left[{\text{Λ}}_i\right]$, allowing for a more compact representation. Finally, since the generating functions do not assume that the entire system is discrete or continuous, we can use the classes of solutions explored throughout this report to solve hybrid systems, with the transcription rate of a CME governed by an SDE. For example, if the transcription rate is given by the gamma Ornstein-Uhlenbeck process, we can solve the hybrid SDE-CME system by appending a “virtual” discrete species that undergoes bursty transcription and splicing (47).

General splicing graphs have analytical solutions

In this subsection, we treat the solutions of CMEs induced by general splicing DAGs. For simplicity, we enforce Eq. 6 holds: all burst processes are independent.

We need to solve Eq. 6, a PDE in n complex variables and one time variable. This is impossible in general. However, using the method of characteristics (30,48,49), we can reduce the PDE's complex degrees of freedom to n particularly simple coupled ordinary differential equations, which can be represented by a matrix equation:

$$\frac{d\mathbf{U}}{ds}=C\mathbf{U}\text{ s}.\text{t}.\mathbf{U}(s=0)=\mathbf{u},$$ (12)

where C is a matrix containing $C_{ij}=c_{ij}$ for all $i\ne j$ and $C_{ii}=-{\sum }_{j=1}^n{c}_{ij}-c_{i0}$. We can compute the characteristics by spectral decomposition:

$$U_i\left(\mathbf{u},s\right)=\sum _{j=1}^n{e}^{-r_{j}s}{\left(V\cdot Diag\left(V^{-1}\mathbf{u}\right)\right)}_{ij}:=\sum _{j=1}^n{e}^{-r_{j}s}{A}_{ij}\left(\mathbf{u}\right),$$ (13)

where $r_j$ are the (strictly nonnegative) eigenvalues of $-C$ and each column of matrix V contains an eigenvector of C. The derivation of this solution procedure is provided in section S2. Once the functional form of $U_i$ is available, it is straightforward to compute the solution of Eq. 6 by quadrature:

$$\phi \left(\mathbf{u},t\right)={\int }_0^t\sum _{i=1}^n{k}_i{M}_i\left(U_i\left(\mathbf{u},s\right)-1\right)ds.$$ (14)

Moments of the splicing graph solutions are tractable by matrix operations

To discuss specific results, such as the correlations between transcripts, we assume that exactly one parent transcript exists, and all other transcripts are produced from it by splicing. Consistently with the conventional model (25,30,50) we assume it is produced in geometrically distributed bursts. This corresponds to defining ${\mathcal{T}}_1$ as the parent transcript and setting $M_1\left(u_1\right)=M\left(u_1\right)=\frac{1}{1-b{u}_1}$ in Eq. 6, with all $k_j,j\ne i$ defined as zero.

To analyze this system, we rewrite Eq. 13 in terms of its marginal components:

$$U_1\left(\mathbf{u},t\right)=\sum _{i=1}^n{u}_i{\psi }_i\left(t\right)\text{ s}.\text{t}.{\psi }_i=\sum _{k=1}^n{a}_{i,k}{e}^{-r_{k}s}.$$ (15)

This form is most convenient for analyzing the summary statistics of a few marginals at a time. If the spectral decomposition is available, converting to this representation amounts to evaluating the coefficient matrix A once: $a_{i,k}=A_{1k}\left({\mathbf{\delta }}_{ij}\right)={\left(V\cdot Diag\left(V^{-1}{\mathbf{\delta }}_{ij}\right)\right)}_{1j}$, where ${\mathbf{\delta }}_{ij}$ is the Kronecker delta vector with a 1 in position i and 0 elsewhere.

The moments of the marginal distribution of species i can be computed directly from the derivatives of the marginal MGF of the formal continuous system with all complex arguments in $\mathbf{u}$ set to zero. We begin by considering $U_1$ as the sum in Eq. 15. To marginalize with respect to all $j\ne i$, we simply set all $u_j$ to zero, obtaining $U_1=u_i{\psi }_i\left(t\right)$. To compute the lower moments of a single species, we take the derivative with respect to $u_i$ and evaluate it at $u_i=0$ with the help of Eq. 15:

$$\mathbb{E}\left[{\text{Λ}}_i\right]=e^{\phi }\frac{\partial }{\partial u_i}{k}_1{\int }_0^{\infty }\left[\frac{1}{1-b{u}_i{\psi }_i\left(s\right)}-1\right]{ds|}_{u_i=0}=k_{1}b{\int }_0^{\infty }{\psi }_i\left(s\right)ds=k_{1}b\sum _{k=1}^n\frac{a_{i,k}}{r_k}.$$ (16)

Per the standard properties of mixed Poisson distributions (41), the value of ${\mu }_i$ is identical for the underlying continuous process and the derived discrete process.

The covariances can be computed directly from the derivatives of the marginal PGF with $u_q=0$ for all $q\ne i,l$. By construction, $U_1\left(u_i,u_l;s\right)=u_i{\psi }_i\left(s\right)+u_l{\psi }_l\left(s\right)$, where each ψ is the exponential sum corresponding to the marginal of the species in question. Taking the partial derivatives yields the following equation:

$$\text{Cov}\left({\text{Λ}}_i,{\text{Λ}}_l\right)=2k_1{b}^2\sum _{j,k=1}^n\frac{a_{i,j}{a}_{l,k}}{r_j+r_k}.$$ (17)

From standard identities, the covariance of a mixed bivariate Poisson distribution with no intrinsic covariance forcing is identical to the covariance of the mixing distribution (41). The marginal variances can be found by plugging in $l=i$, and the standard properties of Poisson mixtures (41) allow conversion to the discrete domain, with $\mathbb{V}\left[X_i\right]=\mathbb{V}\left[{\text{Λ}}_i\right]+{\mu }_i$. Since mixing decreases variance but not covariance, the correlation coefficient of the discrete system will always be lower than that of its continuous or hybrid analog. These lower moments are straightforward to compute, but do not appear to have an easily amenable analytical form for general graphs.

General burst distributions are tractable and encode physics with no free parameters

The relevance of CME to modern transcriptomic experimental data is tempered by the simplicity of tractable models. The model we have presented so far can describe the splicing cascade of a single gene, but does not naturally extend to multigene networks. Yet we know that genes often belong to coexpression modules that are identifiable by similarity metrics (2,21,23). Therefore, we are faced with the challenge of integrating multiple genes in a physically meaningful way.

Instead of building intractable “top-down” models that encode complex networks (51), we may build “bottom-up” models that extend analytical solutions. For example, we can consider sets of synchronized genes that experience bursting events at the same time. This model represents the bursty limit of multiple genes with transcription rates governed by a single telegraph process, up to scaling; a conceptually similar model has previously been used to describe correlations between multiple copies of one gene (52). This model retains the appeal of physical interpretability—for example, gene modules may be regulated by the same molecule—but does not excessively complicate the mathematics, and offers an incremental step toward more detailed descriptions.

For convenience of notation, we omit any discussion of the details of the downstream splicing networks, as the results derived above hold with no change. We have thus far assumed the $R_{tx,i}$ in Eq. 2 are independent, i.e., their bursts are unsynchronized. However, more sophisticated models can be built, and encode gene-gene correlations. Most generally, the differential of the log-PGF in Eq. 6 takes the following functional form:

$$\frac{\partial \phi \left(\mathbf{u},t\right)}{\partial t}=\sum _{\ell =1}^n\sum _{q=1}^{\omega }{k}_{\ell ,q}\left(M_{\ell ,q}\left(\mathbf{U}\left(\mathbf{u},t\right)\right)-1\right).$$ (18)

The full derivation is provided in section S1.4, and relies on iterative application of Cauchy products to conditional PGFs. This rather formal expression states that up to n species in the system may be cotranscribed in a single module. For a particular module of $\ell$ genes with synchronized transcription times, there are $\omega =\left(\begin{array}{l}n\\ \ell \end{array}\right)$ possible combinations of species that can be cotranscribed, indexed by q. The independent case emerges from setting all $k_{\ell ,q}$ to zero for $\ell >1$. The vector defining $U_1,\dots ,U_n:=\mathbf{U}$ is modular, as it is independent of bursting dynamics.

Example: Two-promoter bursty model, no synchronization

To begin, consider a system with two independent promoters that fire reactions $\varnothing \stackrel{k_{\mathrm{1,1}}}{\to }{B}_1\times {\mathcal{T}}_1$ and $\varnothing \stackrel{k_{\mathrm{1,2}}}{\to }{B}_2\times {\mathcal{T}}_2$. If ${\mathcal{T}}_1$ can be converted to ${\mathcal{T}}_2$, this model can describe an internal promoter (53) that generates molecules that cover only a part of the gene. In this formulation, the following special case of Eq. 6 holds:

$$\frac{\partial \phi \left(\mathbf{u},t\right)}{\partial t}=k_{\mathrm{1,1}}\left(M_1\left(U_1\left(\mathbf{u},t\right)\right)-1\right)+k_{\mathrm{1,2}}\left(M_2\left(U_2\left(\mathbf{u},t\right)\right)-1\right).$$ (19)

In the parlance of Eq. 18, we set $n=2$ and $k_{\mathrm{2,1}}=0$. Therefore, the stationary log-PGF takes the simple form:

$$\phi \left(\mathbf{u},t\right)={\int }_0^t[k_{\mathrm{1,1}}\left(M_1\left(U_1\left(\mathbf{u},s\right)\right)-1\right)+k_{\mathrm{1,2}}\left(M_2\left(U_2\left(\mathbf{u},s\right)\right)-1\right)]ds,$$ (20)

i.e., the joint distribution of RNA can be obtained with a single application of quadrature.

If $U_1$ and $U_2$ are disjoint (e.g., ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$ are products from two different genes), this expression reduces to the trivial case $\phi \left(\mathbf{u}\right)={\phi }_1\left(u_1\right)+{\phi }_2\left(u_2\right)$: intuitively, independent transcription processes produce statistically independent distributions. If only a single parent transcript exists ($U_1=U_2=U$), the model can represent a particular class of multistate promoters with two distinct short-lived active states, recapitulating the unsynchronized model in section S1.3. Finally, if the burst distributions are identical ($M_1=M_2=M$), the system becomes equivalent to a one-locus system with burst frequency $k_{\mathrm{1,1}}+k_{\mathrm{1,2}}$. This accords with the superposition property of the Poisson process driving transcription.

Example: Two-gene bursty model, with burst time synchronization

We continue by considering the instructive model of two genes influenced by the same regulator: the active periods of these genes are synchronized in time. However, the burst sizes are not coupled, and may indeed come from different distributions. Such a process has the transcription reaction $\varnothing \stackrel{k_{\mathrm{2,1}}}{\to }{B}_1\times {\mathcal{T}}_1+B_2\times {\mathcal{T}}_2$, where each ${\mathcal{T}}_i$ may be degraded or processed into further downstream species with total efflux rate $r_i$. In the parlance of Eq. 18, we set $k_{\ell ,q}$ to 0 for $\ell =1$.

Assuming that $B_1\sim Geom\left(b_1\right)$ and $B_2\sim Geom\left(b_2\right)$—i.e., the marginals are consistent with the standard bursty model—we can exploit the independence of $B_1$ and $B_2$ to write down the joint distribution:

$$M\left(\mathbf{U}\left(\mathbf{u},t\right)\right)=M_1\left(U_1\left(\mathbf{u},t\right)\right)M_2\left(U_2\left(\mathbf{u},t\right)\right),$$ (21)

which follows immediately from standard MGF identities. We propose a physical model leading to this burst size distribution in section S1.3. The expression in Eq. 18, with Eq. 21 used as the transcriptional burst size distribution, has the following solution:

$$\phi =k_{\mathrm{2,1}}{\int }_0^t[M_1\left(U_1\left(\mathbf{u},s\right)\right)M_2\left(U_2\left(\mathbf{u},s\right)\right)-1]ds=k_{\mathrm{2,1}}{\int }_0^t\left[\frac{1}{\left(1-b_1{U}_1\left(\mathbf{u},s\right)\right)\left(1-b_2{U}_2\left(\mathbf{u},s\right)\right)}-1\right]ds.$$ (22)

This expression is numerically integrable, but does not afford an analytical solution. We can obtain its lower moments by differentiating the log-PGF. Defining $U_i=u_i{\psi }_i$ and $U_l=u_l{\psi }_l$ for two transcript species generated from distinct genes, we yield:

$$\text{Cov}\left({\text{Λ}}_i,{\text{Λ}}_l\right)=k_{\mathrm{2,1}}{b}_1{b}_2{\int }_0^{\infty }{\psi }_i{\psi }_{l}ds=k_{\mathrm{2,1}}{b}_1{b}_2\sum _{j,k=1}^n\frac{a_{i,j}{a}_{l,k}}{r_j+r_k}.$$ (23)

Usefully, this expression is agnostic of the actual identity of $i,l$, so the expression holds for any of the species downstream of ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$. Finally, if we would like to compute the covariance between the two parent species, we simply plug in ${\psi }_i=e^{-r_{1}s}$ and ${\psi }_l=e^{-r_{2}s}$:

$$\text{Cov}\left({\text{Λ}}_1,{\text{Λ}}_2\right)=\frac{k_{\mathrm{2,1}}{b}_1{b}_2}{r_1+r_2}.$$ (24)

This covariance corresponds to the following Pearson correlation coefficient:

$$\rho =\frac{\text{Cov}\left({\text{Λ}}_1,{\text{Λ}}_2\right)}{{\sigma }_1{\sigma }_2}=\frac{\sqrt{r_1/r_2}}{1+r_1/r_2}\times \sqrt{\frac{1}{\left(1+1/b_1\right)\left(1+1/b_2\right)}}.$$ (25)

The first term achieves a global maximum of $1/2$ at $r_1=r_2$. The second is strictly smaller than 1, but asymptotically approaches 1 as $b_1,b_2$ jointly approach infinity. All downstream processes are stochastic and desynchronize molecular observables. Therefore, $1/2$ is the supremum of gene-gene correlations in this class of models.

Example: Two-gene bursty model, with perfect burst time and size synchronization

Conversely, we can consider the two-gene problem assuming that the burst distributions are identical and perfectly correlated. Physically, this model may correspond to coupling of initiation processes, e.g., this may occur when two genes are controlled by a single promoter. This burst distribution has the following joint PGF:

$$F\left(x_1,x_2\right)=\sum _{i,j}{x}_1^i{x}_2^j{p}_{i,j}=\sum _{i,j}{x}_1^i{x}_2^j{p}_i\delta \left(i-j\right)=\frac{1}{1+b-b{x}_1{x}_2}.$$ (26)

Upon inserting the characteristics and taking the requisite partial derivatives, we yield the following correlation structure:

$$\rho =\frac{\sqrt{r_1/r_2}}{1+r_1/r_2}\times \left(1+\frac{b}{b+1}\right).$$ (27)

As in the case of uncoupled gene sizes reported in Eq. 25, the first term is at most $1/2$. The second term asymptotically approaches 2 as $b\to \infty$. Therefore, there are no intrinsic model constraints on Pearson correlation coefficients of two-gene products; constraints arise as the effect of the burst size correlation structure.

Example: Two-gene bursty model, with partial burst time and size synchronization

The models described above are useful for understanding limiting cases, but somewhat restrictive: the model solved in Eq. 19 enforces $\rho =0$, the synchronized burst time model in Eq. 22 enforces $\rho \in \left(\mathrm{0,1}/2\right)$, and the perfectly synchronized burst size model in Eq. 26 requires burst sizes to be identical. Thus, we need to construct models consistent with observations, recapitulating both the multigene correlation structure and the diversity of burst sizes evident from marginals.

This is most easily tractable using the continuous formulation: we can impose perfect correlation between Lévy jump sizes. Conceptually, we suppose the overall driving process $L_t$ for N genes is given by a compound Poisson process with average jump size b and jump distribution $J\sim Exp\left(b^{-1}\right)$. The driving process for a single gene i is given by $L_{i,t}=w_i{L}_t$, with average jump size $b{w}_i$ and ${\sum }_{i=1}^N{w}_i=1$. We propose a physical model leading to this burst size distribution in section S1.3. Since all jump sizes are scalar multiples of each other, they are perfectly correlated. The joint jump distribution has the following MGF:

$$M\left(\mathbf{u}\right)=\mathbb{E}\left[\text{exp}\left(\sum _{i=1}^N{u}_i{J}_i\right)\right]=\mathbb{E}\left[\text{exp}\left(J\sum _{i=1}^N{u}_i{w}_i\right)\right]=\frac{1}{1-b{\sum }_{i=1}^N{u}_i{w}_i},$$ (28)

where the third equality stems from recognizing that the joint MGF is simply the univariate exponential MGF evaluated at ${\sum }_{i=1}^v{u}_i{w}_i$. If we only consider the parent transcripts with efflux rates $r_i$ and characteristics $U_i=u_i{e}^{-r_{i}t}$, we yield the following stationary log-PGF:

$$\phi \left(\mathbf{u}\right)=k_{N,1}{\int }_0^{\infty }\left[\frac{1}{1-b{\sum }_{i=1}^N{u}_i{w}_i{e}^{-r_{i}s}}-1\right]ds.$$ (29)

Finally, setting $N=2$, we can take derivatives of the PGF and compute the correlation structure:

$$\text{Cov}\left({\text{Λ}}_1,{\text{Λ}}_2\right)=\frac{2k_{\mathrm{2,1}}{b}^2{w}_1{w}_2}{r_1+r_2}$$ (30)

$$\rho =\frac{2\sqrt{r_1/r_2}}{1+r_1/r_2}\times \sqrt{\frac{1}{\left(1+\frac{1}{b{w}_1}\right)\left(1+\frac{1}{b{w}_2}\right)}}\in \left(\mathrm{0,1}\right).$$ (31)

As above, this model is appealing since it has no free parameters: the gene-gene correlations are not imposed by an ad hoc correlation parameter, but emerge from the model structure itself. Therefore, we can evaluate the model's performance by comparing true intergene correlations to ones computed based only on the marginals.

Interestingly, single-gene systems with rapid splicing recapitulate the multigene functional form. Consider a source species ${\mathcal{T}}_0$, which is produced in geometrically distributed bursts and converted to species $\left\{{\mathcal{T}}_i\right\}$, with $i=1,\dots ,N$, at rates ${\beta }_i$. These transcripts are degraded at rates $r_i$. Furthermore, suppose all of the ${\beta }_i\sim \mathcal{O}\left({\epsilon }^{-1}\right)$ for small ε, i.e., the source transcript is extremely unstable. In this limit, ${\mathcal{T}}_i$ are produced by a Lévy process with jumps of average size $b{\beta }_i/\beta$, where b is the underlying ${\mathcal{T}}_0$ burst size, $\beta :={\sum }_i{\beta }_i$, and the ratio ${\beta }_i/\beta$ is $O\left(1\right)$. We define corresponding weights $w_i:={\beta }_i/\beta$; by definition, ${\sum }_i{w}_i=1$. This yields:

$$U_0\left(\mathbf{u},t\right)=C{e}^{-\beta t}+\sum _{i=1}^N\frac{{\beta }_i{u}_i}{\beta -r_i}{e}^{-r_{i}t}\to \sum _{i=1}^N{u}_i{w}_i{e}^{-r_{i}t},$$ (32)

where C is a constant in the solution of the characteristic $U_0\left(\mathbf{u},t\right)$ whose value becomes immaterial as β increases. Plugging in the characteristic:

$$M\left(U_0\left(\mathbf{u},t\right)\right)=\frac{1}{1-b{U}_0\left(\mathbf{u},t\right)}=\frac{1}{1-b{\sum }_{i=1}^N{u}_i{w}_i{e}^{-r_{i}t}},$$ (33)

which recapitulates the form of the integrand in Eq. 29. Therefore, the multigene model can be used to describe transcripts arising from a single rapidly processed, unobserved parent molecule, yielding positive, but otherwise unconstrained, correlation between the downstream species.

Example: Anti-correlated two-gene bursty model, with burst time synchronization

Thus far, we have considered the problem of describing synchronized genes, and proposed three models that can produce positive correlations. Putting aside the problem of positing a specific physical mechanism, we can ask whether any joint burst distribution can produce negative correlations in molecule counts, despite perfect synchronization of burst events. Considering the cross moment of mRNA produced at two synchronized loci, with generic joint burst generating function M, we find:

$$\mathbb{E}\left[{\text{Λ}}_1{\text{Λ}}_2\right]=k_{\mathrm{2,1}}{\int }_0^{\infty }\frac{d^{2}M}{d{u}_{1}d{u}_2}ds+{\mu }_1{\mu }_2,$$ (34)

with the partial derivatives evaluated at $u_1=u_2=0$. The second term is strictly positive. The first term is the integral of an exponentially discounted burst cross moment:

$$\frac{d^{2}M}{d{u}_{1}d{u}_2}=\frac{d^{2}M}{d{U}_{1}d{U}_2}\frac{d{U}_1}{d{u}_1}\frac{d{U}_2}{d{u}_2}=\mathbb{E}\left[B_1{B}_2\right]e^{-\left(r_1+r_2\right)s},$$ (35)

where the partial derivatives are yet again evaluated at $u_1=u_2=U_1=U_2=0$, and $B_1$ and $B_2$ denote the SDE jump sizes at the two-gene loci. Supposing the correlation between the burst sizes is $\rho \in [-\mathrm{1,0})$, and considering the covariance between the transcripts:

$$\text{Cov}\left({\text{Λ}}_1,{\text{Λ}}_2\right)=k_{\mathrm{2,1}}\frac{\mathbb{E}\left[B_1{B}_2\right]}{r_1+r_2}=\frac{k_{\mathrm{2,1}}}{r_1+r_2}(\rho {\sigma }_{B_1}{\sigma }_{B_2}+{\mu }_{B_1}{\mu }_{B_2}),$$ (36)

which achieves a minimum at $\rho =-1$. Thus, the covariance has a lower limit:

$$\text{Cov}\left({\text{Λ}}_1,{\text{Λ}}_2\right)\ge \frac{k_{\mathrm{2,1}}}{r_1+r_2}\left({\mu }_{B_1}{\mu }_{B_2}-{\sigma }_{B_1}{\sigma }_{B_2}\right).$$ (37)

Without constructing the joint distribution explicitly, if we suppose the marginal discrete burst distributions are geometric—i.e., the jump sizes are exponential—then ${\mu }_{B_i}={\sigma }_{B_i}=b_i$, and the lower limit on covariance is zero. This means that negative correlations cannot possibly result from a model with geometrically distributed, synchronized jumps. However, other joint burst laws can produce negative correlations, as long as the population correlation coefficient is sufficiently negative and the burst distributions are sufficiently dispersed.

We can demonstrate the existence of processes with negative count correlations induced by synchronized burst events. First, we suppose that the marginal burst distributions are identical and described by a gamma law with shape α and scale θ, enforcing ${\mu }_{B_1}={\mu }_{B_2}=\alpha \theta$ and ${\sigma }_{B_1}^2={\sigma }_{B_2}^2=\alpha {\theta }^2$. Therefore, the covariance of the Poisson intensities takes the following form:

$$\text{Cov}\left({\text{Λ}}_1,{\text{Λ}}_2\right)=\frac{k_{\mathrm{2,1}}}{r_1+r_2}(\rho \alpha {\theta }^2+{\alpha }^2{\theta }^2)=\frac{k_{\mathrm{2,1}}{\theta }^2}{r_1+r_2}(\rho \alpha +{\alpha }^2),$$ (38)

which achieves $\text{Cov}\left({\text{Λ}}_1,{\text{Λ}}_2\right)<0$ whenever $\rho \alpha +{\alpha }^2<0$. Therefore, for any $\rho \in \left(-\mathrm{1,0}\right)$, every $\alpha \in \left(0,-\rho \right)$ meets this criterion.

It remains to confirm that a bivariate gamma distribution with a negative correlation can exist. Such a distribution was constructed by Moran, and permits all $\rho \in \left(-\mathrm{1,1}\right)$ (54,55). Applying the Cauchy-Schwartz inequality to the marginals guarantees that the joint MGF of the correlated bivariate gamma distribution exists (56). This demonstrates the existence of continuous moving average processes with negative stationary correlation, driven by a common Poisson process arrival process. Finally, the corresponding Poisson mixture has identical covariance, and must also have a negative correlation. Therefore, a CME with marginal negative binomial burst distributions and a carefully chosen joint structure can achieve negative molecular correlations, even if the bursts are synchronized.

Certain models of heterogeneity are analytically tractable

Thus far, we have reported a toolbox of models that can represent Markovian systems with fairly general splicing graphs and burst distributions, and demonstrated that their solutions exist and are computable. By design, these models by themselves describe homogeneous populations of cells, with deterministic parameters. Using standard statistical approaches, they can be reassembled to describe heterogeneity in parameters (57):

$$P\left(\mathbf{m},t\right)=\underset{\text{Θ}}{\int }P(\mathbf{m},t;\theta )d{f}_{\theta }={\mathbb{E}}_{\text{Θ}}\left[P(\mathbf{m},t;\theta )\right]$$ (39)

$$G\left(\mathbf{x},t\right)=\underset{\text{Θ}}{\int }G(\mathbf{x},t;\theta )d{f}_{\theta }={\mathbb{E}}_{\text{Θ}}\left[G(\mathbf{x},t;\theta )\right].$$ (40)

Equation 39 is essentially the definition of a mixture model: the parameter vector θ may itself be distributed according to the statistical law $f_{\theta }$ over a state space $\text{Θ}$. To determine the resulting probability distribution, we need to integrate with respect to this law. By linearity, we can exchange the generating function sum in Eq. 4 and the integral in Eq. 39 to obtain Eq. 40.

This expression is extremely generic; the base case of a homogeneous cell population with parameter vector $\overline{\theta }$ is obtained by setting $d{f}_{\theta }=\delta \left(\theta -\overline{\theta }\right)$, where δ is a multivariate Dirac delta functional. Unfortunately, analytical solutions are only available in several highly restrictive cases.

Example: A finite number of cell types

Multimodality in single cells can emerge from the existence of multiple long-lived subpopulations, which are conventionally fit to a finite mixture distribution (58). We can formalize this model for an arbitrary number of populations. Consider a population of cells with J disjoint “cell types,” indexed by j. Each cell type has the parameter vector ${\theta }_j$ and relative abundance $w_j$. The probability distribution of the entire population can be computed by the law of total probability, conditioning on the cell type, or by setting $d{f}_{\theta }={\sum }_{j=1}^J{w}_j\delta \left(\theta -{\theta }_j\right)$ in (39), (40):

$$P\left(\mathbf{m},t\right)=\sum _{j=1}^J{w}_{j}P\left(\mathbf{m},t;{\theta }_j\right)G\left(\mathbf{x},t\right)=\sum _{j=1}^J{w}_{j}G\left(\mathbf{x},t;{\theta }_j\right).$$ (41)

This formulation can produce J-modal distributions. This reduces to the standard model when $J=1$ or when all ${\theta }_j$ are identical.

Correlations can emerge from the existence of multiple cell types. For simplicity, we set $J=2$ and $n=2$, and suppose the molecule distributions are independent Poisson, whether as an effect of constitutive production or as the limit of a bursty distribution. For gene i and cell type j, the average expression is ${\lambda }_{i,j}$, implying that the stationary distribution takes the following form:

$$G\left(\mathbf{u}\right)=\sum _{j=1}^2{w}_{j}G\left(\mathbf{u};{\lambda }_{1,j},{\lambda }_{2,j}\right)=\sum _{j=1}^2{w}_{j}G\left(u_1,{\lambda }_{1,j}\right)G\left(u_2,{\lambda }_{2,j}\right)=\sum _{j=1}^2{w}_j{e}^{{\lambda }_{1,j}{u}_1}{e}^{{\lambda }_{2,j}{u}_2}.$$ (42)

The correlation can be found by differentiation. Setting $w_1=w_2=\frac{1}{2}$ and supposing ${\lambda }_{i,1}=0$ (i.e., cell type 1 does not express either gene), we yield:

$$\rho =\sqrt{\frac{{\lambda }_{\mathrm{1,2}}{\lambda }_{\mathrm{2,2}}}{\left({\lambda }_{\mathrm{1,2}}+2\right)\left({\lambda }_{\mathrm{2,2}}+2\right)}}\in \left(\mathrm{0,1}\right).$$ (43)

Supposing now ${\lambda }_{\mathrm{1,2}}={\lambda }_{\mathrm{2,1}}=0$ (i.e., gene 1 is a perfectly specific marker for cell type 1 and gene 2 is a marker for cell type 2):

$$\rho =-\sqrt{\frac{{\lambda }_{\mathrm{1,1}}{\lambda }_{\mathrm{2,2}}}{\left({\lambda }_{\mathrm{1,1}}+2\right)\left({\lambda }_{\mathrm{2,2}}+2\right)}}\in \left(-\mathrm{1,0}\right).$$ (44)

Therefore, correlations can emerge even in the absence of transcriptional synchronization. To account for these correlations, it is necessary to build mixture models, investigate living systems with low cell type diversity, or use ad hoc filtering to extract putative homogeneous cell populations.

Example: Extrinsic noise in burst frequency

Even within a homogeneous cell type, the parameter values may not be perfectly synchronized. We can thus define extrinsic noise, which encodes the stochastic parameter distribution (24,59). This description presupposes that the noise, if generated by a stochastic process, evolves much slower than the transcriptional dynamics (47). There does not appear to be a general solution for parameter mixing, but a set of solutions is available for systems with random burst frequencies. Suppose there is a single parent transcript with a burst frequency described by the random variable $K_i$. We can immediately write down a solution for the overall count PGF:

$$G\left(\mathbf{x},t\right)={\int }_0^{\infty }G(\mathbf{x},t;k_i)d{f}_{K_i}={\int }_0^{\infty }{e}^{k_i{\phi }^{\ast }\left(\mathbf{x},t\right)}d{f}_{K_i}=M_K\left[{\phi }^{\ast }(\mathbf{x},t)\right],$$ (45)

where $M_{K_i}$ is the MGF of the burst frequency distribution and ${\phi }^{\text{∗}}$ is a nominal log-PGF with unity burst frequency. The degenerate case is recovered by constraining $K_i$ to a Dirac delta distribution at $k_i$, with MGF $M_{K_i}\left(z\right)=e^{k_{i}z}$. Equation 45 immediately extends to integrals of Eq. 18 by defining a multivariate burst frequency distribution and computing its MGF.

Example: Extrinsic noise in burst size

Burst size modulation has been heavily implicated in the regulation of cell size (60, 61, 62). For systems with a distribution of static cell sizes, not governed by the cell cycle, we can at least formally postulate a model:

$$G\left(\mathbf{x},t\right)={\int }_0^{\infty }G\left(\mathbf{x},t;\mathbf{b}\left(z\right)\right)d{f}_Z\left(z\right),$$ (46)

where $\mathbf{b}$ is the vector of average burst sizes, governed by a common univariate random variable Z with realizations z, e.g., $b_i=z{c}_i$. Z thus models the “cell size” in a mechanistic fashion. Unfortunately, despite this relevance to physiology, this general form is intractable: the burst size parameter cannot be “factorized” out. However, certain special cases can be connected to previous work.

Consider the case of a single mRNA species produced in geometric bursts with a random cell-specific burst size. If the inverse burst size distribution is given by the law $\mathcal{Z}$, the distribution of mRNA is given by the $\mathcal{Z}$ -gamma-Poisson PMF. Only a few $\mathcal{Z}$ -gamma distributions have been studied in depth. If $\mathcal{Z}$ is gamma (i.e., the burst size is inverse-gamma distributed), gamma-gamma compounding yields a beta distribution of the second kind (63), with a rather complicated MGF available in terms of Lauricella functions (64).

Transient burst dynamics are solvable

Thus far, we have primarily focused on stationary systems with time-independent parameters. Nevertheless, there are classes of physiological phenomena, such as differentiation and cell cycling, where transient behaviors are crucial, particularly since these processes occur on timescales comparable with the mRNA lifetimes (1,65). Usually, the regulatory events underpinning these processes are modeled by variation in DNA-localized transcriptional parameters (66, 67, 68, 69).

By examining Eq. 18, it is easy to see that the current framework can be extended to any deterministic variation in k and M, with solutions available at arbitrary times t:

$$\phi \left(\mathbf{u},t\right)={\int }_0^t\sum _{\ell =1}^n\sum _{q=1}^{\left(\begin{array}{l}n\hfill \\ \ell \hfill \end{array}\right)}{k}_{\ell ,q}\left(s\right)\left(M_{\ell ,q}\left(\mathbf{U}\left(\mathbf{u},s\right),s\right)-1\right)ds.$$ (47)

Therefore, burst frequencies, burst distributions, and even the coexpression modules can vary, continuously or discontinuously, as long as the variation is deterministic. This can be exploited to model a variety of phenomena, such as variation in gene copy numbers over the cell cycle (62,66) and the concentration of high-abundance regulators not coupled to the mRNA under investigation. If the reaction rates within $\mathbf{U}$ change over time, the generating function PDE becomes intractable; however, some simple models, such as piecewise constant, can be solved by splitting the integral.

We have further assumed $m_i(t=0)=0$ for all species i. However, if nonzero molecule counts are present at $t=0$, it is straightforward to compute the resulting log-PGF by separately defining the homogeneous generating function ${\phi }^h$ with $m_i(t=0)=0$ and the generating function of the initial condition ${\phi }^{init}$:

$$\phi \left(\mathbf{u},t\right)={\phi }^h\left(\mathbf{u},t\right)+{\phi }^{init}\left(\mathbf{U}\left(\mathbf{u},t\right)\right)$$ (48)

$$\phi \left(\mathbf{u},t\right)={\phi }^h\left(\mathbf{u},t\right)+\sum _{i=1}^n{m}_i^{\left(0\right)}\text{ln}\left(1+U_i\left(\mathbf{u},t\right)\right),$$ (49)

where $U_i$ are the characteristics. Eq. 48 relates the general form of the conditional distribution, whereas Eq. 49 produces the particular form with deterministic initial molecule counts $m_i^{\left(0\right)}$, as discussed elsewhere (70). Therefore, the current approach can be used to compute the likelihoods of entire trajectories of observations, and thus perform parameter estimation on live-cell data.

Example: Cell cycling

Using the conditioning relation in Eq. 49, we can solve models of certain cell-cycle phenomena. Suppose that a “cell cycle” consists of two stages with durations ${\text{Δ}}_1$ and ${\text{Δ}}_2$ and parameters $b^{\left(j\right)},{\gamma }^{\left(j\right)},k_1^{\left(j\right)}$ in stage j. The PGF of the joint transcript distribution at the end of the first stage, $t={\text{Δ}}_1$, is given by Eq. 48, yielding the PGF $G^{\left(1\right)}\left(\mathbf{u}\right)$. Now supposing the stage transition involves the binomial partitioning of all molecules, the distribution of mRNA upon entering the second stage is $G^{\left(1\right)}\left(1+\mathbf{u}/2\right)$. This identity results from the law of total expectation, and amounts to asserting that the probability of retaining each molecule is $1/2$, with a per-molecule Bernoulli retention PGF of $\frac{1}{2}\left(1+x\right)$. This result has been derived in previous models of cell cycling (25,62) and proposed in more generality in our recent discussion of technical noise (16).

Considering the specific example of a single transcript with initial PGF $G^{\left(0\right)}$, we can adapt Eq. 11 (44) to yield:

$$G^{\left(1\right)}\left(u,{\Delta }_1\right)=G^{\left(0\right)}\left(u{e}^{-{\gamma }^{\left(1\right)}{\text{Δ}}_1}\right){\left(\frac{1-b^{\left(1\right)}u{e}^{-{\gamma }^{\left(1\right)}{\text{Δ}}_1}}{1-b^{\left(1\right)}u}\right)}^{\frac{k_1^{\left(1\right)}}{{\gamma }^{\left(1\right)}}}.$$ (50)

This is the generating function immediately before partitioning. The generating function immediately after simply inserts $\frac{1}{2}\left(2+u\right)$ in place of u to account for partitioning. Finally, to compute the generating function at the end of the cycle, we multiply through by the transient PGF and insert the characteristic $u{e}^{-{\gamma }^{\left(2\right)}t}$ into the initial condition:

$$G^{\left(2\right)}\left(u,{\Delta }_1+{\Delta }_2\right)=G^{\left(0\right)}\left(\frac{1}{2}\left(2+u{e}^{-{\gamma }^{\left(2\right)}{\Delta }_2}\right)e^{-{\gamma }^{\left(1\right)}{\Delta }_1}\right){\left(\frac{1-b^{\left(1\right)}\frac{1}{2}\left(2+u{e}^{-{\gamma }^{\left(2\right)}{\Delta }_2}\right)e^{-{\gamma }^{\left(1\right)}{\Delta }_1}}{1-b^{\left(1\right)}\frac{1}{2}\left(2+u{e}^{-{\gamma }^{\left(2\right)}{\Delta }_2}\right)}\right)}^{\frac{k_1^{\left(1\right)}}{{\gamma }^{\left(1\right)}}}{\left(\frac{1-b^{\left(2\right)}u{e}^{-{\gamma }^{\left(2\right)}{\Delta }_2}}{1-b^{\left(2\right)}u}\right)}^{\frac{k_1^{\left(2\right)}}{{\gamma }^{\left(2\right)}}}.$$ (51)

Although solutions of this type are somewhat unwieldy to write down explicitly, they can always be computed by composition of functions for the one-species system.

The general solution, with arbitrary burst distributions, splicing networks, and deterministic regulatory dynamics, can be computed by working backward from the last stage of cell cycle and incrementally adding “initial condition” contributions from previous stages. As an illustration, we define a system with zero molecules at $t=0$, with a bursty promoter that produces a single parent isoform with the characteristic $U_1\left(\mathbf{u},s\right)$. For convenience, we assume the splicing and degradation are time independent. We can immediately write down the generating function for the system state before partitioning at $t={\Delta }_1+{\Delta }_2$:

$${\phi }^{\left(2\right)}\left(\mathbf{u},{\Delta }_1+{\Delta }_2\right)=\left(k_1^{\left(1\right)}\underset{0}{\overset{{\Delta }_1}{\int }}\left[\frac{1}{1-b^{\left(1\right)}{U}_1\left(\frac{1}{2}\left(2+\mathbf{U}\left(\mathbf{u},{\Delta }_2\right)\right),s\right)}-1\right]ds\right)+\left(k_1^{\left(2\right)}\underset{0}{\overset{{\Delta }_2}{\int }}\left[\frac{1}{1-b^{\left(2\right)}{U}_1\left(\mathbf{u},s\right)}-1\right]ds\right).$$ (52)

This generalizes the systems studied previously (62) by relaxing the assumption of timescale separation between transcripts, while maintaining the assumption of bursty gene dynamics; transient coupling between cell size and burst size (such as the exponential form in (62)) can be incorporated by appropriately defining a time-varying burst distribution in Eq. 47. The solution has previously been extended to describe Erlang-distributed stochastic time intervals (25,71). This requires defining a CME coupled to a multistate Markov chain governing the transcriptional parameters and yields a series of coupled PDEs that take a form reminiscent of multistate promoter equations (72), but are not generally tractable by quadrature.

Results

Ultimately, we would like to use these solutions to fit real data, and represent entire data sets using a small set of physically interpretable parameters for each gene, potentially with some higher-level structure encoding cell types (as in Eq. 41) or gene-gene synchronization (as in Eq. 29). Unfortunately, the experimental and computational infrastructure to do this does not exist yet: as we discuss at length in section S5, single-cell, single-molecule, full-length sequencing methods are in their nascence, the structure of splicing processes is not well characterized on a genome-wide scale, and both biology and sequencing involve obscure sources of noise.

However, we can take the first steps in this direction by exploiting some of the simpler results to explain correlations in real data. In Eqs. 33 and 29, we report two models that give positive correlations for coexpressed transcripts. We cannot yet use these models to recapitulate entire data sets. The physics are too complex to explicitly describe: the model is a priori misspecified because we disregard other sources of noise. Furthermore, the inference procedure requires some care, as the joint distributions are too large to compute. If we try to fit distributions two at a time, the results will be inconsistent (e.g., fitting genes 1 and 2 will yield an estimated ${\hat{b}}_1$ different from the one obtained by fitting genes 1 and 3), and still suffer from model misspecification.

We can sacrifice some statistical power but improve interpretability by treating the genes one at a time. The models' correlation structure, given in Eq. 31, has no free parameters: it is fully determined by the marginal distributions. Given marginal estimates of gene-specific parameters (straightforward to compute by maximum likelihood estimation with the negative binomial law), we can predict the correlation structure and compare predictions to experimental ground truth. We interpret these predictions as upper bounds in the absence of all other noise: if additional sources of stochasticity are present, the correlations should degrade relative to the model. As the correlations predicted by Eq. 31 are strictly less than 1, they are nontrivial.

To perform this analysis, we obtained data from the recent FLT-seq (full-length transcript sequencing by sampling) protocol (73). As this experimental technique has molecular and cellular barcodes, the data are interpretable as discrete transcript counts sampled from a distribution. To minimize transient effects, such as cell cycling and differentiation, we selected a data set generated from cultured mouse stem cells. To limit biological heterogeneity due to discrete cell subpopulations (as in Eq. 41), we filtered for cell barcodes corresponding to the activated cell subset (136 barcodes) according to the authors' annotations. In all downstream analyses, we treated this filtered data set as biologically homogeneous up to intrinsic stochasticity.

The FLT-seq protocol produces full-length reads, which can be used to discover new isoforms, but does not reveal causal relationships between those isoforms. Nevertheless, we can use the tools of discrete mathematics to partially infer these relationships. Splicing removes introns, but cannot insert them. We can use this relationship to constrain the splicing DAG: if transcript ${\mathcal{T}}_j$ can be obtained by removing part of the sequence in transcript ${\mathcal{T}}_i$, there must be a path from ${\mathcal{T}}_i$ to ${\mathcal{T}}_j$. On the other hand, if ${\mathcal{T}}_i$ contains the sequence $I_i$ but omits the sequence $I_j$, whereas ${\mathcal{T}}_j$ contains the sequence $I_j$ but omits the sequence $I_i$, the transcripts are mutually exclusive and must be generated from the parent transcript by disjoint processes.

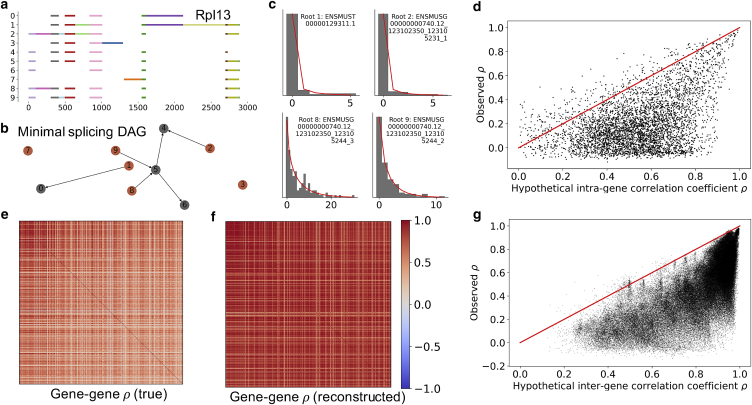
For each gene, we enumerate the transcripts observed in the data and split them into elementary intervals, contiguous stretches that are either present or absent in each transcript (denoted by the colors in Fig. 1 a). These elementary intervals constrain the relationships between transcripts, and we can use their presence or absence in each transcript to construct an accessibility graph. The internal structure of this graph is underspecified, but immaterial: the negative binomial model implied by the generating functions in Eqs. 33 and 29 describes the roots, mutually exclusive transcripts that must be generated directly from the parent transcript (indicated in orange in Fig. 1 b, and solved in Eq. 33). We fit the distributions of these roots, discarding any data that are underdispersed (variance lower than mean), overly sparse (fewer than five molecules in the entire data set), or fail to converge to a fit. The satisfactory fits for the sample gene Rpl13 are shown in Fig. 1 c.

Figure 1.

Leveraging the synchronized burst model to predict transcript-transcript correlations. (a) By inspecting exon coexpression structures in long-read sequencing data, we can split genes into elementary intervals. (b) Although sequencing data are not sufficient to identify the relationships between various transcripts, they can provide information about “roots” of the splicing graph (highlighted in orange), which must be produced from the parent transcript by mutually exclusive processes. (c) The root transcript copy-number distributions are well described by negative binomial laws (gray histograms, raw marginal count data; red lines, fits). (d) The intrinsic noise model is not sufficient to accurately predict transcript-transcript correlations, but does serve as a nontrivial upper bound: few sample correlations exceed the model-based predictions obtained from Eq. 31 (points, transcript-transcript correlation matrix entries for mutually exclusive “root” transcripts of a single gene; red line, theory/experiment identity line). (e) The highest-expressed transcripts across the top 500 genes show distinctive, and generally positive correlation patterns. (f) We can use an analogous model to predict and reconstruct the correlation matrix based solely on marginal data. (g) As before, the model (Eq. 31) is not sufficient to accurately predict gene-gene correlations, but provides an effective and nontrivial upper bound (points, transcript-transcript correlation matrix entries; red line, theory/experiment identity line). To see this figure in color, go online.

The negative binomial fit yields transcript-specific burst sizes $b{w}_i$ and efflux rates $r_i$ (nondimensionalized by setting burst frequency to unity). We plug these quantities into Eq. 31, compute hypothetical correlations ${\rho }_{theo}$, and compare them to sample correlations ${\rho }_{samp}$ in Fig. 1 d. These results represent the 4,885 nontrivial correlation matrix entries between 1,978 transcripts from 500 genes. A total of 302 transcripts were rejected due to underdispersion, 542 due to sparsity, and 100 due to poor fits. The theoretical constraint (sample correlation equal to or lower than predicted correlation) was met in 4,606 cases (94.3%).

The results suggest that the model is not sufficient to recapitulate the full dynamics, but does provide an effective, and nontrivial, theoretical constraint. We hypothesize that the “consistent” regime (${\rho }_{samp}\in \left(0,{\rho }_{theo}\right)$, 3,856 entries) represents the degradation of correlations due to technical noise in the sequencing process and stochastic intermediates. The “inconsistent” regime (${\rho }_{samp}\in \left({\rho }_{theo},1\right)$, 279 entries) may stem from model misidentification, and could be explained by coupling between splicing events, resulting in a burst model closer to Eq. 26. Some of these apparently inconsistent correlations may also be due to the small sample sizes, as discussed in section S5.1. Finally, the “negative” regime (${\rho }_{samp}<0$, 750 entries) technically meets the constraint, but cannot actually be reproduced by the model. This does not appear to be an artifact of sample sizes, as evident from the strong negative peak in Figure S8 a. Instead, we speculate that enrichment in negative correlations is the signature of a more complicated regulatory schema that preferentially synthesizes some isoforms to the exclusion of others, rather than choosing the splicing pathway randomly (as encoded in the derivation of Eq. 33).

We can exploit the analogous intergene model, encoded in Eq. 29, to try to predict the gene-gene correlation matrix (Fig. 1 e) based solely on the marginals, supposing all 500 highest-expressed genes fire simultaneously as a limiting case. For each gene, we consider the highest-abundance root transcript that can be fit by a negative binomial distribution, and identify its marginal burst size and efflux rate. Plugging these parameter estimates into Eq. 26, we obtain theoretical correlations ${\rho }_{theo}$ and reconstruct the correlation matrix (Fig. 1 f). Finally, we compare the intragene sample correlations ${\rho }_{samp}$ to the theoretical values in Fig. 1 g. These results represent the 119,805 nontrivial correlation matrix entries based on the 490 genes with well-fit roots. The theoretical constraint (sample correlation equal to or lower than predicted correlation) was met in 119,503 cases (99.7%).

Yet again, the model provides a nontrivial bound. We hypothesize that the consistent regime (${\rho }_{samp}\in \left(0,{\rho }_{theo}\right)$, 117,542 entries) represents the degradation of correlations due to stochastic effects outside the model, much as before. The correlations in the inconsistent regime (${\rho }_{samp}\in \left({\rho }_{theo},1\right)$, 302 entries) lie very close to the identity line, so we hypothesize they are mostly explained by small sample sizes, as discussed in section S5.1. Finally, the “negative” regime (${\rho }_{samp}<0$, 1,961 entries) is rare and does not appear to produce a strong signal in the correlation distribution (Figure S8 b), so we expect they also emerge from small sample sizes.

Conclusions

We have described a broad extension of previous work pertaining to monomolecular reaction networks coupled to a bursty transcriptional process. In particular, by exploiting the standard properties of reaction rate equations, we have demonstrated the existence of all moments and cross moments. Furthermore, we have derived the analytical expressions for the generating functions and demonstrated their existence. The following expression gives the general solution for the joint PGF G:

$$G\left(\mathbf{u},t\right)={\mathbb{E}}_{\text{Θ}}\left[G^{\left(0\right)}\left(\mathbf{U}\left(\mathbf{u},t\right)\right)\text{exp}\left({\int }_0^t\sum _{\ell =1}^n\sum _{q=1}^{\text{ω}}{k}_{\ell ,q}\left(s\right)\left(M_{\ell ,q}\left(\mathbf{U}\left(\mathbf{u},s\right),s\right)-1\right)ds\right)\right].$$ (53)

This expression is modular with respect to $\mathbf{U}$, the set of characteristics defining the splicing and degradation network, $M_{\ell ,q}$, the joint generating functions governing the bursting dynamics for all possible cotranscribing modules, $G^{\left(0\right)}$, the initial condition, and $f_{\theta }$, the law governing the parameter distributions. The burst frequency and distribution can be time dependent, and describe deterministic driving by a latent process or regulator. By iteratively applying the dependence on the initial condition, we can write down analogous expressions for certain cell-cycle processes. The integral in Eq. 53 cannot be solved analytically for any but the simplest $M_{\ell ,q}$. However, the form guarantees that the dynamics of a general system can be solved using quadrature and do not require matrix-based methods.

Special cases of Eq. 53 can be solved to provide useful insights into model complexity necessary to capture the summary statistics of living cells. To attempt to describe high gene-gene correlations, we have investigated several models for synchronized transcription, and found that geometric burst size coordination is required to achieve transcript count correlations $\rho >1/2$. Furthermore, we test whether negative correlations are feasible under the assumption of synchronized bursts at multiple gene loci, and find that $\rho <0$ are impossible with geometric bursts, but can be achieved with negative binomial bursts. These results substantially constrain and inform the space of models that can recapitulate the combination of bursty dynamics (6) and high absolute gene-gene correlations (2,23) observed in living cells.

We compared the theoretical constraints with experimental data generated by FLT-seq, a recent long-read, single-cell, single-molecule sequencing method. Investigating a set of 500 genes, we found that the constraints were met for 95.3% of the intragene transcript-transcript correlations and 99.7% of the intergene transcript-transcript correlations. Nevertheless, the model was insufficient to recapitulate the precise quantitative details, suggesting that more detailed biophysical models of regulated splicing and technical noise are necessary.

The formal computational complexity of this procedure is $O\left(\mathcal{N}\text{log}\mathcal{N}\right)$ in state space size. However, this complexity ostensibly arises from the inverse Fourier transform. In the practical regime (with a state space up to approximately ${10}^3$), the scaling is sub-linear; unfortunately, full joint distributions are essentially intractable due to the “curse of dimensionality”—the space complexity of holding an array of size $\mathcal{N}$ in memory (potentially requiring petabytes of storage even for small splicing networks, as in section S4.1) for the inverse Fourier transform. Nevertheless, this method can compute marginals without having to solve the entire joint system, which would be intractable with matrix-based methods.

Curiously, this class of analytical solutions to reaction networks can be adapted to a subset of diffusion problems. General diffusion on a multidimensional lattice is not directly solvable, because it violates the assumption of acyclic graph structure. However, percolation through a DAG coupled to a source and a set of sinks can be described using the current mathematical formalism. Furthermore, such a percolation can represent the incremental movement of RNA polymerase along a DNA strand, integrating discrete copy-number statistics with submolecular details in a single analytical framework (74,75).

Finally, we briefly touch upon the class of delay chemical master equations, and survey several recent advances in the field in section S6. Due to the non-Markovian nature of delayed systems, general probabilistic solutions are rare (76) and represent an open area of study. In our discussion, we motivate delays as a limit of numerous, fast isomerization processes, and clarify the challenges inherent in applying the analysis of delay CMEs to bursty systems.

Code availability

Google Colab Python notebooks that reproduce the analyses and benchmarking are available at https://github.com/pachterlab/GP_2021_2.

Author contributions

L.P. and G.G. designed the research and wrote the article. G.G. derived and implemented the analytical solutions, validated them against simulations, and performed the sequencing data analysis.

Editor: Ramon Grima.

Supporting citations

References (77, 78, 79, 80, 81, 82, 83, 84, 85) appear in the supporting material.