ICON: Learning Regular Maps Through Inverse Consistency

Abstract

Learning maps between data samples is fundamental. Applications range from representation learning, image translation and generative modeling, to the estimation of spatial deformations. Such maps relate feature vectors, or map between feature spaces. Well-behaved maps should be regular, which can be imposed explicitly or may emanate from the data itself. We explore what induces regularity for spatial transformations, e.g., when computing image registrations. Classical optimization-based models compute maps between pairs of samples and rely on an appropriate regularizer for well-posedness. Recent deep learning approaches have attempted to avoid using such regularizers altogether by relying on the sample population instead. We explore if it is possible to obtain spatial regularity using an inverse consistency loss only and elucidate what explains map regularity in such a context. We find that deep networks combined with an inverse consistency loss and randomized off-grid interpolation yield well behaved, approximately diffeomorphic, spatial transformations. Despite the simplicity of this approach, our experiments present compelling evidence, on both synthetic and real data, that regular maps can be obtained without carefully tuned explicit regularizers, while achieving competitive registration performance.

1. Motivation

Learning maps between feature vectors or spaces is an important task. Feature vector maps are used to improve representation learning [7], or to learn correspondences in natural language processing [4]. Maps between spaces are important for generative models when using normalizing flows [24] (to map between a simple and a complex probability distribution), or to determine spatial correspondences between images, e.g., for optical flow [16] to determine motion from videos [12], depth estimation from stereo images [25], or medical image registration [39, 40].

Regular maps are typically desired; e.g., diffeomorphic maps for normalizing flows to properly map densities, or for medical image registration to map to an atlas space [20]. Estimating such maps requires an appropriate choice of transformation model. This entails picking a parameterization, which can be simple and depend on few parameters (e.g., an affine transformation), or which can have millions of parameters for 3D nonparametric approaches [14]. Regularity is achieved by 1) picking a simple transformation model with limited degrees of freedom, 2) regularization of the transformation parameters, 3) or implicitly through the data itself. Our goal is to demonstrate and understand how spatial regularity of a transformation can be achieved by encouraging inverse consistency of a map. Our motivating example is image registration/optical flow, but our results are applicable to other tasks where spatial transformations are sought.

Registration problems have traditionally been solved by numerical optimization [28] of a loss function balancing an image similarity measure and a regularizer. Here, the predominant paradigm is pair-wise image registration¹ where many maps may yield good image similarities between a transformed moving and a fixed image; the regularizer is required for well-posedness to single out the most desirable map. Many different regularizers have been proposed [14, 28, 33] and many have multiple hyperparameters, making regularizer choice and tuning difficult in practice. Deep learning approaches to image registration and optical flow have moved to learning maps from many image pairs, which raises the question if explicit spatial regularization is still required, or if it will emanate as a consequence of learning over many image pairs. For optical flow, encouraging results have been obtained without using a spatial regularizer [10, 32], though more recent work has advocated for spatial regularization to avoid “vague flow boundaries and undesired artifacts” [18, 19]. Interestingly, for medical image registration, where map regularity is often very important, almost all the existing work uses regularizers as initially proposed for pairwise image registration [36, 42, 2] with the notable exception of [3] where the deformation space is guided by an autoencoder instead.

Limited work explores if regularization for deep registration networks can be avoided entirely, or if weaker forms of regularizations might be sufficient. To help investigate this question, we work with binary shapes (where regularization is particularly important due to the aperture effect [15]) and real images. We show that regularization is necessary, but that carefully encouraging inverse consistency of a map suffices to obtain approximate diffeomorphisms. The result is a simple, yet effective, nonparametric approach to obtain well-behaved maps, which only requires limited tuning. In particular, the in practice often highly challenging process of selecting a spatial regularizer is eliminated.

Our contributions are as follows: (1) We show that approximate inverse consistency, combined with off-grid interpolation, results in approximate diffeomorphisms, when using a deep registration model trained on large datasets. Foregoing regularization is insufficient; (2) Bottleneck layers are not required and many network architectures are suitable; (3) Affine preregistration is not required; (4) We propose randomly sampled evaluations to avoid transformation flips in texture-less areas and an inverse consistency loss with beneficial boundary effects; (5) We present good results of our approach on synthetic data, MNIST, and a 3D magnetic resonance knee dataset of the Osteoarthritis Initiative (OAI).

2. Background and Analysis

Image registration is typically based on solving optimization problems of the form

$${\theta }^{*}=\underset{\theta }{\text{argmin}}{\mathcal{L}}_{\text{sim}}\left(I^A\circ {\Phi }_{\theta }^{-1},I^B\right)+\lambda {\mathcal{L}}_{\text{reg}}(\theta ),$$ (1)

where I^A and I^B are moving and fixed images, ${\mathcal{L}}_{\text{sim }}(\cdot ,\cdot )$ is the similarity measure, ${\mathcal{L}}_{\text{reg }}(\cdot )$ is a regularizer, θ are the transformation parameters, Φ_θ is the transformation map, and λ ≥ 0. We consider images as functions from ${ℝ}^N$ to $ℝ$ and maps as functions from ${ℝ}^N$ to ${ℝ}^N$. We write ∥f∥_p for the L^p norm on a scalar or vector-valued function f.

Maps, Φ_θ, can be parameterized using few parameters (e.g., affine, B-spline [14]) or nonparametrically with continuous vector fields [28]. In the nonparametric case, parameterizations are infinite-dimensional (as one deals with function spaces) and represent displacement, velocity, or momentum fields [2, 36, 42, 28]. Solutions to Eq. (1) are classically obtained via numerical optimization [28]. Recent deep registration networks are conceptually similar, but predict ${\tilde{\theta }}^{*}$, i.e., an estimate of the true minimizer θ*.

There are three interesting observations: First, for transformation models with few parameters (e.g., affine), regularization is often not used (i.e., λ = 0). Second, while deep learning (DL) models minimize losses similar to Eq. (1), the parameterization is different: it is over network weights, resulting in a predicted θ* instead of optimizing over θ directly. Third, DL models are trained over large collections of image pairs instead of a single (I^A, I^B) pair. This raises the following questions: Q1) Is explicit spatial regularization necessary, or can we avoid it for nonparametric registration models? Q2) Is using a single neural network parameterization to predict all θ* beneficial? For instance, will it result in simple solutions as witnessed for deep networks on other tasks [35] or capture meaningful deformation spaces as observed in [42]? Q3) Does a deep network parameterization itself result in regular solutions, even if only applied to a single image pair, as such effects have, e.g., been observed for structural optimization [17]?

Regularization typically encourages spatial smoothness by penalizing derivatives (or smoothing in dual space). Commonly, one uses a Sobolev norm or total variation. Ideally, one would like a regularizer adapted to deformations one expects to see (as it encodes a prior on expected deformations e.g., as in [29]). In consequence, picking and tuning a regularizer is cumbersome and often involves many hyperparameters. While avoiding explicit regularization has been explored for deep registration / optical flow networks [10, 32], there is evidence that regularization is beneficial [18].

Our key idea is to avoid complex spatial regularization and to instead obtain approximate diffeomorphisms by encouraging inverse consistent maps via regularization.

2.1. Weakly-regularized registration

Assume we eliminate regularization (λ = 0) and use the p-th power of the L^p norm of the difference between the warped image, $I^A\circ {\Phi }_{\theta }^{-1}$, and the fixed image, I^B, as similarity measure. Then, our optimization problem becomes

$${\theta }^{*}=\underset{\theta }{\text{arg}\text{min}}\int {\left(I^A\left({\Phi }_{\theta }^{-1}(x)\right)-I^B(x)\right)}^p\text{d}x,p\ge 1,$$ (2)

i.e., the image intensities of I^A should be close to the image intensities of I^B after deformation. Without regularization, we are entirely free to choose Φ_θ. Highly irregular minimizers of Eq. (2) may result as each intensity value I^A is simply matched to the closest intensity value of I^B regardless of location. For instance, for a constant I^B(x) = c and a moving image I^A(y) with a unique location y_c, where I^A(y_c) = c, the optimal map is ${\Phi }_{\theta }^{-1}(x)=y_c$, which is not invertible: only one point of I^A will be mapped to the entire domain of I^B. Clearly, more spatial regularity is desirable. Importantly, irregular deformations are common optimizers of Eq. (2).

Optimal mass transport (OMT) is widely used in machine learning and in imaging. Such models are of interest to us as they can be inverse consistent. An OMT variant of the discrete reformulation of Eq. (2) is

$${\theta }^{*}=\underset{\theta }{\text{arg}\text{min}}\text{d}x\sum _{i=1}^S{\left(I^A\left({\Phi }_{\theta }^{-1}\left(x_i\right)\right)-I^B\left(x_i\right)\right)}^p,p\ge 1$$ (3)

for p ≥ 1, where i indexes the S grid points x_i, ${\Phi }_{\theta }^{-1}\left(x_i\right)$ is restricted to map to the grid points y_i of I^A, and dx is the discrete area element. Instead of considering all possible maps, we attach a unit mass to each intensity value of I^A and I^B and ask for minimizers of Eq. (3) which transform the intensity distribution of I^A to the intensity distribution of I^B via permutations of the values only. As we only allow permutations, the optimal map will be invertible by construction. This problem is equivalent to optimal mass transport for one-dimensional empirical measures [31]. One obtains the optimal value by ordering all intensity values of $I^A\left(I_1^A\le \cdots \le I_S^A\right)$ and $I^B\left(I_1^B\le \cdots \le I_S^B\right)$. The minimum is the p-th power of the p-Wasserstein distance $(p\ge 1){\mathcal{W}}_p^p={\sum }_i{\left|I_i^A-I_i^B\right|}^p$. In consequence, minimizers for Eq. (2) are related to sorting, but do not consider spatial regularity. Note that solutions might not be unique when intensity values in I^A or I^B are repeated. Solutions via sorting were empirically explored for registration in [34] to illustrate that they, in general, do not result in spatially meaningful registrations. At this point, our idea of using inverse consistency (i.e., invertible maps) as the only regularizer appears questionable, given that OMT often provides an inverse consistent model (when a matching, i.e., a Monge solution, is optimal), while resulting in irregular maps (Fig. 2).

Figure 2:

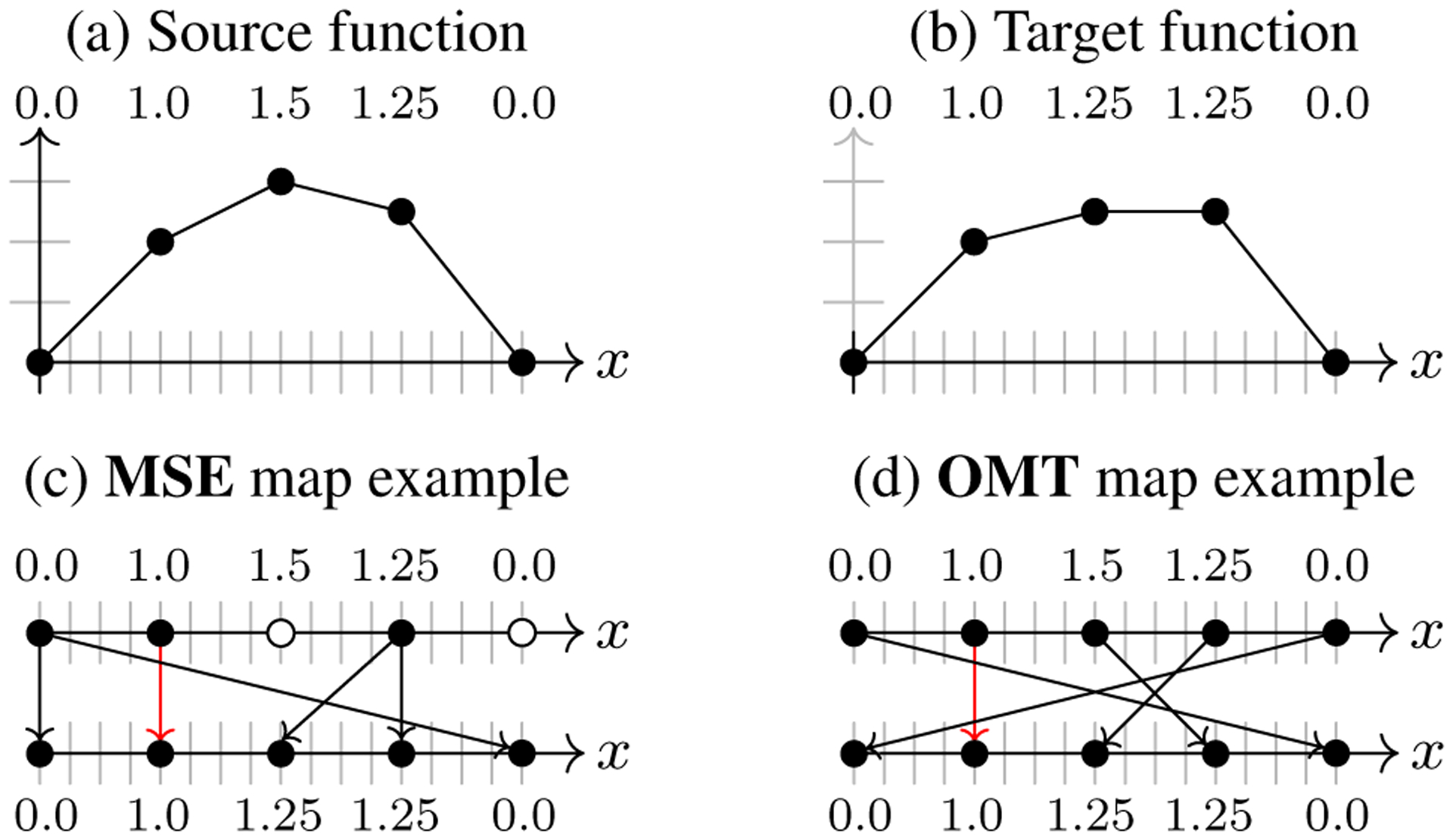
Source and target functions for a 1D registration example. Panels (c) and (d) show two possible solutions for mean square error (MSE) and OMT, respectively. In both cases, solutions may not be unique. However, for OMT, matching solutions will be one-to-one, i.e., invertible. OMT imposes a stronger constraint than MSE on the obtainable maps, but irregular maps are still permissible.

Yet, we will show that a registration network, combined with an inverse consistency loss, encourages map regularity.

2.2. Avoiding undesirable solutions

Simplicity.

The highly irregular maps in Fig. 2 occur for pair-wise image registration. Instead, we are concerned with training a network over an entire image population. Were one to find a global inverse consistent minimizer, a network would need to implicitly approximate the sorting-based OMT solution. As sorting is a continuous piece-wise linear function [5], it can, in principle, be approximated according to the universal approximation theorem [26]. However, this is a limit argument. Practical neural networks for sorting are either approximate [27, 11] or very large (e.g., O(S²) neurons for S values [6]). Note that deep networks often tend to simple solutions [35] and that we do not even want to sort all values for registration. Instead, we are interested in more local permutations, rather than the global OMT permutations, which is what we will obtain for neural network solutions with inverse consistency.

Invertibility.

Requiring map invertibility implies searching for a matching (a Monge formulation in OMT) which is an optimal permutation, but which may not be continuous². Instead, our goal is a continuous and invertible map. We therefore want to penalize deviations from

$${\Phi }_{\theta }^{AB}\circ {\Phi }_{\theta }^{BA}=\text{Id},$$ (4)

where ${\Phi }_{\theta }^{AB}$ denotes a predicted map (by a network with weights θ) to register image I^A to I^B; ${\Phi }_{\theta }^{BA}$ is the network output with reversed inputs and Id denotes the identity map.

Inverse consistency of maps has been explored to obtain symmetric maps for pair-wise registration [13, 8] and for registration networks [43, 36]. Related losses have been proposed on images (instead of maps) for registration [22, 21] and for image translation [44]. However, none of these approaches study inverse consistency for regularization. Likely, because it has so far been believed that additional spatial regularization is required for nonparametric registration.

2.3. Approximate inverse consistency

As we will show next, approximate inverse consistency by itself yields regularizing effects in the context of pairwise image registration.

Denote by ${\Phi }_{\theta }^{AB}(x)$ and ${\Phi }_{\theta }^{BA}(x)$ the output maps of a network for images (I^A, I^B) and (I^B, I^A), respectively. As inverse consistency by itself does not prevent discontinuous solutions, we propose to use approximate inverse consistency to favor C⁰ solutions. We add two vector-valued independent spatial white noises n₁(x), $n_2(x)\in {ℝ}^N$ (x ∈ [0, 1]^N with N=2 or N=3 the image dim.) of variance 1 for each space location and dimension to the two output maps and define

$${\Phi }_{\theta \epsilon }^{AB}(x)={\Phi }_{\theta }^{AB}(x)+\epsilon n_1\left({\Phi }_{\theta }^{AB}(x)\right),$$

$${\Phi }_{\theta \epsilon }^{BA}(x)={\Phi }_{\theta }^{BA}(x)+\epsilon n_2\left({\Phi }_{\theta }^{BA}(x)\right),$$

with ε > 0. We then consider the loss $\mathcal{L}=\lambda {\mathcal{L}}_{\text{inv}}+{\mathcal{L}}_{\text{sim}}$, with inverse consistency component $\left({\mathcal{L}}_{\text{inv }}\right)$

$${\mathcal{L}}_{\text{inv}}={\Vert {\Phi }_{\theta \epsilon }^{AB}\circ {\Phi }_{\theta \epsilon }^{BA}-\text{Id}\Vert }_2^2+{\Vert {\Phi }_{\theta \epsilon }^{BA}\circ {\Phi }_{\theta \epsilon }^{AB}-\text{Id}\Vert }_2^2$$ (5)

and similarity component $\left({\mathcal{L}}_{\text{sim}}\right)$

$${\mathcal{L}}_{\text{sim}}={\Vert I^A\circ {\Phi }_{\theta }^{AB}-I^B\Vert }_2^2+{\Vert I^B\circ {\Phi }_{\theta }^{BA}-I^A\Vert }_2^2.$$ (6)

Importantly, note that there are multiple maps that can lead to the same $I^A\circ {\Phi }_{\theta }^{AB}$ and $I^B\circ {\Phi }_{\theta }^{BA}$. Therefore, among all these maps, minimizing the loss $\mathcal{L}$ drives the maps towards those that minimize the two terms in Eq. (5).

Assumption. Both terms in Eq. (5) can be driven to a small value (of the order of the noise), by minimization.

We first Taylor-expand one of the two terms in Eq. (5) (the other follows similarly), yielding

$${\Vert {\Phi }_{\theta \epsilon }^{AB}\circ {\Phi }_{\theta \epsilon }^{BA}-\text{Id}\Vert }_2^2\approx {\Vert {\Phi }_{\theta }^{AB}\circ {\Phi }_{\theta }^{BA}+\epsilon n_1\left({\Phi }_{\theta }^{AB}\circ {\Phi }_{\theta }^{BA}\right)+{\text{dΦ}}_{\theta \epsilon }^{AB}\left(\epsilon n_2\left({\Phi }_{\theta }^{BA}\right)\right)-\text{Id}\Vert }_2^2.$$

Defining the right-hand side as A, developing the squares and taking expectation, we obtain

$$\begin{gathered} \mathbb{E}[A]={\Vert {\Phi }_{\theta }^{AB}\circ {\Phi }_{\theta }^{BA}-\text{Id}\Vert }_2^2 \\ +{\epsilon }^2\mathbb{E}\left[{\Vert n_1\circ \left({\Phi }_{\theta \epsilon }^{AB}\circ {\Phi }_{\theta \epsilon }^{BA}\right)\Vert }_2^2\right] \\ +{\epsilon }^2\mathbb{E}\left[{\Vert {\text{dΦ}}_{\theta \epsilon }^{AB}\left(n_2\right)\circ {\Phi }_{\theta }^{BA}\Vert }_2^2\right], \end{gathered}$$ (7)

since, by independence, all the cross-terms vanish (the noise terms have 0 mean value). The second term is constant, i.e.,

$$\begin{gathered} \mathbb{E}\left[{\Vert n_1\circ \left({\Phi }_{\theta \epsilon }^{AB}\circ {\Phi }_{\theta \epsilon }^{BA}\right)\Vert }_2^2\right]= \\ \int \mathbb{E}\left[{\Vert n_1\Vert }_2^2(y)\right]\text{Jac}\left({\left({\Phi }_{\theta \epsilon }^{BA}\right)}^{-1}\circ {\left({\Phi }_{\theta \epsilon }^{AB}\right)}^{-1}\right)\text{d}y=\text{ const}., \end{gathered}$$ (8)

where we performed a change of variables and denoted the determinant of the Jacobian matrix as Jac. The last equality follows from the fact that the variance of the noise term is spatially constant and equal to 1. By similar arguments, the last expectation term in Eq. (7) can be rewritten as

$$\begin{gathered} \mathbb{E}\left[{\Vert {\text{dΦ}}_{\theta \epsilon }^{AB}\left(n_2\right)\circ {\Phi }_{\theta }^{BA}\Vert }_2^2\right]= \\ \int \text{Tr}\left(\text{d}{\left({\Phi }_{\theta \epsilon }^{AB}\right)}^{\top }{\text{dΦ}}_{\theta \epsilon }^{AB}\right)\text{Jac}\left({\left({\Phi }_{\theta }^{BA}\right)}^{-1}\right)\text{d}y, \end{gathered}$$ (9)

where Tr denotes the trace operator. As detailed in the suppl. material, the identity of Eq. (9) relies on a change of variable and on the property of the white noise, n₂, which satisfies null correlation in space and dimension $\mathbb{E}\left[n_2(x)n_2{\left(x^{\prime }\right)}^{\top }\right]={\text{Id}}_{{ℝ}^N}$ if x = x′ and 0 otherwise.

Approximation & H¹ regularization.

We now want to connect the approximate inverse consistency loss of Eq. (5) with H¹ norm type regularization. Our assumption implies that ${\Phi }_{\theta }^{AB}\circ {\Phi }_{\theta }^{BA}$, ${\Phi }_{\theta }^{BA}\circ {\Phi }_{\theta }^{AB}$ are close to identity, therefore one has $\text{Jac}\left({\left({\Phi }_{\theta }^{BA}\right)}^{-1}\right)\approx \text{Jac}\left({\Phi }_{\theta }^{AB}\right)$. Assuming this approximation holds, we use it in Eq. (9), together with the fact that, ${\Phi }_{\theta \epsilon }^{AB}\approx {\Phi }_{\theta }^{AB}+O(\epsilon )$ to get at order ε² (see suppl. material for details) to approximate ${\mathcal{L}}_{\text{inv }}$, i.e.,

$$\begin{gathered} {\mathcal{L}}_{\text{inv}}\approx {\Vert {\Phi }_{\theta }^{AB}\circ {\Phi }_{\theta }^{BA}-\text{Id}\Vert }_2^2+{\Vert {\Phi }_{\theta }^{BA}\circ {\Phi }_{\theta }^{AB}-\text{Id}\Vert }_2^2 \\ +{\epsilon }^2{\Vert d{\Phi }_{\theta }^{AB}\sqrt{\text{Jac}\left({\Phi }_{\theta }^{AB}\right)}\Vert }_2^2+{\epsilon }^2{\Vert d{\Phi }_{\theta }^{BA}\sqrt{\text{Jac}\left({\Phi }_{\theta }^{BA}\right)}\Vert }_2^2 \end{gathered}$$ (10)

We see that approximate inverse consistency leads to an L² penalty of the gradient, weighted by the Jacobian of the map. This is a type of Sobolev (H¹ more precisely) regularization sometimes used in image registration. In particular, the H¹ term is likely to control the compression and expansion magnitude of the maps, at least on average, on the domain. Hence, approximate inverse consistency leads to an implicit H¹ regularization, formulated directly on the map.

Inverse consistency with no noise and the implicit regularization of inverse consistency.

Turning the noise level to zero also leads to regular displacement fields in our experiments when predicting maps with a neural network. In this case, we observe that inverse consistency is only approximately achieved. Therefore, one can postulate that the error made in computing the inverse entails the H¹ regularization as previously shown. The possible caveat of this hypothesis is that the inverse consistency error might not be independent of the displacement fields, which was assumed in proving the emerging H¹ regularization. Last, even when the network should have the capacity to exactly satisfy inverse consistency for all data, we conjecture that the implicit bias due to the optimization will favor more regular outputs.

A fully rigorous theoretical understanding of the regularization effect due to the data population and its link with inverse consistency is important, but beyond our scope here.

3. Approximately diffeomorphic registration

We base our registration approach on training a neural network $F_{\theta }^{AB}$ which, given input images I^A and I^B, outputs a grid of displacement vectors, $D_{\theta }^{AB}$, in the space of image I^B, assuming normalized image coordinates covering [0, 1]^N. We obtain continuous maps by interpolation, i.e.,

$${\Phi }_{\theta }^{AB}=D_{\theta }^{AB}+\text{Id},\hspace{1em}{D}_{\theta }^{AB}=\text{interp}\left(F_{\theta }^{AB}\right)$$ (11)

where $I^A\circ {\Phi }_{\theta }^{AB}\approx I^B$. Under the assumption of linear interpolation (bilinear in 2D and trilinear in 3D), ${\Phi }_{\theta }^{AB}$ is continuous and differentiable except on a measure zero set. Building on the considerations of Sec. 2 we seek to minimize

$$\mathcal{L}(\theta )={\mathbb{E}}_{p\left(I^A,I^B\right)}\left[{\mathcal{L}}_{\text{sim }}^{AB}+\lambda {\mathcal{L}}_{\text{inv }}^{AB}\right],$$ (12)

where λ ≥ 0 and p(I^A, I^B) denotes the distribution over all possible image pairs. The similarity and invertibility losses depend on the neural network parameters, θ, and are

$$\begin{gathered} {\mathcal{L}}_{\text{sim}}^{AB}={\mathcal{L}}_{\text{sim}}\left(I^A\circ {\Phi }_{\theta }^{AB},I^B\right)+{\mathcal{L}}_{\text{sim}}\left(I^B\circ {\Phi }_{\theta }^{BA},I^A\right) \\ {\mathcal{L}}_{\text{inv }}^{AB}={\mathcal{L}}_{\text{inv }}\left({\Phi }_{\theta }^{AB},{\Phi }_{\theta }^{BA}\right)+{\mathcal{L}}_{\text{inv }}\left({\Phi }_{\theta }^{BA},{\Phi }_{\theta }^{AB}\right) \end{gathered}$$ (13)

with

$${\mathcal{L}}_{\text{sim}}(I,J)={\Vert I-J\Vert }_2^2,{\mathcal{L}}_{\text{inv}}(\varphi ,\psi )={\Vert \varphi \circ \psi -\text{Id}\Vert }_2^2.$$ (14)

For simplicity, we use the squared L² norm as similarity measure. Other measures, e.g., normalized cross correlation (NCC) or mutual information (MI), can also be used. When ${\mathcal{L}}_{\text{inv }}^{AB}$ goes to zero, ${\Phi }_{\theta }^{AB}$ will be approx. invertible and continuous due to Eq. (11). Hence, we obtain approximate C⁰ diffeomorphisms without differential equation integration, hyperparameter tuning, or transform restrictions. Our loss in Eq. (12) is symmetric in the image pairs due to the symmetric similarity and invertibility losses in Eq. (13).

Displacement-based inverse consistency loss.

A general map ${\Phi }_{\theta }^{AB}$ may map points in [0, 1]^N to points outside [0, 1]^N. Extrapolating maps across the boundary is cumbersome. Hence, we only interpolate displacement fields as in Eq. (11). We rewrite the inverse consistency loss as

$$\begin{gathered} {\mathcal{L}}_{\text{inv}}\left({\Phi }_{\theta }^{AB},{\Phi }_{\theta }^{BA}\right)={\Vert \left(D_{\theta }^{AB}+\text{Id}\right)\circ \left(D_{\theta }^{BA}+\text{Id}\right)-\text{Id}\Vert }_2^2 \\ ={\Vert \left(D_{\theta }^{AB}\right)\circ {\Phi }_{\theta }^{BA}+D_{\theta }^{BA}\Vert }_2^2 \end{gathered}$$ (15)

and use it for implementation, as it is easier to evaluate.

Random evaluation of inverse consistency loss.

${\mathcal{L}}_{\text{inv }}^{AB}$ can be evaluated by approximating the L² norm, assuming constant values over the grid cells. In many cases, this is sufficient. However, as Fig. 3 illustrates, swapped locations may occur in uniform regions where a registration network only sees uniform background. This swap, composed with itself, is the identity as long as it is only evaluated at the center of pixels/voxels. Hence, the map appears invertible to the loss. However, outside the centers of pixels/voxels, the map is not inverse consistent when combined with linear interpolation. To avoid such pathological cases, we approximate the L² norm by random sampling. This forces interpolation and therefore results in non-zero loss values for swaps. Fig. 4 shows why off-grid sampling combined with inverse consistency is a stronger condition than only considering deformations at grid points. In practice, we evaluate the loss

$$\begin{gathered} {\mathcal{L}}_{\text{inv }}\left({\Phi }_{\theta }^{AB},{\Phi }_{\theta }^{BA}\right) \\ ={\Vert \left(D_{\theta }^{AB}\right)\circ {\Phi }_{\theta }^{BA}+D_{\theta }^{BA}\Vert }_2^2 \\ ={\mathbb{E}}_{x~\mathcal{U}{(0,1)}^N}{\left[\left(D_{\theta }^{AB}\right)\circ {\Phi }_{\theta }^{BA}+D_{\theta }^{BA}\right]}^2(x) \\ \approx 1/N_p{\sum }_i{\left(\left[\left(D_{\theta }^{AB}\right)\circ \left(D_{\theta }^{BA}+\text{Id}\right)+D_{\theta }^{BA}\right]\left(x_i+{ϵ}_i\right)\right)}^2 \\ =1/N_p{\sum }_i([D_{\theta }^{AB}\circ \left(D_{\theta }^{BA}\circ \left(x_i+{ϵ}_i\right)+x_i+{ϵ}_i\right) \\ {+D_{\theta }^{BA}\circ \left(x_i+{ϵ}_i\right)])}^2 \end{gathered}$$ (16)

where N_p is the number of pixels/voxels, $\mathcal{U}{(0,1)}^N$ denotes the uniform distribution over [0, 1]^N, x_i denotes the grid center coordinates and ϵ_i is a random sample drawn from a multivariate Gaussian with standard deviation set to the size of a pixel/voxel in the respective spatial directions.

Figure 3:

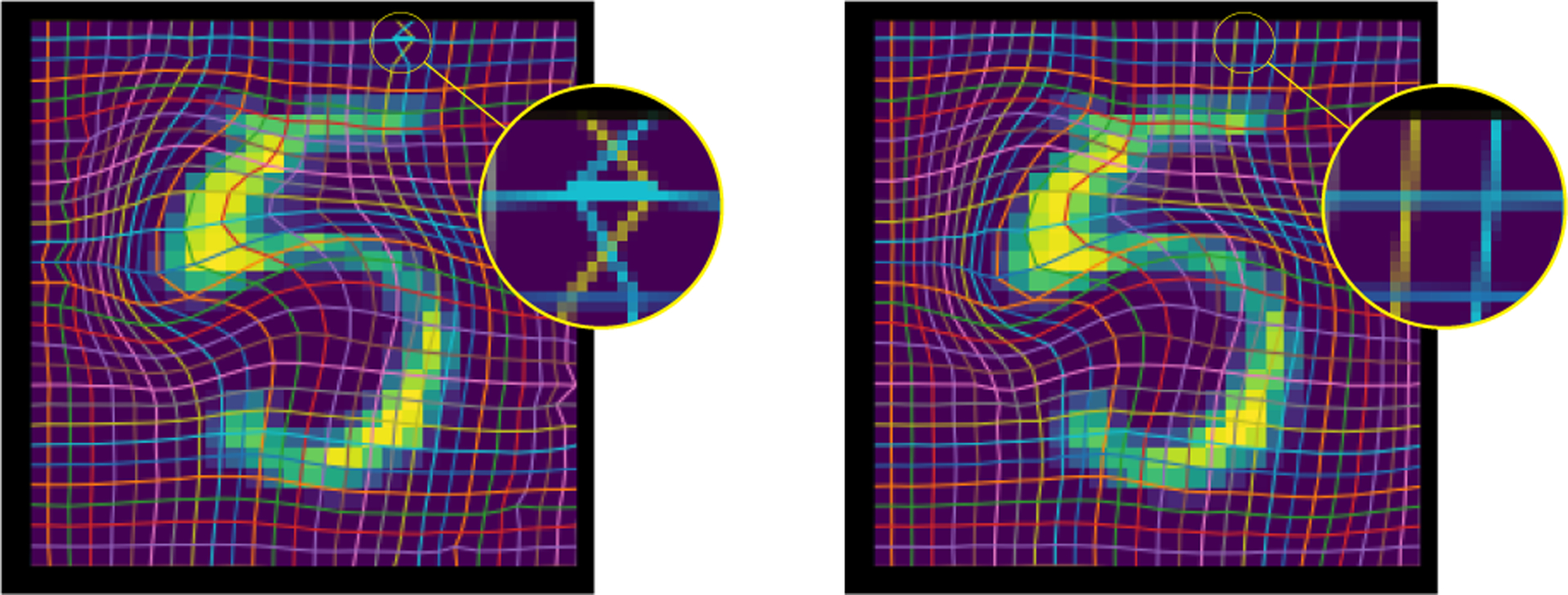
The left output is generated by a network trained with inverse consistency, evaluated on a grid instead of randomly. As a result, the loss cannot detect that maps generated by this network flip the pair of pixels in the upper right corner, as that error is not represented in the composed map. The right output is obtained from a network trained with random evaluation off of lattice points.

Figure 4:

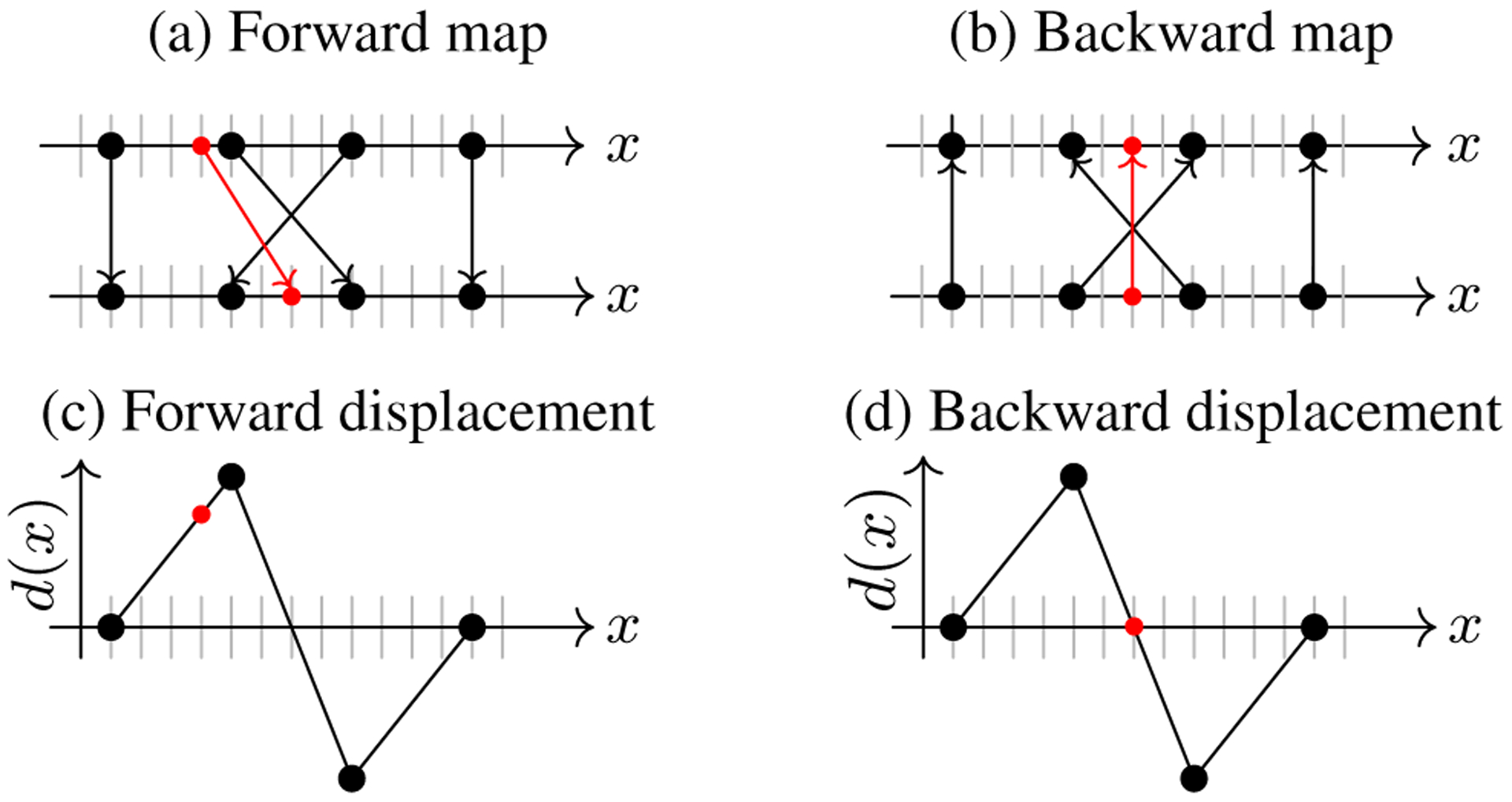
In this example, grid points (solid black discs) map to each other inverse consistently. The forward map (a) is inverted by the backward map (b). However, folding of the space occurs as the middle two points swap positions. Off-grid points map under linear interpolation according to (c/d). We see that the interpolated displacements for the small solid red disc () do not result in an invertible map. Hence, this mismatch would be penalized by the inverse consistency loss, but only when evaluated off-grid.

4. Experiments

Our experiments address several aspects: First, we compare our approach to directly optimizing the maps Φ^AB and Φ^BA on a 2D toy dataset of 128 × 128 images. Second, on a 2D toy dataset of 28 × 28 images, we assess the impact of architectural and hyperparameter choices. Finally, we assess registration performance on real 3D magnetic resonance images (MRI) of the knee.

4.1. Datasets

MNIST.

We use the standard MNIST dataset with images of size 28 × 28, restricted to the number “5” to make sure we have semantically matching images. For training/testing, we rely on the standard partitioning of the dataset.

Triangles & Circles.

We created 2D triangles and circles (128 × 128) with radii and centers varying uniformly in [.2, .4] and [.4, .7], respectively. Pixels are set to 1 inside a shape and smoothly decay to −1 on the outside. We train using 6,000 images and test on 6,000 separate images³.

OAI knee dataset.

These are 3D MR images from the Osteoarthritis Initiative (OAI). Images are downsampled to size 192 × 192 × 80, normalized such that the 1th percentile is set to 0, the 99th percentile is to 1, and all values are clamped to be in [0, 1]. As a preprocessing step, images of left knees are mirrored along the left-right axis. The dataset contains 2,532 training images and 301 test pairs.

4.2. Architectures

We experiment with four neural network architectures. All networks output displacement fields, $D_{\theta }^{AB}$. We briefly outline the differences below, but refer to the suppl. material for details. The first network is an MLP with 2 hidden layers and ReLU activations. The output layer is reshaped into size 2 × W × H. Second, we use a convolutional encoderdecoder network (Enc-Dec) with 5 layers each, reminiscent of a U-Net without skip connections. Our third network uses 6 convolutional layers without up- or down-sampling. The input to each layer is the concatenation of the outputs of all previous layers (ConvOnly). Finally, we use a U-Net with skip and residual connections. The latter is similar to Enc-Dec, but uses LeakyReLU activations and batch normalization. In all architectures, the final layer weights are initialized to 0, so that optimization starts at a network outputting a zero displacement field.

4.3. Regularization by approx. inverse consistency

Sec. 2.3 formalized that approximate inverse consistency results in regularizing effects. Specifically, when ${\Phi }_{\theta }^{AB}$ is approximately the inverse of ${\Phi }_{\theta }^{BA}$, the inverse consistency loss ${\mathcal{L}}_{\text{inv }}^{AB}$ can be approximated based on Eq. (10), highlighting its implicit H¹ regularization. We investigate this behavior by three experiments: Pair-wise image registration (1) with artificially added noise (noise) and (2) without (no noise) artificially added noise, and (3) population-based registration via a U-Net. Fig. 5 shows some sample results, supporting our theoretical exposition of Sec. 2.3: Pair-wise image registration without noise results in highly irregular transformations even though the inverse consistency loss is used. Adding a small amount of Gaussian noise with standard deviation of 1/8th of a pixel (similar to the inverse consistency loss magnitudes we observe for a deep network) to the displacement fields before computing the inverse consistency loss, results in significantly more regular maps. Lastly, using a U-Net yields highly regular maps. Notably, all three approaches result in approximately inverse consistent maps. The behavior for pair-wise image registration elucidates why inverse consistency has not appeared in the classical (pair-wise) registration literature as a replacement for more complex spatial regularization. The proposed technique only results in regularity when inverse consistency errors are present.

Figure 5:

Comparison between U-Net results and direct optimization (no neural network; over ${\Phi }_{\theta }^{AB}$ and ${\Phi }_{\theta }^{BA}$) w/ and w/o added noise, using the inverse consistency loss with λ = 2,048. Direct optimization w/o noise leads to irregular maps, while adding noise or using the U-Net improves map regularity (best viewed zoomed).

In summary, our theory is supported by our experimental results: approximate inverse consistency regularizes maps.

4.4. Regularization for different networks

Sec. 4.3 illustrated that approximate inverse consistency yields regularization effects which translate to regularity for network predictions, as networks will, in general, not achieve perfect inverse consistency. A natural next question to ask is “how much the results depend on a particular architecture”? To this end, we assess four different network types, focusing on MNIST and the triangles & circles data. We report two measures on held-out images: the Dice score of pixels with intensity greater than 0.5, and the mean number of folds, i.e., pixels where the volume form dV of Φ is negative.

One hypothesis as to how network design could drive smoothness would be that smoothness is induced by convolutional layers (which can implement a smoothing kernel). If this were the case, we would expect the MLP to produce irregular maps with a high number of folds. Vice versa, since the MLP has no spatial prior, obtaining smooth transforms would indicate that smoothness is promoted by the loss itself. The latter is supported by Fig. 6, showing regular maps even for the MLP when λ is sufficiently large. Note that λ = 0 in Fig. 6 corresponds to an unregularized MSE solution, as discussed in Sec. 2.1; maps are, as expected, highly irregular and regularization via inverse consistency is clearly needed.

Figure 6:

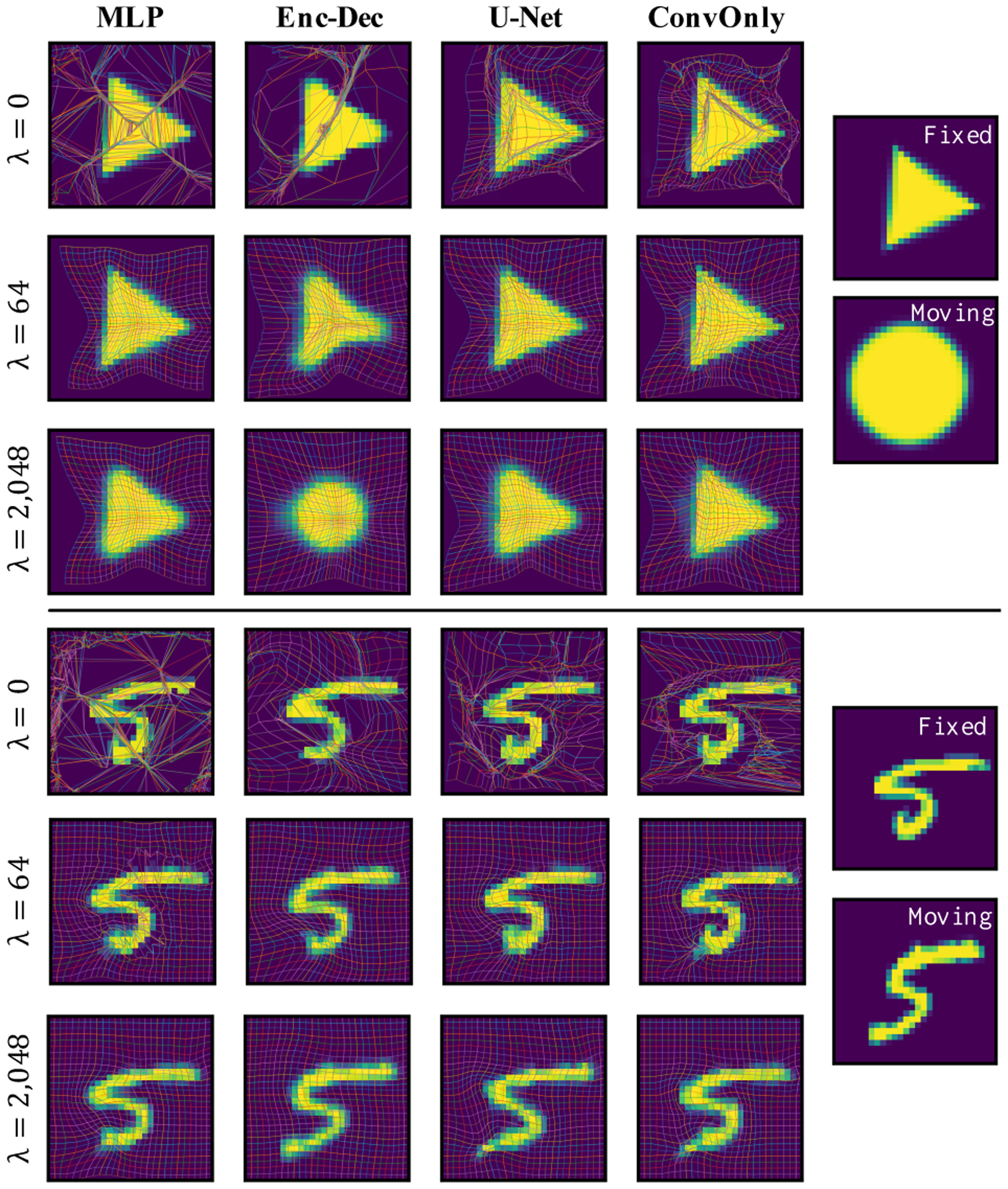
Comparison of networks as a function of λ. U-Net and MLP show the best performance due to their ability to capture long and short range dependencies. Enc-Dec and ConvOnly, which capture only long range and only short range dependencies, resp., also learn regular maps, but for a narrower range of λ. In all cases, maps become smooth for sufficiently large λ. Best viewed zoomed.

A second hypothesis is that regularity results from a bottleneck structure within a network, e.g., a U-Net. In fact, Bhalodia et al. [3] show that autoencoders tend to yield smooth maps. To assess this hypothesis, we focus on the Enc-Dec and ConvOnly type networks; the former has a bottleneck structure, while the latter does not. Fig. 6 shows some support for the hypothesis that a bottleneck promotes smooth maps: for a specific λ, Enc-Dec appears to have more strongly regularized outputs compared to U-Net, with ConvOnly being the most irregular. Yet, higher values of λ (e.g., 1,024 or 2,048) for ConvOnly yield equally smooth maps. Overall, a bottleneck structure does have a regularizing effect, but regularity can also be achieved by appropriately weighing the inverse consistency loss (see Tab. 1).

Table 1:

Network performance across architectures and regularization strength λ. MLP / U-Net perform best. All methods work.

MNIST
Network →	MLP		Enc-Dec		U-Net		ConvOnly
λ ↓	Dice	Folds	Dice	Folds	Dice	Folds	Dice	Folds
64	0.92	26.61	0.80	0.15	0.93	3.87	0.93	30.20
128	0.92	9.95	0.77	0.08	0.92	1.45	0.90	16.27
256	0.91	2.48	0.72	0.01	0.90	0.41	0.88	7.17
512	0.90	0.72	0.66	0.03	0.89	0.09	0.85	3.12
1,024	0.88	0.34	0.62	0.06	0.86	0.02	0.81	0.54
2,048	0.87	0.16	0.63	0.00	0.73	0.09	0.76	0.07
Triangles & Circles
Network →	MLP		Enc-Dec		U-Net		ConvOnly
λ ↓	Dice	Folds	Dice	Folds	Dice	Folds	Dice	Folds
64	0.98	1.24	0.94	3.50	0.98	2.74	0.97	12.57
128	0.98	0.73	0.90	2.71	0.98	1.59	0.96	10.15
256	0.98	0.27	0.88	1.11	0.97	1.14	0.96	8.49
512	0.97	0.10	0.87	0.65	0.96	0.70	0.94	6.61
1,024	0.96	0.03	0.86	0.22	0.95	0.25	0.92	3.91
2,048	0.95	0.03	0.85	0.15	0.94	0.09	0.89	2.18

In summary, our experiments indicate that the regularizing effect of inverse consistency is a robust property of the loss, and should generalize well across architectures.

4.5. Performance for 3D image registration

For experiments on real data, we focus on the 3D OAI dataset. To demonstrate the versatility of the advocated inverse consistency loss in promoting map regularity, we refrain from affine pre-registration (as typically done in earlier works) and simply compose the maps of multiple U-Nets instead. In particular, we compose up to four U-Nets as follows: A composition of two U-Nets is initially trained on low-resolution image pairs. Weights are then frozen and this network is composed with a third U-Net, trained on high-resolution image pairs. This network is then optionally frozen and composed with a fourth U-Net, again trained on high-resolution image pairs. During the training of this multi-step approach, the weighting of the inverse consistency loss is gradually increased. We train using ADAM [23] with a batch size of 128 in the low-res. stage, and a batch size of 16 in the high-res. stage. MSE is used as image similarity measure.

We compare our approach, InverseConsistentNet (ICON), against the methods of [36], in terms of (1) cartilage Dice scores between registered image pairs [1] (based on manual segmentations) and (2) the number of folds. The segmentations are not used during training and allow quantifying if the network yields semantically meaningful registrations. Tab. 2 lists the corresponding results, Fig. 1 shows several example registrations. Unlike the other methods in Tab. 2, except where explicitly noted, ICON does not require affine pre-registration. Since affine maps are inverse consistent, they are not penalized by our method. Notably, despite its simplicity, ICON yields performance (in terms of Dice score & folds) comparable to more complex, explicitly regularized methods. We emphasize that our objective is not to outperform existing techniques, but to present evidence that regular maps can be learned without carefully tuned regularizers.

Table 2:

Comparison of ICON against the methods in [36], on cross-subject registration for OAI knee images.

Method	${\mathcal{L}}_{sim}$	Dice	Folds	Time [s]
Demons	MSE	63.47	19.0	114
SyN	CC	65.71	0	1330
NiftyReg	NMI	59.65	0	143
NiftyReg	LNCC	67.92	203	270
vSVF-opt	LNCC	67.35	0	79
Voxelmorph (w/o affine)	MSE	46.06	83	0.12
Voxelmorph	MSE	66.08	39.0	0.31
AVSM (7-Step Affine, 3-Step Deformable)	LNCC	68.40	14.3	0.83
ICON (2 step ½ res., 2 step full res., w/o affine)	MSE	68.29	118.4	1.06
ICON (2 step ½ res., 1 step full res., w/o affine)	MSE	66.16	169.4	0.57
ICON (2 step ½ res., w/o affine)	MSE	59.36	49.35	0.09

Figure 1:

Example inverse consistent network (ICON) registration results for OAI knee images (see §4), obtained from a U-Net trained for inverse consistency (without any explicit loss to promote map regularity). All four panels show (left to right) the (1) moving image, (2) fixed image, (3) warped moving image and the (4) corresponding transformation grid (colored). Transformations are, as desired, smooth.

In summary, using the proposed inverse consistency loss yields (1) competitive Dice scores, (2) acceptable folds, and (3) fast performance.

5. Limitations, future work, & open questions

Several questions remain and there is no shortage of theoretical/practical directions, some of which are listed next.

Network architecture & optimization.

Instead of specifying a spatial regularizer, we now specify a network architecture. While our results suggest regularizing effects for a variety of architectures, we are still lacking a clear understanding of how network architecture and numerical optimization influence solution regularity.

Diffemorphisms at test time.

We simply encourage inverse consistency via a quadratic penalty. Advanced numerical approaches (e.g., augmented Lagrangian methods [30]) could more strictly enforce inverse consistency during training. Our current approach is only approximately diffeomorphic at test time. To guarantee diffeomorphisms, one could explore combining inverse consistency with fluid deformation models [14]. These have been used for deep registration networks [42, 41, 36, 37, 9] combined with explicit spatial regularization. We would simply predict a velocity field and obtain the map via integration. By using our loss, sufficiently smooth velocity fields would likely emerge. Alternatively, one could use diffeomorphic transformation parameterizations by enforcing positive Jacobian determinants [38].

Multi-step.

Our results show that using a multi-step estimation approach is beneficial; successive networks can refine deformation estimates and thereby improve registration performance. What the limits of such a multi-step approach are (i.e., when performance starts to saturate) and how it interacts with deformation estimates at different resolution levels would be interesting to explore further.

Similarity measures.

For simplicity, we only explored MSE. NCC, local NCC, and mutual information would be natural choices for multi-modal registration. In fact, there are many opportunities to improve registrations e.g. using more discriminative similarity measures based on network-based features, multi-scale information, or side-information during training, e.g., segmentations or point correspondences.

Theoretical investigations.

It would be interesting to establish how regularization by inverse consistency relates to network capacity, expressiveness, and generalization. Further, establishing a rigorous theoretical understanding of the regularization effect due to the data population and its link with inverse consistency would be important.

General inverse consistency.

Our work focused on spatial correspondences for registration, but the benefits of inverse consistency regularization are likely much broader. For instance, its applicability to general mapping problems (e.g., between feature vectors) should be explored.

6. Conclusion

We presented a deliberately simple deep registration model which generates approximately diffeomorphic maps by regularizing via an inverse consistency loss. We theoretically analyzed why inverse consistency leads to spatial smoothness and empirically showed the effectiveness of our approach, yielding competitive 3D registration performance.

Our results suggest that simple deep registration networks might be as effective as more complex approaches which require substantial hyperparameter tuning and involve choosing complex transformation models. As a wide range of inverse consistency loss penalties lead to good results, only the desired similarity measure needs to be chosen and extensive hyperparameter tuning can be avoided. This opens up the possibility to easily train extremely fast custom registration networks on given data. Due to its simplicity, ease of use, and computational speed, we expect our approach to have significant practical impact. We also expect that inverse consistency regularization will be useful for other tasks, which should be explored in future work.