Two-step hypothesis testing to detect gene-environment interactions in a genome-wide scan with a survival endpoint

Abstract

Defined by their genetic profile, individuals may exhibit differential clinical outcomes due to an environmental exposure. Identifying subgroups based on specific exposure-modifying genes can lead to targeted interventions and focused studies. Genome-wide interaction scans (GWIS) can be performed to identify such genes, but these scans typically suffer from low power due to the large multiple testing burden. We provide a novel framework for powerful two-step hypothesis tests for GWIS with a time-to-event endpoint under the Cox proportional hazards model. In the Cox regression setting, we develop an approach that prioritizes genes for Step-2 G × E testing based on a carefully constructed Step-1 screening procedure. Simulation results demonstrate this two-step approach can lead to substantially higher power for identifying gene-environment ( G × E ) interactions compared to the standard GWIS while preserving the family-wise error rate over a range of scenarios. In a taxane-anthracycline chemotherapy study for breast cancer patients, the two-step approach identifies several gene expression by treatment interactions that would not be detected using the standard GWIS.

1 |. INTRODUCTION

The study of gene-environment (G × E) interactions is critical for understanding how individuals with diverse genetic backgrounds (G) can be differentially affected by exposure to an environmental factor (E). In an epidemiological study, interest may lie in studying how genetic susceptibility might predispose subgroups of the population to enhanced effects of an environmental exposure. Alternatively, one may be interested in studying how exposure to an environmental factor may regulate the expression of a gene which will, in turn, lead to disease. Randomized trials with large-scale omic- biomarkers can be also thought of as gene-environment studies where the treatment is considered an environmental exposure. Identifying such interactions can lead to more focused studies with the goal of improving targeted therapeutics and personalized medicine. For example, Fu et al. (2017)¹ demonstrated an antagonistic effect between chemotherapy and erlotinib and Epidermal Growth Factor Receptor (EGFR) mutation on overall survival. Recently, a comprehensive study by Nguyen et al. (2019)² found that human genetic associations of potential drug target proteins can both predict the therapeutic efficacy of a drug and the likelihood of side effects.

In general, possible exposures of interest in a gene-environment study include exogenous environmental factors (e.g., air pollution), personal exposures (e.g., smoking, drinking, treatment), or personal characteristics (e.g., sex, age, race). In this paper, we use the term “gene” to broadly encapsulate any of a variety of genomic measurements (e.g., SNPs, gene expression levels, methylation levels). While G × E studies concerning a disease (e.g., cancer, cancer-free mortality, etc.) often treat the endpoint as binary, investigators are becoming increasingly interested in studying the length of time it takes to observe a disease (e.g., age at onset, progression-free survival). In doing so, a binary phenotype can be reformulated to a time-to-event outcome and can increase power.³

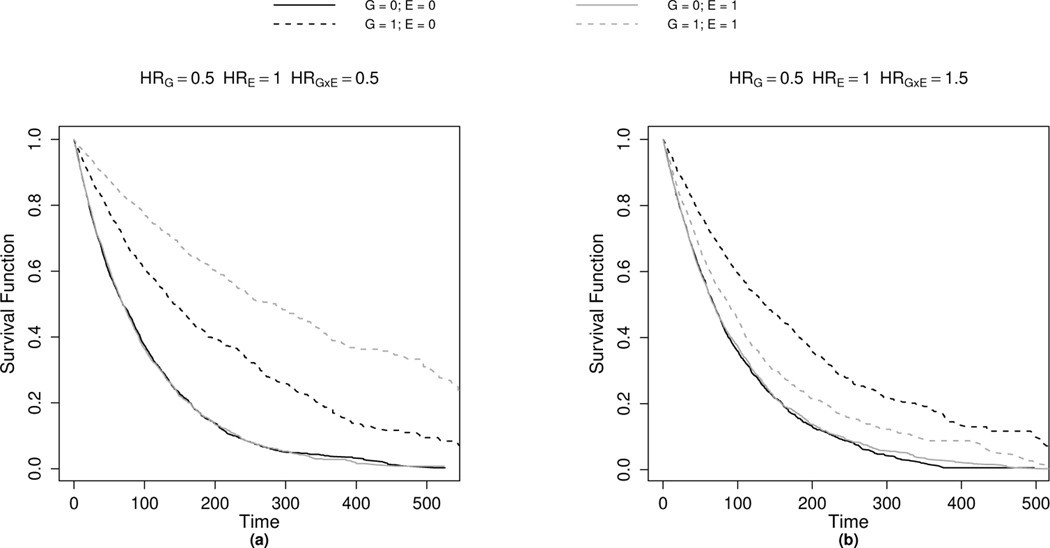
As an example, Figure 1 provides Kaplan-Meier⁴ curves for a simulated right-censored data set of 10,000 individuals to demonstrate hypothetical subgroup (exposure)-specific effects on survival. For simplicity and visualization purposes, we assume that G is binary (e.g., carrier vs. non-carrier of a variant allele or high vs. low for gene expression level) in this example; although G can, in general, also be categorical or continuously measured. In both panels (1(a) and 1(b)), we simulate the data so that no main exposure effect E is present (hazard ratio (HR_E) = 1) and that survival is only influenced through both the genetic component (G) and its interaction with the exposure (G × E). The exposure has no effect on survival for individuals where G = 0 (overlapping solid line curves). However, we see that individuals with G = 1 levels (dotted lines) experience a survival benefit when compared to individuals where G = 0. We also observe differences in survival within the subgroup of individuals with G = 1. More specifically, in Figure 1a, individuals that are exposed (E = 1) have a better prognosis than those who are unexposed (E = 0). The converse is true in Figure 1b where exposed individuals have an elevated risk of death compared those who are unexposed.

FIGURE 1.

Kaplan-Meier curves for G × E combinations on a simulated data set of N = 10,000. Data were generated using an exponential model with binary G and E values under the model: $h(t\mid G,E)=0.01\ast \exp ({\gamma }_{G}G+{\gamma }_{E}E+{\gamma }_{G\times E}(G\times E)$. Independent censoring times were generated using an exponential model with rate 0.005. The exposure (E) is assumed to have a null main effect (HR_E = 1) but affects survival through its interaction (G×E) with G. Panel 1a: Synergistic interaction effect (HR_G×E = 0.5). Panel 1b: Antagonistic interaction effect (HR_G×E = 1.5).

For the purpose of identifying G × E interactions, a computationally appealing approach is a genome-wide interaction scan (GWIS) which estimates G × E interactions one-at-a-time by modeling the individual gene, environmental exposure, and the corresponding interaction term. The G × E association can be based on testing the significance of the interaction term based on, for example, the Wald statistic. To control the family-wise error rate (FWER) at a significance level α, a standard GWIS will typically test each G × E interaction to an adjusted significance level α*. The basic standard for genome-wide association studies (GWAS) or GWIS studies is to set α* = 5 × 10⁻⁸. Alternatively, one can adopt the standard Bonferroni correction⁵ of α* = α∕M, where M is the number of genes to be tested. Either approach will most likely be underpowered in detecting significant interactions.

A variety of statistical methods have been developed that aim to improve power for GWIS, mostly in the epidemiological setting. We refer readers to Gauderman et. al. (2017)⁶ and references therein for a comprehensive review on the subject. Two-step GWIS methods have been proposed to improve the power of a G × E analysis while controlling the FWER and have been well studied for disease^7,8,9,10,11 and quantitative traits.^12,13 These methods use independent information from the data to perform an initial screening (the first step) to prioritize genes that are more likely to be involved in an interaction. In a second step, only the genes that pass the screening step are formally tested for an interaction, thus reducing the multiple testing burden.^7,8 Two commonly-used Step 1 screening tests for case-control studies are 1) the marginal disease-gene association which can be obtained by modeling the outcome on each gene on the disease individually⁷ and 2) the marginal exposure-gene association which models each gene on the exposure.⁸ While the former can also be adopted for quantitative traits,¹³ the latter is only valid in a case-control study since cases have been over sampled. Additional two-step methods that use both aforementioned tests in combination to further improve efficiency have also been explored.^9,10,11 Another, oftentimes more powerful, approach uses the quantitative screening information rather than a pass/no pass screen via a weighted multiple hypothesis testing correction.¹⁴ A key requirement for validity of any two-step procedure is that the statistics used in both Step 1 and Step 2 are independent.¹⁵ Two-step approaches for G × E interaction scans have not been well studied for right-censored time-to-event data.

In this paper, we investigate two-step hypothesis testing for right-censored time-to-event data under the Cox proportional hazards model.¹⁶ We introduce the concept of two-step hypothesis testing under the Cox model (Section 2), provide extensive numerical experiments to validate the method (Section 3) and apply it to discover interactions in a taxane-anthracycline chemotherapy study on breast cancer patients (Section 4). Concluding remarks, limitations and potential avenues for future work are provided in Section 5.

2 |. METHODOLOGY

Consider a study with a time-to-event endpoint where M genes (e.g., genotypes, expression, methylation, etc.) are measured for each of the N subjects such that $G_i=\left(G_{i1},G_{i2},\dots ,G_{iM}\right)$ for $i=1,\dots ,N$ Define E_i to be an environmental factor of interest, measured on each of the N subjects. Lastly let T_i be the true survival time and C_i be the right-censoring time that is assumed to be conditionally independent of T_i given E_i and G_i. With the presence of right censoring, we observe ${\tilde{T}}_i=\min \left(T_i,C_i\right)$ and $D_i=I\left(T_i\le C_i\right)$, where I(⋅) is the indicator function. The data therefore consists of the quadruple ${\left\{\left({\tilde{T}}_i,D_i,G_i,E_i\right)\right\}}_{i=1}^n$ which we assume are independent and identically distributed across the N subjects. Furthermore, one may augment our collection to include V_i, a set of subject-level adjustment covariates if necessary.

2.1 |. Genome-wide Interaction Scans (GWIS) for Right-Censored Data Using the Cox Proportional Hazards Model

With right-censored time-to-event data, a pivotal quantity to estimate is the hazard function $h(t)={\text{lim}}_{\text{Δ}t\to 0}\mathrm{Pr}(t\le T\le t+\text{Δ}t\mid T\ge t)/\text{Δ}t$ which describes the instantaneous risk of the event of interest for an individual, given that the individual has not yet experienced the event. When interest is in quantifying the associations between covariates (e.g., genes) and the time-to-event, one can model the conditional hazard using the Cox proportional hazards model. In the context of a GWIS, this model has the form:

$$h\left(t\mid G_j,E\right)=h_{0j}(t)\exp \left({\gamma }_{G_j}{G}_j+{\gamma }_{E}E+{\gamma }_{G_j\times E}{G}_j\times E\right),$$ (1)

where $h\left(t\mid G_j,E\right)$ is the hazard at time t conditional on G_j and environmental factor E, $h_{0j}(t)$ is an unspecified baseline hazard, and $\gamma ={\left({\gamma }_G,{\gamma }_E,{\gamma }_{G\times E}\right)}^T$ corresponds to a vector of log-hazard ratios. Extensions to include subject-level covariates are straightforward; however, for ease of exposition, we do not include them in this manuscript. The gene-by-environment (G × E) association between each gene and the time-to-event can be based on testing the null hypothesis $H_0:{\gamma }_{G_j\times E}=0$ for $j=1,\dots ,M$. We denote this type of analysis as the standard GWIS as we are interested in applying model (1) genome wide. The primary advantage of the standard GWIS is its computationally efficiency. The test statistic S_j provided by, for example, the Wald test will be used to identify interactions that are associated with the outcome. An adjustment for multiple comparisons can be applied to preserve the family-wise Type I error rate (FWER) at a prespecified significance level α (e.g., α^∗ = 5 × 10⁻⁸ or α* = α∕M). Either correction will lead to low power in detecting a G × E interaction.

To improve power, two-step methods for hypothesis testing have been proposed to conduct a GWIS while simultaneously preserving the FWER.^7,8,14 Hypothesis testing for the interaction effects will still be based on S_j (Step 2 testing); however, the significance level assigned to each of the M tests will be based on an initial screening step (Step 1 screening) via a screening statistic. Two popular approaches to two-step hypothesis testing have been widely adopted: subset testing⁷ and weighted hypothesis testing.¹⁴ In the former, each of the M screening statistics are compared to a prespecified significance threshold α₁.The test statistics S_j for the m genes that pass the Step 1 screen are then compared against the Bonferroni-corrected significance level α∕m to preserve the FWER. Note here that $m<<M$, and therefore the S_j that pass Step 1 are compared against a less stringent significance value than in the standard approach.

Instead of filtering out genes in Step 1, one can test all M test statistics in Step 2 using a weighted hypothesis test. Ionita-Laza et. al. (2007)¹⁴ proposed modifying the significance level assigned to each test statistic based on the ordered p-values (or ordered screening statistics) from Step 1. Let B be a prespecified initial bin size. Based on the results from Step 1, the B most significant genes are evaluated in Step 2 at significance level (α∕2)∕B, the next 2B genes are evaluated at (α∕2²)∕(2B), the next 4B at (α∕2³)∕(4B), etc. Using this scheme ensures that the overall significance level for the entire procedure does not exceed α while also allowing the top genes from Step 1 to be tested at a more liberal significance threshold than α∕M and, in most cases, α∕m. Oftentimes, using this weighted testing approach in Step 2 has been shown to be more powerful than using the subset approach. The choice of α₁ and B can be thought of as auxiliary tuning parameters that, while not affecting the FWER, can affect the power.¹⁷ For demonstrative purposes we selected values α₁ = 0.05 (recommended by Kooperberg and Leblanc, 2008⁷ and Murcray et al., 2009⁸) and B = 5 (recommended by Ionita-Laza et. al., 2007¹⁴) respectively. We leave a discussion on the selection of these auxiliary tuning parameters in our concluding remarks.

2.2 |. Two-step hypothesis testing for the Cox model

We investigate the performance of two-step hypothesis testing for the Cox model. First, we must derive a statistic to be used for the screening step. A common screening statistic used for continuous and binary outcomes is obtained from the marginal association between the gene and the outcome.^7,8,13 When dealing with right-censored survival data, an analogous quantity would be the test statistic ($S_j^{\ast }$) corresponding to the univariate Cox model

$$h\left(t\mid G_j\right)=h_{0j}^{\ast }(t)\exp \left({\beta }_{G_j}{G}_j\right).$$ (2)

Thus one may conduct a two-step GWIS by testing the statistical significance of S_j at an adjusted significance threshold determined by the size of $S_j^{\ast }$, which follows a N(0,1) distribution under the null hypothesis $H_0:{\beta }_{G_j}=0$. We will refer to this approach as mG|G × E, where mG denotes the use of the marginal association with G in the first step. A necessary requirement for the validity of the two-step testing procedure is (asymptotic) independence between the Step 1 and Step 2 statistics. Dai et. al. (2012)¹⁵ established asymptotic independence between the marginal association and interaction test for generalized linear models under a canonical link. Furthermore, they proved that the estimator for the marginal association in a Cox model is asymptotically independent of the case-only estimator¹⁸ of the interaction in the event that the endpoint is rare (see Proposition 2 in Dai et. al., 2012¹⁵). However, a general result for the asymptotic independence between the marginal effect association and interaction for the Cox model has not been shown. As we will show in Section 3, β_G and γ_G×E are in fact asymptotically correlated when a marginal E effect is present. This may be explained by the joint effect both G and E have on the time to event that is ignored in modeling their effects univariately.

It is well known that the regression parameter estimates for the Cox model are not robust to omitted covariates.^19,20 If important covariates are omitted from the model, the estimated effects of the retained covariates are biased towards zero.¹⁹ This phenomenon was further corroborated by Haller and Ulm (2018)²¹ who conducted a simulation study for identifying biomarker-treatment interactions in randomized trials. Although ${\beta }_{G_j}$ and its test statistic $S_j^{\ast }$ are not of primary interest, they play a crucial role in the filtering and ordering of genes for the second-step hypothesis test. Furthermore, as we will show in our simulation studies, using $S_j^{\ast }$ in Step 1 of a two-step procedure can lead to inflated Type I error rates for the overall GWIS across several scenarios.

2.3 |. A new Step 1 screening statistic for the two-step time-to-event GWIS

To preserve Type I error and increase power, we propose using a conditional model to assess the effect of G on survival while conditioning on the environmental factor

$$h\left(t\mid G_j,E\right)={\tilde{h}}_{0j}(t)\exp \left({\omega }_{G_j}{G}_j+{\omega }_{E}E\right).$$ (3)

where ω_G and ω_E correspond to the main effects associated with G and E, respectively. We now use ${\tilde{S}}_j$, the test statistic for the conditional parameter ω_G, to screen genes in Step 1 rather than $S_j^{\ast }$. We denote this screening and testing procedure as $cG\mid G\times E$ to emphasize its conditional dependence on E. We provide formal justification of the asymptotic independence between ${\widehat{\omega }}_{G_j}$ and ${\widehat{\gamma }}_{G_j\times E}$ under the null hypothesis provided that (1) is correctly specified.

Theorem 1.

Consider a study with a right-censored time-to-event endpoint where the data are composed of N subjects, each with $(\tilde{T},\delta ,G,E)$ as defined in Section 2. Consider the two Cox proportional hazards models (1) and (3) and suppose that (1) is correctly specified. Then under the null hypothesis $H_0:{\gamma }_{G_j\times E}=0$, the maximum log-partial likelihood estimators for ${\widehat{\omega }}_{G_j}$ and ${\widehat{\gamma }}_{G_j\times E}$ are asymptotically independent.

The proof of our theorem is provided in the appendix and holds under the regularity conditions proposed by Andersen and Gill (1982).²² While Theorem 1 assumes that model (1) must be correctly specified, which will not be true in most cases, our empirical results in Section 3 provide evidence of asymptotic independence between the Step 1 and Step 2 statistic under mild model misspecification.

3 |. SIMULATION STUDIES

3.1 |. Independence of Step 1 and Step 2 statistics

The validity of the two-step testing procedures relies on the asymptotic independence between the filtering statistic in Step 1 (β_G or ω_G) and the testing statistic in Step 2 (γ_G×E). As in Dai et al. (2012),¹⁵ we examine the empirical correlation coefficients between β_G and γ_G×E and ω_G and γ_G×E for increasing values of N = 1,000, 2,000, 5,000, and 8,000. Survival times were drawn from an exponential model with baseline hazard h₀(t) = 0.01 and γ = (0,γ_E,0), where γ_E ∈ {0,log(0.8),log(0.6)} corresponds to no, a mild, and a modest exposure effect, respectively. A binary environmental exposure was randomly generated from a Bernoulli(π_E) distribution, where π_E = 0.5 corresponds to equal allocation to the exposed (E = 1) and unexposed (E = 0) groups. We simulate G to either be binary(G ~ Bernoulli(0.4))or measured continuously (G ~ N(0,1)).Independent censoring times were generated from an exponential distribution with rate parameter 0.005, corresponding to a censoring percentage of 33 − 40% across the various simulation scenarios we considered. Results are average over 10,000 replicate datasets.

When no exposure effect is present, we observe that both sets of empirical correlations, the correlation between β_G and γ_G×E and ω_G and γ_G×E, are nearly zero (Table 1 ). As the exposure effect becomes stronger, the correlation between β_G and γ_G×E increases. Additionally, this correlation does not diminish as N increases. In all scenarios the correlation between ω_G and γ_G×E remains close to zero.

TABLE 1.

Empirical correlations of the G×E interaction parameter ${\widehat{\gamma }}_{G\times E}$ with the marginal $\left({\widehat{\beta }}_G\right)$ and conditional $\left({\widehat{\omega }}_G\right)$ genetic effect parameters averaged over 10,000 Monte Carlo simulations with varying sample size 𝑛. The censoring rate was roughly between 34 − 50%. G and E were simulated as independent Bernoulli random variables where Pr(G = 1) = 0.30 and Pr(E = 1) = 0.5. Parameter estimates are from the following models: $h(t\mid G)=h_0^{\ast }(t)\exp \left({\beta }_{G}G\right);h(t\mid G,E)={\tilde{h}}_0(t)\exp \left({\omega }_{G}G+{\omega }_{E}E\right)$; $h(t\mid G,E)=h_0(t)\exp \left({\gamma }_{G}G+{\gamma }_{E}E+{\gamma }_{G\times E}G\times E\right)$.

			N = 1,000	2, 000	5,000	8, 000
			${\gamma }_{G\times E}$	${\gamma }_{G\times E}$	${\gamma }_{G\times E}$	${\gamma }_{G\times E}$
$G\sim Bern(0.4)$	${\gamma }_E=0$	${\beta }_G$	−0.001	−0.029	0.014	0.004
		${\omega }_G$	−0.001	−0.030	0.014	0.004
	log(0.8)	${\beta }_G$	0.060	0.083	0.065	0.086
		${\omega }_G$	−0.010	0.014	−0.005	0.016
	log(0.6)	${\beta }_G$	0.141	0.14G	0.134	0.145
		${\omega }_G$	0.000	0.004	−0.010	0.004
$G\sim N(0,1)$	${\gamma }_E=0$	${\beta }_G$	−0.000	0.001	0.004	0.008
		${\omega }_G$	−0.000	0.001	0.004	0.008
	log(0.8)	${\beta }_G$	0.068	0.055	0.072	0.072
		${\omega }_G$	0.000	−0.013	0.000	0.002
	log(0.6)	${\beta }_G$	0.143	0.139	0.14G	0.154
		${\omega }_G$	0.004	−0.005	0.001	0.013

3.2 |. Family-wise error rate and power

We first compare the family-wise error rates (FWER) for the proposed two-step approaches, mG|G × E and cG|G × E, to the standard GWIS approach for continuously (e.g., gene expression levels) measured genes. In all simulations, we generated 10,000 replicate data sets, each consisting of N = 1,000 subjects and M = 10,000 genes. The M genes were simulated using a multivariate normal density N_p(0,Σ_x), where Σ_x = I_p assumes independence across all the genes. Similar to Section 3.1, survival times were drawn from an exponential model with baseline hazard h₀(t) = 0.01 and γ = (0,log(0.6),0), the binary exposure variable was randomly generated from a Bernoulli(0.5), and independent censoring times were generated from an exponential distribution with rate parameter 0.005. We refer to the model corresponding to these particular set of parameters as our “base model”.

For each replicate data set, we performed genome-wide analyses of the G × E interaction using the following methods: 1) the standard GWIS approach where we test S_j at a Bonferroni-adjusted significance level of α∕10,000, and 2) two-step GWIS approach mG|G × E, and 3) two-step GWIS approach cG|G × E. Both subset testing and weighted hypothesis testing were considered for the two-step GWIS methods. Subset testing was performed using a screening threshold α₁ = 0.05 and the initial bin size of weighted hypothesis testing used an initial bin size B = 5.

As expected, the standard GWIS approach has close to nominal Type I error (α = 0.05) across all scenarios (Table 2 Row 1). Likewise, the cG|G × E approach has comparable Type I error rate to the standard GWIS approach. On the other hand, the Type I error rate for the mG|G × E test is inflated. We also considered several alternative models where we vary the simulation parameters and notice similar trends in the FWER. While the cG|G × E approach appears to retain the FWER, inflation is still present for the mG|G×E approach. Additionally, the degree of inflation for the cG|G×E approach is influenced by the values of γ_E, with increasing FWER as the exposure effect becomes stronger.

TABLE 2.

Estimated Type I error rates for tests of G × E interaction across several parameter settings for a continuously-measured genes (Section 3.2). Each estimate of Type I error is based on the proportion of 10,000 replicate datasets for which the indicated procedure identified at least one statistically significant result (at the 0.05 level) among the 𝑀 = 10,000 genes. For the subset screening step, a filtering statistic of α₁ = 0.05 was used. For the weighted Bonferroni test, an initial bin size of B = 5 was used. See Section 3.2 for details on the simulation settings. The Base Model corresponds to the following simulation parameters: γ = (0,log(0.6),0), π_E = 0.5, event rate ≈ 40−44%, Σ_X = I_P, N = 1,000. AR(ᵨ) corresponds to an autoregressive correlation structure with correlation parameter ᵨ.

	Standard	Two-Step Methods
		mG|𝐺 × 𝐸		cG|𝐺 × 𝐸
	GWIS	Subset	Weighted	Subset	Weighted
Base Model	0.048	0.084	0.107	0.050	0.047
γE = log(1)	0.051	0.048	0.048	0.049	0.048
γE = log(0.8)	0.046	0.059	0.062	0.051	0.047
γE = log(0.4)	0.051	0.130	0.175	0.052	0.053
γG = log(0.8); 𝛾𝐸 = log(0.8)	0.048	0.057	0.064	0.051	0.054
γG = log(0.8); γE = log(0.6)	0.046	0.080	0.097	0.051	0.052
γG = log(0.6); γE = log(0.8)	0.051	0.056	0.056	0.052	0.052
γG = log(0.6); γE = log(0.6)	0.047	0.070	0.074	0.054	0.049
γG = log(1.2); γE = log(0.6)	0.047	0.083	0.100	0.051	0.051
ΣX = log (0.3)	0.050	0.085	0.108	0.052	0.051
ΣX = log (0.6)	0.054	0.083	0.098	0.054	0.049
πE = 0.4	0.055	0.088	0.102	0.050	0.048
πE = 0.2	0.056	0.074	0.088	0.054	0.052
Event rate ≈ 0.79	0.051	0.108	0.140	0.051	0.052
Event rate ≈ 0.24	0.051	0.059	0.061	0.053	0.050
N = 2,000	0.052	0.084	0.105	0.049	0.049

Our simulation results show that the cG|G × E two-step approach retains the FWER when the model is correctly specified. However, it is often the case that model will be misspecified (e.g., when an interaction effect is present, the exposure effect is modeled incorrectly, or if important confounding covariates are omitted from the model). To compare the FWER under model misspecification, we generate survival times using the parameters from the “base model” except that survival times are drawn from the following exponential model: h(t) = 0.01exp{E × log(0.6) + V × log(HR_v )}, where V is an omitted covariate from the model with HR_v ∈ {0.4,0.6,0.8,1.2,1.4}. Our results (in Supplemental Table S1) show that both the GWIS and cG|G×E approach retain the FWER at the nominal level for various effect sizes and values of V.

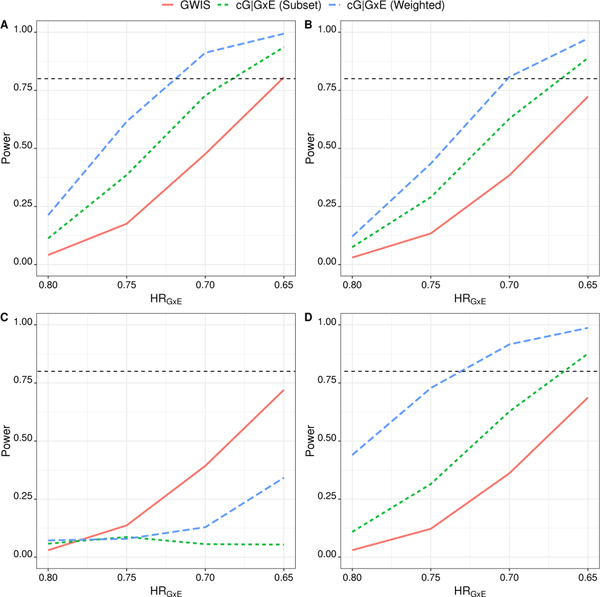
To compare power, we designate one gene as the risk-associated factor (RAF), assumed to have a G × E interaction effect on survival. The remaining 9,999 genes are assumed to have no association with the outcome. Power was estimated as the proportion of replicates in which the RAF was identified as statistically significant. In addition, we estimated the FWER which was defined as the proportion of replicates in which at least one of the M−1 non-RAF genes was declared statistically significant at a FWER of α = 0.05. We adopted the same simulation parameters as the base model while varying γ_G×E. Since the cG|G×E two-step GWIS preserves the FWER under the Base Model, we compare its power to the standard GWIS approach. The inflation in Type I error prohibits a fair power comparison using the mG|G × E approach and is thus not considered. Across a range of interaction effect sizes (γ_G×E), the two-step GWIS (cG|G × E) provides greater power than the standard GWIS (Figure 2 Panel A). Moreover, weighted hypothesis testing provides greater power than subset hypothesis testing. Under these parameters, the cG|G × E two-step GWIS can detect a minimum interaction hazards ratio of γ_G×E ≈ 0.73 with 80% power. For the same interaction effect size, the power using the standard GWIS is only 38%. To achieve 80% power using the standard GWIS, the minimum detectable interaction hazards ratio in this scenario would have to be stronger, at γ_G×E ≈ 0.66.

FIGURE 2.

Power comparison between the standard GWIS approach and the cG|G×E two-step GWIS across different values of HR_G×E = exp(γ_G×E). Panel A) γ = (0,0,γ_G×E); Panel B) γ = (0,log(0.6), γ_G×E); Panel C) γ = (log(1.2),log(0.6), γ_G×E); Panel D) γ = (log(0.8),log(0.6), γ_G×E). See Section 3.2 for details of the simulation setup (Standard GWIS - Solid Red Line; cG|G × E with weighted screening - Dashed Green Line; mG|G × E with weighted screening - Dashed Blue Line).

In addition to the base model, we explore the power to detect an interaction under several combinations of γ_G and γ_E. We see similar trends in power when no main exposure effect is present (Panel B) and when both the main genetic effect and interaction are protective (Panel D). When the sign of the gene effect differs in different exposure groups (Panel C), we observe that the standard GWIS has better power than the cG|G × E GWIS. This is to be expected, since the ‘crossing-style’ interaction (e.g., the main and interaction effects are in opposite directions) in Panel C makes the test based on Model 3 an ineffective screening tool as previously reported by Wason and Dudbridge (2012).²³ We show, in the supplemental material (Figure S1), that power improves for both cG|G×E approaches as the interaction effect size increases in this scenario. By allowing for one true G×E interaction, the model is misspecified for the other 9,999 genes. We also calculate the FWER, identifying at least one statistically significant result among the 9,999 non-risk associated genes, across all four settings. The FWER was retained at the nominal level for the standard GWIS and cG|G × E approach (Table 3 ) across all settings, providing further empirical evidence that the cG|G × E approach works well under mild model misspecification.

TABLE 3.

Estimated Type I error rates for tests of G × E interaction across several parameter settings for a continuousl-ymeasured genes (Section 3.2). Each estimate of Type I error is based on the proportion of 10,000 replicate datasets for which the indicated procedure identified at least one statistically significant result (at the 0.05 level) among the M = 9,999 non-risk associated genes. For the subset screening step, a filtering statistic of α₁ = 0.05 was used. For the weighted Bonferroni test, an initial bin size of B = 5 was used. See Section 3.2 for details on the simulation settings. The Base Model corresponds to the following simulation parameters: γ = (0,log(0.6),0), π_E = 0.5, event rate ≈ 40 − 44%, Σ_X = I_P, N = 1,000. AR(ᵨ) corresponds to an autoregressive correlation structure with correlation parameter ᵨ. Asterisk denotes FWER that are not within the 95% confidence interval for 0.05.

				Standard	Two-Step Methods
					mG|𝐺 × 𝐸		cG|𝐺 × 𝐸
Panel	γ G	γ E	γ G×𝐸	GWIS	Subset	Weighted	Subset	Weighted
A	0	0	log(0.80)	0.055	0.054	0.046	0.054	0.045
			log(0.75)	0.056	0.057	0.048	0.055	0.048
			log(0.70)	0.056	0.059	0.052	0.059	0.051
			log(0.65)	0.058	0.061	0.056	0.059	0.054
B	0	log(0.60)	log(0.80)	0.050	0.090	0.110	0.054	0.050
			log(0.75)	0.052	0.092	0.110	0.057	0.048
			log(0.70)	0.053	0.102	0.116	0.058	0.046
			log(0.65)	0.053	0.106	0.119	0.057	0.046
C	log(1.2)	log(0.60)	log(0.80)	0.049	0.076	0.090	0.056	0.051
			log(0.75)	0.053	0.082	0.094	0.055	0.051
			log(0.70)	0.053	0.086	0.099	0.055	0.052
			log(0.65)	0.052	0.087	0.103	0.054	0.053
D	log(0.80)	log(0.60)	log(0.80)	0.055	0.095	0.108	0.054	0.049
			log(0.75)	0.055	0.096	0.115	0.054	0.050
			log(0.70)	0.054	0.108	0.125	0.057	0.053
			log(0.65)	0.055	0.115	0.135	0.058	0.059

4 |. APPLICATION

We compare the cG|G × E approach to the standard GWIS in a concerted taxane-anthracycline chemotherapy study for breast cancer patients.^24,25 Taxane-based chemotherapy has been shown to significantly improve progression-free and overall survival of patients.²⁶ The data are publicly available from the Gene Expression Omnibus database (http://www.ncbi.nlm.nih.gov/geo; GSE 16446 and 25066 ). The data consists of 22,277 gene expression levels ( Affymetrix array ) measured on N = 614 breast cancer patients receiving anthracycline-based adjuvant chemotherapy with (GSE25066; n = 507) or without (GSE16446; n = 107) taxane. In this example, genes refer to gene expression levels while the treatment (anthracycline with or without taxane) is considered the environmental exposure. Overlapping descriptive characteristics of the patients in both studies can be found in Table S3 of the Online Supplemental Material. Since the data come from two gene expression studies, cross-platform normalization was performed using Frozen RMA²⁷ and XPN.²⁸ Lastly, the number of candidate genes was reduced by filtering out those with an interquartile range less than or equal to one.²⁹ We refer readers to Ternes et al. (2017)³⁰ for more information on the preprocessing, filtering, and normalization procedures. Of the 22,277 probes that were initially available, M = 1,689 were retained after preprocessing. The outcome of interest was distant-relapse free survival (DRFS), experienced by approximately 22% (134/614). A standard GWIS was performed for which each of the G×E p-values was compared to a Bonferroni-corrected significance threshold of 0.05∕1,689 ≈ 3×10⁻⁵. We also applied our proposed two-step cG|G ×E approach using a screening threshold α₁ = 0.05 for subset testing and B = 5 for weighted hypothesis testing.

Based on the standard GWIS, significant interactions were identified for expression at three probes (Table 4 ). In addition to identifying the same three loci – all three via subset testing and two of three by weighted hypothesis testing – the two-step approaches also identified four additional probes that were not identified via standard GWIS. Thus, our two-step approach was able to identify novel G × E effects that were missed by a standard GWIS.

TABLE 4.

Significant G × E (gene-environment) interactions identified for the taxane-anthracycline chemotherapy study in Section 4. GWIS - Standard GWIS approach; Weighted - cG|G ×E approach using weighted hypothesis testing with initial bin size B = 5; Subset - cG|G×E approach using subset hypothesis testing with initial bin size α₁ = 0.05 Y indicates that the G×E interaction was statistically significant at a FWER of α = 0.05 by the corresponding approach. Sites unique to either two-stage approaches are bolded. Parameter (log-hazard ratio) estimates $\left({\widehat{\gamma }}_G,{\widehat{\gamma }}_E,{\widehat{\gamma }}_{G\times E}\right)$ were estimated for each probe using model 1.

Probe ID	Gene	GWIS	Weighted	Subset	${\widehat{\gamma }}_G$	${\widehat{\gamma }}_E$	${\widehat{\gamma }}_{G\times E}$
204533_at	CXCL10	Y	-	Y	−0.46	−0.01	0.76
202089_s_at	SLC39A6	Y	Y	Y	0.52	−0.17	−1.20
208682_s_at	MAGED2	Y	Y	Y	0.27	−0.18	−1.03
2OO810_s_at	CIRBP	-	Y	-	0.16	−0.13	−0.75
2O2O88_at	SLC39A6	-	Y	-	0.34	−0.13	−0.92
205158_at	RNASE4	-	-	Y	0.50	−0.18	−1.02
210962_s_at	AKAP9	-	-	Y	0.44	−0.05	−0.94

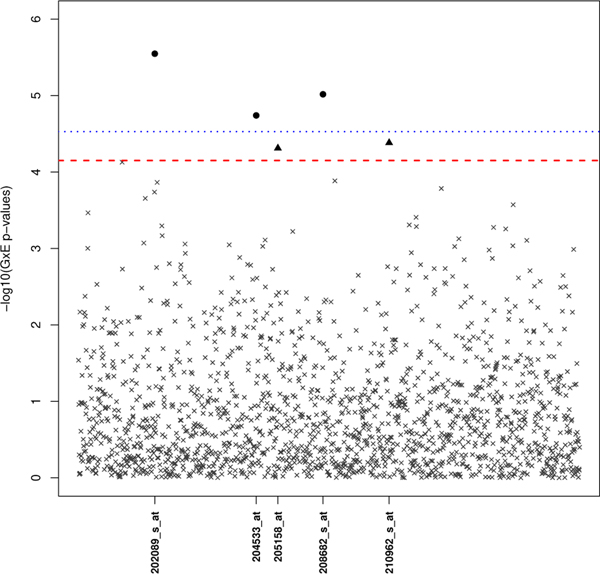
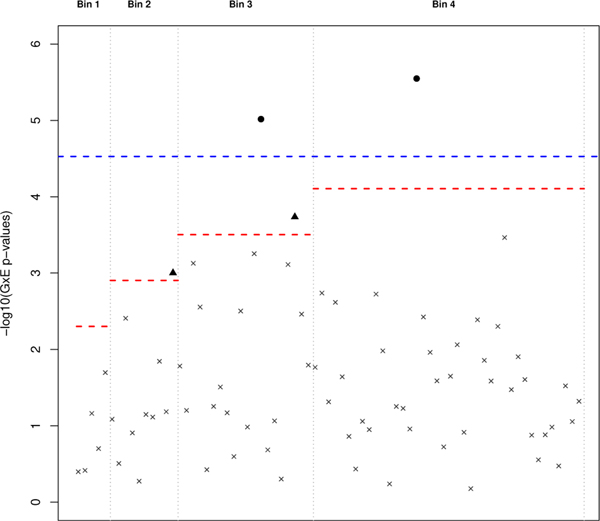
Of the 1,689 probes, 707 passed the screening threshold of α₁ = 0.05. The interaction effect of the 707 probes, estimated from Model 1, are tested at a significance level of 0.05∕707 ≈ 7×10⁻⁵ (Figure 3). It is clear from Figure 3 that each interaction effect is tested at a less stringent threshold using the two-step subset test (red dotted line) when compared to the standard GWIS (blue dotted line). For each of the identified interactions, the corresponding exposure effects were all modest (HR_E ∈ (0.80,0.96)). As shown in the Manhattan plot of Figure 4, ordered left to right in ascending order by their conditional p-values, the four probes identified by weighted hypothesis testing are located in the first four bins, whose respective bin-specific significance thresholds (red-dotted line) are larger than the standard Bonferroni correction. The one probe (204533_at) identified by the standard GWIS but missed in the weighted Bonferroni was placed in Bin 5 (not shown in Figure 4) and was tested against a more conservative significance threshold than the standard Bonferroni correction. The weighted hypothesis testing approach selected four probes; however, two of the probes (202088_at and 202089_s_at) are from the same locus (SLC39A6).

FIGURE 3.

Manhattan Plot of G × E p-values (on the -log10 scale) from the taxane-anthracycline chemotherapy study in Section 4 using subset testing. Loci marked by a black dot or triangle represent G × E p-values that passed the subset-adjusted significance threshold (red dotted line). As a comparison, the standard GWIS significance threshold is also included (blue dotted line) with the black dot indicating a significant finding.

FIGURE 4.

Manhattan Plot of G × E p-values (on the -log10 scale) from the taxane-anthracycline chemotherapy study in Section 4 using weighted Bonferroni testing. G × E p-values for each loci are arranged left to right in ascending order of their respective conditional p-values. Loci marked by a black dot or triangle represent G×E p-values that passed the subset-adjusted significance threshold (red dotted line). As a comparison, the standard GWIS significance threshold is also included (blue dotted line) with the black dot indicating a significant finding.

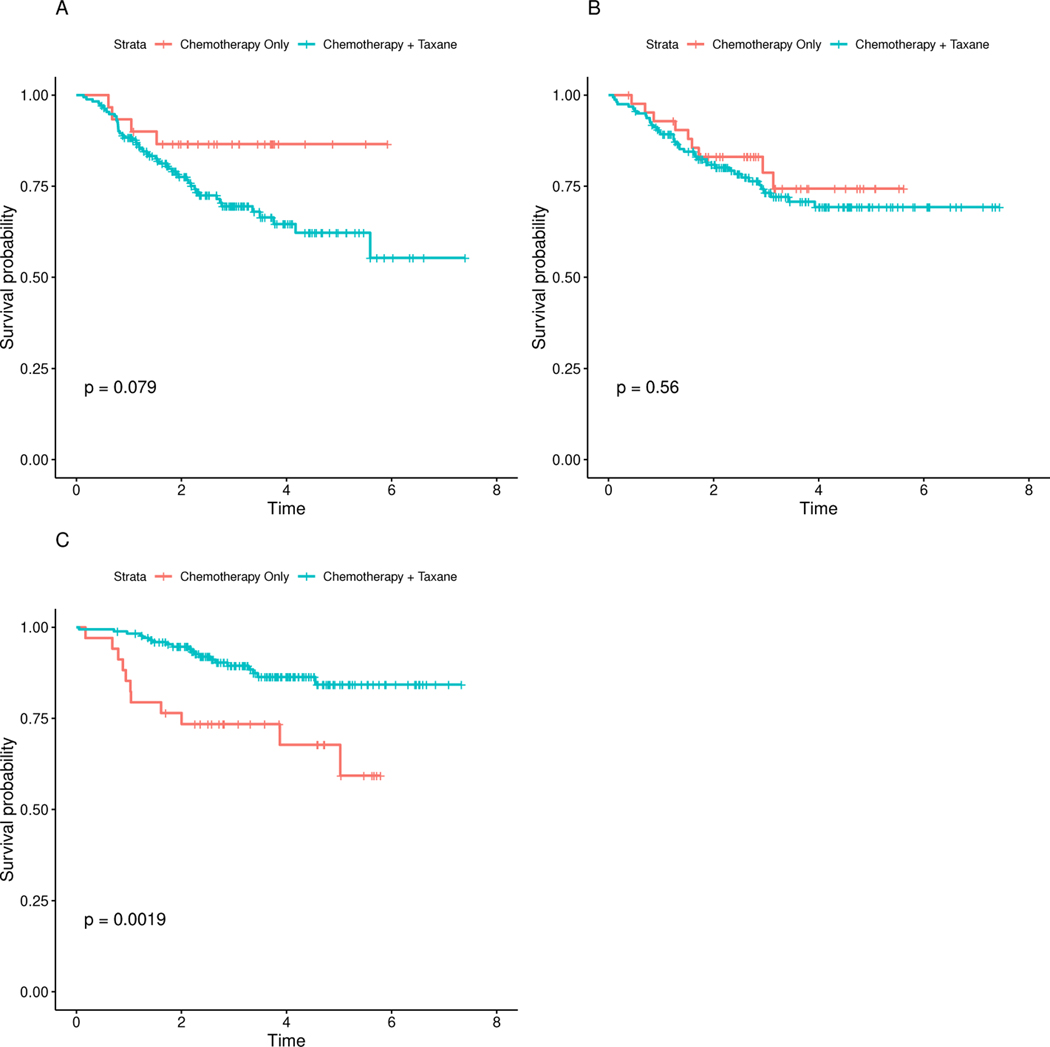
We focus our attention on AKAP9, a locus that was identified using the subset-based approach. This loci is on a particular region of chromosome 7q that has been suggested as a fundamental mechanism of acquired resistance to taxane-based therapy.^31,32 To further investigate this interaction effect, we divide the gene expression levels into tertiles and compute the Kaplan-Meier estimates for both treatment groups at each tertile (Figure 5). The post-hoc analysis suggests that the combination of chemotherapy and taxane has a negative effect on survival for those with suppressed levels of AKAP9 (Panel 5A). However, the combination therapy performs better for those at the highest tertile (Panel 5C). We see a similar relationship between Chemotherapy + Taxane and RNASE4 (Supplemental Figure S2), a gene that is located in the same region and share the same promoters as ANG, which has been associated with the transition of normal breast tissue into invasive breast carcinoma.³³ To the best of our knowledge, no previous study to elucidate the relationship between RNASE4 and taxane-based therapies has been conducted. Further studies are warranted to understand the biological interaction between the the loci and taxane-based therapy.

FIGURE 5.

Kaplan-Meier curves comparing AKAP9-treatment effects on distant relapse-free survival.AKAP9 gene expression levels were divided into tertiles; A) Low AKAP9 levels ≤ −0.516); B) Medium AKAP9 levels (−0.516,0.268); C) High AKAP9 levels ≥ 0.268. P-values are calculated using an unweighted log-rank test.

5 |. DISCUSSION

We provide a framework for two-step hypothesis testing that aims to improve power for identifying G×E interactions compared to standard genome-wide scans under the Cox proportional hazards model. As a consequence, we highlight the necessity of including the exposure in the screening step in order to preserve the FWER, a result that has not been observed for other types of outcome data. We demonstrate that a two-step approach to GWIS can provide substantially greater power to detect G × E interactions. Additionally, we observe that rather than using the unadjusted marginal association between genes and the time-to-event as a screening statistic, one should use the gene association conditional on the exposure via a conditional main effects model.

Our simulation results illustrate that accounting for the exposure in Step 1 is crucial in preserving the FWER under several different scenarios. In general, screening via the marginal genetic association tends to inflate the FWER especially when a strong exposure effect is present. This inflation may lead to false conclusions in studies where we expect the exposure to have some a priori effect on the time to event (e.g., a treatment in a RCT). Using the two-step approach, we were able to identify four G×E interactions that were missed by the standard GWIS in a taxane-anthracycline chemotherapy study. Although our simulations suggests that weighted hypothesis testing can, on average, typically provide greater power than subset-based hypothesis testing, our application illustrates that while some genes are identified by all three approaches, others are only identified by one or two. Further exploration of the specific type of Step 2 testing and the setting of corresponding tuning parameters (α₁ and B) is warranted. The results provide genes that have been previously associated with resistance to taxane-based therapy (AKAP9) or have potential to be investigated further (RNASE4/ANG). We note that substantial blocks of correlated genes exist within our study (Figure S3 in the Online Supplemental Material). As is the case for all discovery-based methods (one step or two step), identification of the true causal gene among a set of correlated genes is always challenging. Validation of the discovered G × E interactions in future targeted studies is necessary to understand the biological mechanism behind taxane-based resistance.

The Step 1 screening statistic proposed for the cG|G × E GWIS approach requires the calculation of the Wald statistic, which requires fitting a separate alternative models for each gene and can be computationally expensive for large N and M. Additionally, for genotype data with low-frequency variants, the Wald test may not control the Type I error rate when testing low-frequency variants and/or when the event rate is low due to the skewness of the underlying normal distribution.^34,35 Refinements to develop a scalable and accurate approach for genome-wide scale single-variant Cox’s regression have recently been proposed.³⁶ We are currently exploring coupling the two-step Cox GWIS with algorithms that scale to the size of electronic health records databases and biobanks.³⁷

Our findings are based on estimated G×E interactions one-at-a-time, that, for example, ignores potential joint G×E effects. While the final estimates in our approach will be biased (due to misspecification, the winner’s curse, etc.), the goal of the two-step hypothesis test is to discover genes that interact with an exposure for future studies. In our formulation, several assumptions are made about the underlying environmental exposure. First, we assume that the exposure has a proportional effect on the event of interest. This can be relaxed if one considers a stratified Cox model where the stratification is performed on a categorical factor. Stratified Cox’s regression is also a popular approach to remedy non-proportional hazards, which may occur when we omit the environmental factor from the screening step. Additionally, our current work falls under the stratified Cox regression framework where the nonparametric baseline hazards are proportional to each other (i.e., h₀₁(t) = exp($\beta$_E)h₀₀(t)). Second, Theorem 1 is valid provided that the model is correctly specified. It remains to be shown that ω_G and γ_G×E are asymptotically independent under model misspecification. A possible solution is to perform testing and screening using a robust standard error as opposed to a model-based standard error.^38,39,40 To show asymptotic independence between the screening and testing statistics under a misspecificed model, one must take into account the sandwich estimator.¹⁵ Doing so is not trivial for the Cox model and we leave this for future research. Our primary focus for this paper was on a binary exposure variable. While our proposed two-step approach approach for Cox regression should also be applicable to a continuous E, specific assessment of this scenario in terms of Type I error and power compared to standard GWIS is left for future research.

Lastly, as noticed in our real data application, gene expression levels are typically highly correlated, which can impact both the screening and testing steps. The screening statistics are estimated one-at-a-time and can reduce power of the overall procedure if there exists substantial correlation among genes.⁴¹ Wang et. al. (2021)⁴² proposed a two-step approach to identify biomarker-treatment interactions using a multivariate screening strategy via penalized regression for continuous outcomes and demonstrate a substantial gain in power when compared to the one-at-a-time screening procedure in highly correlated data. We expect that multivariate screening strategies will lead to similar improvements in performance for time-to-event data. While it has been shown that accounting for correlation can improve power by modifying the screening step, the impact of correlation on the testing step is relatively unknown. A Bonferroni-type correction is still applied in Step 2 for both the subset or weighted hypothesis tests. When substantial correlation exists (within the subset of genes that pass Step 1 for subset testing or within bins for weighted hypothesis testing), the Bonferroni correction is likely to be too conservative. Methods to improve power in the presence of correlation include techniques to adjust the p-value for each test,^43,44 permutation-based testing,^45,46 and replacing the denominator in the Bonferroni correction by the effective number of tests rather than the actual number of tests.^47,48 Refinements to both steps for right-censored data, and in general, all data types, to account for genetic correlation is a novel avenue of research in the field of G × E discovery.

Abbreviations:

FWER

family-wise error rate

GWIS

genome-wide interaction scans

RCT

randomized controlled trial