Abstract
Extant literature suggests that performance on visual arrays tasks reflects limited-capacity storage of visual information. However, there is also evidence to suggest that visual arrays task performance reflects individual differences in controlled processing. The purpose of this study is to empirically evaluate the degree to which visual arrays tasks are more closely related to memory storage capacity or measures of attention control. To this end, we conducted new analyses on a series of large data sets that incorporate various versions of a visual arrays task. Based on these analyses, we suggest that the degree to which the visual arrays is related to memory storage ability or effortful attention control may be task-dependent. Specifically, when versions of the task require participants to ignore elements of the target display, individual differences in controlled attention reliably provide unique predictive value. Therefore, at least some versions of the visual arrays tasks can be used as valid indicators of individual differences in attention control.
Keywords: attention control, change detection, visual arrays, working memory capacity
The visual arrays task, also known as the change-detection task, is one of the most commonly used tools to understand the cognitive and neurophysiological nature of visual working memory (Fukuda et al., 2010; Luck & Vogel, 1997). The task is typically interpreted as a fairly pure measure of visual memory storage capacity. However, the mechanisms reflected by these measures have been questioned. Engle and colleagues (Draheim et al., 2021; Shipstead et al., 2014) have suggested that the standard visual storage interpretation may be incomplete. In particular, they have shown a strong relationship between visual arrays tasks and attention control at the latent construct level that does not align with a strict visual working memory explanation. Although this finding does not preclude interpreting the visual arrays as a memory storage (i.e., working memory capacity) task, it does warrant further exploration of the nature of its relationship with constructs other than visual storage. Additionally, there are various types of visual arrays tasks that include differences in task design that may alter which construct(s) causally contribute to change detection accuracy. Therefore, our question is: Which theoretical construct(s) does the visual arrays task reflect and does this depend on the task design?
We approach this question by reviewing a subset of the literature on the visual arrays task and, using data collected in our lab over the last 10+ years, to empirically assess the extent to which performance on visual arrays metrics is uniquely predicted by both working memory capacity and attention control at the latent level. Crucially, our review is selective and informed by a theoretical approach which assumes that the working memory system comprises of both mechanisms for memory storage and attentional control processes related to the active maintenance and manipulation of the contents of working memory (Engle et al., 1999; Engle & Martin, 2018). Our intent is not to create the impression that no viable theoretical alternatives exist (e.g., Oberauer & Lin, 2017) but rather to narrow the scope and focus of this project toward an evaluation of the prevailing interpretation of visual arrays tasks as measures of visual storage capacity. We do, however, discuss alternative interpretations of our results based on multiple frameworks of attention and working memory.
Visual Arrays Tasks: An Introduction
The general procedure of a visual arrays task is to briefly present a target array of items (e.g., colored squares) on a computer monitor, typically for a duration of 100 ms. After a short interval, a probe array appears and the test-taker must decide whether or not one of the items has changed on some dimension (e.g., color) relative to the target array. When the target array includes 3–4 items, accuracy tends to be nearly perfect. As items are added to the display, performance declines in a linear manner (Luck & Vogel, 1997). This trend is typically interpreted as an indication that people can store a finite number of information chunks in visuospatial memory (Cowan et al., 2005; Rouder et al., 2011; but see Ma et al., 2014). Scores on these tasks are determined based on an equation originally developed by Pashler (1988) by which one can calculate a capacity score (denoted as k) for an individual’s performance on the task. This k capacity score is thought to reflect the number of items one can store in visual working memory (Cowan, 2010). Moreover, k values reach asymptote around 3 or 4, suggesting that most individuals can maintain three to four chunks in visual working memory at a time, a value that accords well with estimates of memory storage capacity derived from other measures (Cowan, 2010).
However, and critical to our empirical tests, there are different versions of the visual arrays task that may change what cognitive processes the resulting k capacity score represents. In particular, in visual arrays with a selection component, participants are cued to focus on only a subset of the items presented in the target array. Participants are asked to attend to only these cued items rather than the entire array, and the cued dimension can vary on location, color, size, shape, and so forth We will refer to the traditional visual arrays task as nonselective visual arrays and those that require ignoring some elements of the target array as selective visual arrays.
If the nonselective and selective visual arrays tasks are fundamentally the same (that is, they measure the same exact construct[s] to the same degree), then k scores should be constant across the two. In fact, mean k scores on selective visual arrays are typically lower, about half, compared with the typical three to four k scores observed with nonselective visual arrays (Shipstead et al., 2014; Shipstead & Yonehiro, 2016). To explain this dissociation, task specific aspects must be considered. Specifically, nonselective visual arrays tasks have no explicit attentional filtering/selection component and no distractors. By contrast, in the selective visual arrays tasks, ineffective selection/filtering would lead to nontarget elements of the target array being represented in working memory, effectively doubling the set-size of items attended and resulting in a lower k score (i.e., performance on a set-size of three items becomes equivalent to performance on a set-size of six items). Thus, the source of individual variability may be different depending on the nature of the visual arrays task in question (i.e., nonselective vs. selective tasks). Currently, there are two proposed sources of variability: storage capacity, which we have addressed (Cowan et al., 2005; Rouder et al., 2011 )m and attention control (Draheim et al., 2021; Shipstead et al., 2014), to which we now turn.
Attention Control
The ability to control and direct attention is necessary for the successful execution of many tasks (Redick et al., 2016; Shipstead et al., 2016). However, the degree to which a specific task reflects this ability to control attention varies.1 According to the executive attention account of working memory capacity, the executive attention system is responsible for maintaining and ignoring distraction in the service of executing a given task (Engle et al., 1999; Shipstead et al., 2016). In storage-based tasks, a principal function of the executive attention system is to actively maintain information in working memory and reduce interference by preventing the storage of irrelevant information. More interference diminishes available storage for relevant memory items, leading to lower scores on capacity tasks (Oberauer, 2002).
A critical feature of this theoretical approach is that there may be multiple sources of interference, some more obvious than others. For instance, interference can occur while trying to actively maintain items in memory by requiring the completion of a secondary task at the same time, such as in complex memory span tasks (Conway et al., 2005). Interference can also occur proactively, when memory items from previous trials interfere with memory items on the current trial (Kane & Engle, 2000; Lustig et al., 2001). Interference can even occur as a result of intrusive and off-task thoughts (McVay & Kane, 2010). Given this executive attention account of working memory capacity, it would be expected that even nonselective visual arrays would depend on the executive attention system to reduce interference from previous trials or from intrusive and off-task thoughts. We will now consider evidence for the role of attention control in nonselective and selective visual arrays tasks.
Attention Control in Nonselective Visual Arrays
First, most studies assessing individual variability in visual arrays performance include set-sizes exceeding the average capacity-limit of three to four items. From a pure storage capacity interpretation, low and high-capacity individuals should be similarly impacted by larger set-sizes. If k merely represents storage capacity independent of controlled processing, then k scores should plateau at their maximum limit for all subjects. In a large sample (N = 495), Fukuda et al. (2015) examined the change in k scores from a set-size of 4 to a set-size of 8. Whereas the mean k score was slightly lower for a set-size of eight, the variability in mean k scores nearly doubled. The main reason for this increased variability was that low-capacity subjects performed much worse on set-size eight compared with set-size four, whereas high-capacity subjects showed only a small difference in performance on set-size eight.
The variability in performance decrements at larger set-sizes is more readily explained within an attentional control framework. Fukuda et al. (2015) suggest that upon the initial presentation of a target array, there is a global attentional capture to all of the elements comprising the array. This capture becomes overwhelming at large set-sizes since not all items can be stored in working memory, and controlled processing is required to reorient attention to only a manageable subset of items. High-capacity individuals engage these control processes more quickly and effectively, leading to fairly stable performance across larger set-sizes. For low-capacity individuals, however, the ineffective execution of controlled processing causes a performance decrement at larger set-sizes.
To explore this interpretation further, Fukuda et al. (2015) increased the duration for which the target array was presented. Consistent with their controlled processing explanation, only low-capacity subjects benefited from the longer exposure. High-capacity individuals already effectively reorient their attention during the encoding phase, and therefore show no benefit from the extra time. This suggests that low-capacity individuals are unable to effectively engage controlled processing unless given more time do so and therefore show lower k scores even on nonselective visual arrays tasks. These results corroborate those from Fukuda and Vogel (2011), where low-capacity individuals were much slower at disengaging from attention capture than high-capacity subjects on a variant of a visual arrays task. Therefore, although these results are difficult to reconcile from a pure storage capacity interpretation of nonselective visual arrays performance, they do follow naturally from an attention control explanation.
In addition, there may be other aspects of attention control at play in visual arrays task besides dealing with larger set-sizes. Shipstead and Engle (2013) manipulated the length of the intertrial interval (ITI; the delay between the probe for trial n and the target for trial n + 1) and interstimulus interval (ISI; the delay period between target array and probe array for the same trial). They assumed that shorter ITIs would create more proactive interference. Consistent with this prediction, the correlation between working memory capacity and nonselective visual arrays capacity, k, was highest when the ITI was short and ISI was long. This makes sense, given the executive attention view of working memory capacity. Nonselective visual arrays performance showed a strikingly different relationship with fluid intelligence, which was most strongly related to k capacity scores with long ITIs and long ISIs. This finding suggests that high fluid intelligence individuals took advantage of the longer ITI to reduce proactive interference from previous trials (cf., Shipstead et al., 2016). This study provides some evidence that even the nonselective visual arrays tasks do not reflect a pure measure of storage capacity but also reflect individual differences in reducing interference.
Finally, asserting that individual differences in attention control are a determining factor in nonselective visual arrays capacity scores is consistent with theoretical accounts of other working memory capacity measures (see Shipstead et al., 2014). For instance, in complex working memory span tasks there is a long retention interval during which a secondary task is performed. In the nonselective visual arrays tasks, the retention interval is very short and there is no explicit interference or distractors. Given these differences, it would be expected that nonselective visual arrays would provide a more pure measure of storage capacity in working memory and complex-span tasks would reflect more active maintenance and interference reduction (i.e., controlled processing). The differences between these measures of working memory capacity have likely given face-validity to the interpretation of the nonselective visual arrays as a pure measure of visual working memory capacity. If this were the case, then it would be expected that complex-span measures of working memory capacity would be more highly related to tasks that measure the control of attention than would nonselective visual arrays. To the contrary, Shipstead et al. (2015) found that a nonselective visual arrays factor contributed unique variance to an attention control factor (i.e., antisaccade, Stroop, & flanker tasks) above and beyond complex-span measures of working memory capacity. Therefore, despite the face-validity of the visual arrays as a pure measure of storage capacity, there is evidence which suggests that individual variability in visual arrays performance reflects processes related to controlled processing in nonmemory based attention tasks.
Attention Control in Selective Visual Arrays
Even though the selective visual arrays have more face-validity to the involvement of attention control, these tasks are also typically considered as relatively pure measures of visual storage capacity. However, there are physiological and behavioral evidence that are more consistent with an attention control interpretation. A commonly used EEG signature in visual arrays tasks is the contralateral delay activity. It is obtained in selective visual arrays tasks in which participants are cued to only attend to either the left or right side of the target array and is characterized by a negative slow-wave event related potential (ERP) on the contralateral (opposite) side of the brain as attended items. As the number of memory items presented in the target array increases, so should arousal, effort, or task difficulty; however contralateral delay activity reaches a maximum at around three to four items, mirroring the capacity indicated by behavioral indices such as the k score (Vogel & Machizawa, 2004). This provides evidence that contralateral delay activity is sensitive to the number of items stored in visual working memory (Feldmann-Wüstefeld et al., 2018). Fukuda et al. (2015) observed a similar contralateral ERP response across larger set-sizes for both low and high-capacity subjects (as indexed by k score values). However, they also observed that low-capacity subjects showed an increase in ipsilateral (corresponding to the side with irrelevant items) ERP response with increasing set-size, but high-capacity subjects did not. This suggests that low-capacity individuals stored irrelevant items from the uncued side of the display, whereas high-capacity individuals effectively filtered out the irrelevant items. Therefore, in selective visual arrays tasks, attention control may determine k scores because failing to sort the irrelevant items would lead to a lower k score.
Additionally, Vogel, McCollough, et al. (2005) assessed whether high- and low-capacity individuals (as determined by k scores) were equally capable of selectively attending elements of a target array. To do so, they manipulated the set-size and number of irrelevant items in a selective visual arrays task in which participants had to respond to the orientation of a probed rectangle, but only in the target color (red (dark gray) or blue (light gray)). A cue before the target array presentation indicated whether to attend to red (dark gray) or blue (light gray) rectangles. There were three conditions (a) a two-item array with no distractors (e.g., two red (dark gray) rectangles), (b) a two-item array with two distractors (e.g., two red (dark gray) rectangles and two blue (light gray) rectangles), and (c) a four-item array with no distractors (e.g., four red (dark gray) rectangles). To the extent that an individual effectively ignores distractors, the contralateral delay activity for the first two conditions should be equivalent, because both are of set-size two. To the extent that an individual does not effectively ignore distractors and stores them in working memory, the contralateral delay activity for the second and third conditions should be equivalent, since both have four total items in the display. High-capacity individuals exhibited the former pattern, whereas low-capacity individuals exhibited the latter.
These studies converge on the interpretation that, for selective visual arrays tasks, high-capacity individuals are those who can effectively ignore irrelevant items in the target array. Low-capacity individuals cannot ignore irrelevant items and tend to store the irrelevant items in working memory, diminishing available capacity. Based on the different pattern of contralateral delay activity as a function of whether or not items were successfully selected, Vogel et al. (2005) concluded that control-led processes were an important determinant of which items are stored in visual working memory, and thereby one’s visual working memory capacity. Several other EEG investigations indicate that filtering efficiency in selective visual arrays is sensitive to the effects of sleep deprivation (Drummond et al., 2012), aging (Jost et al., 2011), and Parkinson’s disease (Lee et al., 2010), further supporting to the notion that selective visual arrays are affected by attentional processes.
Finally, domain-generality is a core feature of how attention control has been conceptualized (cf., Kane et al., 2004), and therefore is an important benchmark for viewing the selective visual arrays as reflecting attention control.2 Shipstead and Yonehiro (2016) found that selective visual arrays performance reflects two factors, one domain-general and one visuospatial. The domain-general factor correlated with reasoning ability, regardless of whether reasoning occurred in the visual or verbal domains. The visuospatial factor, meanwhile, was strictly related to visual reasoning. Shipstead et al. (2014) also found that, despite their heavily visuospatial nature, selective visual arrays performance correlated with verbal retrieval (i.e., secondary memory; see Unsworth & Engle, 2007). Moreover, this retrieval ability also partially mediated the correlation between selective visual arrays performance and fluid intelligence. Therefore, there is evidence that selective visual arrays performance reflects a unique domain-general resource beyond static visual storage capacity.3
The Current Study
The evidence reviewed so far calls into question the interpretation that visual arrays tasks only reflect individual differences in visual storage capacity and is therefore a relatively pure measure of capacity in visual working memory. With two diverging interpretations of what abilities the visual arrays task reflects (visual storage capacity and/or attention control), we find ourselves confronted with two questions, both theoretical and practical in nature:
Are visual arrays tasks more closely related to storage-based measures of working memory capacity or resistance-to-interference aspects of attention control?
Does the nature of the visual arrays task (i.e., nonselective or selective) influence which constructs that type of visual arrays task primarily reflects?
Four potential answers follow these questions:
All visual arrays tasks primarily reflect visual storage capacity related to working memory capacity measures.
All visual arrays tasks primarily reflect differences in controlled attention independent of storage.
All visual arrays tasks reflect both visual storage capacity and differences in controlled attention to the same degree.
The degree to which a visual array task primarily reflects visual storage capacity or controlled attention is task-(selection) dependent.
To answer these questions, we conducted three sets of analyses on four entirely separate data sets collected over an 11-year period by different groups of graduate students, postdoctoral researchers, and undergraduate research personnel. Common to all these data sets are measures of working memory capacity (mainly but not exclusively defined by complex span tasks), attention control (specifically the antisaccade, flanker, and Stroop tasks), and at least one visual arrays task. Each set of analyses was intended to identify whether various visual arrays tasks were more closely related to working memory capacity or attention control. These analyses were all novel; none of these results have been previously published in journals nor presented at conferences. The same set of analyses was used on each of the four data sets.
We began with an exploratory factor analysis. Exploratory factor analysis is a data-driven approach to defining the latent factor structure in a set of tasks. If the visual arrays task is more closely related to working memory capacity, then they should load more with those tasks than measures of attention control. Alternatively, if visual arrays measures are more closely related to measures of attention control, then they should load more consistently with measures of attention control than measures of working memory capacity.
Next, we conducted a structural equation model in which working memory capacity and attention control latent factors uniquely predict individual differences in visual arrays k capacity scores. This allowed us to assess whether individual differences in k capacity scores from the visual arrays tasks reflects primarily storage capacity, attention control, or both.
Finally, we conducted additional structural equation models to further understand the processes underlying individual differences in visual arrays performance. In two separate models, we tested (a) whether visual arrays predicts attention control over and above of working memory capacity and (b) whether visual arrays predicts working memory capacity over and above attention control.
Method
We analyzed data from four different data sets collected over 11 years (the total number of subjects are listed for each set of analyses, and the full population details for each data set are outlined in the Appendix A and Appendix B). In each data set, there were three or more measures of working memory capacity, three measures of attention control, and at least one visual arrays task. Participants for each data set were recruited from the Georgia Institute of Technology, surrounding universities, and the greater Atlanta community. At minimum, half of our population was recruited from outside of Georgia Tech to provide a sample which reflected a diverse background of socioeconomic status, race, gender, and education.
The studies from which the data are reported were all approved by the Georgia Institute of Technology IRB. The data were collected under four independent protocol numbers/titles. They are listed from most recent to oldest. (a) Protocol #H17116 “Understanding the nature of attention control,” (b) #H16322 “Differentiating between working memory capacity and fluid intelligence (Part II),” (c) #H12234 “The relationships among working memory tasks and their relations to fluid intelligence and higher-order cognition,” and (d) #H11309 “Relating the scope and control of attention within working memory.”
Visual Arrays Tasks
Four variations of the visual arrays task were used (see Figure 1). Two tasks explicitly involved a selection component (VA-color-S and VA-orient-S) which required participants to ignore specific distractor items (either those of a given color or those on one side of the array). Two did not (VA-color and VA-orient). The category listed after VA is the dimension on which individuals are making a yes/no change evaluation (i.e., did a box change color, or did a bar change orientation). In calculating the dependent variable, k, N was always defined as the number of valid target-items on a screen. Thus, if ten target/items are presented, but five are to-be-ignored, then N equaled 5. Two tasks required test-takers to decide whether a relevant characteristic of any item in the display had changed (VA-orient and VA-color-S). For these tasks, k was calculated using the whole display correction of Pashler (1988): k = N × (%hits − %false alarms/[1 − %false alarms]). Two tasks required test-takers to respond as to whether a relevant characteristic of a probed item had changed (VA-color and VA-orient-S). For these tasks, k was calculated using the single probe correction of Cowan et al. (2005): k = N × (%hits + %correct rejections −1). In all cases, k was first computed for each set size, and then the set sizes were averaged. In all tasks, participants responded via keypress. Change and no-change trials occurred with 50% probability and, along with set sizes, were randomly distributed. Items were presented within a silver 19.1° × 14.3° visual field at a distance of roughly 45 cm. Items were separated from one another by at least 2° and were all at least 2° from a central fixation point.
Figure 1. Examples of Visual Arrays Tasks Used in the Present Study.
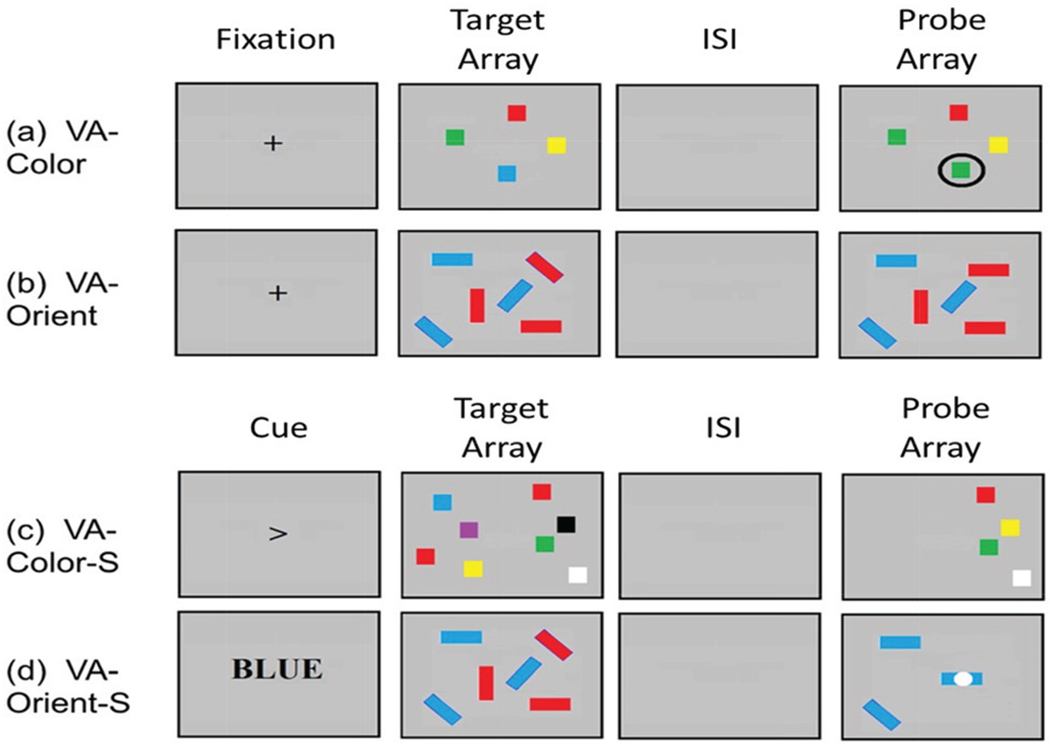
Note. Visual arrays, with either a color change judgment or an orientation change judgment. The labeling of each task is based on the following criteria: VA-[the category of the change-based judgment] - [is there a selection component]. The two potential judgements for change are color or orientation (i.e., has a square changed color, or has a bar changed orientation. The selection components direct an individual to a pay attention to half of the array (either one side [the right or left subset] or one subset of stimuli [blue (light gray) or red (dark gray) bars only]). Going forward, (a) and (b) will be referred to as nonselection versions as all array information is needed for retrieval. In versions (c) and (d) the –S indicates a selection component as evidenced by the cue in lieu of a fixation. (a) and (b) begin with fixation, which is followed by a target array of to-be-remembered items, then an interstimulus interval (ISI). For (a) the test-taker must indicate whether the encircled box has changed colors. For (b) the test-taker must indicate whether any box has changed its orientation. (c) and (d) begin with a cue that indicates which information will be relevant. This is followed by the array of to-be-remembered items, along with distractors. After the ISI, the probe array appears with only cued information presented. For (c) the test-taker must indicate whether any box has changed color. For (d) the test-taker must indicate whether the box with the white dot has changed orientation. VA = visual arrays. See the online article for the color version of this figure.
VA-Color (Color Judgment Task)
Array sets were four, six, or eight colored blocks. Possible colors included white, black, red (dark gray), yellow, green, blue (light gray), and purple. Arrays were presented for 250 ms followed by a 900 ms ISI. Participants responded as to whether or not one circled item had changed color. Twenty-eight trials of each set size were included; 14 were no-change, 14 were change (see Figure 1a).
VA-Orient (Orientation Judgment Task)
The orientation judgment task was based on one of the conditions used by Luck and Vogel (1997). Arrays consisted of five or seven colored bars, each of which was either horizontal, vertical, or slanted 45° to the right or left. Participants needed to judge whether any bar had changed orientation. Colors included red (dark gray) and blue (light gray) and did not change within a trial. Forty trials of each set size were included; 20 were no-change and 20 were change (see Figure 1b).
VA-Color-S (Selective Color Judgment Task)
This task was based on Experiment 2 from Vogel, Woodman, et al. (2005) and was speeded relative to other tasks. Each trial began with a left- or right-pointing arrow at the center of a computer monitor indicating which side of the array participants needed to focus on. This arrow was presented for 100 ms, followed by a 100-ms interval. Next, two equally sized arrays of colored blocks were presented on the right and left sides of the screen for 100 ms. The array on each side contained either four, six, or eight items. After a 900-ms delay, the boxes on the side indicated by the arrow reappeared. Participants indicated whether any of these relevant boxes had changed color. Twenty-eight trials of each set size were included; 14 were no-change, 14 were change, and they occurred equally often on the right and left sides of the screen (see Figure 1c).
VA-Orient-S (Selective Orientation Judgment Task)
This task was based on the first experiment of Vogel, Woodman, et al. (2005). Single probe report was used. Each trial began with presentation of a word, either RED (dark gray) or BLUE (light gray) indicating the color of the items to be attended (the selection instruction) for 200 ms, followed by a 100-ms interval. Next, 10 or 14 bars were presented for 250 ms. Half of all bars were printed in the to-be-attended color, that is set size was either five or seven. Following a 900-ms delay, only the to-be-attended bars returned. The critical item was identified at test by a white dot superimposed on one of the bars. Test takers judged whether the orientation of the item indicated by the dot had changed, relative to the initial presentation. No other changes could occur within the display. Forty trials of each set size were included; 20 were change, and 20 were no-change (see Figure 1d).
Working Memory Capacity Tasks
Operation Span (OSpan; Kane et al., 2004; Turner & Engle, 1989)
This task required subjects to remember a series of letters presented in alternation with simple math equations which they were required to solve. On each trial, subjects first solved a simple math equation where they decided whether a solution was correct (e.g., “[2 × 2] + 1 = 5) or not (e.g., “[3 × 4] − 3 = 8”) followed by the presentation of a single letter. After a variable set size, participants attempted to recall the letters in their correct serial order. There were a total of 14 trials (two blocks of seven trials), set-sizes ranged from three to eight,4 and each set-size occurred twice (once in each block). The dependent variable was the partial span score, which is the total number of letters recalled in proper serial position (Conway et al., 2005).
Symmetry Span (SymSpan; Unsworth et al., 2009)
This task required subjects to judge whether remember a 16 × 16 matrix of black and white squares was symmetrical about the vertical midline and while memorizing the locations of a red (dark gray) square in a 4 × 4 matrix. Participants first made the symmetry judgment and were then presented with the to-be-remembered spatial location. This alternation continued until a variable set-size of spatial locations had been presented. There was a total of 12 trials (two blocks of six trials), set-sizes ranged from two to seven, and each set-size occurred twice (once in each block). The dependent variable was the partial span score, which is the total number of square locations recalled in proper serial position.
Rotation Span (RotSpan; Kane et al., 2004)
This task required subjects to solve a mental rotation task in which they had to mentally rotate and decide whether a letter was mirror reversed or not. Afterward, subjects were presented with a to-be-remembered arrow with a specific direction (eight possible directions; the four cardinal and four ordinal directions) and specific size (small or large).This alternation continued until a variable set-size of arrows had been presented, at which point participants attempted to recall the arrows in their correct serial order. There as a total of 12 trials (two blocks of six trials), set-sizes ranged from two to seven, and each set-size occurred twice (once in each block). The dependent variable was the partial span score, which is the total number of arrows recalled in proper serial position.
Running Letter Span (Broadway & Engle, 2010)
The automated running letter span presented a series of five to nine letters and required participants to remember the last three to seven. Participants were informed of how many items they would need to remember at the beginning of a block of three trials. Blocks were randomly presented. There as a total of 15 trials. Items were presented for 300 ms followed by a 200-ms pause.
Running Spatial Span (Harrison et al., 2013)
The running-spatial-span task was identical to the running-letter-span task, except that matrix locations on a 4 × 4 matrix were the to-be-remembered stimuli.
Rapid Running Digit Span (Cowan et al., 2005)
The automated running digit span presented a series of 12–20 digits and required participants to remember the last 6. Participants performed 18 critical trials. Digits were presented at the rate of four per second via headphones.
Attention Control Tasks
Antisaccade (Hallett, 1978; Hutchison, 2007; Kane et al., 2001)
Subjects saw a central fixation cross lasting a random amount of time between 2,000–3,000 ms followed by an alerting tone for 300 ms. After the alerting tone, an asterisk appeared for 300 ms at 12.3° visual angle to the left or the right of the central fixation followed immediately by a target “Q” or an “O” for 100 ms on the opposite side of the screen from the asterisk. The location of the asterisk and target letter were both masked for 500 ms by “##.” The subject’s goal was to avoid looking at the asterisk and instead look to the opposite side of the screen to catch the target “Q” or “O.” Subjects had as much time as needed to respond to which letter appeared by pressing the associated key on the keyboard. Subjects completed 72 trials, with trial-by-trial feedback for 500 ms following each response, and then a 1,000-ms waiting period until the fixation cross appeared again to indicate a new trial was beginning. The dependent variable was the number of correctly identified target letters.
Arrow Flanker (RT Flanker; Eriksen & Eriksen, 1974)
Subjects were presented with a target arrow in the center of the screen pointing left or right along with two flanking arrows on both sides. The flanking arrows were either all pointing in the same direction as the central target (congruent trial; for example, ← ← ← ← ←) or all in the opposite direction (incongruent trial; for example, ← ← → ← ←)5. The subject was asked to indicate direction the central arrow was pointing by pressing the “z” (left) or “/” (right) key. These keys had the words LEFT and RIGHT taped onto them to assist with response mapping. A total of 144 trials were administered; 96 congruent and 48 incongruent, with a randomized 400- to 700-ms ITI. The dependent variable was the flanker interference effect: the RT cost of the incongruent trials calculated by subtracting each subject’ s mean RT on congruent trials from their mean RT on incongruent trials, excluding inaccurate trials.
Color Stroop (RT Stroop; Stroop, 1935)
Subjects were shown the word “red (dark gray),” “green,” or “blue (light gray)” in red (dark gray), green, or blue (light gray) font. The words were either congruent with the color (for example, red (dark gray)), or incongruent with the color (for example, blue (light gray)). The subject’s task was to indicate which color the word was printed by pressing the “1,” “2,” or “3” key on the number pad. To assist with response mapping, the keys had a piece of paper of the corresponding color taped onto them. A total of 144 trials were administered; 96 congruent and 48 incongruent, with a randomized 400-to 700-ms ITI and a 5,000-ms response deadline. The dependent variable was the Stroop interference effect: the RT cost of the incongruent trials calculated by subtracting each subject’s mean RT on congruent trials from their mean RT on incongruent trials, excluding inaccurate trials.
Data Analysis
For each data set we ran the same general set of analyses. Before analysis we removed subjects that had missing data on any of the visual arrays tasks. We used the same criteria across all data sets and each visual array task. See Appendix A Table A1 for task reliabilities, and Appendix B Tables B1–B4 for correlation tables.
Exploratory Factor Analysis
For each data set we included all the working memory capacity, attention control, and visual arrays tasks that were available from that study. We used an oblimin rotation, and the number of factors was determined by taking into account numerous methods; the Kaiser criterion of eigenvalues greater than 1, scree plot, and parallel analysis.
Structural Equation Models
For our primary analyses we used structural equation modeling. For each data set we conducted four models to better understand the processes related to individual differences in visual arrays performance. (a) We conducted a structural equation model with both working memory capacity and attention control latent factors as correlated predictors of each visual arrays task. Rather than forming a latent visual arrays factor (Data Sets 3 and 4 only) we used each visual arrays task as a separate dependent variable. This model allowed us to assess the unique contributions of working memory capacity and attention control to individual differences in k capacity scores at the task level for each visual array task.6 In Data Sets 3 and 4, we essentially have an experimental manipulation where the only difference between task versions (besides the judgment dimension) is whether there is a selective component or not. This allowed us to evaluate whether the degree to which a visual arrays task primarily reflects visual storage capacity or controlled attention is dependent on there being a selective component. (b) We tested whether visual arrays performance can predict attention control over and above working memory capacity and (c) whether visual arrays performance can predict working memory capacity over and above attention control. For these models, in Data Sets 3 and 4, we formed latent nonselective and selective visual arrays factors. (d) Finally, we also conducted additional structural equation models testing whether working memory capacity and processing speed mediate the relationship between attention control and visual arrays. For processing speed, we used the mean RT from Flanker and Stroop congruent trials. This allowed us to assess whether speed of processing is a viable explanation for any attention control and visual arrays relationship. This is important because no task or latent factor is “process pure.” Therefore, we can rule out potential confounding factors by establish incremental validity.
Analyses were conducted in R statistical software (R Core Team, 2018). The R package psych (Revelle, 2018) was used to conduct the exploratory factor analysis. The R package lavaan (Rosseel, 2012) was used for all structural equation models, treatment of missing values was set to full-information maximum likelihood. Where necessary, we statistically compared models using the Bayes Information Criteria (BIC) to provide an estimate of the Bayes Factor value for the probability of one model over another (Bollen et al., 2014; Wagenmakers, 2007).
Results
Data Set 1
Data Set 1 consisted of OSpan, SymSpan, and RotSpan for working memory capacity; antisaccade, flanker, and Stroop for attention control; and VA-orient-S for visual arrays. There was a total of 397 subjects, with no more than 5% missing data for any one task. The data analyzed in this study was part of a larger data collection sample that occurred from 2017–2018. The following link has a summary of the larger data collection procedure and a reference list of all publications to come out of this data collection sample with information on which tasks were used for each publication: https://osf.io/yc48s/.
Exploratory Factor Analysis
We conducted an exploratory factor analysis using principal axis factoring with two factors and an oblimin rotation (Table 1). Two factors were specified because two factors had eigenvalues greater than 1, both scree plot and parallel analysis suggested that the number of factors was two. The OSpan, SymSpan, and RotSpan loaded most strongly onto the first factor (a working memory capacity factor). The VA-orient-S, antisaccade, flanker, and Stroop all loaded most strongly onto the second factor (an attention control factor). However, the flanker loading was poor for both factors, each under .30. The two factors moderately correlated at r = .6. The exploratory factor analysis supported the interpretation of VA-orient-S as being more similar to attention control measures.
Table 1.
Data Set 1 – Exploratory Factor Analysis With Oblimin Rotation
| Factor |
||
|---|---|---|
| Variable | F1 | F2 |
| OSpan | 0.74 | −0.13 |
| SymSpan | 0.76 | 0.06 |
| RotSpan | 0.62 | 0.24 |
| VA-orient-S | 0.12 | 0.57 |
| Antisaccade | 0.08 | 0.59 |
| Flanker | 0.02 | −0.29 |
| Stroop | 0.20 | −0.43 |
Note. VA = visual arrays.
Structural Equation Models
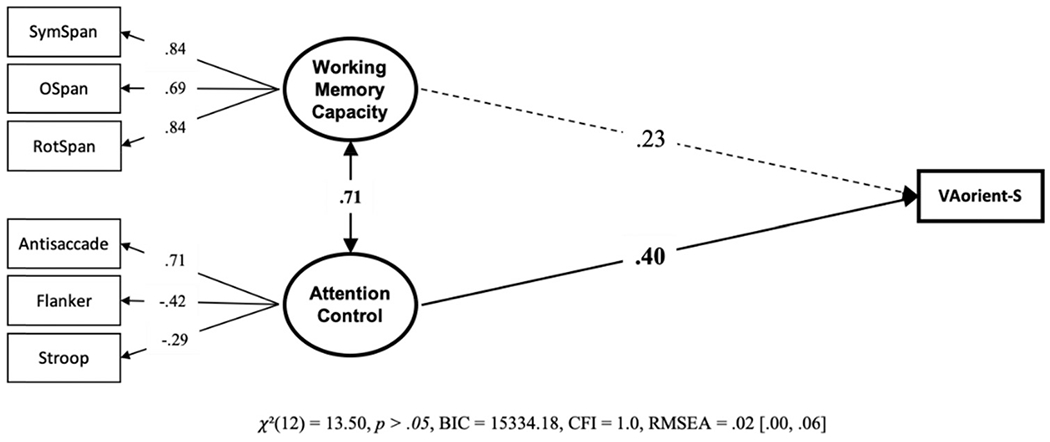
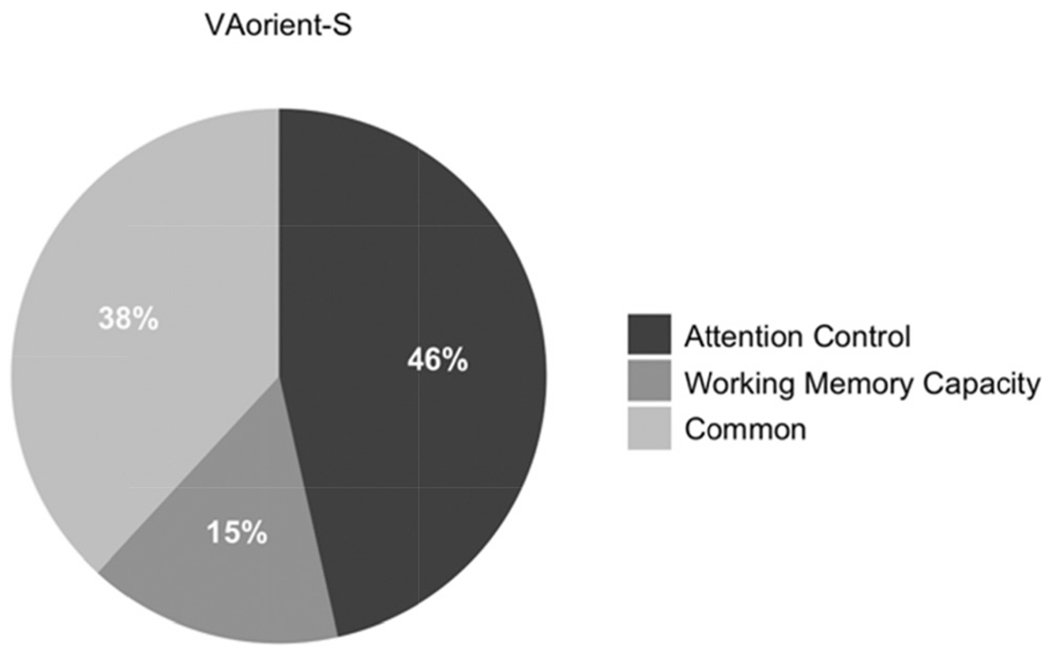
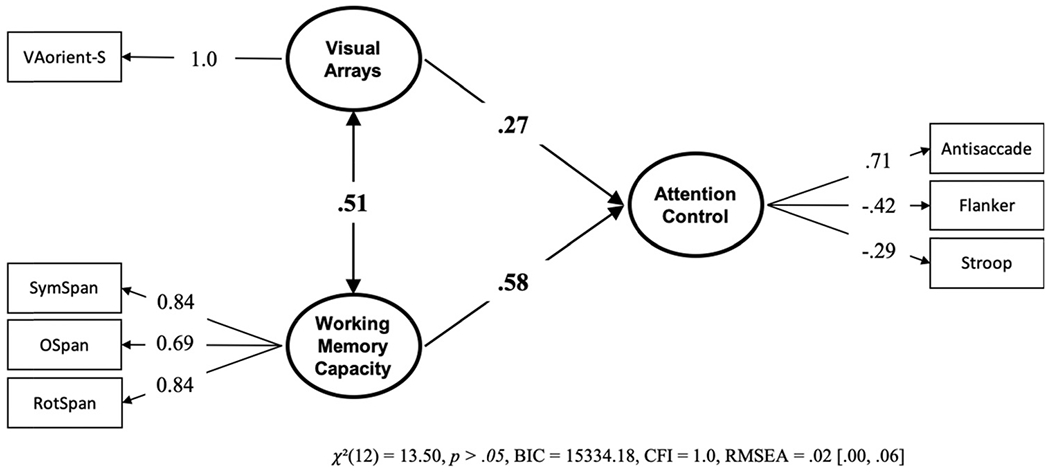
Our primary question of interest is; are individual differences in visual arrays k capacity score explained more by differences in working memory capacity, attention control, or both? To answer this, we conducted a structural equation model with working memory capacity and attention control predicting k capacity scores on the VA-orient-S task (see Figure 2). Attention control, but no working memory capacity, uniquely predicted k capacity scores in the VA-orient-S task. We compared this model with a “null” model in which the working memory capacity – VA-orient-S path was set to zero. The “null” model was 10.63 times more likely; BF01 = 10.63, P(H0 | Data) = .91. We also compared this model with a model where the predictive paths for attention control and working memory capacity were constrained to equality. This model was also preferred, being 6.03 times more likely than the freely estimated model, BF01 = 6.03, P(H0 | Data) = .86. We thus find evidence both for the hypothesis that the predictive path from working memory capacity is statistically unnecessary and that it does not reliably differ from the significant predictive path from attention control. To gain clarity on this apparent contradiction, we compared the Bayes Factors of the two constrained models. This reveals that the null model is slightly preferred over the model with equality constraints, BF01 = 1.76, P(H0 | Data) = .64, although the magnitude of the preference appears negligible. Figure 3 visualizes the contributions of working memory capacity and attention control relative to the 41% of explained variance in VA-orient-S.
Figure 2. Structural Equation Model From Data Set 1 With the Unique Relationships of Working Memory Capacity and Attention Control to VA-Orient-S.
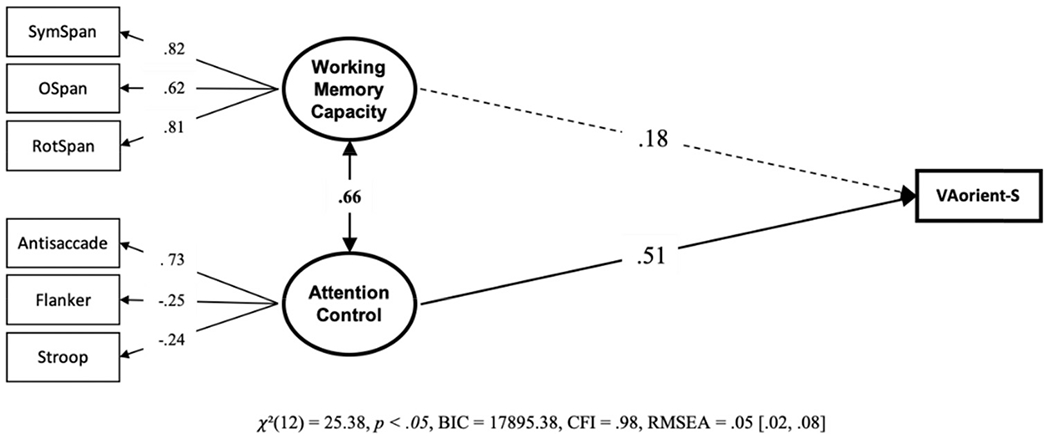
Note. Bold numbers indicate significant values based on p < .05. VA = visual arrays.
Figure 3. Pie Chart Representing the Contributions Uniquely From Working Memory Capacity/Attention Control and Common Variance in the 41% of Explained Variance in VA-Orient-S.
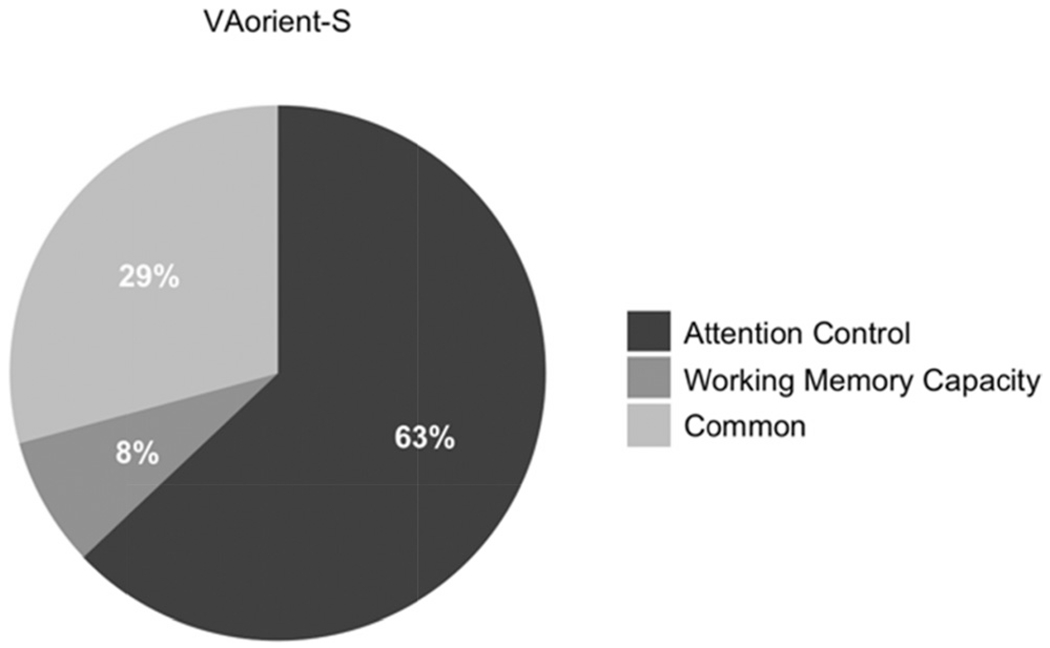
Note. VA = visual arrays
To better understand what individual variability in visual arrays performance reflects, we tested the relationship of unique variance in visual arrays with working memory capacity and attention control.7 First, we tested whether visual arrays capacity can predict attention control uniquely from working memory capacity. If variance in visual arrays reflects nothing more than the capacity of working memory, then visual arrays should not predict unique variance in attention control. However, the model (see Figure 4) does show that VA-orient-S uniquely predicts attention control above and beyond working memory capacity, uniquely accounting for 21.2% of the variance in attention control (based on squaring the path value of .46 between visual arrays and attention control). Furthermore, this freely estimated model is strongly preferred over a model where the selective visual arrays task and working memory tasks are loaded on a single predictive factor, BF01 = 119,593.70, P(H0 | Data) > .999. This is consistent with the notion that individual differences in selective visual arrays performance represents more than just the number of items stored in visual working memory.
Figure 4. Structural Equation Model From Data Set 1 With the Unique Relationships of Visual Arrays and Working Memory Capacity to Attention Control.
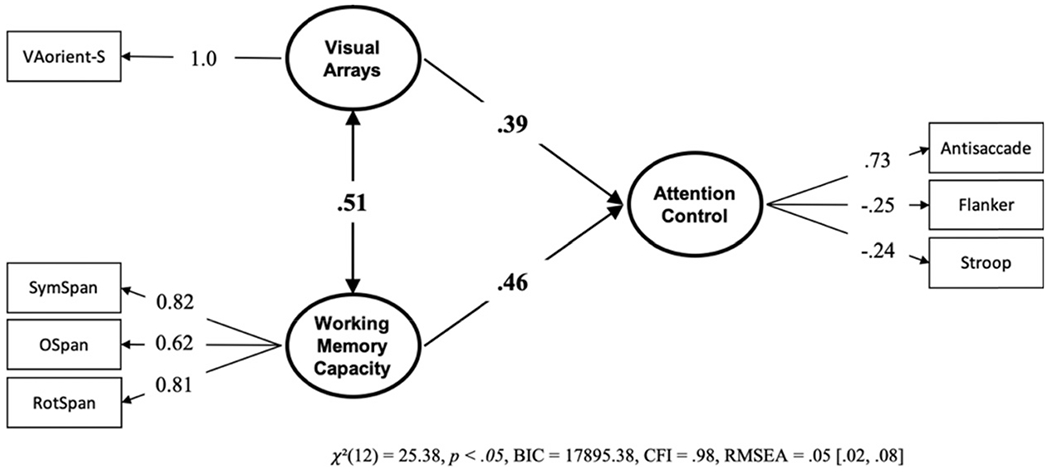
Note. Bold numbers indicate significant values based on p < .05. VA = visual arrays.
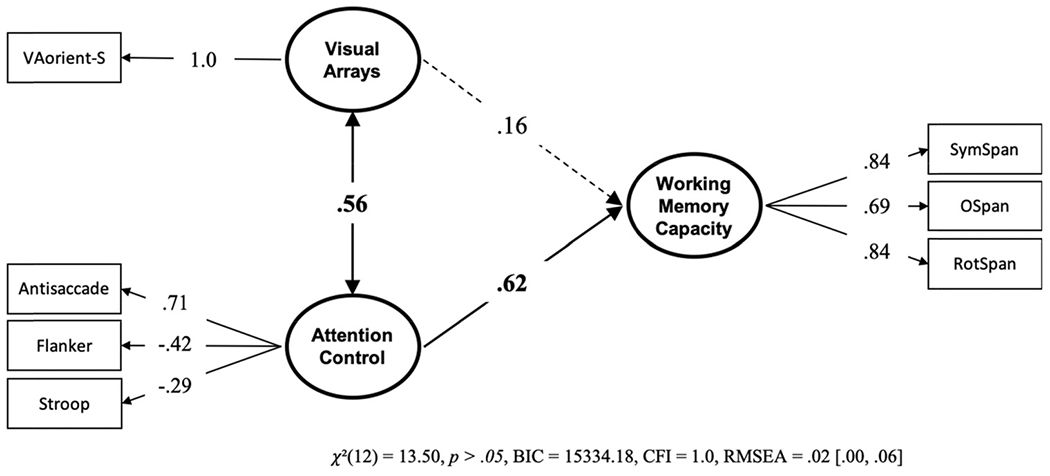
Next, we conducted a model with visual arrays and attention control uniquely predicting working memory capacity. If storage capacity, independent of attention control, is reflected in visual arrays capacity score, then it would be expected to predict working memory capacity uniquely from attention control. The model (see Figure 5) suggests that this is not the case. The k capacity score on VA-orient-S did not predict working memory capacity above and beyond attention control, and a model with a null predictive path from the selective visual arrays factor was preferred over a model where this path was estimated, BF01 = 10.633, P(H0 | Data) = .914.8 However, a model with the two predictive paths were constrained to equality was also preferred to the freely estimated model, BF01 = 3.279, P(H0 | Data) = .766, indicating that the two paths are not reliably different from one another.
Figure 5. Structural Equation Model From Data Set 1 With the Unique Relationships of Visual Arrays and Attention Control to Working Memory Capacity.
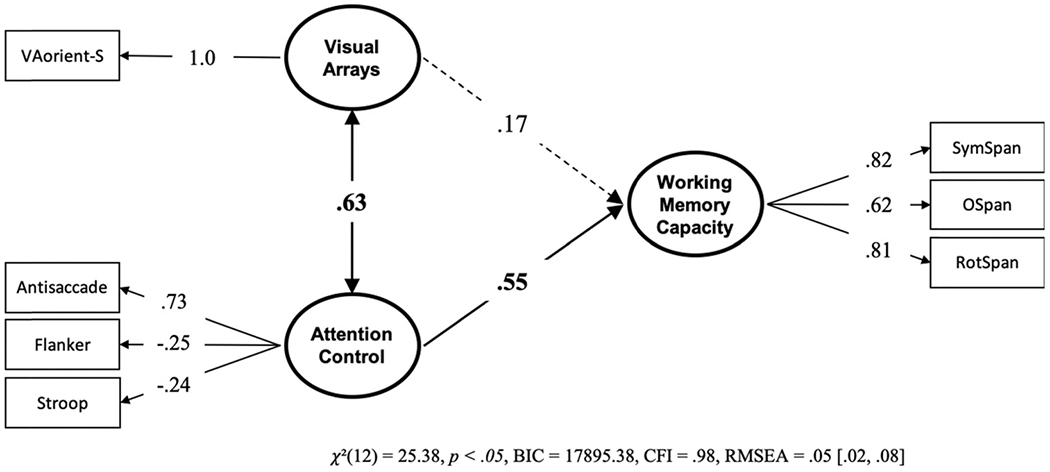
Note. Bold numbers indicate significant values based on p < .05. VA = visual arrays.
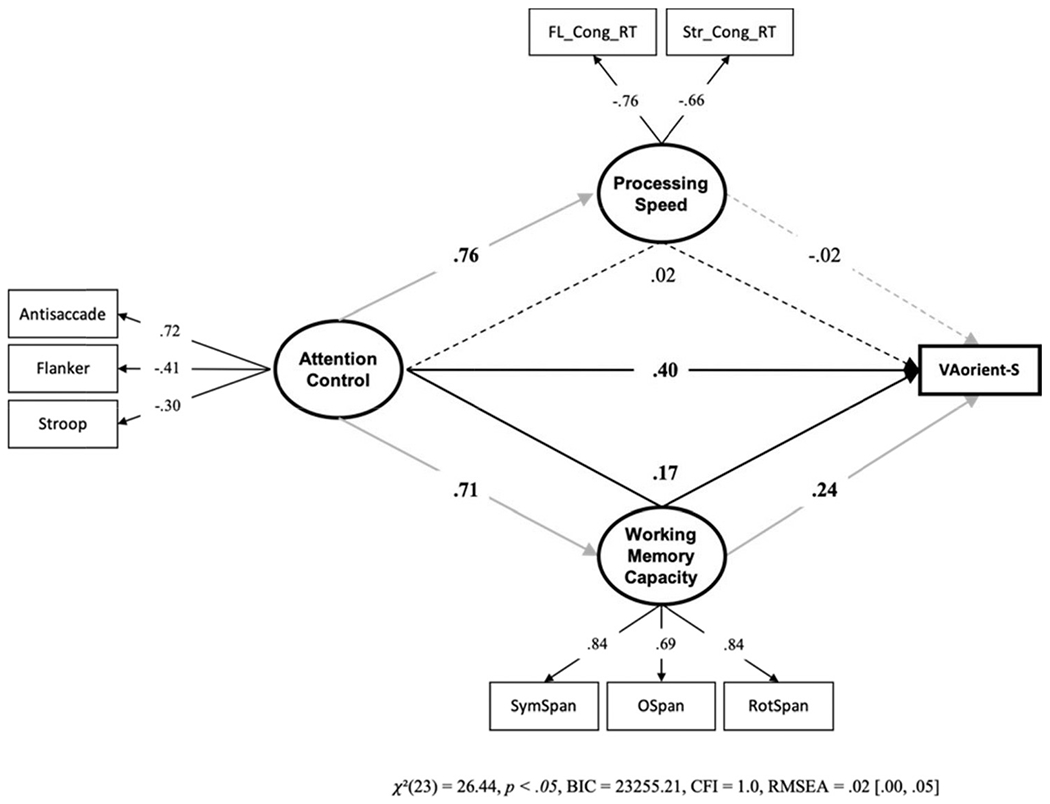
We conducted a final structural equation model to rule out processing speed as a potential confounding factor. We tested whether processing speed and working memory capacity can mediate the attention control – VA-orient-S relationship (see Figure 6).9 Working memory capacity only partially mediated the path from attention control to VA-orient-S; processing speed did not mediate the path from attention control to VA-orient-S. Therefore, the direct effect of attention control on individual differences in k capacity scores cannot be attributed to processing speed or working memory capacity.
Figure 6. Structural Equation Model With Processing Speed and Working Memory Capacity Mediating the Attention Control – VA-Orient-S Relationship.
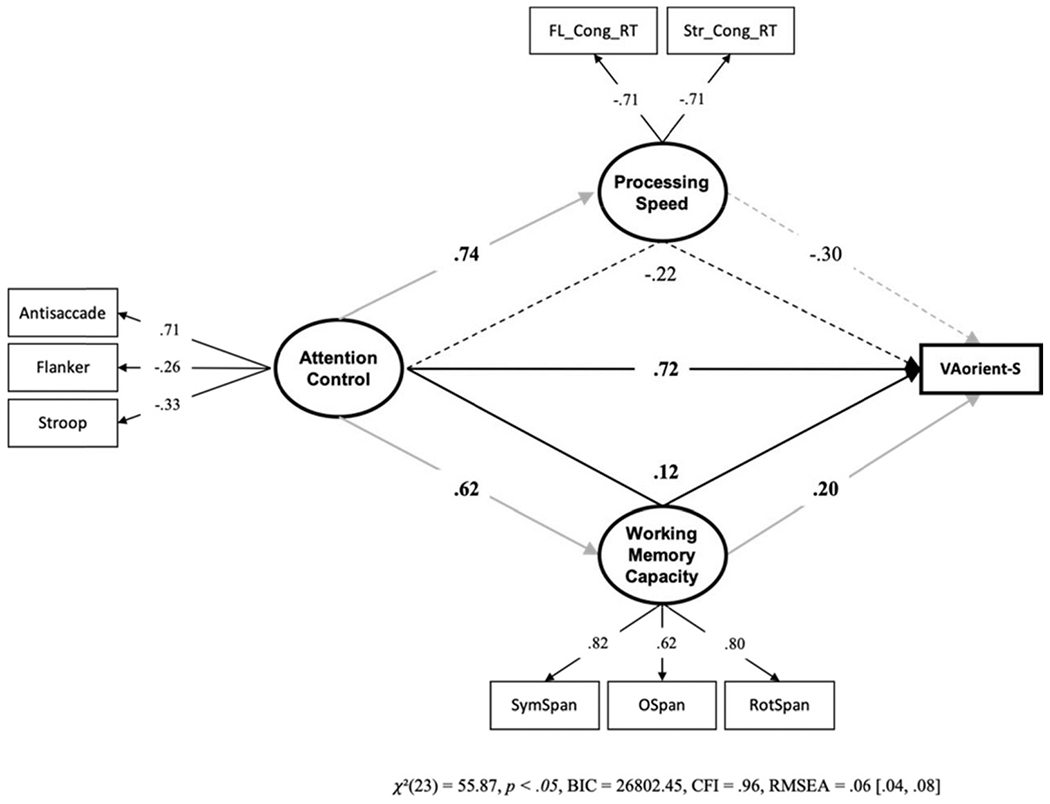
Note. FL_Cong_RT = mean reaction time on congruent trials in the Flanker task; Str_Cong_RT = mean reaction time on congruent trials in the Stroop task. We multiplied the FL_Cong_RT and Str_Cong_RT values by −1 to reflect shorter reaction times as higher processing speed. To make this evident in the figure, the loadings onto the processing speed factor are shown to be negative. Dotted lines represent paths that were not statistically significant, p > .05. VA = visual arrays. Bold numbers indicate significant values based on p < .05. The indirect effect through working memory capacity, but not processing speed, was statistically significant.
In summary; the exploratory analysis revealed that the selective visual arrays loaded more so with measures of attention control than working memory capacity and the structural equation model revealed that only attention control, not working memory capacity, uniquely predicted variance in VA-orient-S. Likewise, after controlling for working memory capacity, VA-orient-S predicted additional variance in attention control. Finally, processing speed was not able to account for the attention control – VA-orient-S relationship. Overall, the results from Data Set 1 suggest that the VA-orient-S task shares substantial variance with attention control independently from working memory capacity. These findings are consistent with studies by Fukuda and Vogel (2009, 2011) showing an important role for attention control processes in visual arrays performance.
Data Set 2
The tasks used in Data Set 1 and Data Set 2 were very similar. There were some differences in the number of trials in the flanker and Stroop tasks. Also, the Stroop task in Data Set 2 included neutral trials (though they were excluded from the present analysis). Other than that, there were no major differences in the administration of the tasks. In Data Set 2 there were a total of 342 subjects with no more than 7% missing values for any one task. These data were collected from 2015–2017 and are associated with the following publications: Draheim et al. (2018) and Tsukahara et al. (2016). The same set of analyses were conducted for this data as in Data Set 1.
Exploratory Factor Analysis
We conducted an exploratory factor analysis using principal axis factoring with two factors and an oblimin rotation (Table 2). Two factors were specified because scree plot and parallel analysis suggested that the number of factors was two, although only one factor had an eigenvalue greater than 1. The OSpan, SymSpan, and RotSpan loaded most strongly onto the first factor (a working memory capacity factor). The antisaccade and flanker all loaded most strongly onto the second factor (an attention control factor). The Stroop task had poor loadings on both factors, each under .20. The VA-orient-S, meanwhile, loaded very similarly on both factors. The two factors correlated moderately at r = .6. The exploratory factor analysis supports the view that the VA-orient-S task shares considerable variance with putative measures of attention control independent of working memory capacity but relates to both constructs to a similar degree.
Table 2.
Data Set 2 – Exploratory Factor Analysis With Oblimin Rotation
| Factor |
||
|---|---|---|
| Variable | F1 | F2 |
| OSpan | 0.71 | −0.03 |
| SymSpan | 0.84 | −0.03 |
| RotSpan | 0.80 | 0.06 |
| VA-orient-S | 0.31 | 0.33 |
| Antisaccade | −0.01 | 0.78 |
| Flanker | −0.04 | −0.37 |
| Stroop | −0.16 | −0.13 |
Note. VA = visual arrays.
Structural Equation Models
We conducted a structural equation model with working memory capacity and attention control predicting k capacity scores on the VA-orient-S task (see Figure 7). Only attention control uniquely predicted variance in the VA-orient-S task. We compared this model to a “null” model in which the working memory capacity – VA-orient-S path was set to zero. The “null” model was 6.07 times more likely; BF01 = 6.07, P(H0 | Data) = .86. However, as in Data Set 1, the predictive paths did not reliably differ and a model where both paths were constrained to equality was preferred to the freely estimated model, BF01 = 13.79, P(H0 | Data) = .93. Comparing the “null” and “equal” models, the latter was slightly preferred, BF10 = 2.26, P(H1 | Data) = .70. Figure 8 visualizes the relative contributions of working memory capacity and attention control to the 34% of explained variance in VA-orient-S.
Figure 7. Structural Equation Model From Data Set 2 With the Unique Relationships of Working Memory Capacity and Attention Control to VA-Orient-S.
Note. VA = visual arrays. Bold numbers indicate significant values based on p < .05.
Figure 8. Pie Chart Representing the Contributions Uniquely From Working Memory Capacity/Attention Control and Common Variance Between the Two in the 34%o of Explained Variance in VA-Orient-S.
Note. VA = visual arrays.
Next, we tested whether visual arrays capacity can predict attention control uniquely from working memory capacity. If variance in visual arrays reflects nothing more than the capacity of working memory, then visual arrays should not predict unique variance in attention control. However, the model (see Figure 9) does show that VA-orient-S uniquely predicts attention control above and beyond working memory capacity. Furthermore, the predictive factors could not be combined without loss of fit, and the depicted model was strongly preferred, BF10 = 25.81, P(H1 | Data) = .96. This is further evidence that individual differences in VA-oreint-S performance represents more than just the number of items stored in visual working memory.
Figure 9. Structural Equation Model From Data Set 2 With the Unique Relationships of Visual Arrays and Working Memory Capacity to Attention Control.
Note. VA = visual arrays. Bold numbers indicate significant values based on p < .05.
We then conducted a model with visual arrays and attention control uniquely predicting working memory capacity. If storage capacity, independent of attention control, is reflected in visual arrays capacity score, then it would be expected to predict working memory capacity uniquely from attention control. The model (see Figure 10) suggests that this is not the case. The k capacity score on VA-orient-S did not predict working memory capacity above and beyond attention control. Furthermore, a “null” model where the predictive visual arrays path was set to zero was preferred to the freely estimated model, BF01 = 6.06, P(H0 | Data) = .86.
Figure 10. Structural Equation Model From Data Set 2 With the Unique Relationships of Visual Arrays and Attention Control to Working Memory Capacity.
Note. VA = visual arrays. Bold numbers indicate significant values based on p < .05.
Additionally, and contrary to Data Set 1, the freely estimated model was slightly preferred to a model with the predictive paths constrained to equality, BF10 = 2.09, P(H1 | Data) = .68. Thus, for Data Set 2, estimating the predictive path from visual arrays to working memory capacity was statistically superfluous. Put differently, attention control accounted for the relationship between selective visual arrays and working memory capacity in this model.
Finally, we conducted a structural equation model to rule out processing speed as a potential confounding factor.10 We tested whether processing speed and working memory capacity can mediate the attention control – VA-orient-S relationship (see Figure 11). Working memory capacity only partially mediated the path from attention control to VA-orient-S; processing speed did not mediate the path from attention control to VA-orient-S. Therefore, the effect of attention control on individual differences in k capacity scores cannot be attributed to processing speed or working memory capacity.
Figure 11. Structural Equation Model With Processing Speed and Working Memory Capacity Mediating the Attention Control – VA-Orient-S Relationship.
Note. FL_Cong_RT = mean reaction time on congruent trials in the Flanker task; Str_Cong_RT = mean reaction time on congruent trials in the Stroop task. We multiplied the FL_Cong_RT and Str_Cong_RT values by −1 to reflect shorter reaction times as higher processing speed. To make this evident in the figure, the loadings onto the processing speed factor are shown to be negative. Dotted lines represent paths that were not statistically significant, p > .05. VA = visual arrays. Bold numbers indicate significant values based on p < .05. The indirect effect through working memory capacity, but not processing speed, was statistically significant.
Overall, the results replicated what was found in Data Set 1. However, the unique relationship of attention control was numerically weaker than in Data Set 1. Converging evidence from all four models suggested that VA-orient-S reflects attention control to a greater degree than storage capacity. The exploratory analysis was not as clean as in Data Set 1, but it still suggested that VA-orient-S wanted to load with measures of attention control (no memory storage demand) just as much with working memory capacity tasks (high memory storage demand). The structural equation models showed that attention control, but not working memory capacity, uniquely predicted variance in k capacity scores on the VA-orient-S task. The total variance in VA-orient-S was less than in Data Set 1, and more of the variance explained was contributed by common variance between attention control and working memory capacity. On the one hand, our theoretical position identifies much of the variability in working memory capacity with individual differences in attention control (Engle et al., 1999). On the other hand, we hesitate to endorse this explanation for the pattern of results in Data Set 2 because the current data are not conducive to a stringent test and disconfirmation of that hypothesis. Finally, processing speed was not able to account for the attention control-visual arrays relationship.
Data Set 3
The tasks in Data Set 3 are more diverse than in Data Sets 1 and 2. There were three different versions of the visual arrays task; VA-color, VA-orient, VA-orient-S. There were also two additional measures of working memory capacity, the Running Spatial and Running Digit Spans. The attention control tasks were the same as those used in Data Set 2. Because there were additional visual arrays tasks, we were able to test additional models to better understand what factors might affect the degree to which visual arrays performance reflects visual working memory or attention control. In Data Set 3, there were 568 subjects and no more than 2% missing values on any task. These data were collected from 2011–2013 and are associated with the following publications: Draheim et al. (2016, 2018), Martin et al. (2019), and Shipstead et al. (2016).
Exploratory Factor Analysis
We conducted an exploratory factor analysis using principal axis factoring with two factors and an oblimin rotation (Table 3). Only one factor had an eigenvalue greater than 1, scree plot suggested two factors, and parallel analysis suggested three factors. When a model with three factors was specified only the Stroop task loaded onto the third factor, so we decided on a two-factor model. The OSpan, SymSpan, RotSpan, RunSpatial, and RunDigit loaded most strongly onto the first factor (a working memory capacity factor). The visual arrays task all loaded strongly onto the second factor. The antisaccade loaded about equally on both factors. The flanker and Stroop did not load well onto either factor, each loading under .30. The two factors were highly correlated, r =.8.
Table 3.
Data Set 3 – Exploratory Factor Analysis With Oblimin Rotation
| Factor |
||
|---|---|---|
| Variable | F1 | F2 |
| OSpan | 0.80 | −0.11 |
| SymSpan | 0.72 | 0.06 |
| RotSpan | 0.76 | 0.02 |
| RunSpatial | 0.49 | 0.37 |
| RunDigit | 0.57 | 0.11 |
| VA-color | 0.06 | 0.72 |
| VA-orient | −0.08 | 0.81 |
| VA-orient-S | 0.11 | 0.69 |
| Antisaccade | 0.33 | 0.31 |
| Flanker | −0.07 | −0.18 |
| Stroop | −0.28 | −0.04 |
Note. VA = visual arrays.
Structural Equation Models
We conducted a structural equation model with working memory capacity and attention control predicting k capacity scores on each visual arrays task (see Figure 12). The nonselective visual arrays task, VA-color and VA-orient, were uniquely predicted by only working memory capacity. The selective visual array task, VA-orient-S, was uniquely predicted only by attention control. We tested this model against a “null” model in which all the nonsignificant paths were set to zero. The “null” model was greater than 1,100 times more likely than the freely estimated model, BF01 = 1115.78, P(H0 | Data) > .99. We also tested a model where each predictive path from attention control and working memory capacity were constrained to equality (within task) across the three visual arrays task types. This model was also strongly preferred to the freely estimated model, BF01 = 3596.19, P(H0 | Data) > .99. Thus, the magnitude of prediction for working memory capacity versus attention control cannot be said to vary across task type.
Figure 12. Structural Equation Model From Data Set 3 With the Unique Relationships of Working Memory Capacity and Attention Control to Each Visual Arrays Task.
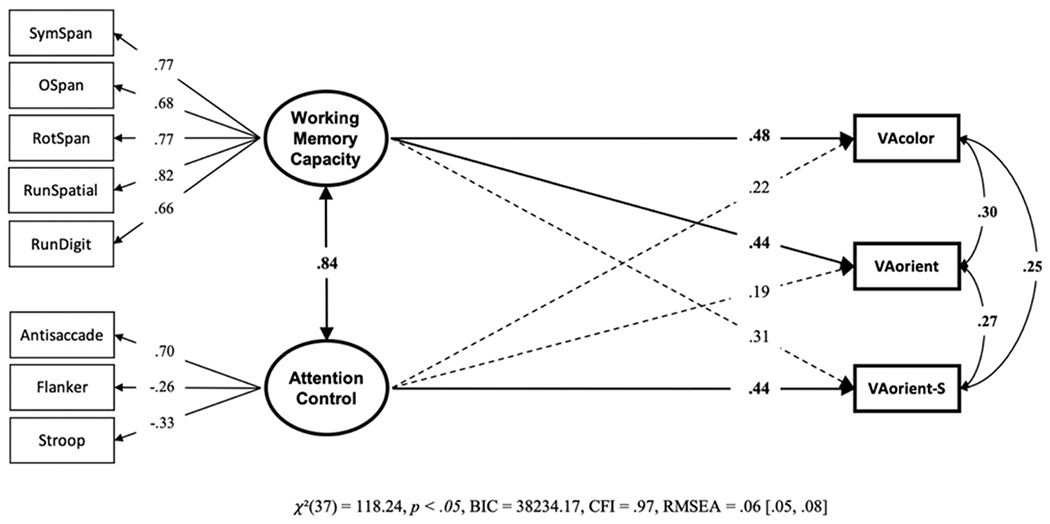
Note. VA = visual arrays. Bold numbers indicate significant values based on p < .05.
Keeping the important caveat that the magnitude of the working memory capacity and attention control predictive paths do not reliably differ for selective versus nonselective visual arrays, the pattern of added incremental validity favors the interpretation that attention control adds prediction over and above working memory capacity only for selective visual arrays, but not nonselective visual arrays. For nonselective visual arrays, the pattern is reversed. This is not to say that attention control does not play any role in nonselective visual arrays tasks, nor that individual differences in working memory capacity are orthogonal to selective visual arrays performance. There is, after all, a considerable amount of common variance explaining performance in each task type. However, it is consistent with the notion that having a selective component in the visual arrays task increases attention control demands. The unique and common contributions of working memory capacity and attention control relative to the amount of explained variance in each visual array task is illustrated in Figure 13. In the model, working memory capacity and attention control explained 45% of variance in the VA-color task, 37% of variance in the VA-orient task, and 52% of variance in the VA-orient-S task.
Figure 13. Pie Chart Representing the Contributions Uniquely From Working Memory Capacity/Attention Control and Common Variance Between the Two.

Note. The model explained 45% of variance in the VA-color task, 37% of variance in the VA-orient task, and 52% of variance in the VA-orient-S task. VA = visual arrays.
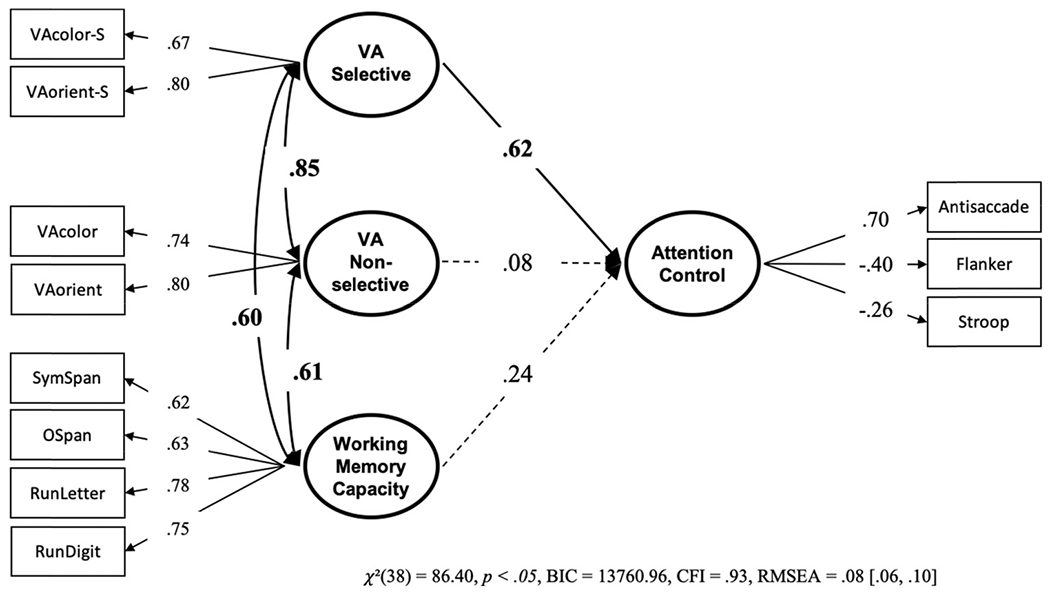
As discussed in the Introduction, there may be differences between the different versions of visual arrays. The VA-color and VA-orient do not require selecting/or filtering out any items in the display, whereas the VA-color-S and VA-orient-S do. Vogel and colleagues have shown that effectively filtering out distractor items from target items in the visual arrays tasks differentiates high capacity and low capacity individuals (Vogel & Machizawa, 2004; Vogel, McCollough, et al., 2005). To test for a differentiation between the selective and nonselective visual arrays tasks we conducted a structural equation model with VA-orient-S loading onto its own VA Selective factor and VA-color and VA-orient loading onto a VA nonselective factor. The results of the model (see Figure 14) showed that working memory capacity and the VA selective factor uniquely predicted attention control, but the VA nonselective factor did not, although the path values do not reliably differ, BF01 = 22.43, P(H0 | Data) = .96. This suggests that the selective filtering in the visual arrays task predicts attention control over and above the nonselective versions.
Figure 14. Structural Equation Model From Data Set 3 Testing the Unique Relationships of VA Selective, VA Nonselective, and Working Memory Capacity to Attention Control.
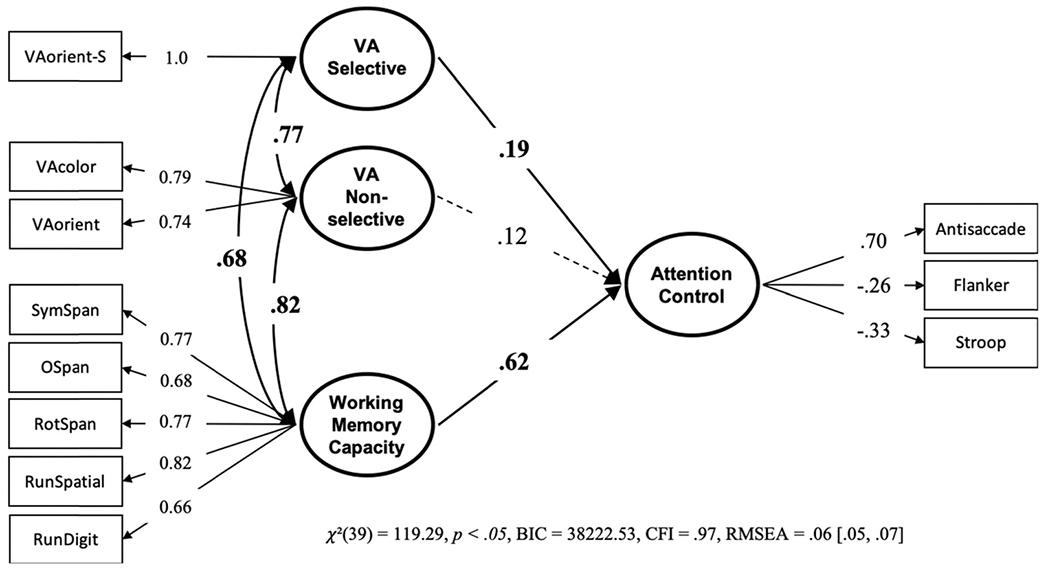
Note. VA = visual arrays. Bold numbers indicate significant values based on p < .05.
Next, we conducted a model with visual arrays and attention control uniquely predicting working memory capacity. If storage capacity, independent of attention control, is reflected in visual arrays capacity score then it would be expected to predict working memory capacity uniquely from attention control. Again, we split the visual arrays task into selective and nonselective factors. The model showed that only attention control and nonselective visual arrays were uniquely predictive of working memory capacity (see Figure 15). Setting the nonsignificant path from selective visual arrays to zero did not harm model fit, BF01 = 22.83, P(H0 | Data) = .96. We also tested a model where the predictive paths for the two visual arrays factors were constrained to be equal. While this constrained factor was slightly preferred over the freely estimated model, BF01 = 2.66, P(H0 | Data) = .73, adding this constraint did decrease model fit according to a chi-square test, Δχ2(1) = 4.39, p = .04.11
Figure 15. Structural Equation Model From Data Set 3 Testing the Unique Relationships of VA Nonselective, and Attention Control to Working Memory Capacity.
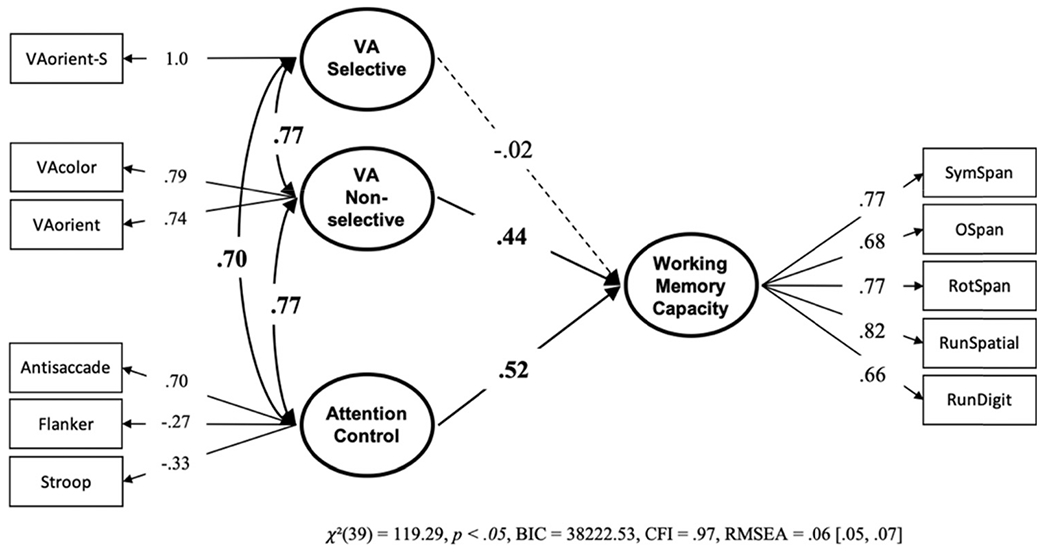
Note. VA = visual arrays. Bold numbers indicate significant values based on p < .05.
Data Set 4
In Data Set 4 there were a total of 215 subjects, each with less than 3% missing data for any task. These data were collected from 2009–2010 and are related to the following publications: Shipstead et al. (2012, 2014, 2015).
The tasks in Data Set 4 are similar to those in Data Set 3. The main difference is that there was an additional visual arrays task for a total of four versions of the task; VA-color, VA-orient, VA-color-S, and VA-orient-S. This is the only data set that has more than one of each visual array version (selective and nonselective), which allows us to more strongly test differentiation between these versions. However, the sample size is not very large. Data Set 4 also does not contain the Rotation Span and Running Spatial Span, but it does include the Running Letter span.
Exploratory Factor Analysis
In an exploratory factor analysis (Table 4), three factors had an eigenvalue greater than 1, scree plot suggested two factors, and parallel analysis suggested three factors. The visual arrays tasks and antisaccade preferred to load onto the first factor. The RunLetter and RunDigit preferred to load onto their own factor (the second factor) and the OSpan, SymSpan, and Stroop preferred to load together. The flanker did not load well onto any factor, each loading under .30. The factors correlated from .4–.5 with each other. Although the exploratory factor analysis suggests the running span and complex span tasks can be treated as separate factors, for the sake of comparison with the previous data sets we conducted further models combing the tasks onto a single working memory capacity factor. Note that we did run the analysis with them separated but the overall interpretation of the models remained the same.
Table 4.
Data Set 4 – Exploratory Factor Analysis With Oblimin Rotation
| Factor |
|||
|---|---|---|---|
| Variable | F1 | F2 | F3 |
| OSpan | −0.08 | 0.31 | 0.52 |
| SymSpan | 0.20 | 0.04 | 0.64 |
| RunLetter | −0.05 | 0.69 | 0.23 |
| RunDigit | 0.13 | 0.82 | −0.08 |
| VA-color | 0.64 | 0.04 | 0.06 |
| VA-orient | 0.72 | 0.05 | −0.02 |
| VA-color-S | 0.67 | −0.02 | −0.01 |
| VA-orient-S | 0.74 | 0.04 | −0.01 |
| Antisaccade | 0.54 | 0.01 | 0.13 |
| Flanker | −0.29 | 0.10 | −0.21 |
| Stroop | −0.16 | 0.22 | −0.38 |
Note. VA = visual arrays.
Structural Equation Models
We conducted a structural equation model with working memory capacity and attention control predicting k capacity scores on each visual array task (see Figure 16). Only attention control, not working memory capacity, uniquely predicted individual differences in visual arrays k capacity scores, regardless of the type of visual arrays task. We compared this model against a “null” model in which all the nonsignificant working memory capacity paths were set to zero, the “null” model was strongly preferred, BF01 = 13,889.01, P(H0 | Data) > .99. However, as with Data Set 3, constraining paths from working memory capacity and attention control to equality for each visual array task did not worsen model fit, BF01 = 2098.20, P(H0 | Data) > .99. However, of the constrained models, the “null” model was preferred, BF01 = 6.62, P(H0 | Data) = .87. The unique and common contributions of working memory capacity and attention control relative to the amount of explained variance in each visual array task is illustrated in Figure 17. In the model, working memory capacity and attention control explained 35% of variance in the VA-color task, 34% of variance in the VA-orient task, 35% of variance in the VA-color-S task, and 42% of variance in the VA-orient-S task. The model (see Figure 16) is also explaining most of the variance between the visual arrays tasks (this is indicated by the residual correlations on the far right of the model).
Figure 16. Structural Equation Model From Data Set 4 With the Unique Relationships of Working Memory Capacity and Attention Control to Each Visual Array Task.
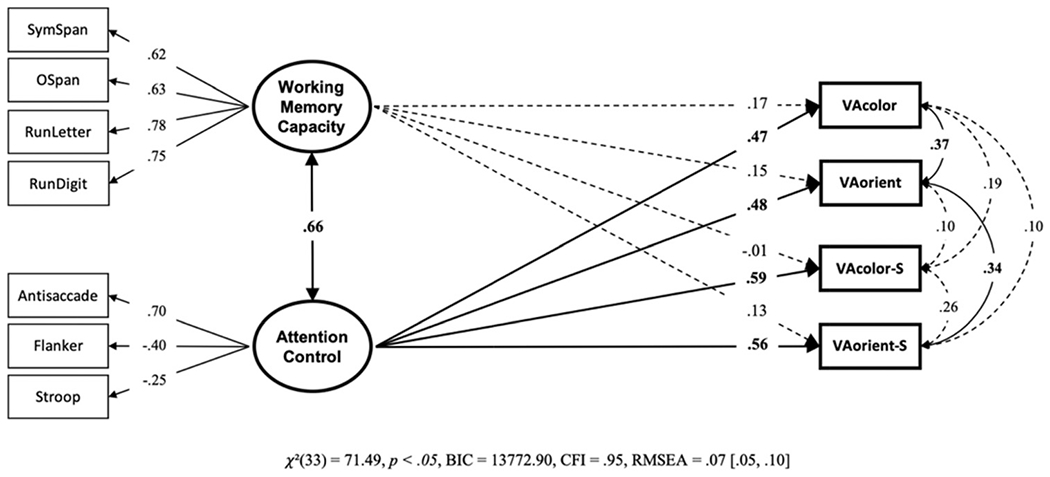
Note. VA = visual arrays. Bold numbers indicate significant values based on p < .05.
Figure 17. Pie Chart Representing the Unique Contributions From Working Memory Capacity/Attention Control and Common Variance Between the Two.
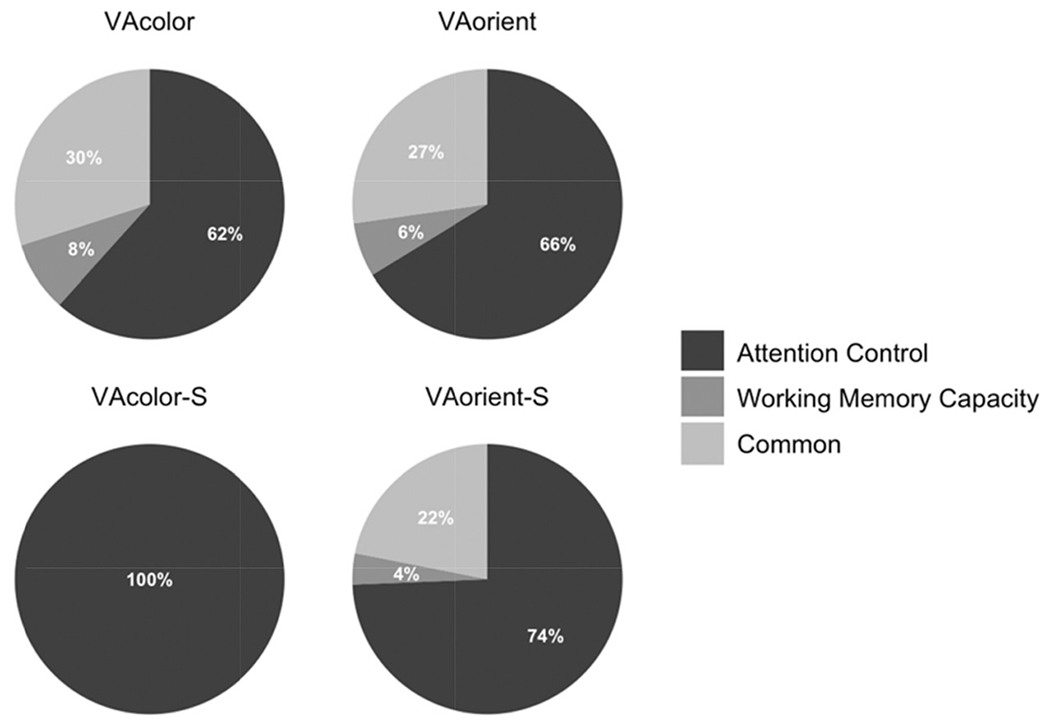
Note. The model explained 35% of variance in the VA-color task, 34% of variance in the VA-orient task, 35% of variance in the VA-color-S task, and 42% of variance in the VA-orient-S task. VA = visual arrays.
The VA-color and VA-color-S both contained trials with set-sizes four, six, and eight. This allowed us to compare the effects of set-size and selective components of the task. We conducted a structural equation model with the set-size and selective components separated out as; VA-color-4, VA-color-6, VA-color-8, VA-color-S-4, VA-color-S-6, and VA-color-S-8 (see Figure 18). Overall, the model does not suggest much of an effect of set-size; in fact, working memory capacity and attention control are slightly more related to visual arrays performance at smaller set-sizes—contrary to a purely storage account of visual arrays. The largest path numerically, from attention control to visual arrays occurred at set-size 4 with a selective component. Admittedly post hoc, this does make sense given an attention control view of visual arrays. Successful filtering of nonrelevant items on a set-size of four (eight total items in the display) can maximally reduce the load from eight items to four items. Given that performance tends to peak at around four items, successful filtering of nonrelevant items can lead to optimal performance. Compare this to successful filtering of nonrelevant items on a set-size of eight (16 total items in the display). Successful filtering, at most, would lead to reducing the load from 16 to 8. While this would likely improve performance, one would still be under non-optimal load regardless of whether there is a selective component to the task. Therefore, although attention control would be involved in performance at lower and higher set-sizes, the impact on performance would be greatest at lower set-sizes. However, this would have to be studied more systematically in future studies to draw any strong conclusions from this pattern of findings.
Figure 18. Structural Equation Model From Data Set 4 With the Unique Relationships of Working Memory Capacity and Attention Control to Visual Arrays Broken Down Into Set-Sizes and Selective Components.
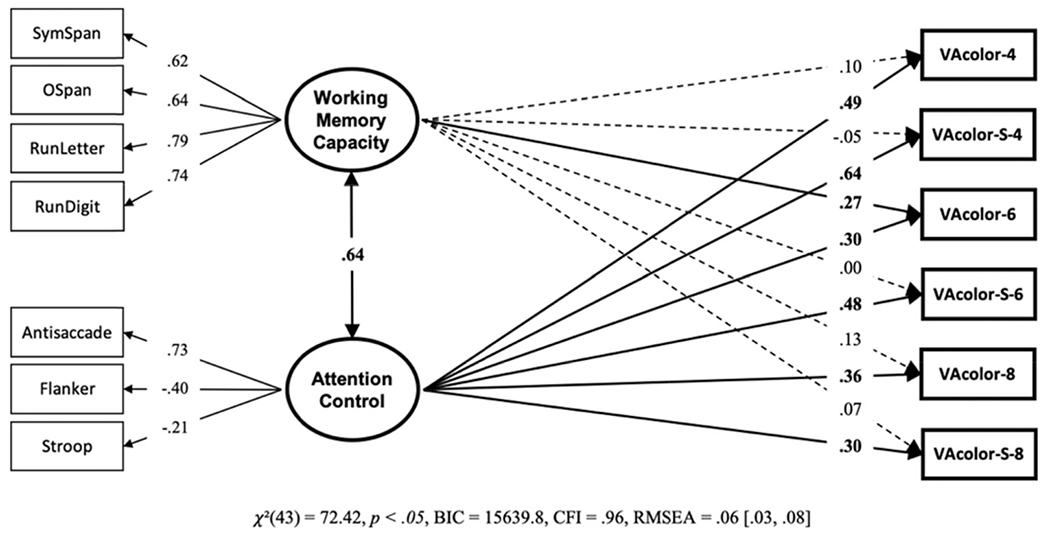
Note. VA = visual arrays. Bold numbers indicate significant values based on p < .05.
Next, we tested the same structural equation models as in Data Set 3 in which we separated out selective and nonselective factors. In this Data Set, however, we had two task indicators on the selective factor instead of just one. The model (see Figure 19) showed that only the selective visual arrays latent factor had unique variance predictive of attention control. Meanwhile, the nonselective visual arrays and working memory capacity factors were not uniquely related to attention control. setting all nonsignificant paths to zero did not decrease model fit, and this model was preferred to the freely estimated one, BF01 = 40.61 P(H0 | Data) = .98. Further, while constraining the paths from the visual arrays factors to equality also did not harm model fit, BF01 = 8.67, P(H0 | Data) = .90, the “null” model was the preferred model, BF01 = 4.66, P(H0 | Data) = .82.
Figure 19. Structural Equation Model From Data Set 4 Testing the Unique Relationships of VA Selective, VA Nonselective, and Working Memory Capacity to Attention Control.
Note. VA = visual arrays. Bold numbers indicate significant values based on p < .05.
In a model in which selective and nonselective visual arrays are predicting working memory capacity, neither set of tasks uniquely predicted working memory capacity (see Figure 20). But note the path values for attention control and VA nonselective (.46 and .27, respectively). The nonsignificance of these path values could have had to do with power issues as this study only had 215 subjects. This is supported by the fact that the path values in Data Set 4 are similar to that in Data Set 3 (in which they were significant). This would support the conclusion that the nonselective visual arrays tasks do include storage capacity related variance that is independent of attention control. However, the selective visual arrays tasks may not.12
Figure 20. Structural Equation Model From Data Set 4 Testing the Unique Relationships of VA Selective, VA Nonselective, and Attention Control to Working Memory Capacity.

Note. VA = visual arrays. Bold numbers indicate significant values based on p < .05.
Summary
We began this project as an empirical test of the theoretical nature of visual arrays tasks. Specifically, we tested whether:
visual arrays tasks are more closely related to storage-based measures of working memory capacity or to resistance-to-interference aspects of attention control, and
the nature of the visual arrays task (i.e., non-selective or selective) influences which constructs that type of visual arrays task primarily reflects
To address these questions, we conducted a series of statistical tests across four independently collected data sets. The conservative interpretation of the overall pattern which emerged across all four data sets is that visual arrays tasks (as a collective) are at the very least not a pure measure of working memory capacity but are multiply determined in terms of attention control and working memory capacity. The more liberal interpretation is that visual arrays tasks will reflect attention control more so than working memory capacity when a selection component is included in the task. Our pattern of results suggests that whereas nonselective measures of visual arrays reflect some attention control properties in addition to storage properties of working memory capacity, selective visual arrays tasks reflect the ability to control and manipulate attention more so than nonselection versions. Although the archival nature of these data limits the ability to make causal interpretations, the body of results as a whole, and their consistent replication call into question the traditional interpretation of visual arrays tasks as measures of visual storage capacity. Results and implications are outlined below.
In all four data sets, the exploratory factor analyses showed that both nonselective and selective visual arrays tasks loaded onto a separate factor from accepted working memory capacity tasks, preferring to load with other attention control tasks, or at least with the antisaccade task (our most reliable measure of attention control). Model fit and parsimony were generally optimized when the selective visual arrays task was predicted by an attention control factor only (i.e., when the path from working memory capacity to visual arrays was set to zero), rather than by both attention control and working memory capacity, although these simultaneously estimated paths were not statistically different from one another. Furthermore, selective visual arrays tasks uniquely predicted attention control over and above working memory capacity and nonselective visual arrays. In contrast, nonselective visual arrays tasks uniquely predicted working memory capacity over and above attention control and selective visual arrays. These results suggest that attention control related variance is at least as predictive of selective visual arrays than is working memory capacity related variance, if not more so. This is not necessarily the case for nonselective visual arrays tasks.
Discussion
We have already outlined areas of support for the role of attention control in selective and nonselective visual arrays, including domain generality, set-size and timing manipulations, and neurophysiological data. We will not readdress that evidence here, but we would like to highlight a few additional interpretations that are particularly relevant to the overlap in storage and attention control processes in nonselective and selective visual arrays.
Generally speaking, we believe these results call into question the idea that visual arrays measures are strictly visuospatial storage tasks (Luck & Vogel, 1997). Our results echo other findings which initially broadened the interpretation of the nature of nonselective visual arrays tasks. Morey and Cowan (2004; see also Saults & Cowan, 2007), for example, found that when a high verbal load was added, nonselective visual arrays performance decreased. As they argued, maintaining the higher verbal load required central resources (see Baddeley & Hitch, 1974) and when these resources were occupied, less attention was available for visual arrays performance. This effect was apparent in the performance decrements. In other words, visual arrays performance seemed to be drawing on central resources rather than visual-specific working memory resources.
Because this research is archival in nature, we did not propose a specific mechanistic account of how attention control contributes causally to performance on selective visual arrays tasks, we find explanations offered by other researchers appealing. Fukuda et al. (2015) proposed that attention must be reoriented to only a subset of manageable items after an initial global capture to the overwhelming number of items in the display. Work by Emrich and Busseri (2015) suggests that the return from attention capture or reorientation toward the array is not the defining feature of performance on visual arrays tasks. Rather, contralateral delay activity preceding the array presentation and the subsequent engagement of the intention to filter was the primary indicator of performance. This preparatory interpretation also fits with work by Adams et al. (2015), which suggests that performance on the visual arrays can be considered in terms of a density function of attention deployed not only within trial but over the course of the session. These studies suggest that controlled processes for goal-maintenance and preventing lapses of attention also play an important role in visual arrays performance.
Limitations and Alternative Explanations
Although we have discussed many studies providing evidence for mechanisms of attention control in visual arrays performance, it is difficult to determine the extent to which individual variability is due to one process over another, because causal closure is nearly impossible to achieve (or to know whether it has been achieved). If we have failed to adequately measure one or more of our constructs of interest, this could potentially undermine the presented analyses. This was especially true of Data Sets 1 and 2 in which working memory capacity was defined solely by complex span measures. Although this is less of a concern for the other data sets, the possibility exists, nonetheless. Furthermore, although we would argue that selective visual arrays have strong face validity as indicators of attention control, face validity can also mislead us about what underlying processes are at play. This is perhaps especially true given that these results are explicitly interpreted within the context of the executive attention framework of working memory capacity. As such, it is important to consider possible explanatory alternatives.
A potential challenge to these results comes from models of working memory that do not require any kind of supervisory attention processes (and thus attention control) to account for differences in interference. One apparently competing framework to the one offered here proposes that the ability to flexibly make, break, and update arbitrary bindings between items in working memory accounts for many interference effects (Oberauer, 2002; Oberauer et al., 2007; Schubert & Rey-Mermet, 2019; Wilhelm et al., 2013). This perspective posits no explicit role for supervisory or controlled attention to form or remove bindings. One way this interpretation might account for performance on a trial of a selective visual arrays task resembles that of Fukuda et al. (2015) and proceeds thus: Upon the first presentation of a target array, all items within the array are bound together into a single memory representation. Individual differences in unbinding will determine the degree to which a person successfully removes nontarget items from the memory representation. Successfully (and rapidly) removing nontargets may improve change-detection accuracy by reducing memory storage demands and increasing the likelihood that memory targets will be successfully retrieved in time to respond to the test array.
We do not regard this binding account as problematic. In fact, we regard it as being potentially compatible with our own, provided that binding and unbinding are construed as capacity-limited control processes (Allen et al., 2014; Fukuda & Vogel, 2009, 2011; Fukuda et al., 2015; Martin et al., 2019; Rizio & Dennis, 2013; Shipstead et al., 2016; Wang et al., 2019; but see Allen et al., 2006). According to the executive attention account of working memory capacity, whereas individual differences in working memory represent the ability to form and maintain bindings, the role of executive attention is twofold in nature, both allowing for the creation of bindings as well as unbinding or disengaging from no longer relevant information. This unbinding aspect, which is present in the selection but absent in the nonselection visual arrays, would explain this difference between variance shared with and independent of working memory capacity (for a more thorough discussion on the functions of maintenance and disengagement as they relate to binding and unbinding of memory representations, see also Martin et al., 2019; Shipstead et al., 2016). The main difference between the executive attention and binding accounts seems to be a disagreement on whether this process of binding and unbinding is related to the control of attention (Shipstead et al., 2016).
Additionally, we have received a significant amount of feedback regarding the nature of other processes that might underlie performance on the visual arrays task including, but not limited to, speed of processing and capacity. One possibility, for example, is that individuals who are able to process data more rapidly are better able to encode the arrays, resulting in higher performance (Vogel et al., 2006). Alternatively, those with faster speed of processing may be able to perform all the necessary information processing steps (whatever they may be) more quickly and completely than those with slower speed of processing. This is especially concerning given the time pressures typically imposed by the visual arrays paradigm (as well as the antisaccade task) and is compounded by concerns that our attention control tasks are contaminated by construct-irrelevant sources of variation (e.g., speed and capacity demands). To address this concern, we conducted post hoc mediation models where we attempted to eliminate the effect of attention control on visual arrays performance by way of speed of processing and working memory capacity. For selective visual arrays, we were consistently unable to do so. This indicates that the observed relationships between attention control and selective visual arrays are not a mere measurement artifact due to speed of processing. One important caveat, however, is that speed of processing in these models is indicated by RT on congruent Stroop and flanker trials, to which we were limited by the archival nature of these data. Future studies should include additional processing speed measures, such as one or more inspection time tasks (Kranzler & Jensen, 1989), to further explore this possibility.
A second alternative explanation of our results is that the complex-span measures, running span measures, and visual arrays measures are reflecting distinct aspects of working memory capacity. In fact, our results do suggest that the nonselection visual arrays tasks are, in some instances, better explained by the more traditional span measures of working memory capacity. However, the selective visual arrays tasks were always closely related to nonstorage measures. Even entertaining the possibility that measures such as the antisaccade do impose some burden on memory storage (which seems inevitable), such burden is likely minimal compared with the measures of working memory capacity included here (see Roberts et al., 1994). Regardless of the specific mechanisms one might propose between the attention control tasks and visual arrays tasks, these data provide evidence that the selective visual arrays tasks are primarily associated with tasks that have little burden on storage capacity than with tasks that place a heavy burden on memory storage.
One final possibility related to the previous one is that both the visual arrays task and the antisaccade task might measure some facet of rapid visual encoding related to working memory and/or attention rather than something akin to domain-general attention control. The present analyses do not rule out this interpretation, but a recent study by Tsukahara et al. (in press) gives reason to doubt it. They found that an attention control factor, defined by the antisaccade, Stroop, and flanker (all visual tasks), fully mediated the relationships between working memory capacity, fluid intelligence, and auditory discrimination ability. They were similarly able to account for the relationship between working memory capacity and fluid intelligence using a factor defined by the antisaccade, a selective visual arrays task (VA-orient-S), and another visual task argued to reflect attention control. It is arguable why the above mediations obtained, but what seems clear is that the antisaccade and selective visual arrays are not reducible merely to indices of rapid visual attention/memory encoding, since they account for the predictive relationship between domain-general working memory capacity and fluid intelligence13 and a domain-specific auditory ability (see also Shipstead & Yonehiro, 2016).
Conclusion
We hope that these results highlight the need for detailed and repeated testing of changes in task design to improve our understanding of the constructs reflected by our tasks. Even small changes in a task may change the cognitive components reflected by the scores on that task. Although we believe these results to be convincing in terms of identifying the constructs underlying visual arrays performance, further inquiry is needed with regard to differences in the nature of nonselective and selective visual arrays tasks.
Moreover, these results pose a more general demand to the field: we cannot assume that tasks reflect the same construct based on their name, superficial characteristics, or scoring procedure alone. Determining construct validity requires relying on many different aspects, psychometric properties, and even sample demographics (for an integrative framework on construct validity see; Embretson, 1983; Embretson, 2017). Experimental studies provide a necessary source of construct validity by clarifying the mechanisms underlying the response processes in a given task (Cronbach, 1957). But we also have to consider correlational studies as a source of external validity showing convergent and divergent relationships with other tasks and latent factors (Engle & Martin, 2018). We believe these results are theoretically important not only to individuals who study differences in working memory capacity and attention control, but also to the experimental community who may be using a single type of visual arrays task and assuming the results generalize to all other visual arrays tasks.
Context of Research
This project was inspired by feedback related to our broader program of research defining and measuring attention control (see Draheim et al., 2018, 2021). Specifically, in this line of research we have been testing the degree to which theoretical versus measurement concerns contribute to poor convergence among tasks used to measure controlled attention. We have received significant, warranted pushback regarding this line of research. We have consistently found that versions of the visual arrays (change detection) task are reliable indicators of controlled attention, particularly when an attentional filtering/selection component is incorporated the task (see also Tsukahara et al., in press). However, given the history of the visual arrays as a measure of visual storage capacity, we have had several reviewers disagree with this position. To address these concerns, we reexamined more than a decade of research to provide an empirical test of our position. We believe these data support the position that the visual arrays task (with a selection component) reflects individual differences in attention control. We believe that by testing an experimental manipulation at the latent level, we can better understand the extent to which task manipulations can impact theoretical relationships.
Supplementary Material
Acknowledgments
This work was supported by Grant N00014-12-1-1011 from the Office of Naval Research to Randall W. Engle and Grant N00014-12-1-0972 to Edward K. Vogel.
Appendix A. Task Reliability
Table A1.
| Task | Reliability | Task | Reliability |
|---|---|---|---|
|
| |||
| Data Set 1 |
Data Set 2 |
||
| SymSpan | .80 | SymSpan | .80 |
| OSpan | .63 | OSpan | .73 |
| RotSpan | .80 | RotSpan | .83 |
| VA-orient-S | .75 | VA-orient-S | .74 |
| Antisaccade | .92 | Antisaccade | .91 |
| Flanker | .69 | Flanker | .83 |
| Stroop | .72 | Stroop | .75 |
|
| |||
| Data Set 3 |
Data Set 4 |
||
| SymSpan | .84 | SymSpan | .84 |
| OSpan | .86 | OSpan | .85 |
| RotSpan | .87 | RunLetter | .81 |
| RunSpatial | .84 | RunDigit | .88 |
| RunDigit | .90 | VA-color | .78 |
| VA-color | .84 | VA-orient | .74 |
| VA-orient | .73 | VA-color-S | .54 |
| VA-orient-S | .79 | VA-orient-S | .70 |
| Antisaccade | .81 | Antisaccade | .85 |
| Flanker | .66 | Flanker | .81 |
| Stroop | .60 | Stroop | .92 |
Note. VA = visual arrays. Reliabilities for Data Sets 3 and 4 are based on values reported in (Shipstead et al., 2014, 2015). The following methods were used to calculate reliabilities for Data Sets 1 and 2. For SymSpan, OSpan, and RotSpan, the total number of items recalled in the correct serial position on each trial was used to calculate cronbach’s α as an estimate of reliability. For the VA-orient-S task, within each set size (five and seven), half of the trials (even/odd split) were used to calculate k scores resulting in a total of four k score; even and odd k scores for each set size. The k scores from each set size were averaged to obtain two split-half k scores for the task to calculate a split-half reliability with a spearman-brown correction as an estimate of reliability. For the antisaccade task, accuracy on each trial was used to calculate a Cronbach’s α as an estimate of reliability. For the flanker and Stroop tasks, within each condition (congruent and incongruent), half of the trials (even/odd split) were used to calculate mean reaction time per condition. A difference score (incongruent – congruent) was calculated for even and odd trials resulting in two interference effects that were used to calculate a split-half reliability with a spearman-brown correction as an estimate of reliability.
Appendix B. Correlation Tables
Table B1.
Data Set 1
| Variable | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1. OSpan | |||||||||
| 2. SymSpan | .53 | ||||||||
| 3. RotSpan | .46 | .63 | |||||||
| 4. Antisaccade | .27 | .32 | .43 | ||||||
| 5. Flanker | −.09 | −.15 | −.17 | −.16 | |||||
| 6. Stroop | .02 | −.11 | −.09 | −.17 | .17 | ||||
| 7. VAorient_S_k | .24 | .39 | .44 | .46 | −.14 | −.16 | |||
| 8. FL_Cong_RT | −.12 | −.21 | −.21 | −.37 | .15 | .25 | −.15 | ||
| 9. Str_Cong_RT | −.12 | −.23 | −.26 | −.34 | .12 | .32 | −.28 | .49 |
Note. FL_Cong_RT = mean reaction time on congruent trials in the Flanker task; Str_Cong_RT = mean reaction time on congruent trials in the Stroop task; VA = visual arrays. Computed correlation used Pearson-method with pairwise-deletion. Correlations in bold are statistically significant, p < .05.
Table B2.
Data Set 2
| Variable | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1. OSpan | |||||||||
| 2. SymSpan | .57 | ||||||||
| 3. RotSpan | .57 | .69 | |||||||
| 4. Antisaccade | .31 | .38 | .45 | ||||||
| 5. Flanker | −.21 | −.25 | −.18 | −.30 | |||||
| 6. Stroop | −.16 | −.18 | −.24 | −.16 | .16 | ||||
| 7. VAorient_S_k | .35 | .41 | .46 | .41 | −.20 | −.14 | |||
| 8. FL_Cong_RT | −.25 | −.28 | −.33 | −.41 | .22 | .16 | −.29 | ||
| 9. Str_Cong_RT | −.25 | −.25 | −.31 | −.33 | .11 | .26 | −.30 | .48 |
Note. FL_Cong_RT = mean reaction time on congruent trials in the Flanker task; Str_Cong_RT = mean reaction time on congruent trials in the Stroop task; VA = visual arrays. Computed correlation used Pearson-method with pairwise-deletion. Correlations in bold are statistically significant, p < .05.
Table B3.
Data Set 3
| Variable | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. OSpan | |||||||||||||
| 2. SymSpan | .54 | ||||||||||||
| 3. RotSpan | .53 | .68 | |||||||||||
| 4. RunSpatial | .53 | .61 | .60 | ||||||||||
| 5. RunDigit | .52 | .44 | .49 | .56 | |||||||||
| 6. Antisaccade | .38 | .45 | .44 | .48 | .40 | ||||||||
| 7. Flanker | −.11 | −.15 | −.17 | −.22 | −.14 | −.19 | |||||||
| 8. Stroop | −.30 | −.19 | −.18 | −.24 | −.23 | −.22 | .09 | ||||||
| 9. VAcolor_k | .43 | .47 | .48 | .59 | .47 | .42 | −.15 | −.23 | |||||
| 10. VAorient_k | .36 | .46 | .43 | .55 | .35 | .38 | −.18 | −.17 | .59 | ||||
| 11. VAorient_S_k | .43 | .51 | .50 | .58 | .47 | .50 | −.16 | −.21 | .60 | .58 | |||
| 12. FL_Congruent_RT | .25 | .28 | .27 | .42 | .35 | .39 | −.37 | −.22 | .30 | .28 | .35 | ||
| 13. Str_Congruent_RT | .27 | .31 | .40 | .40 | .30 | .31 | −.15 | −.24 | .37 | .30 | .42 | .50 |
Note. FL_Congruent_RT = mean reaction time on congruent trials in the Flanker task; Str_Congruent_RT = mean reaction time on congruent trials in the Stroop task; VA = visual arrays. Computed correlation used Pearson-method with pairwise-deletion. Correlations in bold are statistically significant, p < .05.
Table B4.
Data Set 4
| Variable | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. OSpan | |||||||||||||||||||
| 2. SymSpan | .50 | ||||||||||||||||||
| 3. RunLetter | .48 | .45 | |||||||||||||||||
| 4. RunDigit | .40 | .36 | .65 | ||||||||||||||||
| 5. Antisaccade | .20 | .40 | .33 | .34 | |||||||||||||||
| 6.. Flanker | −.16 | −.23 | −.15 | −.18 | −.28 | ||||||||||||||
| 7. Stroop | −.16 | −.25 | −.12 | −.03 | −.13 | .20 | |||||||||||||
| 8. VAcolor_k | .29 | .40 | .29 | .40 | .41 | −.24 | −.12 | ||||||||||||
| 9. VAorient_k | .26 | .39 | .29 | .39 | .42 | −.20 | −.09 | .59 | |||||||||||
| 10. VAcolor_S_k | .19 | .31 | .25 | .33 | .42 | −.23 | −.15 | .47 | .40 | ||||||||||
| 11. VAorient_ S_k | .21 | .36 | .36 | .42 | .45 | −.22 | −.23 | .44 | .59 | .54 | |||||||||
| 12. VAcolor_k.4 | .23 | .36 | .26 | .34 | .42 | −.20 | −.07 | .83 | .50 | .38 | .35 | ||||||||
| 13. VAcolor_k.6 | .28 | .35 | .31 | .38 | .35 | −.18 | −.11 | .85 | .51 | .40 | .41 | .68 | |||||||
| 14. VAcolor_k.8 | .22 | .32 | .20 | .31 | .31 | −.22 | −.12 | .88 | .50 | .41 | .38 | .60 | .54 | ||||||
| 15. VAcolor_S_k.4 | .19 | .30 | .24 | .30 | .46 | −.23 | −.10 | .54 | .51 | .64 | .48 | .45 | .46 | .48 | |||||
| 16. VAcolor S_k.6 | .16 | .20 | .24 | .22 | .36 | −.18 | −.09 | .35 | .33 | .72 | .46 | .33 | .34 | .27 | .46 | ||||
| 17. VAcolor_S_k.8 | .11 | .23 | .15 | .26 | .24 | −.15 | −.14 | .29 | .22 | .85 | .36 | .21 | .23 | .28 | .31 | .33 | |||
| 18. FL_Cong_RT | .20 | .38 | .20 | .24 | .45 | −.83 | −.27 | .36 | .27 | .36 | .32 | .33 | .30 | .30 | .39 | .23 | .26 | ||
| 19. Str_Cong_RT | .15 | .42 | .26 | .30 | .36 | −.16 | −.24 | .44 | .38 | .39 | .37 | .41 | .39 | .36 | .37 | .21 | .33 | .43 |
Note. FL_Cong_RT = mean reaction time on congruent trials in the Flanker task; Str_Cong_RT = mean reaction time on congruent trials in the Stroop task; VA = visual arrays. Computed correlation used the Pearson method with pairwise-deletion. Correlations in bold are statistically significant, p < .05.
Footnotes
A preprint of this project is available on PsychArXiv using the following link: https://psyarxiv.com/u92cm/. A selection of these data has also been reported to the Office of Naval Research as part of our annual program review on June 9, 2020. These data have been released on OSF at the following link: https://doi.org/10.17605/OSF.IO/23NZU.
Furthermore, researchers currently disagree on how best to characterize and measure attention control as a psychometric construct, with some researchers arguing that there is no such coherent latent attention control ability (Frischkorn et al., 2019; Keye et al., 2009; Rey-Mermet et al., 2019; Rouder et al., 2019; von Bastian et al., 2016; Whitehead et al., 2019; but see Draheim et al., 2018, 2021). Although this is a contentious area warranting careful review, this is outside the scope of the present project. However, we devote portions of the discussion section to consideration of some of these issues.
We should note that we regard domain-generality as a necessary but not sufficient benchmark for demonstrating the importance of attention control to visual arrays performance, as there are other plausible domain-general processes that could come into play. For example, Lerche et al. (2020) recently demonstrated that variability in drift rates (the diffusion model parameter associated with information processing speed) derived from many cognitive tasks has both domain-general and domain-specific components.
We also note that there is some evidence for domain-generality in nonselective visual arrays (see Morey & Cowan, 2004).
Owing to an error in programming of the advanced operation span task, trials in which the set-size was supposed to be nine only displayed a set-size of eight. This resulted in the set-size of eight occurring twice as often as intended, a total of four trials compared with two trials for each other set-size.
Note that the arrow flanker task often has three trial types: congruent, incongruent, and a neutral type in which dashes flank the central arrow. Similarly, in the Stroop task a neutral trial type is often present in which the word is not a color. Here we use only incongruent and congruent trials.
In addition to the structural model, we present pie charts representing the contribution of unique attention control, unique working memory capacity, and their common variance relative to the total variance explained in visual arrays performance. The values in the pie chart were calculated based on the path values in the structural equation models. The unique working memory capacity contribution was calculated by squaring the path value from working memory capacity to the visual arrays task divided by the total proportion of variance explained in the visual arrays task. The same was done for the unique attention control contribution. Although the variance from common variance is not explicit in the structural model diagram, it does contribute to the total variance explained in the visual arrays task. To calculate the common variance, the three path values from the model (the covariance between working memory capacity and attention control, working memory capacity to visual arrays, and attention control to visual arrays) are multiplied together and then doubled. It can also be calculated indirectly by subtracting the total from the sum of the unique contributions. In the pie charts, this common variance is then divided by the total variance explained in the visual arrays task.
Note that all models in this section are mathematically equivalent in terms of how well they explain the underlying covariance structure (i.e., their fit indices are identical). Thus, these models should not be regarded as independent pieces of evidence, as they all model exactly the same overall covariance. However, apportioning this covariance in different ways is useful for modeling and assessing the plausibility of alternative models and the effects of placing constraints upon those (equally explanatory) models. The same is true for similar models in our other data sets.
It should be noted that this test is equivalent to test in which the VA-orient-S task is loaded directly onto the attention control factor.
As specified, this model (and all such models we construct) assumes that working memory capacity and processing speed share no residual correlation beyond that explained by their mutual relationship with attention control. To test this assumption, we specified a post hoc structural equation model with attention control predicting both working memory capacity and processing speed and estimated the residual correlation between the latter factors (Figure S1). This revealed a large but nonsignificant negative correlation (r = −.67, p = .26) between the residual nonattention control-related working memory capacity and processing speed variance. Because this residual correlation was not significant, and because this path would be tangential to the goal of explaining away the direct effect relating attention control to VA-orient-S performance, we do not estimate the correlation in our mediation analyses.
As in Data Set 1, we conducted a post hoc structural equation model estimating the residual correlation between working memory capacity and processing speed, accounting for attention control (see Figure S2). This was done because the mediation model tacitly assumes no residual correlation between working memory capacity and processing speed independent of attention control, which could contribute to lack of model fit (although model fit was excellent). The residual correlation was not significant (r = −.08, p = .70).
We also conducted a model with working memory capacity and processing speed mediating the attention control-visual arrays relationship; the interpretation was the same as in Data Sets 1 and 2 (see Figure S3 and Figure S4).
We also conducted a model with working memory capacity and processing speed mediating the attention control-visual arrays relationship; the interpretation was the same as in Data Sets 1 and 2 (see Figure S5 and Figure S6).
Working memory capacity was defined by two spatial complex spans (the symmetry and rotation spans) and one verbal task (the operation span). Fluid intelligence was defined by one spatial reasoning tests (Raven’s Advanced Progressive Matrices) and two verbal reasoning tests (Letter sets [Ekstrom et al., 1976] and Number Series [Thurstone, 1938]).
References
- Adams KCS, Mance I, Fukuda K, & Vogel EK (2015). The contribution of attentional lapses to individual differences in visual working memory capacity. Journal of Cognitive Neuroscience, 27(8), 1601–1616. 10.1162/jocn_a_00811 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen RJ, Baddeley AD, & Hitch GJ (2006). Is the binding of visual features in working memory resource-demanding? Journal of Experimental Psychology: General, 135(2), 298–313. 10.1037/0096-3445.135.2.298 [DOI] [PubMed] [Google Scholar]
- Allen RJ, Baddeley AD, & Hitch GJ (2014). Evidence for two attentional components in visual working memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 40(6), 1499–1509. 10.1037/xlm0000002 [DOI] [PubMed] [Google Scholar]
- Baddeley AD, & Hitch G (1974). Working memory. In G. H. Bower (Ed.), The psychology of learning and motivation: Advances in research and theory (pp. 47–89). Academic Press. [Google Scholar]
- Bollen KA, Harden JJ, Ray S, & Zavisca J (2014). BIC and alternative bayesian information criteria in the selection of structural equation models. Structural Equation Modeling, 21(1), 1–19. 10.1080/10705511.2014.856691 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broadway JM, & Engle RW (2010). Validating running memory span: Measurement of working memory capacity and links with fluid intelligence. Behavior Research Methods, 42(2), 563–570. 10.3758/BRM.42.2.563 [DOI] [PubMed] [Google Scholar]
- Conway ARA, Kane MJ, Bunting MF, Hambrick DZ, Wilhelm O, & Engle RW (2005). Working memory span tasks: A methodological review and user’s guide. Psychonomic Bulletin Review, 12(5), 769–786. [DOI] [PubMed] [Google Scholar]
- Cowan N (2010). The magical mystery four: How is working memory capacity limited, and why? Current Directions in Psychological Science, 19(1), 51–57. 10.1177/0963721409359277 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, Elliott EM, Saults JS, Morey CC, Mattox S, Hismjatullina A, & Conway AR (2005). On the capacity of attention: Its estimation and its role in working memory and cognitive aptitudes. Cognitive Psychology, 51(1), 42–100. 10.1016/j.cogpsych.2004.12.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cronbach LJ (1957). The two disciplines of scientific psychology. American Psychologist, 12(11), 671–684. 10.1037/h0043943 [DOI] [Google Scholar]
- Draheim C, Harrison TL, Embretson SE, & Engle RW (2018). What Item Response Theory can tell us about the complex span tasks. Psychological Assessment, 30(1), 116–129. 10.1037/pas0000444 [DOI] [PubMed] [Google Scholar]
- Draheim C, Hicks KL, & Engle RW (2016). Combining reaction time and accuracy: The relationship between working memory capacity and task-switching as a case example. Perspectives on Psychological Science, 11(1), 133–155. 10.1177/1745691615596990 [DOI] [PubMed] [Google Scholar]
- Draheim C, Tsukahara JS, Martin JD, Mashburn CA, & Engle RW (2021). A toolbox approach to improving the measurement of attention control. Journal of Experimental Psychology: General, 150(2), 242–275. 10.1037/xge0000783 [DOI] [PubMed] [Google Scholar]
- Drummond SP, Anderson DE, Straus LD, Vogel EK, & Perez VB (2012). The effects of two types of sleep deprivation on visual working memory capacity and filtering efficiency. PloS ONE, 7(4), e35653. 10.1371/journal.pone.0035653 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ekstrom RB, French JW, Harman HH, & Dermen D (1976). Manual for kit of factor referenced cognitive tests. Educational Testing Service. [Google Scholar]
- Embretson S (1983). Construct validity: Construct representation versus nomothetic span. Psychological Bulletin, 93(1), 179–197. 10.1037/0033-2909.93.1.179 [DOI] [Google Scholar]
- Embretson S (2017). An integrative framework for construct validity. In Rupp AA & Leighton JP (Eds.), The Handbook of cognition and assessment: Frameworks, methodologies, and applications (pp. 102–123). John Wiley & Sons, Inc. [Google Scholar]
- Emrich SM, & Busseri MA (2015). Re-evaluating the relationships among filtering activity, unnecessary storage, and visual working memory capacity. Cognitive, Affective & Behavioral Neuroscience, 15(3), 589–597. 10.3758/s13415-015-0341-z [DOI] [PubMed] [Google Scholar]
- Engle RW, & Martin JD (2018). Is a science of the mind even possible? Reply to Logie (2018). Journal of Applied Research in Memory & Cognition, 7(4), 493–498. 10.1016/j.jarmac.2018.10.002 [DOI] [Google Scholar]
- Engle RW, Tuholski SW, Laughlin JE, & Conway ARA (1999). Working memory, short-term memory and general fluid intelligence: A latent variable approach. Journal of Experimental Psychology: General, 128(3), 309–331. 10.1037//0096-3445.128.3.309 [DOI] [PubMed] [Google Scholar]
- Eriksen BA, & Eriksen CW (1974). Effects of noise letters upon the identification of a target letter in a nonsearch task. Perception & Psychophysics, 16(1), 143–149. 10.3758/BF03203267 [DOI] [Google Scholar]
- Feldmann-Wüstefeld T, Vogel EK, & Awh E (2018). Contralateral decay activity indexes working memory storage, not the current focus of spatial attention. Journal of Cognitive Neuroscience, 20(8), 1185–1196. 10.1162/jocn_a_01271 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frischkorn GT, Schubert A-L, & Hagemann D (2019). Processing speed, working memory, and executive functions: Independent or interrelated predictors of general intelligence. Intelligence, 75, 95–110. 10.1016/j.intell.2019.05.003 [DOI] [Google Scholar]
- Fukuda K, Awh E, & Vogel EK (2010). Discrete capacity limits in visual working memory. Current Opinion in Neurobiology, 20(2), 177–182. 10.1016/j.conb.2010.03.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukuda K, & Vogel EK (2009). Human variation in overriding attentional capture. Journal of Neuroscience, 29(27), 8726–8733. 10.1523/JNEUROSCI.2145-09.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukuda K, & Vogel EK (2011). Individual differences in recovery time from attentional capture. Psychological Science, 22(3), 361–368. 10.1177/0956797611398493 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukuda K, Woodman GF, & Vogel EK (2015). Individual differences in visual working memory capacity: Contributions of attentional control to storage. In Jolicoeur P, Lefebvre C & Martinez-Trujilo J (Eds.), Mechanisms of sensory working memory: Attention and perfomance XXV (105–139). Elsevier. [Google Scholar]
- Hallett PE (1978). Primary and secondary saccades to goals defined by instructions. Vision Research, 18(10), 1279–1296. 10.1016/0042-6989(78)90218-3 [DOI] [PubMed] [Google Scholar]
- Harrison TL, Shipstead Z, Hicks KL, Hambrick DZ, Redick TS, & Engle RW (2013). Working memory training may increase working memory capacity but not fluid intelligence. Psychological Science, 24(12), 2409–2419. 10.1177/0956797613492984 [DOI] [PubMed] [Google Scholar]
- Hutchison KA (2007). Attentional control and the relatedness proportion effect in semantic priming. Journal of Experimental Psychology: Learning, Memory, and Cognition, 33(4), 645–662. 10.1037/0278-7393.33.4.645 [DOI] [PubMed] [Google Scholar]
- Jost K, Bryck RL, Vogel EK, & Mayr U (2011). Are old adults just like low working memory young adults? Filtering efficiency and age differences in visual working memory. Cerebral Cortex, 21(5), 1147–1154. 10.1093/cercor/bhq185 [DOI] [PubMed] [Google Scholar]
- Kane MJ, Bleckley MK, Conway AR, & Engle RW (2001). A controlled-attention view of working-memory capacity. Journal of Experimental Psychology: General, 130(2), 169–183. 10.1037/0096-3445.130.2.169 [DOI] [PubMed] [Google Scholar]
- Kane MJ, & Engle RW (2000). Working-memory capacity, proactive interference, and divided attention: Limits on long-term memory retrieval. Journal of Experimental Psychology: Learning, Memory, and Cognition, 26(2), 336–358. 10.1037//0278-7393.26.2.336 [DOI] [PubMed] [Google Scholar]
- Kane MJ, Hambrick DZ, Tuholski SW, Wilhelm O, Payne TW, & Engle RW (2004). The generality of working memory capacity: A latent variable approach to verbal and visuospatial memory span and reasoning. Journal of Experimental Psychology: General, 133(2), 189–217. 10.1037/0096-3445.133.2.189 [DOI] [PubMed] [Google Scholar]
- Keye D, Wilhelm O, Oberauer K, & van Ravenzwaaij D (2009). Individual differences in conflict-monitoring: Testing means and covariance hypothesis about the Simon and the Eriksen Flanker task. Psychological Research, 73(6), 762–776. 10.1007/s00426-008-0188-9 [DOI] [PubMed] [Google Scholar]
- Kranzler JH, & Jensen AR (1989). Inspection time and intelligence: A meta-analysis. Intelligence, 13(4), 329–347. 10.1016/S0160-2896(89)80006-6 [DOI] [Google Scholar]
- Lee E, Cowan N, Vogel EK, Rolan T, Valle-Inclan F, & Hackley SA (2010). Visual working memory deficits in Parkinson’s patients are due to both reduced storage capacity and impaired ability to filter out irrelevant information. Brain, 133(9), 2677–2689. 10.1093/brain/awq197 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lerche V, von Krause M, Voss A, Frischkorn GT, Schubert A-L, & Hagemann D (2020). Diffusion modeling and intelligence: Drift rates show both domain-general and domain-specific relations with intelligence. Journal of Experimental Psychology: General, 149(12), 2207–2249. 10.1037/xge0000774 [DOI] [PubMed] [Google Scholar]
- Luck SJ, & Vogel EK (1997). The capacity of visual working memory for features and conjunctions. Nature, 390(6657), 279–281. 10.1038/36846 [DOI] [PubMed] [Google Scholar]
- Lustig C, May CP, & Hasher L (2001). Working memory span and the role of proactive interference. Journal of Experimental Psychology: General, 130(2), 199–207. 10.1037/0096-3445.130.2.199 [DOI] [PubMed] [Google Scholar]
- Ma WJ, Husain M, & Bays PM (2014). Changing concepts of working memory. Nature Neuroscience, 17(3), 347–356. 10.1038/nn.3655 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin JD, Shipstead Z, Harrison TL, Redick TS, Bunting M, & Engle RW (2019). The role of maintenance and disengagement in predicting reading comprehension and vocabulary learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 46(1), 140–154. 10.1037/xlm0000705 [DOI] [PubMed] [Google Scholar]
- McVay JC, & Kane MJ (2010). Adrift in the stream of thought: The effects of mind wandering on executive control and working memory capacity. Handbook of individual differences in cognition (pp. 321–334). Springer. [Google Scholar]
- Morey CC, & Cowan N (2004). When visual and verbal memories compete: Evidence of cross-domain limits in working memory. Psychonomic Bulletin & Review, 11(2), 296–301. 10.3758/bf03196573 [DOI] [PubMed] [Google Scholar]
- Oberauer K (2002). Access to information in working memory: exploring the focus of attention. Journal of Experimental Psychology: Learning, Memory, and Cognition, 28(3), 411–421. [PubMed] [Google Scholar]
- Oberauer K, & Lin H-Y (2017). An interference model of visual working memory. Psychological Review, 124(1), 21–59. 10.1037/rev0000044 [DOI] [PubMed] [Google Scholar]
- Oberauer K, Süß H-M, Wilhem O, & Sander N (2007). Individual differences in working memory capacity and reasoning ability. In Conway ARA, Jarrold C, Kane MH, Miyake A, Towse JN (Eds.), Variation in working memory (pp. 49–75). Oxford University Press. [Google Scholar]
- Pashler H (1988). Familiarity and visual change detection. Perception & Psychophysics, 44(4), 369–378. 10.3758/bf03210419 [DOI] [PubMed] [Google Scholar]
- R Core Team. (2018). R: A language and environment for statistical computing. [Google Scholar]
- Redick TS, Shipstead Z, Meier ME, Montroy JJ, Hicks KL, Unsworth N, Kane MJ, Hambrick DZ, & Engle RW (2016). Cognitive predictors of a common multitasking ability: Contributions from working memory, attention control, and fluid intelligence. Journal of Experimental Psychology: General, 145(11), 1473–1492. 10.1037/xge0000219 [DOI] [PubMed] [Google Scholar]
- Revelle W (2018). Psych: Procedures for personality and psychological research. Northwestern University, Evanston. [Google Scholar]
- Rey-Mermet A, Gade M, Souza AS, von Bastian CC, & Oberauer K (2019). Is executive control related to working memory capacity and fluid intelligence? Journal of Experimental Psychology: General, 148(8), 1335–1372. 10.1037/xge0000593 [DOI] [PubMed] [Google Scholar]
- Rizio AA, & Dennis NA (2013). The neural correlates of cognitive control: Successful remembering and intentional forgetting. Journal of Cognitive Neuroscience, 25(2), 297–312. 10.1162/jocn_a_00310 [DOI] [PubMed] [Google Scholar]
- Roberts RJ, Hager LD, & Heron C (1994). Prefrontal cognitive processes: Working memory and inhibition in the antisaccade task. Journal of Experimental Psychology: General, 123(4), 374–393. 10.1037/0096-3445.123.4.374 [DOI] [Google Scholar]
- Rosseel Y (2012). Lavaan: An R package for structural equation modeling and more. Version 0.5–12 (BETA. ). Journal of Statistical Software, 48(2), 1–36. 10.18637/jss.v048.i02 [DOI] [Google Scholar]
- Rouder JN, Kumar A, & Haaf JM (2019). Why most studies of individual differences with inhibition tasks are bound to fail. PsyArxiv. 10.31234/osf.io/3cjr5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouder JN, Morey RD, Morey CC, & Cowan N (2011). How to measure working memory capacity in the change detection paradigm. Psychonomic Bulletin & Review, 18(2), 324–330. 10.3758/s13423-011-0055-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saults JS, & Cowan N (2007). A central capacity limit to the simultaneous storage of visual and auditory arrays in working memory. Journal of Experimental Psychology: General, 136(4), 663–684. 10.1037/0096-3445.136.4.663 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schubert A-L, & Rey-Mermet A (2019). Does process overlap theory replace the issues of general intelligence with the issues of attentional control? Journal of Applied Research in Memory & Cognition, 8(3), 277–283. 10.1016/j.jarmac.2019.06.004 [DOI] [Google Scholar]
- Shipstead Z, & Engle RW (2013). Interference within the focus of attention: Working memory tasks reflect more than temporary maintenance. Journal of Experimental Psychology: Learning, Memory, and Cognition, 39(1), 277–289. 10.1037/a0028467 [DOI] [PubMed] [Google Scholar]
- Shipstead Z, Harrison TL, & Engle RW (2015). Working memory capacity and the scope and control of attention. Attention, Perception, & Psychophysics, 77(6), 1863–1880. 10.3758/s13414-015-0899-0 [DOI] [PubMed] [Google Scholar]
- Shipstead Z, Harrison TL, & Engle RW (2016). Working memory capacity and fluid intelligence: Maintenance and disengagement. Perspectives on Psychological Science, 11(6), 771–799. 10.1177/1745691616650647 [DOI] [PubMed] [Google Scholar]
- Shipstead Z, Lindsey DR, Marshall RL, & Engle RW (2014). The mechanisms of working memory capacity: Primary memory, secondary memory, and attention control. Journal of Memory and Language, 72(1), 116–141. 10.1016/j.jml.2014.01.004 [DOI] [Google Scholar]
- Shipstead Z, Redick TS, Hicks KL, & Engle RW (2012). The scope and control of attention as separate aspects of working memory. Memory, 20(6), 608–628. 10.1080/09658211.2012.691519 [DOI] [PubMed] [Google Scholar]
- Shipstead Z, & Yonehiro J (2016). The domain-specific and domain-general relationships of visuospatial working memory to reasoning ability. Psychonomic Bulletin & Review, 23(5), 1504–1512. 10.3758/s13423-016-1021-x [DOI] [PubMed] [Google Scholar]
- Stroop JR (1935). Studies of interference in serial verbal reactions. Journal of Experimental Psychology, 18(6), 643–662. 10.1037/h0054651 [DOI] [Google Scholar]
- Thurstone LL (1938). Primary mental abilities. University of Chicago Press. [Google Scholar]
- Tsukahara JS, Harrison TL, Draheim C, Martin JD, & Engle RW (in press). Attention control: The missing link between sensory discrimination and intelligence. Attention, Perception, & Psychophysics. [DOI] [PubMed] [Google Scholar]
- Tsukahara JS, Harrison TL, & Engle RW (2016). The relationship between baseline pupil size and intelligence. Cognitive Psychology, 91, 109–123. 10.1016/j.cogpsych.2016.10.001 [DOI] [PubMed] [Google Scholar]
- Turner ML, & Engle RW (1989). Is working memory capacity task dependent? Journal of Memory and Language, 28(2), 127–154. 10.1016/0749-596X(89)90040-5 [DOI] [Google Scholar]
- Unsworth N, & Engle RW (2007). The nature of individual differences in working memory capacity: Active maintenance in primary memory and controlled search from secondary memory. Psychological Review, 114(1), 104–132. 10.1037/0033-295X.114.1.104 [DOI] [PubMed] [Google Scholar]
- Unsworth N, Redick TS, Heitz RP, Broadway JM, & Engle RW (2009). Complex working memory span tasks and higher-order cognition: A latent-variable analysis of the relationship between processing and storage. Memory, 17(6), 635–654. 10.1080/09658210902998047 [DOI] [PubMed] [Google Scholar]
- Vogel EK, & Machizawa MG (2004). Neural activity predicts individual differences in visual working memory capacity. Nature, 428(6984), 748–751. 10.1038/nature02447 [DOI] [PubMed] [Google Scholar]
- Vogel EK, McCollough AW, & Machizawa MG (2005). Neural measures reveal individual differences in controlling access to working memory. Nature, 438(7067), 500–503. 10.1038/nature04171 [DOI] [PubMed] [Google Scholar]
- Vogel EK, Woodman GF, & Luck SJ (2005). Pushing around the locus of selection: Evidence for the flexible-selection hypothesis. Journal of Cognitive Neuroscience, 17(12), 1907–1922. 10.1162/089892905775008599 [DOI] [PubMed] [Google Scholar]
- Vogel EK, Woodman GF, & Luck SJ (2006). The time course of consolidation in visual working memory. Journal of Experimental Psychology: Human Perception and Performance, 32(6), 1436–1451. 10.1037/0096-1523.32.6.1436 [DOI] [PubMed] [Google Scholar]
- von Bastian CC, Souza AS, & Gade M (2016). No evidence for bilingual cognitive advantages: A test of four hypotheses. Journal of Experimental Psychology: General, 145(2), 246–258. 10.1037/xge0000120 [DOI] [PubMed] [Google Scholar]
- Wagenmakers EJ (2007). A practical solution to the pervasive problems of p values. Psychonomic Bulletin and Review, 14(5), 779–804. 10.3758/BF03194105 [DOI] [PubMed] [Google Scholar]
- Wang TH, Placek K, & Lewis-Peacock JA (2019). More is less: Increased processing of unwanted memories facilitates forgetting. The Journal of Neuroscience, 39(18), 3551–3560. 10.1523/JNEUROSCI.2033-18.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitehead PS, Brewer GA, & Blais B (2019). Are cognitive control processes reliable? Journal of Experimental Psychology: Learning, Memory, and Cognition, 45(5), 765–778. 10.1037/xlm0000632 [DOI] [PubMed] [Google Scholar]
- Wilhelm O, Hildebrandt A, & Oberauer K (2013). What is working memory capacity, and how can we measure it? Frontiers in Psychology, 4, 433. 10.3389/fpsyg.2013.00433 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


