Evaluation of Deep Learning Architectures for Aqueous Solubility Prediction

Abstract

Determining the aqueous solubility of molecules is a vital step in many pharmaceutical, environmental, and energy storage applications. Despite efforts made over decades, there are still challenges associated with developing a solubility prediction model with satisfactory accuracy for many of these applications. The goals of this study are to assess current deep learning methods for solubility prediction, develop a general model capable of predicting the solubility of a broad range of organic molecules, and to understand the impact of data properties, molecular representation, and modeling architecture on predictive performance. Using the largest currently available solubility data set, we implement deep learning-based models to predict solubility from the molecular structure and explore several different molecular representations including molecular descriptors, simplified molecular-input line-entry system strings, molecular graphs, and three-dimensional atomic coordinates using four different neural network architectures—fully connected neural networks, recurrent neural networks, graph neural networks (GNNs), and SchNet. We find that models using molecular descriptors achieve the best performance, with GNN models also achieving good performance. We perform extensive error analysis to understand the molecular properties that influence model performance, perform feature analysis to understand which information about the molecular structure is most valuable for prediction, and perform a transfer learning and data size study to understand the impact of data availability on model performance.

Introduction

Because molecular aqueous solubility is a key performance determiner across many applications, its prediction is one of the key steps in many material selection pipelines. For example, solubility is a critical physical property for drug development and for electrolyte development which determines the performance of devices such as batteries, sensors, and solar cells. In particular, molecular solubility is a key performance driver for redox flow batteries (RFBs) based on organic active materials. These are a promising energy storage technology with potential to address the cost, safety, and functionality needs of the grid-scale energy storage systems forming a critical component of our future electric grid for renewable integration and grid modernization.¹ The key feature of RFB technology is that the energy-bearing redox-active ions/molecules are dissolved in a supporting liquid electrolyte, which, in the case of aqueous RFBs, is water. Traditional transition metal ions commonly used for RFBs are facing many challenges, such as cost and limited chemical space,² which has led to the search for inexpensive and sustainable organic molecules to support growing grid energy storage needs. Because the solubility of candidate organic molecules dictates their maximum concentration in an electrolyte, and thus the energy density of a RFB system, solubility is a key molecular design factor. The need to quickly screen and explore potential candidate molecules for their expected performance in the RFB, motivates us to develop improved models for solubility prediction that can perform well at the high solubility regime (>0.5 mol/L) required for these technologies. Such property prediction models are also a key capability needed for the inverse design of molecules with targeted properties.³⁻⁵

Solubility prediction has been an intensive research area for many years. Major approaches include the general solubility equation,⁶ the Hildebrand and Hansen solubility parameters,^7,8 COSMO-RS,⁹ and methods leveraging molecular dynamics simulations.^10,11

Solubility prediction efforts have increasingly turned to the use of statistical and machine learning methods. Early computational solubility prediction efforts based on the molecular structure were mainly based on developing regression models to predict solubility using the structural and electronic properties of the molecules as input. For example, regression models were developed which leveraged connectivity indices and a polarizability factor,¹² structural and atomic charge-based properties,¹³ and molecular fragments.¹⁴ As high-performance computers and large training data sets became available, artificial neural networks and deep learning which are capable of leveraging the raw molecular structure as input grew in popularity for molecular property prediction. In recent years, these methods have proven to be promising in predicting thermal conductivity, toxicity, lipophilicity, bioactivity, water solubility, protein structure band gap, heat capacity, and scent descriptors, among other properties.¹⁵⁻²¹ These efforts have explored a range of molecular representations and deep learning modeling architectures, including molecular fingerprints and fully connected neural networks,²²⁻²⁷ simplified molecular-input line-entry system (SMILES) strings and recurrent neural networks,²⁸⁻³⁰ molecular graphs and graph neural networks (GNNs),^{15,16,18,31−33} and spatially aware architectures such as SchNet.^34,35

These types of techniques have also been previously applied to the problem of solubility prediction. The most often applied graph-based neural network techniques include DAG recursive neural networks,¹⁵ graph convolutional networks,³⁶ message passing neural networks (MPNNs),³⁷ and MPNN models with self-attention.¹⁸ Other efforts have explored alternative architectures such as Cui et al.³⁸ who compare the performance of shallow neural networks with deeper ResNet-like networks for solubility prediction. These efforts generally rely on small data sets, ranging from 100 to 1297 molecules, with the exception of Cui et al.,³⁸ which leverages a data set with around 10,000 molecules.

Despite these developments, the prediction of solubility remains challenging.³⁹ Several of the major challenges for this task include the complexity of the solvation process, the existence of measurement noise and data quality issues, the diversity and scale of the molecular structure space, and the broad range of solubility values which span many orders of magnitude. Many of the described challenges and limitations are driven by the limited size of available data sets, which do not have the needed diversity or capacity for models to learn the complex relationships between structure and solubility. Another direction for addressing these challenges is through the development of improved molecular representations and the application of models with the capacity to learn complex structure–property relationships.

In this work, we explore the predictive capacity of different commonly used molecular representation approaches and deep learning model variants on the largest and most diverse collection of organic solubility measurements to date. We do not aim to develop a novel modeling architecture, but instead aim to evaluate the effect of commonly employed modeling choices on our unprecedentedly large and diverse data set. Toward this aim, we make several key contributions.

First, we perform a comparison across all commonly used representations and modeling approaches on the same data set to determine which are best suited to extract the underlying structure–property relationships. This contrasts with previous efforts which typically focus on a single modeling approach compared with simple baselines, making it difficult to perform comparisons of different representations and architectures. We demonstrate that feed-forward networks leveraging molecular descriptors outperform other approaches. While it is challenging to make a direct comparison with previous efforts, due to differences in the evaluation data sets, we find that the combination of our models and training data set lead to equivalent or improved performance on most previously used solubility prediction data sets, demonstrating the impact of large training sets on model generalizability.

Second, we perform detailed exploration of the errors made by the resulting models to understand the types of molecular structures for which the prediction is successful and the types for which it is more challenging. We analyze the importance of different feature types to support accurate solubility prediction and find that 2D molecular descriptors provide the best predictive signal which is not strongly improved by the inclusion of 3D information, experimental melting points, or Sterimol parameters. We introduce a novel evaluation approach to specifically probe the ability of models to distinguish the solubility of isomer groups and identify the prediction of solubility within these groups as a key challenge for future development. Finally, we demonstrate the impact of data set size on the predictive capabilities of the model through a transfer learning evaluation and an exploration of performance on smaller data subsamples. We find that doubling the data size is associated with a reduction in the root-mean-square error (RMSE) of 0.06 orders of magnitude and that using transfer learning provides a performance boost for models that leverage raw molecular structure as inputs but not those that rely on precomputed descriptors.

Data

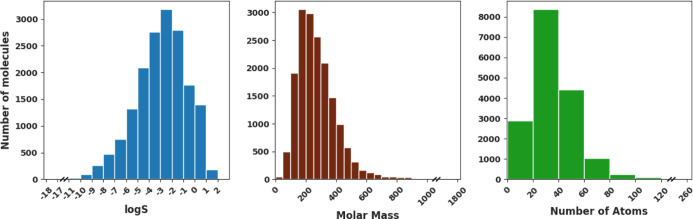
In order to train our deep learning models we leverage a large data set compiled by Gao et al.⁴⁰ containing data for 11,868 molecules collected from various data sources (including OChem,⁴¹ Beilstein,⁴² and Aquasol⁴³) combined with data made available by Cui et al.³⁸ and a commercial data set obtained from Reaxys.⁴² Molecules for which RDKit Mol objects could not be successfully created were discarded from the data set. The final data set consists of 17,149 molecules with sizes ranging from 1 to 273 atoms and with molecular masses ranging from 16 to 1819. The measured aqueous solubilities of these molecules range from 3.4 × 10^–18 to 45.5 mol/L. The distributions of log solubility values, molecular mass, and number of atoms are shown in Figure 1. Throughout this paper, log S stands for base 10 logarithm value of solubility S, which is in the units of mol/L, where L stands for the volume of the solvent in liters.

Figure 1.

Distributions of log solubility, molar mass (g/mol), and number of atoms for molecules in our data set.

In order to study the relationship between solubility and molecular properties as well as to develop features for input to the models, we generate several different sets of features derived from the molecular structure—two-dimensional (2D) molecular features, three-dimensional (3D) molecular features, functional group features, and density functional theory (DFT)-based quantum descriptor features. First, we employed 2D molecular descriptors as implemented in the Mordred package.⁴⁴ In total, this package can generate 1613 descriptors derived from 2D molecular structures. However, the descriptor generation failed for some molecules in our data set, and we therefore relied on 743 features which could be successfully generated for all the molecules (these are listed in Tables S1 and S2). This set of features will be referred to as 2D descriptors in the remainder of the text.

Additionally, we calculated a set of features describing the 3D structure of the molecules (which we will refer to as 3D descriptors). Atomic coordinates for these calculations were generated using the Pybel package.⁴⁵ The coordinates are optimized using MMFF94 force fields with 550 optimization steps. There were 36 molecules for which coordinate generation failed, which we dropped from the data set. Using the approximated coordinates, we calculated counts of atoms within six concentric layers around the centroid of the molecule as described in Panapitiya et al.⁴⁶ to be used as features. Another set of features that contain information about the distribution of atoms has been proposed by Ballester and Richards.⁴⁷ To calculate these features, the distances to all the atoms with respect to three locations in the molecule (centroid, closest atom to the centroid, and farthest atom to the centroid) are calculated. Next, we calculate the statistical moments of the atomic distance distributions from order 1 to 10. These features encode information about the shape of the molecule. We also calculated the volume enclosed by all the atoms in a molecule using the ConvexHull function implemented in the SciPy package.^46,48 In total, there are 37 resulting 3D descriptors.

In addition to the molecular descriptor features, we included counts of molecular fragments and functional groups present in the molecules. First, we identified a set of fragments to use as features. We used RDKit⁴⁹ to identify molecular fragments attached to benzene-like structures (hexagonal ring with six atoms) in our data set. From the resulting fragments, we selected the 52 most common fragments in addition to seven other functional groups commonly found in chemical compounds. These 59 fragments are shown in Figure S1. Combining the 2D descriptors, 3D descriptors, and fragment counts, there are 839 molecular descriptors used as features.

Finally, in order to assess the impact of features derived from DFT, we leveraged a set of quantum descriptors, including the solvation energy (kcal/mol), molecular volume (Ang³), molecular surface area (Ang²), dipole moment (Debye), dipole moment/volume (Debye/A³), and quadrupole moments as calculated using the NWChem package.⁵⁹ Due to the high computational resources it takes to optimize large molecular structures using DFT quantum descriptors, only 7764 molecules containing at most 83 atoms have been used. Therefore, in our primary analysis we exclude these features but perform a study of their impact on the models in the Feature Analysis section.

In order to compare the performance of our models with the results of previous efforts, we perform an evaluation using 13 previously existing data sets, including those from Delaney,⁵⁰ Huuskonen,⁵² Boobier et al.,⁵¹ Tang et al.,¹⁸ Llinàs et al.,⁵³ Cui et al.,³⁸ Llinas et al.,³⁹ and Boobier et al.⁵⁴ A summary of different properties of these data sets are given in Tables 1 and S3 and Figure S2. Except for the Cui data set, the others consist of molecules containing at most eight rings. While the Cui data set does contain complex molecules, our data set introduces even further diversity. Because the data sets contain duplicate entries with potentially differing solubilities, for the purposes of our analysis, we treat duplicate entries across these data sets according to a method similar to what is used in Sorkun et al.⁴³ (described in detail in the Supporting Information).

Table 1. Comparison of the Diversity of Different Data Sets, Showing the Range of Values Observed in the Data Sets^a.

data set	N	log S	atoms	AromAtom	rings
ours	17,149	–17.5 to 1.7	1–273	0–64	0–33
Delaney50	1100	–11.6 to 1.6	4–119	0–28	0–8
Tang18	1310	–11.6 to 1.6	5–94	0–23	0–7
Cui38	9979	–18.2 to 1.7	1–216	0–60	0–16
Boobier51	100	–8.8 to 2.0	10–67	0–20	0–7
Huuskonen52	1011	–11.6 to 1.6	5–94	0–23	0–7
Sol. Challenge 153	114	–7.7 to −1.1	13–76	0–19	1–5
Sol. Challenge 2 SET139	100	–6.8 to −1.2	15–196	0–26	1–7
Sol. Challenge 2 SET239	32	–10.4 to −1.2	21–123	0–30	1–8
water set wide54	900	–12.8 to 1.6	4–80	0–26	0–6
water set narrow54	560	–4.0 to 1.0	4–61	0–17	0–6
Hou SET155,56	21	–8.1 to 0.4	18–57	0–18	0–4
Hou SET255,57	120	–10.4 to 1.0	6–57	0–18	0–5
Wang58	1640	–11.6 to 1.6	4–119	0–28	0–8

^aN, log S, atoms, AromAtom, and rings refer to the number of molecules, log solubility (mol/L), number of atoms, number of aromatic atoms, and number of rings, respectively.

To support the prediction of solubility, we also explore the use of transfer learning by leveraging large molecular data sets (QM9 and PC9), which do not include solubility labels, but do contain significantly more molecules than our solubility data set. The QM9 data set contains 133,885 small molecules with sizes up to nine atoms and composed of only H, C, N, O, and F atoms.⁶⁰ For each molecule, the data set contains 17 energetic, thermodynamic, and electronic properties along with the SMILES structure corresponding to B3LYP relaxation.⁶⁰ The PC9 data set contains 99,234 unique molecules that are equivalent to those in QM9 in terms of the atomic composition and the maximum number of atoms, but the data set is designed to improve upon the chemical diversity in comparison with QM9.⁶¹

Solubility Prediction

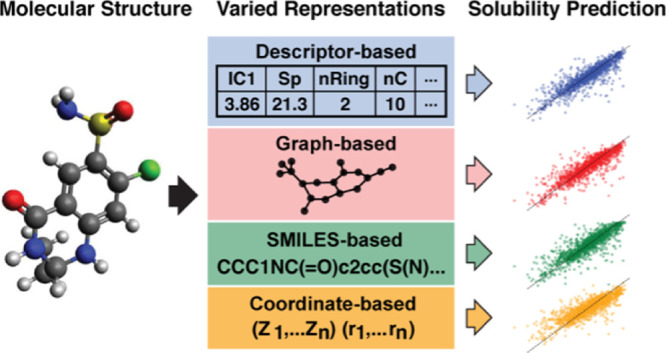
We aim to develop deep learning models that can infer the solubility of a molecule by exploiting the patterns that exist between structural molecular properties and measured molecular solubility. We include an exploration of such patterns in our data set in the Supporting Information. In order to train models that can automatically recognize such patterns, there are various ways of representing a molecule for computational purposes along with associated deep learning architectures designed to learn from such representations. Of these, representing a molecule as a vector of structural/electro-chemical features, as a SMILES string, as a molecular graph, and as a set of 3D atomic coordinates are widely used methods. We use these four representations and associated deep learning architectures to explore which representations and models are best suited toward high-accuracy solubility prediction.

The first representational approach relies on a large suite of molecular descriptors which quantify the structural and electro-chemical properties of the molecule. We leverage a fully connected neural network to predict the solubility, given this set of features. The feature set we use includes the 2D descriptors, 3D descriptors, and fragment counts. Before training the models, the features in the training, validation, and test sets were scaled to zero mean and unit variance using transformation parameters based on the training set. We refer to this model as the molecular descriptor model (MDM).

Our second model is based on using the SMILES string representation of each molecule as an input to a character-level long short-term memory neural network,⁶² which is designed to process sequential data such as the character sequences that comprise SMILES strings. We refer to this model as the SMILES model.

Our third model is a GNN. In the material science domain, GNNs have been widely used for material property prediction and inverse material design.^{3,15,18,63,64} Our model relies on a molecular graph representation, where the atoms and bonds become nodes and edges of a graph, respectively, and a graph convolutional network, which consists of graph convolutional and edge convolutional layers. Each node is initially assigned with a set of features. For this work, we used the features defined in the “atom_features” function of the DeepChem library⁶⁵ which include atomic symbol, degree, implicit valence, total number of hydrogen atoms, and hybridization of the atom as a one-hot encoded vector, whether the atom is aromatic or not as a boolean feature, and the formal charge of the atom (refer to the Supporting Information for more details). The GNN then learns to update the node and edge features through an iterative process called message passing. We refer to this model as the GNN model.

Finally, we apply a model designed to learn from the full 3D atomic coordinate representation of the molecules called SchNet, originally developed to predict molecular energy and interatomic forces.³⁵ The SchNet architecture is built upon three types of sub-networks: atom-wise layers, interaction layers, and continuous filter-networks, which learn atom-level representations based on the observed distances between atoms. We refer to this model as the SchNet model.

The average time (in seconds) required to generate input representations for a single molecule for the MDM, SMILES, GNN, and SchNet models are 0.52, 0.0004, 0.0029, and 0.03 using a Dual Intel(R) Xeon(R) CPU (E5-2620 v4 @ 2.10 GHz) with 64 GB memory. The code for all the models is accessible at https://github.com/pnnl/solubility-prediction-paper.

Optimization

For the purposes of model development and training, we split our full data set into three components for training, validation, and testing. Prior to splitting, the solubility values were binned into 6 folds as shown in Figure S10. Next, 85, 7.5, and 7.5% of the data were chosen using stratified sampling from the bins for the training, validation, and testing splits, respectively. This procedure ensures that high and low solubility molecules are sampled into each of the three splits. Hyperparameter tuning was carried out using the hyperopt python package.⁶⁶ Due to the different training times required by the different models, we were able to perform a larger search of the hyperparameter space for some of the models. For the MDM and GNN models, we considered 1000 different unique combinations, whereas for the SchNet and SMILES models, only 50 and 20 combinations, respectively, were evaluated. Details on the tuned hyperparameters, their explored ranges, and the final selected parameter values can be found in the Supporting Information.

All the models were trained while monitoring the mean squared error of the validation set and saving the model parameters corresponding to the lowest validation error. Training was stopped if the validation error did not improve for 25 consecutive steps. This early stopping procedure ensures that the models are not over-fitted.

Results and Discussion

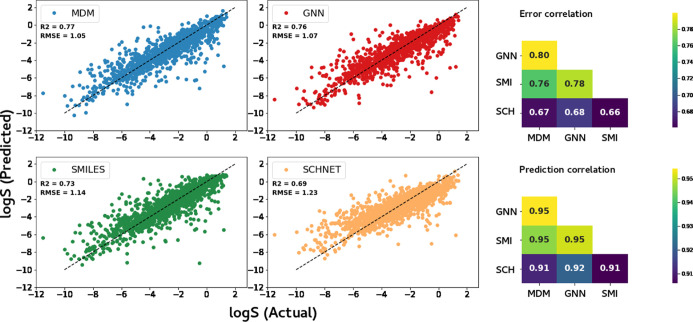
We evaluate the performance of each of our representation and modeling approaches using two error metrics, RMSE and mean absolute error (MAE), and two correlational metrics, R² and Spearman correlation. The error metrics allow us to evaluate the mean levels of error observed in the model predictions, while the correlational metrics allow us to observe if the models perform well at ranking the molecules in terms of solubility, even if the exact predictions are not correct. The performance results for each of the models are given in Table 2 for a fixed test set and Table 3 using a cross validation approach. The predicted versus actual solubility values for all four models are shown in Figure 2 (left). We find that the best performance is achieved by the MDM model, showing that the models which leverage raw structural information alone are not able to outperform the predictions using pre-derived molecular features on this predictive task. The cross validation results show that the performance differences between models are robust and reproducible across test set sampling.

Table 2. Evaluation Results for the Four Models on the Test Set.

			RMSE	MAE
model	R2	Spearman	(log S)	(log S)
MDM	0.7719	0.8787	1.0513	0.6887
GNN	0.7628	0.8708	1.0722	0.7256
SMILES	0.7337	0.8603	1.1360	0.7609
SCHNET	0.6883	0.8337	1.2291	0.8892

Table 3. Evaluation Results (Mean and Standard Deviation) Using Fivefold Cross Validation.

			RMSE	MAE
model	R2	Spearman	(log S)	(log S)
MDM	0.7676±0.0067	0.8797±0.0038	1.0841±0.0312	0.7173±0.0132
GNN	0.7539 ± 0.0103	0.8713 ± 0.0043	1.1156 ± 0.0378	0.7504 ± 0.0196
SMILES	0.7369 ± 0.0083	0.8643 ± 0.0035	1.1536 ± 0.0381	0.7843 ± 0.0268
SCHNET	0.6946 ± 0.0105	0.8411 ± 0.0046	1.2429 ± 0.0327	0.8702 ± 0.0273

Figure 2.

Left: scatter plots of predicted versus actual log solubilities obtained by four models considered in this study. Right: Pearson correlation of errors (top) and predictions (bottom) between different pairs of models.

Of the three models that rely on raw molecular structure information, we find the GNN model achieves the highest performance, almost equaling the performance by the molecular feature model. This shows that GNNs have the capability to learn almost all the information embedded in the molecular features using only a relatively small number of atomic properties.

We also study the strengths and weaknesses of the different representations and modeling approaches by observing whether the different models make similar errors. In Figure 2 (right), we show the correlation in the predictions and errors for each pair of the models. The high correlation values of the predictions (>0.9) and errors (>0.65) show that although the models are using different features and representations of the molecules, they are making very similar predictions. This indicates that the molecules which are easy and hard to predict are largely held in common across the different models, rather than different models excelling for different groups of molecules.

Comparison with Previous Results

To validate the predictive ability of our models, we compared the performance of our modeling approaches with the results obtained in previous solubility prediction studies using 13 different data sets. These comparison efforts are complicated by the use of differing data sets across many different previous studies, by the fact that previous efforts largely used significantly smaller data sets and by the overlap of the molecules across the different data sets. In this comparison, we are aiming to evaluate the impact of both the modeling approach as well as the use of a large and diverse training set of solubility values.

The previous studies used two different strategies for model validation—a fixed test/train split approach and a cross-validation approach where performance is averaged across multiple random splits. For comparison purposes, we replicate the evaluation approach used by each paper. When the external data sets consist of separate train and test sets, we leverage their training set in combination with ours and test the resulting model performance on the external test set. For external data sets where the previous authors did not provide separate train/test sets, we used 10-fold cross validation to obtain test results for external data sets. The folds were generated by randomly splitting the external data in 10 portions and adding 9 of the portions to our training data and using the remaining split as the test set. The final results were calculated by cycling through all 10 folds as the test set and averaging the results. We do not perform any new hyperparameter tuning for these models but rely on the parameters determined by optimizing on our data set alone.

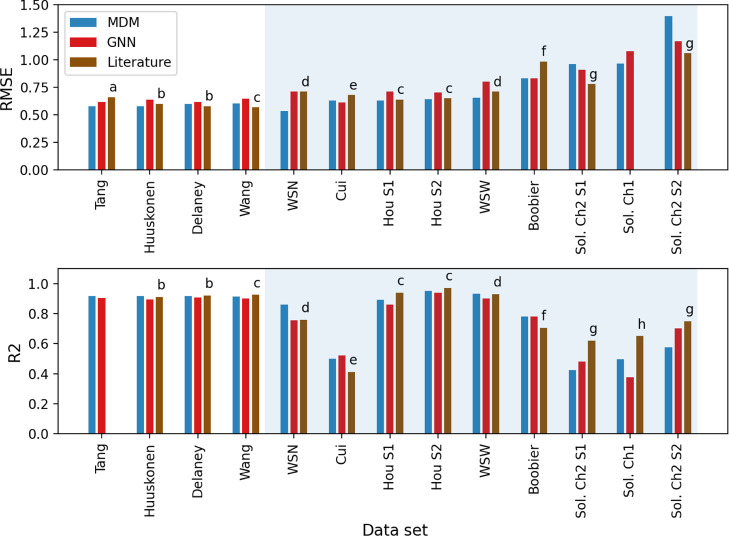
The resulting model accuracies for the 13 external data sets are given in Figure 3. Note that due to data cleaning and duplicate removal steps carried out in this work, the number of molecules that we used to obtain the prediction accuracies for these data sets may be different than the number of molecules the above authors used to obtain their results. For example, Delaney and Huuskonen data sets used by Lusci et al.¹⁵ contain 1144 and 1026 molecules, whereas our cleaned sets consist of 1100 and 1011 molecules, respectively. When a data set contains duplicates, it can cause train-test contamination that leads to artificial inflation of the measured performance. For example, when we evaluate our model on a non-deduplicated version of the Delaney data set we find that our MDM R² improves from 0.92 to 0.93 and our RMSE improves from 0.6 to 0.55 which are better than the previous best results of 0.92 and 0.58. However, such results are misleading due to the train-test contamination introduced by the repeated molecules. Therefore, our cleaned and deduplicated data set versions are more reflective of the true expected performance of the model on unseen molecules but may not be directly comparable to the previously existing results on these data sets. The number of molecules in our cleaned sets are given in Table 1.

Figure 3.

RMSE (top) and R² (bottom) values of predictions obtained by MDM and GNN for different data sets using different data set splitting methods. The data sets on a white background were evaluated using cross-validation and those on a blue background were evaluated using a fixed train-test split. Letters (a–i) correspond to the previous work that report current/previous best prediction accuracies for these data sets. (a): Tang et al.,¹⁸ (b): Lusci et al.,¹⁵ (c): Wu et al.,⁶⁷ (d): Boobier et al.,⁵⁴ (e): Cui et al.,³⁸ (f): Boobier et al.,⁵¹ (g): Llinas et al.,³⁹ and (h): Hopfinger et al.⁶⁸

We can see that the accuracies obtained for other data sets are similar to or better than previous results for most of the data sets. In particular, for the three data sets which appear the easiest (Delaney, Huuskonen, and Tang), with low RMSE and high R² values already previously achieved, our models roughly equal the previously existing performance. This could indicate that there is limited room for predictive performance improvement on these simpler data sets which may already be limited by measurement uncertainties. In contrast, we find that we achieve significant performance improvement for the more challenging Boobier and Cui data sets which have previous R² results of only 0.71 and 0.42, respectively. These results indicate the potential of a large, diverse data set in combination with highly expressive deep learning models to learn generalizable structure–property patterns applicable across many different data sets.

The solubility challenge data sets have proven to be the most difficult for our models. For Solubility Challenge 1, we find that the molecules for which our models have the highest error are those for the which the challenge competitors also had low accuracy and that these molecules are very insoluble in water.⁶⁸ This is consistent with our observation that machine learning models generally find it difficult to accurately predict low solubilities, which agrees with our results shown in Figures 6 and S14. Solubility Challenge 2 consists of two test sets. SET1 consists of highly accurate solubility values of 100 drugs whose log S ranges from −1.2 to −6.8 with interlaboratory reproducibility of approximately 0.17 in log units. SET2 consists of molecules whose log S values range from −1.2 to −10.4 with a interlaboratory reproducibility of 0.62 log unit. Our GNN model outperforms the mean performance of the competitors for both data sets, achieving an RMSE of 0.91 on SET1 and 1.17 on SET2 compared with a mean of 1.14 and 1.62, respectively, for the competitors. Our model would rank 5th for SET1 and 4th for SET2 (in terms of RMSE) among the competitors whose train sets have been confirmed not to be contaminated with the competition’s test molecules. Also, when finding our rank, we did not assign separate ranks for competitor entries whose accuracies were identical. That is, all the competitors with the same prediction accuracy get the same rank. The best RMSE values achieved by any competitor for these sets are 0.78 and 1.06, respectively. It is interesting to note that our GNN model outperforms our MDM model for these two data sets, which is in contrast with the model performance on most data sets.

Figure 6.

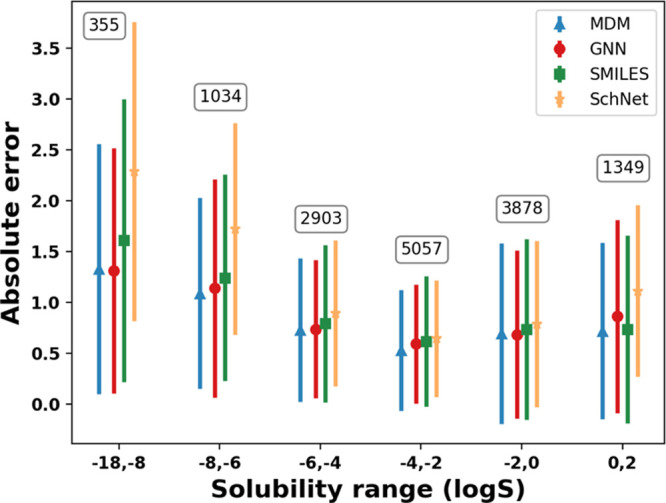
Test set error by solubility range (in log S) for the four models with the number of test molecules in each bin annotated on the plot, showing the mean and standard deviation per bin.

Error Analysis

Next we perform detailed analysis of the errors made by the models to understand the factors leading to improved and reduced predictive performance. We perform several different analyses of the errors, including manual examination of easy and difficult molecules and performance comparison on molecules of different types.

Qualitative Examination

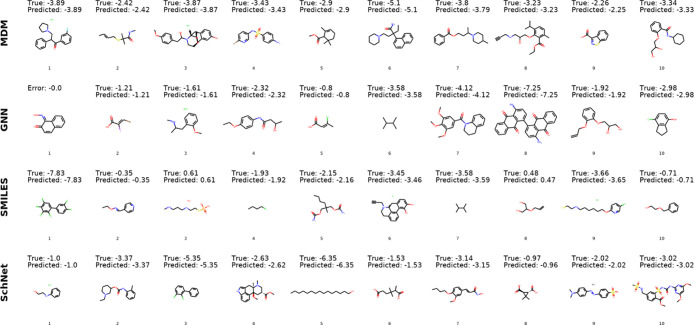
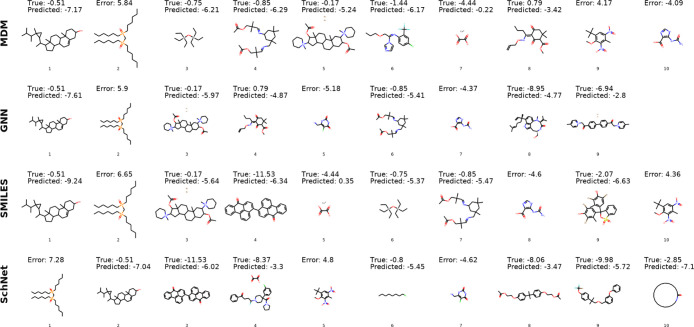
First, we observe the molecules for which the models have exceptionally low or high error values to illustrate the general types of molecules that are well and poorly predicted. Figures 4 and 5 show the top 10 molecules with lowest and highest error for each model. We find that the low error predictions of the MDM model are for molecules with log solubilities in the range of −2.26 to −5.1, showing that the greater data availability for this range of solubilities may improve predictions. While there are no common molecules among the low error instances across all four models, we do observe a significant overlap in the molecules that proved most difficult for the different models.

Figure 4.

Ten lowest error molecules for each model. For molecules from the commercial database Reaxys, we list error values (true-predicted) rather than providing the true solubility measurement.

Figure 5.

Highest error molecules with absolute errors greater than 4 log S. For molecules from the commercial database Reaxys, we list error values (true-predicted) rather than providing the true solubility measurement.

By examining the set of high error molecules, we can identify several potential data labeling issues in the data set. For example, we find that the original reference solubility for molecule 4 (Figure 5) from the high MDM errors is actually the solubility of the decomposed aldehyde product rather than the solubility of the full molecule. For molecule 6 from the high MDM errors, there are two values that exist in the literature, log S = −1.44,⁶⁹ which is the value in the current database, and log S = −4.54,⁷⁰ which is in better agreement with the model prediction.

When collecting measurement data from multiple online sources to compile a large database, the existence of some level of noise and errors in the data cannot be easily avoided. The process of manual validation of measurements is time-consuming and would not be tractable to perform on a database with 17K molecules. The qualitative examination performed here shows that errors made by the predictive models can be used as a signal to identify potential issues arising in the data, informing improvements to future versions of the database. By showing that low performance on some of these molecules can be attributed to data issues rather than true model errors, we also increase confidence in the predictive capabilities of the models.

Errors by Solubility

Next, we observe whether there is any relationship between model error and measured solubility of the molecules. We binned the molecules into solubility ranges and calculated mean and standard deviation of model errors on the test set in each bin, as shown in Figure 6. The corresponding number of training data points for each range is also shown. We find that generally solubility ranges with more data are easier to predict, showing the impact of training data size on model performance. We also find that the models generally have worse errors for low solubility molecules, with higher solubility molecules being easier to predict. However, we should also keep in mind that the predictive task is performed on log solubility, which means that an absolute error of 2 orders of magnitude represents a much smaller actual error for low solubility bins than it does for high solubility bins. It is also known that experimental limitations make it challenging to measure very low solubility values⁷¹ and these measurements are likely associated with high uncertainties.

To further investigate whether the inclusion of low solubility inhibits the performance of our models, we retrained MDM and GNN models using the molecules corresponding to log S greater than −10, −7, −5, −4, and −2. As shown in Table 4, for both MDM and GNN, we observe a significant improvement in the RMSE and MAE for predictions made on high solubility data compared to low solubility ones, indicating that there is likely less absolute uncertainty in the high solubility molecules. However, we find that the correlational metrics gets worse as the data are filtered, showing that the relative solubility of the low solubility molecules still provides a useful signal to the models to learn to distinguish high solubility molecules from low solubility molecules.

Table 4. Change in the Test Set Performance as the Low Solubility Molecules are Filtered out of the Data Set^a.

	MDM				GNN
log S thresh	R2	RMSE	Spearman	MAE	R2	RMSE	Spearman	MAE
–10	0.7654	1.0604	0.8763	0.6975	0.7627	1.0663	0.8740	0.7333
–7	0.7461	0.9580	0.8644	0.6351	0.7289	0.9899	0.8576	0.6846
–5	0.7093	0.8423	0.8343	0.5790	0.6910	0.8684	0.8244	0.6153
–4	0.6817	0.7597	0.8106	0.5447	0.6620	0.7828	0.7955	0.5759
–2	0.5206	0.6134	0.6850	0.4564	0.5101	0.6201	0.6572	0.4707

^aResults given in each row were obtained using molecules with log S > “log S thresh”.

Errors by Molecule Type

Next, we aim to determine whether certain types of molecules are more challenging for the model to predict. We select several subsets of our data set by molecule type, such as chiral molecules and inorganic molecules and analyze the model performance for these subsets. The results of this analysis are shown in Table 5. It is interesting to note that chiral compounds can be predicted with better than average accuracies given that the input molecular representations may be less sensitive to stereochemistry. We also find that molecules in our data set that fall into groups of isomers are relatively easy to predict. However, we will show in the Molecule Group Evaluation section that it is difficult for models to distinguish the solubility of molecules within individual groups of isomers. Even though there are 2580 salts and organo-metallic compounds in the training set, the model has found it difficult to learn a generalized mapping function for this group of compounds as we see reduced performance of this group compared with chiral molecules and isomers. It should also be noted that 99% of molecules in this subset are composed of multiple fragments.

Table 5. Test Set Errors by Molecule Type^a.

		MDM		GNN
group	N	R2	RMSE	R2	RMSE
all		0.77	1.05	0.76	1.07
chiral	142	0.85	0.92	0.81	1.03
salts and org.M	230	0.77	1.08	0.76	1.11
isomers	90	0.90	0.76	0.87	0.89
all other	857	0.74	1.08	0.74	1.08

^aN is the number of molecules of each type in the test set; org.M stands for organo-metallic compounds.

Cluster Analysis

To better understand what might be driving the patterns in which molecules are easier and harder to predict, we expand our analysis beyond these predefined molecular classes. We would like to analyze whether particular molecular properties influence the predictive ability of the models. We first checked whether the model errors are correlated with any of the molecular features and found that the highest Pearson correlation coefficient was fairly low at around 0.3.

To move beyond analysis at the individual feature level, we aim to determine groups of similar molecules and compare the achieved error levels on these groups. To identify groups of similar molecules, we apply k-means clustering and manually selected 15 clusters to obtain a small set of molecule groups to analyze. We scaled all the features to zero mean and unit variance to ensure the differing magnitudes of different features does not cause certain features to be more influential in the clustering. We drop six of the resulting clusters that contain less than 10 members. The test errors of the remaining nine clusters are plotted in Figure 7 in ascending order of mean absolute errors of the MDM and GNN models. For each cluster, the 10 molecules closest to the cluster center are shown in Figure S12. We note that for the majority of clusters, the two different modeling and representation approaches show very similar error patterns across the groups. This reinforces our earlier conclusion that despite the difference in information available to the two models, they are able to learn similar structure–property relationship patterns.

Figure 7.

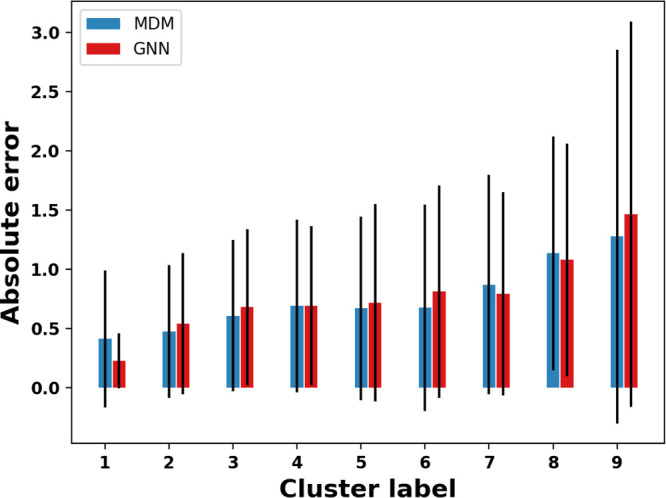
Mean errors by cluster. Error bars indicate the standard deviation across molecules in each cluster.

We observe that there are significant mean error differences across the different clusters and seek to explain which molecular properties of clusters can best explain observed differences in their error levels by looking for correlations between the average errors across clusters and the average molecular descriptors across clusters. Correlation values of highly correlated features with the error are given in Figure S13. Scatter plots of averaged property values with respect to averaged error are shown in Figure S14. We first observe that the cluster errors do not appear to be driven primarily by molecular size, with a correlation of only 0.48 between average error and number of atoms. We do find a moderate negative correlation of mean cluster error with mean cluster solubility (−0.65). This observation reinforces results in Figure 6, which shows molecules with low solubilities are more difficult to predict.

The descriptors *C(C)=O and cenM9 show the highest correlation with the average cluster errors, with Pearson coefficients of 0.95 and 0.92, respectively. *C(C)=O is the count of *C(C)=O fragments in the molecule. cenM9 is a descriptor that quantifies the shape of the molecule and is defined as the 9th statistical moment of the distribution of distances between the centroid and all the atomic positions of a molecule. Another descriptor that has a high positive correlation with the cluster error is SRW05, which is defined as the number of self-returning walk counts of length 5 in the molecular graph. Such self-returning walks can only exist in the presence of three- or five-membered rings, with higher values for molecules with a greater number of such rings. The features cenM9 and SRW05 can be thought of as measures of the complexity of a molecule. Therefore, it seems that the more complex the molecular structure, the more difficult it is to make predictions for such molecules.

Molecule Group Evaluation

We next analyze the ability of the models to accurately distinguish solubilities of structurally similar molecules. For this analysis, we considered three sets of molecules: (1) positional isomers, (2) molecules with same core structures but different functional groups, and (3) molecules containing same type of functional groups attached to different core structures. For example, there are 468 groups of molecules in the isomer set, where each such group consists of n molecules that are isomers of each other. Correspondingly, there are 176 groups of molecules with the same core structure (we excluded isomers from this set) and 21 groups of molecules having the same type of functional groups but different core structures. The details on how these three sets were determined are given in the Supporting Information. The median number of molecules in isomer, same-core, and same-functional-group sets are 2, 4, and 37, respectively.

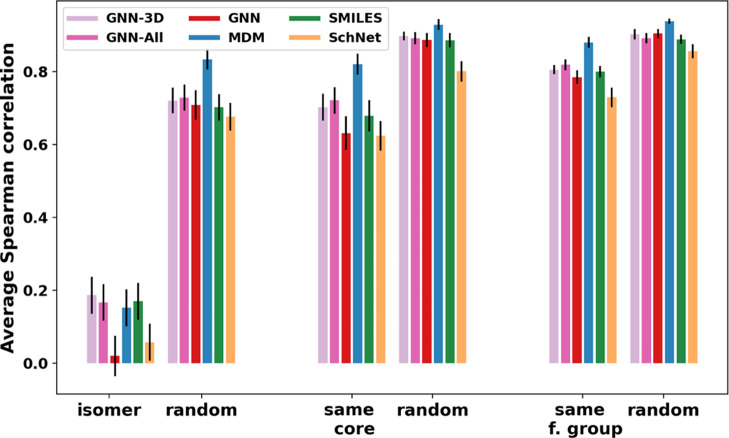
For each sub-group of similar molecules, we calculated the Spearman correlation coefficient between the predicted and actual solubility values. This measure indicates whether the models are able to correctly rank the molecules within the group from highest to lowest solubility. We then average the Spearman correlation across all sub-groups within each of the three sets. The averaged Spearman correlation for each set is shown in Figure 8. We compare the Spearman correlation observed for these groups of molecules with the correlation achieved for randomly selected groups of molecules of the same size. We find that, for the same core and functional group sets, the MDM model is able to correctly rank molecules almost as well as it can for random groups of molecules. This is a particular strength of that model over the other three architectures.

Figure 8.

Spearman correlation of actual and predicted solubilities in groups of similar molecules compared with groups of random molecules. We show results for the four main models (GNN, MDM, SMILES, and SchNet) as well as two GNN variants (GNN-3D and GNN-All) discussed in the Feature Analysis section.

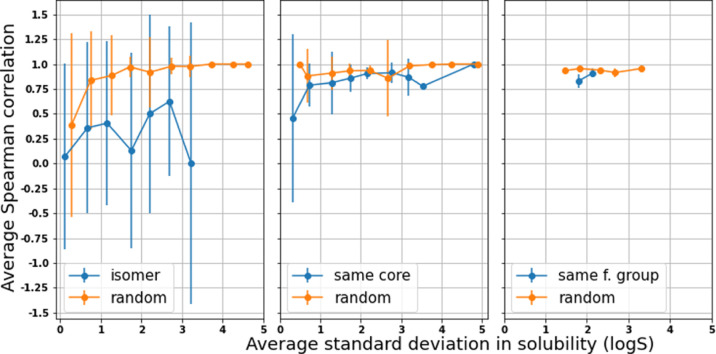
However, the ability to rank order the solubilities of molecules in the isomer set is significantly more challenging compared with the other two sets. This result could potentially be explained using the fact that the solubilities in the isomer set do not vary as much as those in a randomly chosen sample (see Figure S8). However, in Figure 9, we show the Spearman correlation between predicted and actual solubility values versus the level of variability within the group of molecules (as measured by the standard deviation). We see that the Spearman correlation is significantly lower for groups of isomers than for groups of random molecules even after controlling for the level of solubility variation within the group. This shows that the ability to distinguish the effect of functional group positioning on solubility is a key area of improvement for future modeling efforts.

Figure 9.

Spearman correlation versus the within-group standard deviation for isomer/same core/same functional groups for the MDM model.

Feature Analysis

We next seek to analyze the importance of different feature types on the ability of the MDM model to accurately predict the solubility. We do this by training alternate versions of the model with certain feature sets added or removed.

While there is a benefit to the development of models that do not depend on inputs requiring computationally and temporally expensive calculations such as DFT, we tested the effect of adding such inputs to our models using a subset of the data for which the quantum descriptors were available. Table 6 summarizes the effect of adding these features. It is interesting to note that by using only eight quantum descriptors, the model can achieve reasonable accuracies, even though these accuracies are not as high as those obtained with Mordred-generated molecular descriptors. However, the combination of both quantum mechanical and Mordred-generated features does not result in an improvement compared with the accuracies obtained using the molecular descriptors alone.

Table 6. Comparison of the Cross Validated Model Performance due to the Inclusion of Different Types of Features in the MDM and GNN Models^a.

model	features	R2	RMSE	Spearman
MDM	DFTb	0.68 ± 0.02	1.23 ± 0.02	0.79 ± 0.01
	Mol.b	0.79±0.02	0.99±0.02	0.88±0.01
	Mol. + DFTb	0.79±0.02	0.99±0.02	0.88±0.01
MDM	2Dc	0.77±0.01	1.08±0.02	0.88±0.01
	3Dc	0.39 ± 0.01	1.76 ± 0.03	0.61 ± 0.01
	2D + 3Dc	0.77±0.01	1.08±0.03	0.88±0.01
	2D + 3Datom-typec	0.76 ± 0.01	1.10 ± 0.03	0.88 ± 0.01
MDM	w/o MPb	0.79 ± 0.01	1.04 ± 0.02	0.89 ± 0.00
	with MPb	0.79 ± 0.01	1.03 ± 0.02	0.89 ± 0.01
MDM	w/o WSb	0.79 ± 0.01	0.96 ± 0.04	0.89 ± 0.01
	with WSb	0.79 ± 0.01	0.96 ± 0.03	0.89 ± 0.00
GNN	w/o 3D coordinatesb	0.73±0.01	1.15±0.05	0.86±0.01
	with 3D coordinatesb	0.71 ± 0.01	1.20 ± 0.04	0.85 ± 0.00
MetaLayer	2Dc	0.74±0.02	1.16 ± 0.04	0.87±0.00
	3Dc	0.71 ± 0.03	1.20 ± 0.07	0.85 ± 0.02
	2D + 3Dc	0.74±0.02	1.15±0.04	0.87±0.00

^a2D denotes 743 2D descriptors and 59 molecular fragments. 3D denotes 37 3D descriptors. 3D_atom-type denotes 3D descriptors containing atom type information. MP and WS represent melting point and Sterimol parameters.

^bObtained using the entire data set.

^cObtained using the molecules for which the relevant descriptors were available or able to be calculated.

We want to understand the importance of 3D molecular shape information on supporting solubility prediction. Therefore, we compare the effect of 2D and 3D descriptors on model performance. In Table 6, we list the MDM model accuracies obtained using 2D descriptors alone, 3D descriptors alone, and the combination of both 2D and 3D descriptors. Even with just 2D descriptors, MDM is capable of outperforming our GNN model. The 3D descriptors alone do not have significant predictive power. More surprisingly, we do not see a boost in performance when 3D descriptors were added to the 2D model. While we expect 3D structural information to be relevant to determine solubility, it may be that the approximated 3D coordinates calculated using force field methods implemented in Pybel do not provide sufficient accuracy for fully extracting the structure-solubility relationship. If these coordinates, which might not be as accurate as the ones generated using first-principal’s calculations, do not correspond to the actual geometry, it could adversely affect the quality and effectiveness of models trained on these descriptors. Additionally, the 3D information may provide a benefit for certain subsets of the solubility prediction task, such as distinguishing the solubility of very structurally similar molecules, without providing a significant boost to the overall predictive performance. Our 3D descriptors only encode information about the 3D layout of the molecule but are missing information about the types of atoms in the molecule. In order to check whether 3D descriptors equipped with atom type information can improve the prediction accuracy, we modified two of the current 3D descriptors. Instead of just considering the number of atoms in concentric layers around the centroid, we considered different types of atoms in concentric layers. The descriptors proposed by Ballester and Richards⁴⁷ which encode the shape of the molecule were also modified to consider the distributions of distances to different types of atoms from the centroid, closest atom to the centroid, and farthest atom to the centroid. Ten atom types that are most common in our data set were used to calculate these descriptors. After removing four descriptors that have only one unique value, the resultant number of new descriptors is 176. In Table 6, we show the prediction accuracies obtained when type-independent 3D descriptors were replaced by type-dependent ones. The use of type-dependent descriptors resulted in slightly worse prediction accuracies than what have been already achieved using the type-independent counterparts. It is likely that the new descriptors are still not sufficiently informative and the increase in the total number of features could have introduced some noise to the data set. In a future work, we plan to design new complex 3D descriptors coupled with feature selection to encode more structural information.

Melting point and solubility are considered to be inversely proportional.⁷² Using 4652 molecules for which measured melting point values are available, we tested the effect of using the melting point as a feature for solubility prediction. Interestingly, as shown in Table 6, we do not see a significant effect due to using melting point as a feature, showing that using structural information alone provides as much predictive power as the use of relevant experimental measurements. Not only does melting point not provide additional predictive power beyond structural information but it also appears to provide little predictive power on its own for this data set. Using melting point as the only feature achieved an R² of 0.02 and an RMSE of 2.26 which provides little improvement over the RMSE of 2.28 from simply using the mean log S value as the prediction.

Motivated by several works that have studied the relationship between steric effects and solvation, we tested the importance of Sterimol parameters for solubility prediction.^73,74 This comparison has been especially frequently established when discussing sterics as a part of common organic chemical reactions.⁷⁵ Sterimol parameters have been developed to describe the steric effects in molecules.⁷⁶⁻⁷⁸ More details on the Sterimol parameters are presented in the Supporting Information. We find that our MDM model does not seem to be improved due to adding three Sterimol parameters, B₁, B₅, and L₁ as features. Additionally, training a model using only these parameters as input resulted in an RMSE of 2.09 and an R² around 0.02.

The node features of our GNN model depend only on the 2D structural representation of the molecule. As an initial test to check whether incorporating any 3D information have an effect on GNN model accuracy, we added atomic coordinates as node features. These coordinates were generated using Pybel and some molecules were discarded after they failed in this generation. We find that adding 3D atomic coordinates as node features does not improve the GNN model performance. Learning the relevant 3D structural features of the compound using atomic coordinates alone as node features seems to be challenging.

An alternate method to add 3D information to the GNN model is to leverage the 3D descriptors as an additional input to the model. Recently, the MetaLayer model⁷⁹ has been proposed as a graph neural architecture which is capable of learning from properties “global” to the entire graph structure, which allows us to use the molecular descriptors as an additional input to our GNN model. The results given in Table 6 shows, consistent with the MDM results, that the 2D descriptors are individually more informative than the 3D descriptors. However, the addition of the molecular descriptors is not strong enough to surpass the accuracies obtained by our original GNN model.

While the MetaLayer model does not improve on the overall performance, we find that this approach can achieve better accuracies for groups of similar molecules compared to the original GNN model, which may suffer from a lack of 3D information needed to distinguish isomers. These results are shown in comparison with the original GNN model in Figure 8. We see the MetaLayer model that uses only 3D descriptors outperforms all the other models in rank-ordering the solubility values in each isomer group.

Effects of Data Size

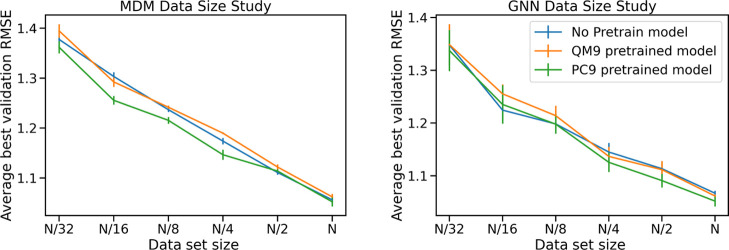
While deep learning models have been shown to excel at learning complex patterns such as those involved in structure–property relationships, they also typically have large data requirements to achieve good performance at these complex tasks. We perform several analyses to study the impact of data set size on our model performance. First, we study the impact of transfer learning by pretraining models on large external data sets before fine-tuning on the solubility prediction task. Second, we evaluate our models with smaller subsamples of our data.

Transfer Learning

Transfer learning is a machine learning technique in which the knowledge a model gains from training on one task is transferred to improve performance on a second task. We apply transfer learning to the solubility prediction task by first pretraining our models on two large data sets, QM9 and PC9. While these data sets do not contain solubility labels, they are 9 and 7 times larger than our solubility database, respectively, and can help the model learn patterns that relate molecular structure to molecular properties. To perform transfer learning, we first train MDM and GNN models to predict all the molecular properties included with the QM9 and PC9 data sets and then, starting from weights learned on the QM9 or PC9 data set, we perform further training using the solubility data.

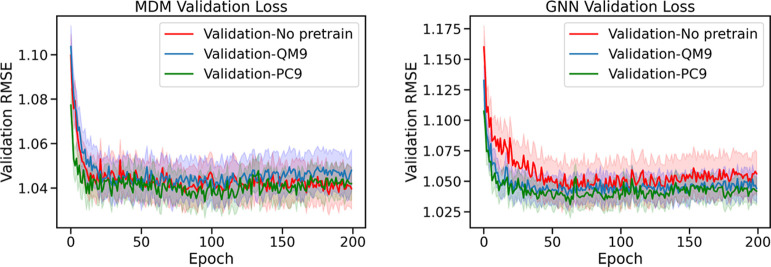
In Figure 10, we show the learning curves of the MDM and GNN models both with and without pretraining, showing how the RMSE decreases during training. We find that pretraining with PC9 data improves the initial performance of the models at the start of training for both the MDM and GNN models. However, for the MDM model the pretraining on the external data sets does not seem to improve the ultimate achieved performance after fine-tuning. The GNN model on the other hand, benefits from pretraining with both PC9 and QM9 throughout the training process and pretrained models achieve improved final performance compared with the non-pretrained model with RMSE dropping from 1.0722 to 1.0656 due to pretraining. Because the GNN model learns from raw molecular structure while the MDM model learns from pre-derived features, the GNN model benefits more from the additional training data, which can help it learn the complex relationship between the raw molecular structure and resulting properties.

Figure 10.

Learning curves for the MDM model (left) and the GNN model (right) with and without pretraining.

We also observe that across the different results, the PC9 data set provides a bigger boost in performance compared with the QM9 data set. This gives evidence for the assertion in Glavatskikh et al.⁶¹ that the PC9 data set improves upon the chemical diversity of QM9, leading to better generalization of the patterns learned from the data set to other data sets and tasks.

Data Size Sensitivity

To investigate the effect of increasing the size of our data set, we conducted a data ablation study by decreasing the size of the training data set, with a fixed test set, and analyzed the final test accuracy for each training data set size. The data set sizes were calculated by taking the full data set and dividing by increasing integer powers of two, 2⁰, 2¹, 2², 2³, and 2⁴. This results in data sets that are 100, 50, 25, 12.5, and 6.25% of the total size. We trained the MDM model and GNN model on each data set size in three configurations—from a random weight initialization, from the pretrained QM9 weights, and from the pretrained PC9 weights. Each model and configuration was trained five times on a given data set size using the Adam optimizer with a learning rate = 0.001 for 100 epochs.

Figure 11 shows the mean and standard deviation of the best validation root-mean-squared-error for each data set size both with and without pretraining. We can see the root-mean-squared-error is still decreasing as the data set size is increased from half to full, suggesting that increasing our data set size will continue to improve results. However, it should be noted that as the x-axis is the power of two dividing the full data set size, this improvement in results will have diminishing returns with respect to the number of data examples added to training. For example, by extrapolating the observed trajectory, we would expect to need to double the training set size to reduce the RMSE below 1 order of magnitude for the MDM model.

Figure 11.

Model performance (RMSE) as a function of training set size for the MDM model (left) and the GNN model (right).

This study also shows some interesting patterns with regard to the combined impact of pretraining and data size. For the MDM, PC9 appears to have a benefit on performance for small solubility data sets but not for large ones. In contrast, the benefit of PC9 pretraining appears for larger data sets using the GNN model. This difference is likely due to the different requirements of the two models. The MDM model needs to learn a transformation from high-level structural descriptors to the target labels, while the GNN needs to learn a transformation from raw structure information to the target labels. The GNN may need a larger solubility data set in order to learn to adapt the patterns that it learned from PC9 to the new solubility target. Meanwhile, the patterns the MDM must learn are simpler so it can quickly adapt the learning from PC9 with a smaller solubility data set, and, given a large enough data set, it can eventually learn the structure-solubility relationship well enough that it cannot be improved by pretraining.

Conclusions and Future Work

We performed a comparison of different deep learning modeling approaches and molecular representations for the prediction of aqueous solubility using the largest set of solubility measurements to date. Through the use of large, diverse data sets combined with deep learning methods, we demonstrate equal or improved performance on many existing solubility prediction data sets. Overall, we found the best performing approach leveraged a set of derived molecular features which comprehensively describe the molecular structure rather than approaches which leverage raw molecular structure information directly. This contrasts with previous studies which have shown the power of deep learning for learning structure–property relationships directly from raw structure.^18,38 Of the models which did rely on raw structure, graph-based molecular representation showed the strongest performance, almost equaling the MDM model in overall performance but showing reduced ability to distinguish the solubilities of similar groups of positional isomers.

The superior performance of the MDM model is likely due to its ability to create a better representation for molecules by mixing a large number of information-rich structural descriptors without the need to learn from raw structure. However, given that the GNN model is the only one that does not use any 3D information, its achieved performance accuracies are noteworthy. Additionally, even though SchNet was designed to harness the structural information from 3D atomic coordinates, it significantly underperformed the other modeling approaches. We suspect the small training set size compared to the data sets originally used for the SchNet model might have played a role in this result. Computational requirements also limited the hyper-parameter optimization we were able to perform with this architecture.

There are also considerations other than model accuracy in terms of practical implementation of the different models, including speed and efficiency of computation. In addition to its high accuracy, the MDM is fast to train compared to the other modeling approaches which leverage more complex architectures. However, this model requires the generation of molecular features, which is slow, and if 3D features are to be included, then atomic coordinates are required. The best form of 3D coordinates is the ones obtained experimentally, but this is not tractable for large data sets. The next best alternative is to optimize geometries using first-principles calculations. These calculations are time-consuming and obtaining these coordinates for large molecules is not practical. Approximated 3D coordinates can be calculated relatively quickly; however, these coordinates are often not reproducible, which could lead to inconsistent results.

In addition to the evaluation of the overall performance of the models, we performed extensive analysis of the errors observed for different modeling approaches. This error analysis leads to several key findings. Models with differing data representations and architectures make highly correlated errors, showing that they are learning similar structure–property relationships. Model errors are lower for molecules with higher solubility and for solubility ranges with larger amounts of training data and higher for more complex molecules. The models struggle to infer the effect of small structural changes, such as functional group position, on the molecular solubility. Contrary with expectations, 3D information about molecular structure has a limited impact on overall model accuracy. However, it does lead to improved, but still limited, performance on solubility prediction for isomer groups.

Our analyses identify several key directions for improving the predictive performance of solubility prediction models. We determined that pretraining models with large external data sets can provide a performance boost for model architectures which rely on raw structural inputs. While we have initially explored only two such data sets, there is potential for significant improvements using even larger supervised or unsupervised pretraining. We have also confirmed that the number of data points available for training plays a significant role in predictive performance, motivating the collection of additional solubility measurements. However, for some solubility ranges, such as those in the lower or higher ranges, gathering more data can be difficult. Targeting data collection to achieve good coverage in the target solubility ranges of interest for a given application will be key. It is also clear that improvements are needed in the prediction of solubilities of very similar molecules and molecules with multiple fragments, which is likely related to both limitations of the available training data and limitations of current molecular representations and architectures. The collection of focused data sets designed to supervise the improved performance on these molecular types as well as the development of novel representations and model techniques should be targeted for achieving performance improvements.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c00642.

• Descriptors used for MDM model; comparison of structural properties of different data sets; duplicate removal process; structure-solubility exploration; GNN architecture; binning solubilities for stratified splitting of the database into train/test and validation folds; hyper-parameter tuning; molecular fragment analysis; and cluster analysis (PDF)

• Solubility data (XLSX)

The authors declare no competing financial interest.

Notes

The source code is available on GitHub at https://github.com/pnnl/solubility-prediction-paper. Part of the data set prepared by Gao et al.⁴⁰ is accessible at https://figshare.com/s/6258a546a27a2373bf2a and the other part is provided as part of the Supporting Information.