Abstract
We present fast classification techniques for sparse generalized linear and additive models. These techniques can handle thousands of features and thousands of observations in minutes, even in the presence of many highly correlated features. For fast sparse logistic regression, our computational speed-up over other best-subset search techniques owes to linear and quadratic surrogate cuts for the logistic loss that allow us to efficiently screen features for elimination, as well as use of a priority queue that favors a more uniform exploration of features. As an alternative to the logistic loss, we propose the exponential loss, which permits an analytical solution to the line search at each iteration. Our algorithms are generally 2 to 5 times faster than previous approaches. They produce interpretable models that have accuracy comparable to black box models on challenging datasets.
1. INTRODUCTION
Our goal is to produce sparse generalized linear models or sparse generalized additive models from large datasets in under a minute, even in the presence of highly-correlated features. Specifically, our interest is in the following problem:
| (1) |
with the logistic loss
or the exponential loss
where is the i-th observation, and yi ∈ {−1, 1} is the label of the i-th data sample. The logistic loss tends to yield nicely calibrated probability estimates, which explains its broad appeal. The exponential loss, used in boosting, has been overlooked as an approach to sparse additive modeling, but like logistic regression, it also yields direct probability estimates. It has the advantage of analytical solutions for line search, dramatically improving convergence rates.
A small ℓ2 regularization is used with the logistic loss to speed up convergence, as discussed later:
| (2) |
We do not include ℓ1: since we are looking for very sparse and accurate models, ℓ1 regularization would degrade the quality of the solution compared to true sparsity regularization with ℓ0. The ℓ0 penalty term makes Problems (1) or (2) NP-hard.
Problems (1) or (2) can produce generalized additive models (Lou et al., 2016; Hastie and Tibshirani, 2017; Nori et al., 2019; Rudin et al., 2022) through a transformation of the input variables, replacing each continuous feature x·,j with a set of dummy variables , for θ set to be each realized value of feature j in the dataset. Then, solving (1) or (2) yields a generalized additive model where component function j is a sum of the weighted dummy variables for feature j. This transformation yields a large feature set with many correlated features, but the approaches provided here can handle such sizes.
There are at least two general approaches for tackling these problem (besides relaxing the ℓ0 term to ℓ1 and suffering the associated bias). The first uses call-backs to a mathematical programming solver, such as a mixed-integer programming (MIP) solver (Sato et al., 2016; Ustun and Rudin, 2017; Sato et al., 2017; Bertsimas and King, 2017; Bertsimas et al., 2021; Ustun and Rudin, 2019). This approach can solve the problem exactly. However, it cannot handle large feature spaces or highly-correlated features. A solver might take several days or run out of memory on even a modestly-sized problem. The second approach to Problems (1) or (2) is to use coordinate descent with local swap operations for best subset search, similar to simulated annealing, Metropolis-Hastings, or other MCMC methods (Metropolis et al., 1953; Kirkpatrick et al., 1983; Del Moral et al., 2006). Our approach is of this second type, though it is important to note that a solution from our method could be used as a warm-start for one of the MIP solvers; a better warm-start is the key to finding optimal solutions faster with MIP.
There are two main steps per iteration in these types of algorithms: (i) coordinate descent steps involving a line search along the objective function, often using a local surrogate function, and (ii) local swaps, where the support set (the set of features permitted to have nonzero coefficients) changes over iterations. Our work advances both of these steps over previous work. For (i), we show that a natural surrogate for the logistic loss used in previous work leads to inefficiency, in that its step sizes are provably too conservative. We propose a more aggressive step. This opens up the possibility of using cutting planes or quadratic cuts. Cuts often help us rapidly prune the search space: by comparing the lower bound from the cuts with the current best loss, we are often able to prove that there is no possible step size we could take that would reduce our objective, in which case we will try a more promising direction in the search space. The ℓ2 penalty term permits us to use quadratic cuts. When we do not want the ℓ2 term (i.e., λ2 = 0), we can use cutting planes. For (ii), we find that the order in which we evaluate features plays an important role, which has been previously overlooked. We use a priority queue to dynamically manage the order of evaluating features. The priority queue discourages us from checking features that are unlikely to change the model’s support set, making the process of finding high-quality solutions more efficient.
In addition, for (i), improving the speed of the coordinate descent steps, we propose to use the exponential loss, which has a major advantage over the logistic loss in that the line search taken at each coordinate descent iteration has an analytical solution. Another appealing property of the exponential loss is that its probabilistic interpretation is extremely similar to that of logistic regression. Also, minimizing the exponential loss is known to provably maximize a proxy for the Area Under the ROC Curve (Ertekin and Rudin, 2011), making it an ideal choice for this problem.
Our contributions are:
We prove that previous work on surrogate loss optimization yields step sizes that are too conservative (Theorem 4.1).
When λ2 = 0, we propose a linear cutting plane algorithm that prunes the search space by efficiently determining whether adding a feature could potentially reduce the objective.
With a small amount of ℓ2 regularization, we propose a quadratic cut algorithm giving a tighter lower bound than the linear cutting plane algorithm.
We propose a method using the exponential loss, which is cleaner and simpler.
For more efficient best subset search, we use a priority queue to dynamically manage the order of checking features.
Our algorithms provide a dramatic improvement over previous approaches, often achieving the same results in less than half the time, and are able to produce models for thousands of features and observations in seconds. For instance, on the challenging FICO dataset from the 2018 Explainable Machine Learning Challenge, which, after the transformation to dummy variables, has 1,917 dummy features and 10K observations, we produce a generalized additive model of 19 total dummy variables, with performance comparable to black-box performance, in under 5 seconds.
2. BACKGROUND
Coordinate descent is popular in machine learning. Other techniques that use variations of it include AdaBoost (Freund and Schapire, 1997) and Sequential Minimal Optimization used for support vector machines (Platt, 1998). Surrogate functions are also common, e.g., they are used by Expectation Maximization (Dempster et al., 1977). We begin with background, following Patrascu and Necoara (2015) and Dedieu et al. (2021).
The loss function in Problem (2) can be rewritten as:
with .
Let us optimize along coordinate j starting at point wt at iteration t. Let ∇jG(wt) denote the j-th component of the gradient of G(wt), and let Lj be the Lipschitz constant for ∇jG(wt). For any :
where ej is a vector with all components equal to 0 except for the j-th component, which is equal to 1. A surrogate upper bound on G(wt + ejd) is thus:
| (3) |
Instead of minimizing the original loss function with respect to coordinate j (as would be typical in coordinate descent), we can minimize this quadratic upper bound with the new coefficient :
Following previous work (Dedieu et al., 2021), we have an analytical solution for the above problem:
| (4) |
where .
If a solution cannot be improved by coordinate descent using this surrogate and thresholding function, we say this solution is surrogate 1-OPT, meaning that no single coordinate can be changed to improve the objective when using this surrogate for the line search.
As discussed earlier, local swap, add, and remove operations are useful for best subset search and other local search problems. These govern the support of the coefficient vector, determining which coefficients are permitted to be nonzero. We use S to denote the support of the feature vector; that is, the set of features that are permitted to have nonzero coefficients. We can swap some features in the current support, denoted by S1 ⊆ S, for other features not in the support, denoted by S2 ⊆ Sc. After each swap, we optimize the coefficients that are permitted to be nonzero.
To reduce computational cost, while evaluating a possible swap, we use an approximate evaluation procedure where we update only the coefficients of the swapped features and keep coefficients of other unswapped features fixed. If such a swap leads to a better loss, we add S2 to the support, remove S1 from the support, and update all coefficients for the features in the new support. We will focus on single feature swaps (i.e. |S1| = |S2| = 1) in this work. If no allowed swap appears to improve the loss, then we call the solution a swap 1-OPT solution.
3. OVERVIEW OF FAST SPARSE LOGISTIC REGRESSION
Let us focus on the logistic loss. Given an initial solution, we optimize one feature’s coefficient at a time, and swap features within the support set to improve the solution. Our technique evaluates whether it could be worthwhile to swap two features. It is based on a theorem showing that thresholding from (4) yields step sizes that are too conservative. Using this information, we develop an algorithm that uses quadratic cuts. Typically, cutting planes (Kelley, 1960) are used in mathematical programming solvers, whereas here, we use cuts as part of efficient feature elimination within coordinate descent. Our second technique uses a priority queue to manage the search order for pairs of features to swap. At each outer iteration, we drop a feature j in the support and at each inner iteration, we evaluate adding a feature j′. The full pseudocode is in Appendix B. The main steps are:
Remove and find alternatives. According to the priority queue, try removing feature j from the current support. Find J′ features outside the support as alternatives for feature j. These alternative features are picked according to orthogonal matching pursuit (Lozano et al., 2011). For each feature j′ ∈ J′, we evaluate whether it is worthwhile to include it in our support as a replacement of feature j. This is done using the following procedures.
Aggressive step. Given a new feature j′ that we may want to include in our support, we wish to find two values on opposite sides of the optimal coefficient . However, at current value wj′, the thresholding results stay on a single side of the optimal value (as we will prove in Theorem 4.1). Thus, we take an aggressive step by going double the distance suggested by thresholding, or triple the distance if necessary. If this triple-sized step does not get to the opposite side of , we iteratively apply thresholding (4) to get a near-optimal coefficient and move to Step 6.
Binary search. Suppose we have found two values a and b on opposite sides of . We then perform one binary search step to get a point closer to by setting c to be the midpoint, . If c is on the same side of a, we replace a with c; if not, we replace b with c. We use quadratic cuts (via the Quadratic Cut Bound, Theorem 4.3) at points a and b to obtain a lower bound on the objective for the optimal coefficient of the feature. In the case of no ℓ2 regularization, we use cutting planes instead. More detail on this is in the next section.
Eliminate. If the lower bound is larger than the current best loss we have encountered so far, the new feature can be eliminated from consideration; we do not add this feature into our support. We move onto the next possible feature and start again from Step 2.
Line search. If the lower bound is smaller than the current best loss we have encountered, then feature j′ could lead to a better solution. Therefore, we iteratively use thresholding (4) to obtain a near-optimal coefficient for the line search. (Alternatively, we could continue binary search for the minimum.)
Complete the step. We then calculate the loss with respect to this near-optimal coefficient for the line search. If the loss is higher than the current best loss, we eliminate this feature and move to the next best alternative feature; if the loss is lower, we add this new feature j′ into the support to make up for the removed feature j and optimize all of the coefficients, completing a successful swap step.
Update priority queue. If no alternative feature can replace feature j, we add feature j back into the support and rate feature j less promising in our priority queue. This allows us to explore features that have a better chance of being swapped with an alternative feature next time.
4. SURROGATE QUADRATIC CUTS
Let us provide the theorem motivating our coordinate descent method for the logistic loss, which shows that the step sizes from thresholding in (4) are too conservative. Recall that thresholding is derived by minimizing a quadratic upper bound of the loss function. The coefficient of the quadratic function is the Lipschitz constant, which defines the maximum curvature the loss function can achieve. These connections imply:
Theorem 4.1. (Thresholding is too conservative.) Let wt be the current solution at iteration t, be the coefficient for the j-th feature, and let be the optimal value on the j-th coefficient while keeping all other coefficients fixed to their values at time t. Furthermore, let , where ej is a vector with 1 on the j-th component and 0 otherwise and T (j, wt) is the thresholding operation with the support set fixed (i.e., λ0 = 0). Then we have the following inequalities:
| (5) |
| (6) |
| (7) |
This result shows that the thresholding operation will move the coefficient of the j-th feature closer to the optimal value with a smaller loss value, as shown by (7). However, the coefficients before and after the thresholding operation will always remain on the same side of , as shown by either (6) or (5). To see this, consider (6). We have two scalars of the same sign: and . If were on the opposite side of w* than , the product of these two scalars would instead be negative. Alternatively, by (5), if the slope of G at wt is negative, the slope at wt+1 is also negative, indicating that we have not yet passed the minimum (of our convex logistic loss). Thus, this theorem indicates that the step size provided by the surrogate is too conservative; the distance is always too small to reach . Figure 1 (left) illustrates this issue. The algorithm may make several steps before becoming sufficiently close to .
Figure 1:
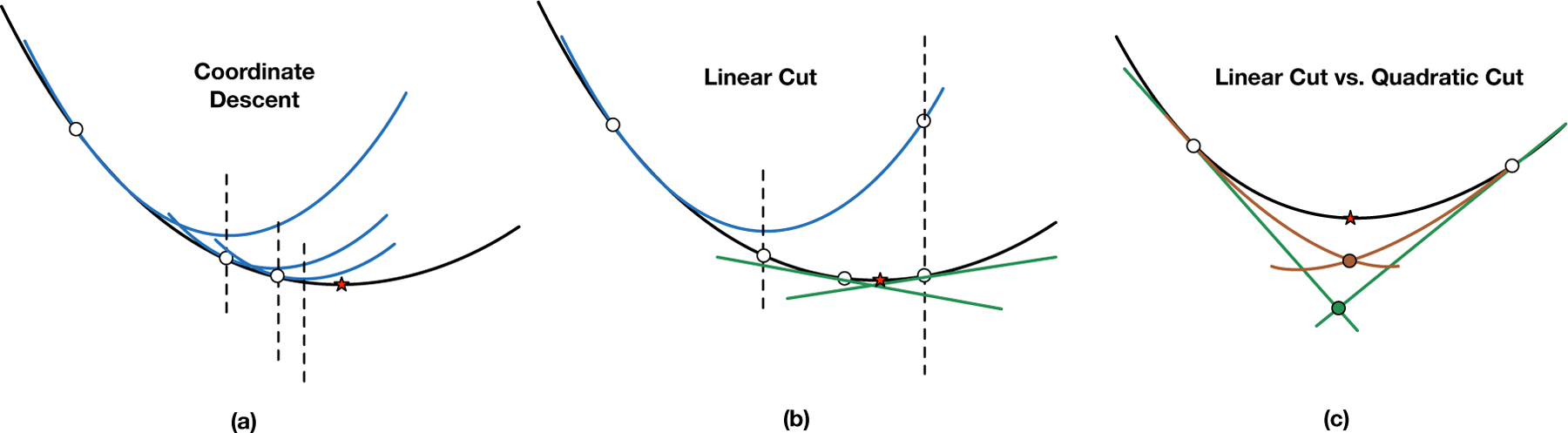
(a) We repeatedly apply coordinate descent until convergence to get the optimal coefficient (shown by the red star) and then calculate the loss. (b) We calculate a lower bound of the optimal loss by constructing two cutting planes. We can rule out the new feature if the lower bound of the loss from the cutting planes is larger than the best current loss. (c) Quadratic cuts (in red) form the lower bound instead and are tighter.
Our technique chooses an aggressive step size that takes us beyond , in order to use cuts to produce a lower bound on the loss at w*. If the lower bound is too high, we can exclude the feature all together.
The first type of cut we introduce is classical cutting planes, which provide a linear lower bound on the loss. This can be used even if we have only ℓ0 regularization on the logistic loss (i.e., if λ2 in (2) is 0). With an additional ℓ2 penalty term, we can obtain a strictly tighter lower bound on the loss, yielding quadratic cuts. We introduce both types of cuts next, starting with cutting planes.
Theorem 4.2. (Classical cutting planes, not novel to this paper) Suppose f(x) is convex and differentiable on domain . Let α1 and α2 be slopes of tangent lines of f(x) at locations x1 and x2. If α1α2 ≤ 0, there is a lower bound on the optimal value f(x*):
| (8) |
This method originates from a first-order approximation of function f(x). Figure 1(b) shows linear cuts.
With an additional ℓ2 penalty term, we can obtain a strictly tighter lower bound on the loss via quadratic cuts. The ℓ2 term makes G(w) strongly convex, which means for any two points w and w′ in the domain:
Using this strongly convex property, we can tighten the lower bound given in Theorem 4.2 as follows:
Theorem 4.3. (Quadratic Cut Bound) Suppose f(x) is strongly convex and differentiable over with λ2 for the coefficient of the quadratic term. Let α1 be the slope of the tangent line to f(x) at location x1. Then, there is a lower bound on the optimal value f(x*):
| (9) |
Let α2 be the slope of the tangent line to f(x) at another location x2. If α1α2 ≤ 0, a lower bound on the optimal value f(x*) is as follows:
| (10) |
Since this method originates from a second-order approximation of the function f(x), we name this bound the Quadratic Cut Bound. Either this bound or cutting planes helps us decide when not to include a potential feature in our support, even without knowing its optimal coefficient from the line search.
5. FAST SPARSE CLASSIFICATION WITH EXPONENTIAL LOSS
Let us now switch from logistic loss to the exponential loss, optimizing:
Though exponential loss typically is not used for sparse classification, it has no clear disadvantages over the logistic loss and even has several advantages. First we point out that exponential loss and logistic loss have remarkably similar probabilistic interpretations under the assumption that we have captured the correct set of features. While logistic regression estimates conditional probabilities as where f(x) = wTx, the exponential loss has almost the same probabilistic model: . Thus, both loss functions are equally relevant for modeling conditional probabilities.
The main benefit of exponential loss is that it has an analytical solution for the line search at each iteration when features are binary (−1 and 1). This avoids the necessity for cutting planes, quadratic cuts, or even surrogate upper bounds. Following the derivation of AdaBoost as a coordinate descent method (Schapire and Freund, 2013), its line search solution follows the formula , where d− indicates the weighted misclassification error of the feature chosen at iteration t (here we are interpreting each weak classifier as an individual feature, and the weak learning algorithm picks one of these features per iteration). AdaBoost’s weight update step avoids calculation of the exponential loss at each iteration, and the full procedure is extremely efficient. (The main difference between our method and this reduced version of AdaBoost is that AdaBoost is not designed to yield sparse models.) In the following theorem, we provide a condition under which our method would decline to add a new feature at iteration t, because it does not provide an overall benefit to our objective. We use with zi = yixi to succinctly represent the product between yi and xi. The objective can be then rewritten as:
where .
Theorem 5.1. Let wt be the coefficient vector at iteration t, Ht ≔ H(wt) and λ0 be the regularization constant for the ℓ0 penalty. For the j-th coordinate, we update the coefficient according to:
- Suppose . Let , with ci = exp(−(wt)Tzi). If d− is within the interval:
then set to 0. Otherwise set . - Suppose . Let , with . Let . If D− is within the interval:
then set to 0. Otherwise, set .
Another potential benefit of the exponential loss is that it is a surrogate for the AUC, i.e., Area Under the ROC Curve (Ertekin and Rudin, 2011). Thus, we have reason to expect good AUC performance when optimizing the exponential loss.
6. DYNAMIC FEATURE ORDERING
Now that we can optimize along the coordinates using either logistic loss (Sections 3 and 4) or exponential loss (Section 5), we discuss the important swap steps that help the algorithm drop features that have promising swap candidates. As stated in Section 3, after coordinate descent is run until a local minimum is reached, we alternate between coordinate descent steps and swap steps. The technique proposed here is broadly applicable and can improve the speed not only for the logistic loss and the exponential loss but also for the squared loss in linear regression (see Appendix D.1).
We focus on the swap 1-OPT solutions (i.e., |S1| = |S2| = 1). The order of checking features in S1 for possible swaps is key to improving the efficiency. Instead of checking features in S1 sequentially based on feature indices (Dedieu et al., 2021), we dynamically order these features via a priority queue. We provide an example in Figure 2 to illustrate the key difference between the two approaches.
Figure 2:

Sequential Ordering vs. Dynamic Ordering. Upper: We check each feature sequentially. Whenever we find a better feature, we always start from the beginning to find the next possible swap. Lower: We order the list, checking the feature that has failed the least amount of times first. We hold off checking less promising features until the end, saving substantial computational time.
Suppose we have an initial solution with support on features 1, 3, 7, 9, 11, and 15, and features 3 and 9 are suboptimal. We can swap feature 3 with feature 5 and feature 9 with feature 10 to get a lower total loss. The first method checks features sequentially and always starts from the first index in the support after a successful swap. The algorithm terminates if we have checked all features without making any swaps. This method implicitly assumes that each feature in the support has an equal probability of having a successful swap. However, a feature that has not been swapped for many iterations is likely to be important and therefore unlikely to be swapped in the near future. It is better to check more promising features first.
To achieve this, we record how many times a feature has failed to swap. The features are ranked in ascending order of the number of failure times. Features that have never been checked are kept at the top of our priority queue. This local search process terminates when all features have been evaluated (i.e., the full priority queue) without making a successful swap. This accelerates the process to reach a swap 1-OPT solution.
7. EXPERIMENTS
Our evaluation answers the following questions: (1) How well do our early pruning technique, priority queue ordering, and proposed exponential loss perform in terms of run time relative to the state-of-the-art? (§7.1) (2) How well do our methods perform in terms of AUC, accuracy, and sparsity relative to state-of-the-art algorithms on simulated and real datasets? (§7.2)
We compare our methods to ℓ1 regularized logistic regression (LASSO) via the glmnet package (Friedman et al., 2010), MCP via the ncvreg package (Breheny and Huang, 2011), and L0Learn (Dedieu et al., 2021). We use the fast C++ linear algebra libraries of L0Learn in our implementation. For all datasets, we run 5-fold cross validation and report the mean and standard deviation. Appendix C presents the experimental setup, datasets, and evaluation metrics, and Appendix D presents additional experimental results. Our methods are denoted as LogRegQuad-L0 (logistic loss and quadratic cuts) and Exp-L0 (exponential loss).
7.1. Computational Efficiency
To examine the impact of the quadratic cuts and dynamic ordering, we first run our algorithm with only quadratic cuts and then enable dynamic ordering on the FICO dataset from the Explainable Machine Learning Challenge (FICO et al., 2018). We also run this experiment using Exp-L0. L0Learn is used as a baseline. (MCP and LASSO use continuous regularization terms, which provides them with a run-time advantage, though these methods do not perform as well, as shown in the next subsections.) The ℓ0 parameters we used are {0.8, 1, 2, 3, 4, 5, 6, 7} and the ℓ2 parameters used are {0.00001, 0.001}.
Figure 3 shows the training time and AUC values on the FICO dataset. The methods achieve performance comparable with Chen et al. (2021), who reported best black-box AUC ~0.8. Our method using only linear cuts (purple bars) runs faster than the baseline (orange bars, L0Learn) for all regularization options. With ℓ2 regularization coefficient λ2 = 0.001, the time is reduced when we switch from using linear cuts to quadratic cuts (green bars) due to the tighter lower bound, as in Figure 1. The training time is further reduced by using both quadratic cuts and dynamic ordering (blue bars, which is LogRegQuad-L0). Exp-L0 (red bars) is the fastest approach. Again, this speed-up owes to the analytical line search and fast update.
Figure 3:
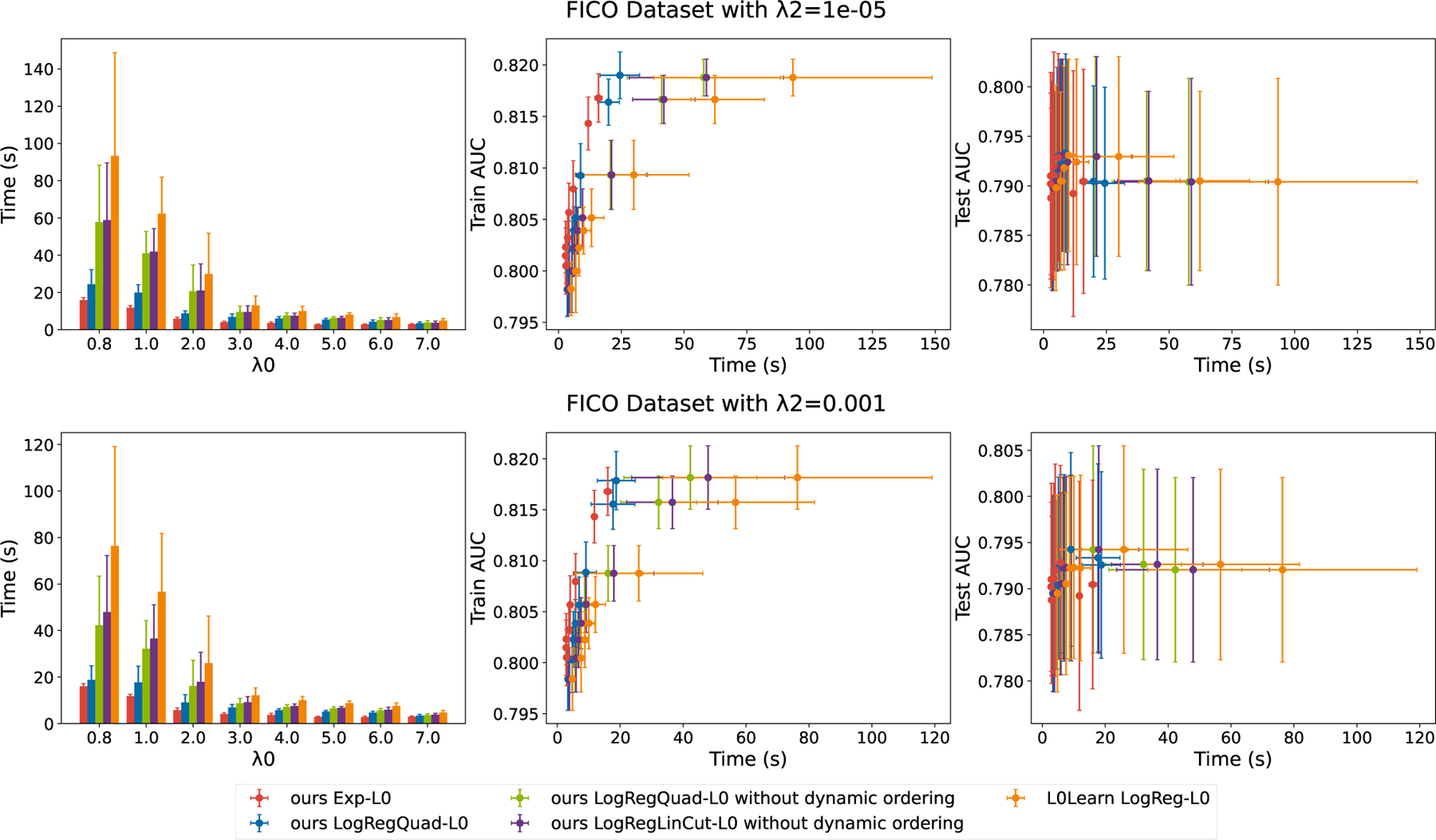
Computational times of different methods. “Exp” stands for exponential loss, “LogReg” stands for logistic loss, “LinCut” stands for linear cuts, and “Quad” stands for quadratic cuts. Note that there is no ℓ2 penalty for the exponential loss. Our Exp-L0 method is generally about 4 times faster than L0Learn. Note that the AUC axes indicate practically similar performance for these particular methods; the training time is what differentiates the methods. Additionally, when the ℓ2 penalty increases from λ2 = 1e − 05 to λ2 = 0.001, there is a computational speedup from using the linear cut to the quadratic cut due to the tighter lower bound.
From the four rightmost subfigures, we find that our improvement in training time does not negatively impact training/test AUC scores, as our methods (red and blue dots) form a “left frontier” with respect to the baseline L0Learn (orange dots). Results for additional datasets are in Appendix D.2.
7.2. Solution Quality
We next evaluate sparsity vs. performance. In addition to AUC on the datasets, we calculate Recovery-F1 score to measure how well we captured the ground truth support (ground truth coefficients w* are known for simulated datasets). Recovery-F1 score is , where is the precision and is the recall. supp(·) stands for the support (indices with nonzero coefficients) of a solution. We can use Recovery-F1 score for synthetic data only, since we need to know w* to calculate it.
Synthetic Data:
Figure 4 shows sparsity/AUC tradeoffs and sparsity/Recovery-F1 tradeoffs on a synthetic dataset consisting of highly correlated features. Our methods are generally tied for the best results. LASSO (pink curves) and MCP (green curves) do not fully optimize the AUC, nor recover the correct support. For the full regularization path, the AUC’s of L0Learn and our method largely overlap. However, as demonstrated in the previous subsection, our method runs much more quickly than L0Learn.
Figure 4:
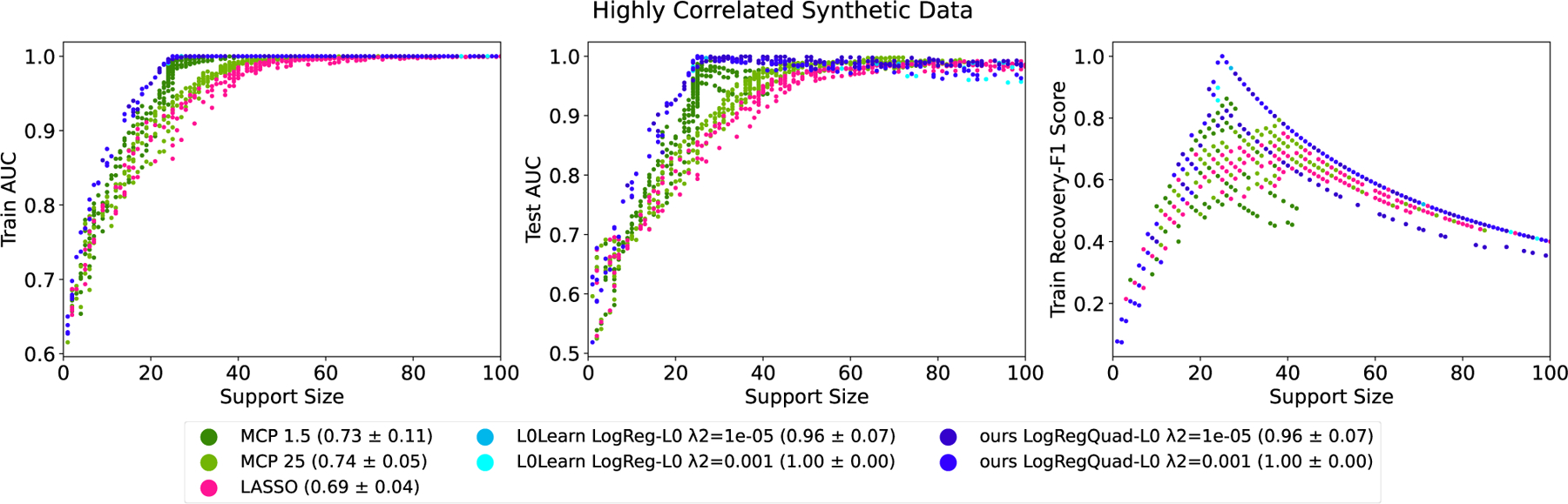
Results from all 5 datasets (each dataset generated by a different random seed) and parameter choices on highly correlated synthetic datasets. The parentheses contain the best Recovery-F1 scores averaged over all 5 datasets. MCP is shown with γ fixed at 1.5 and 25, and all other choices for γ lie between the shown regions. Our methods and L0Learn outperfom MCP and LASSO in terms of the AUC (left and middle), and better recover the true support (right). L0Learn’s performance heavily overlaps with our methods. Our methods have a computational advantage over L0Learn as shown in the last section.
Since the features for this synthetic dataset are continuous (and we chose not to binarize them), Exp-L0 cannot be applied; its advantage comes from exploiting its analytical line search for binary features.
Real Datasets:
Figure 5 shows sparsity-AUC tradeoffs and sparsity-accuracy tradeoffs on the COMPAS and NETHERLANDS datasets. LASSO and MCP do not achieve high prediction accuracy on training and test sets. L0Learn and our proposed methods have higher AUC and accuracy. Again, while L0Learn and our methods are tied for the best performance (which could be the optimal possible performance for this problem), our methods have major advantages in speed. More results are in Appendix D.3.
Figure 5:
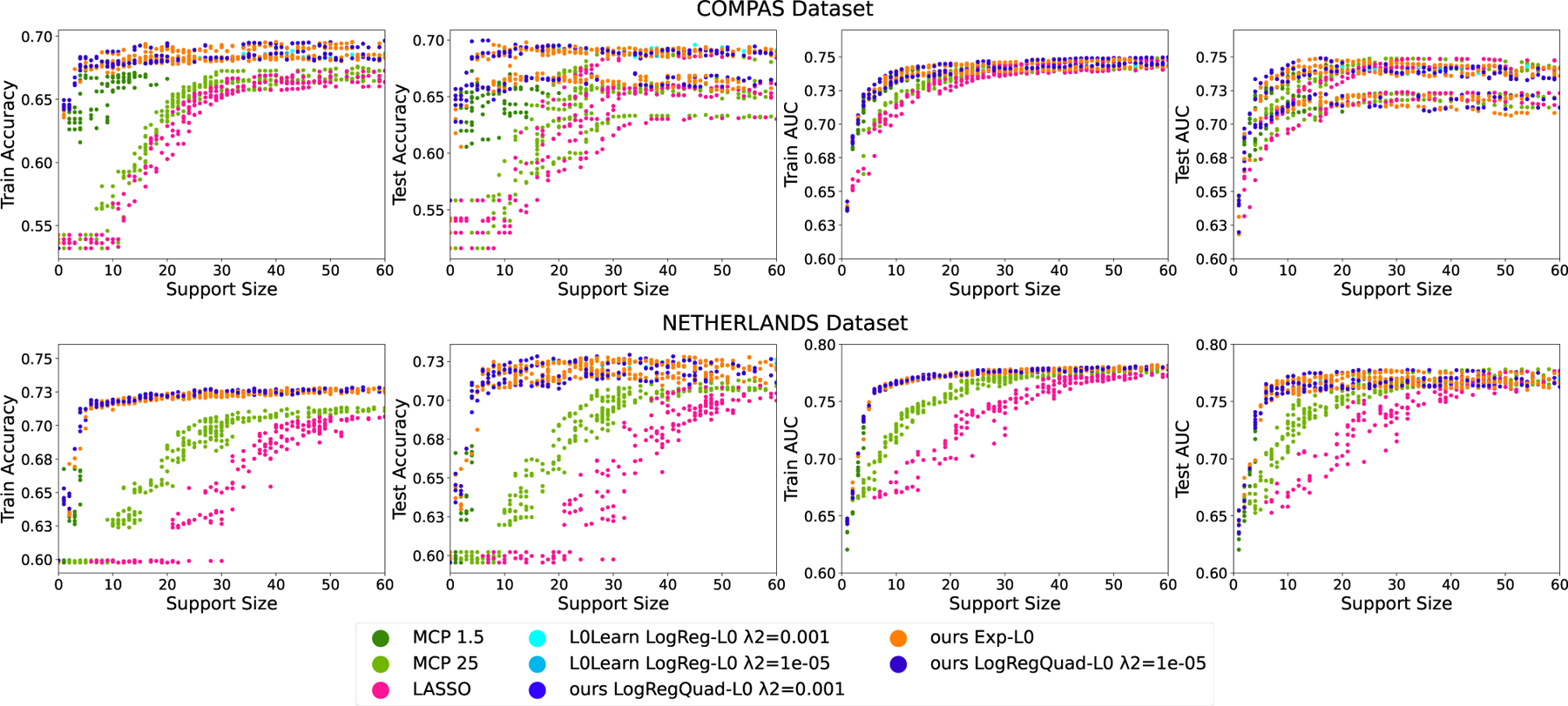
Results from all folds and parameter choices on real datasets: COMPAS and NETHERLANDS. We can see from the first and second columns (training and test accuracies) that MCP and LASSO do not perform well. Our methods and L0Learn (overlapping) outperform all other methods. Our methods are more computationally efficient than L0Learn.
8. RELATED WORK
Mixed Integer Optimization.
There have been many approaches to finding the optimal solution to logistic regression either with an ℓ0 regularization or cardinality constraint (Sato et al., 2016, 2017; Ustun and Rudin, 2017; Bertsimas and King, 2017; Bertsimas et al., 2021; Sakaue and Marumo, 2019; Ustun and Rudin, 2019). In general, these approaches formulate the problem as a mixed-integer optimization problem (see Bertsekas, 1997; Wolsey and Nemhauser, 1999). The problem can then be solved using branch-and-bound search (see Land and Doig, 2010) or cutting-plane methods (Kelley, 1960; Gilmore and Gomory, 1961, 1963). However, even with the recent advances in hardware and software, MIP solvers are orders of magnitude slower than the methods we consider here and requires relatively large ℓ2 regularization to work well (Bertsimas et al., 2021; Dedieu et al., 2021).
Gradient-based Heuristic Methods.
One of the most widely used methods to promote sparsity is LASSO (Tibshirani, 1996), which relaxes the ℓ0 penalty to ℓ1. However, ℓ1 simultaneously promotes sparsity and shrinks the coefficients, leading to bias. Several new methods obtain solutions under cardinality constraints or ℓ0 penalty terms. One method is Orthogonal Matching Pursuit (OMP) (Lozano et al., 2011; Elenberg et al., 2018), which greedily selects the next-best feature based on the current support and gradients on coefficients. Other methods include Iterative Hard Thresholding (IHT) (Blumensath and Davies, 2009), coordinate descent (Beck and Eldar, 2013; Patrascu and Necoara, 2015; Dedieu et al., 2021), GraSP (Bahmani et al., 2013), and NHTP (Zhou et al., 2021). These methods enjoy fast computation, but their solutions suffer when the feature dimension is high or features are highly correlated because they can get stuck at local minima (Dedieu et al., 2021).
Local Feature Swaps.
Some recent work considers swapping features on a given support. One such example is ABESS (Zhu et al., 2020; Zhang et al., 2021), which ranks features based on their contribution to the loss objective. Then, they swap only unimportant features in the support with features outside the support. Our experiments show that ABESS often returns “nan” values for its coefficients, thus in its current form was not able to be included in our experiments. Another work is L0Learn (Hazimeh and Mazumder, 2020; Dedieu et al., 2021), which exhaustively tries replacing every feature in the support with better features.
To the best of our knowledge, our work is the first where quadratic cuts (or exponential loss) and dynamic ordering have been used for sparse classification.
9. CONCLUSION
We have shown substantial speedups over other techniques for best subset search for probabilistic models with high-quality solutions. Our advances are due to several key ideas: (1) the use of cutting planes and quadratic cuts to form lower bounds, telling us when exploring a feature further is not worthwhile, (2) the use of the exponential loss, which has an analytical form, obviating the manipulations needed for logistic loss, (3) the use of a priority queue with a useful ordering function.
Supplementary Material
Acknowledgements
We acknowledge support from the U.S. National Institutes of Health under NIDA grant DA054994-01, and the National Science Foundation under grant DGE-2022040. We also acknowledge the support of the Natural Sciences and Engineering Research Council of Canada (NSERC).
Footnotes
Proceedings of the 25th International Conference on Artificial Intelligence and Statistics (AISTATS) 2022, Valencia, Spain. PMLR: Volume 151. Copyright 2022 by the author(s).
Code Availability
Implementations of the fast sparse classification method discussed in this paper are available at https://github.com/jiachangliu/fastSparse.
References
- Bahmani Sohail, Raj Bhiksha, and Boufounos Petros T. Greedy sparsity-constrained optimization. Journal of Machine Learning Research, 14 (Mar):807–841, 2013. [Google Scholar]
- Beck Amir and Eldar Yonina C. Sparsity constrained nonlinear optimization: Optimality conditions and algorithms. SIAM Journal on Optimization, 23(3): 1480–1509, 2013. [Google Scholar]
- Bertsekas Dimitri P. Nonlinear programming. Journal of the Operational Research Society, 48(3):334–334, 1997. [Google Scholar]
- Bertsimas Dimitris and King Angela. Logistic regression: From art to science. Statistical Science, pages 367–384, 2017. [Google Scholar]
- Bertsimas Dimitris, Pauphilet Jean, and Van Parys Bart. Sparse classification: a scalable discrete optimization perspective. Machine Learning, 110(11):3177–3209, 2021. [Google Scholar]
- Blumensath Thomas and Davies Mike E. Iterative hard thresholding for compressed sensing. Applied and Computational Harmonic Analysis, 27(3):265–274, 2009. [Google Scholar]
- Breheny Patrick and Huang Jian. Coordinate descent algorithms for nonconvex penalized regression, with applications to biological feature selection. Annals of Applied Statistics, 5(1):232–253, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Chaofan, Lin Kangcheng, Rudin Cynthia, Shaposhnik Yaron, Wang Sijia, and Wang Tong. A holistic approach to interpretability in financial lending: Models, visualizations, and summary-explanations. Decision Support Systems, page 113647, 2021. [Google Scholar]
- Daubechies Ingrid, Defrise Michel, and De Mol Christine. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Communications on Pure and Applied Mathematics: A Journal Issued by the Courant Institute of Mathematical Sciences, 57(11):1413–1457, 2004. [Google Scholar]
- Dedieu Antoine, Hazimeh Hussein, and Mazumder Rahul. Learning sparse classifiers: Continuous and mixed integer optimization perspectives. Journal of Machine Learning Research, 22(135):1–47, 2021. [Google Scholar]
- Del Moral Pierre, Doucet Arnaud, and Jasra Ajay. Sequential monte carlo samplers. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 68(3):411–436, 2006. [Google Scholar]
- Dempster Arthur P, Laird Nan M, and Rubin Donald B. Maximum likelihood from incomplete data via the em algorithm. Journal of the Royal Statistical Society: Series B (Methodological), 39(1):1–22, 1977. [Google Scholar]
- Elenberg Ethan R, Khanna Rajiv, Dimakis Alexandros G, and Negahban Sahand. Restricted strong convexity implies weak submodularity. The Annals of Statistics, 46(6B):3539–3568, 2018. [Google Scholar]
- Ertekin Şeyda and Rudin Cynthia. On equivalence relationships between classification and ranking algorithms. Journal of Machine Learning Research, 12:2905–2929, 2011. [Google Scholar]
- FICO, Google, Imperial College London, MIT, University of Oxford, UC Irvine, and UC Berkeley. Explainable Machine Learning Challenge. https://community.fico.com/s/explainable-machine-learning-challenge, 2018.
- Freund Yoav and Schapire Robert E. A decision-theoretic generalization of on-line learning and an application to boosting. Journal of Computer and System Sciences, 55(1):119–139, 1997. [Google Scholar]
- Friedman Jerome, Hastie Trevor, and Tibshirani Robert. Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software, 33(1):1–22, 2010. [PMC free article] [PubMed] [Google Scholar]
- Friedman Jerome H. Greedy function approximation: a gradient boosting machine. Annals of Statistics, pages 1189–1232, 2001. [Google Scholar]
- Gilmore Paul C and Gomory Ralph E. A linear programming approach to the cutting-stock problem. Operations Research, 9(6):849–859, 1961. [Google Scholar]
- Gilmore Paul C and Gomory Ralph E. A linear programming approach to the cutting stock problem—part ii. Operations Research, 11(6):863–888, 1963. [Google Scholar]
- Hastie Trevor J and Tibshirani Robert J. Generalized additive models. Routledge, 2017. [DOI] [PubMed] [Google Scholar]
- Hazimeh Hussein and Mazumder Rahul. Fast best subset selection: Coordinate descent and local combinatorial optimization algorithms. Operations Research, 68(5):1517–1537, 2020. [Google Scholar]
- Kelley James E Jr. The cutting-plane method for solving convex programs. Journal of the Society for Industrial and Applied Mathematics, 8(4):703–712, 1960. [Google Scholar]
- Kirkpatrick Scott, Gelatt C Daniel, and Vecchi Mario P. Optimization by simulated annealing. Science, 220(4598):671–680, 1983. [DOI] [PubMed] [Google Scholar]
- Land Ailsa H and Doig Alison G. An automatic method for solving discrete programming problems. In 50 Years of Integer Programming 1958–2008, pages 105–132. Springer, 2010. [Google Scholar]
- Larson J, Mattu S, Kirchner L, and Angwin J. How we analyzed the COMPAS recidivism algorithm. ProPublica, 2016. [Google Scholar]
- Lou Yin, Bien Jacob, Caruana Rich, and Gehrke Johannes. Sparse partially linear additive models. Journal of Computational and Graphical Statistics, 25(4):1126–1140, 2016. [Google Scholar]
- Lozano Aurelie, Swirszcz Grzegorz, and Abe Naoki. Group orthogonal matching pursuit for logistic regression. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, pages 452–460, 2011. [Google Scholar]
- Metropolis Nicholas, Rosenbluth Arianna W, Rosenbluth Marshall N, Teller Augusta H, and Teller Edward. Equation of state calculations by fast computing machines. The Journal of Chemical Physics, 21(6):1087–1092, 1953. [Google Scholar]
- Nori Harsha, Jenkins Samuel, Koch Paul, and Caruana Rich. Interpretml: A unified framework for machine learning interpretability. arXiv preprint arXiv:1909.09223, 2019. [Google Scholar]
- Patrascu Andrei and Necoara Ion. Random coordinate descent methods for ℓ0 regularized convex optimization. IEEE Transactions on Automatic Control, 60 (7):1811–1824, 2015. [Google Scholar]
- Platt John. Sequential minimal optimization: A fast algorithm for training support vector machines. Technical Report MSR-TR-98–14, April 21 1998.
- Rudin Cynthia, Chen Chaofan, Chen Zhi, Huang Haiyang, Semenova Lesia, and Zhong Chudi. Interpretable machine learning: Fundamental principles and 10 grand challenges. Statistics Surveys, 16:1–85, 2022. [Google Scholar]
- Sakaue Shinsaku and Marumo Naoki. Best-first search algorithm for non-convex sparse minimization. arXiv preprint arXiv:1910.01296, 2019. [Google Scholar]
- Sato Toshiki, Takano Yuichi, Miyashiro Ryuhei, and Yoshise Akiko. Feature subset selection for logistic regression via mixed integer optimization. Computational Optimization and Applications, 64(3):865–880, 2016. [Google Scholar]
- Sato Toshiki, Takano Yuichi, and Miyashiro Ryuhei. Piecewise-linear approximation for feature subset selection in a sequential logit model. Journal of the Operations Research Society of Japan, 60(1):1–14, 2017. [Google Scholar]
- Schapire Robert E and Freund Yoav. Boosting: Foundations and algorithms. Kybernetes, 2013. [Google Scholar]
- Tibshirani Robert. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58(1):267–288, 1996. [Google Scholar]
- Tollenaar Nikolaj and Van der Heijden PGM. Which method predicts recidivism best?: a comparison of statistical, machine learning and data mining predictive models. Journal of the Royal Statistical Society: Series A (Statistics in Society), 176(2):565–584, 2013. [Google Scholar]
- Ustun Berk and Rudin Cynthia. Optimized risk scores. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pages 1125–1134, 2017. [Google Scholar]
- Ustun Berk and Rudin Cynthia. Learning optimized risk scores. J. Mach. Learn. Res, 20:150–1, 2019. [Google Scholar]
- Wolsey Laurence A and Nemhauser George L. Integer and Combinatorial Optimization, volume 55. John Wiley & Sons, 1999. [Google Scholar]
- Zhang Yanhang, Zhu Junxian, Zhu Jin, and Wang Xueqin. Certifiably polynomial algorithm for best group subset selection. arXiv preprint arXiv:2104.12576, 2021. Code version: December 8, 2021. [Google Scholar]
- Zhou Shenglong, Xiu Naihua, and Qi Hou-Duo. Global and quadratic convergence of newton hard-thresholding pursuit. J. Mach. Learn. Res, 22(12): 1–45, 2021. [Google Scholar]
- Zhu Junxian, Wen Canhong, Zhu Jin, Zhang Heping, and Wang Xueqin. A polynomial algorithm for best-subset selection problem. Proceedings of the National Academy of Sciences, 117(52):33117–33123, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


