Searching for a mechanistic description of pairwise epistasis in protein systems

Abstract

When two or more amino acid mutations occur in protein systems, they can interact in a nonadditive fashion termed epistasis. One way to quantify epistasis between mutation pairs in protein systems is by using free energy differences: ϵ = ΔΔG_1,2 - (ΔΔG₁ + ΔΔG₂) where ΔΔG refers to the change in the Gibbs free energy, subscripts 1 and 2 refer to single mutations in arbitrary order and 1,2 refers to the double mutant. In this study, we explore possible biophysical mechanisms that drive pairwise epistasis in both protein-protein binding affinity and protein folding stability. Using the largest available datasets containing experimental protein structures and free energy data, we derived statistical models for both binding and folding epistasis (ϵ) with similar explanatory power (R²) of 0.299 and 0.258, respectively. These models contain terms and interactions that are consistent with intuition. For example, increasing the Cartesian separation between mutation sites leads to a decrease in observed epistasis for both folding and binding. Our results provide insight into factors that contribute to pairwise epistasis in protein systems and their importance in explaining epistasis. However, the low explanatory power indicates that more study is needed to fully understand this phenomenon.

1. Introduction

Multiple amino acid mutations can interact in biological systems, leading to nonadditive effects termed epistasis. While a general understanding of the concept of epistasis has existed for many years, the prevalence of epistasis, or its importance in biological systems, is still a matter of debate^1-5. Some believe it is a major force in evolution, either by constraining the available pathways for systems to evolve, by counteracting mutations that reduce fitness through compensatory effects, or by contributing to a more rugged fitness landscape^6-18. Others have explored the epistatic effect between sets of beneficial mutations, finding that epistasis is pervasive and a key aspect of adaption, but leading to diminishing returns or negative epistasis^{10,19,20,20-22}. Other studies using RNA viruses have shown that epistasis is prevalent and likely a mechanism for their evolution^23-28. Epistasis has also been shown to be a likely contributing factor to drug and antibody resistance of influenza A, HIV-1 and other pathogens^12,24,29,30, and for general disease susceptibility in humans³¹. Finally, the complexity that epistasis provides in understanding mutation effects must be accounted for in protein engineering and design^32-35.

For pairs of simultaneous mutations in proteins (we will refer to these as “double mutations”), epistasis can be expressed in terms of free energy differences:

$$ϵ=\Delta \Delta {\mathrm{G}}_{1,2}\text{-}(\Delta \Delta {\mathrm{G}}_1+\Delta \Delta {\mathrm{G}}_2)$$ (EQ 1)

Where ΔΔG_1,2 corresponds to the change in the folding or binding free energy due to the double mutation, and ΔΔG₁ + ΔΔG₂ refers to the sum of the constituent single mutation free energy changes. There are other definitions for epistatic effects such as ratios of folding changes³⁴. However, our null assumption was the case of perfect additivity (ϵ=0) leading to our definition for epistasis being deviations from additivity. This nonadditivity can be caused by direct interactions between mutational sites, or by indirect effects such as conformational perturbations. Epistasis is positive when the double mutant is more stabilizing than the sum of the constituent singles (ϵ < 0) and negative when the double mutant is more destabilizing than the sum of the constituent singles (ϵ > 0).

Despite its importance to understanding biological systems, a comprehensive mechanistic picture of the drivers of epistasis in proteins is not known. An early attempt to explain epistasis mechanisms is a study by Wells³⁶; they concluded that features like separation distance, electrostatic interactions, and conformational perturbations were likely contributors. However, this conclusion was based on a small data set containing a total of 12 folding and binding systems, with less than 75 total multiple mutations. More recent studies have examined specific protein systems like TEM-1 β-lactamase^37,38 and the IgG-binding domain of protein G³⁹, finding pervasive negative epistasis. Long-range epistasis has also received attention. Gromiha et al. proposed that distant residues that are part of a specific local group (they defined this as a rigid cluster) could lead to epistasis⁴⁰. Other researchers have used tools like molecular dynamics to analyze if networks of interactions can mediate long-range epistasis⁴¹. Classification systems have also been developed. Jemimah et al. used structural features to build a model to classify whether mutational pairs would be additive (i.e., not epistatic)⁴². These previous studies provide a basis for understanding possible contributors to epistasis and some even offer predictive capability, however they do not provide a complete understanding of epistasis mechanisms and their interactions.

In this study, we determine biophysical drivers of pairwise epistasis in protein systems and rank their contribution to the observed epistasis, ϵ (EQ 1). We used protein structural data, protein-protein binding affinities, and protein folding stabilities from the largest, most diverse datasets currently available. We explored possible relationships between the observed epistasis and features that are intrinsic to both the proteins and the mutated residues. A statistical model selection procedure was performed to determine the features that are most important to explaining the observed epistasis. The models determined for binding and folding have similar and modest predictive power. Both models contain similar features that include separation distance and charge interactions. Our work serves as a stepping stone to further our understanding of the biophysical drivers of epistasis, and to build future models with more complex features and interactions.

2. Methods

2.1: Curating experimental data

Experimental binding affinity data was obtained from SKEMPI v2.0 ⁴³ and folding stability data from ProTherm 4⁴⁴. Since the focus of our study is pairwise epistasis, we extracted a subset of the data consisting of all instances where there was data for a double mutant and the corresponding constituent singles. For both folding and binding data, values were converted to kcal/mol. A temperature of 298 K was used if not specified in the dataset. Averages were calculated for mutations that included multiple free energy values. The attributes in the resulting curated folding and binding datasets used in our study include the PDB ID, protein complex name, the mutation(s), and either binding or folding free energy values. The total number of data points for double mutants with constituent single mutants were 572 from 58 protein-protein complexes for binding, and 204 from 30 protein systems for folding. Epistasis was calculated for each double mutation data point using EQ 1, that is, by taking the difference between the free energy change due to the double mutation and the sum of the free energy changes due to the constituent single mutations. Protein structures used for analysis were acquired from the RCSB Protein Data Bank (PDB)⁴⁵.

2.2: Extracting Features as Possible Drivers of Epistasis

For electrostatics, and other categorical features described below, the explicit wildtype-mutant pairs are henceforth denoted separated by a semicolon for simplicity: wt₁wt₂;mut₁mut₂.

Amino Acid Properties

To investigate the effect of electrostatics on epistasis, we classified amino acids as positively charged (+), negatively charged (−), or neutral (0). To incorporate every wildtype-mutant pair state would be infeasible due to overparameterization, as it would result in 3⁴=81 possible categories (++;−−, ++;−+, ++;+−, +−;−−, …). To avoid overparameterization, we explored various abstractions of this data, incorporating this into our model selection process (detailed below). The resulting charge contribution was given by a simplified charge-interaction scheme with pairs belonging to one of three categories: attractive (+− or −+, denoted “A”), repulsive (−− or ++, denoted “R”), and neutral (all other cases, denoted “0”). The reverse of each wildtype-mutant states were classified as the same (e.g. 0;A = A;0), resulting in four categories: 0A, 0R, AR, and 00 to capture all possible electrostatic interactions. Note that the AR case was not present in either dataset.

To include the change in size for the constituent amino acids we used the van der Waals volume in Å. To capture the net effect due to the change in size for both sites we used the metric (referred to as size_net.

$${\text{size}}_{\text{net}}=\mid {\text{size}}_{\mathrm{m}1}\text{-}{\text{size}}_{\text{wt}1}\mid +\mid {\text{size}}_{\mathrm{m}2}\text{-}{\text{size}}_{\text{wt}2}\mid$$ (EQ 2)

where wt and m correspond to the wildtype and mutant amino acids, respectively, and 1 and 2 denote the amino acid sites in an arbitrary order. Under this scheme, if one or both sites undergo a large/small change in volume occupancy the corresponding metric will be large/small respectively, even if they are in opposing directions.

To include the effect of hydrophobicity, each residue is classified as either “H” for hydrophobic or “P” for polar. Using all possible 16 categories would be possible, but risk overfitting. We instead found the following abstraction: a boolean value (“0” or “1”) that denotes whether the net hydrophobicity of the pair changed upon mutation. For example, HP;PH would give 0 since the net hydrophobicity remained the same. By contrast, PP;HP or PP;HH would both give 1, since the net hydrophobic state changed upon mutation.

Structural Properties

Separation distance was defined as the Cartesian separation between the alpha carbons for each mutational site. This Euclidean distance r was calculated using the x, y, z coordinates for the mutation sites via the standard formula:

$$r=\sqrt{(x_{wt1}-x_{wt2}{)}^2+(y_{wt1}-y_{wt2}{)}^2+(z_{wt1}-z_{wt2}{)}^2}$$ (EQ 3)

Secondary structure information was included by considering whether a given mutational site was located in an alpha helix (“H”), beta sheet (“S”), or loop (“L”). Secondary structure content was determined using a PyMol script⁴⁶. As with other categorical features overparameterization may be a concern, though in this case the explicit consideration only has nine possible cases. We tested the possible abstractions, ranging from explicit consideration of the structures at each site (e.g., HL,LL,LS,…) to the simplest case of a boolean value denoting whether both sites belong to the same type of structure (“0”) or different structures (“1”).

We also considered the effect of solvent accessible surface area (SASA): a metric describing whether a residue is exposed or buried. To calculate the SASA, we first prepared the PDB files using pdbfixer from the OpenMM software suite⁴⁷, to add missing residues, replace non-standard residues with their standard equivalents, and add missing hydrogens. The repaired structures were then processed with FoldX⁴⁸ to generate mutations using the BuildModel command. DSSP v 3.0.0⁴⁹ was then used to calculate the absolute SASA (SASA_abs) for each residue of interest. Both absolute and relative SASA were considered, relative SASA (SASA_rel) was calculated using the empirical max accessible surface area (ASA_max) generated by Tien et al⁵⁰ via the formula:

$${\text{SASA}}_{\text{rel}}={\text{SASA}}_{\text{abs}}∕{\text{ASA}}_{\max }.$$ (EQ 4)

Since SASA changes affect both wildtype and mutant residues, we used a modified version of EQ 2 replacing size_net with SASA.

We also included classification information. For binding, we included the type of protein-protein complex broken into five categories, based on the information provided in the SKEMPI v2.0 database: antibody-antigen (AB/AG), T cell receptor-peptide bound major histocompatibility complex (TCR/pMHC), Cytokine-Cytokine receptor (Cyto/Cyto), GTPase-other, and non-specific protein-protein interaction (Pr/PI) which functioned as the reference category for the statistical models. We also included a boolean value indicating whether or not the mutational sites occur on the same (“0”) or different (“1”) protein chains, as sites which occur on the same chain may have a different effect on binding than if they occur on opposing chains. For folding, we included the system size given by the total number of residues acquired from the PDB.

2.3: Statistical Analysis

To analyze the relationship between epistatic effect and separation distance, we conducted a likelihood ratio test that compares a null model (where separation distance is unrelated to epistasis) against an alternative model (where epistasis decays with increasing separation). More precisely, we defined the null model to be that epistasis values are sampled from a normal distribution that is independent of the separation between residues. For the alternative model, epistasis values are sampled from a normal (same mean as the null case) with a standard deviation that decays exponentially as a function of separation according to a e^αr where r is the separation between residue site alpha-carbons (EQ 3) and a and α are the curve’s parameters estimated by maximum likelihood for the dataset. This maximum likelihood was determined by a grid-search method, considering all possible a and α, taking the resulting model with the largest likelihood. The likelihood ratio is given by the ratio of the log of the two likelihoods of the data under the two models:

$$\Lambda (ϵ)=\frac{\mathcal{L}({\theta }_0\mid ϵ)}{\mathcal{L}({\theta }_1\mid ϵ)}\to log(\Lambda (ϵ))=log(\mathcal{L}({\theta }_0\mid ϵ))-log(\mathcal{L}({\theta }_1\mid ϵ))$$ (EQ 5)

where $\mathcal{L}$ refers to the likelihood, log is the natural logarithm, and θ₀ θ₁ correspond to the null and alternative models respectively. Small values of Λ indicate that the alternative model has more explanatory power than the null. We first calculated the likelihood ratio for the experimental data, Λ_exp. In order to determine statistical significance of Λ_exp we then obtained the distribution of Λ under the null through parametric simulation. Specifically, we simulated datasets using the mean and standard deviation of the experimental epistasis data. We then repeated the fitting exercise used on the real dataset for the simulated dataset, using the same separation data, and calculated Λ. This process was repeated 1000 times to obtain the distribution of Λ under the null: Λ_sim. The p-value for the test was then calculated as the proportion of Λ_sim less than or equal to Λ_exp.

Linear statistical models were used to determine the biophysical features that are best able to explain the observed epistasis. The absolute value of the epistasis, ϵ, was used as a response variable for our model building. The choice to use the absolute value was necessary to ensure a monotonic relationship between the features and the response variable, as assumed when using linear models. One could imagine analyzing positive and negative epistasis separately; however, this was not possible due to small sample sizes. All features described above were considered in a standard model selection procedure, including all pairwise interactions terms. For any features where we considered more than one level of abstraction, only one level was included in any given model. To evaluate model performance, the corrected Akaike information criterion (AICc) was used. The corrected criterion was chosen over the standard AIC due to the potential for overfitting models that contain a large number of terms given a small amount of data⁵¹. Models were generated and tested using R software⁵² by considering all permutations of abstracted and non-abstracted features. Model selection was performed using a modified form of stepAIC from the MASS⁵³ package to perform forward and backward selection based on AICc (further verified by the AICc function of AICcmodavg⁵⁴ and compared to standard AIC). Forward selection explores model space by starting with a term-less model and systematically adding terms to find the model with the best value for a given criterion. Conversely, backward selection starts with the complete full-term model and removes terms to find the best model. This model selection process was performed twice with randomized input terms to avoid potential ordering bias (terms treated differently based on their position in the initial list) and the lowest AICc values were compared for consistency. Once we verified that there was no ordering bias, the model with the lowest AICc for both binding and folding was used for further analysis.

To rank the importance of features present in the final statistical models for their effect on epistasis we compared R² values with and without each feature and its interactions. Features with larger explanatory power of the observed epistasis will have a larger change in R² when removed.

2.4 -. Quantification of Experimental Error and Model Validation

In order to develop a model for epistasis, it is important to quantify how much of the observed epistasis could be attributed to error, or noise, in the experimental data. Quantification of overall error is based on the error in three values (ΔΔG_1,2, ΔΔG₁, ΔΔG₂), each of which were determined using a broad range of techniques and conditions from diverse studies (e.g., 60+ for binding). A survey of six studies that contained some of the largest observed epistasis for binding showed the experimental standard error for ΔΔG to be in the range 0.05 - 0.3 kcal/mol⁵⁵-⁵⁷. However, some studies do explicitly include the error for epistasis (frequently termed the coupling energy). For example, in the case of barnase-barstar, Schreiber et al., reports errors in ϵ from 0.2 - 0.39 kcal/mol across 33 mutation pairs⁵⁸ and Goldman et al. reports an error of 0.3 kcal/mol across 13 pairs for an Idiotype-AntiIdiotype Protein-Protein complex⁵⁹. There are outliers, such as the study from Pielak, et al. with six mutational pairs in the Iso-1-cytochrome C Peroxidase complex⁶⁰ found to have an error range of 0.4 - 1.0 kcal/mol with an average error of 0.75 kcal/mol for six samples; an unusually large error. In summary, the reported error for our curated binding and folding datasets are in the range of 0.2 - 1.0 kcal/mol, with mean around 0.4 kcal/mol. For the remainder of this study, we will use a slightly more conservative estimated error of 0.5 kcal/mol to quantify the amount of observed epistasis.

Since our binding and folding data comes from many different protein systems collected by a diversity of methodologies and laboratories, there is an inherent imbalance in the quantity and quality of data for each system. To test the robustness of our model to this bias, we applied a modified “leave-one-out” procedure. We randomly removed 10% of the protein systems and their data, creating a subset from the remaining 90% of systems. The model selection procedure was performed on this subset to generate a new model. This process of removing 10% of the systems and running model selection was repeated 100 times. The resulting 100 subset models were analyzed and compared to determine which terms appeared, their frequency of appearance, and average performance or ranking when present in a model.

3. Results

To build a statistical model for epistasis in proteins we used data for binding curated from SKEMPI v2.0 (572 mutation pairs), and for folding curated from ProTherm 4 (204 mutation pairs). We first considered the extent to which epistasis was present in our data set. To determine this, we defined an epistasis cutoff; values where ∣ϵ∣ is larger than the cutoff are considered epistatic, and other values are not. Ideally, the cutoff would be chosen based on the experimental error or uncertainty, however, given that our data come from a broad spectrum of methods and sources, this is not possible to determine for the dataset as a whole (see supplemental Figure S1 for the dataset divisions with various cutoffs).

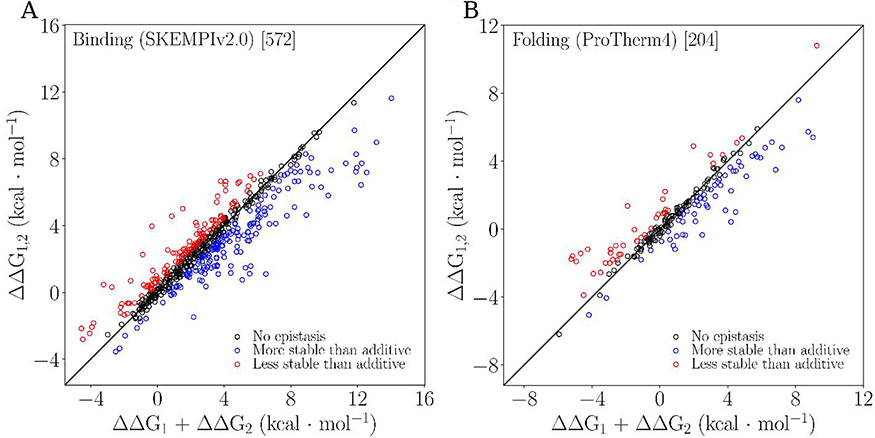
Figure 1 shows the free energy change of the double mutant as a function of the sum of individual free energies for both binding and folding datasets with a cutoff of 0.5 kcal/mol. Both figures 1 and 2 show that epistasis is present in binding and folding. In both datasets there is a marked trend for large sums of constituent single mutations (sum in EQ 1) to correspond to a double mutant with free energy falling below the 1:1 line (i.e., more stabilizing that predicted by additivity). The opposite is true for constituent mutations with smaller sums.

Figure 1:

Epistasis scatterplots for binding (A) and folding (B). Both figures use a cutoff of 0.5 kcal/mol and show data characterized as no epistasis (black), positive epistasis (blue), and negative epistasis (red).

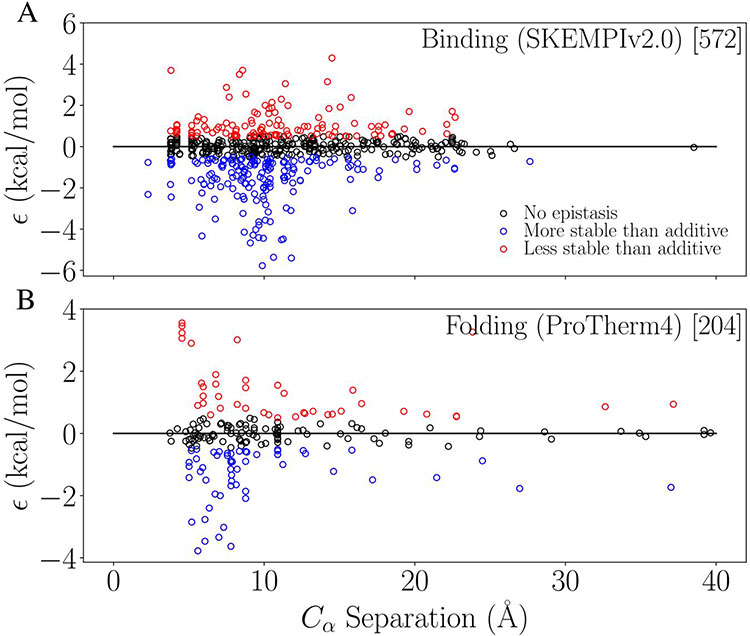
Figure 2:

Observed epistasis as a function of alpha-carbon separation between mutation sites for binding (A) and folding (B). Black indicates no-epistasis using our cutoff of 0.5 kcal/mol, and blue and red indicate positive and negative epistasis, respectively.

After ascertaining the extent to which epistasis is present in our data, we investigated how well the separation between mutation sites could explain the epistatic effect. Figure 2 shows the relationship between separation distance and the observed epistasis for binding (top) and folding (bottom). Both show the general expected trend of less epistasis as separation increases. Both also show a larger number of data points for distances with the largest ϵ values, or spread in ϵ (around 6-10 Å).

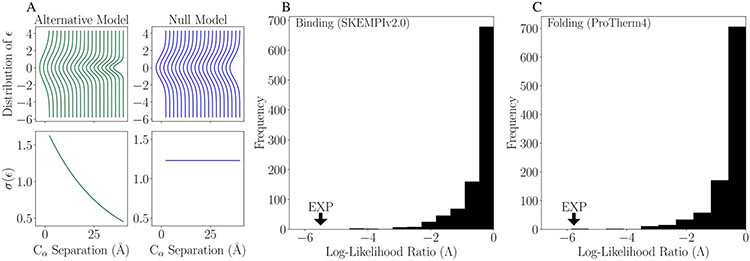
Figure 3 shows our analysis to determine whether the apparent decrease in epistasis with increasing separation distance (Figure 2) is due to an actual relationship or a consequence of the larger number of data points at small distances. Figure 3A shows null model (σ(ϵ) is not a function of r) and alternative model (σ(ϵ) exponentially decreases as a function of r) for the likelihood ratio analysis. Figure 3B and 3C show the simulated distribution of the likelihood ratio, Λ,from the analysis with 1000 samples for binding and folding respectively. The experimentally observed likelihood ratio is well outside the distribution of null ratios given by the label “EXP” and has a value of −5.50 compared with the tail of the simulation distribution minimum of −4.59 in the case of binding. In simple terms, this results in a p-value of p < 1/1000 (p<0.001) in strong support of the alternative model.

Figure 3:

(A) Comparison between the alternative (left) and null (right) models for epistatic effect, ϵ, as a function of separation distance, r. Results of log(likelihood) ratio test for separation distance with 1000 samples for simulated data for binding affinity (B) and folding stability (C). These plots show the alternative model is a significantly better explanation of the data than the null model.

Table 1 shows a summary of the binding (1A) and folding (1B) statistical models for epistasis in protein systems. Both models have similar predictive power in the range of 25-30%. The final selected binding model contains all features that we considered except for hydrophobicity (seven features, 28 terms including interactions) and depends on SASA_abs and secondary structure in addition to binding specific features like the complex type. The folding model is simpler (five features, 12 terms with interactions), and depends on hydrophobicity and SASA_rel. Features are listed in order according to their relative contribution to the explanatory power of the full model. That is, the highest-ranked feature is the one whose removal leads to the greatest reduction in R². For the binding epistasis model, the largest contributor was the complex type, with a change in R² of 0.128 upon removal followed by charge with a change in R² of 0.078 upon its removal. The remaining terms each contribute ~5% or less to the predictive power of the binding model. For the folding epistasis model, the largest contributor was hydrophobicity with a change in R² of 0.151 upon removal, followed by both size and charge with similar contributions (change in R² of 0.0765 and 0.0695 with their removal respectively). The remaining terms each contribute ~4.5% or less to the predictive power of the folding model.

Table 1:

Summaries of epistasis models for binding (A) and folding (B). The leftmost column (column one) contains features. Any categorical abstractions are listed directly below the category with right justification. Column two gives the specific number of mutation pairs for a given category, where applicable. For complex type specifically, the number of complexes of that type are indicated in parentheses. Column three is the change in R² (ΔR²), i.e., how much poorer the model fits the data after removing this feature. In the case of the full model, column three is the R². Removal of a feature also removes all subcategories and any interaction terms involving the feature. Column four lists coefficients for the feature/interaction term in the full model. The rightmost column contains p-values for the features, and features within a given category.

1A: Binding Model
Feature	CategoricalBreakdown	Removal (ΔR2)	Coefficient	P-value
Full Model	572	0.2991
Intercept			0.6994	0.0000
Complex Type		0.1275
AB/AG	66 (8)		−0.8401	0.0120
Cyto/Cyto	69 (4)		0.4677	0.3738
GTPase/other	85 (7)		−0.4134	0.3153
TCR/pMHC	58 (9)		−1.0090	0.0071
Pr/PI	294 (30)		0.0000	0.0000
Charge		0.0778
0	450		0.0000	0.0000
0A	69		1.0195	0.0041
0R	53		−0.7424	0.0131
Separation		0.0522	−0.0025	0.8074
Interaction Side		0.0464	0.5889	0.0055
1	399
0	173
Sizenet		0.0427	0.0022	0.1345
SASAabs		0.0327	−0.0060	0.0002
Secondary Structure		0.0162	0.5837	0.0014
1	315
0	257
Binding Model Interaction Terms
Feature1:Feature2			Coefficient	P-value
Separation:Secondary Structure			−0.0331	0.0246
Sizenet:Interaction Side			−0.0052	0.0081
Separation:Charae
0A			−0.0882	0.0001
0R			0.0454	0.0401
SASAabs:Complex Type
AB/AG			−0.0140	0.0207
Cyto/Cyto			0.0072	0.2340
GTPase/other			0.0072	0.0789
TCR/pMHC			0.0062	0.1631
Sizenet:Complex Type
AB/AG			0.0130	0.0000
Cyto/Cyto			0.0023	0.4650
GTPase/other			0.0008	0.7843
TCR/pMHC			0.0060	0.0754
Interaction Side:Charge
0A			0.7289	0.0089
0R			0.1460	0.5625
Interaction Side: Complex Type
AB/AG			0.1376	0.6577
Cyto/Cyto			−1.4297	0.0004
GTPase/other			−0.3189	0.3331
TCR/pMHC			0.0062	0.9824
1B: Folding Model
Feature	Categorical Breakdown	Removal (ΔR2)	Coefficient	P-value
Full Model	204	0.2578
Intercept			−0.0607	0.8513
HP		0.1506	0.0746	0.0018
0	133
1	71
Sizenet		0.0765	0.0120	0.0000
Charge		0.0695
0	174		0.0000	0.0000
0A	13		1.8631	0.0015
0R	17		−0.7356	0.0133
Separation		0.0446	−0.0416	0.0054
SASArel		0.0383	0.3269	0.8546
Folding Model Interaction Terms
Feature1:Feature2			Coefficient	P-val
SASArel:Sizenet			−0.0437	0.0174
SASArel:Separation			0.1577	0.1324
Sizenet:HP			−0.0103	0.0085
SASArel:HP			2.7022	0.0459
HP:Charge
0A			−2.0467	0.0016
0R			0.8380	0.0391

Table 2 shows the results of 100 trials of our "leave-10%-out" robustness test where 10% of the available systems were randomly removed. These results show that both of our full models are highly robust -- with the binding model being slightly more robust than the folding model. All terms present in the full models are present in the leave-10%-out analysis, most occurring in all trials. Additionally, the mean ranks of most terms are identical to the full-data binding model with more variance in the folding model. Graphical representation of our robustness tests shown in supplemental Figure S2.

Table 2:

Results from 100 trials of our “leave-10%-out” model robustness test for binding (A) and folding (B). The feature is indicated by the first column. The second column indicates the average rank across all trials the given feature appeared in, lower numbers suggest more robust features. The third column shows the standard error associated with the average. The fourth column indicates the average ΔR² from all trials the feature appeared in (higher numbers suggest more robustness), the fifth column indicates the total number of trials a given feature occurred in out of 100 possible, the sixth column indicates whether the feature was present in the full model, and the last column indicates the rank of the feature in the full model.

2A Binding Validation
Feature	Mean Rank	Mean Rank SE	Average ΔR2	Number of Models (/100)	In Full Model	Full Model Rank
Complex Type	1.04	0.02	0.134	100	Yes	1
Charge	2.01	0.036	0.082	100	Yes	2
Separation	3.66	0.118	0.0560	100	Yes	3
Sizenet	4.45	0.097	0.047	100	Yes	5
Interaction side	4.66	0.118	0.046	100	Yes	4
SASA	5.64	0.097	0.0380	100	Yes	6
Secondary Structure	6.68	0.087	0.022	97	Yes	7
Hydrophobicity	7.469	0.018	0.018	32	No	N/A
2B Folding Validation
Feature	Mean Rank	Mean Rank SE	Average ΔR2	Number of Models (/100)	In Full Model	Full Model Rank
Hydrophobicity	1.212	0.062	0.15	99	Yes	1
Charge	3.083	0.122	0.082	96	Yes	3
SecondaryStructure	3.213	0.164	0.0810	47	Yes	N/A
Sizenet	3.22	0.127	0.074	100	Yes	2
Separation	3.98	0.126	0.058	100	Yes	4
SASA	4.897	0.092	0.041	97	Yes	5
Number Residues	5.269	0.113	0.0380	26	No	N/A

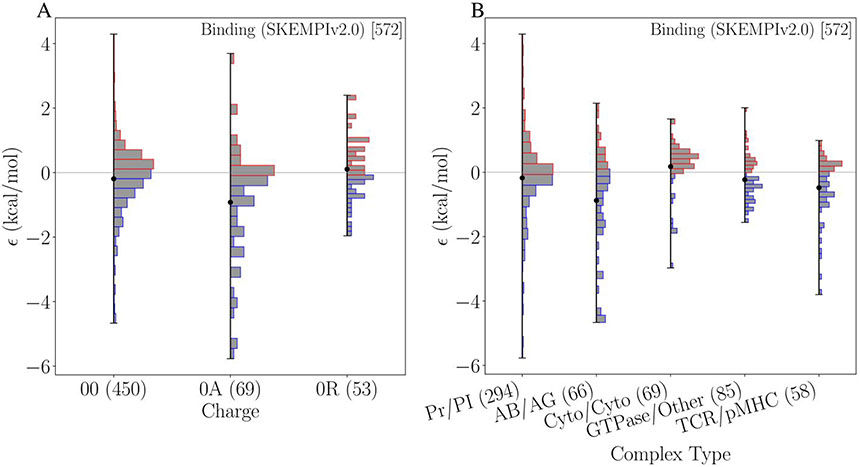
Figure 4 further illustrates the results of our statistical model for epistasis in binding. For charge, the subcategory for interactions involving an attractive pairing (0A) contains the most strongly epistatic mutations. While mutations in this subcategory cover a broad range of values, many tend towards positive epistasis; the largest value belongs to this subcategory. Neutral or constant charge states (00) show a near normal distribution centered on zero with some low levels of epistasis. Changes involving a repulsive interaction (0R) contain the least number of data and have a narrow distribution, with fewer large values for ϵ in either direction. For the complex type category, the antibody-antigen subcategory shows the most epistasis, including the most positive. TCR/pMHC also contains a large amount of positive epistasis. Cytokine-cytokine is the only subcategory with a negative mean suggesting that mutations in this subcategory tend to have negative epistasis. Generic protein-protein complexes show similar behavior to the neutral charge category; centered on zero, broad spread, but low numbers of epistatic data points. Other categorical features are shown in supplemental Figure S3.

Figure 4:

Comparison of binding model of epistasis for the categories of charge (A) and complex type (B). The mean value for a given subcategory is indicated by a black dot. The barplots show the histograms within the categories. In parenthesis is the number of mutation pairs belonging to each category. For the complex type, the number of complexes belonging to each category are shown in square brackets.

4. Discussion

Before building linear models we first determined the extent to which our datasets contain meaningful epistasis. That is, considering there is uncertainty in the data, where should we draw the line between epistatic and non-epistatic values of ϵ? We estimated (see Methods) that the error for both datasets fall between 0.2 - 1.0 kcal/mol with an average around 0.5 - 0.6 kcal/mol. From this, we estimated a cutoff of 0.5 kcal/mol, i.e., ∣ϵ∣ > 0.5 kcal/mol are considered epistatic. There are further limitations of our dataset; the data is not from randomized studies. Instead, the experiments were generally conducted in a targeted fashion with a priori knowledge of function. This may explain why we find more positive epistasis (more stabilizing that additivity predicts) than negative epistasis (more destabilizing that additivity predicts) as shown in Figure 1. Alternatively, it is possible that more positive epistasis is present in the data because negative epistasis could lead to protein misfolding or non-binding events in the experiments. The former reasoning is an artifact of how the data was generated, and the latter is related to biophysical features of the proteins; both carry different implications for the dataset and warrant future work.

Separation distance is the most intuitive feature expected to contribute to epistasis, because residues that are near each other are more likely to interact than those far apart. Simple comparisons show a decreasing spread of epistasis with increasing distance (Figure 2). The folding data show this most strongly with a sharp peak around the shortest separation distances of approximately 6 Å, dropping to near zero at larger distances. The binding data show a possible peak around 10 Å, however, the trend is not as clear. Additionally, with binding there is a paucity of data from 25 Å to 40 Å with only one data point around 40 Å. Our tests using likelihood ratio methods (Figure 3) confirm that separation does play a role in epistasis for both binding and folding. Our alternative model (width of possible ϵ values depends on separation) was a better explanation than the null model (no relationship between separation and ϵ), with a p-value of p < 0.001 in the case of binding, and p < 0.002 in the case of folding. The effect of separation is also confirmed in our models (Table 1) where both folding and binding models have negative coefficients for separation distance, which corroborates the results from the likelihood ratio analysis. In the folding model, a 10 Å increase in separation between residues results in a decrease in epistasis of 0.416. In the binding model, the effect of separation alone is an order of magnitude less than the folding model and has less significance in the model (p=0.8074). Instead, the effect of separation in the binding model is most strongly characterized by the interaction with charge. With charge alone, changes involving attractive pairings show an increase in epistatic effect whereas changes involving a repulsive pairing show a decrease. The interaction between charge and separation contributes an opposing effect: as separation between residues increases, changes involving attractive and repulsive pairings cause a decrease and increase in epistatic effect respectively. Intuitively, as separation between charged residues, regardless of categorization, increases the net effect of charge on epistasis tends towards zero (Δϵ_charge + Δϵ_{charge:separation} ~ 0). Furthermore, interaction terms can drive the inclusion of terms with low linear significance. For example, “separation:charge_0A” and “separation:charge_0R” have p-values of 0.0001 and 0.0401 respectively, orders of magnitude less than the p-value of the linear separation term (p=0.8074). Due to the high significance in the interaction terms, the separation must also be included in the model as a linear variable (albeit with low significance).

In addition to separation distance, amino acid size is present in both models. Size is another feature one might intuitively expect to contribute to epistasis: large absolute changes in size imply that voids are created when residues change from larger to smaller, or that smaller to larger residues create steric clashes. In both models the coefficient is positive (increases in ϵ occur with change in size) with more of an effect in the case of folding (on the order of 10⁻² vs 10⁻³ in the case of binding). Size interaction terms differ between binding and folding. In the case of binding, when there are changes in size that occur on different protein chains, there is a reduction in epistasis as indicated by the negative coefficient for the interaction term in Table 1 (size_net:interaction side). Otherwise, for all complex types, changes in size lead to an increase in epistasis, most strongly with Antibody-antigen complexes. For folding, size_net interacts with hydrophobicity and SASA_rel leading to decreases in epistasis. This will be discussed further with the features specific to the folding model.

In the case of both binding and folding, there are unique features that contribute significantly to the observed epistasis. In the case of binding, these elements only apply to binding interactions such as the type of complex (defined by function) and whether both mutations occur on the same side of the binding interaction. Complex type is the most significant contributor to the observed epistasis (ΔR² = 0.17) with most complexes showing less epistatic effect compared to the reference category of generic protein-protein complexes. There is an exception with Cytokine-cytokine complexes that shows a small increase in epistasis with a coefficient of +0.4677. The interaction side is a smaller contributor compared to complex type (ΔR² = 0.0465), with a slight increase in epistatic effect when mutations occur on opposite sides of the binding interaction. This is consistent with intuition; if both mutations are near the binding interface and on opposite sides, they are more likely to directly interact, or propagate effects at the interface. Additional features that contribute to epistasis in binding are secondary structure and SASA_abs. Secondary structure has a minor contribution, with a slight increase in epistatic effect when residues belong to different secondary structure types. This is counterbalanced by an interaction with separation distance, where residues that occur in different secondary structures, and are also far apart, lead to a decrease in epistatic effect. This could be due to direct interactions between sites; if they are close together but belong to different secondary structures, they can change these structures either directly or indirectly. This is less likely to happen if they are further apart. SASA_abs is the penultimate feature in the model ranking with a very small coefficient (−0.006). This implies that changes in the total exposed surface area due to the two mutations lead to small reductions in the epistatic effect.

Unique to the folding model, hydrophobicity is present, and is the strongest contributor to epistasis with a ΔR² of 0.1506. Changes in the net hydrophobicity lead to an increase in the observed epistasis. This is consistent with other studies that have shown that hydrophobicity contributes to predicting folding stabilities with double mutations⁶¹. Most of the other terms present in the folding model interact with hydrophobicity leading to a stronger effect on epistasis, and a reduction when paired with changes in size, and changes in charge involving attractive interactions.

Since our statistical models for both binding and folding explain approximately 25-30% of the observed epistasis, an important question is: what explains the other 70-75%? We believe the answer lies in dynamical properties that are beyond the scope of what we investigated here. Protein complexes are not static objects, thus static features like those considered in this study are only likely to capture some of the true physical effect they can have on these systems. While a tool like molecular dynamics could potentially help address this question, given the number of mutations and systems considered here, the computational cost would be unreasonably large and will be left as a topic for future study.

Given the size of our datasets, and the imbalanced nature of the data in terms of protein systems, we performed a “leave-10%-out” validation procedure to test the robustness of our models and determine whether there are system-specific effects (see Table 2). We found that our binding model was very robust; all terms appearing in the full model were also present in the validation trials effectively 100% of the time (the least significant term, secondary structure, was missing from three trials). The mean rank was also consistent between the validation trials and the full model ranking for the three most significant terms, the 4th and 5th are switched but close enough to be within a margin of error, the 6th and 7th were also consistently ranked. The folding model was slightly less robust. The effect of hydrophobicity was very robust being ranked first in the full model and appearing in 99 of the 100 validation trials with a mean rank of one. The remaining folding model terms appear between 96% to 100% of the time, however their mean rankings are generally inconsistent with their full model rank, indicating that while they are important to explaining epistasis we cannot be as certain of their relative contribution.

A limitation in the current study, that is also a limitation for all similar studies, is the lack of comprehensive, diverse, and unbiased datasets. Given the challenges associated with measuring binding or folding free energies for a large number of mutants, these datasets are built with narrow focus and small sample sizes. Such databases tend to be biased toward systems of particular interest. Additionally, they will not contain mutations that result in a nonviable protein or system. This does not make the data any less relevant since in nature proteins must be viable, and thus we should expect similar results (e.g., the preponderance of positive epistasis observed in this study). If we want to understand the nature of epistasis at the level of protein stability, we need to study it across more protein systems in a more systematic fashion. To build a truly predictive model of epistasis, dynamic properties would need to be considered and a larger, more representative sample of data would need to be accessible.

5. Conclusion & Future Work

In this study we investigated possible mechanisms and determined statistical models for pairwise epistasis in proteins based on the largest, most diverse, experimental data available. Mechanistic features were investigated that are intrinsic to the mutating amino acids (e.g., charge, hydrophobicity) or to the proteins (e.g. secondary structure, distance between mutational sites). Using a model selection procedure we ranked these features by their power in explaining the observed epistasis. The resulting models for both binding and folding had similar explanatory power of 25-30% and were composed of similar high-ranked features. The features included in both models were charge, separation distance, and residue size. The largest contributing features were complex type for binding, and hydrophobicity for folding. Our results shed some light on the mechanisms for pairwise epistasis in proteins, and highlights the need for larger datasets. Our study also suggests that development of a truly predictive model for epistasis will likely require difficult to ascertain features such as conformational changes, bond formation, and other propagated mutational effects.

Supplementary Material

1

Figure S1: Comparison of cutoffs for epistasis for both binding affinity (left) and folding stability (right). Purple bars correspond to mutants characterized as epistatic while black indicates non-epistatic. Within the sign breakdown, blue indicates negative epistasis and red indicates positive.

Figure S2: Leave-10-percent-out test results for both binding (left) and folding (right) that demonstrate our models are robust. The top plots show the ΔR² (y-axis) for the 100 runs with complexes removed (run indicated on x-axis). The color coding corresponds to a given feature. Abstracted features were combined to a single heading for that feature for simplicity. The bottom plots indicate the range of ΔR² given by an error bar. The y-axis (and color coding) indicates the feature.

Figure S3: Comparison of epistasis by subcategory for categorical or boolean features. The mean value for a given subcategory is indicated by a black dot. The barplots show the histograms within the categories. In parenthesis is the number of mutation pairs belonging to each category. For the complex type, the number of complexes belonging to each category are shown in square brackets.

Data availability:

All data and scripts used for the analysis in this manuscript are available at the Ytreberg-Patel lab Github repository: https://github.com/YtrebergPatelLab/EpistasisStats