Molecular Dynamics Simulations to Understand Glycosaminoglycan Interactions in the Free and Protein-Bound States

Abstract

Natural glycosaminoglycans (GAGs) are informational molecules with astounding structural diversity. Understanding the behavior of GAGs in the free and protein-bound states is critical for harnessing this diversity. Molecular dynamics (MD) offers atomistic insight into principles governing GAG recognition by proteins. Here, we discuss how MD can be used to understand local and global properties of GAGs in free solution including torsions, puckering, hydrogen bonding, flexibility, and energetics. We discuss MD studies on GAG–protein complexes, which help elucidate the strength of interacting residues, role of water, energetics, etc. MD results accumulated so far suggest that GAG recognition of proteins is a continuum from the highly selective on one end to the fully non-selective on the other with intermediate levels of selectivity including moderately selective and plastic. Advancements in MD technology, such as coarse-grained MD, coupled with really long simulations will help understand macroscale molecular movements in the future.

Introduction

From the simplistic thinking that glycosaminoglycans (GAGs) exist to lubricate joints and cartilage, GAGs are now being described more as informational molecules with distinct biological activities. Structurally, GAGs present the highest diversity known for any linear biopolymer because of the sheer number (>100) of basic hexuronate–hexosamine building blocks found in nature. These repeating disaccharide units when inter-linked through either 1➔4 or 1➔3 glycosidic bonds give rise to different classes of GAGs, including heparin/heparan sulfate (Hp/HS), chondroitin sulfate/dermatan sulfate (CS/DS), hyaluronic acid (HA) and others. The large number of sulfate and carboxylate moieties of GAGs coupled with their prime location either on the surface of cells (as constituents of proteoglycans (PGs)) or in the extracellular matrix affords them major opportunities to interact with numerous proteins (>800) belonging to multiple physiological and/or pathological systems, e.g., hemostasis/thrombosis, growth/differentiation, immune regulation, chromatin remodeling, viral invasion, neuronal regulation and others [1,2]. Yet, GAG recognition by the vast majority of these proteins remains poorly understood.

Understanding the conformational dynamics of GAGs, especially oligosaccharides, is key to unraveling the mysteries of their biological functions. Not only are GAGs structurally diverse, their conformational diversity adds another layer of complexity that plays a major role in protein recognition. Ring puckers of iduronic acid (IdoA), especially ¹C₄, ²S_O, and ⁴C₁, and variations in glycosidic torsions, i.e., Φ and Ψ [3,4], enable GAG sequences in free solution to sample interesting local and global topologies that exist in thermodynamic equilibrium. The consequences of such equilibria in terms of protein recognition has been difficult to pinpoint because a diverse library of GAG sequences is still not readily available. In this context, computational modeling and dynamical studies of GAGs in free solution have provided much information in recent times [5–7]. When used in conjunction with dynamical studies of GAGs in the protein-bound state, a high-resolution insight into GAG recognition of proteins becomes possible [8–11].

In the past decade, molecular dynamics (MD) has been used for understanding conformational dynamics, inter- and intra- molecular interactions, energetics of complexation, and atomistic structure–function relationships for both free and protein-bound GAGs. Even non-computational researchers with access to commercial software/hardware and analytical scripts/tools can perform fairly advanced MD experiments. Here, we present a focused summary of the technology, its capabilities, and recent advances. The reader is also directed to some excellent reviews that offer more background on development of GAG structure parameters, forcefields, etc. for MD studies [12–15]

Fundamentals of MD in Aqueous Medium

MD leverages Newton’s 2nd law of motion to simulate the behavior of a molecule in water. Over the past 50 years, sophisticated Molecular Mechanics (MM) forcefields have been developed, especially for GAGs, that have revealed increasingly detailed properties of GAGs. Of these, the GLYCAM forcefield seems to have an advantage because of availability of parameters for unsaturated uronic acids [16]. Although several studies show that the three commonly used forcefields (GLYCAM, CHARMM, and GROMOS) yield fairly similar results [16–19], subtle differences have been documented [9].

MD simulations start with a 3D model of either the GAG or GAG–protein complex immersed in a simulated box of water (see Figure S1 for the methodology). The majority of studies have been performed using three-point (TIP3P) model of water, which is computationally less taxing while simulating solvent interactions fairly well [10,20–23]. Counterions (e.g., Na⁺) are introduced to achieve formal charge neutrality of the system, which comprises of the test and solvent molecules under periodic boundary conditions [24]. Likewise, conditions mimicking physiology, such as pH and ionic strength, are simulated by ensuring appropriate charge states of amino acid residues and number of salt molecules in the solvent box. The entire system is then minimized and equilibrated to the desired thermodynamic conditions before performing productive simulations during which data are collected at a defined rate, e.g., 10 ps/step, for hundreds of nanoseconds. The advances in computational power these days have allowed for trajectory evolution of >100 ns per day for most proteins, thereby affording the possibility of observing even slower conformational changes that occur over μs time scale (Figure S1). An interested reader is advised to review several reviews [14,15,25] and references cited within to learn of foundational aspects on the subject.

MD of Free GAGs

MD experiments reveal a wealth of atomic (e.g., torsions, puckering, and hydrogen bonding), molecular (e.g., global shape), and thermodynamic (e.g., potential energy) information (Figure 1). The Ramachandran plot, classically developed for proteins, is also visually appealing for GAGs because it directly conveys favored glycosidic torsions (Φ and Ψ), thereby quickly revealing local similarities and differences. Likewise, MD studies reveal hopping, or lack thereof, of ring puckers, e.g., from ⁴C₁ to ²S_O to ¹C₄ for IdoA. These results have also been supported by NMR studies, which is an independent approach to understanding GAG structure. In fact, MD and NMR provide a synergistic approach to understand preferred conformational states in solution of GAGs [26–30].

Figure 1. MD simulations of GAGs offers information on A) local as well as B) global properties.

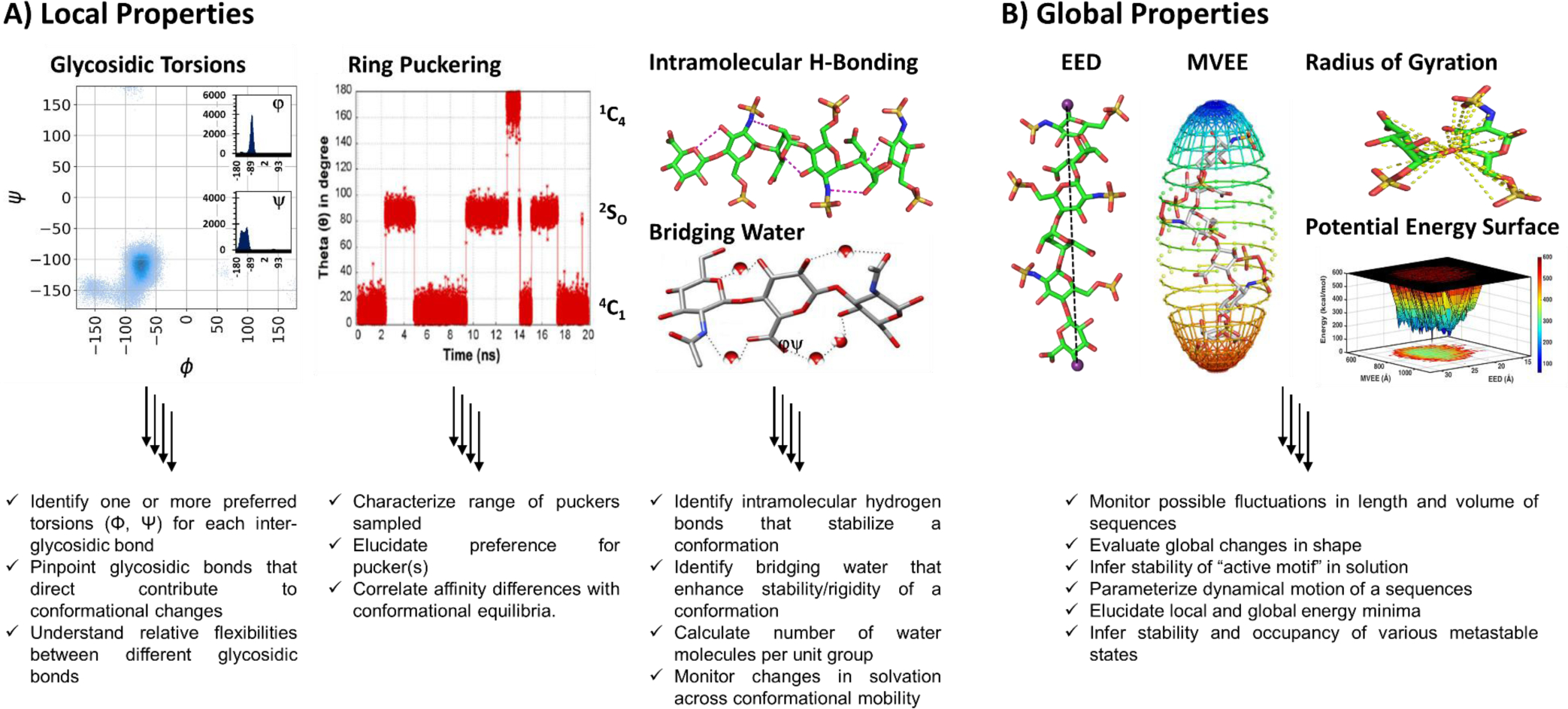
Local properties include i) preferred Φ,Ψ (shown is a UA➔GlcN glycosidic linkage), where dark blue areas correspond to areas of higher frequency and the inset shows the corresponding histogram for Φ and Ψ; ii) ring pucker changes plotted in terms of Cremer-Pople parameter θ as a function of time; and iii) nature of intramolecular (within GAG) or intermolecular (between GAG and water) H-bonds. Global properties include End-to-End Distance (EED) and Minimum Volume Enclosing Ellipsoid (MVEE) parameters; EED is the Euclidean distance between the farthest oxygen atoms in the GAG and approximates its length in solution, whereas MVEE is the minimalist fit of the atomic coordinates of the GAG into the smallest possible 3D-ellipsoid to approximate its volume. MD also offers R_g, the radius of gyration, which sums the squared distances between all atoms and the center of mass. Leveraging EED and MVEE simultaneously allows elucidation of the potential energy surface (PES) of the GAG sequence in water. Detailed analysis of PES can provide the local and global energy minima. The color scheme on the right refers to the energy scale, wherein low energy corresponds to blue areas and high energy to red.

A deeper understanding of free GAG structures, e.g., the strength and stability of intra- and inter-molecular hydrogen-bonds (H-bonds) that form the basis for GAG flexibility, is also possible to achieve through MD (Figure 1A). For analysis at the molecular level, several newer tools, i.e., EED (end-to-end distance), MVEE (minimum volume eclipsing ellipsoid) and R_g (radius of gyration), have been developed. Application of these tools to each MD frame, which may number >1000, reveals global shape changes in detail [6,18,31]. Newer tools have been also developed to derive an insightful view of the classical potential energy surface (Figure 1B). Assimilation of these parametric changes provides deeper insight into the structure and dynamical behavior of free GAGs in solution.

Glycosidic Torsions.

A summative observation from MD studies has been that the preferred Φ and Ψ torsions for GAGs tend to stay bound within a narrow region as long as the type of glycosidic linkage remains same, e.g., β1➔3 or β1➔4, irrespective of the GAG (see Figure S2 for the definitions of two torsion angles). Prior work on neutral sugars showing absence of ring puckering effects on glycosidic torsions [4] supports this narrow range of Φ and Ψ in GAGs. This implies that the linear sequences adopt a fairly consistent helical shape; although torsional populations may change as a function of sulfation. A recent study on MD of 106 GAG sequences found only three major glycosidic topologies at the disaccharide level [7]. Yet, biologically active sequences are usually longer than disaccharides, which begs the question about overall topological changes as the polymer length increases. A case in point is that certain IdoA2S➔GlcN linkages in Hp displayed more than one torsional pairs, which implies that despite an overall helical shape, Hp can display local conformational variations [32].

Ring Puckering.

A large number of MD studies with mono- and di- saccharides have been performed to understand ring flexibility and transitions in GAGs [32–35]. The studies uniformly indicate that most GAG residues exhibit only one preferred ring form (e.g., ⁴C₁), except for IdoA and IdoA2S, which exist in at least ⁴C₁, ¹C₄ or ²S_O forms. A growing understanding in the field is that the occupancy of multiple puckers by IdoA/IdoA2S drives induced-fit recognition of proteins. For example, IdoA2S, as in Arixtra, displays more stable ²S_O form and a better recognition of antithrombin [36]. Interestingly, IdoA2S has been found to favor the ⁴C₁ form, instead of the ¹C₄ form, as its location changes from the non-reducing end to the reducing end (Figure 2A) [37]. Thus, despite many studies, much remains to be deciphered regarding IdoA-induced conformational biases.

Figure 2. Important deductions from MD simulations of GAGs.

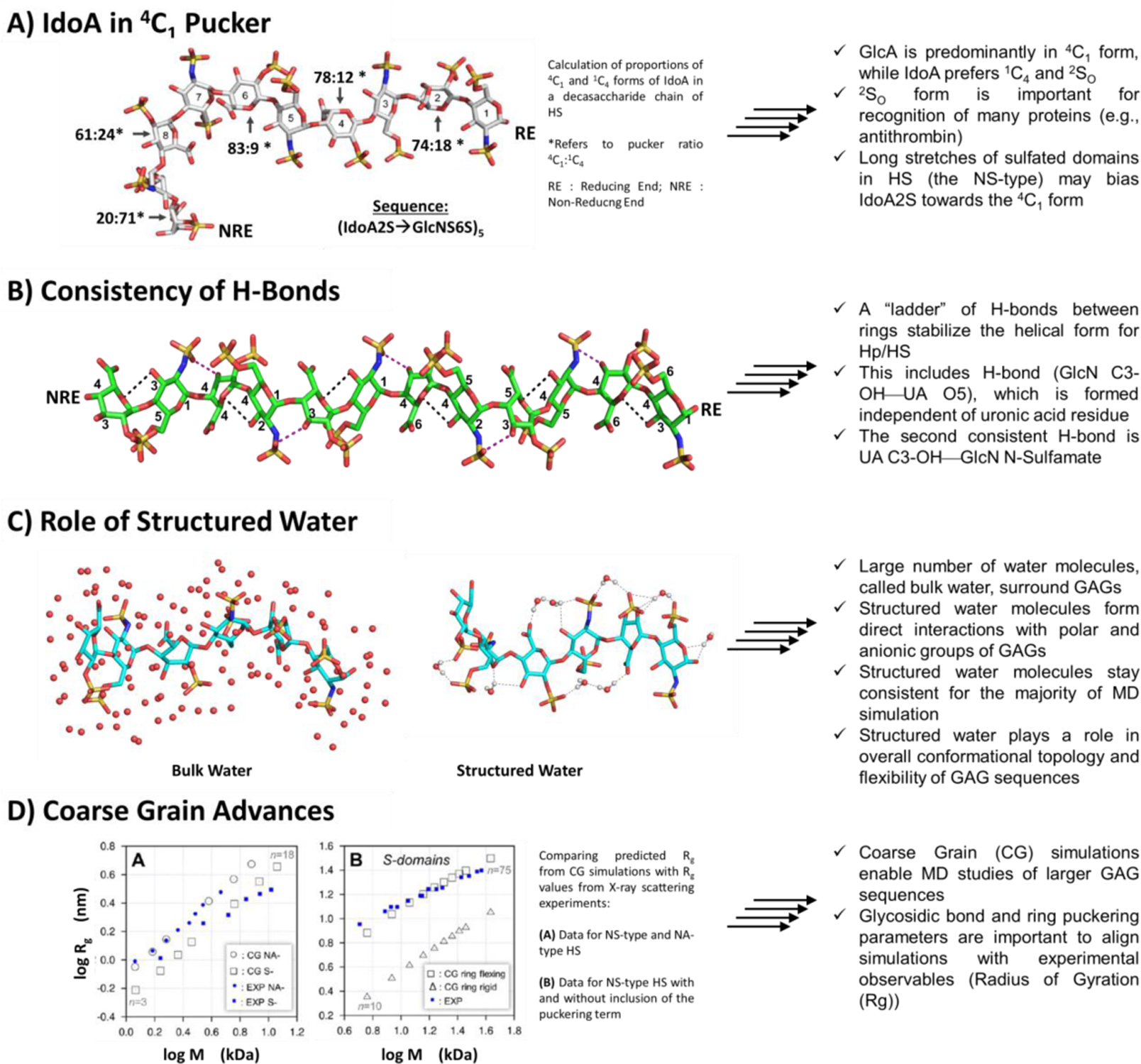
Over the years, MD has offered key insights in the conformational behavior of GAG sequences in water including A) the dependence of IdoA pucker as a function of its location in the GAG chain; B) the high consistency of intramolecular H-bonds that favor secondary structure formation; C) the importance of structured water in 3D topology of GAGs; and (D) the importance of torsions and puckers in dynamical motion of GAGs in solution. A) Although most IdoA in Hp/HS chains found in the PDB exist in the ¹C₄ and ²S_O forms, recent studies have shown that long, heavily sulfated (NS type) HS chains exhibit IdoA in the ⁴C₁ form, which is more populated as chain length increases. Shown are results (⁴C₁ : ¹C₄ ratio for IdoA2S residues) derived for the sequence (IdoA2S–GlcNS6S)₅. B) Hp/HS is known to adopt a coiled shape in solution, which is also referred to as ‘linear’ cylindrical shape. Interestingly, this overall shape is stabilized by two consistent H-bonds of each disaccharide unit, i.e., GlcN C3 OH—UA O5 and UA C3 OH—GlcN NH. A ‘ladder’ of these intramolecular H-bonds stabilizes the coiled shape. (C) In the manner of proteins, GAGs sequester ‘structured’ water, which is different from bulk water. Structured water contributes to stabilization of the overall topology and dynamical motion of GAGs. (D) Considering the incredible structural heterogeneity within a GAG, the number of computations increases exponentially with each additional disaccharide in an MD simulation. Coarse-grained MD simulations cut down on computational cost by utilizing a simplified set of pseudo atoms, and have aided in studying larger GAGs. However, recent studies have shown that inclusion of a ring puckering term is essential for agreeance with macroscopic experimental observables (R_g).

Hydrogen-bonding.

MD simulations are particularly suited to assess the strength and stability of H-bonds. One way to accomplish this is the H-bond occupancy, which refers to the proportion of MD frames that display the target H-bond. Such analysis has shown that intramolecular H-bonds are critical for the formation of two- and three- fold helices of GAGs [38]. In fact, a ‘ladder’ of H-bonds between rings help stabilize helix formation in GAGs, which reminds one of the formation and stabilization of α-helices in proteins. More specifically, two H-bonds between adjacent residues (GlcNC3-OH—UA O5 and UA C3-OH—GlcN NH) are formed fairly consistently to mimic a ‘ladder’ (Figure 2B). In addition, several other high occupancy H-bonds arise in GAGs that help stabilize the overall topology [39–42]. Importantly, changes in IdoA pucker induces local structure-dependent changes in intramolecular H-bonding, as observed for DS [38]. Finally, an intra-residue H-bond between NH and 3-O-sulfonate of the GlcNS3S6S of Hp/HS shows a H-bond occupancy drop of ~25% upon ²S_O to ¹C₄ conversion [41], which is a reminder that local conformational variations do dictate flexibility and topology.

Bridging Water.

The inter-molecular interaction of GAGs with solvent water molecules modulates not only their characteristic viscoelastic properties, but also their local conformation, global fold, flexibility and recognition of other molecules. Useful tools have been developed, that can calculate the water occupancy of each group, e.g., COO⁻, OSO₃⁻, OH, etc., of GAGs as a function of the MD trajectory [43]. Thus, water-induced stabilization of helical folds [44,45] and water-mediated stabilization of the bound protein have been deduced from MD [46–49]. Another tool is the pair distribution function, defined as the average distribution of water molecules around an atom at thermodynamic equilibrium, which has revealed the presence of structured and bulk water around GAG chains (Figure 2C). Several studies have estimated nearly 20 structured water molecules per disaccharide, with the majority around the −OH and −OSO₃⁻ groups [43]. The high number of structured water molecules around GAGs appear to facilitate conformational switching of IdoA residues [42], which could be important for protein binding.

Global Properties.

A major opportunity for understanding the overall shape and flexibility of longer GAG sequences is unfolding these days through MD studies. A recent application of two tools – MVEE and EED – have led to visualization of the potential energy surfaces. The key take home message was that the oligosaccharide samples multiple local minima, which are within reach from the global minimum in solution [6]. These tools have also been to test the GAG-mimicking potential of synthetic GAG mimetics [20]. Another advance that is likely to be of special interest to GAGs is the development of coarse grained (CG) ‘force-fields’. A recent study using CG models conveys that information on local conformations (IdoA ring puckering) could be derived using experimental radius of gyration (R_g) data collected from light scattering experiments (Figure 2D) [35].

MD of GAG–Protein Complexes

Although a large number of computational studies on GAG–protein complexes are being performed today [10,11,50–52], very few studies incorporate an MD arm. Relying only on molecular docking enhances the risk of misinterpretations on the strength and stability of GAG–protein complexes. While MD studies on GAG–protein systems are time consuming and challenging, they are essential for full and true understanding on how GAGs recognize proteins. The first step in this direction is to prepare coordinates of the desired GAG–protein co-complex. These may be available from public databases [e.g., rcsb.org; gagdb.glycopedia.eu; etc.]. However, these currently contain only about 100 GAG–protein structures with the vast majority presenting only the common GAG sequence found in nature. Thus, molecular docking has remained the preferred method to obtain the starting coordinates of the GAG–protein complexes. One robust approach for this purpose is the combinatorial virtual library screening (CVLS) algorithm [13], which provides reliable starting coordinates but also offers key information on the GAG binding site on the protein and the most optimal GAG sequence. Other docking approaches to avail of GAG–protein coordinates include open source tool AUTODOCK (autodock.scripps.edu), a web-based tool ClusPro (cluspro.bu.edu) and HADDOCK (wenmr.science.uu.nl/). Following GAG–protein complex selection, a series of steps are implemented before performing productive MD simulations (Figure S1).

Once MD trajectories are collected at high-enough resolution, a host of analyses can be performed including the nature and energetic contributions of interacting residues, the role and extent of bridging water molecules, the role and extent of interactions of specific moieties/residues, e.g., sulfate groups of GAGs and non-ionic residues of the protein (Figure 3). Such analyses have been performed for a host of GAG–protein systems over the past two decades starting with the first simulation of heparin–antithrombin (AT), which revealed domain movement and relative residue contributions [53]. An MD study of HS06–FGF2 found minimal rolling of the hexasaccharide [10], while MD of HS–CXCL8 complex showed a minimal requirement of at least four sulfated residues [22]. When GAG-binding site is not established, information from mutagenesis could be used for MD studies, as shown for HS binding to CLEC14A [54]. MD has also been used to understand the role of cations in GAG recognition of proteins [55]. Here is it important to recognize the role of pH in GAG recognition. The protonation states of amino acid residues, especially histidine, is critically dependent on the pH and contributes substantially to GAG recognition [23]. Finally, while it is advisable to perform microsecond scale simulations, it may not be necessary for many systems as shown in the study on the role of GAGs in FGF1 [51]. As a group, chemokines are perhaps the most studied for GAG binding using MD [22,23,46,56–59]. While the vast majority of MD studies have been performed with the GAG sequences commonly occurring in nature, MD of some unique CS oligosaccharides binding to TGFβ−2 have also been performed. Interestingly, the study identified two sites of binding, which when simultaneously occupied provide higher free energy of binding (~2-fold) than unitary occupation (Figure S3) [11], an observation supported by literature [60]. Newer techniques/tools, such as dynamic molecular docking (DMD) [9], co-solvent MD [50], coarse-grained MD [61], etc., are also being developed to predict GAG binding and selectivity to proteins. Finally, it is important to note that MD can simulate all lock & key interactions and many induced-fit processes; however, major movements of domains may not be simulated fully because the process may be too slow on the MD timescale.

Figure 3. Key insights possible to derive from MD trajectory analysis of GAG–protein complexes.

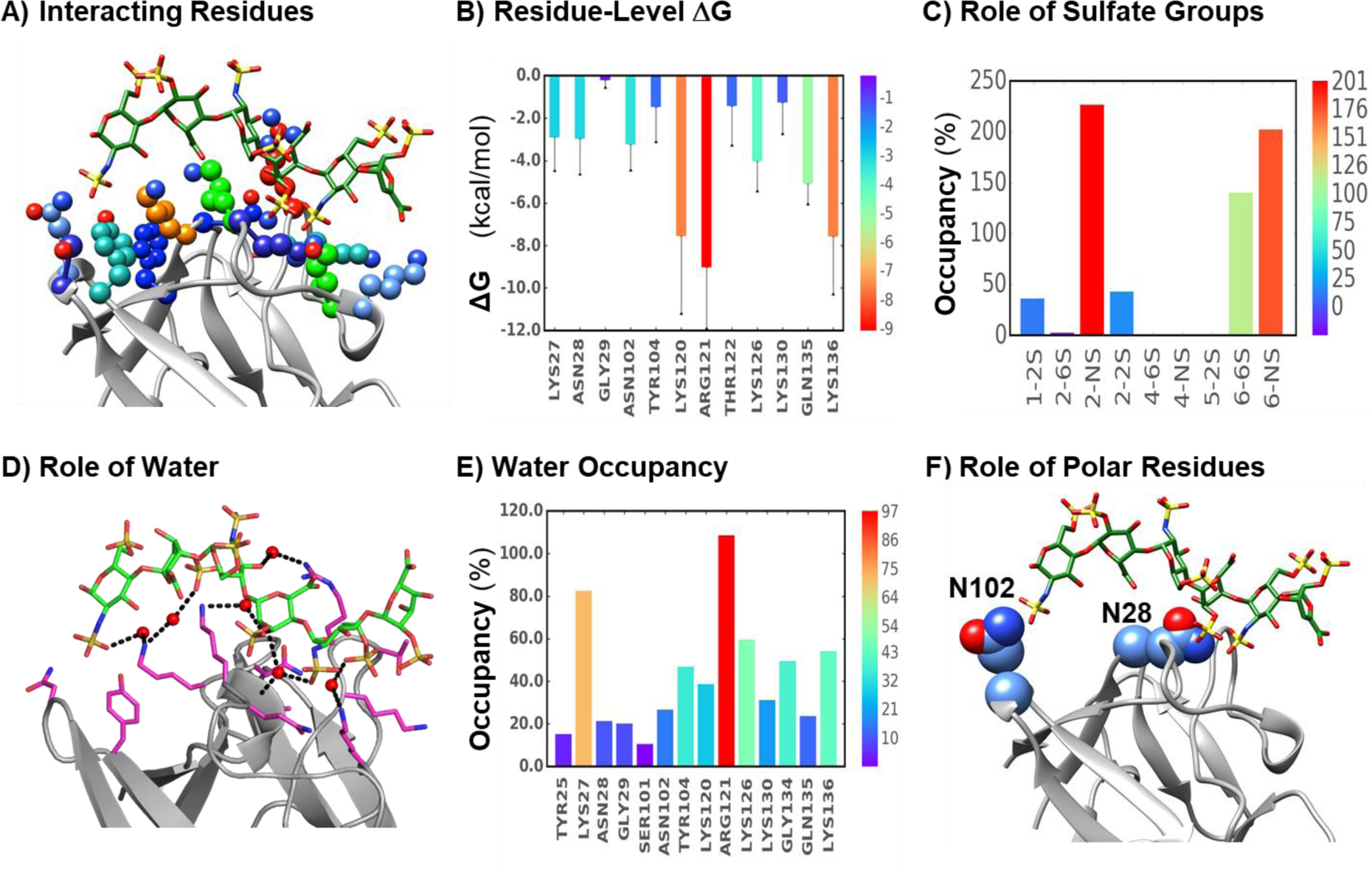
These include interacting residues (A) and their energetic contributions (B), the role of GAG sulfate groups (C), the nature of bridging water molecules (D) and their propensities across the MD timescale (E), and the role of non-ionic, polar residues (F). Protein residues shown in (A) are color coded to match their energetic contributions to GAG binding (B, Error bars show ±SEM). Blue dotted lines in (D) show donor/acceptor interactions mediated by water molecules (red spheres; hydrogen’s not shown). (E) shows the residue level occupancy of water-mediated H-bond occupancy upon GAG binding. In the manner of energy contributions derived for single residues, hydrogen bond occupancies of individual sulfate groups (e.g., group of the non-reducing end (NRE) saccharide; group of residue #2 from the NRE; etc.) can also be derived (C). Interestingly, analysis of MD trajectories has shown that non-ionic residues of proteins also contribute to GAG binding, e.g., Asn102 and Asn28 group of FGF2. Note: Energetic contributions or occupancies are rainbow color-coded with the scale shown on the right.

Residue-Level Energetic Contributions.

The stability of GAG–protein complex throughout the MD simulation, especially when the GAG settles into one or few defined pose(s), is a powerful indicator of a reliable site of binding on the protein. Such a scenario provides much insight into the nature of GAG and protein features that contribute high binding energy. A recent simulation of the HS06–FGF2 complex, where the IdoA residues were either in ¹C₄ or ²S_O form clearly showed that amino acid residues do not bind to both puckers equally all the time (Figures S4A and S4B) [20]. On the flip side, the corresponding sulfate groups of the two puckers also form H-bond at widely different levels with the binding site residues (Figures S4C and S4D). This has also been observed for several other systems where the two forms are differentially populated [57,62,63]. Because both ¹C₄ or ²S_O forms would be populated in solution, the overall binding energy would be expected to be the weighted average, which can be readily collected from MD trajectories. This simple fact remains under-appreciated. Also, in the manner of energy contributions derived for single residues, hydrogen bond occupancies of individual sulfate groups can also be derived, which help support energy contributions of residues (e.g., group of the non-reducing end (NRE) saccharide; group of residue #2 from the NRE; etc.) (see Figure 3C).

Despite the value, calculations on binding energies from MD trajectories remain involved. Different methods are used including the Poisson-Boltzmann (PBSA)/Generalized Born methods (GBSA) [8–10,20] and linear interaction energy (LIE) approximation [64]. The advantage of the former is that individual residue-wise contributions can be deduced, which provides detailed insight into the nature and strength of interaction points (Figures 3A, 3B & 3C). It is also possible to derive and compare the importance of key functional groups using PBSA/GBSA, as shown by Sood et al. [65] This allows for rational design of protein and GAG variants for biological analysis, as achieved for growth factors, chemokines, serum amyloid A and others [8–10,46,47,49,55,64,66].

Influence of Bridging Water.

MD trajectories are especially useful for characterizing the role of water molecules in GAG recognition of proteins. As stated above, free GAGs in solution carry numerous water molecules, many of which are replaced because of direct binding to protein residues. MD simulations reveal that some water molecules are actually not replaced, but are trapped in-between and are referred to as H-bonded bridging water molecules (Figures 3D & 3E). Depending upon the strength of H-bonding, bridging water molecules may function as ‘structured’ water that lend critical binding energy and recognition features. This has been observed in several GAG–protein systems, e.g., FGF2, CD44, CXCL5, CXCL1, and others [46,47,49,56,63].

Role of Non-Ionic, Polar Residues.

Although most researchers assume that ionic residues, i.e., Arg, Lys, and some His, mediate GAG binding, it is becoming clear that selected non-ionic, polar residues play important roles too. In fact, in a number of cases, e.g., antithrombin, 3-O-sulfotransferases, and others, Asn and Gln residues strategically located within the GAG binding site contributed significant interaction forces while also enhancing the selectivity of recognition [67]. Several MD studies have recently documented this to a higher level of detail. For example, a long MD study of FGF2–HS06 (¹C₄ or ²S_O) complex shows that Asn28, Asn102 and Asn135 form strong H-bonds with HS06 (Figures 3E & S3A) [10,20]. Mouse chemokines MIP2 and KC bind to HS oligosaccharides through two polar residues each (Figures S5B & S5C). Likewise, FGF1, CCL2, and procathepsin B have been shown to engage one or more Asn/Gln residues [21,68,69]. Thus, detailed MD trajectory analysis, as described above, is particularly useful in highlighting the role of these polar, non-ionic residues in governing selectivity of GAG recognition.

Inferences on Selectivity, Plasticity and Non-Selectivity from MD

MD offers a unique opportunity to understand the type of GAG recognition by proteins. Most researchers assume that GAG binding to proteins is non-selective because electrostatic forces drive these interactions. Electrostatic forces, i.e., positive/negative charge–charge interactions, are non-directional in nature resulting in poor selectivity. Yet, H-bonding forces also play major roles in stabilizing GAG–protein complexes, as noted above (Figures 3D & 3E). H-bonding is highly directional, thereby playing a major role in the induction of selectivity. Additionally, less recognized is the role of asymmetric distribution of basic residues, e.g., Arg and Lys, in enhancing selectivity, which has been shown earlier [10,20].

GAG–protein systems rely on varying levels of contributions from directional and non-directional forces. Thus, it is naive to segregate them into only two bins – ‘selective’ and ‘non-selective’ systems. Rather, GAG–protein systems exhibit a continuum of selectivity from the ‘highly selective’ to ‘moderately selective’ through ‘plastic’ and ‘fully non-selective’ (Figure 4). The ‘highly selective’ GAG–protein systems exhibit very high consistency in mode, directionality and type of interactions in the site of binding. A classic prototype is antithrombin–heparin system [70], which involves unique interactions between sulfate groups of heparin pentasaccharide and basic residues of antithrombin. Binding modes outside of this unique mode are possible but are dramatically weaker and essentially unpopulated. An MD study of HS06 exhibits highly consistent binding and interaction with multiple Lys residues of KC, the mouse homolog of hCXCL1 suggestive of highly selective recognition (Figure 4, Movie S1) [56].

Figure 4. Inference on GAG recognition by proteins.

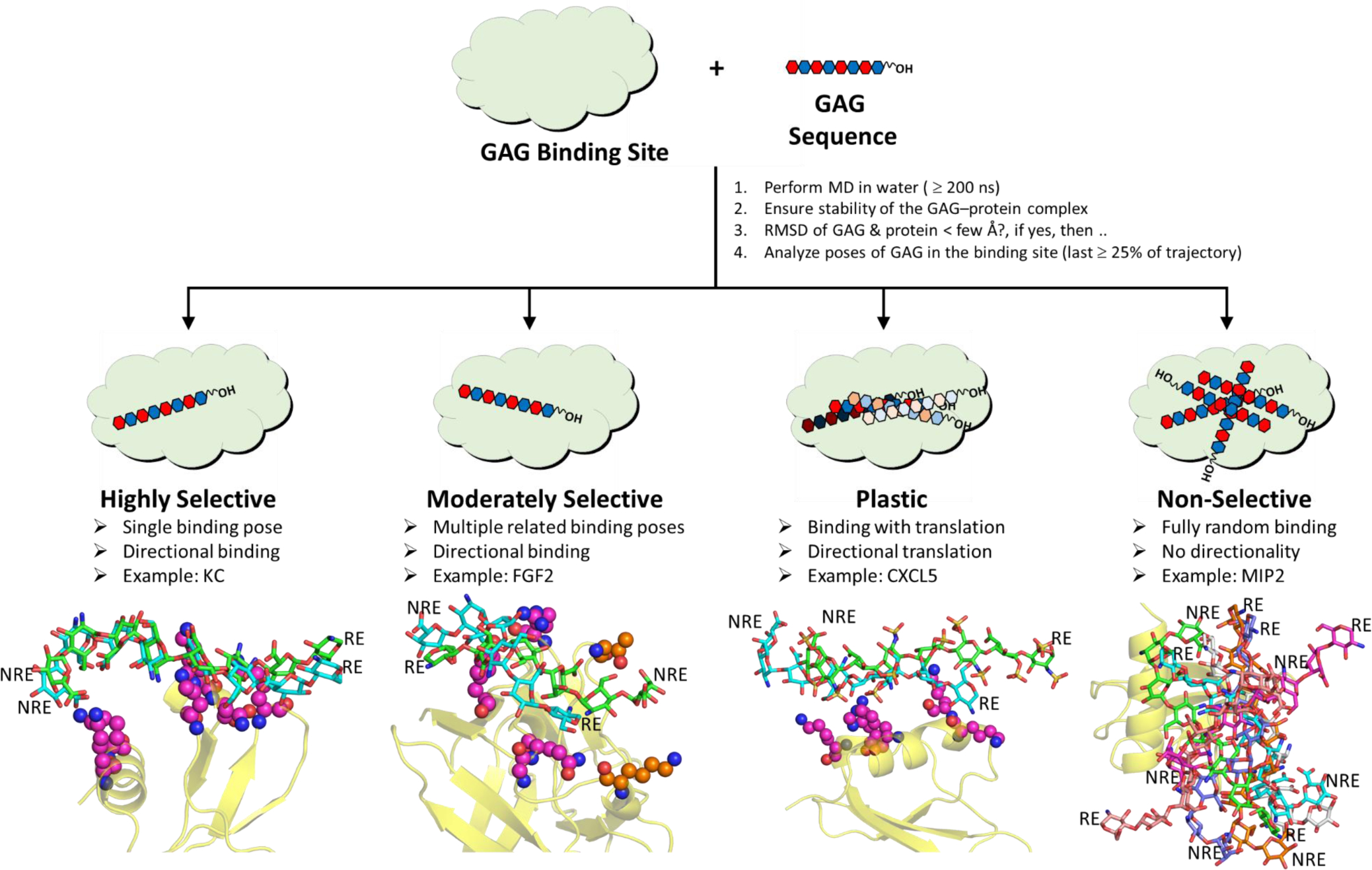
Although GAGs are generally believed to bind to proteins in an essentially non-selective manner, MD studies have revealed a much more wider spectrum of recognition ranging from the highly selective to moderately selective and plastic through fully non-selective. The figure describes definitions and properties of four categories. MD studies in combination with molecular docking studies offer a truly high-resolution view of GAG recognition of proteins.

In the category of ‘moderate selectivity’ is GAG binding to some proteins, e.g., FGF2 [20]. Here, the GAG exhibits major preference in terms of directionality of binding, i.e., chain polarity. Yet, GAG sequences exhibit several poses that utilize different sets of protein residues for binding (Figure 4, Movie S2). This is an intermediate level of selectively, which is crucially important in biological context because it enhances the probability of GAG interaction, and therefore function, dramatically. Moderately selective proteins are able to rapidly bind to a number of closely related GAG sequences, which statistically enhance the probability of interaction in comparison to the very few highly selective GAG sequences.

A different type of selectivity arises when the GAG chain slides along the site of binding on the protein while maintaining the directionality of chain. This is the case of HS06 binding to hCXCL5 (Figure 4, Movie S3) [46]. Biologically, this equates to translational movement of proteins on polymeric GAG chains present on cell surfaces as a part of proteoglycans. Such a translational motion is critical in chemokine-mediated chemotaxis of neutrophils [71] or viral glycoproteins-mediated internalization of herpesvirus into host cells. Such a movement can be referred to as ‘plasticity’ and is likely a fundamental property of many GAG–protein systems.

Finally, a GAG–protein system that displays no preference for either the GAG sequence or the binding pose is fully non-selective. The classic prototype for this class is the GAG–thrombin system, which accommodates any anionic polymer in exosite 2 of thrombin in multiple different binding poses. Another system that exhibits this property in MD simulations is MIP2, the mouse version of hCXCL2, which seems to recognize anionic groups with no particular preference for orientation or directionality (Figure 4D, Movie S4) [56].

Challenges and Future of MD Experimentation

Despite much successes to date, MD simulations remain challenging for most researchers to perform. Simulating GAG structures, especially with the multiplicity of IdoA conformations, requires laborious cross-checking and rigor. Validating MD results, which require solution-based experiments, may not be easy or feasible. At the level of experimentation, even with the power of parallel processing, all-atom MD simulations of GAGs are still limited to mono- to dodeca- saccharides. Longer chains present major hurdles because of exponential rise in the number of degrees of freedom. Yet, the MD field is rapidly advancing in terms of developments in experimental techniques. One advance is the development of coarse-grained (CG) MD parameters, which involve the concept of pseudo-atoms, which reduce a structural group, e.g., IdoA ring or NHCOCH₃, to an ‘atom’ of appropriate properties [50,72]. This has enabled CG studies of polymeric CS and HA under various pH, ionic strengths, cation type and cation levels [5,73]. While the early CG models gave up some information to enhance simplicity, a recent study has shown that only when IdoA ring puckering was incorporated into CG pseudo-atoms was it possible to simulate the R_g data collected from light scattering experiments [37]. Finally, a recent CG model developed 28 pseudo-atoms corresponding to functional groups from 17 different GAG residues and a parameter set that is compatible to the AMBER force field [5].

MD experimentation also suffers from the possibility of insufficient sampling of the conformational space, especially when using classical simulations. Energy barriers may not be overcome due to the nature of GAG polymers. Advanced MD methods, such as replica exchange molecular dynamics (REMD), have been developed to address this possibility on a classical MD timescale. REMD attempts to access the conformational space exhaustively by launching multiple simulations of the same system (‘replicas’) at different temperatures or Hamiltonians [74]. The REMD method has been used for conformational analysis of methyl-IdoA and methyl-GlcA [75]. The method when applied to idraparinux analogs showed conformational changes at the either ends of the pentasaccharide [76]. The method has also been used to predict 21 protein–GAG structures, of which 19 correlated well with experimental structures [77].

Metadynamics is another advanced sampling method where recently visited minima are ‘filled’ during the simulation to incentivize exploration of new minima [78]. Metadynamics simulations on β-D-glucose with various force fields (GLYCAM, CHARMM, GROMOS, OPLS) indicated that although ⁴C₁ was the ubiquitous global energy minimum, ¹C_4, ²S_O, and other intermediate boat and skew-boat conformers were sampled [79]. IdoA is arguably a more pertinent monosaccharide for advanced studies due to its higher ring dynamism [80]. Interestingly, metadynamics simulations of methyl-IdoA and methyl-IdoA2S showed strong correspondence between scaling (reduction) of 1–4 electrostatics and population of IdoA(⁴C₁) [81].

Adaptively-Biased Molecular Dynamics (ABMD) attempts to shrink energy barriers by artificially flattening the energy surface so as to encourage transition to other possible conformers. Using the ABMD method, a strong affinity of Ca²⁺, but not of Na⁺, was observed for the GlcA-COO⁻ in CS disaccharides [82]. The same study showed that 4-O-sulfation of GalNAc in GlcA➔GalNAc and GlcA➔GalNAc6S disaccharides destabilized a secondary Φ,Ψ minima present in the unsulfated counterparts, likely by breaking a key intramolecular hydrogen bond between GlcA-COO⁻ and GalNAc-C4OH. Other advanced MD methods include umbrella sampling [83], targeted MD [84], linear interaction energy (LIE) [85], and CG [50,72,73], many of which focus on lowering computational cost and time.

Majority of above advanced MD techniques are in the early phase of development, where smaller saccharides are being studied. Their promise will be better realized when methodology for their use in designing pharmaceutically relevant sequences would be developed. These sequences are typically in the range of tetra- to octa- saccharides. To date, application of MD to huge range of these sequences (>1000s) remains challenging, especially at a high-throughput level. The pathway forward in this case has been to first explore molecular modeling technologies, e.g., combinatorial virtual library screening (CVLS) [11,13,86], to identify promising sequences and then implement MD. Yet, MD helps understand how nature exploits the diversity of polymeric GAGs to steer biological responses, e.g., chemotaxis, viral invasion, etc. [71], remains a formidable challenge. This also implies that the impact of the initial evidence of plasticity in GAG recognition of proteins present above is yet to be fully recognized. Finally, MD is also expected to have major impact on the discovery of GAG-based drugs. In this specific case, although most GAG–protein systems should be druggable in principle, not many highly selective systems have been identified. Considering that MD has tremendous potential to reveal the true nature of selectivity of GAG–protein systems, rigorous implementation of MD tools will enhance the probability of success in identifying GAG-druggable proteins.