Abstract
Motivation
Large-scale and high-dimensional genome sequencing data poses computational challenges. General-purpose optimization tools are usually not optimal in terms of computational and memory performance for genetic data.
Results
We develop two efficient solvers for optimization problems arising from large-scale regularized regressions on millions of genetic variants sequenced from hundreds of thousands of individuals. These genetic variants are encoded by the values in the set . We take advantage of this fact and use two bits to represent each entry in a genetic matrix, which reduces memory requirement by a factor of 32 compared to a double precision floating point representation. Using this representation, we implemented an iteratively reweighted least square algorithm to solve Lasso regressions on genetic matrices, which we name snpnet-2.0. When the dataset contains many rare variants, the predictors can be encoded in a sparse matrix. We utilize the sparsity in the predictor matrix to further reduce memory requirement and computational speed. Our sparse genetic matrix implementation uses both the compact two-bit representation and a simplified version of compressed sparse block format so that matrix-vector multiplications can be effectively parallelized on multiple CPU cores. To demonstrate the effectiveness of this representation, we implement an accelerated proximal gradient method to solve group Lasso on these sparse genetic matrices. This solver is named sparse-snpnet, and will also be included as part of snpnet package. Our implementation is able to solve Lasso and group Lasso, linear, logistic and Cox regression problems on sparse genetic matrices that contain 1 000 000 variants and almost 100 000 individuals within 10 min and using less than 32GB of memory.
Availability and implementation
1 Introduction
Constantly growing biobanks have provided scientists and researchers with unprecedented opportunities to understand the genetics of human phenotypes. One component is to predict phenotypes of an individual using genetic data. However, datasets of increasing size also pose computational challenges for this task. On the statistics side, genetic datasets are usually high dimensional, meaning the number of genetic variants is larger than the number of sequenced individuals. High-dimensional statistics have been studied for more than two decades with well understood solutions. One such solution is to ‘bet on sparsity’: the assumption that only a small subset of variables is associated with the response. The sparsity assumption is usually embodied through an objective function that encourages sparsity in the solution. Well known examples include the Lasso and the group Lasso. On the computation side, a statistical estimator that describes the relationship between the genetic variants and the response of interest are often obtained by optimizing an objective function involving the genetic matrix. While off-the-shelf solvers may exist for these optimization problems, they are usually not optimal for genetics data. First, these general-purpose solvers require loading a floating point predictor matrix in memory before optimization can be done. This can demand a very large amount of memory for biobank scale data. For example, loading a matrix with 200 000 rows and 1 000 000 columns as double precision floating point numbers takes 1.6 terabytes, much larger than the RAM size of most machines. In particular, they do not exploit the fact that genetic variants can take on only four possible values. Secondly, many of these solvers do not fully utilize modern hardware features such as multi-core processors, which leaves lots of performance on the table. Thirdly, a large number of variants in exome and whole genome sequencing data are rare variants. If a variant is encoded as the number of copies of the minor allele, then the corresponding genetic matrix is sparse. In the UK Biobank’s exome sequencing data (Szustakowski et al., 2020), more than 99% of the variants in the targeted regions have minor allele frequency <1%. As a result, more than 98% of the entries of the corresponding genetic matrix are zero. The sparsity in the predictor matrix can potentially be exploited to improve both memory requirements and computational speed.
The main result of this work is an extremely efficient regularized regression solver for problems with sparse genetic predictors, named sparse-snpnet. The main features of this solver are the following:
A compact, two bits representation of genetic variants based on PLINK2’s (Chang et al., 2015) pgen files.
Good scalability to multi-core processors.
A simplified version of the compressed sparse block format so that arithmetic operations on the genetic matrices are more amenable to parallelism.
In addition, we provide an extension to the popular package glmnet (Friedman et al., 2010; Simon et al., 2011) specifically for Lasso problems involving genetic matrices. This extension exploits the compact representation and is multi-threaded, but does not assume sparsity of the input genetic matrix. We incorporate this solver to the screening framework (Qian et al., 2020) in snpnet and name it snpnet-2.0. Both solvers are implemented in and wrapped as part of the package snpnet, which is available at https://github.com/rivas-lab/snpnet/tree/compact. We refer the readers to Section 5 for comparisons between these two methods.
2 Materials and methods
2.1 Optimization algorithm
We focus on regularized regression problems whose objective functions are in the following form:
| (1) |
where is a genetic matrix, is the parameter vector, is usually the negative log-likelihood function of a generalized linear model (Hastie and Tibshirani, 1986), and is always assumed to be smooth and convex. We have omitted the dependence of h on the response vector to simplify the notation. is a regularization function, and represents the strength of regularization. Here are some examples of h:

Linear regression: for a response vector .
Logistic regression: write for a binary response .
Cox regression (Cox, 1972): Write for a survival time vector and an event indicator .
The regularization function is usually a seminorm but not always. Some examples are:
Lasso (Tibshirani, 1996): .
Elastic net (Zou and Hastie, 2005): for some .
Group Lasso (Yuan and Lin, 2006): , where represents a subset of variables.
To minimize (1), we apply an accelerated proximal gradient descent algorithm (Beck and Teboulle, 2009; Daubechies et al., 2004; Nesterov, 1983) with backtracking line search to determine the step size. This algorithm has fast convergence rate, essentially no tuning parameter, and is particularly suitable for the simple regularization functions that we use. In short, this algorithm alternates between a gradient descent step that decreases the value of , and a proximal step that ensures that the regularization term is not too large. Note that the gradient here refers to the gradient of with respect to β. The regularization function is usually not differentiable at 0. The proximal operator is defined as:
| (2) |
When the regularization function is one of the examples above, the corresponding proximal operator has explicit expression. We summarize this process in the pseudo-code in algorithm 1.
We observe that in this algorithm, the only operations that involve the predictor matrix X are matrix-vector multiplications and XTr, where . When X is dense, these two operations are also the most computationally intensive ones in this algorithm, having complexity , whereas all other operations are either or . This, together with the need to reduce the amount of memory required to load X, motivate a more compact and efficient representation of the genetic predictor matrix X.
2.2 Sparse genotype matrix representation
In this section, we describe the format we use to represent sparse genetic matrices. First of all, we pack each entries in the matrix to two bits. 0, 1, 2 and are represented by 00, 01, 10 and 11, respectively. The compressed sparse column (CSC) format is a popular way to store a sparse matrix. The PLINK 2.0 library (Chang et al., 2015) provides functions that make loading a genetic matrix into this format straightforward. Under CSC, a matrix with n rows, d columns and nnz non-zero entries are represented by three arrays:
A column pointer array of size d + 1.
A row index array row_idx of size nnz.
A value array val of size nnz.
For each column , the non-zero entries in that column are stored from the col_ptr[j]th (inclusive) entry to the (col_ptr[j + 1] - 1)th entry of row_idx and val, where row_idx stores the row index of the non-zero entry and val stores the non-zero value. Figure 1 provides an illustration of a sparse genetic matrix under CSC format.
Fig. 1.
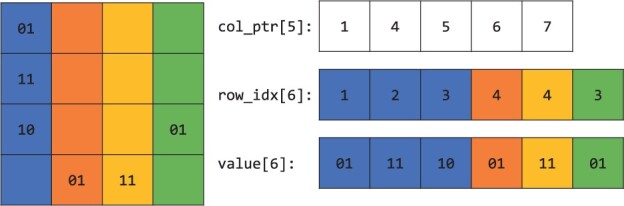
A sparse genetic matrix represented in the compressed sparse column format. The zero entries on the left are omitted. Color indicates that the non-zero entries in the same column are stored contiguously in the memory
When a sparse matrix is stored in CSC format, accessing a particular column is simple. As a result, one can trivially parallellize the computation of . For example, thread j can compute the inner product of the jth column of X and r and write to the jth entry of the output without interfering with other threads. However, same thing can’t be said about . We can’t directly access a row of X stored in CSC format, so there is no easy way to make each thread compute the inner product between β and a row of X. Another way is to, say, have thread j add βj times the jth column of X to the output, but doing this in parallel leads to data race. Alternatively, one can store X in the compressed sparse row format, which makes parallelizing easy but difficult.
Our implementation uses a simplified version of the compressed sparse block (CSB) format proposed in Buluç et al. (2009). In this format, the sparse matrix is partitioned into a grid of smaller, rectangular sub-matrices with same dimensions, which are referred to as blocks. When partitioned to B blocks, a matrix with n rows, d columns, and nnz non-zero entries are represented by four arrays:
A block pointer array blk_ptr of size B + 1.
A row index array row_idx of size nnz.
A column index array col_idx of size nnz.
A value array val of size nnz.
In this representation, non-zero entries in a block (as oppose to those in a column in CSC format) are stored contiguously. The row indices, column indices and values of the non-zero values in a block are stored in row_idx, col_idx and val, starting at the index blk_ptr[b] and ending at the index blk_ptr[b + 1]-1. In the original CSB paper, the non-zero elements in each block has a Z-Morton ordering (Morton, 1966), while the blocks can have any order. In our simplified version, we store the blocks and the non-zero elements within a block in a column major fashion. Figure 2 provides an illustration.
Fig. 2.

A sparse genetic matrix represented in the compressed sparse block format. The zero entries on the left are omitted. The color indicates that the non-zero elements in each block are stored contiguously
Under this representation accessing a block in the sparse matrix is easy. As a result, parallellizing both and XTr are straightforward. For example, if X is the matrix in Figure 2, then to compute we can have thread 1 compute the inner product of the first three rows of X and β, thread 2 compute the inner product of row 4–6 and β, etc. Similarly, to compute XTr thread b will compute the inner product between r and the columns in X for .
Since our implementation uses 2 bits to store a matrix entry and 32 bits to store each index, the genetic CSB format (compared to a dense representation) will only save memory when the matrix is sufficiently sparse (approximately of entries are non-zero). While there are many techniques to reduce the number of bits needed to represent the indices (such as storing the indices relative to the start of the block, differential encoding, bit packing), the current version of our software does not implement these techniques. For variants with high minor allele frequency, we store the corresponding columns in dense format and keep track of their column indices. We also keep an additional array of length d to store the mean imputation of the missing values in X.
3 Benchmarks
3.1 Performance on dense matrix-vector multiplications
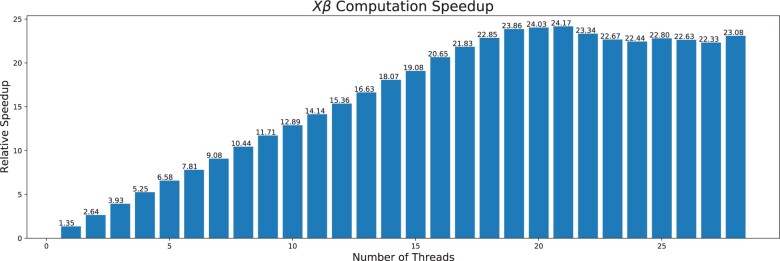
In the first benchmark, we evaluate the performance improvement when the predictor matrix uses the two-bit compact representation, but not the sparse format described in the last section. The genetics data are dense and simulated through the plink2–dummy command. The matrix have n = 200 000 rows and d = 30 000 columns with ∼5% entries NAs. In Figure 3, we show the relative speedup of the compact matrix as a function of the number of threads used. The baseline is ’s builtin matrix-vector multiplication function for double precision matrices (a basic, single-threaded BLAS implementation). The numbers reported are based on the median wall time of 10 runs. Figure 3 demonstrates a more than 20 folds of speedup over the baseline, and good performance scalability in the number of threads for up to almost 20 threads. Unless otherwise specified, all computational experiments in this article are done on an Intel Xeon Gold 6258R. For most of our applications, 16 out of the 28 CPU cores that come with this CPU are used.
Fig. 3.
A bar plot demonstrating the relative speedup in computing when the compact representation is used. The baseline is the R’s builtin matrix-vector multiplication function for double precision matrices. The horizontal axis is the number of threads. The vertical axis is the ratio of between time spent in the baseline and the time spent with the compact representation. The baseline for is 9.8 s
3.2 Performance on solving large-scale lasso problems
In the second benchmark, we compare the performance of the two-bit compact genetic matrix representation when it is incorporated in the software packages glmnet and snpnet to solve large-scale Lasso problems where the predictors are mostly single-nucleotide polymorphisms (SNPs) (with perhaps a few real-valued covariates such as age). As mentioned in the introduction, we call this implementation snpnet-2.0. The main performance gain comes from these factors [the readers can refer to Qian et al. (2020); Li et al. (2020) for the definitions of some terms below]:
glmnet fitting is based on the iteratively reweighted least square (IRLS) algorithm, where the main bottleneck is computing inner-products between columns of X and a real-valued vector. This is done using the two-bit compact representation and is multi-threaded in snpnet-2.0.
snpnet uses a screening procedure named the batch screening iterative Lasso (BASIL). At each BASIL iteration, a different set of predictors is used to fit a model. Using the compact representation reduces the amount of memory traffic needed.
snpnet-2.0 uses reduced precision floating point numbers (float32 instead of float64) to do Karush–Kuhn–Tucker (KKT) conditions checking.
Warm start support, as well as more relaxed convergence criteria, for binomial model and Cox model.
The data used here are a combination of directly genotyped variants [release version 2 of Sudlow et al. (2015)], the imputed allelotypes in human leukocyte antigen allelotypes (Venkataraman et al., 2020), and copy number variations described in Aguirre et al. (2019), resulting in a genotype matrix of 1 080 968 variants, as described in Sinnott-Armstrong et al. (2021). The study population consists of 337 129 unrelated participants of white British ancestry described in DeBoever et al. (2018). We randomly select 70% of the study population as the training set, 10% as the validation set and 20% as the test set. The computational performance is summarized in Table 1. In this table, we compare snpnet-2.0, snpnet and bigstatsr (Privé et al., 2018), which provides efficient Lasso solver for larger-than-RAM data based on memory-mapping. In addition to computational performance, we also run benchmarks on the test set prediction performance of our methods. Here, we compare our method against a few other commonly used polygenic risk score methods including bigstatsr (Privé et al., 2018), BOLT-LMM (Loh et al., 2015) and LDpred2 (Privé et al., 2020). For BOLT-LMM, the input matrix is the combined training and validation data, and we use the -LMM flag, which also produces linear mixed model association testing of the variants. This partially explains the longer runtime of BOLT-LMM in Table 1. For LDpred2, we use the training set to compute the summary statistic, the validation set to compute the genetic correlation matrices by chromosome, and we use the ‘auto’ option to automatically find the hyper-parameters. Once the LDpred2 returns the coefficients, we retrain a linear or logistic model on the training set on the covariates and the polygenic scores to obtain the final prediction (same is done for BOLT-LMM but only for binary response). We published the code used in this benchmark at https://github.com/rivas-lab/snpnet-2.0-paper. The results are summarized in Table 2. The original snpnet paper (Qian et al., 2020) provides more detailed comparison and discussion on prediction performance against PRS-CS (Ge et al., 2019) and SBayesR (Lloyd-Jones et al., 2019).
Table 1.
Speed comparison between snpnet-2.0, snpnet and bigstatsr
| snpnet-2.0 | snpnet | bigstatsr | BOLT-LMM | |
|---|---|---|---|---|
| High cholesterol (B) | 21.9 | 109.8 | 44.98 + 26.81 | 334.27 |
| Asthma (B) | 21.7 | 130.0 | 40.71 + 29.18 | 278.22 |
| Standing height (Q) | 99.9 | a | 41.04 + 217.91 | 1148.32 |
| BMI (Q) | 51.5 | a | 40.38 + 78.84 | 517.12 |
| Other hypothyroidism (S) | 13.5 | 71.5 | 44.23 + 25.80 | 265.61 |
| Thyrotoxicosis (S) | 3.6 | 10.0 | 41.33 + 24.54 | 243.52 |
Note: Time is measured in min. (B) indicates the response is binary, (Q) indicates the response is quantitative and (S) indicates that the response is a survival time. For bigstatsr, the first number we report is the total duration of the time spent on attaching the genetic matrix to a file and mean imputation, which can be shared among multiple responses if they use the same training set split. The second number is the duration of the model fitting function (big_spLinReg and big_spLogReg). For snpnet-2.0 and snpnet, data loading and mean imputation are always done on the fly and are taken into account for this benchmark. For BOLT-LMM, the total runtime also includes time spent on running single-variate regression and association testing on the variants.
The machine we used for most of the applications here has a dual-socket architecture, each having around 400 GB of local memory. The memory requirements by the old version snpnet for both standing height and BMI exceeds the capacity of the local memory of a single socket in this machine. As a result, we ran these two experiments on an Intel Xeon Gold 6130 (also 16 cores) machine with more memory.
Table 2.
Test set prediction accuracy comparison between snpnet-2.0, snpnet, bigstatsr, BOLT-LMM and LDpred2
| snpnet-2.0 | snpnet | bigstatsr | BOLT-LMM | LDpred2 | Covariates only | |
|---|---|---|---|---|---|---|
| High cholesterol (B) | 0.72533 | 0.72531 | 0.72705 | 0.70236 | 0.71240 | 0.69261 |
| Asthma (B) | 0.61609 | 0.61608 | 0.62257 | 0.62638 | 0.61112 | 0.53540 |
| Standing height (Q) | 0.71096 | 0.71100 | 0.71632 | 0.72169 | 0.67515 | 0.53789 |
| BMI (Q) | 0.11408 | 0.11412 | 0.12223 | 0.12869 | 0.094198 | 0.010859 |
| Other hypothyroidism (S) | 0.75194 | 0.75205 | 0.73818 | 0.71908 | 0.72158 | 0.66073 |
| Thyrotoxicosis (S) | 0.71020 | 0.71021 | 0.70432 | 0.67106 | 0.69009 | 0.64888 |
Note: For binary response, the test metric is the area under the ROC curve (AUC). For quantitative response, the metric is the R-squared. For survival response, the metric is the C-index. The results of bigstatsr, and LDpred2 on survival responses are based on regularized logistic regression on the disease indicator with age as an additional covariate. The results of BOLT-LMM on binary data, and LDpred2 on both binary and quantitative data, are obtained by refitting a logistic or linear regression using the polygenic score and the covariates on the training set.
For time-to-event (survival time) responses, both snpnet and snpnet-2.0 are able to fit regularized Cox regression on these responses, which takes into account of both survival time and right-censoring. Since the other methods cannot perform Cox regression, we model instead the binary response , where is the indicator function, T is the underlying survival time (such as age of onset), and is either the age of last follow-up if by then the individual did not develop the disease, or the age of diagnosis if the individual had the disease. We use the other methods to fit regularized logistic regression on this binary response with as an additional covariate. Since this model completely specifies the distribution of T, we are able to evaluate C-index on the fitted models. The last two rows of Tables 1 and 2 describes the computational and predictive performance of these models.
The tables show that snpnet-2.0 achieves better computational performance over the other methods while achieving similar test set prediction performance. We note that for standing height, more than 80 000 variants are selected by snpnet to fit the model. Since the predictor matrix is duplicated in its fitting process, snpnet requires more than 400GB to successfully finish. On the other hand, 32GB of memory is sufficient for snpnet-2.0.
3.3 Performance of the sparse format
In the third benchmark, we evaluate the performance improvement when the genetic predictors make use of both the two-bit compact representation, and the sparse representation described in the last section. In this case, we use real exome data from the UK Biobank. The raw data have 200 643 individuals and 17 777 950 variants. For this benchmark, we only use variants with least three individuals having the minor allele and with missing rate at most 10%. The result is a sparse genetic matrix with 200 643 rows and 7 462 671 columns. For our application, in the next section, the number of variants used to fit models will be smaller since the training set will be a subset of the entire population in this data. On average each column of this matrix has 1399.5 non-zero entries, half of the columns have <7 non-zero entries, and 90% of the columns have <91 non-zero entries. In our sparse representation, we divide this matrix into 16 × 16 = 256 blocks, each with dimension 12 540 by 466 416 (the size of the blocks is a tuning parameter), except at the boundary the block size could be larger. As we mentioned in the last section, storing dense blocks using our version of the compressed sparse block format is not memory efficient, so if a column has a large number of non-zero entries, we store all entries of that column separately. For this particular matrix, 223 596 variants does not use the sparse representation. In Table 3, we present the amount of time to load the matrix and to compute using the sparse matrix representations. Again 16 cores are used for the computation. Loading such matrix would take almost 12 terabytes of memory if the entries are stored as double precision floating point numbers.
Table 3.
The loading and computation time in seconds when the genetic matrix is stored in sparse format
| Loading | ||
|---|---|---|
| 56.5 | 1.86 | 1.80 |
Note: This matrix has 200 643 rows and 7 462 671 columns with more than 10 billion non-zero entries. The computation time are the median of 10 runs using 16 cores.
4 Applications to UK biobank exome sequencing data
In this section, we put our method into practice. Specifically, we use the exome data described in the last part of Section 3 to fit group-sparse linear models on multiple phenotypes. The method described in this section is implemented in sparse-snpnet. In this case, the regularization term will be the sum of the two-norms of the predefined groups. For our applications, the groups are defined by the gene symbol of the variants. For example, the objective function for a Gaussian model is:
| (3) |
where is a collection of indices corresponding to variants with the same gene symbol. , the number of element in the group, is part of the regularization term so that groups of same size are penalized by the same degree. is the sub-vector of β corresponding to the indices in g. We do not allow overlapping groups, so needs to be a partition of all variables. That is, and . One can show that the proximal operator for this regularization function satisfies:
| (4) |
| (5) |
In practice, we would like to adjust for covariates such as age, sex and other demographic information when fitting a regression model. In our application, we first fit an unregularized regression model of the response on these covariates and fit the regularized model of the residual on the genetic variants. The number of covariates are usually much smaller compared to the number of individuals, so the first fitting is not computationally or statistically challenging. To be more precise, let be the covariates that we would like to adjust for. Using the same notation in (1). We fit a model in two steps:
- First, we fit an unregularized model using the covariates:
(6) - Then, we fit the regularized model on the ‘residuals’ using the variants:
(7)
For example, if we write the predicted value of the covariates as , then for a Gaussian model, the objective function of the second step above is:
| (8) |
For logistic regression this becomes:
| (9) |
For Cox model, the objective function is
| (10) |
We optimize these objective functions for a decreasing sequence of λs starting from one such that the solution just becomes non-zero. The initial value for the proximal gradient method of the next λ is initialized from the solution from the current λ (warm start). As alluded in the last section, we randomly assign 70% of the white British individuals in this dataset to the training set, 10% to the validation set and 20% to the test set. We remove individuals whose phenotype value is missing, keeping variants with at least three minor allele count, has an associated gene symbol, has <10% of missing value, and the ratio of the missing value and minor allele is <10. We further filter out the variants that are not protein truncating or protein altering. Depending on the number of missing values in the phenotype, the number of individuals and variants used for fitting could be different. In all of the examples here the training set has more than 90 000 individuals and the number of genetic variants used are over 1 000 000. The covariates are the sex, age and 10 principal components of the genetic data described in the second benchmark of Section 3.2.
To evaluate the fitted model, we use the R-squared value for quantitative phenotype, the area under the receiver operating characteristic (ROC) curve (AUC) for binary phenotype, and the concordance index (C-index) for time-to-event phenotype. These metrics will be computed on the validation set to determine the optimal regularization parameter λ and on the test set to evaluate the model corresponding to the λ used. Once the validation metric starts to decrease, we stop the fitting process and do not compute the solutions for smaller λ values. Figures 4–6 illustrate a few Lasso path plots obtained from our implementation. To evaluate whether this grouping by genes improves the prediction performance, we also run Lasso on these phenotypes with the same predictors. For the applications and grouping used here, we do not observe significant change in prediction performance in Group Lasso compared to Lasso (Table 4).
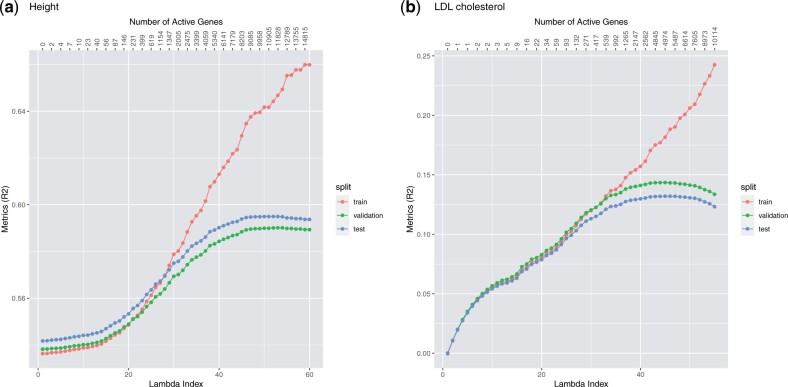
Fig. 4.
Lasso path plots for the quantitative phenotypes height and LDL cholesterol. The horizontal axis is the index of the regularization parameter λ, the vertical axis are the R-squared of the solution corresponding to each λ index. The numbers on the top are the number of genes with non-zero coefficients at the corresponding λ indices. The color corresponds to the train, validation and test set. The duration of training these two models (including data loading and mean imputation) are 8.34 and 8.35 min, respectively. Plots a and b correspond to the phenotypes height and LDL cholesterol, respectively.
Table 4.
Comparison between Group Lasso and Lasso in the prediction performance on quantitative (Q), binary (B) and survival (S) phenotypes
| Group Lasso | Lasso | |
|---|---|---|
| Height (Q) | 0.59495 | 0.59385 |
| LDL cholesterol (Q) | 0.13207 | 0.13390 |
| High cholesterol (B) | 0.70421 | 0.70690 |
| Asthma (B) | 0.56523 | 0.56296 |
| Alzheimer (S) | 0.71559 | 0.71633 |
| hypothyroidism (S) | 0.70587 | 0.70211 |
Here, the grouping are defined by variants in the same gene.
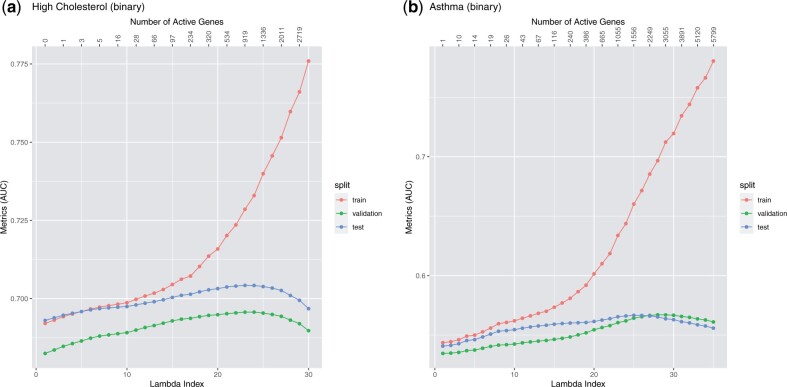
Fig. 5.
Lasso path plots for the binary phenotypes high cholesterol and asthma. The horizontal axis is the index of the regularization parameter λ, the vertical axis are the AUC values of the solution corresponding to each λ index. The numbers on the top are the number of genes with non-zero coefficients at the corresponding λ indices. The color corresponds to the train, validation and test set. The duration of training these two models (including data loading and mean imputation) are 6.88 and 8.27 min, respectively. Plots a and b correspond to the binary phenotypes high cholesterol and asthma, respectively.
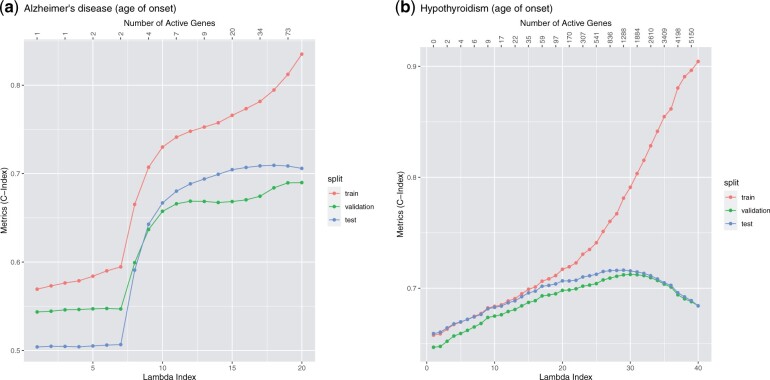
Fig. 6.
Lasso path plots for the time-to-event phenotypes Alzheimer’s disease and hypothyroidism. The horizontal axis is the index of the regularization parameter λ, the vertical axis are the C-index of the solution corresponding to each λ index. The numbers on the top are the number of genes with non-zero coefficients at the corresponding λ indices. The color corresponds to the train, validation and test set. The duration of training these two models (including data loading and mean imputation) are 6.12 and 6.92 min, respectively. Plots a and b correspond to the survival phenotypes age of onset of Alzheimer's disease and hypothyroidism, respectively.
In terms of computation, unlike in snpnet (or the 2.0 version), the optimization in sparse-snpnet are all done without variable screening, and the entire training data (in sparse format) is loaded in memory before fitting starts. This eliminates all the I/O operations carried out in the KKT checking step of snpnet. The applications in this section successfully finished when we allocate 32GB of memory to these jobs. In addition, while the applications in this article focus on Gaussian, logistic and Cox families and group Lasso regularization, our implementation uses abstractions in so it is easy to extend to other generalized linear models and regularization functions.
5 Discussions
We present two fast and memory efficient solvers for generalized linear models with regularization on large genetic data. Both methods utilize a two-bit compact representation of genetic variants and are accelerated though multi-threading on CPUs with multiple cores. The first solver implements the iteratively-reweighted least square algorithm in glmnet, and its goal is to provide boosted computational and memory performance to the large-scale Lasso solver described in (Li et al., 2020; Qian et al., 2020). The second solver implements an accelerated proximal gradient method that’s able to solve more general regularized regression problems. One important feature of this solver is that it combines a version of compressed sparse block format for sparse matrices and the two-bit encoding of genetic variants. We summarize the characteristics of these two solvers in Table 5. We demonstrate the effectiveness of our methods through several benchmarks and UK Biobank exome data applications. We believe our method will be a useful tool as whole genome sequencing data becomes more common.
Table 5.
A comparison between the two solvers we present in this article
| snpnet-2.0 | sparse-snpnet | |
|---|---|---|
| Algorithm | IRLS | Proximal gradient |
| Use variable screening | Yes | No |
| Easy to extend to other GLMs | Yes | Yes |
| Easy to extend regularizations | No | Yes |
| Use two-bit representation of variants | Yes | Yes |
| Use sparse matrix format | No | Yes |
| Multi-threaded | Yes | Yes |
Acknowledgements
We thank all the participants in the study. The primary and processed data used to generate the analyses presented here are available in the UK Biobank access management system (https://amsportal.ukbiobank.ac.uk/) for application 24983, ‘Generating effective therapeutic hypotheses from genomic and hospital linkage data’ (http://www.ukbiobank.ac.uk/wp-content/uploads/2017/06/24983-Dr-Manuel-Rivas.pdf). All of the computing for this project was performed on the Nero and Sherlock clusters. We would like to thank Stanford University and the Stanford Research Computing Center for providing computational resources and support that contributed to these research results.
Funding
Y.T. was supported by a Funai Overseas Scholarship from the Funai Foundation for Information Technology and the Stanford University School of Medicine. M.A.R. was supported by Stanford University and a National Institute of Health center for Multi and Trans-ethnic Mapping of Mendelian and Complex Diseases grant (5U01 HG009080). This work was supported by National Human Genome Research Institute (NHGRI) of the National Institutes of Health (NIH) under awards R01HG010140. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. R.T. was partially supported by NIH grant 5R01 EB001988-16 and NSF grant 19 DMS1208164. T.H. was partially supported by grant DMS-1407548 from the National Science Foundation, and grant 5R01 EB 001988-21 from the National Institutes of Health. This research has been conducted using the UK Biobank Resource under application number 24983.
Conflict of Interest: none declared.
Data availability statement
The data that support the findings of this study are available for approved research. Access to the data can be applied through UK Biobank's website https://www.ukbiobank.ac.uk/enable-your-research/apply-for-access
Contributor Information
Ruilin Li, Institute for Computational and Mathematical Engineering, Stanford University, Stanford, CA 94305, USA.
Christopher Chang, Grail, Inc, Menlo Park, CA 94025, USA.
Yosuke Tanigawa, Department of Biomedical Data Science, Stanford University, Stanford, CA 94305, USA.
Balasubramanian Narasimhan, Department of Biomedical Data Science, Stanford University, Stanford, CA 94305, USA; Department of Statistics, Stanford University, Stanford, CA 94305, USA.
Trevor Hastie, Department of Biomedical Data Science, Stanford University, Stanford, CA 94305, USA; Department of Statistics, Stanford University, Stanford, CA 94305, USA.
Robert Tibshirani, Department of Biomedical Data Science, Stanford University, Stanford, CA 94305, USA; Department of Statistics, Stanford University, Stanford, CA 94305, USA.
Manuel A Rivas, Department of Statistics, Stanford University, Stanford, CA 94305, USA.
References
- Aguirre M. et al. (2019) Phenome-wide burden of copy-number variation in the UK biobank. Am. J. Hum. Genet., 105, 373–383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck A., Teboulle M. (2009) A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Img. Sci., 2, 183–202. [Google Scholar]
- Buluç A. et al. (2009). Parallel sparse matrix-vector and matrix-transpose-vector multiplication using compressed sparse blocks. In: Proceedings of the Twenty-First Annual Symposium on Parallelism in Algorithms and Architectures, SPAA ’09, page 233–244, New York, NY, USA. Association for Computing Machinery. [Google Scholar]
- Chang C. et al. (2015) Second-generation plink: rising to the challenge of larger and richer datasets. GigaScience, 4. doi: 10.1186/s13742-015- 0047-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox D.R. (1972) Regression models and life-tables. J. R. Stat. Soc. Series B, 34, 187–220. [Google Scholar]
- Daubechies I. et al. (2004) An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math., 57, 1413–1457. [Google Scholar]
- DeBoever C. et al. (2018) Medical relevance of protein-truncating variants across 337,205 individuals in the UK biobank study. Nat. Commun., 9, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J. et al. (2010) Regularization paths for generalized linear models via coordinate descent. J. Stat. Software, 33, 1–22. [PMC free article] [PubMed] [Google Scholar]
- Ge T. et al. (2019) Polygenic prediction via Bayesian regression and continuous shrinkage priors. Nat. Commun., 10, 1776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastie T., Tibshirani R. (1986) Generalized additive models. Stat. Sci., 1, 297–310. [DOI] [PubMed] [Google Scholar]
- Li R. et al. (2020) Fast Lasso method for large-scale and ultrahigh-dimensional Cox model with applications to UK Biobank. Biostatistics. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lloyd-Jones L.R. et al. (2019) Improved polygenic prediction by Bayesian multiple regression on summary statistics. Nat. Commun., 10, 5086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loh P.-R. et al. (2015) Efficient Bayesian mixed-model analysis increases association power in large cohorts. Nat. Genet., 47, 284–290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morton G. (1966) A Computer Oriented Geodetic Data Base and a New Technique in File Sequencing. Technical Report, Ottawa, Canada: IBM Ltddy. [Google Scholar]
- Nesterov Y. (1983). A method for solving the convex programming problem with convergence rate . Proc. USSR Acad. Sci., 269, 543–547. [Google Scholar]
- Privé F. et al. (2018) Efficient analysis of large-scale genome-wide data with two R packages: bigstatsr and bigsnpr. Bioinformatics (Oxford, England), 34, 2781–2787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Privé F. et al. (2020) LDpred2: better, faster, stronger. Bioinformatics, 36, 5424–5431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian J. et al. (2020) A fast and scalable framework for large-scale and ultrahigh-dimensional sparse regression with application to the UK biobank. PLoS Genet., 16, e1009141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon N. et al. (2011) Regularization paths for cox’s proportional hazards model via coordinate descent. J. Stat. Software, 39, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinnott-Armstrong N. et al. ; FinnGen. (2021) Genetics of 38 blood and urine biomarkers in the UK biobank. Nat. Genet., 53, 185–194. [CrossRef][10.1038/s41588-020-00757-z] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sudlow C. et al. (2015) UK biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Medicine, 12, e1001779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szustakowski J.D. et al. (2020) Advancing human genetics research and drug discovery through exome sequencing of the UK biobank. https://www.medrxiv.org/content/10.1101/2020.11.02.20222232v1 [DOI] [PubMed]
- Tibshirani R. (1996) Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. Series B (Methodological), 58, 267–288. [Google Scholar]
- Venkataraman G.R. et al. (2020) Pervasive additive and non-additive effects within the HLA region contribute to disease risk in the UK biobank. bioRxiv.
- Yuan M., Lin Y. (2006) Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Series B, 68, 49–67. [Google Scholar]
- Zou H., Hastie T. (2005) Regularization and variable selection via the elastic net. J. R. Stat. Soc. Series B (Statistical Methodology), 67, 301–320. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available for approved research. Access to the data can be applied through UK Biobank's website https://www.ukbiobank.ac.uk/enable-your-research/apply-for-access