High Resolution Fluorescence Lifetime Maps from Minimal Photon Counts

Abstract

Fluorescence lifetime imaging microscopy (FLIM) may reveal subcellular spatial lifetime maps of key molecular species. Yet, such a quantitative picture of life necessarily demands high photon budgets at every pixel under the current analysis paradigm, thereby increasing acquisition time and photodamage to the sample. Motivated by recent developments in computational statistics, we provide a direct means to update our knowledge of the lifetime maps of species of different lifetimes from direct photon arrivals, while accounting for experimental features such as arbitrary forms of the instrument response function (IRF) and exploiting information from empty laser pulses not resulting in photon detection. Our ability to construct lifetime maps holds for arbitrary lifetimes, from short lifetimes (comparable to the IRF) to lifetimes exceeding interpulse times. As our method is highly data efficient, for the same amount of data normally used to determine lifetimes and photon ratios, working within the Bayesian paradigm, we report direct blind unmixing of lifetimes with subnanosecond resolution and subpixel spatial resolution using standard raster scan FLIM images. We demonstrate our method using a wide range of simulated and experimental data.

Fluorescence microscopy has significantly contributed to our understanding of biological processes as they unfold within their native cellular environment.¹⁻⁷ One such microscopy technique is fluorescence lifetime imaging microscopy (FLIM), performed using pulsed or modulated illumination.⁸ The sensitivity of fluorescent probe lifetimes in FLIM has been exploited to spatially resolve the following: (1) temperature variations across environments;⁹⁻¹² (2) refractive indices¹³ that may serve as proxies to local concentrations of proteins;¹³⁻¹⁵ and (3) molecular concentrations of mixtures of species across environments.¹⁶⁻¹⁹ For instance, molecular concentrations deduced from FLIM data have been used to quantify metabolic changes in cells¹⁷⁻²¹ tied to changes in free versus bound states of reduced nicotinamide adenine dinucleotide (NADH).

Of recent interest is the potential of quantitative lifetime imaging using single-photon avalanche diode (SPAD) arrays in the life sciences.^22,23 Thanks to the popularization of such novel detection modalities, it is now possible to achieve widefield FLIM with picosecond time-stamping, a high photon detection rate, and low dark noise. Such developments now make SPAD arrays a promising venue for FLIM-guided oncology research to help discriminate healthy versus cancerous tissues.^24,25

Yet, bringing quantitative lifetime image analysis to the next level, whether through the simultaneous detection of various regions of space through SPAD arrays or through spot scanning, demands a novel mathematical framework in which the key modeling challenges are addressed. For example, currently, FLIM data collected in either pulsed or modulated illumination result in a temporal emission profile from which the fluorescence lifetimes²⁶ can be deduced using phasor-based methods^8,27 and neural networks,²⁸⁻³⁰ model-based methods that implement direct photon arrival analysis using likelihood,^31,32 or Bayesian methods³³⁻³⁹ or by fitting photon arrival histograms (often termed time correlated single photon counting, TCSPC) through least-squares fitting⁴⁰⁻⁴² and deconvolution.⁴³⁻⁴⁶

Yet these analysis methods are generally limited in their ability to (1) learn the number of species and, as such, often assume one or two species for simplicity;^{28−37,40−42} (2) report full error bars over all unknown quantities propagated from effects such as finiteness of the data or intrinsic breadth of the instrumental response function (IRF);^8,27−30 (3) treat a broad range of lifetimes, including short lifetimes, lifetimes longer than interpulse times, and lifetimes with subnanosecond differences; (4) provide spatial resolutions below the pixel size; and (5) take full advantage of all the available data using direct photon arrivals with no data preprocessing,⁴⁷ such as deconvolving the IRF⁴³⁻⁴⁶ and empty pulses to facilitate blind unmixing of lifetime maps.

In prior work, we focused on problems 1 and 2 above for a single pixel (single confocal spot).⁴⁸ That is, we proposed a method to learn the number of chemical species and associated lifetimes simultaneously and self-consistently report on the full posterior distributions around species and lifetimes from direct analysis of single photon arrivals.⁴⁸ While traditional Bayesian methods report full error bars, such methods are parametric and, therefore, need a known number of lifetime species to be specified a priori. For this reason, in our prior work, we abandoned the parametric Bayesian paradigm and worked within a Bayesian nonparametric (BNP) framework. Within this framework, we placed a prior on all (formally an infinite number) species that could be warranted by the data using a device within BNPs, termed Dirichlet process priors.⁴⁹⁻⁵²

Here, we turn to resolving spatial lifetime maps, even below the spatial dimension of a pixel (subpixel resolution) while reporting full error bars over all the parameters, and in doing so, we directly address problems 2–5. We do so while analyzing photon arrivals that themselves report back on the mixture of species present whose lifetimes are convolved with IRFs. In particular, to address challenge 4 above, namely, to resolve lifetime maps below the pixel size, we ask the following: Of all lifetime maps possible for any mixture of species, can we learn those maps warranted by the data, even if the data are sparsely collected at distinct and well-separated spots? Can we do this while simultaneously learning all other unknowns, such as the lifetime for each species?

Again, this problem is naturally nonparametric, as we must place priors on an infinite number of candidate (static) lifetime maps that may not assume simple analytic forms. To do so, we leverage the power of the Gaussian process (GP) priors within the BNP paradigm.⁵³⁻⁵⁷ Within the GP prior paradigm, each map is comprised of an infinite set of random variables (the values of the concentration for each species at every continuous point in space). As such, GP processes are key toward allowing us to interpolate lifetime maps between spatial observation points.

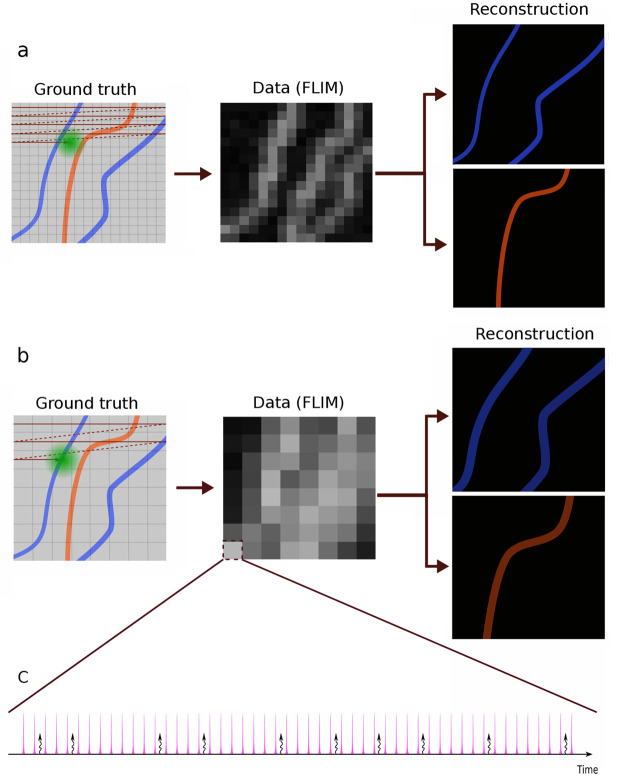
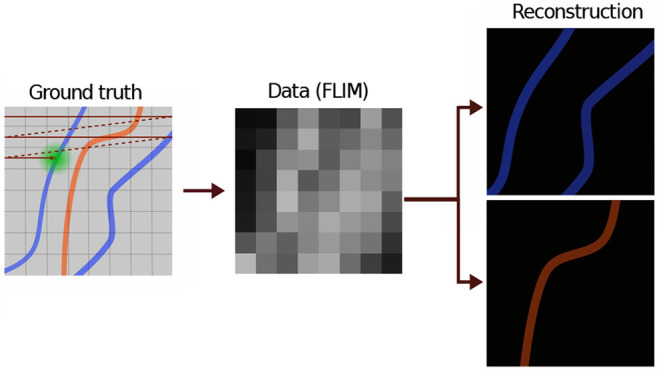
As BNPs are direct logical extensions of their traditional (parametric) Bayesian counterparts,^58,59 the quality of the inferences drawn depend on the physics incorporated into the likelihood. A cartoon example of the type of experiments we wish to interpret is provided in Figure 1. Here, an illumination laser scans a sample at constant speed over straight trajectories separated by pixel size, Figure 1a. Each pixel is therefore illuminated with a certain number of pulses, resulting in excitation of fluorophores. The excited fluorophores, in turn, emit photons that might be recorded by the detector. The probability of detecting a photon is thereby given by a combination of the illumination and detection profiles termed the excitation–detection point spread function (PSF). In principle, the number of detected photons is much smaller than the number of pulses, where both pulses giving rise to photons and “empty pulses” provide information on the underlying lifetime maps.

Figure 1.

A cartoon representation illustrating how a specimen is scanned and the image is deconvolved. Here, we envision a sample stained with two different fluorophores, and the data are collected using a scanning confocal microscope, where the grid represents pixels. (a) The sample is scanned with fine separation between the scanning trajectories. This separation determines the pixel size. We use BNPs to determine the lifetimes of individual species and reconstruct their underlying lifetime map (which may designate the location of cellular structures depending on the stain’s affinity). (b) The sample is scanned using a larger distance between the scanning trajectories (larger pixel size). As an important control of our method, we can ask to what degree BNPs may reconstruct the lifetime maps from such data that would have been obtained from the analysis of the smaller pixel (higher resolution) data. (c) Each pixel is scanned by a train of equally temporally spaced excitation pulses. The pink spikes show laser pulses, and the curly arrows represent detected photons. In the most general case, the pink spikes have a finite width, and it cannot be assumed that photons are generated from an excitation caused by the pulse immediately preceding it.

In what follows, we use the type of data just described and exploit the mathematics of GPs in order to construct lifetime maps (strictly speaking, the product of the excitation probability and concentration at each location) with a subpixel resolution. We do so while rigorously propagating uncertainty through a Bayesian procedure and with no assumption on lifetime durations (whether shorter than the IRF or longer than interpulse times).

Results

Our method’s overarching objective is to learn the lifetime maps, μ_mρ_m(x, y), of each chemical species, indexed m, where μ_m is the average number of excited fluorophores of species m per pulse and related to the quantum yield.⁶⁰ We wish to learn these lifetime maps with subpixel resolution alongside their associated lifetimes, τ_m. As estimates of μ_m are often difficult to obtain directly for in vivo applications and may spatially vary,^19,61−63 in practice, we learn the product μ_mρ_m(x, y) as opposed to absolute concentrations, ρ_m. Here μ_m = μ̂_mδt is a unitless parameter; δt is the average width of the excitation pulse and μ̂_m is excitation rate of fluorophore species.

To be clear, determining the absolute ρ_m(x, y) demands the independent calibration of μ_m for any analysis method, as these quantities appear as products in any theory (whether ours or others).

To make inferences on μ_mρ_m(x, y), designated μρ hereafter for simplicity, over each point in space, as well as τ_m for each species, we require the following: input data (including photon arrival times and which pulses are empty otherwise); the number of species; the IRF; and the excitation–detection PSF of the confocal microscope. With these quantities at hand, we can construct a likelihood of observing the data in the above given model, as described in the Methods section and expanded upon in Supporting Information, Note 1.

Within the Bayesian framework, we must also specify prior distributions on the unknown parameters to arrive at full posterior distributions (as well as derived quantities, such as credible intervals) over all unknowns. Of particular importance is the nonparametric GP prior on the smooth μρ profiles. These profiles are continuous functions over space comprised of infinite sets of parameters (the value of the profile at each point in space). In practice, we learn values of μρ by placing a GP prior over a finite mesh-grid of locations termed test points. The set of test points can be as close as desired and often smaller than the size of the confocal spot and pixel size, as discussed in the Methods section and expanded upon in Supporting Information, Note 2.1–2.

As the nonparametric posterior cannot be assumed to attain an analytic form, we develop a computational scheme to efficiently sample from this posterior. The results presented are therefore in the form of histograms of samples drawn from Markov chains further elaborated in Supporting Information, Note 2.2.

In the following, we benchmark our method using a wide range of realistic simulated and experimental data with μρ profiles of differing levels of spatial heterogeneity (all parameters used in data simulations and analyses are reported in Tables S1 and S2). That is, in the simplest case, we first show that our method recapitulates lifetimes and μρ for the case of spatially uniform μρ using both simulated and experimental data; Figures 2 and S1.

Figure 2.

Lifetime posteriors under uniform μρ profiles. (a, b) The resulting posterior over lifetime and μρ obtained from the data simulated with spatially uniform profiles, as anticipated for any well-stirred solution (in vitro) experiments. (c, d) The resulting lifetime and μρ posteriors from in vitro experiments using a mixture of two fluorophore species (Fluorescein and Coumarin6). The dashed black lines represent ground truths (known for synthetic data and determined using phasor analysis for in vitro data). The blue and brown curves, respectively, correspond to the larger and smaller lifetimes of Fluorescein and Coumarin6, respectively.

As these constitute easier test cases, we relegate smoothly spatially varying profiles to Figures S2–S8 and Supporting Information, Note 3. These profiles are used to demonstrate our method for (1) different photon counts and pixel sizes, see Figures S2–S4 and Supporting Information, Note 3; (2) subnanosecond lifetime resolution (mixture of two lifetimes with 0.5 ns difference), see Figure S5 and Supporting Information, Note 3; (3) learning lifetimes over a wide range from below the IRF to larger than the interpulse time, see Figures S6 and S7 and Supporting Information, Note 3; and (4) data with more than two species, see Figure S8 and Supporting Information, Note 3. Finally, in the main body we present results for more complex μρ profiles (profiles that vary dramatically over space) that recapitulate profiles anticipated in vivo. These results are shown in Figures 3 and 4 for both simulated and in vivo data.

Figure 3.

Simulated μρ profiles meant to mimic more complex patterns observed in vivo. Underlying ground truth μρ profiles for species 1 in panel (a) and for species 2 in panel (b). (c) FLIM data generated using the combination of the ground truth μρ profiles as we observe it in 42 × 42 pixels scanned with a pixel size of 0.2 μm. (d, e) Learned μρ profiles with a subpixel resolution (1/3 of the pixel size). (f, g) Learned μρ profiles where pixels with even columns and rows were ignored. This results in lower resolution data (by a factor of 4) that we subsequently used to obtain our μρ profiles. All scale bars are 1 μm.

Figure 4.

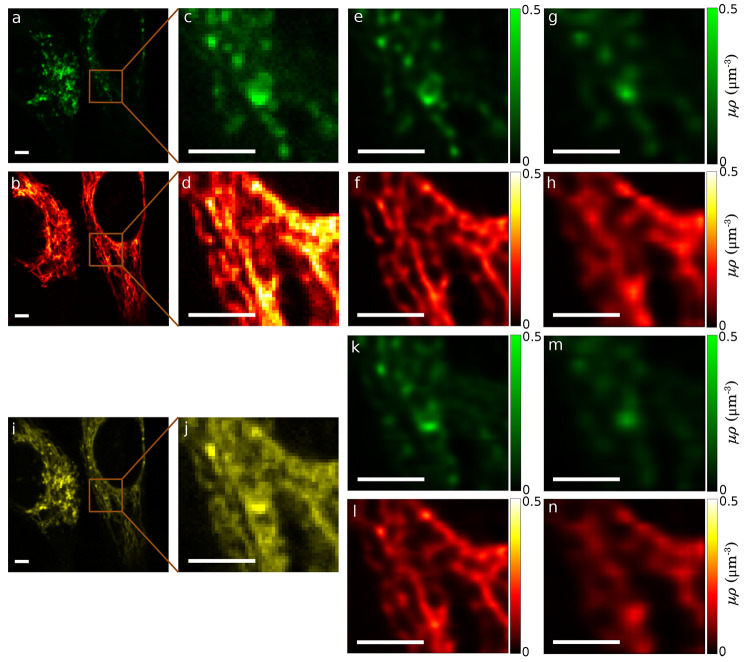
In vivo FLIM data sets acquired from lysosomes and mitochondria labeled with two fluorophore species within HeLa cells. (a, b) Experimental FLIM data images of spectrally resolved lysosomes (green) and mitochondria (red) acquired simultaneously within the same cell. (c, d) Zoomed-in regions inside the boxes in (a) and (b). (e, f) Learned μρ profiles of lysosomes and mitochondria using all the photons in (c) and (d), respectively. (g, h) Learned μρ profiles obtained by ignoring photons from pixels with even rows and columns in (c) and (d), respectively. (i) Shown in yellow is the raw FLIM image of a combination of lysosomes and mitochondria in (a) and (b). (j) Zoomed-in region inside the box in (i). (k, l) Learned μρ profiles of lysosomes and mitochondria, respectively, with a subpixel resolution (1/3 of the pixel size), using all photons in (j). (m, n) Learned μρ profiles of lysosomes and mitochondria, respectively, ignoring photons from pixels with even column and row indices in (j). Scale bars are 4 μm.

Method Validation Using Uniform Profiles

To initially demonstrate our method in learning simple (spatially uniform) μρ profiles, we analyzed both simulated, Figure 2a,b, and in vitro, Figure 2c,d, data sets with two lifetime components and μρ of 1–4. The simple in vitro data sets were uniform (well-stirred) solutions for both species.

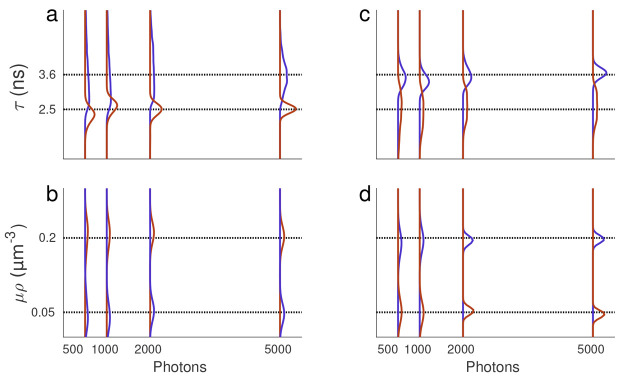
We considered both simulated and experimental data sets with mixtures of close, and thus challenging, lifetimes of 2.5 and 3.6 ns and considered how well we can discriminate between these two lifetime values when analyzing traces containing a different number of photons (500, 1K, 2K, and 5K total photon counts).

Figure 2a,b and c,d show lifetime and μρ posteriors for simulated and experimental data, respectively. Even with as few as 500 total photon counts, the agreement of our lifetime posterior, compared with ground truth (simulated data) and phasor analysis (see Experimental Data Collection section), is in good agreement with ∼7% and 6% differences for the larger and smaller lifetimes in Figure 2a, respectively; the obtained lifetimes are given in Table S3.

It is worth noting that for (spatially homogeneous, uniform solution) in vitro data, the phasor distribution can learn both lifetimes only when one lifetime is specified a priori⁸ (here Coumarin6 with lifetime of 2.5 ns⁶⁴). However, our method learns both lifetimes and the associated μρ without any prior information. In particular, without specifying one of the two lifetimes a priori.

Naturally, as we increase the number of photons incorporated into our analysis, the posterior sharpens; see Figures 2 and S1. Additional analyses, for simpler cases with greater differences in lifetimes, are relegated to Figure S1.

Method Validation Using More Complex Simulated and In Vivo Profiles

We benchmarked our method’s ability to learn more complex μρ profiles initially using simulated data, Figure 3, which recapitulates in vivo data sets. We then analyzed in vivo data sets; Figure 4.

The simulated data was generated with two lifetime components of 1.5 and 5 ns, pixel sizes of 0.2 μm, by scanning 42 × 42 pixels. By contrast, for the in vivo data set, we used two fluorescent labels with affinity for mitochondria and lysosomes, see Figure 4.

Below, we first discuss the results from the simulated data where the ground truth is available. Next, results obtained from the experimental data are discussed.

Figure 3a,b show two simulated cellular structures in an effort to mimic the structures encountered in the subsequent experimental data. As these are synthetic data, we have ground truth profiles for μρ independently for each species.

Figure 3c depicts the generated FLIM data from mixtures of lifetimes in Figure 3a,b, where lifetime species are associated with a larger-scale cellular structure. Figure 3d,e depict the inferred μρ profiles, where μρ is assessed down to a resolution of 1/3 of the pixel size. Here we find that the average of absolute relative differences of our assessment as compared to ground truth lies below 4%. The maps and histograms of relative differences and learned lifetimes are, respectively, depicted in Figures S9–S11. To show that our method is capable of learning the underlying ground truth profiles (as seen in Figures 3a,b), we calculated the relative differences of the ground truths and the learned profiles, given by 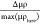, where μρ_ture represents ground truth, returning an average of the absolute relative differences of 1.8% and 3.7% for the structures shown in red and green, respectively; see Figure S9a,b.

As we cannot determine from experiment whether our subpixel assessments of profiles match the ground truth when collecting the highest resolution data available, when analyzing experiments, we must reduce the resolution of the data set by eliminating data obtained from selected pixels. We can then ask to what degree removing pixels deteriorates our assessment of the profile in those regions where no data is collected.

As a first step along these lines, we performed this procedure on synthetic data, where we ignored photons from pixels with even rows and columns. This resulted in a quarter of as many pixels with twice the pixel dimensions. Figure 3f,g shows the resulting μρ profiles that we learned under these more difficult conditions. Despite using a quarter of the data and naively anticipating a deterioration in our assessment of the profiles by ∼75%, our method learns μρ profiles with average absolute relative differences of 2.6% and 7% with respect to the ground truth for structures shown in red and green, respectively; see Figure S9c,d. This was achieved by virtue of rigorously propagating uncertainty from fundamental sources of noise informed by the physics of the process, for example, by including empty pulses in the model.

Next, we evaluated the performance of our method using in vivo data sets with fluorophores that preferentially bind to lysosomes and mitochondria within the same cell. To serve as a control to test our ability to determine where individual lifetime species were located, band-pass filters were used to spectrally discriminate species.⁶⁵Figure 4a,b shows data from these spectrally resolved structures acquired simultaneously (in green and red channels, respectively, primarily identifying lysosomes and mitochondria); with zoomed-in regions, we analyze shown in Figure 4c,d. The μρ profiles in the zoomed-in regions were determined using our method from later Methods section, and the results are shown in Figure 4e,f. These noise-free profiles are what we use as our ground truth.

In order to obtain a challenging data set with two fluorophore species, we mixed the two ground truth data sets (Figure 4a,b) into one in which the cellular structures are highly overlapping; shown in yellow in Figure 4i. We then applied our method to the same region of this data (Figure 4j) to distinguish the two structures and learn their lifetimes. We compare the result, Figure 4k,l, with the ground truth; Figure 4e,f. In an effort to further validate our method, we used the μρ profiles obtained from the spectrally resolved structures (Figure 4e,f) as ground truth. The average absolute relative differences of the learned μρ profiles from the mixture of the two structures (Figure 4k,l) and the obtained ground truth (Figure 4e,f) are 2.3% and 3.4%, respectively; maps of the relative differences are depicted in Figure S12.

Similar to the previously synthetic data, we also ignored photons from pixels with even columns and rows to generate artificially lower resolution data. We then compared our results (Figure 4m,n) to the ground truth (Figure 4e,f) and found average absolute relative differences of 3.5% and 11.2%, respectively.

In order to validate our method against the established phasor technique, we compared the resulting lifetimes from our method and those obtained from the phasor technique; see Figures S13 and S14. The resulting lifetimes from these methods have a difference of ∼0.4 ns, because the phasor method was applied on the entire data set and finds an average lifetime over the field of view. By contrast, our method was used to process a region of the image and finds local lifetimes; see Figure 4i,j. This implies that the lifetimes vary over space for the in vivo data set. To further validate this observation, we applied our method to different regions of the data and found slightly different lifetimes for each region; see Figure S15.

Methods

Here, we briefly describe the mathematical formulation of our method for the analysis of FLIM data acquired using a confocal setup. Further details of the mathematical framework, not provided herein, are otherwise provided in the Supporting Information.

We begin by considering M fluorophore lifetime species, indexed m = 1, ..., M, with the respective photon emission rate λ_m. This rate is the inverse of the excited state lifetime τ_m. To each fluorophore species is associated a concentration, ρ_m(x, y), as well as a unitless excitation probability earlier defined as μ_m. A complete list of all notation is provided in Table S4.

Model Formulation

The average number of detected fluorescence photons from the lth molecule of type m located at X⃗_lm = (x_lm, y_lm, z_lm) during an excitation pulse is given by μ_mPSF(ξ, X⃗_lm), where ξ = vt is the center of the confocal region at time t, v is the speed at which the excitation laser is scanned, and PSF stands for the excitation–detection point spread function.^39,60,66,67 Therefore, the probability of this molecule leading to no photon detection during a pulse is given by

1

In the above equation, every pulse corresponds to a different confocal center. This leads to a complicated formulation and high computational complexity. To simplify the model and decrease the computational time, we assume that the confocal spot moves in discrete steps to new locations, that is, the pixel centers labeled ξⁱ for the ith pixel, and stays there for a period given by (pixel size)/v. Under this assumption, the above equation takes the following form

2

where ξ is demoted to being a subscript, as the PSF is no longer a continuous function of this variable. This approximation leads to errors that propagate into our estimated μρ profiles. The error entailed by this approximation is assessed by generating synthetic data (under the correct, continuous evolution, model) and analyzed using the approximate discrete time-step model. Our simulations showed that this approximation leads to an acceptable ∼2% increase in the average absolute relative differences of the estimated profiles and the ground truth; see Figures S16 and S17. This percentage was obtained by using parameter values for pixel size, PSF, lifetimes, and a laser interpulse time derived from experiment, shown in Figure 4.

Employing eq 2, the probability of no photon detection from molecules of type m in the ith confocal region is given by the product of the probability of every individual molecule giving rise to no detected photon

3

To generalize the above expression to the continuous spatial case, we replace the sum with an integral assuming a continuous distribution of molecules

4

where

5

and hence

6

Associated to each pulse are now three possibilities: an empty pulse with no photons, a pulse resulting in photons coming from one species, and a pulse resulting in photons from multiple species. Each of these is designated with probabilities π₀ⁱ, π_m, and π_*ⁱ, respectively, where

7

8

9

We now make a few assumptions to help simplify our problem: (1) We assume stationarity in time for all physical properties. (2) μρ is a smooth and continuous function with respect to location (X⃗). (3) The detector dead time is often on the order of multiple pulses.^68,69 As such, after a photon has been detected typically no photon can then be detected for multiple subsequent pulses. (4) Most importantly, as a result of low excitation rates, there typically is at most one excited molecule during a single excitation pulse. Thus, we can immediately simplify the second and third terms of eq 9 as we discuss below.

By assumptions 3 and 4, we immediately interpret π_mⁱ as the probability of a single photon emitted from the species m and furthermore assume π_* (the probability of exciting more than one species in a pulse) is zero. As a result, eq 9 simplifies to

10

This approximation is further validated by the observation that, in experiments, on average one in ∼100 pulses give rise to a photon.

By virtue of using empty pulses in the above equation, our method learns absolute μρ for each species as opposed to learning ratios of local μρ values, as was achieved using previous methods.^8,34,35 The basic intuition is as follows: when we remove empty pulses from eq 10, the sum of probabilities is no longer normalized to one. As such, we can at best compare the relative intensity of different local regions, allowing us to determine ratios of local μρ values. By contrast, by accounting for empty pulses, we are able to deduce absolute values at every local region.

Now that we have related pulse excitation probabilities to μρ, we describe the experimental observable. The first observation from a pulse is whether a pulse is empty or not. This is captured using a binary parameter W_kⁱ, reminiscent of flipping a coin. For this reason, the outcome of observing or not observing a photon is drawn from a Bernoulli distribution

11

The above sentence should read as follows: “The probability of observing or not observing a photon in the kth pulse from the ith pixel, W_kⁱ, is a random variable drawn from a Bernoulli distribution parametrized by probability 1 – π₀”.

Next, we introduce the photon arrival time from the kth pulse at the ith pixel, Δt_kⁱ, of a detected photon. In order to discuss this quantity, we must model from what chemical species this photon originates. As we have many discrete options, we use a Categorical distribution with M categories (i.e., total number of species) and associated probabilities, for each category, of π_1:M for the ith pixel

12

Here s_kⁱ is the species label of photons that assigns an emitted photon from the kth pulse in the ith pixel to one of the species, s_k ∈ {1, ..., M}. We call s_kⁱ the indicator parameter also termed a membership parameter in the literature.⁷⁰

We are now in a position to construct the likelihood. The likelihood is the probability of the observations (data), in this case, pulses being empty or nonempty (W_kⁱ) and photon arrival times (Δt_k), given the model parameters that we care to learn. These parameters are the lifetimes τ_m, the indicator parameters s_kⁱ, μρ, and ν_m which is the average of the GP prior for species m (see Supporting Information, Note 2.1), collectively shown by θ

13

The overbars reflect shorthand notation for the set of W_kⁱ and Δt_k across all the pixels and pulses. Since all pulses and photon arrival times are independent, the total likelihood is simply the product of the likelihoods of every individual pulse, P(W_kⁱ|θ), and photon arrival time, P(Δt_k|θ). The likelihood of a pulse being empty or not, P(W_kⁱ|θ), is given by eq 11.

Next, we motivate an explicit expression for P(Δt_kⁱ|θ). In order to derive this expression, we immediately generalize to the case where an excited molecule may emit a photon n pulses after its excitation (including, trivially, 0 where the molecule emits following the pulse that excited it); see Figure S20. The arrival time of such photon recorded by a detector is a function of the time that the molecule spends in the excited state as well as the shape of the IRF (approximated as a Gaussian, see Figure S18 and Supporting Information, Note 1.3). The IRF itself incorporates both of these effects: (1) the finiteness of the excitation pulse and (2) the time required by the detector to record the photon upon arrival.

By accounting for (1) the shape of the IRF, (2) the fluorophore lifetime distribution, and (3) resuming over all possible pulses that could have induced the excitation, that is, all nT for all n before the immediate previous pulse where T is the interpulse time, we arrive at

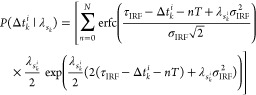14

by convolving the appropriate distributions; see Supporting Information, Note 1.1. Here λ_m, N, and erfc(.) are, in turn, the inverse lifetime of the mth fluorophore species, maximum number prior pulses, and the complementary error function.

Model Inference

In the previous section we defined our likelihood. Within the Bayesian paradigm our goal is to construct the joint probability over all unknowns that we wish to learn, namely, μρ, ν_m, and τ_m for each species, and s_kⁱ, given the data. This object is called a posterior

15

where θ collects all unknowns. To construct the posterior, we must first define priors over all unknowns. In particular, within a Bayesian nonparametric paradigm, as we do not know the shape of the μρ profiles, we will use a GP prior.⁵³⁻⁵⁷ Furthermore, we use the Categorical distribution (eq 12) as prior over the indicator parameters since these parameters can take a value from a finite and discrete set of numbers. For the lifetimes and other associated parameters, we typically opt for conditionally conjugate priors, for the sake of computational efficiency, discussed in further detail in Supporting Information, Note 2.1.

Now we turn to the GP prior on the μρ profiles. These profiles are comprised of a set of spatially correlated random variables (values of μρ at each point in space). As a prior assumption, we can assume that these correlations decay in space and depend inversely on the spatial separation between them.^53,71 The μρ profiles are thus drawn as follows

16

where ν_m and K are the GP prior mean and the covariance matrix; see Supporting Information, Note 2. The means of GP priors, ν_m, are often set to zero. However, since the values associated with μρ profiles are larger than zero, we impose a hyper-prior on ν_m and learn these parameters as well, Supporting Information, Note 2.

With the posterior at hand, we are in a position to draw reasonable values for our parameters of interest from the posterior. As the posterior does not assume an analytic form and cannot be directly sampled from, we invoke a Markov chain Monte Carlo (MCMC) procedure.^{39,48,60,72−75} In particular, we opt for the following Gibbs sampling^60,76 strategy sketched here and discussed further in the Supporting Information, Note 2.2.

As the first step, we initiate the parameter chains to random values taken from the corresponding priors. Next, we iteratively draw new samples from the posterior either directly or by using the Metropolis–Hastings (MH) procedure.^72,73 At every iteration, we sweep the parameters that we wish to learn in the following order: (1) the set of μρ profiles are sampled; (2) the set of GP prior means, ν_m, are sampled; (3) the set of indicator parameters, s_kⁱ, are sampled; (4) the set of lifetimes, τ_m, are sampled. By the end, the resulting parameter sample chains are used for further numerical analyses.

Experimental Data Collection

All data were acquired on an ISS-Alba5 confocal microscope. Excitation was provided by a white light laser (NKT SuperK EXTREME with a repetition of 78093605 Hz) equipped with acousto-optic tunable filters (SuperK SELECT) for selecting an excitation wavelength of 490 nm. Emission was collected by an avalanche photodiode (Excelitas Technologies) and an ISS A320 FastFLIM unit for lifetime determination.

For the in vitro data set in Figure 2, Fluorescein and Coumarin6 were dissolved in ethanol, both at a concentration of 12 μM. A mixture of the two was prepared in a 1:1 ratio, corresponding to a final concentration of 6 μM for each fluorophore. Emission was collected using a band-pass filter 535/50. For the in vivo data sets (HeLa cells; Figure 4), the cells were seeded in a glass-bottom 8-well plate (Ibidi GmbH) previously coated with 2 μg/mL Fibronectin in Dulbecco’s Phosphate Buffer Solution (DPBS) without Ca, Mg, and Phenol Red (GenClone, Genesee). Cells were stained with 1:1000 LysoView 488 (Biotium Inc.) and 100 nM TMRM (Invitrogen) for 20 min, washed twice with DPBS, and subsequently imaged. Emission of the individual samples (LysoView 488 and TMRM) was collected using a band-pass filter (520/35). Emission of the individual sample with TMRM was collected using a band-pass filter at 605/55. The total acquisition time, pixel dwell time, and pixel size were ∼21 s, 16 μs, and 0.196 μm, respectively.

Lifetime measurements using the phasor approach⁸ were performed by visually inspecting the phasor distributions of the stained samples, identifying the presence of components and projecting them onto the universal circle; see Figure S13.

Discussion

FLIM has become a universal tool in probing multiple cellular processes,^1,2 including metabolic changes indicative of cancer metastasis.^77,78 A quantitative assessment of FLIM data requires high resolution lifetime maps typically associated with long data collection, which in turn induces sample phototoxic damage.

Our FLIM framework provides a means to deconvolve lifetime maps from direct photon arrival analysis with subpixel spatial resolutions with limited photon numbers. We do so by leveraging the information provided by each photon as well as empty pulses, one pulse window at a time in order to address challenges 2–5 that we listed at the beginning of this Article. These included, briefly summarized, reporting full error bars, providing a method robust over a broad range of lifetimes, resolving spatial features of the lifetimes maps below the pixel size, and taking advantage of all data directly with no preprocessing.

The conceptual progress required in order to address all five challenges simultaneously (to which we would add the task of learning the number of species) would necessarily involve a doubly nonparametric formulation. That is, we would need to be nonparametric in terms of the number of species and in terms of the lifetime map profiles. While verifying the consistency of single nonparametric processes is now routine,^49,59 the mathematics required to assess the consistency of doubly nonparametric processes satisfactorily deserve future attention.

We benchmarked our method on three different types of data sets: (1) a wide range of synthetic data; (2) in vitro data of a mixture of two fluorophore species with uniform concentrations; (3) in vivo data with highly overlapping inhomogeneous concentration profiles.

Using synthetic data, we assessed the performance of our method under various levels of difficulty including variable concentration profiles, different pixel sizes, photon counts and increasingly small changes between lifetimes down to subnanosecond differences. While the in vitro data set may appear simple, we challenged our method by probing a case involving a mixture of two species with a small difference in lifetimes. The in vivo data, in turn, was acquired by introducing two fluorophore species into a cell with high affinity for lysosomes and mitochondria, respectively. Here, we tested our ability to resolve individual cellular structures when observing photon arrivals from two species at once.

While the BNP framework comes with multiple advantages including high lifetime resolution over a wide range, subpixel spatial resolution, it also comes with two caveats: (1) interpretational issues arising from fundamental model indeterminacy and (2) computational cost. For example, by virtue of the nature of the data itself, the mathematics cannot resolve whether two exponential components coincide with different chemical entities or biexponential decays of a single chemical entity. Strongly correlated spatial distributions of these species may strongly suggest biexponential decay but falls short of a firm proof that these are not different chemical entities. On the computational front, our method scales linearly with the number of species, photon counts per pixel, and number of pixels. As such, for the typical values that we selected, analyzing homogeneous profiles presented in Figure 2 took ∼4 h on an AMD Ryzen 3.8 GHz 12-core processor. On the other hand, for more difficult problems with inhomogeneous profiles over large regions, such as those presented in Figure 3, it took ∼48 CPU hours.

The data used in this paper were collected using a confocal setup with an approximately Gaussian PSF. However, the model presented in the Methods section is not restricted to any specific PSF model and is capable of analyzing data acquired with an arbitrary PSF shape. The model can also be modified to work with any shape of IRF by adapting eq 14.

In addition, we can envision extending the method to incorporate axial spatial information and learning inhomogeneous μρ along this axis by collecting data across multiple axial planes. Based on the intuition built from Figures S5–S7, we anticipate that we could further extend our method to accommodate a mixture of multiple sub-IRF lifetimes given precise IRF calibration and adequate photon counts with arrival times recorded in fine resolutions.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphotonics.1c01936.

• Supplementary figures, tables and details of the mathematical framework (PDF)

• Software Package (ZIP)

Author Contributions

S.P. conceived and supervised the project. M.F. and S.J. designed the algorithm. M.F. wrote the codes. M.F. performed simulations with help from S.J. The experimental data was provided by A.V., L.S., E.G., and M.A.D. M.F. wrote the manuscript with help from S.P. All the authors reviewed and commented on the manuscript.

S.P. acknowledges the support from NIH Grants R01GM134426 and R01GM130745. Image and data acquisition were made possible through access to the Laboratory for Fluorescence Dynamics, a shared resource center supported by the National Institutes of Health (Grant No. P41-GM103540 to L.S., A.V., and E.G.). This study was supported in part by funds from the National Science Foundation (Grant Nos. DMS1763272 and 1847005 to M.A.D.) and a grant from the Simons Foundation (594598 QN to M.A.D.). Part of the simulations for this paper were performed on Arizona State University cluster AGAVE.

The authors declare no competing financial interest.