Discovering giant magnetoelasticity in soft matter for electronic textiles

SUMMARY

We discovered a giant magnetoelasticity in soft matter with up to 5-fold enhancement of magnetomechanical coupling factors compared to that of rigid metal alloys without an externally applied magnetic field. A wavy chain analytical model based on the magnetic dipole-dipole interaction and demagnetizing field was established, fitting well to the experimental observation. To explore its potentials in electronic textiles, we coupled it with magnetic induction to invent a textile magnetoelastic generator (MEG), a new working mechanism for biomechanical energy conversion, featuring an intrinsic waterproofness, an ultralow internal impedance of approximately 20 Ω, and a high short-circuit current density of 1.37 mA/cm², which is about four orders of magnitude higher than that of other textile generator counterparts. Meanwhile, assisted by machine learning, the textile MEG could continuously monitor the respiratory activities on heavily perspiring skin without any encapsulation, allowing a timely diagnosis of the respiration abnormalities in a self-powered manner. We foresee that this discovery can be extended to wide-range soft-matter systems, emerging as a compelling approach to develop electronic textiles for energy, sensing, and therapeutic applications.

Graphical Abstract

We discovered a giant magnetoelasticity in soft matter with up to 5-fold enhancement of magnetomechanical coupling factors compared to that of rigid metal alloys without an externally applied magnetic field. This discovery was well explained by a wavy chain analytical model. To explore its potentials in electronic textiles, we coupled it with magnetic induction to invent a textile magnetoelastic generator (MEG), a fundamentally new working mechanism for biomechanical energy conversion, featuring ultrahigh current output, ultralow internal impedance, and intrinsic waterproofness.

INTRODUCTION

Conventional magnetoelasticity, defined as the change in magnetic property in certain materials under mechanical deformation (Figure S1), has been observed in rigid metal alloys, such as Tb_xDy_1-xFe₂ (Terfenol-D) and Ga_xFe_1-x (Galfenol), for building vibration control.^1,2 As sketched in Figure S2, it holds a bulky, heavy, and rigid structure. The conventional magnetoelasticity in metal alloys has been rarely adopted to build devices for interfacing with the human body since: (1) human skin and tissues are soft and not easily adapted to these hard metal alloys,³ (2) the optimal magnetomechanical coupling efficiency on these rigid metal alloys always requires a pressure of several megapascals, beyond the range of biomechanical stress, and (3) these rigid metal alloys require external magnetic fields of up to 1,000 Oe when implementing functionality.⁴

Textiles have been concomitant of human civilization for thousands of years.⁵ Nowadays, advances in materials science and nanotechnology facilitate the infusion of electronics and textiles, which has been a compelling approach to realize electronic textiles (e-textiles) with additional functions while maintaining their breathability, biocompatibility, and wearing comfort.^5–12 Given this, abundant e-textiles have been developed to perform various applications on the human body, such as energy harvesting/storage,^13–15 sensing,^16–18 therapy,^19–21 display,^22–24 and even computation.^25–27 Among them, biomechanical energy conversion textiles have attracted a wide range of research interests,⁵ since biomechanical motions on the human body are sustainable, pervasive, and easy to obtain.²⁸ Currently, widely adopted e-textiles for biomechanical energy conversion are based on the triboelectric²⁹ and piezoelectric effects,³⁰ which have been proved to conform well to the human skin for wearable electricity generation. Owing to their capacitive power generation principle via manipulating the electric dipoles at the materials interfaces, the wide-range adoption of such technologies is largely shadowed by a low current density (in the order of 100 nA/cm²) and a high internal impedance (in the order of megaohms).^31,32 Moreover, the generated current relies on electric dipole transfer at the materials interfaces, which is vulnerable to perspiration and ambient humidity, severely limiting their practical on-body applications.^30,33

Herein, we discovered a giant magnetoelasticity in a soft matter and achieved a magnetomechanical coupling factor up to 6.77 × 10⁻⁸ T/Pa without the need for an external magnetic field, which is up to five times larger than that of traditional rigid metal-based counterparts³⁴ (Table S1). Soft matter with giant magnetoelasticity demonstrates a strain of up to 500% and a Young’s modulus as low as 166.2 kPa, which is well comparable to human tissue and skin.⁵ A wavy chain analytical model was established to explain the giant magnetoelasticity in the soft matter, which is well consistent with the experimental observation. To demonstrate its practicability, the giant magnetoelasticity was further coupled with magnetic induction to develop a textile magnetoelastic generator (MEG) as a fundamentally new working mechanism for biomechanical energy conversion. Externally applied pressure on the textile MEG strongly altered its magnetic flux density and a current was induced in the textile coil, which demonstrated a high short-circuit current (I_sc) density of 1.37 mA/cm² and a low internal impedance of ~20 Ω. This current output is about four orders of magnitude higher than that of the triboelectric effect-based³⁵ and piezoelectric effect-based³⁶ textile biomechanical energy-harvesting counterparts. Meanwhile, textile MEGs are fully waterproof without encapsulation because the magnetic fields can pass through water molecules with negligible intensity loss. Therefore, textile MEGs were developed into self-powered sensors for wearable respiratory monitoring with heavy perspiration. With an optimal sensitivity of 0.27 mA/kPa, signal-to-noise ratio (SNR) of 61.8 dB, and response time of 15 ms, this textile MEG-based sensor can continuously monitor the strength, frequency, and patterns of various respiratory activities. Assisted by a random forest-based machine learning algorithm, respiration abnormalities can be continuously recognized, such as cough and rapid breathing, hence allowing for a timely diagnosis of breath-related diseases. The discovered giant magnetoelasticity in soft matter is a new form of mechanical to magnetic conversion, and the invented textile MEG is bringing a fundamentally new working mechanism to the biomechanical energy conversion community. These advancements are expected to make a splash in constructing human body-centered e-textiles for personalized healthcare.

RESULTS AND DISCUSSION

Design of soft matter with giant magnetoelasticity and textile MEGs

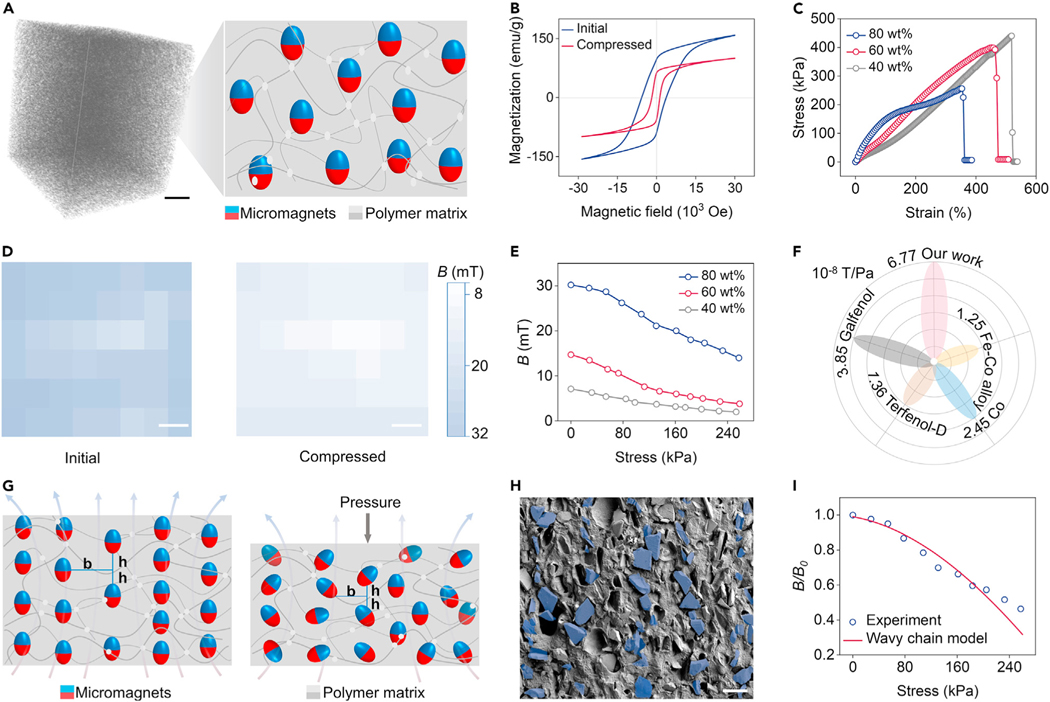
We observed the giant magnetoelasticity in a soft magnetoelastic film consisting of micromagnets and a porous polymer matrix (Figure 1A). After being subjected to an impulse magnetization, the possible rotation and movement of micromagnets in the polymer matrix construct a chain-like arrangement,³⁷ maintaining a large retentivity of 96.5 emu/g (Figure 1B). According to scanning electron microscopy (SEM) (Figure S3) and micro-computed tomography (micro-CT) (Video S1), these micromagnets are evenly distributed in the porous matrix. These micromagnetic particles have a mean diameter of 53.7 μm with a standard deviation of 18.8 μm, and a mean interparticle distance of 139.6 μm with a standard deviation of 34.0 μm (Figure S4). This unique structure gives the soft magnetoelastic film outstanding mechanical properties that favor further on-body biomechanical-to-electrical energy conversion, such as a strain of up to 500% and a Young’s modulus as low as 166.2 kPa (Figures 1C and S5). Figure 1D shows the magnetic flux density mappings of the soft magnetoelastic film with a size of 3 × 3 × 0.2 cm. Under an applied pressure of 257 kPa, the magnetic flux density of the soft magnetoelastic film decreased significantly up to 50%. The relative magnetic flux density decrease of our soft magnetoelastic film rivals that of the traditional magnetoelastic system,³⁸ which needs an extremely high uniaxial stress of more than 10 MPa.³⁹ On this basis, we investigated the values of magnetic flux density variation with different micromagnet concentrations. As shown in Figure 1E, under constant stress, the soft magnetoelastic film with 80 wt % micromagnet concentration has the largest values of magnetic flux density variation of 16 mT compared with those with 60 wt % (10.9 mT) and 40 wt % (5.1 mT) micromagnets. More importantly, this soft magnetoelastic film delivers a magnetomechanical coupling factor of 6.77 × 10⁻⁸ T/Pa without relying on an external magnetic field, which is five times larger than that of the traditional magnetoelasticity in the rigid systems (Figure 1F).³⁴ However, a further increase in loading of the micromagnets could decrease the stretchability (from 500% to 350%) and increase the Young’s modulus (from 166.2 to 433.3 kPa) of the soft magnetoelastic film (Figure S5). To maintain a stretchability applicable to a wearable application and a high magnetomechanical coupling factor, a soft magnetoelastic film with 80 wt % micromagnets was chosen for further study.

Figure 1. Discovering the giant magnetoelasticity in soft matter.

(A) 3D micro-CT of the soft matter and schematics of the internal structure consisted of micromagnets and polymer matrix. Scale bar, 2 cm.

(B) Hysteresis loop of the soft magnetoelastic film with and without uniaxial stress.

(C) Stress-strain curves of the soft magnetoelastic film with different micromagnet concentrations.

(D) Magnetic flux density mappings of the soft magnetoelastic film with/without compression. Scale bar, 0.5 cm.

(E) Magnetoelastic performance of different micromagnet concentrations in terms of applied compressive stress and associated magnetic flux density changes.

(F) Performance comparison of different magnetoelastic systems in terms of the magnetomechanical coupling factor d₃₃.

(G) Wavy chain model to explain the giant magnetoelasticity in soft matter. The dominant parameters are the horizontal center-to-center micromagnet distance b and the vertical center-to-center micromagnet distance h.

(H) SEM images of the soft magnetoelastic film with marked chain structures. Scale bar, 100 μm.

(I) Comparison of the experimental magnetic flux density variation under the applied pressure and the wavy chain model result shows consistency.

To investigate the fundamental science behind the giant magnetoelasticity, we established a wavy chain model.⁴⁰ Without an external pressure, these micromagnets inside the soft magnetoelastic film are well aligned as a wavy chain structure to maintain a stable status after an impulse magnetization (Figure 1G). When an external pressure is applied to the soft magnetoelastic film, the pressure penetrating the polymer matrix could provide a constant energy for these micromagnetic particles to move and rotate, thus decreasing the magnetic flux density. In addition, the relationship between the vertical magnetic field $H_{\perp }$ and principal stretch l could be expressed as⁴⁰:

$$H_{\perp }\approx -\frac{1}{(2a+1){\lambda }^{1.5k}}M+\frac{r^{3}M}{3{\lambda }^3{h}^3}\left(0.3006-f\left(\frac{b}{h{\lambda }^{1.5}}\right)\right),$$ (Equation 1)

where r is the particle radius, a is the aspect ratio of the wavy chain structure, λ is the stretch in the compress direction, M is the magnetization of the micromagnets, k is a constant characterizing the influence of nonideality, neighboring chain-chain interaction, and macroscopic shape effect to the demagnetizing factor under compressive deformation, b and h are the horizontal and vertical distances between the neighboring micromagnets (Figure 1G), respectively, and 0.3006-f(x) is the dipole alignment factor, which describes the contribution of all other dipoles to the vertical magnetic field of a single dipole in the wavy chain. According to the wavy chain model, under external pressure, the compressed chain structure varies and alters the dipole-dipole interaction inside the chain associated with the decrease in magnetic flux density. To verify the accuracy of the wavy chain model, we marked possible chain structures observed in the soft magnetoelastic film (Figure 1H) and measured the parameters b and h. Based on these parameters, we estimated the magnetic flux density variation under the applied pressure, fitting well with the experimental observation (Figure 1I).

The giant magnetoelasticity can generate a localized magnetic flux density change in response to tiny pressure on the soft magnetoelastic film. Combined with a textile coil (Figure 2A), this mechanical energy can be further converted into electricity using Faraday’s law of induction:

$$\epsilon =-N\ast \frac{d\text{Φ}}{dt},$$ (Equation 2)

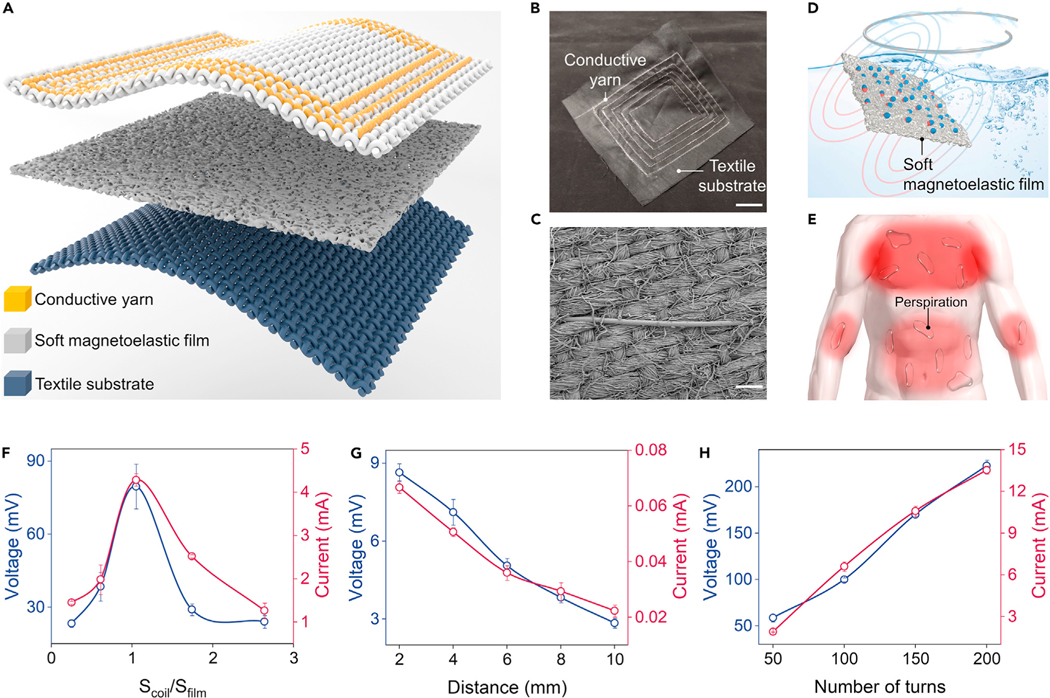
where ε is the electromotive force (EMF), N is the turn of coil, Φ is the magnetic flux, and t is time. In this case, a textile MEG was developed with a soft magnetoelastic film for magnetomechanical coupling and a textile coil for electromagnetic induction (Figure 2B). The textile coil consists of the machine-sewn conducive yarns and a textile substrate (Figure 2C), which could be produced at a factory scale. Meanwhile, textile MEGs are fully waterproof without encapsulation because the magnetic fields can pass through fluid with negligible intensity loss (Figure 2D). This distinct advantage allows textile MEGs to maintain their function even with heavy perspiration (Figure 2E), holding wide practicability for wearable biomechanical-to-electrical energy conversion. It is worth mentioning that our textile MEG is fundamentally different from previously reported wearable electromagnetic generators^41–44: (1) textile MEG is a one-body design that relies on the intrinsic magnetic flux density variation caused by the giant magnetoelasticity, while electromagnetic generators require the magnets to move relative to the circuits (Figure S6). (2) Faraday’s law is a single equation describing two different phenomena: the motional EMF generated by a magnetic force on a relatively moving circuit (electromagnetic generators) and the transformer EMF generated by an electric force due to a changing magnetic field (MEG).

Figure 2. Utilizing the giant magnetoelasticity in soft matter for electricity generation.

(A) Textile MEG is composed of a soft magnetoelastic film, a textile coil, and a textile substrate.

(B) Photograph of the scalable textile coil. Scale bar, 2 cm.

(C) SEM of the textile coil. Scale bar, 100 μm.

(D) Illustration of the waterproof ability of textile MEGs.

(E) Textile MEGs are sweatproof and can be used for a wide range of on-body applications.

(F–H) Dependence of the electric outputs of the textile MEGs against the textile coil size (F), distance (G), and the number of turns (H).

To optimize the biomechanical-to-electrical energy conversion of the textile MEG, we systematically investigated the interaction between the soft magnetoelastic film and the textile coil. First, the dependence of the electric output on the area ratio of the textile coil to the soft magnetoelastic film was plotted (Figure 2F). A smaller textile coil (S_coil/S_film < 1) cannot collect all magnetic flux density variation of the compressed soft magnetoelastic film, while a large textile coil (S_coil/S_film > 1) consists of adverse magnetic field lines canceling each other out (Figure S7). In this case, an approximately similar size of textile coil and soft magnetoelastic film is the optimal ratio to biomechanical-to-electrical energy conversion. Secondly, regarding the distance between the two components, the textile coil closely attached to the soft magnetoelastic film could generate the maximal electric outputs (Figure 2G), since the strength of the magnetic field decreases with distance (Figure S8). Finally, Figure 2H demonstrates that both output voltage and current show a linear relationship with the turns of the textile coil, fitting well with Faraday’s law of induction (Equation 2). Thus, increasing the number of turns in the textile coil is an effective method to enhance the electric outputs.

Textile MEGs for energy conversion

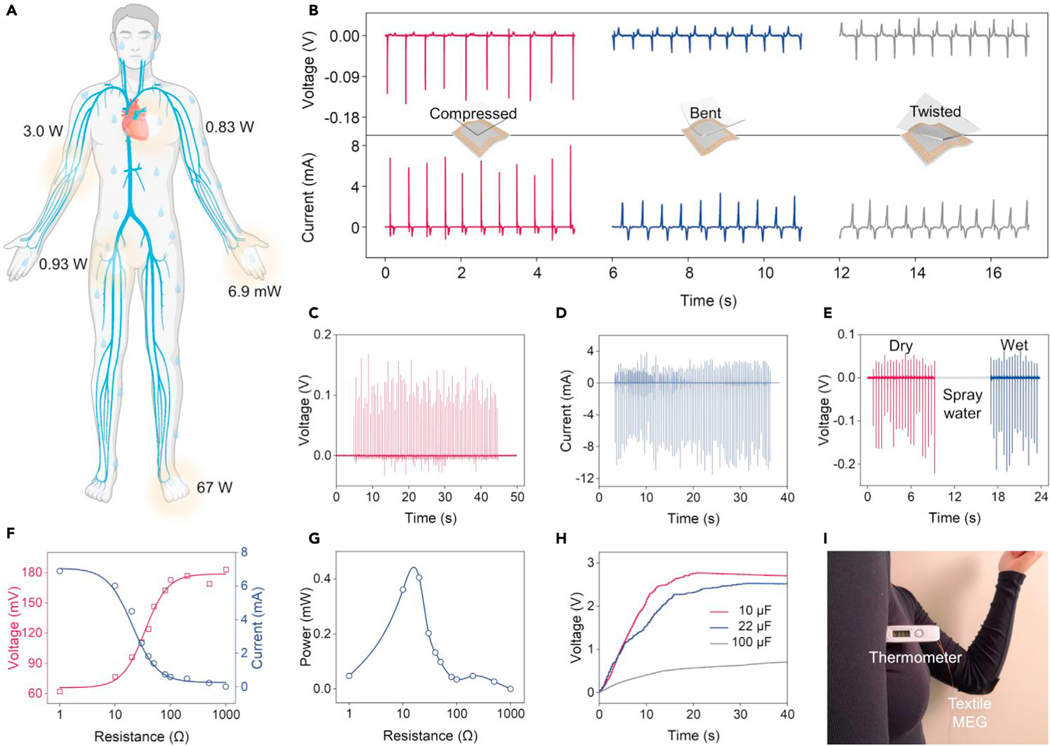
The human body is particularly rich in biomechanical energy,²⁸ which can be explored as a pervasive power source for a wide range of wearable electronics, such as sensors, actuators, and displays.⁵ Typical biomechanical activities, such as blood flow, breathing, upper limb movement, finger typing, and walking contain approximate potential energies of 0.93 W, 0.83 W, 3.0 W, 6.9 mW, and 67 W, respectively (Figure 3A).⁵ Commonly used biomechanical energy conversion technologies rely on triboelectric effect-based²⁹ and piezoelectric effect-based³⁰ nanogenerators. However, these nanogenerators have unavoidable disadvantages, such as a very low current density in the order of 100 nA/cm² and a high internal impedance in the order of megaohms,³² which are caused by their capacitive power generation principle via manipulating the electric dipoles at the materials interfaces. Meanwhile, the generated current originates from the electric dipole transfer at the materials interfaces, which is vulnerable to perspiration and ambient humidity, severely limiting their functionality available to wearable applications.^30,33 Additive encapsulation layers on these nanogenerators, such as silicone rubber,^45–47 have been developed for waterproofness. However, the thickness of the layer would impede the biomechanical energy transfer from the human body to the devices. In contrast, based on the coupling of the giant magnetoelasticity and Faraday’s law of induction, textile MEGs feature a low internal resistance and can generate a high output current in the coil. Additionally, magnetic field variation can penetrate water with negligible intensity loss, endowing textile MEGs with intrinsic waterproof ability. These properties make textile MEGs highly competent in wearable energy conversion for powering bioelectronics.

Figure 3. Textile MEGs for wearable biomechanical energy conversion.

(A) Pervasive biomechanical energy sources on the human body.

(B) Schematics showing three mechanical excitation modes on the textile MEGs and the corresponding measured voltage and current output.

(C) V_oc of the textile MEG under continuous hand tapping.

(D) I_sc of the textile MEG under continuous hand tapping.

(E) Waterproof ability of textile MEGs with respect to electricity generation.

(F) Output current and voltage dependence on the electrical impedance of the textile MEG.

(G) Output power dependence on the electrical impedance of the textile MEG.

(H) Charging of 22, 47, and 100 μF capacitors by hand tapping the textile MEG.

(I) Photograph of the textile MEG for powering a commercial thermometer.

To fulfill this need, a textile MEG consisting of a textile coil with 200 turns was developed for wearable energy conversion. This textile MEG can be conformably attached to the human skin owing to its high flexibility (Figure S9). To optimize the energy conversion performance, we systematically investigated the electric output of textile MEGs under different deformation modes. The textile MEG was compressed, bent, and twisted into various shapes, and the corresponding voltage and current outputs are demonstrated in Figure 3B. Compressed textile MEGs performed best because the vertically applied pressure can strongly decrease the magnetic flux density, while other deformation modes would partially cancel the magnetic field variation (Figure S10). Meanwhile, under compression, the magnetic field variation is vertical to the coil, which could be fully utilized to generate a maximum EMF. Based on the compressive deformation, the textile MEG was continuously tapped by hand, generating an open-circuit voltage (V_oc) of up to 198 mV (Figure 3C) and a short-circuit current (I_sc) of up to 12.4 mA (corresponding to a current density of 1.37 mA/cm²) (Figure 3D). Moreover, the output voltage of the textile MEG remains constant even after being sprayed with water (Figure 3E), demonstrating the ability for wearable energy conversion in a wet environment, such as a heavily perspiring body during exercise. To test the output power of the textile MEG, external resistors were loaded with the circuit. As the load resistance increased from 1 to 1,000 Ω, the output current decreased and the output voltage increased (Figure 3F). The maximum instantaneous power of 0.405 mW could be achieved when the load resistance was approximately 20 Ω (Figure 3G). With a rectifying circuit to convert the alternative output into the direct output (Figure S11), the textile MEG charged the capacitors of 10, 22, and 100 μF to 3, 3, and 1.1 V, respectively, within 20 s instantaneously by gentle touch (<5 N, 5 Hz) (Figure 3H). The collected electricity in the capacitor could drive a commercial thermometer (Figure 3I) for monitoring multiple physiological information.

Textile MEGs for self-powered sensing

Physiological activities inside the human body generate various biomechanical signals,⁴⁸ such as pulse wave, blood flow, intestinal peristalsis, and many others. Self-powered biomechanical sensors can convert these biosignals into electrical signals, providing abundant healthcare information for clinical diagnosis.¹⁶ Typically applied mechanisms of these self-powered biomechanical sensors are triboelectric effect and piezoelectric effect, which rely on their capacitive electricity generation principle via manipulating the electric dipoles at the materials interfaces.^30,33 However, this process is vulnerable to perspiration and ambient humidity from the human body, impeding their wearable applications. Although additive encapsulation layers could enhance their waterproofness, the thickness of the layer would impede biomechanical signals transferring from the human body to the devices, ultimately decreasing sensitivity. In contrast, textile MEGs are fully waterproof without encapsulation because the magnetic fields can pass through fluid with negligible intensity loss. Thus, textile MEGs can also work as self-powered biomechanical sensors for continuously monitoring human physiological signals, especially in heavy perspiration situations, such as exercising and under heat. Relevant biomechanical motions, such as the skin surface fluctuation caused by arterial pressure and chest movement during breathing, can deform the textile MEGs and cause magnetic field distortion, inducing an EMF and generating a current in the textile coil. Meanwhile, textile MEGs feature outstanding wearability, such as breathability and softness, making them conform well when attached to the human body for long-term monitoring.

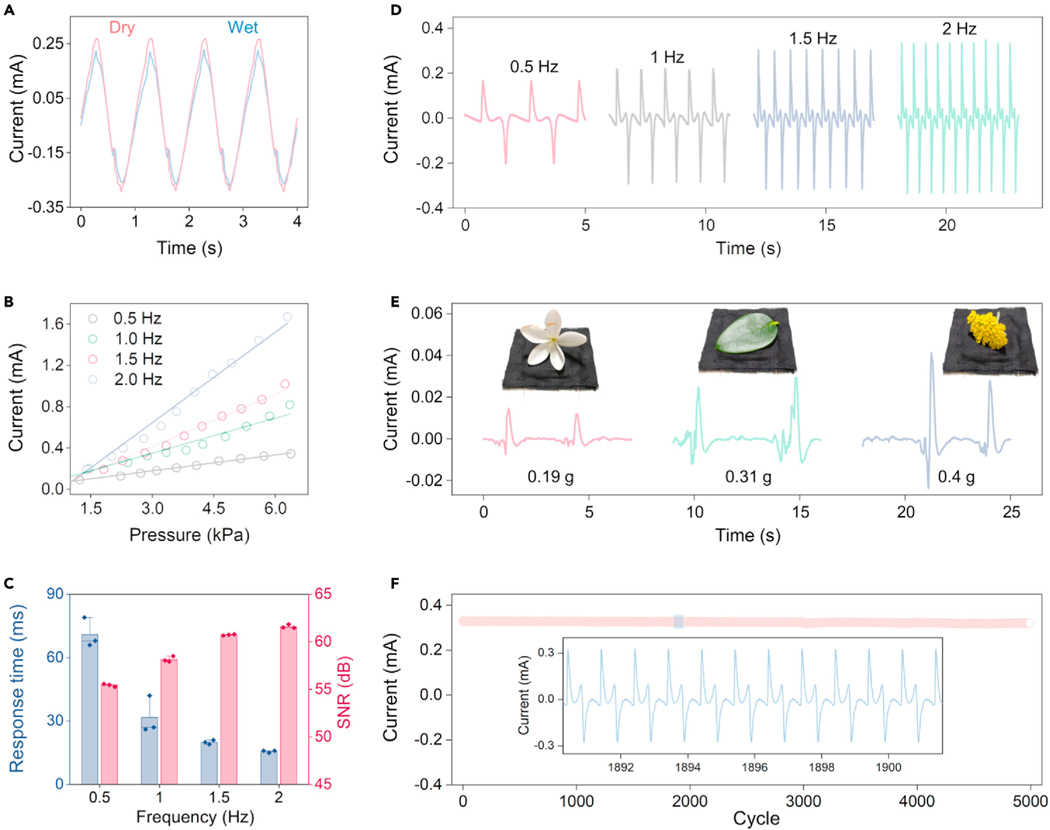
To characterize the sensing performance of textile MEGs in various situations, we established a testing system containing a function generator, power amplifier, electrodynamic shaker, pressure gauge, programmable electrometer, and computer (Figure S12). First, we investigated the waterproofness of the textile MEGs during sensing. As shown in Figure 4A, a textile MEG was deformed by a periodic gentle pressure of 1 Hz with sprayed water, while the acquired current signals are almost the same as the sensing signals from the dry situation. To further test the sensing performance, we measured the sensitivity of the textile MEG by plotting current versus pressure characteristics under diverse frequencies. The testing system applied an external mechanical excitation of up to 6.5 kPa with a frequency of 0.5, 1.0, 1.5, and 2.0 Hz on the textile MEG. As shown in Figure 4B, the output current of the textile MEG increases with an increased applied pressure as well as an increased frequency. Under a frequency of 2 Hz, the maximum sensitivity of 0.27 mA/kPa is realized. Then, we investigated the sensing signal quality of the textile MEG in response to the applied pressure with various frequencies. Under a fixed pressure of 2 kPa, the response time, SNR, and pulse waveforms were measured, as shown in Figures 4C and 4D. With an increased frequency, the output waveforms show a shorter response time (Figure S13) and a higher SNR with a decreased standard deviation (Figure S14). These results show that textile MEGs have a better sensing performance in response to high-frequency excitation, realizing a fast response time (up to 15 ms), a high SNR (61.8 dB), and a stable output. This phenomenon is attributed to the unique working mechanism of textile MEGs. According to Equation 2, the generated EMF is proportional to the variation speed of magnetic flux. Under high-frequency mechanical excitation, the magnetic field of the soft magnetoelastic film changes rapidly, inducing larger electric output signals with higher quality. This novel property enhances the ability of textile MEGs to distinguish the abnormal physiological signals with frequency variation, such as an increased heart rate and breathing rate. We further tested the sensing performance of textile MEGs in an ultralow-pressure range. A tiny white flower (0.19 g), a green leaf (0.31 g), and a yellow flower (0.4 g) were gently dropped onto the textile MEG (Video S2). Figure 4E shows the current signals of the textile MEG in response to the tiny subject loading. High sensitivity indicates that textile MEGs can detect a subtle pressure. Finally, to evaluate the stability of the textile MEG as a self-powered sensor, we measured the output current in response to loading-unloading pressure cycles. An amplitude-fixed 2 kPa pressure with a frequency of 2 Hz was applied to the textile MEG for 5,000 loading-unloading cycles (Figure S15). The peak-to-peak current was recorded (Figure 4F), and the enlarged views of the current waveforms are shown in the inset. These results reveal remarkable repeatability, stability, and durability of textile MEGs, proving their long-term monitoring ability.

Figure 4. Standard evaluation of textile MEGs for self-powered sensing.

(A) Comparison of the sensing signals obtained from the textile MEG under wet and dry conditions.

(B) Sensing signal dependence on the applied pressure frequency and amplitude.

(C) Dependence of the response time and signal-to-noise ratio of the textile MEGs on the applied pressure frequency. Error bars are standard deviations of the results from three samples.

(D) Waveforms of the sensing signals under different applied pressure frequencies.

(E) A tiny white flower, a green leaf, and a yellow flower were gently dropped onto the textile MEG and generated distinct current signals.

(F) Cyclic test of the textile MEGs for more than 5,000 cycles, and an enlarged view of the marked region, showing excellent stability and repeatability.

Machine-learning-assisted respiratory monitoring

Respiration rate is one of the four main vital signs of the human body, providing critical personalized information for diagnosing respiratory diseases, such as pneumonia, asthma, and chronic bronchitis.⁴⁹ Practically, respiration rate could be determined by measuring the rising and falling of the chest. Many wearable respiration sensors have been developed to convert these chest movements into electrical signals,^50,51 creating a promising method for respiratory monitoring and personalized healthcare. However, the human chest is one of the most common areas of sweating, featuring a high mean sweating rate of 1.555 mg cm⁻² min⁻¹.⁵² Many wearable respiration sensors are intolerant to the humidity of sweat, and always need a bulky and airtight layer for encapsulation,⁵³ which might significantly reduce their sensitivity and wearing comfort. In contrast, textile MEGs are instinctively waterproof without any encapsulation, because the magnetic fields can pass through water with negligible intensity loss. Thus, our textile MEGs can be seamlessly sewn on clothes or a chest strap with high air permeability and wearing comfort (Figure 5A), working as a self-powered sensor for respiratory monitoring in the long term even with heavy perspiration.

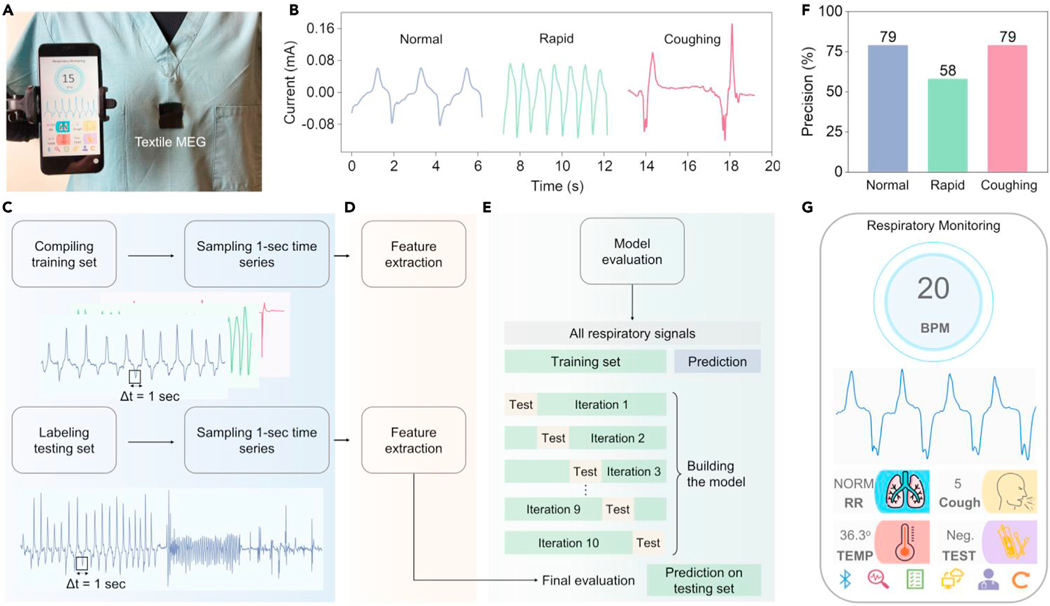
Figure 5. Machine-learning-assisted textile MEGs for wearable respiratory monitoring.

(A) Textile MEGs integrated on the nursing scrubs for respiratory monitoring. A customized cellphone application was developed for data display, storage, and sharing.

(B) Three different kinds of respiratory patterns: normal breathing, rapid breathing, and coughing were monitored by the textile MEG.

(C–E) Machine learning algorithm to classify different respiratory activities, including data preprocessing (C), feature extraction (D), and model training (E).

(F) Classification precision of different respiratory activities.

(G) Customized cellphone application interface to display the sensing results in the front-ends.

To fulfill this need, the textile MEG was directly stitched around the chest area of a nursing scrub. The respiration-caused expansion and contraction of the ribcage deform the textile MEG, generating a current output. Then we tested the sweatproof ability of the textile MEGs by spraying artificial perspiration onto the device-embedded nursing scrub during respiratory monitoring (Figure S16). The acquired respiration signals are almost the same as the signals from the dry situation. These results indicate the excellent sweatproof ability of textile MEGs, which makes them feasible for monitoring of respiratory activities. A 21-year-old man dressed in the textile MEG imitated three different kinds of respiratory patterns: normal breathing, rapid breathing, and coughing, respectively. The acquired waveforms are plotted in Figure 5B. Due to the high sensitivity and stability of textile MEGs, the frequency, intensity, and persistency of different respiratory patterns were distinctly recorded. These data provide enough features for respiratory disease assessment and diagnosis, which necessitate accurate and automated analysis and infrastructure to enable quick medical intervention.

Machine learning is an emerging branch of data science that has shown early promise for personalized healthcare through the extraction of clinically relevant information from imperceptible abnormal biosignals.⁵⁴ On this basis, we established a machine learning framework to classify different respiratory activities according to our sensing signals. A laboratory-scale sensing dataset was collected by our textile MEGs for the machine learning model training, which included more than 300 cycles of normal breathing, 400 cycles of rapid breathing, and 20 cycles of cough. First, these sensing signals were preprocessed by sampling a 1-s time series, generating the training records (Figure 5C). Two types of feature extraction approaches were used, including minimal approaches used to describe the data with the minimum number of features and efficient approaches that have a larger number of features to describe the data (Figure 5D). For both types of feature extraction methods, once the model extracted all features, another step was performed to keep the relevant features only. Two classifiers, decision tree and random forest, were used during the training process to learn these features. Ten-fold cross-validation was used to evaluate machine learning models on these limited samples (Figure 5E). Table S2 summarizes the average accuracy for cross-validation. Random forest with efficient feature extraction gives the most accurate result of up to 90.89% as the cross-validation mean accuracy. The testing sequence to evaluate the algorithm was collected by the same subject at different time periods, beginning with 45 s normal breathing, 25 s rapid breathing, and five forced coughs. Our algorithm demonstrated a classification precision of 0.79, 0.58, and 0.79 for normal breath, rapid breath, and cough, respectively (Figure 5F). Standard metrics of the algorithm performance, i.e., precision, recall, F score, and overall accuracy, are summarized in Tables S3 and S4. This framework can be used to distinguish abnormal respiratory activities, such as rapid breathing and coughing from normal breathing, demonstrating the potential for assessment of respiratory diseases, such as respiratory-based COVID-19 diagnoses.⁵³

We further developed a respiratory monitoring system including the textile MEGs, machine learning algorithms, and a customized cellphone application (APP) for data display, storage, and sharing (Video S3). Respiratory monitoring signals acquired by textile MEGs were first amplified and filtered to obtain a high quality. Then the collected data were processed using our machine learning algorithm to distinguish the respiratory patterns (normal, rapid, and coughing) and calculate the corresponding breaths per minute and cough times. Finally, these data were transmitted to the cellphone APP and displayed in the front-ends (Figures 5G and S17). All these patient-generated data can be one-click forwarded to physicians through email, cloud electronic health records, or messages for further respiratory diseases diagnosis (Figure S18). In brief, textile MEGs assisted by machine learning for respiratory monitoring can serve as a quantitative basis for detecting early signs of respiratory diseases in potential patients, monitoring the symptomatic progression in home settings, and tracking responses to therapeutics in clinical settings.

Conclusions

Giant magnetoelasticity in soft matter can convert the applied pressure into magnetic flux density change through the micromagnet interaction in the polymer matrix without an externally applied magnetic field. To explore this phenomenon, a wavy chain analytical model was established to investigate the scientific principles and a textile MEG was invented to convert the biomechanical motions into electricity. Compared with the existing e-textiles for biomechanical energy harvesting, our textile MEGs feature an intrinsic waterproofness, an ultralow internal impedance, and a high current density output.

From a scientific standpoint, we discovered the giant magnetoelasticity in soft matter without the need for an externally applied magnetic field. It shows a magnetomechanical coupling factor of 6.77 × 10⁻⁸ T/Pa, which is up to five times larger than that of traditional rigid metal-based counterparts under the magnetic field.³⁴ Meanwhile, to understand the scientific principles of the giant magnetoelasticity, a wavy chain model based on the magnetic dipole-dipole interaction was established, fitting well to the experimental observation. From a material standpoint, the developed soft matter is flexible and stretchable, featuring a Young’s modulus of 433.3 kPa and a stretchability of 350%. Compared with the conventional rigid metal alloys with the Young’s modulus of up to 100 GPa, the mechanical properties of our soft matter can be more easily adapted by human skin and tissues. From an application standpoint, we invented a textile MEG by coupling the giant magnetoelasticity in soft matter with Faraday’s law of induction as a new mechanism for biomechanical-to-electrical energy conversion. Our textile MEGs demonstrated an ultralow internal impedance of approximately 20 Ω and a high short-circuit current density of 1.37 mA/cm², corresponding to four orders of magnitude enhancement more than other textile counterparts for biomechanical energy conversion.³⁵ Meanwhile, textile MEGs are intrinsically waterproof and can also work as self-powered sensors for respiratory monitoring on skin with heavy perspiration. Assisted by machine learning, respiration abnormalities could be continuously and precisely detected, demonstrating the potential for assessment of respiratory diseases. This collection of compelling features makes textile MEGs an emerging platform technology for the broad academic community.

In brief, our study discovered a giant magnetoelasticity in soft matter consisting of a polymer matrix and micromagnets, which demonstrated a 5-fold enhancement of magnetomechanical coupling factors more than that of the traditional rigid metal-based counterparts. To understand this phenomenon, a wavy chain analytical model, based on the magnetic dipole-dipole interactions in the soft matter, was established, fitting well to the experimental observation. Then we explored this discovery in e-textiles and coupled it with Faraday’s law of induction to invent a textile MEG for biomechanical-to-electrical energy conversion. The developed textile MEG demonstrates an intrinsic waterproof property, an ultralow internal impedance, and a high current output. Meanwhile, textile MEGs can work as self-powered sensors for respiratory monitoring on skin with heavy perspiration without any encapsulation. Assisted by machine learning, abnormal respiratory activities, such as rapid breathing and coughing, can be precisely distinguished, demonstrating the potential for diagnosis of respiratory diseases. We believe that the discovery of giant magnetoelasticity can branch out into broader soft-matter systems, illuminating the future of e-textiles for developing human body-centered energy, sensing, and therapeutic applications.

EXPERIMENTAL PROCEDURES

Resource availability

Lead contact

Further information and requests for data and resources will be fulfilled by the lead contact, Prof. Jun Chen (jun.chen@ucla.edu).

Materials availability

All materials used in this work are commercially available.

Data and code availability

Data from this paper are available in the article and in the supplemental information.

Fabrication of the soft magnetoelastic film

Ecoflex 00–30 part A (Smooth-on) and Ecoflex 00–30 part B (Smooth-on) with a weight ratio of 1:1 were mixed and pre-cured at room temperature for 10 min. Then neodymium-iron-boron micromagnets (MQFP-B-20076–088) with weight concentrations of 40%, 60%, and 80% were blended with the polymer mixture using a stirring rod. Stirring thoroughly for 10 min introduced air microbubbles for a porous structure. Then the mixture was poured into the template and cured at 70^◦C in an oven (Thermo Fisher Scientific) for 4 h. By using different templates, composited films with the given thickness could be fabricated. Finally, the cured composited film was magnetized by an impulse field (approximately 2.6 T) using an impulse magnetizer (IM-10–30, ASC Scientific) to import the remnant magnetization.

Characterization of the soft magnetoelastic film

Structural characterization of the soft magnetoelastic film was conducted by SEM (Zeiss supra 40VP) and micro-CT (CrumpCAT). Magnetic flux density measurement was realized using a digital Gauss meter (TD8620, Tunkia). Stress was applied on the soft magnetoelastic film, and the Gauss meter with an axial probe measured the vertical component of the magnetic field. The magnetic hysteresis loop was tested using a SQUID magnetometer (MPMS3, Quantum Design). The stress-strain curves were determined by using a dynamic mechanical analyzer (DMA, RSA III). The Young’s modulus was calculated by fitting the experimental curves with a neo-Hookean model.

Fabrication of the textile MEGs

Flexible and thin conductive yarns (Remington Industries 43 HFVP.25) were sewn into the textile substrates to construct the textile coil. These textile coils could be stacked layer by layer to construct a multilayered textile coil with different turns. Then a textile substrate, a soft magnetoelastic film, and the textile coil with different turns were sewn together to construct textile MEGs.

Characterization of the electrical performance of the textile MEGs

The electrical performance characterization system contained a function generator (AFG1062, Newark), a power amplifier (PA-151, Labworks), an electrodynamic shaker (ET-126HF, Labworks), and a pressure meter (HYPX-017). Voltage signals were recorded using a programmable electrometer (Keithley 6514) and the current signals were recorded using a Stanford low-noise current pre-amplifier (model SR570). For electricity generation, a diode bridge rectifier (MBSK16SE) was used to convert the alternative current to a direct current. A toroidal transformer was used to expand the voltage signals.

Machine-learning-assisted respiratory monitoring

For the laboratory-scale sensing dataset collection, a 21-year-old man dressed in the textile MEG performed 300 cycles of normal breath, 400 cycles of rapid breath, and 20 cycles of forced cough. Two classifiers, decision tree and random forest, were trained and tested. Ten-fold cross-validation was used for model training. Two types of feature extraction methods were used, including minimal used to describe the data with the minimum number of features and efficient that have a larger number of features to describe the data. For both types of feature extraction methods, once the model extracted all features, another step was performed to keep the relevant features. Random forest with efficient feature extraction gave the most accurate results. Filtering the features, the accuracy decreased slightly due to less-expensive computational costs. The performance of different classifiers was evaluated on the test set, consisting of 45 s normal breathing, 25 s rapid breath, and five forced coughs. The same feature extraction and feature types were applied on the test set as on the training set.

Mobile APP design

A customized android cellphone APP for data display, storage, and sharing was designed using MIT AI2 Companion. The respiratory patterns and respiration rate were acquired with the assistance of our machine learning algorithms. Then these data were transmitted to the cellphone APP and displayed in the front-end. The body temperature and the testing results were inputted by the users during the self-screening process.

Highlights.

Discover giant magnetoelasticity in soft matter

Establish a wavy chain model based on the magnetic dipole-dipole interaction

Invent essentially new textile MEGs for biomechanical-to-electrical energy conversion

Textile MEGs feature high-output current, low internal impedance, and waterproofness

Progress and potential.

Magnetoelasticity is usually observed in rigid bulky alloys. Our study discovered giant magnetoelasticity in soft matter, which demonstrated a 5-fold enhancement of magnetomechanical coupling factor compared to that of traditional rigid metal-based counterparts without the need for an externally applied magnetic field. A wavy chain analytical model based on the magnetic dipole-dipole interaction and demagnetizing field was established, well consistent with the experimental observation. Then we explored the potentials of this discovery in electronic textiles by coupling it with magnetic induction to invent a textile magnetoelastic generator (MEG) for biomechanical energy conversion, featuring an intrinsic waterproof property, an ultralow internal impedance, and a high current output density. Meanwhile, the textile MEG can work as a self-powered sensor for continuous respiratory monitoring with heavy perspiration without any encapsulation. Assisted by machine learning, respiration abnormalities can be continuously and practically detected. The discovery of giant magnetoelasticity in a soft-matter system is expected to pave new ways to develop electronic textiles for personalized healthcare.