Inferring gene regulation from stochastic transcriptional variation across single cells at steady state

Significance

Deciphering gene regulatory networks can help elucidate the molecular underpinnings that define cellular identity and disease processes. Current approaches to discover regulation compare different cell types or employ cellular perturbations. We show that, with enough data, it should be possible to identify regulatory relationships within a cell type without need for perturbation, by leveraging the intrinsic stochasticity in transcriptional bursting across individual cells at steady-state. Importantly, time-shifted correlations in RNA expression make it possible to distinguish covariation due to regulatory relationships within a cell state from covariation due to undetected cell states. Here, we present a theoretical framework for this approach and discuss future experimental design.

Abstract

Regulatory relationships between transcription factors (TFs) and their target genes lie at the heart of cellular identity and function; however, uncovering these relationships is often labor-intensive and requires perturbations. Here, we propose a principled framework to systematically infer gene regulation for all TFs simultaneously in cells at steady state by leveraging the intrinsic variation in the transcriptional abundance across single cells. Through modeling and simulations, we characterize how transcriptional bursts of a TF gene are propagated to its target genes, including the expected ranges of time delay and magnitude of maximum covariation. We distinguish these temporal trends from the time-invariant covariation arising from cell states, and we delineate the experimental and technical requirements for leveraging these small but meaningful cofluctuations in the presence of measurement noise. While current technology does not yet allow adequate power for definitively detecting regulatory relationships for all TFs simultaneously in cells at steady state, we investigate a small-scale dataset to inform future experimental design. This study supports the potential value of mapping regulatory connections through stochastic variation, and it motivates further technological development to achieve its full potential.

Systematically identifying gene regulatory networks in any specific cellular context has been a long-standing quest that remains unfulfilled. Existing approaches to link transcription factors (TFs) to their regulatory targets based on gene expression data include tracking gene coexpression across different cell states (1–4), perturbing TFs experimentally and measuring transcriptomic changes (5–8), and studying coordinated changes in genes’ expression over dynamic biological processes (9–11). Single-cell RNA sequencing (scRNA-seq) technologies have made it possible to apply these approaches to study gene expression at unprecedented resolution (11–24).

However, systematic interrogation of human gene–gene regulatory interactions in steady-state cellular systems has been limited by the need for targeted experimental perturbation of specific genes (14, 25–27). The ability to learn gene regulation from unperturbed cells would provide a scalable approach applicable to any cell type and state, providing novel insights into the transcriptional programs that shape steady-state cellular identity.

Because all genes are transcribed in stochastic bursts (28–35), even isogenic cells in the same cellular state have substantial variability in gene expression across time (36–41). Cells thus carry out their own natural “perturbation” experiments, as the accumulation or depletion of recent bursts leads to varied messenger RNA (mRNA) abundances for each gene. These natural perturbations have the potential to help reveal gene regulation (42–45). Specifically, a transient increase in the transcription of a TF in a given cell generates a subsequent increase in the abundance of the TF protein, which in turn leads to an increase in mRNA for the target genes of the TF (provided the TF protein is localized to the nucleus).

In this paper, we demonstrate how stochastic fluctuations across individual cells in a single cell state can give rise to time-shifted covariation between the level of TFs and their target genes. Using this information, we lay out a theory for inferring regulatory relationships between TFs and target genes in cells at steady state, based on the time-shifted covariation between TF mRNA levels and target gene mRNA levels; the approach can be used to study simultaneously all TFs and potential targets.

Specifically, we use published ranges for gene-specific parameters to characterize the shape of the time-shifted correlation curve resulting from regulatory relationships. As we discuss, it is important to examine time-shifted correlations rather than just simultaneous correlations between the level of gene pairs at the same time point—because the latter can arise from the undetected presence of multiple cell states, whereas the former should not. Finally, we explore practical considerations in designing future experiments to detect gene regulation by measuring time-shifted correlations, including the sample sizes and improvements in mRNA detection efficiency that will be required.

Results

We first lay out the conceptual framework for the paper. Consider a transcription factor gene, TF, and a possible target gene, Target. Because gene expression occurs in bursts, the number of transcripts of TF and Target will fluctuate over time. (Throughout, Gene^(RNA)_T and Gene^(ΔRNA)_T will denote the amount of a gene’s total and nascent RNA at time t = T. Nascent RNA refers to unspliced, pre-mRNA.)

The key insight is that if TF regulates Target in cells of a given cell state, then the time-shifted correlation with either nascent or total Target RNA—that is, C_T = Corr(TF^(RNA)₀, Target^RNA_T) and C_T^Δ = Corr(TF^(RNA)₀, Target^ΔRNA_T)—is expected to increase and then decrease, as T increases from 0 (Fig. 1 A and B). The reason is simple: Higher levels of TF^(RNA) at t = 0 give rise over time to higher levels of TF^(Protein) and then to higher levels of Target^(ΔRNA) and Target^(RNA), resulting in higher maximum time-shifted correlations, until the relationship eventually breaks down as the initial TF^(RNA) degrades.

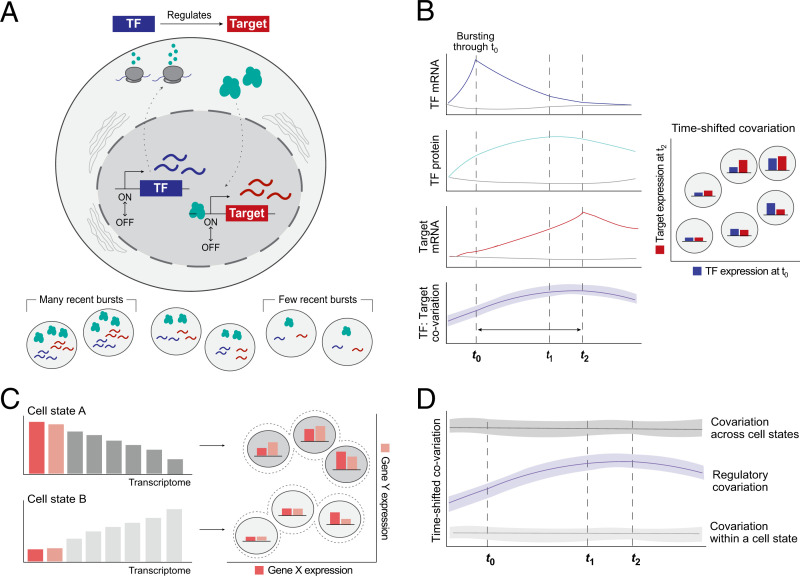
Fig. 1.

Overview of the conceptual framework for inferring TF:Target gene regulation from single cells at steady state. (A) Transcriptional bursting leads to stochastic variation in the mRNA abundance of each gene, even within a population of isogenic cells at steady state. We invoke stochastic transcriptional bursting as a source of TF mRNA heterogeneity across steady-state cell populations. If a TF directly regulates a target gene, we hypothesize that their abundances will be correlated. (B) Idealized representation of the hypothesized time-shifted correlation between a TF and its target gene’s mRNA abundances in the presence of regulation. Colored lines indicate the average behavior of cells that had at least one burst of the TF gene; gray lines represent those that did not have a burst. The time delay reflects the time required for TF mRNA translation into protein, translocation, and target site search in the nucleus. From left to right, dotted lines reflect the time of maximal TF mRNA (t₀), TF protein (t₁), or target mRNA abundance (t₂), respectively. (C) Subpopulations of cells (i.e., cell states, such as cells in different stages of the cell cycle) will also give rise to covariation—in this example, due to different baseline mRNA counts for genes in each state. Thus, correlation does not always imply regulation. (D) We can theoretically distinguish between regulation- and state-based covariation by looking at the shape over time: State-based covariation will tend to be more stable.

The temporal pattern is important because it allows one to distinguish correlation arising due to gene regulation from correlation arising from an important alternative possibility. Specifically, correlated gene expression across cells can also arise if the cells are an undetected mixture of different cell types. However, such correlations will not show the expected pattern of increase and decrease in time-shifted correlation C_T (Fig. 1 C and D).

We now turn to a more quantitative treatment, to study the properties of the time-shifted correlation and determine the feasibility of detecting it experimentally.

Transcriptional Bursting in Cells at Steady State Gives Rise to Temporal Covariation between TFs and Their Target Genes.

We built a quantitative model that describes the processes linking the key quantities for a regulatory gene pair involving a TF and a target gene. The model builds on the traditional model of transcriptional bursting, by extending it to include translation of the TF mRNA and gene regulation of a target gene. The key quantities we track are total TF mRNA abundance [TF^(RNA)], measured in number of transcripts; total TF protein abundance [TF^(P)], measured in thousands of molecules; and target-gene mRNA abundance, assessed as either total RNA [Target^(RNA)] or nascent RNA [Target^(ΔRNA)] (Fig. 2A and Materials and Methods). For each quantity, we can derive from our model the average abundance level, the distribution of abundance levels across cells, and the cross-correlation and auto-correlation between these quantities across cells and time. These values each depend on gene-specific kinetic parameters, which we describe below.

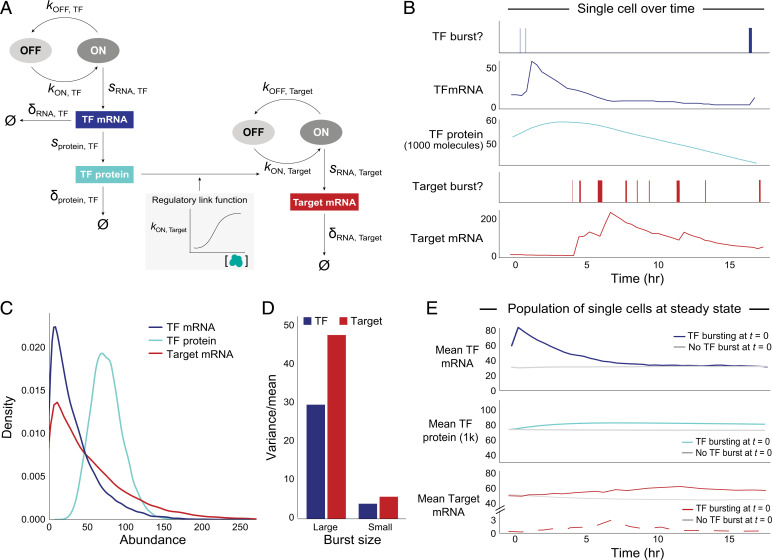
Fig. 2.

Transcriptional bursting yields intrinsic variation for each gene across cells at steady state. (A) Two-state model of transcriptional bursting and regulation for one Regulator–Target pair. Variables: k_ON (burst frequency), k_OFF (1/burst duration), s_RNA (transcription = burst size*k_OFF), s_protein (translation), δ (decay), Ø (no molecules left). Blue: TF, red: Target. (B) Simulation of TF^(RNA), TF^(P), and Target^(RNA) bursting events and abundance for one cell in the presence of direct regulation between a pair of genes. (C) Abundance distributions of TF^(RNA) (μ: 29, CV: 0.84), TF^(P) in thousands (μ: 61, CV: 0.31), and Target^(RNA) (μ: 50, CV: 0.93), for median values of burst parameters, across 20,000 simulated cells. (D) Overdispersion structure (variance/mean) of total mRNA for TF and Target for different burst sizes (large TF: 32 transcripts/burst, large Target: 40 transcripts/burst; small TF: 3, small Target: 4). (E) Mean TF^(RNA) (Top), TF^(P) (Middle), and Target^(RNA) (Bottom) abundance over time, across cells that did have a burst of the TF gene (colored, n = 715) versus those that did not have a burst (gray, n = 715 randomly subsampled cells with no burst) at t = 0 (20,000 total cells). Solid red line indicates TF^(RNA) and dashed red line indicates TF^(ΔRNA). Curves are based on data points at 30 min intervals. (TF mRNA at 30 min shows a sharp peak due to discrete sampling; the actual peak is smooth.)

Transcriptional bursting can be abstracted into a two-state model, whereby transcription of a gene stochastically switches between transcriptional “on” and “off” states (46–50). A gene’s burst frequency (k_on), burst size, and mRNA decay rate determine its cellular mRNA abundance, which—along with the translation and protein decay rates—determines the corresponding protein abundance over time (SI Appendix, Eqs. 1–3 and 5). Following transcription from a burst, each nascent pre-mRNA transcript encoding a TF is spliced into a mature transcript on the order of <10 min (51–53), after which it is translocated into the cytoplasm and translated, also on the order of minutes (54).

While modeling the processes of transcription and translation is straightforward, modeling the impact of changes in TF protein levels on the expression of target genes is more complicated. TF protein levels are generally considered to affect target genes by modulating their bursting frequency (although this is not strictly true in all cases; see refs. 55–64). We modeled the regulation of a target gene by a TF by adjusting the target gene’s rate of burst initiation in a manner dependent on the concentration of the TF protein (SI Appendix, Eq. 7). Here, the derivative of the response function [i.e., the instantaneous ΔTarget^(kon)/ΔTF^(P)] describes the proportional change in bursting frequency relative to the change in TF^(P). We chose a Hill function to reflect the effect of changes in TF^(P) on Target^(kon), although the specific shape of the response curve can also be captured by other models (e.g., Michaelis–Menten).

We note that small fluctuations in TF^(P) levels will only affect target gene transcription when TF^(P) is neither extremely low nor near saturating concentrations. For instance, if a given target gene’s promoter is already occupied with many molecules of a particular TF protein, then a small increase in that protein will likely have minimal to no effect on the target gene’s transcription. In this work, we focus on regulatory relationships that are “meaningful” within a cell type, by which we mean that TF^(P) is near the steep part of the response curve. Since the coefficient of variation for TF^(P) across a population of cells at steady state is relatively small (∼0.3; Fig. 2C), the TF protein abundance for any given cell is not likely to stray too far from the mean. In these cases, the relationship between TF^(P) levels to Target^(kon) is effectively linear, with a slope defined by the Hill coefficient n (SI Appendix, Fig. S2C). (The slope of the Hill coefficient roughly captures the degree of cooperativity in the effect of TF molecules on gene regulation.)

We simulated a TF regulating a target gene in a steady-state population of 20,000 cells, continuously tracking TF^(RNA), TF^(P), Target^(RNA), and Target^(ΔRNA) for 20 h in each cell (Materials and Methods).

For parameters related to transcription and translation, we selected values based on published data in human and mouse cells (40, 55, 65–70) as reported in Table 1.

Table 1.

Range of intrinsic parameter values for TFs and non-TF genes

Parameter	Interquartile ranges	Refs.
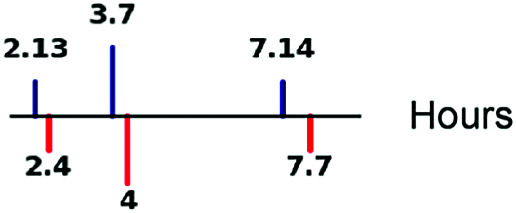
Time between bursts (1/kON)		67, 70
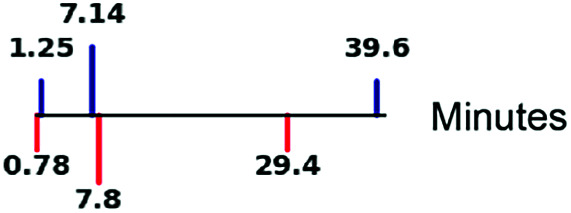
Burst duration (1/kOFF)		67, 70
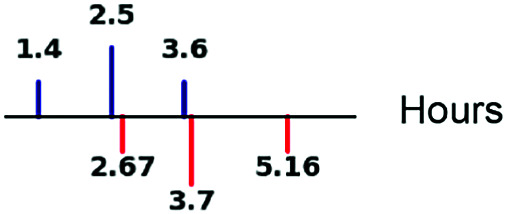
mRNA half-life		65, 69, 81
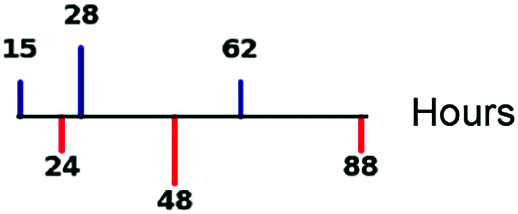
Protein half-life		69
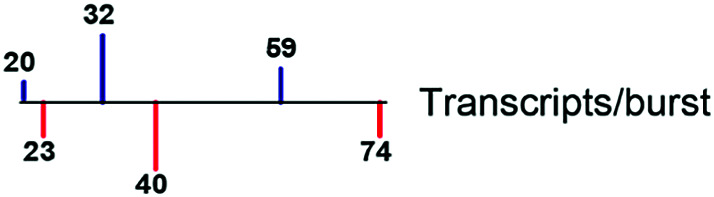
Burst size		55, 67, 74
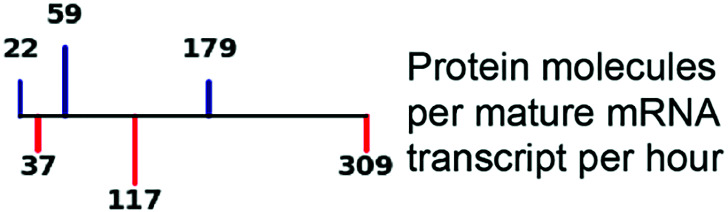
Translation rate		65, 69

Derived from literature, where parameters were estimated and inferred from published experimental data. Lines represent first quartile, median, and third quartile values for TFs (blue) and non-TFs (red), respectively. Burst sizes used in simulations were based on previously published smFISH-based copy numbers, although we note that scRNA-seq data-based estimates are lower due to transcript capture inefficiencies (88–90). k_on = burst frequency; k_off = number of burst ends per hour.

For most gene-specific parameters, the estimates are consistent across studies. However, certain studies (e.g., refs. 71 and 72) suggest that mRNA half-lives may be longer than other estimates by two- to fourfold (65, 70). To be conservative, we used the shorter estimates of half-life in our simulations. We return to this point below, where we discuss the implications of longer half-lives for inferring gene regulation.

For the Hill coefficient of the regulatory response function (connecting changes in TF protein levels to target gene transcription), the value can range from zero (no regulatory effect) to a large positive number (with higher coefficients corresponding to a stronger effect). In our model, we chose a modest value of 2, representing the situation where doubling TF^(P) results in a fourfold increase in the target gene’s burst frequency [Target^(kon)], in bursts per hour (SI Appendix, Fig. S2C). With these parameters, the distributions of TF^(RNA), TF^(P), and Target^(RNA) across cells are consistent with published, experimental measurements (SI Appendix, Fig. S1 A and B) (69, 73, 74).

While our simulations assume a single copy of the TF and target genes, we confirmed that simulations with two alleles at both genes, with each allele having half the bursting rate, produce essentially equivalent results (as expected, because bursting events are infrequent and thus the two alleles are rarely bursting at the same time) (SI Appendix, Fig. S2B). We also confirmed that our simulations produce equivalent results to using Gillespie stochastic simulations for our model (SI Appendix, Fig. S2B) (75).

Applying our model to follow a collection of single cells over time revealed the compounded effects of bursting and decay on each gene’s mRNA abundance fluctuations (Fig. 2B). While much of the variation in TF^(RNA) is buffered at the protein level due to longer protein half-lives, there is an approximately threefold difference in mean TF protein abundance between the top and bottom deciles of TF^(P) (Fig. 2C), which is robust to changes in gene-specific parameter values over relevant ranges (SI Appendix, Fig. S1C). Importantly, the production of mRNA molecules in rapid succession due to bursts results in the overdispersion (variance/mean >1) of mRNA expression, with the amount of mRNA overdispersion directly proportional to the gene’s burst size (Fig. 2D and SI Appendix, Eq. 4).

If we partition cells according to whether or not the TF gene was bursting at time t = 0, we find that cells that were bursting at t = 0 have substantially higher levels of TF^(RNA), TF^(P), and Target^(RNA) over the subsequent hours than cells that were not bursting at t = 0; the difference eventually disappears as the levels converge back to the population mean (Fig. 2E). [As seen in the figure, we note that cells bursting at t = 0 already have higher levels of TF^(RNA) at t = 0, because the burst will have typically begun before t = 0.] The temporal dynamics for each of the quantities is notably different:

• 1)TF^(RNA) rises steeply for nearly  30 minutes, by which time the burst occurring at t = 0 will have ended and mRNA decay will have taken over.
• 2)TF^(P) rises more gradually as the TF mRNA is steadily translated. In cells that were bursting at t = 0, TF^(P) reaches a maximum increase of ∼12% increase at ∼6 h. Elevated levels of TF^(P) persist for many hours, because TF^(P) decays much more slowly than TF^(RNA) (median TF protein half-life = 28 h).
• 3)Target^(ΔRNA) and Target^(RNA) both rise at similar rates; however Target^(ΔRNA) peaks and drops off at ∼7 h, whereas Target^(RNA) continues rising gradually for another > 5 h (approximately two mRNA half-lives). This difference reflects the short lifespan of unspliced transcripts. Target^(ΔRNA) thus provides a sensitive measure of the instantaneous regulatory effect of TF^(P), while Target^(RNA) reflects the accumulation of mRNA over time.

Propagation of Stochastic Variation from TF to Target Genes.

We next analyzed in detail how the variance in a TF’s mRNA level is propagated to a target gene’s mRNA level through translation and then the TF protein’s modulation of the target gene’s transcriptional bursting (Fig. 3A).

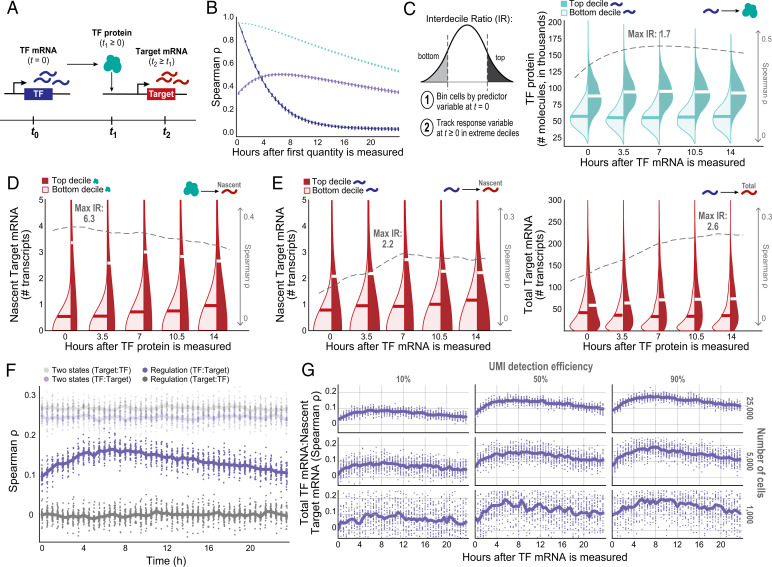
Fig. 3.

Information flow between a TF and its target gene is time-dependent. (A) Schematic of the multistep inference question. (B) TF^(RNA) and TF^(P) Spearman’s ρ autocorrelations and correlations between TF^(RNA) and TF^(P) over time, across 25 simulation runs (each included as its own dot). (C–E) Kernel density estimates comparing the extremes of distributions across cells at t ≥ 0, binned by the predictor molecule abundance at t = 0. Dashed gray line indicates Spearman’s ρ, and “max IR” indicates maximum D10:D1 IR between top- and bottom-binned cells (alternative hypothesis: top decile of the dependent variable is greater than the bottom decile) value at each time point, with the highest magnitude effect listed. (C) TF^(RNA)₀:TF^(P)_T correlation and D10:D1 IR of TF^(P) distribution extremes at t ≥ 0 for cells binned by TF^(RNA) at t = 0. (D) TF^(P)₀:Target^(kon)_T correlation and D10:D1 IR of adjusted Target^(ΔRNA) distribution extremes for cells binned by TF^(P) at t = 0, under the Hill function model of interaction. (E) Relying on mRNA only—C_T^Δ and TF^(RNA)-binned Target^(ΔRNA) D10:D1 IR (Left) and C_T and Target^(RNA) D10:D1 IR (Right)—to infer regulation over time. (F) Correlation between a TF and its putative Target could be a result of cell-state-based structure; if so, the time-shifted correlation would have a stable magnitude over time. (G) Effect of down-sampling the number of cells and/or UMI detection efficiency on estimated TF:Target covariation trends over time (focusing on C_T^Δ). Estimates get both noisier and lower in magnitude due to these two technical considerations.

The amount of TF^(P) in a cell produced from TF^(RNA) present at t = 0 can be expressed by a system of ordinary differential equations governed by translation and degradation rates (SI Appendix, Eq. 5). TF^(P) peaks after a time delay, because protein molecules continue to accumulate until the rate of new TF proteins produced by the remaining mRNA that was present at t = 0 is offset by the slow decay rate of the protein. For the parameters in our model, the TF^(RNA):TF^(P) correlation is initially ∼0.35 at t = 0 [consistent with experimental measurements in single cells (76)] and subsequently rises to a peak of 0.5 at around t = 6 h (SI Appendix, Fig. S2A), before gradually falling again over the subsequent 10+ h, based on the TF protein’s half-life (Fig. 3B).

If we compare cells that were in the top decile (D10) and bottom decline (D1) of TF^(RNA) at t = 0, those that were in the top decile have nearly double the level of TF^(P) at the time of maximum correlation at ∼6 h (D10:D1 interdecile ratio [IR] = 1.7; Fig. 3C), showing how variance is propagated from mRNA to protein.

In addition, cells with high levels of TF^(P) have substantially higher levels of nascent target-gene mRNA (Target^(ΔRNA)), which closely reflects the instantaneous Target^(kon). For our model (regulatory relationship with Hill coefficient = 2), comparison of cells in the top versus bottom decile of TF^(P) (whose IR = 2.8) reveals that the former have approximately sixfold higher levels of Target^(ΔRNA) [maximum Spearman’s ρ = 0.32 between TF^(P) and Target^(ΔRNA); Fig. 3D].

In principle, to compare TF and Target RNA levels, we can look at either C_T or C_T^Δ; the former reaches higher magnitudes (e.g., a peak of 0.23 versus 0.18) but changes more gradually, while the latter peaks earlier and falls more sharply. We measured both of these time-shifted correlations for 0 ≤ T ≤ 15 and focused on C_T^Δ for our analyses. The peak C_T^Δ occurs at around 7 h, not long after the peak TF^(RNA) correlation with TF^(P) (Fig. 3E, Left). The same is true for the D10:D1 IR of Target^(ΔRNA) (SI Appendix, Fig. S2D). This makes sense, because the level of nascent transcripts reflects current transcription rates and thus is closely related to TF protein levels. In contrast, C_T continues to rise for several more hours (Fig. 3E, Right and SI Appendix, Fig. S2B), because transcription continues to occur and total mRNA continues to accumulate.

Sensitivity of Time-Shifted Correlations to Gene-Intrinsic Parameters.

We explored the sensitivity of the magnitude and timing of peak correlations to the choice of parameters in our model, by replacing them with the 25th and 75th percentile values (Table 1).

Broadly, the time-shifted correlation C_T^Δ is robust to variation in most variables, although the magnitude is more sensitive to changes in TF protein half-life and TF burst frequency (SI Appendix, Fig. S2F).

With respect to the time of maximum correlation, increasing the half-life of TF mRNA or TF protein from 25th to 75th percentile delays the time from 5 to 9 h (as expected from SI Appendix, Eq. 6), whereas increasing Target^(kon) shortens the time effect from 12 to 4 h (SI Appendix, Fig. S2 D and F and Table S1).

With respect to the magnitude of the correlation C_T^Δ, increasing the TF mRNA half-life increases TF^(1/koff) (burst duration), which in turn increases the covariation by up to 25%, whereas increasing the TF protein half-life or TF^(kon) decreases the magnitude by up to 60% (SI Appendix, Fig. S2 E and F and Table S1).

These results suggest that experiments to detect regulatory covariation should sample time points across the range of 0 to >12 h in order to capture the start, peak, and decay of the time-shifted correlation curves for most genes.

We also explored the sensitivity of the results to changing the Hill coefficient (SI Appendix, Fig. S2C). Whereas the Hill coefficient of 2 used in our model results in a maximum Spearman’s ρ for TF^(RNA):Target^(ΔRNA) of ∼0.2, larger values increase the magnitude of the covariation (e.g., 0.33 with a Hill coefficient of 4) while lower values decrease the magnitude of the covariation (0.13 with a Hill coefficient of 1, corresponding to no cooperativity).

Distinguishing Cell State-Based Structure from Regulatory Covariation.

While we have focused on how TF:Target regulation gives rise to a characteristic time-shifted correlation C_T^Δ, it should be noted that such regulation also gives rise to simultaneous correlations—that is, when the quantities are measured at the same time point. Specifically. TF^(RNA) and TF^(P), as well as TF^(RNA) and Target^{(RNA or ΔRNA)}, show positive correlation even when the quantities are measured at t = 0 (Fig. 3 B, C, and E; Spearman’s ρ = 0.35 and 0.1, respectively). This is due to the fact that TF mRNA resulting from earlier bursts of transcription persists long enough to overlap target gene expression resulting from those bursts.

Given that TF:Target regulation results in simultaneous correlation in between TF and Target mRNA levels at any given time t, one might ask why bother looking at time-shifted correlation. After all, simultaneous correlation is easier to study, as it can be measured in a simple scRNA-seq experiment. The reason is that, while simultaneous correlation can arise as a consequence of gene regulation, it can also arise from the undetected presence of multiple stable cell states. In drawing inferences about gene regulation, it is important to rule out the latter possibility.

To illustrate the issue, we compared the time-shifted correlation C_T that arises from gene regulation versus a mixture of two stable cell “states” (Materials and Methods and SI Appendix, Fig. S3A). Moreover, we examined both the standard “forward” time-shifted correlation studied above C_T^Δ = Corr(TF_{t = 0}^(RNA):Target_{t ≥ 0}^(ΔRNA)) and, as a negative control, a “reverse” time-shifted correlation Corr(Target^(ΔRNA)₀:TF^(RNA)_T), which assesses whether the Target regulates the transcription of the TF gene (SI Appendix, Fig. S3B).

As expected, the mixture of two stable cell states gives rise to a time-shifted correlation that is roughly constant over time and shows similar results in the forward and reverse directions—in sharp contrast to the results seen for time-shifted correlation arising from gene regulation (Fig. 3F and SI Appendix, Fig. S3B).

Notably, it is easier to distinguish the time-shifted correlation arising from gene regulation from the time-shifted correlation arising from a mixture of cell states when focusing on C_T^Δ rather than C_T. This is because C_T^Δ shows an earlier, sharper peak that is more readily distinguished from the stability of state-based correlations. In contrast, C_T changes more gradually, since the preexisting target-gene mRNA dilutes the acute regulatory effect of TF^(P) at t = 0.

Finally, we note that “stable cell states,” as used above, refers to states that persist for the period over which time-shifted correlations are measured—e.g., at least one cell division. [Stable states thus include both permanent states and meso-stable states (77, 78)]. States that persist for much shorter periods of a few hours are best regarded as “transient states”; they might arise from rapid processes, such as cell cycle progression or temporary activation of neuronal or immune cells. To distinguish transient states from regulation, it will be useful to know gene expression patterns associated with these rapid processes (as are available for cell cycle progression).

From Theory to Experimental Design.

The results above show it should be possible to systematically learn gene regulatory connections from stochastic variation in steady-state cells, provided one can measure transcriptome-wide mRNA levels at pairs of time points in individual cells with sufficient sensitivity and power. We now turn to how one might implement the theory in practice.

Several high-throughput technologies exist for using pulse–chase labeling to distinguish mRNAs synthesized at different time points (68, 71, 72, 79–81). One approach involves 1) pulse-labeling cells with 4-thiouridine (4sU, a uridine analog that incorporates into RNA) to mark transcripts synthesized during an initial interval (t₁, t₁ + δ), 2) chasing the label with uridine, and 3) harvesting and profiling the cells at a later time t₃ using single-cell RNA-seq approaches. By performing chemical conversion of 4sU into cytosine analogs before performing scRNA-seq, one can use the presence of U-to-C substitutions to identify transcripts synthesized during (t₁, t₁ + δ). This approach can be used to study both total mRNA and nascent RNA, via intronic sequences.

Suppose we wish to detect an increase δ in the time-shifted correlation—for example, a doubling from t = 0 to t = 7 (Fig. 3G). In this case, δ = C₇^Δ − C₀^Δ. The power to detect this increase depends on the number of cells studied and the sensitivity to detect transcripts.

First, consider the case of infinitely many cells and perfect transcript detection α = 1 (that is, 100% sensitivity, such that every transcript is represented by a unique molecular identifier [UMI]). There will be no variance in independent correlation estimates. Thus, δ can be estimated perfectly: The coefficient of variation (CV_δ, defined as SD divided by the mean of δ) is zero.

Next, consider the case of a finite number n of cells with perfect transcript detection α = 1. In this case, one must overcome only biological variation across cells. Suppose the true mean abundances are E(X) = 29 and E(Y) = 50 transcripts (Fig. 2C). Simulations show that the time-shifted correlation doubles, from C₀^Δ = 0.09 to C₇^Δ = 0.18 (SI Appendix, Fig. S3C), with δ = 0.09 and CV_δ ≈ 0.36/√(n/1,000), corresponding to CV_δ ≈ 0.17 for n = 2,500 and 0.04 for n = 50,000 (SI Appendix, Fig. S3D). To estimate δ with an SD equal to 25% of the mean (a reasonable level of precision) requires roughly 5,000 cells (SI Appendix, Fig. S3E).

Now, consider the case of a finite number of cells with incomplete transcript detection α < 1 (Fig. 3G). In this case, one must overcome both biological variation and measurement noise. For example, current scRNA-seq methods detect only a small fraction (∼10 to 15%) of the number of mRNA transcripts present in each cell (82), owing to incomplete capture of transcripts(73, 83) and incomplete sequencing of captured transcripts (83–91). If we can detect only 10% of transcripts in the preceding example, we have E(X) = 2.9 and E(Y) = 5.0. Simulations show that the time-shifted correlations are now smaller (roughly, C₀^Δ = 0.04 and C₇^Δ = 0.08) (SI Appendix, Fig. S3C) and the CV_δ is larger (by 2.24-fold) (SI Appendix, Fig. S3F). To estimate δ with CV_δ = 0.25 requires many more cells—roughly 50,000 cells (SI Appendix, Fig. S3G).

Finally, we noted above that some papers have suggested mRNA half-lives may be two- to fourfold longer than previously reported values, which were used in our simulations. Increasing the half-life (while maintaining the mean level) of both the TF and Target mRNA by two- or fourfold increases the value and time of the maximum time-shifted correlation C_T, but it has minimal effect on δ or on the number of cells required (SI Appendix, Fig. S3H).

In summary, to reliably detect relevant increases in time-shifted correlation, it will be necessary to improve current methods for time-resolved labeling by increasing 1) transcript detection efficiency, 2) the number of cells that it is feasible to study, or 3) both. For example, a detection efficiency of 50% would allow the use of 17,500 cells per time point for TF and Target mRNA half-lives of 2.5 and 3.6 h, respectively. Such improvements seem achievable but will require focused efforts.

Leveraging Simultaneous Correlations in a Single-Cell Dataset to Enrich for Gene Regulation.

We noted earlier that regulatory relationships give rise to two types of correlation between TF^(RNA) and Target^(RNA): 1) a positive correlation C₀ between the quantities when measured simultaneously [because TF^(RNA) from past bursts persists long enough in cells to overlap Target^(RNA) due to those bursts] and 2) an increase δ in the time-shifted correlation after an appropriate time interval. Simultaneous correlation has the disadvantage that it could also arise from undetected cell types, whereas the time-shifted correlation approach controls for this possibility.

Because the time-shifted correlation approach is not yet feasible with current labeling methods, we undertook an experiment to examine genes that show simultaneous correlation with a TF, to look for other evidence that some of the correlations may be due to regulation. Using a droplet-based method, scNT-sEq. (71), we generated a temporally resolved scRNA-seq dataset with K562 cells labeled with 4sU for a 24-h pulse phase, followed by a 10-h chase phase with uridine, during which we sampled cells every 2 h (Fig. 4A, SI Appendix, Fig. S4 A–D, and Materials and Methods). We collected ∼1,000 to 4,000 cells at each of six time points (total of 13,679 cells) (SI Appendix, Fig. S4B). We confirmed that burst sizes (SI Appendix, Fig. S4E) and mRNA half-lives (SI Appendix, Fig. S4F) estimated from the K562 data are consistent with recent, published estimates from scRNA-seq data (55, 71, 72, 80), including the longer estimates of mRNA half-lives.

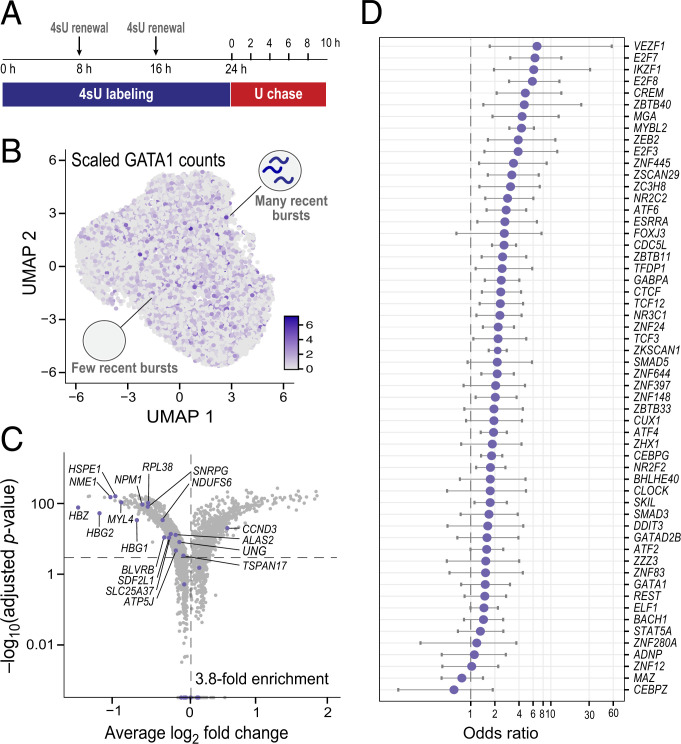
Fig. 4.

Enrichment of gene regulatory signal from simultaneous correlations in scRNA-seq data of K562 cells at steady state. (A) Schematic of the experimental design of a pulse–chase metabolic labeling experiment to capture two temporally resolved snapshots of RNA abundance in the same single cells. U, uridine. (B) UMAP of 13,679 unperturbed K562 single cells across six time points (∼1,000 to 4,000 cells per time point), colored by GATA1 scaled counts. (C) Differentially expressed genes upon GATA1 knockdown, inferred from an orthogonal GATA1 knockdown Perturb-seq experiment in K562 cells (92). The horizontal dotted line represents a Bonferroni-adjusted P value threshold of 0.001, and the vertical one a log₂ fold change of 0. Purple dots denote the set of correlated genes with P < 0.05 at all time points, which have a 3.8-fold enrichment. (D) Enrichment of predicted TF binding from simultaneous Corr(TF^(RNA)_T:non-TF^(RNA)_T) correlations for ChIP-seq binding signal across 56 TFs with ENCODE ChIP-seq data that have at least 15 significantly correlated genes from the K562 data.

We started by considering GATA1, a well-known erythroid regulator, in these steady-state cells (Fig. 4B) and looking for genes whose mRNA levels showed significant correlation with GATA1 mRNA levels across cells (Spearman’s ρ P < 0.05; Materials and Methods). Specifically, we analyzed each time point separately and looked only at those genes that showed significant correlation with GATA1 at all six time points. A total of 36 genes met these criteria. Based on two lines of evidence, many of the correlations seem likely to reflect regulation by GATA1: 1) The genes are enriched (3.8-fold) for genes differentially expressed (92) in an independent GATA1 Perturb-seq knockdown experiment (Fig. 4C, SI Appendix, Fig. S4G¸and Materials and Methods) and 2) 22 of the genes are well-known GATA1 targets (see refs. 93–97 for a few prominent examples), of which 19 are significantly down-regulated and 3 significantly up-regulated upon GATA1 knockdown (SI Appendix, Fig. S4H).

We next calculated mRNA correlations for 342 TFs, finding a total of 17,152 TF:non-TF pairs that showed significant correlations at all six time points (mean number of significant links per TF = 50). We focused on 56 TFs with at least 15 significantly correlated genes whose genome-wide binding sites had been measured in K562 cells using chromatin immunoprecipitation and sequencing (ChIP-seq) in the ENCODE project (98). For each such TF, we identified putative binding sites based on stringent ChIP-seq peaks; we then assigned these sites to a specific gene based on the Activity-By-Contact model (ref. 99 and Materials and Methods). We found that 53/56 (95%) of the TFs were enriched for binding in enhancers and promoters assigned to the significantly correlated genes relative to all other genes expressed in K562 cells (Fig. 4D).

These results suggest that many of the genes that show simultaneous correlations are likely to be regulatory targets, although time-resolved experiments will be necessary to rule out alternative possibilities. If confirmed, this framework would provide a method for identifying regulatory connections in steady-state cells.

Discussion

The ability to infer gene regulation from observations of cells at steady state, without experimental perturbations, would vastly expand the study of regulatory networks in any cell type—providing insight into previously inaccessible realms of biology. Here, we introduce a framework to do so that uses the stochasticity of transcription to identify, in a principled way, all pairs of covarying TF and target genes in cells at steady state.

Our model, which is grounded in experimentally-derived parameters, captures a distinctive, time-shifted correlation curve between the abundance of the mRNA of a TF and nascent RNA of a target gene, which rises and then falls, at time scales reflecting the half-lives of the TF mRNA and TF protein. While we focus on C_T^Δ, we show that C_T (using total Target mRNA) results in a similar curve that increases and decreases more gradually. Importantly, these temporal relationships distinguish correlation due to gene regulation from correlation due to the undetected presence of multiple cell states.

Simulations indicate that identifying regulatory pairs should be feasible, in principle, for genes within typical gene-specific parameter ranges. The key challenge is that current experimental methods lack adequate power. For example, given current transcription detection efficiencies of ∼10%, detecting a two-fold increase in the time-shifted correlation would require ∼50,000 cells sampled per time point, which is not currently practical. We quantify the effects of improving transcript detection and sample sizes on the ability to infer gene regulation.

While simultaneous correlation does not allow us to conclusively distinguish between gene regulation and undetected cell states, we investigated simultaneous correlation between TFs and other genes in K562 cells at steady state. Independent results from Perturb-seq and ChIP-seq strongly suggest that many of the significantly correlated pairs represent true gene regulation. These results support the idea that pairwise correlations of gene mRNA abundances in cells at steady state can highlight potential instances of gene regulation, which can then be tested via patterns of time-shifted correlation.

A reviewer raised an interesting question that is worth addressing: Given that the variation in TF protein levels across cells should cause a positive correlation in bursting between the two alleles of a gene within a cell, why do studies often find no such allelic correlation (100, 101)? The answer is that there is indeed an allelic correlation, but its magnitude is tiny (typically, in the range of 0.003) given the variation of TF protein levels and the regulatory response in our model and thus would be difficult to detect.

Our results have various limitations. Estimates of kinetic parameters from scRNA-seq data remain imperfect. Our simulations assume a regulatory effect size (Hill coefficient) of 2; extremely weak regulatory relationships in a cell type [i.e., corresponding to very high or very low concentrations of TF^(P)] will not be detected but likely constitute less meaningful biology in the cell type. Our model does not currently include such factors as nuclear buffering of mRNA (102), TF autoregulation (76, 103, 104), and posttranslational modifications (105). Such factors could be incorporated, but we believe that the current model provides sufficient guidance for initial experimental designs.

While our work focuses on scRNA-seq–based transcriptomic correlations, technologies to profile complementary aspects of cells broaden the spectrum of informative approaches. Joint protein and mRNA measurements in single cells (106) can enable simultaneous measurement of TF^(P) with the Target^(ΔRNA). Additionally, pairing intronic gene abundances with spatial information (107) could leverage the spatial organization of the nascent transcriptome to yield more nuanced regulatory insights.

Given the critical roles of gene regulatory networks in cell types, we anticipate that the ideas presented here—coupled with improvements in high-throughput single-cell technologies—could provide powerful approaches for understanding biology.

Materials and Methods

Modeling Transcriptional Bursting and Gene Regulation.

The underlying stochastic model (SI Appendix, Eqs. 1 and 2) relies on the following transcriptional burst parameters, which we incorporated in a gene-specific manner: k_on, k_off, and burst size. Parameter values for each gene are based on TF- and non-TF ranges observed experimentally (Table 1). We used a Poisson decay model to enable discrete removal of mRNA transcripts and protein molecules (SI Appendix, Eq. 3). We also incorporated splicing and translation from the literature in a TF- and non-TF-specific manner (Table 1 and SI Appendix, Eqs. 4–6). Transcription rates were calculated as the burst size * k_off for each gene, and the rate of mRNA synthesis was the product of whether bursting was on for that gene and the transcription rate. As a check, we confirmed that the resulting mRNA and protein abundances match those estimated by deterministic ordinary differential equations (SI Appendix, Eq. 5). We modeled the TF^(P):Target^(kon) response function as a Hill function (SI Appendix, Eq. 7), with a Hill coefficient of 2.

Simulating Two-Gene Regulation in a Population of Cells at Steady State.

We wrote a simulation (Python v3.7) based on the two-state stochastic bursting model of gene transcription above and simulated two genes, one TF (regulator) and its target gene, across 20,000 cells. At each time step, we tracked TF^(ΔRNA), TF^(RNA), TF^(P), Target^(ΔRNA), Target^(RNA), and Target^(kon), to reflect the abundance changes between each time point. To assess regulatory signal, we calculated the following time-shifted RNA:RNA Spearman’s ρ correlations between 1) TF₀ and Target_T^Δ (C_T^Δ) and 2) TF₀ and Target_T (C_T), for each time point ranging from 0 h after the burn-in time to up to 2 d after. We have made our simulator code, including code to run the simulator with various parameters, and a notebook with the key analyses included in this paper, available on GitHub (https://github.com/agupta-landerlab/stochastic-regulation-code).

Gene-Specific Parameter Sensitivity Analyses.

We measured the sensitivity of C_T^Δ to gene-specific parameters, with each taking on either the 25th, 50th, or 75th percentile value, taken from the literature (Table 1). We ran 25 independent simulations of 20,000 cells each. In each run, we estimated the regulatory effect using the IR measure (ratio of the mean abundance of the top decile of cells to the mean of the bottom decile of cells) as well as C_T^Δ. We plugged in various values of mRNA and protein half-lives into SI Appendix, Eq. 6 to analytically model each parameter’s effect on protein production from a baseline mRNA abundance at t = 0.

Simulation of State-Based Covariation.

We simulated two cell “states” with no regulation between the TF and Target by removing the link function between TF^(P) and Target^(kon) and creating one “state” with low mRNA abundances and another with high abundances for each gene. Specifically, we varied the basal burst frequency for both the TF and Target to be either their first quartile or third quartile values, depending on the state. At each time point, we then combined the 10,000 cells from each state to yield a total of 20,000 cells that we tracked over time.

Assessing the Effect of Sequencing Inefficiencies and Sample Size.

To mimic the combined effects of capture inefficiencies and read depth in scRNA-seq (which we call “UMI detection efficiency”), we varied the sampling density of counts for each cell by introducing Poisson down-sampling, with the Poisson rate parameter equal to the number of counts*capture_efficiency. We chose the minimum between the raw and down-sampled counts to ensure that we never overestimated the number of counts per cell. To determine the effect of either changing the sample size (number of cells) or UMI detection efficiency on our ability to detect regulation-based covariation, we simulated 25 runs for each pair of capture efficiencies and sample sizes.

Pulse–Chase Experiment with 4sU.

K562 erythroleukemia cells (ATCC, CCL-243) were cultured in RMPI 1640 + l-glutamine, with 10% fetal bovine serum, 1% penicillin/streptomycin, and 1% l-glutamine 200 mM. For 4sU experiments, cells were plated in six-well plates ∼12 h before the start the experiment at a density of 5 × 10⁵ to 8 × 10⁵ cells per mL in 5 mL of fresh media. The 4sU (Sigma, T4509-25MG) in dimethyl sulfoxide (DMSO) was added to culture wells at a final concentration of 100 μM for 24 h, with renewal every 6 to 8 h. Between the pulse and chase phases, the cells were washed twice to remove any residual traces of 4sU. Subsequently, media with saturating concentrations of uridine (Sigma, U6381) at 10 mM was added. Cells were collected at 0, 2, 4, 6, 8, and 10 h. All the samples from each pulse–chase experiment were processed the same day to minimize batch effects. To control for genes induced by the long exposure to 4sU and to uridine, two control samples with chase only or DMSO only were included.

Conventional and Temporally Resolved Single-Cell RNA Sequencing.

The same datasets were used to analyze stochastic transcriptional variation and to calculate gene-specific burst sizes and mRNA half-lives. Our scNT-seq protocol was adapted from previously published methods (71–73), with modifications described in SI Appendix. Details on raw sequencing data demultiplexing, alignment, and doublet detection can also be found in SI Appendix. These scRNA-seq data were deposited to Gene Expression Omnibus (GEO), with accession number GSE202292. We have made code related to the analysis of these real data available on GitHub (https://github.com/agupta-landerlab/stochastic-regulation-code).

Gene-Specific Parameter Estimation from Real Data (mRNA Half-Lives and Burst Sizes).

To estimate gene-specific half-lives from real data, we fit the fraction of labeled counts for each gene at each time point to an exponential decay model (SI Appendix). Genes in which the fraction of labeled counts increased overtime were removed from the analysis. Genes with a fitting r² > 0.6 were plotted for the comparison with half-lives from ref. 71.

Identification of Significantly Correlated TF:non-TF Pairs Using Simultaneous Correlation Analysis.

To determine the list of TFs and non-TF genes, we used a recently published, curated list of human TFs (66). We filtered out cells with low UMI and genes expressed in few cells across time points. We scaled raw counts to account for differences in library size. Correlated genes for each TF were identified based on genes whose expression profiles had a Spearman’s rank correlation with the TF’s expression that fell in the right tail of the null distribution (defined by a permutation test to randomize ranks). We defined significantly correlated genes for each TF as the intersection of correlated genes with a P value <0.05 in all sampling time points.

Enrichment of GATA1 Correlated Genes in Perturb-seq Data.

We compared the genes significantly correlated with GATA1 with a recently published dataset that combined CRISPR interference on GATA1 with a single-cell RNA sequencing readout (92). A guide-cell barcode dictionary with the identity of the perturbation in each cell was obtained from GSE132080. We used a Wilcoxon rank sum test to identify differentially expressed genes between GATA1 KD and nonperturbed cells (Bonferroni-adjusted P < 0.001).

ChIP-seq Enrichment for 56 TFs.

We obtained K562 ChIP data from the ENCODE consortium (98). We linked enhancers to genes using the Activity-By-Contact model (99). For 56 TFs with at least 15 significantly correlated genes, we used Fisher’s exact test to check for enrichment of TF binding: An odds ratio >1 indicates that the ratio of correlated genes with the TF bound to the TF unbound is higher than for uncorrelated genes.

Data, Materials, and Software Availability

scRNA-seq data have been deposited in Gene Expression Omnibus (GSE202292) (108). Code related to the analysis of these data is available on GitHub (https://github.com/agupta-landerlab/stochastic-regulation-code).

Change History

August 25, 2022: An author name has been updated to correct a typographical error: Emanuelle I. Grody.