Summary:
Multi-modality or multi-construct data arise increasingly in functional neuroimaging studies to characterize brain activity under different cognitive states. Relying on those high-resolution imaging collections, it is of great interest to identify predictive imaging markers and inter-modality interactions with respect to behavior outcomes. Currently, most of the existing variable selection models do not consider predictive effects from interactions, and the desired higher-order terms can only be included in the predictive mechanism following a two-step procedure, suffering from potential mis-specification. In this paper, we propose a unified Bayesian prior model to simultaneously identify main effect features and inter-modality interactions within the same inference platform in the presence of high dimensional data. To accommodate the brain topological information and correlation between modalities, our prior is designed by compiling the intermediate selection status of sequential partitions in light of the data structure and brain anatomical architecture, so that we can improve posterior inference and enhance biological plausibility. Through extensive simulations, we show the superiority of our approach in main and interaction effects selection, and prediction under multi-modality data. Applying the method to the Adolescent Brain Cognitive Development (ABCD) study, we characterize the brain functional underpinnings with respect to general cognitive ability under different memory load conditions.
Keywords: Bayesian variable selection, Brain imaging, Cognitive development, Data integration, Interaction effects, Multi-modality
1. Introduction
Functional brain imaging techniques, which measure an aspect of brain activity, have yielded explosive growth in recent decades to characterize neural basis of disease or behavior. Among all, functional magnetic resonance imaging (fMRI) is the dominant whole brain mapping tool, and it gradually becomes common to collect multiple fMRI runs from different cognitive tasks on a single individual. Uncovering brain underpinnings associated with the clinical outcome under these multi-modal imaging measurements as well as understanding how inter-task interaction effects play a role in the mechanism will improve people’s understanding of the associated neurological etiology and guide potential intervention targets.
Our work is motivated by the recent Adolescent Brain Cognitive Development (ABCD) study with an overall goal to investigate brain development from childhood through adolescence (Casey et al., 2018). For each participant, multiple task-based fMRI scans were obtained to measure brain activity under a range of functional domains, and we are particularly interested in the memory-related n-back tasks (Casey et al., 2018). It has been lately shown that functional brain activation under each of the memory task conditions is associated with general cognitive ability (Sripada et al., 2020). Our aim here is to characterize brain functional underpinnings and identify active brain markers corresponding to general cognitive ability by integrating high-dimensional imaging traits from different memory tasks while innovatively considering the interactions between different memory conditions.
To study the prediction of imaging features on a behavior outcome, scalar-on-image regressions have been developed under a single imaging modality or construct (Wang et al., 2017; Kang et al., 2018), though it is always a concern on how the spatial correlation among imaging markers can be accommodated. Recently, with the emergence of big complex data, a considerable amount of efforts have been placed on selecting variables incorporating structural information–the so-called “structural sparsity” which assumes data structure impacts the pattern of risk features. By extending canonical regularized regressions, sparse group lasso (Simon et al., 2013) and its variations with more complex within-group correlation (Danaher et al., 2014; Zhao et al., 2016) have been developed to select grouped variables with selection smoothed over the prior structure. From a Bayesian perspective, variable selection under group structure has also been investigated with an extra benefit of uncertainty quantification. For instance, by introducing both group level and individual level selection indicators, Chen et al. (2016); Zhao et al. (2019) extend stochastic search variable selection (SSVS) to achieve sparse group selection under a nested two-level indicator set. Rockova et al. (2014); Zhang et al. (2014) adopt similar ideas but impose one or both levels of selection with a shrinkage prior. Despite the success of these methods, they are more suitable to accommodate grouped features. Simply assembling voxels into regions of interest (ROIs) may omit the structural details over brain topology within individual ROIs.
Under multi-construct cognitive states, the interaction among information domains on their association to a behavior outcome offers another potential to contribute to the predictive mechanism. Recent works have started to explore the nonlinear impact of single imaging modality on behavior (Mastrovito, 2013), but the interaction effects among collections from different tasks have not yet been studied. From an analytical perspective, joint modeling high-dimensional features and pairwise interaction effects is a non-trivial task due to an inflation of feature space. Under a heredity assumption which requires the inclusion of both main effects if their interaction effect is included in the model (Chipman, 1996), two-step method is dominantly used for model fitting by first identifying main effects and then refitting the model with both main effects and their interaction effects (Hao et al., 2018; Wang et al., 2019). Under Bayesian paradigms, recent works have placed main and interaction terms in one inference system via hierarchical shrinkage priors (Griffin et al., 2017). Due to the non-sparse nature, the heredity assumption has to be relaxed.
In this paper, we develop an innovative Bayesian selection prior to efficiently identify risk features and interaction effects from high dimensional, topologically structured imaging markers collected from multiple modalities. Specifically, we construct nested topological partitions over the brain, and introduce a unified prior model to adaptively search the predictive main effects and inter-modality interaction effects. The group sparsity between adjacent levels allows the signal detection to follow a structural driven path, and the prior dependence between main effect selection and interaction effect selection naturally guarantees the heredity. Such a multi-level learning idea has been adopted previously to construct model stages under different scales to optimize computational efficiency and refine model estimation (Kou et al., 2012). Recently, Zhao et al. (2018) has developed a multiresolution-based Bayesian variable selection model and showed an improved posterior mixing and feature selection accuracy for ultra-high dimensional imaging data. One of the limitations of this method is the resolution parameters are not connected within a joint inference paradigm, leading to hurdles for the fine scale parameters to explore the whole sample space. In this work, we fully address this issue by integrating parameters from different scales under one prior model, which ensures the posterior inclusion probability is nonzero for each unit. Here, we use the word “modality” to refer to a broader concept of technique, domain or construct. Though the motivated study considers measurements from different functional domains collected via the same imaging technology, the analytical framework is general to perform data integration on measurements from different imaging techniques.
Our major contributions are several-fold. First, we remove the linearity constrain among imaging predictors by including spatially-varying interaction effects over the whole brain for an enhanced prediction and interpretation. Rather than resorting to a two-step fashion to select main and interaction effects with potential mis-specification, we jointly identify both components under a heredity condition by naturally adjusting the included features and estimating their contribution to the outcome within one posterior inference framework. Second, we take into consideration the complementary information from different fMRI tasks, and integrate multi-modal imaging to strengthen the neuroimaging signals. Third, we develop a unified Bayesian prior model to achieve a structurally adaptive selection under high dimensional, multi-modal neuroimaging features. The new selection prior model facilitates a sequential incorporation of brain structural information as well as inter-modal correlation, leading to an improved model specification and posterior inference. Overall, the coherence of our modeling framework and its biological plausibility ensures the unique advantage of this method over existing ones on applying to scalar-to-multi-modal image problems.
The rest of the paper is organized as follows. We present the model formulation, proposed prior specification and posterior algorithm in Section 2. We assess the method and compare it with existing alternatives by extensive simulations in Section 3, and implement the method to the ABCD study in Section 4. Finally, we conclude with a discussion in Section 5.
2. Method
For subject i (i = 1, …, n), let yi be a clinical outcome variable, e.g., cognitive assessment. Let denote the collected M-modal imaging measurements over the whole brain with xim referring to the imaging markers associated with modality m. Without loss of generality, we assume all the imaging modalities are registered under the same template space consisting of P voxels. Let si represent a vector of non-imaging covariates with the first element being one. To model the impact of multi-modal imaging traits and their inter-modal interaction effects on a continuous outcome variable, we consider the following high dimensional linear regression with main effects and inter-modality interaction effects
| (1) |
Here, “◦” represents the entry-wise product, β0 denotes non-imaging covariate effects including the intercept effects, βm = (βm1, …, βmP)T represents the voxel-wise main effect of imaging modality m, β<m,m′> = (β<m,m′>1, …, β<m,m′>P)T captures the coefficient for the voxel-wise interaction effects between modalities m and m′, and residual error term . We discuss the case when yi is a categorical variable in the Web Appendix A.
Model (1) describes a clinically meaningful nonlinear association between multi-modal predictors and a scalar outcome. In the ABCD application with the goal to investigate how functional brain activation under different memory conditions associates with general cognitive ability (Sripada et al., 2020), we consider three functional brain activation contrast maps derived from the emotional n-back fMRI data using SPM (Penny et al., 2011) to measure the low memory load brain activity (0-back versus baseline), high memory load brain activity (2-back versus baseline) and working memory brain activity (2-back versus 0-back). It has been shown that working memory brain activity is closely related to fluid intelligence but does not fully explain its variability (Takeuchi et al., 2018). Thus, including interaction effects between brain activities under different memory load conditions offers a great potential to enhance the prediction on general cognitive ability.
2.1. Multi-modal imaging feature selection
Given the total number of imaging predictors in model (1) exceeds M(M+1)P/2, sparsity is an inevitable assumption to facilitate proper model fitting. Meanwhile, besides prediction, it is of great interest to assess the impact of risk neuroimaging traits and their interaction effects on adolescents’ cognition, which will offer a high potential to characterize the mechanism of brain development at younger ages and guide downstream clinical interventions.
Yet it is indeed a challenging task to achieve a joint selection on both multi-modal imaging features and their potential interactions. On the one hand, a commonly used strategy is to select features in a two-step fashion by first selecting main effects and then identifying interactions among selected features, which unavoidably leads to erroneous results as these steps are not independent. On the other hand, there exist correlations among imaging features across brain anatomy and between modalities, and a disregard of such information will sacrifice statistical power and biological interpretation. To address these hurdles by joint selecting both main effects and interaction effects in light of brain structure, as well as accommodating model fitting and computational difficulty, we now describe our proposed Bayesian feature selection model under sequential partitions to enable an efficient stochastic searching, an incorporation of within modal structure, as well as a natural bridge between the selection of main effects and interaction effects.
We start by introducing latent selection indicators. Let δmp ∈ {0, 1} indicate the main effect selection of modality m at voxel p, and δ<m,m′>p ∈ {0, 1} indicate the interaction effect selection between modalities m and m′ at voxel p. The indicator set within each modality is represented as δm = (δm1, …, δmP)T, and between modalities as δ<m,m′> = (δ<m,m′>1, …, δ<m,m′>P)T. Let I0 be the point mass at zero. To impose sparsity, we assign a point mass mixture prior for each corresponding regression coefficient,
| (2) |
under a selection constraint δ<m,m′>p ⩽ δmp × δm′p for 1 ⩽ m,m′ ⩽ M and p = 1, …, P. Such a point mass mixture is the canonical Bayesian feature selection prior, and we will show in the later part the alignment of this prior specification with our unique selection procedure. Compared with shrinkage priors, the point mass mixture prior requires a higher computational involvement and may suffer with poor mixing. For instance, to conduct posterior inference, we could assign δmp ~ Bern(p0), δ<m,m′>p ~ Bern(p1δmpδm′p) with prior inclusion probabilities p0, p1, noninformative prior β0 ~ N(0, ) with a large , residual error variance and hyper-priors , . A direct posterior computation via Gibbs sampler will involve O(P3 M3) operations. When one only updates the main effect coefficients , the time complexity reduces to O(PMT2) if using a block update by chopping β into segments of a size T (Ishwaran et al., 2005). Under moderate to high dimensional case, the latter update scheme becomes the only option due to the computational allocation of large matrices inverse. However, the computational cost for the block update will still be tremendous when P × M is large, e.g. P ~ 50, 000, M = 3 in our data application, which is more challenging as we aim to incorporate both main and interaction effects within the stochastic searching procedure, while simultaneously accounting for structural information.
2.2. A Partition Nested Selection Prior
To jointly select both main and interaction effects with inherent correlation structure under a computational intractable procedure, we propose a partition nested selection prior by replacing the sparsity imposing procedure in Section 2.1 with a sequence of nested sparsity for β that can be naturally expanded to . One unique advantage of a point mass mixture model is we can easily intersect the selection status of each main and corresponding interaction terms by matching the indicator value. First, we adopt the following equivalent prior representation for (2) as
| (3) |
where αmp ~ N(0, ) and α<m,m′>p ~ N(0, ) represent the nonzero main and interaction effects measured at voxel p. We can further summarize (3) as β = δ ◦ α and βinter = δinter ◦ αinter, with δ (δinter) and α (αinter) organized by the index order of β (βinter). The posterior distribution of coefficients β, βinter can be fully captured by those of δ, δinter and α, αinter, providing a straightforward representation for our prior specifications and subsequent posterior inference. In the following sections, we will first discuss the selection prior for main effects, and then direct expand it to a joint interaction selection.
2.2.1. Nested sparsity on main effects
To induce nested sparsity within β, we reconstruct δ into a sequence of nested selection indicators for the corresponding intermediate imaging features partitioned from coarse scales to fine scales. Referring back to the brain anatomy, selecting a proper way to construct such a partition could facilitate the incorporation of structural information and correlation among different imaging modalities. To achieve so, we first partition over brain locations. At level k (k = 1, …, K − 2), we divide the whole brain voxels {1, 2, …, P} into L(k) mutually exclusive voxel groups summarized by their index sets , where for each l = 1, …, L(k+1), there exists l′ ∈ 1, …, L(k) with , i.e. each index set of a partition at level k + 1 is a subset of certain index set of level k. Consequently, the total number of partitions at each level keeps increasing from lower levels to higher levels, until it reaches the voxel scale (level K − 2 with L(K−2) = P) where M modalities are collected from. Within each of the levels, the multi-modal imaging traits collected from the same spatial location are maintained within one union to leverage their correlation with respect to signal searching. To proceed to the actual feature scale, we can directly split each unit into M elements with each element containing an imaging modality at voxel p.
These nested partitions along multi-modal main effect imaging features pave a unique way to represent θ by the accumulative selection information over different partition levels. To first link selection between adjacency levels, we introduce a mapping matrix between levels k and k + 1 as of a dimension L(k+1) × L(k), k = 1, …, K − 2, with indicating whether partition l at level k + 1 is the “child” for partition l′ at level k. Then, we introduce a selection indicator set for partitions at level k (k < K) with indicating whether imaging features within partition l at level k are highly predictive for outcome as a whole; and γ(K−1) characterizes the selection at the actual imaging feature level. Sequentially between adjacent levels, these intermediate selection indicators are linked with each other by the fact that if a partition at a higher level is selected, then its parent partitions from all the lower levels should all been selected. In other words, only if with , contains signals. We can describe this information transition more clearly by summarizing the accumulative selection at level k reflected by all the previous and current levels denoted by δ(k) as
| (4) |
where the selection information of each γ(1), …, γ(k−1) can sequentially pass along through mapping matrices and are combined with γ(k) to determine this overall selection status. Therefore, between adjacent levels, we have δ(k+1) = A(k)δ(k)◦γ(k+1), and we can eventually link the intermediate selections to main effect selection as
| (5) |
where denotes the mapping from level k to the actual main effect feature space, and Ã(K−1) = IM×P. Based on the representation (5), we replace the main effect selection indicator δ by a number of nested intermediate selection indicator sets {γ(1), …, γ(K−1)}. For any k ∈ {1, …, K − 1}, if there exists p ∈ {1, …, P} such that the pth element of the accumulative selection vector Ã(k)γ(k) is zero, then the corresponding pth element of δ will be zero. When it comes to the posterior inference, this means that at each iteration, any unselected partition at a specific level will directly set all its children partitions at higher levels to be noises; and the inference will only concentrate on the partitions containing signals. This effect accumulates from lower levels to higher levels, allowing the algorithm to keep adjusting the potential signal components. Though the original number of features at level K − 1 equals the actual scale, given the active set has been dramatically downsized via “screening” from previous levels, we will have a much more efficient posterior computation and better inference performance upon the refined feature space.
Another appealing feature of this model is reflected by an embedding of structural information, which is highly preferred in the application of neuroimaging data. Given neuroimaging measurements are spatially correlated under such a fine measure scale with respect to brain anatomical structure, biologically, the spatially contingent imaging features should have a higher possibility to be selected or excluded simultaneously. Our model can straightforwardly accommodate this information by constructing contiguous partitions in light of brain anatomical structure; and we also demonstrate the impact of different partition constructions in our numerical studies. Along with the nested selection indicators, we essentially realize a series of sparse group selection; and the smoothing effect of selection status will be sequentially achieved between each pair of adjacent levels.
2.2.2. Connection to the selection of interactions
The developed sequential sparsity along multi-modal imaging features only accomplish two of our goals to incorporate correlated data structure and facilitate an efficient posterior computation. To jointly identify inter-modal interactions which are determined by their own contribution to the outcome and the existence of the corresponding main effects, we can directly expand our sequential sparsity by adding another level K with indicators γ(K) for the selection status of interactions. Specifically, we define a mapping matrix between main effects (level K − 1) and interactions (level K) as with describing whether imaging measure l′ is one of the two parent features of interaction l. It is straightforward to see that each row of A(K) contains two “1” elements with the rest to be zero. Accordingly, the accumulative selection till the interaction level follows
| (6) |
where represents the element-wise indicator function. Model (6) allows us to learn the selection of interactions in a similar fashion as the previous sequential selection procedure by either directly excluding an interaction when at least one of its main effects is unselected, or determining its selection status by the corresponding element in γ(K). In real practice, even though the total number of potential interaction terms is PM(M − 1)/2 which can be tremendous, a majority of them will be directly marked as unselected in our posterior inference. Combining (6) and (5), (4) will finish the prior construction for β and βinter. We name this new prior model as the Bayesian structure-driven sequential sparsity (BSSS) model, and it is well suited to identify either main effects or both main and higher order effects (interaction in our case) in the presence of large-scale structural or correlated predictors.
2.3. Posterior inference.
We move on to the posterior inference, through which we can clearly see the advantage of our BSSS prior to improve the computational efficiency. After constructing K − 2 levels of partition across whole brain voxels, the unknown parameter set for model (1) with M-modal imaging features is Φ = (γ(1), …, γ(K−1), γ(K), α, αinter, β0, , , ). There are different prior choices for selection indicators such as the Bernoulli-Beta hierarchical prior (Stingo et al., 2011) and Ising model (Li and Zhang, 2010), aiming to adjust the posterior selection from different perspectives. To focus on the main message and enhance robustness, we use simple independent Bernoulli prior as an illustration, and one can easily replace it with an Ising model to further smooth the selection.
To conduct posterior computation, we rely on a Markov chain Monte Carlo (MCMC) algorithm. The joint posterior distribution of all the parameters given the data is
where y = (y1, …, yn)T, X = (x1, …, xn)T, , and S = (s1, …, sn)T. For each of the parameters, we can derive the analytical form of its posterior distribution, based on which, we use (block) Gibbs samplers to draw the posterior samples. A detailed description of the MCMC algorithm is provided in the Web Appendix B. Along the posterior inference, the majority computation is concentrated on parameters involved in δ = 1 and δinter = 1, corresponding to the potential signals within main and interaction effects. The sequential update of δ and δinter facilitates a broad signal searching at coarse scales and gradually refines feature identification at fine scales. Compared with existing Bayesian SSVS methods which directly work on the selection of actual feature scale, the posterior inference under our model accumulatively downsizes the searching space within each MCMC iteration in light of structural information, making the whole searching procedure targeted and biologically plausible.
3. Simulations
We evaluate the feature selection and prediction performance of BSSS compared with alternative approaches; and we assess the sensitivity of BSSS on partition choices through a number of simulations. In the first set of simulation, we consider two image dimensions, i.e, a 2D image with 30 × 30 pixels and a 3D image with 24 × 24 × 24 voxels, and vary the sample size to be 100, 300 and 500 for the 2D case, and 500, 1000 for the 3D case. We consider two modalities for all the cases. To generate imaging features for two modalities xi1 and xi2 while ensuring spatial smoothness and inter-modality correlation, we first generate three latent vectors zi0, zi1 and zi2, each with same dimension as the image features.
| (7) |
where represents the spatial coordinate of feature p, and we set τt = 1, t = 0, 1, 2; and lt = 0.12, t = 0; lt = 0.032, t = 1, 2. Those spatially smoothed latent vectors are then used to construct imaging features for each modality by xi1 = zi0 + 0.2zi1; xi2 = zi0 + 0.2zi2. In terms of coefficients, we follow a similar procedure by introducing latent vectors bit, t = 0, 1, 2, where each bit is generated based on (7) under τt = 0.02, lt = 0.12. To impose sparsity across main effects and interactions, we generate each element of β1, β2 and β<1,2> by , and , where , i = 1, …, 4 are the coordinate set, and the corresponding true signal pieces for 2D and 3D images are demonstrated in Figure 1. In this way, each modality contains both positive and negative main effects, and the interaction effects obey the heredity constrain. In addition, we consider different signal-to-noise-ratios with R2 around 0.63 for the high noise, and around 0.83 for the low noise; and simulate 100 datasets for each simulation setting.
Figure 1.
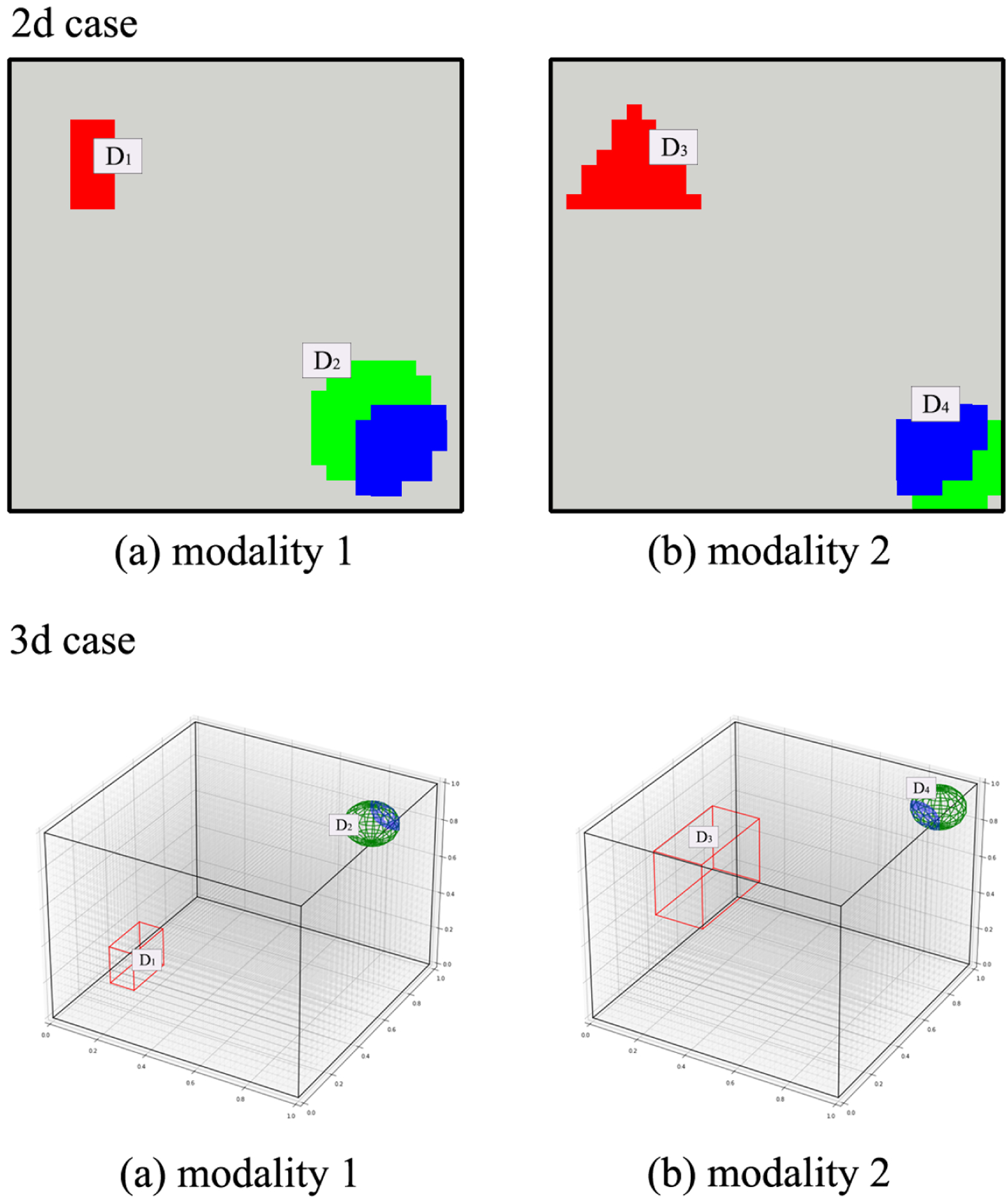
A demonstration of our simulation under 2D and 3D image settings. The true main effect signal pieces for each modality are highlighted under red and green colors, and the inter-modal interaction signals are marked in blue.
We apply the BSSS model to the simulated dataset by noninformatively setting , ασ = bσ = αϵ = bϵ = 1 and each pk = 0.5. To assess the impact of partition construction, we consider two different partition designs for our method under both 2D and 3D images. Specifically, for the 2D case, in the first design (BSSS-P1), we construct six levels of partitions according to the natural order after vectorizing the image features followed by interactions. In the second one (BSSS-P2), we construct six levels of partitions with the first four anatomical partitions showed in the upper panel of Figure 2. For the 3D case, we follow similar considerations with BSSS-P1 and BSSS-P2 containing five and six levels of partition, and the anatomical partitions of BSSS-P2 are presented in the lower panel of Figure 2. For each BSSS method, we run the MCMC algorithm with initial values sampled from priors for 5,000 iterations with 2,000 burn-in, and estimate each parameter by its posterior median. The computational time is 15–30 seconds for the 2D case and 5–6 minutes for the 3D case per thousand iterations on a Mac with M1 chip and 16 GB memory. In terms of competing approaches, given few existing approaches are readily applicable to achieve a joint consideration of intra- and inter-modality feature selection, we resort to the widely used LASSO (Tibshirani, 1996) and horseshoe (Carvalho et al., 2010) implemented by R packages glmnet and horseshoe under a regular two-step procedure by first selecting main effects and then interactions. To evaluate selection accuracy, we calculate the AUC for selecting main effects (AUCmain), interactions (AUCinter) and all features (AUCall); and for the prediction performance, we obtain the out-of-sample R2 based on the test set.
Figure 2.
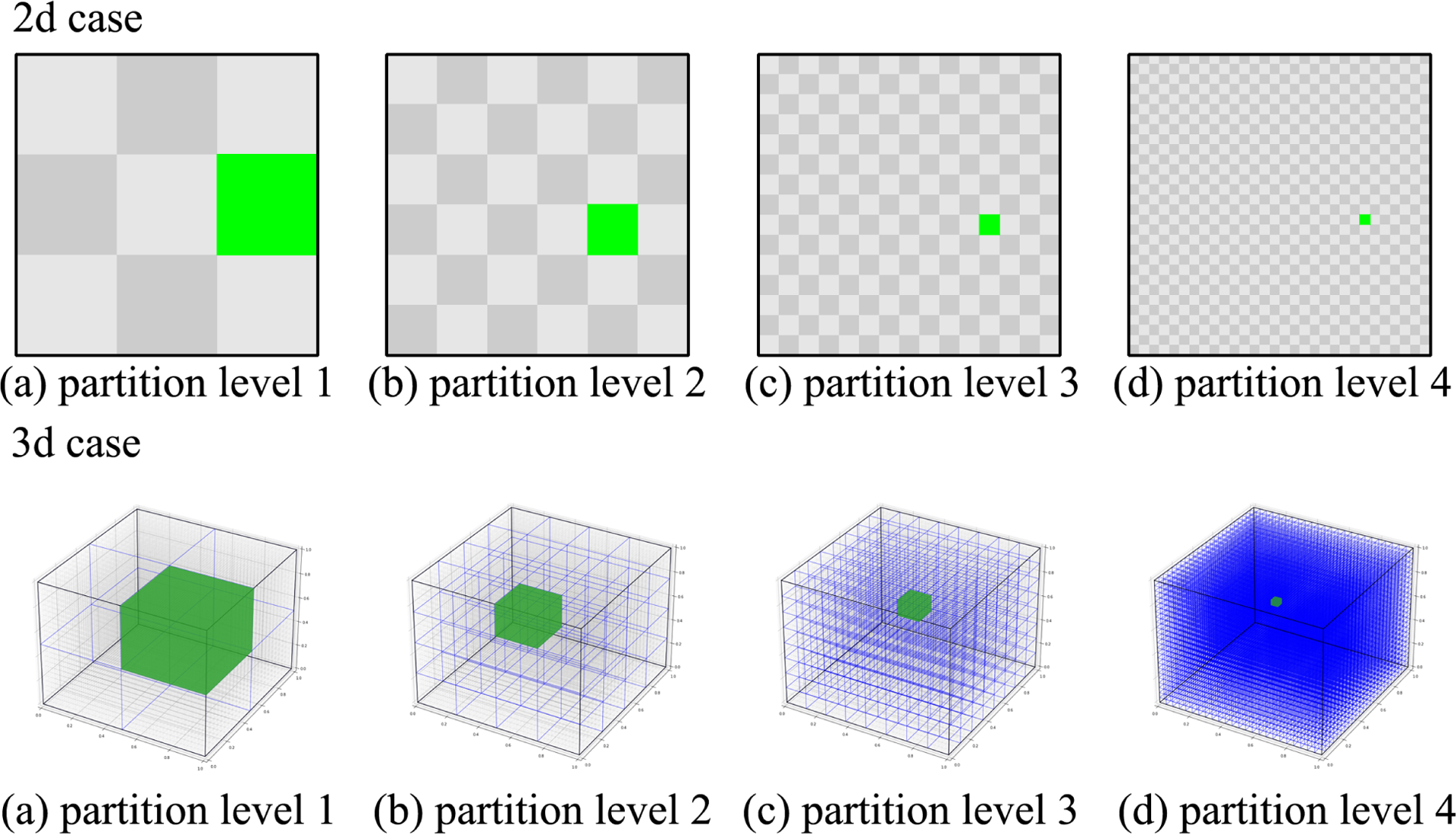
An illustration of the partition design at each level for BSSS-P2 implemented under 2D and 3D image feature space over each modality. Level 4 for each case corresponds to the partition for each pixel(voxel).
We summarize the simulation results in Table 1. Based on the results, the proposed BSSS models achieve the best or among the best performance in both feature selection and prediction under all the settings, and their superiority becomes more pronounced under small sample sizes and high noises. Particularly, besides a much higher selection accuracy on interaction effects (AUCinter), BSSS also substantially improves the selection accuracy for the main effects (AUCmain) compared with the existing frequentist and Bayesian methods under a traditional two-step procedure. This reassures the power of an integrative analysis on main and interaction effects under the same platform. When comparing between two BSSS versions which are under different partition constructions, we confirm the advantage of performing sequential selection in light of structural information for spatially contiguous signals as the case in neuroimaging applications; and when enough spatial structure is considered, BSSS is not sensitive to different partition designs. It is worth noting that we have also tried an alternative way to implement the competing methods (LASSO and horseshoe) by combining imaging features and inter-modality interactions as a whole set of predictors for model fitting and variable selection. However, the performance is even worse than that under the two-step procedure; hence, we only provide the two-step results here.
Table 1.
Simulation results under different image dimensions, sample sizes and noise levels are evaluated by AUCs on identifying features within main effects and interaction (AUCall), main effects only (AUCmain) and interaction only (AUCinter); and out-of-sample prediction (R2). The Monte Carlo standard deviation for each metric is included in the parentheses.
| 2D Image | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Low noise | High noise | ||||||||
| n | Method | AUCall | AUCmain | AUCinter | R 2 | AUCall | AUCmain | AUCinter | R 2 |
| 100 | BSSS-P1 | 0.919(0.018) | 0.914(0.022) | 0.966(0.021) | 0.734(0.058) | 0.902(0.021) | 0.897(0.027) | 0.957(0.025) | 0.509(0.072) |
| BSSS-P2 | 0.962(0.010) | 0.969(0.008) | 0.976(0.009) | 0.744(0.057) | 0.947(0.014) | 0.962(0.012) | 0.970(0.012) | 0.520(0.069) | |
| LASSO | 0.546(0.009) | 0.542(0.010) | 0.573(0.030) | 0.706(0.060) | 0.527(0.007) | 0.526(0.008) | 0.536(0.024) | 0.469(0.084) | |
| horseshoe | 0.593(0.050) | 0.587(0.051) | 0.653(0.095) | 0.620(0.090) | 0.566(0.048) | 0.571(0.045) | 0.607(0.081) | 0.313(0.106) | |
| 300 | BSSS-P1 | 0.939(0.017) | 0.933(0.019) | 0.968(0.027) | 0.783(0.037) | 0.931(0.012) | 0.923(0.016) | 0.974(0.013) | 0.566(0.054) |
| BSSS-P2 | 0.975(0.003) | 0.976(0.003) | 0.980(0.006) | 0.788(0.037) | 0.969(0.006) | 0.973(0.005) | 0.979(0.008) | 0.572(0.054) | |
| LASSO | 0.577(0.011) | 0.570(0.012) | 0.622(0.033) | 0.788(0.035) | 0.553(0.010) | 0.547(0.010) | 0.589(0.030) | 0.565(0.054) | |
| horseshoe | 0.672(0.064) | 0.657(0.067) | 0.749(0.093) | 0.747(0.075) | 0.605(0.058) | 0.592(0.057) | 0.662(0.093) | 0.421(0.122) | |
| 500 | BSSS-P1 | 0.939(0.019) | 0.931(0.020) | 0.967(0.024) | 0.793(0.032) | 0.936(0.015) | 0.929(0.018) | 0.971(0.020) | 0.575(0.042) |
| BSSS-P2 | 0.977(0.003) | 0.977(0.003) | 0.982(0.005) | 0.796(0.032) | 0.973(0.004) | 0.975(0.004) | 0.981(0.006) | 0.579(0.042) | |
| LASSO | 0.595(0.012) | 0.585(0.013) | 0.654(0.035) | 0.802(0.029) | 0.565(0.011) | 0.558(0.012) | 0.604(0.031) | 0.581(0.040) | |
| horseshoe | 0.666(0.064) | 0.651(0.063) | 0.752(0.091) | 0.789(0.036) | 0.617(0.073) | 0.595(0.077) | 0.695(0.102) | 0.495(0.103) | |
| 3D Image | |||||||||
| Low noise | High noise | ||||||||
| n | Method | AUCall | AUCmain | AUCinter | R 2 | AUCall | AUCmain | AUCinter | R 2 |
| 500 | BSSS-P1 | 0.956(0.018) | 0.949(0.018) | 0.964(0.015) | 0.780(0.032) | 0.957(0.017) | 0.947(0.020) | 0.962(0.016) | 0.549(0.037) |
| BSSS-P2 | 0.952(0.034) | 0.940(0.037) | 0.986(0.006) | 0.775(0.033) | 0.959(0.012) | 0.948(0.014) | 0.982(0.008) | 0.546(0.040) | |
| LASSO | 0.539(0.007) | 0.538(0.007) | 0.563(0.040) | 0.767(0.032) | 0.523(0.004) | 0.523(0.004) | 0.527(0.031) | 0.529(0.042) | |
| horseshoe | 0.513(0.012) | 0.514(0.013) | 0.564(0.054) | 0.562(0.048) | 0.511(0.010) | 0.511(0.010) | 0.565(0.062) | 0.249(0.043) | |
| 1000 | BSSS-P1 | 0.950(0.019) | 0.945(0.019) | 0.951(0.032) | 0.789(0.025) | 0.966(0.017) | 0.958(0.017) | 0.968(0.012) | 0.578(0.037) |
| BSSS-P2 | 0.916(0.061) | 0.906(0.062) | 0.987(0.011) | 0.774(0.040) | 0.963(0.021) | 0.952(0.023) | 0.986(0.007) | 0.577(0.037) | |
| LASSO | 0.556(0.007) | 0.555(0.007) | 0.601(0.045) | 0.783(0.026) | 0.534(0.007) | 0.533(0.005) | 0.549(0.039) | 0.566(0.036) | |
| horseshoe | 0.514(0.015) | 0.518(0.015) | 0.576(0.079) | 0.570(0.039) | 0.514(0.012) | 0.514(0.015) | 0.586(0.067) | 0.262(0.037) | |
To further investigate the robustness of BSSS on partition construction, in the second set of simulation, based on 2D images, we consider five different partition designs for the BSSS implementation. The details of the simulation setting, model implementation and results are provided in the Web Appendix C. Through the simulation, we confirm our model is relatively robust with respect to the partition design.
Finally, we perform the third set of simulation in light of the motivated ABCD study to evaluate our model performance under the real data scale compared with competing methods. We directly adopt the multi-modal imaging data from the ABCD study and consider the inter-modality interactions. The details of the simulation setting, model implementation and results are also provided in the Web Appendix C. Based on this set of simulation, we further confirm the superior performance of the BSSS under an ultra-high dimensional case.
4. The Adolescent Brain Cognitive Development Study.
The ABCD (Casey et al., 2018) is an ongoing landmark study to investigate how environmental and socio-cultural factors impact human brain development from childhood through adolescence. The study recruits more than 10,000 9- to 10-year-old children from 21 study sites across the United States; and the study will collect the behavioral, psychosocial and neuroimaging measurements longitudinally from participants for ten years. Our analyses focus on the first release of baseline ABCD data with the detailed imaging processing and acquisition across different sites described in Hagler Jr et al. (2019) and Casey et al. (2018). The task-based fMRI study contains an emotional version of the n-back task, during which the participants were required to respond whether the stimulus was the same as the one shown 2 trials earlier (2-back) or the target stimulus shown at the beginning (0-back). The obtained fMRI data reflects the application of the standard preprocessing steps including gradient-nonlinearity distortions, inhomogeneity correction for structural data, gradient-nonlinearity distortion correction, motion correction and field map correction (Hagler Jr et al., 2019). All the fMRI images are co-registered and normalized into the standard 3mm MNI space which consists of 47,636 voxels in the brain. For each subject, we construct task-related activation contrast maps by fitting voxel-wise general linear models (GLM). We primarily focus on the three task contrasts, i.e. 2-back versus 0-back (2back-0back), 2-back versus baseline (2back), and 0-back versus baseline (0back), characterizing a subject’s working memory brain activity, high memory load brain activity and low memory load brain activity, respectively. Our goal here is to determine the informative imaging markers and inter-contrast interaction effects, as well as quantify their prediction for children’s general intelligence, or G-Factor, which will help pave the way to characterize the neural signature for this life-outcome related factor.
To perform the analysis, we construct the training data under the 20 study sites with the minimum missing values, and the test data based on the remaining site. Of note, the imaging protocol of the ABCD study follows a well-developed harmonization process to remove site effect (see Casey et al. (2018) for details); and we also show balanced residuals based on our predictive model across different sites (see the Web Appendix D), supporting the rationale of our data split. Under the training set, we apply BSSS for the three imaging modalities and inter-modality interactions adjusting for age, gender, race, highest parental education, household marital status and household income. Given the ABCD study also provides the propensity weight for each participated child (Garavan et al., 2018), we straightforwardly adjust our implementation under a weighted regression to accommodate potential recruitment bias. To construct partitions over voxels in light of brain anatomy, we set the first level in light of automated anatomical labeling (AAL) atlas, and each subsequent level by dividing an original partition unit into eight spatially contiguous pieces based on the 3D coordinates with the unit center as the origin. This allows us to reach the actual feature scale at level five and between modality interaction at level six. The hyper-parameter settings closely follow those in the simulations. We implement the MCMC for 10,000 iterations with the first 5,000 as burn-in, and the posterior convergence has been confirmed by both trace plots and GR method (Gelman et al., 1992) as shown in the Web Appendix D.
We first display the significant main and interaction effects identified by our method across the brain from each contrast and contrast interaction in Figure 3, which also showcases our model structure. To examine how the strongest intra- and inter-modality predictive signals are concentrated across different ROIs, we summarize the posterior median proportion of voxels with a posterior inclusion probability higher than 0.95 for each ROI. Table 2 highlights the top five regions with the largest piece of signals under each task contrast and interactions; and the full list of AAL regions and the associated signal proportion under different effects are provided in the Web Appendix D. The results indicate a general consistency among working memory, high and low memory loads on the activated brain locations reflected by the main effects. Specifically, right hippocampus, right parahippocampal gyrus and right calcarine sulcus display strong neural signals for all three task contrasts. Previous literature indicates that hippocampus and parahippocampal gyrus are the two essential brain areas that significantly contribute to memory-based ability during the neurodevelopment (Faridi et al., 2015), and the right hippocampus, right parahippocampal gyrus and calcarine sulcus have been extensively reported to support spatial sense cognition (Mathieu et al., 2018), social cognition (Barber et al., 2013) and visual processing respectively (Tang et al., 2015). In terms of the interactions, different from the main effects, the three interaction units show diverse signal patterns across the brain for different memory process combinations. The clear distinction between the ROIs with strong intra-modality and inter-modality effects suggests a nonlinear relationship on the imaging predictors and indicates a potential oversight of signals if we only emphasize the first-order prediction.
Figure 3.
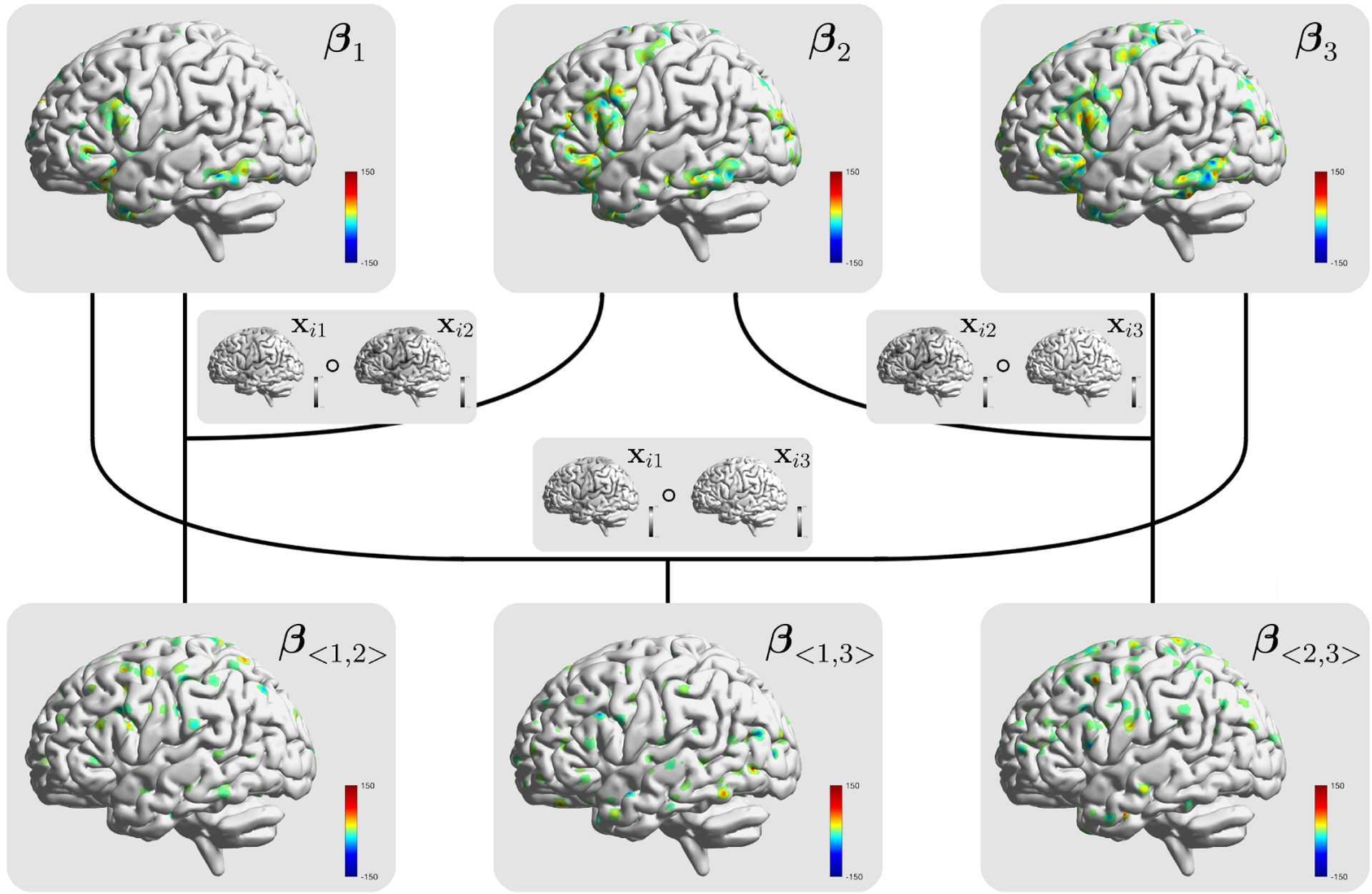
A demonstration of the model structure for BSSS with Xi, i = 1, 2, 3 representing the imaging markers associated with the 2back-0back, 2back-baseline, and 0back-baseline modalities from the ABCD study. Based on the results from the posterior inference, the identified main and interaction effects are displayed by the corresponding heat maps from the coefficients.
Table 2.
The median proportion of the voxels with the posterior inclusion probability higher than 0.95 on the AAL regions from the main and interaction effect results for the ABCD study. The top 5 brain regions under each effect components are bolded.
| 2back-0back | 2back | 0back | |
|---|---|---|---|
| Frontal_Med_Orb_L | 0.151 | 0.147 | 0.191 |
| Insula_R | 0.130 | 0.167 | 0.189 |
| Cingulum_Ant_L | 0.148 | 0.150 | 0.169 |
| Hippocampus_R | 0.160 | 0.194 | 0.212 |
| ParaHippocampal_R | 0.187 | 0.187 | 0.269 |
| Calcarine_R | 0.166 | 0.164 | 0.199 |
| Lingual_L | 0.132 | 0.179 | 0.203 |
| Temporal_Pole_Sup_R | 0.128 | 0.128 | 0.198 |
| 2back-0back × 2back | 2back-0back × 0back | 2back × 0back | |
| Frontal_Inf_Oper_L | 0.086 | 0.037 | 0.071 |
| Frontal_Inf_Orb_R | 0.048 | 0.077 | 0.026 |
| Supp_Motor_Area_L | 0.070 | 0.021 | 0.096 |
| Supp_Motor_Area_R | 0.075 | 0.020 | 0.087 |
| Cingulum_Post_L | 0.080 | 0.036 | 0.066 |
| Parietal_Sup_R | 0.057 | 0.022 | 0.091 |
| Precuneus_L | 0.052 | 0.037 | 0.083 |
| Paracentral_Lobule_L | 0.076 | 0.028 | 0.071 |
| Paracentral_Lobule_R | 0.066 | 0.022 | 0.084 |
| Caudate_L | 0.036 | 0.079 | 0.043 |
| Pallidum_R | 0.026 | 0.105 | 0.013 |
| Thalamus_L | 0.029 | 0.093 | 0.029 |
| Thalamus_R | 0.039 | 0.081 | 0.029 |
| Temporal_Pole_Mid_R | 0.092 | 0.054 | 0.060 |
We further investigate the imaging signals with respect to brain sub-networks (Power et al., 2011) by summarizing the posterior median proportion of the above signals within each functional sub-network in Table 3. Based on the table, sub-networks with the largest activation from the main effects under each contrast focus on the ones controlling auditory, memory retrieval and visual processes. These signal patterns are the most cognition-related ones, reassuring the plausibility of our results. The imaging signals within different memory process interactions again display under distinct sub-network sets. Most of these sub-networks have not been disclosed before for a direct impact on a child cognitive development but the uncovered interaction effects could enrich our understanding on the memory process system and guide future investigation.
Table 3.
The median proportion of the voxels with the posterior inclusion probability higher than 95-percentile on the functional sub-networks from the main and interaction effect results for the ABCD study. The top 3 sub-networks under each effect component are bolded.
| 2back-0back | 2back | 0back | |
|---|---|---|---|
| Sensory/somatomotor Hand | 0.081 | 0.072 | 0.086 |
| Sensory/somatomotor Mouth | 0.071 | 0.071 | 0.119 |
| Cingulo-opercular Task Control | 0.115 | 0.084 | 0.128 |
| Auditory | 0.130 | 0.130 | 0.136 |
| Default mode | 0.078 | 0.080 | 0.095 |
| Memory retrieval | 0.091 | 0.114 | 0.136 |
| Visual | 0.105 | 0.117 | 0.147 |
| Fronto-parietal Task Control | 0.072 | 0.078 | 0.094 |
| Salience | 0.103 | 0.107 | 0.131 |
| Subcortical | 0.027 | 0.054 | 0.071 |
| Ventral attention | 0.024 | 0.035 | 0.059 |
| Dorsal attention | 0.074 | 0.089 | 0.099 |
| Cerebellar | 0.028 | 0.042 | 0.042 |
| 2back-0back × 2back | 2back-0back × 0back | 2backx0back | |
| Sensory/somatomotor Hand | 0.062 | 0.053 | 0.055 |
| Sensory/somatomotor Mouth | 0.048 | 0.048 | 0.048 |
| Cingulo-opercular Task Control | 0.062 | 0.044 | 0.044 |
| Auditory | 0.059 | 0.041 | 0.059 |
| Default mode | 0.046 | 0.046 | 0.054 |
| Memory retrieval | 0.045 | 0.068 | 0.045 |
| Visual | 0.033 | 0.054 | 0.033 |
| Fronto-parietal Task Control | 0.055 | 0.049 | 0.068 |
| Salience | 0.038 | 0.062 | 0.038 |
| Subcortical | 0.054 | 0.080 | 0.036 |
| Ventral attention | 0.059 | 0.012 | 0.106 |
| Dorsal attention | 0.054 | 0.050 | 0.045 |
| Cerebellar | 0.028 | 0.028 | 0.028 |
We also evaluate the prediction performance on the test set, and the correlation between the predicted G-Factor and the actual value is 0.352, which is higher than the previous prediction on the general ability (Sripada et al., 2020). To assess the contribution from the interactions, we rerun BSSS without interaction effect, and the correlation decreases to 0.291. Furthermore, given most of the hyper-priors are noninformative, we perform a sensitivity analysis on impact of partition construction following the strategies in the second simulation to assess the robustness of our model. We have shown that BSSS is mildly sensitive to partition construction with the majority signals maintained. More details have been provided in the Web Appendix D.
5. Discussion
In this article, we propose a unified Bayesian approach that jointly identifies risk first-order markers and inter-modality/construct interactions for analysis of multi-modality neuroimaging data. By constructing a sequential selection prior from the biological architecture and inter-modality relationship, we enhance the computational efficiency and biological plausibility for the stochastic signal searching along high-dimensional structure features and their higher order terms under heredity. Through extensive simulations, we demonstrate the superiority of the proposed methods in both prediction and feature selection. By implementing the proposed model to the ABCD study under different task fMRI contrasts, we identify not only strongly cognition-related brain areas under working memory, high and low memory loads, but also interesting and distinct signal patterns within each inter-contrast interaction that are highly associated with children’s general intelligence. An increase of correlation by 20% from adding interaction effects confirms the crucial role those effects play, though such inter-modal effects have been omitted in previous studies.
Though our current data analyses focus on an integration of functional imaging under different task domains, the proposed method can be directly implemented to combine imaging modalities collected from different technologies with a range of functional, molecular and anatomical information after registration to the same geometrical space. In addition, we currently focus on interactions as higher order terms to explain modality-wise coordination, and our model can be directly modified to accommodate more comprehensive nonlinear support. Meanwhile, besides modeling the interaction effects between different modalities, we can also modify mapping matrices to dissect interaction effects within modalities. Such a general high-order effect consideration, though may not be well-motivated in the current brain imaging studies, is of great interest in molecular data with a converging recognition that interaction between genetic variants, or epistasis contributes to explain phenotypic variance for complex traits.
The construction of partitions contributes to improving biological interpretation and enhancing analytical power, as typically the landscape of the true signals is influenced by the underlying architecture among features. Given the partition design is flexible, in most of the biomedical studies, one can straightforwardly build a set of structurally informative partitions in light of biological information. At the same time, from the aspect to relieve informative prior assumption, one future direction of our work is to parameterize the partition construction within the model inference. By such, we will increase the model complexity but gain more adaptation during signal searching.
Supplementary Material
Acknowledgments
The authors thank the co-editor, associate editor and referee for their valuable comments. This work was partially supported by the National Institutes of Health (NIH) grants RF1 AG068191 (Zhao), R01 DA048993 (Kang), R01 GM124061 (Kang) and R01 MH105561 (Kang) and the National Science Foundation (NSF) grant IIS2123777 (Kang).
Footnotes
Supporting Information
Web Appendices in Sections 2 to 4 are available with this paper at the Biometrics website on Wiley Online Library. R code for BSSS along with implementation details is also provided.
Data Availability Statement
The data that support the findings in this paper are openly available at the NIMH Data Archive (NDA) under Adolescent Brain Cognitive Development Data Repository https://nda.nih.gov/abcd
References
- Barber AD, Caffo BS, Pekar JJ, and Mostofsky SH (2013). Developmental changes in within-and between-network connectivity between late childhood and adulthood. Neuropsychologia 51, 156–167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carvalho CM, Polson NG, and Scott JG (2010). The horseshoe estimator for sparse signals. Biometrika 97, 465–480. [Google Scholar]
- Casey B, Cannonier T, Conley MI, Cohen AO, Barch DM, Heitzeg MM, Soules ME, Teslovich T, Dellarco DV, Garavan H, et al. (2018). The adolescent brain cognitive development (abcd) study: imaging acquisition across 21 sites. Developmental Cognitive Neuroscience 32, 43–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen R-B, Chu C-H, Yuan S, and Wu YN (2016). Bayesian sparse group selection. Journal of Computational and Graphical Statistics 25, 665–683. [Google Scholar]
- Chipman H (1996). Bayesian variable selection with related predictors. Canadian Journal of Statistics 24, 17–36. [Google Scholar]
- Danaher P, Wang P, and Witten DM (2014). The joint graphical lasso for inverse covariance estimation across multiple classes. Journal of the Royal Statistical Society. Series B, Statistical Methodology 76, 373–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faridi N, Karama S, Burgaleta M, White MT, Evans AC, Fonov V, Collins DL, and Waber DP (2015). Neuroanatomical correlates of behavioral rating versus performance measures of working memory in typically developing children and adolescents. Neuropsychology 29, 82–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garavan H, Bartsch H, Conway K, Decastro A, Goldstein R, Heeringa S, Jernigan T, Potter A, Thompson W, and Zahs D (2018). Recruiting the abcd sample: Design considerations and procedures. Developmental Cognitive Neuroscience 32, 16–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman A, Rubin DB, et al. (1992). Inference from iterative simulation using multiple sequences. Statistical Science 7, 457–472. [Google Scholar]
- Griffin J, Brown P, et al. (2017). Hierarchical shrinkage priors for regression models. Bayesian Analysis 12, 135–159. [Google Scholar]
- Hagler DJ Jr, Hatton S, Cornejo MD, Makowski C, Fair DA, Dick AS, Sutherland MT, Casey B, Barch DM, Harms MP, et al. (2019). Image processing and analysis methods for the adolescent brain cognitive development study. Neuroimage 202, 116091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hao N, Feng Y, and Zhang HH (2018). Model selection for high-dimensional quadratic regression via regularization. Journal of the American Statistical Association 113, 615–625. [Google Scholar]
- Ishwaran H, Rao JS, et al. (2005). Spike and slab variable selection: frequentist and Bayesian strategies. The Annals of Statistics 33, 730–773. [Google Scholar]
- Kang J, Reich BJ, and Staicu A-M (2018). Scalar-on-image regression via the soft-thresholded Gaussian process. Biometrika 105, 165–184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kou S, Olding BP, Lysy M, and Liu JS (2012). A multiresolution method for parameter estimation of diffusion processes. Journal of the American Statistical Association 107, 1558–1574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li F and Zhang NR (2010). Bayesian variable selection in structured high-dimensional covariate spaces with applications in genomics. Journal of the American Statistical Association 105, 1202–1214. [Google Scholar]
- Mastrovito D (2013). Interactions between resting-state and task-evoked brain activity suggest a different approach to fMRI analysis. Journal of Neuroscience 33, 12912–12914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathieu R, Epinat-Duclos J, Léone J, Fayol M, Thevenot C, and Prado J (2018). Hippocampal spatial mechanisms relate to the development of arithmetic symbol processing in children. Developmental Cognitive Neuroscience 30, 324–332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penny WD, Friston KJ, Ashburner JT, Kiebel SJ, and Nichols TE (2011). Statistical Parametric Mapping: The Analysis of Functional Brain Images. Elsevier. [Google Scholar]
- Power JD, Cohen AL, Nelson SM, Wig GS, Barnes KA, Church JA, Vogel AC, Laumann TO, Miezin FM, Schlaggar BL, et al. (2011). Functional network organization of the human brain. Neuron 72, 665–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rockova V, Lesaffre E, et al. (2014). Incorporating grouping information in Bayesian variable selection with applications in genomics. Bayesian Analysis 9, 221–258. [Google Scholar]
- Simon N, Friedman J, Hastie T, and Tibshirani R (2013). A sparse-group lasso. Journal of Computational and Graphical Statistics 22, 231–245. [Google Scholar]
- Sripada C, Angstadt M, Rutherford S, Taxali A, and Shedden K (2020). Toward a “treadmill test” for cognition: Improved prediction of general cognitive ability from the task activated brain. Human Brain Mapping 41, 3186–3197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sripada C, Rutherford S, Angstadt M, Thompson WK, Luciana M, Weigard A, Hyde LH, and Heitzeg M (2020). Prediction of neurocognition in youth from resting state fMRI. Molecular Psychiatry 25, 413–3421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stingo FC, Chen YA, Tadesse MG, and Vannucci M (2011). Incorporating biological information into linear models: A Bayesian approach to the selection of pathways and genes. The Annals of Applied Statistics 5, 1978–2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takeuchi H, Taki Y, Nouchi R, Yokoyama R, Kotozaki Y, Nakagawa S, Sekiguchi A, Iizuka K, Hanawa S, Araki T, et al. (2018). General intelligence is associated with working memory-related brain activity: new evidence from a large sample study. Brain Structure and Function 223, 4243–4258. [DOI] [PubMed] [Google Scholar]
- Tang Y, Chen K, Zhou Y, Liu J, Wang Y, Driesen N, Edmiston EK, Chen X, Jiang X, Kong L, et al. (2015). Neural activity changes in unaffected children of patients with schizophrenia: a resting-state fMRI study. Schizophrenia Research 168, 360–365. [DOI] [PubMed] [Google Scholar]
- Tibshirani R (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological) 58, 267–288. [Google Scholar]
- Wang C, Jiang B, and Zhu L (2019). Penalized interaction estimation for ultrahigh dimensional quadratic regression. arXiv preprint arXiv:1901.07147 [Google Scholar]
- Wang X, Zhu H, and Initiative ADN (2017). Generalized scalar-on-image regression models via total variation. Journal of the American Statistical Association 112, 1156–1168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L, Baladandayuthapani V, Mallick BK, Manyam GC, Thompson PA, Bondy ML, and Do K-A (2014). Bayesian hierarchical structured variable selection methods with application to molecular inversion probe studies in breast cancer. Journal of the Royal Statistical Society: Series C (Applied Statistics) 63, 595–620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y, Chung M, Johnson BA, Moreno CS, and Long Q (2016). Hierarchical feature selection incorporating known and novel biological information: Identifying genomic features related to prostate cancer recurrence. Journal of the American Statistical Association 111, 1427–1439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y, Kang J, and Long Q (2018). Bayesian multiresolution variable selection for ultra-high dimensional neuroimaging data. IEEE/ACM transactions on computational biology and bioinformatics 15, 537–550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y, Zhu H, Lu Z, Knickmeyer RC, and Zou F (2019). Structured genome-wide association studies with Bayesian hierarchical variable selection. Genetics 212, 397–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings in this paper are openly available at the NIMH Data Archive (NDA) under Adolescent Brain Cognitive Development Data Repository https://nda.nih.gov/abcd


