Rapid Assessment of T-Cell Receptor Specificity of the Immune Repertoire

Abstract

Accurate assessment of TCR-antigen specificity at the whole immune repertoire level lies at the heart of improved cancer immunotherapy, but predictive models capable of high-throughput assessment of TCR-peptide pairs are lacking. Recent advances in deep sequencing and crystallography have enriched the data available for studying TCR-p-MHC systems. Here, we introduce a pairwise energy model, RACER, for rapid assessment of TCR-peptide affinity at the immune repertoire level. RACER applies supervised machine learning to efficiently and accurately resolve strong TCR-peptide binding pairs from weak ones. The trained parameters further enable a physical interpretation of interacting patterns encoded in each specific TCR-p-MHC system. When applied to simulate thymic selection of an MHC-restricted T-cell repertoire, RACER accurately estimates recognition rates for tumor-associated neoantigens and foreign peptides, thus demonstrating its utility in helping address the large computational challenge of reliably identifying the properties of tumor antigen-specific T-cells at the level of an individual patient’s immune repertoire.

1. Introduction

The advent of new strategies that unleash the host immune system to battle malignant cells represents one of the largest paradigm shifts in treating cancer and has ushered in a new frontier of cancer immunotherapy [1]. Various treatments have emerged, including checkpoint blockade therapy [2], tumor antigen vaccine development [3], and the infusion of a donor-derived admixtures of immune cells [4]. A majority of successful treatments to-date rely on the anti-tumor potential of the CD8+ T-cell repertoire, a collection of immune cells capable of differentiating between malignant cells and normal tissue by recognizing tumor-associated neoantigens (TANs) detectable on the cell surface [5]. Therefore, accurately assessing a T-cell repertoire’s ability to identify cancer cells by recognizing their tumor antigens lies at the heart of optimizing cancer immunotherapy.

A complete understanding of adaptive immune recognition and the tumor-immune interaction has remained a formidable task, owing in part to the daunting complexity of the system. For example, antigens and self-peptides contained in an epitope (i.e. recognizable peptide sequences) space of size ∼ 20⁹ are presented to ∼ 10⁷ unique T-cell clones in each individual [6], a small fraction of the upper limit of TCR diversity (∼ 10²⁰) [7]. Moreover, their behavior is tempered via an elaborate thymic negative selection process in order to avoid auto-recognition [8]. Here, T-cell clones, each with uniquely generated T-cell receptors (TCRs), interface with numerous (∼ 10⁴) self-peptides presented on the major histocompatibility complex (p-MHC) of thymic medullary epithelial cells via TCR CDR3α and β chains, and survive only if they do not bind too strongly [9]. This process, together with systems-level peripheral tolerance [10], imparts T-cells with durable tolerance to major self-peptides and influences many of the recognition properties of the resultant repertoire. The complexity of the adaptive immune system has attracted numerous mathematical modeling efforts quantifying the mechanisms underlying T-cell immune response. Collectively, the field has made significant progress in understanding the population-level effects of tolerance on T-cell recognition and self vs. non-self discrimination [9, 11]. This includes the T-cell repertoire’s effectiveness at discerning tumor from self-antigens [12], its ability to impart immunity against current and future threats [13, 14], and the extent of selection pressure that it exerts on an evolving cancer population [15, 16].

Any attempt at better understanding these system-scale properties must start with a reliable method to evaluate the interaction between specific TCR-p-MHC pairs. Despite this, a comprehensive, biophysical model capable of learning the energy contributions of each contact pair in a TCR-p-MHC system and applying them to new predictions remains elusive. To-date, experimental research has integrated solved crystal structures [17, 18] with peptide sequencing [19, 20] to probe the physiochemical hallmarks of epitope-specific TCRs. Publicly available crystal structures have enabled researchers to identify detailed structural features that influence the binding specificity of TCR-p-MHC pairs, and machine learning algorithms have made progress on the complementary task of accurately predicting peptide-MHC binding [21, 22, 23, 24] as well as TCR-peptide binding [25, 26]. However, the limited number of available structures relative to the diversity in MHC alleles and TCR-peptide combinations complicates extrapolation to unsolved systems. Alternate templatebased structural modeling [27] and docking [28] approaches are limited by calculation speeds (at best one structure-per-minute), thus it is unlikely in the foreseeable future that such strategies can be used to investigate the number of TCR-peptide interactions necessary to study the problem at the immune-repertoire level, as this task easily requires the assessment of more than 10⁹ pairs simultaneously [29]. Prior attempts have approximated binding affinity by implementing statistical scores calculated from docking algorithms [28]. These scores are trained using examples of generic protein binding and thus lose the unique aspects of the TCR-peptide interactions.

To deal with this challenge, we develop a systematic TCR-p-MHC prediction strategy, which we refer to as the Rapid Coarse-grained Epitope TCR (RACER) model, for rapid and accurate assessment of TCR specificity capable of differentiating self- and foreign-antigens. This approach can evaluate 10⁹ similarly MHC-restricted TCR-peptide pairs. This method employs supervised machine learning on known TCR-peptide structures and experimental data to derive a coarse-grained, chemically-accurate energy model governing TCR-p-MHC interaction. This strategy was adapted from earlier efforts to predict protein folding [30, 31, 32, 33, 34, 35] and to screen the binding of small molecules [36, 37]. Confining our predictions to TCRs with a given MHC restriction enables the transferability of the method to TCRs that are not included in the training set, but our approach could be generalized with the use of additional training data. This strategy provides a tractable means for affinity predictions based on similarly restricted TCR-peptide primary sequences. We show that RACER accurately distinguishes binding peptides across various TCRs and validation tests. Lastly, we simulate thymic selection and show agreement with previously established estimates of T-cell binding distributions and peptide recognition rates [38, 39]. Our in silico results share several features observed in experimental data including the degree to which post-selection TCRs recognize foreign antigen and TANs, in addition to the sequence diversity of epitope-specific TCRs. [40, 20]. Taken together, our results demonstrate RACER’s utility in learning the interactions relevant for high-throughput TCR-epitope binding predictions.

2. Results

2.1. Distinguishing peptides based on binding affinity

The RACER optimization protocol (Fig. 1a) utilizes high-throughput deep sequencing data on TCRpeptide interactions across a large peptide library [19], together with known physical contacts between TCRs and peptides obtained from deposited crystal structures [41]. The training data comes from cases where all the peptides are displayed by the same allele of the mouse MHC-II molecule. The binding energy between TCRs and peptides, calculated based on a solvent-averaged coarsegrained pairwise model [35], was used as the metric to assess the TCR-peptide binding affinity. The interaction parameters for this solvent-averaged energy model were reoptimized here for recognizing strong TCR-peptide interactions. Adapting an approach previously implemented for studying protein folding [42, 34], the RACER optimization strategy trains a pairwise energy model which maximizes TCR-peptide binding specificity. The energy model was optimized by maximizing the Z-score defined to separate the affinities of experimentally determined strong-binding peptides, called “strong binders” hereafter, from computationally generated, randomized decoys (The Z-score is defined as the difference between the average binding energies of strong binders versus decoys, divided by the standard deviation of the decoy energies. Throughout this manuscript, we report the absolute value of the calculated Z-score, except for Fig. 5c.). The optimized residue type-dependent energy model is used to evaluate the binding energies of an ensemble of new TCR-peptide systems. As will be shown below, we performed three different levels of test (Fig. 1b), and find the predicted binding energies can differentiate strongly binding peptides from weak ones, provided they are displayed by the same MHC allele as that of the training set. Crucially, accurate predictions can be made even without knowledge of the actual crystal structure, although the predictions are improved when this additional information is available.

Figure 1.

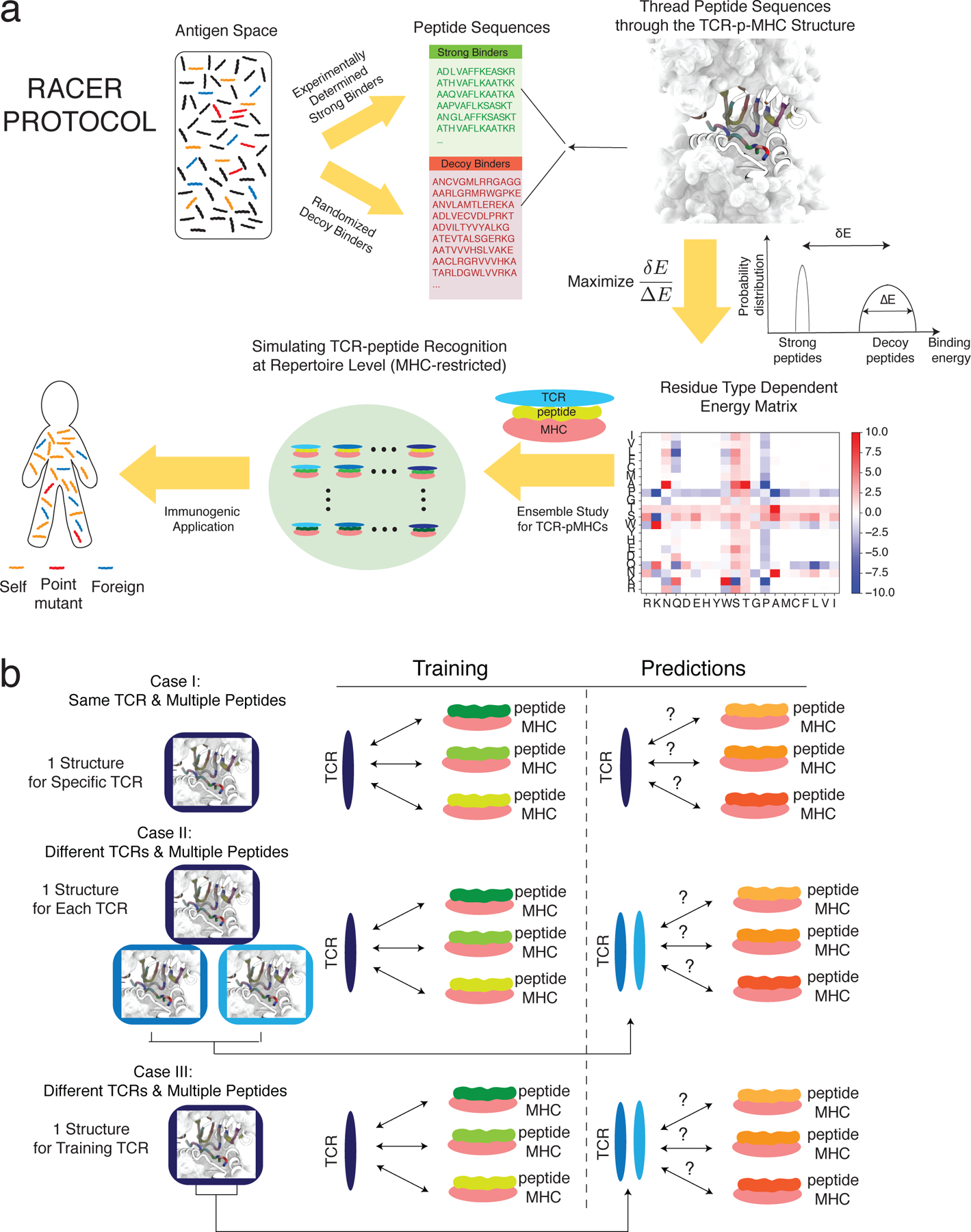
Summary of the modeling approach employed in this study. a. The protocol of RACER optimization (Methods). b. Three tests were conducted to evaluate the performance of RACER. Case I: the training set includes one TCR-p-MHC structure and multiple peptide sequences. The test set includes the same TCR structure and a separate set of peptide sequences. Case II: the training set includes one TCR-p-MHC structure and multiple peptide sequences. The test set includes two different TCR structures (restricted on the same MHC allele) and two separate sets of peptide sequences. Structures for the two additional test TCRs are included in predictions. Case III: The training set includes one TCR-p-MHC structure and multiple peptide sequences. The test set includes only the sequences of two different TCRs (restricted on the same MHC allele) and two separate sets of peptides. Only the structure from the original training TCR was used in prediction (The interactions of interest are indicated by double-sided arrows between TCR and p-MHC).

Figure 5.

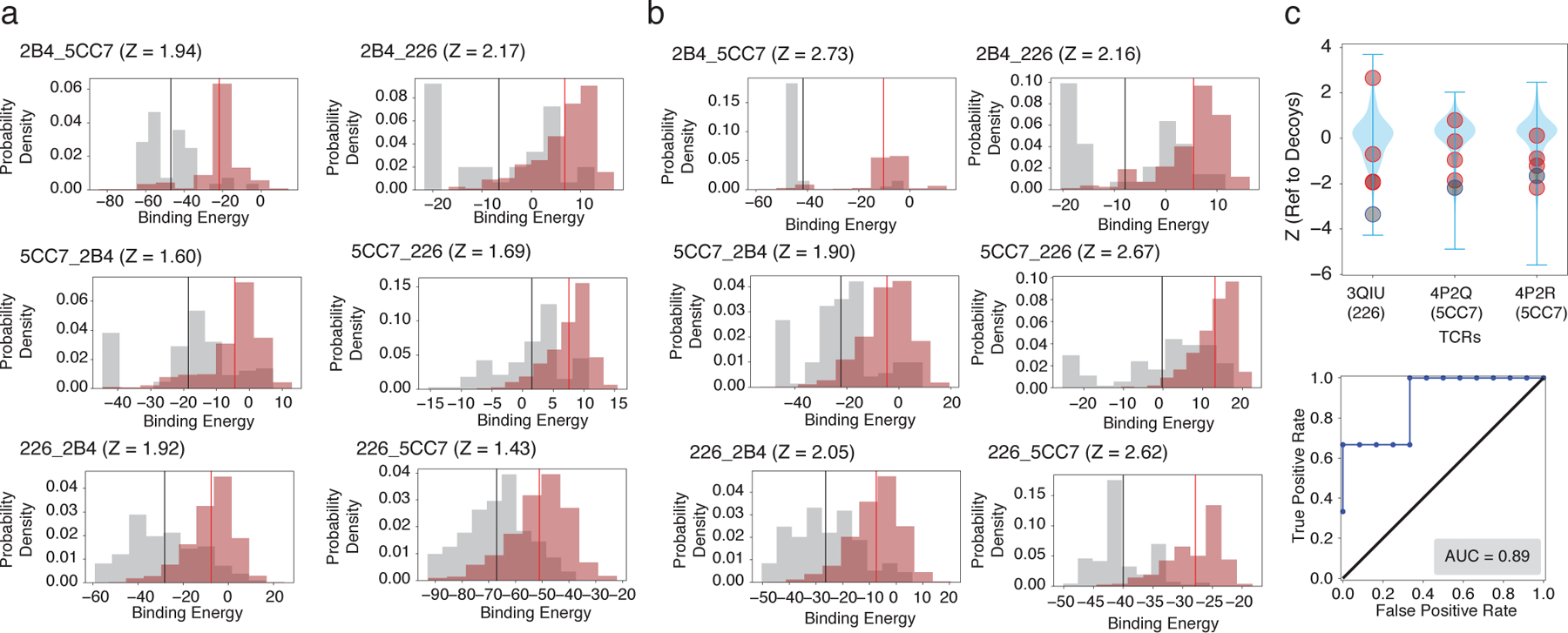
RACER predictive transferability across distinct TCRs. a. Probability density distributions of the predicted binding energies of experimentally determined strong (brown, with mean depicted in red) and weak (grey, with mean depicted in black) binders of each of the three TCRs (2B4, 5CC7 and 226), using another TCR for training. The title of each figure follows the format of “target training TCRs”, e.g., “2B4 5CC7” utilizes the energy model trained on TCR 5CC7 for predicting peptide binding affinities of TCR 2B4. b. Probability density distributions of the predicted binding energies of the same cases as in panel a, but without utilizing any new structure for the new TCR. The panel is formatted in the same way as in panel a. c. Upper panel: The energy model trained on TCR 2B4 is used to predict the binding energies of sequences from the other IEk-associated TCRs [44]. Z-scores of known strong binders (grey) and weak binders (orange) provided by [44] were calculated relative to a set of 1000 decoy peptides with randomized sequences (blue violin plot), with lower Z-scores indicating better predictive performance. Lower panel: The calculated Z-scores of each TCR were used to depict corresponding ROC curve and AUC score (0.89, lower panel).

Fig. 2 summarizes RACER’s predictive performance for a specific TCR (Case I in Fig. 1b). For this fixed TCR, pre-identified strong binding peptides and decoy peptides with randomized sequences were used to train the energy model (Methods). Another set of peptides independently verified experimentally as weak binders constitutes the testing set. The resulting energy model was then applied to calculate binding energies for the strong binders in the training set as well as the peptides in the testing set. This approach was repeated on three independent TCRs that are associated with the IE^k MHC-II allele: 2B4, 5CC7 and 226 (TCR Details in Table S1). Although the experimentally identified weak binders were omitted from the training set, RACER effectively resolves binding energy differences between experimentally determined strong and weak binders having Z-scores, calculated in an analogous way as above by replacing decoys with experimentally-determined poor binders, larger than 3.5 in all cases (Fig. 2a), thus highlighting the predictive power of this approach.

Figure 2.

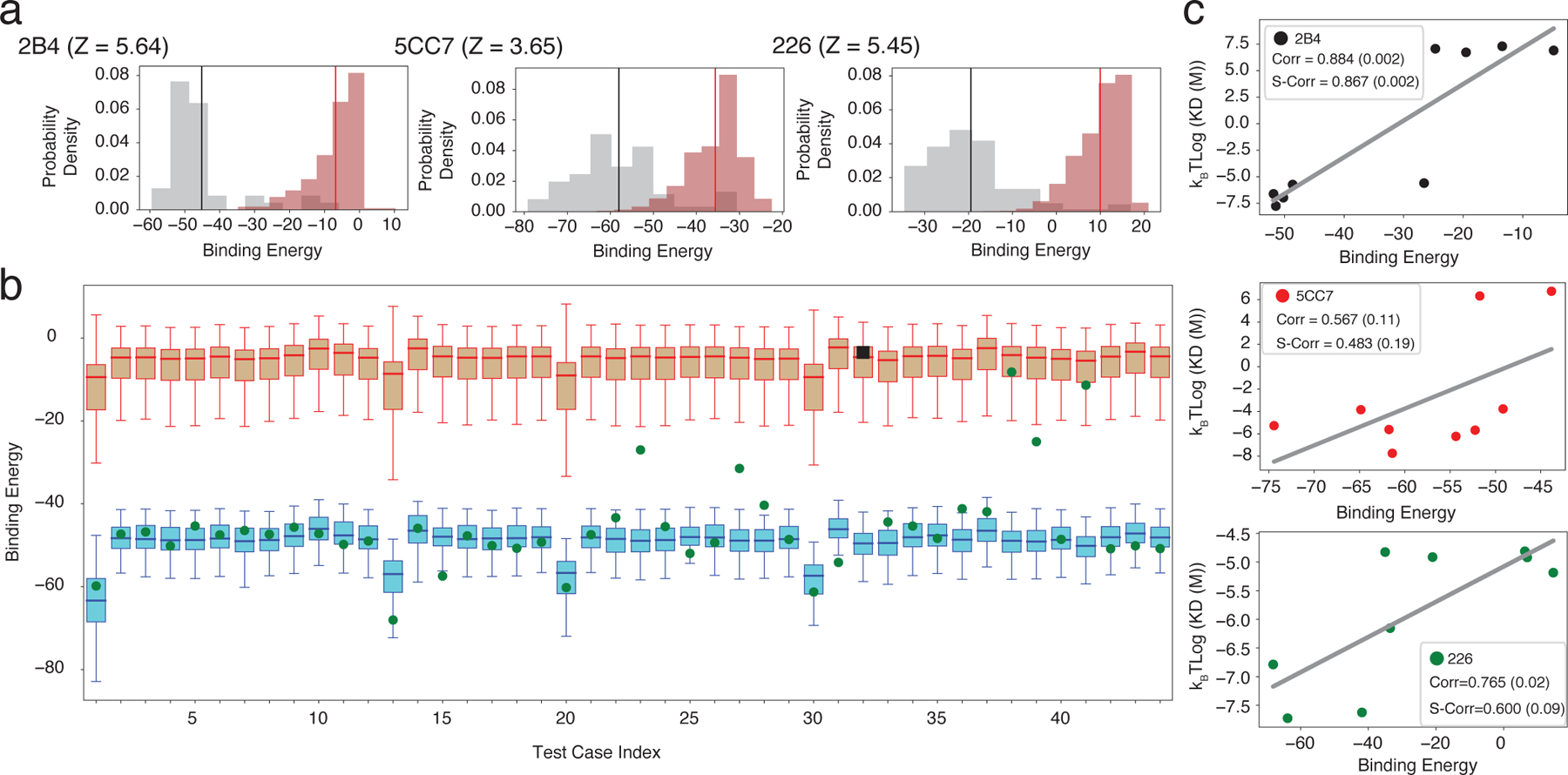
RACER identification of TCR-specific strong and weak binders. a. Probability density distributions of the predicted binding energies of experimentally determined strong (brown, with mean depicted in red) and weak (grey, with mean depicted in black) binders of three TCRs (2B4, 5CC7 and 226). b. Summary of the predicted binding energies from the leave-one-out-cross-validation tests using TCR 2B4. Each test case represents one example using one of the 44 strong binders (green or black), as well as the experimentally determined weak binders (brown) as the test set and the other 43 strong binders as the training set (blue). Each box plot represents the lower (Q1) to upper (Q3) quartiles of the predicted binding energies, and with a horizontal line at the median. Withheld strong binders are depicted in green when being successfully recognized (binding energy lower than the median of the experimentally determined weak binders), and in black square otherwise. The whiskers are placed at the first and last datum points that fall within (m, M), where m = Q1 – 1.5IQR and M = Q3 + 1.5IQR, IQR = Q3 - Q1 represents the interquartile range. c. In a completely independent testing data measured by surface plasmon resonance (SPR) [19], the calculated binding energies of testing peptides were compared with the binding affinity converted from their experimentally determined dissociation constant K_d. Best-fit linear regression is depicted for each case. Corr: Pearson correlation coefficient. S-Corr: Spearman’s rank correlation coefficient. The p-value of each correlation coefficient is reported in the parenthesis.

Despite their relative sparsity in antigen space, strong binders play a central role in T-cell epitope recognition. It is more difficult to predict strong binders than weak binders. To test RACER’s ability to identify strong binders, we performed a leave-one-out cross-validation (LOOCV) test, using data from TCR 2B4 as an example. For each test iteration, one known strong binder was withheld from the training set of 44 strong binders. Our optimization protocol was applied to train the energy model by using the remaining 43 peptides and then predicting the binding energy of the withheld peptide. This prediction was then compared to predicted binding energies of known weak binders, and the procedure was repeated for each of the 44 peptides. Our model is able to accurately distinguish the withheld strong binder in 43 cases (Fig. 2b). This is in contrast to a cluster-based attempt at strong binder identification based on peptide sequences alone, which at best correctly identifies 19 out of 44 strong binders (Supplementary note S1). The same LOOCV test was performed for TCR 5cc7 and 226, which correctly identified 120 out of 126 strong binders of 5cc7, and 267 out of 274 strong binders of 226. To further test the limit of RACER in detecting strong binders that have a more diverse sequence coverage, we performed a more demanding set of hold-out tests on an extended data set from [19]. RACER can recognize peptides sharing little sequence identity (∼0.3) with the native peptide (Figs. S1, S2), and is still able to recognize strong binders when a substantial portion of the training data is withheld (Supplementary note S2, S3 and Fig. S3, S4).

In order to further characterize RACER’s predictive power, an independent set of K_d values measured by surface plasmon resonance (SPR) [19] were compared with predicted affinities. The SPR experiments were performed on 9 independent peptide tests for each of the aforementioned three TCRs. RACER was used to predict the binding energies of each of those TCR-peptide pairs, each modeled with the structure of the corresponding TCR as the template. The free energies, k_BT log(K_d), were compared with calculated binding energies from RACER as a quantitative test of binding affinity prediction accuracy. Lower binding energies indicate stronger binding affinity so that a positive correlation between the k_BT log(K_d) values and calculated binding energies implies a successful prediction. As shown in Fig. 2c, RACER’s prediction of binding affinities for these 9 peptides correlates well with experimental measurement, with an average Pearson correlation coefficient of 0.74. The predicted order of binding affinities is also consistent with those from the experiment, with an average Spearman’s rank correlation coefficient of 0.65.

2.2. Optimized specific interactions for TCR-peptide recognition

The data utilized by RACER includes strong binders and an input crystal structure, as well as TCR and peptide primary sequences, which determine an interaction pattern that was then used to construct a system-specific force field. To illustrate this, we focus on the 2B4 TCR as an example (Fig. 3). The crystal structure of TCR 2B4 (Fig. 3a) reveals that there can be many threonine (T) and asparagine (N) residues on the CDR loops region of the TCR. In the strong binder set, these residues tend to interact with specific peptide residues such as alanine (A), as seen for the specific peptide given in the figure. This notion can be formalized by showing the matrix of observed probabilities of close proximity of specific residue pairs. Thus, we see that certain pairs such as A-T and A-N are significantly enriched in the set of strong binders, while much less so in the decoy set (Fig. 3b). This leads to strongest attractions between the A-T, A-N residue pairs in the optimized energy model (Fig. 3c). In contrast, the TCR tryptophan (W) residue frequently interacts with alanine (A) in both strong binders and decoy peptides. As a result, the optimized energy model does not favor the A-W interaction.

Figure 3.

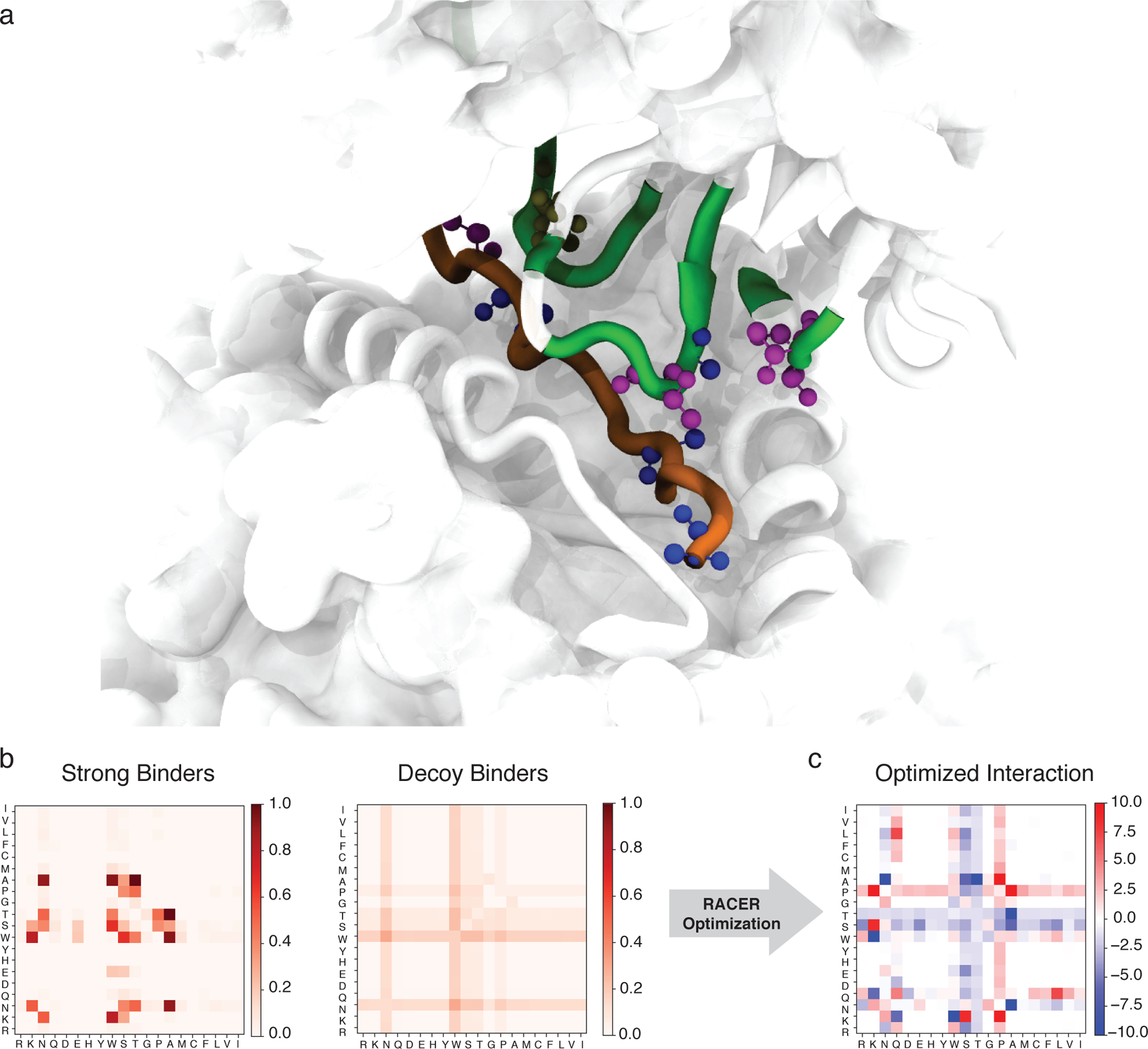
The RACER-derived energy model a. The 3D crystal structure of the 2B4 TCR bound to a specific peptide (PDBID: 3QIB). The parts of the structure that are in contact between the TCR and peptide are color-highlighted as green (TCR) and orange (peptide). Also shown are residues alanine (blue), threonine (magenta) and asparagine (tan) which are discussed in the main text (CPK representation [51]). b. The probability of contact formation (interaction set) between each two of the 20 amino acids in the set of strong binders (left) and the set of randomized decoy binders (right) of TCR 2B4. c. The residue-based interaction strength (energy model) determined by RACER for TCR 2B4. A more negative value indicates a stronger attractive interaction between the corresponding two residues.

This energy model is rather distinct from those typically used for studying protein folding. In order to compare the RACER-derived energy model to well-established force fields described in the protein folding literature, we substitute for our energy model either the standard AWSEM [35] (optimized on deposited folded proteins) force field or the Miyazawa-Jernigan (MJ) statistical potential [43] (constructed using the probability distribution of contacting residues from deposited proteins) and calculate the corresponding binding energy predictions for the TCR 2B4 peptides. We find that neither of them effectively resolves these groups, with Z-scores of 0.69 and 1.28, respectively (Supplementary note S4 and Fig. S5). Similar trends were observed utilizing the peptides corresponding to the 5CC7 and 226 TCRs, demonstrating the necessity of RACER’s de novo identification of pertinent structural information for studying the TCR-peptide system.

2.3. Predicting TCR-peptide binding affinity given the same MHC allele

Given RACER’s accuracy in resolving test peptides presented to the specific TCR used for training, we next explored the feasibility of extending predictions to additional TCR-peptide pairs albeit with the same MHC restriction. Toward this end, we next assessed whether the physical contacts implicitly encoded in RACER’s optimized force field were conserved within IE^k-restricted TCR-peptide pairs. The three IE^k-restricted TCRs considered in our analysis all have been tested with peptides bound to the IE^k mouse MHC molecule. The available crystal structures have a significant degree of structural similarity at the TCR CDR3-peptide binding interface (Fig. 5 of [19]). We further quantified the TCR CDR3-peptide contacts for each pair, constructing a contact map based on their crystal structures (Methods). Our results suggest that, despite differences in TCR and peptide primary sequences, similarly MHC-restricted TCR-peptide pairs share common structural features. In contrast, these contact maps are not preserved across different MHC alleles (Fig. S6).

We next examine RACER’s ability to predict binding peptides of other MHC-restricted TCRs. Toward this end, we apply the energy model optimized using binding data for one of the three TCRs to predict the TCR-peptide binding energies of the remaining two holdout TCRs (Case II in Fig. 1b). To do this, we initially use a known structure for each of the holdouts, and the energy model learned from the training TCR to predict the binding energies of the experimentally determined strong and weak binders of those holdout TCRs. Although the Z-scores measured for these alternate TCRs are lower than those found previously in Sec 2.1, RACER still successfully distinguishes a majority of strong binders from weak binders, with an average Z-score of 1.8 (Fig. 5a). Further incorporation of target TCR structural information in the optimization step improve RACER’s predictive accuracy (Supplementary note S5, Fig. S7).

To provide an additional test and to quantify our discrimination capability, we used an independent dataset from [44]. Four independent TCRs (PDB ID: 3QIB, 3QIU, 4P2Q, 4P2R) from their curated benchmark dataset are associated with the IE^k allele; note that three of these overlap with the TCRs in [19]. To test the performance of RACER for different TCR-peptide pairs, we used the energy model trained based on 2B4 (3QIB) to predict the binding energies of both strong and weak binders for the three remaining TCRs. This calculation again uses the structure found for the one strong binding peptide for each of the 3 TCRs. Our calculation re-emphasizes that RACER can successfully distinguish strong binders even when it is trained based on a different TCR (Fig. 5c), with an AUC of 0.89. As a more comprehensive test of RACER’s transferability, we included other TCR-peptide pairs from [44]. RACER capably recognizes most strong binders across same MHC allele-restricted TCRs with different Vα and Vβ genes, and does so more effectively when there are multiple copies of TCR-peptide pairs available for training (Supplementary note S6, Fig. S8). Of note, when we tested data from the same study involving TCR-p-MHCs with different MHC alleles, RACER could not isolate strong binders, presumably due to the substantially different TCR-peptide interacting patterns (Fig. S6).

Next we examine the necessity to have at least one TCR-p-MHC crystal structure in order to use the optimized energy model for identifying other strong binders (Case III in Fig. 1b). Of course to evaluate the binding energy we must have a structure; the alternative to having a measured structure for a new sequence is to thread that new CDR3 sequence into the crystal structure used for the training data, which potentially introduces an uncertainty in registration. For the cases at hand, this issue arises only for the CDR3α chain as the β chains for all three TCRs all have 12 residues and there is no residual ambiguity. We tested the simplest possible assumption, where all three α chain are aligned to the left [45]. Fig. 5b shows that this procedure again leads to successful discrimination between strong and weak binders, with an average Z-score of 2.36. As a comparison, the best performance of a recent sequence-based predictor trained by using artificial neural networks [26] can recognize the strong binders of TCR 5CC7, but not TCR 2B4 and 226 (Supplementary note S7 and Fig. S10). Similar tests were also performed for the TCR-peptide pairs from [44]. RACER still capably recognizes the strong binders across TCRs with different Vα and Vβ genes (Supplementary note S6, Fig. S9). Thus, we conclude that the MHC-restricted TCR structures are sufficiently similar so that not only can we use the energy model derived from a single TCR training set for other TCRs but we can also use the same structure. This then allows us to make estimates at the repertoire scale without creating extremely large numbers of TCR-p-MHC structures.

2.4. RACER-optimized representation of thymic selection

We apply RACER’s ability to reasonably assess binding strengths using a single crystal structure and associated energy model to study statistical properties of the high-throughput TCR-p-MHC binding observed in thymic negative selection. Using the 2B4 TCR-peptide crystal structure, we simulate 10⁵ TCRs and 10⁴ self-peptides by uniform randomization of the CDR3 and peptide sequences over amino acid space. To avoid registration issues, simulated TCRs were chosen to have the same number of α and β chain residues as TCR 2B4. This was repeated with 2000 TCRs and 10⁴ selfpeptides, this time weighing CDR3-peptide interactions by each of the the three contact maps in Fig. 4. The same approach was applied to a model that assumes a strictly diagonal contact map (motivated by previous analytical work [12]) with randomization of the TCR sequence taken over each non-null position in the contact map.

Figure 4.

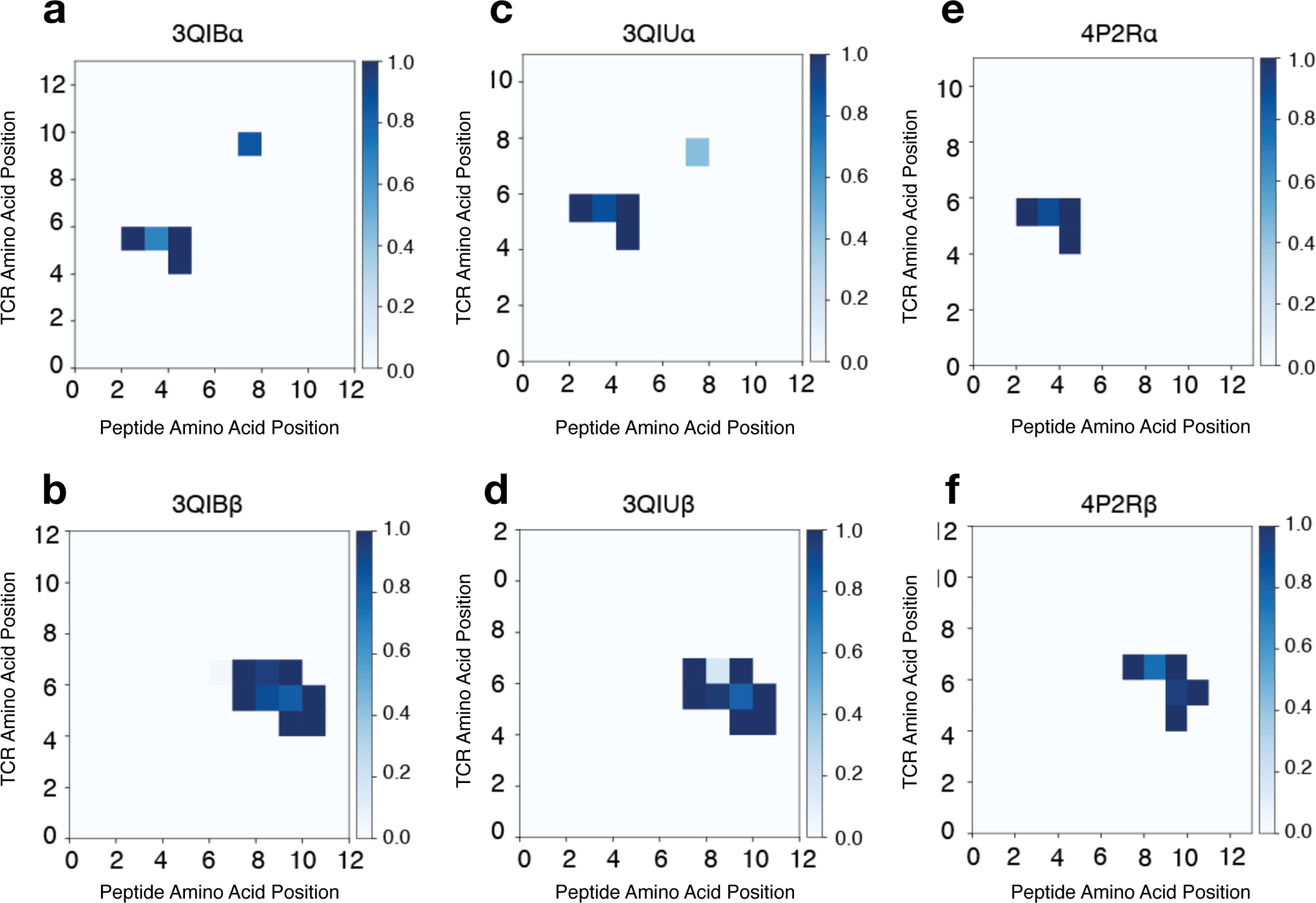
Contact maps for MHC-II IEk-restricted TCR-peptide pairs. Contact maps are calculated using distances from each pairwise TCR-peptide amino acid combination using Eq. 6 for the following MHC-II IEk-restricted TCR-peptide pairs: 3QIB - peptide ADLIAYLKQATK with TCR 2B4 a. CDR3α (AALRATGGNNKLT) and b. CDR3β (ASSLNWSQDTQY) chains; 3QIU – peptide ADLIAYLKQATK with TCR 226 c. CDR3α (AAEPSSGQKLV) and d. CDR3β (ASSLNNANS-DYT) chains; 4P2R - peptide ADGVAFFLTPFKA with TCR 5cc7 e. CDR3α (AAEASNTNKVV) and f. CDR3β (ASSLNNANSDYT) chains. Similarity in interaction topology across TCR-peptide pairs is observed by comparing the contact silhouette of interacting coordinates for the α (top row) and β (bottom row) TCR sequences.

Using this framework, a given TCR survives only if it binds every self-peptide below a fixed activation threshold. The maximum binding interaction over all self-peptides for each TCR defines a selection curve (Fig. 6a), which describes the percentage of negatively-selected T-cells as a function of the cutoff activation threshold. Selection curves for the three TCR sets using Fig. 4 contact maps and RACER energy model compare reasonably to the diagonal contact map motivated by previous analytical work (Fig. 6b red curve). Here, variances are similar in each case with mean-shifts correlated directly with the number of peptide-CDR3 contacts (Fig. 4). These findings reinforce the relevance of TCR-p-MHC-specific structural interactions encoded in the RACER-derived energy potential for binding prediction and T-cell repertoire generation. Although empirical estimates of TCR thymic selection survival rates vary (20%−50%) [46, 47], we assess recognition across all survival rates, restricting our analysis to 50%, when applicable. Given these assumptions, we demonstrate that RACER-generated thymic selection makes reasonable use of available self-peptides (Supplementary note S8, Fig. S11a) and generates a sensible regime of optimal selection, consistent with previous analytical estimates [12] (Supplementary note S8, Fig. S11c).

Figure 6.

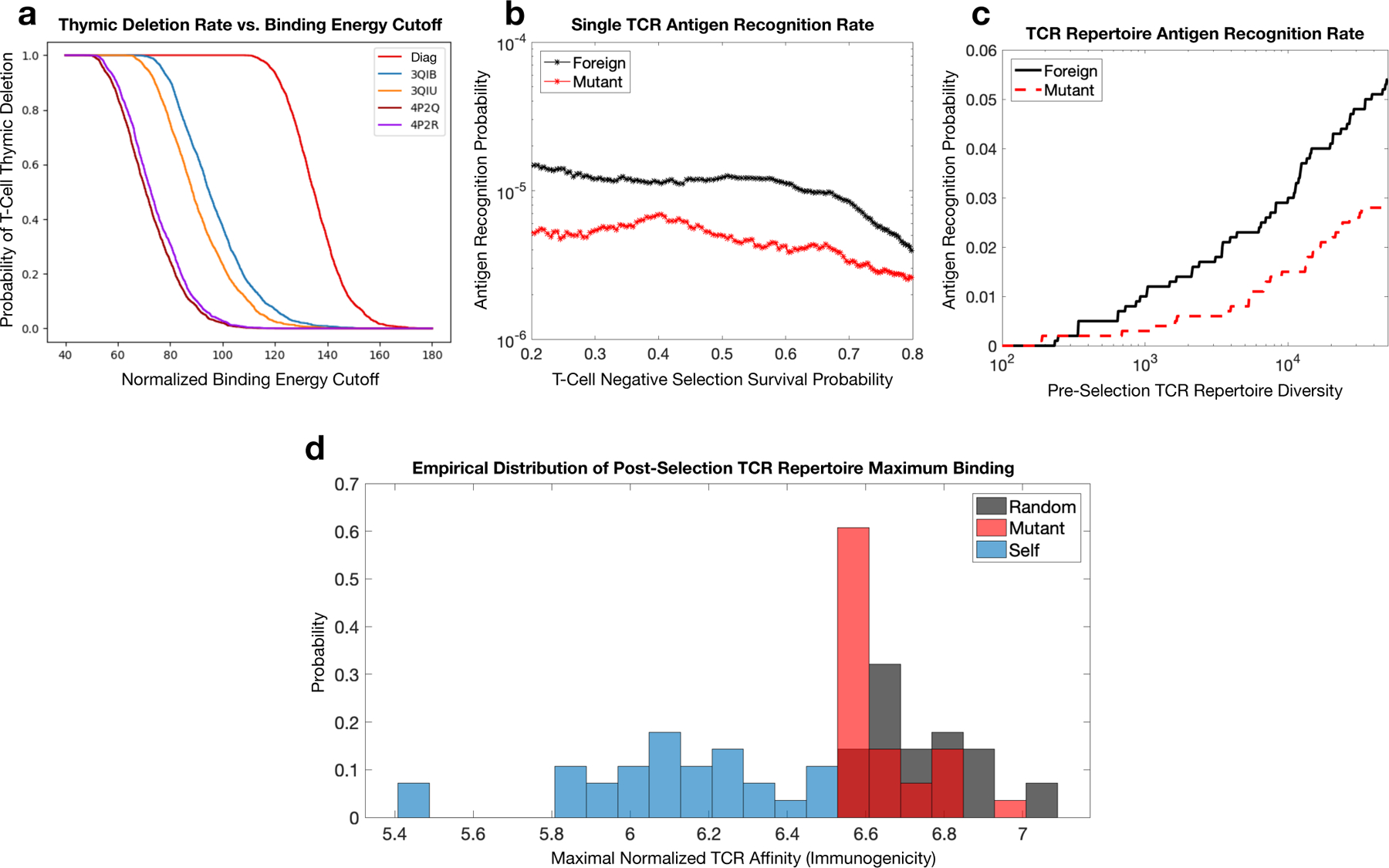
RACER-derived T-cell repertoire simulations of thymic selection and antigen recognition. a. Simulated thymic selection curves (T-cell recognition probability as a function of negative selection binding energy cutoff) incorporating the effects of non-adjacent contacts (given in Fig. 4) using N_n = 10⁴ uniformly randomized self-peptides and N_t = 2000 randomized IE^k-restricted TCRs. 4P2Q and 4P2R (purple) use T-cells generated by randomizing the CDR3 region of TCR 5cc7, while 3QIB (blue) randomizes the CDR3 of TCR 2B4, and 3QIU (yellow) randomizes the CDR3 of TCR 226 (in all cases, randomized CDR3 lengths were unchanged from the original TCR) (red curve uses RACER energy using a diagonal contact map model whose study here is motivated by previous work [12]). b. Utilizing RACER-derived energy assessments from the 2B4 crystal structure, the probability of recognizing foreign and point-mutant antigens for individual post-selection T-cells is plotted as a function of the percentage of TCRs surviving negative selection (ordinate of the graph in panel a, simulations averaged over all post-selection TCRs with pairwise interactions amongst 10³ random peptides and 10³ point-mutant peptides). c. The recognition probability of foreign (black) and mutant (red) peptides by the entirety of the TCR repertoire is plotted as a function of pre-selection TCR repertoire diversity (the number of unique post-selection TCRs), with negative selection thresholds giving 50% survival. d. RACER-derived immunogenicity of foreign, mutant, and self antigen. The distribution of maximum binding affinity over all post-selection T-cells for immunogenic random (gray) and point-mutated self-peptides (red) is compared to that of thymic self-peptides (blue) (There were 28 point-mutated peptides that had at least one T-cell recognition event. To keep an equal number of peptides in each distribution, these were compared with the top 28 similarly ordered foreign peptides and 28 randomly chosen self-peptide groups).

One key issue influencing adaptive immune recognition of tumor-associated neoantigens (TANs) is the recognition of peptides closely related to self (e.g. point-mutants) relative to foreign peptide recognition. The fact that T-cells can in fact recognize tumors suggests that thymic selection leaves intact the ability to strongly bind TANs. Post-selection individual TCR’s exhibit minor recognition differences between foreign peptides and TANs (Fig. 6b) with overlapping variances in line with previous theoretical estimates (Fig. S11B). Moreover, the recognition capacity of the MHCrestricted post-selection T-cell repertoire demonstrates that this minimal difference is maintained at the aggregate immune level (Fig. 6c). These findings explain the ability of the immune system to target cancers in a manner dependent on their mutational load. Moreover, comparisons of RACERderived post-selection T-cell maximal binding energy to the immunogenicity scores for empirically observed thymic self-peptides, foreign peptides, and TANs [40] demonstrates RACER’s ability to capably classify TANs having immunogenicity intermediary to those of foreign and self-peptides with their distribution closer to the foreign group (Fig. 6d). Additional assessments of RACER-derived TCR repertoire CDR3 sequence similarity recapitulate key features observed in experimentally studied repertoires [20] (Supplementary note S8, Fig. S12). Collectively, our results reinforce RACER’s utility for performing realistic post-selection T cell repertoire-level analyses.

3. Discussion

TCR-p-MHC structures encode a system-specific energy model, whose identification can uncover the rules underlying TCR-antigen specificity. The preserved sequence and structural features of TCR-peptide systems [18, 19, 20] limit the physiochemical space explorable by TCR-peptide interface. When optimized on TCR-peptide pairs, the arrangement of the residue contacts between TCR and its cognate peptide (Fig. 4) leads to an energy model (Fig. 3) distinct from the traditional hydrophobic-hydrophilic interaction patterns [48] used for studying protein folding, such as the MJ potential [43]. This system-specifc energy model enables RACER to identify strong binders of corresponding TCRs (Fig. 2) while standard protein-folding energy models fall short (Fig. S5).

RACER offers an approach for developing models that incorporate available protein structural information. Prior investigations have applied artificial neural networks for predicting strong binders of TCR [25, 26] and MHC [49] molecules based only on the primary sequences. Although deep learning can implicitly account for higher-order interactions, such approaches may still be limited by available sequences. RACER alleviates the high demands for sequences by including existing crystal structures in a pairwise potential. To comprehensively characterize RACER’s predictive power, our training set was limited to cases that had pre-identified TCR-peptide pairs given their known crystal structure [19, 44]. While limited by the diversity of experimentally determined strong binders, RACER correctly resolves most of the strong binders even in the most challenging training scenario (Fig. 5b, S7). While the pairwise potential of RACER maintains reasonably high predictive accuracy, it can be further improved by including entropic contributions to affinity (Supplementary note S9).

In cases with available crystal structures, contact map analysis revealed a largely conserved interaction pattern for a variety of TCR-peptide pairs associated with the IE^k MHC-II allele (Fig. 4), providing an explanation for the transferability of RACER-derived interactions when trained on a particular crystal structure. Moreover, these results contributed to variety in the selection behavior of individual TCRs in that TCR-peptide systems having more interactions in their corresponding contact map were correlated with systematic shifts in their mean binding energies, which subsequently correspond to differences in their post-thymic selection inclusion probability (Fig. 6). Previous investigations have characterized the probability distribution for generating particular TCR sequences in VDJ recombination, and have even suggested that the a posteriori observed post-selection TCRs had greater generation probabilities [50, 51], with so-called “public” TCR sequences being observed in multiple individuals. Incorporation of contact maps into our generative model contributes to variations in T-cell survival probability, and may offer a physical interpretation of why public repertoires survive thymic selection at higher rates[52], in addition to providing an explicit means of estimating post-selection T-cell prevalence within a given MHC-class restriction.

RACER’s application to CDR₃ α, β chains obtained from T-cell sequencing, together with possible TAN lists generated by cancer deep sequencing could provide a rapid and reliable method of generating clinically actionable information for cancer specific TCRs in the form of putative TCRTAN pairs, provided those TANs are similarly presented on the original MHC [38, 39]. While we focused our analysis on a single MHC restriction, our approach could also be applied to the crystal structure of another TCR-p-MHC pair, together with several known strong and weak binder candidates. In the future, RACER’s predictive accuracy can be further improved by incorporating additional strong binders and structural data as they become available (Fig. 5b).

The relative efficacy of targeting TANs remains an important question with significant clinical implications. Our findings suggest that thymic selection affords little to no recognition protection of peptides closely related to self, thus supporting the notion that T-cells undergoing central tolerance to thymic self-peptides are essentially memorizing a list of antigens to avoid. Given that a large class of TANs are generated via point-mutations in self-peptide, our results provides a quantitative argument for the efficacy of immunotherapies which target point-mutated neoantigens. We expect that RACER’s ability to identify a diverse set of antigen-specific TCRs within high-dimensional CDR3 sequence space will accelerate therapeutic T-cell discovery by providing a quick and inexpensive screening tool that can then inform more costly confirmatory TCR repertoire sequencing and affinity tests. Currently, we have focused on predicting binding affinities of TCR-peptide pairs restricted to a particular MHC allele, offering a proof-of-principle for epitope identification. This procedure can in general be repeated for other MHC alleles and could be applied to a broad set of clinical scenarios by training on a relatively small number of the most common MHC Class-I alleles, each having ample available crystal structure data.

While important, TCR-p-MHC pairwise interactions are only one factor influencing adaptive immune system recognition. Signaling between other adaptive immune elements and intracellular factors influence antigen generation, abundance, and availability also affect recognition rates. We propose our optimized framework as a tool for understanding general questions regarding the interactions between the T-cell repertoire and relevant antigen landscape. Although we calculate static antigen recognition probabilities, the temporal tumor-immune interaction leads to dynamic co-evolution [16] reliant on the quality, abundance, and systems-level signaling of antigens [53]. The availability of time series assessments of immune cell repertoires, self-peptides, and tumor antigens will enable the development of optimized immunotherapeutic treatments by uncovering the T-cell-tumor-antigen specificity map.

4. Methods

4.1. Protocol of RACER model

The optimization of RACER (Fig. 1a) starts from a series of TCR binders obtained from the deepsequencing experiments [19], as well as the corresponding TCR-p-MHC crystal structures deposited in the database [41]. The sequences of the strong binders, as well as the generated decoy binders from randomizing the non-anchoring sequences of the strong binders, are collected for parameterizing a pairwise energy model which maximizes the energetic gap between the strong binders and a randomized set of decoys. The resulting energy model can be used to quickly evaluate the binding affinities of an ensemble of TCR-peptide interactions at the population level. The calculated binding affinities can be used for simulating the negative selection process in the thymus, as well as measuring the recognition probability of the post-selection TCRs. Finally, this kind of ensemble study can be used for immunogenic applications that require input from an entire T-cell repertoire.

4.2. Energy model

To evaluate the binding energies on the basis of a structurally motivated molecular energy model, the framework of a coarse-grained protein energy model, AWSEM force field [35], was utilized for calculating the binding energies between the T-cell receptors (TCRs) and the peptide displayed on top of a MHC molecule. AWSEM is a coarse-grained model with each residue described by the positions of its 3 atoms – Cα, Cβ and O atoms (except for glycine, which does not have Cβ atoms) [35]. We used the Cβ atom (except for glycine, where the Cα atom was used) of each residue to calculate inter-residue interactions. The original AWSEM energy includes both bonded and nonbonded interactions.

$$V_{\text{total}}=V_{\text{bonded}}+V_{\text{nonbonded}}$$ (1)

Since those residue pairs that contribute to the TCR-peptide binding energy, specifically those from the CDR loops and peptides, are in separate protein chains, only non-bonded interactions are considered. V_nonbonded is composed of three terms:

$$V_{\text{nobonded}}=V_{\text{pairwise}}+V_{\text{burial}}+V_{\text{database}}$$ (2)

Among them, V_burial is a one-body term describing the propensity of residues to be buried in or exposed on the surface of proteins. V_database is a protein sequence-specific term that uses information from existing protein database, such as secondary and tertiary interactions, to ensure locally accurate chemistry of protein structure. Since the TCR-p-MHC system features pairwise interactions between a TCR and its corresponding peptide, only the term V_pairwise is used for this study.

The pairwise energy of AWSEM potential describes the interactions between any two nonbonded residues and can be further separated into two terms:

$$V_{\text{pairwise}}=V_{\text{direct}}+V_{\text{mediated}}$$ (3)

V_direct captures the direct protein-protein interaction of residues that are in between 4.5 and 6.5 Å. The functional form of V_direct is

$$V_{\text{direct}}=\sum _{\begin{array}{c}i\in \text{TCR}\\ j\in \text{peptide}\end{array}}{\gamma }_{ij}\left(a_j,a_j\right){\text{Θ}}_{ij}^{\text{'}}$$ (4)

in which ${\text{Θ}}_{ij}^I=\frac{1}{4}\left(1+\text{tanh}\left[5.0\cdot \left(r_{\text{ij}}-r_{\min }^I\right)\right]\right)\left(1+\tanh \left[5.0\cdot \left(r_{\max }^I-r_{\text{ij}}\right)\right]\right)$ is a switching function capturing the effective range of interactions between two residues (here taken between $r_{\min }^I=4.5\AA$ and $r_{\max }^I=6.5\AA$). Thus, two residues are defined to be “in contact” if their distance falls between 4.5 Å and 6.5 Å. γ_ij(a_i,a_j) describes the residue-type dependent interaction strength, and is the most important parameter that enters the optimization of RACER. V_mediated describes the longer range interactions of two residues and is not used in this study.

4.3. Maximizing specificity of TCR-peptide recognition

For each interaction type, the γ_ij(a_i,a_j) parameters constitute a 20-by-20 matrix of parameters that describes the pairwise interaction between any two residues i, j, each with one of the 20 residue types, a_i, a_j. Guided by the principle of minimum frustration [32], γ_ij(a_i,a_j) was previously optimized self-consistently to best separate the folded states from the misfolded states of proteins. Distilled into mathematical details, the energy model was optimized to maximize the functional δE/∆E, where δE is the energy gap between folded and misfolded proteins, and ∆E measures the standard deviation of the energies of the misfolded states. An energy model was optimized based on a pool of selected protein structures [54], where a series of decoy structures were generated by either threading the sequences along the existing crystal structures, or by biasing the proteins into molten globule structures using MD simulations [34]. The resultant γ parameter thus determines an energy model that facilitates the folding of proteins with given sequences.

Motivated by this idea, RACER was parameterized to maximize the Z-scores for fully separating TCR strong binders from weak ones. Strong binders were chosen to be those top peptides that survive and were amplified to contain to at least 50 copies after four rounds of experimental deep sequencing processes (details in Section Data used in our analyses) [19], together with the peptides present in the deposited crystal structures [41]. In the experiment of [19], to ensure the correct display of peptides on the MHC, limited diversity was introduced for most distal residues and anchoring residues of peptides. The decoy binder sequences were generated by randomizing the non-anchoring residues of each strong binder thereby generating 1000 copies, and excludes the strong-binder sequences. The γ parameters were then optimized to maximize the stability gap between strong and randomized set of decoy binders, δE = A^Tγ, and the standard deviation of decoy energies, ∆E² = γ^TBγ, where the vector A and matrix B are defined as:

$$\begin{gathered} A=〈{〈{\varphi }_{\text{direct}}〉}^{\text{db}}-{\varphi }_{\text{direct}}^{\text{sb}}〉 \\ B=〈{〈{\varphi }_{\text{direct}}{\varphi }_{\text{direct}}〉}^{\text{db}}-{〈{\varphi }_{\text{direct}}〉}^{\text{db}}{〈{\varphi }_{\text{direct}}〉}^{\text{db}}〉 \end{gathered}$$ (5)

In the above Eq. 5, “direct” stands for the interaction type, V_direct. ɸ_direct is the functional form for V_direct. ɸ_direct also summaries the probability of contacts formation (interaction matrix) between pairs of amino acids in a specific TCR-peptide system. The subscripts “db” stands for “decoy binders” and “sb” stands for “strong binders”. The first average is over the 1000 decoy binders generated from one specific strong binder. The second average is over all the strong binders. The maximization of $\delta E/\text{Δ}E=A^T\gamma /\sqrt{{\gamma }^{\text{T}}B\gamma }$ can be performed effectively by maximizing the functional objective R(γ) = A^Tγ − λ₁∆, where ∆² = γ^TBγ. The solution of this optimization gives γ ∝ B⁻¹A. A is a vector containing the difference in the number of interactions of each type in the strong and decoy binders. B is a covariance matrix, which contains information about which types of interactions tend to co-occur in the decoy binders. Finally, γ is a vector that encodes the optimized strengths of the interactions. The dimension of the vector A is (1, 210), that of the matrix B is (210, 210), and that of the vector γ is (210, 1). To aid visual presentation, we reshape the γ vector into a symmetric 20 by 20 matrix in Fig. 3c. Finite sampling of decoy binders introduces noise in the optimization process, particularly in B. As such, a filter is applied to reduce the effects of the noise. The filtering scheme was performed by first diagonalizing the B matrix such that B⁻¹ = PΛ⁻¹P⁻¹, where P is composed of the eigenvectors of B and Λ is made up of B’s eigenvalues. The first N modes of B (sorted in descending order by eigenvalue) are retained and the other (210 - N) eigenvalues in Λ are replaced with the Nth eigenvalue of B. The final result is robust to the choice of N. In practice, N is chosen so that no eigenvalue is close to zero. The Wolynes group performed this optimization in an iterative way where the optimized parameters were used for generating a new set of decoy protein structures [55]. In this study, since different peptides are structurally degenerate on top of MHC as observed from experiments [19], only one round of optimization was performed. Since the optimization leaves a scaling factor as a free parameter, throughout this manuscript, the binding energies are presented with reduced units. To obtain binding energies that have physical units, the scaling factor can be further calibrated to fit the experimentally determined binding affinities, such as the K_d values measured by SPR experiments (Fig. 2c).

4.4. Data input

A deep-sequencing technique was developed to assess the binding affinity of a diverse repertoire of MHC-II-presented peptides towards a certain type of TCR [19]. Specifically, 3 types of TCRs: 2B4, 5CC7 and 226, were used for selecting peptides upon four rounds of purification. The peptides that survived and enriched with multiple copies bind strongly with the corresponding TCR. In contrast, the peptides present initially but become extinct during purification represent experimentally determined weak binders. For each of the 3 TCRs, the peptides that end up with more than 50 copies after the purification process, together with the peptides presented in the crystal structures, were selected as strong binders. 1000 decoy sequences were generated for each of the strong binders by randomizing the non-anchoring residues. Both strong binders and decoys were included in the training set. In addition, to test the performance of RACER, peptides having at least 8 copies initially but disappearing during purification were selected as experimentally determined weak binders and were assigned to the test set for each TCR. To test the transferability of the model, we used weak-binding peptides of two different TCRs (e.g., 5CC7 and 226) as additional test sets distinct from the TCR used in training (e.g., 2B4).

When structural data for a specific TCR-peptide pair of interest is unavailable, we built the structure by homology modeling [45], based on a known TCR-peptide crystal structure incorporating the same TCR. Since potential steric clashes after switching peptide sequences may disfavor the strong binders used in our training set, we used Modeller [45] to refine the structures located at the TCR-peptide interface of strong binders before including them in the training process. Likewise, the binding energies of the experimentally determined weak binders were also evaluated after structural relaxation. The structural relaxation adds several seconds of computational time for each TCRpeptide pair, and thus poses a challenge for large scale repertoire analysis. However, the coarsegrained nature of RACER framework may significantly reduce the probability of side-chain clashes after switching peptide sequences. To test the accuracy of our model prediction without structural relaxation, we calculated the binding energies of strong and weak binders of TCR 2B4 by only switching the peptide sequences, omitting any structural adjustment. Our result (Fig. S13) shows comparable accuracy in separating strong from weak binders, similar to that reported in Fig. 2a. In the same vein, the transferability of RACER was also maintained without structural relaxation (Fig. 5b). Encouraged by the accuracy of our coarse-grained model without relaxation, we modeled large pairwise collections of TCR-peptide interactions by only altering their corresponding sequences.

For an additional independent test of the transferability of RACER under the same MHC allele, we used the benchmark set reported in [44]. Four crystal structures are curated in their benchmark set, including three TCRs: 3QIB (2B4), 3QIU (226), 4P2Q (5CC7) and 4P2R (5CC7). Each of them have one strong-binding peptide presented in the crystal structure, and 4 weakly binding peptides. All the TCR-peptide pairs are associated with MHC-II allele IE^k, and three of them overlap with the main dataset reported in [19]. We therefore used the energy model previously trained from TCR 2B4 to test its transferability for the other three TCR-peptide pairs. The calculated binding energies were converted into a Z score by referencing to a set of 1000 randomized peptides of corresponding TCRs: $Z=\frac{E_{\text{binding}}-E_{\text{decoys}}}{\sigma \left(E_{\text{decoys}}\right)}$, with σ(E_decoys) being the standard deviation of E_decoys. The ROC curve and AUC score were calculated by scanning through different thresholds of the Z score. A further test by including more examples from [44] is available at Supplementary note S6, Fig. S8 and S9.

4.5. Testing the transferability of RACER without target TCR-peptide structure

To test the transferability of RACER without requiring any measured structure for a new TCR, we threaded the sequences of the CDR3 loops of the new TCR on the TCR structure used in our training. The length of CDR3β chain is the same among three TCRs (2B4: ASSLNWSQDTQY; 5cc7: ASSLNNANSDYT, 226: ASSLNNANSDYT), but the length of CDR3α chain is different (2B4: AALRATGGNNKLT; 5cc7: AAEASNTNKVV; 226: AAEPSSGQKLV). In order to accommodate such difference when threading the CDR3α sequences, we used a simple approach: aligning them based on the first two AA residues, leaving two gaps for TCR 5cc7 and 226. Modeller[45] was used to build the new loop structure based on these aligned new sequence, using the single structure in the training set as the template. These homology-modeled structures were then used for calculating the binding energies of the strong and weak binders of the new TCRs, using the trained energy model. We also omitted the step of structural relaxation when replacing a new peptide sequence on the built structure. Such approach is unlikely to reduce RACER’s performance, as demonstrated in Fig. S13.

4.6. The leave-one-out cross validation

The Leave-one-out cross validation (LOOCV) was used to test the predictive power of RACER on its ability to identify strong binders. Specifically, one of the 44 strong binders of TCR 2B4 was removed from the training set, and its predicted binding energy E_pred was compared with the experimentally determined weak binders. If the median of the weak binders’ binding energies is larger than E_pred (a larger binding energy is associated with smaller affinity), the testing strong binder is successfully identified. Similar tests were performed for TCR 5cc7 and TCR 226. The performance of RACER is compared with that from the clustering of peptide sequences using the algorithm from CD-Hit [56] (Supplementary note S1).

4.7. Comparing results from SPR experiments

Surface plasmon resonance (SPR) was performed to assess the binding affinities of the three TCRs towards 9 selected peptides [19]. The correlation between the predicted binding energies from RACER and the dissociation constant K_d evaluated from the SPR experiments thus constitutes a separate set of tests for the accuracy of RACER. We first built a relaxed structure with Modeller [45] for each of those TCR-peptide pairs, using the corresponding TCR structure as the template. We then used the optimized energy model of the corresponding TCR to evaluate the binding energy of each of those TCR-peptide pairs. The K_d values were obtained from fitting the SPR titration curves (Fig. S4f of [19]) using equation $R_{\text{eq}}=\frac{C\cdot R_{\max }}{C+K_{\text{d}}}$ with C, K_d and R_max as free parameters. The Pearson correlation coefficient and the Spearman’s rank correlation coefficient between k_BT log(K_d) and predicted binding energies were used to quantify this correlation.

4.8. Evaluating contact residues of TCR-peptide pairs

The contact map of a given TCR-peptide structure was constructed by measuring the proximity W_i,j between each residue of peptide (residue i) and CDR loops (residue j) based on their mutual distance, using a smoothed step function:

$$W_{\text{ij}}=\frac{1-\tanh \left(d-d_{\max }\right)}{2},\text{\hspace{1em}\hspace{0.17em}\hspace{0.17em}with\hspace{0.33em}}{d}_{\max }=6.5\AA$$ (6)

Only C_β atoms were included in our calculation (except for glycine, where the Cα atom was used). The CDR3 loops were utilized as defined in the IEDB database [57]. The constructed contact map represents those residues that are spatially close to each other in the given crystal structure.

4.9. Evaluation of different TCR-p-MHC interactions used for statistical study

To assess the statistical behavior of the inferential model, we calculated the pairwise binding interactions between a simulated T-cell population of size N_t and collection of N_n = 10⁴ thymic self-peptides. For this proof-of-principle study, we used TCR 2B4 as an example, uniformly varying the 10⁴ amino acids of the peptides, as well as those residues from the TCR that are in spatial contact with the peptide. TCR-peptide pairwise energies were calculated for N_t = 10⁵ randomized TCR sequences using the RACER energy model optimized for TCR 2B4, and N_t = 2000 for each of the TCR-p-IE^k systems given in Fig. 4 using energies weighted according to their contact maps, along with a model using a contact map with diagonal interactions (Fig. 6a). Substitution of TCRpeptide sequences with the newly generated ensemble yielded a total of N_t∗N_n (10⁹ in the 2B4 case; 2∗10⁷ for each of the cases involving the TCR-p-IE^k and diagonal contact maps) TCR-peptide pairs representing interactions occurring during thymic selection. Given our previous results (Fig. S13), we avoid the computationally expensive task of structural relaxation, and instead calculate pairwise interactions with the original structure, requiring 5,000 CPU hours on an Intel(R) Xeon(R) CPU E5–2650 v2 for the large-scale 2B4-optimized simulation.

4.9.1. Thymic selection

Each T-cell survives if the maximal interaction over all self-peptides does not exceed some upper threshold. Selection thresholds were chosen to achieve 50% [7]. In all cases, the RACER-optimized energy model was used for energy assignment. Thymic selection was performed for each of the TCR-p-IE^k examples and their corresponding contact maps given in Fig. 4 (Fig. 6a). For each TCRp-IE^k example, N_t = 2000 pre-selection TCRs were created by varying uniformly the original TCR CDR3 α and β sequences over amino acid space, keeping the sequence lengths unchanged. A similar randomization yielded N_n = 10⁴ randomized peptide sequences representing self-peptides. For each of the 2000 randomized TCRs, binding energies were calculated against the 10⁴ self-peptides by selecting the corresponding entries in the RACER-optimized energy model weighted by the original TCR-p-IE^k contact maps, and the maximum energy was recorded. The fraction of TCRs whose maximal binding energy exceeded the selection threshold E_n traces the survival curves. This procedure, utilizing the RACER-optimized energy model, was repeated for a simplified model that utilizes only adjacent contacts (i.e. a strictly diagonal contact map with each entry having weight one) in the TCR-peptide interaction. The number of diagonal elements in the diagonal contact model was taken to be 20 (10 for each of the CDR3α-peptide and CDR3β-peptide pairs).

4.9.2. Self-peptide potency

Most self-peptides present in thymic selection are expected to participate in the deletion of selfreactive T-cells. Thus, a reasonable model of thymic selection would feature a majority of selfpeptides contributing to the selection of immature T-cells. A rank order of these self-peptides based on their ability to recognize unique T-cells, or potency, characterizes the extent to which each selfpeptide is utilized in thymic selection. The rank order of potency was created for the RACER model utilizing the crystal structure of the 2B4 TCR (PDB ID: 3QIB) and its corresponding energy model derived from the set of experimentally determined strong binders. The thymic selection process using 10⁴ self-peptides and 10⁵ TCRs for the 2B4-optimized RACER model described above generates a total of 10⁹ pairwise binding energies. The negative selection threshold E_n was selected to yield 50% selection, resulting in ∼ 5 · 10⁴ deleted TCRs. The number of TCRs deleted by each self-peptide was recorded. The peptide deleting the most TCRs defines the most potent self-peptide. TCRs recognized by this peptide are removed from the list of total TCRs, and this peptide is similarly removed from the list of self-peptides. This process is repeated on the smaller TCR and self-peptide list to determine the second most potent peptide. Additional iteration until no TCRs remain provides the rank order of self-peptides in decreasing order of potency. The cumulative fraction of deleted relative to total TCRs is plotted in decreasing order of peptide potency.

4.9.3. Antigen recognition probabilities for individual T-cells and T-cell repertoires

Utilizing the same post-selection T-cell repertoire from the previous section, post-selection T-cells were quantified for their ability to recognize random non-self-antigens and tumor neoantigens that differ from the N_n thymic self peptides by one residue. 50% selection of TCRs result in approximately 5 · 10⁴ surviving, for which pairwise interactions are generated against 10³ random and 10³ point-mutated self-peptides, representing foreign and tumor-associated neoantigens, respectively (randomly generated peptides were checked to ensure non-membership in the set of thymic selfpeptides). Estimates of individual TCR recognition probability were calculated by averaging the 5 · 10⁴-by-10³ indicator matrix, having values of 1 (resp. 0) corresponding to recognition (resp. no recognition). The previous quantity estimates an individual TCR’s antigen recognition ability. Estimates of the corresponding recognition probability for the entire post-selection MHC-restricted T-cell repertoire was calculated by assessing the 1-by-10³ vector indicating the presence or absence of at least 1 recognizing TCR. The post-selection individual and repertoire T-cell recognition probabilities of random and point-mutant antigens were then compared with previously derived analytic results for two random energy models [12].

6. Data Availability

The data comprised of the peptides recognized by the three TCRs, used for RACER training and testing, are available from [19]. An extended data set of these three TCRs were uploaded at Github: https://github.com/XingchengLin/RACER.git. The additional data used for training and testing on different MHC-II TCRs can be found in [44]. All other output from this study are available from the corresponding author upon reasonable request.