Abstract
Efficient navigation based on chemical cues is an essential feature shared by all animals. These cues may be encountered in complex spatiotemporal patterns and with orders of magnitude varying intensities. Nevertheless, sensory neurons accurately extract the relevant information from such perplexing signals. Here, we show how a single sensory neuron in Caenorhabditis elegans animals can cell‐autonomously encode complex stimulus patterns composed of instantaneous sharp changes and of slowly changing continuous gradients. This encoding relies on a simple negative feedback in the G‐protein‐coupled receptor (GPCR) signaling pathway in which TAX‐6/Calcineurin plays a key role in mediating the feedback inhibition. This negative feedback supports several important coding features that underlie an efficient navigation strategy, including exact adaptation and adaptation to the magnitude of the gradient's first derivative. A simple mathematical model explains the fine neural dynamics of both wild‐type and tax‐6 mutant animals, further highlighting how the calcium‐dependent activity of TAX‐6/Calcineurin dictates GPCR inhibition and response dynamics. As GPCRs are ubiquitously expressed in all sensory neurons, this mechanism may be a general solution for efficient cell‐autonomous coding of external stimuli.
Keywords: calcineurin/TAX‐6, calcium imaging, GPCR signaling, negative feedback, pulsatile response
Subject Categories: Neuroscience, Signal Transduction
A chemosensory neuron in Caenorhabditis elegans shows remarkable computational capacities to efficiently encode external stimuli. A TAX‐6‐mediated negative feedback loop within the GPCR signaling pathway underlies these computational capacities.
Introduction
Animals' fitness critically depends on efficient coding of environmental signals. For example, chemical cues allow animals to locate food sources, a mating partner, and avoid possible dangers. In nature, chemical cues often form complex spatiotemporal patterns. To support efficient navigation based on chemical cues (a process known as chemotaxis), animals need to accurately extract the relevant signals and robustly relay this information to subsequent neural layers.
There are two major modes by which animals may experience chemical cues. In rapidly changing environments (e.g., wind carrying plumes or abrupt flow changes), animals will sense instantaneous steep changes in stimulus concentration resembling a step‐like function of the stimulus (Murlis et al, 1992). Alternatively, in enclosed and turbulent‐free environments, where diffusion processes dominate, smooth chemical gradients will be formed. Under these conditions, animals will typically experience a gradual change in stimulus concentration. In both cases, stimulus concentrations may vary across several orders of magnitude imposing a great challenge for animals to reliably detect and follow stimulus changes (van As et al, 1985; Shirley et al, 1987; Gaudry et al, 2012; Sourjik & Wingreen, 2012; Levy & Bargmann, 2020).
To efficiently chemotax in complex varying environments, living organisms employ at least two sensory‐coding principles: exact adaptation and logarithmic coding. Exact adaptation implies that the sensory response to a stimulus is transient, and following an initial change, the response resumes to its baseline levels. This way, the sensory system becomes idle to respond upon encountering impending changes in stimulus levels (Berg & Tedesco, 1975; Zufall, 2000; Ferrell, 2016; Tu & Rappel, 2018). Logarithmic coding, also known as the Weber–Fechner law, is a hallmark of sensory systems found across different organisms and sensory modalities (Fechner, 1948; Laughlin, 1989). It dictates that perception depends on the ratio between stimulus change and the background level, thus effectively coding a logarithmic scale of the stimulus. This allows sensory systems to rescale their responses across several orders of magnitude of the signal (Lazova et al, 2011). Interestingly, this feature is thought to be intrinsically implemented in the receptor's thermodynamic properties, where increased ligand concentrations induce receptor allosteric modulations (e.g., phosphorylation), which shift the binding affinity between the receptor and its ligand (Olsman & Goentoro, 2016).
In single‐cell organisms, such as Escherichia coli bacteria, these principles are implemented by intracellular signaling pathways to support a biased‐random walk chemotaxis strategy (Block et al, 1983; Barkai & Leibler, 1997; Tu et al, 2008; Shimizu et al, 2010; Tu, 2013). In this navigation strategy, cells control the probability for making turns: increasing concentrations of an attractant suppress turning probabilities, such that the cells are more prone to continue moving forward, while decreasing concentrations of the attractant increase turning probabilities (Sourjik & Wingreen, 2012). Crucially, to maintain responsiveness over time, cell activity resumes its basal level even if the stimulus remains constantly on (thus implementing exact adaptation), allowing it to be idle to detect and respond to future changes.
In multicellular organisms, equipped with a neural network, one may assume that similar features may be attributed to dynamics within defined neural circuits. Interestingly, however, individual sensory neurons may also implement such computations in a cell‐autonomous manner (Tanimoto et al, 2017; preprint: Desrochers et al, 2018). For example, the nervous system of Caenorhabditis elegans nematodes consists of 302 neurons (White et al, 1986; Cook et al, 2019). A single pair of chemosensory neurons, the AWA neurons, exhibits a range of coding features in response to diacetyl, a chemoattractive food cue secreted from bacteria in decomposing fruits (Choi et al, 2016). Smooth and slowly increasing gradients of diacetyl lead to a pulsatile activity in the AWA neurons, where the frequency and the amplitude of the pulses increase the greater is the temporal derivative of the stimulus (Itskovits et al, 2018). This pulsatile activity was also observed in mutant animals, defective in neurotransmitter and neuropeptide secretion, suggesting that these sensory neurons may implement such intricate computation in a cell‐autonomous manner. Furthermore, following a step‐like increase in diacetyl concentrations, AWA calcium levels quickly rise and then return to near‐baseline levels even when diacetyl levels remain constantly high (exact adaptation). These responses are found for a wide range of diacetyl concentrations spanning seven orders of magnitude (Bargmann et al, 1993; Bargmann, 2006; Hart & Chao, 2009; Larsch et al, 2013, 2015; Itskovits et al, 2018).
Behaviorally, AWA activity facilitates forward locomotion, while a decrease in AWA activity promotes turning events (Larsch et al, 2015; Itskovits et al, 2018). Thus, a pulsatile activity dictates a run and tumble strategy, similar to the biased‐random walk behavior in E. coli (Pierce‐Shimomura et al, 1999). However, while cells typically adapt to the absolute levels of the stimulus, AWA pulsatile activity also adapts to the first derivative of the gradient (Itskovits et al, 2018). This coding principle was shown to support an efficient navigation strategy that outperforms the classical biased‐random walk strategy (Itskovits et al, 2018). An intriguing question then arises: how can a single neuron perform all these computations and efficiently encode complex stimulus patterns?
The AWA neuron exclusively expresses the diacetyl G‐protein‐coupled receptor (GPCR), named ODR‐10 (Bargmann et al, 1993; Sengupta et al, 1996). ODR‐10 activation follows the canonical GPCR signaling pathway: Upon binding of diacetyl, ODR‐10 leads to the dissociation of the trimeric G protein, where the Gα subunit stimulates opening of TRPV channels (Fig 1A), possibly via polyunsaturated fatty acids (Kahn‐Kirby et al, 2004; Larsch et al, 2015). Calcium ions then flow into the cell leading to a partial depolarization that subsequently triggers a much larger influx of calcium through the voltage‐gated calcium channels (EGL‐19), which culminates in a train of spiking events (Larsch et al, 2015; Liu et al, 2018).
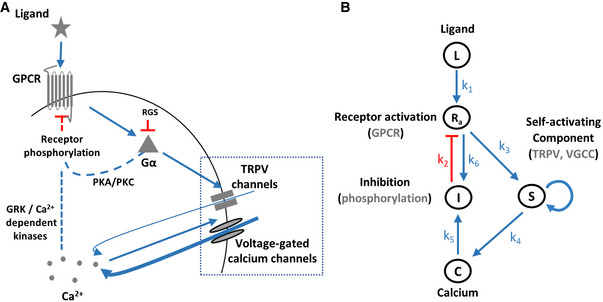
Figure 1. Illustration of the core GPCR signaling pathway and the analogous model.
-
AKey components of the GPCR signaling pathway. Dashed lines mark canonical GPCR pathways, though they have not been verified yet in the AWA neuron.
-
BAn analogous circuit topology that recapitulates the main signaling events related to calcium dynamics. Note that S (TRPV and VGCC) depicts a self‐amplifying module to generate the pulsatile activity. Symbols next to arrows mark the relevant constant in the model's equations. Blue arrows indicate activation, and red lines mark inhibition.
However, the mechanism by which AWA adapts to the odorant signal is unknown, though evidence suggests that it relies on a negative feedback loop (Rahi et al, 2017). A canonical model for GPCR adaptation relies on receptor phosphorylation events via two possible pathways: (i) second messenger‐induced kinases, namely PKA and PKC, which phosphorylate both active and inactive receptors, thus mediating a nonspecific (non‐homologous) adaptation (Fig 1A and B); (ii) G‐protein‐coupled receptor kinases (GRKs) that phosphorylate the active receptors, leading to receptor‐specific (homologous) adaptation. GRKs can be activated by calmodulin, a calcium‐binding protein, suggesting that calcium levels may indirectly regulate receptor adaptation (Lefkowitz, 1998; Zufall, 2000). In addition, regulators of G protein signaling (RGS), which inactivate the Gα subunit via GTP hydrolysis, may also contribute to sensory adaptation (Vries et al, 2000; Fukuto et al, 2004).
In this study, we demonstrate how a simple negative feedback in the GPCR signaling pathway underlies efficient coding of various spatiotemporal patterns of the stimulus. Remarkably, it enables cell‐autonomous translation of smooth gradients into a series of pulses that adapt to the magnitude of the gradient's first derivative. Furthermore, we identified TAX‐6/Calcineurin as a key component required for the negative feedback that leads to receptor adaptation. A simple mathematical model depicts an array of neural responses of both wild‐type (wt) and tax‐6 mutant animals. Given the ubiquitous expression of GPCRs in sensory neurons, this mechanism may account for efficient coding in other animals across different sensory modalities.
Results
A simple feedback model recapitulates experimental observations for coding complex stimulus patterns
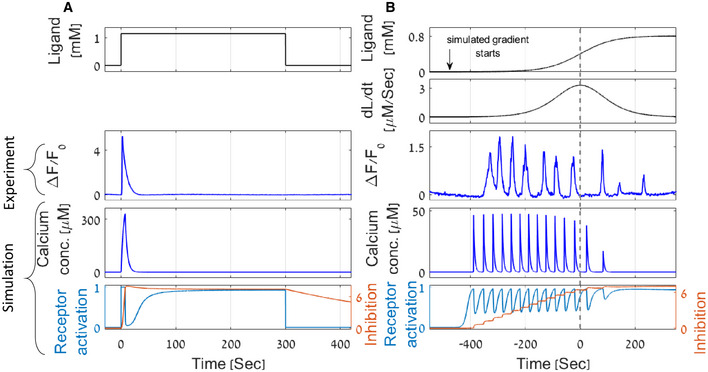
Studies in C. elegans worms revealed that a single sensory neuron type, AWA, cell‐autonomously implements key features required for efficient chemotaxis: (i) It codes the ligand concentration in a logarithmic‐like scale, so that neural responses remain similar across orders of magnitude of ligand concentration (Larsch et al, 2015; Itskovits et al, 2018). (ii) It responds with a single pulse to a step function and with multiple pulses during a continuous gradual increase in the stimulus concentration (Fig 2A; Larsch et al, 2013, 2015; Itskovits et al, 2018). (iii) It shows an exact adaptation following a step function of the stimulus (Fig 2A; Larsch et al, 2015; Itskovits et al, 2018). (iv) The mean frequency and the amplitude of the pulses, induced by smooth increasing stimuli, correlate with the first derivative of the gradient and also adapt to it (Fig 2B; Itskovits et al, 2018). Thus, the steeper the change in the gradient (higher first derivative), the higher are the frequency and the amplitude of the neural activity. On longer timescales, this activity adapts to the magnitude of the stimulus first derivative, such that the frequency and the amplitude of the pulses decrease if not facing increasing first derivative changes in the stimulus.
Figure 2. A parsimonious mathematical model recapitulates experimental results demonstrating exact adaptation, pulsatile coding, and adaptation to the magnitude of the first derivative.
-
A, BExperimental results and model simulations of calcium levels in response to a step function (A) and to a smooth sigmoidal function (B) of the stimulus. (A) Following an on step, and during stimulus presentation, calcium levels rise and then return to their basal levels (exact adaptation in experiment and simulation). Receptor activity () and inhibition levels () reach a new steady state. (B) A sigmoidal gradient of the stimulus elicits a series of calcium pulses that are stronger in the first half of the sigmoid, thus demonstrating adaptation to the gradient's first derivative (dashed line marks the sigmoid midpoint, where the first derivative is maximal). This feature is observed in both experiments and simulations. The stair‐shape inhibition constitutes a discrete memory of previous input levels. Top two panels show the gradient and its derivative. Middle panels depict a representative result of AWA calcium imaging. The two bottom panels present calcium concentrations (), receptor activation (), and inhibition () levels as simulated by the model for the same gradient. Calcium dynamics was measured using a strain expressing GCaMP in the AWA neuron and is denoted as the GCaMP fluorescence fold change from the initial state . Diacetyl (stimulus) was presented to the worm using a custom‐made microfluidic device (see Materials and Methods).
Source data are available online for this figure.
To understand how these intricate coding schemes can be cell‐autonomously implemented, we considered the GPCR signaling pathway and constructed a simple parsimonious model of its known signaling components (Fig 1B). In this model, the stimulus ligand () binds the GPCR to convert it to its active state (). The active state, through the small Gα subunit, activates TRPV and subsequently VGCC (together denoted as ) to depolarize the cell by increasing cytoplasmic calcium levels (). Elevated calcium levels activate an array of proteins, including GRKs (denoted as ), which lead to phosphorylation and eventual inhibition of the GPCRs. Gα‐mediated activation of PKA and PKC also contributes to GPCR inhibition, and this inhibition is also included in the inhibitory component ().
The dynamics of this signaling pathway can be simulated using a set of four equations (equations (1), (2), (3), (4)), where each equation describes the temporal change of one of the main signaling components (see Appendix Note S1 part 1 for extended descriptions).
| (1) |
| (2) |
| (3) |
| (4) |
The fraction of active receptors (, equation (1)) is described by a sigmoid function, where the levels of active receptors scale logarithmically with the concentration of the ligand (as was shown for the dynamics of E. coli receptors; Tu et al, 2008). inhibition (e.g., via phosphorylation) is linearly dependent on the levels of the inhibitors . This representation is motivated by previous reports showing that when the sensor's activity increases logarithmically with ligands' concentration, the negative feedback loop enables logarithmic coding (Tu et al, 2008).
Equation 2 describes a switch‐like transition in the state of TRPV and VGCC (). These channels open once active receptors cross a threshold value, , and close otherwise. The switch‐like dynamics is due to self‐activating voltage‐dependent properties of the VGCCs, through which the majority of the calcium enters the cell. This self‐amplification underlies the pulsatile activity and is a known molecular switch motif (Ferrell & Machleder, 1998; Zhang et al, 2007).
Intracellular calcium concentration () increases upon opening of the channels () while a first‐order removal term decreases it back to baseline levels, (equation 3). The fact that calcium removal is proportional to calcium concentration enables exponential decay in calcium levels, as was also experimentally observed (Itskovits et al, 2018). Finally, equation 4 describes the circuit negative feedback (), where calcium‐dependent (e.g., GRKs, denotes by the arrow) and calcium‐independent (e.g., PKA/PKC, denoted by the arrow) pathways enhance inhibition, and a first‐order removal term suppresses it. Borrowing the exact adaptation concepts developed for the E. coli chemosensory circuit, we posit that inhibition is proportional to the fraction of active receptors (), and the removal term is proportional to the fraction of inactive receptors (). A detailed description and analysis of the mathematical model are available in Appendix Note S1 parts 1–3 and Appendix Table S1.
Remarkably, the simple parsimonious model of a negative feedback in the GPCR signaling pathway captures the key features that we observed experimentally (Fig 2): An on step of the diacetyl stimulus resulted in a single calcium pulse, which decayed to baseline levels even though the stimulus remained constantly present (Fig 2A). Similarly, both the experiments and the simulation results showed pulsatile dynamics in response to smooth sigmoid gradients of the stimulus (Fig 2B). Moreover, the amplitude and the frequency of the pulses increase with the gradient's first derivative but also adapt to it. Thus, in response to a sigmoidal gradient, in which the first derivative is symmetric around the gradient's midpoint, the pulsatile response is stronger in the first half, up to the maximal first derivative point, and decreases thereafter (Fig 2B). Of note, the pulsatile activity greatly varies between individuals (Appendix Fig S3A). This variability, which can be reproduced when simulating the model with slightly different random variables of the parameter space (Appendix Fig S2D–F), manifests in the number of the pulses, their amplitude, as well as in their frequency. Nevertheless, the pulsatile response and the correlation of the pulse's amplitude and frequency with the gradient's first derivative are robust features.
How does the circuit model translate an increasing gradient of the stimulus input into a pulsatile calcium activity, an output that both increases with the input's derivative and adapts to it? Consider a smooth slowly increasing stimulus: At the beginning, calcium levels are close to baseline levels such that the inhibition is relatively constant (equation 4). As stimulus concentration gradually increases, the fraction of active receptors also rises (equation 1). Once it crosses a threshold value, , TRPV, followed by the VGCCs, will open (equation 2), resulting in a calcium pulse (equation 3). The high intracellular calcium concentration enhances a quick inhibition (equation 4), thus reducing the fraction of active receptors below the critical threshold, (equation 2), in which case, the pulse is terminated by exponential removal of the calcium (equation 3). Relaying the signaling output, , to directly facilitate inhibition is known as an integral feedback and underlies exact adaptation (Yi et al, 2000). As time passes and the stimulus concentration increases, this process will repeat itself to produce an additional calcium pulse. Since receptors' activation is logarithmically dependent on the input, the change required in the input levels to elicit a consecutive pulse becomes increasingly larger. For a linear gradient, this implies that the time interval between consecutive pulses will increase, effectively leading to an adaptation to the input gradient. In fact, a detailed mathematical analysis shows that the time interval between consecutive pulses increases exponentially with the pulse index number and is inversely proportional to the linear gradient derivative (Appendix Note S1 part 3).
Our model qualitatively captures additional functional features observed in AWA response dynamics (Appendix Fig S1). In response to repetitive high‐frequency steps of the stimulus, inhibition removal may be too slow, and hence, activity would not be observed in response to all repetitive stimulations, a phenomenon known as periodic skipping (compare Appendix Fig S1B and C and see also experimental evidence in Larsch et al, 2015; Rahi et al, 2017). Furthermore, in response to short on steps, our model predicts gradual adaptation: a decrease in response amplitude between consecutive steps (Appendix Fig S1A), which was also observed experimentally (Larsch et al, 2015; Rahi et al, 2017).
Notably, the main features of the model outputs are robust to changes in the values of the different parameters. We simulated the system behavior while varying each parameter by ∼100‐fold (See Materials and Methods). Despite the broad parameter space, the qualitative dynamics remained largely unaffected, where key features such as exact adaptation and adaptation of the pulsatile activity were maintained (Appendix Fig S2, Appendix Table S1). When simultaneously varying all the model's parameters (except for ) by 10‐fold, the qualitative dynamics remained intact in 75% of the cases (see Materials and Methods). Moreover, the model's output is robust to over 10,000‐fold variation in stimulus concentration, a necessary requirement for a versatile sensory system that can code and robustly respond to a range of concentrations. These results indicate that the model shows robust outputs that are insensitive to the exact values of its variables.
TAX‐6/calcineurin is required for the pulsatile response
A classic feedback circuit that achieves full adaptation requires the inhibition to depend on the circuit output (Barkai & Leibler, 1997; Tu et al, 2008). We therefore analyzed several mutants that had been suggested to affect adaptation in C. elegans worms. These included: odr‐3, which codes the Gα protein, and eat‐16, an RGS homolog regulating Gα activity (Roayaie et al, 1998; Hajdu‐Cronin et al, 1999); grk‐2, which affects G‐protein signaling in sensory neurons (Wood & Ferkey, 2016); osm‐6, which is responsible for cilia integrity and intraflagellar transport (Larsch et al, 2015); arr‐1, an arrestin homolog (Fukuto et al, 2004; preprint: Merritt et al, 2021); and tax‐6, a calcineurin shown to cell‐autonomously mediate adaptation in different sensory neurons (Kuhara et al, 2002).
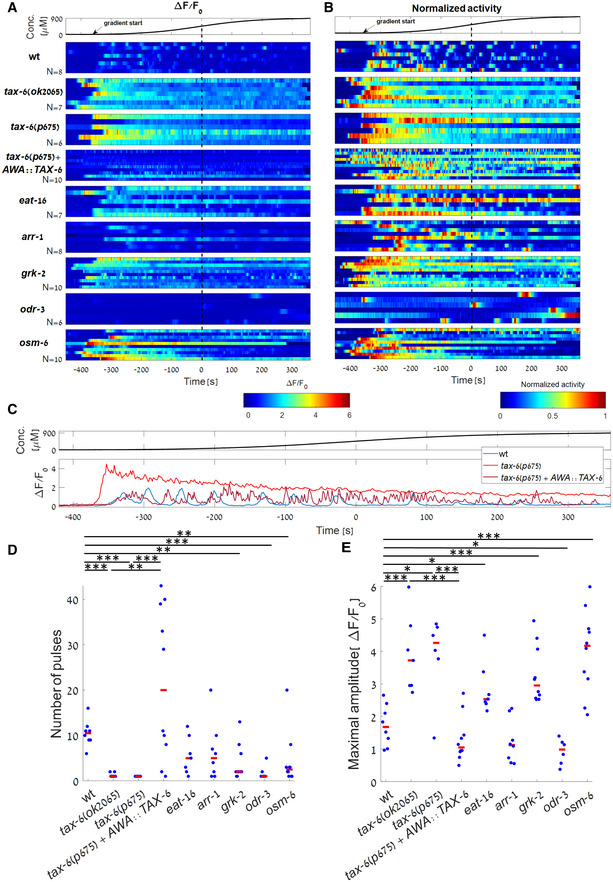
First, we analyzed the capacity of these mutant strains to generate pulsatile activity in response to smooth gradients of the stimulus diacetyl (Fig 3 and Appendix Fig S3). As expected, calcium transients were barely observed in odr‐3 mutants as this protein is the immediate downstream component of the GPCR ODR‐10. Interestingly, robust loss of pulsatile activity was observed in tax‐6 mutants (in both p675 and ok2065 alleles). These mutant animals exhibited a single pulse at the start of the gradient ramp, which then slowly decayed over the entire course of the experiment (Fig 3A–D and Appendix Fig S3B and C). A similar dynamics was observed in grk‐2 mutants (although the effect was less prominent), and in some of the eat‐16 and osm‐6 mutants (though not as consistent as observed in the tax‐6 mutant animals, Fig 3A and D and Appendix Fig S3E and I). In addition, the maximal amplitude of tax‐6 pulses (as well as of grk‐2, eat‐16, and osm‐6) was significantly higher than the maximal amplitude observed in wild‐type worms (Fig 3E). Together, these results suggested that TAX‐6/Calcineurin and GRK‐2 play a key role in inhibiting signaling and reducing intracellular calcium levels, effectively terminating the pulsatile activity.
Figure 3. Analysis of dynamic responses and adaptation in different mutant backgrounds.
-
A, BResponse profiles of individual wt and mutant worms to a sigmoidal gradient (top). Shown are the fold change activity (A) and the normalized activity (B) of wt, tax‐6(ok2065), tax‐6(p675), tax‐6(p675) + AWA::TAX‐6, eat‐16, arr‐1, grk‐2, odr‐3 and osm‐6 mutant worms ( worms, respectively). Due to the high variability of the GCaMP baseline fluorescence, , between and within each of the mutant strains, we considered fluorescence fold change, , when analyzing pulsatile activity. Tax‐6 mutants lacked any pulsatile activity (raw traces are shown in Appendix Fig S3). Time is aligned to the gradient's inflection point, in which the first derivative is maximal (dotted black line). Arrow marks the approximated time in which odorant levels start to rise.
-
CRepresentative traces of wt, tax‐6(p675), and tax‐6(p675) + AWA:TAX‐6 worms (taken from the first row of each strain in panel A).
-
D, ETo quantify the differences in activity between wt worms and the various mutants, we extracted individual pulses (see Materials and Methods). When compared with wt, number of pulses was significantly lower in tax‐6(ok2065), tax‐6(p675), grk‐2, odr‐3, and osm‐6 mutants (, respectively). Maximal amplitude was significantly higher in tax‐6(ok2065), tax‐6(p675), eat‐16, grk‐2, and osm‐6 mutants (P = 0.002, 0.02, 0.02, 0.002, 0.003 respectively) and significantly lower in odr‐3 mutants (P = 0.04). In both tax‐6 mutant alleles (ok2065 and p675), the number of pulses was significantly lower when compared with the rescued strain ( respectively), and the maximal amplitude was significantly higher (, respectively). Wilcoxon rank‐sum test, FDR corrected for the 20 comparisons. Red bar marks the median. *P < 0.05, **P < 0.01, ***P < 0.005.
Source data are available online for this figure.
TAX‐6/calcineurin cell‐autonomously promotes exact adaptation and habituation
As tax‐6 mutants completely lost the ability to generate pulsatile activity in response to smooth gradients, we proceeded with this gene to analyze its capacity to reach exact adaptation, a hallmark of chemosensory coding. Furthermore, as the results for both mutant alleles were essentially similar, we proceeded with the p675 allele only. To analyze the capacity to reach exact adaptation, we exposed the worms to a 5‐min long on‐step of diacetyl (Fig 4A, bottom panels). To analyze possible habituation, a reduction in the neural response between consecutive on steps (Larsch et al, 2015), we inflicted a second short on step following 2 min off step.
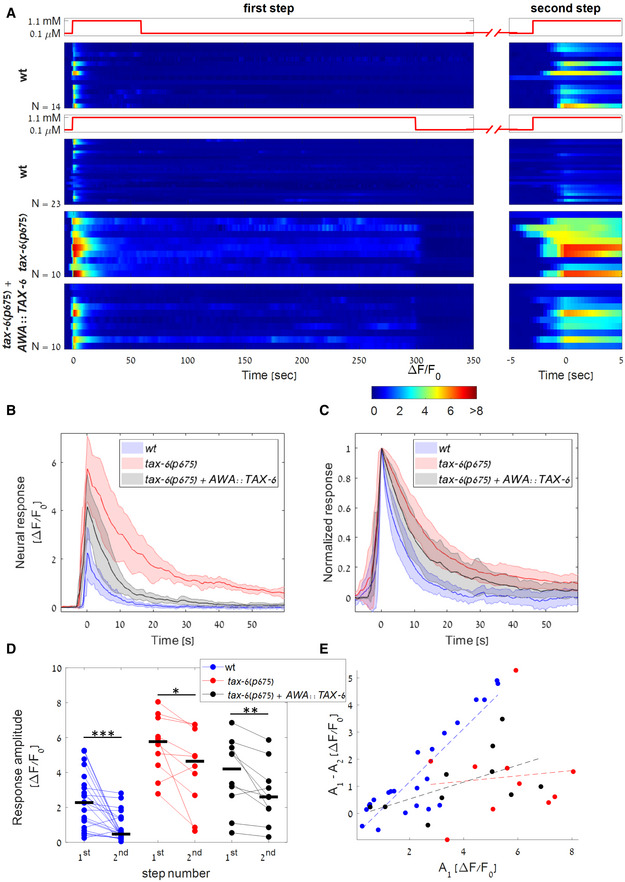
Figure 4. TAX‐6/Calcineurin is required for exact adaptation and habituation.
-
AResponse dynamics of wt, tax‐6(p675), and tax‐6(p675) + AWA::TAX‐6 worms to a two‐step protocol: First step consisting of 5 min (bottom panels, worms respectively) or 1 min (top panel, wt worms. Biological replicates) of on step, followed by a 2 min, or 6 min off step, respectively, before applying a second short step (right panels). Wt worms exposed to the 5‐min step showed stronger habituation compared to worms exposed to the 1‐min‐long step (, Wilcoxon rank‐sum test between the amplitudes of the second steps). Steps are aligned to the maximal amplitude (at time 0).
-
B, CMedian neural activity (B) and normalized neural activity (C) of wt, tax‐6(p675), and tax‐6(p675) + AWA::TAX‐6 worms in response to the first step. Fitting the pulse decay with an exponent of the shape , tax‐6 mutants showed a longer decay time than wt worms, suggesting slower adaptation dynamics ( of and s, respectively, Wilcoxon rank‐sum test, ). of the rescue line was s, which was not significantly different from wt (Wilcoxon rank‐sum test, ). Color‐shaded area marks mean absolute deviation.
-
DComparison of the amplitudes in the first and the second step for wt, tax‐6(p675), and tax‐6(p675) + AWA::TAX‐6 worms (following the longer 5‐min step). All three strains showed a weaker activity in the second step (signed‐rank test, , respectively), with tax‐6(p675) worms having a significantly higher amplitude than wt in both the first and second steps (Wilcoxon rank‐sum test, and respectively). Black bars mark the median. *P < 0.05, **P < 0.01, ***P < 0.005.
-
EThe difference between the response amplitudes of the first and the second steps as a function of the first‐step amplitude. While wt worms show a higher amplitude difference when the response to the first step is stronger (), tax‐6(p675) mutants do not (r = 0.1, P = 0.78), suggesting that calcium influx affects habituation in wt worms but not in tax‐6(p675) mutants. The linear dependency in the rescued animals (tax‐6(p675) + AWA::TAX‐6) is higher than in tax‐6 mutants, though the correlation is not significant ().
Source data are available online for this figure.
Following the first step, the response amplitude of the tax‐6 mutants was significantly higher than that of wt worms, and it was followed by a significantly slower exponential decay (Fig 4B and C). Notably, the neural activity of eight out of the 10 tax‐6 mutants did not return to its baseline levels for the entire duration of stimulus presentation, indicating a failure to perform exact adaptation (Fig 4A, bottom panels). Only when removing the stimulus (following 5 min of on step) did the activity resume to its basal level. Importantly, the failure to reach exact adaptation was not due to the enhanced neural activity since eat‐16 mutants also showed enhanced responses to a sigmoidal gradient (Fig 3E) and yet, reached exact adaptation following an on‐step stimulation (Appendix Fig S4).
Furthermore, both the wt worms and the tax‐6 mutants habituated to the stimuli, showing weaker responses to the second step (Fig 4D). However, only in wt worms this reduction positively correlated with the magnitude of the first pulse (Fig 4E). This suggests that initial stronger pulses, which lead to greater calcium influx, also increase TAX‐6‐mediated adaptation processes (Fig 4E and Appendix Fig S5). Therefore, as TAX‐6/Calcineurin activity is calcium‐dependent, calcium may provide the negative feedback required for the TAX‐6‐mediated adaptation.
We next asked whether factors other than calcium may also contribute to habituation. For this, we compared neural responses of wt animals following either a short or a long on step of the stimulus. The short on‐step stimulus essentially allowed the worms to be off the stimulus for a longer time period before inflicting a second on step (Fig 4A, top panel). While calcium dynamics in both protocols was similar in response to the first step, the response to the second step was significantly reduced following the long‐step protocol where the worms had a shorter time period to recover before the start of the second on step (Fig 4A, compare top two panels). Notably, in both protocols, calcium levels between the onset of the first and the second steps were similar. This suggests that a second, calcium‐independent adaptation mechanism may exist. An alternative explanation is that recovery from adaptation can only occur in the absence of an external stimulus. We found similar results when comparing activity dynamics in response to a multistep protocol and a single long‐step protocol (Appendix Fig S5).
TAX‐6 is widely expressed in the C. elegans nervous system (Kuhara et al, 2002; Taylor et al, 2021). We therefore asked whether TAX‐6 promotes exact adaptation and habituation in the AWA neurons cell‐autonomously or possibly via feedback from other neurons. For this, we introduced TAX‐6 expression in a tax‐6 mutant (p675) exclusively in the AWA neurons (see Materials and Methods). Notably, the wt AWA dynamical features were restored: When facing a stimulus gradient, the pulsatile activity was reestablished (Fig 3A–D and Appendix Fig S3D), and the amplitude of these pulses was reduced to wt levels (Fig 3E). In response to a stimulus step, the heightened amplitude of tax‐6 mutants was reduced to be closer to wt levels, and exact adaptation was observed in a fraction of the tested worms (Fig 4A–D). In addition, the correlation between habituation and the amplitude of the first pulse was partially restored, shifting the tax‐6 response dynamics closer to that of the wt (Fig 4E). These results suggest that TAX‐6 acts cell‐autonomously in the AWA neurons to promote pulsatile activity, exact adaptation, and habituation between consecutive pulses.
TAX‐6/calcineurin‐mediated inhibition does not affect the activity of voltage‐gated calcium channels
The response dynamics of tax‐6 mutants to diacetyl was significantly different than that of wt worms: they exhibited a heightened single calcium pulse, which did not resume to basal levels (hence no exact adaptation). To elucidate how the lack of TAX‐6 inhibition leads to the differential response, we subjected the worms to artificial light‐induced activation using the optogenetic channel Chrimson (Fig 5A). This light activation increases calcium levels that directly affect VGCC opening and thus bypasses the natural activation and signaling through the ODR‐10 GPCR and the TRPV channels (Fig 1A).
Figure 5. wt and tax‐6 mutants show similar response dynamics following optogenetic stimulation.

-
AAWA calcium dynamics of wt and tax‐6(p675) mutants ( worms respectively) in response to three repeated light activations (488 nm). Each worm was illuminated thrice, each for 1‐min long with 1‐min rest between consecutive stimulations. Responses are shown as fold differences in fluorescence from the first captured frame.
-
BPeak amplitudes as measured for each of the activations. Following light activation, and in contrast to the response to diacetyl, response of tax‐6 mutants was not stronger than the response of wt worms ( Wilcoxon rank‐sum test between the amplitudes of wt and tax‐6(p675) in response to the first or third light activation, respectively). Black bars mark the median. Horizontal lines denote the compared groups. *P < 0.05, **P < 0.01, ***P < 0.005.
-
CMedian response dynamics of wt and tax‐6(p675) worms for the first light activation. The two strains show similar activation dynamics. All responses were aligned to their maximal activation levels prior to extraction of the median values. Shaded‐colored area marks mean absolute deviation.
-
DActivations from the same worm tend to cluster together indicating a low in‐worm variability, while the between‐worm variability is high. The first 30 s in each of the three light activations of the 10 wt worms shown in (A) were normalized by the maximal amplitude and decomposed using Principal Component Analysis (PCA). Shown are the projections of each activation to the first two PCs (capturing 90% and 6% of the variance, respectively). Each color represents a single worm (three activations for each worm). Colored dashed lines were added manually.
Source data are available online for this figure.
For this, neurons were light‐activated thrice, each time for 1‐min long, while simultaneously imaging calcium dynamics. During the continuous 1‐min long optogenetic activation, both wt and tax‐6 worms showed a similar fast (∼2 s) increase in calcium levels, which was followed by a slow gradual decrease (Fig 5A). The second and the third light activations elicited responses that were similar to the responses observed after the first light activation, though with a mildly lower amplitude, which may be attributed to bleaching of the fluorescent signal (Fig 5A and B). In fact, both wt and tax‐6 mutants showed similar neural dynamics in response to light activations (Fig 5C). This is in stark contrast to their differential responses to the natural stimulus diacetyl (Fig 4B and C). Since calcium influx mediated by repeated light‐induced activations does not lead to adaptation, this suggests that TAX‐6/Calcineurin mediates calcium feedback inhibition by affecting the signaling cascade between the ODR‐10 receptor (including) and the TRPV channels (see Fig 1).
Another interesting observation is the relative heterogeneity in the responses of individual worms to the light stimulus. While the response pattern of each worm seems highly repetitive, the fine activation dynamics in the different worms varied with respect to the amplitude, the rise time, and decay kinetics (Fig 5A). To visualize the differences of individual responses, we normalized each response by its maximal amplitude and used Principal Component Analysis (PCA) to project each activation pattern of the wt worms on the two main PCs (Fig 5D). Indeed, the three activations of each worm cluster together, indicating a low in‐worm variability and high between‐worms variability. Notably, these idiosyncratic responses were observed in an isogenic population of worms, expressing the same levels of Chrimson (chromosomally integrated), and grown under the exact same conditions. Thus, the animals' cell‐intrinsic state (e.g., expression levels of the different components, channel's functional states) may govern the shape of the response dynamics.
A GPCR negative feedback model recapitulates fine dynamic responses of wt and tax‐6 mutants
The above experiments position calcium and TAX‐6/Calcineurin as key components for GPCR inhibition and exact adaptation. We therefore turned back to our parsimonious model (equations (1), (2), (3), (4) and Figs 1 and 2) and asked whether elimination of TAX‐6/Calcineurin from the circuit will recapitulate the experimental results.
To simulate dynamics of tax‐6 mutants, we nullified the calcium‐dependent term from equation 4 in the original model (by setting ). Hitherto, for simplicity purposes and to allow analytical tractability of the model (Fig 1 and equations (1), (2), (3), (4)), we did not include explicit description of the voltage‐gated channels dynamics in AWA. These details were not crucial for modeling dynamics in wt animals, where the negative feedback was the major drive for exact adaptation. However, in tax‐6 mutants that lack the negative feedback, the role of the voltage‐gated ion channels in reducing calcium levels becomes prominent. Thus, for completeness, we have now included in the model a module that provides the fine details for the initiation and termination of the pulses within the AWA neurons. This module was implemented exactly as it appears in (Liu et al, 2018), who experimentally measured intracellular currents (see details in Appendix Note S1 part 4).
The resulting simulations recapitulated the experimental results. When exposed to increasing gradients of the stimulus, wt animals exhibited a pulsatile activity that adapted to the magnitude of the gradient's first derivative (Fig 6A). In contrast, activity of tax‐6 mutants showed a single pulse whose amplitude was higher than that of the wt worms. However, our simplified model failed to accurately describe the slow decay of the pulse in tax‐6 mutants, probably due to our oversimplification of the two‐states self‐amplification process (equation 2).
Figure 6. A detailed mathematical model recapitulates experimental results of both wt and tax‐6 mutant worms.
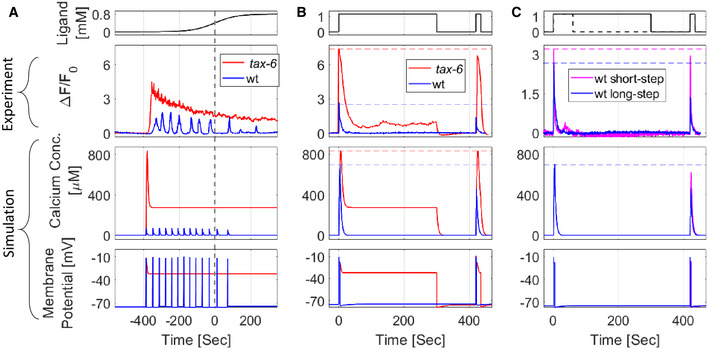
In the detailed model (see Appendix Note S1 part 4), we integrated the available dynamics of the AWA ion channels (Liu et al, 2018). To simulate circuit dynamics of tax‐6 mutants, we set the contribution of calcium‐mediated inhibition to zero ( in equation 4 and shown in Fig 1B).
-
A–CCalcium concentration and membrane potential as simulated by the model, alongside calcium imaging measurements of a representative worm in response to different stimulation patterns (top). (A) In response to a sigmoidal gradient, simulated tax‐6 worms fail to generate pulsatile activity, in agreement with the experimental results. Also, activity does not resume to its baseline levels. (B) Response dynamics following a first long on step (identical to experiment protocol described in Fig 4). Experimental and simulated wt worms exhibit reduced amplitude responses (increased habituation) following the second on step. In contrast, tax‐6 mutants did not show exact adaptation nor a reduced activity in response to the second on step (no habituation). (C) Response dynamics of wt worms following a first long (continues line) or short (dashed line) on step. A second on step following a short on step (and hence a long off step), elicits calcium levels that match the first step (purple). This contrasts with the attenuated response following a long on step (and hence short off step, blue). Even though in both protocols, calcium concentrations returned to baseline levels, the longer the off step, the higher the response activity to a second step (in agreement with experimental results, Fig 4A), suggesting that calcium‐independent processes contribute to the inhibition. Note the different y‐scale for the experimental results in panels (B) and (C).
Source data are available online for this figure.
When considering the responses to discrete on steps of the stimulus, our simulation qualitatively captured the observed experimental results (Fig 6B and C). Wt animals exhibited a single pulse whose dynamics returned to the basal level (exact adaptation), while tax‐6 mutants responded with a single pulse that was higher in amplitude and which remained above basal level for as long as the stimulus remained on. This heightened amplitude of tax‐6 mutants was also observed following the second step, whereas the response of wt worms to the second step was reduced, suggesting that tax‐6 mutants fail to habituate to past experienced stimuli (Fig 6C, Appendix Fig S6).
Finally, to verify that our model also captures calcium‐independent inhibitory processes, we compared the simulated and the experimental response dynamics of wt worms in the two consecutive on‐step stimulation protocols (short and long intervals, Figs 4A and 6C). While calcium responses to the first on step were identical in both protocols, the amplitude of the second pulse, following a short off‐step interval, was lower (Fig 6C), in agreement with the experimental results (Fig 4A). Notably, the lower amplitude observed following the second step was despite the fact that calcium levels already resumed to baseline levels. This suggests that inhibition is also affected by calcium‐independent inhibition processes.
Taken together, our parsimonious model captured the key features that were experimentally observed: calcium‐dependent and calcium‐independent inhibition, exact adaptation, habituation, and the corresponding dynamics in tax‐6 mutants, which lack inhibitory capacity. Notably, these features robustly appear despite the model's large parameter space and the various possible outcomes.
Discussion
In this work, we demonstrated how a simple negative feedback loop in the GPCR signaling pathway promotes efficient coding of complex stimulus patterns. Moreover, we showed how this coding is achieved cell‐autonomously and identified Calcineurin/TAX‐6 as key for the negative feedback. A simple mathematical model recapitulated the experimental results observed in both wt and a calcineurin‐deficient mutant strain, further underscoring the validity of the model and the interpretation of the experimental results.
Notably, the GPCR negative feedback supports several important computational features, including: (i) coding ligand concentration on a logarithmic‐like scale, thus enabling adjusted responses across several orders of magnitude of the stimulus. (ii) Responding with a single pulse to a step function and with multiple pulses when presented with a continuous increasing gradient of the stimulus. (iii) Exhibiting exact adaptation even when the stimulus remains on. (iv) The mean frequency and the amplitude of the pulses correlate with and adapt to the magnitude of the gradient's first derivative. It is therefore remarkable that all these features can be achieved cell‐autonomously with a simple negative feedback loop.
These features are embedded in the signaling pathway in a modular fashion (Fig 7). Adaptation to the first derivative of the gradient and logarithmic‐like coding are achieved by the inherent activity mode of GPCRs (Olsman & Goentoro, 2016). These receptors are logarithmically facilitated by the ligand, but linearly inhibited by intracellular components. Exact adaptation is achieved by calcium‐mediated inhibition. As calcium levels can be viewed as the circuit output, their feedback inhibition forms an integral feedback that underlies exact adaptation, in analogy to the exact adaptation observed in the E. coli chemotaxis system (Barkai & Leibler, 1997; Yi et al, 2000; Tu et al, 2008). Pulsatile coding of smooth gradients is driven by a self‐excitatory element, which converts the graded response into a series of pulses. As the negative feedback loop links all these features together, removing a single element, such as TAX‐6/Calcineurin, disrupts all these functions.
Figure 7. The negative feedback loop can be decomposed into discrete modules where each module fulfills a defined computational role.
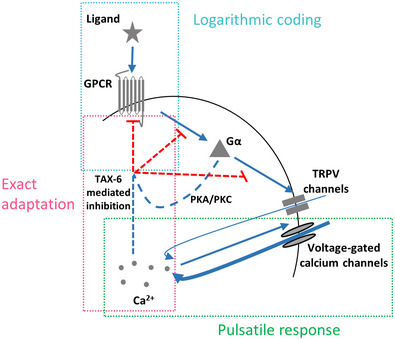
Logarithmic coding is achieved by the logarithmic transformation of ligand levels to receptor's activity, which in turn is linearly inhibited by the system's output (calcium levels). Exact adaptation is achieved by the integral feedback where the system's output inhibits receptor activity in a calcium‐dependent manner. The self‐amplifying activity of the TRPV and VGCC channels underlies the pulsatile activity. TAX‐6/Calcineurin may be acting as a negative feedback on any of the processes marked in red dashed line.
Clearly, this negative feedback necessitates that all the components will be localized to the cilia, the dendrite ending region. Indeed many of the components had been shown to be localized to the dendrites and cilia of C. elegans sensory neurons, including the ODR‐10 GPCR, the Gα subunit ODR‐3, the VGCC EGL‐19, and TAX‐6/Calcineurin (Sengupta et al, 1996; Roayaie et al, 1998; Kuhara et al, 2002; Mukhopadhyay et al, 2008; Shindou et al, 2019). Supporting this hypothesis, we observed calcium pulsatile activity in the AWA dendrite and cilia activity, which was synchronized with the calcium transients observed in the cell soma (Movie EV1).
We discovered that TAX‐6/Calcineurin serves as a key component in inhibiting GPCR signaling: while tax‐6 mutants were unable to generate pulsatile activity and reach exact adaptation in response to the natural stimulus diacetyl (Figs 3 and 4), their calcium dynamics following optogenetic activation was similar to wt worms (Fig 5). This positions the TAX‐6/Calcineurin to mediate inhibition along the pathway between the GPCR to the TRPV (Figs 1 and 7). Importantly, TAX‐6 mediates inhibition cell‐autonomously: when expressing TAX‐6 exclusively in the AWA neurons of tax‐6 mutants, we were able to rescue exact adaptation and pulsatile response (Figs 3 and 4). This rescue was observed in a fraction of the animals, possibly due to the variable expression levels of TAX‐6 that is expressed from an extrachromosomal array. This is also in line with a previous report showing that TAX‐6 can cell‐autonomously control adaptation in a number of sensory neurons and modalities (e.g., the thermosensory AFD neurons, the polymodal ASH neurons, and in the olfactory AWC neurons; Kuhara et al, 2002). For example, tax‐6 mutants are hyper‐adaptive to odorant pre‐exposure and AWC‐specific rescue restores this phenotype. Thus, our observations that tax‐6 mutants show long‐lasting calcium fluxes that fail to resume basal pre‐stimulus levels may explain the hyper‐adaptation phenotypes scored via behavioral outputs (Kuhara et al, 2002). This long‐lasting pulse also prevents formation of sequential pulses, presumably rendering the AWA neurons insensitive to the gradient, thus leading to defective chemotaxis (Movies EV2 and EV3 and Appendix Fig S7).
How could TAX‐6/Calcineurin promote inhibition? Calcineurin is a phosphatase, thus it may indirectly mediates phosphorylation of active GPCRs (Creamer, 2020). Such feedback, where the active receptors that initiate the signaling cascade are also modified, is known as homologous adaptation. For example, homologous adaptation was shown in the C. elegans AWC neuron, where adaptation to one odorant did not lead to adaptation to a second odorant, which is sensed by the same neuron, presumably because it signals through a different receptor (Colbert & Bargmann, 1995). In C. elegans, GPCR phosphorylation is presumably carried out by grk‐1 and grk‐2 (which may work redundantly, as a mutation in grk‐2 alone does not lead to reduced adaptation nor to hypersensitivity; Fukuto et al, 2004), as well as by the calmodulin‐dependent protein kinase II homolog unc‐43 (Hobert, 2013). Interestingly, phosphorylation of active receptors is thought to underlie the logarithmic coding of GPCRs (Olsman & Goentoro, 2016).
It was previously demonstrated that exact adaptation can be achieved when the output signal directly inhibits the sensor in a negative feedback loop (Barkai & Leibler, 1997; Tu, 2013). As calcium drives the main synaptic output of neurons (Katz & Miledi, 1970; Llinás et al, 1976), it constitutes a preferable candidate to mediate adaptation via a calcium‐binding enzyme, such as TAX‐6/Calcineurin. The link between calcium and inhibition is further supported by the correlation between calcium influx and the magnitude of the habituation (Fig 4E). Interestingly, a similar correlation between calcium levels and habituation was also observed in mice (Vinograd et al, 2017), suggesting that similar principles may underlie these processes in higher organisms. As habituation to the stimulus persisted even after calcium levels returned to their baseline levels (Fig 4A), a second, calcium‐independent inhibitory process may also exist.
To better understand the key principles that promote these coding dynamics, we constructed a simple mathematical model that captured key dynamics features of both wt and tax‐6 mutant animals. Notably, rather than accurately fitting the experimental results, the main purpose of this model was to demonstrate how a calcium‐mediated feedback inhibition in the GPCR signaling pathway can robustly explain an array of sensory responses: It enables pulsatile activity as well as adaptation to the first derivative of the gradients; it is responsible for exact adaptation in response to step changes; and it mediates habituation between sequential presentations of the same odorant cue.
Another model for neural activation was proposed by Levy and Bargmann, known as the adaptive‐threshold mechanism (Levy & Bargmann, 2020). According to this mechanism, the threshold for initiating a neural response in the AWC sensory neurons is not fixed, but rather a dynamic variable that changes depending on the history of the perceived stimulus. Our experimental design and modeling results, which considered smooth continuous gradient stimuli, carry such stimulus history, and with few assumptions, our model is mathematically analogous to the adaptive‐threshold model (A detailed mathematical derivation is found in Appendix Note S1 part 5).
When constructing the model, we strived to simplify the detailed signaling cascades, focusing on the key computational components that underlie the observed coding. For this, we grouped components acting together or sequentially and abstracted parts of the system's dynamics. For example, we modeled activities of TRPVs and VGCCs as a single self‐activating component. As AWA neurons generate action potentials (Liu et al, 2018), a more realistic model would include the positive feedback loop between the VGCCs, the potassium channels driving the action potential downstroke, and the membrane potential (dictated in part by calcium). It is conceivable that the calcium pulses may be initiated as a result of a spike train resulting from voltage‐dependent conductance. However, these spikes operate on shorter timescales than the calcium transients and the longer temporal decay of intracellular calcium (on the order of tens of seconds, Fig 3) may be crucial for the negative feedback of the GPCR pathway. This longer timescale also dictates behavioral outputs, as animals maintain a straight trajectory during the pulse when AWA neurons are active and turn once the pulse is terminated (Itskovits et al, 2018).
Interestingly, the activation dynamics in individual animals considerably varied, even in response to identical highly reproducible optogenetic activations (Fig 5). This variability is in line with previous reports demonstrating significant differences between individual worms in neural activity patterns and behavioral outputs (Luo et al, 2014; Gordus et al, 2015; Stern et al, 2017; preprint: Desrochers et al, 2018; Itskovits et al, 2018; preprint: Pritz et al, 2020). Notably, the assayed worms were isogenic and were grown in the exact same conditions. The fact that these neural responses are cell‐autonomous (Itskovits et al, 2018) may suggest that a significant variability between individual animals is due to differences in cell‐specific internal states (Marder & Goaillard, 2006). Nevertheless, despite the inherent noise and the significant differences in response dynamics, all neurons showed exact adaptation and pulsatile activity. This may suggest cell‐autonomous mechanisms that provide robustness in face of noise and variability (Alon et al, 1999). In that respect, the mathematical model suggests that this robustness may be inherently encoded in the negative feedback as the neural outputs were largely insensitive to a wide range of changes in the system's parameters (Appendix Fig S2).
Together, here we delineated how a negative feedback in the GPCR signaling pathway provides an array of key sensory features that together underlie an efficient navigation strategy. We identified TAX‐6/Calcineurin as a major cell‐autonomous inhibitory component and constructed a simple mathematical model that depicts the experimental observations in both wt and tax‐6 mutant animals. While this model simplifies the full dynamics within the neuron, it establishes a convenient framework to understand the principles by which a neuron translates complex stimulus patterns into coherent activity outputs. As GPCR signaling is conserved in all eukaryotes, the same mechanisms may underlie cell‐autonomous coding schemes in different sensory modalities across the animal kingdom.
Materials and Methods
Strains used in this study
ZAS163 [syEx1252(gpa‐6::GCaMP3, pha‐1::PHA‐1); pha‐1(e2123ts); lite‐1(ce314)].
The following strains were crossed with ZAS163:
PR675 [tax‐6(p675) IV] yielding the strain ZAS282
RB1667 [tax‐6(ok2065) IV] yielding the strain ZAS486
PR811 [osm‐6(p811) V] yielding the strain ZAS416
JT609 [eat‐16(sa609) I] yielding the strain ZAS403
RB660 [arr‐1(ok401) X] yielding the strain ZAS402
CX2205 [odr‐3(n2150) V] yielding the strain ZAS482
FG7 [grk‐2(gk268) III] yielding the strain ZAS487
ZAS423 [azrIs423(odr‐7p::Chrimson::SL2::mCherry; elt‐2::mCherry); syEx1252(gpa‐6::GCaMP3, pha‐1::PHA‐1)] was generated by first integrating CX16561(kyEx5662[odr‐7p::Chrimson::SL2::mCherry 5 ng/ul, elt‐2::mCherry]) (Larsch et al, 2015) using UV and backcrossing seven times with wt N2 worms. The resulting strain was then crossed with ZAS163. As GCaMP3 signal was weaker in worms homozygous for the Chrimson, heterozygous worms were picked for imaging.
ZAS424 [tax‐6(p675); azrIs423(odr‐7p::Chrimson::SL2::mCherry; elt‐2::mCherry); syEx1252(gpa‐6::GCaMP3, pha‐1::PHA‐1)] was generated by crossing ZAS423 with PR675[tax‐6(p675)], which yields the genotype azrIs423(odr‐7p::Chrimson::SL2::mCherry; elt‐2::mCherry); syEX1252(gpa‐6::GCaMP3, pha‐1::PHA‐1) in tax‐6 mutant background.
ZAS489 [tax‐6(p675); lite‐1(ce314); pha‐1(e2123); syEX1252(gpa‐6::GCaMP3; pha‐1::PHA‐1); azrEx489(gpa‐6::TAX‐6‐DsRed; unc‐122::GFP)] was generated as following: The TAX‐6 coding sequence was amplified from N2 cDNA library using the following primers: forward ‐ ATGGCCTCGACATCGGC; reverse ‐ TTAGCTATTTGATGGACCATTTTG. It was then cloned into the pPD95.77 plasmid upstream and in frame to DsRed. Next, we fused the pcr segment of TAX‐6‐DsRed from the pPD95.77 plasmid to the gpa‐6 promoter amplified from a genomic DNA (Zaslaver et al, 2015; Bokman et al, 2022). Finally, we injected the linear fragment to ZAS282 together with unc122::GFP. The resulting transgenic animals showed DsRed AWA‐exclusive expression in the head and in another cell in the tail.
Worms were grown at 20°C on NGM plates that were pre‐seeded with overnight culture of OP50 according to (Sulston & Brenner, 1974).
Preparing reagents for calcium imaging
For calcium imaging of the AWA neurons in response to diacetyl, we used two types of solutions: “Stimulus” and “Buffer.” Both solutions were composed of a CTM buffer supplemented with 10 mM Levamisole (Sigma, CAS Number: 16595‐80‐5). Levamisole was used to minimize worms' movement in the microfluidic device during imaging. Importantly, Levamisole does not alter AWA response activities as non‐sedated worms demonstrate similar pulsatile activity (Itskovits et al, 2018). The “Stimulus” input was also supplemented with 1.15 mM diacetyl and 0.5 μM rhodamine. The rhodamine dye was used to directly measure the diacetyl gradient experienced by the worms. Importantly, the AWA neuron does not respond to these concentrations of rhodamine (Itskovits et al, 2018). We also added low levels of diacetyl (0.12 μM) to the “Buffer” solution to reduce the effect of possible abrupt changes in diacetyl concentration that would greatly impact AWA activity.
Calcium imaging setup
We typically imaged one (either left or right) of the bilateral symmetric AWA neurons using an Olympus IX‐83 inverted microscope equipped with a Photometrics sCMOS camera (Prime 95B) and a 40× magnification (0.95 NA) Olympus objective. A dual‐band filter (Chroma 59012) and a two‐led illumination source (X‐cite, Lumen Dynamics) were used to allow alternating imaging of both green and red channels intermittently. Hardware was controlled using Micro‐Manager (Edelstein et al, 2014).
Generating gradients and steps of the stimulus
To generate smooth gradients of diacetyl, we used two computer‐controlled syringe pumps to flow the diacetyl and a diluting buffer into a small‐volume (50 μl) mixing chamber (Itskovits et al, 2018). The content of the chamber was stirred by a magnetic bead and its output was flowed through the nose of the worm while it was constrained in a custom‐made microfluidic device. Generation of step changes were done in an “olfactory chip” (Chronis et al, 2007). Switching between on and off steps was done either manually or using an automated valve (LFYA1218032H, the Lee company) controlled by Arduino.
Image analysis
AWA activity (green) and rhodamine concentration (red) were each imaged at a rate of 1.4 frames/s. For step gradients that did not necessitate continuous measurements of diacetyl concentrations, we imaged the green channel at a frame rate of 3.3 frames/s. Image analysis was done using in‐house developed MATLAB scripts. We extracted the fluorescence values of the neuron at each time and calculated the change in fluorescence relative to the fluorescence before the gradient onset (or before the step): (as in Figs 2, 3, 4). Normalization of raster plots to a range of [0–1] was done using [val – min (val)]/[max (val) – min (val)].
Optogenetic activation
About 12–24 h prior to imaging, L4 worms were picked and placed on NGM plates pre‐seeded with E. coli OP 50 supplemented with 100 μM ATR. Optogenetic activation was done via a 40× magnification (0.95 NA) Olympus objective by an X‐cite blue led illumination source set to 5% of maximal power. As the same LED light source was also used to image calcium levels, the beginning of neural activation was likely to be observed in the first recorded frame. We therefore quantified neural activity by comparing fluorescent levels to the first frame .
Extraction of the pulsatile activity in smooth gradients
Pulses were extracted automatically using the following criterion: a local maximum with an amplitude that exceeds 20% of the maximal measured fluorescence, and which is surrounded by a decay of at least 70% of its amplitude. Data points that obeyed this criterion were considered as pulses. In case no point passed this criterion, the number of pulses was set to 1.
Model construction and parameter evaluation
We used MATLAB (Mathworks© Inc.) for implementing numerical simulations of the dynamical system (equations (1), (2), (3), (4) and Appendix Note S1 part 1). As we did not fit the model to the data, but rather aimed to construct a “toy” model that captures the fine dynamic features observed experimentally, some of the parameters were manually varied by orders of magnitude (see full description in Appendix Table S1). Parameters for which we had experimental evidence were fixed based on available data. Appendix Table S1 provides the description of the parameters and how they were evaluated.
Parameter' scan and analysis of the model robustness
To analyze the robustness of the model to variations in the parameters space, we used two complementing approaches to simulate the model's output while varying the parameters: (i) we systematically varied the parameters one by one in the range of 0.1–10‐fold of their initialized value (100‐fold range in total). (ii) In each simulation, we simultaneously varied multiple parameters (except for , whose dynamic range was found to be relatively small, as seen in Appendix Fig S3). Each parameter was drawn independently from a log‐uniform distribution, with a range that was set to generate a symmetric 10‐fold range around the initially set value (shown in Appendix Table S1). We used this process to generate 10,000 independent sets of parameters.
For each set of parameters, the model was tested for two features: (i) exact adaptation in response to a single step (1.15 mM) of the stimulus. Here, the output criterion was to observe a single pulse whose duration was less than 60 s. (ii) Adaptation of the pulsatile response to the magnitude of the gradient's first derivative (during a sigmoidal smooth gradient as shown in Fig 1C). The output criterion was to observe anywhere between 3 and 100 pulses, where more than 55% of the pulses initiated prior to reaching the middle point of the sigmoid gradient (the point of maximal first derivative, as expected for adaptation to the gradient's first derivative).
Pulses were extracted from the simulation output using the following criteria: a local maximum with an amplitude that exceeds 1% of the global maximal amplitude. A pulse's initiation/termination time was calculated as the time that the output rose/fell more than 10%/90% of its amplitude, respectively. Parameter values that produced activity dynamics obeying these criteria were considered as valid, thus leading to robust behavioral output of the model. To analyze the model's performance in response to various ligand concentrations, we performed each of the above simulations independently while modifying the stimulus amplitude only (the other parameters remained fixed at their initially set values).
Chemotaxis assays
Assays were performed on synchronized‐bleached young adult (65–70 h post bleaching) wt and tax‐6(p675) worms. Worms were grown on standard NGM plates, pre‐seeded with 500 μl E. coli OP 50 culture. Before the experiments, the worms were rinsed off the growth plates and washed three times in CTM (5 mM potassium phosphate, pH 6.0, 1 mM CaCl2, 1 mM MgSO4) to remove bacteria. The worms were then kept food‐deprived in CTM for 45–60 min before loaded on the assay plates. Assays were performed in 9 cm covered CTX plates (25 mM KH2PO4, pH 6.0, 1 mM CaCl2, 1 mM MgSO4, 1.7% agar).
We drew a diameter on the plate's lid (90 mm round plates) and marked on it two points, ∼10 mm equally distant from the lid's edges. We used an agar chunk soaked (15 μl) with diacetyl (11.5 mM) and attached it from the inside of the lid, on one of the points that we marked. On the other point, on the CTX itself, we placed a 15 μl CTM drop of washed worms (100–200, Appendix Fig S7). Chemotaxis assays were imaged using a Photometrics Micropublisher 5 MB camera, using Olympus SZ61 binocular equipped with a 0.5× lens. Movies were acquired at a rate of two frames per second. To minimize day‐to‐day variability, we assayed wt and tax‐6 mutants side by side in parallel. Image analyses and extraction of tracks were done using in‐house tracking software (Itskovits et al, 2017) that was modified to segment worm entities using a deep learning algorithm (available in https://github.com/itskov/WormSegmentation.git).
Author contributions
Rotem Ruach: Resources; data curation; software; formal analysis; validation; investigation; visualization; methodology; writing – original draft; writing – review and editing. Shai Yellinek: Resources; data curation; software; formal analysis; investigation; visualization; methodology; writing – original draft; writing – review and editing. Eyal Itskovits: Data curation; software; formal analysis; validation; investigation; methodology. Noa Deshe: Resources; validation; methodology. Yifat Eliezer: Resources; validation; methodology. Eduard Bokman: Formal analysis; methodology. Alon Zaslaver: Conceptualization; data curation; supervision; funding acquisition; validation; visualization; writing – original draft; project administration; writing – review and editing.
Disclosure and competing interests statement
The authors declare that they have no conflict of interest.
Supporting information
Appendix
Movie EV1
Movie EV2
Movie EV3
Source Data for Figure 2
Source Data for Figure 3
Source Data for Figure 4
Source Data for Figure 5
Source Data for Figure 6
Source Data for Appendix
Acknowledgements
We thank Cori Bargmann for providing strains and reagents. Some strains were provided by the CGC, which is funded by NIH Office of Research Infrastructure Programs (P40 OD010440). This work was supported by the Israeli Science Foundation (1300/17), ERCStG (336803), I‐Core (1902/12), and the Jerusalem Brain Community. AZ is the Greenfield Chair in Neurobiology.
Mol Syst Biol. (2022) 18: e10514
Data availability
The code for the model and the simulations is available in: https://github.com/zaslab/negative_feedback.git.
References
- Alon U, Surette MG, Barkai N, Leibler S (1999) Robustness in bacterial chemotaxis. Nature 397: 168–171 [DOI] [PubMed] [Google Scholar]
- Bargmann C (2006) Chemosensation in C. elegans . WormBook: 1–29 10.1895/wormbook.1.123.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bargmann CI, Hartwieg E, Robert Horvitz H (1993) Odorant‐selective genes and neurons mediate olfaction in C. elegans . Cell 74: 515–527 [DOI] [PubMed] [Google Scholar]
- Barkai N, Leibler S (1997) Robustness in simple biochemical networks. Nature 387: 913–917 [DOI] [PubMed] [Google Scholar]
- Berg HC, Tedesco PM (1975) Transient response to chemotactic stimuli in Escherichia coli . Proc Natl Acad Sci USA 72: 3235–3239 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Block SM, Segall JE, Berg HC (1983) Adaptation kinetics in bacterial chemotaxis. J Bacteriol 154: 312–323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bokman E, Eliezer Y, Zaslaver A (2022) A fusion PCR method for expressing genetic tools in C. elegans . Methods Mol Biol 2468: 205–214 [DOI] [PubMed] [Google Scholar]
- Choi JI, Yoon K‐H, Kalichamy SS, Yoon S‐S, Lee JI (2016) A natural odor attraction between lactic acid bacteria and the nematode Caenorhabditis elegans . ISME J 10: 558–567 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chronis N, Zimmer M, Bargmann CI (2007) Microfluidics for in vivo imaging of neuronal and behavioral activity in Caenorhabditis elegans . Nat Methods 4: 727–731 [DOI] [PubMed] [Google Scholar]
- Colbert HA, Bargmann CI (1995) Odorant‐specific adaptation pathways generate olfactory plasticity in C. elegans . Neuron 14: 803–812 [DOI] [PubMed] [Google Scholar]
- Cook SJ, Jarrell TA, Brittin CA, Wang Y, Bloniarz AE, Yakovlev MA, Nguyen KCQ, Tang LT‐H, Bayer EA, Duerr JS et al (2019) Whole‐animal connectomes of both Caenorhabditis elegans sexes. Nature 571: 63–71 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Creamer TP (2020) Calcineurin. Cell Commun Signal 18: 137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desrochers M, Lang M, Hendricks M (2018) Asymmetric adaptation reveals functional lateralization for graded versus discrete stimuli. bioRxiv 10.1101/411033 [PREPRINT] [DOI]
- Edelstein AD, Tsuchida MA, Amodaj N, Pinkard H, Vale RD, Stuurman N (2014) Advanced methods of microscope control using μManager software. J Biol Methods 1: e10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fechner GT (1948) Elements of psychophysics, 1860. In Readings in the History of Psychology, Dennis W (ed), pp 206–213. East Norwalk, CT: Appleton‐Century‐Crofts; [Google Scholar]
- Ferrell JE Jr (2016) Perfect and near‐perfect adaptation in cell signaling. Cell Syst 2: 62–67 [DOI] [PubMed] [Google Scholar]
- Ferrell JE Jr, Machleder EM (1998) The biochemical basis of an all‐or‐none cell fate switch in xenopus oocytes. Science 280: 895–898 [DOI] [PubMed] [Google Scholar]
- Fukuto HS, Ferkey DM, Apicella AJ, Lans H, Sharmeen T, Chen W, Lefkowitz RJ, Jansen G, Schafer WR, Hart AC (2004) G protein‐coupled receptor kinase function is essential for Chemosensation in C. elegans . Neuron 42: 581–593 [DOI] [PubMed] [Google Scholar]
- Gaudry Q, Nagel KI, Wilson RI (2012) Smelling on the fly: sensory cues and strategies for olfactory navigation in drosophila. Curr Opin Neurobiol 22: 216–222 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordus A, Pokala N, Levy S, Flavell SW, Bargmann CI (2015) Feedback from network states generates variability in a probabilistic olfactory circuit. Cell 161: 215–227 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hajdu‐Cronin YM, Chen WJ, Patikoglou G, Koelle MR, Sternberg PW (1999) Antagonism between G(o)alpha and G(q)alpha in Caenorhabditis elegans: the RGS protein EAT‐16 is necessary for G(o)alpha signaling and regulates G(q)alpha activity. Genes Dev 13: 1780–1793 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hart A, Chao M (2009) From odors to behaviors in Caenorhabditis elegans . In The Neurobiology of Olfaction, Menini A (ed), pp 1–33. Boca Raton, FL: CRC Press; [PubMed] [Google Scholar]
- Hobert O (2013) The neuronal genome of Caenorhabditis elegans . WormBook: 1–106 10.1895/wormbook.1.161.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Itskovits E, Levine A, Cohen E, Zaslaver A (2017) A multi‐animal tracker for studying complex behaviors. BMC Biol 15: 29 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Itskovits E, Ruach R, Kazakov A, Zaslaver A (2018) Concerted pulsatile and graded neural dynamics enables efficient chemotaxis in C. elegans . Nat Commun 9: 2866 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahn‐Kirby AH, Dantzker JLM, Apicella AJ, Schafer WR, Browse J, Bargmann CI, Watts JL (2004) Specific polyunsaturated fatty acids drive TRPV‐dependent sensory signaling in vivo . Cell 119: 889–900 [DOI] [PubMed] [Google Scholar]
- Katz B, Miledi R (1970) Further study of the role of calcium in synaptic transmission. J Physiol 207: 789–801 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhara A, Inada H, Katsura I, Mori I (2002) Negative regulation and gain control of sensory neurons by the C. elegans calcineurin TAX‐6. Neuron 33: 751–763 [DOI] [PubMed] [Google Scholar]
- Larsch J, Ventimiglia D, Bargmann CI, Albrecht DR (2013) High‐throughput imaging of neuronal activity in Caenorhabditis elegans . Proc Natl Acad Sci USA 110: E4266–E4273 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larsch J, Flavell SW, Liu Q, Gordus A, Albrecht DR, Bargmann CI (2015) A circuit for gradient climbing in C. elegans chemotaxis. Cell Rep 12: 1748–1760 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laughlin SB (1989) The role of sensory adaptation in the retina. J Exp Biol 146: 39–62 [DOI] [PubMed] [Google Scholar]
- Lazova MD, Ahmed T, Bellomo D, Stocker R, Shimizu TS (2011) Response rescaling in bacterial chemotaxis. Proc Natl Acad Sci USA 108: 13870–13875 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lefkowitz RJ (1998) G protein‐coupled receptors. J Biol Chem 273: 18677–18680 [DOI] [PubMed] [Google Scholar]
- Levy S, Bargmann CI (2020) An adaptive‐threshold mechanism for odor sensation and animal navigation. Neuron 105: 534–548 [DOI] [PubMed] [Google Scholar]
- Liu Q, Kidd PB, Dobosiewicz M, Bargmann CI (2018) C. elegans AWA olfactory neurons fire calcium‐mediated all‐or‐none action potentials. Cell 175: 57–70 [DOI] [PubMed] [Google Scholar]
- Llinás R, Steinberg IZ, Walton K (1976) Presynaptic calcium currents and their relation to synaptic transmission: voltage clamp study in squid giant synapse and theoretical model for the calcium gate. Proc Natl Acad Sci USA 73: 2918–2922 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo L, Wen Q, Ren J, Hendricks M, Gershow M, Qin Y, Greenwood J, Soucy ER, Klein M, Smith‐Parker HK et al (2014) Dynamic encoding of perception, memory, and movement in a C. elegans chemotaxis circuit. Neuron 82: 1115–1128 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E, Goaillard J‐M (2006) Variability, compensation and homeostasis in neuron and network function. Nat Rev Neurosci 7: 563–574 [DOI] [PubMed] [Google Scholar]
- Merritt DM, MacKay‐Clackett I, Almeida SMT, Tran C, Ansar S, van der Kooy D (2021) Arrestin‐mediated desensitization enables olfactory discrimination in C. elegans . bioRxiv 10.1101/2021.05.02.439367 [PREPRINT] [DOI] [PMC free article] [PubMed]
- Mukhopadhyay S, Lu Y, Shaham S, Sengupta P (2008) Sensory signaling‐dependent remodeling of olfactory cilia architecture in C. elegans . Dev Cell 14: 762–774 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murlis J, Elkinton JS, Cardé RT (1992) Odor plumes and how insects use them. Annu Rev Entomol 37: 505–532 [Google Scholar]
- Olsman N, Goentoro L (2016) Allosteric proteins as logarithmic sensors. Proc Natl Acad Sci USA 113: E4423–E4430 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierce‐Shimomura JT, Morse TM, Lockery SR (1999) The fundamental role of pirouettes in Caenorhabditis elegans chemotaxis. J Neurosci 19: 9557–9569 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritz CO, Itskovits E, Bokman E, Ruach R, Gritsenko V, Nelken T, Menasherof M, Azulay A, Zaslaver A (2020) Principles for coding associative memories in a compact neural network. bioRxiv 10.1101/2020.06.20.162818 [PREPRINT] [DOI] [PMC free article] [PubMed]
- Rahi SJ, Larsch J, Pecani K, Katsov AY, Mansouri N, Tsaneva‐Atanasova K, Sontag ED, Cross FR (2017) Oscillatory stimuli differentiate adapting circuit topologies. Nat Methods 14: 1010–1016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roayaie K, Crump JG, Sagasti A, Bargmann CI (1998) The Gα protein ODR‐3 mediates olfactory and nociceptive function and controls cilium morphogenesis in C. elegans olfactory neurons. Neuron 20: 55–67 [DOI] [PubMed] [Google Scholar]
- Sengupta P, Chou JH, Bargmann CI (1996) Odr‐10 encodes a seven transmembrane domain olfactory receptor required for responses to the odorant diacetyl. Cell 84: 899–909 [DOI] [PubMed] [Google Scholar]
- Shimizu TS, Tu Y, Berg HC (2010) A modular gradient‐sensing network for chemotaxis in Escherichia coli revealed by responses to time‐varying stimuli. Mol Syst Biol 6: 382 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shindou T, Ochi‐Shindou M, Murayama T, Saita E‐I, Momohara Y, Wickens JR, Maruyama IN (2019) Active propagation of dendritic electrical signals in C. elegans . Sci Rep 9: 3430 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shirley SG, Polak EH, Edwards DA, Wood MA, Dodd GH (1987) The effect of concanavalin a on the rat electro‐olfactogram at various odorant concentrations. Biochem J 245: 185–189 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sourjik V, Wingreen NS (2012) Responding to chemical gradients: bacterial chemotaxis. Curr Opin Cell Biol 24: 262–268 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern S, Kirst C, Bargmann CI (2017) Neuromodulatory control of long‐term behavioral patterns and individuality across development. Cell 171: 1649–1662 [DOI] [PubMed] [Google Scholar]
- Sulston JE, Brenner S (1974) The DNA of Caenorhabditis elegans . Genetics 77: 95–104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanimoto Y, Yamazoe‐Umemoto A, Fujita K, Kawazoe Y, Miyanishi Y, Yamazaki SJ, Fei X, Busch KE, Gengyo‐Ando K, Nakai J et al (2017) Calcium dynamics regulating the timing of decision‐making in C. elegans . Elife 6: e21629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor SR, Santpere G, Weinreb A, Barrett A, Reilly MB, Xu C, Varol E, Oikonomou P, Glenwinkel L, McWhirter R et al (2021) Molecular topography of an entire nervous system. Cell 184: 4329–4347 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tu Y (2013) Quantitative modeling of bacterial chemotaxis: signal amplification and accurate adaptation. Annu Rev Biophys 42: 337–359 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tu Y, Rappel W‐J (2018) Adaptation of living systems. Annu Rev Condens Matter Phys 9: 183–205 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tu Y, Shimizu TS, Berg HC (2008) Modeling the chemotactic response of Escherichia coli to time‐varying stimuli. Proc Natl Acad Sci USA 105: 14855–14860 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van As W, Kauer JS, Menco BPM, Köster EP (1985) Quantitative aspects of the electro‐olfactogram in the tiger salamander. Chem Senses 10: 1–21 [Google Scholar]
- Vinograd A, Livneh Y, Mizrahi A (2017) History‐dependent odor processing in the mouse olfactory bulb. J Neurosci 37: 12018–12030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vries LD, De Vries L, Zheng B, Fischer T, Elenko E, Farquhar MG (2000) The regulator of G protein signaling family. Annu Rev Pharmacol Toxicol 40: 235–271 [DOI] [PubMed] [Google Scholar]
- White JG, Southgate E, Thomson JN, Brenner S (1986) The structure of the nervous system of the nematode Caenorhabditis elegans . Philos Trans R Soc Lond B Biol Sci 314: 1–340 [DOI] [PubMed] [Google Scholar]
- Wood JF, Ferkey DM (2016) GRK roles in C. elegans . In Methods in Pharmacology and Toxicology, Gurevich VV, Gurevich EV, Tesmer JJG (eds), pp 283–299. Totowa, NJ: Humana Press; [Google Scholar]
- Yi TM, Huang Y, Simon MI, Doyle J (2000) Robust perfect adaptation in bacterial chemotaxis through integral feedback control. Proc Natl Acad Sci USA 97: 4649–4653 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaslaver A, Liani I, Shtangel O, Ginzburg S, Yee L, Sternberg PW (2015) Hierarchical sparse coding in the sensory system of Caenorhabditis elegans . Proc Natl Acad Sci USA 112: 1185–1189 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X‐P, Cheng Z, Liu F, Wang W (2007) Linking fast and slow positive feedback loops creates an optimal bistable switch in cell signaling. Phys Rev E Stat Nonlin Soft Matter Phys 76: 031924 [DOI] [PubMed] [Google Scholar]
- Zufall F (2000) The cellular and molecular basis of odor adaptation. Chem Senses 25: 473–481 [DOI] [PubMed] [Google Scholar]


