Learning probabilistic protein–DNA recognition codes from DNA-binding specificities using structural mappings

Abstract

Knowledge of how proteins interact with DNA is essential for understanding gene regulation. Although DNA-binding specificities for thousands of transcription factors (TFs) have been determined, the specific amino acid–base interactions comprising their structural interfaces are largely unknown. This lack of resolution hampers attempts to leverage these data in order to predict specificities for uncharacterized TFs or TFs mutated in disease. Here we introduce recognition code learning via automated mapping of protein–DNA structural interfaces (rCLAMPS), a probabilistic approach that uses DNA-binding specificities for TFs from the same structural family to simultaneously infer both which nucleotide positions are contacted by particular amino acids within the TF as well as a recognition code that relates each base-contacting amino acid to nucleotide preferences at the DNA positions it contacts. We apply rCLAMPS to homeodomains, the second largest family of TFs in metazoans and show that it learns a highly effective recognition code that can predict de novo DNA-binding specificities for TFs. Furthermore, we show that the inferred amino acid–nucleotide contacts reveal whether and how nucleotide preferences at individual binding site positions are altered by mutations within TFs. Our approach is an important step toward automatically uncovering the determinants of protein–DNA specificity from large compendia of DNA-binding specificities and inferring the altered functionalities of TFs mutated in disease.

Introduction

Protein–DNA interactions are critical for the proper functioning of a wide range of biological processes within cells. Central among them is the regulation of gene expression, which is orchestrated by a complex network of sequence-specific interactions made by transcription factor (TF) proteins. Although proper gene regulation ensures that the appropriate genes are expressed in each spatiotemporal context, mutations—within either TFs themselves or the particular genomic regions that they are intended to interact with—can alter gene expression programs and lead to disease phenotypes (for review, see Lee and Young 2013). Because of the central importance of TF–DNA interactions in both healthy and disease states, there have been substantial efforts to characterize the determinants of specificity in TF–DNA interactions (for review, see Inukai et al. 2017) and to catalog DNA-binding specificities (Noyes et al. 2008a; Berger and Bulyk 2009; Jolma et al. 2010; Yang et al. 2017) and genomic occupancies (The ENCODE Project Consortium 2012; The ENCODE Project Consortium et al. 2020) of TFs.

To date, DNA-binding specificities and/or context-specific genomic binding regions for thousands of TFs across human and other model organisms have been determined (Weirauch et al. 2014; Kulakovskiy et al. 2018; Castro-Mondragon et al. 2022). These data have enabled large-scale construction of regulatory networks and have revealed the organization of regulatory circuits (Gerstein et al. 2012). Further, these data have been used to train machine learning models to uncover cooperative TF binding and other regulatory “grammars” (Avsec et al. 2021; Miraldi et al. 2021) and to predict the impact of mutations within noncoding regions of the genome (Zhou and Troyanskaya 2015; Martin et al. 2019). However, despite these extensive catalogs of DNA-binding specificities for wild-type TFs, as yet very few methods have been able to use these data in order to uncover the underlying determinants of protein–DNA specificity; this prevents both the prediction of de novo specificities for uncharacterized TFs (e.g., including those in nonmodel organisms or those that have proved difficult to study experimentally) and the prediction of altered DNA-binding specificities owing to mutations or SNPs within TFs (e.g., as observed in several Mendelian disorders [Veraksa et al. 2000], in cancers [Kobren et al. 2020], and across healthy populations [Barrera et al. 2016]). The main challenge is that for the vast majority of TFs for which DNA-binding specificities are known, the specific amino acid–base interactions comprising the underlying interaction interfaces are largely unknown, thus making it difficult to infer base preferences for specific amino acids or to determine which positions within their binding sites, if any, would be altered by mutations at specific amino acid positions.

Here, we introduce recognition code learning via automated mapping of protein–DNA structural interfaces (rCLAMPS), a general probabilistic approach that uses DNA-binding specificities for TFs from the same structural family to simultaneously infer both which nucleotide positions are contacted by particular amino acids within the TF as well as a recognition code that relates base-contacting amino acids to nucleotide preferences at the DNA positions they contact. Our approach leverages the fact that protein–DNA interactions can be classified into structural families (Luscombe and Austin 2000) and that proteins from the same structural family have relatively well-conserved structural interfaces, where analogous positions within TFs tend to interact with the same set of DNA positions and these pairwise amino acid–base interactions define a contact map. rCLAMPS takes as input a collection of position weight matrices (PWMs) representing DNA-binding specificities for TFs from the same structural family and uses a contact map representation of their protein–DNA structural interface. It performs Gibbs sampling to infer for each TF the mapping from its PWM columns to DNA positions within the contact map (i.e., determining which PWM columns across the TFs are analogous to each other) while simultaneously learning the parameters of a linear model that describes the base preferences of amino acids in specific positions of the TFs. Our approach is general and can be applied to PWMs for any family of DNA-binding proteins whose interaction interfaces with DNA are structurally conserved enough to be modeled by a pairwise amino acid–base position contact map.

We show the efficacy of our method by applying it to homeodomains, members of which play critical roles in development and cell fate processes (Bürglin and Affolter 2016), and mutations within which are associated with a plethora of diseases (Chi 2005). We show that rCLAMPS accurately identifies analogous positions across a diverse set of homeodomain PWMs by mapping TF–PWM pairs to a canonical homeodomain contact map. Additionally, we show via extensive testing that rCLAMPS infers a recognition code that has excellent performance in predicting de novo DNA-binding specificities for homeodomain proteins. Furthermore, because rCLAMPS identifies which base positions within a PWM are contacted by specific amino acids within a TF and relies on an underlying linear model, we transfer existing specificity information from wild-type TFs to mutant TFs while making predictions only for the affected base positions and show that this improves the accuracy of predicted specificities for mutant TFs beyond that of de novo predictions. Finally, we show the generality of our framework by applying it to Cys₂-His₂ zinc finger (C2H2-ZF) proteins, the largest and most diverse class of TFs in humans (Vaquerizas et al. 2009; Lambert et al. 2018). Overall, we establish that our probabilistic framework yields a general, effective, and interpretable method that newly enables fully automated analyses of large compendia of known DNA-binding specificities in order to uncover protein–DNA interaction interfaces, infer recognition codes, and characterize mutant TFs.

Further related work

Because of the fundamental importance of sequence-specific protein–DNA interactions in gene regulation, the determinants of TF–DNA interaction specificity have been studied extensively from both structural and statistical perspectives (Luscombe and Austin 2000; Luscombe 2001; Rohs et al. 2009; Persikov and Singh 2011). Sequence-based machine learning methods to predict de novo specificities for TFs have been developed for several structural families, including C2H2-ZFs and homeodomains. Typically, these approaches to infer recognition codes explicitly incorporate prior knowledge of known DNA-contacting residues or curated protein–DNA interface contact maps (Benos et al. 2002; Kaplan et al. 2005; Noyes et al. 2008b; Persikov et al. 2009, 2015; Gupta et al. 2014; Persikov and Singh 2014; Najafabadi et al. 2015). That is, the pairwise contacts between specific amino acids in the protein sequence and the DNA-binding sites are often known via specialized experimental protein–DNA interaction assays that position and orient the TF relative to a potential DNA-binding site in a predetermined way (Noyes et al. 2008a,b; Chu et al. 2012; Persikov et al. 2014; Najafabadi et al. 2015); in contrast, our approach does not require a priori knowledge of these contacts and instead simultaneously infers them while learning a probabilistic recognition code. Alternatively, PWMs representing binding specificities for TFs from the same structural family have been aligned, and subsequently, machine learning models have been trained on them to predict DNA-binding specificities, an approach taken by the earliest method for homeodomains (Christensen et al. 2012); however, because the PWMs for TFs from the same structural family may be quite varied, these types of approaches require some manual intervention, whereas rCLAMPS learns these alignments automatically. Protein–nucleic acid recognition codes have also been inferred from unaligned DNA sequences (Pelossof et al. 2015); although elegant, this approach relies on relating k-mers to quantitative binding measurements, and these are only available for some experimental assays, whereas rCLAMPs uses PWMs and can be applied to binding specificities determined from any technical platform. Additionally, a model for predicting DNA-binding preferences for C2H2-ZF proteins has been learned from unaligned DNA sequences (Kaplan et al. 2005); however, unlike rCLAMPS, this approach uses a manually curated contact map and assumes that nucleotide preferences are largely determined by single amino acid positions. Finally, several computational approaches have investigated large compendia of TFs and their corresponding DNA-binding specificities to learn rules for when the specificity of a characterized TF may be transferrable to an uncharacterized TF of the same family (Weirauch et al. 2014; Lambert et al. 2019); although powerful, these approaches cannot predict how a mutation within a TF will change its specificity. In contrast to previous approaches, we leverage structural information to enable automated, simultaneous inference of protein–DNA interaction interface mappings and an interpretable family-level DNA recognition code; consequently, our approach enables us to determine when and how transfer of specificity information from wild-type to mutant TFs is appropriate at the resolution of individual binding site positions.

Methods

Overview of approach

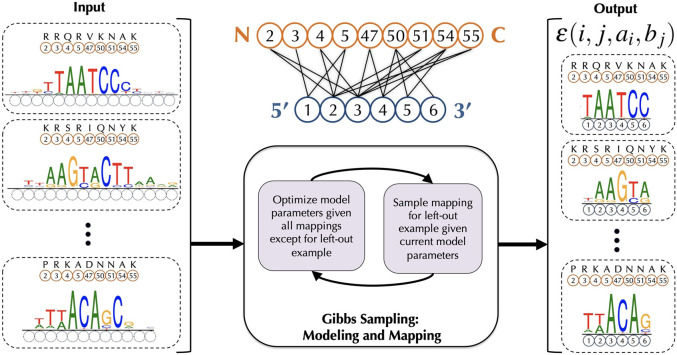
Our framework rCLAMPS takes a corpus of DNA-binding specificities for a set of proteins from the same DNA-binding family; these DNA-binding specificities are represented as PWMs. It also uses protein–DNA co-complex structural data for that DNA-binding family in order to determine conserved pairwise contacts between positions in the proteins and positions within DNA that together comprise a structural interface or “canonical” contact map (Fig. 1, top middle). For all pairs of TF proteins and their corresponding PWMs, the amino acids that correspond to each of the base-contacting positions within the contact map are known; however, the positions within the PWM that are contacted by these amino acids are not known (Fig. 1, left). Our framework assumes that for each base position within the contact map, the base preferences at that position can be described by a linear model with additive contributions from amino acids occupying protein positions that contact that base position; each base position in the model is thus allowed to be involved in interactions with multiple amino acid positions. We use a linear model as its correspondence with the contact map makes it readily interpretable, especially for characterizing the impact of amino acid mutations on DNA-binding specificities. Initially, the parameters of the model are not known. However, if the parameters were known, then the likelihood of the data given each possible mapping of PWM columns to the nucleotide positions within the contact map can be computed. rCLAMPS uses a Markov chain Monte Carlo Gibbs sampling approach (Fig. 1, bottom middle) to simultaneously learn the parameters of the model and determine which columns within the PWMs map to the same base position in the contact map (i.e., which columns across the PWMs are analogous to each other) (Fig. 1, right).

Figure 1.

Schematic of our procedure rCLAMPS for jointly learning protein–DNA interaction interfaces and structure-aware recognition codes for TFs of the same structural family. (Middle, top) Our approach first analyzes protein–DNA co-complex structural data for a TF family to determine commonly observed pairwise contacts between positions in the protein (orange circles) and positions within DNA (blue circles) that together comprise a structural interface or “canonical” contact map. Here we show such a contact map for the homeodomain TF family, with protein positions corresponding to match states in Pfam homeodomain model PF00046 (relabeled as canonical homeodomain positions from Noyes et al. 2008b). (Left) Given a set of TFs and their corresponding DNA-binding specificities as PWMs, the positions (and amino acids) within each TF that interact with DNA are known (orange circles and amino acids above), but initially the positions within the PWMs that are contacted by these amino acids are not known (dotted blue circles). (Middle, bottom) We use a Gibbs sampling approach to map the PWM positions to DNA positions within the contact map wherein base preferences at each nucleotide position are described in terms of additive amino acid–base contact energies. (Right) After Gibbs sampling is complete, we have a mapping of each TF–PWM pair to the TF family contact map, along with a linear recognition code for the TF family that consists of pairwise energy estimates for each amino-to-base pairing in each of the (i, j) amino acid–nucleotide position pairs in the contact map.

Deriving a contact map representation of the protein–DNA structural interface

For a DNA-binding domain of interest (i.e., a structural family of TFs), we obtain from BioLiP (Yang et al. 2013) all co-complex structures of proteins from that family interacting with DNA. For each protein, we run HMMer with a Pfam model for that DNA-binding domain to map protein positions to HMM match states (Finn et al. 2014), thus finding analogous protein positions across the TFs. For each co-complex structure, for each of its amino acids that corresponds to an HMM match state, we then find DNA bases contacted by it, defining a contact as a pair of nonhydrogen atoms between an amino acid side-chain and a DNA base at a distance of at most 3.6 Å. We perform a co-complex structural alignment based on this set of contacts to ascertain which nucleotide positions across structures map to each other (for additional algorithmic and co-complex structure processing details, see Wetzel and Singh 2020). This structural alignment allows computation of an aggregate contact frequency matrix D, where D[i, j] corresponds to the sequence-weighted (Henikoff and Henikoff 1994) fraction of times across the structures that the amino acid in match state i is in contact with the nucleotide in structurally aligned binding site position j. Without loss of generality, we index the binding site positions 5′ to 3′ for the strand that is more frequently contacted by the proteins.

A contact map C (i.e., a set of (i, j) match state-to-binding site position contact pairs) for the TF family is then constructed based on D in the following way: We first identify a set of base-contacting match states based on a contact frequency threshold t_d, 0 < t_d < 1; match state i is included if in at least t_d of sequence-weighted aligned co-complex structures, the amino acid in match state i contacts any base. For each match state i that is base-contacting, we then add contact pair (i, j) to C if D[i, j] ≥ t_e, 0 < t_e < 1. Note that the contact map represents a consensus “canonical” representation of which amino acid and nucleotide position pairs tend to be observed to be in contact across protein–DNA co-complex structures; a co-complex structure need not contain all contacts included in the map.

For the homeodomain contact map derived here from 73 BioLiP structures, we set both t_d and t_e equal to 0.05. This results in a contact map including eight contiguous base positions. We ultimately reduce this contact map to only the central six base positions of this contiguous region, which correspond to the “core” homeodomain binding site illustrated by Noyes et al. (2008b). These eliminated flanking positions of the homeodomain binding sites display on average lower information content in their DNA-binding specificities (see, e.g., Fig. 2 of Christensen et al. [2012], labeled as positions 1, 2, and 9) and less consistency across repeated experiments for the same protein. For our extension of rCLAMPS to C2H2-ZF proteins, which bind DNA via arrays of closely linked individual C2H2-ZF domains (explained in detail below), 287 individual C2H2-ZF domain–DNA interfaces were structurally aligned and converted to a domain–DNA contact map representation as described earlier (Wetzel and Singh 2020). This resulted in a 4-nt domain–DNA contact map spanning four previously described specificity-determining base-contacting residues and nine previously observed amino acid–base contacts (Persikov and Singh 2011).

Figure 2.

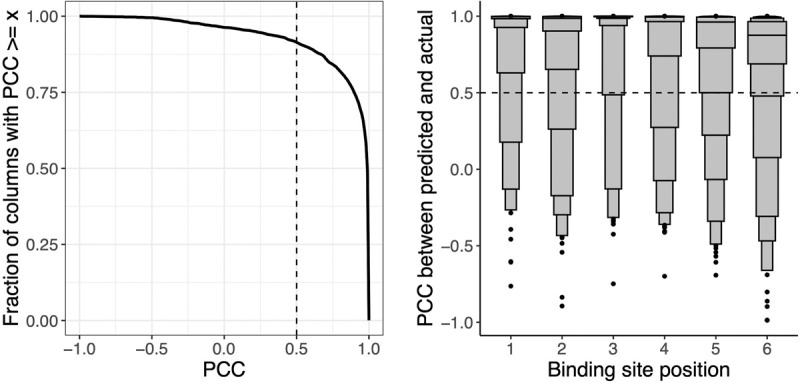
Probabilistic DNA recognition code for homeodomains derived from automatically inferred structural mappings has excellent de novo predictive performance. We compare agreement between predicted PWM columns and corresponding experimental PWM columns for 763 homeodomain proteins in a strict holdout validation setup. (Left) Considering all homeodomain binding site positions together, as different thresholds of PCC are considered (x-axis), the fraction of column pairs that have PCC greater than this threshold is plotted (y-axis). Our nominal threshold for agreement (PCC ≥ 0.5) is shown as a dashed vertical line. (Right) For each binding site position within the homeodomain contact map (x-axis), we display the PCC agreement scores (y-axis) for the paired columns at that binding site position, visualized as letter-value (or boxen) plots. In a letter-value plot, the widest box shows the value range spanned by half the data (from the 25th to 75th percentiles), whereas each successively narrower pair of boxes together show the value range spanned by half the remaining data. The PCCs at the 25th percentile for positions 1–6 are 0.98, 0.90, 1.00, 0.97, 0.79, and 0.69, respectively.

Model representation

For a particular protein–DNA interaction interface, we consider a model in which the free energy of binding is additive over amino acid–binding site position pairs that are in the contact map C. That is, if a_i is the amino acid in base-contacting position i and b_j is the nucleotide in amino acid–contacting position j and if ɛ(i, j, a_i, b_j) represents the energetic contribution arising from the contact between b_j and a_i, then the free energy of the entire protein–DNA interface is given by

$$\sum _j\sum _{i:\left(i,j\right)\in C}\epsilon (i,j,a_i,b_j).$$

The energy contributions of each base j to the free energy of the entire protein–DNA interface is given by

$$\sum _{i:\left(i,j\right)\in C}\epsilon (i,j,a_i,b_j).$$

For a protein–DNA interaction interface, we assume that the identity of a base at any position j of the binding site is conditionally independent of the identity of bases at all other positions, given the amino acid sequence of the protein. For each amino acid position i and binding position j in the contact map, we introduce, respectively, random variables A_i that can take on each of the 20 amino acids and random variables B_j that can take on each of the four nucleotide bases. When considering a specific protein sequence (i.e., where A_i = a_i for all i), the Boltzmann distribution specifies the natural log of the probability that a particular base b is found in binding position j as

$$\ln (Pr(B_j=b|A_i=a_i\mathrm{\forall }i:(i,j)\in C))\propto -\sum _{i:\left(i,j\right)\in C}\epsilon (i,j,a_i,b).$$

That is, if we know the amino acids occupying each position of a protein, we estimate the probability of a particular base at that jth binding site position by considering just the sum of the pairwise binding energies of that base and the amino acids it interacts with according to our contact map C. Initially, these pairwise binding energies are not known, but we describe below how to estimate them from known protein–DNA structural interfaces.

Representations of DNA-binding specificities

For each TF, we assume that its DNA-binding specificity is represented as a PWM F, where entry f_bj is the frequency with which nucleotide b is observed in column j in a set of aligned binding sites of that TF. Note that although binding sites for a single TF are aligned relative to one another, they are not yet mapped to our contact map C. That is, the analogous positions across a set of PWMs for a TF family are not typically known at the outset, and rCLAMPS will infer this. We transform each PWM to an estimated position count matrix (PCM) by simply multiplying each such frequency by 100 and rounding to the nearest integer. We note that our approach can also be applied to PCMs derived directly from aligned binding sites, but most commonly, specificity information for TFs is encapsulated in databases as PWMs. Furthermore, having the same number of total counts for each column of each PCM guarantees that each specificity in our training set contributes equally to the optimization procedure described below.

Estimating pairwise energy terms from mapped protein–DNA structural interfaces

Here we show that if we have a set of TFs and their PWMs along with a mapping of each TF's PWM onto the structural interface (as in Fig. 1, right), then we can estimate the pairwise energy terms of our linear model. We transform each PWM into a PCM as described above. Based on the Boltzmann distribution, for each base position j, we can relate amino acid outcomes to base probabilities via a log-linear model of the following form with one equation for each base outcome b:

$$\ln (Pr(B_j=b|A_i=a_i\mathrm{\forall }i:\left(i,j\right)\in C))=\sum _{i:\left(i,j\right)\in C}\sum _a{\theta }_{i,j,a,b}{X}_{i,j,a,b}-\ln (Z_j),$$

where a ranges over the 20 amino acids, X_i,j,a,b is an indicator variable that is set to one if the amino acid in position i is a, θ_i,j,a,b is the coefficient to be estimated that represents the contact energy contribution when nucleotide b in binding site position j is paired with amino acid a in protein position i, and Z_j is a partition function. In particular, denoting parameters and indicator variables for the equation for base b in position j more compactly as ${\overrightarrow{\theta }}_{j,b}$ and ${\overrightarrow{X}}_{j,b}$, respectively,

$$Z_j=\sum _b{e}^{{\overrightarrow{\theta }}_{j,b}\cdot {\overrightarrow{X}}_{j,b}}$$

enforces $\sum _{b}Pr(B_j=b|A_i=a_i\mathrm{\forall }i:\left(i,j\right)\in C)=1$ for each combination of amino acid settings.

If we fix some an arbitrary base b_o as a “reference” and in turn fix ${\overrightarrow{\theta }}_{j,b_o}=\overrightarrow{0}$, then each θ_i,j,a,b can be interpreted as the expected contribution of a particular amino acid a at protein position i to a change in the energy of binding induced by swapping base b for base b_o in base position j. Equivalently, because ${\overrightarrow{\theta }}_{j,b_o}=\overrightarrow{0}$, θ_i,j,a,b is the expected change in log-odds of observing base b relative to base b_o, given amino acid a at protein position i. Thus, in practice, we solve an equivalent multinomial logistic regression with the scikit-learn Python package and regularize the model by adding pseudocounts to the PCMs, corresponding to a flat Dirichlet prior. Ultimately ɛ(i, j, a_i, b) is set to the negative of its corresponding inferred model coefficient, because custom dictates that more favorable energetic states are more negative whereas more favorable log-odds are positive.

Mapping a PWM to the contact map using the energy terms

We next show that if we know the pairwise free energy binding terms, then we can compute the likelihood of each mapping of the TF's PWM to the contact map. We are given a protein p with PWM F_p = (f_bj) and compute the corresponding PCM K_p = (k_bj). We want to infer S_p, the index of the column of F_p that maps to the first binding site position in the contact map C, as well as the orientation O_p of the PWM with respect to the contact map. If O_p = 1, then F_p is mapped to C, and if O_p = 0, the reverse complement of F_p is mapped to C. For each possible setting of O_p and S_p, we compute the probability of observing the bases occupying the binding site positions in C in the PCM as follows. If O_p = 1 and w is the number of nucleotide positions in our contact map C, then the sum of the natural logs of probabilities of observing the bases in the PCM is proportional to

$$-\sum _{j=1}^w\sum _{i:\left(i,j\right)\in C}\sum _b\epsilon (i,j,a_i,b)\cdot k_{b,S_p+j-1},$$

where b takes on each of the 4 nt. On the other hand, if O_p = 0, we let $\overline{b}$ denote the base complementary to b, and then the sum of the natural logs of probabilities of observing the bases in the PCM is proportional to

$$-\sum _{j=1}^w\sum _{i:\left(i,j\right)\in C}\sum _b\epsilon (i,j,a_i,\overline{b})\cdot k_{\overline{b},S_p-j+1}.$$

We refer to the set of mapping parameters for all proteins together as the registration R = {R_p}, where R_p = (O_p, S_p).

Gibbs sampling to estimate energy and mapping parameters

Initially, the pairwise contact energy terms ɛ are not known to us, and neither is the set of mapping parameters R. However, as we showed above, if the mapping is known, then all the ɛ terms can be estimated. On the other hand, if the ɛ terms are known, we can compute the probability of the observed data for each setting of the mapping parameters R as described in the preceding section.

Thus, we use Gibbs sampling for parameter inference. The Gibbs sampler initializes the mappings R randomly. During any given iteration of the sampling procedure, we hold out a protein p (and corresponding PCM K_p) and estimate the ɛ terms as described above, using the mapping R_−p (i.e., withholding R_p from R). We then sample a new R_p proportional to the probability for each offset and orientation of K_p, corresponding to a length w binding site based on these newly estimated ɛ terms as described in the preceding section. Sampling stops either when the joint probability of the data given the current settings of ɛ terms become bound in a small range over many iterations or, alternatively, when a set maximum number of iterations is reached. In practice, we use a form of block sampling, in which the mapping parameters for proteins with identical residues in their base-contacting positions are held out together and updated jointly (i.e., without recomputing the ɛ terms between members of the same blocks) in order to avoid being drawn into spurious local modes. For homeodomains, we seed the sampling procedure with offset and orientation information for five protein–PWM pairs for which a co-complex structure already exists for the protein and the binding site in the structure aligns unambiguously to the corresponding PWM. For C2H2-ZFs, we seed the sampling with experimentally determined mappings from Enuameh et al. (2013) for six protein–PWM pairs spanning a diverse set of base-contacting amino acid sequences and specificities.

Extending rCLAMPS to C2H2-ZF proteins

rCLAMPS is described above assuming that for each PWM–protein pair in a given data set, there exists only a single protein domain interacting with the DNA represented by the PWM. However, C2H2-ZF proteins specify their DNA-binding sites via tandem arrays of multiple, closely linked C2H2-ZF domains, wherein an individual C2H2-ZF domain binds a contiguous 3-nt subsequence, 3′ to 5′, along with a potential fourth, cross-strand contact that overlaps the target of the N-terminal adjacent C2H2-ZF domain within the same array. In this way, the protein's binding site is composed of partially overlapping specificities corresponding to individual C2H2-ZFs in the array (Persikov et al. 2015). In general, multiple arrays of C2H2-ZF domains may exist within a single protein, and only a subset of contiguous domains within an array may be engaged with the DNA. For simplicity, here we focus on a subset of C2H2-ZF proteins for which a single short array of domains can be assumed a priori to engage the DNA.

To extend rCLAMPS to this subset of C2H2-ZFs, we consider a contact map for domain–DNA interactions in which each domain within a C2H2-ZF array interacts with a 4-nt region of the corresponding PWM. Although the energies are estimated for a single-domain 4-nt interface, each PWM–protein pair is modeled by rCLAMPS as a set of n C2H2-ZF domains, each interacting with a 4-nt binding subsite that overlaps its N-terminal adjacent C2H2-ZF domain's subsite (if one exists). Thus if a protein has n domains, it is considered to have a single length 3n + 1 nt binding site, the registration and orientation of which (within the PWM) are unknown before running rCLAMPs, and the total energetic contribution to binding of a set of contacts is additive across these n domain–DNA interfaces.

De novo prediction of PWMs

Once we have learned pairwise contact energy terms ɛ for a family of DNA-binding proteins as described above, then for a given protein p from that family, we first use Pfam to identify the amino acids within it that comprise the protein positions within the contact map. Next, for each binding site position j within the contact map C, we use

$${\displaystyle \frac{e^{-\sum _{i:\left(i,j\right)\in C}\epsilon (i,j,a_i,b)}}{\sum _b{e}^{-\sum _{i:\left(i,j\right)\in C}\epsilon (i,j,a_i,b)}}}$$

to calculate the probability with which each base b occurs in column j and set element f_bj of a predicted PWM F_p to this value.

For a C2H2-ZF protein with an array of n domains, we predict its PWM by first predicting n PWMs (one for each domain) in the same manner described above. These n PWMs are then combined by concatenating the PWMs for each domain (in C-to-N-terminal order) with a 1-nt overlap, resulting in a single PWM with 3n + 1 columns. In particular, for each pair of adjacent domains (k and k + 1, k < n, C-to-N-terminal order), the fourth PWM position predicted for domain k is averaged with the first PWM position predicted for domain k + 1.

Predicting PWMs for highly similar TFs

If we have two TFs that are nearly identical in the amino acids that comprise the structural interface and if we know the PWM for one of them and this PWM has been mapped to the structural interface, then the PWM for the other TF can be predicted via a hybrid approach that transfers some PWM columns and predicts others de novo. In particular, given a TF p that is extremely sequence-similar to (i.e., is a mutant version of) another TF p′, for which we already know its PWM $F_{p^{\mathrm{\prime }}}$ and mapping $R_{p^{\mathrm{\prime }}}$, we may transfer some information from $F_{p^{\mathrm{\prime }}}$ to infer a new PWM, F_p. Specifically, if the two proteins vary in a single DNA-contacting position i, then for each binding site position j that does not contact protein position i according to our contact map C, we simply set column j of F_p equal to the column of $F_{p^{\mathrm{\prime }}}$ that maps to binding site position j (i.e., according to $R_{p^{\mathrm{\prime }}}$). In practice, because there may be many such near-mutant proteins (like p′) for each given binding site position j, we use a weighted column transfer of the mapped column j across all such proteins, weighting each column by the corresponding near-mutant protein's overall fraction of DNA-binding domain identity to p (considering only match positions and using a minimum identity threshold of 0.8). On the other hand, for each column j where no qualifying near-mutant protein exists in our data set of mapped TF specificities, we simply predict column j of F_p de novo as described in the preceding section.

PWM and protein data sets

PWMs for each of 623 wild-type homeodomain TFs were extracted from the Cis-BP database (build 2.00) (Weirauch et al. 2014), considering only specificities for which a single homeodomain was the only DNA-binding domain in the protein and using the PWM from the most recent publication. Additionally, PWMs for 151 synthetic homeodomains from Chu et al. (2012) and 30 mutant homeodomains from Barrera et al. (2016) were added to our data set. After removing PWMs corresponding to proteins missing DNA-contacting HMM match states, we had PWMs for a total of 763 distinct homeodomain proteins. Before training our models, we rescaled PWMs to account for differences in information content across data sets (using a method described by Najafabadi et al. 2015). Proteins corresponding to each PWM were downloaded from UniProt (using the longest isoform for each) (The UniProt Consortium 2021) and mapped to HMM match states using HMMer v.3 with the PF00046 HMM (Finn et al. 2014). For C2H2-ZF proteins, a total of 263 PWM–protein pairs were extracted from Cis-BP (Weirauch et al. 2014) and Fly Factor Survey (Enuameh et al. 2013), considering only proteins for which the set of C2H2-ZF domains interacting with DNA could be unambiguously determined. Further details on collection of PWM–protein pairs and how the data were split for various testing tasks are described in Supplemental Methods 1.1.

Evaluating agreement between PWMs for the same protein

We compare two PWMs for the same protein based on the Pearson correlation coefficient (PCC) of their corresponding columns when mapped to the binding site positions of our contact map C. For predicted PWMs, this mapping is known. For experimental PWMs for which this mapping is not known, we use the set of contiguous experimental PWM columns that best align to the predicted PWM using a previously described method (Persikov and Singh 2014). PCC is particularly suitable for many of our analyses owing to its insensitivity to information content differences of PWMs across data sets.

Results

We show the effectiveness of our framework to simultaneously learn probabilistic recognition codes and the contacts comprising protein–DNA interaction interfaces from compendia of DNA-binding specificities by applying it to homeodomains and C2H2-ZFs, the largest TF families in metazoans.

Accurate de novo prediction of PWMs via a structure-aware recognition code

We ran rCLAMPS with the homeodomain contact map and a set of 763 homeodomain proteins along with their DNA-binding specificities. Because models explored by Gibbs sampling can be sensitive to starting parameters, we ran Gibbs sampling 100 times and considered the mapping R of PWMs to our contact map C with the highest observed likelihood score. We note that as with any Monte Carlo style algorithm, the more times our algorithm is run, the higher the likelihood of obtaining an optimal solution. Although we have no guarantee that the optimal mapping is found within 100 runs, mappings found from several of the starting points result in likelihoods similar to that of the highest likelihood mapping (Supplemental Fig. S1).

We first show that the inferred mappings of the PWMs can be used to yield recognition codes that are highly effective in predicting the DNA-binding specificities of held-out homeodomain proteins. That is, for each protein z, we re-estimate the energies ε while withholding that protein and any other protein with identical DNA-contacting residues and then predict the protein's DNA-binding specificity de novo as described above. Because we are using the inferred recognition code to make a prediction, the mapping of each column in this predicted PWM to the contact map C is known. We compare this predicted PWM to the corresponding experimental PWM as described above. Over all TFs z, >91% of the predicted columns are in agreement with the corresponding actual columns (i.e., have PCCs ≥ 0.5) (Fig. 2, left). Generally, the experimental PWM columns are more likely to be predicted accurately when their information content is higher or when their amino acid residue contacts have been observed frequently across the data set (Supplemental Fig. S2).

Considering each binding site position separately, the median per-column PCCs when comparing predicted and experimentally measured columns are 1.0, 0.99, 1.0, 0.99, 0.96, and 0.88 for columns 1–6, respectively (Fig. 2, right). We find that 95%, 91%, 97%, 91%, 88%, and 86% of the predicted columns in positions 1–6, respectively, agree with the actual columns. As expected based on the determinants of homeodomain specificity, the strongest agreement is observed for base position 3, corresponding to a highly conserved asparagine-to-adenine contact. Columns also agree quite well for positions 4, 5, and 6, which are among the most variable positions of the core binding site for naturally occurring homeodomains and for which our data set contains synthetic homeodomains explicitly designed to vary specificity in these positions (Chu et al. 2012). Thus, even though the amino acid–base contacts comprising structural interfaces are automatically inferred, models trained assuming that these structural interfaces are correct have excellent predictive performance. Moreover, our structure-aware approach is expressive enough to describe a highly accurate recognition code for homeodomains, yet constrained enough to allow excellent generalization for predicting novel homeodomain specificities.

Linear approach is competitive with state-of-the-art combinatorial models

We compare the predictive performance of rCLAMPS to that of existing state-of-the-art methods for predicting homeodomain DNA-binding specificities. In particular, we consider two random forest approaches: one that was trained using naturally occurring homeodomains (rf_extant) (Christensen et al. 2012) and another that showed the utility of incorporating synthetic homeodomain training data (rf_joint) (Chu et al. 2012). For both of these approaches, the data set of TF–PWM pairs required heuristic alignment of PWMs to uncover corresponding base positions across the PWMs; this was followed by feature selection before a random forest was trained for each base position. To provide a fair comparison of de novo predictive performance across methods on diverse proteins, we reserve half of the synthetic (at random) and all of the mutant homeodomain proteins as a test set and rerun rCLAMPS on the remaining 593 pairs that do not overlap these reserved proteins in terms of DNA-contacting residue combinations. Of the 141 proteins unseen by either rCLAMPS or rf_extant, our model predicts 90% of columns correctly, 5% more than rf_extant. Notably, rCLAMPS displays greater accuracy for five out the six core binding site positions for homeodomains, with the most marked improvements in positions 3 through 5 (Supplemental Fig. S3). This is consistent with earlier observations that rf_extant struggles to predict the more variable DNA-binding specificities in positions 4 through 6 introduced by the synthetic homeodomains (Chu et al. 2012). Our comparison to rf_joint is more limited, as the 77 proteins not in either method's training set cover only 16 distinct DNA-binding residue combinations. Nonetheless, on this limited test set, both methods predict 94% of columns accurately. Although rf_joint predicts one more column correctly in each of binding site positions 1, 2, and 4, our model predicts two more columns correctly in position 5 (Supplemental Fig. S4). Thus, despite the fact that these previous approaches used combinatorial models that required hyperparameter tuning, as well as extensive preprocessing for alignment of PWMs and homeodomain position feature selection (Christensen et al. 2012), our automated probabilistic approach requiring only interpretable linear parameter fitting provides comparable de novo predictive power.

Learning structural mappings allows effective transfer of specificity information from wild-type to mutant TFs

Although de novo DNA-binding specificity prediction is necessary for predicting binding preferences of completely uncharacterized TFs, in the context of natural variation and disease, there is great interest in predicting the changes in DNA-binding specificities induced via single–amino acid alterations to wild-type TFs. Mutated TFs are seen in cancer (Kobren et al. 2020) and in inherited diseases (Chi 2005; Hamosh et al. 2005). If such an alteration occurs in a DNA-contacting residue, as a first approximation, de novo prediction is necessary only for the binding site positions contacted by that altered residue, whereas the specificity for the remaining binding site positions can be transferred directly from the wild type. The primary obstacle preventing such a “hybrid” approach is that for the vast majority of TFs, the underlying amino acid–base contacts involved in the interaction are unknown. However, because rCLAMPS infers both a structural mapping of the underlying amino acid–base contacts and a per-binding site position de novo recognition code, we next use such a hybrid inference approach.

To test our hybrid approach, we considered the 593 proteins given as input to rCLAMPS from the previous section as “wild-type” specificities and inferred specificities for each of 88 “mutant” proteins in the held-out test set. A protein from the held-out set is considered to be a mutant to a given wild-type protein if it is at least 80% identical to the wild type throughout all positions in the match states of the DNA-binding domain and differs in exactly one DNA-contacting residue. Across these 88 mutants’ inferred specificities, our hybrid approach infers 353 of the columns via transfer from corresponding wild-type specificities and requires de novo predictions for 175 columns. Comparing these inferred columns to their experimental counterparts, we find that 90% of the columns predicted de novo are accurate versus 93% for the transferred columns (Fig. 3, left), suggesting a potential advantage to using the transfer approach when possible. Additionally, the transferred columns are more accurate than the identical column positions for the same proteins when predicted de novo by either rCLAMPS or by rf_extant (Fig. 3, right). We note that the rf_joint method includes all but 19 of the mutant proteins in its training set (spanning only eight distinct DNA-contacting residue combinations). On this extremely small and not very diverse set of proteins, both our hybrid approach and rf_joint predict each of the 76 columns for which transfer was possible accurately (Supplemental Fig. S5). Taken together, our results illustrate that the protein–DNA interface mappings inferred by our approach effectively enable transfer of wild-type homeodomain specificity information at the level of individual binding site positions and in turn allow inference of more accurate DNA-binding specificities for mutant homeodomains than de novo prediction alone.

Figure 3.

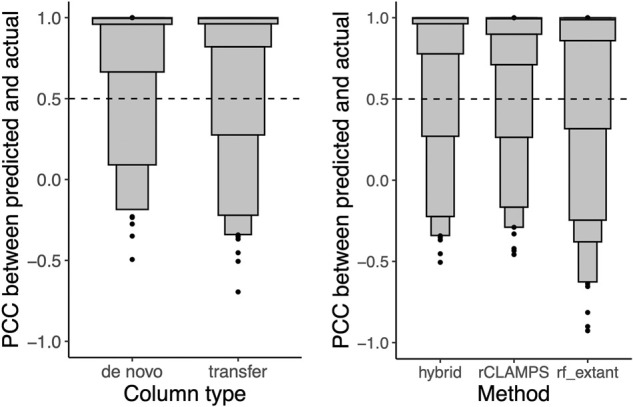
Column transfer via learned structural mappings is highly effective for predicting DNA-binding specificities for mutant TFs. (Left) For the hybrid approach, the PWM columns are binned according to whether they are predicted de novo or via transfer, and the PCCs of the predicted versus actual columns are shown in letter-value plots. Although 90% of de novo predictions are in agreement with their experimentally determined counterparts, an even higher 93% of predictions via transfer are in agreement. (Right) For each of the homeodomains that were also not part of the rf_extant training set and by considering only columns for which transfer was used by our hybrid approach, we compute the PCC between the actual specificity for a column and that predicted by our hybrid approach (hybrid), our de novo linear approach (rCLAMPS), and the rf_extant model (rf_extant). We find that 93% of transferred predictions are in agreement with their experimentally determined counterparts, compared with 91% and 85% of de novo predictions for rCLAMPS and rf_extant, respectively.

Accurate and automated mapping of TF–PWM pairs to a structural interface

Because homeodomain proteins and their DNA-binding specificities are highly conserved across organisms (Nitta et al. 2015), we next use an across-species approach to externally validate our mapping of TF–PWM pairs using previously determined known protein–DNA interfaces. Specifically, in the first large-scale assay of homeodomains in the fruit fly, DNA-binding specificities were characterized in a specialized experimental system that specifically allowed for a global alignment (with known orientation) of all the DNA sequences selected by all the DNA-binding domains assayed (Noyes et al. 2008b). By manually aligning a single PWM from this set relative to the start of our contact matrix and shifting registrations of all others identically, we obtain an experimentally inferred mapping of each of these fly PWMs. Of 593 homeodomains for which rCLAMPS inferred structural mappings, 235 of them map to fly proteins characterized in this previous assay as they are identical in their base-contacting positions. Thus, we compare correspondences between the experimentally determined fly mappings and the mappings of their base-contacting residue-identical counterparts in our data set.

Overall, 97% (228/235) of our inferred mappings are identical to their experimentally determined counterparts (Fig. 4, left, green). Further, after separating the homeodomain proteins according to “specificity groups” as determined by the investigators of the experimental approach via hierarchical clustering of their DNA-binding motifs (Noyes et al. 2008b), we find that the mappings are either completely or nearly completely correct for 10 out of 11 of these diverse specificity groups (Fig. 4, right, green), with poor agreement occurring for only the relatively small Iroquois group.

Figure 4.

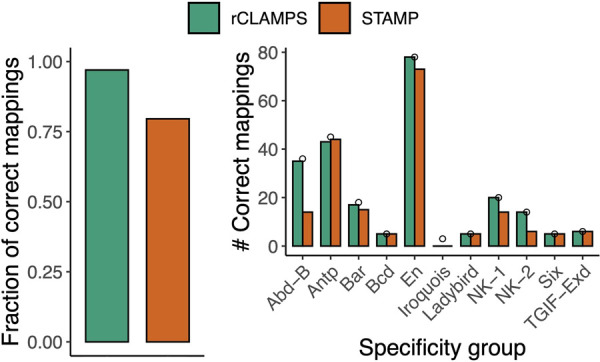
Inferred mappings to contact map are highly accurate. We compare mappings inferred by rCLAMPS (green) and computed based on direct PWM multiple alignment performed by STAMP (red) to those that are known experimentally for TFs that have identical amino acids within their base-contacting positions. (Left) The fraction of predicted mappings that is identical to the experimental mappings. (Right) The number of identical mappings when homeodomains are classified with respect to “specificity groups” as determined by Noyes et al. (2008b). Small circles represent the total number of homeodomains considered in each of these specificity groups.

To illustrate the advantage of our approach that jointly considers the proteins and the binding sites when aligning specificities for a family of TFs, we compare our results to a tool that considers only binding site information. In particular, we consider STAMP (Mahony et al. 2007), which is a multiple PWM alignment tool that uses a guide tree based on pairwise PWM alignments (i.e., without considering the protein sequences associated with the PWMs). We run STAMP on the same set of PWMs and use default parameters. Although STAMP does not map its aligned set of PWMs to the homeodomain contact map, we consider the mapping of the alignment that gives the best possible results for STAMP. This results in a correct mapping for 80% of the TFs (Fig. 4, left, red). STAMP does well on the most abundant groups (e.g., Antp and En); this is as expected because these PWMs are similar to each other and align well to each other. In contrast, STAMP struggles on groups that diverge more substantially from the canonical homeodomain motif pattern (e.g., the NK-2 group) or groups that tend to have reverse palindromic PWMs with more subtle specificity differences between the two sides of the palindrome (e.g., the Abd-B group). This is also as expected, because STAMP's intended use is to align similar PWMs, not a diverse set of PWMs, as can be seen for different TFs from the same structural family. Thus, for TF families with diverse or complex DNA-binding specificity determinants, our framework can effectively harness the shared information between the proteins and their corresponding PWMs to produce a multiple PWM alignment that is in outstanding agreement with a ground truth experimental alignment.

Accurate de novo prediction and interface mapping for C2H2-ZF proteins

To empirically examine the generalizability of our framework, we run our extended version of rCLAMPS using the C2H2-ZF domain–DNA contact map along with 263 C2H2-ZF PWM–protein pairs, sampling 250 random starting positions and orientations for the PWMs, and consider the mapping of protein–DNA interfaces with the highest likelihood across all runs. Despite the fact that the C2H2-ZF family contains by far the most diverse set of DNA-binding specificities, with domains capable of interacting with all 64 DNA triplets via different combinations of DNA-contacting residues (Persikov et al. 2015), our linear recognition code was able to predict C2H2-ZF DNA-binding specificities quite well. Specifically, in a strict holdout validation analogous to that used for homeodomains (i.e., analogous to Fig. 2), 1446 out of 2041 (71%) PWM columns predicted by rCLAMPS de novo agree with corresponding experimental columns (Supplemental Fig. S6, left), with slightly higher performance for PWMs from the Fly Factor Survey (72%) than for other PWMs. We note that C2H2-ZFs have historically been the most difficult family for which to experimentally determine DNA-binding specificities (Barazandeh et al. 2018); indeed in previous work, we examined across-data set agreement of high-throughput specificities for individual C2H2-ZF domains identical in their DNA-contacting residues, finding that they agreed in only 75% of columns even after optimal within-data set regularization (Wetzel and Singh 2020). Considering each binding site position of the C2H2-ZF domain–DNA interface separately, the median per-column PCCs when comparing predicted and experimentally measured columns are 0.86, 0.92, and 0.99 for binding site positions 1 through 3, respectively (Supplemental Fig. S6, right). For 36 of the PWM–protein pairs included in our data set, per-domain PWMs were previously experimentally inferred (Enuameh et al. 2013), allowing for easy inference of the proper starting positions and orientations of the protein–DNA interfaces within the corresponding full-length PWMs. Overall, the mappings inferred by rCLAMPS agree for 30 (83%) of these. Taken together, these results indicate that rCLAMPS is a general and effective approach for automatically inferring both TF family-specific recognition codes and protein–DNA interfaces from large PWM collections.

Discussion

We describe a novel probabilistic framework that enables fully automated analyses of large compendia of TF DNA-binding specificities to jointly discover mappings of underlying sets of amino acid–base contacts and structure-aware TF family-wide recognition codes. In principle, our approach can be applied to PWMs for any family of DNA-binding proteins whose interaction interfaces with DNA are structurally conserved enough to be modeled by a pairwise amino acid–base position contact map. Using the homeodomain family as a test case, we show that the physically interpretable recognition code learned is both expressive enough and generalizable enough to allow state-of-the-art de novo prediction of homeodomain DNA-binding specificities. Furthermore, we show that having extremely accurate mappings of TF–PWM interfaces allows single-base-position resolution transfer of specificity information from wild-type to mutant proteins, in turn enabling inference of even more accurate DNA-binding specificities. Finally, we show the generality of our framework by applying it to a very different TF family from the homeodomains, namely C2H2-ZFs where all C2H2-ZF domains are known to engage with DNA.

Our linear model and set of mapped TF–DNA interfaces can serve as a jumping off point for training models that account for higher-order interactions, and without the need to rely on experimentally curated contact maps (Benos et al. 2002; Kaplan et al. 2005; Noyes et al. 2008b; Persikov et al. 2009, 2015; Persikov and Singh 2014; Najafabadi et al. 2015), specialized experimental setups that place the protein in a fixed orientation with the binding site (Noyes et al. 2008a,b; Chu et al. 2012; Persikov et al. 2014; Najafabadi et al. 2015), or complicated and partly curated multiple motif alignment strategies (Christensen et al. 2012; Chu et al. 2012). Indeed, in a preliminary exploration in which we trained machine learning methods that allow nonlinear effects between amino acids on base preferences (including gradient boosting [Friedman 2000] and random forests [Breiman 2001]) on our set of mapped TF–DNA interfaces, we found that they provide subtle improvements in predictive performance for some base positions. However, we do not report those results here as the pairwise energetic approximation provided by rCLAMPS allows for statistically interpretable coefficients while still providing state-of-the-art predictive performance. Optimizing these nonlinear, more expressive models is likely to be a fruitful avenue for further research. Additionally, exploration of informative priors for the protein–DNA recognition codes learned by rCLAMPS could likely improve its performance and make it possible to predict changes in specificity induced even by amino acid–base contacts not directly observed in the PWM–protein pair training set. For example, one could imagine introducing parameter priors based on more general amino acid–base contacts observed across domains with similar structural motifs (Suzuki 1994; Suzuki and Yagi 1994; Luscombe 2001) or based on previous DNA-recognition patterns observed in large synthetic TF–DNA interaction screens for certain TF families (Najafabadi et al. 2015; Persikov et al. 2015). Further, DNA shape has been shown to be an important determinant for both intrinsic and context-specific DNA recognition by homeodomain and other TF families (Gordân et al. 2013; Dror et al. 2014; Zhou et al. 2015; Mathelier et al. 2016; Yang et al. 2017; Kribelbauer et al. 2020); thus, extending our model to include DNA shape information based on binding sites’ flanking nucleotide contexts may lead to more accurate predictions of the effects of TF mutations on DNA-binding activity.

rCLAMPS can in principle be applied to a broad range of TF families. The primary requirements for applying our framework in its current form are the availability of a set of structural co-complex interfaces from which to infer a family-wide aggregate contact map, availability of a sufficient number of PWM–protein pairs from which to learn a family-wide recognition code, and a priori knowledge for each PWM–protein pair of which DNA-binding domain(s) within the protein interacts with the set of DNA sequences represented by the PWM. In theory, however, rCLAMPS can be extended to relax this third requirement via the use of latent variables, allowing automated inference of more complex situations that can arise in TF–DNA interactions. For example, some C2H2-ZF TFs contain multiple distinct arrays of domains, and it is generally unknown a priori which array or arrays, or even which domains within these arrays, are involved in DNA binding for a given PWM. Such situations could be handled by rCLAMPS via inclusion of additional latent parameters representing the engaged array or arrays, as well as the first and last domain within it that are engaged; alternatively, variable interaction interface alignments could be introduced through clever algorithmic work. On a similar note, many TFs engage their binding sites as homodimers or heterodimers (Jolma et al. 2013). In such a case, although the current implementation of rCLAMPS would find only half-sites within the PWM that are a good match to the learned recognition code, additional latent parameters could be included to help determine whether the PWM is a better match to a single binding site or a pair of half-sites, with or without half-site overlap. Although rigorous testing of such extensions is beyond the scope of this article, they highlight the overall flexibility of the framework and represent opportunities to build upon it.

Overall, we expect that our general approach can be applied to the thousands of extant DNA-binding specificities across a range of organisms and to a diverse set of DNA-binding families; this would drastically improve our understanding of the determinants of DNA-binding specificity and in turn help efforts to predict the potential downstream regulatory impacts of mutations within TFs.

Software availability

Open-source software implementing methods and analyses described in this work, along with examples of how to predict specificities for novel TFs using the models described and how to interpret the models’ learned parameters, are available at GitHub (https://github.com/jlwetzel-slab/rCLAMPS) and as Supplemental Code.

Competing interest statement

The authors declare no competing interests.