Joint modeling under competing risks: Application to survival prediction in patients admitted in Intensive Care Unit for sepsis with daily Sequential Organ Failure Assessment score assessments

Abstract

Joint models of longitudinal process and time‐to‐event data have recently gained attention, notably to provide individualized dynamic predictions. In the presence of competing risks, models published mostly involve cause‐specific hazard functions jointly estimated with a linear or generalized linear model. Here we propose to extend the modeling to full parametric joint estimation of a nonlinear mixed‐effects model and a subdistribution hazard model. We apply this approach on 6046 patients admitted in intensive care unit (ICU) for sepsis with daily Sequential Organ Failure Assessment (SOFA) score measurements. The joint model is built on a randomly selected training set of two thirds of patients and links the current predicted SOFA measurement to the instantaneous risks of ICU death and discharge from ICU, both adjusted on the patient age. Stochastic Approximation Expectation Maximization algorithm in Monolix is used for estimation. SOFA evolution is significantly associated with both risks: 0.37, 95% confidence interval (CI) = [0.35, 0.39] for the risk of death and −0.38, 95% CI = [−0.39, −0.36] for the risk of discharge. A simulation study, inspired from the real data, shows the good estimation properties of the parameters. We assess on the validation set the added value of modeling the longitudinal SOFA follow‐up for the prediction of death compared with a model that includes only SOFA at baseline. Time‐dependent receiver operating characteristic area under the curve and Brier scores show that when enough longitudinal individual information is available, joint modeling provides better predictions. The methodology can easily be applied to other clinical applications because of the general form of the model.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

Joint modeling under competing risk setting has been rarely described in the literature, especially when dealing with nonlinear mixed‐effects models (NLMEMs). Most published models considered a linear biomarker evolution, possibly with spline functions to deal with nonlinearity. One considers an NLMEM model jointly estimated with a cause‐specific multistate model using NONMEM software.

• WHAT QUESTION DID THIS STUDY ADDRESS?

We propose an approach to model joint estimation of NLMEM and competing risks using a parametric subdistribution hazard model. We apply this new approach on a large data set of patients admitted in intensive care unit (ICU) for sepsis, with daily Sequential Organ Failure Assessment (SOFA) score assessments, to predict the risk of death with the competing risk being discharge from ICU.

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

The Stochastic Approximation Expectation Maximization algorithm can be used to provide unbiased estimates of such model parameters. In the real case application, we showed that the joint modeling improves the quality of predictions when sufficient SOFA follow‐up is considered compared with a model that only uses baseline information.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

The methodology can be easily extended to other clinical applications of individualized predictions, which is useful because a competing risk setting arises in many biomedical applications.

INTRODUCTION

A major ambition of precision medicine is to provide every patient with a personalized and adapted medical treatment. Individual dynamic predictions of a clinical outcome based on discrete longitudinal observations of a biomarker fully enter the scope of precision medicine. To get individual predictions that can be updated as more observations become available, a natural approach is to use the fit of a joint model combining (i) the longitudinal model for the evolution of the biomarker and (ii) the time‐to‐event process describing the risk of the clinical outcome in consideration.

This joint modeling approach has recently gained attention, ¹ , ² , ³ , ⁴ mainly for two reasons. First, a much simpler strategy where biomarker observations are included as a time‐varying covariate in a survival model imposes to make a hypothesis about the marker evolution between measurements, neglects measurement errors, and is known to be incorrect because of the endogenous nature of the covariate (i.e., whose existence is directly related to failure status). ⁵ , ⁶ Second, one could consider fitting a first model for the biomarker evolution and then plugging the predicted evolution as a time‐dependent covariate in the survival model, resulting in a so‐called two‐stage procedure. Unfortunately, the dropout process induced by the survival model, that is, the onset of an event that precludes any further biomarker measurements, generates missing data for the biomarker that can be not at random (missing not at random [MNAR]). This leads to possible bias in the estimations as described in a published study. ⁷ The joint modeling approach genuinely overcomes these two methodological issues. A recent publication ⁸ proposes a workflow for a joint model of longitudinal and time‐to‐event data.

Competing risks are frequent in biomedical applications, where patients are at risk of multiple and mutually exclusive events (e.g., death and relapse in oncology or death and discharge in a hospital ward). When dealing with competing events, two distinct risks can be modeled: the cause‐specific hazard (CSH) ⁹ and the subdistribution hazard (SDH). ¹⁰ Although both approaches are essentially two different parametrizations of the same random process, some authors argue that the CSH parameters are more suitable for etiologic studies and SDH parameters for risk prediction. ¹¹ , ¹² We also emphasize that the hypothesis of proportionality of risks on CSH and SDH are generally not compatible. ¹³ Although the cause‐specific approach was the most often used in the context of joint modeling, ³ , ¹⁴ , ¹⁵ , ¹⁶ we decided here to analyze the data assuming that the hypothesis of proportional hazards holds on the SDHs.

The joint estimation with competing risks complicates the analysis, especially when the biomarker evolution is associated with the risk of both events. In the literature, linear ¹⁷ , ¹⁸ , ¹⁹ and nonlinear ¹ , ⁴ , ²⁰ joint models have been extensively described. However, when dealing with competing risks, linear mixed‐effects submodels, possibly involving a combination of spline functions to deal with nonlinearity (using R‐INLA ²¹ or JMbayes ¹⁵ ) are predominant. To our knowledge, only one study ²² considered a nonlinear mixed‐effects model (NLMEM) jointly estimated with a cause‐specific multistate model using NONMEM software (ICON plc).

A popular application when treating of joint models is to derive individual dynamic predictions of both marker evolution and associated risks of event. It consists of considering a so‐called landmark time and predicting, for one individual, the future evolution of the marker and the cumulative incidences of the competing events conditionally to the overall survival up to that landmark time. ¹ , ²³ In that case, the competing risk framework imposes to carefully define the at‐risk population for predictions, in particular when assessing their performances.

In this work, we propose to use Monolix software (Lixoft) to jointly estimate a nonlinear mixed‐effects submodel for modeling the longitudinal trajectory of a biomarker and a parametric SDH submodel for modeling multiple risks of events. This approach is then applied to a subset of OUTCOMEREA database in patients admitted in intensive care unit (ICU) for sepsis, a life‐threatening condition where severe organ dysfunctions are caused by the infection of the organism by a pathogen. ²⁴ We also propose a simulation study to assess performances of the estimation in terms of relative bias and relative root mean square error.

METHODS

General framework

Joint Model

Nonlinear mixed‐effects models

Let N be the number of subjects and $\{y_{i1},\dots ,y_{i{n}_i}\}$ the vector of longitudinal observations of subject i (for i = 1, … , N). Observation y _ij denotes the jth measurement of patient i at time t _ij (for j = 0, … , n _i ). Let m be the known nonlinear function describing the structural model and g the known function describing the error model. The NLMEM writes as follows:

$$y_{\mathit{ij}}=m\left(t_{\mathit{ij}},{\psi }_i\right)+g\left[m\left(t_{\mathit{ij}},{\psi }_i\right),\sigma \right]{ϵ}_{\mathit{ij}}$$ (1)

ψ _i = f(μ, η _i , Z _i ) denotes the individual parameters expressed as a function of population parameters, noted μ; individual random effects, noted η _i ; and an optional vector of individual covariates Z _i . The random effects are assumed to be normally distributed with mean 0 and variance–covariance matrix Ω, and independent of the residual Gaussian error, noted ϵ _ij , of mean 0 and variance 1. σ denotes the vector of the error model parameters.

SDH models

Let the variable T describe the time‐to‐event distribution, C the noninformative censoring time, and K denotes the event type that occurs. For the sake of simplicity, we consider only two events $k\in \left\{1,2\right\}$. We set $\delta =1_{T<C}\times K$ as the event indicator, thus δ = K in case of failure and δ = 0 in case of censoring. The couple $\left(\tilde{T},\delta \right)$ with $\tilde{T}=\min \left(T,C\right)$ is observed for each individual. The cumulative incidence $\mathrm{\mathbb{P}}\left(T<t,K=k\right)$ on event k is modeled with an SDH λ _k associated with the variable T _k defined as: $T_k=T\times 1_{K=k}+\infty \times 1_{K\ne k}$. To model T ₁ and T ₂ and derive cumulative incidences, we introduce two parametric SDH functions ${\lambda }_1$ and ${\lambda }_2$.

Likelihood and estimation

Longitudinal and survival parts are supposed to be linked as described in the following equation:

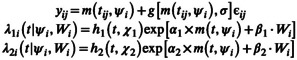(2)

where $h_1$ and $h_2$ are the baseline hazard functions for the risk of event 1 and the risk of event 2, and which depend on vectors of parameters χ ₁ and χ ₂, respectively. ${\alpha }_1$ and ${\alpha }_2$ are the coefficients that link the current predicted value of the marker with the instantaneous risks of event 1 and event 2, respectively. For the sake of clarity, we only considered a linear link between the longitudinal process and the subdistribution risks. Depending on the modeled data, more complex link functions could also be considered (e.g., involving splines or integration). W _i is the optional vector of covariates with coefficient β ₁ or β ₂.

Both longitudinal and survival submodels are linked by shared random effects, and the joint likelihood writes:

$$L\left(\theta \right)=\prod _{i=1}^N{\int }_{{\eta }_i}\left[\left(\prod _{j=0}^{n_i}p\left(y_{\mathit{ij}}|{\eta }_i,Z_i;\theta \right)\right)p\left({\tilde{T}}_i,{\delta }_i|{\eta }_i;\theta \right)p({\eta }_i;\theta )\right]d{\eta }_i$$ (3)

where $\theta =\left\{\mu ,,,\mathrm{\Omega },,,\sigma ,,,{\chi }_1,,,{\chi }_2,,,{\alpha }_1,,,{\alpha }_2,,,{\beta }_1,,,{\beta }_2,\right\}$ is the vector of parameters to estimate. p(y _ij |η _i , Z _i ; θ) is the density function of longitudinal process, p(η _i ; θ) the density function of random effects, and p(t, δ|η _i ; θ) is the density function of the survival process given by:

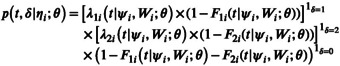(4)

where, for k = {1, 2}, $F_{\mathit{ki}}\left(t|{\psi }_i,W_i;\theta \right)=1-\exp \left(-{\int }_0^t{\lambda }_{\mathit{ki}}\left(u|{\psi }_i,W_i;\theta \right)\mathrm{d}u\right)$ is the individual cumulative incidence function for event k at time t.

The population parameter θ can be estimated by the maximization of the likelihood with the Stochastic Approximation Expectation Maximization (SAEM) algorithm implemented in Monolix (http://lixoft.com). This algorithm has been shown to be powerful, having good theoretical properties and accurately estimating parameters. ²⁵ Variance–covariance matrix Σ of the population parameters is estimated with a stochastic approximation. ²⁶ We note $\widehat{\theta }$ and $\widehat{\mathrm{\Sigma }}$ their estimates.

Individual dynamic predictions

A popular application of joint models is to provide individual dynamic predictions for the biomarker evolution and for survival outcome(s). For a new patient i who has longitudinal observations until a landmark time l, $Y_i\left(l\right)=\left\{y_{\mathit{ij}};0\le t_{\mathit{ij}}\le l\right\}$, we aim at predicting his future marker value at time l + t, denoted m _i (l + t|l), and his event 1 survival probability s _i (l + t|l). The time t is called horizon time. Because dynamic predictions are applied to patients who are event free before time l, we focus on the conditional probability of not experiencing the event of interest expressed as:

$$s_i\left(l+t|l\right)=\mathrm{\mathbb{P}}\left(T_{1i}>l+t|T_i>l,Y_i\left(l\right),Z_i,W_i,\theta \right)$$ (5)

Thus, for each landmark time l, the marker measurements of patient i up to time l and the information provided by the population parameters are used to compute the a posteriori distribution of the individual parameters and infer the desired quantities. But as the a posteriori distribution has no closed form, Markov chain simulation is needed. In particular, some authors ²⁷ compared different software and computing methods to draw a posteriori values and showed that Monolix software and its Metropolis‐Hastings (MH) algorithm are able to provide those quantities with good properties. Then, the Monte Carlo process described in Rizopoulos ²³ can be used to derive R samples of individual parameters. For a repetition r ∈ [1, R],

1. draw ${\theta }^{\left(r\right)}\sim \mathcal{N}\left(\widehat{\theta },,,\widehat{\mathrm{\Sigma }}\right)$ to take into account estimation uncertainty on population parameters

2. draw a realization of ${\eta }_i^{\left(r\right)}$ on the a posteriori distribution: ${\eta }_i^{\left(r\right)}\sim \left\{{\eta }_i,|,T_i>l,,,Y_i\left(l\right),,,Z_i,,,W_i,,,{\theta }^{\left(r\right)}\right\}$ and infer ${\psi }_i^{\left(r\right)}=f\left({\mu }^{\left(r\right)},{\eta }_i^{\left(r\right)},Z_i\right)$

3. compute $m_i^{\left(r\right)}\left(l+t|,{\psi }_i^{\left(r\right)}\right)$ and $\begin{array}{c}{s}_i^{\left(r\right)}\left(l+t,|,{\psi }_i^{\left(r\right)}\right)=\hfill \end{array}$ $\begin{array}{c}\frac{F_{1i}^{\left(r\right)}\left(\infty \right)+F_{2i}^{\left(r\right)}\left(\infty \right)-F_{1i}^{\left(r\right)}\left(l+t\right)-F_{2i}^{\left(r\right)}\left(l\right)}{F_{1i}^{\left(r\right)}\left(\infty \right)+F_{2i}^{\left(r\right)}\left(\infty \right)-F_{1i}^{\left(r\right)}\left(l\right)-F_{2i}^{\left(r\right)}\left(l\right)}\hfill \end{array}$ with $F_{\mathit{ki}}^{\left(r\right)}\left(t\right)=$ $F_{\mathit{ki}}\left(t,,|,,{\psi }_i^{\left(r\right)},,,W_i,;,{\theta }^{\left(r\right)}\right)$.

Estimates of m _i (l + t|l) and π _i (l + t|l) are derived with

$$\begin{array}{l}{\widehat{m}}_i\left(l+t|l\right)=\text{median}\left\{m_i^{\left(r\right)}\left(l+t|{\psi }_i^{\left(r\right)}\right),r=1,\dots ,R\right\}\\ {\widehat{s}}_i\left(l+t|l\right)=\text{median}\left\{s_i^{\left(r\right)}\left(l+t|{\psi }_i^{\left(r\right)}\right),r=1,\dots ,R\right\}\end{array}$$ (6)

Prediction intervals can be derived by reporting the corresponding percentiles.

Performances are assessed in terms of discrimination with the time‐dependent receiver operating characteristic area under the curve (ROC AUC) ²⁸ and calibration with the time‐dependent Brier score. ²⁸ Details on the definition and computation of those indicators can be found in Supplementary Information S1.

Application framework

Data and objectives

Description of the data

The data are a subset of the OUTCOMEREA database composed of patients admitted in the ICU in 30 French centers between 1997 and 2015. Ethical and legal aspects of the database are described in Supplementary Information S2. In this application, we focus on patients included for sepsis or septic shock aged older than 18 years. Exclusion criteria were readmissions, admissions for palliative care, brain deaths, or early decisions not to forego life‐sustaining therapy. The patient set was randomly divided into two subsets to build a training data set composed of two thirds of the data and a validation data set composed of the remaining one third. Daily assessment of the sepsis‐related Sequential Organ Failure Assessment (SOFA) score was available for each patient stay. The SOFA score quantifies the number and the severity of organ dysfunctions between 0 (no organ dysfunction) and 24 (very severe organ dysfunctions). ²⁹ , ³⁰ , ³¹ This score is measured daily from ICU admission to discharge from ICU, but not after. ICU duration stay; status (alive/dead) at the end of the stay; and baseline covariates such as age, sex, and presence of comorbidities (e.g., diabetes, chronic heart failure, chronic kidney diseases, liver cirrhosis, chronic obstructive pulmonary diseases and immunocompromised status) were also available.

Objectives

The objective is to estimate jointly the individual SOFA score evolutions and the associated risk of ICU death and discharge within 30 days after ICU admission. It is worth noting that death and discharge are competing events because the occurrence of discharge precludes the possibility to observe the ICU death. It is also reasonable to presume that discharged patients do not have the same risk of death than other patients still hospitalized in the ICU. In this application, SOFA score evolution is modeled by a parametric NLMEM, death and discharge are modeled by a parametric competing risk subdistribution model with ICU death as the event of interest and discharge from ICU as the competing event. The added value of modeling the longitudinal evolution of the SOFA score is assessed by comparing prediction performances of a baseline model (model that only includes baseline SOFA measurement and other baseline covariates) versus the joint model.

Baseline and joint models

Baseline model

SDHs are parametric functions with a constant baseline hazard noted h ₁ for the risk of death and h ₂ for the risk of discharge. Both instantaneous risks include the baseline SOFA measurement. Covariate selection for age, sex, and number of comorbidities is based on Bayesian information criterion (BIC). All combinations are tested, and the one that minimizes the BIC is added in the baseline model. Briefly, the model writes:

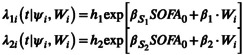(7)

Joint model

To allow monotonous or nonmonotonous evolution (e.g., initial increase of SOFA followed by a decrease or vice versa), the structural model m is defined as:

$$\begin{array}{c}\begin{array}{c}m\left(t_{\mathit{ij}},{\psi }_i\right)=\varphi \left[b_{0i}+a_i\right.\times \left(\exp ,\left(b_{1i}\times \left(t_{\mathit{ij}}-t_{\mathrm{lag},i}\right)\right)\right.\left.\left.-\exp \left(b_{2i}\times \left(t_{\mathit{ij}}-t_{\mathrm{lag},i}\right)\right)\right)\right]\hfill \end{array}\hfill \end{array}$$ (8)

where ϕ is a capping function used to enforce the predicted SOFA score to remain between 0 and 24:

$$\varphi \left(x\right)=\left\{\begin{array}{cc}0 \hfill & \text{if}x<0\hfill \\ x \hfill & \text{if}0\le x\le 24\hfill \\ 24\hfill & \text{if}x>24\hfill \end{array}\right.$$

and we have:

$$\begin{array}{c}\left\{\begin{array}{cc}{b}_{0i}\hfill & ={\mu }_0+{\eta }_{0i}\\ b_{1i}& ={\mu }_1+{\eta }_{1i}\\ b_{2i}& ={\mu }_2+{\eta }_{2i}{\eta }_{\mathit{pi}}\sim \mathcal{N}\left(0,,,{\omega }_p\right)\\ a_i& ={\mu }_a{e}^{{\eta }_{\mathit{ai}}}\\ t_{\mathrm{lag},i}& ={\mu }_{\mathrm{lag}}+{\eta }_{t_{\mathrm{lag}},i}\end{array}\right.\hfill \end{array}$$

The parameter t _lag stands for the delay between symptom onset and the first SOFA evaluation. Details of coefficient interpretations can be found in Supplementary Information S3.

We used a combined error based on a model selection procedure using the BIC criteria. Thus, g[m(t _ij , ψ _i ), σ] = σ _a  + σ _b  × m(t _ij , ψ _i ), with σ = {σ _a , σ _b }. Details referring to error model selection are presented in Table S1 of the Supplementary Materials. In our joint model, the survival part includes baseline covariate(s) to model the dependence between prognosis and a patient's characteristics. In accordance with physicians, we made the hypothesis that the covariates only affect survival, for a given SOFA trajectory, and not the SOFA process itself. Therefore, it was not tested in the longitudinal submodel. Of note, exploring and testing various covariates on each of the five parameters of the structural model would require a careful handling of multiple testing issues.

SDHs are the same parametric functions as presented in the baseline model but including a coefficient linking the longitudinal process and the respective instantaneous risk.

We used Monolix 2018R2 with a maximum of 2000 iterations in the exploratory phase and in the stochastic approximation for both baseline and joint model estimations.

Details and help for readers on practical model implementation can be found in Supplementary Information S4.

Individual dynamic predictions

For both baseline and joint modeling, four landmark times are considered at 0, 3, 6, and 9 days after patient admission. Multiple horizon times are also considered, from landmark time plus 1 day to 30 days after admission.

To assess the performances of the models and according to the methods described, at a landmark time l and an horizon time t, a case is a patient who died in the ICU between l and l + t, and a control is a patient still hospitalized in the ICU or who was discharged between l and l + t. We note that, in our context, no censoring occurs between landmark and horizon times, and there is only an administrative censoring at 30 days. Thus, estimators of the AUC and Brier score in the absence of censoring presented in Supplementary Information S1 are used (Equations 2 and 4).

For the settings of the MH algorithm, we set one chain with three proposal functions that are used in turn: the population distribution, a unidimensional Gaussian random walk, or a multidimensional Gaussian random walk. For the random walks, the variance of the Gaussian is automatically adapted to reach an optimal acceptance ratio of 0.3. The algorithm stops when, for all parameters, the average conditional means and standard deviations of the last 50 iterations do not deviate by more than 5%.

Evaluation of the estimation performances by simulation

We conducted a simulation study to confirm that the SAEM algorithm implemented on Monolix 2018R2 provides good estimation performances of such a joint model. We assessed the estimation accuracy in terms of relative bias and evaluated the incertitude of estimation using relative root mean square errors (RRMSEs).

Simulation setting

We simulated M = 200 data sets of N = 1000 patients assuming that SOFA score measurements were available every day for at most 30 days after the ICU admission. SOFA measurements were reported for each patient until time of ICU death or ICU discharge or also end of the first 30 days of the stay, with no other censoring process.

The longitudinal data were simulated according to the model proposed in the application methods. Thus, this model is used:

$$\begin{array}{c}{y}_{\mathit{ij}}=m\left({\psi }_i,t_{\mathit{ij}}\right)+\left[{\sigma }_a+{\sigma }_b\times m\left({\psi }_i,t_{\mathit{ij}}\right)\right]{\mathrm{ϵ}}_{i,j}\\ m\left(t_{\mathit{ij}},{\psi }_i\right)=\varphi \left[b_{0i}+a_i\times \left(\exp \left(b_{1i}\times \left(t_{\mathit{ij}}-t_{\mathrm{lag},i}\right)\right)-\exp \left(b_{2i}\times \left(t_{\mathit{ij}}-t_{\mathrm{lag},i}\right)\right)\right)\right]\end{array}$$ (9)

with

$$\begin{array}{c}\varphi \left(x\right)=\left\{\begin{array}{cc}0 \hfill & \text{if}x<0\\ x& \text{if}0\le x\le 24\\ 24& \text{if}x>24\end{array}\right.\left\{\begin{array}{cc}{b}_{0i}\hfill & ={\mu }_0+{\eta }_{0i}\\ b_{1i}& ={\mu }_1+{\eta }_{1i}\\ b_{2i}& ={\mu }_2+{\eta }_{2i}\\ a_i& ={\mu }_a{e}^{{\eta }_{\mathit{ai}}}\\ t_{\mathrm{lag},i}& ={\mu }_{\mathrm{lag}}+{\eta }_{t_{\mathrm{lag}},i}\end{array}\right.{\eta }_{\mathit{pi}}\sim \mathcal{N}\left(0,{\omega }_p\right)\hfill \end{array}$$

For the survival part, we considered here two competing events and one categorical covariate W with three modalities. We adapted methods already described ³² , ³³ to generate failure time data. The subdistribution for the event of interest is given by:

$$\begin{array}{c}\mathrm{\mathbb{P}}\left(T_{1i}<t|,{\psi }_i,,,W_i,;,\theta \right)\hfill \\ =1-\exp \left(-{\int }_0^t\frac{p_1{g}_1\exp \left(-g_1\times s\right)\times \lambda \left(s\right)}{1-p_1\left(1-\exp \left(-g_1\times s\right)\right)}\mathrm{d}s\right)\hfill \end{array}$$ (10)

with λ(s) = exp(α ₁ × m(ψ _i , t _ij ) + β ₁ × W _i ). Parameters p ₁ and g ₁ are used to control the number of event 1 at infinite time and the speed of onset. The subdistribution for the competing risk was then obtained using an exponential distribution with rate $\frac{t}{b}$, where b controls the speed of event 2 onset:

$$\begin{array}{c}\mathrm{\mathbb{P}}\left(T_{2i}<t|,{\psi }_i,,,W_i,;,\theta \right)=\left(1-F_1\left(,\infty ,\right)\right)\times \left(1-\exp \left(-\frac{t}{b}\right)\right)\hfill \end{array}$$ (11)

Estimation setting

For each data set $m\in \left\{1,\dots ,M\right\}$, we estimated the following joint model:

$$\begin{array}{c}{y}_{\mathit{ij}}=m\left(t_{\mathit{ij}},{\psi }_i\right)+\left[{\sigma }_a+{\sigma }_b\times m\left({\psi }_i,t_{\mathit{ij}}\right)\right]{\mathrm{ϵ}}_{i,j}\\ {\lambda }_{1i}\left(t|{\psi }_i,W_i\right)=\frac{p_1{g}_1\exp \left(-g_1\times t\right)}{1-p_1\left(1-\exp \left(-g_1\times t\right)\right)}\exp \left[{\alpha }_1\times m\left(t,{\psi }_i\right)+{\beta }_1\cdot W_i\right]\\ {\lambda }_{2i}\left(t|{\psi }_i,W_i\right)=\frac{p_2{g}_2\exp \left(-g_2\times t\right)}{1-p_2\left(1-\exp \left(-g_2\times t\right)\right)}\exp \left[{\alpha }_2\times m\left(t,{\psi }_i\right)+{\beta }_2\cdot W_i\right]\end{array}$$ (12)

Estimation was performed by the maximization of the likelihood using the SAEM algorithm implemented on Monolix 2018 software with the same settings as explained in the application.

Evaluation criteria

We aimed to assess the performances of the estimation on a subset of the vector of parameters, the longitudinal parameters, and the survival parameters for the event of interest (death). We defined $\rho =\left\{\mu ,\omega ,{\alpha }_1,{\beta }_1\right\}$ and $\widehat{\rho }$ its estimate. The model specification for data simulation does not allow α ₂ and β ₂ to be easily identified, which is why the estimation evaluation was based on vector $\widehat{\rho }$. We evaluated the relative bias and the RRMSE of $\widehat{\rho }$ defined as:

$$\begin{array}{c}\text{Relative\hspace{0.17em}bias}=\frac{\mathbb{E}\left[\widehat{\rho }\right]-\rho }{\rho }\times 100\hfill \\ \text{and}\hfill \\ \text{RRMSE}=\sqrt{\frac{\mathbb{E}\left[{\left(\widehat{\rho }-\rho \right)}^2\right]}{\rho }}\times 100\hfill \end{array}$$ (13)

We also provided violin plots of relative estimation errors (REE) defined for each data set $m\in \left\{1,\dots ,M\right\}$ as:

$$\mathrm{REE}=\frac{\widehat{{\rho }^m}-\rho }{\rho }\times 100$$ (14)

RESULTS

Data description

A total of 6046 patients were considered, with 4050 patients included in the training set and 1996 in the validation set. The data flowchart is detailed in Figure 1.

FIGURE 1.

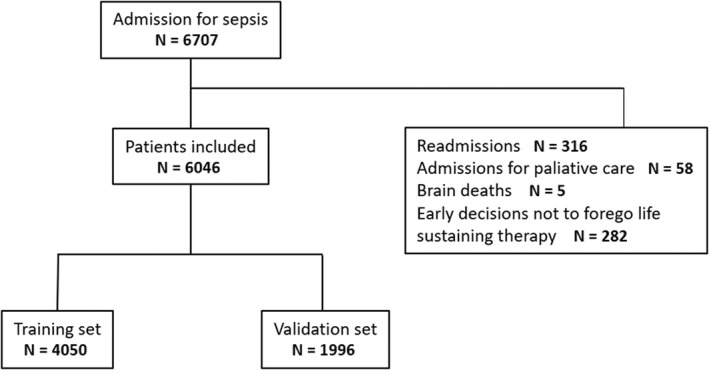
Data flowchart. A total of 6046 patients were included in the analysis, with 4050 in the training set and 1996 in the validation set.

Most of the patients were men (62%), and the median age at admission was 65.1 years ([Q1–Q3]: [52.7–76.2]). About half of the patients had no comorbidity at admission, one third had one, and one third had more than one. Median admission SOFA was 6 and 30 days after admission, about 19% of the patients died, whereas 72% were discharged. Table 1 summarizes the main patient characteristics at admission in both data sets.

TABLE 1.

Main patient characteristics at intensive care unit admission

Variable	Training set	Validation set
	(n = 4050)	(n = 1996)
Age, years, n (%)
<60	1565 (39)	782 (39)
[60, 75]	1333 (33)	682 (34)
$\ge$75	1152 (28)	532 (27)
Sex, n (%)
Male	2491 (61)	1272 (64)
Female	1559 (39)	726 (36)
Comorbidities, n (%)
0	1988 (49)	985 (49)
1	1340 (33)	682 (34)
>1	722 (18)	329 (17)
Admission SOFA, median [Q1–Q3]	6 [4–9]	6 [4–9]
30‐day mortality, n (%)	781 (19)	362 (18)
30‐day discharge, n (%)	2921 (72)	1426 (71)

Abbreviation: SOFA, Sequential Organ Failure Assessment.

Figure 2a shows the longitudinal SOFA trajectories of 100 random patients of the training data set. Figure 2b shows the cumulative incidences of both competing events (death and discharge) on the training set, truncated at day 30.

FIGURE 2.

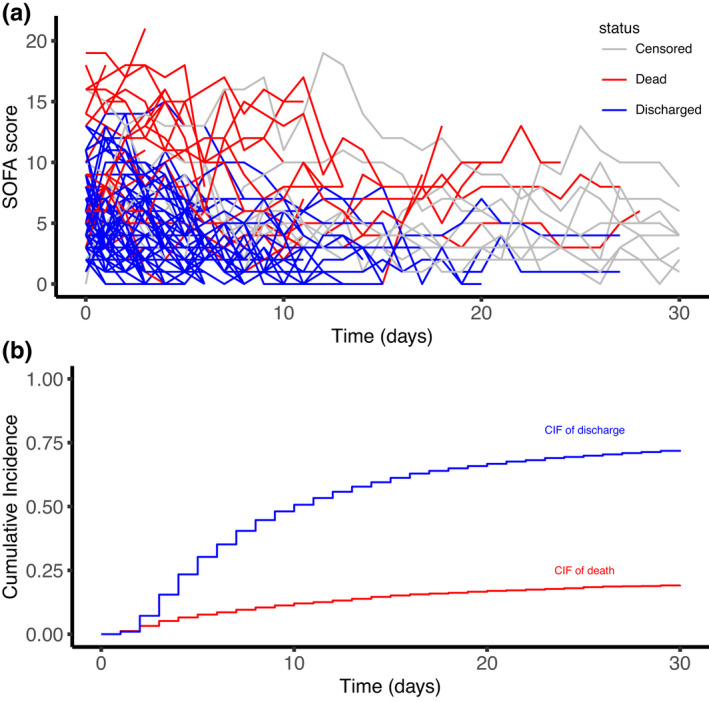
Exploratory plots of longitudinal and competing risk intensive care unit (ICU) data of the training set: (a) the Sequential Organ Failure Assessment (SOFA) score evolution of 100 random patients and (b) the cumulative incidences of ICU death and discharge from ICU (no censoring occurred during the follow‐up). CIF, cumulative incidence function.

Baseline model fit

The baseline model includes the baseline SOFA measurement and the patient age in three categories with cutoffs at 60 and 75 years (see Table S2 of the Supplementary Materials). The baseline SOFA already has a strong effect on the instantaneous risks of death and discharge: at a constant age category, a patient with a one‐point higher baseline SOFA has his instantaneous risk of death multiplied by 1.22 with a 95% confidence interval (CI) of [1.20, 1.24] and his instantaneous risk of discharge divided by 1.13 with a 95% CI of [1.12, 1.14]. Age also has an effect on both risks: for the same baseline SOFA, patients aged [60, 75[years have an instantaneous risk of death multiplied by 1.40 (with 95% CI: [1.18, 1.68]), and patients aged 75 years or older have their risk multiplied by 1.84 (with 95% CI: [1.55, 2.19]), compared with patients aged <60 years. For the risk of discharge from ICU, the effect is more moderate: patients aged [60, 75[years have an instantaneous risk of discharge divided by 1.23 (with 95% CI: [1.14, 1.35]), and patients aged 75 years or older have their risk divided by 1.30 (with 95% CI: [1.19, 1.43]). All parameter estimates can be found in Table S3 of the Supplementary Materials.

Joint model fit

The parameter estimates of the joint model can be found in Table 2.

TABLE 2.

Joint model parameter estimation

Parameter	Value	SE	RSE (%)	p Value a
Longitudinal submodel
Fixed effects
${\mu }_0$	1.69	0.0547	3.23
${\mu }_1$	−0.262	0.0051	1.93
${\mu }_2$	−1.13	0.0188	1.66
${\mu }_a$	10.4	0.135	1.29
${\mu }_{t_{\mathit{lag}}}$	−1.48	0.0286	1.94
Random effects
${\omega }_0$	2.56	0.0424	1.66
${\omega }_1$	0.194	0.00411	2.12
${\omega }_2$	0.494	0.013	2.63
${\omega }_a$	0.459	0.00962	2.10
${\omega }_{t_{\mathit{lag}}}$	0.669	0.02	3.00
Error parameters
${\sigma }_a$	0.887	0.0123	1.39
${\sigma }_b$	0.127	0.00265	2.08
Survival submodel
Death
$h_1$	0.000476	6.52 × 10−5	13.7
${\alpha }_1$	0.371	0.00788	2.12	$<{10}^{-4}$
${\beta }_{1,\mathit{Age}1}\left(\mathit{ref}\right)$	0
${\beta }_{1,\mathit{Age}2}$	0.348	0.0876	25.1	$<{10}^{-4}$
${\beta }_{1,\mathit{Age}3}$	0.766	0.119	15.6	$<{10}^{-4}$
Discharge
$h_2$	0.325	0.00901	2.77
${\alpha }_2$	−0.375	0.00768	2.05	$<{10}^{-4}$
${\beta }_{2,\mathit{Age}1}\left(\mathit{ref}\right)$	0
${\beta }_{2,\mathit{Age}2}$	−0.195	0.0187	9.58	$<{10}^{-4}$
${\beta }_{2,\mathit{Age}3}$	−0.225	0.0302	13.4	$<{10}^{-4}$

Abbreviation: RSE, relative standard error.

^a Wald test p values are reported for link and covariate coefficients.

The parameters are those from (8).

The p values from the Wald test are reported for the link coefficients and those associated with covariate effects. As expected, we showed a significant association between an increase of the SOFA score and a higher risk of death (α ₁ = 0.371 with 95% CI: [0.356, 0.386]) and a lower risk of discharge (α ₂ = −0.375 with 95% CI: [−0.390, −0.360]). We also reported the significant effect of age class on both death and discharge risk. Age has a more important impact on the risk of death, similar to the baseline model: for the same SOFA evolution, patients aged [60, 75[years have an instantaneous risk of death multiplied by 1.42 (with 95% CI: [1.20, 1.68]), and patients aged 75 years or older have their risk multiplied by 2.15 (with 95% CI: [1.70, 2.72]), compared with the reference class age (<60 years).

Some diagnostic plots and indicators that assessed the quality of the longitudinal model and the joint model, respectively, can be found in Supplementary Information S5.

Dynamic predictions

Figure 3 illustrates dynamic predictions for two patients (a and b) of the validation set using the joint model. It shows the observed and predicted SOFA evolution on the top and predicted individual survival probability on the bottom, depending on landmark time. Predicted SOFA evolution and predicted survival are updated at each landmark time. Patient a of the figure shows an initial clinical deterioration, followed by an improvement of his clinical state. The more landmark time increases, better is his predicted survival. The SOFA score of Patient b monotonously increases over time, resulting in his predicted survival at 30 days getting worse as the landmark increases. He finally died on Day 26.

FIGURE 3.

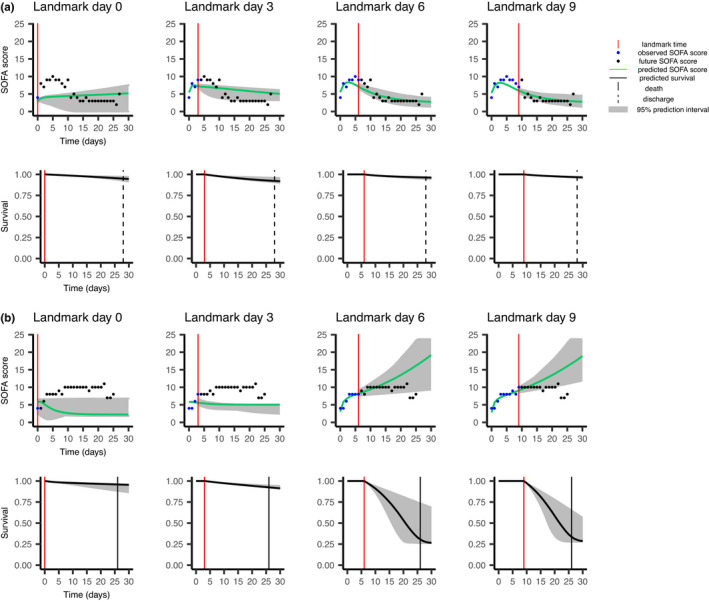
Dynamic predictions for two random patients (a and b) of the validation data set. For each patient, predictions of the Sequential Organ Failure Assessment (SOFA) evolution are on the top, and predictions of the risk of death are on the bottom. Patient a, who is older than 75 years, was discharged 28 days after his intensive care unit admission, whereas Patient b, also older than 75 years, died 26 days after his admission.

To visualize the covariate effect on predictions, in Supplementary Information S6 we added the median [Q1–Q3] survival predictions in the validation population for the three age categories and for baseline SOFA splits in three categories for various landmark times.

To assess the predictive performances of the baseline and joint models, we used the 1996 patients of the validation set. Time‐dependent ROC AUC and the Brier score including 95% CIs within the joint model are presented in Figure 4. The ones for the baseline model are presented in Figure S1 of the Supplementary Materials. The joint modeling approach allows to improve the quality of prediction when the follow‐up is sufficient. For instance, when considering landmark time = 6 and horizon time = 30, AUC = 0.63 (95% CI: [0.58, 0.68]) and AUC = 0.77 (95% CI: [0.74, 0.80]) for the baseline and the joint model, respectively. However, when considering an early landmark where only one SOFA observation is available, the joint model does not perform better than the baseline model (for landmark time = 0 and horizon time = 30, AUC = 0.73, 95% CI = [0.70, 0.77] and AUC = 0.69 with 95% CI = [0.66, 0.72] for the baseline and joint models, respectively).

FIGURE 4.

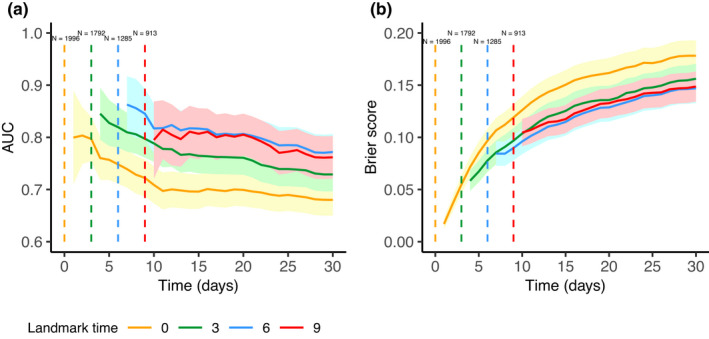
Time‐dependent receiver operating characteristic area under the curve (ROC AUC) (a) and Brier score (b) computed on the validation set depending on landmark time. The 95% confidence intervals are represented by the corresponding colored intervals. Number of at‐risk patients at each landmark time is specified on the top.

Results of the simulation study

Values of parameters (except p ₁, g ₁ and b) used to simulate data were based on estimates obtained by maximization of the likelihood using this model on the OUTCOMEREA database presented previously. The details of the values can be found in Table 3. p ₁, g ₁ were set to 0.01, 0.05, respectively, and b was fixed to 6 to obtain about 20% Cause 1 failures, 78% Cause 2 failures, and 2% administrative censoring at time 30, similar to the application.

TABLE 3.

Estimated relative bias and root mean square errors based on 200 simulations

Parameter	True value	Relative bias (%)	RRMSE (%)
Longitudinal part
Fixed effects
${\mu }_0$	2	2	11
${\mu }_1$	−0.25	5	10
${\mu }_2$	−1	4	8
${\mu }_a$	10	−0.06	5
${\mu }_{t_{\mathit{lag}}}$	−1	6	12
Random effects
${\omega }_0$	3	6	9
${\omega }_1$	0.2	15	18
${\omega }_2$	0.5	−0.5	13
${\omega }_a$	0.5	−14	16
${\omega }_{t_{\mathit{lag}}}$	0.8	6	11
Error parameters
${\sigma }_a$	0.9	−0.3	2
${\sigma }_b$	0.1	3	5
Survival part
${\alpha }_1$	0.35	2	9
${\beta }_{1,\mathit{Age}2}$	0.34	−12	85
${\beta }_{1,\mathit{Age}3}$	0.76	7	39

Abbreviation: RRMSE, relative root mean square error.

The parameters are those from (12).

Table 3 provides the relative biases and RRMSEs expressed in percentage. Relative biases are low for all parameters, which reflects good accuracy. The parameter that links the longitudinal and the survival process (α ₁) was of particular interest. The simulation showed that it is accurately estimated with a relative bias of about 2% and also precisely estimated with a RRMSE about 9%. Overall, the parameters are precisely estimated except parameters associated with the baseline covariate, which have high RRMSEs.

Violin plots can be found in Figure S2A of the Supplementary Materials and provide the same conclusion.

DISCUSSION

In many biomedical applications, the patients are not only at risk of a single event, but of several. Joint modeling under competing risks is seldom explored, particularly in a full parametric setting.

In our application, a significant association was found between the longitudinal evolution of the SOFA and each outcome (death and discharge): an increase of the SOFA score is associated with a higher risk of death and a lower risk of discharge. In the joint model, higher uncertainty was found in the estimates of the baseline age effect when adjusted on the SOFA evolution. Of note, simulations according to the baseline model (see Figure S2B of the Supplementary Materials), which is adjusted on the baseline SOFA value, also reported the same trend: high uncertainty in the estimates of the baseline age effect, which highlights the difficulty in estimating age effect when the SOFA score is in the model.

For landmark time 3 and more, as sufficient information becomes available, individual predictions from the joint model are significantly improved and outperform those from the baseline model. At landmark time 0, no added value of the joint model was shown as there is no longitudinal information available. Individual predictions at any landmark time, using all available SOFA scores at that time, can be very useful for clinicians in routine medical practice as it may help clinical decisions such as therapeutic escalation or limitation, as indeed those decisions arise during the follow‐up and not at admission.

The proposed joint model could probably be improved on some points. First, we could test for the covariate effects in the parameters of the longitudinal submodel. Second, we did not assess graphically the quality of the survival model fit because usual diagnostic plots are, to date, unavailable for this kind of model. This is because these plots rely on simulations, which are currently not available for SDH formulation and would require additional developments that are beyond the scope of this article. Finally, we considered the subdistribution approach to treat the competing risk setting, and sensitivity analyses can be done with a cause‐specific approach.

Our approach with joint modeling is justified when missing data for the longitudinal biomarker are MNAR. However, depending of the richness of the design, missing data can be considered missing at random (MAR), and some authors ³⁴ showed that treating MAR data with a joint modeling approach can lead to bias in estimates.

The simulation study showed that our estimation procedure has good statistical properties with no major bias in longitudinal parameters and in the coefficient that links the longitudinal process with the survival process. However, we cannot evaluate the bias on event 2 because of the model specification in the simulation process. Further developments are thus needed to fully investigate the quality of estimation on both events as well as the type I error and power of statistical tests involving the coefficients.

In conclusion, we showed in this work that Monolix software and its SAEM algorithm can be used for joint modeling with competing events and provide accurate parameter estimates. We also presented a real‐case application with dynamic predictions. The methodology is easy to reproduce and can be easily extended to other clinical applications because of the general form of the model. The longitudinal model can also be extended to ordinary differential equations in a more pharmacometric application.

AUTHOR CONTRIBUTIONS

A.L.‐M. wrote the manuscript. J.‐F.T., F.M., and J.M. designed the research. A.L.‐M. and J.M. performed the research. A.L.‐M. analyzed the data.

FUNDING INFORMATION

Dr. Timsit was supported by the Innovative Medicines Initiative under grant agreement no. 115737‐2–COMBACTE‐MAGNET.

CONFLICT OF INTEREST

The authors declared no competing interests for this work. As Editor‐in‐Chief of CPT: Pharmacometrics & Systems Pharmacology, France Mentre was not involved in the review or decision process for this paper.

Supporting information

Supplementary Information S1

Supplementary Information S2

Supplementary Information S3

Supplementary Information S4

Supplementary Information S5

Supplementary Information S6

Supplementary Information S7

Supplementary Information S8

Supplementary Information S9

Supplementary Information S10

Supplementary Information S11

Supplementary Information S12

Lavalley‐Morelle A, Timsit J‐F, Mentré F, Mullaert J, The OUTCOMEREA network . Joint modeling under competing risks: Application to survival prediction in patients admitted in Intensive Care Unit for sepsis with daily Sequential Organ Failure Assessment score assessments. CPT Pharmacometrics Syst Pharmacol. 2022;11:1472‐1484. doi: 10.1002/psp4.12856