Abstract
The Corona Virus Disease 2019 (COVID-19) has been declared a worldwide pandemic, and a key method for diagnosing COVID-19 is chest X-ray imaging. The application of convolutional neural network with medical imaging helps to diagnose the disease accurately, where the label quality plays an important role in the classification problem of COVID-19 chest X-rays. However, most of the existing classification methods ignore the problem that the labels are hardly completely true and effective, and noisy labels lead to a significant degradation in the performance of image classification frameworks. In addition, due to the wide distribution of lesions and the large number of local features of COVID-19 chest X-ray images, existing label recovery algorithms have to face the bottleneck problem of the difficult reuse of noisy samples. Therefore, this paper introduces a general classification framework for COVID-19 chest X-ray images with noisy labels and proposes a noisy label recovery algorithm based on subset label iterative propagation and replacement (SLIPR). Specifically, the proposed algorithm first obtains random subsets of the samples multiple times. Then, it integrates several techniques such as principal component analysis, low-rank representation, neighborhood graph regularization, and k-nearest neighbor for feature extraction and image classification. Finally, multi-level weight distribution and replacement are performed on the labels to cleanse the noise. In addition, for the label-recovered dataset, high confidence samples are further selected as the training set to improve the stability and accuracy of the classification framework without affecting its inherent performance. In this paper, three typical datasets are chosen to conduct extensive experiments and comparisons of existing algorithms under different metrics. Experimental results on three publicly available COVID-19 chest X-ray image datasets show that the proposed algorithm can effectively recover noisy labels and improve the accuracy of the image classification framework by 18.9% on the Tawsifur dataset, 19.92% on the Skytells dataset, and 16.72% on the CXRs dataset. Compared to the state-of-the-art algorithms, the gain of classification accuracy of SLIPR on the three datasets can reach 8.67%-19.38%, and the proposed algorithm also has certain scalability while ensuring data integrity.
Keywords: COVID-19, Chest X-ray image classification, Noisy label, Label recovery, Feature extraction
1. Introduction
The Corona Virus Disease 2019 (COVID-19), which broke out at the end of 2019, has been recognized as a global pandemic by the World Health Organization. At present, the disease has involved more than 200 countries and regions, infecting more than 600 million people worldwide. The main clinical symptoms of COVID-19 are fever, cough, and fatigue, and it may lead to fatal acute respiratory distress syndrome [1]. At the same time, statistics from the World Health Organization show that the average number of infected people spreading the virus to others in a population without immunity can reach 3.77. Therefore, without medical intervention, COVID-19 will spread rapidly. The main obstacle to controlling the spread of the disease is the lack of efficient detection methods. Although reverse transcription-polymerase chain reaction (RT-PCR) is considered to be the most sensitive method for detecting COVID-19, it takes about 4–6 h to obtain the results [2]. Moreover, RT-PCR has a relatively high false negative rate, requiring repeated tests at intervals of several days to confirm the diagnosis. According to the latest findings, up to 58 % of COVID-19 patients may have initial false negative RT-PCR results, which indicates the necessity to implement more appropriate diagnostic strategies to correctly identify high-risk cases and reduce the burden of disease in the population [3]. In addition, RT-PCR reagents are in short supply in many areas with severe epidemics. In contrast, chest imaging equipment has been widely used in major hospitals. Therefore, experts recommend the diagnosis of suspected cases based on clinical symptoms, chest imaging manifestations, and etiological tests. Common chest imaging examinations include X-ray and computed tomography (CT). CT constructs a clear structure of the lung tissue by performing a three-dimensional tomography scan of the patient's chest, which demonstrates a mass or nodular lesion. X-rays project the three-dimensional structure onto a two-dimensional plane, i.e., the soft tissue of the chest wall and bony structures onto the lung field, and the shadows produced may be confused with the lesion. As a result, X-ray is often more difficult than CT in the diagnosis of disease. However, considering the disadvantages of CT, such as expensive and high radiation dose, X-ray has the advantages of low radiation dose, fast shooting speed, and low price [4]. In clinical practice, X-ray examination can provide the necessary visual support and diagnostic basis for imaging studies and diagnosis of diseases such as COVID-19 [5]. For these reasons, we focus on the study of chest X-ray images.
In the diagnosis of chest X-ray images for COVID-19, radiologists usually have to read dozens or even hundreds of X-rays per day due to the large number of patients to be screened and treated, which is a heavy workload. In addition, the quality of the chest X-rays is easily affected by factors such as the patient's position and the depth of inspiration, which complicates the analysis of chest X-rays and may lead to misdiagnosis. Therefore, the diagnosis of COVID-19 can be carried out by chest X-ray images with the support of artificial intelligence technology. In recent years, deep learning methods represented by convolutional neural networks (CNN) have been widely used in medical image processing and have made important progress in many fields [6], [7], such as skin cancer [8], [9], breast cancer [10], brain disease [11], pneumonia [12], [13], and lung segmentation [14], [15], [16], [17], [18]. At present, many effective algorithms based on deep learning have been proposed, most of which are based on supervised learning strategies that require a large number of correctly labeled training samples to train a well-performing model. However, it is usually difficult to obtain a completely true and effective medical dataset due to insufficient label information, manual mislabeling, subjectivity in the labeling process, and data encoding problems [11]. Noisy labels usually have a negative impact on the performance of classification models [19], [20], [21], and manually correcting noisy labels not only requires consistent expert judgment but is also a time-consuming and impractical task. Although many approaches have been considered to address the problem of noisy labels, it is still a major challenge to eliminate the interference of noisy labels in medical image analysis.
Existing researches on training with noisy labels mainly focus on two directions. (1) Build a robust model for noisy environments [22]. Xue et al [23] proposed an iterative learning framework based on an online uncertainty sample mining method for medical image classification with noisy labels to address the lack of high-quality labeled medical data. Zhu et al [24] proposed a label quality evaluation strategy to select samples and designed an overfitting control module to allow the network to maximally learn from accurate labels during training. Xue et al [25] selected samples with correct labels by a model committee setting and designed a joint optimization framework with label correction to gradually correct noisy labels and improve the performance of the network. Ju et al [26] proposed a framework based on uncertainty estimation to deal with label noise of medical images and introduced a boosting-based curriculum training procedure for robust learning. Lin et al [27] followed the idea of the loss-value weighting strategy and designed a sample weight-adjustment scheme combined with an attention mechanism to evaluate the importance of each sample through the learning process and reduce the impact of noisy samples on the training of the network. Li et al [22] proposed an improved categorical cross entropy to reduce the effect of noisy labels on the training process and improve the robustness of the network. Although the above strategies can eliminate the influence of noisy labels to some extent, it is still necessary to manually specify the form of the weighting or correction functions in practical applications, and the hyper-parameters in the functions usually have to be adjusted by cross-validation, which may affect the stability of the performance of the training model. (2) Remove or relabel noisy samples to obtain a more accurate dataset for training [28]. In [29], the information entropy was calculated based on the probability distribution obtained by the Bayesian classifier, and samples with low entropy and incorrect prediction results were considered noisy samples. Guan et al [30] proposed a sequential ensemble noise filter that generated a noise score for each feature instance to identify noisy labels. Xia et al [31] defined relative density based on the idea that samples surrounded by heterogeneous points were more likely to be the noise than homogeneous points to identify noise [10]. Samples with a relative density greater than or equal to the preset threshold were considered mislabeled. Feng et al [32] proposed an ensemble method based on noise detection metrics that used three different classifiers, namely Bagging, AdaBoost, and k-nearest neighbor, to identify noisy labels. Yuan et al [33] borrowed ideas from co-training and generative adversarial networks, using multiple neural networks that learn and cross-predict labels independently to iteratively update labels of the dataset. Ying et al [34] proposed that samples could be analyzed multiple times by supervised learning methods, and then the resulting predictions were counted and the sample was relabeled using the majority voting algorithm. However, the above methods focus on extracting and analyzing the global features of the images, ignoring the problem that the performance of the classification model is limited when the noise level of the labels is high. Furthermore, COVID-19 chest X-ray images should be analyzed from a different perspective compared with other types of images. The specific features of chest X-ray images of COVID-19 patients are as follows: early on, the lungs (obvious in the outer lung zones) show multiple small patchy shadows and interstitial changes, which subsequently tend to develop into multiple ground-glass manifestations and infiltrative shadows in both lungs, and in severe cases, lung consolidation may be found. It can be noticed that the lesion areas of COVID-19 chest X-rays are smaller and the similarity between images is higher. Nevertheless, most of the algorithms commonly used currently to recover noisy labels usually have the part of interest located in the center of the image or occupying a larger portion of the image. In cases where the critical lesion areas are small, such algorithms may have difficulty capturing subtle differences between images and may be disturbed by the noise outside the lesion area, which will result in limited performance. In conclusion, there is an urgent need to address the challenge of classifying chest X-ray images with noisy labels to better control the spread of COVID-19.
In this paper, we introduce a general classification framework for COVID-19 chest X-ray images with noisy labels and propose a noisy label recovery algorithm based on subset label iterative propagation and replacement (SLIPR). Firstly, the proposed algorithm randomly extracts some samples multiple times to form several subsets. Secondly, global and local features of chest X-rays are extracted and learned with the help of principal component analysis (PCA), low-rank representation (LRR), and neighborhood graph regularization. Then, the samples are analyzed and classified using the k-nearest neighbor (KNN) algorithm, and the iterative results are retained. Finally, multi-level weight distribution and replacement are performed on the label set of the samples, and the noisy labels are recovered according to the idea of label propagation. In addition, the proposed algorithm can also select samples with high confidence as the training set to further improve the stability and accuracy of the classification framework. In this paper, extensive experiments are conducted on three available COVID-19 chest X-ray image datasets and the proposed algorithm is compared with other state-of-the-art algorithms. The results show that SLIPR is effective in recovering the noisy labels and performs better than other algorithms in terms of objective metrics.
This paper is organized as follows: Section 2 presents the introduced framework and the proposed algorithm. Section 3 illustrates the experimental setup. Section 4 details the results of our experiments. Section 5 concludes the paper.
2. Method
2.1. Overview of the framework
To reduce the interference caused by label noise, we take the approach of recovering noisy labels to improve label quality, which has the advantage of being directly applicable to subsequent classification models. Furthermore, the medical features of the chest X-ray images used to diagnose COVID-19 include distinct localized lesion features as well as scattered global features. However, most existing algorithms do not take into account both global and local sample features, which may result in label noise that is difficult to remove or even increase.
To this end, we introduce a general framework for classifying COVID-19 chest X-ray images in the presence of noisy labels (shown in Fig. 1 ), and propose a noisy label recovery algorithm based on subset label iterative propagation and replacement (shown in Fig. 2 ). The framework first divides the dataset into the training set and the testing set, and then simulates the situation where the labels of the training set are noisy. To model the noise, we choose the most commonly used method, namely the random noise method [35]. This method is described in detail in Section 3.2, where the labels of a certain proportion of samples are exchanged randomly. After injecting the label noise, the noisy labels of the training set are recovered using the label recovery module (shown in the blue shaded part of Fig. 1), which is the core of this paper, i.e., the proposed SLIPR algorithm. Finally, the CNN is used to train the label-recovered training set, and the testing set is analyzed and classified.
Fig. 1.
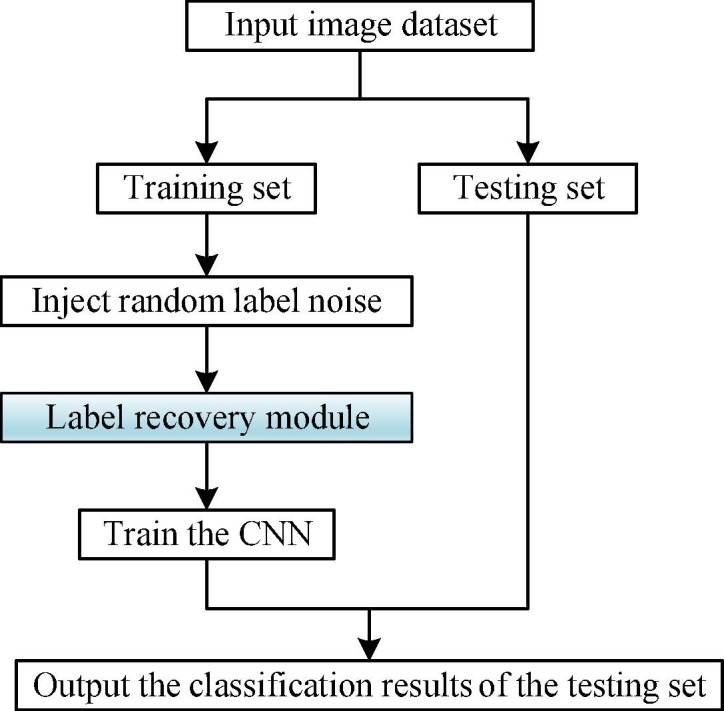
COVID-19 chest X-ray image classification framework with noisy labels.
Fig. 2.
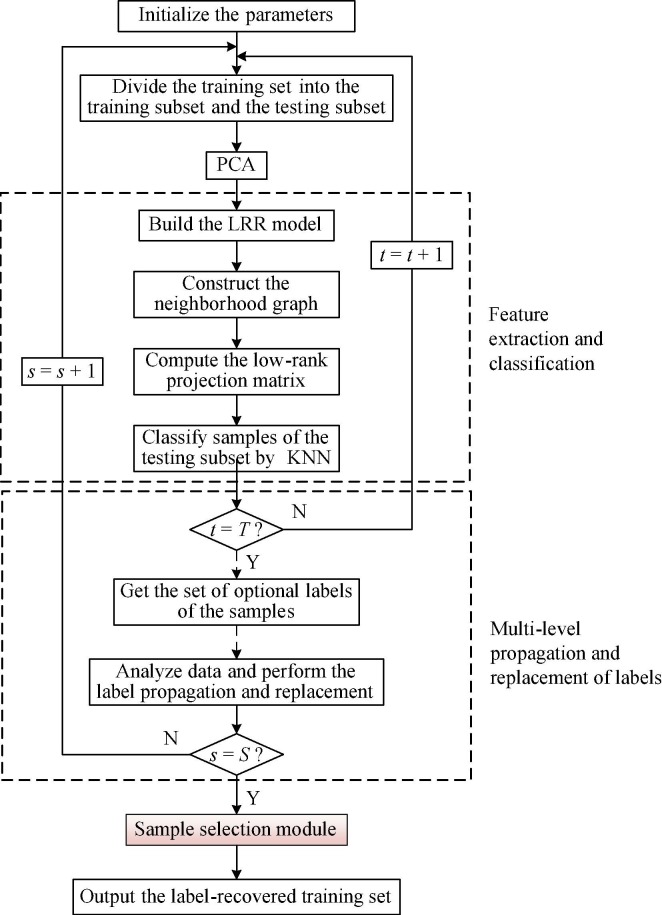
Flow chart of the proposed SLIPR algorithm.
2.2. Proposed algorithm
To correct the noisy labels of COVID-19 chest X-ray images, we propose a noisy label recovery algorithm based on subset label iterative propagation and replacement. As shown in Fig. 2, for the training set after injecting the random noise illustrated in Fig. 1, the proposed algorithm first randomly divides it into the training subset and the testing subset through multiple operations, and then the principal component analysis is used for dimensionality reduction of the training subset for subsequent data analysis [36]. Based on the idea that most of the samples in the dataset have true labels, SLIPR can extract the sample features of the training subset and classify the samples of the testing subset, then propagate the correct labels among similar samples by random learning and updating, and finally cleanse the label noise of the whole training set effectively. Considering the problem of small lesion areas and high similarity between images in COVID-19 chest X-rays, the proposed algorithm adopts the strategy of analyzing both the global and local features of images, which enhances the ability of the algorithm to correct the noisy labels. In addition, during the training process of CNN, easy samples tend to have stable outputs in different learning epochs, while the outputs of hard samples tend to be unstable [37]. Therefore, the proposed algorithm can regard the staged results of its learning process as indicators to measure the confidence of the samples, and select samples with high confidence as the training set of CNN to improve the accuracy of the classification framework.
Feature extraction and classification. First, in order to get low-rank features of the samples, we refer to the method proposed by Yin et al [38] as the LRR-based feature extraction model and it can be defined as:
| (1) |
where denotes the sample data matrix, stands for the row space of the matrix, refers to the column information of the matrix, and is the nuclear norm of the matrix, which is calculated as the sum of all singular values of the matrix. In this case, the low-rank projection matrix not only extracts the principal component information but also preserves the global representation structure of the data.
To prevent the algorithm from converging to a trivial solution during iteration, we introduce two matrices and to approximate and constrain the range of solutions by imposing an orthogonal constraint. The matrix can be regarded as the data reconstruction matrix and is the projection matrix that can accommodate the main energy of the data. Considering that in practical applications, large data have many redundant features that are not conducive to classification, it is desirable to select the most useful features from the redundant data for extraction. Due to the good row-sparsity property of norm [39], [40], to make the algorithm more flexible in the selection of feature dimensions and to have good interpretability, we also impose the following condition on the projection matrix,
| (2) |
| (3) |
| (4) |
where and are the regularization parameters used to balance the importance of the corresponding terms, is the unit matrix in the orthogonal constraint, and is the norm defined as:
| (5) |
where is the number of samples, or the number of rows of the matrix , denotes the row vector of matrix , and denotes the norm.
Although LRR can preserve the global representation structure of the data, it ignores the local relationships of the data and cannot obtain a compact representation of the data in low-dimensional space. In this case, learning a projection that preserves the local structure of the data is also necessary for feature extraction. Manifold learning is widely used in pattern recognition and computer vision owing to its success in revealing the local geometric structure of data [41], [42], [43], [44]. The core idea of manifold learning is that any non-linear manifold can be approximated locally by linear subspaces. If two data points are adjacent in the manifold in which they are distributed, they are also adjacent in the reduced subspace of reconstructed points. Since the relationship between a sample and its neighbors is linear, the local geometric properties of a given sample can be well described based on the linear coefficients of the reconstructed samples of its neighbors. Based on the preceding conclusions, we adopt the method based on neighborhood graph regularization to ensure that the reduced-dimensional data retains its original local structure. Specifically, for the data matrix , the method based on neighborhood graph regularization first constructs the neighborhood graph to represent the local relationships of the samples, and then performs projection learning by solving the following optimization problem,
| (6) |
where is the projection matrix, and denotes the element of the graph . Specially, each of graph can be defined as:
| (7) |
where represents the set of k nearest neighbor samples of sample . = 1 means that sample is the nearest neighbor of sample in the data distribution. It can be considered that these samples are similar and have a large probability of belonging to the same class.
Since the original samples and reconstructed samples have the same neighborhood relationship with those of the original samples, we impose a graph constraint on the reconstruction error between the original and reconstructed samples to preserve the local geometric structure as:
| (8) |
where is the column vector of the matrix , and can be viewed as the reconstructed sample of the original sample .
From the above, the low-rank projection matrix can be obtained by Eqs. (3), (4), and (8). Then we can calculate the low-rank representation matrices of the training and testing subsets through Eq. (9), and use the KNN algorithm to quickly predict the class labels of the samples of the testing subset [45]. In Eq. (9), represents the low-rank representation matrix and represents the original sample data matrix.
| (9) |
Multi-level propagation and replacement of labels. After iterative learning of the algorithm, each sample will obtain multiple optional labels. T denotes the total number of iterations of label propagation and replacement per round, denotes the total number of rounds of label propagation and replacement, then sample can obtain labels in the round, and denotes the set of optional labels for sample in the round. Based on the idea that samples with correct labels are in the majority, we expect that each sample can not only retain the initial label information, but also be guided by sample relabelling based on the learning results of the algorithm. Therefore, the label of sample after the round of training can be updated according to Eqs. (10) and (11).
| (10) |
| (11) |
where is the element of , is the observed label of , and can be seen as a function that assigns the label for each sample.
At this point, the dataset has completed the label propagation and replacement for the current round. Since the subsets are randomly selected, we can perform multiple rounds of label propagation based on the current updated results, and replace the labels of the samples several times until the final results converge to obtain the recovered label set. Algorithm 1 is the pseudo-code of SLIPR.
| Algorithm 1: Label recovery algorithm based on subset label iterative propagation and replacement (SLIPR). |
|---|
| Require: dataset , noisy label set , parameters , , . |
| Ensure: recovered label set . |
| 1: for = to do |
| 2: for = to do |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: |
| 8: |
| // Construct the neighborhood graph |
| 9: |
| 10: while not converged do |
| 11: Update by Eqs. (3), (4), (8) |
| 12: end while |
| 13: |
| 14: |
| // Classify samples by KNN |
| 15: |
| 16: |
| 17: end for |
| 18: for = to do |
| 19: |
| 20: |
| 21: end for |
| 22: |
| 23: end for |
| 24: |
| 25: return |
Selection strategy for high confidence samples. During the training process of CNN, the outputs of simple samples in different learning epochs are usually stable, while the outputs of hard samples tend to be unstable, leading to the degradation of the classification performance of the model. Therefore, as shown in the red shaded part in Fig. 2, without affecting the inherent performance of the classification framework, the proposed algorithm can select high confidence samples as the training set and obtain more stable and accurate samples by removing some hard samples. Specifically, the proposed algorithm draws on the idea of majority voting [46], using the compositional structure of the sample’s optional labels as a reference. A sample is considered to be a high confidence sample if the majority result suggests that it should belong to the same type of label. Based on this mechanism, the performance of the classification model will be effectively improved. However, for different types of classification models, the minimum number of samples required for the training set is different, so the ratio ξ should be given to achieve the selection. The ratio ξ is defined as:
| (12) |
where represents the minimum number of samples required for the classification model. Fig. 3 is the flow chart of the sample selection module described in this section. Since the selection module is an optional part of the proposed algorithm, it is not shown in Algorithm 1.
Fig. 3.

Flow chart of the sample selection module.
Computational Complexity. For the proposed algorithm, the main computational costs are the singular value decomposition (SVD) of the matrix and the inverse operation. Assuming that the total number of iterations of the algorithm is , the computational complexity is approximately for the data matrix of . To reduce the training time of the proposed algorithm, the graphics processing unit (GPU) device can be used instead of the central processing unit (CPU) device for computation, thus allowing the algorithm to be applied to large-scale datasets.
2.3. Convolutional neural network
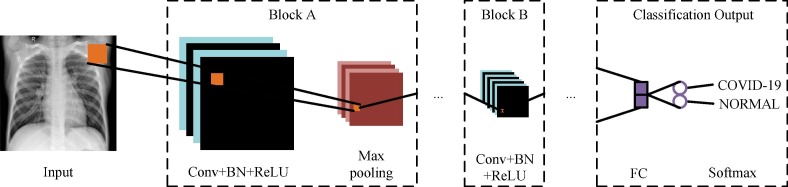
The CNN has excellent performance in image classification tasks. As shown in Fig. 4 , the CNN used in this paper consists of an input, two block A, one block B, and a classification output. Block A consists of the convolutional (Conv) layer, the batch normalization (BN) layer, the rectified linear unit (ReLU) layer, and the max pooling layer. Block B, unlike block A, does not contain the max pooling layer. The classification output consists of the fully connected (FC) layer and the softmax layer. The network parameters of the CNN are shown in Table 1 . In addition, as a label recovery module, the proposed SLIPR algorithm can be directly combined with CNNs of different structures. Therefore, we choose the CNN with a simple structure as the reference for subsequent experiments and analysis, and the structure of the CNN can be changed flexibly according to the requirements.
Fig. 4.
Structure of the CNN.
Table 1.
Network parameters of the CNN.
| Module | Parameters |
|---|---|
| Input | 224 × 224 × 1 |
| Conv Layer | 2-D convolutional layer with 16/32/64 filters of size [3 3] and padding of size 1 |
| BN Layer | / |
| ReLU Layer | / |
| Max Pooling Layer | 2 × 2 max pooling with stride [2 2] |
| FC Layer | 2 hidden neurons |
| Softmax Layer | / |
| Classification Output | 2 classes, "1" for COVID-19, and "2" for NORMAL |
3. Experimental setup
The experimental environment is an Intel® Core™ i7-10710U CPU @ 1.10 GHz on a Windows 10 PC with 16 GB RAM and an NVIDIA GeForce MX350 graphics card. The model is built and trained under MATLAB R2020a. The initial learning rate used is 0.0003, the optimization algorithm used is the stochastic gradient descent with momentum, and the batch size is 64. To decrease the contingency of the experimental results, the experiments are repeated 10 times and the average values are tabulated.
3.1. Datasets
Three publicly available COVID-19 chest X-ray image datasets are introduced in this paper. All datasets use posterior-to-anterior (AP)/anterior-posterior (PA) images of chest X-rays, as radiologists use this perspective of radiography extensively in clinical diagnosis.
Tawsifur[47], [48] dataset includes 362 COVID-19 chest X-rays and 569 normal chest X-rays from various publicly available datasets, online sources, and published articles. Furthermore, the images gathered were of varying sizes, depending on the resolution of the X-ray machine and the articles supplying the images. As a result, the dataset's creators undertook the time-consuming task of uniformly processing the chest X-ray images and ensuring that no duplicates were present.
Skytells1 dataset is comprised of 448 COVID-19 chest X-rays and 569 normal chest X-rays. The dataset is primarily derived from examples in publications, as these images are already available with a high degree of certainty. Subjects in the Skytells dataset have differences in gender, age, ethnicity, and nationality. Furthermore, the dataset contains chest X-ray images of the same person at various stages of the disease, as symptoms differ at different levels of COVID-19 infection.
CXRs dataset consists of 818 samples, including 304 COVID-19 chest X-rays from the COVID-19 collection2 and 512 normal chest X-rays from the Pneumonia collection3 . Joseph Paul Cohen, Paul Morrison, and Lan Dao assembled the COVID-19 collection from published articles and online resources on GitHub. The images in the dataset were reviewed by trained radiologists, and the condition was confirmed by clinical history, vital signs, and laboratory tests. Chest X-rays from paediatric patients at the Guangzhou Women and Children's Medical Centre who were between the ages of one and five make up the Pneumonia collection, a publicly accessible Kaggle dataset. An initial quality control check was performed on each chest X-ray to eliminate any poor or illegible images. The chest X-rays were then evaluated and examined for diagnostic outcomes by two experienced doctors. The Pneumonia collection's normal chest X-ray images were utilized to construct the CXRs dataset.
All datasets are pre-processed to resize the chest X-rays to meet the requirement that the size of the input images for the CNN should be 224 × 224 × 1.
3.2. Label noise settings
To simulate the noise, we select the most standard and widely used method, the random noise method [35], [49], in which a given proportion of samples have their labels randomly exchanged. Specifically, represents the input image dataset, represents the corresponding true label set, and represents the observed noisy label set. The parameter stands for the label noise level [50] indicating the probability that the label of a sample is flipped to another type, and the parameter can be mathematically formalized as:
| (13) |
where stands for the true label of the sample , is introduced to represent the noisy label observed for the sample , and denotes the number of categories of the sample. For instance, when = 0.2, it means that for a sample labelled as , there is a 20 % probability of being labelled as another type ().
For the three datasets described in the previous section, we inject random noise with values ranging from 0.05 to 0.4 at an interval of 0.05 on the label sets of the datasets. In addition, the random number generator selects the same seeds to generate repeated random noise in different situations, which ensures a fairer and more effective experiment.
3.3. Evaluation metrics
To evaluate the effectiveness of the proposed algorithm, three metrics are used in our experiment, including overall accuracy (OA), removal efficiency (RE), and false negative rate (FNR). True positive (TP), false positive (FP), true negative (TN), and false negative (FN) are the four main components involved in the calculating of the OA and FNR metrics. TP represents the number of samples correctly classified as COVID-19; FP represents the number of samples incorrectly classified as COVID-19; TN represents the number of normal samples correctly classified; FN represents the number of samples misclassified as normal.
The overall accuracy which demonstrates the ability of the model to classify correctly is calculated as follows.
| (14) |
The removal rate which reflects the ability of the algorithm to recover noisy labels correctly is calculated as follows.
| (15) |
where represents the number of removed noisy samples, and represents the total number of samples.
The false negative rate which measures the classification efficiency of the model is calculated as follows.
| (16) |
4. Results and analysis
In this section, the performance of the proposed algorithm is quantitatively measured and evaluated using metrics such as OA, RE, and FNR in three publicly available COVID-19 chest X-ray image datasets (i.e., Tawsifur, Skytells, and CXRs datasets).
4.1. Performance analysis of COVID-19 chest X-ray image classification framework with noisy labels
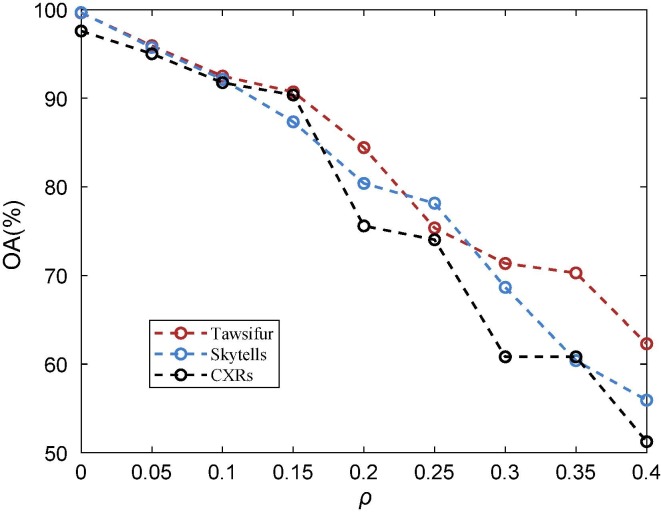
To illustrate the importance of the label recovery algorithm, we investigate the impact of noisy labels on the performance of the chest X-ray image classification framework (as shown in Fig. 1) in this section. The noisy-label-based algorithm (NLA) [50] is chosen as the label recovery module (i.e., the blue shaded part in Fig. 1) in the image classification framework. In short, the NLA method does not perform any processing on noisy labels. Fig. 5 shows the impact of noisy labels on the classification accuracy of the chest X-ray image classification framework, where the noise level changes from 0 to 0.4 at an interval of 0.05. Obviously, as the noise level increases, the performance of the image classification framework shows a significant downward trend. When the noise level reaches 0.4, its classification accuracy has dropped from 90 % to about 50 %. The experimental results demonstrate the necessity of the label recovery algorithm and the large room for improvement of the algorithm.
Fig. 5.
Overall accuracy of the COVID-19 chest X-ray image classification framework at different noise levels.
4.2. Parameter analysis of the proposed algorithm
According to the previous section, the proposed algorithm consists of a total of four parameters. (1) The parameter indicates the ratio of the number of samples in the training subset selected in each iteration to the total number of samples in the training set. (2) The parameter indicates the total number of iterations used to perform one round of label propagation and replacement. (3) The parameter indicates the total number of rounds of label propagation and replacement. (4) The parameter indicates the proportion of high confidence samples selected for the training of the CNN.
In order to measure the influence of parameters on the noise reduction performance of the algorithm more intuitively, for parameters , and , we compare the proposed algorithm with NLA under the image classification framework shown in Fig. 1. As for the parameter , we only compare whether the proposed algorithm includes the sample selection module under the image classification framework shown in Fig. 1. OA and RE are used to evaluate the algorithms. The experiments in this section only test the performance of the algorithms when = 0.3. In fact, similar conclusions can be drawn at other noise levels.
Table 2 shows the RE and OA scores of the proposed algorithm under different values of . Here the parameter is 5, is 4, and is 0.8. The experimental results of NLA used for comparison are described in the note below Table 2. It can be seen from the table that although the optimal value of the parameter differs for different datasets. But in general, SLIPR can make the classification framework perform better when , with the RE scores up to 90.70 % and the OA scores up to 30.82 %.
Table 2.
Performance of the proposed algorithm under different values of .
| Dataset | Metric | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 |
|---|---|---|---|---|---|---|
| Tawsifur | Noise number | 21 | 21 | 38 | 56 | 118 |
| RE (%) | 89.18 | 89.18 | 80.41 | 71.13 | 39.18 | |
| OA (%) | 99.36 | 99.50 | 97.86 | 96.79 | 91.86 | |
| Skytells | Noise number | 20 | 26 | 36 | 53 | 108 |
| RE (%) | 90.70 | 87.91 | 83.26 | 75.35 | 49.77 | |
| OA (%) | 99.48 | 98.82 | 97.25 | 95.41 | 94.36 | |
| CXRs | Noise number | 91 | 70 | 60 | 58 | 120 |
| RE (%) | 47.09 | 59.30 | 65.12 | 66.28 | 30.23 | |
| OA (%) | 80.57 | 82.86 | 85.14 | 89.55 | 76.57 |
Note: bold numbers represent the best results. Experimental results of NLA are as follows: Noise number = 194, OA = 71.36 % (Tawsifur dataset); Noise number = 215, OA = 68.66 % (Skytells dataset); Noise number = 172, OA = 60.82 % (CXRs dataset).
Table 3 shows the RE and OA scores of the proposed algorithm under different values of . Here the parameter is 0.2, is 4, and is 0.8. The experimental results of NLA used for comparison are described in the note below Table 3. From the table, we can find that the proposed algorithm performs better when = 4. At this point, its RE can reach up to 87.91 % and its OA can increase to 29.18 %.
Table 3.
Performance of the proposed algorithm under different values of .
| Dataset | Metric | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Tawsifur | Noise number | 63 | 29 | 41 | 38 | 30 |
| RE (%) | 67.53 | 85.05 | 78.87 | 80.41 | 84.54 | |
| OA (%) | 93.43 | 99.36 | 97.86 | 98.07 | 99.07 | |
| Skytells | Noise number | 72 | 28 | 26 | 36 | 35 |
| RE (%) | 66.51 | 86.98 | 87.91 | 83.26 | 83.72 | |
| OA (%) | 90.95 | 97.77 | 97.84 | 97.18 | 97.25 | |
| CXRs | Noise number | 43 | 73 | 37 | 60 | 48 |
| RE (%) | 75.00 | 57.56 | 78.49 | 65.12 | 72.09 | |
| OA (%) | 84.18 | 79.10 | 85.14 | 81.55 | 83.92 |
Note: bold numbers represent the best results. Experimental results of NLA are as follows: Noise number = 194, OA = 71.36 % (Tawsifur dataset); Noise number = 215, OA = 68.66 % (Skytells dataset); Noise number = 172, OA = 60.82 % (CXRs dataset).
Table 4 shows the RE and OA scores of the proposed algorithm under different values of . Here the parameter is 0.2, is 4, and is 0.8. The experimental results of NLA used for comparison are described in the note below Table 4. Obviously, the performance of SLIPR generally shows an upward trend as increases and has a significant advantage over NLA. When the value of is 8, the RE scores of the proposed algorithm can reach up to 93.49 % and the OA scores can increase up to 32 %.
Table 4.
Performance of the proposed algorithm under different values of .
| Dataset | Metric | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|
| Tawsifur | Noise number | 41 | 38 | 36 | 31 | 29 |
| RE (%) | 78.87 | 80.41 | 81.44 | 84.02 | 85.05 | |
| OA (%) | 97.86 | 98.07 | 98.14 | 98.43 | 98.57 | |
| Skytells | Noise number | 26 | 19 | 16 | 16 | 14 |
| RE (%) | 87.91 | 91.16 | 92.56 | 92.56 | 93.49 | |
| OA (%) | 97.84 | 98.62 | 98.75 | 98.75 | 99.48 | |
| CXRs | Noise number | 37 | 29 | 34 | 31 | 27 |
| RE (%) | 78.49 | 83.14 | 80.23 | 81.98 | 84.30 | |
| OA (%) | 85.14 | 90.69 | 89.63 | 89.88 | 92.82 |
Note: bold numbers represent the best results. Experimental results of NLA are as follows: Noise number = 194, OA = 71.36 % (Tawsifur dataset); Noise number = 215, OA = 68.66 % (Skytells dataset); Noise number = 172, OA = 60.82 % (CXRs dataset).
Table 5 shows the OA scores of the proposed algorithm under different values of . Here the parameter is 0.2, is 4, and is 8. To compare the performance of the algorithms more intuitively, we use SLIPR-c to represent the proposed SLIPR algorithm that includes the sample selection module. It is not difficult to find that the sample selection module allows for more accurate training of the classification framework. In particular, SLIPR-c performs best when the value of is 0.8. Compared with the SLIPR algorithm without the sample selection module, its OA score can be improved by 1.83 %.
Table 5.
OA (%) of the proposed algorithm under different values of .
| Dataset | Method | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|
| Tawsifur | SLIPR | 99.21 | 99.21 | 99.21 | 99.21 | 99.21 |
| SLIPR-c | 99.21 | 99.93 | 99.93 | 100 | 99.93 | |
| Skytells | SLIPR | 97.84 | 97.84 | 97.84 | 97.84 | 97.84 |
| SLIPR-c | 99.21 | 99.41 | 99.41 | 99.67 | 99.02 | |
| CXRs | SLIPR | 92.82 | 92.82 | 92.82 | 92.82 | 92.82 |
| SLIPR-c | 92.89 | 92.90 | 92.90 | 93.06 | 87.84 |
Note: bold numbers represent the best results.
4.3. Experimental results and analysis
To verify the effectiveness of the proposed algorithm, we compare it with other state-of-the-art label recovery algorithms in the chest X-ray image classification framework shown in Fig. 1 at the typical noise level . All algorithms are described as follows:
-
•
Noisy-label-based algorithm (NLA)[50]: the algorithm does not deal with noisy labels, but trains the classification model directly on the noisy dataset.
-
•
Iterative cross learning (ICL)[33]: the algorithm selects multiple neural networks to learn independently and cross-predict the labels to identify the learned differences, and then iteratively updates the labels of the samples.
-
•
Multi-class relative density noise filtering (mRD)[31]: the algorithm calculates the relative density and sets a threshold to identify the noise.
-
•
Subset-divided iterative projection bagging (SIPB)[34]: subsets are extracted several times for supervised learning, and all labels are selected and updated according to the majority voting algorithm.
-
•
SLIPR: the proposed label recovery algorithm based on subset label iterative propagation and replacement extracts both global and local features of the samples for analysis and classification, and then performs multi-level weight distribution and replacement of the labels to correct the noisy labels.
-
•
SLIPR-c: the algorithm can be regarded as an extension of SLIPR. It counts the training results of SLIPR and selects samples with high confidence as the training set of the CNN to improve the stability and classification accuracy of the framework.
In this section, we set the parameters of SLIPR and SLIPR-c according to the findings of the previous section, i.e., is 0.2, is 4, is 8, and is 0.8.
Firstly, Table 6 shows the RE scores of all algorithms at each noise level on the three datasets. From the table, it can be seen that the proposed SLIPR algorithm generally outperforms the other algorithms in cleansing noise as the noise level gradually increases. In terms of the average RE, SLIPR is 42.23 %, 40.59 %, and 39.19 % higher than ICL, 49.09 %, 48.70 %, and 57.73 % higher than mRD, and 17.04 %, 13.62 %, 14.18 % higher than SIPB respectively on the Tawsifur dataset, the Skytells dataset, and the CXRs dataset.
Table 6.
Comparison of RE (%) for different methods at different noise levels.
| Dataset | Method | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| Tawsifur | ICL | 37.04 | 46.43 | 64.13 | 4.51 | 44.72 | 50.00 | 19.09 | 9.20 | 37.99 |
| mRD | 55.56 | 44.64 | 34.78 | 33.08 | 22.98 | 15.98 | 10.91 | 7.20 | 31.13 | |
| SIPB | 92.59 | 89.29 | 73.91 | 69.92 | 58.39 | 44.85 | 36.82 | 25.20 | 63.18 | |
| SLIPR | 92.59 | 89.29 | 97.83 | 96.24 | 93.79 | 85.05 | 74.09 | 61.60 | 80.22 | |
| Skytells | ICL | 50.00 | 34.92 | 43.27 | 46.98 | 55.87 | 26.05 | 29.80 | 15.58 | 40.98 |
| mRD | 46.67 | 42.86 | 42.31 | 32.89 | 27.93 | 22.33 | 15.10 | 14.49 | 32.87 | |
| SIPB | 86.67 | 84.13 | 81.73 | 71.81 | 60.34 | 51.16 | 39.59 | 26.09 | 67.95 | |
| SLIPR | 63.33 | 90.48 | 95.19 | 96.64 | 91.06 | 93.49 | 72.65 | 58.70 | 81.57 | |
| CXRs | ICL | 8.70 | 10.20 | 34.18 | 17.39 | 21.58 | 25.00 | 29.44 | 31.42 | 20.93 |
| mRD | 0 | 6.12 | 5.06 | 4.35 | 2.16 | 0.58 | −1.52 | −0.44 | 2.39 | |
| SIPB | 39.13 | 55.10 | 62.03 | 44.35 | 42.45 | 37.21 | 31.47 | 15.49 | 45.94 | |
| SLIPR | 8.70 | 42.86 | 58.23 | 80.87 | 73.38 | 84.30 | 78.68 | 75.22 | 60.12 |
Note: bold numbers represent the best results.
Secondly, Table 7 shows the OA and average OA scores of the different algorithms at each noise level on the three datasets. From the results, we can conclude that the proposed algorithm enables the classification framework to show better performance than other algorithms in almost all situations (especially when the noise level is high). In terms of average OA, the gains of SLIPR over NLA are very impressive on the three datasets, e.g., 18.05 %, 18.46 %, and 15.98 %. Compared with ICL and mRD, the average OA of SLIPR is improved by the range of 10.71 %-18.64 %. Compared with SIPB, the gains of SLIPR can reach 7.85 %, 7.21 %, and 6.97 % in average OA respectively on the Tawsifur dataset, the Skytells dataset, and the CXRs dataset. In addition, SLIPR-c has also improved the classification performance of the framework. Compared with the method using only SLIPR to deal with noisy labels, the average OA of the image classification framework after selecting samples using SLIPR-c can be improved by 0.85 %, 1.46 %, and 0.74 % respectively on the three datasets.
Table 7.
Comparison of OA (%) for different methods at different noise levels.
| Dataset | Method | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| Tawsifur | NLA | 95.93 | 92.50 | 90.72 | 84.43 | 75.36 | 71.36 | 70.29 | 62.29 | 80.36 |
| ICL | 96.79 | 95.43 | 94.14 | 76.36 | 88.50 | 85.79 | 75.29 | 62.43 | 84.34 | |
| mRD | 97.71 | 94.93 | 92.29 | 90.43 | 79.86 | 70.00 | 74.50 | 59.57 | 82.41 | |
| SIPB | 99.21 | 99.17 | 97.50 | 96.29 | 93.14 | 86.86 | 79.14 | 73.14 | 90.56 | |
| SLIPR | 99.64 | 99.36 | 99.64 | 99.43 | 98.93 | 98.57 | 96.64 | 95.07 | 98.41 | |
| SLIPR-c | 100 | 99.64 | 100 | 100 | 99.93 | 100 | 97.36 | 97.14 | 99.26 | |
| Skytells | NLA | 95.74 | 92.13 | 87.34 | 80.39 | 78.16 | 68.66 | 60.39 | 55.93 | 77.34 |
| ICL | 99.02 | 93.77 | 87.41 | 87.01 | 85.57 | 81.12 | 77.05 | 69.77 | 85.09 | |
| mRD | 97.90 | 95.54 | 90.82 | 87.87 | 84.92 | 81.97 | 63.87 | 60.72 | 82.95 | |
| SIPB | 99.34 | 98.69 | 98.43 | 96.53 | 89.84 | 81.44 | 75.44 | 68.98 | 88.59 | |
| SLIPR | 98.82 | 98.75 | 98.82 | 99.08 | 97.97 | 99.48 | 91.41 | 82.10 | 95.80 | |
| SLIPR-c | 99.54 | 99.02 | 99.48 | 99.02 | 99.61 | 99.67 | 94.43 | 87.28 | 97.26 | |
| CXRs | NLA | 95.02 | 91.76 | 90.37 | 75.59 | 74.04 | 60.82 | 60.82 | 61.80 | 76.28 |
| ICL | 95.51 | 91.18 | 92.74 | 78.20 | 75.1 | 74.69 | 70.61 | 66.45 | 80.56 | |
| mRD | 95.51 | 94.04 | 84.90 | 78.20 | 70.37 | 55.35 | 56.98 | 53.63 | 73.62 | |
| SIPB | 96.57 | 93.39 | 93.55 | 90.49 | 89.39 | 82.78 | 72.25 | 63.92 | 85.29 | |
| SLIPR | 93.88 | 92.82 | 90.69 | 95.02 | 91.84 | 92.82 | 90.78 | 90.20 | 92.26 | |
| SLIPR-c | 94.29 | 94.37 | 89.39 | 95.59 | 92.33 | 93.06 | 91.43 | 93.55 | 93.00 |
Note: bold numbers represent the best results.
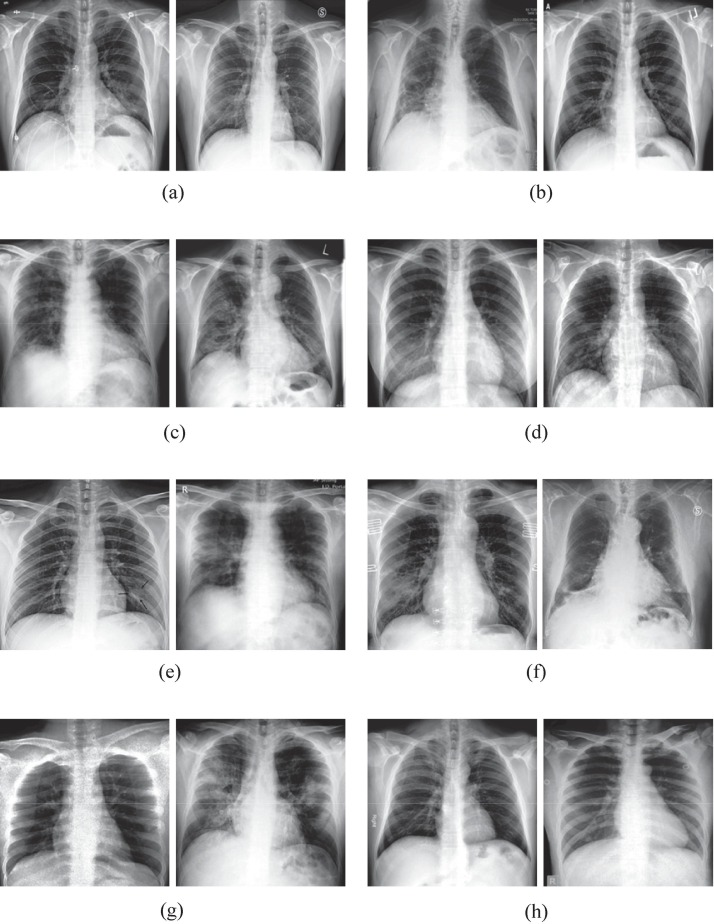
Then, Fig. 6 shows the detection results of different algorithms for some samples with label noise of the Tawsifur dataset. Specifically, all samples shown are COVID-19 chest X-ray images with label noise, which means that their observed labels are “NORMAL” and their true labels are “COVID-19″. Fig. 6 (a) to Fig. 6 (g) represent samples with label noise that ICL, MRD, and SIPB may not be able to detect, but the proposed algorithm is able to accurately identify and correct the label noise. Fig. 6 (h) shows the noisy samples that are correctly detected by all algorithms. The COVID-19 chest X-ray image in Fig. 6 may be difficult to read due to the lack of annotation indicating the location of the lesion. However, even a non-expert can notice that some of the samples contain large and distinct shadows, whereas others can hardly be considered abnormal as they have relatively small and fuzzy areas. Based on the experimental results shown in Fig. 6, it can be seen that the ICL, mRD, and SIPB are relatively ineffective in detecting label noise, while the SLIPR successfully detects and corrects label noise for all of the images presented. In summary, the proposed algorithm has the best detection capability for samples with label noise, which contributes to the classification accuracy of the image classification framework.
Fig. 6.
Detection results of different algorithms for samples with label noise in the Tawsifur dataset. (a) Samples with false detection by ICL; (b) Samples with false detection by mRD; (c) Samples with false detection by SIPB; (d) Samples with false detection by ICL and mRD; (e) Samples with false detection by mRD and SIPB; (f) Samples with false detection by ICL and SIPB; (g) Samples with false detection by ICL, mRD and SIPB; (h) Samples detected correctly by all algorithms.
Finally, to evaluate the performance of the proposed algorithm in improving the diagnostic efficiency of COVID-19, Table 8 compares the FNR scores of NLA and the proposed algorithm at different noise levels. Compared with the FNR of RT-PCR, which is about 58 %, the FNR of SLIPR and SLIPR-c are only about 2 %, which is 23 %-34 % better than NLA. It can be seen that the proposed algorithm has a lower FNR, which can improve the diagnostic efficiency of COVID-19 and effectively reduce the risk of missed diagnosis.
Table 8.
Comparison of FNR (%) for different methods at different noise levels.
| Dataset | Method | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| Tawsifur | NLA | 3.12 | 9.91 | 34.31 | 19.63 | 50.09 | 21.10 | 30.09 | 26.61 | 24.36 |
| SLIPR | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| SLIPR-c | 0.37 | 0 | 0 | 0 | 0.37 | 0 | 0 | 0.37 | 0.14 | |
| Skytells | NLA | 4.18 | 7.91 | 7.16 | 17.01 | 19.55 | 42.24 | 48.81 | 43.73 | 23.82 |
| SLIPR | 0.75 | 0.60 | 0.75 | 0.60 | 0.30 | 0.30 | 0 | 0 | 0.41 | |
| SLIPR-c | 0.90 | 0.45 | 0.60 | 0.60 | 0.30 | 0.30 | 0 | 0 | 0.39 | |
| CXRs | NLA | 12.09 | 12.97 | 12.09 | 32.97 | 32.75 | 61.10 | 51.43 | 76.48 | 36.49 |
| SLIPR | 1.25 | 1.91 | 2.48 | 0.64 | 1.39 | 1.87 | 1.98 | 0.57 | 1.51 | |
| SLIPR-c | 1.71 | 1.65 | 3.52 | 1.03 | 1.41 | 1.82 | 2.70 | 0.46 | 1.79 |
Note: bold numbers represent the best results.
In summary, the proposed algorithm has the best overall performance for label recovery, which can effectively improve the robustness and stability of the image classification framework. As a label recovery module in the image classification framework, the proposed algorithm can be directly combined with other types of CNNs. Therefore, we choose the CNN with a simple structure as the reference for experimental analysis, and similar conclusions can be drawn in practice with the combination of other CNNs. It is worth mentioning that although SLIPR-c can be considered as an extension of SLIPR, it requires specifying the proportion of high confidence samples to be selected to ensure that the inherent performance of the classification framework is not affected, which makes it more complicated in practical applications. And this strategy has the potential to lead to noise in training, which in some cases may instead lead to a loss of classification accuracy. Moreover, when the noise level is small, the initial labels of the samples account for a relatively small proportion of the label recovery process of the proposed algorithm, resulting in a comparatively insignificant performance advantage of SLIPR compared to other algorithms. This also motivates us to further improve the design of the algorithm in future work.
5. Conclusion
The combination of CNN and medical image processing is extremely beneficial for the diagnosis of COVID-19, and label quality is particularly important in the classification of chest X-rays. Existing classification models tend to assume that the labels of the samples are completely true and effective. However, due to the lack of information, the subjectivity of human judgment or human mistakes, and data encoding problems, the existing COVID-19 chest X-ray image datasets inevitably suffer from label noise. Noisy labels will mislead the training of the model, and severely affect its classification performance, potentially leading to misdiagnosis. Moreover, as COVID-19 chest X-rays contain medical features that distinguish them from general images, existing generic label recovery algorithms will be limited. To reduce the interference caused by label noise, we introduce a general training framework for COVID-19 chest X-ray image classification with noisy labels and propose a label recovery algorithm based on subset label iterative propagation and replacement (SLIPR). Firstly, the SLIPR randomly extracts a certain number of samples to form a subset several times. Secondly, since the medical features of COVID-19 chest X-rays include localized lesion features and scattered global features, the SLIPR employs a combination of PCA, LRR, neighborhood graph regularization, and other techniques to extract both global and local features of the samples. Then, the samples are classified quickly by KNN. Finally, the concept of label propagation is used to select and replace the labels of the samples at multiple levels to recover the noisy labels. Furthermore, the proposed algorithm can also select high confidence samples as the training set of CNN to achieve more accurate and stable classification results. Experimental results on three publicly available datasets demonstrate that the proposed algorithm can effectively recover the noisy labels, and improve the accuracy of the classification framework by 18.9 % on Tawsifur dataset, 19.92 % on Skytells dataset, and 16.72 % on CXRs dataset. Compared with the state-of-the-art algorithms, the proposed algorithm also has a significant advantage with a classification accuracy of 8.67 %-19.38 % higher on the three datasets. In addition, as a novel data processing module, the proposed algorithm is scalable and of great practical value as it can be directly integrated into existing image classification frameworks.
In this paper, we simply utilize random noise to simulate noisy situations. However, in practical situations, the form and number of noisy labels may be unpredictable, and how to deal with such label noise needs further exploration. The selection of subsets and iterative training increase computational complexity. Studying the adaptive selection mechanism of subsets and iterative thresholds should also be our future work. In addition, the proposed algorithm is theoretically applicable to recovering noisy labels from other types of images, but its efficiency remains to be investigated.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
We thank all the anonymous reviewers for their valuable comments and constructive suggestions. This research is supported by the Graduate Student Innovation Fund of Donghua University (No. GSIF-DH-M-2022011) and the National Natural Science Foundation of China (No. 62001099).
Footnotes
This paper was recommended for publication by Prof Guangtao Zhai.
https://github.com/skytells-research/COVID-19-XRay-Dataset
https://github.com/ieee8023/covid-chestxray-dataset
https://www.kaggle.com/paultimothymooney/chest-xray-pneumonia/
Data availability
No data was used for the research described in the article.
References
- 1.Chen N., Zhou M., Dong X., et al. Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in Wuhan, China: a descriptive study. Lancet. 2020;395(10223):507–513. doi: 10.1016/S0140-6736(20)30211-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ai T., Yang Z., Hou H., et al. Correlation of chest CT and RT-PCR testing in coronavirus disease 2019 (COVID-19) in China: a report of 1014 cases. Radiology. 2020;296(2):32–40. doi: 10.1148/radiol.2020200642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pecoraro V., Negro A., Pirotti T., et al. Estimate false-negative RT-PCR rates for SARS-CoV-2 A systematic review and meta-analysis. Eur. J. Clin. Invest. 2022;52:e13706. doi: 10.1111/eci.13706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sahin M.E. Deep learning-based approach for detecting COVID-19 in chest X-rays. Biomed. Signal Process. Control. 2022;78 doi: 10.1016/j.bspc.2022.103977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Qi A., Zhao D., Yu F., et al. Directional mutation and crossover boosted ant colony optimization with application to COVID-19 X-ray image segmentation. Comput. Biol. Med. 2022;148 doi: 10.1016/j.compbiomed.2022.105810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yan L., Zhang H., Goncalves J., et al. An interpretable mortality prediction model for COVID-19 patients. Nat. Mach. Intell. 2020;2:283–288. [Google Scholar]
- 7.Mebarkia M., Meraoumia A., Houam L., et al. X-ray image analysis for osteoporosis diagnosis: From shallow to deep analysis. Displays. 2023;76 [Google Scholar]
- 8.Lu Y., Lai Z., Xu Y., et al. Low-rank preserving projections. IEEE Trans. Cybern. 2016;46(8):1900–1913. doi: 10.1109/TCYB.2015.2457611. [DOI] [PubMed] [Google Scholar]
- 9.Srivastava G., Shao M., Fu Y. Proceedings of the IEEE International Conference and Workshops on Automatic Face and Gesture Recognition. 2013. Low-rank embedding for semisupervised face classification, in; pp. 1–6. [Google Scholar]
- 10.Zhu X., Wu X. Class noise vs. attribute noise: A quantitative study. Artif Intell Rev. 2004;22:177–210. [Google Scholar]
- 11.Frénay B., Verleysen M. Classification in the presence of label noise: a survey. IEEE Trans. Neural Netw. Learn Syst. 2014;25(5):845–869. doi: 10.1109/TNNLS.2013.2292894. [DOI] [PubMed] [Google Scholar]
- 12.Nettleton D.F., Orriols-Puig A., Fornells A. A study of the effect of different types of noise on the precision of supervised learning techniques. Artif. Intell. Rev. 2010;33:275–306. [Google Scholar]
- 13.Fan X., Feng X., Dong Y., et al. COVID-19 CT image recognition algorithm based on transformer and CNN. Displays. 2022;72 doi: 10.1016/j.displa.2022.102150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Angluin D., Laird P. Learning from noisy examples. Mach. Learn. 1988;2:343–370. [Google Scholar]
- 15.Liu T., Tao D. Classification with noisy labels by importance reweighting. IEEE Trans. Pattern Anal. Mach. Intell. 2016;38(3):447–461. doi: 10.1109/TPAMI.2015.2456899. [DOI] [PubMed] [Google Scholar]
- 16.Tu B., Zhou C., He D., et al. Hyperspectral classification with noisy label detection via superpixel-to-pixel weighting distance. IEEE Trans. Geosci. Remote Sens. 2020;58(6):4116–4131. [Google Scholar]
- 17.Wang X., Yuan Y., Guo D., et al. SSA-Net: spatial self-attention network for COVID-19 pneumonia infection segmentation with semi-supervised few-shot learning. Med. Image Anal. 2022;79 doi: 10.1016/j.media.2022.102459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang X., Wang L., Sheng Y., et al. Automatic and accurate segmentation of peripherally inserted central catheter (PICC) from chest X-rays using multi-stage attention-guided learning. Neurocomputing. 2022;482:82–97. [Google Scholar]
- 19.Garcia L.P.F., de Carvalho A.C., Lorena A.C. Effect of label noise in the complexity of classification problems. Neurocomputing. 2015;160:108–119. [Google Scholar]
- 20.Zhang C., Bengio S., Hardt M., et al. Understanding deep learning (still) requires rethinking generalization. Commun. ACM. 2021;64(3):107–115. [Google Scholar]
- 21.Chen P., Liao B.B., Chen G., et al. In: Proceedings of the International Conference on Machine Learning. 2019. Understanding and utilizing deep neural networks trained with noisy labels; pp. 1062–1070. [Google Scholar]
- 22.Li P., He X., Cheng X., et al. An improved categorical cross entropy for remote sensing image classification based on noisy labels. Expert Syst. Appl. 2022;205 [Google Scholar]
- 23.Xue C., Dou Q., Shi X., et al. In: Proceedings of the IEEE International Symposium on Biomedical Imaging. 2019. Robust learning at noisy labeled medical images: Applied to skin lesion classification; pp. 1280–1283. [Google Scholar]
- 24.Zhu H., Shi J., Wu J. Proceedings of the International Conference on Medical Image Computing and Computer Assisted Intervention. 2019. Pick-and-learn: automatic quality evaluation for noisy-labeled image segmentation, in; pp. 576–584. [Google Scholar]
- 25.Xue C., Deng Q., Li X., et al. Proceedings of the International Conference on Medical Image Computing and Computer Assisted Intervention. 2020. Cascaded robust learning at imperfect labels for chest x-ray segmentation, in; pp. 579–588. [Google Scholar]
- 26.Ju L., Wang X., Wang L., et al. Improving medical images classification with label noise using dual-uncertainty estimation. IEEE Trans. Med. Imag. 2022;41(6):1533–1546. doi: 10.1109/TMI.2022.3141425. [DOI] [PubMed] [Google Scholar]
- 27.Lin C., Guo S., Chen J., et al. Deep learning network intensification for preventing noisy-labeled samples for remote sensing classification. Remote Sens. 2021;13(9):1689. [Google Scholar]
- 28.Zhu X., Wu X., Chen Q. Proceedings of the International Conference on Machine Learning. 2003. Eliminating class noise in large datasets, in; pp. 920–927. [Google Scholar]
- 29.Sun J., Zhao F., Wang C., et al. In: Proceedings of the International Conference on Future Generation Communication and Networking. 2007. Identifying and correcting mislabeled training instances; pp. 244–250. [Google Scholar]
- 30.Guan D., Chen K., Han G., et al. A novel class noise detection method for high-dimensional data in industrial informatics. IEEE Trans. Industr. Inform. 2021;17(3):2181–2190. [Google Scholar]
- 31.Xia S., Chen B., Wang G., et al. mCRF and mRD: two classification methods based on a novel multiclass label noise filtering learning framework. IEEE Trans. Neural Netw. Learn Syst. 2022;33(7):2916–2930. doi: 10.1109/TNNLS.2020.3047046. [DOI] [PubMed] [Google Scholar]
- 32.Feng W., Quan Y., Dauphin G. Label noise cleaning with an adaptive ensemble method based on noise detection metric. Sensors (Basel) 2020;20(23):6718. doi: 10.3390/s20236718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.B. Yuan, J. Chen, W. Zhang, et al., Iterative cross learning on noisy labels, in: Proceedings of the IEEE Winter Conference on Applications of Computer Vision, 2018, pp. 757-765.
- 34.Ying X.Q., Liu H., Yuan W.Y., et al. Subset-divided iterative projection bagging for noisy-label recovery. Opt. Precis. Eng. 2020;28(12):2719–2728. [Google Scholar]
- 35.Garcia L.P.F., Lehmann J., de Carvalho A.C., et al. New label noise injection methods for the evaluation of noise filters. Knowl. Based Syst. 2019;163:693–704. [Google Scholar]
- 36.Wang Z., Li J., Zhang T. Discriminative graph convolution networks for hyperspectral image classification. Displays. 2021;70 [Google Scholar]
- 37.D.B. Wang, Y. Wen, L. Pan, et al., Learning from noisy labels with complementary loss functions, in: Proceedings of the AAAI Conference on Artificial Intelligence, 2021, pp. 10111-10119.
- 38.M. Yin, S. Cai, J. Gao, Robust face recognition via double low-rank matrix recovery for feature extraction, in: Proceedings of the IEEE International Conference on Image Processing, 2013, pp. 3770-3774.
- 39.Ye J., Zhang L.H., Jiang B. Hyperspectral image denoising using constraint smooth rank approximation and weighted enhance 3DTV. Displays. 2022;74 [Google Scholar]
- 40.Xiang S., Nie F., Meng G., et al. Discriminative least squares regression for multiclass classification and feature selection. IEEE Trans. Neural Netw. Learn. Syst. 2012;23(11):1738–1754. doi: 10.1109/TNNLS.2012.2212721. [DOI] [PubMed] [Google Scholar]
- 41.M. Belkin, P. Niyogi, Laplacian eigenmaps and spectral techniques for embedding and clustering, in: Proceedings of the International Conference on Neural Information Processing Systems, 2001, pp. 585-591.
- 42.X. He, P. Niyogi, Locality preserving projections, in: Proceedings of the International Conference on Neural Information Processing Systems, 2003.
- 43.D. Cai, X. He, J. Han, Spectral regression: A unified approach for sparse subspace learning, in: Proceedings of the IEEE International Conference on Data Mining, 2007, pp. 73-82.
- 44.Yin M., Gao J., Lin Z. Laplacian regularized low-rank representation and its applications. IEEE Trans. Pattern Anal. Mach. Intell. 2016;38(3):504–517. doi: 10.1109/TPAMI.2015.2462360. [DOI] [PubMed] [Google Scholar]
- 45.Gou J., Sun L., Du L., et al. A representation coefficient-based k-nearest centroid neighbor classifier. Expert Syst. Appl. 2022;194 [Google Scholar]
- 46.Freund Y. Boosting a weak learning algorithm by majority. Inf. Comput. 1995;121(2):256–285. [Google Scholar]
- 47.Chowdhury M.E.H., Rahman T., Khandakar A., et al. Can AI help in screening viral and COVID-19 pneumonia? IEEE Access. 2020;8:132665–132676. [Google Scholar]
- 48.Rahman T., Khandakar A., Qiblawey Y., et al. Exploring the effect of image enhancement techniques on COVID-19 detection using chest X-ray images. Comput. Biol. Med. 2021;132 doi: 10.1016/j.compbiomed.2021.104319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.A. Kalai, R.A. Servedio, Boosting in the presence of noise, in: Proceedings of the Annual ACM Symposium on Theory of Computing, 2003, pp. 195-205.
- 50.Jiang J., Ma J., Wang Z., et al. Hyperspectral image classification in the presence of noisy labels. IEEE Trans. Geosci. Remote Sens. 2019;57(2):851–865. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
No data was used for the research described in the article.