SDPRX: A statistical method for cross-population prediction of complex traits

Summary

Polygenic risk score (PRS) has demonstrated its great utility in biomedical research through identifying high-risk individuals for different diseases from their genotypes. However, the broader application of PRS to the general population is hindered by the limited transferability of PRS developed in Europeans to non-European populations. To improve PRS prediction accuracy in non-European populations, we develop a statistical method called SDPRX that can effectively integrate genome wide association study summary statistics from different populations. SDPRX automatically adjusts for linkage disequilibrium differences between populations and characterizes the joint distribution of the effect sizes of a variant in two populations to be both null, population specific, or shared with correlation. Through simulations and applications to real traits, we show that SDPRX improves the prediction performance over existing methods in non-European populations.

We developed a statistical method, SDPRX, to improve the performance of polygenic risk score (PRS) in non-European populations by jointly modeling GWAS summary statistics from European and non-European populations.

Introduction

The polygenic risk score (PRS) of a complex trait for a given individual is constructed by combining the estimated effect sizes of genetic markers across the genome for this individual. PRS has received great interest recently because of its ability to identify individuals with high disease risk for more effective population screening, diagnosis, and monitoring.¹ However, PRSs for most diseases to date have been primarily developed for Europeans, as most well-powered genome-wide association studies (GWASs) have been performed in cohorts of European ancestry. There can be substantial reduction in prediction accuracy when the PRSs derived from European samples are directly applied to non-European populations, leading to possible health disparities.^2,3

The limited generalizability of PRS across different populations may be attributed but not limited to a number of factors. First, there is a lack of well-powered GWASs for training PRS models in the non-European populations. Second, the pattern of linkage disequilibrium (LD) and the tagging of causal variants can be different across populations. Third, the allele frequencies of variants vary between populations, and some variants can even be population specific. As a general rule, the effect sizes of rarer variants are harder to estimate and GWASs with larger sample size are required in order to provide accurate estimates. Fourth, the effect sizes of one variant can be null (i.e., no effect), population specific (non-zero in one population), or correlated in two populations.^4,5 Therefore, the effect sizes estimated from European GWASs may or may not be directly transferable to other populations.

Great efforts have been made in recent years to improve the genetic diversity of GWASs.^6,7 Increased availability of GWAS summary statistics and biobank data from non-European ancestries creates an opportunity for developing novel methods to improve the accuracy of PRS in different populations. One general approach is to first estimate effect sizes in each population separately and then derive a linear combination of the estimated effect sizes from a validation dataset of the target population.⁸ Other approaches include jointly modeling GWAS summary statistics from multiple populations under the assumption that the causal variants are largely shared across populations.^9,10,11,12

Here, we propose SDPRX, an extension of SDPR,¹³ which integrates GWAS summary statistics and LD matrices from two populations with effect sizes under a hierarchical Bayesian model. SDPRX characterizes the joint distribution of the effect sizes of a SNP (single-nucleotide polymorphism) in two populations to be both null, population specific, or shared with correlation. We compared the performance of SDPRX with existing methods through extensive simulations and applications to 15 traits in the East Asian (EAS) and seven traits in the African (AFR) individuals from the UK Biobank.¹⁴ We show that SDPRX may substantially improve the prediction accuracy in non-European populations over the existing methods.

Material and methods

Overview of SDPRX

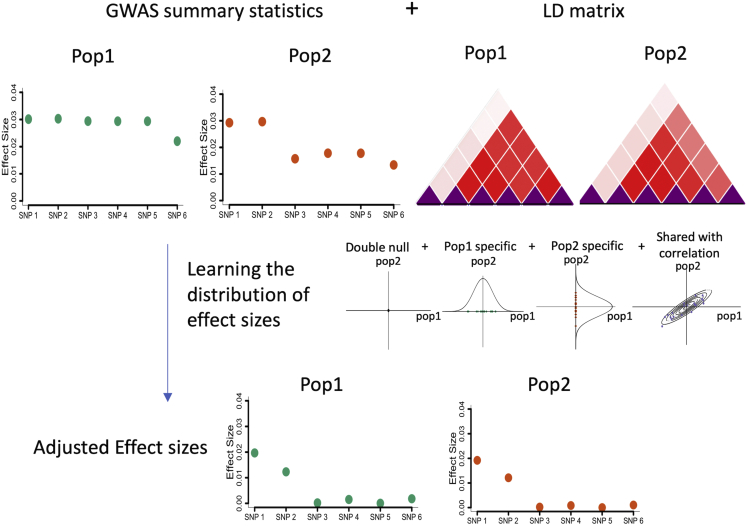
As a hierarchical Bayesian model, SDPRX has two parts—likelihood and prior (Figure 1). The likelihood connects the pair of marginal effect sizes in GWAS summary statistics from the two populations with true effect sizes through a multivariate normal distribution accounting for LD:

$$\begin{array}{l}{\hat{\mathit{\beta }}}_1|\eta ,{\mathit{\beta }}_1\sim N({\mathit{R}}_1\eta {\mathit{\beta }}_1,{\mathit{R}}_1/N_1+a\mathit{I})\hfill \\ {\hat{\mathit{\beta }}}_2|\eta ,{\mathit{\beta }}_2\sim N\left({\mathit{R}}_2\eta {\mathit{\beta }}_2,{\mathit{R}}_2/N_2+a\mathit{I}\right)\hfill \end{array}\text{, }$$ (Equation 1)

where ${\hat{\mathit{\beta }}}_1$ and ${\hat{\mathit{\beta }}}_2$ are the marginal effect sizes, ${\mathit{R}}_1$ and ${\mathit{R}}_2$ are the LD matrices, and $N_1$ and $N_2$ are GWAS sample sizes for populations 1 and 2, respectively. Compared with the commonly used assumption $\hat{\mathit{\beta }}|\mathit{\beta }\sim N(\mathit{R}\mathit{\beta },\mathit{R}/N)$, the function above has two variations.¹³ First, it shrinks the off-diagonal covariance by a constant identity matrix $aI$ to avoid the over-estimation of effect sizes ${\beta }_1$ and ${\beta }_2$ for SNPs in high LD as a result of the mismatch between GWAS summary statistics and reference panel. Second, it introduces a redundant parameter $\eta$ so that the choice of hyperparameters of the prior on the variance components does not constrain the posterior inference.¹⁵ We set $N_{1}a=N_{2}a=1$ and let $\eta \sim N(0,{10}^6)$ based on our SDPR paper as a small shrinkage would allow the algorithm to converge.^13.

Figure 1.

Illustration of the modeling framework of SDPRX

SDPRX integrates GWAS summary statistics and LD matrices from two populations through the likelihood function. The prior characterizes the joint distribution of the effect sizes of a SNP in two populations to be both null, population specific, or shared with correlation. After fitting the model through MCMC, it outputs the adjusted effect sizes for calculation of PRS.

For each SNP $j$, we then specify the following joint distribution as the prior on the effect sizes (${\beta }_{j1}$, ${\beta }_{j2}$) in two populations

$$\begin{array}{l}\left(\begin{array}{l}{\beta }_{j1}\hfill \\ {\beta }_{j2}\hfill \end{array}\right)\sim p_0\left(\begin{array}{l}{\delta }_0\hfill \\ {\delta }_0\hfill \end{array}\right)+p_1\sum _{k=1}^{1000}{\pi }_{1k}\left(\begin{array}{l}N\left(0,{\sigma }_{1k}^2\right)\hfill \\ {\delta }_0\hfill \end{array}\right)+\hfill \\ p_2\sum _{k=1}^{1000}{\pi }_{2k}\left(\begin{array}{l}{\delta }_0\hfill \\ N\left(0,{\sigma }_{2k}^2\right)\hfill \end{array}\right)+\hfill \\ p_3\sum _{k=1}^{1000}{\pi }_{3k}N\left(\left(\begin{array}{l}0\hfill \\ 0\hfill \end{array}\right),{\sigma }_{3k}^2\left(\begin{array}{l}1\rho \hfill \\ \rho 1\hfill \end{array}\right)\right)\hfill \end{array}\text{. }$$ (Equation 2)

This prior characterizes the genetic architecture of one trait in two populations by a mixture of four mutually exclusive components. The first term describes the effect sizes of one SNP as zero (Dirichlet delta distribution) in both populations. The second, third, and fourth terms represent the effect sizes of one SNP as non-zero in population 1 only, non-zero in population 2 only, or non-zero and correlated in both populations. We note that if a SNP is only present in one population, it will be assigned to the first term (null) or one of the second and third terms (population specific).

We further assigned a Dirichlet distribution prior on the probability of each SNP to be null ($p_0$), population 1 specific ($p_1$), population 2 specific ($p_2$), and shared with correlation ($p_3$).

$$\begin{array}{l}\left(p_0,p_1,p_2,p_3\right)\sim Dir\left(1\right)\hfill \end{array}$$ (Equation 3)

In simulation and real data analysis, we often found that SDPRX over-estimated the proportion of SNPs with population-specific effects and under-estimated the proportion of SNPs with shared effects, which was due to the identifiability issues caused by SNPs in high LD (Figure S1). To fix this issue, we introduce an option for SDPRX assuming no population-specific effects for shared variants ($p_0=0.25,p_1=p_2=0,p_3=0.25$). We found that this option improved the prediction accuracy for most traits in real data analysis, suggesting that the genetic effects for most complex traits are indeed shared across ancestries. We recommend the user to run both options and select the better result based on the validation dataset.

SDPRX adopts the idea of Bayesian nonparametric prior from SDPR, which is adaptive to different parametric assumptions. Specifically, for the second (population 1 specific), third (population 2 specific), and fourth terms (shared with correlation), we used the truncated stick-breaking process to represent the variance components and probability of assignments.¹⁶ The truncation needs to be applied so that the maximum number of components of the mixture model is finite. We found that setting the maximum components to 1,000 was sufficient for our simulation and real data application because the number of non-trivial components, to which SNPs were assigned, was way fewer than 1,000. For example, for the second term (population 1 specific), we had:

$$V_{1k}\sim Beta\left(1,{\alpha }_1\right),k=1,\dots ,1000$$

$${\pi }_{11}=V_{11}$$

$${\pi }_{1k}=\prod _{m=1}^{k-1}\left(1-V_{1m}\right)V_{1k},k=2,\dots 1000$$

$${\sigma }_{1k}^2\sim IG(.5,.5)$$

$$\begin{array}{l}{\alpha }_1\sim Gamma\left(0.1,0.1\right)\hfill \end{array}\text{.}$$ (Equation 4)

The cross-population genetic correlation $\rho$ can be obtained from software like Popcorn.¹⁷ We set rho to the estimated value in simulation and real data analysis. To reduce the computational burden, SDPRX partitioned the LD matrix (element-wise maximum of LD matrices from two populations) into approximately independent LD blocks.^13,18 We developed a Markov chain Monte Carlo (MCMC) algorithm based on the Gibbs sampler to fit the model (supplemental methods). In practice, we used 1,000 MCMC iterations and the first 200 iterations as the burn-in. We outputted the mean posterior effect sizes $\eta {\beta }_1$ and $\eta {\beta }_2$ as the weights to derive PRS for two populations. When an independent validation dataset is available, one can also perform a convex combination of the output weights ($\alpha$ increased from 0 to 1 by a step of 0.05) and select the best $\alpha$ to further optimize the performance:

$$\begin{array}{l}{\beta }_{target}=\alpha {\beta }_1+\left(1-\alpha \right){\beta }_2\hfill \end{array}\text{.}$$ (Equation 5)

Existing methods

We compared the performance of SDPRX with five other methods: (1) PRS-CSx as implemented in the PRS-CSx software; (2) LDpred2 as implemented in the bigsnpr package; (3) XPASS as implemented in the XPASS package; (4) DBSLMM as implemented in the DBSLMM package; and (5) Lassosum as implemented in the Lassosum package. For PRS-CSx, the global shrinkage parameter was specified as {1e−6, 1e−4, 1e−2, 1, auto}. For LDpred2, we ran LDpred2-inf, LDpred2-auto, and LDpred2-grid and reported the best performance of three options. The grid of hyperparameters was set as non-sparse, p in a sequence of 21 values from 10⁻⁵ to 1 on a log-scale, and h² within {0.7, 1, 1.4} of h²_LDSC. For XPASS, population-specific effects were included in both populations (p < 10⁻¹⁰, clump_r² = 0.1, clump_kb = 1,000). For DBSLMM, p value threshold was iterated within {10⁻⁵, 10⁻⁶, 10⁻⁷, 10⁻⁸}, r² was iterated within {0.05, 0.1, 0.15, 0.2, 0.25}, and h² was set as h²_LDSC. For Lassosum, lambda was set in a sequence of 20 values from 0.001 to 0.1 on a log-scale and s within {0.2, 0.5, 0.9, 1}. In real data analysis, we also performed a linear regression of phenotype on the PRS of two populations on the validation dataset to learn the weights for combination of effect sizes.

Simulations

To simulate individual-level genotypes from the 1000 Genomes Phase 3 haplotype, we first randomly selected 3,000 SNPs from the first 30,000 common SNPs (minor allele frequency [MAF] > 0.05 in East Asians (EAS), Europeans (EUR), and Africans (AFR)) on chromosomes 1 to 10. The curated haplotypes reduced the computational burden of Hapgen2 while still providing a good representation of the real population structure. The simulated genotypes all passed the quality control (MAF > 0.05, genotype missing rate < 0.1, p value of Hardy-Weinberg Equilibrium test (pHWE) > 10⁻⁶).

We generated the simulated effect sizes of SNPs for two populations (EUR + EAS or EUR + AFR) according to the following model:

$$\begin{array}{l}\left(\begin{array}{l}{\beta }_{j1}\hfill \\ {\beta }_{j2}\hfill \end{array}\right)\sim (1-p_1-p_2-p_3)\left(\begin{array}{l}{\delta }_0\hfill \\ {\delta }_0\hfill \end{array}\right)+p_1\left(\begin{array}{l}N\left(0,\frac{0.2h^2}{M{p}_1}\right)\hfill \\ {\delta }_0\hfill \end{array}\right)+\hfill \\ p_2\left(\begin{array}{l}{\delta }_0\hfill \\ N\left(0,\frac{0.2h^2}{M{p}_2}\right)\hfill \end{array}\right)+\hfill \\ p_{3}N\left(\left(\begin{array}{l}0\hfill \\ 0\hfill \end{array}\right),\frac{0.8h^2}{M{p}_3}\left(\begin{array}{l}1\rho \hfill \\ \rho 1\hfill \end{array}\right)\right),\hfill \end{array}$$

where $h^2=0.3$ and $M=\mathrm{30,000}$. We mainly considered four scenarios by increasing the proportions of population-specific and shared causal variates: (1) $p_1=p_2=p_3=0.0005$, (2) $p_1=p_2=p_3=0.005$, (3) $p_1=p_2=p_3=0.05$, and (4) $p_1=p_2=0.05,p_3=0.9$. We also varied the cross-population genetic correlation $\rho$ in {0.4, 0.6, 0.8}. Additionally, we considered one simulation setting based on scenario 3 to evaluate the performance of each method on admixed individuals. We then generated phenotypes from simulated effect sizes by using GCTA-sim, and we performed marginal linear regression analysis on the training data to obtain summary statistics by using PLINK2.^19,20

UK Biobank analysis

We downloaded GWAS summary statistics from GIANT, DIAGRAM, GLGC, BBJ, and PAGE consortia.^{6,7,21,22,23,24,25,26} We followed the guideline of LDHub to perform quality control on the GWAS summary statistics for each population.²⁷ We removed strand-ambiguous (A/T and G/C) SNPs, insertions and deletions (INDELs), and SNPs with an effective sample size less than 0.67 times the 90^th percentile of sample size. We did not restrict to SNPs present in two GWAS summary statistics so that population-specific SNPs would be retained. Table 1 shows the number of SNPs present in the summary statistics for each trait after intersecting with reference panel and test dataset. The number of SNPs may not be optimal to achieve the best performance for each trait, but it did allow a fair comparison of different methods. We used the 1000 Genomes EUR, EAS, and AFR samples as the LD reference panel for EUR, EAS, and AFR (admixed populations for PAGE study) summary statistics, respectively. For UK Biobank, we first performed principal-component analysis (PCA) together with 1000 Genomes samples. We then trained a random forest classifier to assign UK Biobank samples to one of five super populations (EUR, EAS, AFR, South Asians [SAS], Admixed Americans [AMR]) on the basis of the top ten PCs (Figure S2). We retained 2,091 unrelated EAS and 6,829 unrelated AFR samples with a predicted probability greater than 0.9 to form the validation and test datasets. We also selected 410 self-reported Black admixed individuals from UK Biobank, as we found that the random forest classifier was not able to accurately identify admixed individuals. We obtained a total of around 800K Hapmap3 (HM3) SNPs after intersecting with the SNPs of summary statistics and reference panel.

Table 1.

Summary of sample size and SNPs in GWAS summary statistics and UK Biobank datasets

	GWAS sample size (EUR/EAS/AFR)	1KG HM3 and GWAS and UKB SNPs (EAS)	1KG HM3 and GWAS and UKB SNPs (AFR)	UKB EAS sample size (EAS)	UKB AFR sample size (AFR)
Height	252,23021/159,09526/49,7816	775,077	753,371	2,081	6,727
BMI	233,76622/158,28425/49,3356	755,775	832,542	2,078	6,715
HDL	885,5407/116,4047/90,8047	711,038	832,494	398	1,610
LDL	840,0067/79,6937/87,5597	772,482	832,494	440	1,710
Total cholesterol	929,7327/144,5797/92,5547	445,763	832,494	440	1,714
Triglycerides	860,5477/81,0717/89,4677	772,505	832,494	440	1,714
Eosinophils	563,08528/62,07629/N/A	757,167	N/A	2,026	N/A
Lymphocytes	563,08528/62,07629/N/A	757,167	N/A	2,026	N/A
Monocytes	563,08528/62,07629/N/A	757,167	N/A	2,026	N/A
Neutrophils	563,08528/62,07629/N/A	757,167	N/A	2,026	N/A
Red blood cells	563,08528/108,79429/N/A	757,167	N/A	2,028	N/A
White blood cells	563,08528/107,96429/N/A	757,167	N/A	2,028	N/A
Platelets	563,08528/108,20829/N/A	757,167	N/A	2,028	N/A
Coronary artery disease	61,29430/101,09131/N/A	761,770	N/A	1,116	N/A
Type 2 diabetes	156,10923/191,76424/14,4806	570,266	722,296	1,263	4,809

The union of SNPs in GWAS summary statistics of two populations passing the quality control were intersected with the 1000 Genomes Hapmap3 reference panel and UK Biobank to form the final SNP list.

Phenotypes were selected on the basis of the relevant data fields (50 for height, 21001 for BMI, 30780 for low-density lipoprotein [LDL], 20760 for high-density lipoprotein [HDL], 20690 for total cholesterol [TC], 30870 for triglycerides [TG], 30150 for count of eosinophil [EOS], 30120 for lymphocyte [LYM], 30130 for monocyte [MON], 30140 for neutrophil [NEU], 30010 for red blood cell [RBC], 30000 for white blood cell [WBC], 30080 for platelet [PLT], and self-report questionnaire and in-hospital record for coronary artery disease [CAD] and type 2 diabetes). For 13 quantitative traits, we reported the prediction R² of PRS (variance explained by PRS) defined as $R^2=1-\frac{SS1}{SS0}$, where $SS0$ is the sum of squares of the residuals of the restricted linear regression model with covariates (an intercept, age, sex, top ten PCs of the genotype data) and SS1 is the sum of squares of the residuals of the full linear regression model (covariates above and PRS). For two binary traits, we reported the area under the curve (AUC) of PRS only for better comparison of different methods. The percentage of the improvement of method A over method B was defined as (metric_A – metric_B)/metric_B.

Results

Simulations

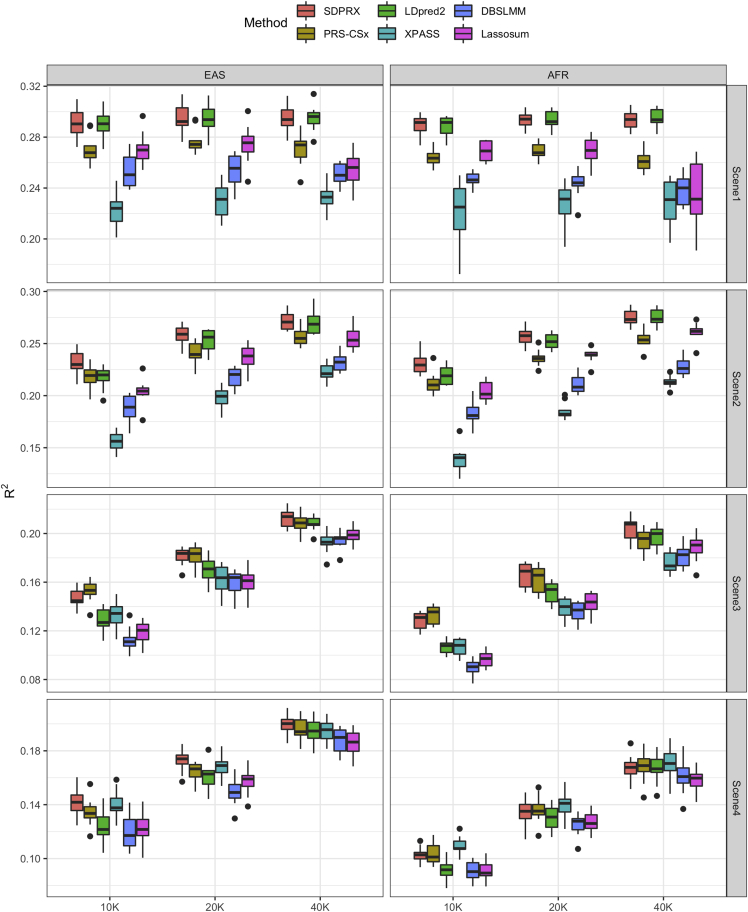
We first evaluated the prediction performance of each method via simulations across different genetic architectures and training sample sizes. We focused on six methods—SDPRX, PRS-CSx,¹⁰ LDpred2,³² XPASS,⁹ DBSLMM,³³ and Lassosum.³⁴ LDpred2, DBSLMM, and Lassosum are single population methods that take non-EUR GWAS summary statistics as input, while SDPRX, PRS-CSx, and XPASS are multi-discovery methods that jointly integrate GWAS summary statistics from multiple populations. We used Hapgen2 to simulate individual-level genotypes of European (EUR), East Asian (EAS), and African (AFR) populations by using the 1000 Genomes Phase 3 as the reference haplotypes.^35,36 We also used admix-simu to simulate admixed individuals by a model of one pulse of admixture nine generations ago with 80% contribution from AFR and 20% from EUR.³⁷ Due to computational constraints, we only included 30,000 SNPs in total by selecting 3,000 SNPs from each of chromosomes 1 to 10. The training cohort consisted of 40K EUR individuals and varying sample sizes (10, 20, 40K) of EAS and AFR individuals. The reduced sample size of non-EUR populations aligns with the fact that the sample size of most non-EUR GWASs is smaller than EUR GWASs. The validation and test datasets consisted of 5K individuals of each population. The genetic architecture was simulated for two populations (EUR + EAS or EUR + AFR) as follows. Effect sizes of one SNP in two populations can be both zero, population specific (non-zero in population 1 or population 2), or correlated with the cross-population genetic correlation. We fixed the total heritability to be 0.3 and assumed that 80% of the total heritability was explained by SNPs with correlated effect sizes between the two populations (material and methods). The proportion of SNPs with population 1-specific, population 2-specific, and correlated effect sizes was equally set to be 0.05% (scenario 1), 0.5% (scenario 2), and 5% (scenario 3). For scenario 4, the proportion of SNPs with population 1-specific and population 2-specific effect sizes were set to 5% and the proportion of SNPs with shared effect sizes was set to 90%. The cross-population genetic correlation was set to be 0.8 (Figure 2), 0.6 (Figure S3), and 0.4 (Figure S4). Each simulation setting was repeated 10 times. Further details of simulation can be found in the material and methods section.

Figure 2.

Prediction performance of different methods on simulated data

The proportion of SNPs with population 1-specific, population 2-specific, and correlated effect sizes was equally set to be 0.05% (scenario 1), 0.5% (scenario 2), and 5% (scenario 3). For scenario 4, the proportion of SNPs with population 1-specific and population 2-specific effect sizes were set to 5% and the proportion of SNPs with shared effect sizes was set to 90%. The cross-population genetic correlation was set to be 0.8 and the heritability was 0.3. Simulation in each scenario was repeated for 10 times. For each boxplot, the central mark is the median and the lower and upper edges represent the 25^th and 75^th percentiles.

We generated summary statistics via regression analysis of the training cohort as the input to SDPRX, PRS-CSx,¹⁰ LDpred2,³² XPASS,⁹ DBSLMM,³³ and Lassosum.³⁴ We used the validation dataset to estimate LD matrix for each method and tune parameters for LDpred2, PRS-CSx, DBSLMM, and Lassosum. The prediction performance was assessed by the square of Pearson correlation of PRS and simulated phenotype in the independent test dataset. We mainly focused on the results in EAS and AFR because our main purpose is to jointly utilize EUR GWAS data to improve the performance of PRS in non-EUR populations.

Overall, all methods performed better as the proportion of causal SNPs decreased (Figure 2 and Table S1). Under a highly sparse genetic architecture (scenario 1), the increase of sample size provided minimal benefits because the effect size per causal SNP was large enough for accurate estimation. In contrast, the improvement with an increasing sample size became apparent when the genetic architecture was polygenic (scenarios 3 and 4). Among all methods, XPASS did not perform well in the sparse setting as the simulated data violated its assumption that all SNPs are causal. LDpred2 had descent accuracy when the genetic architecture was sparse or the sample size was large. However, there was clear advantage of cross-population methods (SDPRX and PRS-CSx) over LDpred2 when the genetic architecture was polygenic (scenarios 3 and 4) and the sample size was small (10 and 20K). Results were similar for lower genetic correlations (Figures S3 and S4; Tables S2 and S3) and admixed population (Figure S5). These results suggest that jointly modeling EUR and non-EUR GWASs can improve the prediction accuracy in non-EUR populations if non-EUR GWAS alone was not well powered. We can see that SDPRX outperformed the other methods in most cases.

Prediction performance for UK Biobank traits

We next compared the performance of SDPRX with other methods in predicting 13 quantitative traits (height, body mass index, high-density lipoproteins, low-density lipoproteins, total cholesterol, triglycerides, count of eosinophil, lymphocyte, monocyte, neutrophil, red blood cell, white blood cell and platelet) and two binary traits (type 2 diabetes and coronary artery disease) for EAS individuals in UK Biobank. For AFR individuals, the performance was compared with six quantitative traits and one binary trait because of the limited number of publicly available summary statistics. For AMR individuals, the comparison was limited to height and BMI, as fewer than 100 individuals had records for other traits in UK Biobank. We obtained public GWAS summary statistics and performed quality control to standardize the input (details in material and methods; Table 1). Individuals in the GWAS do not overlap with individuals in UK Biobank. EUR, EAS, and AFR samples from the 1000 Genomes Project were used to construct the reference LD matrix for each method. We selected unrelated EAS and AFR individuals in UK Biobank on the basis of a random forest classifier (Figure S2). AMR individuals were selected on the basis of self-reported questionnaire. For each population, we randomly assigned 1/3 of participants to the validation dataset for parameter tuning and learning the linear combination of effect sizes. The remaining participants formed the test dataset for evaluation of the prediction performance. The random assignment was repeated for 20 times. We reported the prediction R² of PRS (variance explained by PRS) for 13 quantitative traits and the AUC of PRS for two binary traits.

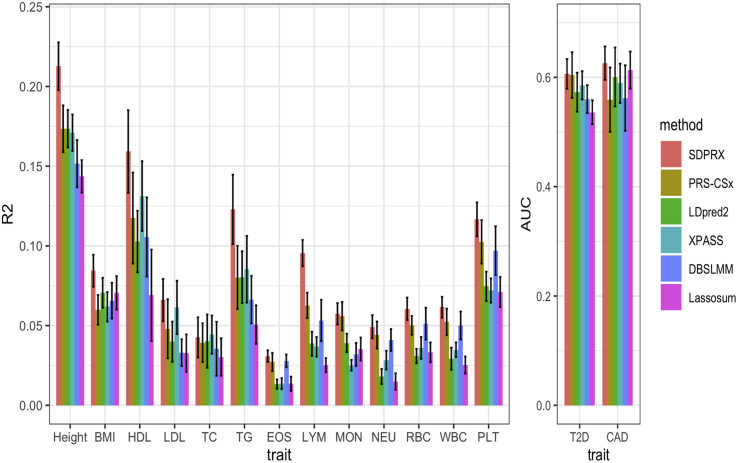
We first investigated the prediction accuracy of each method in EAS (Figure 3 and Table S4) without learning the linear combination of effect sizes. Consistent with simulations, SDPRX achieved the highest prediction accuracy in all traits. The average improvement of SDPRX was 67% over LDpred2, 40% over DBSLMM, and 86% over Lassosum, suggesting that jointly modeling EUR and EAS GWAS summary statistics indeed provided benefits compared with using EAS GWAS summary statistics alone. SDPRX was also on average 23% and 56% better than PRS-CSX and XPASS. We then linearly combined EUR and EAS effect sizes for each method by weights learned on the validation dataset. SDPRX remained the best method for ten traits with an average 11%, 28%, 19%, 17%, and 43% improvement over PRS-CSX, LDpred2, XPASS, DBSLMM, and Lassosum (Figure S6 and Table S5), respectively.

Figure 3.

Prediction performance of different methods for 13 quantitative traits and two binary traits in EAS samples from UK Biobank without the linear combination of effect sizes

Selected participants with corresponding phenotypes were randomly split to form the validation (1/3) and test datasets (2/3). The mean and standard deviation of R² (quantitative trait) and AUC (binary trait) across 20 random splits are showed on the bar plot.

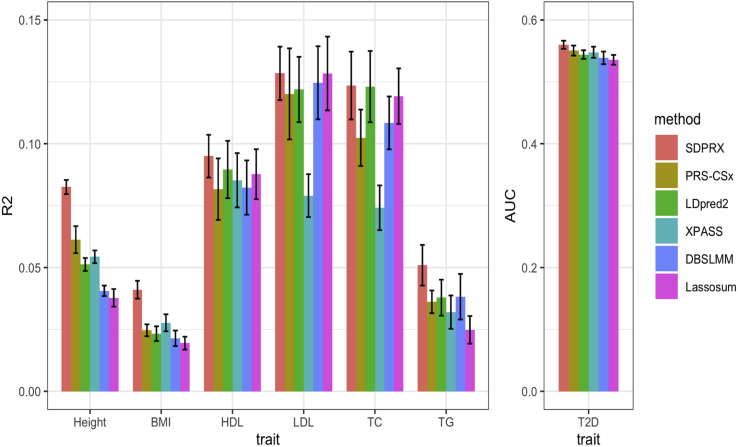
Results for AFR were similar to results for EAS (Figure 4 and Table S6). SDPRX performed best in most traits regardless of learning the linear combination of effect sizes. The average improvement of SDPRX over PRS-CSx, LDpred2, XPASS, DBSLMM, and Lassosum was 27%, 12%, 44%, 38%, and 51% before the linear combination and 17%, 36%, 37%, 24%, and 42% after the linear combination (Figure S7 and Table S7). We also evaluated the performance of each method for height and BMI for the limited number of AMR individuals in UK Biobank and found that SDPRX outperformed the other methods as well (Figure S8).

Figure 4.

Prediction performance of different methods for six quantitative traits and one binary trait in AFR samples from UK Biobank without the linear combination of effect sizes

Selected participants with corresponding phenotypes were randomly split to form the validation (1/3) and test datasets (2/3). The mean and standard deviation of R² (quantitative trait) and AUC (binary trait) across 20 random splits are showed on the bar plot.

Discussion

SDPRX takes GWAS summary statistics from two populations as input and thus is able to leverage shared information from two populations to better estimate the effect sizes of SNPs compared with single population methods such as LDpred2. The prior assumption made by SDPRX is more general than XPASS and PRS-CSx. Unlike SDPRX, XPASS assumes that the genetic architecture is polygenic and all SNPs have non-zero effect sizes while empirically methods assuming only part of SNPs having non-zero effect sizes often have better performance. Compared with PRS-CSx, SDPRX directly incorporates the cross-population genetic correlation into the model for better estimation of shared effect sizes. These points, taken together, may explain why SDPRX outperformed the other methods in both simulation and real data analyses.

Although SDPRX improves the prediction accuracy in non-EUR populations, it is far from overcoming the gap between performance of PRS in EUR and non-EUR populations. We think developing computational methods alone will not be able to solve this issue, and there are two points that may explain the gap based on the results presented in this paper. First, the sample sizes of non-EUR GWASs are limited. Results in EAS were overall better than results in AFR because of the larger sample size of EAS GWASs. Second, other factors such as genetic architecture may be different for some traits in two populations. For example, the performance of HDL, LDL, TC, and TG was different in EAS and AFR in spite of similar GWAS sample sizes. We also note that social, environmental, and familial factors were not considered in this study because we primarily focused on comparison of methods, though they may play an important role in the transferability of PRS.³

The computational time and memory usage of all methods are listed in Table S8. For SDPRX and PRS-CSx, we paralleled computation over 22 chromosomes and used three threads per chromosome for the linear algebra library (22 × 3 = 66 threads in total). The time and memory usage are reported for the longest chromosome, which was the rate-limiting step. LDpred2 was run in the genome-wide mode with ten threads for parallel computation. DBSLMM and Lassosum were run with three threads for parallel computation. No parallelization was used for XPASS. One should keep in mind that the number of MCMC iterations and threads for parallel computation affects the computation time significantly, though we did not explore it in this paper. Overall, the methods that do not need to perform MCMC (XPASS, DBSLMM, and Lassosum) were faster than the methods that need to perform MCMC (SDPRX, PRS-CSx, and LDpred2). SDPRX was able to finish the job in 10 h without consuming a large amount of memory.

Lastly, we note three limitations of our current work that we will address in the future. First, similar to other studies (e.g., PRS-CSx), we restricted to HM3 SNPs for an easy comparison of different methods, which is not optimal, as it might not include some informative SNPs. Second, SDPRX is currently not designed for admixed populations, which is challenging as the LD pattern would be heterogenous and difficult to capture with a single LD matrix. To our knowledge, how to connect the marginal effect sizes in the GWAS summary statistics derived from admixed populations with true effect sizes is also less clear, which may deal with the adjustment of local ancestry and covariates.^38,39 Third, methods utilizing functional annotation have shown to improve the performance in both single and cross-population settings.^40,41 Incorporating functional annotation may further improve the performance of SDPRX.

Published: December 1, 2022

Web resources

• Admix-simu, https://github.com/williamslab/admix-simu

• BBJ summary statistics, http://jenger.riken.jp/en/result

• BCX summary statistics, ftp://ftp.sanger.ac.uk/pub/project/humgen/summary_statistics/UKBB_blood_ cell_traits/

• CARDIoGRAMplusC4D summary statistics, http://www.cardiogramplusc4d.org/data-downloads/

• DIAGRAM summary statistics, https://diagram-consortium.org/downloads.html

• GIANT summary statistics, https://portals.broadinstitute.org/collaboration/giant/index.php/GIANT_consortium_data_files-GIANT_Consortium_2012-2015_GWAS_Summary_Statistics

• GLGC summary statistics, http://csg.sph.umich.edu/willer/public/glgc-lipids2021/results/ancestry_specific/

• LDpred2, https://github.com/privefl/bigsnpr

• PAGE summary statistics, https://www.ebi.ac.uk/gwas/studies/GCST008053

• PLINK, https://www.cog-genomics.org/plink/

• Popcorn, https://github.com/brielin/Popcorn

• PRS-CSx, https://github.com/getian107/PRScsx

• XPASS, https://github.com/YangLabHKUST/XPASS

Data and code availability

SDPRX is available at https://github.com/eldronzhou/SDPRX. The code used in this paper is available at https://github.com/eldronzhou/SDPRX_paper. The links to summary statistics can be found in the web resources.